Visual Navigation Using Depth Estimation Based on Hybrid Deep Learning in Sparsely Connected Path Networks for Robustness and Low Complexity

Abstract

Robot navigation refers to a robot’s ability to determine its position within a reference frame and plan a path to a target location. Visual navigation, which relies on visual sensors such as cameras, is one approach to this problem. Among visual navigation methods, Visual Teach and Repeat (VT&R) techniques are commonly used. To develop an effective robot navigation framework based on the VT&R method, accurate and fast depth estimation of the scene is essential. In recent years, event cameras have garnered significant interest from machine vision researchers due to their numerous advantages and applicability in various environments, including robotics and drones. However, the main gap is how these cameras are used in a navigation system. The current research uses the attention-based UNET neural network to estimate the depth of a scene using an event camera. The attention-based UNET structure leads to accurate depth detection of the scene. This depth information is then used, together with a hybrid deep neural network consisting of a Convolutional Neural Network (CNN) and Long Short-Term Memory (LSTM), for robot navigation. Simulation results on the DENSE dataset yield an RMSE of 8.15, which is an acceptable result compared to other similar methods. This method not only provides good accuracy but also operates at high speed, making it suitable for real-time applications and visual navigation methods based on VT&R.

1. Introduction

The surge in robotics interest over the past few years has led to extensive use across various industries and societal applications [1]. Robots are now prevalent in manufacturing (from assembly and dispensing to handling and picking) [2], transportation (from tourist guidance and elderly assistance to structural health monitoring) [3], and service and cleaning (from dust removal to disinfection) [4]. The primary benefits of robotics include cost reduction, enhanced safety, increased speed, and improved mobility [5].

Mobile robotics, a key discipline within this field, focuses on developing systems and components that enable robots to move autonomously through their environment [6]. Autonomy here refers to the robot’s ability to complete its movements without human intervention. Navigation is a crucial component of mobile robotics, making it a significant and compelling topic for research [7]. An example of a robot navigation problem is shown in Figure 1. For path C, a shorter and smoother path is shown, indicating less energy loss and higher efficiency, while ensuring the safety of the mobile robot [8].

Figure 1. Robot navigation problem [9].

While no comprehensive solution exists for mobile robot navigation, numerous methods have been proposed. These methods are categorized based on factors such as the types of sensors used, the environment, the need for prior knowledge, and the connection between perception and action [10]. The VT&R method [11] is a popular approach used in robot navigation to enable effective navigation in known environments. In this research, VT&R has been employed as the foundational routing method. VT&R involves teaching the robot a path by manually guiding it along the desired route while recording sensory data, such as images or laser scans. This data is then used to create a visual map or model of the environment.

After the initial path training in the VT&R method, the robot can navigate independently along the same path by relying on visual perception. The main advantages of the VT&R method are its simplicity and efficiency. This method eliminates the need for complex environmental mapping or localization techniques such as Simultaneous Localization and Mapping (SLAM) [12]. Additionally, this approach enables robots to navigate dynamic environments by primarily relying on visual perception rather than sensor measurements or laser scans.

Due to the compatibility of visual recognition algorithms, the VT&R method demonstrates robustness against perceptual changes, such as lighting variations or the presence of temporary obstacles. This makes it suitable for various applications, including indoor navigation, warehouse automation, and even space navigation, provided there are enough visual cues. VT&R allows robots to autonomously navigate previously trained paths using visual perception, simplifying the navigation process and providing a reliable and efficient solution for robot navigation in known environments. Visual navigation finds application across various types of mobile robots, including autonomous land vehicles, unmanned aerial vehicles, and autonomous underwater vehicles [13].

Regardless of the type of robot, visual navigation can generally be categorized into two approaches [14]: those that rely on prior knowledge of the entire environment for perception and navigation, and those that operate without such prior knowledge by perceiving and navigating the environment in real time [15]. Additionally, methods in visual navigation can be further classified into those that utilize maps, such as metric and topological mapping systems, and mapless navigation techniques [16]. The latter often employ reactive strategies based on visual cues derived from segmented images or real-time environmental perception, which involves object recognition or tracking specific landmarks [17].

Effective robot routing using the VT&R method requires an accurate depth image of the scene. Various methods exist to obtain this essential information from the environment. Most systems rely on monocular or binocular (stereo) setups, although trinocular configurations are also available. Recently, all-in-one cameras have gained popularity as well. Given that robots typically utilize monochrome cameras, an integrated VT&R system proves invaluable in practical applications, enabling navigation tasks that were previously unachievable. In recent developments, approaches incorporating depth-sensitive sensors such as Lidar, RGBD, and stereo systems [18] have been proposed. For our research, event cameras will be employed to capture scene imagery.

Event cameras operate by establishing a logarithmic scale of light intensity at each pixel [19]. At any given moment, the camera compares the current light intensity at each pixel with its established baseline. When the difference exceeds a certain threshold, an event is generated for that pixel. Following each event, the baseline or logarithmic intensity is updated to maintain camera functionality. Each event includes coordinates (x, y) indicating the pixel location, a timestamp (t) indicating when the event occurred, and polarity information indicating whether the light intensity increased or decreased. Event cameras are data-driven, meaning they only transmit information when there is a change in the environment. Unlike traditional cameras, which continuously capture frames, event cameras produce sparse data—often just a few events per transmission—while other pixels remain inactive.

The main gap in the past research is the lack of sufficient attention to the efficiency of these cameras in designing a robot navigation system. In this study, a completely innovative framework for robot navigation based on the VT&R method is presented, which combines event camera-based depth estimation and a deep hybrid CNN-LSTM network for the first time. The main innovation of this work is to eliminate the heavy recurrent structure of existing models and replace it with the attention mechanism in the UNET architecture, which increases speed, reduces computational complexity, and improves the accuracy of depth estimation. In addition, the resulting depth output is directly used in the hybrid network for navigation with three left, right, and straight decisions, and a complete integration between depth estimation and navigation is achieved. This combination has resulted in the presentation of a lightweight, fast, and accurate system for the VT&R-based navigation literature. In short, the main innovation of the current paper is the simultaneous integration of VT&R, depth estimation, and navigation decision-making in an end-to-end framework. Unlike classical VT&R methods that are based on feature matching and pre-stored maps, our proposed end-to-end framework uses deep learning to simultaneously extract visual information, depth, and navigation command. So far, no such research has been presented that performs all operations in an end-to-end framework.

2. Related Works

In this section, related works are reviewed in two categories. In the first category, robot navigation methods based on VT&R are reviewed. In the second category, the methods of estimating the depth of the images are examined.

2.1. Robot Navigation Methods Based on VT&R

The literature contains numerous studies focusing on robotic navigation [20]. For instance, Patel et al. [20] proposed different classifications for navigation methods, broadly categorizing them into classical and reactive approaches. Classical methods, initially pioneering in this field [21,22], have gradually fallen out of favor due to their reliance on precise measurement mechanisms, susceptibility to uncertainty, susceptibility to local minima trapping, and high computational costs.

In contrast, reactive approaches such as ant colony optimization [23], fuzzy logic [24,25], particle swarm optimization [26], fire algorithms [27], and neural networks [28,29,30] have gained popularity for their smart implementation, resilience to uncertainty, reduced complexity, and overall efficiency. Despite being complex to design, requiring longer computation times, extensive memory usage, and a learning phase, reactive methods are increasingly favored for their lower computational demands and robustness against uncertainty.

Newly emerging approaches like Deep Neural Networks [31,32], Visual and Deep Learning repetition [33,34], and Deep Reinforcement Learning [35,36,37] are currently receiving significant attention for navigation tasks. For example, Symeonidis et al. [32] demonstrated a vision-based autonomous UAV landing system using Deep Neural Networks, while Arnes et al. [38] proposed a method employing Deep Neural Networks to handle uncertainty in variable inputs. Although these methods perform comparably in sufficiently complex scenarios, further advancements are continually being explored, particularly in VT&R methods.

Recently, reinforcement learning methods in deep learning have received significant attention for their robust learning capabilities. For instance, Miroski et al. [39] framed the navigation problem within a reinforcement learning framework, leveraging multimodal sensory inputs to achieve enhanced performance and efficiency. Similarly, Kulhánek et al. [40] introduced a map-free approach trainable and optimized for specific environments. However, these methods have primarily demonstrated their effectiveness in small-scale indoor settings (such as small office environments) or simulated environments, lacking validation in real-world long-distance navigation scenarios.

In addressing sparse path networks, Swedish et al. [34] proposed a deep visual training and repetition method, while Zhao et al. [33] presented a scalable real-time navigation approach using topological maps.

Despite the advancements, only a few studies, such as those by Swedish et al. [34] and papers [41,42,43], have explored the integration of deep neural networks with visual training and repetition scenarios. These approaches often rely on trained classifiers for path identification and struggle with continuous path following and navigating uncharted routes, limiting their applicability in most VT&R scenarios. Recognizing this research gap, the current work aims to bridge this divide by effectively combining the strengths of deep neural networks with the specific demands of visual training and repetition scenarios.

2.2. Depth Estimation Methods

2.2.1. Depth Estimation Methods Based on RGB Images

Methods for estimating image depth based solely on RGB images constitute a category that relies exclusively on RGB inputs to infer depth information [40].

Some of the most significant methods in this category will be reviewed. One notable approach, presented in [41], introduces a novel method for depth estimation in RGB images using a two-stream deep adversarial network. The first stream employs an encoder–decoder architecture with residual concepts to extract coarse-level depth features. In parallel, the second stream focuses on fine-level depth estimation, leveraging residual architecture for detailed refinement. Furthermore, a feature map sharing mechanism enhances residual learning, allowing the decoder module of the first stream to share learned feature maps. The efficacy of this approach has been evaluated on the NYU RGB-D v2 dataset, with both qualitative and quantitative analyses demonstrating its superior performance in depth prediction compared to existing methods [41]. However, this method imposes a significant computational burden, rendering it impractical for deployment on resource-constrained platforms such as robots. In this branch, there are many other articles such as [44,45,46], which can be studied in order to better examine them.

2.2.2. Depth Estimation Methods Based on Event Images

Problems related to RGB images can be solved largely by using event cameras. Therefore, depth estimation methods based on event images have also been of interest to researchers [47,48]. For example, ref. [47] proposes a recurrent architecture that outperforms conventional feed-forward approaches as shown in Figure 2. Specifically, their method generates detailed depth predictions using a monocular setup, a capability not previously demonstrated. To train their model, ref. [47] utilizes a novel dataset collected from the CARLA simulator, which includes events and depth maps. Finally, they evaluate their approach to the Multi Vehicle Stereo Event Camera dataset (MVSEC) [49], demonstrating its effectiveness and superiority. Recently, transformer networks have also become one of the accurate methods for estimating scene depth [50]. These networks can estimate scene depth with high accuracy from both RGB and depth images [19,49].

Figure 2. Neural network architecture in study [47].

Despite these advantages, these methods face a fundamental challenge: they are typically unsuitable for tasks such as robot navigation due to their recursive structure and slow processing speed. To address this challenge, the current research introduces an attention-based mechanism designed to overcome these limitations.

3. Proposed Method

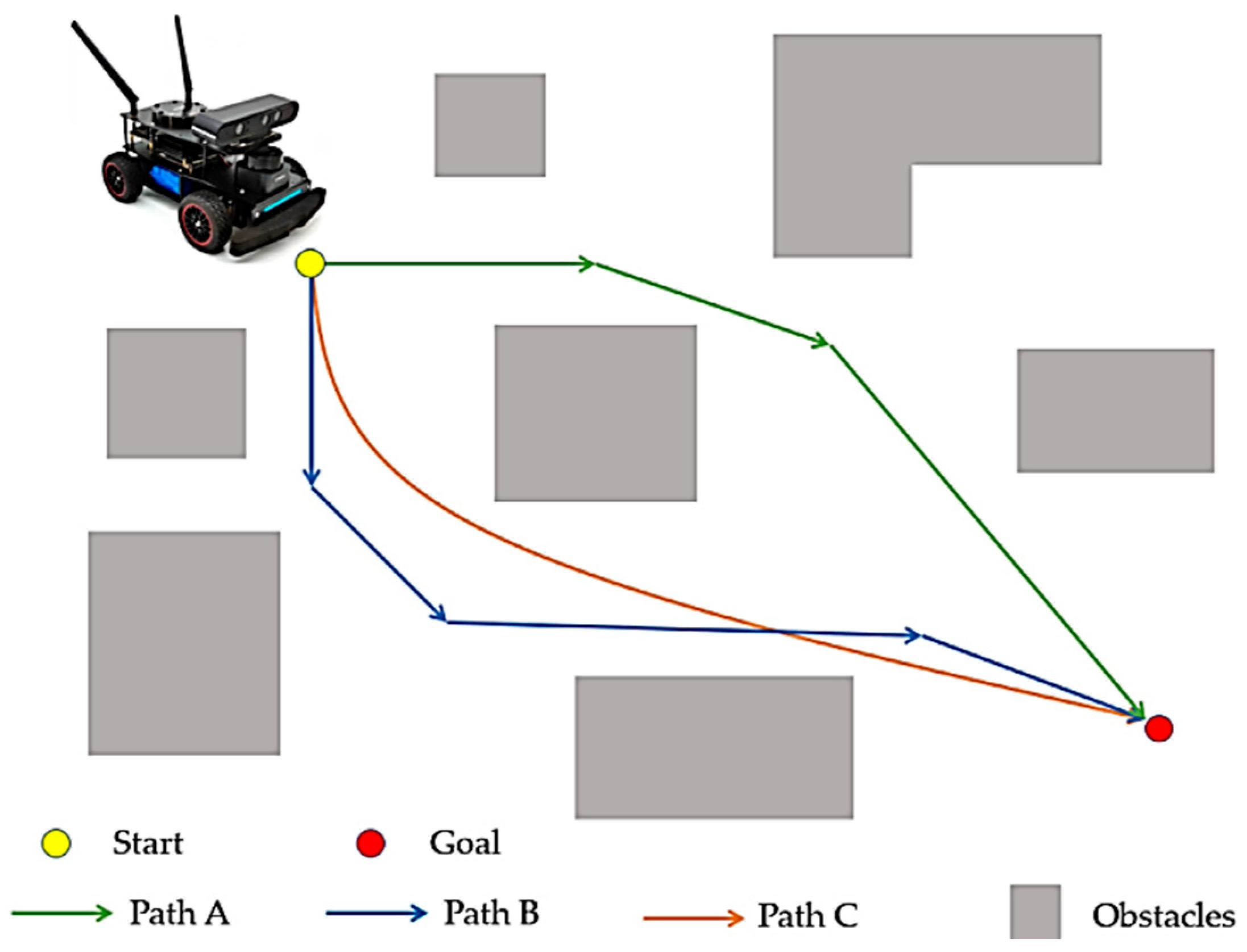
3.1. Definition of the Problem

The problem of this research is described in two general stages according to Table 1. Initially, images are captured by the event camera. Subsequently, the deep neural network provided is employed for depth estimation of the scene (first network). This depth image serves as the basis for training the robot using the VT&R method. Finally, navigation is executed based on the trained robot (second network).

Table 1. Stages of the proposed method.

Specifications	Depth Estimation Stage	Visual Navigation Stage
Input	Event stream	Depth Map
Output	Depth Map	Navigation of Robot
Model	UNET	CNN-LSTM

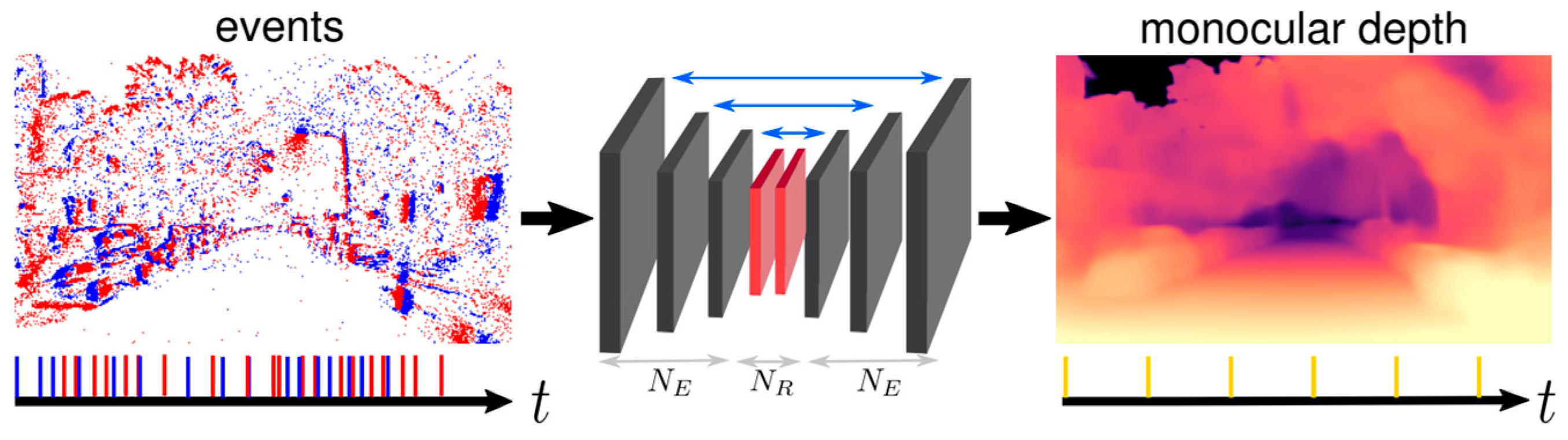
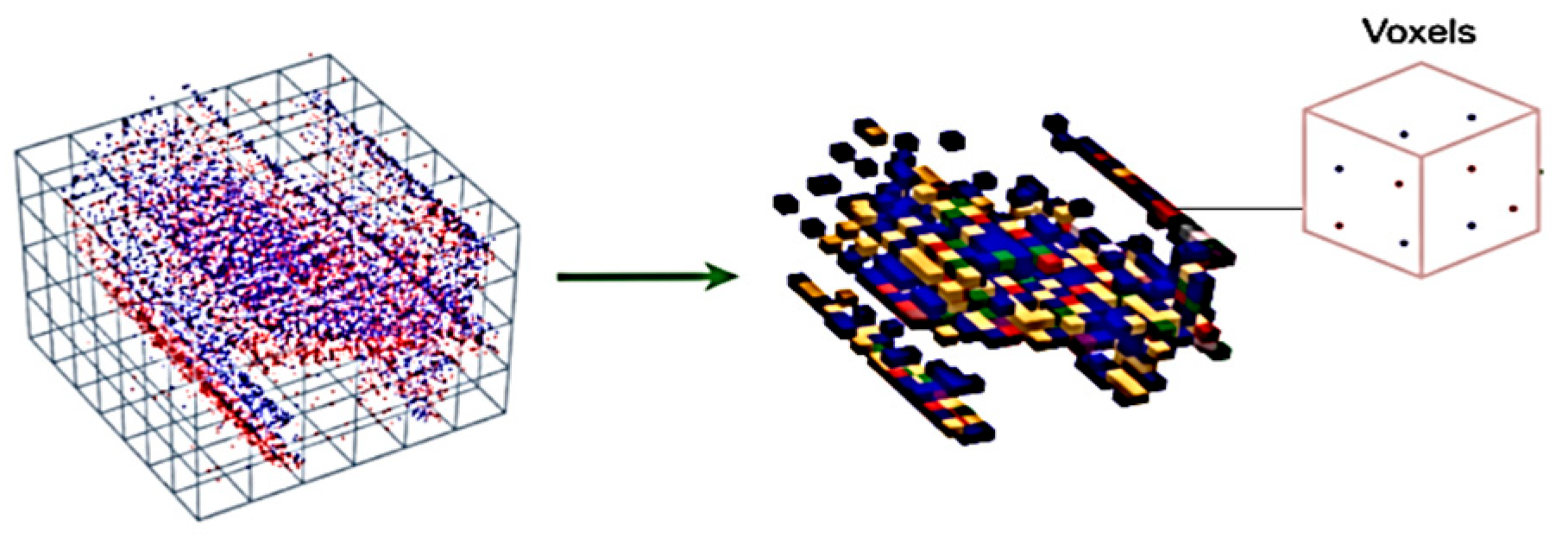
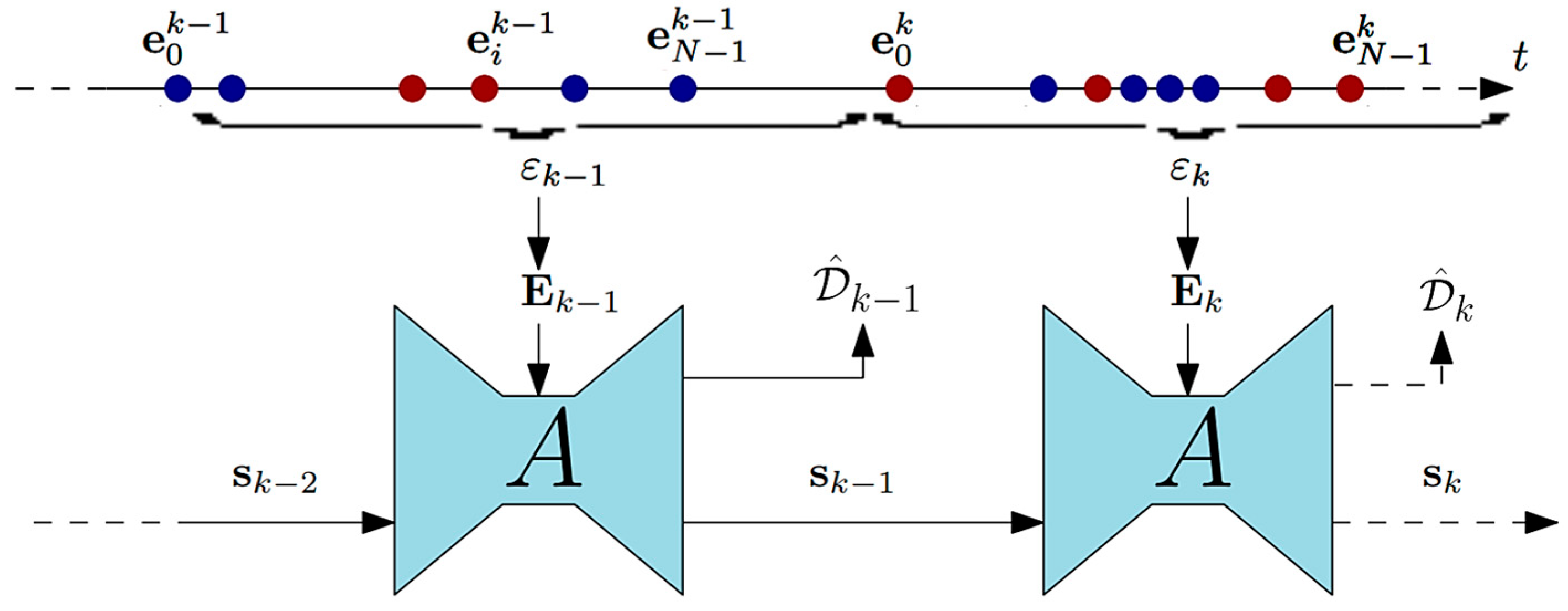
3.2. Event Stream

The proposed method initially requires depth data input. Thus, the output of the event camera is represented as shown in Figure 3.

$${\mathit{e}}_{\mathit{i}}=({\mathit{u}}_{\mathit{i}},{\mathit{t}}_{\mathit{i}},{\mathit{p}}_{\mathit{i}})$$

(1)

Figure 3. Converting stream to the voxel grid structure [47].

Assuming the sensor’s ideal performance, $t_i$ represents the time at which a new event is generated due to brightness changes in pixel $u_i=\left[\begin{array}{c}{x}_i\\ y_i\end{array}\right]$. These brightness changes, characterized by a threshold of ±C with polarity $p_i$, indicate alterations in brightness sign. To estimate depth from the continuous stream of $e_i$, the proposed method employs subsequent non-overlapping window processing, as depicted in Model 2.

$${\mathit{ϵ}}_{\mathit{k}}={\left\{{\mathit{e}}_{\mathit{i}}\right\}}_{\mathit{i}}^{\mathit{N}-1}$$

(2)

Each of these windows exists within the fixed interval $∆T=t_{N-1}^k-t_0^k$, and within each window, the subsequent depth map is estimated.

$$\left\{\widehat{{\mathit{D}}_{\mathit{k}}}\right\}\in {\left[0,1\right]}^{\mathit{W}\times \mathit{H}}$$

(3)

3.3. Deep Network 1 (UNET)

The proposed neural network for depth estimation adopts the structure of UNET, incorporating an internal state referred to as $s_k$. Training the network follows a supervised learning approach, utilizing ground truth depth maps. Initially, training occurs in a simulated environment using synthetic events with comprehensive ground truth data. Subsequently, the network undergoes refinement using real event sequences. Implementation of the proposed method involves utilizing a voxel grid structure as input. This structure aims to represent events in terms of their location, time, and polarity. Consequently, the generated data becomes 4-dimensional, portraying location and time within a 3-dimensional framework while also preserving polarity information.

The data is represented using the following relationship, where ΔT signifies the time intervals during which events are gathered, and B denotes the number of temporal bins. These two hyperparameters are adjusted based on the method outlined in reference [47].

$${\mathit{E}}_{\mathit{k}}\left({\mathit{u}}_{\mathit{k}},{\mathit{t}}_{\mathit{n}}\right)=\sum _{{\mathit{e}}_{\mathit{i}}}{\mathit{p}}_{\mathit{i}}\mathit{\delta }\left({\mathit{u}}_{\mathit{i}}-{\mathit{u}}_{\mathit{k}}\right)\max \left(0,1-\left|{\mathit{t}}_{\mathit{n}}-{\displaystyle \frac{\mathit{B}-1}{\Delta \mathit{T}}}\left({\mathit{t}}_{\mathit{i}}-{\mathit{t}}_0\right)\right|\right)$$

(4)

Based on the above relationship, initially, all existing events are segmented into a specific number of inputs with predetermined time intervals ΔT. Subsequently, the events within these intervals are categorized into B groups according to the defined relationship. Following this categorization, a normalization operation is applied to ensure a mean of zero and a variance of one across the voxel grids. The neural network architecture employed in this research is a fully convolutional recurrent neural network based on the UNET architecture. This network comprises several layers, including a header layer H, recursive encoder layers NE(Ei), recursive blocks NR(Rj), and decoder layers NE Dl. The output of the network is generated by a final depth prediction layer P. The neural network architecture utilized in this study is illustrated in Figure 4.

Figure 4. UNET neural network architecture (adapted from [47]).

The basic architecture employed follows the specifications outlined in [47]. The sole distinction between our architecture and that of [47] lies in the utilization of an attention mechanism instead of a recurrent mechanism, aimed at accelerating the network. Specifically, spatial attention is adopted to emphasize important regions in the feature maps at each layer. Spatial attention computes a weighted map over the spatial locations in the feature maps, highlighting important regions while eliminating irrelevant regions. This mechanism allows the network to focus on critical depth cues in the scene, improving accuracy without significantly increasing computational cost. This design improves computational efficiency while preserving critical depth details. Constants of the basic neural network architecture are listed in Table 2.

Table 2. Constants of the basic neural network architecture.

$\mathsf{\Delta }\mathit{T}$	$50\mathbf{ms}$
$B$	5
NE	3
NR	2
Nb	32
L	40

According to the presented architecture, an event tensor ${\mathit{E}}_k$ at time step k along with the previous network state has been defined.

$${\mathit{s}}_{\mathit{k}}=\left\{{\mathit{c}}_{\mathit{k}-1}^1,\dots ,{\mathit{c}}_{\mathit{k}-1}^{{\mathit{N}}_{\mathit{E}}}\right\}$$

(5)

Based on these inputs, this architecture conducts the following operations:

$$x_k^h=H\left(E_k\right)$$

(6)

$$h_k^i,c_k^i={\epsilon }^i(h_{k-1}^i,c_{k-1}^i)$$

(7)

The details of neural network layers are shown in Figure 5.

Figure 5. Details of deep neural network layers (adapted from [47]).

Two types of objective functions are employed for neural network training. The first type, known as scale-invariant loss, is defined by the following equation:

$${\mathcal{L}}_{\mathrm{k},\mathrm{si}}={\displaystyle \frac{1}{\mathit{n}}}\sum _{\mathit{u}}{\left({\mathcal{R}}_{\mathit{k}}\left(\mathit{u}\right)\right)}^2-{\displaystyle \frac{1}{{\mathit{n}}^2}}{\left(\sum _{\mathit{u}}{\mathcal{R}}_{\mathit{k}}\left(\mathit{u}\right)\right)}^2$$

(8)

The subsequent relationship is also defined as multi-scale scale-invariant and is computed at each scale within the network. The equation for this objective function is provided as follows:

$${\mathcal{L}}_{\mathrm{k},\mathrm{grad}}={\displaystyle \frac{1}{\mathit{n}}}\sum _{\mathit{s}}\sum _{\mathit{u}}\left|{\nabla }_{\mathit{x}}{\mathcal{R}}_{\mathit{k}}^{\mathit{s}}\left(\mathit{u}\right)\right|+\left|{\nabla }_{\mathit{y}}{\mathcal{R}}_{\mathit{k}}^{\mathit{s}}\left(\mathit{u}\right)\right|$$

(9)

Therefore, by combining these two introduced functions, the final objective function is reached:

$${\mathcal{L}}_{\mathit{tot}}=\sum _{\mathit{k}=0}^{\mathit{L}-1}{\mathcal{L}}_{k,\mathit{si}}+\mathit{\lambda }{\mathcal{L}}_{k,\mathit{grad}}$$

(10)

The final objective function for depth estimation, as defined in Equation (10), combines the scale-invariant loss and the multi-scale gradient loss to ensure both global depth consistency and preservation of local depth variations. The weight λ balances the contribution of the gradient term relative to the scale-invariant component. In all experiments, λ is set to 1, which provides an equal emphasis on both terms, facilitating stable and accurate depth learning. This setup allows the network to maintain fine structural details while minimizing overall depth estimation error.

The depth estimation problem is commonly applied to various tasks such as semantic segmentation, robot navigation, and autonomous driving. In this research, our focus lies on robot navigation. Therefore, it is imperative for the algorithm to be lightweight, fast, and devoid of heavy computational burdens. However, the basic network introduced, which utilizes a recursive structure, cannot achieve such objectives. As an innovative approach, the feedback loop is mitigated or weakened. Clearly, the presence of a recurrent structure in the depth estimation neural network can be substituted with an attention mechanism ($UNe{t}_{att}$). The resulting network, referred to as deep network 1, embodies a swift and precise structure for scene depth detection.

3.4. Routing Based on VT&R Method

Depth images outperform RGB images in the VT&R algorithm for robot navigation due to their provision of more detailed environmental information. Unlike RGB images, which merely capture surface appearances, depth images offer insights into object distances within the scene. This depth information proves vital for the VT&R algorithm, facilitating precise robot localization and navigation. For instance, depth images aid in obstacle detection, depth map estimation for navigation planning, and comprehension of the environment’s 3D structure. Consequently, employing depth images as input enhances the robot’s ability to perceive and navigate complex environments. During robot navigation operations, the robot utilizes a three-state function to select its path at each stage.

$$\mathit{f}\left(\mathit{x}\right)=\left\{\begin{array}{c}\mathit{L} \mathit{c}\mathit{a}\mathit{s}\mathit{e} 1:\mathit{L}\mathit{e}\mathit{f}\mathit{t}\\ \mathit{R} \mathit{c}\mathit{a}\mathit{s}\mathit{e} 2:\mathit{R}\mathit{i}\mathit{g}\mathit{h}\mathit{t}\\ \mathit{F} \mathit{c}\mathit{a}\mathit{s}\mathit{e} 3:\mathit{F}\mathit{o}\mathit{r}\mathit{w}\mathit{a}\mathit{r}\mathit{d} \end{array}\right.$$

(11)

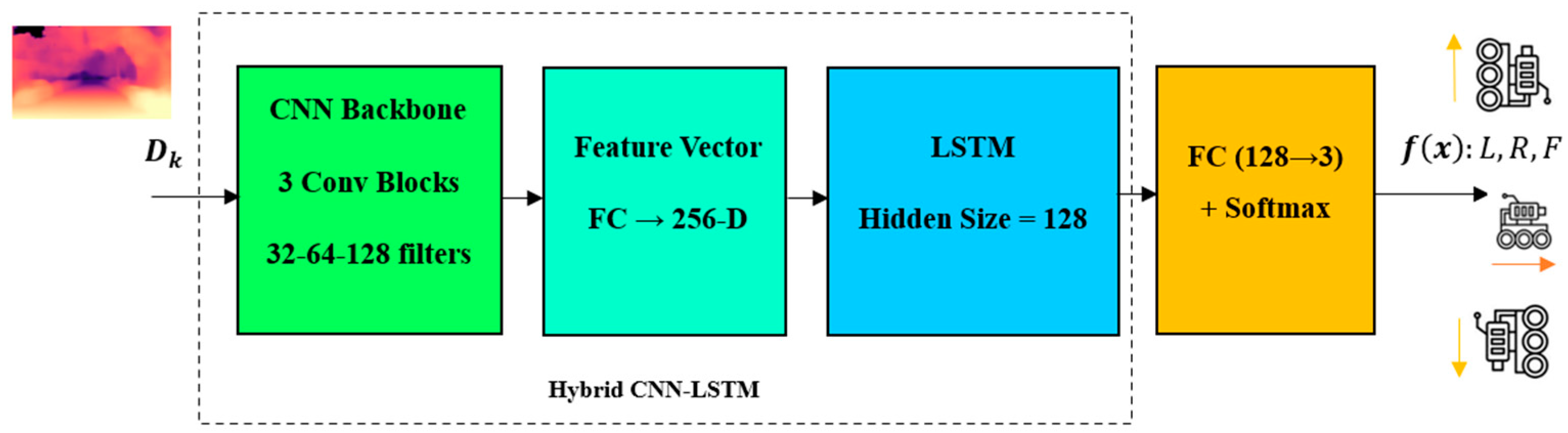
3.5. Deep Network 2 (Hybrid CNN-LSTM)

To utilize the estimated depth images as input to the VT&R algorithm, a hybrid CNN-LSTM network can be employed. Here is a step-by-step explanation of how to utilize the grid:

• Input data: The network receives a sequence of estimated depth images as input. Let us assume the input sequence has a length of T, and each depth image is denoted by ${\mathit{D}}_{\mathit{k}}$;
• CNN Backbone: The initial step involves passing each depth image ${\mathit{D}}_{\mathit{k}}$ through a CNN backbone to extract meaningful features. This process is denoted by CNN(${\mathit{D}}_{\mathit{k}}$), yielding the feature map ${\mathit{F}}_{\mathit{t}}$ for the depth image;

  $${\mathit{F}}_{\mathit{t}}=\mathit{C}\mathit{N}\mathit{N}\left({\mathit{D}}_{\mathit{k}}\right)$$

  (12)
• Feature Encoding: The feature maps derived from the CNN backbone need to be encoded into a representation with fixed dimensions. This encoding facilitates the retention of timing information across the sequence. A commonly employed method for this task is to utilize an LSTM network.
  • LSTM input: The input to the LSTM at time t is denoted as ${\mathit{X}}_{\mathit{t}}$ and can be computed as follows:

    $${\mathit{X}}_{\mathit{t}}=\mathit{E}\mathit{n}\mathit{c}\mathit{o}\mathit{d}\mathit{e}\mathit{r}\left({\mathit{F}}_{\mathit{t}}\right)$$

    (13)
  • LSTM hidden state update: The LSTM retains a hidden state ${\mathit{H}}_{\mathit{t}}$, capturing temporal dependencies within input sequences. The hidden state at time $\mathit{t}$, denoted by ${\mathit{H}}_{\mathit{t}}$, can be updated utilizing the input ${\mathit{X}}_{\mathit{t}}$ and the previous hidden state ${\mathit{H}}_{(\mathit{t}-1)}$ as follows:

    $${\mathit{H}}_{\mathit{t}}=\mathit{L}\mathit{S}\mathit{T}\mathit{M}({\mathit{X}}_{\mathit{t}},{\mathit{H}}_{(\mathit{t}-1)})$$

    (14)
  • LSTM output: The LSTM output at time $\mathit{t}$, denoted by ${\mathit{Y}}_{\mathit{t}}$, represents the encoded representation of the feature map at that specific time step.

    $${\mathit{Y}}_{\mathit{t}}=\mathit{L}\mathit{S}\mathit{T}\mathit{M}\mathit{o}\mathit{u}\mathit{t}\mathit{p}\mathit{u}\mathit{t}\left({\mathit{H}}_{\mathit{t}}\right)$$

    (15)
• VT&R Algorithm: The encoded representations obtained from the LSTM can now be employed within the VT&R algorithm for robot navigation. The features of this algorithm are contingent upon the particular approach utilized.
  • VT&R Loss: In the VT&R algorithm, the usual procedure entails comparing the robot’s current observations with previously observed sequences. The loss for VT&R can be defined based on the ${\mathit{Y}}_{\mathit{t}}$ coded representations and the desired target sequence:

    $$\mathit{L}\mathit{o}\mathit{s}\mathit{s}=\mathit{V}\mathit{T}\&\mathit{R}\mathit{L}\mathit{o}\mathit{s}\mathit{s}({\mathit{Y}}_{\mathit{t}},\mathit{T}\mathit{a}\mathit{r}\mathit{g}\mathit{e}\mathit{t})$$

    (16)
  • Training: The entire network, comprising the CNN, LSTM, and VT&R modules, can undergo end-to-end training. Network parameters can be updated utilizing gradient-based optimization techniques, such as backpropagation.

In summary, the proposed method shows how the estimated depth images are converted into navigation commands after feature extraction and temporal analysis. The structure of this part of the proposed method is shown in Figure 6. In this structure, first, each depth image is fed into the CNN section and important spatial features are extracted from it. These features are then fed to the LSTM layer to learn the temporal dependencies between frames and the robot’s motion changes along the path. The output of the LSTM is a encoded feature vector rich in spatio-temporal information that is sent to the VT&R module. This module generates a steering decision (left, right, or straight) by comparing the current observations with the trained path. This input–processing–decision flow provides a structured and integrated map of how the hybrid network is used for robot navigation.

Figure 6. Robot navigation based on deep hybrid network.

Although the overall structure of the CNN-LSTM hybrid model in Figure 6 shows the process of converting depth images into navigation commands, it is necessary to provide details of the architecture of this model to achieve complete transparency and repeatability of the method. In the CNN section, convolutional layers with 3 × 3 filters and an increasing number of channels are used to extract depth spatial features with greater accuracy. After each layer, batch normalization and the ReLU activation function are used for training stability. The output of this section is converted into a fixed-dimensional feature vector that forms the input base of the LSTM layers. In the LSTM section, a layer with a fixed hidden state vector size is used to continuously model the temporal dependencies between frames and the robot’s motion changes. This detailed description takes the model framework out of the conceptual state and allows for its fair evaluation and comparability.

Also, to complete the VT&R-based navigation process, it is necessary to provide a more precise definition of the loss function and the feature matching mechanism. In the present method, the output vectors of the LSTM are compared with the trained path feature sequence, and the spatio-temporal difference between them is calculated as a measure of the VT&R error. This cost function, by giving balanced weight to the vector differences, trains the network in such a way that a more accurate match is created with the reference path. In the decision-making stage, three classes “left”, “right”, and “straight” are selected based on minimizing the difference between the current observation and the reference state. For training phase, the entire network is trained end-to-end and learns the correct path with VT&R Loss. Table 3 details the detailed architecture of the hybrid network as well as other specifications of the network training process.

Table 3. Hybrid network architecture and training process specifications.

Component of Hybrid Network	Specification
Input	${\mathrm{D}}_{\mathrm{k}}$, sequence length (T)
CNN Backbone (3 Convolutional Blocks)	Conv Layer 1: 3 × 3 kernel, 32 filters, BatchNorm, ReLU Conv Layer 2: 3 × 3 kernel, 64 filters, BatchNorm, ReLU Conv Layer 3: 3 × 3 kernel, 128 filters, BatchNorm, ReLU Output flattened to Feature Vector (FC → 256D)
LSTM	Input: 256D Feature Vector Hidden State: 128 Captures temporal dependencies between frames Output: Encoded feature representation (${\mathrm{Y}}_{\mathrm{t}}$)
Fully Connected + Softmax	FC Layer: 128 → 3 Softmax activation for navigation command selection
Loss Function	Categorical Cross-Entropy–Spatio-temporal difference
Training	End-to-end training with backpropagation (30–70%)
Output Classes	3 classes: Left, Right, Forward

4. Simulation of the Proposed Method

4.1. Simulation Dataset

The simulation for this research is conducted using Python 3.11. The training utilized the Adam optimizer, a multi-scale scale-invariant objective function with weight and lambda set to 1, a batch size of 8, and a learning rate of 0.0003. The model has been exposed to 100 epochs. Leveraging the robust computing power and ample memory of GPUs, two models with identical settings have been concurrently trained on each GPU, resulting in four models being trained simultaneously at each stage, thereby saving time. The simulation employed the DENSE dataset, introduced in 2020 alongside the E2Depth model, which was prepared within a simulator environment. The input images in this dataset are sized at 260 × 346. Additionally, the MVSEC dataset [49,51,52] was also utilized during the training process.

This dataset currently stands as the sole real dataset prepared to employ an event camera in authentic scenes, accompanied by depth information as a label. It encompasses several segments categorized by vehicle carrying the camera and the imaging environment. Within this dataset, four distinct categories are delineated based on the vehicle carrying the camera: (1) UAV, (2) human, (3) machine, and (4) engine.

Additionally, concerning the environment, there are two primary categories: indoor and outdoor as depicted in Figure 7, further subdivided based on time (for cars and motorbikes, segmented according to the geographical area of imaging).

Figure 7. MVSEC dataset in indoor and outdoor views [51].

• The MVSEC dataset comprises two sets of features: Indoor Vicon and Outdoor Qualisys;
• Indoor Vicon:

  -

  The Indoor Vicon setup covers a space measuring 88 × 22 × 15 ft, enabling the tracking system to capture movements within this area;

  -

  It employs 20 Vicon Vantage VP-16 cameras to track the movement of objects or individuals within the designated area;

  -

  The dataset offers pose updates at a frequency of 100 Hz, indicating that the position and orientation of objects are recorded 100 times per second;

• Outdoor Qualisys:

  -

  The outdoor setup of the Qualisys system covers a larger area, which is 100 × 50 × 50 ft. This allows for tracking movements in a more extensive outdoor environment;

  -

  It deploys 34 Qualisys Opus 700 cameras to capture the movements and positions of objects in the designated outdoor area;

  -

  Like the Indoor Vicon system, the Outdoor Qualisys system provides pose updates at a frequency of 100 Hz, meaning that the position and orientation of objects are recorded 100 times per second.

The MVSEC dataset was divided into indoor and outdoor subsets for both training and evaluation: training was primarily conducted on the indoor sequences, while outdoor sequences were used for testing to assess cross-domain generalization. This experimental split ensures that the network is exposed to diverse environments and validates the robustness of the proposed method across different settings.

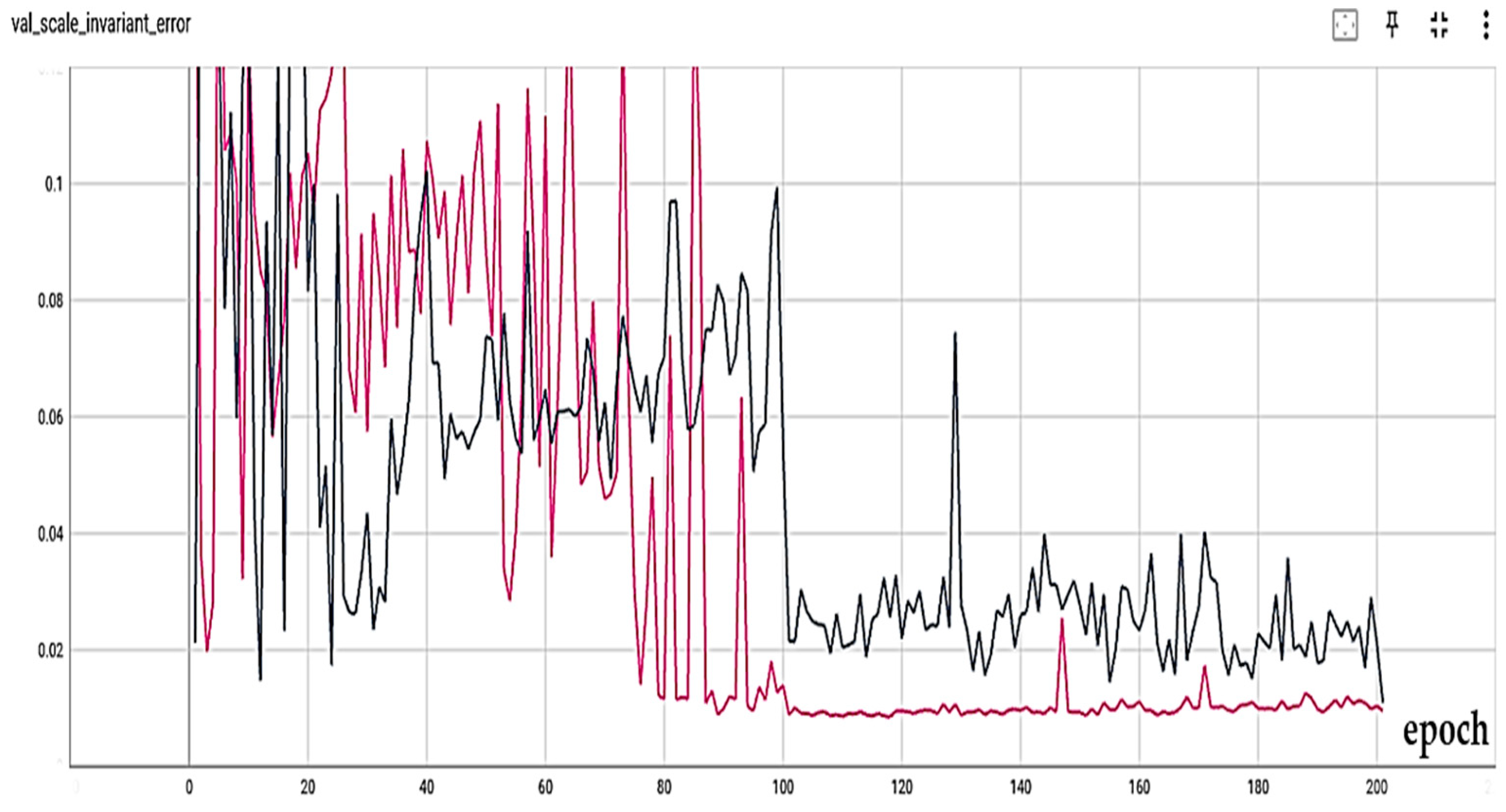
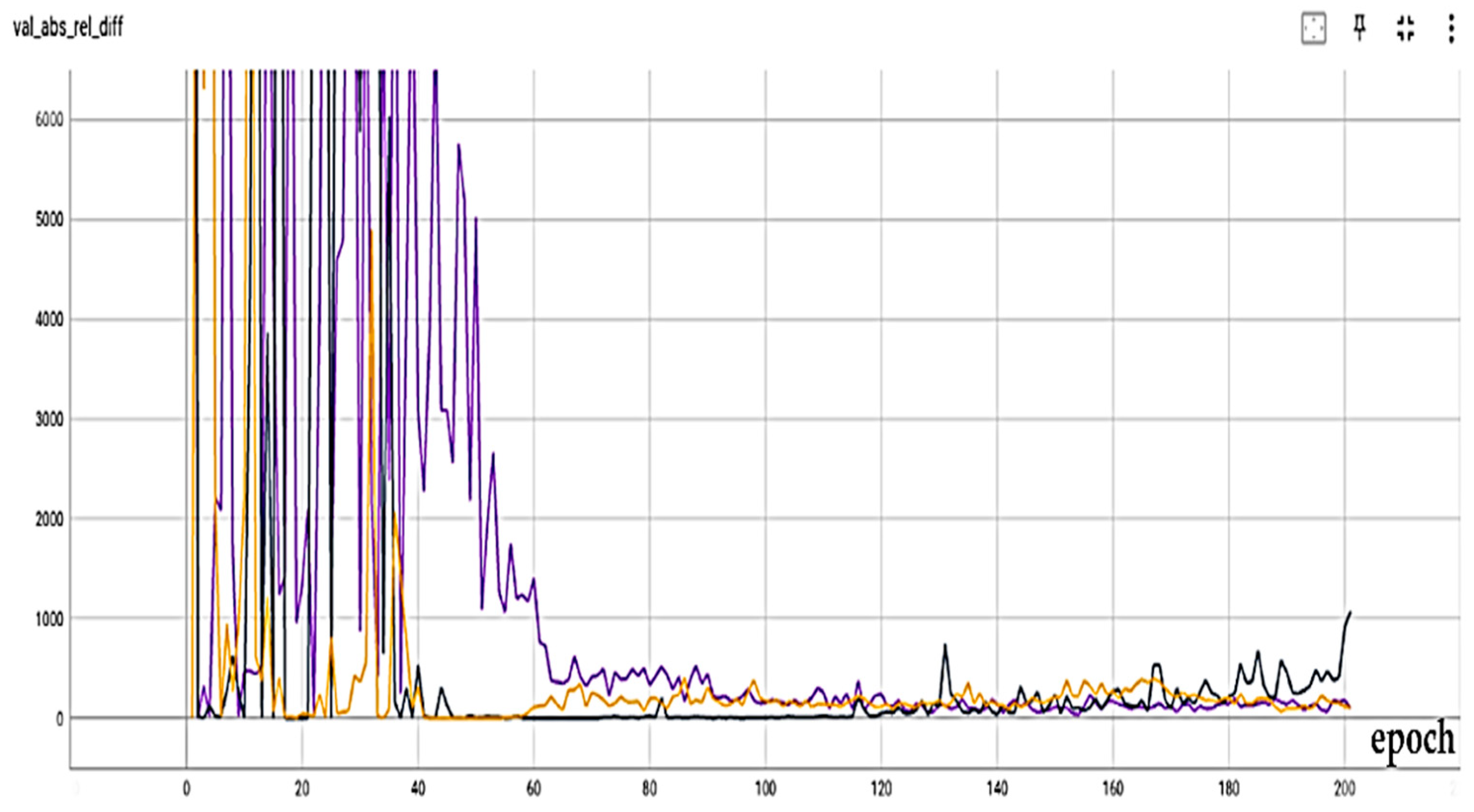
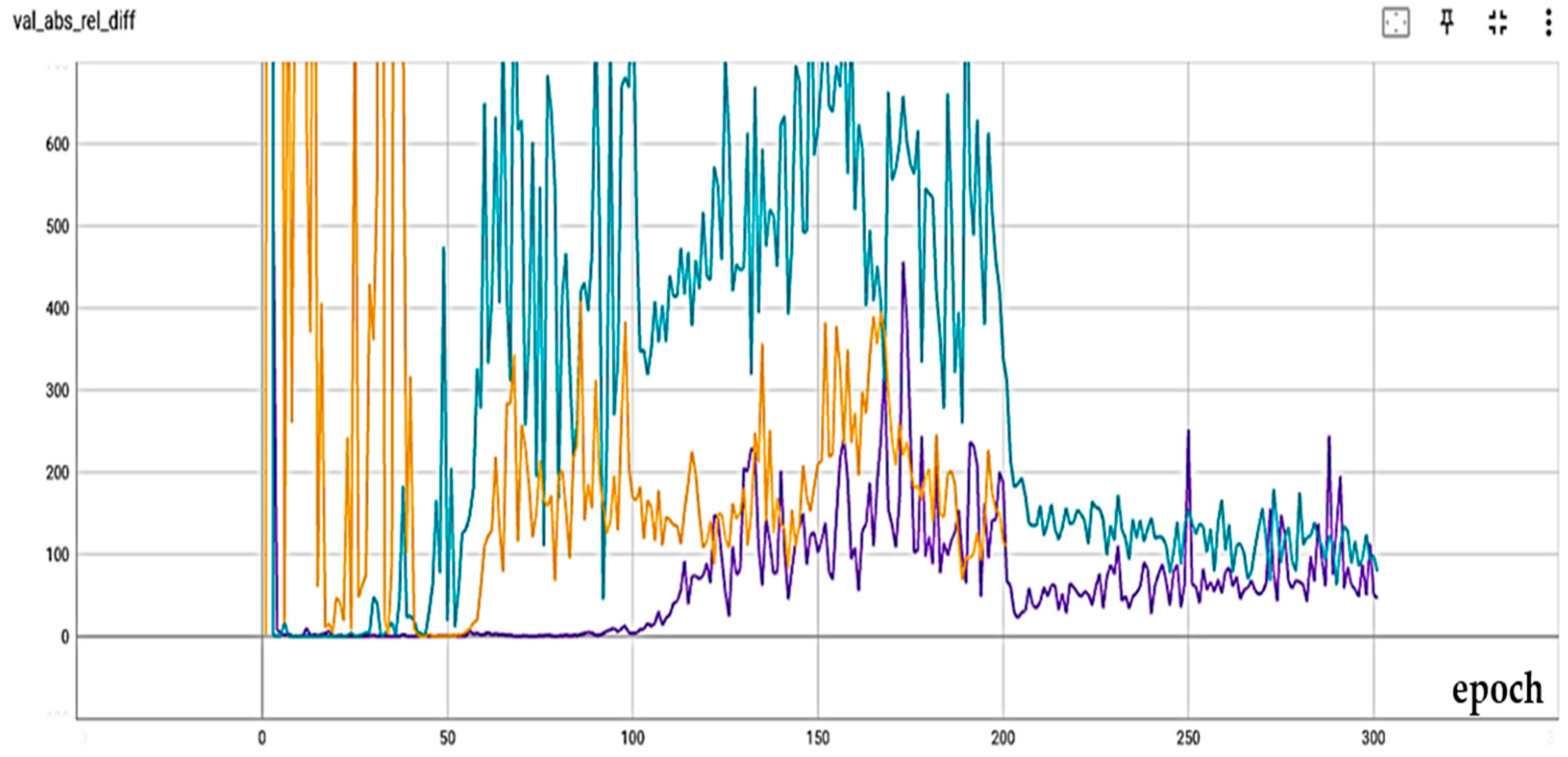
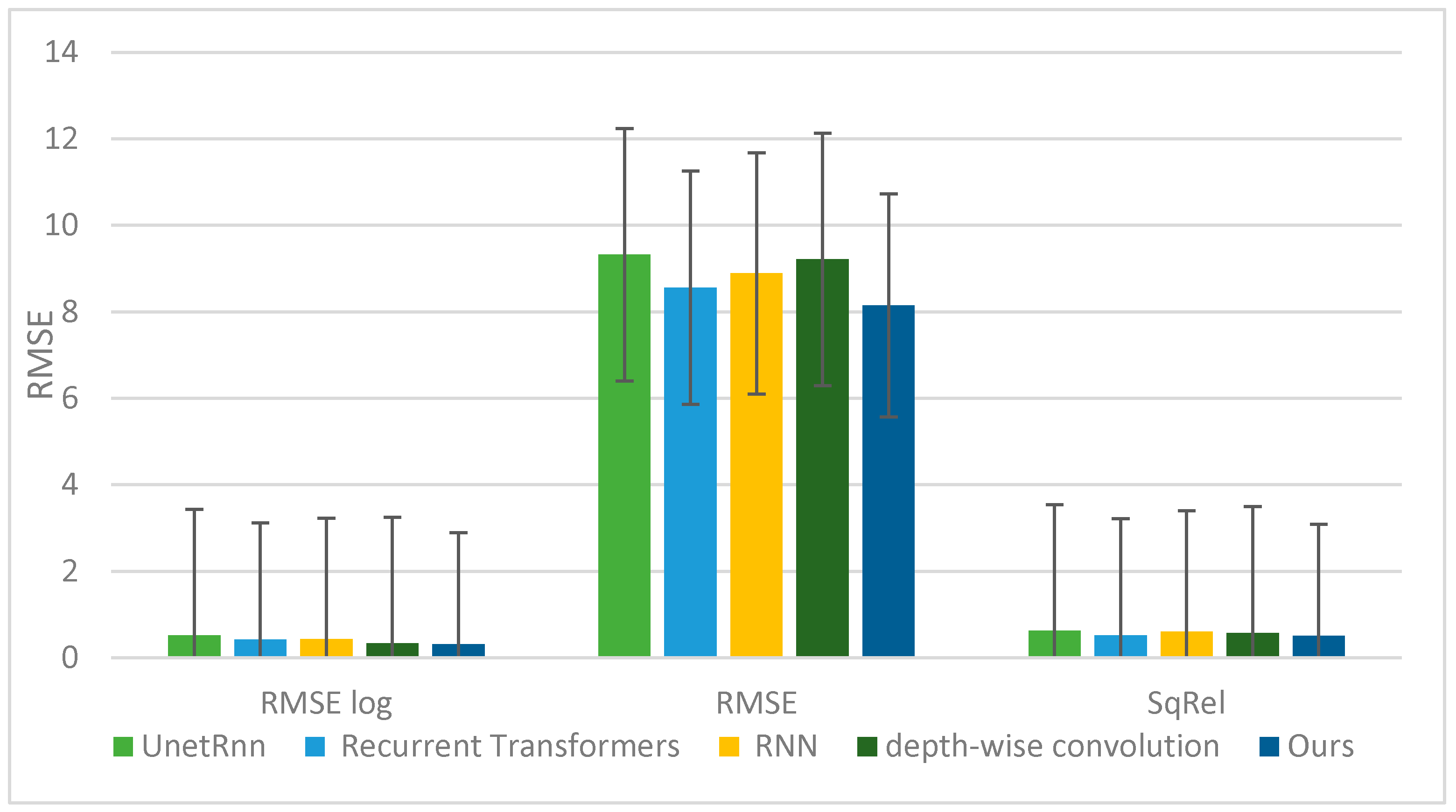
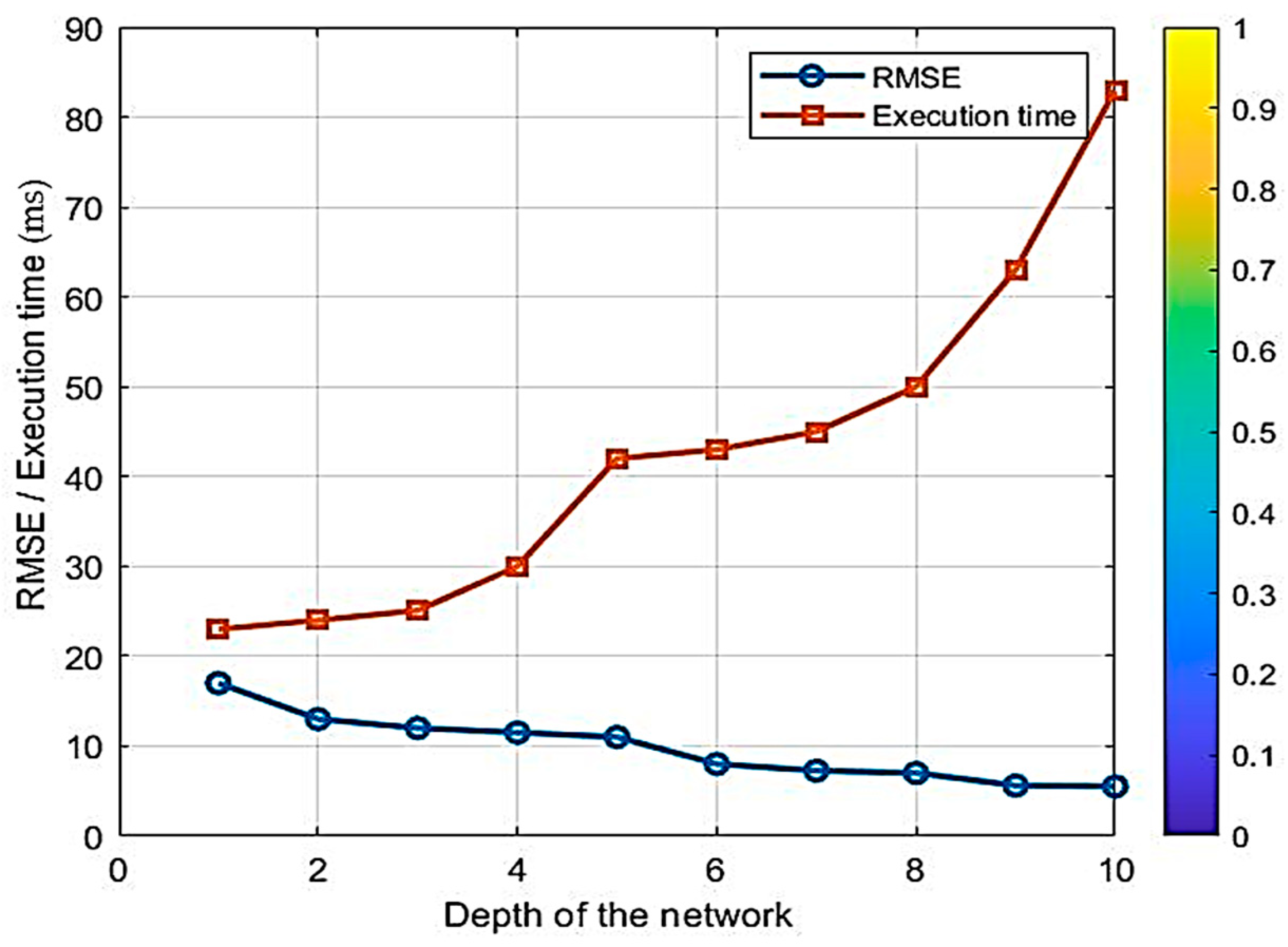
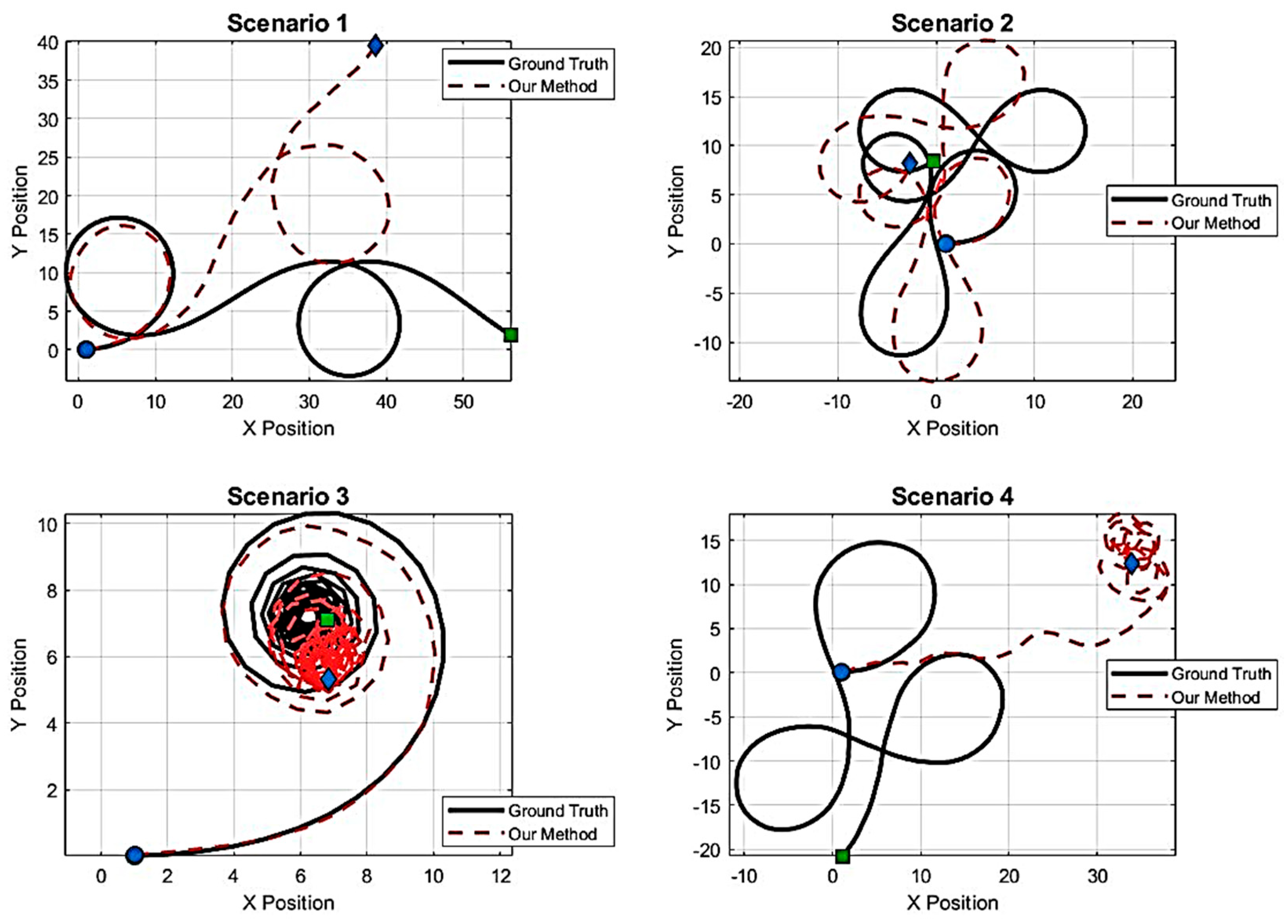
4.2. Results and Discussion

The criteria for evaluating the efficiency of depth map estimation for assessing the proposed method comprise three items. Given the estimated depth map D and the corresponding true criterion $D^{*}$, $D_i$ and $D_i^{*}$ represent the values of the estimated depth map and the true criterion depth at the pixel indexed by i, respectively. N represents the total number of pixels for which both the true and estimated depths are available. For the quantitative comparison of the estimated depth map and the true criterion, the common evaluation criteria are listed below.

The Root Mean Square Error (RMSE) is defined as follows:

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum _N{\left|D_i^{*}-D_i\right|}^2}$$

(17)

The Logarithm Root Mean Square Error (log RMSE) is defined as follows:

$$RMSE log=\sqrt{{\displaystyle \frac{1}{N}}\sum _N{\left|\mathit{log}\left(D_i^{*}\right)-\mathit{log}\left(D_i\right)\right|}^2}$$

(18)

The Squared Relative Difference (Sq Rel) is calculated as the average value across all pixels in the image, incorporating the L_2 distance between the accurate measurement and the estimated depth, scaled by the estimated depth itself.

$$SqRel={\displaystyle \frac{1}{N}}\sum _N{\displaystyle \frac{{\left|D_i^{*}-D_i\right|}^2}{D_i}}$$

(19)

To evaluate the other different models, the tensorboard tool has been used to record and visualize the performance records of the model during training. The Adam optimizer, batch size equal to 8 and a learning rate of 0.0003 were used for training. Also, items such as Clip Distance have been used to control large gradients. In each training, due to the high computational power of GPUs and their large memory, we trained two models of the same settings simultaneously in each GPU. In other words, in each stage of training, four modes were trained simultaneously, which saved time. Also, considering that the two trainings have been performed from the simultaneous mode, their comparison is valid and reliable.

To better examine the attention mechanism, two spatial attention mechanisms (A-B) have been examined with different settings. In Figure 8, the scale-invariant error criterion for the no-attention (black) and attention A (pink) modes without the Recurrent part is presented. Also, in Figure 9, the results of the absolute relative difference criterion for the no-attention state (black), attention A (purple), and attention B (orange) are presented. As the results show, with a slight difference from attention A, attention B has the best result. Also, in Figure 10, the results of the absolute relative difference criterion for the no-attention state (blue), attention B (purple) with the Recurrent part, and attention B (orange) without the Recurrent part are shown. An example of the output results is also shown in Figure 11. In this Figure, the output of the best models in the last step is as follows: the left column is for the no-Recurrent state and the right column is for the Recurrent state. Also, the first row is for no attention, the second row is for attention A, and the third row is for attention B.

Figure 8. Scale-invariant error measure for no attention (black) and attention A (pink) without recurrent part.

Figure 9. Absolute relative difference measure results for no attention (black), attention A (purple), and attention B (orange).

Figure 10. Absolute relative difference measure results for no attention (blue), attention B (purple) with recurrent part, and attention B (orange) without recurrent part.

Figure 11. Output results (left column: no recurrent condition, right column: with recurrent condition).

The proposed method in this research represents a novel approach to utilizing event-based depth estimation in robot routing. To the best of our knowledge, there exists no study that comprehensively addresses this specific issue. However, this method can be effectively compared with several significant and relevant studies in the field of depth estimation. The comparison of the results obtained from this research with those of other related studies is presented in Table 4.

Table 4. Comparison of the proposed method with other methods.

Method	$\mathit{R}\mathit{M}\mathit{S}\mathit{E} \mathit{l}\mathit{o}\mathit{g}$	$\mathit{R}\mathit{M}\mathit{S}\mathit{E}$	$\mathit{S}\mathit{q}\mathit{R}\mathit{e}\mathit{l}$
UnetRnn [47]	0.514	9.321	0.627
Recurrent Transformers [52]	0.421	8.564	0.516
RNN [53]	0.436	8.891	0.609
Depthwise Convolution [54]	0.333	9.21	0.576
Fusion of Event Camera and Sparse LiDAR [55]	-	9.70	-
Ours	0.315	8.15	0.510

The simulation results show that replacing the recurrent model in [47] with the attention model has resulted in error reduction. Evidently, depth estimation, although primarily employed for tasks such as semantic segmentation, robot navigation, and autonomous driving, serves as the focus of this research, particularly in the context of robot navigation. Consequently, it is imperative for this algorithm to prioritize lightness, speed, and minimal computational load.

Better results can be achieved by eliminating or weakening the recursive structure introduced in [47]. Consequently, as an innovative approach, we have either eliminated or weakened the recursive cycle. Integrating the output of the depth estimation algorithm into the robot navigation process through a deep hybrid network has yielded a path selection accuracy of 91.11%, surpassing the normal image mode by 11.09%. In this study, the data was split into “Indoor” and “Outdoor” training sets from the MVSEC dataset to assess the model’s generalization ability under heterogeneous conditions. An accuracy of 91.11% was reported based on the same protocol and with multiple replicate experiments to stabilize the results. A key constraint in implementing this method lies in the accessibility of robots to the event camera. Should this challenge be fully addressed in the future, our proposed method exhibits significant potency, promising high accuracy in robot navigation.

To contextualize the comparison of attention mechanisms in the proposed method, ref. [54] emerges as particularly relevant. In [54], long-range information is acquired through a depth-wise convolution network. Additionally, a novel attention trap is introduced, strategically placing multiple traps across a broad spatial range for each pixel. This formation of the attention mechanism is based on preserving the complexity window feature ratio. Through this design, quadratic computational complexity is effectively transformed into a linear format. Subsequently, the method progresses to create an encoder-–decoder trap depth estimation network.

The network introduces an optical transformer as an encoder and employs trap attention to estimate depth from a single image in the receiver. In comparison to other methods, the proposed approach demonstrates higher accuracy, indicated by reduced errors. Figure 12 provides a comprehensive comparison between the proposed method and others.

Figure 12. Comparison of different error measures between ours and other methods.

The balance between accuracy and lightness may vary based on the specific requirements and constraints of the depth estimation task. When accuracy is the primary concern and ample computational resources are available, the optimal choice is an attention mechanism with a recurrent structure. Conversely, if real-time processing and model lightness are prioritized, an attention mechanism without recurrence might be more suitable. A recurrent structure can also serve as a compromise between accuracy and lightweight design, albeit with a slight reduction in speed compared to a non-recurrent attention-based model. Additionally, the depth of the proposed network is a crucial factor to consider.

The research methodology reveals that the network’s depth is appropriately calibrated. It is crucial to note that if the network has insufficient depth and lacks a recurrent mode, the addition of attention mechanisms will decrease accuracy. Conversely, incorporating a recurrent mode increases the network’s depth, thereby enhancing accuracy but reducing speed. Our research aims to develop a lightweight model that achieves favorable results with minimal training. By integrating attention mechanisms, we can attain the same or similar accuracy as the original model with fewer steps. Therefore, in this research, a network with a recurrent structure of appropriate depth, coupled with an attention mechanism that balances accuracy and speed, has been utilized. As illustrated in Figure 13, increasing the network’s depth enhances accuracy (reducing error) while simultaneously reducing the model’s lightness (increasing execution time). The data in the table is normalized.

Figure 13. Trade-off between accuracy and lightness.

It should be noted that altering the attention-based hyperparameters of the UNET network can significantly impact the error rate of the depth estimation algorithm. The attention mechanism in the UNET network enhances the network’s ability to focus on relevant features while suppressing irrelevant ones, thereby improving the network’s understanding of the depth-related information in the input image.

Adjusting meta-parameters such as attention scale or attention weighting power can modulate the network’s ability to capture critical depth cues. Increasing the scale of attention may prioritize salient depth information, resulting in lower error rates as the network focuses more on relevant features. Conversely, decreasing the scale of attention might cause the network to overlook important depth details, leading to higher error rates.

Similarly, adjusting the strength of attention weights can influence network performance. Increasing the attention weight can enhance the impact of depth-related features, potentially improving the accuracy of depth estimation.

Conversely, lower attention weights can diminish the importance of depth cues, leading to suboptimal algorithm performance. Modifying the attention-based meta-parameters within the proposed UNET network can significantly impact the error rate of the depth estimation algorithm. Fine-tuning these hyperparameters enables a balance between emphasizing critical depth features and optimizing overall network performance. These aspects warrant further investigation in future research.

To investigate the performance of the proposed method, it has been evaluated in four different VT&R-based navigation scenarios. The results are shown in Figure 14. In the first three scenarios, which included gentle undulating paths, relatively sharp turns, and paths with long curves, the UNET network based on the attention mechanism was able to reconstruct the event-based depth map with high accuracy, and the CNN-LSTM hybrid model also learned the temporal pattern of these paths correctly and produced paths very close to the Ground Truth. The deviations observed in these three paths have been limited to natural motion noises, and the system behavior remained stable and converged. However, in the fourth scenario, the path has rapid and nonlinear changes, which caused an instantaneous error in the depth estimation and the subsequent propagation of this error in the LSTM temporal memory. This caused the VT&R matching module to fail to align the visual features correctly and the output path gradually deviated from the benchmark path. This scenario shows that although the model performs accurately and reliably under normal conditions, there is a need for error compensation or path readjustment mechanisms in highly unstable or highly fluctuating paths.

Figure 14. Comparison of the performance of the proposed method in route selection.

Various studies have been reviewed to compare the navigation part. However, in the VT&R research literature, there is no specific source that states exactly that VT&R and depth estimation are used simultaneously. Most VT&R studies focus on navigation with images only for iterative path and localization and take depth from LiDAR or Stereo/Visual-inertial sensors or separate this part, examples of which are presented in [56,57,58]. In this respect, the architecture of the current method is presented for the first time in an end-to-end framework. Table 5 presents a comparison between our method and other methods. As it is clear, no research has used event camera-based depth images for visual navigation so far, so the results of this research can be promising for practical applications in the future.

Table 5. Comparison of the architecture of our method with other VT&R-based methods.

Method	Model	Hybrid Model	Depth Estimation	Sensor Type
[56]	CNN	✘	✘	RGB
[57]	ViewNet-VelocityNet	✓	✘	RGB
[58]	Neural Radiance Field (NeRF)	✘	✓	LiDAR
Ours	CNN-LSTM	✓	✓	Event

5. Conclusions

Robot navigation is a crucial aspect of robotics that involves determining its position within a reference frame and planning a path to a target location. Visual navigation methods, particularly those employing cameras, are extensively utilized, with VT&R techniques being a prominent example. Achieving accurate and rapid robot navigation based on VT&R necessitates precise and swift depth estimation of the scene. In recent years, event cameras have garnered significant attention from machine vision researchers due to their numerous advantages and applicability in various environments, such as robots and drones. This research proposes utilizing a fast neural network for depth estimation with event cameras, in conjunction with a hybrid deep neural network for robot navigation. Simulation results on the DENSE dataset indicate that the proposed method achieves an RMSE=8.15, offering both accuracy and speed, thus making it suitable for real-time applications and visual navigation methods based on VT&R. Future research could achieve better results by focusing on the attention mechanism and domain adaptation. Furthermore, navigation for a small, low-cost autonomous surface/underwater vehicle is one area where the results of this research could lead to improvements. Obviously, this area will become more applicable in the future and more research is needed on it. It should be noted that one of the major limitations of the proposed approach is the further development of event cameras for real-world performance. These cameras need to become cheaper and more commercially mass-produced before they can be used in practical applications. However, recent research shows a bright future.