An Efficient Petrov–Galerkin Scheme for the Euler–Bernoulli Beam Equation via Second-Kind Chebyshev Polynomials

Abstract

The current article introduces a Petrov–Galerkin method (PGM) to address the fourth-order uniform Euler–Bernoulli pinned–pinned beam equation. Utilizing a suitable combination of second-kind Chebyshev polynomials as a basis in spatial variables, the proposed method elegantly and simultaneously satisfies pinned–pinned and clamped–clamped boundary conditions. To make PGM application easier, explicit formulas for the inner product between these basis functions and their derivatives with second-kind Chebyshev polynomials are derived. This leads to a simplified system of algebraic equations with a recognizable pattern that facilitates effective inversion to produce an approximate spectral solution. Presentations are made regarding the method’s convergence analysis and the computational cost of matrix inversion. The efficiency of the method described in precisely solving the Euler–Bernoulli beam equation under different scenarios has been validated by numerical testing. Additionally, the procedure proposed in this paper is more effective compared to other existing techniques.

1. Introduction

The beam ranks among the most fundamental and practical mechanical structures in engineering issue modeling. Beams are used to create models of real-life structures like bridges, machine components, wind turbines, aircraft wings, and helicopter blades. Scientific and engineering professionals can simplify three-dimensional difficulties using beam theories. One can find several beam theories in many sources. Popular theories include the classical beam theory (Euler–Bernoulli), the Reddy beam theory, and the Timoshenko beam theory [1]. Many authors are interested in investigating beam problems from various aspects. For example, the authors of [2] developed analytic solutions for Euler–Bernoulli beams. Other analytic solutions were developed in [3] to nonlocal Euler–Bernoulli beam equations. In [4], A closed-form solution for non-uniform Euler–Bernoulli beams was presented. Other types of beam equations were given in [5]. From a numerical perspective, the beam types of equations were handled by many methods. For example, the authors of [6] applied a finite difference method for the Euler–Bernoulli beam equation, two collocation approaches were followed in [7,8], and the Lagrange interpolation method was used in [9]. One can refer to [10,11,12,13] for other contributions.

In recent times, spectral methods have become increasingly popular in computational mechanics and applied mathematics due to their effectiveness and accuracy in solving various differential equations. These methods provide substantial accuracy and efficiency benefits for numerous applications in scientific computing, engineering, and physics, particularly for issues with smooth solutions; see, for example, [14,15,16]. There are different methods of spectral methods and their variants. The three main methods are the tau, collocation, and Galerkin methods. To apply the different spectral methods, one should choose two families of functions, namely, test and trial functions. The choice of these functions varies from one method to another. To apply the Galerkin method, we must select the basis functions to fulfill the underlying boundary conditions; see, for example, [17,18]. This restriction is unnecessary when applying the tau method; see, for example, [19,20]. The collocation method can be applied without any restrictions on the basis functions. In addition, it can be applied to all types of differential equations; see, for example, [21,22,23].

As a modification of the standard Galerkin method, the Petrov–Galerkin scheme is notable for its proficiency in handling intricate boundary conditions. This paper presents an application of the spectral Petrov–Galerkin method to solve the fourth-order uniform Euler–Bernoulli beam equation, which is very important in structural engineering and biomechanics. The fourth-order uniform Euler–Bernoulli Beam Equation encapsulates the dynamic response of slender beams under diverse loading conditions. Its fractional derivative term accounts for non-local effects, making it a powerful tool for modeling viscoelastic materials and systems with memory. Considering both the clamped–clamped and pinned–pinned cases, we encompass a broad spectrum of practical scenarios encountered in engineering applications. For recent advances in Euler–Bernoulli beam theory, see [24,25,26,27].

At the core of our methodology lies the utilization of second-kind Chebyshev polynomials, with [28] as a foundation in spatial variables. These polynomials possess distinct characteristics that render them highly suitable for spectral methods, notably their capability to accommodate multiple types of boundary conditions simultaneously. This adaptability is crucial in tackling the Euler–Bernoulli beam equation, which commonly involves clamped–clamped and pinned–pinned boundary conditions in practical settings.

The Petrov-Galerkin method [29,30,31,32,33] is a mathematical approach employed to approximate solutions of partial differential equations that involve terms with odd orders and where the test function and solution function reside in distinct function spaces. It can be considered an expansion of the Bubnov–Galerkin method, wherein the bases of test and solution functions coincide. From an operator standpoint of the differential equation, the Petrov–Galerkin method involves applying a projection that may not be orthogonal, unlike the Bubnov–Galerkin method.

To simulate memory and hereditary characteristics in real-life phenomena, fractional calculus and differential equations are important in this regard. Applications include simulating blood flow, drug distribution, and nerve impulses in physiology, as well as tackling viscoelasticity, heat conduction, and fluid dynamics problems in engineering physics and civil engineering. See the seminal textbook on fractional differential equations ([34,35]) for more in-depth information.

The organization of this paper is as follows: Section 2 provides an overview of the preliminaries underlying our work, including relevant properties of the Chebyshev polynomials of the second kind. Section 3 details the spectral Petrov–Galerkin method employed to solve the Euler–Bernoulli beam equation, elucidating the explicit formulas derived for inner products and the resulting system of algebraic equations. In Section 5, we delve into the convergence analysis of the method. Section 6 accounts for the computational complexity of the resulting matrix system. Section 7 presents numerical examples demonstrating the efficacy and applicability of our approach. Finally, Section 8 offers concluding remarks and avenues for future research, consolidating the contributions and implications of our work in advancing the field of computational mechanics.

2. Shifted Second-Kind Chebyshev Polynomials

This section presents some fundamental formulas of the shifted second kind of Chebyshev polynomials (S2KCPs). Additionally, a novel formula will be given to represent the moments of the derivatives of these polynomials.

2.1. Some Basic Formulas of S2KCPs

Let $U_j^{*}\left(\zeta \right)$ be shifted S2KCPs on $[0,1]$ denoted by $U_j^{*}\left(\zeta \right)=U_j(2\zeta -1)$. These have the following form [36,37]:

$$U_j^{*}\left(\zeta \right)=\sum _{r=0}^j{\displaystyle \frac{2^{2r}{(-1)}^{j+r}(j+r+1)!}{(2r+1)!(j-r)!}}{\zeta }^r,j\ge 0.$$

(1)

They are orthogonal regarding $\omega \left(\zeta \right)=\sqrt{\zeta -{\zeta }^2}$ in the sense that [36]

$${\int }_0^1\omega \left(\zeta \right)U_m^{*}\left(\zeta \right)U_n^{*}\left(\zeta \right)d\zeta =b_{m,n},$$

(2)

where

$$b_{m,n}={\displaystyle \frac{\pi }{8}}\left\{\begin{array}{cc}1,\hfill & \mathrm{if}m=n,\hfill \\ 0,\hfill & \mathrm{if}m\ne n,\hfill \end{array}\right.$$

(3)

and they can be generated by the following recurrence relation:

$$U_m^{*}\left(\zeta \right)=2\left(2\zeta -1\right)U_{m-1}^{*}\left(\zeta \right)-U_{m-2}^{*}\left(\zeta \right),$$

(4)

where $U_0^{*}\left(\zeta \right)=1,U_1^{*}\left(\zeta \right)=2\zeta -1.$

In addition, we have the following expression [36]:

$${\zeta }^k=\sum _{\ell =0}^k{B}_{\ell ,k}{U}_{\ell }^{*}\left(\zeta \right),j\ge 0,$$

(5)

where

$$B_{\ell ,k}={\displaystyle \frac{4\mathsf{\Gamma }\left(k+\frac{3}{2}\right)((\ell +1)!k!)}{\sqrt{\pi }\ell !(k-\ell )!(\ell +k+2)!}}.$$

(6)

Formula (5) is equivalent to

$${\zeta }^k=(2k+1)!\sum _{\ell =0}^k{\displaystyle \frac{2^{1-2k}(1+k-\ell )}{(2k-\ell +2)!\ell !}}{U}_{k-\ell }^{*}\left(\zeta \right).$$

(7)

The following moment formula of S2KCPs2 is also important ([38]):

$${\displaystyle {\zeta }^m{U}_i^{*}\left(\zeta \right)=\frac{1}{2^{2m}}\sum _{s=0}^{2m}\left(\genfrac{}{}{0pt}{}{2m}{s}\right)U_{i+m-s}^{*}\left(\zeta \right).}$$

(8)

The following is the structure formula of S2KCPs:

$$U_j^{*}\left(\zeta \right)={\displaystyle \frac{1}{4(j+1)}}\left(D{U}_{j+1}^{*}\left(\zeta \right)-D{U}_{j-1}^{*}\left(\zeta \right)\right).$$

(9)

From the above formula, the q-times repeated indefinite integrals of S2KCPs can be derived. The following lemma presents this result:

Lemma 1. 

Assume j and q are two positive integers with $j\ge q$. One has

$$\stackrel{qtimes}{\overbrace{\int \int \cdots \int }}{U}_j^{*}\left(\zeta \right)\stackrel{qtimes}{\overbrace{d\zeta d\zeta \dots d\zeta }}={\displaystyle \frac{q!}{2^{2q}}}\sum _{\ell =0}^q{\displaystyle \frac{{(-1)}^{\ell }(1+j-2\ell +q)(j-\ell )!}{\ell !(-\ell +q)!(j-\ell +q+1)!}}{U}_{j+q-2\ell }^{*}\left(\zeta \right)+{\pi }_{q-1}\left(\zeta \right),$$

(10)

and ${\pi }_{q-1}\left(\zeta \right)$ is a polynomial whose degree is $\le q$.

Proof. 

A particular case of a formula that was given in [39]. □

2.2. Moments of the Derivatives of S2KCPs

This section is confined to presenting an important theorem regarding S2KCPs, which will be the backbone for deriving our numerical algorithm.

Now, we give a new formula that expresses the moments of the derivatives of S2KCPs as combinations of their original polynomials.

Theorem 1. 

Consider the three non-negative integers m, q, and i with $i\ge q$. The following formula holds:

$$\begin{array}{cc}\hfill {\zeta }^m{D}^q{U}_i^{*}\left(\zeta \right)=& {\displaystyle \frac{2^{1-2m+2q}i!(2(1+i+m-q)-1)!}{(i-q)!}}\sum _{s=0}^{i+m-q}{\displaystyle \frac{1+i+m-s-q}{s!(2i+2m-s-2q+2)!}}\times \hfill \\ \hfill & {}_{4}F_3\left(\begin{array}{c}-{\displaystyle \frac{1}{2}}-i,-s,-i+q,-2-2i-2m+s+2q\\ -1-2i,-{\displaystyle \frac{1}{2}}-i-m+q,-i-m+q\end{array}{\displaystyle |}1\right)U_{i+m-q-s}^{*}\left(\zeta \right).\hfill \end{array}$$

(11)

Proof. 

The analytic form in (1) enables one to obtain the following expression for ${\zeta }^m{D}^q{U}_i^{*}\left(\zeta \right)$ in the following form:

$${\displaystyle {\zeta }^m{D}^q{U}_i^{*}\left(\zeta \right)=\sum _{r=0}^i\frac{{(-1)}^r{2}^{2(i-r)}(2i-r+1)!{(1+i-q-r)}_q}{r!(2i-2r+1)!}{\zeta }^{m+i-r-q},}$$

(12)

which can be transformed into the following formula after applying the inversion Formula (7):

$$\begin{array}{cc}\hfill {\zeta }^m{D}^q{U}_i^{*}\left(\zeta \right)=& 2^{1-2m+2q}\sum _{r=0}^i{\displaystyle \frac{{(-1)}^r(2i-r+1)!{(1+i-q-r)}_q}{r!(2i-2r+1)!}}\times \hfill \\ \hfill & \sum _{\ell =0}^{m+i-r-q}{\displaystyle \frac{(1+i+m-q-r-\ell )\left(2\right(1+i+m-q-r)-1)!}{\ell !\left(2\right(i+m-q-r+1)-\ell )!}}{U}_{i+m-r-q-\ell }^{*}\left(\zeta \right).\hfill \end{array}$$

(13)

The last formula, after some algebraic computations, can be rewritten in the following more convenient form:

$$\begin{array}{cc}\hfill {\zeta }^m{D}^q{U}_i^{*}\left(\zeta \right)=& 2^{1-2m+2q}\sum _{s=0}^{i+m-q}(1+i+m-s-q)\times \hfill \\ \hfill & \sum _{r=0}^s{\displaystyle \frac{{(-1)}^r(2i-r+1)!(2(1+i+m-q-r)-1)!{(1+i-q-r)}_q}{(s-r)!r!(2i-2r+1)!(2i+2m-s-2q-r+2)!}}{U}_{i+m-q-s}^{*}\left(\zeta \right).\hfill \end{array}$$

(14)

If the following transformation is used,

$$\begin{array}{cc}& \sum _{r=0}^s{\displaystyle \frac{{(-1)}^r(2i-r+1)!(2(1+i+m-q-r)-1)!{(1+i-q-r)}_q}{(s-r)!r!(2i-2r+1)!(2i+2m-s-2q-r+2)!}}\hfill \\ & ={\displaystyle \frac{i!\left(2\right(1+i+m-q)-1)!}{s!(i-q)!(2i+2m-s-2q+2)!}}\times {}_{4}F_3\left(\begin{array}{c}-{\displaystyle \frac{1}{2}}-i,-s,-i+q,-2-2i-2m+s+2q\\ -1-2i,-{\displaystyle \frac{1}{2}}-i-m+q,-i-m+q\end{array}|1\right),\hfill \end{array}$$

then the following formula is

$$\begin{array}{cc}\hfill {\zeta }^m{D}^q{U}_i^{*}\left(\zeta \right)=& {\displaystyle \frac{2^{1-2m+2q}i!(2(1+i+m-q)-1)!}{(i-q)!}}\sum _{s=0}^{i+m-q}{\displaystyle \frac{1+i+m-s-q}{s!(2i+2m-s-2q+2)!}}\times \hfill \\ & {}_{4}F_3\left(\begin{array}{c}-{\displaystyle \frac{1}{2}}-i,-s,-i+q,-2-2i-2m+s+2q\\ -1-2i,-{\displaystyle \frac{1}{2}}-i-m+q,-i-m+q\end{array}|1\right)U_{i+m-q-s}^{*}\left(\zeta \right).\hfill \end{array}$$

This proves Theorem 1. □

As a consequence of Theorem 1, the following important derivative expression of S2KCPs are combinations of their original polynomials. The following corollary exhibits this result.

Corollary 1. 

The derivative expression of the S2KCPs is

$$D^q{U}_i^{*}\left(\zeta \right)=2^{2q}\sum _{s=0}^{⌊{\displaystyle \frac{i-q}{2}}⌋}{\displaystyle \frac{(1-2s+i-q){\left(q\right)}_s}{s!{(1-s+i)}_{1-q}}}{U}_{i-q-2s}^{*}\left(\zeta \right),i\ge q.$$

(15)

Proof. 

Setting $m=0$ in (11) yields

$$\begin{array}{cc}\hfill D^q{U}_i^{*}\left(\zeta \right)=& {\displaystyle \frac{2^{1+2q}i!(1+2i-2q)!}{(i-q)!}}\sum _{s=0}^{i-q}{\displaystyle \frac{1+i-q-s}{(2+2i-2q-s)!s!}}\times \hfill \\ \hfill & {}_{3}F_2\left(\begin{array}{c}-s,-{\displaystyle \frac{1}{2}}-i,-2-2i+2q+s\\ -1-2i,-{\displaystyle \frac{1}{2}}-i+q\end{array}|1\right)U_{i-q-s}^{*}\left(\zeta \right).\hfill \end{array}$$

(16)

The above ${}_{3}F_2\left(1\right)$ can be summed using Watson’s identity ([40]) to give the following formula:

$${}_{3}F_2\left(\begin{array}{c}-s,-{\displaystyle \frac{1}{2}}-i,-2-2i+2q+s\\ -1-2i,-{\displaystyle \frac{1}{2}}-i+q\end{array}|1\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\left(i-\frac{s}{2}\right)!\mathsf{\Gamma }\left(\frac{1+s}{2}\right){\left(q\right)}_{\frac{s}{2}}}{\sqrt{\pi }i!{\left(\frac{3}{2}+i-q-\frac{s}{2}\right)}_{\frac{s}{2}}},}\hfill & s\mathrm{even},\hfill \\ 0,\hfill & s\mathrm{odd}.\hfill \end{array}\right.$$

(17)

Accordingly, the following formula can be obtained:

$$D^q{U}_i^{*}\left(\zeta \right)=2^{2q}\sum _{s=0}^{⌊{\displaystyle \frac{i-q}{2}}⌋}{\displaystyle \frac{(1-2s+i-q){\left(q\right)}_s}{s!{(1-s+i)}_{1-q}}}{U}_{i-q-2s}^{*}\left(\zeta \right).$$

(18)

Hence, Formula (15) is obtained. □

3. Spectral Approach for Fourth-Order Partial Differential Equations

In this section, we consider the following fourth-order partial differential equations (FPDE):

$${\partial }_{tt}\xi (\zeta ,t)+\alpha {\partial }_{\zeta \zeta }\xi (\zeta ,t)+\mu {\partial }_{\zeta \zeta \zeta \zeta }\xi (\zeta ,t)=f(\zeta ,t),(\zeta ,t)\in (0,1)\times (0,1),$$

(19)

constrained by the following initial and boundary conditions:

$$\begin{array}{cc}\hfill \xi (\zeta ,0)=& p_1\left(\zeta \right),{\partial }_t\xi (\zeta ,0)=p_2\left(\zeta \right),0<\zeta <1,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\left.\xi (\zeta ,t)\right|}_{\zeta =0,1}=& {\left.(1-\theta ){\partial }_{\zeta }\xi (\zeta ,t)\right|}_{\zeta =0,1}={\left.\theta {\partial }_{\zeta \zeta }\xi (\zeta ,t)\right|}_{\zeta =0,1}=0,0<t<1,\hfill \end{array}$$

(21)

where $\alpha ,\mu$ are arbitrary positive constants, $p_1\left(\zeta \right),p_2\left(\zeta \right)$ are given continuous functions, and $f(\zeta ,t)$ is the source term.

Remark 1. 

The parameter θ may be 0 or 1 in the following circumstances: 

• If $\theta =0$, the boundary conditions (21) will be ${\left.\xi (\zeta ,t)\right|}_{\zeta =0,1}={\left.{\partial }_{\zeta }\xi (\zeta ,t)\right|}_{\zeta =0,1}=0.$
• If $\theta =1$, the boundary conditions (21) will be ${\left.\xi (\zeta ,t)\right|}_{\zeta =0,1}={\left.{\partial }_{\zeta \zeta }\xi (\zeta ,t)\right|}_{\zeta =0,1}=0.$

3.1. The Integral Form of Fourth-Order Partial Differential Equations

By integrating Equation (19) twice concerning the variable t to reduce the number of conditions, one gets the following:

$$\xi (\zeta ,t)+\alpha {\int }_0^t{\int }_0^t{\partial }_{\zeta \zeta }\xi (\zeta ,t)dtdt+\mu {\int }_0^t{\int }_0^t{\partial }_{\zeta \zeta \zeta \zeta }\xi (\zeta ,t)dtdt=\widehat{f}(\zeta ,t),(\zeta ,t)\in (0,1)\times (0,1),$$

(22)

subject to

$${\left.\xi (\zeta ,t)\right|}_{\zeta =0,1}={\left.(1-\theta ){\partial }_{\zeta }\xi (\zeta ,t)\right|}_{\zeta =0,1}={\left.\theta {\partial }_{\zeta \zeta }\xi (\zeta ,t)\right|}_{\zeta =0,1}=0,0<t<1,$$

(23)

where

$$\widehat{f}(\zeta ,t)={\int }_0^t{\int }_0^{t}f(\zeta ,t)dtdt+p_1\left(\zeta \right)+t{p}_2\left(\zeta \right).$$

(24)

Therefore, Equation (22) may be solved under condition (23) instead of solving Equation (19) under the conditions (20) and (21).

3.2. The Petrov–Galerkin Algorithm

This section analyzes the PGM to treat (22) governed by (23). We will suggest basis functions and, after that, apply the PGM.

Consider the following basis functions:

$${\mathcal{E}}_i^{*}\left(\zeta \right)=\zeta (1-\zeta )\left({\displaystyle \frac{3\theta }{2i^2+4i+3}}-{\zeta }^2+\zeta \right)U_i^{*}\left(\zeta \right),$$

(25)

along with $U_j^{*}\left(t\right)$ defined in (1).

Consider the following spaces:

$$\begin{array}{cc}& {\mathcal{A}}^N=\mathrm{span}\{{\mathcal{E}}_i^{*}\left(\zeta \right)U_j^{*}\left(t\right):i,j=0,1,\dots ,N\},\hfill \\ & {\mathcal{B}}^N=\{\xi \in {\mathcal{A}}^N:{\left.\xi (\zeta ,t)\right|}_{\zeta =0,1}={\left.(1-\theta ){\partial }_{\zeta }\xi (\zeta ,t)\right|}_{\zeta =0,1}={\left.\theta {\partial }_{\zeta \zeta }\xi (\zeta ,t)\right|}_{\zeta =0,1}=0\}.\hfill \end{array}$$

(26)

Then, ${\xi }^N(\zeta ,t)\in {\mathcal{B}}^N$ can be expressed as follows:

$${\xi }^N(\zeta ,t)=\sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{\mathcal{E}}_i^{*}\left(\zeta \right)U_j^{*}\left(t\right).$$

(27)

The residual $\mathcal{R}(\zeta ,t)$ of Equation (22) has the following form:

$$\begin{array}{cc}\hfill \mathcal{R}(\zeta ,t)& ={\xi }^N(\zeta ,t)+\alpha {\int }_0^t{\int }_0^t{\partial }_{\zeta \zeta }{\xi }^N(\zeta ,t)dtdt+\mu {\int }_0^t{\int }_0^t{\partial }_{\zeta \zeta \zeta \zeta }{\xi }^N(\zeta ,t)dtdt-\widehat{f}(\zeta ,t)\hfill \\ & =\sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{\mathcal{E}}_i^{*}\left(\zeta \right)U_j^{*}\left(t\right)+\alpha \sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{\mathcal{E}}_i^{{*}^{″}}\left(\zeta \right){\int }_0^t{\int }_0^t{U}_j^{*}\left(t\right)dtdt\hfill \\ & +\mu \sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{\mathcal{E}}_i^{{*}^{⁗}}\left(\zeta \right){\int }_0^t{\int }_0^t{U}_j^{*}\left(t\right)dtdt-\widehat{f}(\zeta ,t).\hfill \end{array}$$

(28)

The application of the PGM implies the following:

$$\begin{array}{cc}& {\left(\mathcal{R}(\zeta ,t),U_r^{*}\left(\zeta \right)U_s^{*}\left(t\right)\right)}_{\overline{\omega }(\zeta ,t)}=0,0\le r,s\le N,\hfill \end{array}$$

(29)

where $\overline{\omega }(\zeta ,t)=\omega \left(\zeta \right)\omega \left(t\right).$ Now, Equation (29) turns into

$$\sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{a}_{ir}{b}_{js}+\alpha \sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{g}_{ir}{k}_{js}+\mu \sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{\overline{h}}_{ir}{k}_{js}={\widehat{f}}_{rs},$$

(30)

where

$${\widehat{f}}_{rs}={\left(\widehat{f}(\zeta ,t),U_r^{*}\left(\zeta \right)U_s^{*}\left(t\right)\right)}_{\overline{\omega }(\zeta ,t)},a_{ir}={\left({\mathcal{E}}_i^{*}\left(\zeta \right),U_r^{*}\left(\zeta \right)\right)}_{\omega \left(\zeta \right)},b_{j,s}={\left(U_j^{*}\left(t\right),U_s^{*}\left(t\right)\right)}_{\omega \left(t\right)},$$

$$g_{ir}={\left({\mathcal{E}}_i^{{*}^{″}}\left(\zeta \right),U_r^{*}\left(\zeta \right)\right)}_{\omega \left(\zeta \right)},{\overline{h}}_{ir}={\left({\mathcal{E}}_i^{{*}^{⁗}}\left(\zeta \right),U_r^{*}\left(\zeta \right)\right)}_{\omega \left(\zeta \right)},$$

and

$$k_{js}={\left({\int }_0^t{\int }_0^t{U}_j^{*}\left(t\right)dtdt,U_s^{*}\left(t\right)\right)}_{\omega \left(t\right)}.$$

Now, Equation (30) constitutes a system of algebraic equations of order ${(N+1)}^2$ that may be solved using the Gauss elimination procedure.

Theorem 2. 

The elements $a_{ir},b_{js},g_{ir},{\overline{h}}_{ir}$ and $k_{js}$ are given by the following:

$$\begin{array}{cc}& \left(a\right){\int }_0^1{\mathcal{E}}_i^{*}\left(\zeta \right)U_r^{*}\left(\zeta \right)\omega \left(\zeta \right)d\zeta =a_{ir}\hfill \\ & \left(b\right){\int }_0^1{D}^2{\mathcal{E}}_i^{*}\left(\zeta \right)U_r^{*}\left(\zeta \right)\omega \left(\zeta \right)d\zeta =g_{ir}\hfill \\ & \left(c\right){\int }_0^1{D}^4{\mathcal{E}}_i^{*}\left(\zeta \right)U_r^{*}\left(\zeta \right)\omega \left(\zeta \right)d\zeta ={\overline{h}}_{ir}\hfill \\ & \left(d\right){\int }_0^1{U}_j^{*}\left(t\right)U_s^{*}\left(t\right)\omega \left(t\right)dt=b_{j,s},\hfill \\ & \left(e\right){\int }_0^1\left({\int }_0^t{\int }_0^t{U}_j^{*}\left(t\right)dtdt\right)U_s^{*}\left(t\right)\omega \left(t\right)dt=k_{js},\hfill \end{array}$$

(31)

where

$$\begin{array}{cc}\hfill a_{ir}& ={(-1)}^{{\displaystyle \frac{i-r}{2}}}\pi \times \left\{\begin{array}{cc}{\displaystyle \frac{5+24\theta }{1024},}\hfill & \mathit{if}r=i=0,\hfill \\ {\displaystyle \frac{15+20i+10i^2+96\theta }{2048(3+4i+2i^2)},}\hfill & \mathit{if}r=i=1,\hfill \\ {\displaystyle \frac{3(3+4i+2i^2+16\theta )}{1024(3+4i+2i^2)},}\hfill & \mathit{if}r=i,\hfill \\ {\displaystyle \frac{15+20i+10i^2+48\theta }{2048(3+4i+2i^2)},}\hfill & \mathit{if}r=i+2\mathit{and}i=0,\hfill \\ {\displaystyle \frac{3+4i+2i^2+12\theta }{512(3+4i+2i^2)},}\hfill & \mathit{if}r=i+2,\hfill \\ {\displaystyle \frac{15+20i+10i^2+48\theta }{2048(3+4i+2i^2)},}\hfill & \mathit{if}r=i-2\mathit{and}i=2,\hfill \\ {\displaystyle \frac{3+4i+2i^2+12\theta }{512(3+4i+2i^2)},}\hfill & \mathit{if}r=i-2,\hfill \\ {\displaystyle \frac{1}{2048},}\hfill & \mathit{if}|r-i|=4,\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill g_{ir}& {\displaystyle =\frac{\pi (r+1)}{2i^2+4i+3}\times \left\{\begin{array}{cc}{\displaystyle \frac{(2i^2+4i+3)(r+2)}{128},}\hfill & \mathit{if}r-i=2,\hfill \\ {\displaystyle \frac{3\theta (r+2)}{8}+\frac{(2i^2+4i+3)(r+1)}{64}\left\{\begin{array}{cc}2,\hfill & \mathit{if}r=0,\hfill \\ 1,\hfill & \mathit{otherwise}.\hfill \end{array}\right.,}\hfill & \mathit{if}r=i,\hfill \\ {\displaystyle -\frac{3\theta }{4}+\frac{(2i^2+4i+3)}{128}\left\{\begin{array}{cc}0,\hfill & \mathit{if}r=0,\hfill \\ 1,\hfill & \mathit{otherwise}.\hfill \end{array}\right.,}\hfill & \mathit{if}r-i=-2,\hfill \\ {\displaystyle -\frac{3\theta }{4},}\hfill & \mathit{if}(i-r)\mathit{even},i>r,\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.}\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill {\overline{h}}_{ir}& =\pi \times \left\{\begin{array}{cc}{\displaystyle \frac{(i+1)(i+2)(i+3)(i+4)}{8},}\hfill & \mathit{if}i=r,\hfill \\ {\displaystyle -\frac{3(r+1)\left(\right(r-2\left)\right(r+4)-5i(i+2\left)\right)(-\theta (i-r\left)\right(i+r+2)+2i(i+2)+3)}{8\left(2i\right(i+2)+3)},}\hfill & \mathit{if}i>r,(i-r)\mathit{even},\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill k_{js}& {\displaystyle =\frac{\pi }{128}\times \left\{\begin{array}{cc}{\displaystyle -\frac{2}{j(j+2)},}\hfill & \mathit{if}j=s,\hfill \\ {\displaystyle \frac{1}{j(j+1)},}\hfill & \mathit{if}j-s=2,\hfill \\ {\displaystyle \frac{1}{(j+1)(j+2)},}\hfill & \mathit{if}s-j=2,\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.}\hfill \end{array}$$

(35)

and $b_{j,s}$ is given in (3).

Proof. 

The proof of Theorem 2 is based on Formulas (8), (15) and (11) after some lengthy manipulations.

• First, to compute $a_{i,r}$, we write ${\mathcal{E}}_i^{*}\left(\zeta \right)$ in the following form:

  $${\mathcal{E}}_i^{*}\left(\zeta \right)=\zeta (1-\zeta )(A_{i,\theta }+\zeta -{\zeta }^2)U_i^{*}\left(\zeta \right),$$

  (36)

  with

  $$A_{i,\theta }={\displaystyle \frac{3\theta }{2i^2+4i+3}}.$$

  Therefore, we have

  $$a_{i,r}={\int }_0^1\left({\zeta }^2-2{\zeta }^3+{\zeta }^4+\zeta A_{i,\theta }-{\zeta }^2{A}_{i,\theta }\right)U_i^{*}\left(\zeta \right)U_r^{*}\left(\zeta \right)\sqrt{\zeta -{\zeta }^2}d\zeta .$$

  Based on the moment Formula (8) together with the orthogonality relation, it is not difficult to find the matrix form of $a_{i,r}$ in (32).
• To find the elements $g_{i,r}$ we note from (36) that $D^2{\mathcal{E}}_i^{*}\left(\zeta \right)$ takes the following form:

  $$\begin{array}{cc}\hfill D^2{\mathcal{E}}_i^{*}\left(\zeta \right)=& \zeta (1-\zeta )\left(A_{i,\theta }+\zeta -{\zeta }^2\right)D^2{U}_i^{*}\left(\zeta \right)+2\left(2\zeta -6{\zeta }^2+4{\zeta }^3+A_{i,\theta }-2\zeta A_{i,\theta }\right)D{U}_i^{*}\left(\zeta \right)\hfill \\ & +\left(2-12\zeta +12{\zeta }^2-2A_{i,\theta }\right)U_i^{*}\left(\zeta \right).\hfill \end{array}$$

  Formula (11) along with (8) yields, after some tedious computations, the elements of the matrix in (33). The elements ${\overline{h}}_{i,r}$ given in (34) can be obtained following similar steps. The elements $k_{j,s}$ can be obtained using the repeated integrals Formula (10) (for q = 2) along with the orthogonality property.
• Finally, the elements $b_{j,s}$ can be directly computed from the orthogonality relation. □

4. An Extension to Fractional Case

In this section, we consider the following time-fractional fourth-order partial differential equations (TFFPDE):

$$D_t^{\alpha }\xi (\zeta ,t)+\alpha {\partial }_{\zeta \zeta }\xi (\zeta ,t)+\mu {\partial }_{\zeta \zeta \zeta \zeta }\xi (\zeta ,t)=f(\zeta ,t),1<\alpha <2,$$

(37)

subject to the initial and boundary conditions (20) and (21), where $D_t^{\alpha }$ is the Caputo’s fractional derivative defined as follows ([34]):

$${\displaystyle D_z^{\alpha }Y\left(z\right)=\frac{1}{\mathsf{\Gamma }(r-\alpha )}{\int }_0^z{(z-t)}^{r-\alpha -1}{Y}^{\left(r\right)}\left(t\right)dt,\alpha >0,z>0,}$$

(38)

$$r-1<\alpha \le r,r\in {\mathbb{Z}}^{+}.$$

The residual $\overline{\mathcal{R}}(\zeta ,t)$ of Equation (37) has the following form:

$$\overline{\mathcal{R}}(\zeta ,t)=D_t^{\alpha }{\xi }^N(\zeta ,t)+\alpha {\partial }_{\zeta \zeta }{\xi }^N(\zeta ,t)+\mu {\partial }_{\zeta \zeta \zeta \zeta }{\xi }^N(\zeta ,t)-f(\zeta ,t).$$

(39)

The application of the PGM implies that

$$\begin{array}{cc}& {\left(\overline{\mathcal{R}}(\zeta ,t),U_r^{*}\left(\zeta \right)U_s^{*}\left(t\right)\right)}_{\overline{\omega }(\zeta ,t)}=0,0\le r,s\le N,\hfill \end{array}$$

(40)

which can be rewritten as follows:

$$\sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{a}_{ir}{\lambda }_{js}+\alpha \sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{g}_{ir}{b}_{js}+\mu \sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{\overline{h}}_{ir}{b}_{js}=f_{rs},0\le r,s\le N-1,$$

(41)

where $a_{ir},b_{js},g_{ir},{\overline{h}}_{ir}$ are those defined in Theorem 2, and

$$f_{rs}={\left(f(\zeta ,t),U_r^{*}\left(\zeta \right)U_s^{*}\left(t\right)\right)}_{\overline{\omega }(\zeta ,t)},{\lambda }_{js}={\left(D_t^{\alpha }{U}_j^{*}\left(t\right),U_s^{*}\left(t\right)\right)}_{\omega \left(t\right)}.$$

In addition, the conditions in (20) lead to the following equations:

$$\begin{array}{cc}\hfill & \sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{a}_{ir}{U}_j^{*}\left(0\right)={(p_1\left(\zeta \right),U_r^{*}\left(\zeta \right))}_{\omega \left(t\right)},0\le r\le N-1,\hfill \\ & \sum _{i=0}^N\sum _{j=0}^N{c}_{ij}{a}_{ir}{U^{*}}_j^{\prime }\left(0\right)={(p_2\left(\zeta \right),U_r^{*}\left(\zeta \right))}_{\omega \left(t\right)},0\le r\le N.\hfill \end{array}$$

(42)

Now, Equations (41) and (42) yield a linear system of algebraic equations of dimension ${(N+1)}^2$ in the unknown expansion coefficients $c_{ij}$, which can be solved using the Gaussian elimination procedure.

Theorem 3. 

The elements ${\lambda }_{js}$ are given by the following:

$${\int }_0^1{D}_t^{\alpha }{U}_j^{*}\left(t\right)U_s^{*}\left(t\right)\omega \left(t\right)dt={\lambda }_{js},$$

(43)

where

$$\begin{array}{cc}\hfill {\lambda }_{js}=& \sum _{k=2}^j{\displaystyle \frac{\pi 4^{k-1}(s+1)k!{\tau }^{2-\alpha }{(-1)}^{j+k+s}(j+k+1)!\mathsf{\Gamma }\left(k-\alpha +\frac{3}{2}\right)}{\mathsf{\Gamma }(2k+2)(j-k)!\mathsf{\Gamma }(k-\alpha +1)}}\times \hfill \\ & {}_3\tilde{F}_2\left.\left(\begin{array}{c}-s,s+2,-\alpha +k+{\displaystyle \frac{3}{2}}\\ \\ {\displaystyle \frac{3}{2}},-\alpha +k+3\end{array}\right|1\right),\hfill \end{array}$$

(44)

where ${}_3\tilde{F}_2\left(z\right)$ is the regularized hypergeometric function.

Proof. 

The application of Caputo’s fractional derivative (38) enables us to write

$$D_t^{\alpha }{t}^k={\displaystyle \frac{k!}{\mathsf{\Gamma }(k+1-\alpha )}}{t}^{k-\alpha },\mathrm{if}k\in {\mathbb{Z}}^{\ge 0}andk\ge \lceil \alpha \rceil .$$

(45)

Using the previous property along with relation (1), one can write

$$\begin{array}{cc}\hfill {\lambda }_{js}=& {\int }_0^1\omega \left(t\right)\left[D_t^{\alpha }{U}_j^{*}\left(t\right)\right]U_s^{*}\left(t\right)dt\hfill \\ & =\sum _{k=2}^j{\displaystyle \frac{2^{2k}k!{(-1)}^{j+k}(j+k+1)!}{(2k+1)!(j-k)!\mathsf{\Gamma }(k-\alpha +1)}}{\int }_0^1{U}_s^{*}\left(t\right)t^{k-\alpha }\omega \left(t\right)dt\hfill \\ & =\sum _{k=2}^j{\displaystyle \frac{2^{2k}k!{(-1)}^{j+k}(j+k+1)!}{(2k+1)!(j-k)!(k-\alpha )!}}\sum _{n=0}^s{\displaystyle \frac{\sqrt{\pi }{2}^{2n-1}{(-1)}^{n+s}(n+s+1)!\mathsf{\Gamma }\left(k+n-\alpha +\frac{3}{2}\right)}{(2n+1)!(s-n)!\mathsf{\Gamma }(k+n-\alpha +3)}}.\hfill \end{array}$$

(46)

Inserting the following identity [41] in the previous equation can obtain the desired result:

$$\begin{array}{cc}& \sum _{n=0}^s{\displaystyle \frac{\sqrt{\pi }{2}^{2n-1}{\tau }^{2-\alpha }{(-1)}^{n+s}(n+s+1)!\mathsf{\Gamma }\left(k+n-\alpha +\frac{3}{2}\right)}{(2n+1)!(s-n)!\mathsf{\Gamma }(k+n-\alpha +3)}}\hfill \\ & ={\displaystyle \frac{1}{4}}\pi {(-1)}^s(s+1){\tau }^{-\alpha +2}\mathsf{\Gamma }\left(k-\alpha +{\displaystyle \frac{3}{2}}\right){}_3\tilde{F}_2\left.\left(\begin{array}{c}-s,s+2,-\alpha +k+{\displaystyle \frac{3}{2}}\\ {\displaystyle \frac{3}{2}},-\alpha +k+3\end{array}\right|1\right).\hfill \end{array}$$

(47)

This completes the proof of this theorem. □

5. Error Analysis

This section analyzes the error analysis of the proposed approximate expansion.

Theorem 4 

([36]). Consider the function $u\left(\zeta \right)\in C^n[0,1]$, where $n>3,$ is expanded as

$$u\left(\zeta \right)=\sum _{i=0}^{\infty }{\widehat{u}}_i{U}_i^{*}\left(\zeta \right).$$

(48)

Then, we have the following estimates:

$$\left|{\widehat{u}}_i\right|\lesssim {\displaystyle \frac{1}{i^n}},\forall i>n,$$

(49)

where $A\lesssim B$ implies the existence of a generic constant c independent of N and any function with $A\le nB.$

Theorem 5. 

Consider the function $v(\zeta ,t)=g_1\left(\zeta \right)g_2\left(t\right)\in C^n\left(\mathsf{\Omega }\right)$, $\mathsf{\Omega }=(0,1)\times (0,1),$ such that $g_1^{\left(n\right)}\left(\zeta \right)$ and $g_2^{\left(n\right)}\left(t\right)$ are bound for $n>3$, and $v(\zeta ,t)$ is expanded as

$$v(\zeta ,t)=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{c}_{ij}{U}_i^{*}\left(\zeta \right)U_j^{*}\left(t\right).$$

(50)

The series in (50) converges uniformly to $v(\zeta ,t)$. Moreover, the following inequality holds:

$$\left|c_{ij}\right|\lesssim {\displaystyle \frac{1}{i^n{j}^n}},\forall i,j>n.$$

(51)

Proof. 

The expansion in (5), together with the orthogonality property of $U_i^{*}\left(\zeta \right)$, yields

$$c_{ij}={\displaystyle \frac{64}{{\pi }^2}}{\int }_0^1{\int }_0^{1}v(\zeta ,t)U_i^{*}\left(\zeta \right)U_j^{*}\left(t\right)\overline{\omega }(\zeta ,t)d\zeta dt.$$

(52)

The Theorem’s assumption enables one to express $c_{ij}$ as follows:

$$c_{ij}={\displaystyle \frac{64}{{\pi }^2}}\left({\int }_0^1\omega \left(\zeta \right)g_1\left(\zeta \right)U_i^{*}\left(\zeta \right)d\zeta \right)\left({\int }_0^1\omega \left(t\right)g_2\left(t\right)U_j^{*}\left(t\right)dt\right).$$

(53)

It is possible to achieve the desired result using similar steps as in Theorem 4. □

Corollary 2. 

Consider the function $\xi (\zeta ,t)=\zeta (1-\zeta )\left({\displaystyle \frac{3\theta }{2i^2+4i+3}}-{\zeta }^2+\zeta \right)g_1\left(\zeta \right)g_2\left(t\right)\in C^q\left(\mathsf{\Omega }\right)$, such that $g_1^{\left(n\right)}\left(\zeta \right)$ and $g_2^{\left(n\right)}\left(t\right)$ are bound for $n>3$, and $\xi (\zeta ,t)$ is expanded as

$$\xi (\zeta ,t)=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{c}_{ij}{\mathcal{E}}_i^{*}\left(\zeta \right)U_j^{*}\left(t\right).$$

(54)

The above series is uniformly convergent to $\xi (\zeta ,t)$. Moreover, the expansion coefficients in (54) satisfy the following:

$$\left|c_{ij}\right|\lesssim {\displaystyle \frac{1}{i^n{j}^n}},\forall i,j>n.$$

(55)

Proof. 

The hypothesis of this corollary enables us to write

$$\begin{array}{cc}\hfill \xi (\zeta ,t)& =\zeta (1-\zeta )\left({\displaystyle \frac{3\theta }{2i^2+4i+3}}-{\zeta }^2+\zeta \right)g_1\left(\zeta \right)g_2\left(t\right)\hfill \\ & {\displaystyle =\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{c}_{ij}{\mathcal{E}}_i^{*}\left(\zeta \right)U_j^{*}\left(t\right)}\hfill \\ & =\zeta (1-\zeta )\left({\displaystyle \frac{3\theta }{2i^2+4i+3}}-{\zeta }^2+\zeta \right)\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{c}_{ij}{U}_i^{*}\left(\zeta \right)U_j^{*}\left(t\right).\hfill \end{array}$$

(56)

In virtue of Theorem 5, the following inequality can be obtained:

$$\left|c_{ij}\right|\lesssim {\displaystyle \frac{1}{i^n{j}^n}},\forall i,j>n.$$

This ends the proof. □

Theorem 6. 

The following truncation error estimate is valid:

$$|\xi (\zeta ,t)-{\xi }^N(\zeta ,t)|\lesssim {\displaystyle \frac{1}{N^{n-2}}}.$$

(57)

Proof. 

It is easy to show that this theorem is true by following the same steps as in [36] and using two inequalities:

$${\mathcal{E}}_i^{*}\left(\zeta \right)<{\displaystyle \frac{(4\theta +1)(i+1)}{16}},\mathrm{and}{U}_j^{*}\left(t\right)\le j+1.\square$$

6. Computational Complexity

In numerical linear algebra, the computational expense of computing a matrix’s inverse significantly influences the viability and effectiveness of different algorithms. For pentadiagonal matrices, distinguished by their sparse nature featuring only five nonzero diagonals, the computational workload is notably diminished compared to denser matrices. As highlighted in “Matrix Computations” by Gene H. Golub and Charles F. Van Loan [42], sparse matrices, such as pentadiagonal matrices, offer significant computational advantages due to their sparsity. Specialized algorithms tailored for solving systems involving pentadiagonal matrices, while not as well-known as those for tridiagonal systems, exhibit computational complexities on the order of $O\left(n\right)$, where n represents the size of the matrix. This contrasts sharply with the $O\left(n^3\right)$ complexity typically associated with dense matrix inversions. Thus, utilizing efficient algorithms tailored for pentadiagonal matrices underscores a marked reduction in computational cost, making them a preferred choice for various numerical computations in engineering, physics, and other scientific domains.

As a direct conclusion from the system of Equation (30), we ended up with the following comment on the computational complexity of the method. The efficient structure of the system of algebraic equations derived from the Euler–Bernoulli beam problem using the Petrov–Galerkin approach is notable. The system becomes a combination of tridiagonal, pentadiagonal, and diagonal matrices through temporal and spatial discretization. Interestingly, this combination results in a final pentadiagonal matrix that captures the essence of the situation. With the help of the Thomas method designed specifically for pentadiagonal systems, the inversion procedure exhibits a computational complexity of $O(nlogn)$, which is significantly less than that of denser matrices. This tactical approach guarantees both numerical stability and efficient solution procedures, making it especially appropriate for solving complex structural dynamics in engineering and related fields.

For example, the matrices $a_{ir},g_{ir},{\overline{h}}_{i,r},b_{j,s}$ and $k_{j,s}$ take the following forms for $N=6$:

$$a_{ir}=\left(\begin{array}{ccccccc}{\displaystyle \frac{\pi (24\theta +5)}{1024}}& 0& -{\displaystyle \frac{\pi (16\theta +5)}{2048}}& 0& {\displaystyle \frac{\pi }{2048}}& 0& 0\\ 0& {\displaystyle \frac{\pi (32\theta +15)}{6144}}& 0& -{\displaystyle \frac{\pi (4\theta +3)}{1536}}& 0& {\displaystyle \frac{\pi }{2048}}& 0\\ -{\displaystyle \frac{\pi (48\theta +95)}{38912}}& 0& {\displaystyle \frac{3\pi (16\theta +19)}{19456}}& 0& -{\displaystyle \frac{\pi (12\theta +19)}{9728}}& 0& {\displaystyle \frac{\pi }{2048}}\\ 0& -{\displaystyle \frac{\pi (4\theta +11)}{5632}}& 0& {\displaystyle \frac{\pi (16\theta +33)}{11264}}& 0& -{\displaystyle \frac{\pi (4\theta +11)}{5632}}& 0\\ {\displaystyle \frac{\pi }{2048}}& 0& -{\displaystyle \frac{\pi (4\theta +17)}{8704}}& 0& {\displaystyle \frac{\pi (16\theta +51)}{17408}}& 0& -{\displaystyle \frac{\pi (4\theta +17)}{8704}}\\ 0& {\displaystyle \frac{\pi }{2048}}& 0& -{\displaystyle \frac{\pi (12\theta +73)}{37376}}& 0& {\displaystyle \frac{3\pi (16\theta +73)}{74752}}& 0\\ 0& 0& {\displaystyle \frac{\pi }{2048}}& 0& -{\displaystyle \frac{\pi (4\theta +33)}{16896}}& 0& {\displaystyle \frac{\pi (16\theta +99)}{33792}}\end{array}\right),$$

(58)

$$g_{ir}=\left(\begin{array}{ccccccc}-{\displaystyle \frac{1}{32}}\pi (8\theta +1)& 0& {\displaystyle \frac{3\pi }{32}}& 0& 0& 0& 0\\ 0& -{\displaystyle \frac{1}{16}}\pi (4\theta +1)& 0& {\displaystyle \frac{5\pi }{32}}& 0& 0& 0\\ -{\displaystyle \frac{3\pi \theta }{76}}& 0& -{\displaystyle \frac{9\pi (32\theta +19)}{1216}}& 0& {\displaystyle \frac{15\pi }{64}}& 0& 0\\ 0& \pi \left({\displaystyle \frac{1}{64}}-{\displaystyle \frac{\theta }{22}}\right)& 0& -{\displaystyle \frac{1}{44}}\pi (10\theta +11)& 0& {\displaystyle \frac{21\pi }{64}}& 0\\ -{\displaystyle \frac{\pi \theta }{68}}& 0& \pi \left({\displaystyle \frac{3}{64}}-{\displaystyle \frac{3\theta }{68}}\right)& 0& -{\displaystyle \frac{5\pi (48\theta +85)}{1088}}& 0& {\displaystyle \frac{7\pi }{16}}\\ 0& -{\displaystyle \frac{3\pi \theta }{146}}& 0& \pi \left({\displaystyle \frac{3}{32}}-{\displaystyle \frac{3\theta }{73}}\right)& 0& -{\displaystyle \frac{9\pi (28\theta +73)}{1168}}& 0\\ -{\displaystyle \frac{\pi \theta }{132}}& 0& -{\displaystyle \frac{\pi \theta }{44}}& 0& {\displaystyle \frac{5\pi (33-8\theta )}{1056}}& 0& -{\displaystyle \frac{7\pi (64\theta +231)}{2112}},\end{array}\right),$$

(59)

$${\overline{h}}_{i,r}=\left(\begin{array}{ccccccc}3\pi & 0& 0& 0& 0& 0& 0\\ 0& 15\pi & 0& 0& 0& 0& 0\\ {\displaystyle \frac{18}{19}}\pi (19-8\theta )& 0& 45\pi & 0& 0& 0& 0\\ 0& {\displaystyle \frac{20}{11}}\pi (33-12\theta )& 0& 105\pi & 0& 0& 0\\ {\displaystyle \frac{16}{17}}\pi (51-24\theta )& 0& {\displaystyle \frac{45}{17}}\pi (51-16\theta )& 0& 210\pi & 0& 0\\ 0& {\displaystyle \frac{135}{73}}\pi (73-32\theta )& 0& {\displaystyle \frac{252}{73}}\pi (73-20\theta )& 0& 378\pi & 0\\ {\displaystyle \frac{31}{33}}\pi (99-48\theta )& 0& {\displaystyle \frac{30}{11}}\pi (99-40\theta )& 0& {\displaystyle \frac{140}{33}}\pi (99-24\theta )& 0& 630\pi \end{array}\right),$$

(60)

$$b_{j,s}=\left(\begin{array}{ccccccc}{\displaystyle \frac{\pi }{8}}& 0& 0& 0& 0& 0& 0\\ 0& {\displaystyle \frac{\pi }{8}}& 0& 0& 0& 0& 0\\ 0& 0& {\displaystyle \frac{\pi }{8}}& 0& 0& 0& 0\\ 0& 0& 0& {\displaystyle \frac{\pi }{8}}& 0& 0& 0\\ 0& 0& 0& 0& {\displaystyle \frac{\pi }{8}}& 0& 0\\ 0& 0& 0& 0& 0& {\displaystyle \frac{\pi }{8}}& 0\\ 0& 0& 0& 0& 0& 0& {\displaystyle \frac{\pi }{8}}\end{array}\right),$$

(61)

$$k_{j,s}=\left(\begin{array}{ccccccc}-{\displaystyle \frac{\pi }{960}}& 0& {\displaystyle \frac{\pi }{2560}}& 0& 0& 0& 0\\ 0& -{\displaystyle \frac{\pi }{1536}}& 0& {\displaystyle \frac{\pi }{3840}}& 0& 0& 0\\ {\displaystyle \frac{\pi }{3840}}& 0& -{\displaystyle \frac{\pi }{2240}}& 0& {\displaystyle \frac{\pi }{5376}}& 0& 0\\ 0& {\displaystyle \frac{\pi }{5376}}& 0& -{\displaystyle \frac{\pi }{3072}}& 0& {\displaystyle \frac{\pi }{7168}}& 0\\ 0& 0& {\displaystyle \frac{\pi }{7168}}& 0& -{\displaystyle \frac{\pi }{4032}}& 0& {\displaystyle \frac{\pi }{9216}}\\ 0& 0& 0& {\displaystyle \frac{\pi }{9216}}& 0& -{\displaystyle \frac{\pi }{5120}}& 0\\ 0& 0& 0& 0& {\displaystyle \frac{\pi }{11520}}& 0& -{\displaystyle \frac{\pi }{6336}}\end{array}\right).$$

(62)

7. Some Illustrative Examples

This section presents some illustrative examples to show the applicability and efficiency of our proposed algorithm.

Test Problem 1. 

Consider the following equation,

$${\partial }_{tt}\xi (x,t)+{\partial }_{xx}\xi (x,t)+{\partial }_{xxxx}\xi (x,t)=f(x,t),(x,t)\in (0,1)\times (0,1),$$

(63)

governed by the below conditions:

$$\begin{array}{cc}& \xi (x,0)={\partial }_t\xi (x,0)=0,0<x<1,\hfill \\ & {\left.\xi (x,t)\right|}_{x=0,1}={\left.{\partial }_{xx}\xi (x,t)\right|}_{x=0,1}=0,0<t<1,\hfill \end{array}$$

(64)

where $f(x,t)$ is chosen such that the exact solution is $\xi (x,t)=t^{2}sin\left(\pi x\right).$

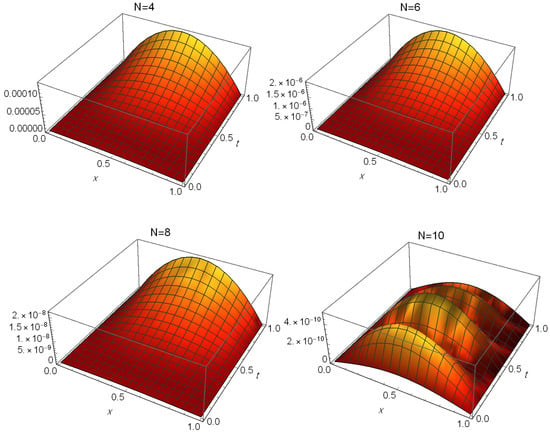
The precision of the suggested approach is demonstrated in Figure 1, which shows the distribution of absolute errors (AEs) throughout the domain at different values of N. We see in this figure that the proposed method is accurate for small choices of N.

Table 1. The AEs of Test Problem 1 at $N=10$.

x	$\mathit{t}=0.1$	$\mathit{t}=0.4$	$\mathit{t}=0.6$	$\mathit{t}=0.8$
0.1	$1.368\times {10}^{-10}$	$1.18505\times {10}^{-10}$	$8.09423\times {10}^{-11}$	$1.08948\times {10}^{-10}$
0.2	$2.60273\times {10}^{-10}$	$2.24334\times {10}^{-10}$	$1.51527\times {10}^{-10}$	$2.11563\times {10}^{-10}$
0.3	$3.58277\times {10}^{-10}$	$3.07781\times {10}^{-10}$	$2.06324\times {10}^{-10}$	$2.95169\times {10}^{-10}$
0.4	$4.21189\times {10}^{-10}$	$3.61156\times {10}^{-10}$	$2.41043\times {10}^{-10}$	$3.49669\times {10}^{-10}$
0.5	$4.42839\times {10}^{-10}$	$3.79519\times {10}^{-10}$	$2.52935\times {10}^{-10}$	$3.68573\times {10}^{-10}$
0.6	$4.21115\times {10}^{-10}$	$3.61168\times {10}^{-10}$	$2.41053\times {10}^{-10}$	$3.49648\times {10}^{-10}$
0.7	$3.58158\times {10}^{-10}$	$3.07802\times {10}^{-10}$	$2.06341\times {10}^{-10}$	$2.95135\times {10}^{-10}$
0.8	$2.60157\times {10}^{-10}$	$2.24356\times {10}^{-10}$	$1.51546\times {10}^{-11}$	$2.11528\times {10}^{-10}$
0.9	$1.36732\times {10}^{-10}$	$1.18521\times {10}^{-10}$	$8.09551\times {10}^{-11}$	$1.08926\times {10}^{-10}$

displays the AEs at different values of t when $N=10$. In addition,

Table 2. The MAEs of Test Problem 1.

	$\mathit{N}=4$	$\mathit{N}=6$	$\mathit{N}=8$	$\mathit{N}=10$
MAE	$1.00843\times {10}^{-6}$	$1.55871\times {10}^{-8}$	$1.62508\times {10}^{-10}$	$1.368\times {10}^{-10}$
CPU time	8.281	57.689	116.655	258.5

shows the maximum absolute errors (MAEs) and CPU time used. These results demonstrate the advantages of our method for obtaining accurate solutions for small values of N.

Test Problem 2. 

Consider the following equation,

$${\partial }_{tt}\xi (x,t)+{\partial }_{xxxx}\xi (x,t)=f(x,t),(x,t)\in (0,1)\times (0,1),$$

(65)

governed by the below conditions:

$$\begin{array}{cc}& \xi (x,0)=sin\left(\pi x\right),{\partial }_t\xi (x,0)=0,0<x<1,\hfill \\ & {\left.\xi (x,t)\right|}_{x=0,1}={\left.{\partial }_{xx}\xi (x,t)\right|}_{x=0,1}=0,0<t<1,\hfill \end{array}$$

(66)

where $f(x,t)$ is chosen such that the exact solution is $\xi (x,t)=cos\left(t\right)sin\left(\pi x\right).$

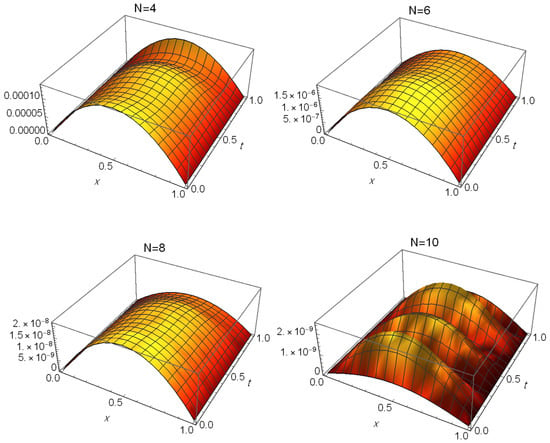
The AEs obtained via the suggested method at different values of N are shown in Figure 2, indicating that it is effective in providing a highly precise approximation of the exact solution.

Table 3. Comparison of MAEs of Test Problem 2.

Our Method	Method in [43]	Method in [44]	Method in [45]	Method in [46]	Method in [47]	Method in [48]
$7.35149\times {10}^{-10}$	$9.8\times {10}^{-7}$	$4.9\times {10}^{-7}$	$1.0\times {10}^{-6}$	$1.5\times {10}^{-7}$	$4.9\times {10}^{-8}$	$1.4\times {10}^{-7}$

gives a comparison of the MAEs between our method at $N=10$ and the methods in different literature.

Table 4. The MAEs of Test Problem 2.

	$\mathit{N}=4$	$\mathit{N}=6$	$\mathit{N}=8$	$\mathit{N}=10$
MAE	$1.3529\times {10}^{-4}$	$1.94993\times {10}^{-6}$	$2.10315\times {10}^{-8}$	$7.35149\times {10}^{-10}$
CPU time	8.235	31.25	62.202	141.203

also shows the MAEs and CPU time used. We see in these tables that the results are accurate for small choices of N. Also, this comparison reveals the superior performance of our technique over methods in [43,44,45,46,47,48].

Test Problem 3. 

Consider the following equation:

$${\partial }_{tt}\xi (x,t)+{\partial }_{xxxx}\xi (x,t)=f(x,t),(x,t)\in (0,1)\times (0,1),$$

(67)

subject to the following initial and boundary conditions,

$$\begin{array}{cc}& \xi (x,0)=0,{\partial }_t\xi (x,0)=0,0<x<1,\hfill \\ & {\left.\xi (x,t)\right|}_{x=0,1}={\left.{\partial }_x\xi (x,t)\right|}_{x=0,1}=0,0<t<1,\hfill \end{array}$$

(68)

where $f(x,t)$ is chosen such that the exact solution the exact solution of this problem is$\xi (x,t)=t^{5/2}{e}^{-t}{\left(x(1-x)\right)}^{7/2}.$

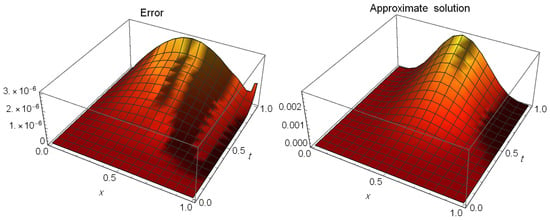
The approximate solution (right) and AEs (left) at $N=16$ are shown in Figure 3. This figure verifies that the suggested approach reduces errors consistently throughout the domain and shows good agreement between the approximate solution and the exact one. The MAEs obtained using the suggested method at different values of N when $0<t<1$ are shown in

Table 5. The MAEs of Test Problem 3 when $0<t<1$.

x	$\mathit{N}=10$	$\mathit{N}=12$	$\mathit{N}=14$	$\mathit{N}=16$
0.1	$3.03327\times {10}^{-6}$	$1.9058\times {10}^{-6}$	$1.27838\times {10}^{-6}$	$9.16472\times {10}^{-7}$
0.2	$5.88801\times {10}^{-6}$	$3.67112\times {10}^{-6}$	$2.44756\times {10}^{-6}$	$1.74034\times {10}^{-6}$
0.3	$8.28164\times {10}^{-6}$	$5.12965\times {10}^{-6}$	$3.40535\times {10}^{-6}$	$2.40799\times {10}^{-6}$
0.4	$9.9287\times {10}^{-6}$	$6.12247\times {10}^{-6}$	$4.05339\times {10}^{-6}$	$2.8565\times {10}^{-6}$
0.5	$1.05207\times {10}^{-5}$	$6.47742\times {10}^{-6}$	$4.28445\times {10}^{-6}$	$3.01428\times {10}^{-6}$
0.6	$9.9287\times {10}^{-6}$	$6.12244\times {10}^{-6}$	$4.05354\times {10}^{-6}$	$2.8512\times {10}^{-6}$
0.7	$8.28164\times {10}^{-6}$	$5.12959\times {10}^{-6}$	$3.40563\times {10}^{-6}$	$2.39142\times {10}^{-6}$
0.8	$5.88801\times {10}^{-6}$	$3.67104\times {10}^{-6}$	$2.44786\times {10}^{-6}$	$1.79274\times {10}^{-6}$
0.9	$3.03327\times {10}^{-6}$	$1.90573\times {10}^{-6}$	$1.27854\times {10}^{-6}$	$8.46683\times {10}^{-6}$

, indicating that it is effective in providing a highly precise approximation of the exact solution. These results indicate the advantage of our method for obtaining the AEs and MAEs at small values of $N.$

Extension to the Fractional Case

In this subsection, we demonstrate how the methodologies proposed in this paper can be extended to address the Euler–Bernoulli beam differential problem in the context of fractional-order temporal derivatives.

Test Problem 4. 

Consider the following equation,

$$D_t^{\alpha }\xi (x,t)+{\partial }_{xx}\xi (x,t)+{\partial }_{xxxx}\xi (x,t)=f(x,t),$$

(69)

governed by the below conditions:

$$\begin{array}{cc}& \xi (x,0)={\partial }_t\xi (x,0)=0,0<x<1,\hfill \\ & {\left.\xi (x,t)\right|}_{x=0,1}={\left.{\partial }_{xx}\xi (x,t)\right|}_{x=0,1}=0,0<t<1,\hfill \end{array}$$

(70)

where $f(x,t)$ is chosen such that the exact solution is $\xi (x,t)=t^{4}sin\left(\pi x\right).$

Table 6. The AEs of Test Problem 4 at $\alpha =1.5$.

x	$\mathit{t}=0.2$	$\mathit{t}=0.5$	$\mathit{t}=0.8$
0.1	$1.27149\times {10}^{-7}$	$1.39299\times {10}^{-7}$	$9.37741\times {10}^{-6}$
0.2	$2.38797\times {10}^{-7}$	$6.245\times {10}^{-8}$	$1.9771\times {10}^{-5}$
0.3	$3.26526\times {10}^{-7}$	$1.84643\times {10}^{-7}$	$3.03553\times {10}^{-5}$
0.4	$3.83385\times {10}^{-7}$	$5.49473\times {10}^{-7}$	$4.01641\times {10}^{-5}$
0.5	$4.04875\times {10}^{-7}$	$9.54307\times {10}^{-7}$	$4.79327\times {10}^{-5}$
0.6	$3.89306\times {10}^{-7}$	$1.29387\times {10}^{-6}$	$5.20707\times {10}^{-5}$
0.7	$3.38097\times {10}^{-7}$	$1.42315\times {10}^{-6}$	$5.05786\times {10}^{-5}$
0.8	$2.55201\times {10}^{-7}$	$1.17327\times {10}^{-6}$	$4.1195\times {10}^{-5}$
0.9	$1.42578\times {10}^{-7}$	$5.62259\times {10}^{-7}$	$2.31558\times {10}^{-5}$

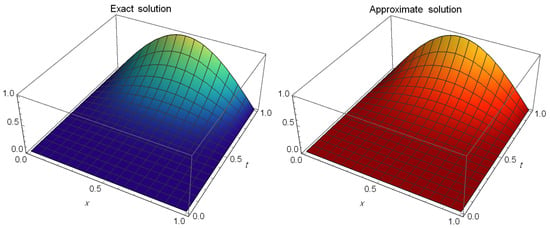
displays the AEs at different values of t, $N=5$, and $\alpha =1.5.$ 

Table 7. The AEs of Test Problem 4 at $\alpha =1.7$.

x	$\mathit{t}=0.3$	$\mathit{t}=0.6$	$\mathit{t}=0.9$
0.1	$2.02443\times {10}^{-8}$	$2.27676\times {10}^{-6}$	$2.24042\times {10}^{-6}$
0.2	$2.48855\times {10}^{-8}$	$4.17195\times {10}^{-6}$	$4.21335\times {10}^{-5}$
0.3	$2.7778\times {10}^{-8}$	$5.77414\times {10}^{-6}$	$5.88819\times {10}^{-5}$
0.4	$3.85244\times {10}^{-8}$	$7.11046\times {10}^{-6}$	$7.20788\times {10}^{-5}$
0.5	$6.24176\times {10}^{-8}$	$8.14662\times {10}^{-6}$	$8.09045\times {10}^{-5}$
0.6	$9.8603\times {10}^{-8}$	$8.76068\times {10}^{-6}$	$4.1739\times {10}^{-5}$
0.7	$1.39636\times {10}^{-7}$	$8.74139\times {10}^{-6}$	$8.03384\times {10}^{-5}$
0.8	$1.68818\times {10}^{-7}$	$7.75602\times {10}^{-6}$	$6.73457\times {10}^{-5}$
0.9	$1.41928\times {10}^{-7}$	$5.09533\times {10}^{-6}$	$4.15315\times {10}^{-5}$

also displays the AEs at different values of t at $N=5$ and $\alpha =1.7.$ These tables indicate that the presented method is effective in providing a highly precise approximation of the exact solution. Figure 4 shows the exact solution (left) and the approximate solution (right) at $N=5$ and $\alpha =1.9.$

8. Conclusions

The current study employed second-kind Chebyshev polynomials in conjunction with the Petrov–Galerkin method to handle the important Euler–Bernoulli beam problem. The analysis of the proposed numerical algorithm was based on solving the corresponding integral equation to the investigated problem and, after that, using a closed form of some specific integrals involving combinations of Chebyshev polynomials. The advantage of this approach is that it simultaneously treats the pinned–pinned and clamped–clamped boundary conditions, which were both successfully handled. We reduced the computational method by deriving a set of algebraic equations that can be numerically treated. Experimental results showed that the approach was accurate and applicable. As an expected future work, we aim to employ the developed theoretical results in this paper along with suitable spectral methods to treat some other problems with variable coefficients or external forces.