Hermite–Hadamard-Type Inequalities for Harmonically Convex Functions via Proportional Caputo-Hybrid Operators with Applications
Abstract
1. Introduction
2. Preliminaries
- (1)
- Beta function:
- (2)
- Hypergeometric function:
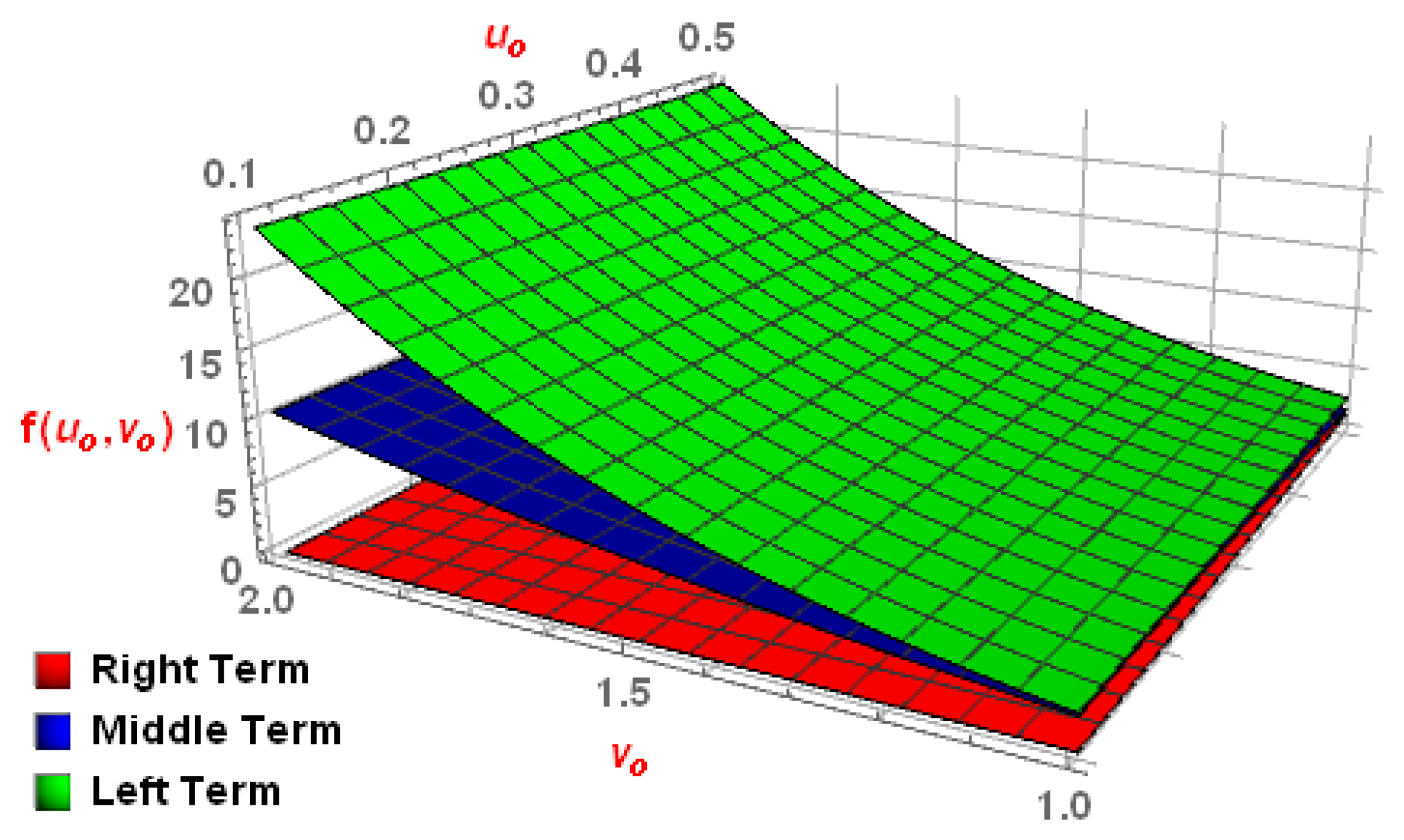
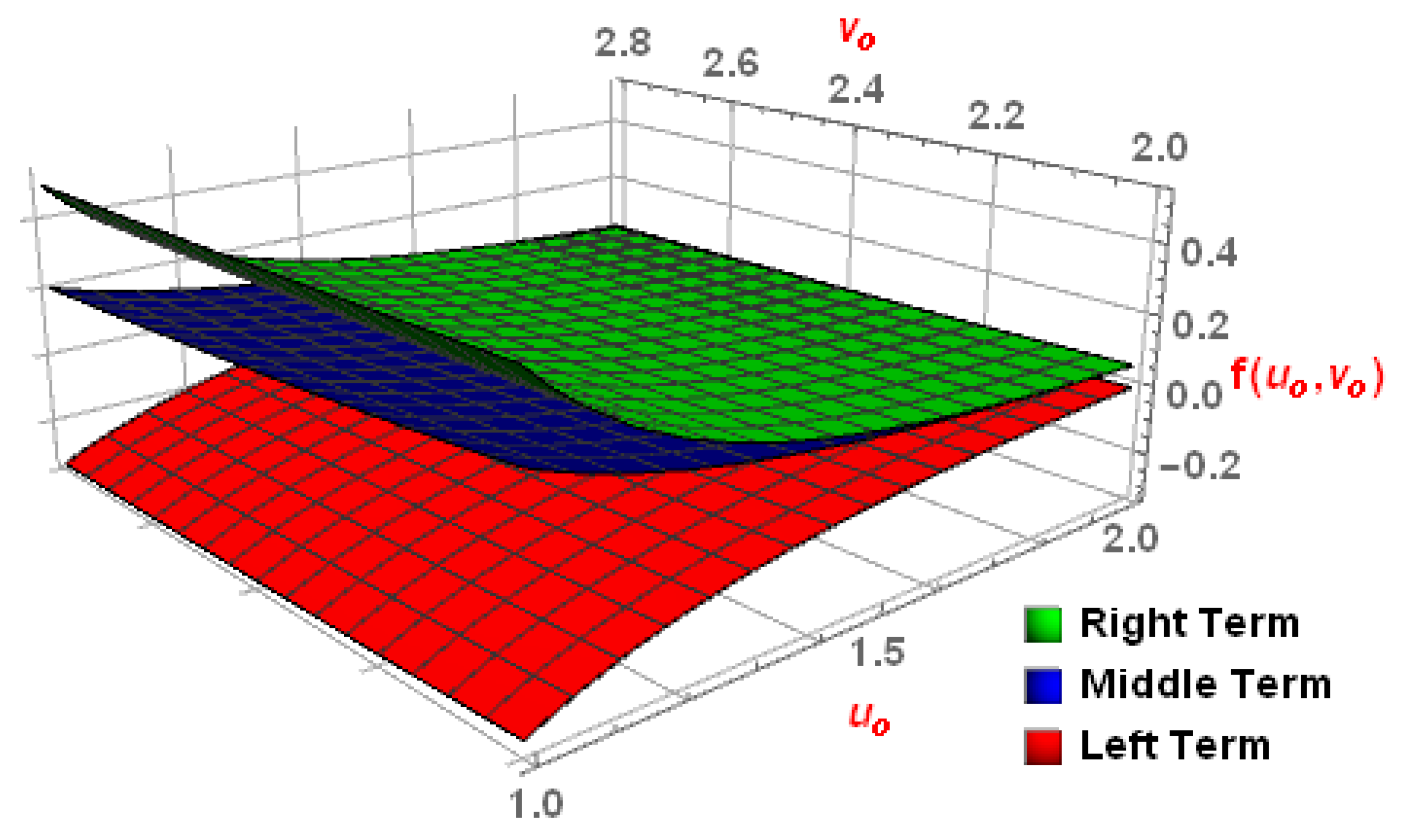
3. Main Result
- (i)
- By letting in Lemma 3, it become Lemma 1.
- (ii)
- By letting in Lemma 3, it becomes the following equality:
- (iii)
- Letting in Lemma 3, we obtain
4. Applications to Bessel Function
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niculescu, C.P.; Persson, L.E. Old and new on the Hermite-Hadamard inequality. Real Anal. Exch. 2004, 29, 663–686. [Google Scholar] [CrossRef]
- Pečarić, J.; Tong, Y.L. Convex Functions, Partial Orderings and Statistical Applications; Academic Press: New York, NY, USA, 1992. [Google Scholar]
- Dragomir, S.S.; Agarwal, R. Two inequalities for differentiable mappings and applications to special means of real numbers and to trapezoidal formula. Appl. Math. Lett. 1998, 11, 91–95. [Google Scholar] [CrossRef]
- Nápoles Valdés, J.E.; Rabossi, F.; Samaniego, A.D. Convex functions: Ariadne’s thread or Charlotte’s Spiderweb? Adv. Math. Model. Appl. 2020, 5, 176–191. [Google Scholar]
- Du, T.; Long, Y. The multi-parameterized integral inequalities for multiplicative Riemann-Liouville fractional integrals. J. Math. Anal. Appl. 2025, 541, 128692. [Google Scholar] [CrossRef]
- Butt, S.I. Generalized Jensen-Hermite-Hadamard Mercer type inequalities for generalized strongly convex functions on fractal sets. Turk. J. Sci. 2024, 8, 51–63. [Google Scholar]
- Vivas-Cortez, M.; Kérus, P.; Nápoles Valdés, J.E. Some generalized Hermite-Hadamard-Fejér inequality for convex functions. Adv. Differ. Equ. 2021, 2021, 199. [Google Scholar] [CrossRef]
- Pearce, C.E.; Pečarić, J. Inequalities for differentiable mappings with application to special means and quadrature formulae. Appl. Math. Lett. 2000, 13, 51–55. [Google Scholar] [CrossRef]
- Kirmaci, U.S.; Özdemir, M.E. On some inequalities for differentiable mappings and applications to special means of real numbers and to midpoint formula. Appl. Math. Comput. 2004, 153, 361–368. [Google Scholar]
- Vivas-Cortez, M.; Ali, M.A.; Budak, H.; Kalsoom, H.; Agarwal, P. Some new Hermite-Hadamard and related inequalities for convex functions via (p, q)-integral. Entropy 2021, 23, 828. [Google Scholar] [CrossRef]
- Mehrez, K.; Agarwal, P. New Hermite-Hadamard type integral inequalities for convex functions and their applications. J. Comput. Appl. Math. 2019, 350, 274–285. [Google Scholar] [CrossRef]
- Varošanec, S. On h-convexity. J. Math. Anal. Appl. 2007, 326, 303–311. [Google Scholar] [CrossRef]
- Kadakal, M.; İşcan, İ.; Agarwal, P.; Jleli, M. Exponential trigonometric convex functions and Hermite-Hadamard type inequalities. Math. Slovaca 2021, 71, 43–56. [Google Scholar] [CrossRef]
- Anderson, G.D.; Vamanamurthy, M.K.; Vuorinen, M. Generalized convexity and inequalities. J. Math. Anal. Appl. 2007, 15, 1294–1308. [Google Scholar] [CrossRef]
- Íşcan, Í. Hermite-Hadamard inequalities for harmonically convex functions. Hacet. J. Math. Stat. 2014, 43, 935–942. [Google Scholar]
- Dimitrijev, S. Effective mass in semiconductors. Bart J. Van Zeghbroeck. 1997.
- Noor, M.A.; Noor, K.I. Harmonic variational inequalities. Appl. Math. Inform. Sci. 2016, 10, 1811–1814. [Google Scholar] [CrossRef]
- Íşcan, Í.; Wu, S. Hermite-Hadamard type inequalities for harmonically convex functions via fractional integrals. Appl. Math. Comput. 2014, 238, 237–244. [Google Scholar]
- Gao, W.; Kashuri, A.; Butt, S.I.; Tariq, M.; Aslam, A.; Nadeem, M. New inequalities via n-polynomial harmonically exponential type convex functions. AIMS Math. 2020, 5, 6856–6873. [Google Scholar] [CrossRef]
- Du, T.S.; Awan, M.U. Hermite-Hadamard type inequalities for harmonically-convex functions using fuzzy integrals. Filomat 2022, 36, 4099–4110. [Google Scholar]
- Butt, S.I.; Agarwal, P.; Yousaf, S.; Guirao, J.L.G. Generalized fractal Jensen and Jensen-Mercer inequalities for harmonic convex function with applications. J. Inequal. Appl. 2022, 2022, 1. [Google Scholar]
- Özcan, S.; Butt, S.I. Hermite-Hadamard type inequalities for multiplicatively harmonic convex functions. J. Inequal. Appl. 2023, 2023, 120. [Google Scholar] [CrossRef]
- Balachandran, K.; Matar, M.; Annapoorani, N.; Prabu, D. Hadamard functional fractional integrals and derivatives and fractional differential equations. Filomat 2024, 38, 779–792. [Google Scholar] [CrossRef]
- Ledesma, C.E.T.; Sousa, J.V.D.C. Fractional integration by parts and Sobolev-type inequalities for ψ-fractional operators. Math. Meth. Appl. Sci. 2022, 45, 9945–9966. [Google Scholar] [CrossRef]
- Khan, T.U.; Khan, M.A. New generalized mean square stochastic fractional operators with applications. Chaos Solitons Fractals 2021, 142, 110452. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Dahmani, Z.; Kiris, M.E.; Ahmad, F. (k,s)-Riemann-Liouville fractional integral and applications. Hacet. J. Math. Stat. 2016, 45, 77–89. [Google Scholar]
- Verma, S.; Viswanathan, P. A note on Katugampola fractional calculus and fractal dimensions. Appl. Math. Comput. 2018, 339, 220–230. [Google Scholar]
- Fernandez, A.; Ustaoğlu, C. On some analytic properties of tempered fractional calculus. J. Comput. Appl. Math. 2020, 366, 112400. [Google Scholar] [CrossRef]
- Ledesma, C.E.T.; Gutierrez, H.A.C.; Rodriguez, J.P.A.; Vera, W.Z. Some boundedness results for Riemann-Liouville tempered fractional integrals. Fract. Calc. Appl. Anal. 2024, 27, 818–847. [Google Scholar] [CrossRef]
- Cheng, Q.J.; Luo, C.Y. Analytical properties, fractal dimensions and related inequalities of (k,h)-Riemann-Liouville fractional integrals. J. Comput. Appl. Math. 2024, 450, 115999. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Sabzikar, F.; Meerschaert, M.M.; Chen, J. Tempered fractional calculus. J. Comput. Phys. 2015, 293, 14–28. [Google Scholar] [CrossRef] [PubMed]
- Sun, W. On generalization of some inequalities for generalized harmonically convex functions via local fractional integrals. Quaest. Math. 2019, 42, 1159–1183. [Google Scholar] [CrossRef]
- Butt, S.I.; Khan, D. Integral inequalities of h-superquadratic functions and their fractional perspective with applications. Math. Method. Appl. Sci. 2024, 48, 1952–1981. [Google Scholar] [CrossRef]
- Benaissa, B.; Budak, H. General (k,p)-Riemann-Liouville fractional integrals. Filomat 2024, 38, 2579–2586. [Google Scholar]
- Sun, W. Some new inequalities for generalized h-convex functions involving local fractional integral operators with Mittag-Leffler kernel. Math. Methods Appl. Sci. 2021, 44, 4985–4998. [Google Scholar] [CrossRef]
- Sarikaya, M.Z. On Hermite-Hadamard type inequalities for proportional Caputo-hybrid operator. Konuralp. J. Math. 2023, 11, 31–39. [Google Scholar]
- Balenau, D.; Ferrandez, A.; Akgül, A. On a fractional operator combining proportional and classical differintegrals. Mathematics 2020, 8, 13. [Google Scholar] [CrossRef]
- Demir, İ. A new approach of Milne-type inequalities based on proportional Caputo-hybrid operator. J. Adv. Appl. Comput. Math. 2023, 10, 102–119. [Google Scholar] [CrossRef]
- Demir, İ.; Tunç, T. A new approach to Simpson-type inequality with proportional Caputo-hybrid operator. Math. Methods Appl. Sci. 2024, 48, 93–106. [Google Scholar] [CrossRef]
- Lakhdari, A.; Bin-Mohsin, B.; Jarad, F.; Xu, H.; Meftah, B. A parametrized approach to generalized fractional integral inequalities: Hermite–Hadamard and Maclaurin variants. J. King Saud Univ.-Sci. 2024, 36, 103523. [Google Scholar] [CrossRef]
- Peng, Y.; Özcan, S.; Du, T. Symmetrical Hermite–Hadamard type inequalities stemming from multiplicative fractional integrals. Chaos Solitons Fractals 2024, 183, 114960. [Google Scholar] [CrossRef]
- Li, H.; Meftah, B.; Saleh, W.; Xu, H.; Kiliçman, A.; Lakhdari, A. Further Hermite-Hadamard-type inequalities for fractional integrals with Exponential Kernels. Fractal Fract. 2024, 8, 345. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, C.; Zhou, Y. New generalized Hermite-Hadamard type inequalities and applications to special means. J. Inequal. Appl. 2013, 2013, 325. [Google Scholar] [CrossRef]
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Khan, D.; Butt, S.I. Superquadraticity and its fractional perspective via center-radius cr-order relation. Chaos Solitons Fractals 2024, 182, 114821. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butt, S.I.; Umar, M.; Khan, D.; Seol, Y.; Tipurić-Spužević, S. Hermite–Hadamard-Type Inequalities for Harmonically Convex Functions via Proportional Caputo-Hybrid Operators with Applications. Fractal Fract. 2025, 9, 77. https://doi.org/10.3390/fractalfract9020077
Butt SI, Umar M, Khan D, Seol Y, Tipurić-Spužević S. Hermite–Hadamard-Type Inequalities for Harmonically Convex Functions via Proportional Caputo-Hybrid Operators with Applications. Fractal and Fractional. 2025; 9(2):77. https://doi.org/10.3390/fractalfract9020077
Chicago/Turabian StyleButt, Saad Ihsan, Muhammad Umar, Dawood Khan, Youngsoo Seol, and Sanja Tipurić-Spužević. 2025. "Hermite–Hadamard-Type Inequalities for Harmonically Convex Functions via Proportional Caputo-Hybrid Operators with Applications" Fractal and Fractional 9, no. 2: 77. https://doi.org/10.3390/fractalfract9020077
APA StyleButt, S. I., Umar, M., Khan, D., Seol, Y., & Tipurić-Spužević, S. (2025). Hermite–Hadamard-Type Inequalities for Harmonically Convex Functions via Proportional Caputo-Hybrid Operators with Applications. Fractal and Fractional, 9(2), 77. https://doi.org/10.3390/fractalfract9020077




