A Novel Approach to the Dynamics of a Fractional-Order Neural Networks with Delay Through Two-Point Self-Mapped Contraction

Abstract

The paper explores the uniform stability and equilibrium characteristics of a class of neural networks of fractional order with time delay. The two-point self-mapped contraction theorem is used in order to establish sufficient conditions for the uniform stability of the system. Further, the existence, uniqueness, and uniform stability of the equilibrium point are established. A set of numerical examples is presented to proclaim the validity and usefulness of the proposed results.

1. Introduction

Fractional calculus (an extension of classical integer-order calculus) has, in turn, become a significant mathematical method of modeling complex systems with memory and hereditary behaviour [1,2,3]. Although somewhat hampered by theoretical issues and a dearth of applications, recent decades have seen the revival of interest in fractional-order systems in a variety of scientific and engineering fields and data, such as in viscoelastic materials, biological processes, electromagnetic theory, as well as in financial modeling [4,5] (for more applications, we refer the reader to [6,7,8]). Fractional derivatives are especially applicable in describing a system in which historic states affect current dynamics, and therefore, they provide more modeling accuracy in such a system than integer-order methods.

The combination of fractional operators offers significant benefits for neural networks. As Lundstrom et al. revealed, a fractional differentiation provides neurons with higher computational functions, such as efficient information processing and anticipating stimuli [9]. In the same manner, Anastasio [10] proposed the oculomotor integrator to be a fractional-order system, and Anastassiou [11] demonstrated that the fractional neural networks had a high rate of approximation. Overall, these results suggest that the field of fractional-order neural networks is a significant contribution not only to theoretical neuroscience but also to practical applications, whether estimating parameters of a specific problem or recognizing a specific pattern.

In a recent research, E. Kaslika and S. Sivasundaram studied different classes of fractional-order neural networks in [12]. Thereafter, they have explored stability properties, multi-stability properties, chaos, and synchronization. However, the incorporation of time delays—a crucial feature of biological and artificial neural systems—introduces additional complexity to fractional-order network analysis. Time delays can induce oscillations, instability, or rich dynamical behaviors, making their rigorous treatment essential for both theoretical understanding and practical implementation (see, for example, [13,14]).

Previous stability analyses of delayed neural networks have predominantly relied on integer-order models [15,16], with results often obtained through Lyapunov functional methods. These approaches do not readily extend to fractional-order systems due to the non-local nature of fractional derivatives. Consequently, establishing stability criteria for fractional-order delayed neural networks remains an open challenge. Some researchers have applied contraction mapping principles to prove equilibrium existence and uniqueness in fractional-order neural networks [17,18,19,20]. Analysis and review of fractional order neural networks can be seen in [21]. The extension of the admissible class of neural models of a fractional-order nature, as well as the analysis of periodicity and the asymptotic behaviour of Cohen-Grossberg-type networks by using Riemann–Liouville fractional operators, are presented in [22]. Various stability results under appropriate sufficient conditions with systematic fixed-point structures in complex-valued contexts can be found [23,24,25]. In [26,27], the authors have investigated the finite-time stability of Caputo fractional-order neural networks.

On the other hand, contractive mappings are a fundamental notion in nonlinear analysis and have become a highly important tool for existence and uniqueness problems in scientific and engineering models. There are classes of contractions known as Kannan contraction, defined by Kannan [28] in 1968, and described by the inequality

$$\mathbb{D}(\mathrm{H}\mathbb{q},\mathrm{H}\mathbb{r})\le \gamma \left[\mathbb{D}(\mathbb{q},\mathrm{H}\mathbb{q})+\mathbb{D}(\mathbb{r},\mathrm{H}\mathbb{r})\right],0\le \gamma <{\displaystyle \frac{1}{2}},$$

has become a strong substitute to the classical Banach contraction principle. Unlike the Lipschitz-type dependence of $\mathbb{D}(\mathbb{q},\mathbb{r})$ being used in the framework of Banach, the Kannan condition is based on the self-distance terms of $\mathbb{D}(\mathbb{q},\mathrm{H}\mathbb{q})$ and $\mathbb{D}(\mathbb{r},\mathrm{H}\mathbb{r})$ which allow fixed-point results in the case where continuity or direct contractiveness between pairwise distances are not always true. This structural property has seen generalizations of Kannan-type operators being widely used in numerous contemporary mathematical contexts, including partial metric spaces [29], b-metric spaces [30], fuzzy and probabilistic metric spaces [31,32], and a host of other types of metrical structure of the type of fractional and integral operators. These developments and many recent studies have shown that Kannan-type contractions are useful for solving nonlinear functional, integral, and integro-differential equations and for studying the stability of complex dynamical systems found in science and engineering, including fractional-order models [33,34,35], fractals, as well as iterative numerical schemes [36]. Therefore, Kannan contractions still have a strong analytical structure, especially in those cases where classical methods do not assure convergence.

In contrast to Lyapunov methods, the Kannan theorem does not impose a classical differentiable or continuous requirement on the system; only a Lipschitz condition is required. This is more in line with the fractional-order context. Whereas Banach contractions require the mapping to decrease distances between any two points, Kannan mappings satisfy a property requiring distances between points and their images. It is a minor yet important difference that opens new possibilities for stability analysis of the fractional-order delayed neural networks. Although the condition is numerically more restrictive, it has alternative analytical properties, which can be useful in particular situations, especially when mixed with other methods, or in applications to systems with a given structural property.

Motivated by the above, we present an alternative analytical framework for studying fractional-order delayed neural networks by employing the two-point self-mapped contraction theorem. Unlike the Banach contraction principle used in previous works, the two-point self-mapped contraction theorem provides distinct sufficient conditions for the existence of unique fixed points. We derive a novel stability criterion based on this approach and prove the existence of unique and uniformly stable equilibrium points for a class of fractional-order neural networks with constant delays. Our results complement existing literature by offering an alternative mathematical pathway with different parametric constraints.

This paper is organized as follows: Section 2 briefs the fractional-order delayed neural network model and necessary mathematical preliminaries, including the two-point self-mapped contraction theorem. Section 3 presents our main results: sufficient conditions for uniform stability and an analysis of equilibrium points using the two-point self-mapping contraction theorem. Section 4 provides a few numerical examples validating the theoretical findings, and Section 5 concludes the paper.

2. Basic Definitions and Briefing on Fractional-Order Neural Network Model

Definition 1

([1,2]). The fractional integral of order $\varpi \in {\mathbb{R}}^{+}$ for a function $\mathbb{q}(t)$ is defined as follows:

$${\mathrm{D}}_{t_0,t}^{-\varpi }\mathbb{q}(t)={\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_{t_0}^t{(t-\tau )}^{\varpi -1}\mathbb{q}(\tau )d\tau ,\varpi >0,$$

(1)

where $\Gamma (·)$ is the Gamma function, $\Gamma (\varpi )={\int }_0^{\infty }{t}^{\varpi -1}{e}^{-t}dt$.

Definition 2

([1,2]). The Riemann–Liouville derivative of fractional order ϖ of function $\mathbb{q}(t)$ is as follows:

$${}_{RL}\mathrm{D}_{t_0,t}^{\varpi }\mathbb{q}(t)={\displaystyle \frac{d^n}{d{t}^n}}{\mathrm{D}}_{t_0,t}^{-(n-\varpi )}\mathbb{q}(t)={\displaystyle \frac{d^n}{d{t}^n}}{\displaystyle \frac{1}{\Gamma (n-\varpi )}}{\int }_{t_0}^t{(t-\tau )}^{n-\varpi -1}\mathbb{q}(\tau )d\tau ,$$

(2)

Here, we have noted that $n-1<\varpi <n\in {\mathbb{Z}}^{+}$.

Definition 3

([1,2]). The Caputo derivative of fractional order ϖ of function $\mathbb{q}(t)$ is as follows:

$${}_C\mathrm{D}_{t0,t}^{\varpi }\mathbb{q}(t)={\mathrm{D}}_{t_0,t}^{-(n-\varpi )}{\displaystyle \frac{d^n}{d{t}^n}}\mathbb{q}(t)={\displaystyle \frac{1}{\Gamma (n-\varpi )}}{\int }_{t_0}^t{(t-\tau )}^{n-\varpi -1}{\mathbb{q}}^{(n)}(\tau )d\tau ,$$

(3)

where $n-1<\varpi <n\in {\mathbb{Z}}^{+}$.

Lemma 1

([3]). If $\mathbb{q}(t)\in C^m[0,\infty )$ and $m-1<\varpi <m\in {\mathbb{Z}}^{+}$, which implies the following:

$$\begin{array}{cc}& (1){\mathrm{D}}^{-\varpi }{\mathrm{D}}^{-\vartheta }\mathbb{q}(t)={\mathrm{D}}^{-(\varpi +\vartheta )}\mathbb{q}(t),\varpi ,\vartheta \ge 0,\hfill \\ & (2){\mathrm{D}}^{\varpi }{\mathrm{D}}^{-\vartheta }\mathbb{q}(t)=\mathbb{q}(t),\varpi =\vartheta \ge 0,\hfill \\ & (3){\mathrm{D}}^{-\varpi }{\mathrm{D}}^{\vartheta }\mathbb{q}(t)=\mathbb{q}(t)-\sum _{k=0}^{m-1}{\displaystyle \frac{t^k}{k!}}{\mathbb{q}}^{(k)}(0),\varpi =\vartheta \ge 0.\hfill \end{array}$$

Remark 1.

The Caputo derivative has the advantage that initial conditions take the same form as for integer-order differential equations. Moreover, the Caputo derivative of a constant is zero. Therefore, throughout this paper, we use the Caputo fractional derivative operator ${\mathrm{D}}^{\varpi }$ to model our neural network system.

The dynamic behavior of a continuous fractional-order delayed neural network is described by the following:

$${\mathrm{D}}^{\varpi }{\mathbb{q}}_i(t)=-c_i{\mathbb{q}}_i(t)+\sum _{j=1}^n{a}_{ij}{\eta }_j({\mathbb{q}}_j(t))+\sum _{j=1}^n{b}_{ij}{\omega }_j({\mathbb{q}}_j(t-\tau ))+I_i,$$

(4)

for $i\in \mathbb{N}$, $t\in [0,T]$ and $T<\infty$ with $0<\varpi <1$. Equivalently, in vector form:

$${\mathrm{D}}^{\varpi }\mathbb{q}(t)=-C\mathbb{q}(t)+\mathrm{A}\eta (\mathbb{q}(t))+\mathrm{B}\omega (\mathbb{q}(t-\tau ))+I,$$

(5)

where

• $\mathbb{q}(t)={({\mathbb{q}}_1(t),\dots ,{\mathbb{q}}_n(t))}^{\top }\in {\mathbb{R}}^n$ is the state vector;
• $C=\mathrm{diag}(c_1,\dots ,c_n)$ with $c_i>0$;
• $\mathrm{A}=(a_{ij})$ and $\mathrm{B}=(b_{ij})$ are connection weight matrices;
• $\eta (\mathbb{q}(t))={({\eta }_1({\mathbb{q}}_1(t)),\dots ,{\eta }_n({\mathbb{q}}_n(t)))}^{\top }$ and $\omega (\mathbb{q}(t))={({\omega }_1({\mathbb{q}}_1(t)),\dots ,{\omega }_n({\mathbb{q}}_n(t)))}^{\top }$ are activation functions;
• $\tau >0$ is the transmission delay;
• $I={(I_1,\dots ,I_n)}^{\top }$ is the external bias vector.

The initial conditions associated with system (6) are as follows:

$${\mathbb{q}}_i(t)={\phi }_i(t)\mathrm{and}{\phi }_i(0)=0;\mathrm{where}t\in [-\tau ,0]\mathrm{and}i\in N,$$

(6)

where ${\phi }_i\in C([-\tau ,0],\mathbb{R})$. The norm on $C([-\tau ,0],\mathbb{R})$ is defined as follows:

$$\parallel \phi (t)\parallel =\sum _{i=1}^n\underset{t\in [-\tau ,0]}{sup}|e^{-t}{\phi }_i(t)|.$$

(7)

Definition 4

([28]). Let $(\mathcal{N},\mathbb{D})$ be a metric space. A self-mapping $\mathrm{H}:\mathcal{N}\to \mathcal{N}$ is said to be a two-point self-mapped contraction if there exists a constant $\gamma \in [0,{\displaystyle \frac{1}{2}})$ such that

$$\mathbb{D}(\mathrm{H}\mathbb{q},\mathrm{H}\mathbb{r})\le \gamma \left(\mathbb{D}(\mathbb{q},\mathrm{H}\mathbb{q})+\mathbb{D}(\mathbb{r},\mathrm{H}\mathbb{r})\right),$$

(8)

for all $\mathbb{q},\mathbb{r}\in \mathcal{N}$.

Theorem 1

(Kannan Fixed Point Theorem [28]). Let $(\mathcal{N},\mathbb{D})$ be a complete metric space and let $\mathrm{H}:\mathcal{N}\to \mathcal{N}$ be a mapping satisfying

$$\mathbb{D}(\mathrm{H}\mathbb{q},\mathrm{H}\mathbb{r})\le \gamma \left(\mathbb{D}(\mathbb{q},\mathrm{H}\mathbb{q})+\mathbb{D}(\mathbb{r},\mathrm{H}\mathbb{r})\right),0\le \gamma <{\displaystyle \frac{1}{2}},$$

(9)

for all $\mathbb{q},\mathbb{r}\in \mathcal{N}$. Then $\mathrm{H}$ possesses a fixed point ${\mathbb{q}}^{*}$ in $\mathcal{N}$, that is unique, and for any ${\mathbb{q}}_0\in \mathcal{N}$, the sequence

$${\mathbb{q}}_{n+1}=\mathrm{H}{\mathbb{q}}_n$$

converges to ${\mathbb{q}}^{*}$.

Remark 2.

The Kannan contraction is often referred to as a Two-point Self-mapped Contraction because the contractive condition

$$\mathbb{D}(\mathrm{H}\mathbb{q},\mathrm{H}\mathbb{r})\le \gamma \left[\mathbb{D}(\mathbb{q},\mathrm{H}\mathbb{q})+\mathbb{D}(\mathbb{r},\mathrm{H}\mathbb{r})\right],0\le \gamma <{\displaystyle \frac{1}{2}},$$

does not depend on the direct distance $\mathbb{D}(\mathbb{q},\mathbb{r})$ between two distinct points $\mathbb{q}$ and $\mathbb{r}$, unlike the classical Banach contraction. Instead, it depends solely on the self-distances of each point from its own image under $\mathrm{H}$, namely $\mathbb{D}(\mathbb{q},\mathrm{H}\mathbb{q})$ and $\mathbb{D}(\mathbb{r},\mathrm{H}\mathbb{r})$. Thus, the contraction property is determined through two points and their self-mapped distances, making it an intrinsic contraction based on how far each point is from its transformation.

Assumption A1.

There exist positive constants ${\Lambda }_j,{{\rm Y}}_j$ such that for all $u,v\in \mathbb{R}$:

$$|{\eta }_j(\kappa )-{\eta }_j(\mathcal{l})|\le {\Lambda }_j|\kappa -\mathcal{l}|,|{\omega }_j(\kappa )-{\omega }_j(\mathcal{l})|\le {{\rm Y}}_j|\kappa -\mathcal{l}|.$$

Assumption A2.

The system parameters satisfy the following:

$$\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel <{\displaystyle \frac{1}{3}}{c}_{min},$$

where

$$a_i^{*}=\underset{1\le j\le n}{max}\{|a_{ij}|{\Lambda }_j\},b_i^{*}=\underset{1\le j\le n}{max}\{|b_{ij}|{{\rm Y}}_j\},$$

$$\parallel {\mathrm{A}}^{*}\parallel =\sum _{i=1}^n{a}_i^{*},\parallel {\mathrm{B}}^{*}\parallel =\sum _{i=1}^n{b}_i^{*},$$

$$c_{min}=\underset{1\le i\le n}{min}{c}_i,c_{max}=\underset{1\le i\le n}{max}{c}_i.$$

For $T>0$, let $\Omega =C([0,T],{\mathbb{R}}^n)$ with the norm:

$$\parallel \mathbb{q}(t)\parallel =\sum _{i=1}^n\underset{t\in [0,T]}{sup}{e}^{-t}|{\mathbb{q}}_i(t)|.$$

For initial functions $\phi \in C([-\tau ,0],{\mathbb{R}}^n)$, define:

$$\parallel \phi \parallel =\sum _{i=1}^n\underset{t\in [-\tau ,0]}{sup}{e}^{-t}|{\phi }_i(t)|.$$

Remark 3.

Above-stated Assumption 2, $\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel <{\displaystyle \frac{1}{3}},c_{min}$ is an algebraic and easy-to-check sufficient condition, distinct from the usual contraction condition $\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel <c_{min}$. It is stricter but sometimes easier to satisfy in parameter design.

Definition 5.

The solution of (4) is uniformly stable if for any $ϵ>0$, there exists $\delta >0$ such that for any two solutions $\mathbb{q}(t)$ and $\mathbb{r}(t)$ with initial conditions φ and ϱ, respectively, $\parallel \phi -\varrho \parallel <\delta$ implies $\parallel \mathbb{r}(t)-\mathbb{q}(t)\parallel <ϵ$ for all $t\ge 0$.

3. Existence, Uniqueness, and Uniform Stability Results

Theorem 2.

Under Assumptions 1 and 2, and if $c_{max}<{\displaystyle \frac{3}{4}}$, then system (4) is uniformly stable.

Proof. 

Let $\mathbb{q}(t)={({\mathbb{q}}_1(t),\dots ,{\mathbb{q}}_n(t))}^T$ and $\mathbb{r}(t)={({\mathbb{r}}_1(t),\dots ,{\mathbb{r}}_n(t))}^T$ be any two solutions of (4) with different initial conditions ${\phi }_i(s)$ and ${\varrho }_i(s)$ for $s\in [-\tau ,0]$, where ${\phi }_i,{\varrho }_i\in C([-\tau ,0],\mathbb{R})$ and ${\phi }_i(0)={\varrho }_i(0)=0$. Let ${\hslash }_i(t)={\mathbb{r}}_i(t)-{\mathbb{q}}_i(t)$. Then from (4) we have the following:

$${\mathrm{D}}^{\varpi }{\hslash }_i(t)=-c_i{\hslash }_i(t)+\sum _{j=1}^n{a}_{ij}[{\eta }_j({\mathbb{r}}_j(t))-{\eta }_j({\mathbb{q}}_j(t))]+\sum _{j=1}^n{b}_{ij}[{\omega }_j({\mathbb{r}}_j(t-\tau ))-{\omega }_j({\mathbb{q}}_j(t-\tau ))].$$

(10)

The inverse fractional integral operator ${\mathrm{D}}^{-\varpi }$ is applied on both sides of Equation (10) with the known Caputo property of ${\mathrm{D}}^{-\varpi }{\mathrm{D}}^{\varpi }\hslash (t)=\hslash (t)-\hslash (0)$ and $\hslash (0)=0$. Then we can get that which comes about is the integrative form as below:

$${\hslash }_i(t)={\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^t{(t-s)}^{\varpi -1}\left[-c_i{\hslash }_i(s)+\sum _{j=1}^n{a}_{ij}({\eta }_j({\mathbb{r}}_j(s))-{\eta }_j({\mathbb{q}}_j(s)))+\sum _{j=1}^n{b}_{ij}({\omega }_j({\mathbb{r}}_j(s-\tau ))-{\omega }_j({\mathbb{q}}_j(s-\tau )))\right]ds.$$

(11)

Now multiply both sides by $e^{-t}$ and take absolute values:

$$e^{-t}|{\hslash }_i(t)|\le {\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^t{(t-s)}^{\varpi -1}{e}^{-t}\left[c_i|{\hslash }_i(s)|+\sum _{j=1}^n|a_{ij}|{\Lambda }_j|{\hslash }_j(s)|+\sum _{j=1}^n|b_{ij}|{{\rm Y}}_j|{\hslash }_j(s-\tau )|\right]ds.$$

(12)

Using $e^{-t}=e^{-(t-s)}{e}^{-s}$, we obtain the following:

$$\begin{array}{cc}\hfill e^{-t}|{\hslash }_i(t)|& \le {\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^t{(t-s)}^{\varpi -1}{e}^{-(t-s)}[c_i{e}^{-s}|{\hslash }_i(s)|\hfill \\ \hfill & +\sum _{j=1}^n|a_{ij}|{\Lambda }_j{e}^{-s}|{\hslash }_j(s)|+\sum _{j=1}^n|b_{ij}|{{\rm Y}}_j{e}^{-s}|{\hslash }_j(s-\tau )|]ds.\hfill \end{array}$$

(13)

Now, estimate the right-hand side as follows. We consider each term in the integrand separately and use appropriate bounds:

$$\begin{array}{cc}\hfill e^{-t}|{\hslash }_i(t)|& \le {\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^t{(t-s)}^{\varpi -1}{e}^{-(t-s)}{c}_i{e}^{-s}|{\hslash }_i(s)|ds\hfill \\ \hfill & +{\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^t{(t-s)}^{\varpi -1}{e}^{-(t-s)}\sum _{j=1}^n|a_{ij}|{\Lambda }_j{e}^{-s}|{\hslash }_j(s)|ds\hfill \\ \hfill & +{\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^t{(t-s)}^{\varpi -1}{e}^{-(t-s)}\sum _{j=1}^n|b_{ij}|{{\rm Y}}_j{e}^{-s}|{\hslash }_j(s-\tau )|ds.\hfill \end{array}$$

(14)

Let us denote $M_i(t)={sup}_{0\le s\le t}{e}^{-s}|{\hslash }_i(s)|$, $M(t)={\sum }_{i=1}^n{M}_i(t)$, and $N={\sum }_{i=1}^n$${sup}_{\theta \in [-\tau ,0]}{e}^{-\theta }|{\varrho }_i(\theta )-{\phi }_i(\theta )|$.

For the first integral, change the variable $\kappa =t-s$:

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^t{(t-s)}^{\varpi -1}{e}^{-(t-s)}{c}_i{e}^{-s}|{\hslash }_i(s)|ds& ={\displaystyle \frac{c_i}{\Gamma (\varpi )}}{\int }_0^t{\kappa }^{\varpi -1}{e}^{-\kappa }{e}^{-(t-\kappa )}|{\hslash }_i(t-\kappa )|d\kappa \hfill \\ \hfill & \le {\displaystyle \frac{c_i}{\Gamma (\varpi )}}\underset{0\le s\le t}{sup}\left(e^{-s}|{\hslash }_i(s)|\right){\int }_0^t{\kappa }^{\varpi -1}{e}^{-\kappa }d\kappa \hfill \\ \hfill & \le c_i{M}_i(t){\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^{\infty }{\kappa }^{\varpi -1}{e}^{-\kappa }d\kappa \hfill \\ \hfill & =c_i{M}_i(t).\hfill \end{array}$$

For the second integral, using $|a_{ij}|{\Lambda }_j\le a_i^{*}$:

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{\Gamma (\varpi )}}& {\int }_0^t{(t-s)}^{\varpi -1}{e}^{-(t-s)}\sum _{j=1}^n|a_{ij}|{\Lambda }_j{e}^{-s}|{\hslash }_j(s)|ds\hfill \\ \hfill & \le \sum _{j=1}^n|a_{ij}|{\Lambda }_j\underset{0\le s\le t}{sup}\left(e^{-s}|{\hslash }_j(s)|\right){\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^t{(t-s)}^{\varpi -1}{e}^{-(t-s)}ds\hfill \\ \hfill & \le \sum _{j=1}^n|a_{ij}|{\Lambda }_j{M}_j(t){\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^{\infty }{\kappa }^{\varpi -1}{e}^{-\kappa }d\kappa \hfill \\ \hfill & =\sum _{j=1}^n|a_{ij}|{\Lambda }_j{M}_j(t)\hfill \\ \hfill & \le a_i^{*}\sum _{j=1}^n{M}_j(t)=a_i^{*}M(t).\hfill \end{array}$$

For the third integral, we split the integration domain into two parts: $s\in [0,\tau ]$ and $s\in [\tau ,t]$ (if $t>\tau$).

Case 1: $\mathit{s}\in [\mathbf{0},\mathit{\tau }]$ (or $s\in [0,min(t,\tau )]$). In this case, $s-\tau \in [-\tau ,0]$, so $|{\hslash }_j(s-\tau )|=|{\varrho }_j(s-\tau )-{\phi }_j(s-\tau )|$. Also, $e^{-s}=e^{-\tau }{e}^{-(s-\tau )}$. Thus,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^{min(t,\tau )}{(t-s)}^{\varpi -1}{e}^{-(t-s)}\sum _{j=1}^n|b_{ij}|{{\rm Y}}_j{e}^{-s}|{\hslash }_j(s-\tau )|ds\hfill \\ \hfill & \le \sum _{j=1}^n|b_{ij}|{{\rm Y}}_j\underset{\theta \in [-\tau ,0]}{sup}{e}^{-\theta }|{\varrho }_j(\theta )-{\phi }_j(\theta )|e^{-\tau }{\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^{min(t,\tau )}{(t-s)}^{\varpi -1}{e}^{-(t-s)}ds\hfill \\ \hfill & \le b_i^{*}N{e}^{-\tau }{\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^{\infty }{\kappa }^{\varpi -1}{e}^{-\kappa }d\kappa \hfill \\ \hfill & =b_i^{*}N{e}^{-\tau }\le b_i^{*}N.\hfill \end{array}$$

Case 2: $\mathit{s}\in [\mathit{\tau },\mathit{t}]$ (if $t>\tau$). Let $\sigma =s-\tau$. Then $s=\sigma +\tau$ and $e^{-s}=e^{-\tau }{e}^{-\sigma }$. Also, when $s=\tau$, $\sigma =0$; when $s=t$, $\sigma =t-\tau$. Thus,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_{\tau }^t{(t-s)}^{\varpi -1}{e}^{-(t-s)}\sum _{j=1}^n|b_{ij}|{{\rm Y}}_j{e}^{-s}|{\hslash }_j(s-\tau )|ds\hfill \\ \hfill & ={\displaystyle \frac{e^{-\tau }}{\Gamma (\varpi )}}{\int }_0^{t-\tau }{(t-\sigma -\tau )}^{\varpi -1}{e}^{-(t-\sigma -\tau )}\sum _{j=1}^n|b_{ij}|{{\rm Y}}_j{e}^{-\sigma }|{\hslash }_j(\sigma )|d\sigma \hfill \\ \hfill & \le e^{-\tau }\sum _{j=1}^n|b_{ij}|{{\rm Y}}_j\underset{0\le \sigma \le t}{sup}\left(e^{-\sigma }|{\hslash }_j(\sigma )|\right){\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^{t-\tau }{(t-\sigma -\tau )}^{\varpi -1}{e}^{-(t-\sigma -\tau )}d\sigma \hfill \\ \hfill & \le e^{-\tau }{b}_i^{*}M(t){\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^{\infty }{\kappa }^{\varpi -1}{e}^{-\kappa }d\kappa \hfill \\ \hfill & =e^{-\tau }{b}_i^{*}M(t)\le b_i^{*}M(t).\hfill \end{array}$$

Combining the estimates for the third integral, we obtain the following:

$${\displaystyle \frac{1}{\Gamma (\varpi )}}{\int }_0^t{(t-s)}^{\varpi -1}{e}^{-(t-s)}\sum _{j=1}^n|b_{ij}|{{\rm Y}}_j{e}^{-s}|{\hslash }_j(s-\tau )|ds\le b_i^{*}(N+M(t)).$$

Now, putting all three estimates together into (14), we have the following:

$$e^{-t}|{\hslash }_i(t)|\le c_i{M}_i(t)+a_i^{*}M(t)+b_i^{*}(N+M(t)).$$

Taking the supremum over $t\ge 0$ on the left-hand side and summing over $i=1,\dots ,n$, we obtain the following:

$$\begin{array}{cc}\hfill \sum _{i=1}^n\underset{t\ge 0}{sup}{e}^{-t}|{\hslash }_i(t)|& \le \sum _{i=1}^n{c}_i\underset{t\ge 0}{sup}{e}^{-t}|{\hslash }_i(t)|+\sum _{i=1}^n{a}_i^{*}M+\sum _{i=1}^n{b}_i^{*}(N+M)\hfill \\ \hfill & =\sum _{i=1}^n{c}_i\underset{t\ge 0}{sup}{e}^{-t}|{\hslash }_i(t)|+\parallel {\mathrm{A}}^{*}\parallel \parallel \hslash \parallel +\parallel {\mathrm{B}}^{*}\parallel (N+\parallel \hslash \parallel ),\hfill \end{array}$$

where $\parallel \hslash \parallel ={\sum }_{i=1}^n{sup}_{t\ge 0}{e}^{-t}|{\hslash }_i(t)|$, and also note that $N=\parallel \varrho -\phi \parallel$. Since $c_i\le c_{max}$ for all i, we have the following:

$$\sum _{i=1}^n{c}_i\underset{t\ge 0}{sup}{e}^{-t}|{\hslash }_i(t)|\le c_{max}\sum _{i=1}^n\underset{t\ge 0}{sup}{e}^{-t}|{\hslash }_i(t)|=c_{max}\parallel \hslash \parallel .$$

Thus,

$$\parallel \hslash \parallel \le c_{max}\parallel \hslash \parallel +\parallel {\mathrm{A}}^{*}\parallel \parallel \hslash \parallel +\parallel {\mathrm{B}}^{*}\parallel (\parallel \varrho -\phi \parallel +\parallel \hslash \parallel ).$$

Rearranging terms gives the following:

$$\left(1-(c_{max}+\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel )\right)\parallel \hslash \parallel \le \parallel {\mathrm{B}}^{*}\parallel \parallel \varrho -\phi \parallel .$$

(15)

Under Assumption 2, we have $\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel <{\displaystyle \frac{1}{3}}{c}_{min}$. Since $c_{min}\le c_{max}$, it follows that $\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel <{\displaystyle \frac{1}{3}}{c}_{max}$. Therefore,

$$c_{max}+\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel <c_{max}+{\displaystyle \frac{1}{3}}{c}_{max}={\displaystyle \frac{4}{3}}{c}_{max}.$$

If $c_{max}<{\displaystyle \frac{3}{4}}$, then ${\displaystyle \frac{4}{3}}{c}_{max}<1$, and hence $1-(c_{max}+\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel )>0$. Consequently,

$$\parallel \hslash \parallel \le {\displaystyle \frac{\parallel {\mathrm{B}}^{*}\parallel }{1-(c_{max}+\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel )}}\parallel \varrho -\phi \parallel .$$

(16)

Now for any $ϵ>0$, we can choose $\delta ={\displaystyle \frac{1-(c_{max}+\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel )}{\parallel {\mathrm{B}}^{*}\parallel }}ϵ>0$.

Then, if $\parallel \varrho -\phi \parallel <\delta$, we have the following:

$$\parallel \hslash \parallel <ϵ.$$

This implies the following:

$$\sum _{i=1}^n\underset{t\ge 0}{sup}{e}^{-t}|{\mathbb{r}}_i(t)-{\mathbb{q}}_i(t)|<ϵ,$$

which means that $\parallel \mathbb{r}(t)-\mathbb{q}(t)\parallel <ϵ$ for all $t\ge 0$. Therefore, system (4) is uniformly stable. □

Theorem 3.

Under Assumptions 1 and 2, there exists a unique equilibrium point ${\mathbb{q}}^{*}$ of the system (4).

Proof. 

The equilibrium point ${\mathbb{q}}^{*}$ satisfies the following:

$$-c_i{\mathbb{q}}_i^{*}+\sum _{j=1}^n{a}_{ij}{\eta }_j({\mathbb{q}}_j^{*})+\sum _{j=1}^n{b}_{ij}{\omega }_j({\mathbb{q}}_j^{*})+I_i=0,i=1,\dots ,n.$$

Let ${\kappa }_i=c_i{\mathbb{q}}_i^{*}$. Then,

$${\kappa }_i=\sum _{j=1}^n{a}_{ij}{\eta }_j\left({\displaystyle \frac{{\kappa }_j}{c_j}}\right)+\sum _{j=1}^n{b}_{ij}{\omega }_j\left({\displaystyle \frac{{\kappa }_j}{c_j}}\right)+I_i.$$

Define the mapping $\Theta :{\mathbb{R}}^n\to {\mathbb{R}}^n$ by the following:

$${\Theta }_i(\kappa )=\sum _{j=1}^n{a}_{ij}{\eta }_j\left({\displaystyle \frac{{\kappa }_j}{c_j}}\right)+\sum _{j=1}^n{b}_{ij}{\omega }_j\left({\displaystyle \frac{{\kappa }_j}{c_j}}\right)+I_i.$$

We show that $\Theta$ satisfies the two-point self-mapped contraction condition on the complete metric space $({\mathbb{R}}^n,\parallel ·{\parallel }_s)$, where ${\parallel \kappa \parallel }_s={\sum }_{i=1}^n|{\kappa }_i|$. For any $u,v\in {\mathbb{R}}^n$, using Assumption 1, we have the following:

$$\begin{array}{cc}\hfill |{\Theta }_i(\kappa )-{\Theta }_i(\mathcal{l})|& \le \sum _{j=1}^n|a_{ij}|{\Lambda }_j{\displaystyle \frac{|{\kappa }_j-{\mathcal{l}}_j|}{c_j}}+\sum _{j=1}^n|b_{ij}|{{\rm Y}}_j{\displaystyle \frac{|{\kappa }_j-{\mathcal{l}}_j|}{c_j}}\hfill \\ & \le {\displaystyle \frac{1}{c_{min}}}\sum _{j=1}^n\left(|a_{ij}|{\Lambda }_j+|b_{ij}|{{\rm Y}}_j\right)|{\kappa }_j-{\mathcal{l}}_j|\hfill \\ & \le {\displaystyle \frac{1}{c_{min}}}(a_i^{*}+b_i^{*})\sum _{j=1}^n|{\kappa }_j-{\mathcal{l}}_j|.\hfill \end{array}$$

Summing over i:

$${\parallel \Theta (\kappa )-\Theta (\mathcal{l})\parallel }_s\le {\displaystyle \frac{1}{c_{min}}}\sum _{i=1}^n(a_i^{*}+b_i^{*}){\parallel \kappa -\mathcal{l}\parallel }_s={\displaystyle \frac{\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel }{c_{min}}}{\parallel \kappa -\mathcal{l}\parallel }_s.$$

Thus, $\Theta$ is Lipschitz with constant $L={\displaystyle \frac{\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel }{c_{min}}}$. By Assumption 2, $L<{\displaystyle \frac{1}{3}}$. Now, for any $\kappa ,\mathcal{l}\in {\mathbb{R}}^n$,

$${\parallel \Theta (\kappa )-\Theta (\mathcal{l})\parallel }_s\le L{\parallel \kappa -\mathcal{l}\parallel }_s.$$

Using the triangle inequality:

$${\parallel \kappa -\mathcal{l}\parallel }_s\le {\parallel \kappa -\Theta (\kappa )\parallel }_s{+\parallel \Theta (\kappa )-\Theta (\mathcal{l})\parallel }_s+{\parallel \mathcal{l}-\Theta (\mathcal{l})\parallel }_s.$$

Substituting the Lipschitz bound:

$${\parallel \Theta (\kappa )-\Theta (\mathcal{l})\parallel }_s\le L\left({\parallel \kappa -\Theta (\kappa )\parallel }_s{+\parallel \Theta (\kappa )-\Theta (\mathcal{l})\parallel }_s+{\parallel \mathcal{l}-\Theta (\mathcal{l})\parallel }_s\right).$$

Rearranging yields the following:

$${(1-L)\parallel \Theta (\kappa )-\Theta (\mathcal{l})\parallel }_s\le L\left({\parallel \kappa -\Theta (\kappa )\parallel }_s+{\parallel \mathcal{l}-\Theta (\mathcal{l})\parallel }_s\right).$$

Since $L<{\displaystyle \frac{1}{3}}$, we have $1-L>0$ and $\lambda ={\displaystyle \frac{L}{1-L}}<{\displaystyle \frac{1}{2}}$. Thus,

$${\parallel \Theta (\kappa )-\Theta (\mathcal{l})\parallel }_s\le \lambda \left({\parallel \kappa -\Theta (\kappa )\parallel }_s+{\parallel \mathcal{l}-\Theta (\mathcal{l})\parallel }_s\right),$$

with $\lambda \in [0,{\displaystyle \frac{1}{2}})$. Hence, $\Theta$ satisfies the two-point self-mapped contraction condition. By two-point self-mapped contraction theorem, $\Theta$ has a unique fixed point ${\kappa }^{*}\in {\mathbb{R}}^n$. Then ${\mathbb{q}}^{*}={({\kappa }_1^{*}/c_1,\dots ,{\kappa }_n^{*}/c_n)}^T$ is the unique equilibrium of system (4). □

Theorem 4.

Under Assumptions 1 and 2, and if $c_{max}<{\displaystyle \frac{3}{4}}$, then the unique equilibrium point ${\mathbb{q}}^{*}$ of system (4) is uniformly stable.

Proof. 

The existence and uniqueness of ${\mathbb{q}}^{*}$ follow from Theorem 3. For any solution $\mathbb{q}(t)$ of (4) with initial condition $\phi$, let $\mathbb{r}(t)\equiv {\mathbb{q}}^{*}$ be the constant equilibrium solution. By Theorem 1, we have

$$\parallel \mathbb{q}(t)-{\mathbb{q}}^{*}\parallel \le {\displaystyle \frac{\parallel {\mathrm{B}}^{*}\parallel }{1-(c_{max}+\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel )}}\parallel \phi -{\phi }^{*}\parallel ,$$

where ${\phi }^{*}$ is the constant function equal to ${\mathbb{q}}^{*}$ on $[-\tau ,0]$. For any $ϵ>0$, choose $\delta ={\displaystyle \frac{1-(c_{max}+\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel )}{\parallel {\mathrm{B}}^{*}\parallel }}ϵ$. Then if $\parallel \phi -{\phi }^{*}\parallel <\delta$, we have $\parallel \mathbb{q}(t)-{\mathbb{q}}^{*}\parallel <ϵ$ for all $t\ge 0$. Hence, ${\mathbb{q}}^{*}$ is uniformly stable. □

Remark 4.

The condition $c_{max}<{\displaystyle \frac{3}{4}}$ ensures positivity of $1-(c_{max}+\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel )$. This can be relaxed by using a weighted norm with rate $\lambda >0$, leading to ${\lambda }^{-\varpi }(c_{max}+\parallel {\mathrm{A}}^{*}\parallel +e^{\lambda \tau }\parallel {\mathrm{B}}^{*}\parallel )<1$.

Remark 5.

The two-point self-mapped contraction condition $\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel <{\displaystyle \frac{1}{3}}{c}_{min}$ is stronger than the contraction condition $\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel <c_{min}$ but provides an alternative fixed-point approach.

Remark 6.

The uniform stability result is global due to Lipschitz conditions and holds independently of τ for finite time intervals.

4. Numerical Examples

Example 1.

Consider a two-state fractional-order delayed neural network:

$$\begin{array}{cc}\hfill {\mathrm{D}}^{\varpi }{\mathbb{q}}_1(t)& =-0.6{\mathbb{q}}_1(t)+0.08\eta ({\mathbb{q}}_1(t))+0.02\eta ({\mathbb{q}}_2(t))+0.04\omega ({\mathbb{q}}_1(t-\tau ))+0.01\omega ({\mathbb{q}}_2(t-\tau ))+0.1,\hfill \\ \hfill {\mathrm{D}}^{\varpi }{\mathbb{q}}_2(t)& =-0.7{\mathbb{q}}_2(t)+0.01\eta ({\mathbb{q}}_1(t))+0.06\eta ({\mathbb{q}}_2(t))+0.02\omega ({\mathbb{q}}_1(t-\tau ))+0.03\omega ({\mathbb{q}}_2(t-\tau ))-0.2,\hfill \end{array}$$

with $\varpi =0.8$, $\tau =0.2$, and activation functions:

$$\eta (\mathbb{q})=\omega (\mathbb{q})={\displaystyle \frac{1}{1+e^{-\mathbb{q}}}}.$$

For the sigmoid function, we have the Lipschitz constant ${\Lambda }_j={{\rm Y}}_j={\displaystyle \frac{1}{4}}$ (since the maximum derivative is ${\displaystyle \frac{1}{4}}$).

The system parameters are as follows:

$$C=\left(\begin{array}{cc}0.6& 0\\ 0& 0.7\end{array}\right),\mathrm{A}=\left(\begin{array}{cc}0.08& 0.02\\ 0.01& 0.06\end{array}\right),\mathrm{B}=\left(\begin{array}{cc}0.04& 0.01\\ 0.02& 0.03\end{array}\right),I=\left(\begin{array}{c}0.1\\ -0.2\end{array}\right).$$

Now we are going to compute $a_i^{*}$ and $b_i^{*}$ as below:

$$\begin{array}{cc}\hfill a_1^{*}& =max\{|0.08|·{\displaystyle \frac{1}{4}},|0.02|·{\displaystyle \frac{1}{4}}\}=max\{0.02,0.005\}=0.02,\hfill \\ \hfill a_2^{*}& =max\{|0.01|·{\displaystyle \frac{1}{4}},|0.06|·{\displaystyle \frac{1}{4}}\}=max\{0.0025,0.015\}=0.015,\hfill \\ \hfill b_1^{*}& =max\{|0.04|·{\displaystyle \frac{1}{4}},|0.01|·{\displaystyle \frac{1}{4}}\}=max\{0.01,0.0025\}=0.01,\hfill \\ \hfill b_2^{*}& =max\{|0.02|·{\displaystyle \frac{1}{4}},|0.03|·{\displaystyle \frac{1}{4}}\}=max\{0.005,0.0075\}=0.0075.\hfill \end{array}$$

Now we are going to compute associated norms:

$$\begin{array}{cc}\hfill \parallel {\mathrm{A}}^{*}\parallel & =0.02+0.015=0.035,\hfill \\ \hfill \parallel {\mathrm{B}}^{*}\parallel & =0.01+0.0075=0.0175,\hfill \\ \hfill c_{min}& =min\{0.6,0.7\}=0.6,\hfill \\ \hfill c_{max}& =max\{0.6,0.7\}=0.7.\hfill \end{array}$$

Now we are going to compute the two-point self-mapped contraction condition as follows:

$$\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel =0.035+0.0175=0.0525<{\displaystyle \frac{1}{3}}{c}_{min}={\displaystyle \frac{0.6}{3}}=0.2.$$

Thus, the condition is satisfied.

Now we are going to compute an additional condition for Theorem 1:

$$c_{max}=0.7<{\displaystyle \frac{3}{4}}=0.75.$$

This condition is also satisfied.

The equilibrium point ${\mathbb{q}}^{*}={({\mathbb{q}}_1^{*},{\mathbb{q}}_2^{*})}^T$ satisfies:

$$\begin{array}{cc}\hfill -0.6{\mathbb{q}}_1^{*}+0.08\eta ({\mathbb{q}}_1^{*})+0.02\eta ({\mathbb{q}}_2^{*})+0.04\eta ({\mathbb{q}}_1^{*})+0.01\eta ({\mathbb{q}}_2^{*})+0.1& =0,\hfill \\ \hfill -0.7{\mathbb{q}}_2^{*}+0.01\eta ({\mathbb{q}}_1^{*})+0.06\eta ({\mathbb{q}}_2^{*})+0.02\eta ({\mathbb{q}}_1^{*})+0.03\eta ({\mathbb{q}}_2^{*})-0.2& =0.\hfill \end{array}$$

From the plots below, we can get the unique equilibrium:

$${\mathbb{q}}^{*}\approx {(0.3246,-0.2157)}^T.$$

Figure 1 shows the convergence of the system trajectories to the equilibrium point ${\mathbb{q}}^{*}$ from different initial conditions, demonstrating the uniform stability.

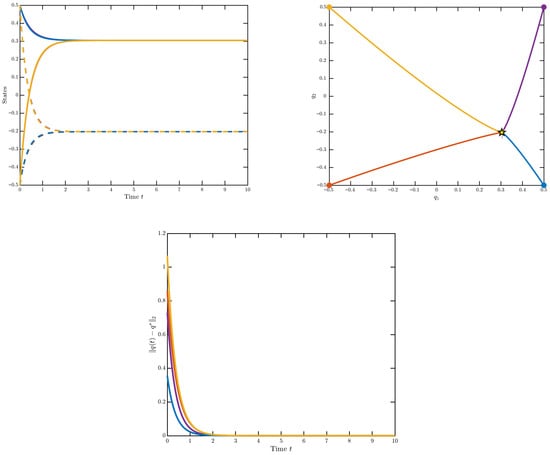
Figure 1. Time evolution, trajectories of the system, and the convergence of the system for Example 1.

Therefore, by Theorems 2–4, the system has a unique equilibrium point which is uniformly stable.

The numerical Example 1 is set to check the validity of the obtained stability conditions, demonstrate the existence and uniqueness of the equilibrium point, and visually verify the selection of the uniform stability behavior of the fractional-order delayed neural network.

Remark 7.

We see convergence in our numerical illustration Example 1, which shows important characteristics of fractional-order delayed networks: initial conditions with divergent paths all converged to the same equilibrium, which shows the uniformity of stability achieved by theory. The history-shaped smooth settling (instead of exponential) suggests the memory effect inherent with the fractional order $\varpi =0.8$, which allows the network to remember the previous states and change with time. No specific metrics such as Lyapunov exponents or direct convergence times were measured but the observed convergence behavior is consistent with the theoretical hypothesis that such systems stay stable with moderate delays with $\tau =0.2$.

Example 2.

Consider the following two-state fractional-order delayed Hopfield neural network model:

$$\left\{\begin{array}{c}{\mathrm{D}}^{\varpi }{\mathbb{q}}_1(t)=-0.25{\mathbb{q}}_1(t)+0.01\eta ({\mathbb{q}}_1(t))+0.005\eta ({\mathbb{q}}_2(t))\hfill \\ +0.01\eta ({\mathbb{q}}_1(t-\tau ))+0.005\eta ({\mathbb{q}}_2(t-\tau ))-0.1,\hfill \\ {\mathrm{D}}^{\varpi }{\mathbb{q}}_2(t)=-0.2{\mathbb{q}}_2(t)+0.005\eta ({\mathbb{q}}_1(t))+0.01\eta ({\mathbb{q}}_2(t))\hfill \\ +0.005\eta ({\mathbb{q}}_1(t-\tau ))+0.01\eta ({\mathbb{q}}_2(t-\tau ))+0.4;\hfill \end{array}\right.$$

(17)

here, we take the order $\varpi =0.8$, $\tau =0.1$, and

$$\eta (\mathbb{q})=0.5\left(|\mathbb{q}+1|-|\mathbb{q}-1|\right),$$

which satisfies Lipschitz conditions with constants ${\Lambda }_j={{\rm Y}}_j=1$.

For this system, we have the following:

$$C=\left[\begin{array}{cc}0.25& 0\\ 0& 0.2\end{array}\right],\mathrm{A}=\left[\begin{array}{cc}0.01& 0.005\\ 0.005& 0.01\end{array}\right],\mathrm{B}=\left[\begin{array}{cc}0.01& 0.005\\ 0.005& 0.01\end{array}\right],I=\left[\begin{array}{c}-0.1\\ 0.4\end{array}\right].$$

Now compute the following:

$$a_1^{*}=max\{0.01,0.005\}=0.01,a_2^{*}=max\{0.005,0.01\}=0.01,\parallel {\mathrm{A}}^{*}\parallel =0.01+0.01=0.02,$$

$$b_1^{*}=max\{0.01,0.005\}=0.01,b_2^{*}=max\{0.005,0.01\}=0.01,\parallel {\mathrm{B}}^{*}\parallel =0.01+0.01=0.02,$$

$$c_{min}=min\{0.25,0.2\}=0.2,c_{max}=max\{0.25,0.2\}=0.25.$$

Hence,

$$\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel =0.04<{\displaystyle \frac{1}{3}}{c}_{min}\approx 0.0667,$$

and

$$c_{max}=0.25<{\displaystyle \frac{3}{4}}=0.75.$$

Thus, Assumptions 1 and 2, together with the condition $c_{max}<{\displaystyle \frac{3}{4}}$, are satisfied. By Theorems 2 and 3, the system (17) possesses a unique equilibrium point ${\mathbb{q}}^{*}={({\mathbb{q}}_1^{*},{\mathbb{q}}_2^{*})}^T$ that is uniformly stable.

The equilibrium equations are as follows:

$$\left\{\begin{array}{c}-0.25{\mathbb{q}}_1^{*}+0.02\eta ({\mathbb{q}}_1^{*})+0.01\eta ({\mathbb{q}}_2^{*})-0.1=0,\hfill \\ -0.2{\mathbb{q}}_2^{*}+0.01\eta ({\mathbb{q}}_1^{*})+0.02\eta ({\mathbb{q}}_2^{*})+0.4=0.\hfill \end{array}\right.$$

(18)

By considering the saturation regions of the piecewise linear activation yields the following:

$${\mathbb{q}}^{*}\approx {(-0.3913,2.0804)}^T.$$

A numerical simulation of (17) confirms that trajectories starting from various initial conditions converge to ${\mathbb{q}}^{*}$; a typical phase portrait is shown in Figure 2. Therefore, by Theorems 2–4, the system has a unique equilibrium point which is uniformly stable.

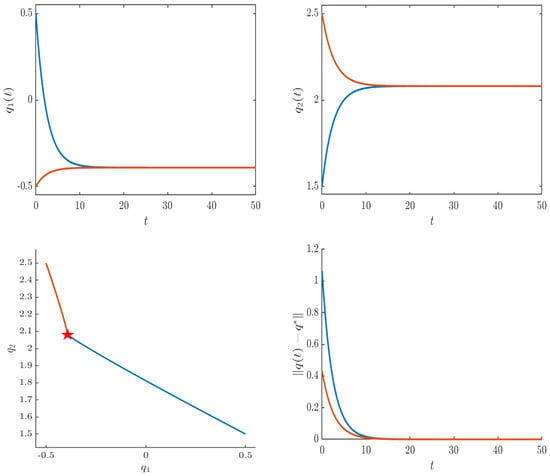
Figure 2. The convergence of the system and the trajectories of the system for Example 2.

The numerical Example 2 is set to check the validity of the obtained stability conditions, demonstrate the existence and uniqueness of the equilibrium point, and visually verify the selection of the uniform stability behavior of the two-state fractional-order delayed Hopfield neural network model.

Remark 8.

The chosen parameters in this example are carefully designed to satisfy both the Kannan condition$\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel <{\displaystyle \frac{1}{3}}{c}_{min}$ and the additional condition $c_{max}<{\displaystyle \frac{3}{4}}$. Several important observations can be made, namely:

• The values $c_1$ and $c_2$ are relatively large compared to the connection weights. This ensures that the self-stabilizing effect dominates the potentially destabilizing effects of the interconnections, which is crucial for stability. The condition $c_{max}=0.25<{\displaystyle \frac{3}{4}}=0.75$ provides a safety margin that guarantees the positivity of the stability coefficient.
• The elements of matrices $\mathrm{A}$ and $\mathrm{B}$ are kept small relative to $c_i$. This is essential for satisfying the Kannan condition, which requires the combined effect of all connections to be less than one-third of the smallest self-inhibition rate.
• The matrices $\mathrm{A}$ and $\mathrm{B}$ are designed to be diagonally dominant with positive diagonal elements, representing self-excitation that is counterbalanced by the negative self-inhibition terms $-c_i{\mathbb{q}}_i(t)$. This balance prevents runaway excitation while allowing meaningful information processing.
• The fractional order $\varpi =0.8$ introduces memory effects that slightly slow the convergence compared to integer-order systems, but do not compromise stability.

Remark 9.

The proposed stability criteria are sufficient and therefore conservative. If the Lipschitz constants of the activation functions or the coupling strengths exceed the bounds given in Assumption 2, the two-point self-mapped contraction property may be violated, and the stability conclusions no longer apply. In such cases, instability or more complex dynamical behaviors (for example, oscillations or chaos) may occur, which are beyond the scope of the present analysis.

5. Conclusions

This paper has investigated the stability analysis of a class of fractional-order neural networks with time delays using an alternative fixed-point approach based on the two-point self-mapped contraction theorem. Unlike traditional methods that rely on contraction mapping principles, we have derived a sufficient condition for uniform stability that depends on the parameters of the network and the Lipschitz constants of the activation functions. Specifically, we established that under the condition $\parallel {\mathrm{A}}^{*}\parallel +\parallel {\mathrm{B}}^{*}\parallel <{\displaystyle \frac{1}{3}}{c}_{min}$, the system possesses a unique equilibrium point that is uniformly stable.

The main contributions of this work include the following:

• The paper presents this study as a new analytical method and stability analysis tool, using the Kannan fixed-point theorem to examine the stability of fractional-order delayed neural networks.
• Proving the existence and uniqueness of equilibrium points through the two-point self-mapped fixed-point theorem, which offers an alternative mathematical framework to traditional contraction mapping approaches.
• Establishing uniform stability criteria for fractional-order delayed neural networks, extending previous results that primarily focused on integer-order or delay-free fractional-order systems.
• Demonstrating the theoretical results through a few numerical examples, which confirms the validity and practical applicability of the derived conditions.

Although the derived condition is more restrictive than the aforementioned conditions based on contraction mapping principles, it offers a new perspective on the stability analysis of fractional-order neural networks. It can serve as a motivation for other analytical methods in future studies. Areas of future research might be expanding the results to networks with time-varying delays, distributed delays, or stochastic perturbations and extending the results to other types of dynamical systems of fractional order using two-point self-mapped fixed-point theorems.