Complementary Metal-Oxide Semiconductor (CMOS) Circuit Realization of Elliptic Low-Pass Filter of Order (1 + α)

Abstract

In this paper, complementary metal-oxide semiconductor (CMOS) circuit realization of a low-pass elliptic filter of order (1 + α) is realized using the inverse follow-the-leader feedback (IFLF) topology. The transfer functions to approximate the passband and stopband ripple characteristics of the second-order elliptic low-pass filter are synthesized using the nonlinear least squares (NLS) optimization routine. The elliptic filters of orders 1.4, 1.6, and 1.8 are designed using a cross-coupled operational transconductance amplifier (OTA) in the United Microelectronics Corporation (UMC) 180 nm CMOS process. The dynamic range of the filter was found to be 49.7 dB, 52.08 dB, and 54.02 dB for an order of 1.4, 1.6, and 1.8, respectively. The circuit simulation results such as magnitude, phase, transient, and group delay plots, are validated with the MATLAB simulation plots. Monte Carlo and PVT analyses have demonstrated the accuracy and robustness of the design. The proposed approach supports quality education and industry, innovation, and infrastructure.

1. Introduction

Continuous time (CT) filters play a vital role in signal processing, serving to extract desired signal components while attenuating undesired or noise-related components from the input signal. Frequency-selective applications such as ECG, EEG, sensor systems, acoustic systems, control systems, robotics, automation, and military or submarine communications demand suitable filters. To enhance performance across these domains, the design of analog filters has increasingly incorporated fractional calculus [1,2], leading to the development of fractional order (FO) filters. Fractional calculus, which generalizes differentiation and integration to non-integer orders, has enabled significant advancements in the aforementioned applications. The distinctive features of fractional-order filters—such as constant phase response, tunable stopband notch frequency and gain [3], passband shaping [4], and stopband ripple control [5]—have made them an attractive area of research. The improvement in the accuracy of passband and stopband shaping has been achieved by incorporating asymmetrical frequency bands into the optimization routine [6]. Furthermore, critical parameters such as the half-power frequency and quality factor can be orthogonally controlled [7].

In general, filter circuits are designed using transfer functions rather than time-domain representations, and this approach remains valid when fractional-order concepts are incorporated in the design process. Fractional-order capacitors (FOCs) serve as essential components of fractional-order systems. Although FOCs are not yet commercially available, significant research efforts are underway to realize their practical implementation [8,9]. Since ideal fractional-order capacitors (FOCs) are not yet realizable, several approximation techniques have been developed to implement fractional-order filters effectively. At present, fractional-order elements are emulated using RC networks over a limited frequency range [10,11]. Various techniques, such as fractional-order capacitor (FOC) or fractional-order inductor (FOL) emulation [12,13], and integer-order approximations based on polynomial coefficient fitting, have been employed to obtain network-realizable transfer functions [14,15,16]. A detailed analysis of fractional-order analog filter realizations and implementation strategies can be found in [2].

CMOS-based realization of the elliptic fractional-order filter remains unexplored in the literature. In this study, a fractional-order elliptic filter of order (1 + α), representing a generalized second-order filter with a 3 dB passband ripple and a 50 dB stopband ripple, is designed. The proposed fractional-order elliptic filter is implemented using the inverse follow-the-leader feedback (IFLF) configuration. This study employs a cross-coupled CMOS operational transconductance amplifier (OTA) [15,17] for the realization of the fractional-order filter. The transconductance of the OTA can be controlled by varying either the biasing current or the external resistor, providing flexibility in filter tuning. In realizing the fractional-order filter (FOF), the term $s^{\alpha }$ is approximated by a rational transfer function using methods such as Oustaloup, Matsuda, Valsa, or CFE [18]. The circuit complexity and the accuracy of both magnitude and phase responses are largely determined by the type and order of the approximation employed. Compared to the Oustaloup, Valsa, and Matsuda methods, the CFE approximation yielded results that more closely matched the expected response around the half-power and right phase frequencies [18]. To realize an approximated elliptic fractional order filter, the coefficients are computed using the fotf (fractional order transfer function) optimization routine [4,5,19].

The design methodology of the elliptic fractional-order filter, including numerical analysis, least-squares curve fitting, and transfer function approximations, is presented in Section 2. The CMOS circuit realization of the elliptic fractional-order filter using a cross-coupled OTA is discussed in Section 3. The simulation results and performance parameters, and concluding remarks are presented in Section 4 and Section 5, respectively.

2. Design of the Elliptic Fractional Order Filter

2.1. The Literature on the Elliptic Fractional Order Filter

Elliptic filters are extensively used in biopotential signal acquisition [20,21] due to their sharp frequency selectivity and high roll-off rate, enabling effective noise suppression within a limited bandwidth. The precise amplitude and phase control of elliptic FoFs make them ideal for applications such as ECG, EEG, and EMG signal processing. Elliptic fractional-order filters (FOFs) [6,19] are considered to be superior to other fractional filter types (Butterworth, Chebyshev-I/II, Bessel, etc.) because they simultaneously exploit elliptic optimality and fractional-order flexibility. Elliptic FOFs give the sharpest roll-off with the smallest order. The elliptic FOFs provide a superior stopband and precise control over notch depth (due to fractional zeros) in comparison to other FOFs like Butterworth and Bessel. The elliptic FOFs offer improved interference rejection and a higher stopband attenuation rate per decade, which are particularly beneficial in mixed-signal circuit design, biomedical and sensor interfaces, and noise-limited communication front ends.

The design and validation of a (1 + α) low-pass elliptic FO analog filter response [19] was studied using MATLAB ® R2024a. Further, responses of a (1 + α) low-pass elliptic FOF were validated using SPICE [6] using two op-amp topologies realized with approximated fractional-order capacitor (FOC) implementation using Foster 1 topology. Ashu Soni et al. [22] have discussed the effect of bandwidth on the FO elliptic filter and observed that the fractional and integer order elliptic filter gives a better response as compared to the Chebyshev filter in the terms of order reduction and stability. Further, the SPICE simulation of a (1  +  α)-order low-pass elliptic filter using a fractional capacitor [23] has been considered. A CMOS-based realization of the elliptic fractional-order filter has not been addressed in existing studies.

The synthesis of elliptic FOFs can be carried out using optimization-based techniques, including least-squares curve fitting and the fitmagfrd frequency-response fitting function, which employs nonlinear least-squares optimization to match the desired magnitude response [6,19]. These elliptic FOF filters were realized using op-amp and passive RC ladder networks (approximating the FoC component). The integer-order approximation of the fractional-order transfer function is discussed next.

2.2. Overview

The specification set of a low-pass filter [24] is given by

$$\begin{gathered} S=\left\{f_p,f_s,A_p,A_s\right\} \\ {f}_p,f_s\in \left[\mathrm{0,1}\right] \end{gathered}$$

(1)

where $\left\{f_p,f_s\right\}$ are the passband edge frequency (Hz) and the stopband edge frequency (Hz), respectively, and are normalized from 0 to 1. $\left\{A_p,A_s\right\}$ represent the maximum allowable ripple in the passband (dB) and minimum stopband attenuation (dB), respectively.

A second-order elliptic filter can be realized with a low-pass notch (LPN) circuit, which is characterized by

$$E_{INT}^2\left(s\right)=k{\displaystyle \frac{\left[s^2+{{\omega }_z}^2\right]}{s^2+s\frac{{\omega }_o}{Q_o}+{\omega }_o^2}}$$

(2)

k is the gain factor. A second-order elliptic filter was designed to meet the specifications of a 0.01 Hz passband edge, 0.1 Hz stopband edge, 3 dB passband ripple, and 50 dB stopband attenuation. The specifications of the normalized elliptic biquad filter are presented in Table 1, while the corresponding magnitude response obtained from MATLAB simulations is illustrated in Figure 1.

Table 1. Specification details of a second-order normalized elliptic filter.

Description	Notation	Value
Pole frequency	${\omega }_o$	$0.0526$ rad/sec
	$f_o$	$0.0083$ Hz
Notch or zero frequency	${\omega }_n$	$0.788$ rad/sec
	$f_n$	0.125 Hz
Pass band edge frequency	$f_p$	0.01 Hz
Stop band edge frequency	$f_s$	0.1 Hz
Passband ripple	$A_p$	3 dB
Stopband attenuation	$A_s$	50 dB
Quality factor	$Q_p$	1.309

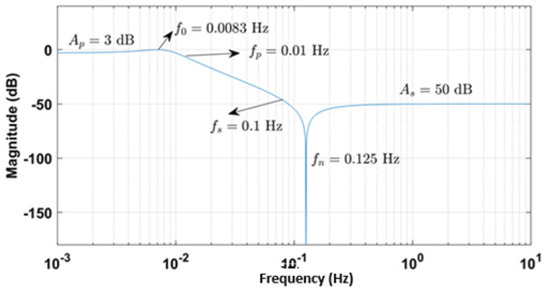
Figure 1. Simulated magnitude response of second-order low-pass elliptic filter for specification details in Table 1.

The transfer function of the normalized second-order elliptic filter realized using the LPN circuit for the specifications in Table 1 is given by

$${\mathrm{E}}_{\mathrm{I}\mathrm{N}\mathrm{E}}\left(\mathrm{s}\right)=0.003162\ast \left\{{\displaystyle \frac{{\mathrm{s}}^2+0.6211}{{\mathrm{s}}^2+0.04022\mathrm{s}+0.002774}}\right\}$$

(3)

The MATLAB Control System Toolbox supports the creation of transfer function models with specified frequency and attenuation parameters. The function ellipord determines the minimum filter order (N) and cut-off frequency required to meet the given design specifications, while ellip computes the numerator and denominator coefficients of the corresponding filter transfer function. A DC gain of −3 dB and a high-frequency gain (HFG) of −50 dB are anticipated for the desired response. To obtain such a magnitude characteristic, both poles and zeros are required to realize the specified ripples in the passband and stopband. In contrast, Butterworth and Chebyshev filters utilize only poles for their realization, thereby distinguishing them from the elliptic filter, which incorporates zeros in addition to poles. The fractional-order (1 + α) transfer function, when approximated using a second-order model, provides a close representation of the desired passband and stopband ripple characteristics and enables the realization of fractional-order poles and zeros.

The fractional-order filters can be synthesized using the lsqcurvefit function, a nonlinear optimization tool that approximates the desired filter characteristics by fitting a mathematical model to the given data points.

2.3. Least-Squares Fitting Function

The fractional-order filters are synthesized using the lsqcurvefit function, a nonlinear optimization algorithm that approximates the desired filter characteristics by fitting a mathematical model to the given data points. The optimal coefficients of the elliptic low-pass filter are determined through the following procedure:

• Defining the transfer function incorporating the fractional-order terms along with the corresponding coefficients.
• Specifying the target frequency response characteristics based on the design specifications provided in Equation (3) and illustrated in Figure 1.

$$E_{FOF}^{1+\alpha }\left(s\right)={\displaystyle \frac{k_4\left[k_1{s}^{1+\alpha }+1\right]}{k_2{s}^{1+\alpha }+k_3{s}^{\alpha }+1}}$$

(4)

The lscurvefit function in MATLAB is used to minimize the difference between the actual model and the desired response by adjusting the coefficients, as given in (5)

$$\underset{x}{\mathit{min}}{‖\left|E_{FOF}\left(x,\omega \right)\right|-\left|E_{INE}\left(\omega \right)\right|‖}_2^2={\displaystyle \genfrac{}{}{0pt}{}{\underset{\mathit{x}}{\mathit{min}}}{s.\mathit{t\; x}>0.1}}{\sum }_{i=1}^k{\left(\left|E_{FOF}\left(x,{\omega }_i\right)\right|-\left|E_{INE}\left({\omega }_i\right)\right|\right)}^2$$

(5)

where ${\mathrm{E}}_{\mathrm{F}\mathrm{O}\mathrm{F}}$ is the elliptical fractional order filter given in (4) and ${\mathrm{E}}_{\mathrm{I}\mathrm{N}\mathrm{E}}$ is the second-order elliptic filter given in (3).

2.3.1. Stability

The mapping from the $s^{\alpha }$ plane to the W plane [16,25] yields the following characteristic equation:

$${\mathrm{k}}_2{\left(\mathrm{W}\right)}^{\mathrm{m}+\mathrm{k}}+{\mathrm{k}}_3{\mathrm{W}}^{\mathrm{k}}+1=0$$

(6)

where $\mathrm{W}={\mathrm{s}}^{1/\mathrm{m}}$ and m, k > 0 are integers.

The roots of (6) were computed for $\alpha =0.1$ to $0.9$ with $m=10$, yielding $W$ in the range of 16.37° to 9.49°. These results satisfy the minimum root condition ${\theta }_W>{\displaystyle \frac{{180}^{\circ }}{2m}}$ (i.e., 9°), confirming that each transfer function obtained using the coefficients of the derived fractional-order filter is stable [25]. However, when ${\theta }_W>{\displaystyle \frac{{180}^{\circ }}{m}}$ (i.e., 18°), the corresponding systems are not physically realizable [26]. Table 2 presents the coefficients of the fractional-order filter polynomials corresponding to orders 1.4, 1.6, and 1.8, which form the basis for the subsequent filter circuit implementation.

Table 2. Coefficient values for (1 + $\alpha$) fractional-order elliptic filter.

Parameter	α = 0.4	α = 0.6	α = 0.8
${\mathrm{k}}_1$	0.0187	0.0206	0.0187
${\mathrm{k}}_2$	2.9086	3.2157	3.6248
${\mathrm{k}}_3$	0.0001	0.0001	0.7212
${\mathrm{k}}_4$	0.7356	0.6486	0.7040
${\tau }_1$(µs)	29.11	38.21	49.23
${\tau }_2$(µs)	481.5	774.1	1196.58
${\tau }_3$(µs)	1583	1196.5	940.17
${\theta }_{\mathrm{w}}$	12.864°	11.418°	11.27°
${\mathrm{G}}_0$	217.45	188.68	177.67
${\mathrm{G}}_1$	22.34	18.7	17.81
${\mathrm{G}}_2$	1.3693	1.1158	1.018
${\mathrm{G}}_3$	1	1	1

2.3.2. Transfer Function Approximation

Fractional-order filters utilize the fractional Laplacian operator, expressed as $s^{\alpha }$, in contrast to integer-order filters that use the integer-order operator $s$. The approximation is limited to the second order and substituting $s^{\alpha }$ from [27] yields the Laplacian term given by

$$s^{\alpha }={\displaystyle \frac{a_0{s}^2+a_{1}s+a_2}{a_2{s}^2+a_{1}s+a_0}}$$

(7)

The design equation for coefficients $a_0,a_1,a_2$ [27] in (7) are given as

$$\begin{gathered} a_0={\alpha }^2+3\alpha +2 \\ {a}_1=8-2{\alpha }^2 \\ {a}_2={\alpha }^2-3\alpha +2 \end{gathered}$$

(8)

The integer-order approximation of the fractional-order elliptic filter with order (1 + α) is expressed as

$$H_{FON}^{1+\alpha }\left(s\right)={\displaystyle \frac{k_4}{k_2\ast a_0}}\left[{\displaystyle \frac{A_3\ast s^3+A_2\ast s^2+A_1\ast s+A_0}{s^3+B_2\ast s^2+B_1\ast s+B_0}}\right]$$

(9)

where

$$\begin{gathered} {\mathrm{A}}_3={\mathrm{k}}_1\ast {\mathrm{a}}_0 \\ {\mathrm{A}}_2={\mathrm{k}}_1\ast {\mathrm{a}}_1+{\mathrm{a}}_2 \\ {\mathrm{A}}_1={\mathrm{k}}_1\ast {\mathrm{a}}_2+{\mathrm{a}}_1 \\ {\mathrm{A}}_0={\mathrm{a}}_0 \end{gathered}$$

(10)

$$\begin{gathered} {\mathrm{B}}_2={\displaystyle \frac{{\mathrm{k}}_2{\mathrm{a}}_1+{\mathrm{k}}_3{\mathrm{a}}_0+{\mathrm{a}}_2}{{\mathrm{k}}_2\ast {\mathrm{a}}_0}} \\ {\mathrm{B}}_1={\displaystyle \frac{{\mathrm{k}}_2{\mathrm{a}}_2+{\mathrm{k}}_3{\mathrm{a}}_1+{\mathrm{a}}_1}{{\mathrm{k}}_2\ast {\mathrm{a}}_0}} \\ {\mathrm{B}}_0={\displaystyle \frac{{\mathrm{k}}_2{\mathrm{a}}_2+{\mathrm{a}}_0}{{\mathrm{k}}_2\ast {\mathrm{a}}_0}} \end{gathered}$$

(11)

2.3.3. Functional Block Diagram

The integer-order approximated fractional-order transfer function of the elliptic filter in (9) was implemented using the functional block diagram shown in Figure 2, which is based on the inverse follow-the-leader feedback (IFLF) topology.

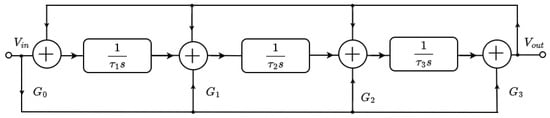
Figure 2. Functional block diagram of IFLF topology.

The transfer function for the filter structure in Figure 2 is shown to be

$${\displaystyle \frac{{\mathrm{V}}_{\mathrm{o}\mathrm{u}\mathrm{t}}}{{\mathrm{V}}_{\mathrm{i}\mathrm{n}}}}={\displaystyle \frac{{\mathrm{G}}_3{\mathrm{s}}^3+\frac{{\mathrm{G}}_2}{{\tau }_1}{\mathrm{s}}^2+\frac{{\mathrm{G}}_1}{{\tau }_1{\tau }_2}\mathrm{s}+\frac{{\mathrm{G}}_0}{{\tau }_1{\tau }_2{\tau }_3}}{{\mathrm{s}}^3+\frac{1}{{\tau }_1}{\mathrm{s}}^2+\frac{1}{{\tau }_1{\tau }_2}\mathrm{s}+\frac{1}{{\tau }_1{\tau }_2{\tau }_3}}}$$

(12)

2.3.4. OTA-C Circuit Realization of Fractional-Order Low-Pass Elliptic Filter

The OTA and capacitance (OTA-C) circuit realization of the fractional-order low-pass elliptic filter of order (1 + α) is shown in Figure 3. The values of feedforward factors $G_i$ (i = 0, 1, 2, 3) and time constants ${\tau }_i$ (i = 0, 1, 2) in the functional block diagram of Figure 2, obtained by equating the polynomial coefficients in (12) and (9), are listed in Table 2.

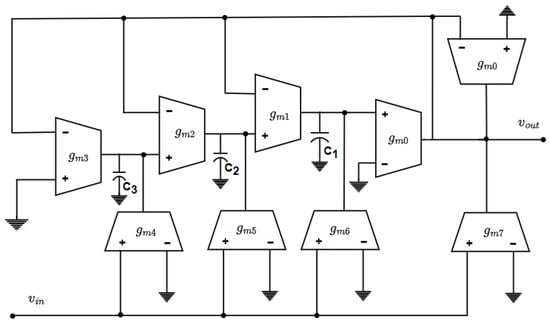
Figure 3. OTA-C realization of fractional order elliptic LPF of order (1 + α).

The expressions for the feedforward factors $G_i$ and the time constants ${\tau }_i$ in terms of transconductances $g_i$ and capacitances $C_i$ of the OTA- C circuit in Figure 3 are given as follows:

$${\mathrm{G}}_0={\displaystyle \frac{{\mathrm{g}}_{\mathrm{m}4}}{{\mathrm{g}}_{\mathrm{m}3}}}; {\mathrm{G}}_1={\displaystyle \frac{{\mathrm{g}}_{\mathrm{m}5}}{{\mathrm{g}}_{\mathrm{m}2}}}; {\mathrm{G}}_2={\displaystyle \frac{{\mathrm{g}}_{\mathrm{m}6}}{{\mathrm{g}}_{\mathrm{m}1}}}; {\mathrm{G}}_3=1$$

(13a)

$${\tau }_1={\displaystyle \frac{{\mathrm{C}}_1}{{\mathrm{g}}_{\mathrm{m}1}}};{\tau }_2={\displaystyle \frac{{\mathrm{C}}_2}{{\mathrm{g}}_{\mathrm{m}2}}}; {\tau }_3={\displaystyle \frac{{\mathrm{C}}_3}{{\mathrm{g}}_{\mathrm{m}3}}};$$

(13b)

3. CMOS Circuit Realization of the Fractional-Order Elliptic Filter

The fractional-order elliptic filters with orders 1.4, 1.6, and 1.8 were synthesized and realized in the UMC 180 nm CMOS process. The design employs a cross-coupled OTA architecture with an integrated common-mode feedback circuit to ensure stable operation.

3.1. CMOS OTA Architecture

The schematic of the cross-coupled (CC) CMOS OTA [17] with its biasing network, used in the realization of the fractional-order elliptic low-pass filter (LPF), is shown in Figure 4a. The required bias currents ($I_{B0},$ $I_{B1},)$ are mirrored from the basic current mirror circuit shown in Figure 4b. The reference current $I_{REF}$ can be generated using precision current reference circuits such as the Proportional to Absolute Temperature (PTAT) [28,29,30] and Complementary to Absolute Temperature (CTAT) [31,32].

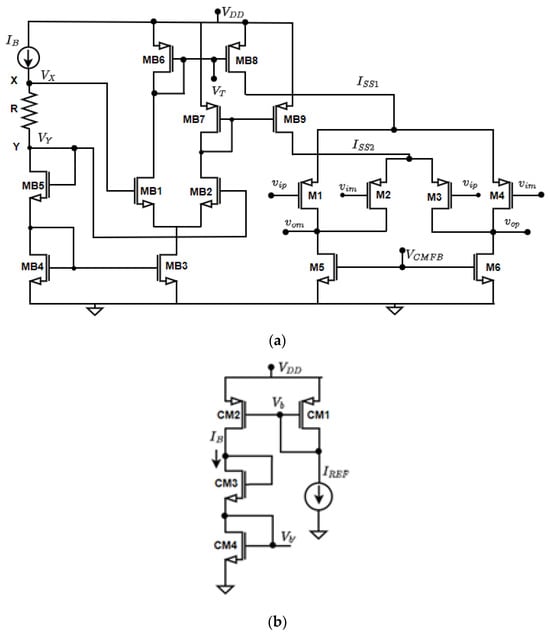
Figure 4. (a) CMOS circuit of CC-OTA with tail current generation [17], (b) current mirror circuit used to realize ${\mathit{I}}_{\mathit{B}}$.

The effective transconductance of the OTA can be tuned by varying the resistor R connected between nodes X and Y, for a given bias current $I_B.$ The overall transconductance of the CC-OTA is determined as the difference between the transconductances of the two source-coupled PMOS differential pairs (M₁–M₄ and M₂–M₃), and is expressed as

$${\mathrm{g}}_{\mathrm{m}\mathrm{e}\mathrm{f}\mathrm{f}}={\mathrm{g}}_{\mathrm{m}1}-{\mathrm{g}}_{\mathrm{m}2}={\displaystyle \frac{{\mathrm{I}}_{\mathrm{S}\mathrm{S}1}}{2\eta {\mathrm{V}}_{\mathrm{T}}}}-{\displaystyle \frac{{\mathrm{I}}_{\mathrm{S}\mathrm{S}2}}{2\eta {\mathrm{V}}_{\mathrm{T}}}}={\displaystyle \frac{{\mathrm{I}}_{\mathrm{S}\mathrm{S}1}-{\mathrm{I}}_{\mathrm{S}\mathrm{S}2}}{2\eta {\mathrm{V}}_{\mathrm{T}}}}={\displaystyle \frac{∆\mathrm{i}}{2\eta {\mathrm{V}}_{\mathrm{T}}}}$$

(14)

where ${\mathbf{g}}_{\mathbf{m}\mathbf{1}}$ and ${\mathbf{g}}_{\mathbf{m}\mathbf{2}}$ are transconductances of PMOS differential pairs M₁–M₄ and M₂–M₃, respectively, which are operated in the sub-threshold region.

The overall transconductance of the CC-OTA is obtained as the difference between the individual transconductances, which serves as an effective technique for achieving low transconductance values. The aspect ratio of MOS transistors (M1–M6 and MB1–MB9) used in CC-OTA for realization of different transconductances ${\mathrm{g}}_{\mathrm{m}0}$ to ${\mathrm{g}}_{\mathrm{m}7}$ (except ${\mathrm{g}}_{\mathrm{m}4}$) in Figure 3 are summarized in Table 3.

Table 3. Transistor size of CC-OTA.

Transistor	Order = 1.4	Order = 1.6	Order = 1.8
	$[\mathrm{m}\ast (\mathrm{W}/\mathrm{L}\left)\right]\mathrm{\mu }\mathrm{m}$
M1, M2, M3, M4	4 ∗ (5/40)	4 ∗ (10/48)	$4\ast (2/40)$
M5, M6	$(0.25/48)$
MB1, MB2	$2\ast (1/48)$
MB3, MB4, MB5	$2\ast (1/48)$
MB6, MB7, MB8, MB9	2 ∗ $\left(10/1\right)$

$m$ is the multiplier and $W/L$ is the aspect ratio.

3.2. Common-Mode Feedback Circuit

The common-mode feedback (CMFB) concept and circuit [33,34] employed to regulate the DC operating point of the fully differential OTA of Figure 4 is shown in Figure 5. The CMFB circuit regulates the common-mode output level of the fully differential OTA by sensing the average of $v_{op}$ and $v_{om}$ through the resistive network and comparing it with the reference $V_{CM}$. The sensing and error-amplifying transistors (MC8–MC11) generate the control voltage $V_{CMFB}$, which adjusts the bias voltage of devices M5–M6 (in Figure 4) to restore the desired common-mode voltage. The transistor size details in CMFB circuit of Figure 5b are given in in Table 4. All of the transistors are working in the saturation region.

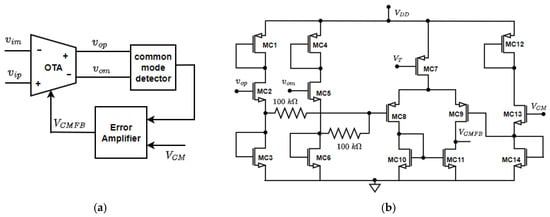
Figure 5. Common-mode feedback scheme: (a) block diagram, (b) CMOS circuit diagram.

Table 4. Transistor size for common-mode feedback circuit in Figure 5b.

Transistor	$\raisebox{1ex}{$\mathit{W}$}\!\left/ \!\raisebox{-1ex}{$\mathit{L}$}\right.$(µm)
MC1, MC3	85/1
MC2, MC4	50/3
MC5, MC6	0.5/18
MC7, MC8	0.5/48
MC9	0.5/30
MC10, MC11	85/1

4. Simulation Results

The schematic entry and circuit simulations of the fractional-order (FO) elliptic filter of orders 1.4, 1.6, and 1.8 (Figure 2) were carried out using the Cadence Virtuoso ® 6.1.6 with Spectre ® circuit simulator (Cadence Design Systems, USA) with UMC 180 nm CMOS technology at a 1.8 V supply. The complete schematic of the FO elliptic filter implemented in Virtuoso is shown in Figure 6. In this design, $V_{CM}$ and $I_B$ represent the common-mode control voltage and the OTA bias current, respectively, while the resistors $R_0,R_1,\dots ,R_7$ are used to tune the transconductances $g_{m0},g_{m1},\dots ,g_{m7}$ of the OTAs employed in the filter architecture of Figure 2. The final design parameters for the FO elliptic filters of orders 1.4, 1.6, and 1.8 used in the simulations are summarized in Table 5.

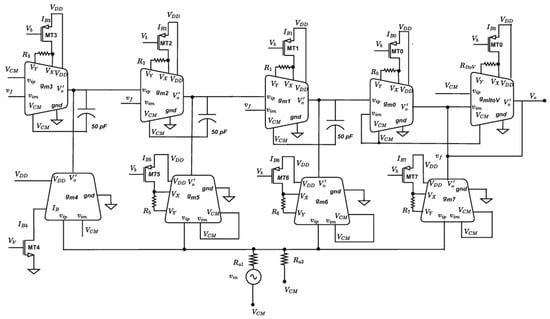
Figure 6. CC-OTA-based elliptic filter of order (1 + $\alpha )$ realised in Cadence Virtuoso.

Table 5. Design values of circuit elements for FO elliptic filter of orders 1.4, 1.6, and 1.8.

Parameter	Transconductance		Resistance		$\mathbf{Current}({\mathit{I}}_{\mathit{B}}$)	Transistor	${(\mathit{W}/\mathit{L})}_{\mathit{m}=2}$
α = 0.4	${\mathrm{g}}_{\mathrm{m}0},{\mathrm{g}}_{\mathrm{m}7},\left(\mathrm{\mu }\mathrm{S}\right)$	1	$R_0$, $R_7$ (kΩ)	900	300 nA	MT0, MT7	$900\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}1}\left(\mathrm{\mu }\mathrm{S}\right)$	1.72	${\mathrm{R}}_1$ (kΩ)	980	230 nA	MT1	$650\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}2}\left(\mathrm{n}\mathrm{S}\right)$	104	${\mathrm{R}}_2$ (kΩ)	105	150 nA	MT2	$390\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}3}\left(\mathrm{n}\mathrm{S}\right)$	33	150 nA	${\mathrm{R}}_3$ (kΩ)	33	MT3	$390\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}4}\left(\mathrm{\mu }\mathrm{S}\right)$	7.09	NA *	NA *	1 µA	MT4	$46\mu /1\mu$
	${\mathrm{g}}_{\mathrm{m}5}\left(\mathrm{n}\mathrm{S}\right)$	1.67	${\mathrm{R}}_5$ (kΩ)	663	200 nA	MT5	$550\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}6}\left(\mathrm{\mu }\mathrm{S}\right)$	1.83	${\mathrm{R}}_6$ (MΩ)	1	250 nA	MT6	$580\mathrm{n}/48\mu$
		${\mathrm{R}}_{\mathrm{a}1}\left(\mathrm{k}\mathrm{\Omega }\right)$		5
		${\mathrm{R}}_{\mathrm{a}2}(\mathrm{\Omega }$)		16.91
α = 0.6	${\mathrm{g}}_{\mathrm{m}0},{\mathrm{g}}_{\mathrm{m}7},\left(\mathrm{\mu }\mathrm{S}\right)$	1	$R_0$, $R_7$ (kΩ)	675	180 nA	MT0, MT7	$520\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}1}\left(\mathrm{\mu }\mathrm{S}\right)$	1.32	${\mathrm{R}}_1$ (MΩ)	1.05		MT1
	${\mathrm{g}}_{\mathrm{m}2}\left(\mathrm{n}\mathrm{S}\right)$	65	${\mathrm{R}}_2$ (kΩ)	39.7		MT2
	${\mathrm{g}}_{\mathrm{m}3}\left(\mathrm{n}\mathrm{S}\right)$	42	${\mathrm{R}}_3$ (kΩ)	256		MT3
	${\mathrm{g}}_{\mathrm{m}4}(\mu \mathrm{S})$	7.69	$\mathrm{N}\mathrm{A}$ *	$\mathrm{N}\mathrm{A}$ *	1 µA	MT4	$23\mathrm{\mu }/1\mu$
	${\mathrm{g}}_{\mathrm{m}5}\left(\mathrm{\mu }\mathrm{S}\right)$	1.215	${\mathrm{R}}_5$ (kΩ)	893	180 nA	MT5	$520\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}6}\left(\mathrm{\mu }\mathrm{S}\right)$	1.487	${\mathrm{R}}_6$ (MΩ)	1.61		MT6
		${\mathrm{R}}_{\mathrm{a}1}\left(\mathrm{k}\mathrm{\Omega }\right)$		5
		${\mathrm{R}}_{\mathrm{a}2}(\mathrm{\Omega }$)		16.61
α = 0.8	${\mathrm{g}}_{\mathrm{m}0},{\mathrm{g}}_{\mathrm{m}7},\left(\mathrm{\mu }\mathrm{S}\right)$	1	$R_0$, $R_7$ (kΩ)	900	200 nA	MT0, MT7	$300\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}1}\left(\mathrm{\mu }\mathrm{S}\right)$	1.02	${\mathrm{R}}_1$ (MΩ)	1.37	160 nA	MT1	$430\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}2}\left(\mathrm{n}\mathrm{S}\right)$	40	${\mathrm{R}}_2$ (kΩ)	40.45	150 nA	MT2	$390\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}3}\left(\mathrm{n}\mathrm{S}\right)$	55	${\mathrm{R}}_3$ (kΩ)	55.6		MT3
	${\mathrm{g}}_{\mathrm{m}4}\left(\mathrm{\mu }\mathrm{S}\right)$	9.735	NA *		1 µA	MT4	$12.25\mathrm{\mu }/48\mu$
	${\mathrm{g}}_{\mathrm{m}5}\left(\right(\mathrm{n}\mathrm{S})$	632	${\mathrm{R}}_5$ (kΩ)	824	130 nA	MT5	$330\mathrm{n}/48\mu$
	${\mathrm{g}}_{\mathrm{m}6}\left(\mathrm{\mu }\mathrm{S}\right)$	1.04	${\mathrm{R}}_6$ (kΩ)	848		MT6	$330\mathrm{n}/48\mu$
			${\mathrm{R}}_{\mathrm{a}1}\left(\mathrm{k}\mathrm{\Omega }\right)$	5
			${\mathrm{R}}_{\mathrm{a}2}(\mathrm{\Omega }$)	16.31

* Not applicable.

A large value of $g_{m4}$ was realized using the OTA circuit in Figure 7 without tail current generation and with the different transistor dimensions listed in Table 6.

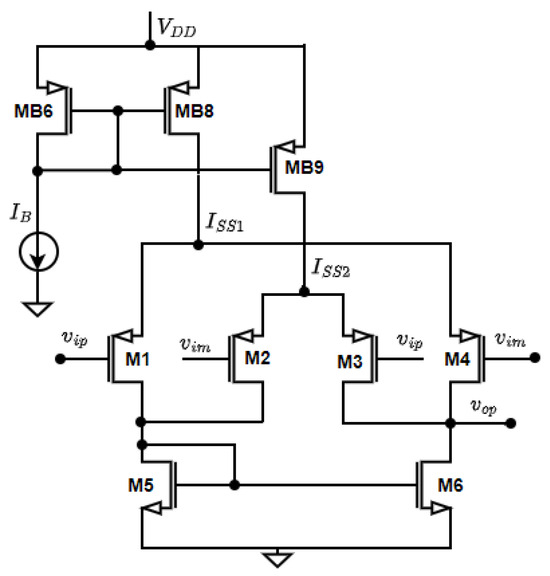
Figure 7. The OTA circuit for ${\mathbf{g}}_{\mathbf{m}\mathbf{4}}$ without tail current generation circuit without CMFB.

Table 6. The transistor size of the OTA $g_{m4}$ for different fractional orders.

Transistors	Order = 1.4	Order = 1.6	Order = 1.8
	${\mathbf{g}}_{\mathbf{m}4}=7.09 \mathbf{\mu }\mathbf{S}$	${\mathbf{g}}_{\mathbf{m}4}=7.69 \mathbf{\mu }\mathbf{S}$	${\mathbf{g}}_{\mathbf{m}4}=9.74 \mathbf{\mu }\mathbf{S}$
	$\mathbf{Aspect}\mathbf{Ratio}[\mathbf{m}\ast (\mathbf{W}/\mathbf{L}\left)\right]\mathbf{\mu }\mathbf{m}$
M1, M2, M3, M4	$8\ast (8.6/40)$	$2\ast (10/40)$	$8\ast (35/40)$
M5, M6	$2\ast (46.6/0.26)$	$2\ast (45/0.26)$	$2\ast (45/0.26)$
MB6	$(20/4)$	$(20/4)$	$(20/4)$
MB8	$(19/4)$	$(19/4)$	$(19/4)$
MB9	$(1/28)$	$(1/28)$	$(1/28)$

4.1. Amplitude Response

The amplitude (in dB) associated with the numerically evaluated ideal transfer functions and the Spectre-simulated implementations of the FO elliptic filters of orders 1.4, 1.6, and 1.8 in Table 7 confirm a high degree of consistency. Figure 8 presents the amplitude responses of FO elliptic filters of orders 1.4, 1.6, and 1.8, comparing the theoretically synthesized responses with the corresponding circuit-level simulation results. A focused view near the cut-off frequency reveals variation between the ideal and simulated responses of 5.82% {(−7.39 + 6.9)/6.9} for a fractional order 1.4. at 150 Hz frequency, 10.8% {(−8.2 + 7.4)/7.4} for a fractional order of 1.6 at 180 Hz, and 0.68% {(−8.2 + 8.256)/8.256} for a fractional order of 1.8 at 200 Hz. The ideal cut-off frequencies for the fractional orders of 1.4, 1.6, and 1.8 are 140 Hz, 179.4 Hz, and 194 Hz, respectively. The corresponding cut-off frequencies obtained from the Spectre-simulated amplitude responses are 152 Hz, 182 Hz, and 199 Hz, resulting in errors of 8.57%, 1.4%, and 2.57%, respectively. The small deviations observed in the Spectre-simulated responses relative to the ideal curves are primarily attributed to the finite output resistance of the OTA and other practical non-idealities, including component tolerances.

Table 7. Magnitude, phase, and group delay of the output waveform of fractional order elliptic filter of orders 1.4, 1.6, and 1.8, across a range of frequencies.

Frequency	Order	Magnitude (dB)		Phase (Deg)		Group Delay (ms)
		Matlab	Cadence	Matlab	Cadence	Matlab	Cadence
50 Hz	1.4	−3.8	−4.8	−25.14	−24.47	1.35	1.35
	1.6	−4.35	−5.2	−20.22	−21.32	1.29	1.28
	1.8	−4.19	−4.7	−16.4	−18.3	1.09	1.17
150 Hz	1.4	−6.9	−7.3	−70.16	−69.91	1.03	1.1
	1.6	−5.8	−6.66	−74.2	−76.44	1.51	1.55
	1.8	−3.92	−4.46	−86.18	−85.84	2.27	2.25
200 Hz	1.4	−9.3	−9.48	−86.2	−87	0.75	0.86
	1.6	−8.69	−9.42	−97.16	−100.3	1	1.8
	1.8	−8.25	−8.2	−116.5	−118.3	1.1	1.3
1 kHz	1.4	−32.66	−33.35	−113.27	−143.1	−0.07	−0.2
	1.6	−35.7	−36.16	−112.7	−138.63	−0.11	−0.03
	1.8	−39.7	−38.8	−125.7	−165.2	−0.11	0.096

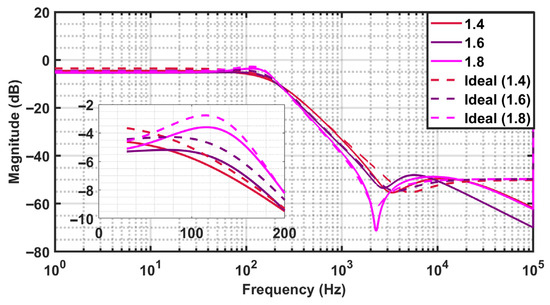
Figure 8. Ideal and simulated magnitude responses of fractional-order elliptic filters of orders 1.4, 1.6, and 1.8, obtained using MATLAB and Cadence Spectre.

4.2. Phase Response

The numerically synthesized ideal phase responses (MATLAB) and the corresponding simulated phase responses (Cadence Spectre) are shown in Figure 9. The phase responses corresponding to the ideal transfer functions and the simulated implementations for the fractional-order elliptic filters of orders 1.4, 1.6, and 1.8 are summarized in Table 7. As can be seen from the phase plot, the phase varies smoothly with an approximately linear trend across the passband, reflecting the controlled dynamic response of the synthesized filter. A pronounced phase transition (phase reversal) occurs at the notch frequency of 2.1 kHz, for the case of a 1.8 fractional order.

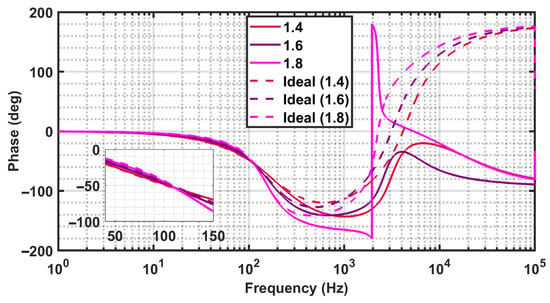
Figure 9. Ideal and simulated phase responses of FO elliptic filters of orders 1.4, 1.6, and 1.8, obtained using MATLAB and Cadence Spectre.

4.3. Group Delay

Group delay (GD) plots for FO elliptic filters of orders 1.4, 1.6, and 1.8 for numerically synthesized ideal responses and circuit-level Spectre simulations are presented in Figure 10. The GD values of the FO elliptic filters of orders 1.4, 1.6, and 1.8 for both the ideal transfer function and the simulated implementation are summarized in Table 7. The plots show preservation of the linear phase over the passband and deviations near the notch frequencies due to practical nonidealities. The nearly linear group delay observed in the passband minimizes waveform distortion, a requirement that is especially important in biomedical signal processing applications—such as ECG, EEG, and EMG—where accurate preservation of temporal features directly affects diagnostic reliability.

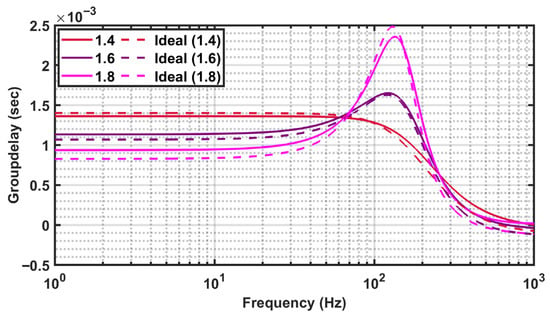
Figure 10. Group delay of the FO elliptic filter of orders 1.4, 1.6, 1.8: numerical synthesis versus circuit-level Spectre simulation.

4.4. Transient Response

The transient simulation of the FO elliptic filter for fractional orders of 1.4, 1.6, and 1.8 was performed using a 50 Hz sinusoidal input signal with a peak-to-peak amplitude of 200 µV, and the resulting time-domain waveforms are shown in Figure 11. The output signals closely follow the input waveform in both shape and frequency, while exhibiting the expected level of attenuation. These time-domain results complement the frequency-domain analysis, further validating the correctness of the filter implementation and confirming its suitability for real-time analog signal-processing applications.

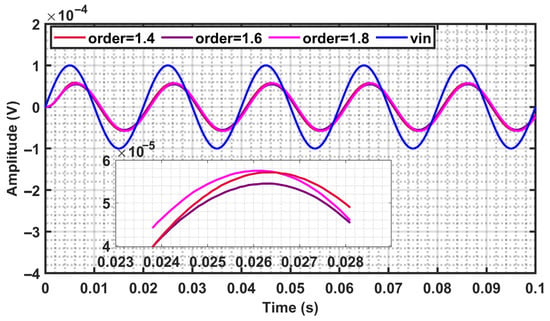
Figure 11. Transient response of the FO elliptic filters with orders 1.4, 1.6, and 1.8, obtained for a 200-µV peak-to-peak sinusoidal input signal at 50 Hz.

4.5. Harmonic Spectrum

The plot of the harmonic spectrum of the FO elliptic filter of order 1.8 is shown in Figure 12. The fundamental component appears at 50 Hz with the highest amplitude, while the subsequent harmonic occurs at an integer multiple of this frequency and exhibits a lower amplitude than the fundamental component. For a sinusoidal input voltage of 200 µV and frequency of 50 Hz, THD is found to be 0.5% (less than 1%).

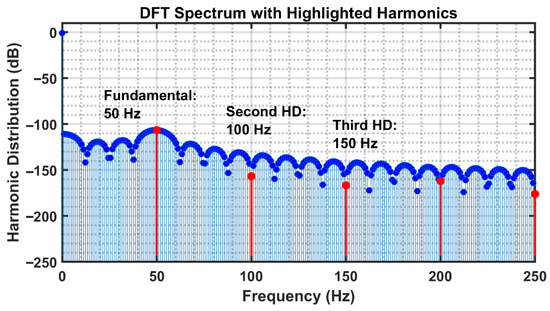
Figure 12. Simulated harmonic spectrum of the FO elliptic filter of order 1.8 with a 200 µV p-p input signal at 50 Hz.

4.6. Monte Carlo Results

Monte Carlo simulations were performed for the FO elliptic filters shown in Figure 6, for orders 1.4, 1.6, and 1.8, with 1000 iterations each, to evaluate the impact of process variations and device mismatch on the cut-off frequency. The resulting plots are presented in Figure 13a–c. From the Gaussian distribution curves for the different orders, shown in distinct colors, it is evident that the pole frequency exhibits minimal variation under process-induced deviations. The mean cut-off frequencies for the fractional orders 1.4, 1.6, and 1.8 are 152.48 Hz, 181.5 Hz, and 199.6 Hz, respectively, and the corresponding Gaussian distributions are well centered around their respective means. The standard deviation (SD) values of the cut-off frequency for fractional orders 1.4, 1.6, and 1.8 are 0.852 Hz, 1.9 Hz, and 2.6 Hz, respectively.

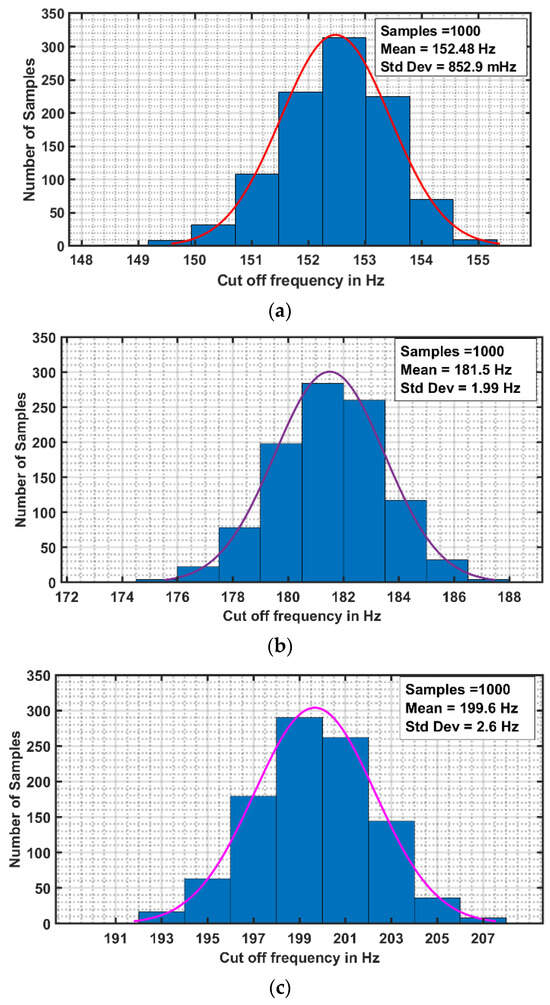
Figure 13. Monte Carlo simulation plots of FO elliptic filter of orders (a) 1.4, (b) 1.6, and (c) 1.8 with respect to cut-off frequency ${\mathrm{f}}_{\mathrm{c}}$.

.

4.7. Effect of PVT and $I_{REF}$

Variations

The implemented FO elliptic filter for fractional orders 1.4, 1.6, and 1.8 were simulated under various PVT (process, voltage, temperature) variations to assess its robustness and performance consistency.

The FO elliptic filters of orders (a) 1.4, (b) 1.6, and (c) 1.8 shown in Figure 6 were simulated across five standard process corners (FF, SNFP, TT, FNSP, and SS) at a temperature of 27 °C and an operating voltage of 1.8 V. The resulting amplitude-response plots are presented in Figure 14a–c. The four standard process corners (FF, SNFP, FNSP, and SS) were compared with the Typical–Typical (TT) corner, which lies at the center of the variation range, and the overall deviation remains within 10%. As the filter order increases, the percentage error in gain also increases.

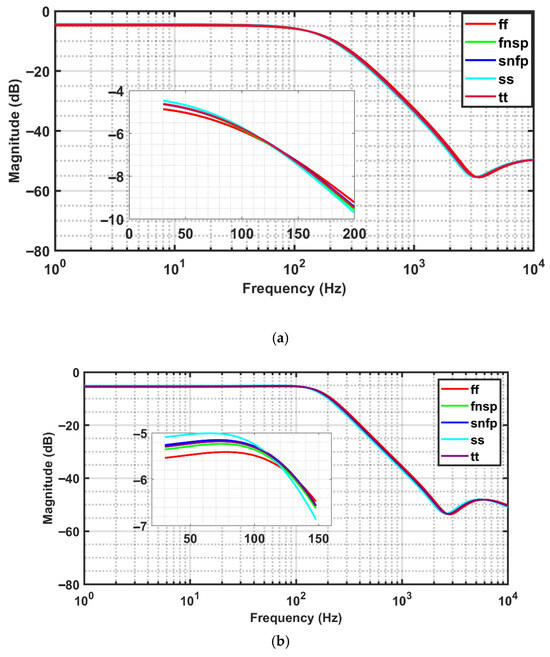
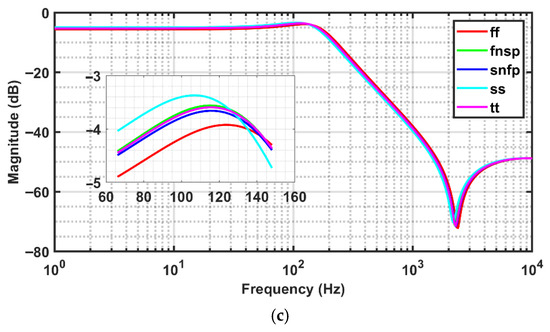
Figure 14. (a–c). Magnitude response of the FO elliptic filter of orders (a) 1.4, (b) 1.6, and (c) 1.8 under different process (P) corners (FF, SNFP, TT, FNSP, and SS) at temperature of 27 °C and an operating voltage of 1.8 V.

The implemented FO elliptic filters of orders 1.4, 1.6, and 1.8 were subjected to a 10% variation in the 1.8 V DC supply voltage (i.e., 1.62 V, 1.8 V, and 1.98 V) at room temperature under the TT process corner. The resulting magnitude-response plots are shown in Figure 15a–c, and the responses are observed to be consistent across the voltage variations. As is indicated in Table 8, the maximum percentage deviation due to voltage variations is 2.2%.

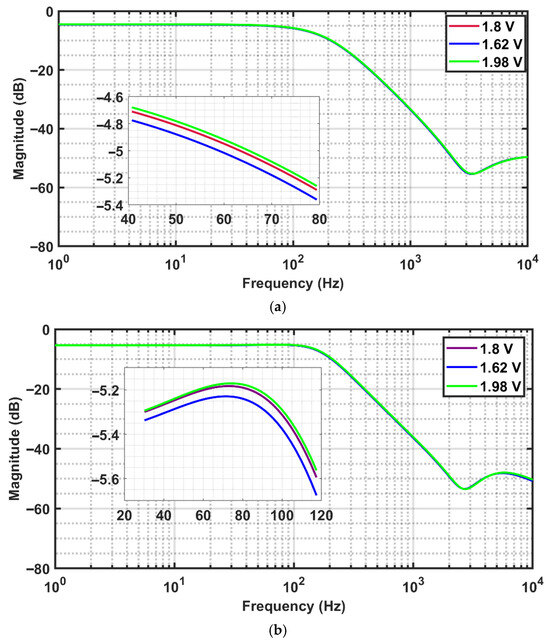
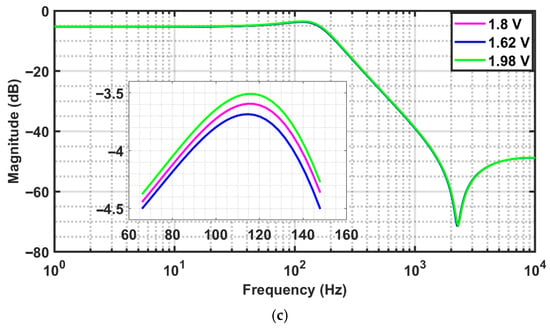
Figure 15. (a–c). Magnitude response of the FO elliptic filter of orders (a) 1.4, (b) 1.6, and (c) 1.8, with respect to 10% voltage variations in 1.8 V DC voltage (1.62, 1.8, 1.98 V) at temperature of 27 °C and at Typical–Typical process corner.

Table 8. Summary of effect of PVT and $I_{REF}$ variations on amplitude response of FO elliptic filter of orders 1.4, 1.6, and 1.8.

Filter Order	Amplitude Value (-dB)$\mathbf{at}{\mathit{f}}_{\mathit{c}}$ Under Normal PVT Conditions (TT, 1.8 V, 27 °C)	Process Variation (FF, SNFP, TT, FNSP, SS)		Voltage Variation (1.62, 1.8, 1.98 V)		$\mathbf{Bias}\mathbf{Current}\left({\mathbf{I}}_{\mathbf{R}\mathbf{E}\mathbf{F}}\right)$$\mathbf{Variation}(\pm 2\mathbf{\%})$		Temperature Variation (0 °C, 27 °C, 80 °C)
		Amplitude Variation (-dB)	Amplitude Variation (%)	Amplitude Variation (-dB)	Amplitude Variation (%)	Amplitude Variation (-dB)	Amplitude Variation (%)	Amplitude Variation (-dB)	Amplitude Variation (%)
1.4	7.4	7.37 to 7.7	0.39 to 3.9	7.42 to 7.54	0.26 to 1.82	7.34 to 7.44	0.1 to 0.68	7.3 to 7.9	1.3 to 6.5
1.6	8.3	7.99 to 8.85	4.81 to 6.24	8.26 to 8.48	0.48 to 2.16	8.09 to 8.43	0.48 to 2.43	7.7 to 9.8	7.2 to 18
1.8	8.1	−7.5 to 9.07	9.7 to 10.8	8.1 to 8.36	2.02 to 2.2	7.89 to 8.57	2.59 to 5.8	6.8 to 10.8	15 to 33

The simulations are carried out for implemented FO elliptic filters in Figure 6 with a variation in temperature of 0 °C, 27 °C, and 80 °C at the TT process corner, and 1.8 V DC voltage resulting amplitude-response plots of orders 1.4, 1.6, and 1.8 are shown in Figure 16a–c. From these plots, the magnitude variation with respect to temperature variations is seen to increase with the increase in order.

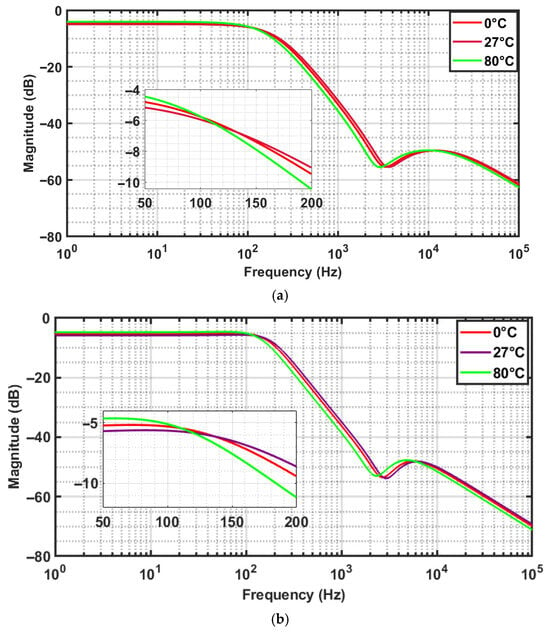
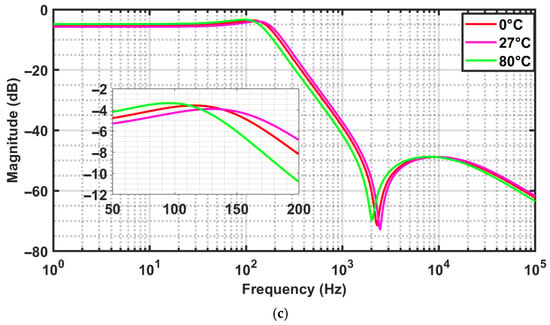
Figure 16. (a–c). Magnitude response of the FO elliptic filter of orders (a) 1.4, (b) 1.6, and (c) 1.8, with respect to temperature 0 °C, 27 °C, and 80 °C at DC voltage 1.8 V and Typical–Typical process corner.

The implemented FO elliptic filters of orders 1.4, 1.6, and 1.8 were subjected to a 2% variation in $I_{REF}$ at the TT process corner, 1.8 V DC supply voltage, and 27 °C room temperature. The resulting magnitude-response plots are shown in Figure 17a–c, and the responses are observed to be consistent across the $I_{REF}$ variations. As is indicated in Table 8, the maximum percentage amplitude deviation due to ±2% ${\mathrm{I}}_{\mathrm{R}\mathrm{E}\mathrm{F}}$ variations are seen to be 5.8%.

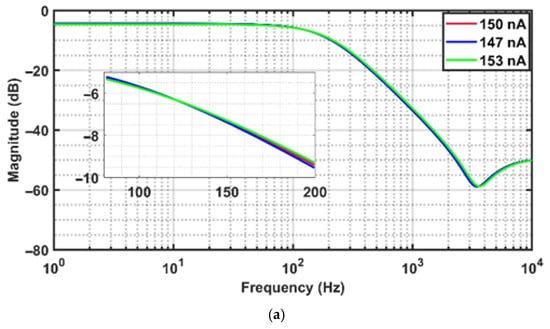
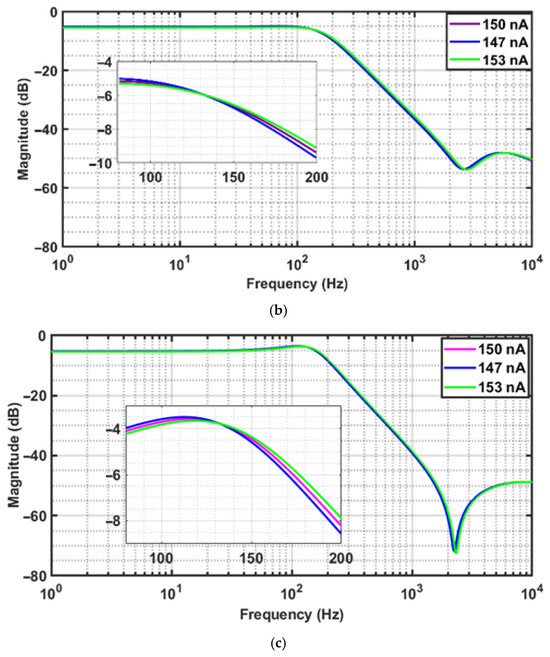
Figure 17. (a–c). Magnitude response of the FO elliptic filter of orders (a) 1.4, (b) 1.6, and (c) 1.8, with respect to 2% $I_{REF}$ variations at Typical–Typical process corner, DC voltage 1.8 V, and a temperature of 27 °C.

A consolidated summary of the effect of PVT variations and $I_{REF}$ variations on amplitude response for these three filter orders is presented in Table 8.

4.8. Output Noise

Figure 18 illustrates the simulated output noise voltage of the FO elliptic filter. The results indicate that flicker noise is the predominant contributor up to approximately 50 Hz, beyond which thermal noise becomes the major component. At 50 Hz, the equivalent output noise levels for the filter orders 1.4, 1.6, and 1.8 are 95.5 nV, 88 nV, and 73.9 nV, respectively.

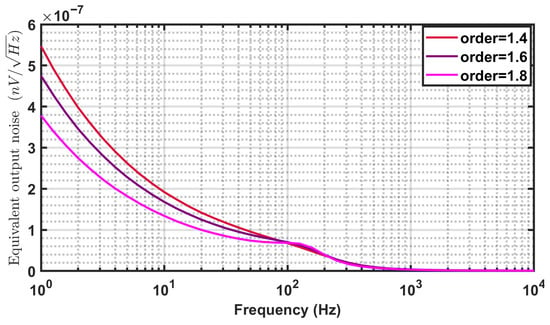
Figure 18. Output noise response of the FO elliptic filter shown in Figure 6 for filter orders 1.4, 1.6, and 1.8.

5. Evaluation of Performance Metrics

The key performance metrics of the FO elliptic filters shown in Figure 6, as obtained from Cadence Spectre simulations for orders 1.4, 1.6, and 1.8, are summarized in Table 9.

Table 9. Summary of performance metrics of FO elliptical filter of orders 1.4, 1.6 and 1.8.

Parameter	Order 1.4	Order 1.6	Order 1.8
Power at $V_{DD}$ = 1.8 V ($\mu \mathrm{W}$)	22	17.9	17.08
Cut-off frequency (Hz)	151 Hz	181 Hz	200 Hz
Attenuation rate (dB/dec)	37.71	39.62	50.78
Attenuation at notch $A_{notch}$(dB)	−55	−55.18	−61.9
Notch frequency $f_0$ (kHz)	5.1	3.3	2.1
Stop band ripple $A_s$(dB)	−50.34	−49.84	−49.78
Input Referred Noise (IRN)$(\mathrm{n}\mathrm{V}/\sqrt{\mathrm{H}\mathrm{z}})$	230.4	$175.8$	140.8
Dynamic range (dB)	49.7	52.08	54.02
Figure of Merit (pJ)	2093	1186	875.35

Dynamic range: The dynamic range (DR) of the filter, evaluated using (15), is found to be approximately 49.7 dB, 52.08 dB, and 54.02 dB for the FO elliptic filter orders 1.4, 1.6, and 1.8, respectively, corresponding to 0.6% total harmonic distortion (THD).

$$\mathrm{D}\mathrm{R}=20\ast \mathrm{l}\mathrm{o}\mathrm{g}{\displaystyle \frac{{\mathrm{V}}_{\mathrm{i}\mathrm{n}\mathrm{m}\mathrm{a}\mathrm{x}}\left(\mathrm{r}\mathrm{m}\mathrm{s}\right)}{\mathrm{I}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t} \mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{d} \mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}\left(\mathrm{r}\mathrm{m}\mathrm{s}\right)}}$$

(15)

Figure of merit (FOM): The figure of merit (FOM) [35] used is as given in (16).

$$\mathrm{F}\mathrm{O}\mathrm{M}={\displaystyle \frac{\mathrm{P}}{\mathrm{D}\mathrm{R}\ast f_c\ast \mathrm{N}}}$$

(16)

where DR, P, ${\mathrm{f}}_{\mathrm{c}},$ and N are the dynamic range, power, cut-off frequency, and order of the filter, respectively. The FOM for the FO elliptic filter orders 1.4, 1.6, and 1.8 are found to be 2093, 1186 and 875 pJ, respectively.

From the simulation results in Figure 8, the stopband attenuation rate is observed to increase significantly with a higher α. A moderate variation in the stopband ripple $A_s$ and the attenuation at the notch frequency $A_{\mathrm{notch}}$ is also noted with changes in filter order. As the filter order increases, the required transconductance values decrease, except for $g_{m4}$ (Table 5), resulting in lower bias currents and reduced power consumption. This trend is confirmed in Table 9, where the total power decreases with increasing α value. Furthermore, a higher filter order yields lower input-referred noise, thereby improving the dynamic range (DR). The figure of merit (FOM) also decreases with increasing α value due to the reduction in power consumption.

A few relevant previously reported research works on FoF are considered for benchmarking the performance metrics of the proposed elliptic FOF. The circuit realization of Butterworth and Chebyshev low-pass and high-pass filters of fractional order ($0<\alpha <1$) using a single current feedback operational amplifier (CFOA) [36] is reported, with the cut-off frequency being independent of the filter order. The design of current-mode FoFs of various filter types using a multi-output second-generation current-controlled conveyor (MO-CCCII) has been reported by Fadile Sen et al. [37]. Sadaf Tasneem et al. have presented the implementation of a low-voltage, low-power fractional-order low-pass filter (FO-LPF) of order (1 + α) using a voltage differencing differential difference amplifier (VDDDA) [38]. Georgia Tsirimokou et al. have discussed the realization of a companding FoF for ultra-low-voltage applications [39]. Ola I. Ahmed et al. [40] have discussed a novel design technique for a tunable FO band-pass filter of order $2\alpha$ and its implementation using an OTA. Table 10 presents a summary of the performance parameters (P, THD, IRN, DR, and FOM) of the implemented elliptic FOF, together with comparative data from various fractional-order filter types previously reported in the literature. The THD of the proposed elliptic FOF is lower than that reported in [11,15,36,37,38]. The implemented filter provides an IRN value comparable to that reported in [36] and exhibits improved noise performance (lower IRN) relative to that in [15]. The proposed elliptic FOF provides a higher DR than the design presented in [39]. The power consumption of the implemented elliptic FOF is comparable to that reported in [15] and lower than that in [11,37,40].

Table 10. Comparison with some FOFs in the literature.

Ref/Fig	[6] Figure 11	[11] Figure 4	[15] Figure 5	[19]	[36] Figure 3, Figure 4 and Figure 6	[39] Figure 15	[37] Figure 3	[40] Figure 7	[38] Figure 8	This Paper, Figure 6
FOF type	LP	LP/HP/BP	LP	LP	LP/HP	Class AB log domain LP	LP/HP/AP/AE	BP	LP	LP
Filter approximation	Elliptic	-	Inverse Chebyshev	Elliptic	Butterworth, Chebyshev	Butterworth	Butterworth	-	Butterworth	Elliptic
FO approximation	CFE	Oustaloup	CFE	CFE	-	CFE	Oustaloup	CFE/Matsuda	CFE	CFE
Curve fitting	LS	-	LS	LS	Fitmagfrd	LS	-	-	LS	LS
Filter order	1.2, 1.8	1.5, 1.6, 1.7, 1.8	1.3, 1.6, 1.9	1.25, 1.75	0.3, 0.5, 0.7	1.3, 1.5, 1.7	0.7, 0.8, 0.9	0.6, 0.7, 0.8, 0.9	1.3,1.5, 1.7,1.9	1.4, 1.6, 1.8
Cut-off frequency (Hz)	10 k	1 k	7.2, 7.9, 8.4	-	15.915, 1591.5, 159.15 k	11.7, 11.9, 11.5	1 k	0.27 (peak frequency)	1 k	151, 181, 200
Active block	Opamp (LT1361)	MCFOA	CC-OTA	-	CFOA	Nonlinear Trans conductor	MO-CCCII	OTA	VDDDA	CC-OTA
Simulation/ technology used	SPICE	PSpice	Cadence/180 nm UMC CMOS	MATLAB	PSpice	Cadence/TSMC 180 nm CMOS	Cadence/TSMC 180 nm CMOS	Cadence/130 nm UMC CMOS	Cadence/TSMC 180 nm CMOS	Cadence/180 nm UMC CMOS
Supply voltage (V)	±2.5 to ±15	±2.5	1.8	-	±15	0.5	2.5	-	±0.3 V	1.8
Power (P)	-	<2 mW	13.5 µW	-	-	10.6, 10.11, 9.87 nW	1 mW	14 mW (CFE), 19 mW (Matsuda)	663 nW	22, 17.9, 17.04 µW
THD	-	<2%	< 1%	-	<1%	≤0.21%	≤0.8%	-	4%	0.6%
IRN	-	67.2 pA/√Hz	4.11, 3.48, 4.98 [µV/√Hz]	-	271.3 nV/√Hz	0.36, 0.64, 0.65 [pA/√Hz]	129.4 pA/√Hz	-	691/767 nV/√Hz (Output noise for pre/post layout)	230.4, 175.8, 140.8 [nV/√Hz]
DR (dB)	-	>80	83, 86.1, 84.7	-	150.1	44.7, 44.7, 44.8	>60	-	-	49.7, 52.08, 54.02
FOM (pJ)	-	-	101.6, 52.73, 49.18	-	-	4.7, 3.9, 3.7	1111.11	-	-	2093, 1186, 875.35

LS: least squares, MCFOA: modified CFOA, TSMC: Taiwan Semiconductor Manufacturing Company, VDDDA: Voltage Differencing Differential Difference Amplifier.

6. Conclusions

An elliptic FO LPF of order (1 + α), for α = 0.4, 0.6, and 0.8, is synthesized using the continued-fraction expansion (CFE) method. The elliptic FOF structures are further optimized using a nonlinear least-squares (NLS) routine to accurately match the desired magnitude response. The FO elliptic filters of orders 1.4, 1.6, and 1.8 are designed for cut-off frequencies of 151 Hz, 181 Hz, and 200 Hz, respectively, using a 1.8 V supply and a CC-OTA architecture with a resistor-averaged CMFB circuit. The FO elliptic LPF circuits are implemented and simulated in the Cadence IC Design Suite 6.1.8 (Virtuoso/Spectre) using the 180 nm UMC CMOS process. The Spectre-simulated amplitude responses show good agreement with the MATLAB-generated results. Key performance metrics, including THD, DR, Input Referred Noise (IRN), power, and FoM, were evaluated and compared against previously reported designs. The circuit simulation outcomes confirm the robustness and accuracy of the proposed FO elliptic filter architecture. The Monte Carlo analysis shows that variations in the cut-off frequency due to process fluctuations and device mismatch are minimal and remain within acceptable limits. In addition, the THD remains below 1%, and the DR exceeds 49 dB. Although the CFE approximation method and NLS-based curve fitting were employed in this study, alternative approximation techniques, such as Oustaloup, Matsuda, and Valsa, along with optimization tools like fitmagfrd, can also be used. As part of future work, the design methodology can be extended to realize elliptic FOFs of generalized order (n + α).