Fractional Long-Range Dependence Model for Remaining Useful Life Estimation of Roller Bearings

Abstract

Estimation of remaining useful life (RUL) of roller bearings is a prevalent problem for predictive maintenance in manufacturing. However, roller bearings are subject to a variety of factors during their operation. As a result, we deal with a slow nonlinear degradation process, which is long-range dependent, self-similar and has non-Gaussian characteristics. Proper data pre-processing enables us to use Pareto’s probability density function (PDF), Generalized Pareto motion (GPm) and its fractional-order extension (fGPm) as the degradation predictive model. Estimation of the Hurst exponent shows that this model has a long-range correlation and self-similarity. Through the analysis of the uncertainty of the end point of the bearing’s RUL and the prediction process, not only did it verify the high adaptability of fGPm in simulating complex degradation processes but also the criteria for judging self-similarity, and LRD characteristics were established. The case study mainly proves the validity of the theory, providing an effective analytical tool for a deeper understanding of the degradation mechanism.

1. Introduction

Predictive models of the RUL of roller bearings can be divided into two categories: data-driven models and physics-of-failure models [1]. The data-driven prediction method uses the data from monitoring during the entire life cycle of the roller bearing as the training set. By learning these data, a prediction model is constructed, and then the RUL is predicted for new monitoring data. This method effectively avoids the limitations of the prediction, based on the physics-of-failure model. In terms of the bearing data statistical characteristic, RUL can be further divided into statistical data-driven methods and artificial intelligence-based methods [2,3]. The statistical data-driven method analyzes historical failure data through probabilistic and statistical methods to calculate the life distribution of the bearing. Its advantage lies in the relatively small dependence on specific failure models, but it is limited by the need for a large amount of historical data, making the prediction for small-sample data a challenge. The prediction models based on the physics of failure are determined by the theoretical framework of expert knowledge and failure mechanisms. Such methods are limited by the complexity of modeling and the applicability to specific scenarios.

For the RUL prediction, traditional machine learning methods such as regression analysis, Support Vector Machine (SVM), and decision trees [4] are widely adopted. reference [5,6] predicted the degradation trend of resistance through a feed-forward Artificial Neural Network (ANN) and explored the influence of noise and the number of hidden neurons; reference [7,8] used the statistical indicators of the Weibull distribution as the input of the ANN, which reduced the influence of noise; Reference [9] combined an ANN with the fatigue damage accumulation theory to effectively predict the RUL of cranes. However, they have drawbacks such as the problem of local optima, high model design and computational costs, and difficulty in directly expressing prediction uncertainty.

Convolutional Neural Networks (CNNs) along with the Long Short-Term Memory Networks (LSTM) represent widely used methods for prediction of the RUL. Harbola et al. [10] developed a one-dimensional CNN model consisting of three convolutional layers and three fully connected layers. The convolutional layers were used to extract features, and fully connected layers were employed to predict the sequence changes. Another approach employs wavelet transformation for extraction of complex information in the time-frequency domain. Then a multi-modal CNN is applied to estimate the RUL [11]. Previous research studies [12,13] successfully predicted the degradation trend of roller bearings by removing the Softmax classification layer in the CNN and introducing three fully connected layers for training. However, a direct description of the temporal input dependence by deep learning models represents a difficulty. To address this issue, study [14] combined multi-scale permutation entropy with LSTM. Multi-scale permutation entropy algorithm was used to detect the abrupt change states of equipment degradation and various trends were input into the LSTM model. According to study [15], the LSTM prediction model for wind turbine roller bearings identifies and analyzes weak fault features in vibration and acoustic signals.

In this paper we develop a prognostic model, which is based on the fundamental notions: non-stationarity and LRD. With the consideration of these features, our approach effectively captures the uncertainties during the degradation process. A number of disadvantages of the existing methods are eliminated and verified by a case study.

The layout of this article is as follows: Section 2 provides the method for calculating long-range dependence and self-similarity. Section 3 deduces a fractional Pareto degradation prediction model and analyzes the model’s characteristics. Section 4 proves the reliability of this prediction model. Section 5 proposes the selection of fault characteristic parameters. Section 6 introduces parameter estimation. Section 7 examines an engineering case. Section 8 gives the conclusion.

2. Long-Range Dependence and Self-Similarity

Recall that if the sum of autocorrelation functions (ACFs) of a discrete-time series does not converge, i.e., ${\sum }_{k=1}^{\infty }R\left(k\right)=\infty$, or for a continuous time sequence, then ${\int }_0^{\infty }R\left(t\right)dt=\infty$ [16,17]. It means that the feature of the LRD in the random time sequence follows a power-law approximation, see Equation (1):

$$R\left(k\right)~k^{2H-2},$$

(1)

where H is the Hurst exponent, which is used to quantify the strength of self-similarity. The Hurst exponent is calculated by collecting historical data of the degradation process, and its value is (0.5, 1), which meets RLD characteristics.

Self-similarity is a statistical property at different scales or time periods. For a stochastic process, self-similarity is the statistical characteristic to remains unchanged under any scale transformation $\mathrm{a}$, shown in Equation (2).

$$X\left(at\right)\triangleq a^{H}X\left(t\right),$$

(2)

Figure 1 shows characteristics of self-similar time sequence from different observation windows. Local fluctuation patterns can be reflected in the global trend and quantified by the Hurst exponent in multi-scale analysis. It is clear that the Hurst exponent links self-similarity with LRD. This LRD is also known as long-term memory effect or persistence indicating that correlations of the asset degradation increments extend over extensive periods. Therefore, future degradation trends are not only influenced by the current condition of the asset but are also deeply linked to its entire degradation history.

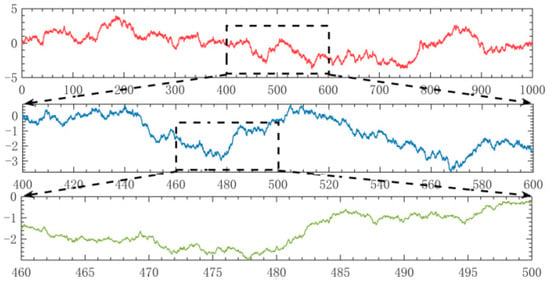
Figure 1. Typical self-similar raw data.

3. Fractional Pareto Degradation Prediction Model

The PDF of the generalized Pareto distribution is shown in Equation (3):

$$f_{GP}\left(x|\mu ,\delta ,\alpha \right)={\displaystyle \frac{1}{\delta }}{\left[1+{\displaystyle \frac{1}{\alpha \delta }}\left(x-\mu \right)\right]}^{-1-\alpha },$$

(3)

where $\alpha$ is a parameter. Small values of $\alpha$ correspond to slow decay rate. $\delta$ is the scale parameter, which represents the dispersion of the random sequence; $\mu$ represents the location parameter.

3.1. Fractional Pareto Motion Model

The fGPm is defined by Riemann–Liouville integral, as shown in Equation (4):

$$P_{H,\alpha }\left(t\right)={\displaystyle \frac{1}{\Gamma \left(H+\frac{1}{2}\right)}}{\int }_0^t{\left(t-\tau \right)}^{H-{\displaystyle \frac{1}{2}}}p\left(d\tau \right),$$

(4)

where $p\left(ds\right)$ represents a generalized Pareto stochastic process with the location parameter $\mu =0$, and the scale parameter $\delta =\left|d\tau \right|$, $\mathrm{\Gamma }\left(.\right)$ is the gamma function. The correlation and self-similarity depend on the parameter $H$ and the tail parameter $\alpha$.

• When $H>{\displaystyle \frac{1}{\alpha }}$, the kernel function $f\left(a,b;t,s\right)$ changes very slowly with the variable $s$, then the fGPm model has long-range dependence;
• When $H<{\displaystyle \frac{1}{\alpha }}$, the fGPm model exhibits short-range dependence;
• When $H={\displaystyle \frac{1}{\alpha }}$, the fGPm model degenerates into the GPm model, which means that the equivalence between the fGPm model and the GPm model holds under specific parameter configurations.

The larger the product of $H$ and $\alpha$ is, the stronger the LRD of the stochastic sequence is, and the sequence shows a more complex changeable trend. When $0<\alpha \le 1$, the fGPm model does not have the LRD because the value of self-similarity $H$ is restricted to the interval $\left(0,1\right)$. Figure 2 explains the relationship between $H$ and $\alpha$.

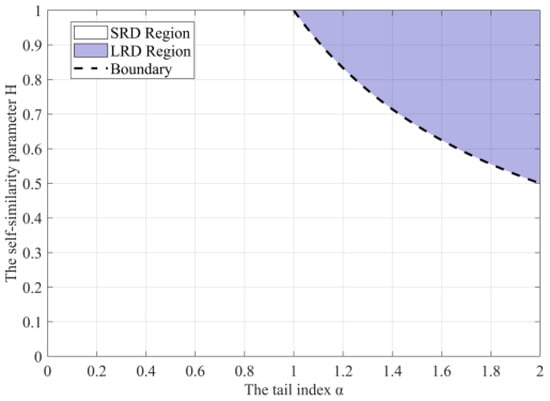
Figure 2. Dependence of the fGPm model.

3.2. fGPm Predictive Model

According to the Itô formula, Black and Scholes introduced the fractional Brownian motion (fBm) model with the LRD characteristics [18], given as (5):

$$d{S}_t={\mu }_s{S}_{t}dt+{\delta }_s{S}_{t}d{B}_H\left(t\right).$$

(5)

Substitution of Equation (4) into Equation (5) gives us the Itô process, driven by the fGPm model. Fluctuations of the random sequence in this process are not only affected by the drift coefficient and diffusion parameter but also depend on the fGPm model. The degenerate model is modeled, shown in Equation (6):

$$Y\left(t\right)=Y\left(0\right)+\lambda {\int }_0^t\mu \left(s;\mathrm{\Theta }\right)ds+\eta P_{H,\alpha }\left(t\right)$$

(6)

where $Y\left(0\right)$ is the initial value of the degenerate process sequence, usually set to 0, $\mu \left(s;\mathrm{\Theta }\right)$ represents the nonlinear drift function, $\lambda$ represents the drift coefficient, $\eta$ represents the diffusion coefficient, and $P_{H,\alpha }\left(t\right)$ represents the fractional Generalized Pareto motion model.

The fGPm of the incremental is expressed as shown in Equation (7):

$$Y(t+\mathrm{\Delta }t)-Y(t)=\lambda {\displaystyle {\int }_t^{t+\mathrm{\Delta }t}\mu (s;\mathrm{\Theta })ds+\eta [P_{H,\alpha }}(t+\mathrm{\Delta }t)-P_{H,\alpha }(t),$$

(7)

where $∆t$ is the time increment.

Set $\mathrm{Y}\left(0\right)=0$ under different parameters, and $\mathrm{Y}\left(t\right)$ are simulated as shown in Figure 3.

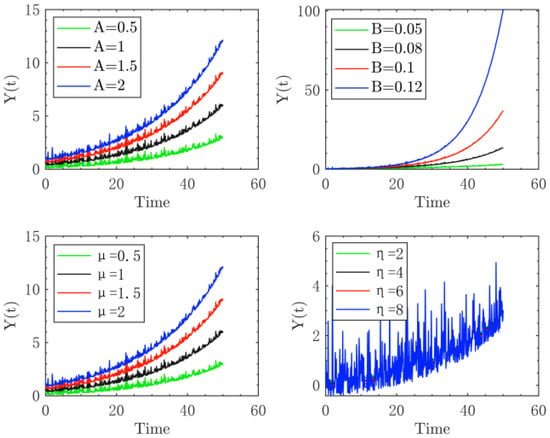
Figure 3. Numerical simulation of the fGPm degradation model.

4. Reliability of the End Point of Remaining Life and Prediction Process

The ‘failure time’ is the bearing falling below a predetermined threshold and is considered to have failed. When the degradation process first exceeds the fault threshold, the point is called the ‘End of Life’ (EOL) of the bearing. The RUL is shown in Equation (8).

$$T_r=\inf \left\{\begin{array}{l}{t}_r:Y(t_c+t_r)\ge HI(T_f)\\ HI(T_e)\le Y(t_c)\le HI(T_f)\end{array}\right\},$$

(8)

where $t_c$ is the time of the degradation process, $t_r$ is the process time of RUL, $HI\left(T_e\right)$ is the FPT, and $HI\left(T_f\right)$ is the set fault threshold.

The fGPm prediction model is a non-stationary stochastic process. When the RUL prediction values are obtained directly from the model, the prediction values have an uncertainty. The degradation process of rolling bearings is characterized as a non-stationary. Therefore, Monte Carlo [19] can be used to simulate the degradation process. Through the statistical analysis of a large number of simulations, the probability distribution of RUL can be obtained, and the peak of probability density is considered as the RUL prediction value (see Figure 4).

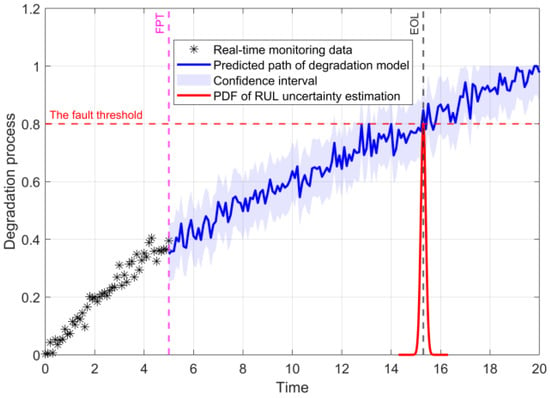
Figure 4. Typical prediction principle of the fGPm model based on Monte Carlo simulation.

5. Selection of Fault Characteristic Parameters

Next, it is required to evaluate how well the sensors correlate with the degradation pattern. Signals that do not properly correlate with a monotonic exponential trend should be removed. To that end, the three prognostic parameter choosing measures of monotonicity degradation, robustness and degradation trendiness are used to identify the meaningful characteristic parameters.

(1)

Monotonicity: Degradation process is a monotonically increasing process. The calculation is as follows:

$$Mon={\displaystyle \frac{1}{J-1}}{\sum }_{j=1}^J\delta \left(Z_{t_{j+1}}-Z_{t_j}\right)-\delta \left(Z_{t_j}-Z_{t_{j+1}}\right)$$

(9)

where $\mathrm{Mon}\in [-1,1],\delta \left(t\right)=\left\{\begin{array}{c}1,t\ge 0\\ 0,t<0\end{array}\right.$ is a pulse function, $Z_{t_j}$ represents multi-domain features of multi-source sensors; $J$ represents the length of the bearing degradation sequence. A measure of Mon close to 1 indicates that the data from the sensor are monotonically increasing.

(2)

Robustness: Represents the anti-interference ability, calculated as follows:

$$Rob={\displaystyle \frac{1}{J}}{\sum }_{j=1}^J\exp \left(-\left|{\displaystyle \frac{Z_{t_j}-\overline{Z}}{Z_{t_j}}}\right|\right),$$

(10)

where $\mathrm{Rob}\in [-1,1]$, and the larger the Rob value, the stronger the robustness. $Z_{t_j}$ is the characteristic value at $t_j$ moment, $\overline{z}$ is the average value of the characteristic sequence.

(3)

Degradation trendiness: Represents the correlation between degenerative characteristic and time series, calculated as follows:

$$Ten={\displaystyle \frac{J{\sum }_{j=1}^J{Z}_{t_j}{t}_j-{\sum }_{j=1}^J{Z}_{t_j}{\sum }_{j=1}^J{t}_j}{\sqrt{\left[K{\sum }_{j=1}^J{t_j}^2-{\left({\sum }_{j=1}^J{t}_j\right)}^2\right]\left[K{\sum }_{j=1}^J{Z_{t_j}}^2-{\left({\sum }_{j=1}^J{Z}_{t_j}\right)}^2\right]}},}$$

(11)

where $Ten\in [-1,1]$, and $t_j$ is the $j$th value of the time series. A greater the value of the trendiness corresponds to a better fit.

The weak fault characteristic parameter CHI is obtained by assigning the corresponding weights to the evaluation indicators (9)–(11) as follows:

$$CHI=p_{1}Mon+p_{2}Rob+p_{3}Ten,$$

(12)

where $p_1+p_2+p_3=1,\mathrm{and}{p}_1,p_2,p_3>0$.

6. Health Indicator Assessment

Then, the maximum likelihood method is applied to identify the parameter $\lambda$ and $\eta$. The sequence generated by the prediction model (7) has a high self-similarity with the future bearing degradation process sequence.

The Hurst exponent is independent of other degradation parameters. A generalized Hurst exponent method is adopted and calculated as follows:

$$H\left(q\right)={\displaystyle \frac{1}{q}}\log {\displaystyle \frac{⟨{\left|X\left(t+\tau \right)-X\left(t\right)\right|}^q⟩}{⟨{\left|X\left(t\right)\right|}^q⟩}},$$

(13)

where $H\left(q\right)$ is the generalized Hurst exponent, which represents the scale dependence of the q order; ⟨∙⟩ represents the average value of a series, and $\tau$ is the time interval. When q = 1, the generalized Hurst exponent becomes the Hurst exponent.

In terms of Equation (7), we can obtain that

$${\mu }_g=\lambda {\int }_t^{t+∆t}\mu \left(s;\mathrm{\Theta }\right)ds,$$

(14)

$${\delta }_g=\eta {∆t}^{H+{\displaystyle \frac{1}{\alpha }}-{\displaystyle \frac{1}{2}}}.$$

(15)

A degraded differential sequence $Z_{\mathbf{1}:\mathit{N}}$ is constructed, and $Z_i=Y_{t_{i+1}}-Y_{t_i}$. For the global mean ${\mu }_g$, the mean of the degraded difference sequence is fitted, that is,

$$\widehat{{\mu }_g}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{Z}_i,$$

(16)

parameters α and ${\delta }_g$ can be estimated by the maximum likelihood estimation. The log-likelihood function for Equation (7) can be written as follows:

$$logL\left(\alpha ,{\mu }_g,{\delta }_g|\left\{Z_i\right\}\right)={\sum }_{i=1}^n\left[log{\displaystyle \frac{1}{2{\delta }_g}}-\left(1+\alpha \right)\log \left(1+{\displaystyle \frac{\left|Z_i-{\mu }_g\right|}{\alpha {\delta }_g}}\right)\right],$$

(17)

Then a MATLAB 10.0 function ‘fminserch’ was applied to solve the log-likelihood estimators of parameters α and ${\delta }_g$.

7. Case Study

In order to demonstrate the effectiveness of our approach, consider the XJTU-SY bearing dataset [20] as the case study (see Figure 5). The experimental object is the roller bearing LDK UER204. The temporal dependence of the amplitude along the horizontal direction is shown in Figure 6.

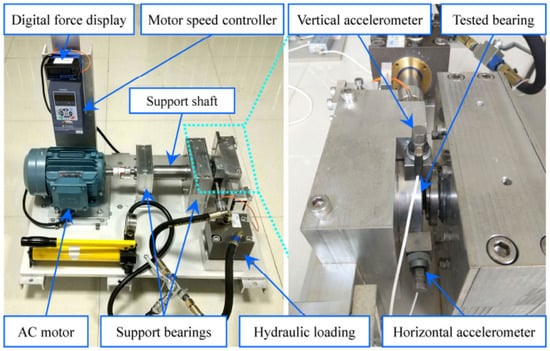
Figure 5. Test bench of the roller bearings.

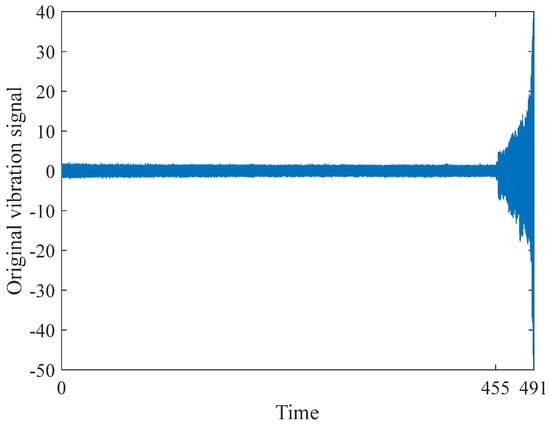
Figure 6. The original vibration sequence.

It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn. When the rolling bearing is operating normally, the degradation sequence exhibits the characteristics of a stationary random sequence. Once a weak fault occurs, the characteristics of the degradation sequence will change from a stationary random sequence to a non-stationary random sequence. Figure 7 shows that there is an obvious fluctuation at the 1418th point. After this point, the characteristic values of the degradation process suddenly change significantly and fluctuate violently. This stage is considered to be the slow failure stage of the rolling bearing; see Figure 7.

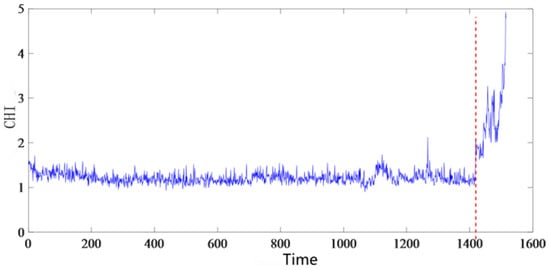
Figure 7. Degradation characteristic series of bearings.

Let us refer to the exponential drift ${\int }_0^{t_k}\mu \left(s;\mathrm{\Theta }\right)ds=A{e}^{Bt}$ of the fGPm. Table 1 shows the maximum likelihood parameter identification of the fGPm degradation model at different prediction starting points. Figure 8 shows the RUL prediction results of the fGPm model (M1) with an adaptive drift function and the fGPm model (M2) without an adaptive drift function at multiple starting points. Figure 9 shows the uncertainty estimation results of M1 and M2 models at different prediction starting points. The analysis results indicate that an adaptive drift term can significantly improve the accuracy of prediction results.

Table 1. Parameter estimating for different starting points.

Starting Point	A	B	H	${\mathit{\delta }}_{\mathit{g}}$	$\mathit{\alpha }$
1442	0.2	0.05	0.6894	4.9847 × 10−7	1.2769
1446	0.2	0.05	0.6616	0.00045276	1.2244
1450	0.2	0.05	0.6915	0.00029006	1.0930
1454	0.2	0.05	0.7078	0.00036754	1.0800
1458	0.2	0.05	0.7252	0.00055092	1.0987
1462	0.2	0.05	0.7481	0.00049252	1.0728
1466	0.2	0.05	0.7776	0.00054661	1.1677
1470	0.2	0.05	0.8090	0.00046149	1.1459
1474	0.2	0.05	0.8291	0.00045164	1.1525
1478	0.2	0.05	0.8447	0.00047855	1.2648
1482	0.2	0.05	0.8569	0.00045776	1.0546
1486	0.2	0.05	0.8660	0.00057272	1.0978
1490	0.2	0.05	0.8737	0.00058506	1.0863
1494	0.2	0.05	0.8815	0.00060035	1.0755

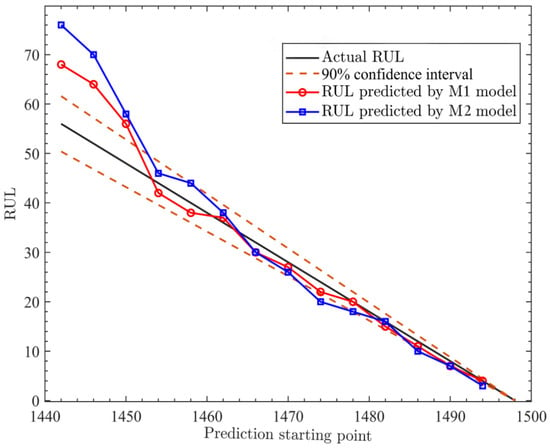
Figure 8. Predictions with and without drift parameters.

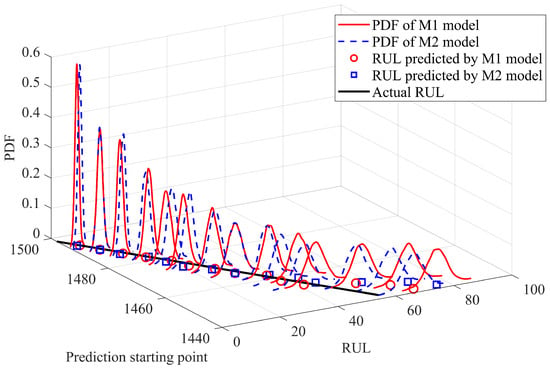
Figure 9. Comparison of PDF with and without drift parameters.

The obtained results are compared with other models: the fLSm degradation model with adaptive drift ability (M3), the fBm degradation model (M4), the Brownian motion (Bm) degradation model (M5), and the LSTM (M6). Table 2 shows the prediction accuracy, result score, health assessment, and reliability. M1 not only has the lowest values on RMSE (5.7268) and MAE (3.8856) and the smallest error between its predicted and actual values but also obtained the highest scores on SOR (0.91935) and HD (0.99574).

Table 2. Predicting error compared with other models.

	SOR	RMSE	MAE	HD	PICP	MPIW
M1	0.91935	5.7268	3.8856	0.99574	58.145%	9.65
M2	0.90740	8.3370	5.3428	0.87532	58.177%	9.821
M3	0.90421	7.0155	5.8813	0.89761	38.100%	10.863
M4	0.8999	8.7726	7.4721	0.83541	37.765%	10.971
M5	0.87680	9.1491	7.6839	0.83487	21.759%	10.9375
M6	0.87684	11.482	8.6592	0.82143	21.593%	11.0113

8. Conclusions

This article does not discuss the setting of fault diagnosis parameters, fault thresholds, and parameter maximum likelihood identification for the degradation process.

(1)

The degradation process of bearings has a non-stationary stochastic process with long-range dependence and self-similarity.

(2)

The accuracy of RUL in this article is better than other methods.

(3)

Because the degradation process of all equipment and components is a gradual non-stationary process, this method can be extended to other fields.

Future research directions will focus on multimodal factors because the practice operating conditions are random multimodal.