Distributed Energy Storage Configuration Method for AC/DC Hybrid Distribution Network Based on Bi-Level Optimization

Abstract

Aiming at prominent voltage quality problems in AC/DC hybrid distribution networks with a high proportion of distributed energy and diversified loads, this paper proposes a bi-level energy storage system (ESS) optimization model. The upper level optimizes the ESS configuration with the goal of minimizing the cost, and the lower level optimizes the real-time running state of the ESS. Considering multiple constraints, the improved PSO algorithm and the Gurobi solver are used to solve the problem. The test on the modified IEEE-33 node system verified that the model effectively improved voltage quality and reduced power system costs, which provides theoretical and engineering support for the scientific configuration of the ESS.

1. Introduction

With the rapid advancement of distributed generation and innovative loads integrated into grids, traditional distribution networks are transforming into active, smart ones with bidirectional energy transfer [1]. However, random fluctuations in distributed photovoltaic (PV) output and innovative loads exacerbate voltage variations, even causing voltages to exceed safety limits and threatening network stability [2,3,4]. Traditional mitigation strategies fail to take advantage of an energy storage system (ESS). The ESS not only alleviates supply–demand imbalances during peak load periods but also addresses the inability of reactive power devices to promptly compensate for active power shortages, thus enhancing the supply capacity of distribution networks and resolving undervoltage issues [5,6].

Since the location, capacity, and scheduling of ESSs exert a significant impact on voltage quality and the economic operation of distribution networks, research on the economically optimal ESS configuration for distribution systems is particularly imperative [7]. In recent years, researchers have conducted extensive and in-depth research on the potential of ESSs in achieving cost-effective configurations and improving the voltage quality of distribution networks. In reference [8], a bi-level programming-based optimal configuration strategy for an ESS is presented. To tackle the uncertainty associated with PV output, the K-means clustering algorithm is adopted for data processing; subsequently, an improved multi-objective particle swarm optimization algorithm is employed to solve the proposed model. Case validation results demonstrate that the method can effectively reduce voltage deviations, smooth load fluctuations, and cut down on system operational costs. Reference [9] proposes a bi-level optimal ESS configuration scheme based on an improved voltage sensitivity strategy. It extracts typical PV output scenarios via K-means clustering, identifies highly sensitive nodes using an improved voltage sensitivity algorithm, solves the problem with an improved niche particle swarm optimization algorithm, and enhances voltage regulation accuracy and cost-effectiveness. In reference [10], a bi-level optimization model oriented toward power loss reduction is developed on the basis of source–grid–load–storage coordination. This model is proven to possess robust adaptability across distribution networks with different scales. Moreover, the coordinated deployment of an ESS is shown to boost the integration capability of PV systems and electric vehicles, realizing the dual optimization of economic returns and technical performance. It should be noted, nevertheless, that all the above-mentioned references conduct their validation and analysis in the context of conventional pure AC distribution networks, and none of them addresses the voltage regulation properties specific to AC/DC hybrid distribution networks.

As power electronics technology advances rapidly, DC transmission technology based on voltage source converters (VSCs) has witnessed remarkable progress in recent decades. The AC distribution network is evolving into an AC/DC hybrid distribution network. Some achievements have been made in control strategies, modeling and analysis, and application scenarios. However, the existing achievements still have obvious deficiencies in the coordination of ESS configuration and voltage regulation and the comprehensiveness of uncertainty responses, which cannot provide complete support for the scientific configuration of ESSs.

Reference [11] only focuses on the power flow calculation of an AC/DC distribution network with VSC, and realizes the effective solution of power flow by modifying the active power imbalance equation of VSC boundary nodes. However, it does not involve the related content of ESS optimization configuration, nor is it related to the core requirements of engineering, such as voltage quality improvement and cost control, which is only the research of basic calculation tools. In reference [12], although the flexibility of the system is explored through VSC power flow control, MTDC control mode switching, and flexible load scheduling, an ESS is not included in the flexible resource system, and the quantitative correlation between flexibility improvement and voltage quality and operation economy is not established, which lacks direct support for actual engineering decision-making. In reference [13], an optimal scheduling model of an AC/DC hybrid distribution network considering converter station control mode is proposed, which can effectively balance load rate and improve voltage distribution. Reasonable selection of converter station control mode can reduce DC-side voltage deviation without deteriorating AC-side voltage deviation. ESS scheduling also conforms to the law of electricity prices to reduce operating costs. In reference [14], a bi-level programming model of an AC/DC hybrid distribution network is proposed. At the same time, the collaborative optimization operation of source–grid–load–storage coordination is comprehensively considered. Although both of the aforementioned references incorporate ESSs into their research scope, the former only conducts analyses and calculations under scenarios where the ESS location and capacity are predefined. Moreover, neither of them has carried out research that integrates an ESS configuration with VSC control strategies.

Therefore, it is particularly imperative to carry out research on the optimal configuration of an ESS in AC/DC hybrid distribution networks based on bi-level optimization. This paper focuses on analyzing voltage quality, with a specific emphasis on voltage deviation. This paper is specifically tailored to the topological characteristics of AC/DC hybrid distribution networks. It constructs a more comprehensive multi-dimensional objective and constraint system, designs an efficient and synergistic solution mechanism, and conducts adaptability verification tests across multiple scenarios. It addresses the limitations of the existing studies, including an overemphasis on traditional AC distribution networks, a simplistic objective and constraint framework, overreliance on a single solution mechanism, and insufficient scenario-based verification. In doing so, it provides a targeted approach for the rational configuration of an ESS in AC/DC hybrid distribution networks.

2. Materials and Methods

2.1. ESS, VSC, and PV Uncertainty Models

2.1.1. ESS Model

ESSs are renowned for their rapid response capability and high operational flexibility. These inherent characteristics render them a pivotal technology for effectively mitigating the intermittency and volatility of renewable energy generation, such as PV power, and curbing unnecessary energy wastage. The operational constraints of ESSs are defined in Equations (1)–(6).

(1) ESS power and capacity constraints

$${\displaystyle \frac{P_{ess,N,t}\Delta t}{\eta }}=(SOC(t-1)-SOC(t))E_m$$

(1)

In the equation, $SOC(t)$ denotes the SOC of the ESS at time t; $E_m$ refers to the rated capacity of the ESS; $\eta$ represents the charge–discharge efficiency of the ESS; $P_{ess,N,t}$ is the charge–discharge power of the ESS at time t, noting that charging and discharging operations cannot be performed simultaneously, but only at distinct time points; $\Delta t$ indicates the time interval, which is set to 1 h.

(2) ESS charging and discharging constraints

$$-P_{ess\_N}\le P_{ess,N,t}\le P_{ess\_N}$$

(2)

In the equation, $P_{ess\_N}$ denotes the rated power capacity of the N-th ESS.

(3) ESS state of charge (SOC) constraints

$$SO{C}_{\min }\le SOC(t)\le SO{C}_{\max }$$

(3)

$$SO{C}_{\min }\le SOC(1)\le SO{C}_{average}\le SO{C}_{\max }$$

(4)

$$SO{C}_{average}\le {\displaystyle \frac{1}{24}}{\displaystyle \sum _{t=1}^{T}SOC(t)}$$

(5)

$$SOC(1)=SOC(24)=55\%SO{C}_{\max }$$

(6)

In the equation, $SO{C}_{\min }$ and $SO{C}_{\max }$ represent the lower and upper limits of the SOC of the ESS, respectively; $SOC(1)$ denotes the initial SOC value of the ESS; $SOC(24)$ refers to the SOC value of the ESS at the final time step; $SO{C}_{average}$ indicates the average SOC of the ESS.

2.1.2. VSC Model

A steady-state structure of a VSC is illustrated in Figure 1. The VSC model is appropriately simplified, and the constraints to be satisfied by the VSC are defined in Equations (7)–(9). Specifically, Equations (7) and (8) quantify the active and reactive power balance states of the VSC, respectively, while Equation (9) clarifies the dynamic correlation between the AC-side and DC-side voltages of the VSC.

$$P_{a,t}-I_{ac,t}^2{R}_{ac}=P_{d,t}$$

(7)

$$Q_{a,t}-I_{ac,t}^2{X}_{ac}=-Q_{c,t}$$

(8)

$$U_{c,t}={\displaystyle \frac{\sqrt{3}}{3}}\overline{\mu }M{U}_{d,t}$$

(9)

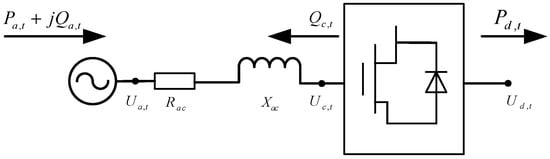
Figure 1. A steady-state structure diagram of a VSC.

In the equation, $P_{a,t}$ and $Q_{a,t}$ denote the active and reactive power input to the AC-side VSC at time t, respectively; $P_{d,t}$ represents the active power output on the DC side; $R_{ac}$ and $X_{ac}$ refer to the equivalent branch resistance and reactance of the VSC, respectively; $Q_{c,t}$ represents the internal reactive power equivalent to VSC; $U_{c,t}$ and $U_{d,t}$ indicate the internal voltage of the VSC and the DC-side voltage, respectively; $\overline{\mu }$ stands for the DC voltage utilization factor, where it takes a value of 0.866 when sinusoidal pulse width modulation (SPWM) is adopted; M represents the modulation degree of the VSC, where its variation range is constrained to 0 ≤ M ≤ 1. In the field of power electronics technology, the VSC can realize independent and precise control of active power and reactive power through a decoupling control strategy in the d-q coordinate system. The d-axis of the converter can be controlled by constant voltage control and droop control; when the constant voltage control is adopted, $U_{d,t}$ remains a fixed value, and when droop control is adopted, the DC-side power and voltage must satisfy the droop characteristics, as defined in Equation (10).

$$U_{\mathrm{d},t}-U_{\mathrm{d},\mathrm{ref}k}-\rho (P_{\mathrm{d},t}-P_{\mathrm{d},\mathrm{ref}k})=0$$

(10)

In the equation, $U_{\mathrm{d},\mathrm{ref}k}$ and $P_{\mathrm{d},\mathrm{ref}k}$ denote the reference values of DC voltage and DC power, respectively; $\rho$ represents the droop coefficient.

2.1.3. PV Uncertainty Model

In the configuration of the ESS, the diversity of PV operating scenarios is taken into account to maximize the ESS’s operational benefits while minimizing resource waste, thereby ensuring that the power system can maintain real-time dynamic stability under each scenario. However, incorporating all PV operating scenarios over several years would lead to excessive computational complexity, and redundant solutions are prone to arising due to scenario similarity. Therefore, this paper employs the synchronous backward substitution method to reduce the historical actual output data of PV over several years. Each day of PV operation corresponds to one scenario, and a set of typical PV output scenarios is derived accordingly. The occurrence probability of each typical scenario is calculated as follows:

$${\overline{\sigma }}_{pv}=\left[{\overline{\sigma }}_{f1},{\overline{\sigma }}_{f2},{\overline{\sigma }}_{f3},\dots ,{\overline{\sigma }}_{fk}\right],k\in R_{sc}$$

(11)

In the equation, $R_{sc}$ denotes the number of typical scenarios derived via data reduction; ${\overline{\sigma }}_{pv}$ represents the probability set corresponding to the reduced typical PV scenarios; ${\overline{\sigma }}_{fk}$ indicates the occurrence probability of the k-th typical PV scenario.

2.2. Case Description

The case study in this paper employs an AC/DC hybrid distribution network derived from the IEEE-33 bus system [15]. Based on the placement of the VSC, the network is partitioned into two separate AC and DC sub-grids [16,17,18,19]. The power system is configured with five PV units and three distributed ESSs. The power system topology is depicted in Figure 2, where the installed capacity of each PV unit is specified as 0.1 MVA. For the case study in this paper, the YALMIP toolbox in MATLAB R2024a is adopted, with the optimization solver Gurobi invoked for problem solution. The voltage security range of each bus is specified as 0.95–1.05 p.u., while the maximum allowable current of both AC and DC branches is 1 p.u. The service lifetime of the ESSs is set to 5 years, with a discount factor β of 0.33 and a charge–discharge efficiency of 90%. In terms of electricity pricing, the peak-period tariff is 0.6 CNY/(kWh) and the valley-period tariff is 0.35 CNY/(kWh), where the peak period is defined as 08:00–21:00 and the valley period is defined as 01:00–07:00 [20]. The relevant parameter of the particle swarm optimization (PSO) algorithm is as follows: the size of the particle swarm is set to 20; the maximum number of iterations is defined as 15; the upper limit of the individual learning factor for each particle is 2.5, the lower limit is 0.5; the upper limit of the social learning factor for each particle is 2.5, the lower limit is 0.5; the upper limit of inertia weight is 0.9, the lower limit of inertia weight is 0.4 [21]. The optimal configuration of the ESS and voltage quality under the bi-level optimization model is analyzed. The focus of the case analysis is to verify the impact of the ESSs on operational economy and voltage stability in the AC/DC hybrid distribution network.

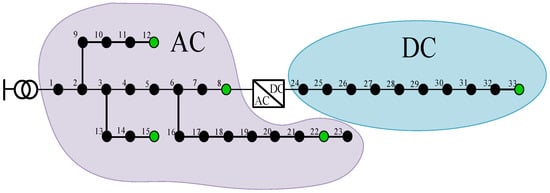
Figure 2. The topology of the AC/DC hybrid distribution network.

2.3. Bi-Level Optimal Configuration Model of ESS in AC/DC Hybrid Distribution Network

2.3.1. Upper-Level Objective Function

Aiming at complex ESS investment decision-making, this study focuses on a multi-objective optimization strategy to improve system bus voltage quality while ensuring economic feasibility. The objective function includes ESS investment cost, line loss cost, main network purchase cost, and overall bus voltage deviation cost:

$$\min f_{up}=F_1+F_2+F_3+\mu \Delta U_{\mathrm{n}}$$

(12)

In the equation, $F_1$, $F_2$, $F_3$, and $\Delta U_{\mathrm{n}}$ are ESS investment cost, line loss cost, main network electricity purchase cost, and overall bus voltage deviation, respectively. $\mu$ is the scale coefficient of dimensional unified conversion. The specific calculation equation of each objective function is as follows:

(1) The ESS investment cost $F_1$ calculation equation is as follows [22]:

$$\begin{array}{ll}{F}_1& =\beta {\displaystyle \sum _1^N(C_{pess\_N}{P}_{ess\_N}+C_{eess\_N}{E}_{ess\_N})}\hfill \\ & ={\displaystyle \frac{\tau {(1+\tau )}^y}{{(1+\tau )}^y-1}}{\displaystyle \sum _1^N(C_{pess\_N}{P}_{ess\_N}+C_{eess\_N}{E}_{ess\_N})}\hfill \end{array}$$

(13)

In the equation, $N$ refers to the actual number of installed ESSs; $\tau$ is the annual interest rate; y represents the operational lifespan of the ESSs; $\beta$ is the discount rate, where it is used to discount the initial investment cost of the ESSs according to the annual average value; $C_{pess\_N}$ represents the unit power cost of the ESSs; $C_{eess\_N}$ represents the unit capacity cost of the ESSs; $E_{ess\_N}$ represents the rated energy capacity of the N-th ESS.

(2) The calculation equation of line loss cost $F_2$ is as follows:

$$F_2=C_{ep}{\displaystyle \sum _1^{365}{\displaystyle \sum _{t=1}^{24}\Delta t{\displaystyle \sum _1^j{P}_{loss,j,t}}}}$$

(14)

In the equation, $P_{loss,j,t}$ is the active power loss of the j-th branch at time t; $C_{ep}$ is the cost of unit line loss, CNY/kWh.

(3) The main network electricity purchase cost calculation equation $F_3$ is as follows:

$$F_3=F_{buy}-F_{ess}$$

(15)

$$F_{buy}=C_{ebuy}{\displaystyle \sum _1^{365}{\displaystyle \sum _{t=1}^{24}{P}_{load,t}}}\Delta t$$

(16)

$$F_{ess}=C_{ebuy}{\displaystyle \sum _1^{365}{\displaystyle \sum _{t=1}^{24}\Delta t{\displaystyle \sum _1^N{P}_{ess,N,t}}}}$$

(17)

In the equation, $F_{buy}$ is the electricity purchase cost when the ESS is not connected; $P_{load,t}$ denotes the total load of the system at time t when the ESS is not connected; $C_{ebuy}$ is the peak-valley unit electricity price; $F_{ess}$ is the ESS’s participation in the regulation of the main network electricity purchase cost.

(4) The overall bus voltage deviation $\Delta U_{\mathrm{n}}$ calculation equation is as follows:

$$\Delta U_{\mathrm{n}}={\displaystyle \sum _{i=1}^{N_{bus}}{\displaystyle \sum _{t=1}^{24}\left|\frac{U_{\stackrel{-}{i,}t}-U_N}{U_N}\right|}}$$

(18)

In the equation, $U_{\stackrel{-}{i,}t}$ is the voltage of the i-th bus at time t; $U_N$ represents the rated value of bus voltage during the investigation period; $N_{\mathrm{bus}}$ represents the number of system buses.

(5) The calculation equation of the dimensional unified conversion coefficient $\mu$ is as follows:

$$\mu =C_{\mathrm{ep}}dw$$

(19)

In the equation, $d$ denotes the number of days in a year; the proportional conversion coefficient $w$ of active power loss and bus voltage deviation is set to 500 kW/p.u. [23].

2.3.2. Upper-Level Constraints

(1) Power balance constraints

$$P_m=P_{m-1}-R_{m-1}(P_{m-1}^2+Q_{m-1}^2)/U_{m-1}^2-P{L}_m+x_m{P}_{ess\_N}$$

(20)

$$Q_m=Q_{m-1}-X_{m-1}(P_{m-1}^2+Q_{m-1}^2)/U_{m-1}^2-Q{L}_m+x_m{Q}_{ess\_N}$$

(21)

In the equation, $P_m$ and $Q_m$ represent the active and reactive power injected into bus m, respectively; $R_m$ and $X_m$ are the resistance and reactance between bus m–1 and bus m, respectively; $P{L}_m$ and $Q{L}_m$ stand for the active and reactive loads of the buses, respectively; $U_m$ indicates the bus voltage; $x_m$ is a binary decision variable, where 1 means that the bus is connected to the ESS, and vice versa is 0.

(2) Bus voltage constraints

$$U_{\min }\le U_{m,t}\le U_{\max }$$

(22)

In the equation, $U_{\min }$ is the lower limit of the bus voltage amplitude in the t period; $U_{\max }$ represents the upper limit of the bus voltage amplitude in the t period.

(3) ESS allowable installed power capacity

$$P_{ess,\min }\le P_{ess\_N}\le P_{ess,\max }$$

(23)

In the equation, $P_{ess,\min }$ and $P_{ess,\max }$ denote the lower and upper bounds of the allowable installed power capacity for the ESS, respectively.

(4) ESS installation of the candidate bus constraints

$${\displaystyle \sum _{m=1}^N{x}_m=}{N}_{ess}$$

(24)

In the equation, $N_{ess}$ represents the number of ESSs connected to the system.

2.3.3. Lower-Level Objective Function

In order to ensure that the ESS power scheduling of the system at each moment can be directly integrated into the upper decision-making model, this study introduces the output of the ESS as the key control parameter and minimizes the load standard deviation as the optimization goal.

$$\min f_{down}=\sqrt{{\displaystyle \sum _{t=1}^T{(P_t-P_{average})}^2/T}}$$

(25)

$$P_{average}={\displaystyle \frac{1}{T}}{\displaystyle \sum _{\mathrm{t}=1}^T{P}_t}$$

(26)

$$P_{load,t}=P_t+{\displaystyle \sum _1^N{P}_{ess,N,t}}$$

(27)

In the equation, T represents the duration of a day, which is 24 h; $P_t$ is the total active load after the system is connected to the ESS at time t; $P_{average}$ is the average active load during a day; $P_{load,t}$ is the active load when the system is not connected to the ESS at time t.

2.3.4. Lower-Level Constraints

(1) AC network power flow equation constraints

$$\left\{\begin{array}{l}{\displaystyle \sum _{k\in \delta (j)}{P}_{jk,t}}-{\displaystyle \sum _{i\in \pi (j)}\left(P_{ij,t}-I_{ij,t}^2{R}_{ij}\right)}=P_{j,t},\forall j\in N^{\mathrm{A}}\hfill \\ {\displaystyle \sum _{k\in \delta (j)}{Q}_{jk,t}}-{\displaystyle \sum _{i\in \pi (j)}\left(Q_{ij,t}-I_{ij,t}^2{X}_{ij}\right)}=Q_{j,t},\forall j\in N^{\mathrm{A}}\hfill \\ P_{j,t}=P_{j,t}^{\mathrm{PV}}+P_{j,t}^{\mathrm{ESS}}-P_{j,t}^{\mathrm{load}},\forall j\in N^{\mathrm{A}}\hfill \\ Q_{j,t}=Q_{j,t}^{\mathrm{PV}}+Q_{j,t}^{\mathrm{ESS}}-Q_{j,t}^{\mathrm{load}},\forall j\in N^{\mathrm{A}}\hfill \end{array}\right.$$

(28)

In the equation, $\delta (j)$ is the set of all the tail buses of the first bus $j$; $\pi (j)$ is the set of all the first buses of the tail bus $j$; $P_{jk,t}$ and $Q_{jk,t}$ represent the active and reactive powers, respectively, flowing from bus $j$ to the connected bus k; $P_{ij,t}$ and $Q_{ij,t}$ represent the active and reactive powers flowing through the branch $ij$, respectively; $I_{ij,t}$, $R_{ij}$, and $X_{ij}$ represent the current, resistance, and reactance of branch $ij$, respectively; $U_{j,t}$ and $U_{i,t}$ are the voltage amplitudes of bus $j$ and bus $i$, respectively; $P_{j,t}$ and $Q_{j,t}$ are the active and reactive powers of the injected bus $j$, respectively; $P_{j,t}^{\mathrm{load}}$ and $Q_{j,t}^{\mathrm{load}}$ are the active load and reactive load of bus $j$, respectively; $N^{\mathrm{A}}$ denotes the set of AC nodes.

(2) AC voltage and current equation constraints

$$U_{j,t}^2=U_{i,t}^2-2\left(P_{ij,t}{R}_{ij}+Q_{ij,t}{X}_{ij}\right)+I_{ij,t}^2\left(R_{ij}^2+X_{ij}^2\right),\forall ij\in L^{\mathrm{A}}$$

(29)

$$I_{ij,t}^2={\displaystyle \frac{P_{ij,t}^2+Q_{ij,t}^2}{U_{i,t}^2}},\forall ij\in L^{\mathrm{A}}$$

(30)

In the equation, $L^{\mathrm{A}}$ denotes the set of AC branches.

(3) DC network power flow equation constraints

$$\left\{\begin{array}{cc}{\displaystyle \sum _{k\in \delta (j)}{P}_{jk,t}}-{\displaystyle \sum _{i\in \pi (j)}\left(P_{ij,t}-I_{ij,t}^2{R}_{ij}\right)}=P_{j,t},\hfill & \forall j\in N^{\mathrm{D}}\hfill \\ P_{j,t}=P_{j,t}^{\mathrm{PV}}+P_{j,t}^{\mathrm{ESS}}-P_{j,t}^{\mathrm{load}},\hfill & \forall j\in N^{\mathrm{D}}\hfill \end{array}\right.$$

(31)

In the equation, $N^{\mathrm{D}}$ denotes the set of DC nodes.

(4) DC voltage and current equation constraints

$$V_j^2=V_i^2-2P_{ij}{r}_{ij}+I_{ij}^2{r}_{ij}^2,\forall ij\in L^D$$

(32)

$$I_{ij}^2={\displaystyle \frac{P_{ij}^2}{V_i^2}},\forall ij\in L^D$$

(33)

In the equation, $L^D$ denotes the set of DC branches.

(5) Network security constraints

$$-\pi \le {\theta }_{ij}\le \pi$$

(34)

$$I_{ij\min }\le I_{ij}\le I_{ij\max }$$

(35)

$$V_{j\min }\le V_j\le V_{j\max }$$

(36)

In the equation, ${\theta }_{\mathrm{ij}}$ is the voltage phase angle of bus $i$; $I_{ij\min }$ and $I_{ij\max }$ are the lower and upper limits of the current amplitude of branch $ij$, respectively; $V_{j\min }$ and $V_{j\max }$ are the lower and upper bound constraints of the bus $j$ voltage amplitude, respectively.

(6) PV active and reactive power upper and lower limits constraints

$$0\le P_{w,t}\le P_{w,t}^A$$

(37)

$$0\le Q_{w,t}\le Q_{w,t}^A$$

(38)

In the equation, $P_{w,t}$ is the active output power of PV in the t-th time period; $Q_{w,t}$ is the reactive output power of PV in the t-th time period; $P_{w,t}^A$ is the predicted active output power of PV; $Q_{w,t}^A$ is the predicted reactive output power of PV.

2.4. Convexity Transformation Method

In order to improve the calculation accuracy and efficiency, the nonlinear constraint is relaxed by a second-order cone. The second-order cone programming relaxation of AC/DC network constraints is performed on Equations (39)–(44):

$$\left\{\begin{array}{ll}{\displaystyle \sum _{k\in \delta (j)}{P}_{jk,t}}-{\displaystyle \sum _{i\in \pi (j)}\left(P_{ij,t}-I_{ij,t}{R}_{ij}\right)}=P_{j,t},\hfill & \forall j\in N^{\mathrm{A}}\hfill \\ {\displaystyle \sum _{k\in \delta (j)}{Q}_{jk,t}}-{\displaystyle \sum _{i\in \pi (j)}\left(Q_{ij,t}-I_{ij,t}{X}_{ij}\right)}=Q_{j,t},\hfill & \forall j\in N^{\mathrm{A}}\hfill \end{array}\right.$$

(39)

$$v_{j,t}=v_{i,t}-2\left(P_{ij,t}{R}_{ij}+Q_{ij,t}{X}_{ij}\right)+I_{ij,t}\left(R_{ij}^2+X_{ij}^2\right),\forall ij\in L^{\mathrm{A}}$$

(40)

$${‖{\left[\begin{array}{ccc}2P_{ij,t}\hfill & 2Q_{ij,t}\hfill & I_{ij,t}-v_{i,t}\hfill \end{array}\right]}^{\mathrm{T}}‖}_2⩽I_{ij,t}+v_{i,t}$$

(41)

$${\displaystyle \sum _{k\in \delta (j)}{P}_{jk,t}}-{\displaystyle \sum _{i\in \pi (j)}\left(P_{ij,t}-l_{ij,t}{R}_{ij}\right)}=P_{j,t},\forall j\in N^{\mathrm{D}}$$

(42)

$$v_{j,t}=v_{i,t}-2P_{ij,t}{R}_{ij}+l_{ij,t}{R}_{ij}^2,\forall ij\in L^{\mathrm{D}}$$

(43)

$${‖{\left[\begin{array}{cc}2P_{ij,t}\hfill & l_{ij,t}-v_{i,t}\hfill \end{array}\right]}^{\mathrm{T}}‖}_2⩽l_{ij,t}+v_{i,t}$$

(44)

2.5. Solving Steps

Figure 3 shows a bi-level optimal configuration method for the ESS in AC/DC hybrid distribution networks, split into upper planning and lower operation levels. The upper level, with minimum comprehensive cost as the objective, uses an improved particle swarm optimization algorithm to initialize ESS location and capacity. The lower level, targeting minimum load standard deviation, adopts the commercial solver Gurobi for accurate optimization to determine system operating parameters and costs. The upper and lower levels realize collaborative optimization through a feedback mechanism: the lower level feeds back operating parameters to update the upper-level plan, while the upper-level ESS configuration serves as the lower-level input to form a complete model. This method realizes the integrated optimal configuration of location, capacity, and operation control of the ESS in the distribution network, taking into account economy, operational efficiency, and system feasibility.

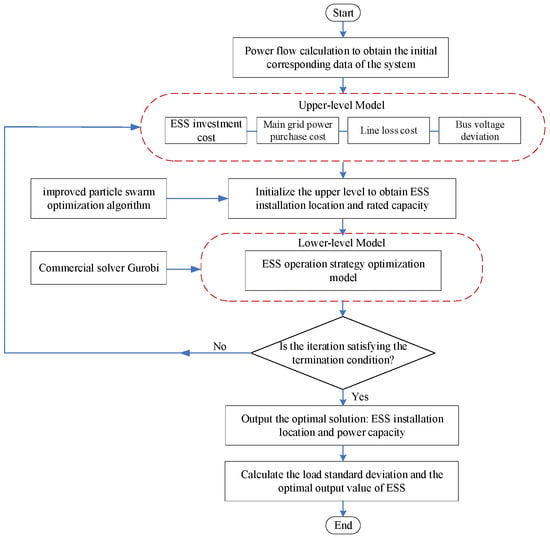
Figure 3. An overall solution flow chart.

3. Results and Discussion

3.1. Analysis of ESS Capacity and Location Impacts on Key Cost Items

• Scenario (1): Optimal configuration of the ESS.
• Scenario (2): Optimal configuration of the ESS with different capacities at the same site.
• Scenario (3): Optimized configuration of the ESS at different sites.
• Scenario (4): Optimized configuration of the ESS at different capacities and different sites.

From the Table 1 of the influence of ESS capacity and location on various costs, it can be seen that the cost difference among the four configuration scenarios is essentially the trade-off result of capacity adjustment and location change on core cost items such as network power purchase, line loss, voltage deviation, and investment.

Table 1. Comparison of ESS capacity and location impacts on key cost items.

Scenario	Planning Bus	Planning Capacity (kWh)	Main Network Electricity Purchase Cost (CNY/Day)	Line Loss Cost (CNY/Day)	Bus Voltage Deviation Cost (CNY/Day)	ESS Investment Cost (CNY/Day)	Total Cost (CNY/Day)
1	7	163	30,316	473	3415	735	34,939
	15	210
	28	244
2	7	240	33,203	835	2097	772	36,907
	15	200
	28	180
3	3	163	32,617	834	2107	985	36,543
	23	210
	25	244
4	5	240	33,458	834	2113	685	37,091
	22	176
	27	160

Scenario 1 is the optimal configuration scenario. Although the power purchase cost of the main network is the lowest among the four scenarios, the voltage deviation cost is significantly higher than that of other scenarios, and the final total cost is the lowest among the four scenarios, which is suitable for the scenario where the voltage stability requirement is relatively low and the total cost is given priority in control. Scenario 2 maintains the same location but adjusts the capacity. The increase in ESS capacity greatly reduces the cost of voltage deviation, but also increases the cost of power purchase in the main network, which reflects the characteristics of increasing capacity to improve voltage quality but increasing power purchase expenditure. Scenario 3 switches to different locations and keeps the capacity unchanged. The investment cost is the highest in the four scenarios, the cost of no overvoltage deviation is reduced, and the line loss cost is also maintained at a low level. Scenario 4 adjusts the location and capacity at the same time, and the investment cost is minimized, but the main network purchase cost becomes the highest among the four scenarios, and the total cost also increases.

On the whole, the capacity and location of the ESS should not be optimized in a single dimension; instead, it is necessary to integrate the goals of meeting voltage stability requirements, controlling main grid power purchase costs, and managing ESS investment costs, while making trade-offs between core cost components. For instance, pursuing the minimization of total cost entails accepting a certain level of voltage deviation and, thus, higher voltage deviation cost, whereas emphasizing voltage quality improvement requires bearing higher main grid power purchase costs or ESS investment costs.

3.2. Analysis of Economically Optimal Configuration of ESS Under Different Control Modes

• Scenario (1): The VSC control mode is constant power, and the ESS is optimized.
• Scenario (2): The VSC control mode is constant voltage, and the ESS is optimized.
• Scenario (3): The VSC control mode is droop control, and the ESS is optimized.

Table 2 illustrates the comparison of the economically optimal configuration schemes for the ESS across various control modes. In Scenario 1, the main grid electricity purchase cost is relatively low, and the ESS power configuration adopts a simplified scheme; however, its voltage deviation cost is the highest among all scenarios, with the total cost ranking in the middle.

Table 2. Comparison of ESS economically optimal configurations under different control modes.

Scenario	Planning Bus	Planning Capacity (kWh)	Planning Power (kW)	Main Network Electricity Purchase Cost (CNY/Day)	Line Loss Cost (CNY/Day)	Bus Voltage Deviation Cost (CNY/Day)	ESS Investment Cost (CNY/Day)	Total Cost (CNY/Day)
1	7	163	100	30,316	473	3415	735	34,939
	15	210	100
	28	244	100
2	5	239	61	32,450	826	1836	855	35,968
	19	188	68
	31	224	64
3	10	225	100	30,259	400	2710	703	34,074
	19	196	100
	29	170	100

Scenario 2 features its core advantage in the lowest voltage deviation cost and optimal power supply stability. Nevertheless, it exhibits the highest main grid electricity purchase cost and line loss cost, accompanied by larger ESS total capacity, higher ESS investment cost, and the highest total cost.

Scenario 3 achieves the lowest main grid electricity purchase cost, line loss cost, and ESS investment cost among the three scenarios, with the optimal total cost performance. Additionally, its voltage deviation cost is superior to that of Scenario 1, presenting the most balanced comprehensive performance; the only drawback is that its voltage accuracy is slightly inferior to that of Scenario 2.

3.3. Analysis of ESS-Induced Voltage Quality Improvement Under Different Control Modes

Section 3.3 focuses on analyzing and comparing the bus voltage conditions of AC/DC hybrid distribution networks under different control modes. Figure 4 presents the load curve of the AC/DC hybrid distribution network. During the 00:00–18:00 period, the original total load exhibits an overall upward trend, reaching a peak load of 3715 kW at 18:00; in contrast, the total load fluctuation becomes more significant after the integration of PV and ESS, while the load level generally remains lower than the original load. After 18:00, both load curves decrease rapidly: the original load drops to 1858 kW, and the load with PV and ESS integration decreases to 1557 kW. On the whole, this figure clearly illustrates the changes in the fluctuation characteristics of the total load power induced by the integration of PV and the ESS, and effectively verifies that PV and ESS integration reduces the overall power level of the total load.

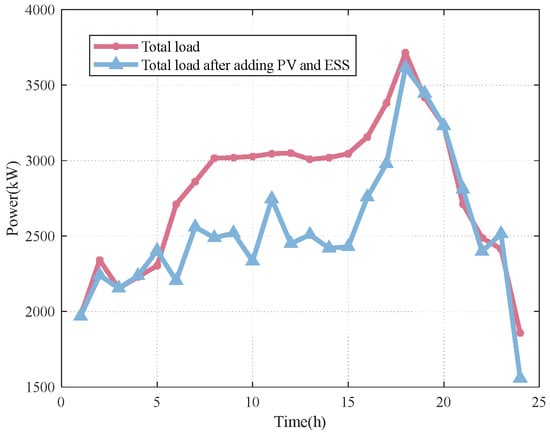
Figure 4. The load curve of the AC/DC hybrid distribution network.

Figure 5 corresponds to the voltage distribution of the AC/DC hybrid distribution network at three typical moments—12:00 (maximum PV output), 18:00 (maximum load), and 24:00 (minimum load)—under three control modes, and further compares the voltage regulation performance of these three control modes. Specifically, at all three moments, the voltage in the constant power control scenario drops sharply to 0.95 p.u. after node 24, which significantly deviates from the rated bus voltage and poses a risk of voltage over-limit. In contrast, under both constant voltage control and droop control, the voltage stability of each node can be constrained within the reasonable range of 0.97–1.05 p.u. at 12:00, 18:00, and 24:00. Among these two control modes, constant voltage control exhibits optimal voltage stability, while droop control also maintains voltage within the limit without over-limit risks. These results indicate that during the three typical periods, both constant voltage control and droop control can effectively improve system voltage quality, and their performance is significantly superior to that of the constant power control mode.

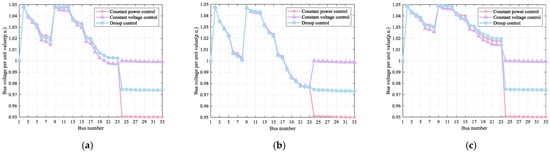
Figure 5. Voltage distribution curves of three scenarios: (a) The voltage distribution at 12:00 (maximum PV output); (b) The voltage distribution at 18:00 (maximum load); (c) The voltage distribution at 24:00 (minimum load).

As shown in Table 3, the minimum voltage value in Scenario 1 is only 0.95 p.u., while those in Scenario 2 and Scenario 3 are increased to 0.9773 p.u. and 0.9731 p.u., respectively. Although the maximum voltage values of the three scenarios are relatively close, the voltage variation range of Scenario 1 is significantly wider than that of Scenario 2 and Scenario 3. In terms of voltage stability, the voltage deviation in Scenario 1 is as high as 2.0633 p.u., with the most severe fluctuations. By contrast, the voltage deviation in Scenario 3 is reduced to 1.6181 p.u., and that of Scenario 2 is further compressed to 1.0659 p.u., which means it exhibits optimal stability. In summary, from voltage extreme values and variation ranges to deviation levels, Scenario 2 outperforms Scenario 3, and the voltage quality performance of both scenarios is significantly superior to that of Scenario 1.

Table 3. Analysis of bus voltage quality under different control methods.

Scenario	Maximum Voltage (p.u.)	Minimum Voltage (p.u.)	Average Voltage (p.u.)	Range of Voltage (p.u.)	Voltage Deviation (p.u.)
1	1.0489	0.95	1.002	0.95–1.0489	2.0633
2	1.0487	0.9773	1.0161	0.9773–1.0487	1.0659
3	1.0498	0.9731	1.0098	0.9731–1.0498	1.6181

3.4. Analysis of ESS Energy Variation and System Power Balance Under Different Control Modes

Section 3.4 focuses on analyzing ESS energy variation and system power balance under different control modes. By synthesizing the three control methods, the ESS energy variation characteristics presented in Figure 6 can be summarized. This figure illustrates the energy characteristics of the ESS under the three control modes. In Scenario 1, the SOC of the ESS is basically maintained around 0.5, with gentle fluctuations in charging and discharging powers. In Scenario 2, the SOC fluctuation range is expanded, and the power response exhibits higher activity. Scenario 3 further enhances the peak-shaving capability and frequency of power regulation; meanwhile, the dynamic fluctuation of the SOC with power changes becomes more significant. This phenomenon intuitively reflects the transition of different control strategies from non-intervention to active regulation, as well as the impact of control modes on the stability of the ESS state and the flexibility of the power response. Figure 7 presents the power balance status of the AC/DC hybrid distribution network under the three control strategies.

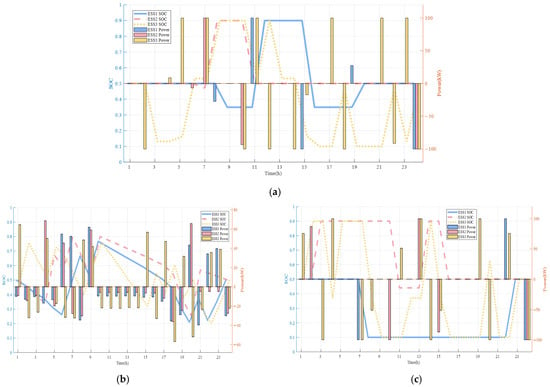
Figure 6. ESS energy variation under different control modes: (a) The variation of ESS energy under the constant power control mode; (b) The variation of ESS energy under the constant voltage control mode; (c) The variation of ESS energy under the droop control mode.

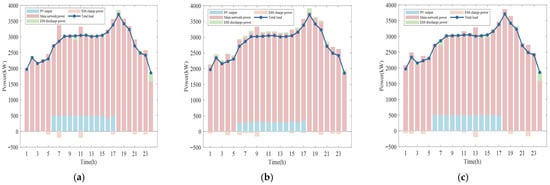
Figure 7. System power balance status under different control modes: (a) System power balance status under the constant power control mode; (b) System power balance status under the constant voltage control mode; (c) System power balance status under the droop control mode.

3.5. Sensitivity Analysis of Objective Function to ESS Parameters

Section 3.5 focuses on analyzing the sensitivity of the objective function to ESS parameters. Figure 8a illustrates that as the ESS power upper limit and the number of ESS access points increase, the load standard deviation decreases continuously. This phenomenon indicates that an ESS with a larger capacity and more access points can effectively stabilize load fluctuations and enhance system stability. Figure 8b shows that the impact of ESS parameters on the comprehensive cost is relatively moderate: the comprehensive cost decreases slightly with the increase in the power upper limit, and then rises slightly as the number of access points increases. On the whole, the ESS configuration needs to balance the improvement in load stability and the control of comprehensive costs. Specifically, by reasonably selecting the ESS power upper limit and the number of access points, the optimal matching between system stability and cost control can be achieved.

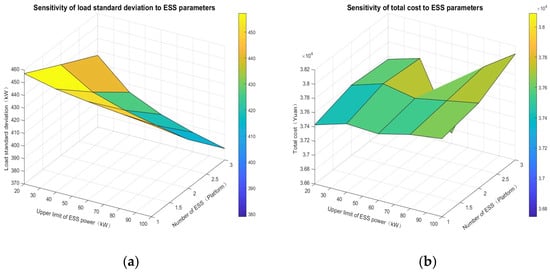
Figure 8. Sensitivity analysis of the objective function to ESS parameters: (a) Sensitivity of load standard deviation to ESS parameters; (b) Sensitivity of total cost to ESS parameters.

3.6. Analysis of Uncertainty Scenarios in AC/DC Hybrid Distribution Network ESS Configuration

Section 3.6 focuses on a comparative analysis of PV uncertainty scenarios. Specifically, Figure 9 presents an uncertainty scenario analysis of PV output. Figure 9a illustrates the PV basic scenarios, showing the original fluctuation curves of multiple groups of PV output. These curves reflect the randomness and volatility of PV output within a single day. Figure 9b depicts typical PV scenarios, where five groups of typical output curves with different probabilities (probability distributions: 0.34, 0.13, 0.22, 0.1, 0.21) are extracted from basic scenarios. This extraction not only retains the uncertainty characteristics of PV output but also simplifies the analysis dimensions through the selection of typical scenarios. Overall, this figure clearly demonstrates the uncertainty of PV output by means of basic scenarios showing fluctuations and typical scenarios refining patterns. It further provides a scenario-based foundation for subsequent system analysis, such as ESS configuration robustness verification in the AC/DC hybrid distribution network.

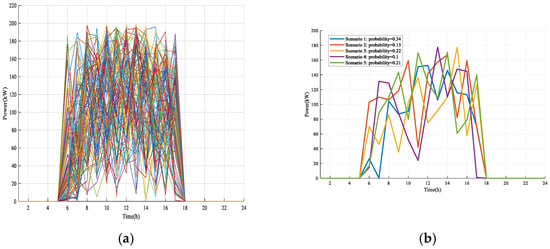
Figure 9. Analysis of PV output uncertainty scenarios: (a) Basic PV scenarios; (b) Typical PV scenarios.

Figure 10 illustrates the voltage distribution curves of the three control methods across five scenarios. The ESS configuration scenarios proposed in Section 3.2 were applied to five different PV uncertainty scenarios for comparative verification, with the voltage distribution curves at 18:00 selected for focused analysis. At this time point, the terminal bus voltage is at risk of falling below the lower limit due to high load demand and reduced PV output. From the analysis results, it can be concluded that all configuration scenarios are capable of meeting the voltage quality requirements of the power system, among which Scenario 2 exhibits optimal voltage quality performance.

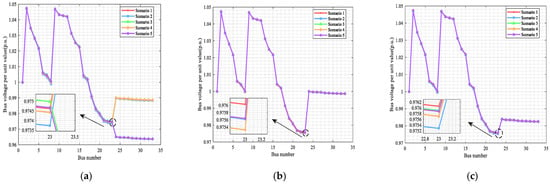
Figure 10. Voltage distribution curves of the three control methods across five scenarios: (a) Voltage distribution curves of the constant power control methods across five scenarios; (b) Voltage distribution curves of the constant voltage control methods across five scenarios; (c) Voltage distribution curves of the droop control methods across five scenarios.

As shown in Table 4, the variations in ESS configuration parameters and cost components across different scenarios reflect the influence of diverse PV output conditions on both the economically optimal configuration of the ESS and its daily operating costs.

Table 4. Comparison of ESS economically optimal configurations under different scenarios.

Scenario	Planning Bus	Planning Capacity (kWh)	Planning Power (kW)	Main Network Electricity Purchase Cost (CNY/Day)	Line Loss Cost (CNY/Day)	Bus Voltage Deviation Cost (CNY/Day)	ESS Investment Cost (CNY/Day)	Total Cost (CNY/Day)
1	7	176	100	30,018	655	3441	701	34,816
	23	167	100
	33	245	100
2	7	211	82	32,329	833	2000	975	36,139
	18	210	75
	32	185	72
3	7	212	72	32,748	833	1995	770	36,348
	18	209	82
	32	184	68
4	7	161	71	32,804	835	2128	780	36,549
	15	209	80
	28	244	56
5	3	158	72	32,421	820	2208	780	36,231
	14	242	82
	31	202	76

3.7. Analysis of Seasonal Scenarios in AC/DC Hybrid Distribution Network ESS Configuration

Section 3.7 focuses on the analysis of seasonal scenarios. Specifically, the maximum load scenarios in summer and winter of a specific region are selected to verify the impact of load scenario variations on the ESS configuration scheme. Table 5 presents the ESS configuration parameters and cost indicators under these two scenarios. As indicated in the table, differences exist in ESS installation locations, rated capacities, and cost components across the two load scenarios, which confirms that changes in load scenarios exert a direct influence on the ESS configuration scheme.

Table 5. Comparison of ESS economically optimal configurations under different seasonal scenarios.

Scenario	Planning Bus	Planning Capacity (kWh)	Planning Power (kW)	Main Network Electricity Purchase Cost (CNY/Day)	Line Loss Cost (CNY/Day)	Bus Voltage Deviation Cost (CNY/Day)	ESS Investment Cost (CNY/Day)	Total Cost (CNY/Day)
1	11	230	95	38,789	991	1982	758	42,522
	14	213	84
	32	163	64
2	7	154	80	36,321	932	2019	756	40,030
	22	249	81
	29	188	60

Figure 11 presents the voltage distribution curves corresponding to the two seasonal scenarios at the moment of maximum load. Specifically, the maximum load time at 14:00 in summer and the maximum load time at 18:00 in winter were selected for targeted analysis and verification. The results confirm that the proposed ESS configuration scenarios are fully capable of meeting the voltage level requirements of the power system.

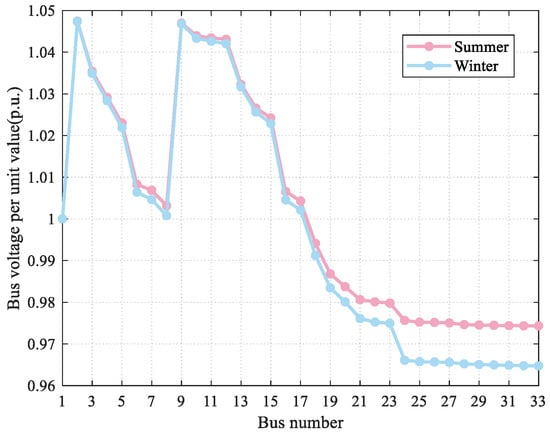
Figure 11. Voltage distribution curves at the maximum load time of the two seasonal scenarios.

3.8. Analysis of Algorithm Convergence and Computational Efficiency

Section 3.8 focuses on an analysis of convergence and computational efficiency of the algorithm employed for ESS configuration optimization. Specifically, Figure 12 presents a comparison of the convergence processes across three control scenario groups: constant power control, constant voltage control, and droop control. The results indicate that the algorithms corresponding to the constant power control and droop control scenarios converge rapidly after the third iteration, while the algorithm for the constant voltage control scenario initiates convergence at the fourth iteration.

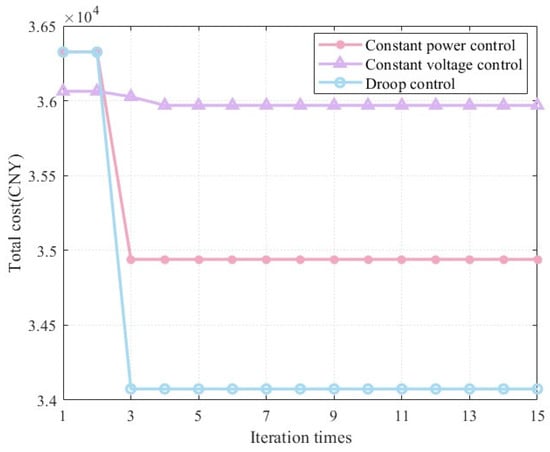
Figure 12. Convergence verification of algorithms for three control scenarios.

Table 6 presents the computational efficiency of the algorithms corresponding to the three control scenarios proposed in Section 3.2. Specifically, the solution time of the algorithm under the constant power control mode is 164,153 s, while that under the constant voltage control mode is 181,849 s, and the droop control mode corresponds to a solution time of 182,612 s. As indicated in Table 6, although the droop control mode exhibits optimal convergence performance, its solution time is slightly longer than that of the other two control modes.

Table 6. Analysis of computational efficiency of algorithms under different control scenarios.

Scenario	Computational Efficiency (Seconds)
1	164,153
2	181,849
3	182,612

4. Conclusions

In this paper, a bi-level optimal configuration method of an ESS for an AC/DC hybrid distribution network considering voltage quality is proposed. The optimal configuration results of the ESS under different control modes of a VSC are fully considered. The results show the following:

(1) The proposed bi-level optimal configuration method of the ESS in the AC/DC hybrid distribution network, considering voltage quality, can effectively eliminate the risk of bus voltage violation and reduce voltage deviation. Specifically, under the condition of the parameters of the case used, compared with the scenario without a voltage optimal control strategy, the overall voltage deviation is reduced by 48.34%, and the power system voltage is maintained at an ideal level.

(2) Among the various control modes of the VSC investigated, the constant voltage control mode demonstrates the most significant effect on voltage quality improvement, while the droop control mode achieves the highest comprehensive cost-effectiveness. These findings provide valuable technical guidance for formulating practical operation strategies for AC/DC hybrid distribution networks.

(3) The scientific configuration of the ESS in AC/DC hybrid distribution networks requires the integration of multi-objective optimization considerations. In this paper, a rational balance is achieved between two core objectives: ESS cost control and power system voltage stability. These research outcomes effectively address the existing research gap regarding the coordination of ESS configuration and voltage regulation in AC/DC hybrid distribution networks.