Data-Driven State-of-Health Estimation by Reconstructing Virtual Full-Charge Segments

Abstract

The rapid growth of new energy vehicles necessitates accurate battery state of health (SOH) assessment to ensure safety and reliability. However, real-world SOH estimation is challenging because users rarely perform full charge–discharge cycles, leaving only fragmented charging segments that obscure true battery capacity. To address this, we propose a data-driven method that reconstructs a virtual full-charge cycle. By clustering charging segments based on temperature and current, the approach creatively splices multiple incomplete curves from similar mileages and conditions into a complete charging profile. This enables robust full-capacity estimation on a large-scale real-world vehicle dataset, achieving estimation errors below 2% when compared with offline validation tests. The method offers a practical and scalable solution for SOH monitoring and fleet management using field data.

1. Introduction

Lithium-ion batteries serve as the primary energy source for propulsion in new energy vehicles (NEVs) [1]. The state of health (SOH) is a pivotal metric that reflects the extent of electrochemical degradation within the battery system and directly governs the NEV’s performance, safety, and operational reliability [2,3,4]. Over prolonged cycling, side reactions such as solid electrolyte interphase (SEI) growth, lithium plating, and transition metal dissolution induce capacity fading, internal resistance increase, and heat generation, collectively deteriorating the available power and energy output [5,6]. These degradation phenomena not only constrain the driving range and acceleration capability but also elevate the risk of thermal runaway and mechanical failure [7,8]. Consequently, accurate and real-time SOH estimation is indispensable for energy optimization, and the safe, long-term management of NEVs [9,10].

Beyond its technical significance, precise SOH estimation also has profound economic and environmental implications [11,12]. Reliable SOH assessment provides a scientific basis for operational decision making, including usage optimization, maintenance scheduling, and end-of-life management, thereby reducing life-cycle costs and enhancing system sustainability [13,14]. Moreover, SOH serves as a key criterion for second-life applications, determining whether a retired battery retains sufficient functionality for echelon utilization in distributed energy storage or other low-demand scenarios [15,16]. In this context, SOH estimation constitutes the scientific foundation for extending the life-cycle value chain of retired lithium-ion batteries [17].

Presently, estimation methodologies for battery SOH are broadly categorized into model-driven and data-driven approaches [18]. Model-driven methods rely on physics-based electrochemical models or equivalent circuit models (ECMs) to interpret degradation behaviors from a mechanistic perspective [19,20]. Conversely, data-driven methods leverage statistical analysis and machine learning to capture degradation trends by mining large-scale historical operational data [21]. With the rapid development of big data analytics and artificial intelligence, data-driven SOH estimation has become a prominent research frontier, offering enhanced adaptability and scalability for real-world NEV applications [22,23].

Nonetheless, conventional model-driven methods exhibit significant limitations when applied to real-world vehicle operations [24]. These approaches are typically developed under controlled laboratory conditions and depend on specific features or parameters extracted from experiments conducted at constant temperature or under constant-current/constant-voltage protocols [25]. During real-world driving and charging, however, the operating conditions are highly dynamic and nonlinear, making it impossible to satisfy these stringent laboratory prerequisites. This mismatch between theoretical model assumptions and practical conditions leads to substantial discrepancies between estimated and actual SOH values [26].

While data-driven methods are inherently better suited to practical operating conditions, they face their own challenges [27]. Most existing techniques require pre-labeled SOH data as the ground truth for model training [28,29]. These labels are typically derived from costly, time-consuming laboratory tests or inferred from the vehicle’s battery management system (BMS)  [30]. However, the SOH values reported by onboard BMSs are prone to estimation errors, causing error propagation and limiting the achievable estimation precision of data-driven models [31].

A fundamental bottleneck common to both categories of methods lies in the incompleteness of real-world operational data [32]. Due to the stochastic and user-dependent nature of charging behavior, NEV batteries are seldom charged from a low state of charge to full capacity [33]. Consequently, historical datasets are dominated by incomplete charging records, which hinder the construction of accurate degradation features and impose an upper limit on achievable estimation accuracy [34].

To address these challenges, this study proposes a novel SOH estimation framework that integrates data-driven techniques with a clustering-based feature reconstruction strategy. The proposed method operates exclusively on real-world data and eliminates the dependence on pre-labeled SOH values. A clustering algorithm leveraging statistical indicators of temperature and current is introduced to partition complex operating conditions and mitigate the influence of variable thermal and loading profiles. Most critically, a charging segment splicing strategy is developed, which identifies and concatenates multiple incomplete charging segments from the same vehicle that share similar operating conditions and close mileage proximity. This reconstruction yields a virtually complete charging profile, enabling robust capacity estimation. By averaging the charge capacity across spliced segments, the proposed framework significantly reduces estimation bias caused by anomaly segments and effectively overcomes the accuracy bottleneck imposed by the lack of fully charged data.

2. Theoretical Framework for Virtual Capacity Reconstruction

The SOH of a battery is fundamentally defined as the ratio of its current maximum available capacity $C_{curr}\left(t\right)$ at a specific time t (or mileage m) to its initial, beginning-of-life (BOL) capacity $C_{initial}$  [35]. This relationship is mathematically formulated as

$$SOH\left(t\right)={\displaystyle \frac{C_{curr}\left(t\right)}{C_{initial}}}$$

(1)

Therefore, obtaining an accurate measurement of the current full capacity, $C_{curr}\left(t\right)$, is the physical basis for any SOH estimation. Yet, in real-world operation, charging processes are frequently interrupted by stochastic user behavior, resulting in field data dominated by incomplete charging segments.

A common method to estimate the current full capacity $C_{seg,i}$ from a single incomplete segment i is to divide the measured charge accumulation $\Delta Q_i$ by the corresponding change in state of charge (SOC) $\Delta SO{C}_i$  [36]. This relationship is formulated as

$$C_{seg,i}={\displaystyle \frac{\Delta Q_i}{\Delta SO{C}_i}}={\displaystyle \frac{{\int }_{t_{start,i}}^{t_{end,i}}I\left(t\right)dt}{SOC\left(t_{end,i}\right)-SOC\left(t_{start,i}\right)}}$$

(2)

However, the $SOC\left(t\right)$ value used in the denominator is itself an onboard estimation and is subject to errors from model inaccuracies, sensor drift, and temperature variations [37]. The estimation error in the denominator propagates directly into the capacity calculation, introducing significant uncertainty and bias in the estimated segment capacity $C_{seg,i}$.

To address these limitations, we propose a novel approach for reconstructing a virtual full-charge capacity, denoted as $C_{virtual}$. This method synthesizes a complete and physically consistent charging profile by splicing multiple incomplete charging segments extracted from real-world operation. The theoretical soundness of this reconstruction is established based on two key assumptions:

• Quasi-static degradation: Within a sufficiently small mileage window $\Delta M$, the lithiumion battery’s capacity degradation is considered negligible. For any two mileages $m_i$ and $m_j$ within this window,

  $$|m_i-m_j| \le \Delta M⟹C_{curr}\left(m_i\right)\approx C_{curr}\left(m_j\right)$$

  (3)
• Consistency of polarization via clustering: Ideally, the capacity integration intervals should be defined based on the open-circuit voltage (OCV) to reflect thermodynamic equilibrium. However, real-world BMS data typically provides only terminal voltage ($V_{terminal}$), which differs from OCV due to ohmic potential drop and polarization effects:

  $$V_{terminal}=V_{OCV}+I·R_{int}+V_{pol}$$

  (4)
  Direct usage of $V_{terminal}$ for data splicing across heterogeneous operating conditions would introduce significant systematic errors, as the voltage drop would vary drastically. To validate the use of $V_{terminal}$, we employ a strict clustering strategy based on the dominant operating factors, including current and temperature. By ensuring that all segments within a specific cluster share statistically similar current and temperature profiles, we impose a constraint where the polarization terms remain consistent across spliced segments:

  $${(I·R_{int}+V_{pol})}_i\approx {(I·R_{int}+V_{pol})}_j\approx C_{pol}$$

  (5)
  Under this condition, aligning segments based on $V_{terminal}$ becomes mathematically equivalent to aligning them based on $V_{OCV}$ with a constant offset $C_{pol}$. This effective alignment preserves the physical validity of the capacity integration $\Delta Q$ within the standardized voltage intervals, despite the lack of OCV measurements. While internal resistance increases with long-term aging, the proposed method reconstructs capacity profiles locally within a narrow mileage window. Consequently, the impedance and polarization characteristics are considered distinct for each reconstruction instance but consistent within the splicing set, thereby isolating the aging effect from the reconstruction process.

In practical automotive applications, lithium-ion batteries predominantly exhibit a linear degradation trajectory during their primary lifespan. The end-of-life (EOL) threshold is conventionally defined as 80% of the nominal capacity which is typically reached after a cumulative mileage ranging from 80,000 to 150,000 km. Taking a conservative estimation where an electric vehicle reaches 80% SOH at 80,000 km, the average degradation rate is approximately 0.025% per 100 km. Consequently, within the proposed sliding window of $\Delta M=2000$ km, the theoretical capacity loss is limited to approximately 0.5%. This magnitude is significantly lower than the inherent sensor noise and the algorithmic tolerance margin of 2%. Furthermore, although lithium-ion batteries may exhibit nonlinear aging or capacity diving phenomena in their late life-cycle stages, the degradation curve remains locally linear within such a narrow mileage interval. Therefore, the capacity variation within closely spaced driving intervals is statistically insignificant and can be reasonably considered quasi-static.

Our methodology reconstructs the capacity by discretizing the standardized, full voltage range $[V_{min},V_{max}]$ into N small, non-overlapping intervals, $\Delta V_j=[V_j,V_{j+1}]$ (e.g., $\Delta V=0.01V$). The current capacity $C_{curr}\left(t\right)$ can thus be represented as the sum of the incremental capacities $q_j$ required to charge through each interval $\Delta V_j$,

$$C_{curr}\left(t\right)=\sum _{j=1}^N{q}_j\left(t\right)\mathrm{where}{q}_j\left(t\right)={\int }_{V_j}^{V_{j+1}}I\left(V\right){\displaystyle \frac{dt}{dV}}dV$$

(6)

To ensure operating condition consistency, all charging segments are first partitioned into k distinct clusters. For a target charging segment i at mileage $m_i$ belonging to cluster k, we first collect a set $S_k\left(m_i\right)$ of n adjacent charging segments that satisfy the two assumptions.

$$S_k\left(m_i\right)=\{r\mid \mathrm{vehicle}\left(r\right)=\mathrm{vehicle}\left(i\right),\mathrm{cluster}\left(r\right)=k,|m_r-m_i| \le \Delta M\}$$

(7)

For each voltage interval $\Delta V_j$, we then gather the set of all available incremental capacity measurements $\left\{q_{r,j}\right\}$ from all segments $r\in S_k\left(m_i\right)$ that cover this specific voltage interval. A robust average, ${\overline{q}}_j(m_i,k)$, is then calculated for this interval by applying a statistical filter to remove outliers from the set $\left\{q_{r,j}\right\}$,

$${\overline{q}}_j(m_i,k)=\mathrm{RobustAverage}\left(\{q_{r,j}\mid \forall r\in S_k\left(m_i\right)\mathrm{and}\Delta V_j\subseteq [V_{start,r},V_{end,r}]\}\right)$$

(8)

The virtual full-charge capacity $C_{virtual}(m_i,k)$ for the target segment i is defined as the sum of these robustly averaged incremental capacities ${\overline{q}}_j$ across the entire standardized voltage range $[V_{min},V_{max}]$.

$$C_{virtual}(m_i,k)=\sum _{j=1}^N{\overline{q}}_j(m_i,k)$$

(9)

The reconstructed $C_{virtual}(m_i,k)$ serves as a robust and physically consistent approximation of the current full capacity $C_{curr}\left(m_i\right)$ under operating condition k. By substituting the reconstructed capacity into the fundamental definition of SOH, the SOH corresponding to segment i at mileage $m_i$ and condition k can be expressed as

$$SOH(m_i,k)={\displaystyle \frac{C_{virtual}(m_i,k)}{C_{initial}}}$$

(10)

This formulation enables accurate SOH estimation by reconstructing a complete and physically meaningful capacity profile from fragmented real-world data, thereby effectively overcoming the inherent limitations imposed by incomplete charging records.

3. Algorithmic Implementation for SOH Calculation

The implementation of the proposed SOH estimation framework comprises four major stages: (1) data acquisition and feature engineering, (2) operating condition classification through clustering analysis, (3) virtual capacity reconstruction via charging segment splicing, and (4) SOH calibration coupled with anomaly detection. The overall architecture of this process is depicted in Figure 1.

3.1. Data Acquisition and Feature Engineering

The foundational dataset utilized in this study comprises historical time-series data uploaded from the BMS of NEVs to the cloud platform during charging events. For each charging segment i, the raw dataset $D_i$ contains timestamps t, current $I\left(t\right)$, individual cell voltages $V_{cell,j}\left(t\right)$, and temperatures $T\left(t\right)$.

For each cell, the incremental capacity $q_{i,j}$ charged within each predefined voltage interval $\Delta V_j$ (e.g., $\Delta V=0.01$ V) is calculated using the Ampere-hour integration method. The charge $\Delta Q_k$ accumulated between two consecutive timestamps $t_k$ and $t_{k+1}$ is given by

$$\Delta Q_k={\int }_{t_k}^{t_{k+1}}I\left(t\right)dt$$

(11)

By mapping the calculated $\Delta Q_k$ values to their corresponding voltage intervals $\Delta V_j$, the set of incremental capacities $\left\{q_{i,j}\right\}$ is derived for each charging segment i. Concurrently, to facilitate the subsequent clustering analysis, a comprehensive series of statistical features is extracted, including the cumulative mileage $m_i$ as well as the maximum, minimum, and mean values of both temperature ($T_{max,i},T_{min,i},T_{mean,i}$) and current ($I_{max,i},I_{min,i},I_{mean,i}$). These indicators comprehensively characterize the electrical and thermal loading conditions of each segment, thereby establishing a robust foundation for the classification of operating conditions.

3.2. Operating Condition Classification via K-Means Clustering

To account for the substantial influence of operating conditions on charging behavior, all charging segments are partitioned into k distinct clusters representing different thermal–electrical modes. The k-means algorithm is adopted for this purpose, owing to its efficiency and stability in handling high-dimensional continuous features and its suitability for unsupervised partitioning of large-scale battery datasets [38]. For each segment i, a feature vector $X_i$ is constructed from its most representative indicators, including the maximum, minimum, and mean values of temperature and current. It should be noted that mileage is not included in the clustering features, as it serves as a prerequisite criterion for sample selection; only charging segments with a mileage difference smaller than a predefined threshold $\Delta M$ are grouped together prior to clustering. A feature vector $X_i$ is constructed for each segment i using its most influential features:

$$X_i=[T_{max,i},T_{min,i},T_{mean,i},I_{max,i},I_{min,i},I_{mean,i}]$$

(12)

To ensure that each feature contributes equally to the distance calculation, the features are first normalized to the range $[0,1]$ using min-max scaling:

$$x^{\prime }={\displaystyle \frac{x-x_{min}}{x_{max}-x_{min}}}$$

(13)

The k-means algorithm aims to minimize the within-cluster sum of squares (SSE)  [39], which is defined as

$$J=\sum _{k=1}^K\sum _{X_i\in S_k}{\parallel X_i-{\mu }_k\parallel }^2$$

(14)

where $S_k$ denotes the set of charging segments belonging to cluster k, as defined in Equation (7), and ${\mu }_k$ represents the centroid of that cluster. The optimal number of clusters K is determined through a comprehensive evaluation that combines the Elbow method and the Silhouette coefficient across a range of candidate K values [40,41]. Each resulting cluster $S_k$ represents a distinct charging operating condition.

3.3. Virtual Capacity Reconstruction via Splicing

The algorithm for computing the virtual full-charge capacity $C_{virtual}$ is implemented for each target charging segment i based on the mathematical framework established in Section 2. The procedure proceeds sequentially through adjacent segment filtering, incremental capacity aggregation, robust statistical averaging, and final capacity summation.

In the adjacent segment filtering stage, a sequence-based filtering mechanism is applied using a sliding window of length $\Delta M$. Starting from the mileage corresponding to each target segment i (with mileage $m_i$ and cluster index k), the algorithm iteratively slides the window forward along the mileage axis to identify all charging segments belonging to the same vehicle and operating condition cluster, where the mileage difference satisfies $|m_r-m_i| \le \Delta M$ (typically $\Delta M=2000$ km). Consistent with the theoretical derivation in Section 2, this interval corresponds to a conservative capacity loss of approximately 0.5%, which is statistically negligible compared to the algorithmic tolerance margin, thereby strictly satisfying the quasi-static assumption. The resulting set of filtered segments, denoted as $S_{adj}$, forms the local neighborhood used for virtual capacity reconstruction.

Once the set $S_{adj}$ is defined, the algorithm aggregates all available incremental capacity data. A temporary data structure $Q_{collector}$ is created. $Q_{collector}$ is an array of lists, where each index j corresponds to a specific voltage interval $\Delta V_j$ in the standardized range $[V_{min},V_{max}]$. The algorithm iterates through every segment $r\in S_{adj}$. For each segment, it reads its pre-calculated incremental capacity data $\left\{q_{r,j}\right\}$ and appends each $q_{r,j}$ to the corresponding list in the collector:

$$Q_{collector}\left[j\right]=\{q_{r,j}\mid \forall r\in S_{adj}\mathrm{and}\Delta V_j\mathrm{is}\mathrm{covered}\mathrm{by}r\}$$

(15)

After this step, $Q_{collector}\left[j\right]$ holds all measured incremental capacity values for the j-th voltage interval from all relevant neighboring segments.

A simple mean of $Q_{collector}\left[j\right]$ is highly susceptible to outliers and may be distorted by anomalous values from individual segments. To enhance robustness, a statistical filtering procedure is applied to each list $Q_{collector}\left[j\right]$ prior to averaging. Specifically, a standard boxplot-based interquartile range (IQR) filter is employed to remove outliers and retain only statistically consistent values, as detailed in Algorithm 1.

Algorithm 1 Robust Statistical Filtering for Virtual Capacity Calculation

Require: List of incremental capacities $Q_{collector}\left[j\right]=\{q_1,q_2,\dots ,q_n\}$ for voltage interval j

Ensure: Robust average ${\overline{q}}_j$

1: Compute the first and third quartiles: $$Q{1}_j=\mathrm{Quantile}(Q_{collector}\left[j\right], 0.25),Q{3}_j=\mathrm{Quantile}(Q_{collector}\left[j\right], 0.75)$$  2: Calculate the interquartile range: $IQ{R}_j=Q{3}_j-Q{1}_j$  3: Define acceptance bounds: $$Lower\_Boun{d}_j=Q{1}_j-1.5\times IQ{R}_j,Upper\_Boun{d}_j=Q{3}_j+1.5\times IQ{R}_j$$  4: Filter outliers to form a new list: $$Q_{collector}^{\prime }\left[j\right]=\{q\in Q_{collector}\left[j\right]\mid Lower\_Boun{d}_j\le q\le Upper\_Boun{d}_j\}$$  5: Compute the robust mean: $${\overline{q}}_j={\displaystyle \frac{1}{|Q_{collector}^{\prime }\left[j\right]|}}\sum _{q\in Q_{collector}^{\prime }\left[j\right]}q$$  6: return ${\overline{q}}_j$

Finally, the total virtual capacity $C_{virtual}(m_i,k)$ is computed by summing the robust averages ${\overline{q}}_j$ for all N intervals across the standardized voltage range $[V_{min},V_{max}]$ as described in Equation (9). This single scalar value is the output of the algorithm for segment i. It represents the robustly estimated full capacity at mileage $m_i$ for operating condition k.

4. Results and Discussion

This section presents the experimental validation of the proposed SOH estimation methodology. The algorithm was applied to an extensive dataset of real-world operational data collected from a fleet of electric vehicles. The following subsections detail the dataset characteristics, the intermediate clustering results, the final SOH estimation accuracy, and specific validation cases.

4.1. Experimental Dataset Overview

The dataset utilized in this study consists of historical charging data collected from a fleet of 108 real-world electric vehicles of the same model. All vehicles are equipped with the same battery pack specifications, featuring a configuration of Nickel–Cobalt–Manganese (NCM) cells with a nominal capacity of 145 Ah. Comprising a total of 65,250 charging segments, the dataset captures detailed time-series records of current, cell voltages, temperature, and cumulative mileage for each charging event. The aggregated data spans a broad operational spectrum, with vehicle mileages ranging from 0 km to approximately 250,000 km, covering the entire life-cycle from fresh to highly degraded states. Figure 2 illustrates the mileage distribution of the fleet, demonstrating a comprehensive and data-rich sample across various degradation stages.

4.2. Operating Condition Clustering Results

As outlined in the methodology, partitioning the data by operating condition is a prerequisite for accurate splicing. While the full estimation model employs a comprehensive set of six statistical features, specifically the maximum, minimum, and mean values of both temperature and current as clustering inputs, for the purpose of clear visualization, the k-means clustering results are demonstrated here using two simplified representative features, average charging current and average charging temperature. Figure 3 depicts the results for $k=7$. The clusters effectively segregate distinct charging behaviors, clearly distinguishing between low-power/low-temperature scenarios and high-power/high-temperature scenarios. This separation is essential to ensure that the virtual capacity reconstruction strategy strictly splices segments that share comparable electrochemical conditions.

4.3. Comparison with Industrial Baseline

Figure 4 presents a comparative analysis of the SOH degradation trajectory for a representative vehicle, estimated by the proposed splicing methodology versus the conventional Ampere-hour integration method calculating capacity via $\Delta Q/\Delta SOC$. The separation of the high-temperature cluster (red) into two groups along the mileage axis in Figure 4 is attributed to the multi-year duration of the dataset, which covers more than one summer season.

It is important to acknowledge that the Ampere-hour integration method serves as a baseline with known limitations, primarily due to its heavy reliance on the onboard BMS-estimated SOC, which inherently suffers from measurement drift and estimation errors. To faithfully reproduce the real-world performance constraints of legacy systems, the baseline capacity is calculated directly utilizing the raw SOC values reported by the BMS, without the application of additional filtering. However, as this method remains the prevailing standard in many legacy industrial systems, this comparison is essential. Its purpose is not to benchmark against ideal laboratory models, but to highlight a critical advantage of the proposed approach, which is the ability to decouple SOH estimation from unreliable SOC inputs.

The results illustrated in Figure 4 clearly demonstrate this benefit. The Ampere-hour integration method exhibits significant volatility and non-physical fluctuations, directly attributable to the SOC estimation noise discussed in Section 2. In contrast, the proposed virtual charge-splicing method yields a stable, monotonic, and physically plausible degradation trend, effectively filtering out the noise inherent in single-segment estimations and providing a robust metric for real-world applications.

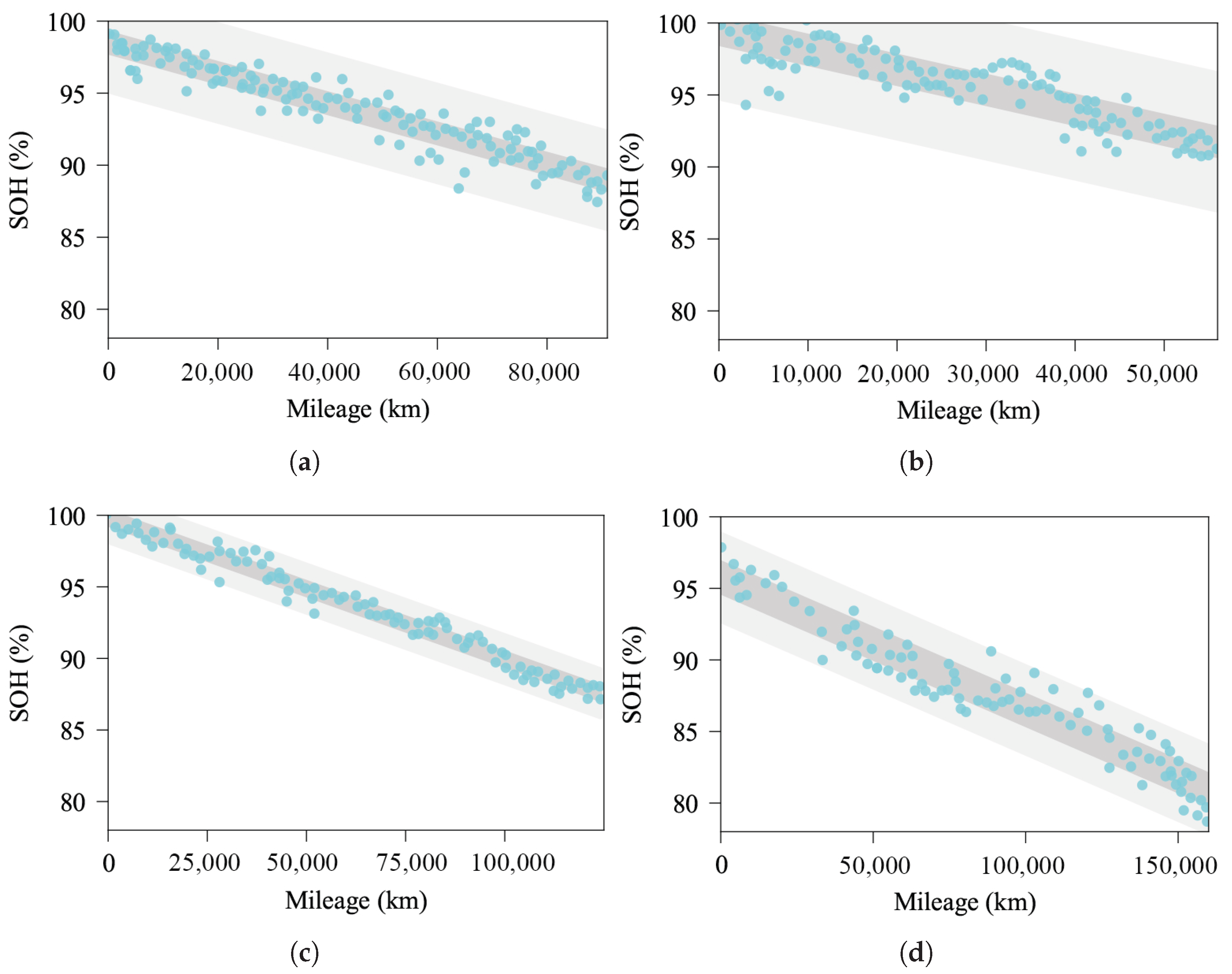
4.4. SOH Estimation Performance on Randomly Selected Vehicles

To evaluate the method’s adaptability across individual instances, four vehicles were randomly selected from the fleet: X143, X228, X251, and X287. Their SOH estimation results are plotted against mileage in Figure 5a–d. A linear degradation model was fitted to the data for each vehicle to represent its specific aging trajectory. The shaded regions in the plots indicate the estimation error bands. As observed, the estimated SOH points for all four vehicles cluster tightly around their respective fitted degradation lines. Quantitative analysis reveals that the average error band is less than 1%, with the maximum outlier deviation remaining within 4%. These results demonstrate that the proposed virtual capacity reconstruction method maintains high consistency and precision across different individual vehicles, effectively capturing the linear aging trend despite the randomness of real-world charging behaviors.

4.5. Field Validation via Controlled Full-Charge Experiments

To rigorously validate the absolute accuracy of the algorithm against a reliable physical benchmark, controlled field experiments were conducted on randomly selected operational vehicles (X761, X655, and X117). Distinct from the statistical analysis based on historical data mining, this validation involved active intervention coordinated with fleet operators. The procedure was strictly controlled, beginning with the scheduling of target vehicles during their operational downtime. To reach the lower SOC limit required for a full cycle, the vehicles were actively discharged through a combination of test driving and continuous operation of the air conditioning system. Subsequently, the vehicles were fully charged from this lower limit to 100% utilizing calibrated high-precision charging equipment. The equipment employed for this validation features a measurement precision of 0.1% F.S. (full scale) for both voltage and current, thereby ensuring that the measured charged capacity served as a precise ground truth for the current SOH.

The algorithmic SOH estimates, derived exclusively from historical incomplete segments, were benchmarked against the physically measured ground truth. The quantitative results, summarized in

Table 1. Comparison of field validation results between the splicing algorithm and calibrated measurements.

Vehicle No.	Mileage (km)	Measured SOH	Estimated SOH	Error
X761	39,565	0.962	0.949	1.3%
X655	89,841	0.910	0.928	1.8%
X117	248,778	0.815	0.796	1.9%

, reveal exceptional precision across the vehicle lifespan. Notably, the validation covers a broad mileage spectrum, ranging from early-stage operation (approx. 40,000 km) to an advanced aging stage (approx. 250,000 km). In all cases, the relative estimation error remains strictly below 2%, with a maximum deviation of only 1.9% observed at the highest mileage. This empirical evidence confirms that the proposed virtual capacity reconstruction strategy effectively aligns with the true physical capacity measured under controlled conditions.

5. Conclusions

This paper proposes a novel data-driven methodology for estimating the SOH of power batteries based on a virtual full-charge reconstruction strategy. Designed to overcome the fundamental challenges of real-world vehicle data, the method successfully eliminates the dependence on pre-labeled SOH values and unreliable onboard SOC estimations. By employing a k-means clustering algorithm based on statistical features of temperature and current, the framework effectively partitions complex charging data into distinct operating modes to ensure electrochemical consistency. A key innovation lies in the charging segment splicing strategy which synthesizes a comprehensive capacity profile from multiple incomplete charging segments. This approach effectively resolves the primary bottleneck of fragmented data and mitigates errors associated with small voltage integration intervals. Coupled with robust statistical averaging, the method ensures high resilience against anomalies in individual charging events. Validation through both large-scale fleet analysis and controlled field experiments demonstrates high precision with estimation errors consistently maintained below 2%. Consequently, the proposed method offers a scalable and reliable solution for the health management of new energy vehicle fleets.

Future investigations could explore advanced clustering algorithms such as density-based spatial clustering or Gaussian mixture models to identify more nuanced operating conditions. Additionally, the incorporation of nonlinear degradation models could capture long-term aging behaviors with greater accuracy. A significant objective is to optimize the algorithm for computational efficiency to enable deployment for real-time estimation on cloud-based battery management platforms. Furthermore, the applicability of the splicing concept should be evaluated on different battery chemistries and diverse electric platforms. Finally, integrating this high-precision SOH estimation into a holistic BMS could significantly improve the accuracy of related metrics including SOC and SOE.