Oscillation of a Liquid Column in an Eccentric Annulus

Abstract

The velocity distribution of flow in an eccentric cylindrical annulus is determined in an attempt to investigate the vertical capillary rise in the channel. The critical values of the radii ratio and the eccentricity at which the capillary rise changes from oscillatory to monotone or vice versa are determined. For a particular aspect ratio, the rise becomes monotonic as the eccentricity increases. The oscillations are also dampened as the annulus becomes thinner. These critical values depend on Galileo and Bond numbers as well as the contact angle. The results reduce to the limiting cases of concentric and fully eccentric annuli. The critical values are also calculated for the special arrangements when the radii ratios are 1 and 0. The latter limit is in perfect agreement with the conditions found in the literature for the classical circular channel.

1. Introduction

Capillary rise, the phenomenon where a liquid spontaneously ascends within a narrow space due to intermolecular forces, plays a crucial role in numerous scientific and industrial processes. Studying the capillary rise of liquids in thin tubes is important due to its numerous applications. For example, a porous medium was modeled as a bundle of capillary tubes, De Gennes et al. [1], Quéré [2], and Lago and Araujo [3]. Other applications that essentially require a thorough understanding of the interesting phenomenon include applications in the paper, ink, and textile industries, Delgado [4].

While extensively studied in simple geometries such as circular tubes, the behavior of capillary rise in more complex geometries, like an eccentric annulus, remains less understood yet equally significant. An eccentric annulus, formed between two cylinders with different radii that are offset from each other, presents unique challenges and opportunities for understanding fluid dynamics.

The study of capillary rise in an eccentric annulus is important for several reasons. First, many natural and engineered systems feature non-concentric cylindrical geometries, where precise fluid management is critical. Applications range from enhanced oil recovery in porous media to microfluidic devices, where controlling fluid distribution in narrow, eccentric spaces can improve efficiency and performance. Furthermore, the behavior of capillary rise in an eccentric annulus can offer insights into the design of advanced materials and systems. For example, in porous media, where the pores can be modeled as bundles of capillary tubes with varying degrees of eccentricity, understanding capillary behavior can inform the development of more effective filtration and absorption materials. In the textile and paper industries, where fibers and sheets can create similar eccentric geometries, predicting fluid movement is essential for optimizing processes like dyeing, printing, and coating. Investigating capillary rise in an eccentric annulus not only fills a critical gap in the fundamental understanding of fluid dynamics but also has significant implications for a wide range of practical applications across various industries.

The mathematical modeling of capillary rise in a tube dates back to Ampt [5], Lucas [6], and Washburn [7]. Since then, the literature has been quite rich on all aspects of this phenomenon. The original celebrated Lucas–Washburn equation ignores gravity and kinetic effects. A model that includes both effects is given by Masoodi et al. [8], Szekely et al. [9], and Fries [10]. The model in abstract symbols reads as $y y^{\prime }+y+\omega d(y y^{\prime })/dt=1$ with $\omega$ being the parameter that hosts the liquid and tube properties, and $y$ is some dimensionless version of the height of the column. An interesting behavior is found near the equilibrium height of the rise. For some range of $\omega$, the rise oscillates around its equilibrium destination, while for others, the oscillations are completely dampened, as shown in Figure 1 (a gif file in Supplementary Materials file is also attached), Płociniczak and Świtała [11].

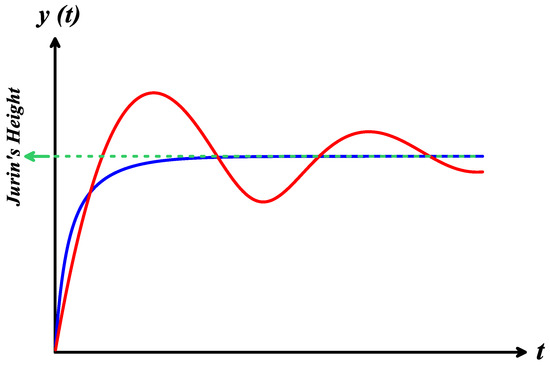
Figure 1. Oscillations of capillary rise.

Masoodi et al. [8] determined that the condition $\omega >1/4$ leads to the onset of oscillations. The findings of this fundamental work were rigorously proven by Płociniczak and Świtała [11].

Numerous studies have been performed on the flow between two vertical plates (see, for example, [12,13,14,15,16]) and on the capillary rise in tubes. The bulk of the research on capillary rise has been related to circular tubes. In this research, we investigate the capillary rise in an eccentric annulus from which a circular tube is a special case. The research is interesting from an application point of view as many instruments involve capillary rise in the annulus of tubes. The annulus is not always, intentionally or unintentionally, perfectly centered. The eccentricity of the annulus can be of significant magnitude. In the study presented herein, we determine the velocity distribution and investigate the effect of the radii ratio and the eccentricity on the transition from monotone to oscillatory rise. To the best of our knowledge, no such work has been carried out.

2. Velocity Profile

Consider an axial flow in an eccentric cylindrical annulus with inner radius $r_1$, outer radius $r_2$, and center-to-center distance $D$, as shown in Figure 2.

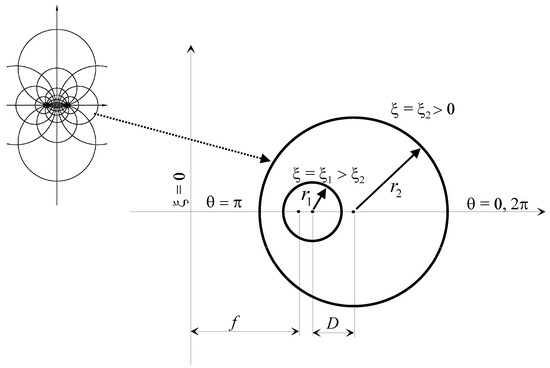
Figure 2. Problem configuration.

The steady developed flow in the annulus is assumed to obey the Poiseuille equation

$${\nabla }^{2}u={\displaystyle \frac{1}{\mu }}{\displaystyle \frac{dP}{dz}}$$

(1)

where $u$ is the velocity in the axial direction $z$, $\mu$ is the viscosity, and $P$ is the pressure.

The solution of (1), i.e., the velocity profile, can be obtained using the naturally fit bipolar cylindrical coordinates system $\left(\theta , \xi , z\right)$. This system is a three-dimensional orthogonal coordinates system whose projection on a plane perpendicular to the z-axis is composed of two sets of Apollonian circles, as shown in Figure 2. For more details on the coordinates system, the reader is referred to the work of Moon and Spencer [17] and Alassar and El-Gebeily [18]. The Cartesian coordinates system is related to the bipolar system by the relations

$$x={\displaystyle \frac{a \sinh \xi }{\cosh \xi -\cos \theta }}, y={\displaystyle \frac{a \sin \theta }{\cosh \xi -\cos \theta }}, z=z$$

(2)

with $0\le \theta \le 2\pi$ and $-\infty <\xi <\infty$. The inner and the outer cylinders are identified, respectively, by ${\xi }_1={\sinh }^{-1}(f/r_1)$ and ${\xi }_2={\sinh }^{-1}(f/r_2)$, where $f$ is the focal length given by

$$f={\displaystyle \frac{\sqrt{(D-r_1-r_2)(D-r_1+r_2)(D+r_1-r_2)(D+r_1+r_2)}}{2D}}$$

(3)

The bipolar coordinates system has the scale factors

$$h_{\theta }= h_{\xi }={\displaystyle \frac{a}{\cosh \xi -\cos \theta }}, h_z=1$$

(4)

It is standard procedure, Arfken [19], to cast Equation (1) in any orthogonal coordinates system using the appropriate scale factors. In bipolar coordinates, Equation (1) takes the form

$${\displaystyle \frac{{\partial }^{2}u}{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial {\theta }^2}}={\displaystyle \frac{1}{\mu }}{\displaystyle \frac{dP}{dz}}{\displaystyle \frac{f^{ 2}}{{\left(\cosh \xi -\cos \theta \right)}^2}}$$

(5)

At the surfaces of the cylinders, no-slip conditions ($u(\theta ,{\xi }_1)=u(\theta ,{\xi }_2)=0$) are considered.

Though inspection, one can notice that ${\displaystyle \frac{f^{ 2}}{2 \mu }}{\displaystyle \frac{dP}{dz}}{\displaystyle \frac{\cosh \xi }{\cosh \xi -\cos \theta }}$ is a particular solution of (5). Considering the symmetry of the problem, we then assume a solution of the form

$${\displaystyle \frac{u}{-\frac{r_2^2}{\mu }\frac{dP}{dz}}}={\displaystyle \frac{- f^{ 2} \cosh \xi }{2 r_2^2 \left(\cosh \xi -\cos \theta \right)}}+a_1+a_2 \xi +{\displaystyle \sum _{n=1}^{\infty }\left[A_n\sinh n(\xi -{\xi }_1)+B_n\sinh n(\xi -{\xi }_2)\right]}\cos n\theta$$

(6)

It is noted here that the velocity has been scaled by $-{\displaystyle \frac{r_2^2}{\mu }}{\displaystyle \frac{dP}{dz}}$ to make it dimensionless. The assumed solution (6) has the same form as that given by Alassar [20] for the flow in eccentric annuli but with slip. It can be shown, however, that the coefficients in (6) which were calculated numerically by Alassar [20] due to their coupled nature, decouples in the present no-slip case and can be obtained exactly in closed form. The coefficients are found to be

$$\begin{array}{l}{a}_1=-{\displaystyle \frac{{\sinh }^2{\xi }_2}{2}} {\displaystyle \frac{{\xi }_2 \coth {\xi }_1-{\xi }_1 \coth {\xi }_2}{{\xi }_1-{\xi }_2}}, a_2=-{\displaystyle \frac{{\sinh }^2{\xi }_2}{2}} {\displaystyle \frac{\coth {\xi }_2-\coth {\xi }_1}{{\xi }_1-{\xi }_2}}\\ A_n={\sinh }^2{\xi }_2{\displaystyle \frac{e^{-n {\xi }_2} \coth {\xi }_2}{\sinh n({\xi }_2-{\xi }_1)}}, B_n={\sinh }^2{\xi }_2{\displaystyle \frac{e^{-n {\xi }_1} \coth {\xi }_1}{\sinh n({\xi }_1-{\xi }_2)}}\end{array}$$

(7)

To obtain (7), one needs, in addition to the standard orthogonality relations of the trigonometric functions, the three special integrals

$$\begin{array}{l}{\displaystyle \underset{ 0}{\overset{ 2 \pi }{\int }}\frac{\cos n \theta }{ \cosh \xi -\cos \theta }d\theta = \frac{2 \pi e^{ - n \xi }}{\sinh \xi }}\\ {\displaystyle \underset{ 0}{\overset{ 2 \pi }{\int }}\frac{1}{{(\cosh \xi -\cos \theta )}^3}d\theta = \frac{\pi (2+\cosh 2\xi )}{{\sinh }^5\xi }}\\ {\displaystyle \underset{ 0}{\overset{ 2 \pi }{\int }}\frac{\cos n \theta }{{(\cosh \xi -\cos \theta )}^2}d\theta = \frac{2 \pi (n+\cosh \xi ) e^{ - n \xi }}{{\sinh }^2\xi }}\end{array}$$

(8)

The average dimensionless velocity, $\overline{w}=\overline{u}/(-{\displaystyle \frac{r_2^2}{\mu }}{\displaystyle \frac{dP}{dz}})$, can now be calculated as

$$\begin{array}{l}\overline{w}={\displaystyle \frac{\overline{u}}{-\frac{r_2^2}{\mu }\frac{dP}{dz}}}=-{\displaystyle \frac{1+2 \cosh 2{\xi }_2+3 {\mathrm{csch}}^2{\xi }_1 {\sinh }^2{\xi }_2}{8}}+a_1+{\displaystyle \frac{\coth {\xi }_2-\coth {\xi }_1+{\xi }_2 {\mathrm{csch}}^2{\xi }_2-{\xi }_1 {\mathrm{csch}}^2{\xi }_1}{\left({\coth }^2{\xi }_2-{\coth }^2{\xi }_1\right)}}{a}_2 \\ +{\displaystyle \frac{1}{2 \left({\coth }^2{\xi }_2-{\coth }^2{\xi }_1\right)}}{\displaystyle \sum _{n=1}^{\infty }\left[\begin{array}{l}{A}_n e^{-n {\xi }_1}(2n \coth {\xi }_2-2n \coth {\xi }_1-\frac{e^{2n({\xi }_1-{\xi }_2)}-1}{{\sinh }^2{\xi }_2})\\ +B_n{e}^{-n {\xi }_2}(2n \coth {\xi }_2-2n \coth {\xi }_1+\frac{e^{2n({\xi }_2-{\xi }_1)}-1}{{\sinh }^2{\xi }_1})\end{array}\right]}\end{array}$$

(9)

In summary, the velocity and the average velocity are completely determined if both the radii and the center-to-center distance are known. The center-to-center distance can be replaced by the eccentricity, $\epsilon$,

$$\epsilon =D/(r_2-r_1)={\displaystyle \frac{D/r_2}{1-r_1/r_2}}$$

(10)

The focal distance is then

$$f={\displaystyle \frac{\sqrt{(1-{\epsilon }^2)({(r_2+r_1)}^2-{\epsilon }^2{(r_2-r_1)}^2)}}{2 \epsilon }}$$

(11)

The two numbers representing the two surfaces of the cylinders, ${\xi }_1$ and ${\xi }_2$, are thus determined. Figure 3 shows a typical velocity profile ($r_1/r_2=1/4$ and $\epsilon =1/2$).

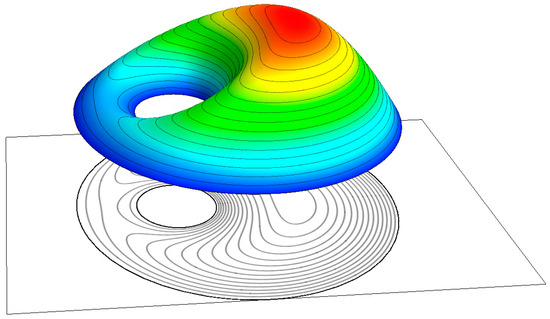
Figure 3. Velocity profile for the case $r_1/r_2=1/4$ and $\epsilon =1/2$.

3. Capillary Rise

Consider a liquid of density $\rho$ and viscosity $\mu$ rising in a vertical capillary channel of cross-sectional area $A$ and perimeter $C$. The height of the liquid column, $h(t)$, is governed by Newton’s second law of motion

$${\displaystyle \frac{d}{dt}}(\rho A h {\displaystyle \frac{dh}{dt}} )=\gamma \cos \theta C+\Delta P A-\rho g h A$$

(12)

where $\gamma$ is the surface tension, $\theta$ is the contact angle, $\Delta P$ is the pressure drop in the channel, and $g$ is the gravitational acceleration, Masoodi et al. [8]. From (9), the pressure drop in a liquid column of height $L$ can be written as

$$\Delta P = {\displaystyle \frac{\mu }{r_2^2 \overline{w}}}L \overline{u} = {\displaystyle \frac{\mu }{r_2^2 \overline{w}}} h {\displaystyle \frac{dh}{dt}}$$

(13)

There are several ways to cast (12) into dimensionless form, Fries and Dreyer [21]. Using $H={\displaystyle \frac{\rho g A}{\gamma C \cos \theta }} h$ and $\tau =\sqrt{{\displaystyle \frac{\rho g^{2}A}{\gamma C \cos \theta }}} t$, Equation (12) can be rewritten as

$${\displaystyle \frac{d}{d\tau }}(H {\displaystyle \frac{dH}{d\tau }} )+{\displaystyle \frac{{(1-r_1/r_2)}^2}{8 \overline{w}}}\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}H{\displaystyle \frac{dH}{d\tau }}+H=1$$

(14)

where $Ga={\displaystyle \frac{g R^3 {\rho }^2}{{\mu }^2 }}$ is the Galileo number, $Bo={\displaystyle \frac{\rho g R^2}{\gamma }}$ is the Bond number, and $R={\displaystyle \frac{2A}{C}}=r_2-r_1$ is the hydraulic radius.

It has been shown that, under consistent boundary conditions (i.e., $H(0)=0, H^{\prime } (0)=1$) and depending on the value of ${\displaystyle \frac{{(1-r_1/r_2)}^2}{8 \overline{w}}}\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}$ (i.e., the coefficient of $H{\displaystyle \frac{dH}{d\tau }}$ in (14)), the solution of Equation (14) progresses in time either monotonically or oscillates about its equilibrium height. The equilibrium height, known as Jurin’s height, is usually used for the measurement of surface tension. It is obtained from (12) as $h_{ e}={\displaystyle \frac{\gamma C \cos \theta }{\rho g A}}={\displaystyle \frac{2 \gamma \cos \theta }{\rho g R}}$ or the dimensionless value $H_{ e}=1$.

According to Płociniczak and Świtała [11], the solution of (12) remains monotone as long as ${\displaystyle \frac{{(1-r_1/r_2)}^2}{8 \overline{w}}}\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}>2$ or equivalently

$$\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}>{\displaystyle \frac{16 \overline{w}}{{(1-r_1/r_2)}^2}}$$

(15)

It is important to observe that, for a specific liquid and tube material, the condition (15) is purely geometric. We define the equality $\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}={\displaystyle \frac{16 \overline{w}}{{(1-r_1/r_2)}^2}}$ as the critical condition at which the rise changes from oscillatory to monotone or vice versa.

Figure 4 quantifies the expected effect of the radii ratio and the eccentricity on this critical value. As the eccentricity decreases, the rise becomes more oscillatory. In other words, eccentric annuli tend to dampen oscillations. The oscillations are also reduced when the radii ratio increases as a result of the annulus becoming narrower.

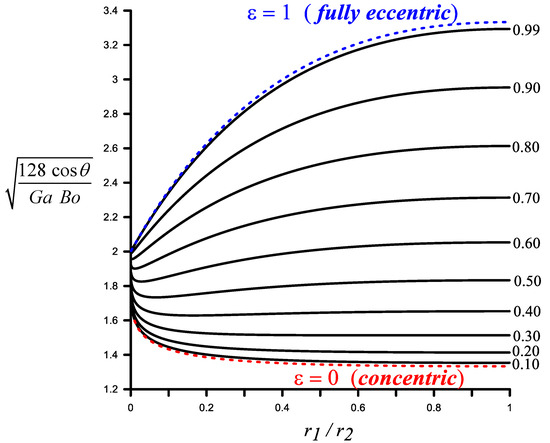
Figure 4. Critical $\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}$ for monotone rise.

It is noted here that for a circular tube (i.e., as $r_1/r_2\to 0$), we obtain the well-known result $\overline{w}\to {\displaystyle \frac{1}{8}}$, and the limiting critical values is $\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}=2$. The bottom and top curves in Figure 4 correspond to, respectively, the concentric ($\epsilon =0$) and the fully eccentric ($\epsilon =1$) cases. The critical values for these two limiting cases can be written, in order, as

$${\left.\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}\right|}_{concentric}= 2{\displaystyle \frac{1-{(r_1/r_2)}^4+{\left[1-{(r_1/r_2)}^2\right]}^{ 2}/\ln (r_1/r_2)}{ {(1-r_1/r_2)}^2 \left[1-{(r_1/r_2)}^2\right]}}$$

(16)

$${\left.\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}\right|}_{eccentric}= 2{\displaystyle \frac{1-{(r_1/r_2)}^4 - 4 {(r_1/r_2)}^2 {\psi }_1(\frac{1}{1-r_1/r_2})}{{(1-r_1/r_2)}^2 \left[1-{(r_1/r_2)}^2\right]}}$$

(17)

where ${\psi }_1$ is the second Polygamma function. The condition in (17) is based on the velocity profile given by MacDonald [22]. For both cases, again, $\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}=2$ as $r_1/r_2\to 0$. As $r_1/r_2\to 1$, one can show, perhaps for only theoretical curiosity, that the critical value for the fully eccentric case $\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}\to {\displaystyle \frac{10}{3}}$, while for the concentric case, $\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}\to {\displaystyle \frac{4}{3}}$.

Figure 4 is fundamental in determining the dimensions of a channel that supports monotone rise. The following paragraph explains the process.

Given that $R=r_2-r_1$ and $\sqrt{{\displaystyle \frac{128 \cos \theta }{Ga Bo}}}=\sqrt{{\displaystyle \frac{128 \gamma {\mu }^2 \cos \theta }{{\rho }^3 g^2 R^5}}}$, one can, for specific values of the radii ratio $r_1/r_2$ and the eccentricity $\epsilon ={\displaystyle \frac{D/r_2}{1-r_1/r_2}}$, find the maximum radius of the outer (equivalently the inner) cylinder that maintains monotone rise. The condition for maintaining monotone then reduces from (15) as

$$r_2< \sqrt[5 ]{{\displaystyle \frac{\gamma {\mu }^2 \cos \theta }{2 (1-r_1/r_2) {\overline{w}}^{ 2} {\rho }^3 g^2}}}$$

(18)

In other words, the value $r_2= \sqrt[5 ]{{\displaystyle \frac{\gamma {\mu }^2 \cos \theta }{2 (1-r_1/r_2) {\overline{w}}^{ 2} {\rho }^3 g^2}}}$ is the largest outer radius before oscillations appear. As $r_1/r_2\to 0$, condition (18) reduces to $r_2< 2 \sqrt[5 ]{{\displaystyle \frac{\gamma {\mu }^2 \cos \theta }{ {\rho }^3 g^2}}}$, which is identical to that obtained by Masoodi et al. [8] for a circular tube.

Figure 5 shows the variation in the maximum value of $r_2$ required to maintain monotonicity, with the radii ratio and the eccentricity for water at $20$ °C ($\rho =998.23 \mathrm{kg}{.\mathrm{m}}^{-3}$, $\mu =1.002 \mathrm{mPa}.\mathrm{s}$, $\gamma =72.86 \mathrm{mN}.{\mathrm{m}}^{-1}$, and $\theta =0^{\circ }$). The corresponding Jurin’s heights are also plotted in Figure 6. As $r_1/r_2\to 0$, $h_{ e}\to \sqrt[5 ]{{\displaystyle \frac{{\gamma }^4 {\cos }^4\theta }{{\rho }^2 g^3 {\mu }^2}}}$ ($\sim$31.26 mm for water at $20$ °C). The calculations can be repeated easily for any other liquid.

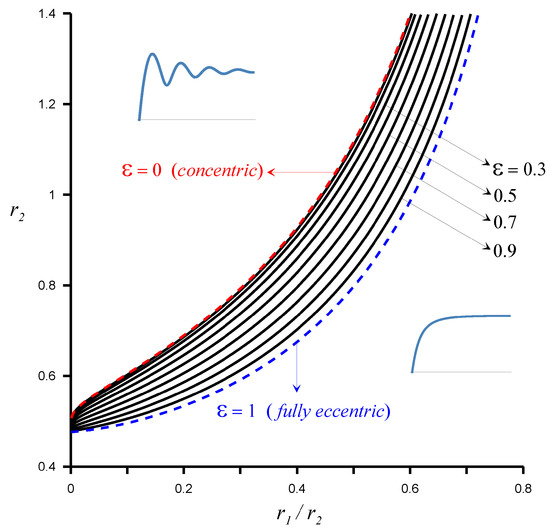
Figure 5. Maximum $r_2$ to maintain monotone rise for water at 20 °C.

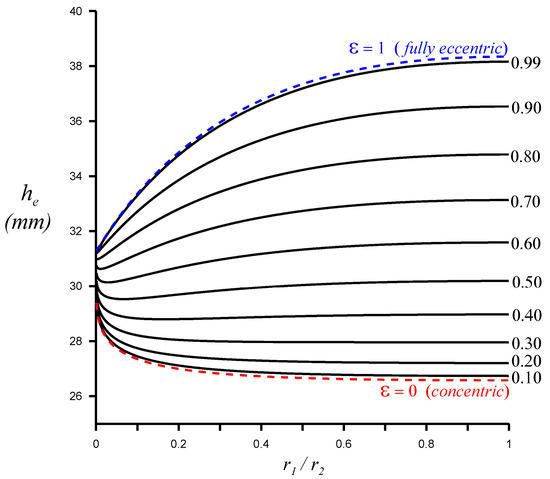
Figure 6. Equilibrium heights at maximum $r_2$ which maintain monotone rise for water at $20$ °C.

4. Conclusions

The investigation has successfully determined the critical values of the radii ratio and eccentricity at which the behavior of capillary rise within an eccentric annulus shifts from oscillatory to monotonic or vice versa. These critical transitions are pivotal in understanding fluid dynamics within such geometries, as they offer insights into how various parameters influence capillary behavior. Specifically, for a given aspect ratio, it has been observed that the rise transitions to a monotonic behavior as the eccentricity increases, indicating a direct relationship between these variables. Moreover, the study reveals that as the annulus becomes thinner, the amplitude of the oscillations in the capillary rise is significantly dampened, further contributing to the shift toward monotonic behavior. These critical values, illustrated in Figure 4 and mathematically described explicitly by Equations (15) and (18), highlight the dependence on the key dimensionless numbers, the Galileo and Bond numbers, in addition to the contact angle. The results are robust, as they reduce to the well-established limiting cases of concentric and fully eccentric annuli given by Equations (16) and (17). This provides a strong validation of the findings, as they align with the known behavior in these simpler arrangements. Additionally, critical values have been calculated for special configurations where the radii ratio and eccentricity take on the particular values $r_1/r_2\to 1$ and $r_1/r_2\to 0$. Notably, the limit $r_1/r_2\to 0$ corresponds to the classical condition found in the literature for capillary rise in a circular channel, further reinforcing the accuracy and relevance of the results.