Numerical Analysis of the Submerged Horizontal Plate Device Subjected to Representative Regular and Realistic Irregular Waves of a Sea State
Abstract
1. Introduction
2. Operating Principle, Historical Review, and State of the Art of the SHP Device
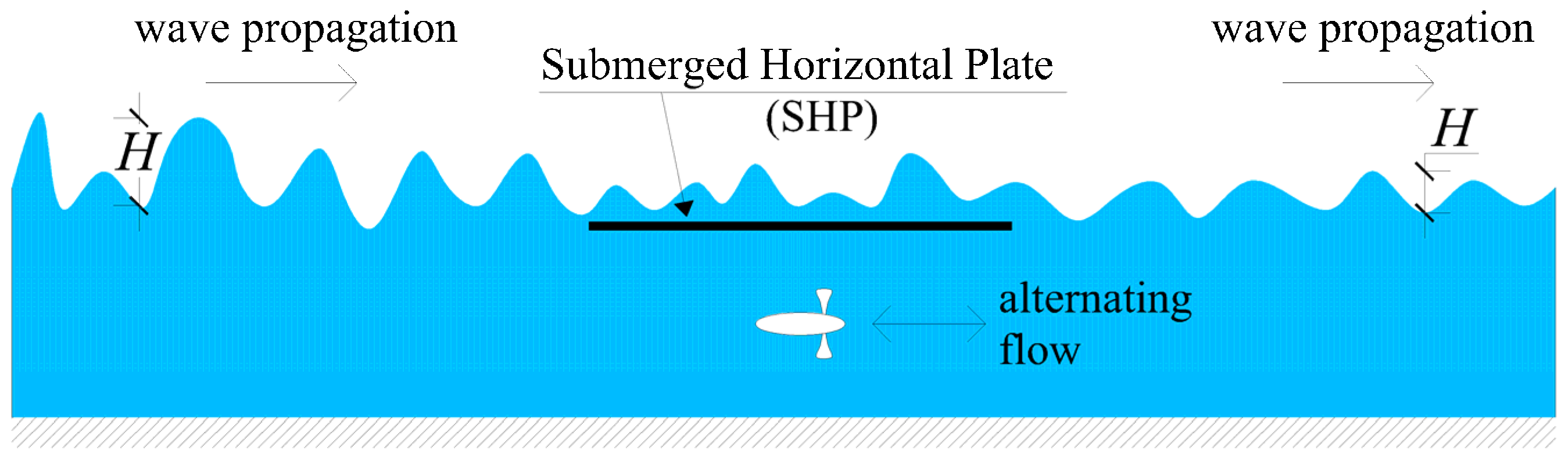
2.1. Hydrodynamic Principle of the SHP
2.2. Studies of the SHP as Breakwater
2.3. Studies of the SHP as WEC
2.4. Studies of the SHP as Breakwater and WEC
3. Materials and Methods
3.1. Computational Model
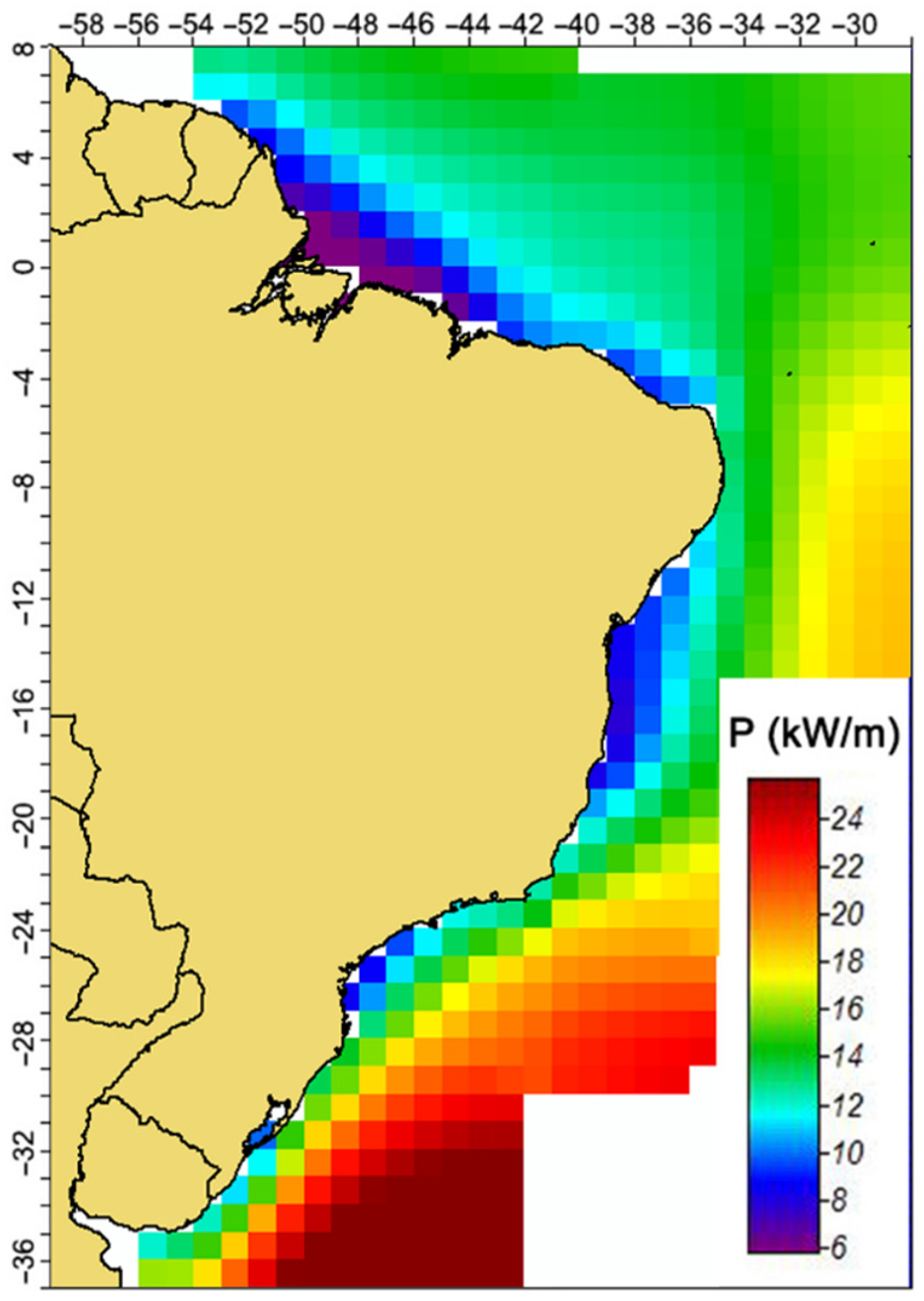
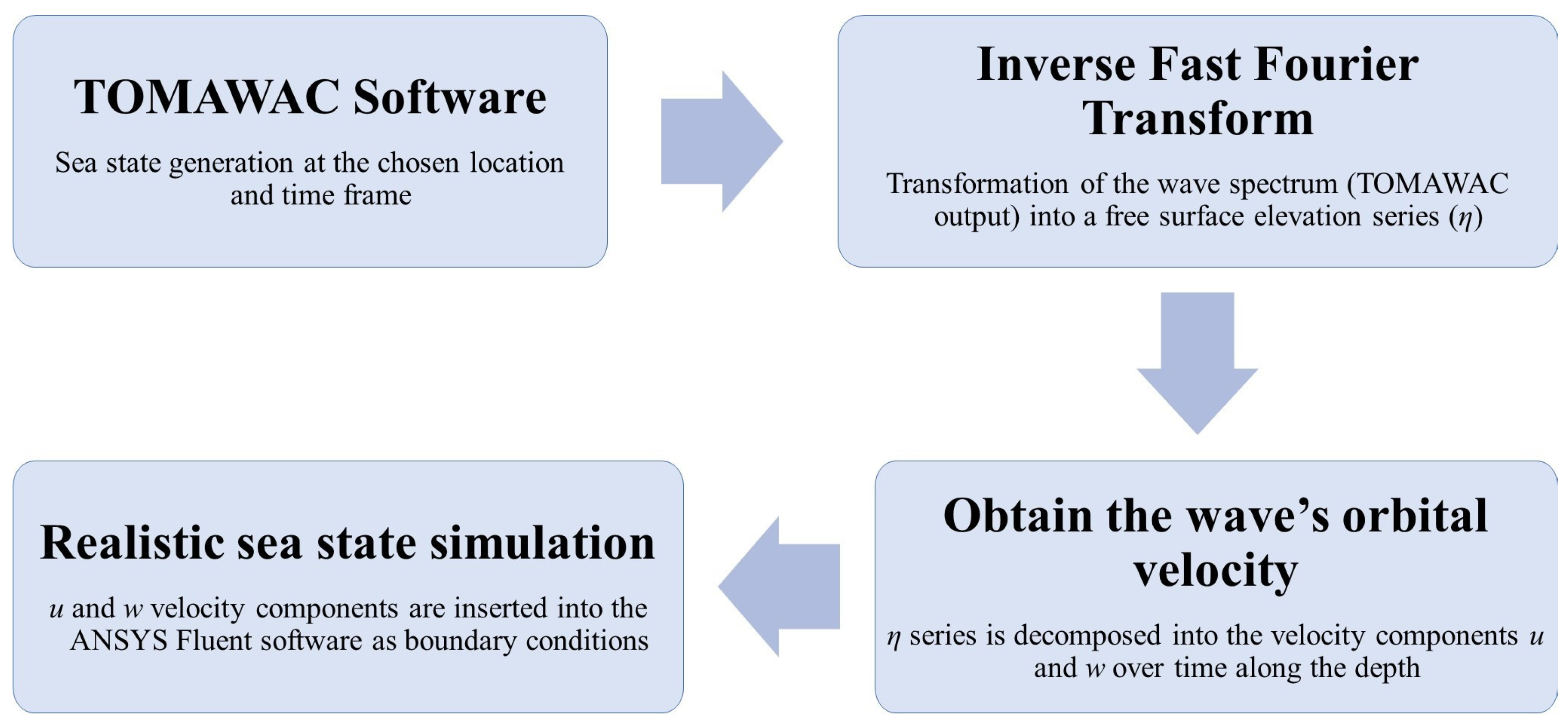
3.2. Representative Regular and Realistic Irregular Waves of a Sea State
3.3. Verification and Validation Procedures
3.3.1. Verification of the WaveMIMO Methodology
3.3.2. Validation of the Computational Model in a Laboratory Scale with SHP
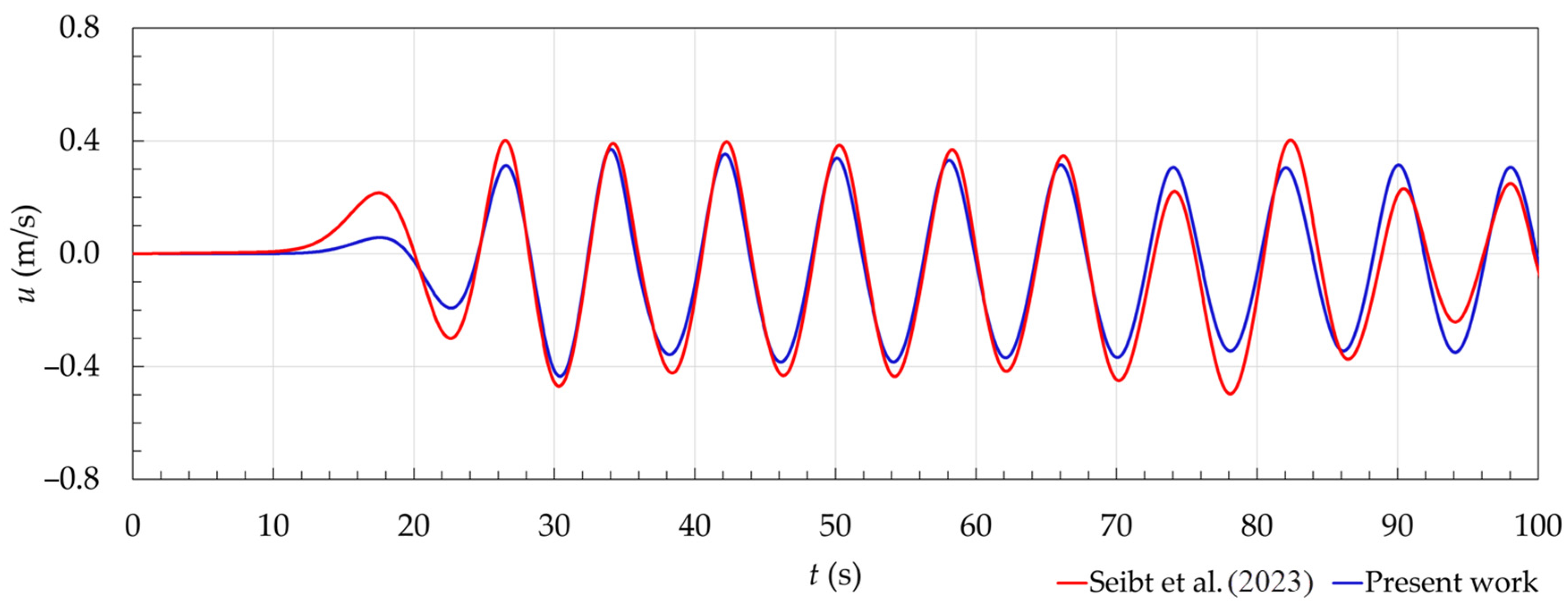
3.3.3. Verification of the Full-Scale Computational Model with SHP
3.3.4. Verification of the OCEANLYZ Software
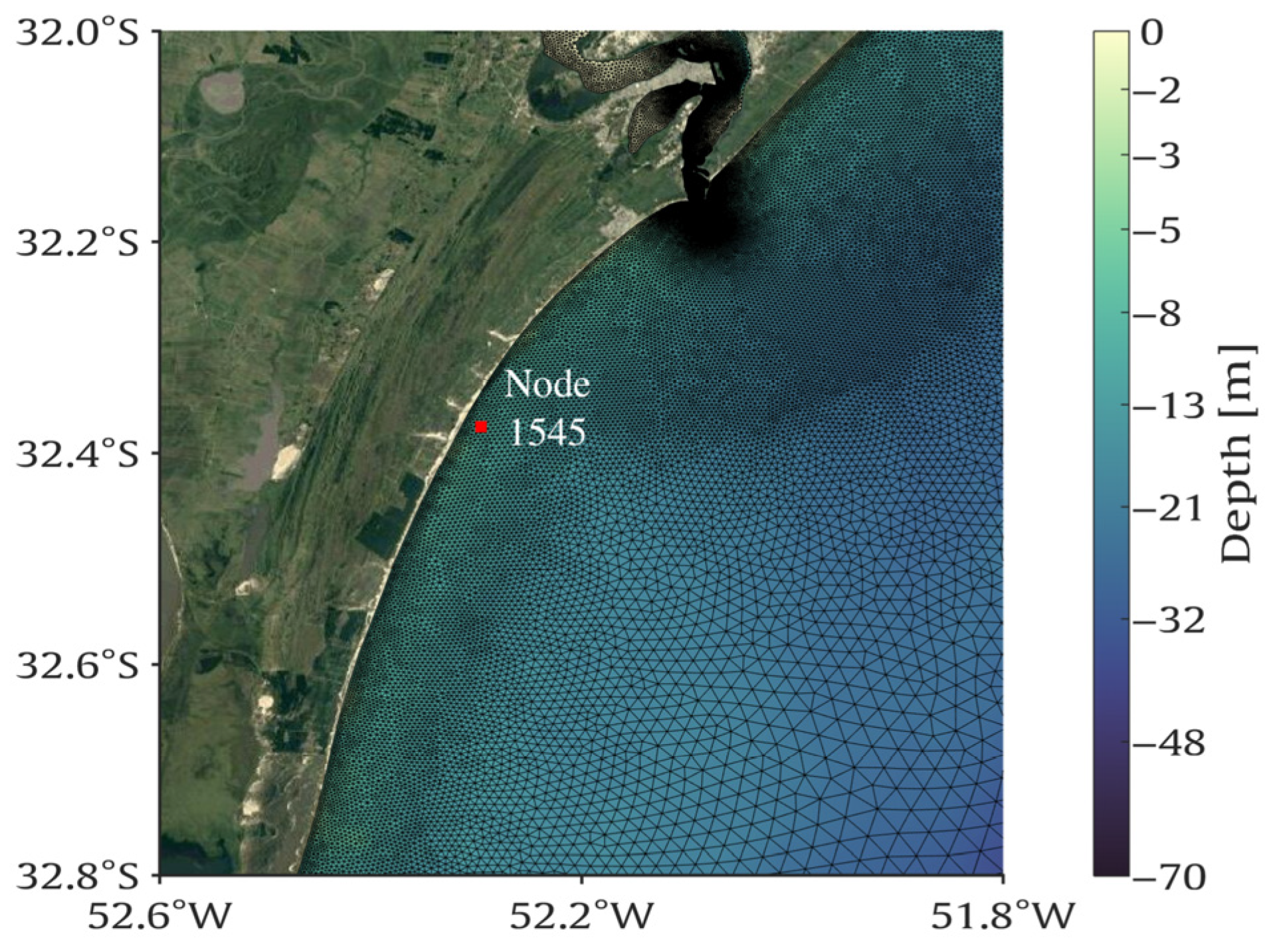
3.4. Case Study Methodology
4. Results and Discussion
4.1. Verification and Validation Results
4.1.1. Verification of the WaveMIMO Methodology
4.1.2. Validation of the Computational Model in a Laboratory Scale with SHP
4.1.3. Verification of the Full-Scale Computational Model with SHP
4.1.4. Verification of the OCEANLYZ Software
4.2. Results from the Case Study
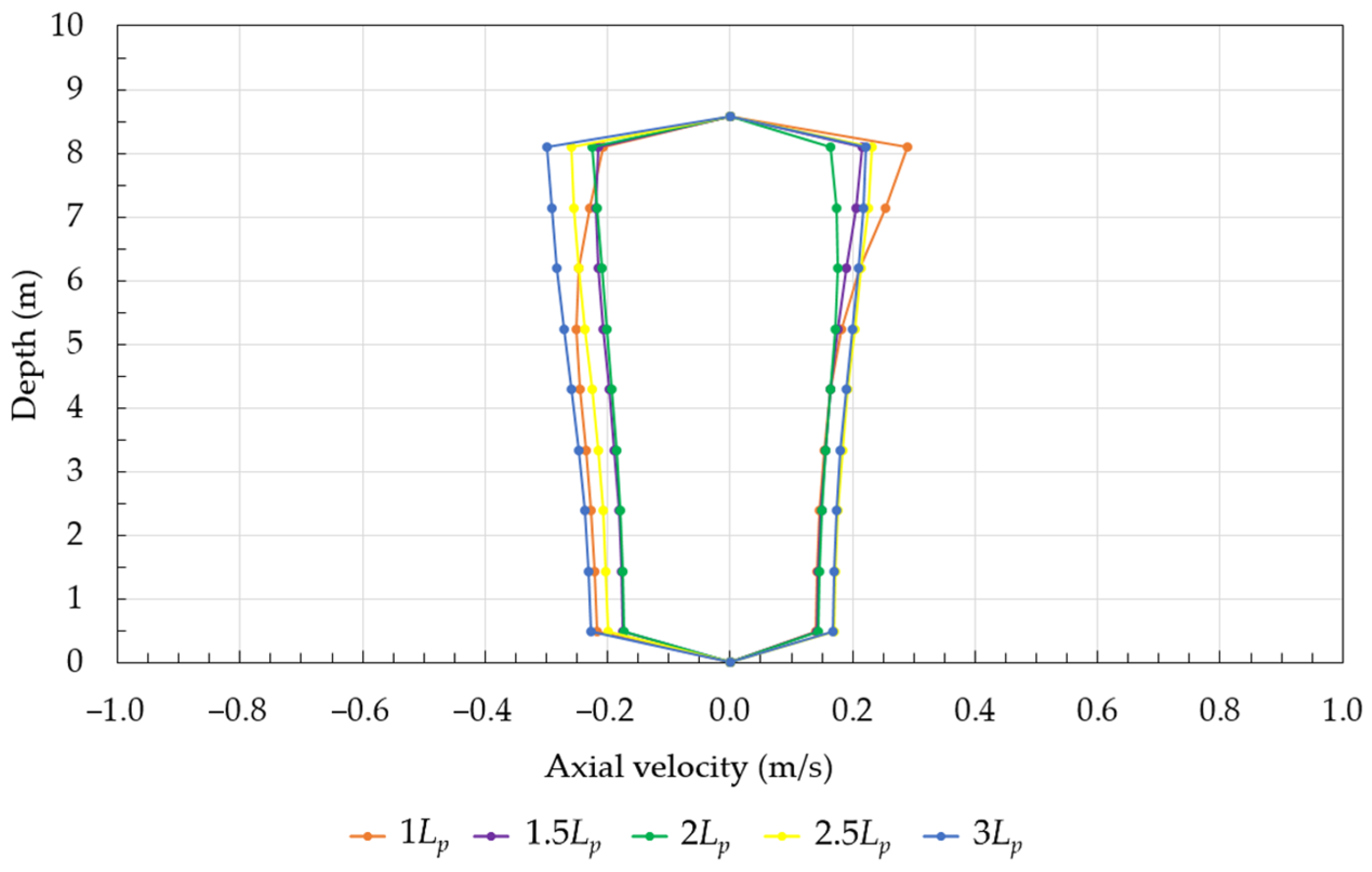
4.2.1. SHP under the Incidence of the Representative Regular Waves
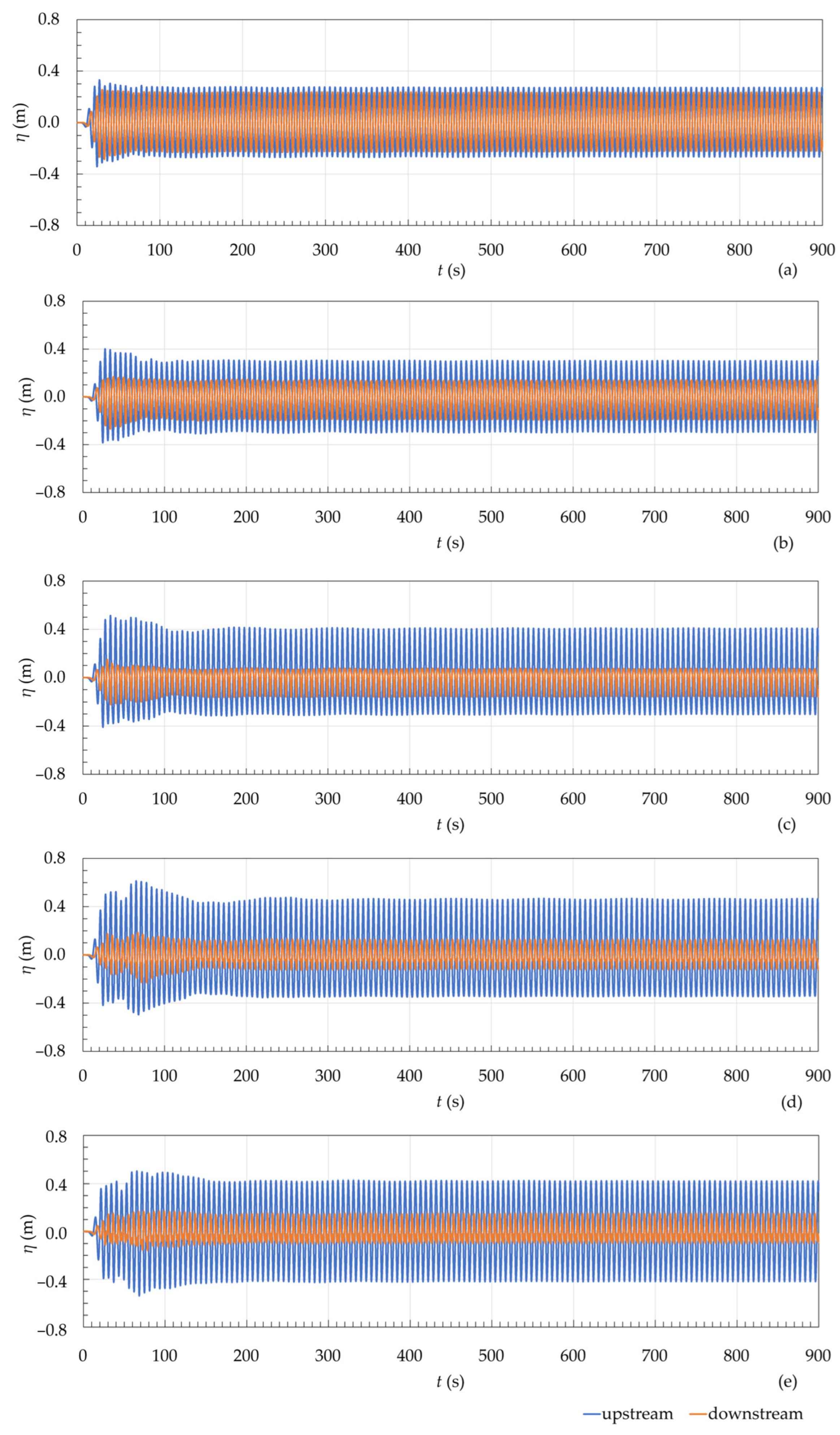
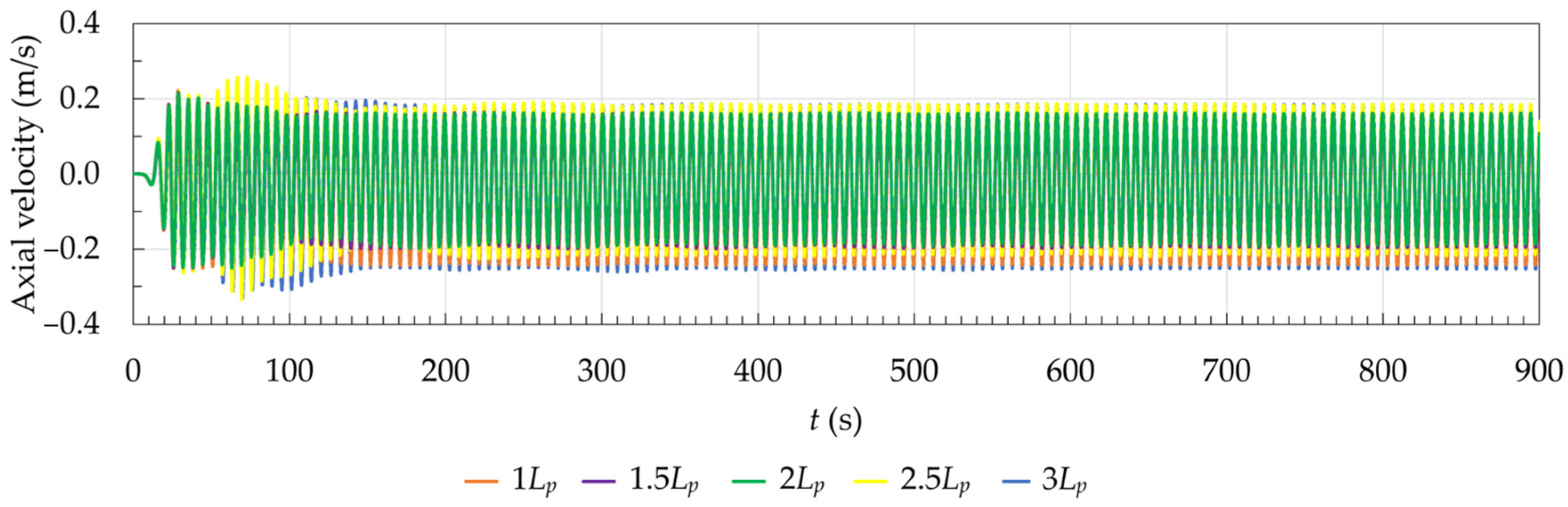
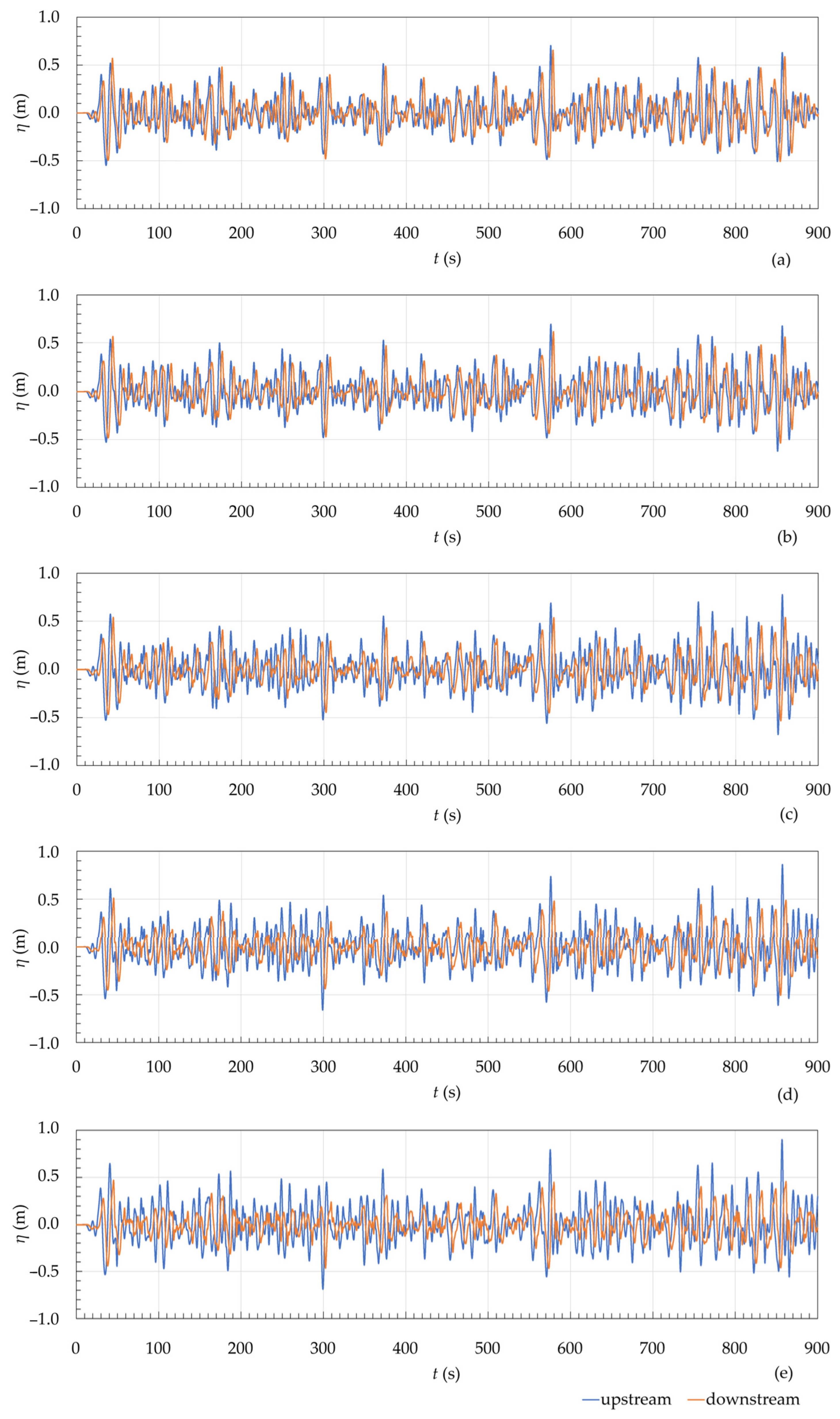
4.2.2. SHP under the Incidence of the Irregular Realistic Waves
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations Framework Convention on Climate Change. Paris Agreement. In Proceedings of the Conference of Parties 17; United Nations Framework Convention on Climate Change: Paris, France, 2015; p. 32. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement (accessed on 13 July 2024).
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development. Resolution Adopted by the General Assembly on 25 September 2015. Available online: https://www.un.org/en/development/desa/population/migration/generalassembly/docs/globalcompact/A_RES_70_1_E.pdf (accessed on 13 July 2024).
- González, A.T.; Dunning, P.; Howard, I.; McKee, K.; Wiercigroch, M. Is Wave Energy Untapped Potential? Int. J. Mech. Sci. 2021, 205, 106544. [Google Scholar] [CrossRef]
- UNESCO. The Science We Need for the Ocean We Want: Report; Intergovernmental Oceanographic Commission: Paris, France, 2019; Available online: https://en.unesco.org/news/science-we-need-ocean-we-want (accessed on 13 July 2024).
- Tavakoli, S.; Khojasteh, D.; Haghani, M.; Hirdaris, S. A Review on the Progress and Research Directions of Ocean Engineering. Ocean Eng. 2023, 272, 113617. [Google Scholar] [CrossRef]
- Wahyudie, A.; Jama, M.A.; Susilo, T.B.; Saeed, O.; Nandar, C.S.A.; Harib, K. Simple Bottom-up Hierarchical Control Strategy for Heaving Wave Energy Converters. Int. J. Electr. Power Energy Syst. 2017, 87, 211–221. [Google Scholar] [CrossRef]
- Seibt, F.M.; Dos Santos, E.D.; Isoldi, L.A.; Rocha, L.A.O. Constructal Design on Full-Scale Numerical Model of a Submerged Horizontal Plate-Type Wave Energy Converter. Mar. Syst. Ocean Technol. 2023, 18, 1–13. [Google Scholar] [CrossRef]
- Espindola, R.L.; Araújo, A.M. Wave Energy Resource of Brazil: An Analysis from 35 Years of ERA-Interim Reanalysis Data. PLoS ONE 2017, 12, e0183501. [Google Scholar] [CrossRef] [PubMed]
- Dias, F.; Dutykh, D.; Ghidaglia, J.-M. A two-fluid model for violent aerated flows. Comput. Fluids 2010, 39, 283–293. [Google Scholar] [CrossRef]
- Kim, S.P. CFD as a seakeeping tool for ship design. Int. J. Nav. Archit. Ocean Eng. 2011, 3, 65–71. [Google Scholar] [CrossRef]
- Dutykh, D.; Poncet, R.; Dias, F. The VOLNA code for the numerical modeling of tsunami waves: Generation, propagation and inundation. Eur. J. Mech. B Fluids 2011, 30, 598–615. [Google Scholar] [CrossRef]
- Rafiee, A.; Dutykh, D.; Dias, F. Numerical Simulation of Wave Impact on a Rigid Wall Using a Two–phase Compressible SPH Method. Procedia IUTAM 2015, 18, 123–137. [Google Scholar] [CrossRef]
- Wang, J.; Wan, D. CFD Investigations of Ship Maneuvering in Waves Using naoe-FOAM-SJTU Solver. J. Marine. Sci. Appl. 2018, 17, 443–458. [Google Scholar] [CrossRef]
- Liu, S.; Gatin, I.; Obhrai, C.; Ong, M.C.; Jasak, H. CFD simulations of violent breaking wave impacts on a vertical wall using a two-phase compressible solver. Coast. Eng. 2019, 154, 103564. [Google Scholar] [CrossRef]
- Jiao, J.; Huang, S.; Guedes Soares, C. Viscous fluid–flexible structure interaction analysis on ship springing and whipping responses in regular waves. J. Fluids Struct. 2021, 106, 103354. [Google Scholar] [CrossRef]
- Liu, B.; Park, S. CFD Simulations of the Effects of Wave and Current on Power Performance of a Horizontal Axis Tidal Stream Turbine. J. Mar. Sci. Eng. 2023, 11, 425. [Google Scholar] [CrossRef]
- Amini, M.; Memari, A.M. CFD Evaluation of Regular and Irregular Breaking Waves on Elevated Coastal Buildings. Int. J. Civ. Eng. 2024, 22, 333–358. [Google Scholar] [CrossRef]
- Liao, X.-Y.; Xia, J.-S.; Chen, Z.-Y.; Tang, Q.; Zhao, N.; Zhao, W.-D.; Gui, H.-B. Application of CFD and FEA Coupling to Predict Structural Dynamic Responses of a Trimaran in Uni- and Bi-Directional Waves. China Ocean Eng. 2024, 38, 81–92. [Google Scholar] [CrossRef]
- Opoku, F.; Uddin, M.N.; Atkinson, M. A Review of Computational Methods for Studying Oscillating Water Columns—The Navier-Stokes Based Equation Approach. Renew. Sustain. Energy Rev. 2023, 174, 113124. [Google Scholar] [CrossRef]
- Machado, B.N.; Oleinik, P.H.; de Paula Kirinus, E.; Rocha, L.A.O.; das Neves Gomes , M.; Conde, J.M.P.; Isoldi, L.A. WaveMIMO Methodology: Numerical Wave Generation of a Realistic Sea State. J. Appl. Comput. Mech. 2021, 7, 2129–2148. [Google Scholar] [CrossRef]
- Muehe, D. Erosão E Progradação Do Litoral Brasileiro; Ministério do Meio Ambiente: Brasília, Brazil, 2006. [Google Scholar]
- Trombetta, T.B.; Marques, W.; Guimarães, R.C.; Kirinus, E.D.P.; Silva, D.V.D.; Oleinik, P.H.; Leal, T.F.; Isoldi, L.A. Longshore Sediment Transport on the Brazilian Continental Shelf. Sci. Plena 2019, 15. [Google Scholar] [CrossRef]
- Heins, A.E. Water Waves Over a Channel of Finite Depth with a Submerged Plane Barrier. Can. J. Math. 1950, 2, 210–222. [Google Scholar] [CrossRef]
- Greene, T.R.; Heins, A.E. Water Waves Over a Channel of Infinite Depth. Appl. Math. 1953, XI, 201–214. [Google Scholar] [CrossRef]
- Dick, T.M.; Brebner, A. Solid and Permeable Submerged Breakwaters. In Coastal Engineering; American Society of Civil Engineers: London, UK, 1968; pp. 1141–1158. [Google Scholar]
- Graw, K. Is the Submerged Plate Wave Energy Converter Ready to Act as a New Coastal Protection System? In Proceedings of the XXIV Convegno Di Idraulica e Costruzioni Idrauliche, Napoli, Italy, 20–22 September 1994. [Google Scholar]
- Lima, S.F.; Almeida, L.E.; Toldo, E., Jr. Estimativa da Capacidade de Transporte Longitudinal de Sedimentos a partir de Dados de Ondas para a Costa do Rio Grande do Sul. Pesqui. Em Geociências 2001, 28, 99. [Google Scholar] [CrossRef]
- Yu, X. Functional Performance of a Submerged and Essentially Horizontal Plate for Offshore Wave Control: A Review. Coast. Eng. J. 2002, 44, 127–147. [Google Scholar] [CrossRef]
- Hayatdavoodi, M.; Ertekin, R.C.; Valentine, B.D. Solitary and Cnoidal Wave Scattering by a Submerged Horizontal Plate in Shallow Water. AIP Adv. 2017, 7, 065212. [Google Scholar] [CrossRef]
- Karmakar, D.; Soares, C.G. Wave Motion Control Over Submerged Horizontal Plates. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Siew, P.F.; Hurley, D.G. Long Surface Waves Incident on a Submerged Horizontal Plate. J. Fluid. Mech. 1977, 83, 141–151. [Google Scholar] [CrossRef]
- Wang, K.-H.; Shen, Q. Wave Motion over a Group of Submerged Horizontal Plates. Int. J. Eng. Sci. 1999, 37, 703–715. [Google Scholar] [CrossRef]
- Cheng, Y.; Ji, C.; Ma, Z.; Zhai, G.; Oleg, G. Numerical and Experimental Investigation of Nonlinear Focused Waves-Current Interaction with a Submerged Plate. Ocean Eng. 2017, 135, 11–27. [Google Scholar] [CrossRef]
- Fang, Q.; Yang, C.; Guo, A. Hydrodynamic Performance of Submerged Plates During Focused Waves. J. Mar. Sci. Eng. 2019, 7, 389. [Google Scholar] [CrossRef]
- Aghili, M.; Ghadimi, P.; Faghfoor Maghrebi, Y.; Nowruzi, H. Simulating the Interaction of Solitary Wave and Submerged Horizontal Plate Using SPH Method. Int. J. Phys. Res. 2014, 2, 16–26. [Google Scholar] [CrossRef][Green Version]
- Orer, G.; Ozdamar, A. An Experimental Study on the Efficiency of the Submerged Plate Wave Energy Converter. Renew. Energy 2007, 32, 1317–1327. [Google Scholar] [CrossRef]
- Wagner, J.J.; Wagner, J.R.; Hayatdavoodi, M. Hydrodynamic analysis of a submerged wave energy converter. In Proceedings of the 4th Marine Energy Technology Symposium METS2016, Washington, DC, USA, 25–27 April 2016. [Google Scholar]
- Xu, Y.; Zhang, G.; Wan, D.; Chen, G. MPS Method for Study of Interactions between Solitary Wave and Submerged Horizontal Plate. In Proceedings of the 29th International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019. [Google Scholar]
- Seibt, F.M.; Couto, E.C.; Dos Santos, E.D.; Isoldi, L.A.; Rocha, L.A.O.; Teixeira, P.R.D.F. Numerical Study on the Effect of Submerged Depth on the Horizontal Plate Wave Energy Converter. China Ocean Eng. 2014, 28, 687–700. [Google Scholar] [CrossRef]
- Carter, W.R. Wave Energy Converters and A Submerged Horizontal Plate. Master’s Thesis, Ocean and Resources Engineering, University of Hawaii, Honolulu, HI, USA, 2005. [Google Scholar]
- Seibt, F.M.; Couto, E.C.; Teixeira, P.R.D.F.; Dos Santos, E.D.; Rocha, L.A.O.; Isoldi, L.A. Numerical Analysis of the Fluid-Dynamic Behavior of a Submerged Plate Wave Energy Converter. Comput. Therm. Sci. Int. J. 2014, 6, 525–534. [Google Scholar] [CrossRef]
- Seibt, F.; De, C.; Dos, S.; Das, N.; Rocha, L.; Isoldi, L.; Fragassa, C. Numerical Evaluation on the Efficiency of the Submerged Horizontal Plate Type Wave Energy Converter. FME Trans. 2019, 47, 543–551. [Google Scholar] [CrossRef]
- He, M.; Gao, X.; Xu, W.; Ren, B.; Wang, H. Potential Application of Submerged Horizontal Plate as a Wave Energy Breakwater: A 2D Study Using the WCSPH Method. Ocean Eng. 2019, 185, 27–46. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhou, Y.; Jin, R.; Mu, Y.; He, M.; Zhao, L. Experimental Study on Submerged Horizontal Perforated Plates under Irregular Wave Conditions. Water 2023, 15, 3015. [Google Scholar] [CrossRef]
- Chakrabarti, S.K. Handbook of Offshore Engineering; Elsevier: Amsterdam, The Netherlands, 2005; Volume I, ISBN 978-0-08-044568-7. [Google Scholar]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; Advanced Series on Ocean Engeneering; WSPC: Singapore, 1991; Volume 2, ISBN 981-02-0420-5. [Google Scholar]
- Samad, A.; Sannasiraj, S.A.; Sundar, V.; Halder, P. (Eds.) Ocean Wave Energy Systems: Hydrodynamics, Power Takeoff and Control Systems; Ocean Engineering & Oceanography; Springer International Publishing: Cham, Switzerland, 2022; Volume 14. [Google Scholar]
- Oleinik, P.H.; Tavares, G.P.; Machado, B.N.; Isoldi, L.A. Transformation of Water Wave Spectra into Time Series of Surface Elevation. Earth 2021, 2, 997–1005. [Google Scholar] [CrossRef]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- ANSYS, Inc. Ansys Fluent Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics—The Finite Volume Method; Pearson Education Limited: London, UK, 2007. [Google Scholar]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comp. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Gomes, M.D.N.; Lorenzini, G.; Rocha, L.A.O.; Santos, E.D.D.; Isoldi, L.A. Constructal Design Applied to the Geometric Evaluation of an Oscillating Water Column Wave Energy Converter Considering Different Real Scale Wave Periods. J. Eng. Thermophys. 2018, 27, 173–190. [Google Scholar] [CrossRef]
- Srinivasan, V.; Salazar, A.J.; Saito, K. Modeling the Disintegration of Modulated Liquid Jets Using Volume-of-Fluid (VOF) Methodology. Ap. Math. Mod. 2011, 3710–3730. [Google Scholar] [CrossRef]
- da Cruz Lisboa, R.; de Freita, T.P.R.; Eric, D. Simulação da propagação de ondas regulares e irregulares em um canal bidimensional com praia numérica. In Proceedings of the VII Seminário e Workshop em Engenharia Oceânica, Rio Grande, Brazil, 4 December 2016. [Google Scholar]
- Mavriplis, D.J. Unstructured Grid Techniques. Annu. Rev. Fluid. Mech. 1997, 29, 473–514. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)?—Arguments against Avoiding RMSE in the Literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Kar, C.-J.; Els, P.S. Validation Metric Based on Relative Error. Math. Comput. Model. Dyn. Syst. 2012, 18, 487–520. [Google Scholar] [CrossRef]
- Karimpour, A. OCEANLYZ. Available online: https://github.com/akarimp/Oceanlyz (accessed on 13 July 2024).
- Maciel, R.P.; Oleinik, P.H.; Dos Santos, E.D.; Rocha, L.A.O.; Machado, B.N.; Gomes, M.D.N.; Isoldi, L.A. Constructal Design Applied to an Oscillating Water Column Wave Energy Converter Device under Realistic Sea State Conditions. J. Mar. Sci. Eng. 2023, 11, 2174. [Google Scholar] [CrossRef]
- Maciel, R.P.; Fragassa, C.; Machado, B.N.; Rocha, L.A.O.; Dos Santos, E.D.; Gomes, M.N.; Isoldi, L.A. Verification and Validation of a Methodology to Numerically Generate Waves Using Transient Discrete Data as Prescribed Velocity Boundary Condition. J. Mar. Sci. Eng. 2021, 9, 896. [Google Scholar] [CrossRef]
- Cisco, L.A.; Maciel, R.P.; Oleinik, P.H.; Dos Santos, E.D.; Gomes, M.N.; Rocha, L.A.O.; Isoldi, L.A.; Machado, B.N. Numerical Analysis of the Available Power in an Overtopping Wave Energy Converter Subjected to a Sea State of the Coastal Region of Tramandaí, Brazil. Fluids 2022, 7, 359. [Google Scholar] [CrossRef]
- Hubner, R.G.; Fragassa, C.; Paiva, M.D.S.; Oleinik, P.H.; Gomes, M.D.N.; Rocha, L.A.O.; Santos, E.D.D.; Machado, B.N.; Isoldi, L.A. Numerical Analysis of an Overtopping Wave Energy Converter Subjected to the Incidence of Irregular and Regular Waves from Realistic Sea States. J. Mar. Sci. Eng. 2022, 10, 1084. [Google Scholar] [CrossRef]

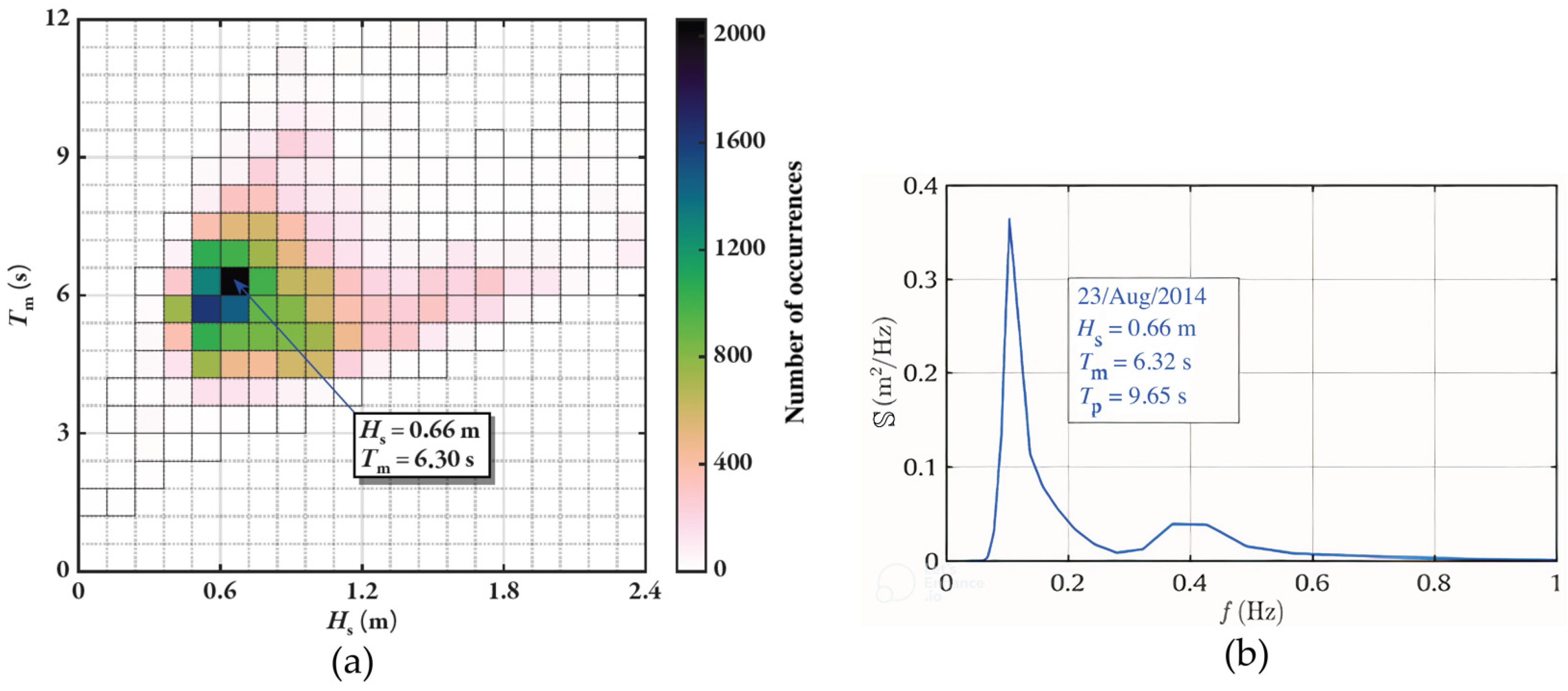
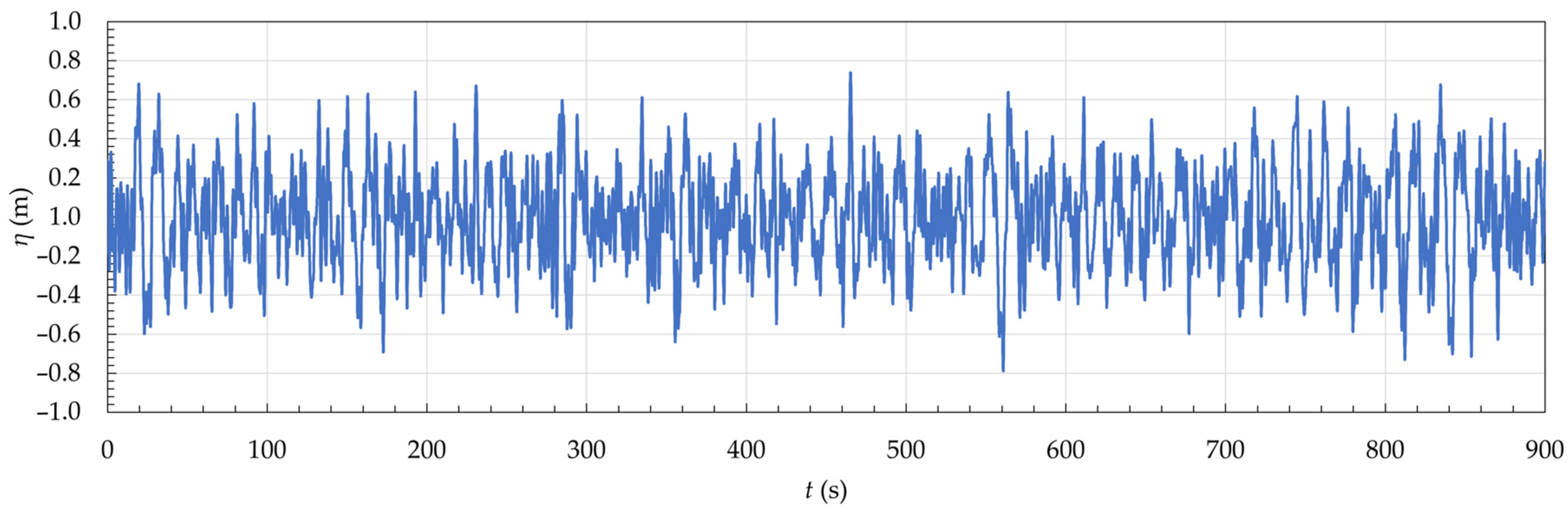


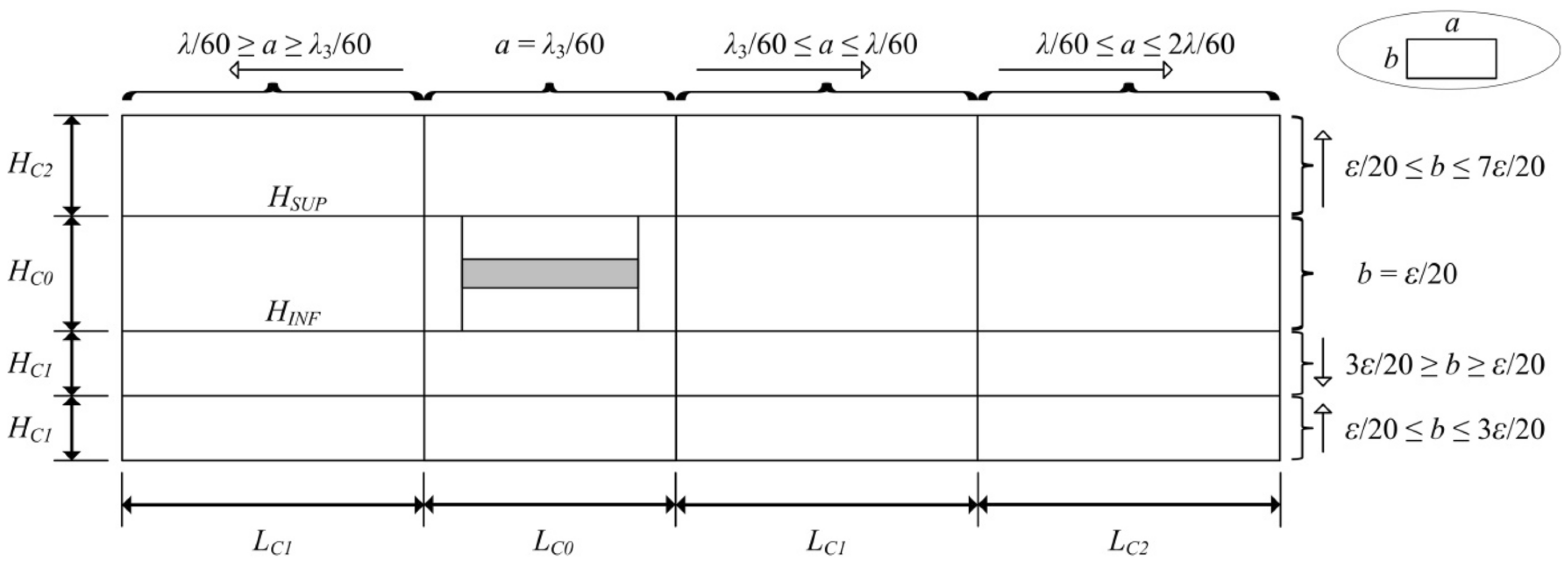
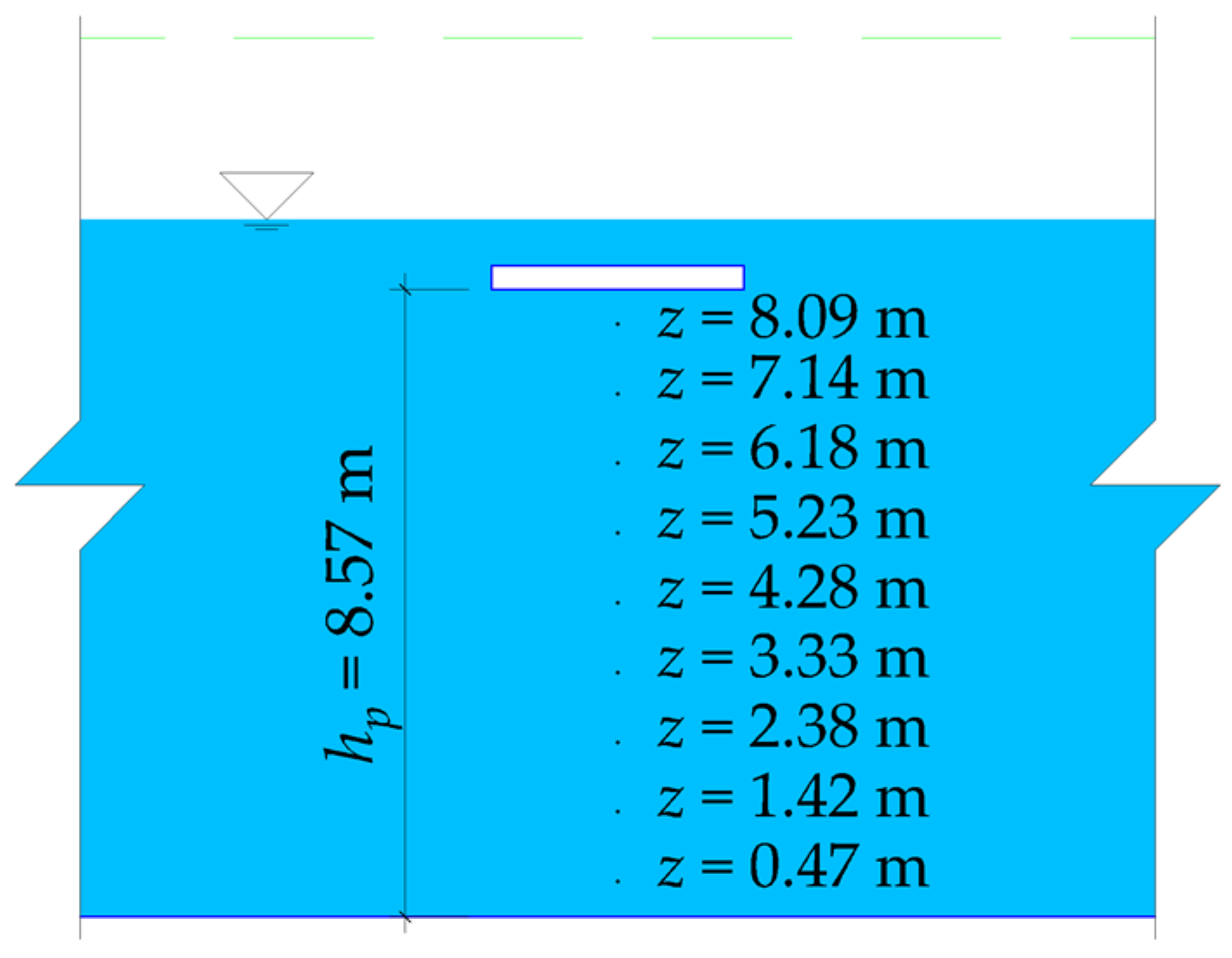
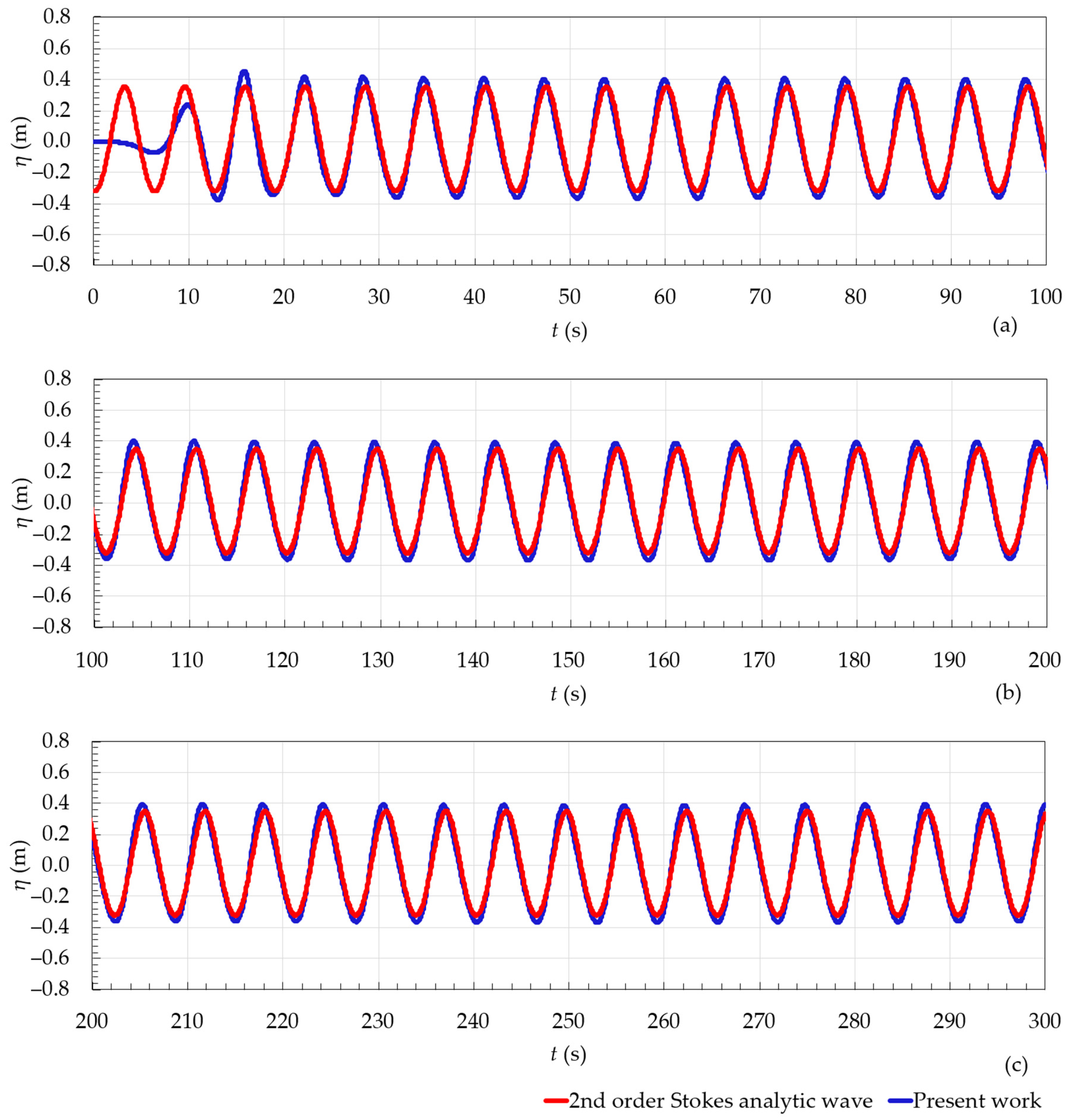
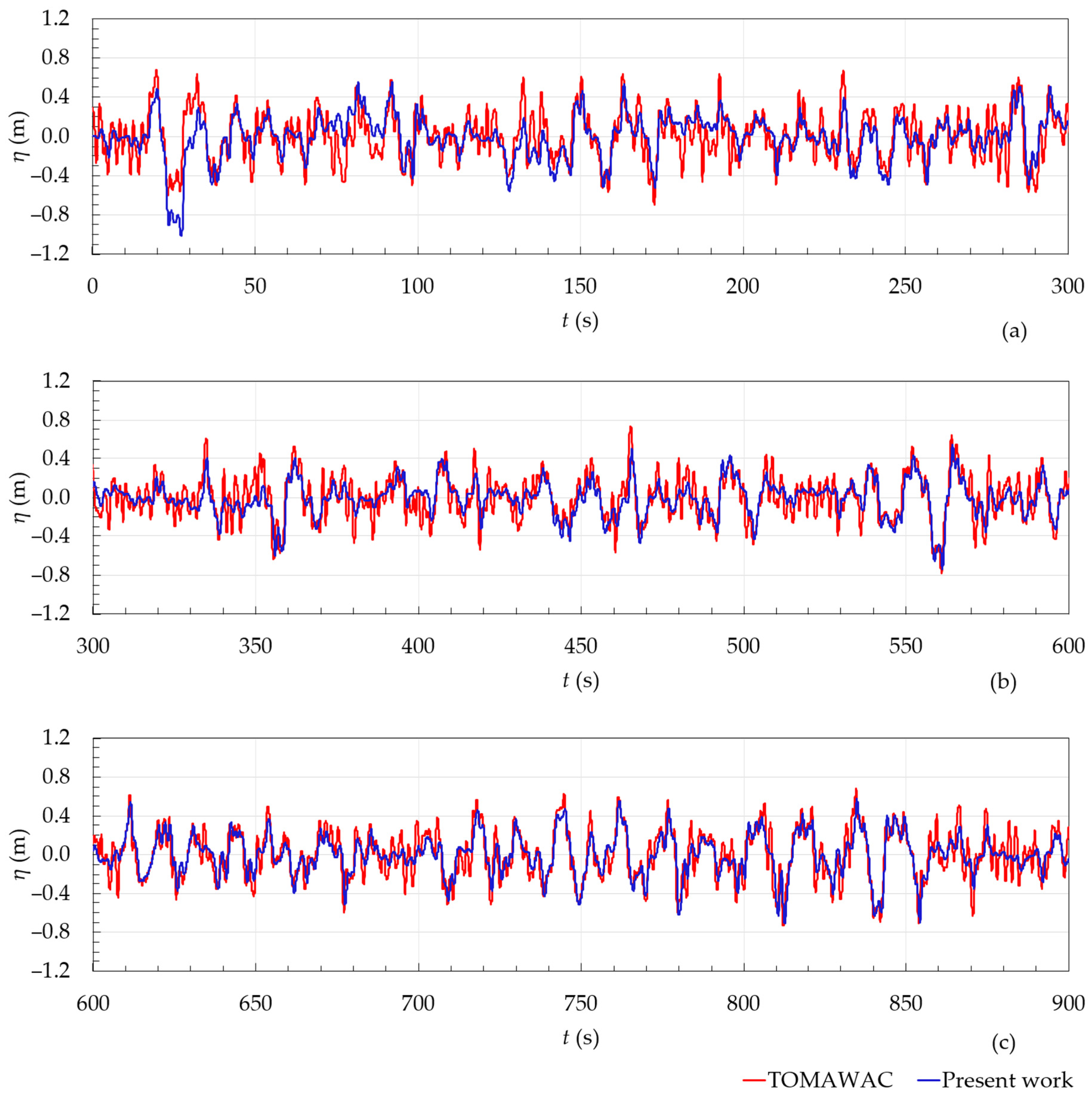
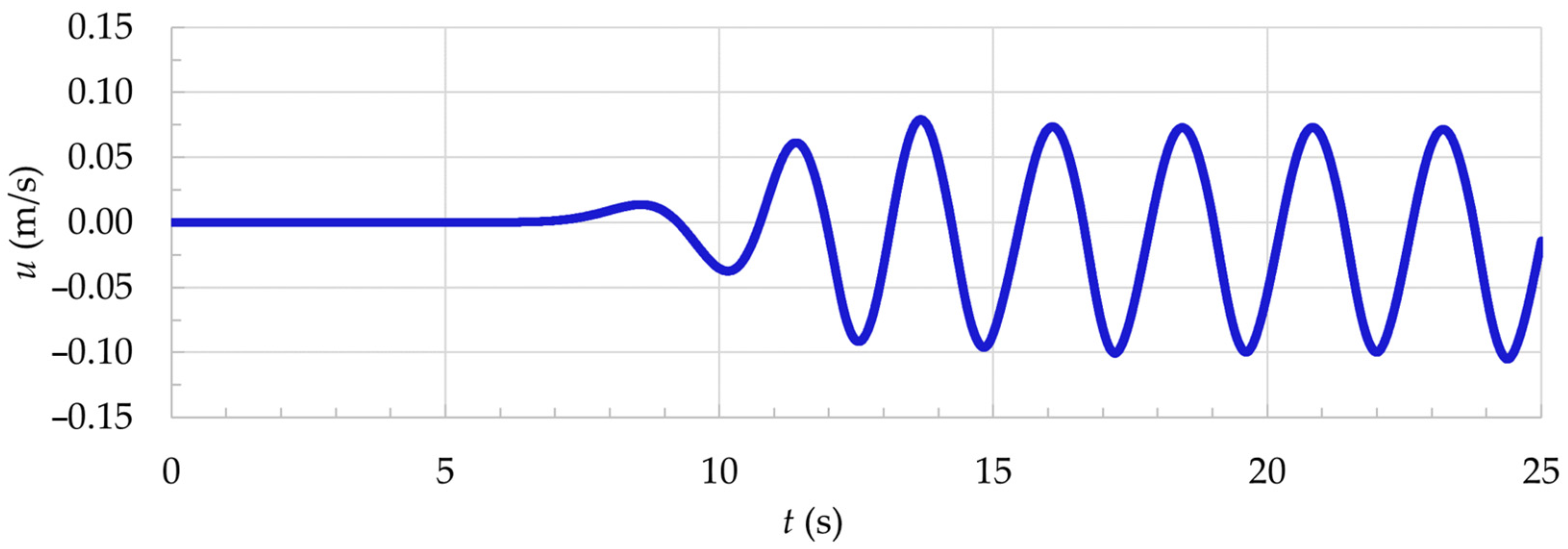
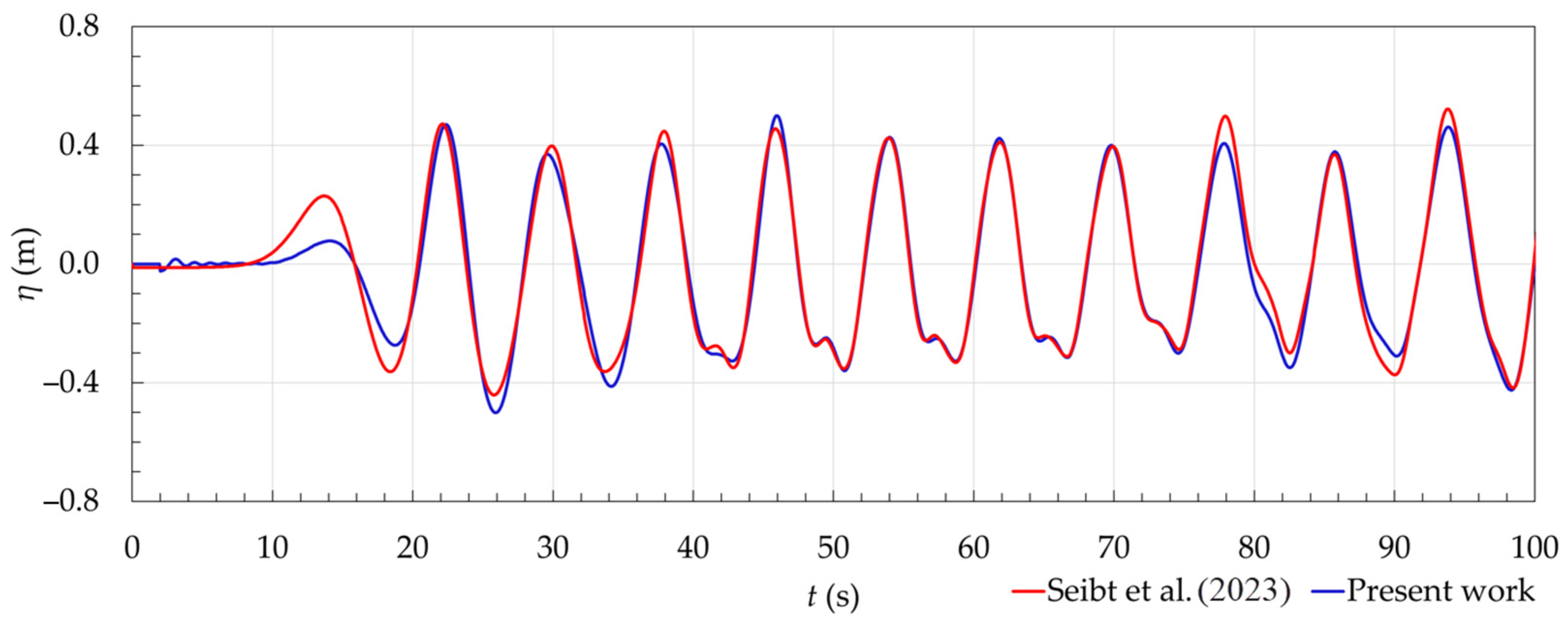

| T (s) | λ (m) | H (m) | d (m) | d/λ |
|---|---|---|---|---|
| 1.87 | 5.37 | 0.06 | 0.60 | 0.11 |
| T (s) | λ (m) | H (m) | d (m) | d/λ |
|---|---|---|---|---|
| 8.00 | 69.79 | 0.96 | 9.60 | 0.14 |
| Case | Lp (m) | Probe Position Downstream of the SHP: x (m) | Probes Position Below the SHP: x (m) |
|---|---|---|---|
| 1Lp | 3.4570 | 116.65 | 104.93 |
| 1.5Lp | 5.1858 | 118.38 | 105.79 |
| 2Lp | 6.9140 | 120.11 | 106.65 |
| 2.5Lp | 8.6420 | 121.84 | 107.52 |
| 3Lp | 10.3710 | 123.57 | 108.38 |
| Experimental Axial Velocity (m/s) | Numerical Axial Velocity (m/s) | Difference (m/s) |
|---|---|---|
| −0.11385 | −0.10505 | −0.0088 |
| Case | 10 m Upstream of SHP (x = 93.2 m) | 10 m Downstream of SHP (x = Varies) | RPE (Hs Reduction) |
|---|---|---|---|
| 1Lp | 0.540 m | 0.461 m | −14.62% |
| 1.5Lp | 0.599 m | 0.329 m | −45.05% |
| 2Lp | 0.713 m | 0.227 m | −68.16% |
| 2.5Lp | 0.812 m | 0.246 m | −69.63% |
| 3Lp | 0.840 m | 0.246 m | −70.70% |
| Case | 10 m Upstream of SHP (x = 93.2 m) | Fixed Probe Downstream of the SHP (x = 128.63 m) | RPE (Hs Reduction) |
|---|---|---|---|
| 1Lp | 0.540 m | 0.456 m | −15.61% |
| 1.5Lp | 0.599 m | 0.309 m | −48.50% |
| 2Lp | 0.713 m | 0.229 m | −67.88% |
| 2.5Lp | 0.812 m | 0.215 m | −73.52% |
| 3Lp | 0.840 m | 0.239 m | −71.61% |
| Case | Maximum Axial Velocity (m/s) | Time of Occurrence t (s) |
|---|---|---|
| 1Lp | −0.244 | 272.05 |
| 1.5Lp | −0.197 | 265.68 |
| 2Lp | −0.192 | 290.74 |
| 2.5Lp | −0.225 | 227.52 |
| 3Lp | −0.258 | 316.60 |
| Case | 10 m Upstream of SHP (x = 93.2 m) | 10 m Downstream of SHP (x = Varies) | RPE (Hs Reduction) |
|---|---|---|---|
| 1Lp | 0.662 m | 0.632 m | −4.52% |
| 1.5Lp | 0.683 m | 0.619 m | −9.31% |
| 2Lp | 0.738 m | 0.594 m | −19.47% |
| 2.5Lp | 0.783 m | 0.560 m | −28.48% |
| 3Lp | 0.829 m | 0.534 m | −35.59% |
| Case | 10 m Upstream of SHP (x = 93.2 m) | Fixed Probe Downstream of SHP (x = 128.63 m) | RPE (Hs Reduction) |
|---|---|---|---|
| 1Lp | 0.662 m | 0.649 m | −1.98% |
| 1.5Lp | 0.683 m | 0.615 m | −9.89% |
| 2Lp | 0.738 m | 0.583 m | −20.97% |
| 2.5Lp | 0.783 m | 0.562 m | −28.19% |
| 3Lp | 0.829 m | 0.511 m | −38.28% |
| Case | Maximum Axial Velocity (m/s) | Time of Occurrence t (s) |
|---|---|---|
| 1Lp | −0.595 | 852.38 |
| 1.5Lp | −0.636 | 852.64 |
| 2Lp | −0.647 | 852.95 |
| 2.5Lp | −0.629 | 853.32 |
| 3Lp | −0.588 | 853.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thum, G.Ü.; Maciel, R.P.; Oleinik, P.H.; Rocha, L.A.O.; dos Santos, E.D.; Seibt, F.M.; Machado, B.N.; Isoldi, L.A. Numerical Analysis of the Submerged Horizontal Plate Device Subjected to Representative Regular and Realistic Irregular Waves of a Sea State. Fluids 2024, 9, 188. https://doi.org/10.3390/fluids9080188
Thum GÜ, Maciel RP, Oleinik PH, Rocha LAO, dos Santos ED, Seibt FM, Machado BN, Isoldi LA. Numerical Analysis of the Submerged Horizontal Plate Device Subjected to Representative Regular and Realistic Irregular Waves of a Sea State. Fluids. 2024; 9(8):188. https://doi.org/10.3390/fluids9080188
Chicago/Turabian StyleThum, Gabrielle Ücker, Rafael Pereira Maciel, Phelype Haron Oleinik, Luiz Alberto Oliveira Rocha, Elizaldo Domingues dos Santos, Flavio Medeiros Seibt, Bianca Neves Machado, and Liércio André Isoldi. 2024. "Numerical Analysis of the Submerged Horizontal Plate Device Subjected to Representative Regular and Realistic Irregular Waves of a Sea State" Fluids 9, no. 8: 188. https://doi.org/10.3390/fluids9080188
APA StyleThum, G. Ü., Maciel, R. P., Oleinik, P. H., Rocha, L. A. O., dos Santos, E. D., Seibt, F. M., Machado, B. N., & Isoldi, L. A. (2024). Numerical Analysis of the Submerged Horizontal Plate Device Subjected to Representative Regular and Realistic Irregular Waves of a Sea State. Fluids, 9(8), 188. https://doi.org/10.3390/fluids9080188











