Dynamics of a Laser-Induced Bubble above the Flat Top of a Solid Cylinder—Mushroom-Shaped Bubbles and the Fast Jet
Abstract
1. Introduction
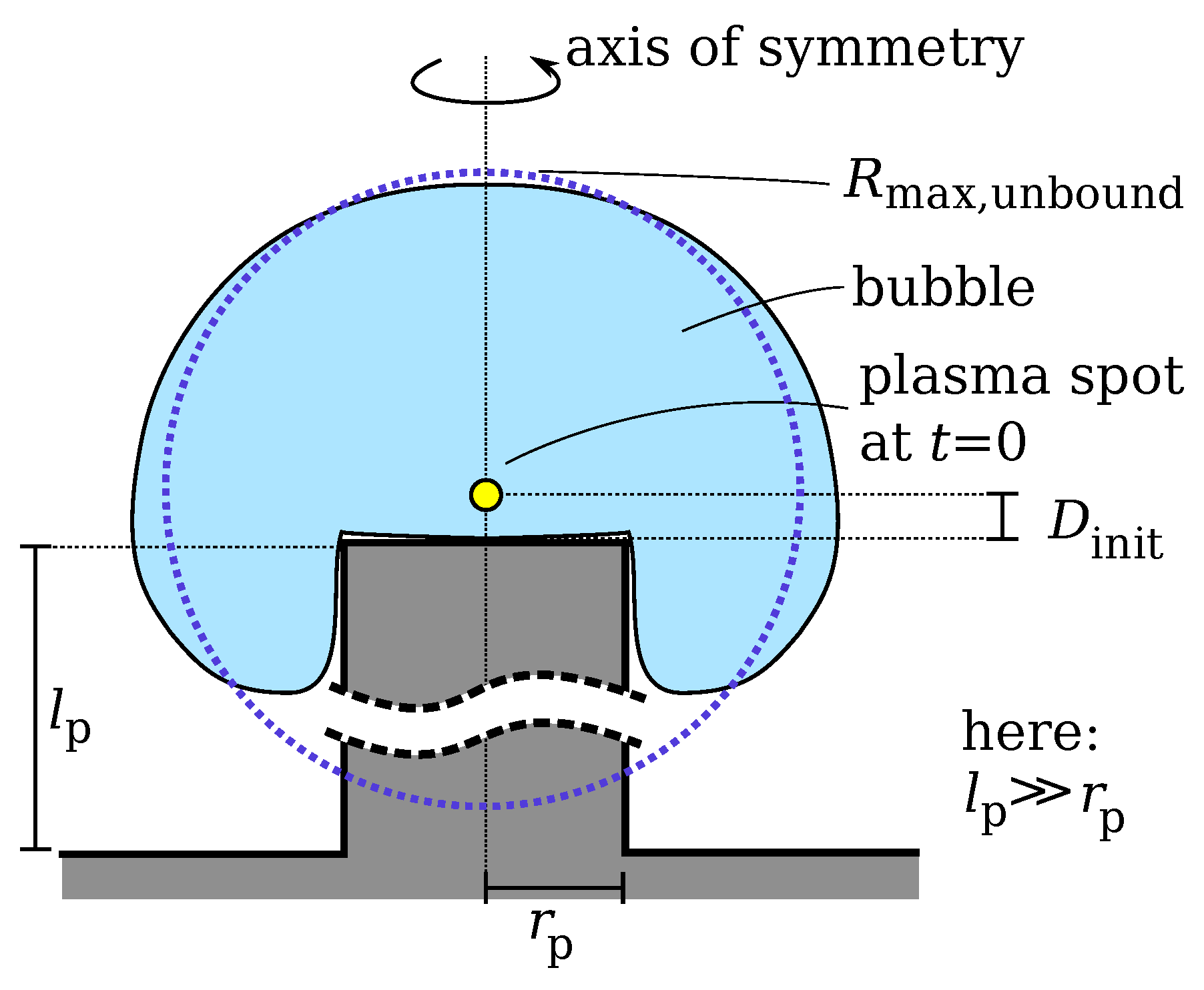
 rp, cannot be neglected. Then it holds for that the case of a bubble in front of a solid plane is approached (irrespective of ). For the limit case studied here is obtained. The transition to pillars of small height would need substantial further work and is not studied here. The present work investigates the details of the dynamics in the parameter range and . This parameter region covers very peculiar bubble dynamics, and, in particular, cases with experimentally observable fast-jet formation are included.
rp, cannot be neglected. Then it holds for that the case of a bubble in front of a solid plane is approached (irrespective of ). For the limit case studied here is obtained. The transition to pillars of small height would need substantial further work and is not studied here. The present work investigates the details of the dynamics in the parameter range and . This parameter region covers very peculiar bubble dynamics, and, in particular, cases with experimentally observable fast-jet formation are included.2. Experimental Methods
3. Numerical Methods
3.1. Bubble Model
3.2. Equations of Motion
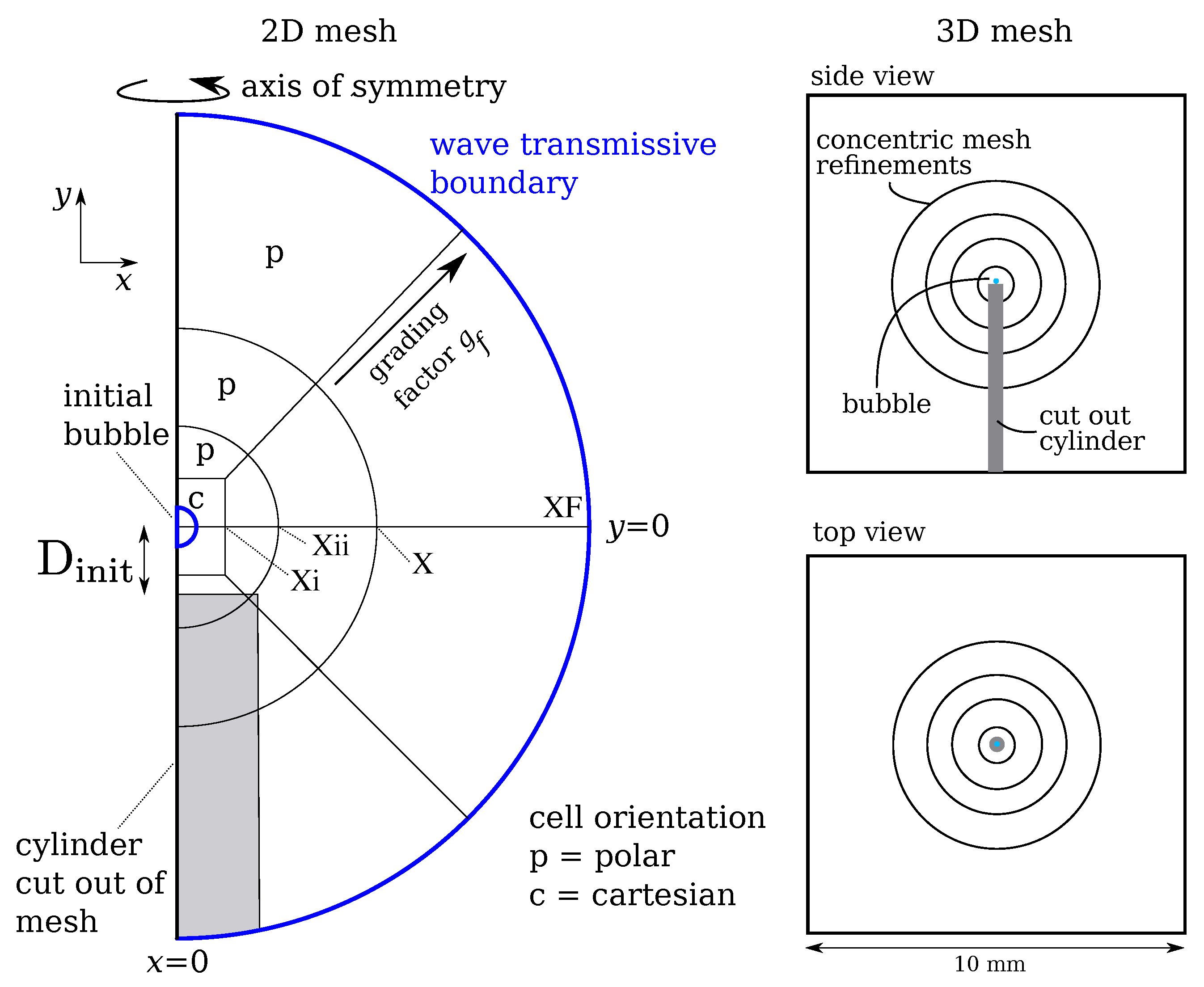
3.3. Initial and Boundary Conditions, Meshes, and Time Steps
3.4. Validation
4. Experimental Results
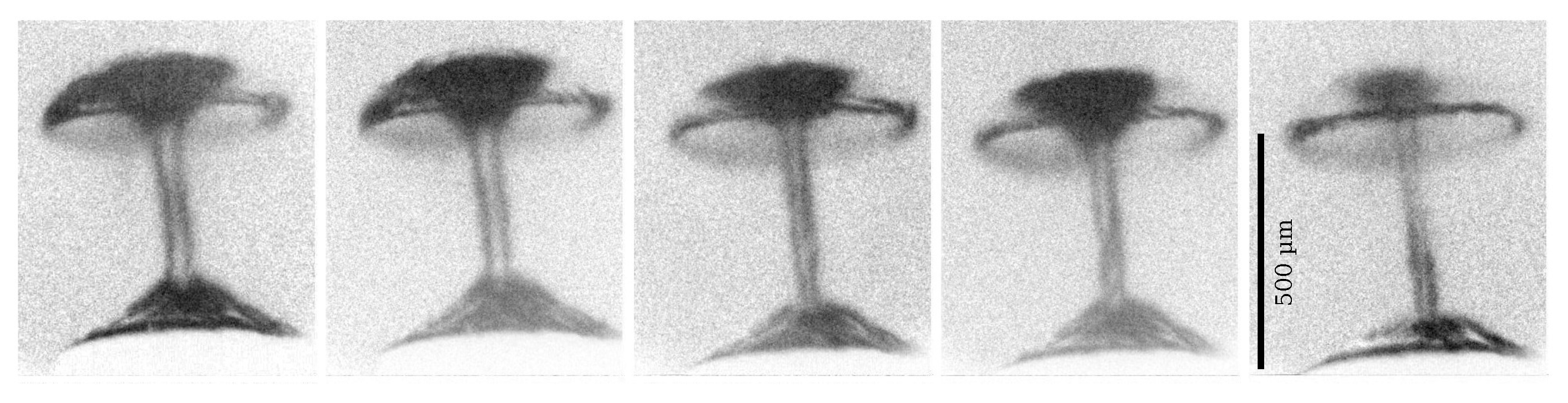
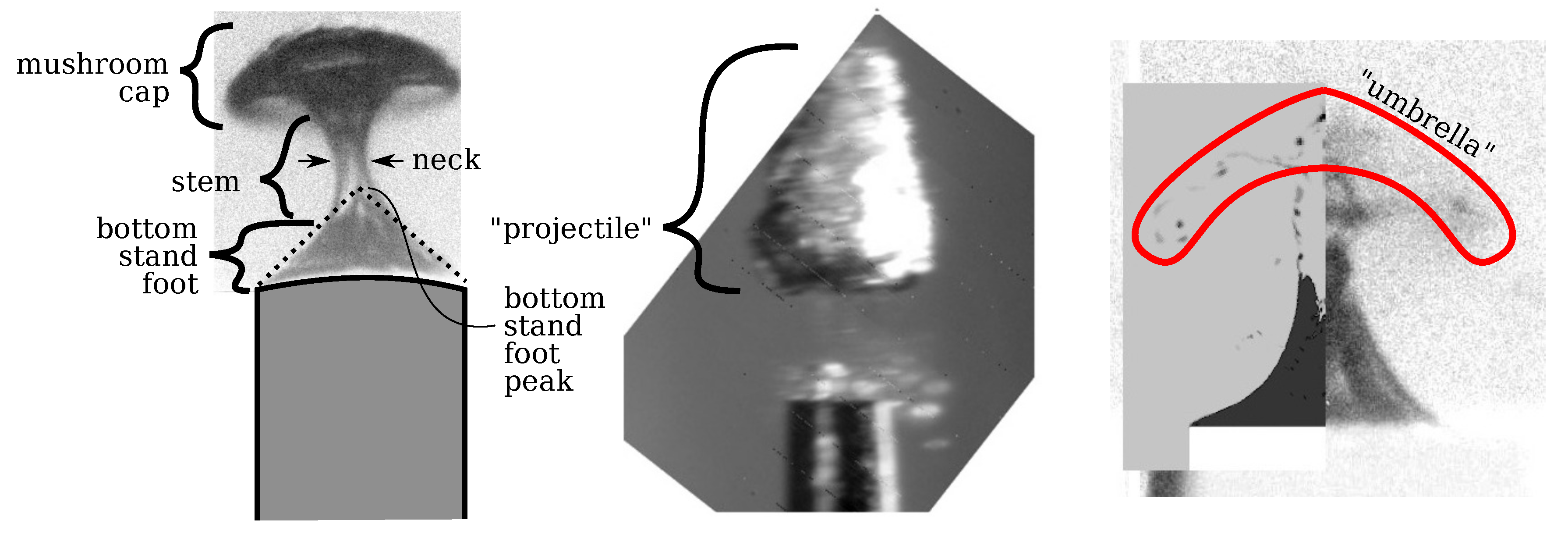
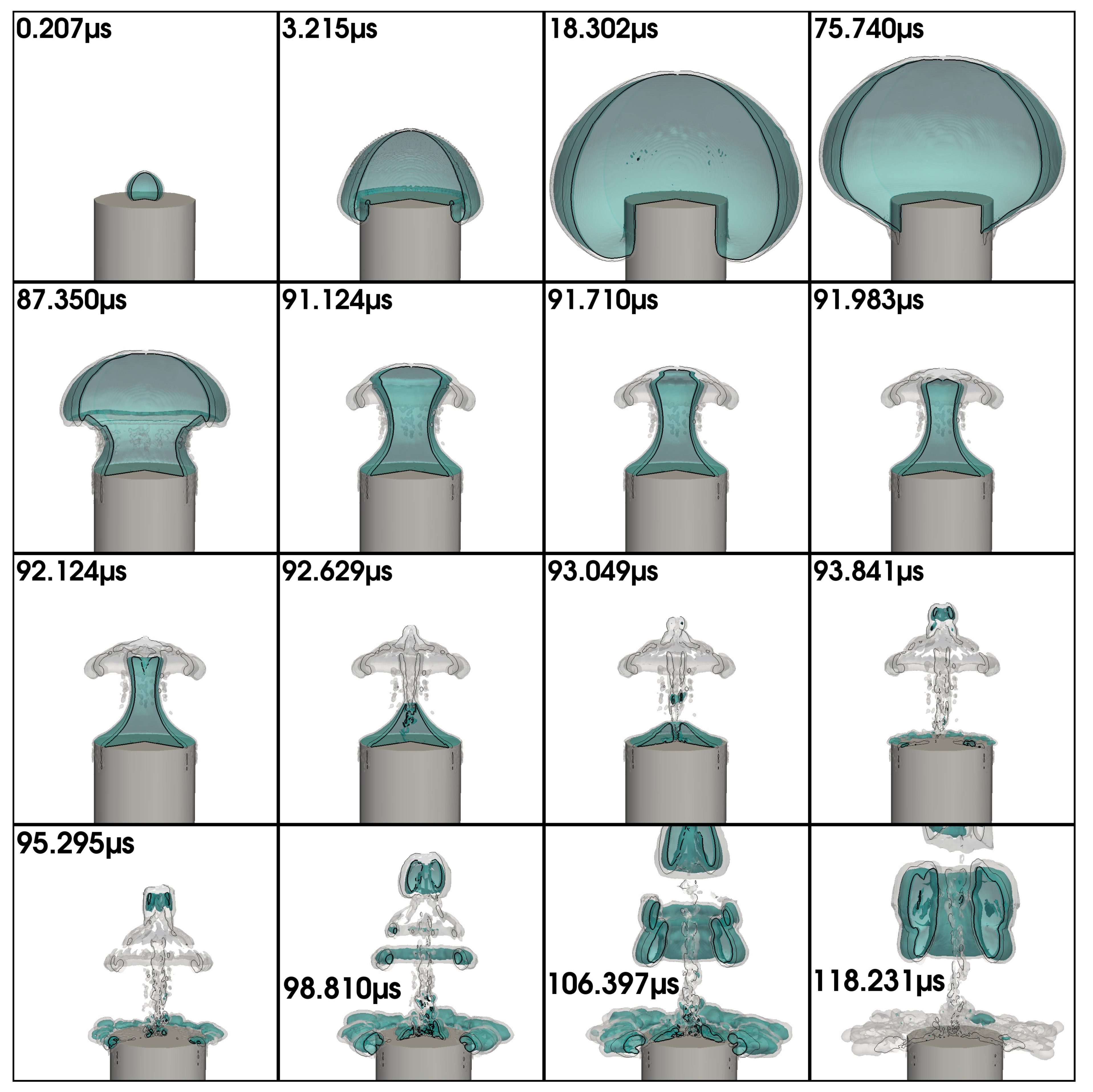
4.1. Typical Mushroom Bubble Dynamics
4.2. Typical Mushroom-Bubble Collapse and Rebound
5. Numerical Results
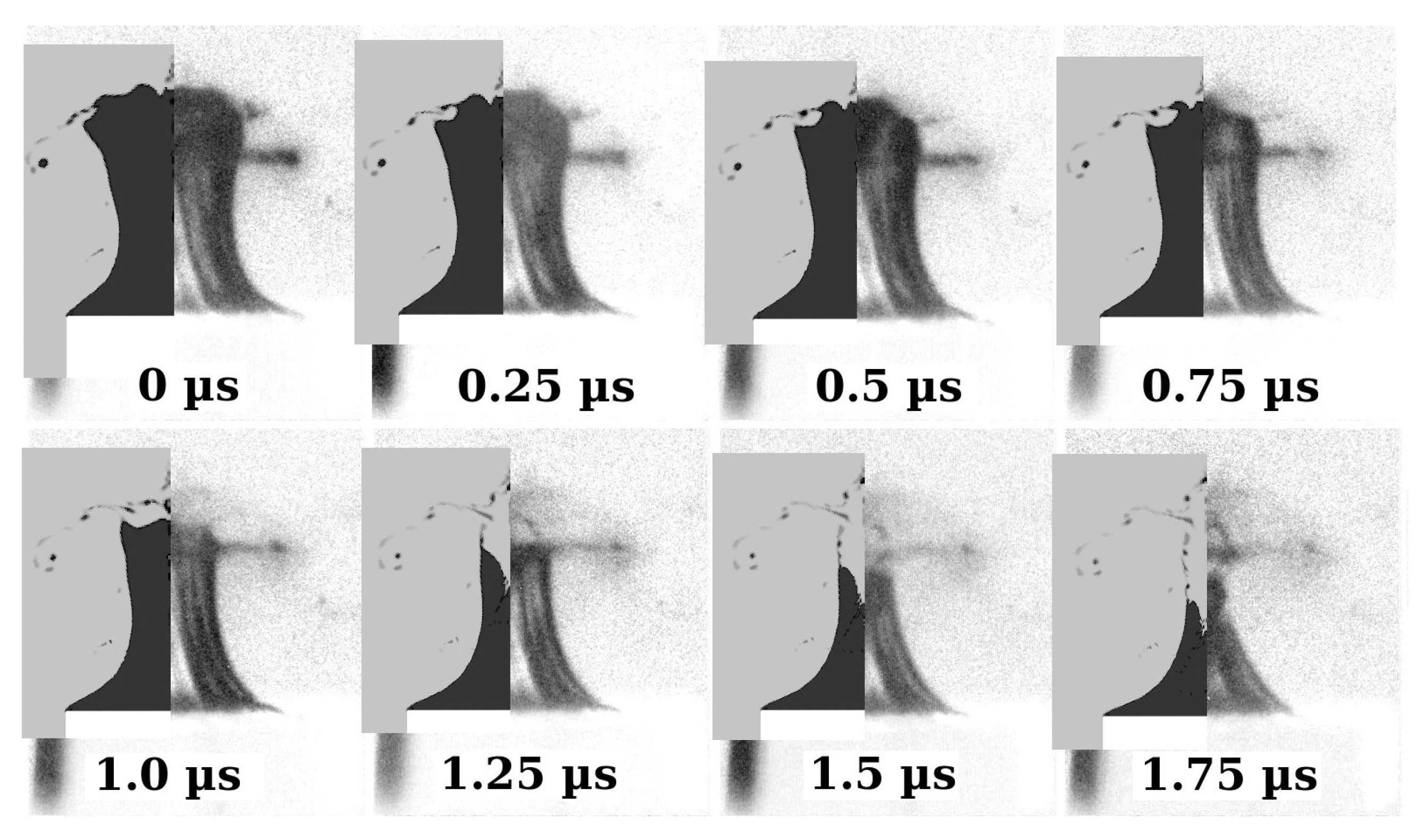
5.1. Comparison of an Experimental Mushroom Bubble with Simulations
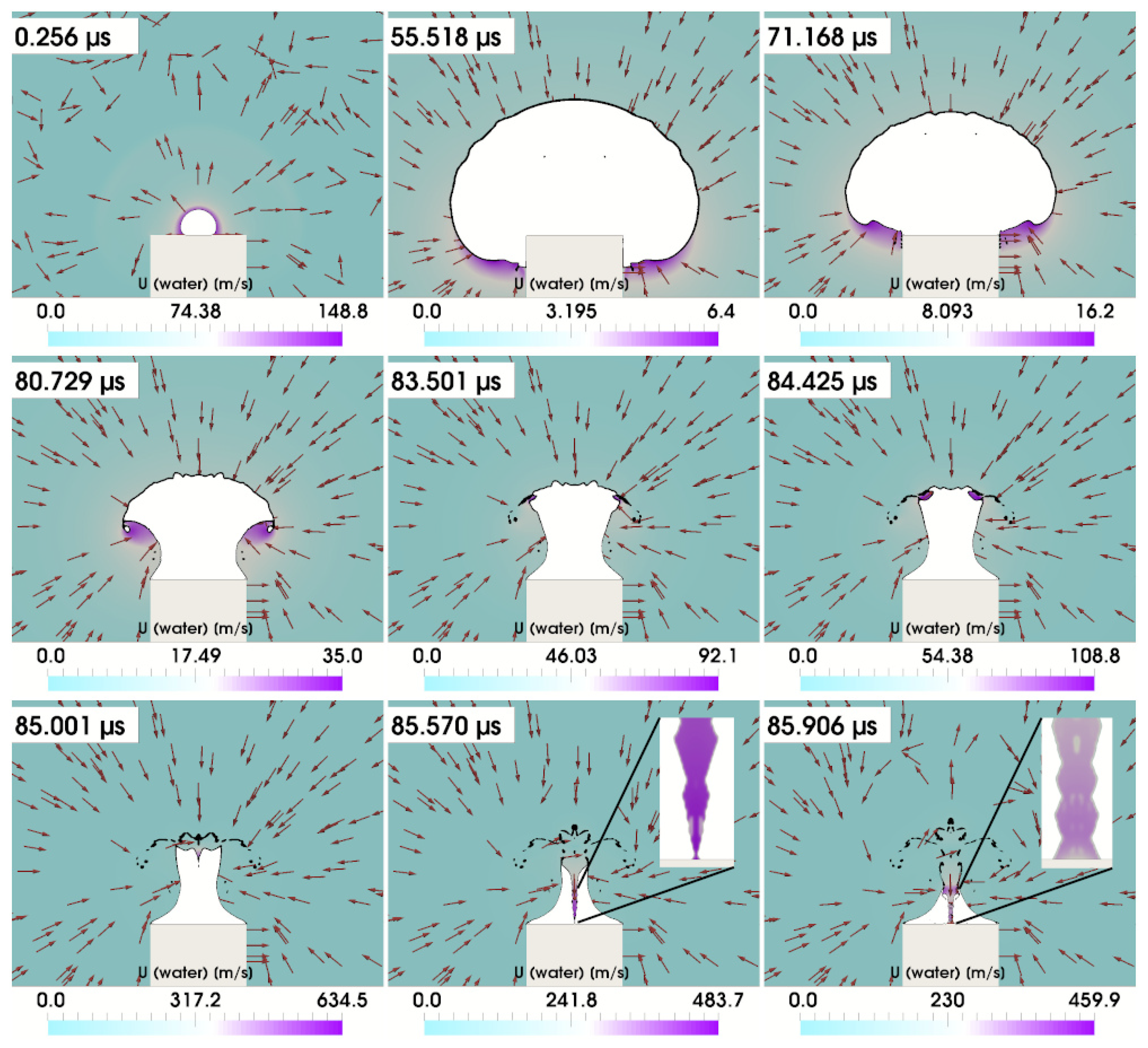
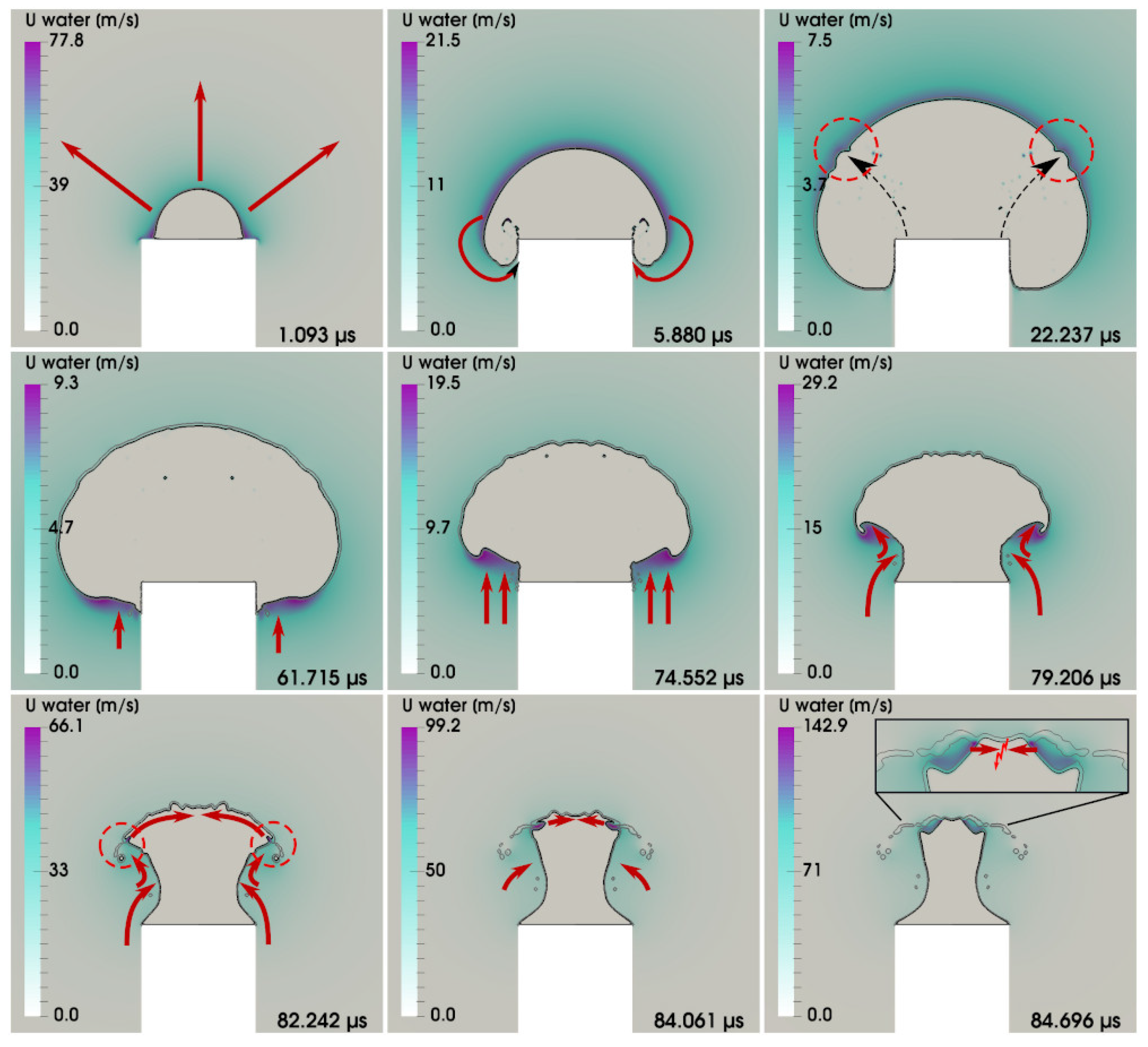
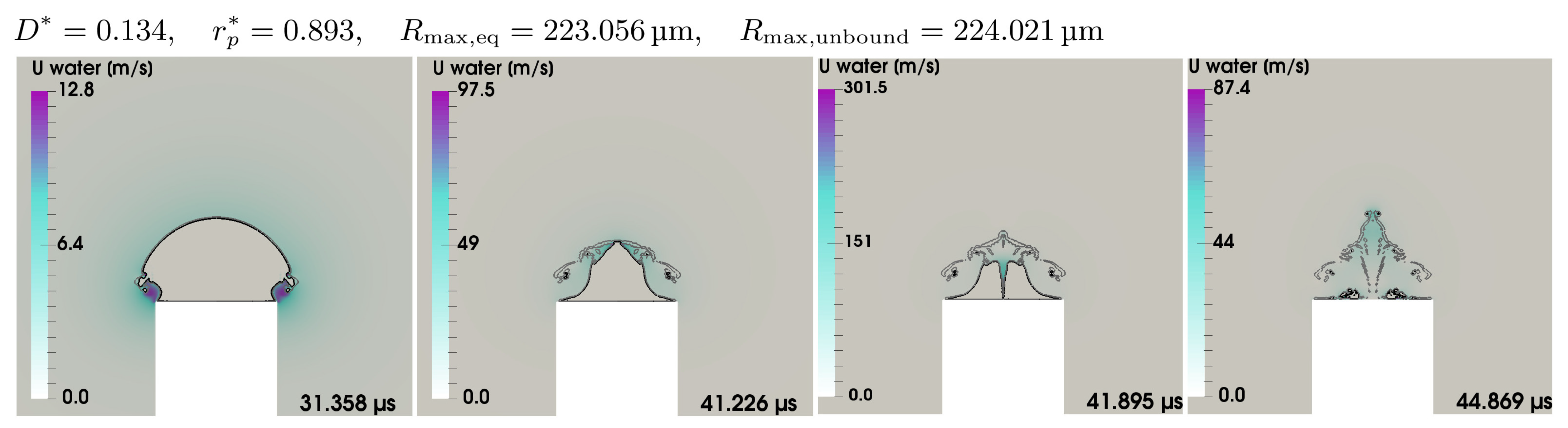
5.2. Pressure, Velocity and Flow Fields of a Mushroom Bubble
5.3. General Dynamics of a Mushroom Bubble
5.4. Simulation in Full 3D
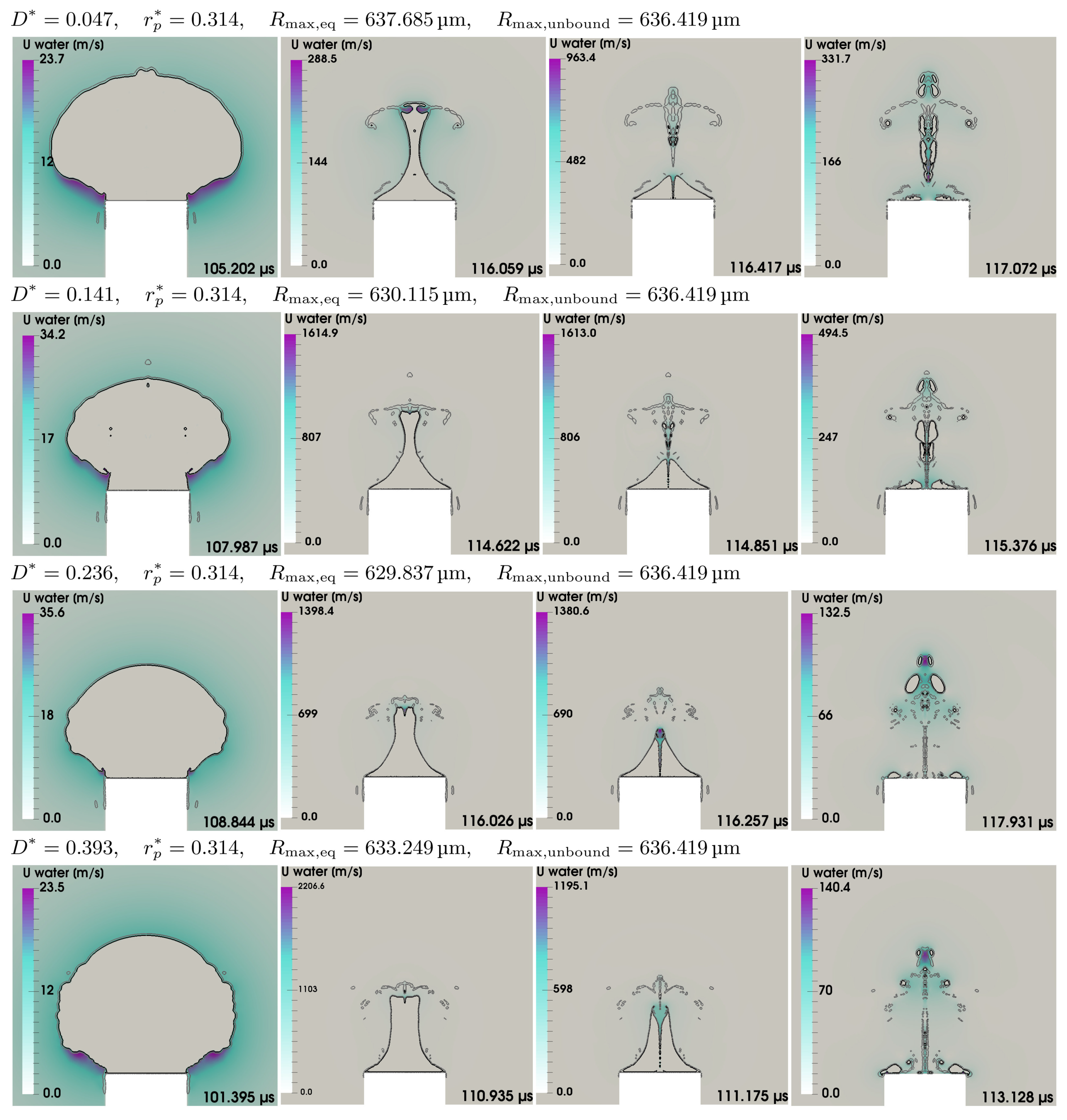
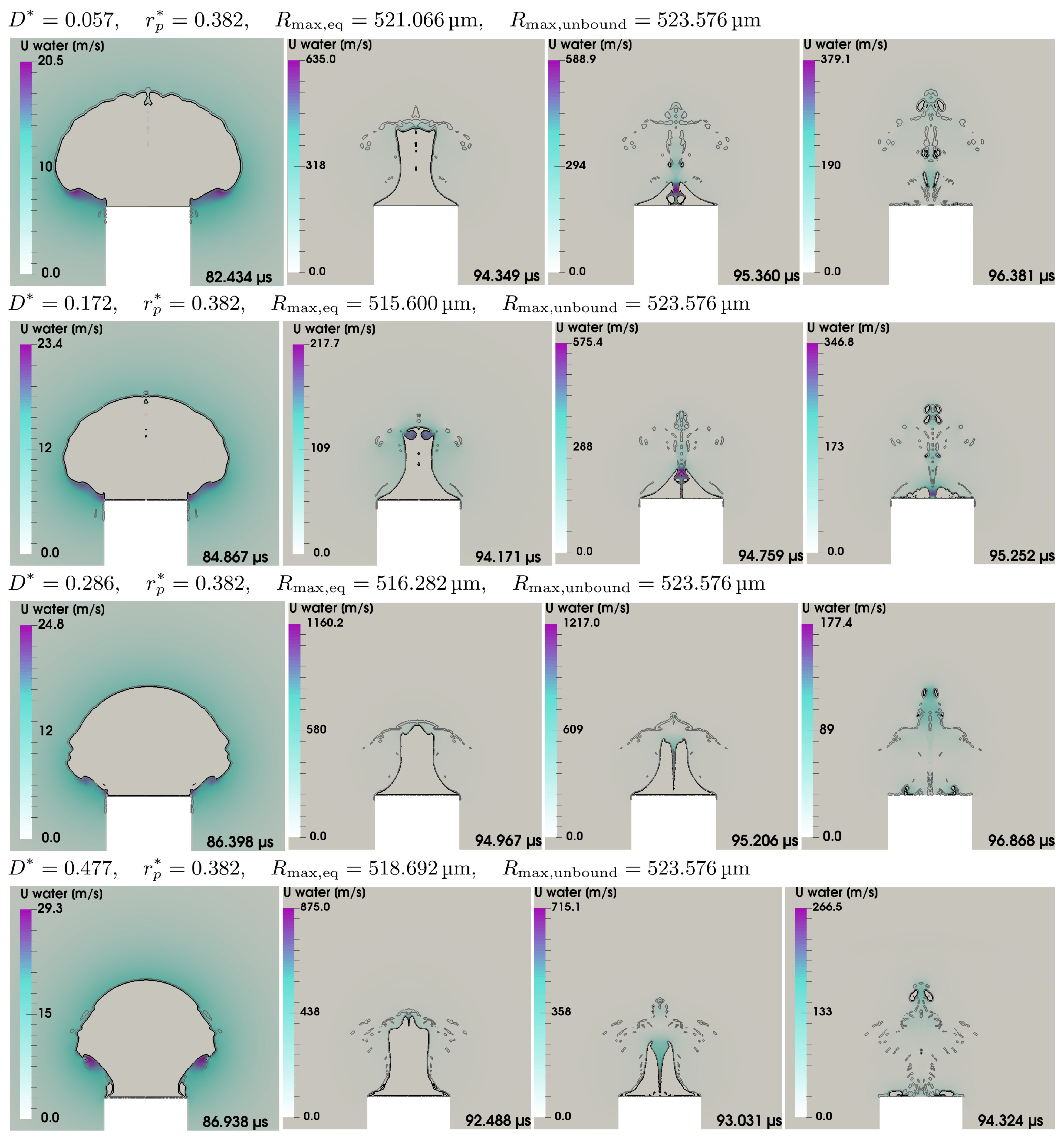
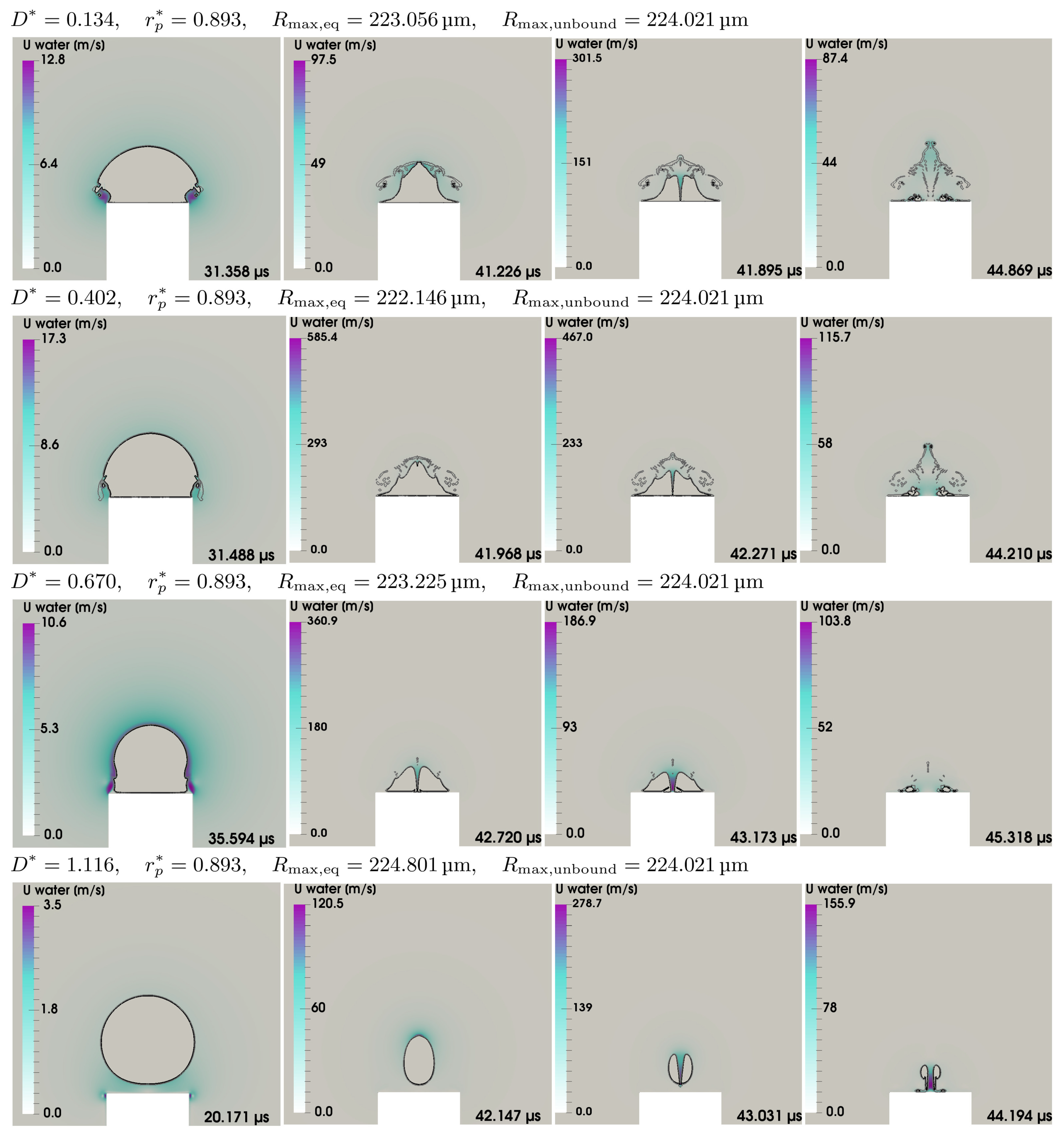
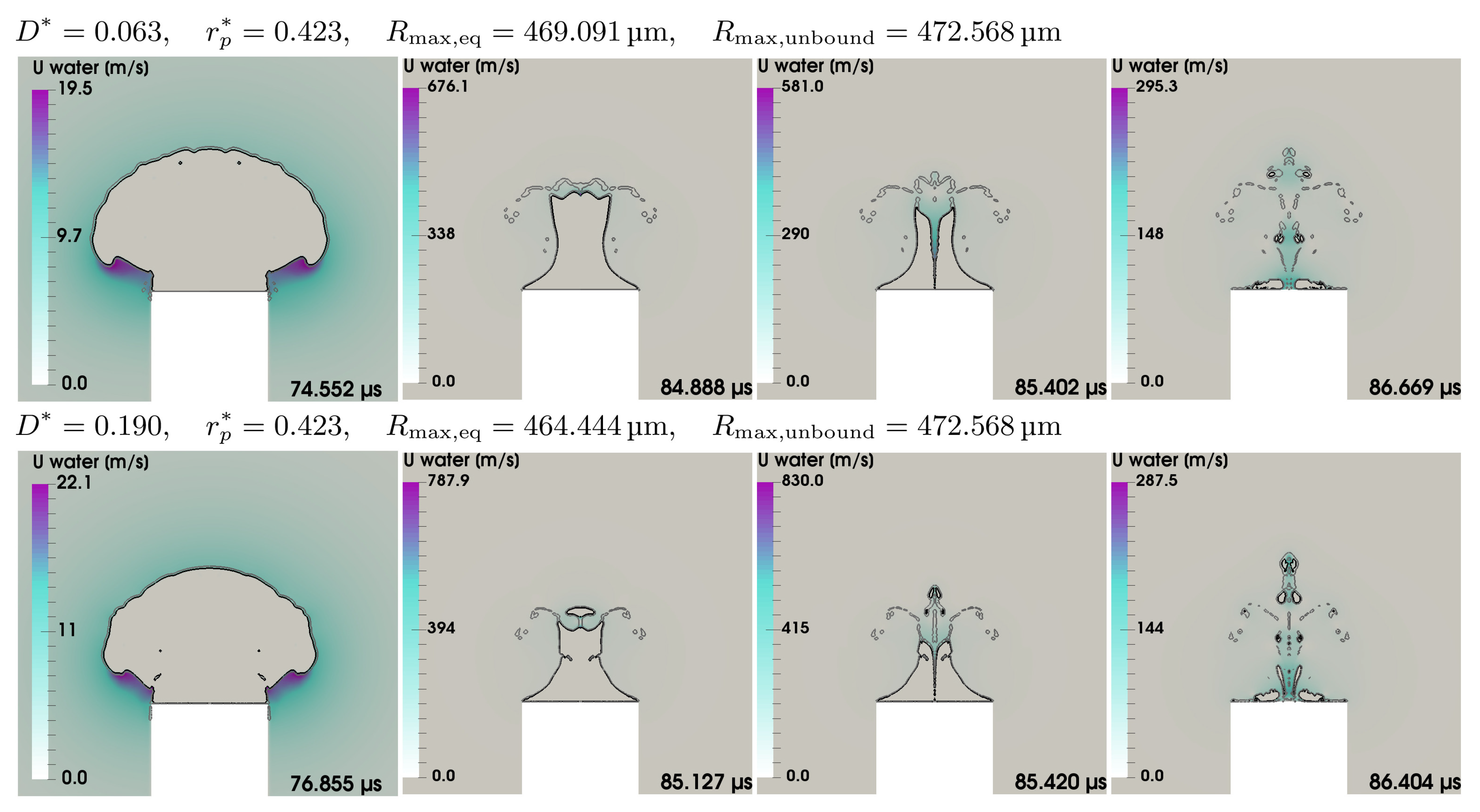
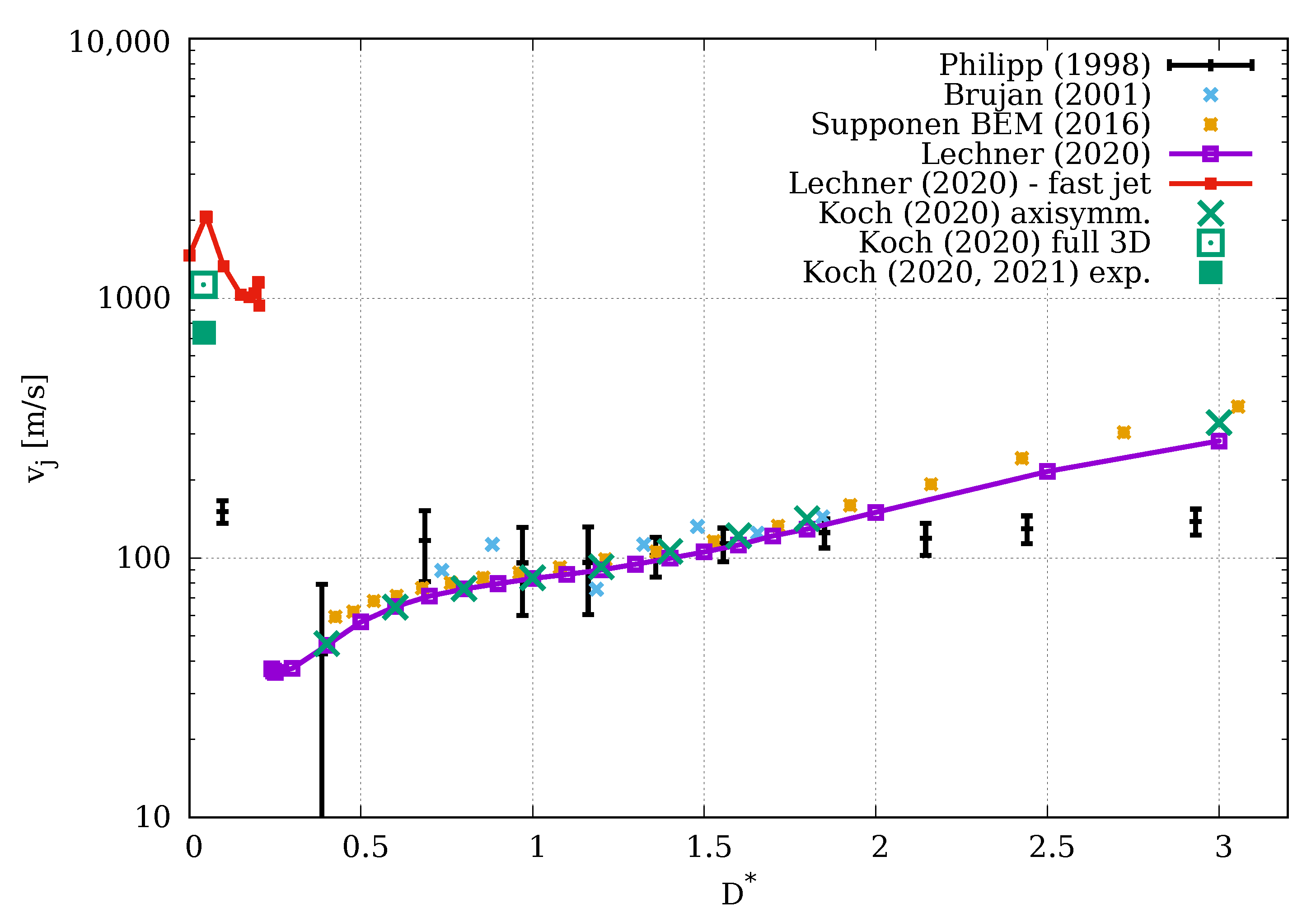
5.5. Parameter Study
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mass Reduction of the Bubble, Validation of the Bubble Model

Appendix B. Mass Error Compensation
Appendix C. Initial Conditions
Appendix D. Calculation of the Advected Color Layer Map
Appendix E. Further Parameter-Study Plots
References
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Kornfeld, M.; Suvorov, L. On the destructive action of cavitation. J. Appl. Phys. 1944, 15, 495–506. [Google Scholar] [CrossRef]
- Leighton, T.G. The Acoustic Bubble; Academic Press: London, UK, 1994. [Google Scholar]
- Lauterborn, W.; Kurz, T. Physics of bubble oscillations. Rep. Prog. Phys. 2010, 73, 106501. [Google Scholar] [CrossRef]
- Askar’yan, G.; Prokhorov, A.; Chanturiya, I.; Shipulo, G. The effects of a laser beam in a liquid. Sov. Phys.—JETP 1963, 17, 1463–1465. [Google Scholar]
- Felix, M.; Ellis, A. Laser-induced liquid breakdown—A step-by-step account. Appl. Phys. Lett. 1971, 19, 484–486. [Google Scholar] [CrossRef]
- Lauterborn, W.; Bolle, H. Experimental investigations of cavitation-bubble collapse in the neighbourhood of a solid boundary. J. Fluid Mech. 1975, 72, 391–399. [Google Scholar] [CrossRef]
- Lauterborn, W. Optic Cavitation. J. Phys. Colloques 1979, 41, C8-273–C8-278. [Google Scholar] [CrossRef]
- Tomita, Y.; Shima, A. High-Speed photographic observations of laser-induced cavitation bubbles in water. Acustica 1990, 71, 161–171. [Google Scholar]
- Tomita, Y.; Robinson, P.B.; Tong, R.P. Growth and collpase of cavitation bubbles near a curved rigid boundary. J. Fluid Mech. 2002, 466, 259–283. [Google Scholar] [CrossRef]
- Blake, J.R.; Taib, B.B.; Doherty, G. Transient cavities near boundaries. Part 1. Rigid boundary. J. Fluid Mech. 1986, 170, 479–497. [Google Scholar] [CrossRef]
- Philipp, A.; Lauterborn, W. Cavitation erosion by single laser-produced bubbles. J. Fluid Mech. 1998, 361, 75–116. [Google Scholar] [CrossRef]
- Tong, R.P.; Schiffers, W.P.; Shaw, S.J.; Blake, J.R.; Emmony, D.C. The role of `splashing’ in the collaspe of a laser-generated cavity near a rigid boundary. J. Fluid Mech. 1999, 380, 339–361. [Google Scholar] [CrossRef]
- Brujan, E.A.; Keen, G.S.; Vogel, A.; Blake, J.R. The final stage of the collapse of a cavitation bubble close to a rigid boundary. Phys. Fluids 2002, 14, 85–92. [Google Scholar] [CrossRef]
- Lindau, O.; Lauterborn, W. Cinematographic observation of the collapse and rebound of a laser-produced cavitation bubble near a wall. J. Fluid Mech. 2003, 479, 327–348. [Google Scholar] [CrossRef]
- Wang, Q. Multi-oscillations of a bubble in a compressible liquid near a rigid boundary. J. Fluid Mech. 2014, 745, 509–536. [Google Scholar] [CrossRef]
- Koukouvinis, P.; Gavaises, M.; Supponen, O.; Farhat, M. Simulation of bubble expansion and collapse in the vicinity of a free surface. Phys. Fluids 2016, 28, 052103. [Google Scholar] [CrossRef]
- Supponen, O.; Obreschkow, D.; Tinguely, M.; Kobel, P.; Dorsaz, N.; Farhat, M. Scaling laws for jets of single cavitation bubbles. J. Fluid Mech. 2016, 802, 263–293. [Google Scholar] [CrossRef]
- Brujan, E.A.; Nahen, K.; Schmidt, P.; Vogel, A. Dynamics of laser-induced cavitation bubbles near an elastic boundary. J. Fluid Mech. 2001, 433, 251–281. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Ellis, A.T. The Collapse of Cavitation Bubbles and the Pressures thereby Produced against Solid Boundaries. Philos. Trans. R. Soc. Lond. Ser. A 1966, 260, 221–240. [Google Scholar]
- Koukouvinis, P.; Gavaises, M.; Supponen, O.; Farhat, M. Numerical simulation of a collapsing bubble subject to gravity. Phys. Fluids 2016, 28, 032110. [Google Scholar] [CrossRef]
- Obreschkow, D.; Tinguely, M.; Dorsaz, N.; Kobel, P.; de Bosset, A.; Farhat, M. The quest for the most spherical bubble: Experimental setup and data overview. Exp. Fluids 2013, 54, 1503. [Google Scholar] [CrossRef]
- Naudé, C.F.; Ellis, A.T. On the mechanism of cavitation damage by nonhemispherical cavities collapsing in contact with a solid boundary. J. Basic. Eng. 1961, 83, 648–656. [Google Scholar] [CrossRef]
- Crum, L.A. Surface oscillations and jet development in pulsating bubbles. J. Phys. Colloques 1979, 41, C8-285–C8-288. [Google Scholar] [CrossRef]
- Plesset, M.S.; Chapman, R.B. Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary. J. Fluid Mech. 1971, 47, 283–290. [Google Scholar] [CrossRef]
- Blake, J.; Taib, B.; Doherty, G. Transient cavities near boundaries: II. Free surface. J. Fluid Mech. 1987, 181, 197–212. [Google Scholar] [CrossRef]
- Blake, J.R.; Hooton, M.C.; Robinson, P.B.; Tong, R.P. Collapsing cavities, toroidal bubbles and jet impact. Proc. R. Soc. Lond. Ser. A 1997, 355, 537–550. [Google Scholar] [CrossRef]
- Blake, J.R.; Tomita, Y.; Tong, R.P. The art, craft and science of modelling jet impact in a collapsing cavitation bubble. Appl. Sci. Res. 1998, 58, 77–90. [Google Scholar] [CrossRef]
- Blake, J.R.; Keen, G.S.; Tong, R.P.; Wilson, M. Acoustic cavitation: The fluid dynamics of non-spherical bubbles. Philos. Trans. R. Soc. Lond. Ser. A 1999, 357, 251–267. [Google Scholar] [CrossRef]
- Vogel, A.; Lauterborn, W.; Timm, R. Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary. J. Fluid Mech. 1989, 206, 299–338. [Google Scholar] [CrossRef]
- Tomita, Y.; Shima, A. Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse. J. Fluid Mech. 1986, 169, 535–564. [Google Scholar] [CrossRef]
- Zhang, S.; Duncan, J.H.; Chahine, G.L. The final stage of the collapse of a cavitation bubble near a rigid wall. J. Fluid Mech. 1993, 257, 147–181. [Google Scholar] [CrossRef]
- Isselin, J.C.; Alloncle, A.P.; Autric, M. On laser induced single bubble near a solid boundary: Contribution to the understanding of erosion phenomena. J. Appl. Phys. 1998, 84, 5766–5771. [Google Scholar] [CrossRef]
- Shaw, S.J.; Schiffers, W.P.; Gentry, T.P.; Emmony, D.C. The interaction of a laser-generated cavity with a solid boundary. J. Acoust. Soc. Am. 2000, 107, 3065–3072. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Yeo, K.S.; Khoo, B.C.; Wang, C. 3D Jet Impact and Toroidal Bubbles. J. Comput. Phys. 2001, 166, 336–360. [Google Scholar] [CrossRef]
- Johnsen, E.; Colonius, T. Numerical simulations of non-spherical bubble collapse. J. Fluid Mech. 2009, 629, 231–262. [Google Scholar] [CrossRef] [PubMed]
- Ochiai, N.; Iga, Y.; Nohmi, M.; Ikohagi, T. Numerical Analysis of Nonspherical Bubble Collapse Behavior and Induced Impulsive Pressure during First and Second Collapses near the Wall Boundary. J. Fluid Sci. Technol. 2011, 6, 860–874. [Google Scholar] [CrossRef][Green Version]
- Lauer, E.; Hu, X.; Hickel, S.; Adams, N. Numerical modelling and investigation of symmetric and asymmetric cavitation bubble dynamics. Comput. Fluids 2012, 69, 1–19. [Google Scholar] [CrossRef]
- Chahine, G.L. Modeling of Cavitation Dynamics and Interaction with Material. In Advanced Experimental and Numerical Techniques for Cavitation Erosion Prediction. Fluid Mechanics and Its Applications; Kim, K.H., Chahine, G., Franc, J.P., Karimi, A., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 106, pp. 123–161. [Google Scholar] [CrossRef]
- Hsiao, C.T.; Jayaprakash, A.; Kapahi, A.; Choi, J.K.; Chahine, G.L. Modelling of material pitting from cavitation bubble collapse. J. Fluid Mech. 2014, 755, 142–175. [Google Scholar] [CrossRef]
- Tiwari, A.; Pantano, C.; Freund, J. Growth-and-collapse dynamics of small bubble clusters near a wall. J. Fluid Mech. 2015, 775, 1–23. [Google Scholar] [CrossRef]
- Koch, M.; Lechner, C.; Reuter, F.; Köhler, K.; Mettin, R.; Lauterborn, W. Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM. Comput. Fluids 2016, 126, 71–90. [Google Scholar] [CrossRef]
- Aganin, A.A.; Ilgamov, M.A.; Kosolapova, L.A.; Malakhov, V.G. Dynamics of a cavitation bubble near a solid wall. Thermophys. Aeromech. 2016, 23, 211–220. [Google Scholar] [CrossRef]
- Reuter, F.; Gonzalez-Avila, S.R.; Mettin, R.; Ohl, C.D. Flow fields and vortex dynamics of bubbles collapsing near a solid boundary. Phys. Rev. Fluids 2017, 2, 064202. [Google Scholar] [CrossRef]
- Lechner, C.; Koch, M.; Lauterborn, W.; Mettin, R. Pressure and tension waves from bubble collapse near a solid boundary: A numerical approach. J. Acoust. Soc. Am. 2017, 142, 3649–3659. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhang, A.M.; Wang, S.P.; Cui, J. Dynamic characteristics of large scale spark bubbles close to different boundaries. Phys. Fluids 2017, 29, 092107. [Google Scholar] [CrossRef]
- Ma, X.; Huang, B.; Li, Y.; Chang, Q.; Qiu, S.; Su, Z.; Fu, X.; Wang, G. Numerical simulation of single bubble dynamics under acoustic travelling waves. Ultrason. Sonochem. 2018, 42, 619–630. [Google Scholar] [CrossRef] [PubMed]
- Beig, S.A.; Aboulhasanzadeh, B.; Johnsen, E. Temperatures produced by inertally collapsing bubbles near rigid surfaces. J. Fluid Mech. 2018, 852, 105–125. [Google Scholar] [CrossRef]
- Lauterborn, W.; Lechner, C.; Koch, M.; Mettin, R. Bubble models and real bubbles: Rayleigh and energy-deposit cases in a Tait-compressible liquid. IMA J. Appl. Math. 2018, 83, 556–589. [Google Scholar] [CrossRef]
- Dular, M.; Požar, T.; Zevnik, J.; Petkovšek, R. High speed observation of damage created by a collapse of a single cavitation bubble. Wear 2019, 418–419, 13–23. [Google Scholar] [CrossRef]
- Sagar, H.J.; el Moctar, O. Dynamics of a cavitation bubble near a solid surface and the induced damage. J. Fluids Struct. 2020, 92, 102799. [Google Scholar] [CrossRef]
- Denner, F.; Evrard, F.; van Wachem, B. Modeling acoustic cavitation using a pressure-based algorithm for polytropic fluids. Fluids 2020, 5, 69. [Google Scholar] [CrossRef]
- Lechner, C.; Lauterborn, W.; Koch, M.; Mettin, R. Jet formation from bubbles near a solid boundary in a compressible liquid: Numerical study of distance dependence. Phys. Rev. Fluids 2020, 5, 093604. [Google Scholar] [CrossRef]
- Gonzalez-Avila, S.; Denner, F.; Ohl, C.D. The acoustic pressure generated by the cavitation bubble expansion and collapse near a rigid wall. Phys. Fluids 2021, 33, 032118. [Google Scholar] [CrossRef]
- Trummler, T.; Schmidt, S.J.; Adams, N.A. Effect of stand-off distance and spatial resolution on the pressure impact of near-wall vapor bubble collapses. Int. J. Multiph. Flow 2021, 141, 103618. [Google Scholar] [CrossRef]
- Trummler, T.; Schmidt, S.J.; Adams, N.A. Numerical investigation of non-condensable gas effect on vapor bubble collapse. Phys. Fluids 2021, 33, 096107. [Google Scholar] [CrossRef]
- Požar, T.; Agrež, V.; Petkovšek, R. Laser-induced cavitation bubbles and shock waves in water near a concave surface. Ultrason. Sonochem. 2021, 73, 105456. [Google Scholar] [CrossRef]
- Koch, M. Laser Cavitation Bubbles at Objects: Merging Numerical and Experimental Methods. Ph.D. Thesis, Georg-August-Universität Göttingen, Third Physical Institute, Göttingen, Germany, 2020. [Google Scholar]
- Koch, M.; Rosselló, J.M.; Lechner, C.; Lauterborn, W.; Eisener, J.; Mettin, R. Theory-assisted optical ray tracing to extract cavitation-bubble shapes from experiment. Exp. Fluids 2021, 62, 60. [Google Scholar] [CrossRef]
- Lechner, C.; Lauterborn, W.; Koch, M.; Mettin, R. Fast, thin jets from bubbles expanding and collapsing in extreme vicinity to a solid boundary: A numerical study. Phys. Rev. Fluids 2019, 4, 021601. [Google Scholar] [CrossRef]
- Pishchalnikov, Y.A.; Behnke-Parks, W.M.; Schmidmayer, K.; Maeda, K.; Colonius, T.; Kenny, T.W.; Laser, D.J. High-speed video microscopy and numerical modeling of bubble dynamics near a surface of urinary stone. J. Acoust. Soc. Am. 2019, 146, 516–531. [Google Scholar] [CrossRef] [PubMed]
- Voinov, O.V.; Voinov, V.V. On the process of collapse of a cavitation bubble near a wall and the formation of a cumulative jet. Sov. Phys. Dokl. 1976, 21, 133–135. [Google Scholar]
- Olaf, J. Oberflächenreinigung mit Ultraschall (Cleaning of surfaces by the use of ultrasonics). Acustica 1957, 7, 253–263. [Google Scholar]
- Gale, G.; Busnaina, A. Roles of cavitation and acoustic streaming in megasonic cleaning. Part. Sci. Technol. 1999, 17, 229–238. [Google Scholar] [CrossRef]
- Okorn-Schmidt, H.F.; Holsteyns, F.; Lippert, A.; Mui, D.; Kawaguchi, M.; Lechner, C.; Frommhold, P.E.; Nowak, T.; Reuter, F.; Banchs Piqué, M.; et al. Particle Cleaning Technologies to Meet Advanced Semiconductor Device Process Requirements. ECS J. Solid State Sci. Technol. 2014, 3, N3069–N3080. [Google Scholar] [CrossRef]
- Mason, T.J. Ultrasonic cleaning: An historical perspective. Ultrason. Sonochem. 2016, 29, 519–523. [Google Scholar] [CrossRef]
- Vlachomitrou, M.; Pelekasis, N. Numerical study of the interaction between a pulsating coated bubble and a rigid wall. Phys. Rev. Fluids 2021, 6, 013602-1–013602-33. [Google Scholar] [CrossRef]
- Ohl, C.D.; Arora, M.; Dijkink, R.; Janve, V.; Lohse, D. Surface cleaning from laser-induced cavitation bubbles. Appl. Phys. Lett. 2006, 89, 074102. [Google Scholar] [CrossRef]
- Reuter, F.; Mettin, R. Mechanisms of single bubble cleaning. Ultrason. Sonochem. 2016, 29, 550–562. [Google Scholar] [CrossRef]
- Reuter, F.; Lauterborn, S.; Mettin, R.; Lauterborn, W. Membrane cleaning with ultrasonically driven bubbles. Ultrason. Sonochem. 2017, 37, 542–560. [Google Scholar] [CrossRef]
- Kim, T.H.; Kim, H.Y. Disruptive bubble behaviour leading to microstructure damage in an ultrasonic field. J. Fluid Mech. 2014, 750, 355–371. [Google Scholar] [CrossRef]
- Kauer, M.; Belova-Magri, V.; Cairós, C.; Linka, G.; Mettin, R. High-speed imaging of ultrasound driven Cavitation bubbles in blind and through holes. Ultrason. Sonochem. 2018, 48, 39–50. [Google Scholar] [CrossRef] [PubMed]
- Karri, B.; Pillai, K.S.; Klaseboer, E.; Ohl, S.W.; Khoo, B.C. Collapsing bubble induced pumping in a viscous fluid. Sens. Actuators A Phys. 2011, 169, 151–163. [Google Scholar] [CrossRef]
- Trummler, T.; Bryngelson, S.H.; Schmidmayer, K.; Schmidt, S.J.; Colonius, T.; Adams, N.A. Near-surface dynamics of a gas bubble collapsing above a crevice. J. Fluid Mech. 2020, 899, A16. [Google Scholar] [CrossRef]
- Andrews, E.D.; Rivas, D.F.; Peters, I.R. Cavity collapse near slot geometries. J. Fluid Mech. 2020, 901, A29. [Google Scholar] [CrossRef]
- Quah, E.W.; Karri, B.; Ohl, S.W.; Klaseboer, E.; Khoo, B.C. Expansion and collapse of an initially off-centered bubble within a narrow gap and the effect of a free surface. Int. J. Multiph. Flow 2018, 99, 62–72. [Google Scholar] [CrossRef]
- Gonzalez-Avila, S.R.; van Blokland, A.C.; Zheng, Q.; Ohl, C.D. Jetting and shear stress enhancement from cavitation bubbles collapsing in a narrow gap. J. Fluid Mech. 2020, 884, A23-1–A32-23. [Google Scholar] [CrossRef]
- Li, S.; Zhang, A.M.; Han, R.; Liu, Y.Q. Experimental and numerical study on bubble-sphere interaction near a rigid wall. Phys. Fluids 2017, 29, 092102. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, F.; Zhang, Y.; Zhang, Y.; Du, X. Experimental investigations of interactions between a laser-induced cavitation bubble and a spherical particle. Exp. Therm. Fluid Sci. 2018, 98, 645–661. [Google Scholar] [CrossRef]
- Li, S.; Zhang, A.M.; Han, R.; Ma, Q. 3D full coupling model for strong interaction between a pulsating bubble and a movable sphere. J. Comput. Phys. 2019, 392, 713–731. [Google Scholar] [CrossRef]
- Zevnik, J.; Dular, M. Cavitation bubble interaction with a rigid spherical particle on a microscale. Ultrason. Sonochem. 2020, 69, 105252. [Google Scholar] [CrossRef]
- Palanker, D.; Vankov, A.; Miller, J.; Friedman, M.; Strauss, M. Prevention of tissue damage by water jet during cavitation. J. Appl. Phys. 2003, 94, 2654–2661. [Google Scholar] [CrossRef]
- Kim, D.; Kim, D. Underwater bubble collapse on a ridge-patterned structure. Phys. Fluids 2020, 32, 053312. [Google Scholar] [CrossRef]
- Kadivar, E.; el Moctar, O.; Skoda, R.; Löschner, U. Experimental study of the control of cavitation-induced erosion created by collapse of single bubbles using a micro structured riblet. Wear 2021, 486–487, 204087. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, X.; Zhang, X.; Tang, N.; Zhang, Y. Collapsing dynamics of a laser-induced cavitation bubble near the edge of a rigid wall. Ultrason. Sonochem. 2020, 67, 105157. [Google Scholar] [CrossRef]
- Senegačnik, M.; Kunimoto, K.; Yamaguchi, S.; Kimura, K.; Sakka, T.; Gregorčič, P. Dynamics of laser-induced cavitation bubble during expansion over sharp-edge geometry submerged in liquid – an inside view by diffuse illumination. Ultrason. Sonochem. 2021, 73, 105460. [Google Scholar] [CrossRef]
- Wang, Q.; Mahmud, M.; Cui, J.; Smith, W.R.; Walmsley, A.D. Numerical investigation of bubble dynamics at a corner. Phys. Fluids 2020, 32, 053306. [Google Scholar] [CrossRef]
- Koch, S.; Garen, W.; Hegedűs, F.; Neu, W.; Reuter, R.; Teubner, U. Time-resolved measurements of shock-induced cavitation bubbles in liquids. Appl. Phys. B 2012, 108, 345–351. [Google Scholar] [CrossRef]
- Garen, W.; Hegedűs, F.; Kai, Y.; Koch, S.; Meyerer, B.; Neu, W.; Teubner, U. Shock wave emission during the collapse of cavitation bubbles. Shock Waves 2016, 26, 385–394. [Google Scholar] [CrossRef]
- Fujikawa, S.; Akamatsu, T. Effects of the non-equilibrium condensation of vapour on the pressure wave produced by the collapse of a bubble in a liquid. J. Fluid Mech. 1980, 97, 481–512. [Google Scholar] [CrossRef]
- Akhatov, I.; Lindau, O.; Topolnikov, A.; Mettin, R.; Vakhitova, N.; Lauterborn, W. Collapse and rebound of a laser-induced cavitation bubble. Phys. Fluids 2001, 13, 2805–2819. [Google Scholar] [CrossRef]
- Akhatov, I.; Vakhitova, N.; Topolnikov, A.; Zakirov, K.; Wolfrum, B.; Kurz, T.; Lindau, O.; Mettin, R.; Lauterborn, W. Dynamics of laser-induced cavitation bubbles. Exp. Therm. Fluid Sci. 2002, 26, 731–737. [Google Scholar] [CrossRef]
- Gopala, V.R.; van Wachem, B.G.M. Volume of fluid methods for immiscible-fluid and free-surface flows. Chem. Eng. J. 2008, 141, 204–221. [Google Scholar] [CrossRef]
- Miller, S.; Jasak, H.; Boger, D.; Paterson, E.; Nedungadi, A. A pressure-based, compressible, two-phase flow finite volume method for underwater explosions. Comput. Fluids 2013, 87, 132–143. [Google Scholar] [CrossRef]
- Hentschel, W.; Lauterborn, W. Acoustic emission of single laser-produced cavitation bubbles and their dynamics. Appl. Sci. Res. 1982, 38, 225–230. [Google Scholar] [CrossRef]
- Brujan, E.A.; Nahen, K.; Schmidt, P.; Vogel, A. Dynamics of laser-induced cavitation bubbles near elastic boundaries: Influence of the elastic modulus. J. Fluid Mech. 2001, 433, 283–314. [Google Scholar] [CrossRef]
- Reuter, F.; Kaiser, S.A. High-speed film-thickness measurements between a collapsing cavitation bubble and a solid surface with total internal reflection shadowmetry. Phys. Fluids 2019, 31, 097108. [Google Scholar] [CrossRef]
- Lauterborn, W. Cavitation bubble dynamics—New tools for an intricate problem. Appl. Sci. Res. 1982, 38, 165–178. [Google Scholar] [CrossRef]
- Zhang, D.; Gökce, B.; Barcikowski, S. Laser synthesis and processing of colloids: Fundamentals and applications. Chem. Rev. 2017, 117, 3990–4103. [Google Scholar] [CrossRef] [PubMed]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koch, M.; Rosselló, J.M.; Lechner, C.; Lauterborn, W.; Mettin, R. Dynamics of a Laser-Induced Bubble above the Flat Top of a Solid Cylinder—Mushroom-Shaped Bubbles and the Fast Jet. Fluids 2022, 7, 2. https://doi.org/10.3390/fluids7010002
Koch M, Rosselló JM, Lechner C, Lauterborn W, Mettin R. Dynamics of a Laser-Induced Bubble above the Flat Top of a Solid Cylinder—Mushroom-Shaped Bubbles and the Fast Jet. Fluids. 2022; 7(1):2. https://doi.org/10.3390/fluids7010002
Chicago/Turabian StyleKoch, Max, Juan Manuel Rosselló, Christiane Lechner, Werner Lauterborn, and Robert Mettin. 2022. "Dynamics of a Laser-Induced Bubble above the Flat Top of a Solid Cylinder—Mushroom-Shaped Bubbles and the Fast Jet" Fluids 7, no. 1: 2. https://doi.org/10.3390/fluids7010002
APA StyleKoch, M., Rosselló, J. M., Lechner, C., Lauterborn, W., & Mettin, R. (2022). Dynamics of a Laser-Induced Bubble above the Flat Top of a Solid Cylinder—Mushroom-Shaped Bubbles and the Fast Jet. Fluids, 7(1), 2. https://doi.org/10.3390/fluids7010002






