Abstract
The sharp decline in streamflow prediction accuracy with increasing lead times remains a persistent challenge for effective water resources management and flood mitigation. In this study, we developed a coupled deep learning model for daily streamflow prediction in the Hanjiang River Basin, China. The proposed model integrates self-attention (SA), a one-dimensional convolutional neural network (1D-CNN), and bidirectional long short-term memory (BiLSTM). The model’s effectiveness was assessed during flood events, and its predictive uncertainty was quantified using kernel density estimation (KDE). The results demonstrate that the proposed model consistently outperforms baseline models across all lead times. It achieved Nash-Sutcliffe Efficiency (NSE) scores of 0.92, 0.86, and 0.79 for 1-, 3-, and 5-days, respectively, showing particular strength at these extended lead time predictions. During major flood events, the model demonstrated an enhanced capacity to capture peak magnitudes and timings. It achieved the highest NSE values of 0.924, 0.862, and 0.797 for the 1-, 3-, and 5-day forecasting horizons, respectively, thereby showcasing the strengths of integrating CNN and SA mechanisms for recognizing local hydrological patterns. Furthermore, KDE-based uncertainty analysis identified a high prediction interval coverage in different forecast periods and a relatively narrow prediction interval width, indicating the strong robustness of the proposed model. Overall, the proposed SA-CNN-BiLSTM model demonstrates significantly improved accuracy, especially for extended lead times and flood events, and provides robust uncertainty quantification, thereby offering a more reliable tool for reservoir operation and flood risk management.
1. Introduction
Accurate and timely streamflow prediction is fundamental to sustainable water resource management, underpinning critical applications ranging from short-term flood control and emergency response to mid- and long-term drought mitigation, hydropower optimization, and infrastructure planning [1,2,3]. Consequently, enhancing the reliability of streamflow forecasts remains a cornerstone of hydrological research. Over recent decades, methodologies for streamflow simulation and prediction have broadly diverged into two main paradigms: physical process-based models (PBMs) and data-driven models [4,5].
PBMs such as the Soil and Water Assessment Tool (SWAT) [6] and the Variable Infiltration Capacity (VIC) [7] model employ extensive mathematical equations to describe physical processes, allowing a clear explanation of model behavior and providing strong physical interpretability [8]. However, these models require comprehensive knowledge—including physical, biological, and socioeconomic aspects—to properly define model structures, and any deficiencies in this information can amplify uncertainty and error propagation [9]. Additionally, the increasing complexity of streamflow generation mechanisms—driven by rapid urbanization, land-use alterations, and climate change—has further constrained the practical application of PBMs in certain contexts [10,11,12]. In contrast, the emergence of data-driven approaches, particularly deep learning (DL), has revolutionized hydrological modeling by effectively capturing nonlinear relationships in complex environmental systems without explicit physical assumptions [13,14]. Among these, Long Short-Term Memory (LSTM) networks [15,16], convolutional neural networks (CNNs) [17], and transformer-based models [18] have demonstrated superior performance in handling hydrological data. Unlike traditional statistical models, DL methods excel at learning intricate nonlinear patterns from observational data and offer an alternative approach for streamflow prediction, though they typically lack the ability to provide physical information about hydrological processes [19].
Despite the successes of DL in hydrological modeling, several persistent challenges impede their broader operational adoption and reliability. Firstly, a significant concern is the degradation of predictive accuracy over longer forecasting horizons (i.e., increasing lead times), largely attributable to the accumulation of errors [20]. This issue is often exacerbated during extreme events, such as floods, where models may underperform due to imbalanced data distribution and insufficient learning of extreme hydrological dynamics [21]. While techniques like LSTM aim to capture temporal dependencies and mitigate error propagation, and hybrid models (e.g., CNN-LSTM [22,23], SA-BiLSTM [24]) show promise by combining architectural strengths for enhanced feature extraction, maintaining robust performance at extended lead times remains a key objective. Secondly, the “black-box” nature of many DL models limits their interpretability, hindering the understanding of how model decisions are made and which hydrological drivers are most influential [25]. Although post-hoc explanation methods such as Shapley Additive Explanations (SHAP) [26,27] and Local Interpretable Model-agnostic Explanations (LIME) [28] have been applied to uncover mechanisms captured by deep learning models in hydrology, a systematic understanding of basin-specific streamflow drivers across different temporal scales remains underdeveloped. Thirdly, the majority of DL-based streamflow studies focus on deterministic point predictions, often neglecting the crucial aspect of uncertainty quantification [29]. Reliable prediction intervals are essential for risk-informed decision-making, yet methods like kernel density estimation (KDE) for constructing these intervals face challenges, notably the critical selection of optimal bandwidth, which is rarely addressed systematically in hydrological contexts.
To address the critical challenges of maintaining predictive accuracy at extended lead times and providing reliable uncertainty quantification, this study proposed an integrated deep learning framework. This framework uniquely combined advanced architectural designs and adaptive uncertainty methods for robust daily streamflow prediction in the Hanjiang River Basin, China. The main contributions of this study are as follows: (1) We propose a novel hybrid architecture, SA-CNN-BiLSTM, which synergistically combines Self-Attention (SA), a 1D Convolutional Neural Network (1D-CNN), and a Bidirectional Long Short-Term Memory (BiLSTM) network. This design aims to enhance multiscale feature extraction from hydrometeorological time series and improve predictive accuracy, particularly over extended forecasting horizons, by effectively capturing both local patterns and long-range dependencies. (2) We implement a robust uncertainty quantification approach based on KDE with an adaptive bandwidth selection strategy, aiming to generate reliable and informative prediction intervals. The efficacy of the proposed model is rigorously evaluated against several baseline models, with a specific focus on its performance during flood events and its ability to provide well-calibrated uncertainty estimates.
2. Methodology
2.1. Study Area
The Hanjiang River originates from Shangfeng in Zijin County, Guangdong Province, and is the second largest river basin in Guangdong outside the Pearl River Basin. The upper reaches of the Hanjiang River are formed by the confluence of the Meijiang River and the Ting River, after which the main stream of the Hanjiang River flows into the Hanjiang River delta river network before ultimately discharging into the South China Sea. The main stream of the Hanjiang River is 470 km long and drains a total area of approximately 30,100 km2. The basin is distributed across three provinces: Guangdong (59.4%), Fujian (40.1%), and Jiangxi (0.5%).
The Hanjiang River Basin, geographically located in eastern Guangdong and southwestern Fujian, Hanjiang River Basin, is situated within 115.22–117.15° E longitude and 23.28–26.08° N latitude (Figure 1). The region experiences a subtropical monsoon climate, characterized by a mild climate, abundant precipitation, and high vegetation coverage. The multi-year mean temperature ranges from 20 °C to 21.5 °C, and the mean annual precipitation is approximately 1620 mm. However, influenced by the topography, precipitation exhibits marked spatial variability and uneven seasonal distribution. This variability leads to substantial streamflow fluctuations between wet and dry seasons, increasing the risk of flood events and posing a significant challenge to water resource management. Currently, the water management infrastructure in the Hanjiang River Basin includes four major reservoirs: the Cotton Beach Reservoir, with a capacity of approximately 1 billion m3, and three reservoirs on Meijiang River tributaries with a combined capacity of approximately 200 million m3. However, the effective operation and dispatching of these reservoirs depend on the availability of accurate runoff forecasts.
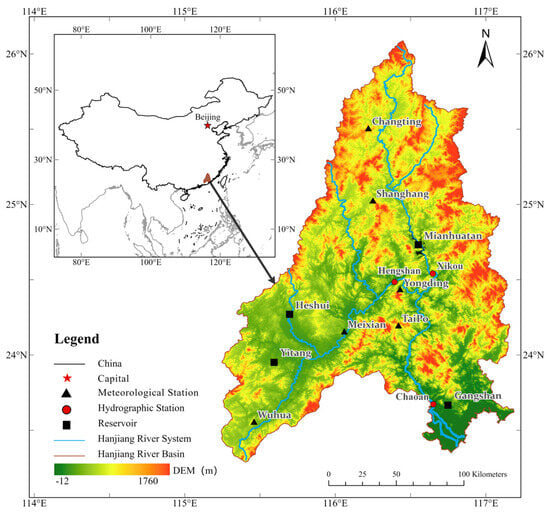
Figure 1.
The location and DEM of the Hanjiang River Basin.
2.2. Dataset
Daily streamflow data were sourced from the Hanjiang River Basin Management Bureau, encompassing three hydrological stations: Chaoan, Hengshan, and Xikou. Basic information on these stations is summarized in Table 1. These hydrological records span from 2001 to 2010, providing a reliable foundation for model development due to their high data quality and temporal continuity. Meteorological data were obtained from the China Meteorological Data Network (CMDN) daily dataset V3 [30], which encompasses observations from 699 national benchmark and basic stations from 1951 to 2010. Finally, six meteorological stations within the basin—Changting, Shanghang, Yongding, Dabu, Meixian, and Wuhua—were selected (Table 2). To address missing values, the cubic spline interpolation method was applied. Soil water content data were retrieved from the ERA5-Land reanalysis dataset provided by the European Centre for Medium-Range Weather Forecasts (ECMWF). This dataset provides hourly estimations for four soil layers: 0–7 cm, 7–28 cm, 28–100 cm, and 100–289 cm at a spatial resolution of 0.1°. Subsequently, catchment-level averages for the upstream hydrometeorological variables were derived using the Thiessen polygon method.

Table 1.
Basic information of major streamflow control stations of Hanjiang River.

Table 2.
Basic information of meteorological stations in Hanjiang River Basin.
The final dataset compiled for the model comprises streamflow at the Chaoan station and 21 hydrometeorological factors and upstream streamflow (detailed in Table 3). In total, this dataset consists of 3532 daily records, covering the period from 1 May 2001 to 31 December 2010.

Table 3.
Streamflow prediction dataset information.
To improve model efficiency and reduce multicollinearity, feature selection was conducted using the Maximum Information Coefficient (MIC) method [31]. This process yielded nine predictors: temperature, air pressure, precipitation, evapotranspiration, relative humidity, soil water content, and upstream streamflow. These variables, detailed in Table 4, demonstrated strong associations with the Chaoan station streamflow, with precipitation, soil water content, and upstream streamflow exhibiting particularly high MIC values—underscoring their predictive relevance. Further details regarding the MIC calculation and selection process are provided in the Supplementary Materials.

Table 4.
Results of feature screening for streamflow prediction models.
2.3. Deep Learning Models
In this study, the baseline models were selected from commonly used streamflow prediction models, including Multilayer Perceptron (MLP), one-dimensional CNN (1D-CNN, hereinafter referred to as CNN), gated recurrent unit (GRU), BiLSTM, and SA mechanisms.
2.3.1. MLP
MLP is a classic feed-forward neural network architecture composed of an input layer, one or more hidden layers with nonlinear activation functions, and an output layer [32,33]. Each layer comprises interconnected neurons through which data propagate unidirectionally, from input to output. The network is trained using the backpropagation algorithm and is well-suited for capturing complex nonlinear relationships in data. In hydrology, MLPs have been extensively employed for daily streamflow forecasting and have frequently demonstrated superior performance compared to traditional statistical models [34,35,36]. In this study, an MLP with several hidden layers was implemented to model the nonlinear relationships between hydroclimatic inputs (e.g., precipitation and temperature) and daily streamflow.
2.3.2. CNN
Unlike conventional two-dimensional convolutional neural networks designed for image processing, the 1D-CNNs used in this study are capable of processing one-dimensional vector input, enabling efficient feature extraction and temporal pattern extraction. Due to their simplified structures and fewer parameters, 1D-CNNs can employ larger convolutional kernels to achieve broader receptive fields while maintaining a relatively small number of network parameters [37]. Specifically, 1D-CNNs have been demonstrated as effective models for daily runoff prediction [38]. The mathematical formulation of the 1D-CNN is given by the following:
where yi denotes the i-th element of the output sequence; xi+m is the corresponding input element; f is the activation function; wm is the m-th weight in the convolution kernel of size k, and b is the bias term. Additionally, multiple convolution kernels can be used to extract a variety of features from the input sequence.
2.3.3. GRU and BiLSTM
Traditional neural networks struggle to capture long-term dependencies within sequential data. To address this, an LSTM network was developed, offering enhanced capabilities for modeling such temporal relationships [39]. Furthermore, simultaneously analyzing both forward and backward temporal patterns within sequence data is an effective strategy for enhancing model performance in time series prediction. Unlike conventional LSTMs, BiLSTM comprises distinct forward and backward LSTMs, allowing for bidirectional flow of sequence information. This bidirectional processing enables simultaneous processing of sequence information in both directions, leading to a more comprehensive capture and recognition of temporal dependencies within the data. Therefore, BiLSTM was used to simulate streamflow in this study. Compared with LSTM, GRU is faster to train and less prone to overfitting due to its simpler structure with fewer parameters, but it may be less effective than LSTM at capturing long-term dependencies in complex sequences.
2.3.4. SA
The attention mechanism, inspired by the human cognitive ability for selective focus, assigns differential weights to input data, thereby prioritizing more salient information. In time series forecasting, such mechanisms have led to significant improvements in both model performance and generalization capabilities [40]. Conventional attention mechanisms typically operate on intermediate hidden states or outputs when applied within neural networks, which may limit their capacity to capture global contextual information effectively. In contrast, the SA mechanism directly processes the entire input sequence by calculating pairwise importance scores between all elements, thereby effectively capturing long-term dependencies without relying on sequential processing. In the self-attention framework, the input vector X is projected into three representations: queries (Q), keys (K), and values (V), using shared weight matrices Wq, Wk, and Wv, respectively. The process of SA can be summarized as follows:
where dk is the dimensionality of the key vectors, used for scaling to stabilize gradients. This formulation allows the model to capture complex dependencies and dynamically adjust the importance of different time steps in the input sequence.
2.3.5. Coupled Model
As the forecasting horizon extends, the predictive performance of standalone models may be insufficient for practical application. To address this limitation, a hybrid SA-CNN-BiLSTM model was proposed for multi-step daily streamflow prediction. Within this hybrid architecture, the 1D-CNN is first employed to extract local patterns from the time series input. These patterns are then processed by the SA to assess the relative importance of different time steps for the prediction task. Finally, the BiLSTM captures long-term temporal dependencies from the SA output. The output from the BiLSTM layer is subsequently fed into a fully connected layer, mapping the learned representations to the final multi-step streamflow predictions.
2.3.6. Training and Hyperparameter Optimization
In this study, the dataset was divided into training, validation, and test sets sequentially by time at a ratio of 7:1:2, prior to Z-score normalization. The input sequence length for the BiLSTM model was fixed at 10 steps, while the output sequence length corresponded to the selected prediction horizons. Each model was optimized using the AdamW optimizer with a mean-squared error (MSE) loss function, and the Rectified Linear Unit was employed as the activation function. AdamW [41] is a variant of the Adam optimization algorithm that improves weight decay handling of Adam, thereby enhancing momentum stability and convergence speed [42]. The initial learning rate was set to 0.001, while the training epoch was set to 50 to ensure sufficient model convergence. Additionally, L1 regularization was incorporated into the loss function to mitigate overfitting.
To obtain the optimal model, Bayesian optimization (BO) was employed to search for the best hyperparameter combination according to predefined ranges [43]. Further details on the BO method and hyperparameter search space are provided in the Supplementary Materials. Specifically, this study utilized a BO implementation known as Optuna [44], an open-source automated hyperparameter optimization framework based on the Tree-structured Parzen Estimator (TPE) algorithm. TPE efficiently explores the hyperparameter space by modeling conditional probabilities. Additionally, Optuna incorporates an asynchronous successive halving algorithm for pruning, which terminates unpromising trials early, thereby focusing computational resources on more promising hyperparameter combinations [44]. The optimization process aimed to maximize the Nash-Sutcliffe Efficiency (NSE) on the validation set and consisted of 500 trials, with pruning initiated after the first 10 trials.
2.4. Model Evaluation Method
In this study, model performance on the test set was evaluated using a combination of three commonly applied metrics: NSE, root-mean-square error (RMSE), and mean-absolute error (MAE). NSE measures the overall consistency between model predictions and observations, with values closer to 1 indicating a higher accuracy. RMSE and MAE quantify the average degree of discrepancy between predicted and observed values. While NSE is bounded above by 1, RMSE and MAE are unbounded but provide intuitive measures of error magnitude—lower values indicate better model performance. Furthermore, RMSE is more sensitive to large errors due to its squared term, whereas MAE provides a linear measure of average absolute error. In addition to these metrics, the Diebold-Mariano (DM) test was then employed to determine whether the performance differences between models are statistically significant. The DM test is a non-parametric statistical hypothesis test designed to compare the forecasting performance of two time series forecasting models, proposed in Diebold and Mariano [45] 2002. Additional details regarding the formulas for metrics and the DM test are provided in the Supplementary Materials.
2.5. Flood Event Recognition
Accurate prediction of peak streamflow is crucial for effective flood forecasting and mitigation. To assess the proposed model’s effectiveness in flood prediction, this study employed the Peak Over Threshold (POT) method to identify flood events during the test period. The model’s performance was then specifically assessed on these sequences. In contrast to the widely used method Annual Maximum series approach [46], the POT method was more robust for the relatively short duration of the test period, as it allows for the identification of multiple flood events within a given timeframe. Additionally, it should be noted that, in this context, the term “flood” refers to peak streamflow events identified by the POT method and does not necessarily correspond to events causing catastrophic or destructive impacts in a socio-economic sense.
2.6. Prediction Interval Estimation
Methods for estimating probability density functions (PDFs) are broadly classified into parametric and non-parametric. Among these methods, KDE is a widely used non-parametric technique. A key advantage of non-parametric approaches is their suitability when the underlying data distribution is unknown, as they avoid potential biases stemming from incorrect distributional assumptions [47]. In this study, KDE was utilized to construct prediction intervals (PIs) for streamflow forecast errors at designated confidence levels with a Gaussian kernel function. A critical parameter in KDE is the bandwidth, which influences the smoothness of the density estimate. Optimal bandwidths for each horizon were determined experimentally using the training set, yielding values of 13.565 (1-day), 15.272 (3-day), and 16.686 (5-day). Furthermore, the Prediction Interval Coverage Probability (PICP) and the Prediction Interval Normalized Average Width (PINAW) metrics were then used to quantitatively evaluate the prediction interval. More details can be found in the Supplementary Materials.
2.7. Shapley Additive Explanations
SHAP is a model-agnostic interpretability framework proposed by Lundberg and Lee [26] in 2017, grounded in cooperative game theory. It provides a consistent and theoretically sound method for quantifying the contribution of each input feature to the model’s predictions. In SHAP, each feature is treated as a “player” in a game, and its contribution is measured as its SHAP value, reflecting the change it causes in the predicted output when added to different combinations of features. A positive SHAP value indicates a positive influence on the prediction, while a negative value indicates a negative effect. Furthermore, the absolute magnitude of a feature’s SHAP value reflects its importance in the model, with larger values indicating greater influence [48].
3. Results and Discussion
3.1. Model Performance Evaluation
Figure 2, Figure 3 and Figure 4 illustrate the predictive performance of different models at the Chaoan station over 1-, 3-, and 5-day forecasting horizons, respectively. At the 1-day lead time, most models achieved an NSE higher than 0.7, with MAE below 200 m3 s−1 and RMSE below 300 m3 s−1. The integration of advanced components such as BiLSTM, SA, and CNN consistently enhanced model performance. Among all models, the SA-CNN-BiLSTM model demonstrated superior performance, achieving the highest NSE of 0.92, with the lowest MAE and RMSE.
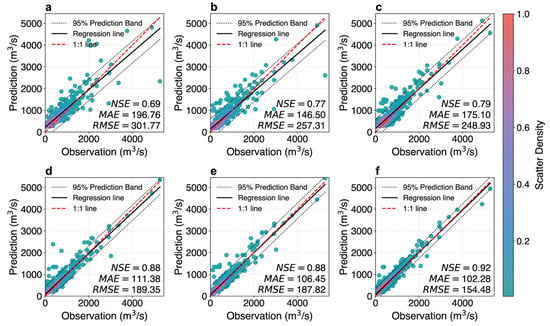
Figure 2.
Scatter density plots of comparisons between predicted and observed streamflow across different models at a 1-day forecast period: (a–f) represent MLP, GRU, BiLSTM, SA-BiLSTM, CNN-BiLSTM, and SA-CNN-BiLSTM, respectively.
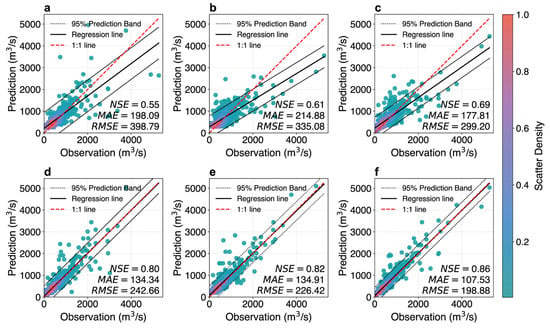
Figure 3.
Scatter density plots of comparisons between predicted and observed discharge across different models at a 3-day forecast period: (a–f) represent MLP, GRU, BiLSTM, SA-BiLSTM, CNN-BiLSTM, and SA-CNN-BiLSTM, respectively.
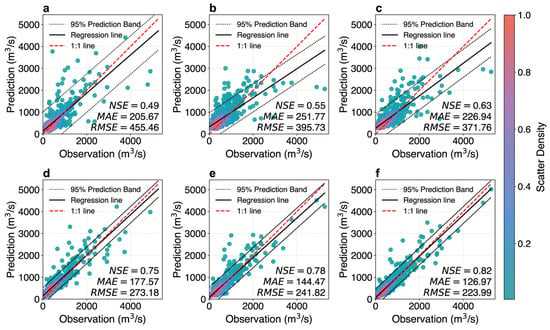
Figure 4.
Scatter density plots of comparisons between predicted and observed discharge across different models at a 5-day forecast period: (a–f) represent MLP, GRU, BiLSTM, SA-BiLSTM, CNN-BiLSTM, and SA-CNN-BiLSTM, respectively.
As the forecasting horizon increased, all models experienced a noticeable decline in performance. Specifically, benchmark models exhibited NSE reductions ranging from 6.82% to 20.77% when the lead time increased from 1 day to 3 days, while the SA-CNN-BiLSTM model showed a comparatively smaller decrease of 6.52%. Similarly, when the lead time increased from 3 days to 5 days, NSE for benchmarks decreased by 4.88% to 10.91%, compared to a more modest decline of 4.65% for the proposed model. These results indicate that incorporating either SA or CNN can efficiently improve the ability to maintain temporal information, thereby mitigating the performance degradation of BiLSTM over longer forecasting horizons. Moreover, the combination of SA and 1D-CNN yielded additional gains in predictive accuracy.
To statistically validate these performance differences, the DM test was employed. As shown in Table 5, the SA-CNN-BiLSTM model significantly outperformed all baseline models at all forecast horizons (1-, 3-, and 5-day), with p-values < 0.05 indicating statistical significance. Positive DM values further confirm that the proposed model consistently yielded more accurate predictions than its counterparts.

Table 5.
DM test results comparing the proposed model and other benchmark models across three lead times at the Chaoan station.
3.2. Flood Event Performance Analysis
Deep learning models such as LSTM are well-suited for general streamflow prediction but often struggle with extreme events, which pose challenges for flood control applications. Therefore, all models were explicitly evaluated during flood events. The four largest flood peaks were identified by the POT method within the test period: 2 June 2010; 13 July 2010; 21 July 2010; and 29 September 2010. These peaks occurred within three separate flood events, with the second event (from approximately 9 July to 25 July 2010) exhibiting a bimodal structure.
Figure 5, Figure 6 and Figure 7 present the streamflow prediction results for all models across the different forecasting horizons, focusing specifically on these three flood events. The results show that all models manage to capture these four peaks at a 1-day lead time. However, the performance of the standalone models—MLP, GRU, and BiLSTM—declined significantly in terms of accuracy. The MLP model produced significantly skewed predictions, while GRU and BiLSTM exhibited noticeable discrepancies compared to the observations. In contrast, the coupled models demonstrated superior performance in capturing streamflow dynamics during high-flow periods, even as the forecasting horizon extended to 5 days. Among these models, the SA-CNN-BiLSTM model consistently outperformed the others by effectively integrating the strengths of SA and CNN. Specifically, the SA-CNN-BiLSTM model achieved the highest prediction accuracy during the three flood events, with average NSE values of 0.924, 0.862, and 0.797 for the 1-, 3-, and 5-day forecasting horizons, respectively. These results highlight the model’s robustness in forecasting extreme hydrological events and underscore its potential value for operational flood prediction.
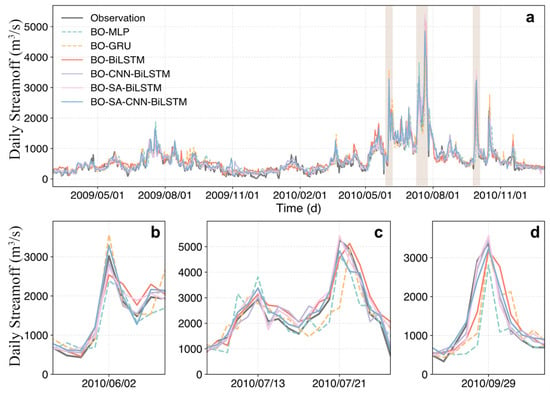
Figure 5.
Comparison of streamflow predictions during the test period (a) and three flood events (b–d) between different models under a 1-day lead time. The shaded areas represent the three flood events identified by the POT method, corresponding to subplots (b), (c), and (d), respectively.
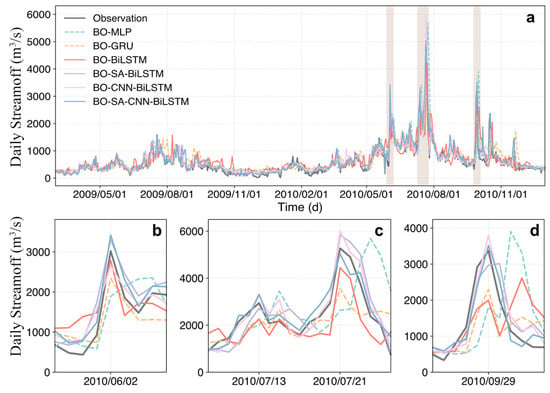
Figure 6.
Comparison of streamflow predictions during the test period (a) and three flood events (b–d) between different models under a 3-day lead time. The shaded areas represent the three flood events identified by the POT method, corresponding to subplots (b), (c), and (d), respectively.
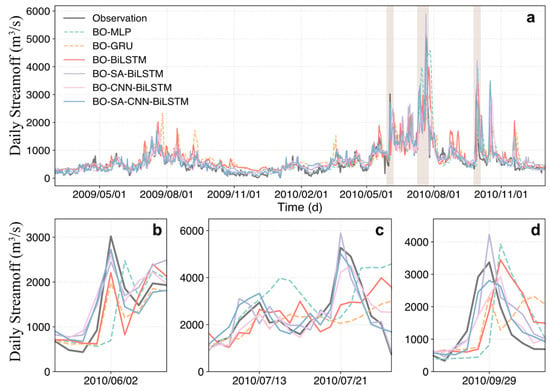
Figure 7.
Comparison of streamflow predictions during the test period (a) and three flood events (b–d) between different models under a 5-day lead time. The shaded areas represent the three flood events identified by the POT method, corresponding to subplots (b), (c), and (d), respectively.
3.3. Interval Prediction of Daily Streamflow for Different Lead Times
The SA-CNN-BiLSTM model’s capability in generating daily streamflow intervals was evaluated across multiple confidence intervals (CIs) (80%, 85%, 90%, 95%) and forecast horizons (1-day, 3-day, 5-day) in Table 6. As expected, both PICP and PINAW increase with higher confidence levels and longer forecast periods. The results consistently highlight the model’s effectiveness, with the key indicator of reliability, PICP, consistently exceeding the corresponding nominal confidence levels (NCLs) in all tested scenarios. Notably, even under the stringent 95% NCL, the model achieved empirical coverage rates of 96.13%, 97.17%, and 96.57% for 1-, 3-, and 5-day forecasts, respectively. This consistent performance (PICP > NCL) suggests that the generated PIs are highly reliable and slightly conservative, ensuring that the observed streamflow is captured within the predicted bounds more often than nominally required. Additionally, PINAW increases with both higher confidence levels (e.g., from 10.33% at 80% CI to 28.24% at 95% CI for a 5-day forecast) and longer forecast horizons (e.g., from 13.58% at 1-day to 18.39% at 5-day under 90% CI), reflecting the expected growth in predictive uncertainty. Importantly, PINAW remains within reasonable bounds, indicating that the intervals are informative without being overly wide. For instance, a 13.58% PINAW for the 90% CI at the 1-day forecast indicates a relatively tight bound, underscoring the model’s ability to balance high reliability with practical precision.

Table 6.
Performance evaluation of daily streamflow interval predictions.
Moreover, at lower confidence levels (e.g., 80%), the model maintains relatively narrow intervals (e.g., 8.54% PINAW for the 1-day lead time) while still achieving reasonable coverage (PICP = 82.71%), suggesting good calibration. The increasing PINAW across the forecast horizons further confirms that the model appropriately represents the growing uncertainty over time. In summary, the model demonstrates well-calibrated and adaptive uncertainty quantification, maintaining a strong trade-off between interval sharpness (PINAW) and reliability (PICP) across different settings.
Figure 8 illustrates the error cumulative distribution functions (CDFs) for each horizon and highlights the derivation of the 90% confidence interval as an example. Specifically, for the 90% confidence level, the derived error intervals were [−323.22, 296.14] m3/s (1-day), [−381.49, 333.33] m3/s (3-day), and [−440.75, 398.34] m3/s (5-day). These results show a broadening of the error range with increasing lead time, reflected in the PINAW values. The dynamic behavior of the 95% PIs, which adapt to flow conditions by widening during high-flow and high-variability periods (e.g., mid-2010 flood events) and narrowing during stable, low-flow periods. This heteroscedastic behavior is consistent with hydrological expectations. In summary, the proposed model not only delivers accurate streamflow predictions but also generates reliable and context-aware uncertainty intervals, making it a valuable tool for operational hydrological forecasting and risk-informed water resource management at Chaoan Station. The corresponding CDFs of the prediction errors were calculated via integration to determine the upper and lower bounds corresponding to the target confidence levels, and the complete daily streamflow prediction intervals at the 90% confidence were then reconstructed in Figure 9.
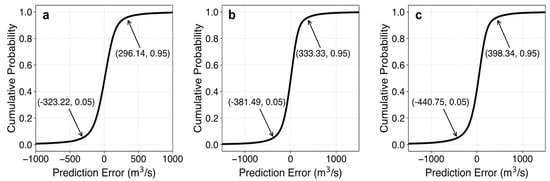
Figure 8.
CDF curves of prediction errors under different lead times (“α” = 90%): (a) 1 day, (b) 3 days, and (c) 5 days.
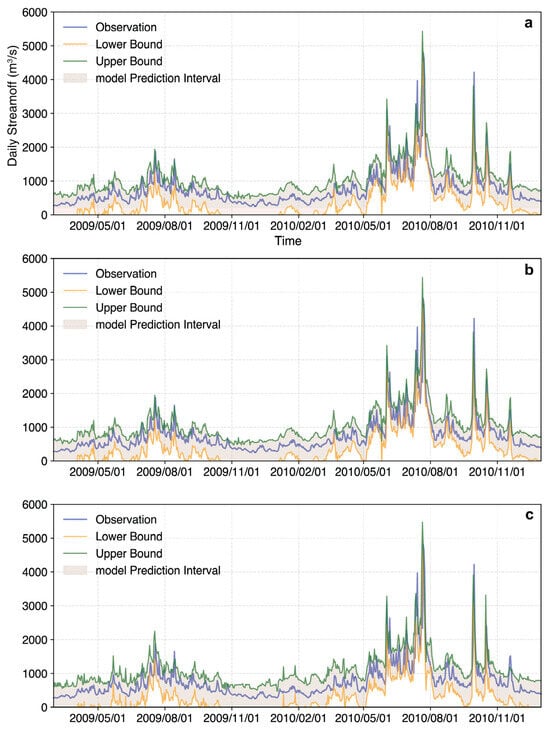
Figure 9.
Daily streamflow prediction interval of the Chaoan Station with forecast periods of 1d (a), 3d (b), and 5d (c). (“α” = 90%).
3.4. Feature Importance
To enhance model interpretability, the SHAP method was employed to quantify the relative importance of each feature for the 1-day forecasting period. Figure 10 reveals that streamflow on the previous day at Hengshan Station (RHS, 1D) and Chaoan Station (RCA, 1D) exerts the most significant influence on streamflow at the Chaoan Station. Other key features included precipitation (DP1D), streamflow at Xikou and Chaoan stations two days prior (RCA, 2D; RXK, 2D), and soil water content (SMC1D). Generally, antecedent streamflow exhibits greater importance than precipitation. Additionally, variables such as minimum daily surface temperature (e.g., ST2D), average daily air pressure (e.g., AP2D), and evapotranspiration (e.g., ET1D) in the previous period also have a measurable influence on streamflow predictions. Notably, variables temporally closer to the prediction time do not necessarily have a stronger influence on the forecast, suggesting that temporal proximity is not the sole determinant of feature importance in the model.
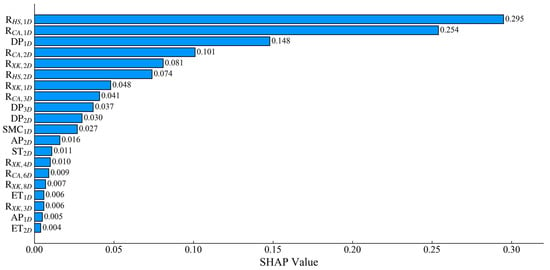
Figure 10.
Feature importance ranked by SHAP at a 1-day lead time (the number in the variable subscript indicates the lead time).
3.5. Research Gaps and Future Work
Despite the promising results, several limitations offer opportunities for further research. First, potential impacts of human activities (e.g., land use changes, reservoir operations) or subsurface hydrological conditions on streamflow are not explicitly modeled in this study. Incorporating broader datasets encompassing these factors may further enhance prediction accuracy and offer more comprehensive insights into predicting streamflow dynamics. Second, the model’s spatial generalization remains limited, as it primarily captures temporal dependencies through a data-driven lens. Integrating spatially explicit architectures, such as graph neural networks or GANs, could better leverage topological information across river networks and meteorological stations. Additionally, hybrid modeling approaches that integrate deep learning components with process-based hydrological models may improve model interpretability and promote physically consistent predictions. Such hybrid frameworks could bridge the gap between data-driven flexibility and process-based transparency, yielding more reliable tools for operational hydrological forecasting.
4. Conclusions
This study established an integrated SA-CNN-BiLSTM framework for daily streamflow prediction, demonstrating significant advancements in both deterministic accuracy and uncertainty quantification in the Hanjiang River Basin. The key findings and conclusions are summarized as follows:
The proposed model consistently achieved superior deterministic prediction performance across 1-, 3-, and 5-day prediction horizons, notably outperforming all benchmark models. This superior performance was statistically validated by the DM test, which confirmed the significant outperformance of our proposed model across all tested horizons (p < 0.05). Its advantage was particularly pronounced for longer horizons, achieving NSE values of 0.92, 0.86, and 0.79 for 1-, 3-, and 5-day lead times, respectively. Beyond general performance, the model exhibited exceptional robustness during major flood events, consistently achieving high average NSE values of 0.924, 0.862, and 0.797 for 1-, 3-, and 5-day forecasts during flood periods, respectively. These results underscore its critical potential for operational flood prediction and early warning systems, an area where traditional deep learning models often struggle due to imbalanced data.
Furthermore, the successful implementation of an adaptive KDE approach enabled the generation of highly reliable and informative prediction intervals. The proposed model consistently achieved PICP that exceeded nominal confidence levels (e.g., 96.13% at 95% NCL for 1-day forecast) while maintaining a relatively narrow PINAW, demonstrating a robust performance. Additionally, the application of SHAP for feature importance analysis further enhanced the interpretability of our integrated model. The results revealed that streamflow from upstream stations and precipitation from the previous day exert the most important effect on the prediction process.
In conclusion, the SA-CNN-BiLSTM framework significantly improves the performance of short-to-medium-range streamflow forecasting (up to 5 days), while effectively quantifying predictive uncertainty. These advancements provide valuable tools for hydrological forecasting and decision-making in water resources management, particularly in flood-prone regions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/hydrology12070168/s1, Figure S1: Heat map of maximum information coefficient between different variables; Table S1: Hyperparameter search range for each streamflow prediction model. References [31,45,47,49,50,51,52,53,54,55] are cited in the Supplementary Materials.
Author Contributions
Conceptualization, H.H. and X.C.; funding acquisition, X.C.; methodology, J.H., J.C. and X.C.; software, J.H. and J.C.; validation, J.C.; visualization, H.H.; writing—original draft, J.H. and H.H.; writing—review and editing, X.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (42375165) and the National Key Research and Development Program of China (2023YFF0805501). We thank, for the technical support, the National Large Scientific and Technological Infrastructure “Earth System Numerical Simulation Facility” (https://cstr.cn/31134.02.EL).
Data Availability Statement
Daily meteorological data were from the China Meteorological Data Service Center (http://data.cma.cn/en, accessed on 22 May 2024). Daily streamflow data were from the Hanjiang River Basin Management Bureau through a project collaboration. Soil moisture data were from the European Centre for Medium-Range Weather Forecasts ReAnalysis 5-Land (ERA5-Land) reanalysis dataset (https://cds.climate.copernicus.eu/datasets/reanalysis-era5-land-timeseries, accessed on 22 May 2024).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Granata, F.; Di Nunno, F. Neuroforecasting of Daily Streamflows in the UK for Short- and Medium-Term Horizons: A Novel Insight. J. Hydrol. 2023, 624, 22. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Bari, M.A.; Kabir, A.; Hasan, M.M.; Woldemeskel, F.M.; Gamage, N.; Sunter, P.D.; Zhang, X.S.; Robertson, D.E.; Bennett, J.C.; et al. Development of a National 7-Day Ensemble Streamflow Forecasting Service for Australia. Hydrol. Earth Syst. Sci. 2022, 26, 4801–4821. [Google Scholar] [CrossRef]
- Matrenin, P.; Safaraliev, M.; Dmitriev, S.; Kokin, S.; Eshchanov, B.; Rusina, A. Adaptive Ensemble Models for Medium-Term Forecasting of Water Inflow When Planning Electricity Generation under Climate Change. Energy Rep. 2022, 8, 439–447. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, Y.; Zhang, C.; Wang, B. Are Hybrid Models Integrated with Data Preprocessing Techniques Suitable for Monthly Streamflow Forecasting? Some Experiment Evidences. J. Hydrol. 2015, 530, 137–152. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–Runoff Modelling Using Long Short-Term Memory (Lstm) Networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A Simple Hydrologically Based Model of Land Surface Water and Energy Fluxes for General Circulation Models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An Overview of Current Applications, Challenges, and Future Trends in Distributed Process-Based Models in Hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef]
- Shen, C.P.; Appling, A.P.; Gentine, P.; Bandai, T.; Gupta, H.; Tartakovsky, A.; Baity-Jesi, M.; Fenicia, F.; Kifer, D.; Li, L.; et al. Differentiable Modelling to Unify Machine Learning and Physical Models for Geosciences. Nat. Rev. Earth Environ. 2018, 4, 552–567. [Google Scholar] [CrossRef]
- Freire, P.K.D.M.; Santos, C.A.G.; da Silva, G.B.L. Analysis of the Use of Discrete Wavelet Transforms Coupled with Ann for Short-Term Streamflow Forecasting. Appl. Soft Comput. 2019, 80, 494–505. [Google Scholar] [CrossRef]
- Dehghani, A.; Moazam, H.M.Z.H.; Mortazavizadeh, F.; Ranjbar, V.; Mirzaei, M.; Mortezavi, S.; Ng, J.L.; Dehghani, A. Comparative Evaluation of LSTM, CNN, and ConvLSTMfor Hourly Short-Term Streamflow Forecasting Using Deep Learning Approaches. Ecol. Inform. 2023, 75, 12. [Google Scholar] [CrossRef]
- Wagena, M.B.; Goering, D.; Collick, A.S.; Bock, E.; Fuka, D.R.; Buda, A.; Easton, Z.M. Comparison of Short-Term Streamflow Forecasting Using Stochastic Time Series, Neural Networks, Process-Based, and Bayesian Models. Environ. Model. Softw. 2020, 126, 10. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Niu, J.; Sun, Y.Q.; Liu, Q.; Li, S.; Li, P.; Sun, L.Q.; Li, Q.L. Study on Streamflow Response to Land Use Change over the Upper Reaches of Zhanghe Reservoir in the Yangtze River Basin. Geosci. Lett. 2020, 7, 12. [Google Scholar] [CrossRef]
- Mohammed Ji, B.G. Streamflow Modeling under the Impact of Climate Change. (Case Study of Dabus River Sub-Basin, Ethiopia). Topology 2020, 12, 7. [Google Scholar]
- Williams, A.P.; Livneh, B.; McKinnon, K.A.; Hansen, W.D.; Mankin, J.S.; Cook, B.I.; Smerdon, J.E.; Varuolo-Clarke, A.M.; Bjarke, N.R.; Juang, C.S.; et al. Growing Impact of Wildfire on Western Us Water Supply. Proc. Natl. Acad. Sci. USA 2022, 119, 8. [Google Scholar] [CrossRef]
- Huang, H.; Feng, G.; Cao, Y.; Feng, G.; Dai, Z.; Tian, P.; Wei, J.; Cai, X. Simulation and Driving Factor Analysis of Satellite-Observed Terrestrial Water Storage Anomaly in the Pearl River Basin Using Deep Learning. Remote Sens. 2023, 15, 3983. [Google Scholar] [CrossRef]
- Ahmed, Y.; Al-Faraj, F.; Scholz, M.; Soliman, A. Assessment of Upstream Human Intervention Coupled with Climate Change Impact for a Transboundary River Flow Regime: Nile River Basin. Water Resour. Manag. 2019, 33, 2485–2500. [Google Scholar] [CrossRef]
- Yin, H.; Guo, Z.; Zhang, X.; Chen, J.; Zhang, Y. Rr-Former: Rainfall-Runoff Modeling Based on Transformer. J. Hydrol. 2022, 609, 127781. [Google Scholar] [CrossRef]
- Awchi, T.A. River Discharges Forecasting in Northern Iraq Using Different Ann Techniques. Water Resour. Manag. 2014, 28, 801–814. [Google Scholar] [CrossRef]
- Fidal, J.; Kjeldsen, T.R. Accounting for Soil Moisture in Rainfall-Runoff modelling of Urban Areas. J. Hydrol. 2020, 589, 125122. [Google Scholar] [CrossRef]
- Malakoutian, M.M.A.; Samaei, S.Y.; Khaksar, M.; Malakoutian, Y. A Prediction of Future Flows of Ephemeral Rivers by Using Stochastic Modeling (Ar Autoregressive Modeling). Sustain. Oper. Comput. 2022, 3, 330–335. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Krebs, P. Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Ghimire, S.; Yaseen, Z.M.; Farooque, A.A.; Deo, R.C.; Zhang, J.; Tao, X. Streamflow Prediction Using an Integrated Methodology Based on Convolutional Neural Network and Long Short-Term Memory Networks. Sci. Rep. 2021, 11, 17497. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Chen, Y.; Liu, J. Application of a New Hybrid Deep Learning Model That Considers Temporal and Feature Dependencies in Rainfall–Runoff Simulation. Remote Sens. 2023, 15, 1395. [Google Scholar] [CrossRef]
- Ghaith, M.; Siam, A.; Li, Z.; El-Dakhakhni, W. Hybrid Hydrological Data-Driven Approach for Daily Streamflow Forecasting. J. Hydrol. Eng. 2020, 25, 9. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 10. [Google Scholar]
- Zhao, Z.; Huang, H.; Wang, J.; Feng, G.; Li, L.; Sun, T.; Li, Y.; Wei, J.; Cai, X. Impacts of the Grain for Green Project on Soil Moisture in the Yellow River Basin, China. Hydrol. Process. 2025, 39, e70112. [Google Scholar] [CrossRef]
- Tulio Ribeiro, M.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. arXiv 2016, arXiv:1602.04938. [Google Scholar]
- Tiwari Dk, T.N.R. Geomorphology-Wavelet Based Approach to Rainfall Runoff Modeling for Data Scarce Semi-Arid Regions, Kolar River Catchment, India. J. Eng. Res. 2022, 10, 29–40. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Feng, H.H.; He, H.; Zhou, J.H.; Zhang, Y.L. Evaluation of Soil Moisture Climatology and Anomaly Components Derived from Era5-Land and Gldas-2.1 in China. Water Resour. Manag. 2021, 35, 629–643. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting Novel Associations in Large Data Sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Murtagh, F. Multilayer Perceptrons for Classification and Regression. Neurocomputing 1991, 2, 183–197. [Google Scholar] [CrossRef]
- Hasan, M.M.; Nilay, M.S.M.; Jibon, N.H.; Rahman, R.M. Lulc Changes to Riverine Flooding: A Case Study on the Jamuna River, Bangladesh Using the Multilayer Perceptron Model. Results Eng. 2023, 18, 101079. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F.; Pham, Q.B. A Novel Additive Regression Model for Streamflow Forecasting in German Rivers. Results Eng. 2024, 22, 102104. [Google Scholar] [CrossRef]
- Sammen, S.S.; Ehteram, M.; Abba, S.I.; Abdulkadir, R.A.; Ahmed, A.N.; El-Shafie, A. A New Soft Computing Model for Daily Streamflow Forecasting. Stoch. Environ. Res. Risk Assess. 2021, 35, 2479–2491. [Google Scholar] [CrossRef]
- Köyceğiz, C.; Büyükyıldız, M. Estimation of Streamflow Using Different Artificial Neural Network Models. Osman. Korkut Ata Üniv. Fen Bilim. Enst. Derg. 2022, 5, 1141–1154. [Google Scholar] [CrossRef]
- Wang, K.; Ma, C.; Qiao, Y.; Lu, X.; Hao, W.; Dong, S. A Hybrid Deep Learning Model with 1DCNN-LSTM-Attention Networks for Short-Term Traffic Flow Prediction. Phys. A Stat. Mech. Its Appl. 2021, 583, 126293. [Google Scholar] [CrossRef]
- Xie, Y.; Sun, W.; Ren, M.; Chen, S.; Huang, Z.; Pan, X. Stacking Ensemble Learning Models for Daily Runoff Prediction Using 1d and 2d CNNs. Expert Syst. Appl. 2023, 217, 119469. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Sathi, K.A.; Hosain, M.K.; Hossain, M.A.; Kouzani, A.Z. Attention-Assisted Hybrid 1D CNN-BiLSTM Model for Predicting Electric Field Induced by Transcranial Magnetic Stimulation Coil. Sci. Rep. 2023, 13, 2494. [Google Scholar] [CrossRef]
- Srivastava, R.; Mittal, V. Adaw: Age Decay Accuracy Weighted Ensemble Method for Drifting Data Stream Mining. Intell. Data Anal. 2021, 25, 1131–1152. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Frazier, P.I. A Tutorial on Bayesian Optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. arXiv 2019, arXiv:1907.10902. [Google Scholar]
- Diebold, F.X.; Mariano, R.S. Comparing Predictive Accuracy (Reprinted). J. Bus. Econ. Stat. 2002, 20, 134–144. [Google Scholar] [CrossRef]
- Mangini, W.; Viglione, A.; Hall, J.; Hundecha, Y.; Ceola, S.; Montanari, A.; Rogger, M.; Salinas, J.L.; Borzì, I.; Parajka, J. Detection of Trends in Magnitude and Frequency of Flood Peaks across Europe. Hydrol. Sci. J. 2018, 63, 493–512. [Google Scholar] [CrossRef]
- Terrell Gr, S.D.W. Variable Kernel Density Estimation. Ann. Stat. 1992, 20, 1236–1265. [Google Scholar] [CrossRef]
- Aumann, R.J.; Hart, S. Handbook of Game Theory with Economic Applications; Elsevier: Amsterdam, The Netherlands, 1992; Volume 2. [Google Scholar]
- Liu, H.; Motoda, H. Feature Selection for Knowledge Discovery and Data Mining; Springer Science & Business Media: New York, NY, USA, 2012; Volume 454. [Google Scholar]
- Brochu, E.; Cora, V.M.; de Freitas, N. A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning. arXiv 2010, arXiv:1012.2599. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar]
- Shahriari, B.; Swersky, K.; Wang, Z.Y.; Adams, R.P.; de Freitas, N. Taking the Human out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Routledge: London, UK, 2018. [Google Scholar]
- Abebe, N.A.; Ogden, F.L.; Pradhan, N.R. Sensitivity and Uncertainty Analysis of the Conceptual Hbv Rainfall–Runoff Model: Implications for Parameter Estimation. J. Hydrol. 2010, 389, 301–310. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).