Abstract
The study of localized surface plasmons (LSPs) in nanoscale structures is an essential step towards identifying optimal plasmonic modes that can facilitate robust optomechanical coupling and deepen our understanding of light–matter interactions at the nanoscale. This paper investigates, numerically, using the finite element method, LSP modes in a design comprising two coupled nano-ridges deposited on a gold layer with an interposing polymer spacer layer. Such a structure, usually referred to as a particle-on-mirror structure, shows exquisite optical properties at the nanoscale. We first examine the LSP modes of a single nano-ridge through the analysis of its scattering cross-section in the visible and infrared ranges. To enhance the plasmonic response, a thin polymer layer is placed at the middle of the ridge, which introduces additional LSP modes confined within the former. Then, we extend the analysis to the dimer configuration, which exhibits more complex and enhanced plasmonic behavior compared to a single nano-ridge. In particular, the dimer configuration yields LSP resonances with a quality factor enhancement of approximately threefold relative to a single nano-ridge. Furthermore, the presence of the polymer layer within the ridges significantly improves plasmon field localization and the quality factor. These findings underscore the potential of nano-ridge-based structures in advancing optomechanical coupling and offering valuable insights for the development of high-performance acousto-plasmonic devices. In particular, the proposed device could help significantly improve the design of nano-acousto-optic modulators, operating in the visible or in the near-infrared ranges, that require an enhanced light–phonon coupling rate.
1. Introduction
Plasmonics and its applications are based on the optical processes that occur in metallic nanostructures involving the coupling of light and collective oscillations of conduction band electrons (known as plasmons) at the metal–dielectric interface. The sizes, shapes, and compositions of the nanostructures can be engineered to manipulate the properties of the plasmons, such as their resonance frequency and localization, which, in turn, can enable a wide range of applications in various fields [1,2,3,4,5]. Notably, advanced concepts such as plasmonically induced transparency (PIT) have emerged lately; such resonance is shown to allow the precise on-chip control of light at the nanoscale [6]. Recent studies have explored the realization of PIT using graphene nanoribbons, providing robust methodologies to achieve transparency effects that are highly tunable and resilient to structural perturbations [7,8].
In addition, the application of plasmonics represents a good opportunity for nano-optomechanics to explore the interaction between light and mechanical motion at the nanoscale, enabling ultra-sensitive mass detection, the precision measurement of forces, and advancements in quantum information processing [9,10,11,12]. These systems typically utilize nanoscale resonators where light controls and measures mechanical vibrations. Achieving strong optomechanical coupling relies on the ability to localize and enhance electromagnetic fields at the nanoscale. Metallic nanostructures possess the ability to confine light below the diffraction limit via the excitation of localized surface plasmons (LSPs), the oscillations of free electrons at the surfaces of metallic nanostructures, offering a powerful means of confining light to sub-wavelength dimensions [13,14]. LSPs can interact with mechanical vibrations, making them ideal for studying nanoscale mechanical oscillations and enhancing optomechanical interactions [15,16,17]. Such strong acousto-plasmonic coupling could be harnessed in a multitude of advanced applications like ultra-sensitive accelerometers, force sensors, and optical signal processing [18], in the designing of multifunctional sensors with the possibility of integration into a wireless network [19], and in quantum computing [20]. Investigating systems with high LSP confinement is crucial for advancing nano-optomechanical applications.
Among the nanostructures supporting highly confined LSPs, one can cite nanoparticle-on-mirror (NPOM) structures (or film-coupled nanoparticles) [21,22], where a metal nanoparticle is separated from a metal film by a thin dielectric layer acting as a spacer; these structures have attracted significant attention due to their ease of fabrication [23] and the ability to trap plasmon modes in ultrasmall volumes [24,25,26]. The response of NPOM structures can be significantly influenced by the thickness of the metal film [27,28], as thinner metal films tend to result in stronger coupling between the nanoparticle and the film, leading to more pronounced plasmonic effects, while thicker films may reduce this interaction and broaden the resonance linewidths. Similarly, the interspacing between the gold film and the nanoparticles [29] and the shapes of the nanoparticles play crucial roles in determining the plasmonic properties [30]. Also, NPOM structures with dimers or trimers atop the metal film, as opposed to monomers, are expected to exhibit more interesting and/or improved features such as narrower plasmon linewidths and more pronounced scattered intensity [16,31].
This paper focuses on investigating, numerically, based on the finite element method (FEM), LSPs in a structure design in the category of NPOM devices, consisting of nano-ridges deposited on a gold layer, with a polymer layer acting as a spacer. It is worth mentioning that such a design could be readily fabricated experimentally given the state-of-the-art technology [32]. We first investigate the LSP modes of a single ridge by examining its scattering cross-section in the visible and near-infrared ranges. To introduce additional LSP modes, we insert a thin polymer layer at the middle of the ridge, which results in new LSPs confined within such a layer. Then, we explore the dimer configuration, which has been proven to show more interesting characteristics [16,31]. Our findings indicate that dimerization, achieved by positioning two ridges in close proximity, enhances the interaction between the modes, leading to LSP resonances with significantly improved quality factors—approximately a threefold enhancement compared to a single monomer. Additionally, the polymer layer at the middle of the ridges plays an important role in enhancing the localization of the plasmon field and the quality factor of the different modes as compared to previous reports [16]. In a recent paper [33], we studied localized mechanical vibrations in similar monomer and dimer structures. Here, we show, prospectively, based on the dimer LSP modes’ effective volumes, how such modes would couple with the localized mechanical vibrations in the dimer, thereby enabling their classification in terms of optomechanical coupling intensity.
This paper is organized as follows. In Section 2, we present a detailed investigation of the LSPs of a single gold nano-ridge positioned atop a multilayer structure. In Section 3, we extend this analysis to coupled gold nano-ridges, examining how the dimer configuration influences the localization and enhancement of the plasmonic modes. In Section 4, we provide an analysis of the mode volume for each LSP mode, enabling the classification of the different LSP modes and discussing their potential applications in acousto-plasmonic interactions.
2. Localized Surface Plasmons of a Single Gold Nano-Ridge
The proposed design is shown in Figure 1a. It consists of a gold nano-ridge with a thin polymer layer lying in the middle, deposited above a polymer thin spacer layer made of the same material, that covers a gold thick film beneath. Experimentally speaking, the whole design could be grown on a silicon dioxide substrate (SiO2), but in terms of simulations, the thick gold film absorbs and reflects all incident light before reaching SiO2. Hence, the latter medium is excluded from simulations. Due to the system’s symmetry along the y-axis, all calculations were performed in the x–y plane.
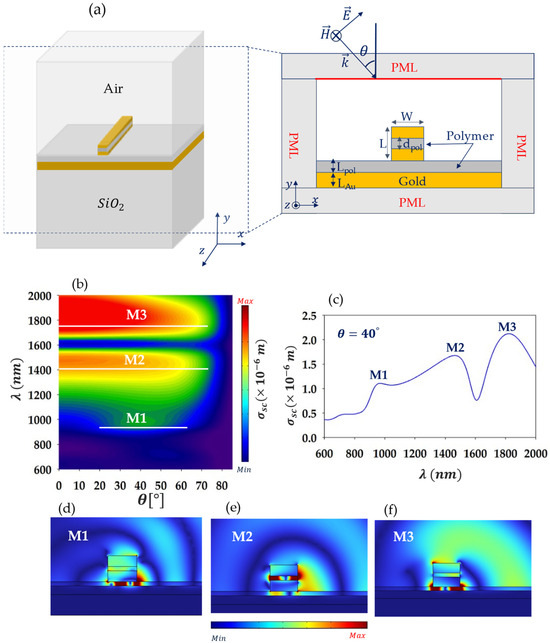
Figure 1.
(a) Design of the 3D studied system composed of a gold nano-ridge with a thin polymer layer of thickness in the middle, placed above a gold layer with a polymer layer acting as a spacer in between. A 2D cross-section of the studied structure is shown on the right side. (b) Simulated scattering cross-section of the system in (a) as a function of wavelength and the angle of incidence . (c) Same as in (b), but for the fixed incidence angle . (d–f) Field maps of the scattered electric field within and around the nano-ridge corresponding to modes M1, M2, and M3 shown in (c) at wavelengths ~975 nm, ~1493 nm, and ~1689 nm, respectively.
The modeled cross-section of the system is depicted in Figure 1a. The parameters of the studied system are as follows: W is the nano-ridge width while L is its height, dpol is the thickness of the polymer layer inserted in the middle of the ridge, Lpol is the thickness of the polymer spacer layer, and LAu is the thickness of the gold layer beneath. The simulation results presented in this work were obtained using electromagnetic frequency domain analysis based on the FEM using COMSOL Multiphysics software. In order to excite the system, a plane light-wave with TM polarization is launched from the incidence medium at the top at oblique incidence onto the latter, as shown in Figure 1a. To eliminate undesirable reflections at the edges of the system, perfectly matched layers (PMLs) have been placed on all boundaries. The materials used include a polymer with the refractive index while, for dispersive materials, namely the gold metal, a frequency-dependent complex-valued relative permittivity based on the Lorentz–Drude model is adopted [34]:
Here, the sum over m corresponds to different oscillators, is the high-frequency contribution to the relative permittivity, is the plasma frequency of free electrons, is the oscillator strength, is the resonance frequency, and is the damping coefficient. We use M = 6 damped harmonic oscillators in order to take the inter-band transitions of gold. The values of the different parameters have been taken from [35] and are listed in Table 1. Throughout the paper, unless stated otherwise, the geometrical parameters are taken as follows: , , , , and .

Table 1.
Lorentz–Drude parameters values adopted for modeling the relative permittivity of gold.
To obtain the dispersion relation of the system, we have simulated the scattering cross-section as a function of both the angle of incidence in the range [] and the wavelength in the range of interest [], which covers the visible and near-infrared domains. The corresponding results are shown in Figure 1b in the color scale. Let us indicate that the red color indicates the maximum scattering intensity while blue indicates the minimum (scattering) intensity. Three distinctive modes are observed, highlighted with horizontal white lines as a guide for the eye. We refer to these modes as M1 for the lower-wavelength (or higher-frequency) mode, M2 for the middle-wavelength mode, and M3 for the higher-wavelength mode. It is worth noting that modes M2 and M3 are excited for nearly all values of while mode M1 is only excited in the range of θ between approximately and . To give an idea about the behavior of these modes in the scattering spectra, Figure 1c shows as a function of wavelength at , indicating three peaks corresponding to LSP resonances at wavelengths 975 nm (mode M1), 1493 nm (mode M2), and 1689 nm (mode M3). Figure 1d–f displays the maps of the scattered electric field at these wavelengths, respectively. The field localization shows the presence of two types of modes: one confined underneath the ridges (modes M1 and M3) and one at the middle of the ridge (mode M2). A characteristic that is common between the modes is the fact that they are trapped in between two metal materials within a dielectric, which suggests that they correspond to metal–insulator–metal (MIM)-type modes. To explore, in more detail, this aspect of the modes and their general behavior versus the key geometrical parameters, we analyze the effect of the nano-ridge width in Figure 2a, where is plotted as a function of both the wavelength and the nano-ridge width, . The remaining parameters are kept as in Figure 1 while the incidence angle is set to , ensuring the excitation of the three modes. One notes that the resonance wavelengths of the three modes (corresponding to the scattering maximum/peaks) increase linearly with an increase in W. This trend is typical in an effective plasmonic cavity acting as a Fabry–Pérot cavity, where MIM-type resonances correspond to confined plasmonic standing waves [16,36]. Accordingly, the thin dielectric layers either underneath or at the middle of the nano-ridge, where the modes are localized, act as an effective plasmonic Fabry–Pérot cavity (PFPC) of nominal length . In particular, the plasmonic MIM standing waves build up due to reflections off the PFPC edges on each side. The resonance wavelength of the (plasmonic) modes can be expressed as [36]:
Here, is the effective refractive index of the of the propagating MIM-like plasmon in the cavity, is its wave vector, is the wavevector in the vacuum, and , 2, 3, … is an integer representing the mode number. This equation is derived from the resonance condition corresponding to a round-trip of the wave in the cavity, namely, , where is the phase shift due to the reflection off the edges of the nano-ridge, whose value can be approximated as [36], where is the apparent length extension of the mode off the nano-ridge edges. Therefore, is actually replaced by the length, . By fitting the LSP resonance wavelengths (shown with open white circles in Figure 2a), we estimate to be approximately for mode M1, for mode M2, and for mode M3. As for the values of for each mode, these can be determined from the plot of the localized field inside the PFPC along the -axis. From Figure 1d–f, we can deduce that m = 2 for mode M1 while for modes M2 and M3, m = 1. To provide an example of the calculation of the phase shift off the ridge edges, , we use the relation such that , where is the resonance wavelength of the mode, and (effective refractive index) is estimated numerically using a MIM waveguide model in Comsol. We calculate the values of at the incidence angle and for the ridge width (with the remaining parameters being set as in Figure 1). The phase shifts are approximately found to be , , and for modes M1, M2, and M3, respectively. The solid white lines in Figure 2a represent the fits of the numerical data (white open circles) using Equation (3). We observe, using the PFPC model based on the latter equation, that we have successfully fitted the numerical results (Figure 2a), which confirms the mechanism behind the LSP modes (M1, M2, and M3) formation.
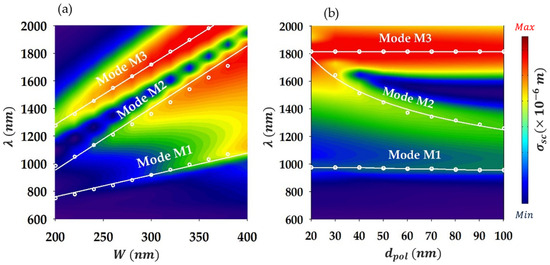
Figure 2.
(a) Scattering cross-section as a function of wavelength and the width of the nano-ridge W. White open circles indicate the position of the LSP resonances for various values of W while white solid lines represent a fit of these points using the MIM-like waveguide model (Equation (2)). (b) Same as in (a), except that the scattering cross-section is plotted as a function of wavelength and the thickness of the polymer layer at the middle of nano-ridge.
In order to better understand the physics behind these modes, we examine, in Figure 2b, the effect of the polymer layer thickness in the middle of the nano-ridge for . The rest of the parameters are set similar to Figure 1. Let us recall that the field is essentially confined inside the polymer layer for mode M2, whereas for modes M1 and M3, the field is localized underneath the ridge. This means that only mode M2 should be sensitive to , which is evident in Figure 2b as only mode M2 is affected by changes in . In particular, one remarks that the resonance wavelength of mode M2, , drops nearly hyperbolically as increases. This trend reminds us of the effective refractive index () of a metal–insulator–metal-type waveguide versus its width, whereby changes as the inverse of the guide width i.e., [37]. This relationship can be exploited to explain the behavior of versus considering what we mentioned above, namely, mode M2 (or M1/M3) arises out of the trapping of a MIM-type mode in an effective plasmonic cavity (in the form of a MIM standing wave). Hence, the effective refractive index of such MIM plasmonic modes should change as , which enables one to estimate the resonance wavelength as follows:
Here, is a fitting parameter. Applying Equation (3), we have fitted the numerically calculated (FEM) resonance wavelength of mode M2 in Figure 2b. Note that modes M1 or M3 have not been fitted given their insensitivity to . The curve based on Equation (3) is depicted in a white solid line while the FEM results are shown in white open circles; we can notice the very good agreement achieved. The fitting provided in Figure 2 using Equations (2) and (3) enables us to definitely validate the physical mechanism behind the formation of modes M1, M2, and M3 mentioned above. It is important to note that the plasmonic modes investigated in this paper are not to be confused with the localized surface plasmons associated with metallic nanoparticles. As is well known, the latter modes are optical eigen-modes of the particles that depend on their shapes, the surrounding medium, and the nature of metal. They correspond to coherent collective vibrations of free electrons in the metal constituting the nanoparticle and are localized near the latter surface boundary.
3. Localized Surface Plasmons of Coupled Gold Nano-Ridges (Dimer)
In this section, we investigate the effect of two identical coupled nano-ridges that form a dimer. This configuration is expected to enhance the localization of the plasmonic field and the quality factors of the modes, leading to stronger light–matter interaction [16]. The two nano-ridges are set to be separated by a distance , as shown in the 2D (x–y) plane of the simulated system in Figure 3a. Note that is a key parameter as it enables one to control the coupling magnitude in between the nano-ridges (forming the dimer). Figure 3b shows the simulated scattering cross-section as a function of wavelength and incidence angle, with , while the other parameters are set as earlier (Figure 1). The plot reveals that for , the modes are indistinguishable and not excited but rather correspond to large scattering bands. However, for , four modes, labelled D1, D2, D3, and D4, show up. To examine these modes more closely, Figure 3c shows the scattering cross-section at θ = 55° as a function of wavelength (blue line), where four peaks are clearly identified at roughly 816 nm (D1), 975 nm (D2), 1483 nm (D3), and 1690 nm (D4). A significant observation is that the quality factor of the modes in the dimer case is improved by approximately a factor of 3 compared to the single monomer case (red dashed line). For instance, if we focus on modes D3 and D4, which are the most strongly confined within the dimer, their quality factors are estimated as and , respectively. In comparison, mode M3 (of the monomer), which is the closest in terms of wavelength, has a quality factor of . This improvement is attributed to the coupling between the ridges, which enhances the localization of the electric field as is evident from the field maps of the scattered field shown in Figure 3d–g. This enhanced localization is particularly evident for modes D2 and D4, where the field is strongly confined underneath and between the ridges, as well as inside the polymer layers in the middle of the ridges. For mode D2, the field is primarily localized in the polymer layers at the middle, but also in between the ridges. In contrast, mode D1 exhibits weaker localization, having antenna-like components associated with multipolar localizations at the edges, that causes the field to radiate. Let us mention that the enhanced quality factor of the dimer modes comparing with the monomer case has been reported elsewhere [16,31].
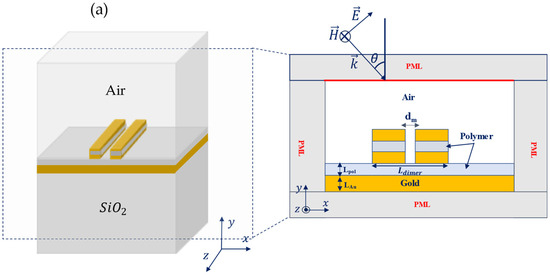
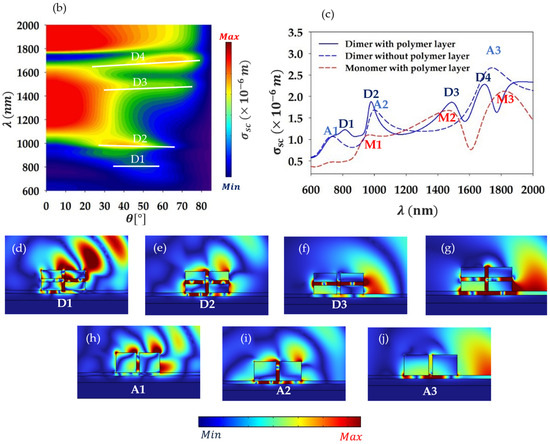
Figure 3.
(a) Two-dimensional schematic representation of the simulated system consisting of two nano-ridges sitting atop a multilayer structure, separated by a distance dm. (b) Scattering cross-section of the system in (a) as a function of wavelength λ and the incidence angle ϴ. (c) Same as in (b), but at , for the monomer structure (red dashed lines), the dimer structure with the polymer layer is set at the middle of the ridges (blue solid line) and the dimer structure without the polymer layer is at the middle (blue dashed line). (d–g) Scattered field map of the modes D1, D2, D3, and D4 in the case of the nano-ridges with a thin polymer layer placed at the middle at wavelengths , , , and , respectively. (h–j) Same as in (d–g) but for the modes A1, A2, and A3 of the nano-ridges without the polymer layer at wavelengths , , and , respectively.
As a matter of comparison, we have simulated the scattering cross-section as a function of wavelength for θ = 55° for the dimer structure without the polymer layer inserted in the middle of the ridges (blue dashed line). The curve is overlaid with that of dimer (blue solid line) and monomer (red dashed line) structures with the polymer layer set in the middle as shown in Figure 3c. We can observe that the insertion of the thin polymer layers within the dimer ridges results in an improved quality factor for the modes. In addition, the spectrum is quite richer in the latter case as additional localized surface plasmons (with four modes) show up as compared to the case of no layers in the ridges (three modes). Furthermore, the localization of the field is significantly better with the polymer layer, as seen in Figure 3d–g, compared to the field maps in the case where no layer is inserted (Figure 3h–j).
To analyze the impact of geometrical parameters on the dimer modes and the physical origins of the latter, we examine how variations in the width of the dimer , and the thickness of the polymer layer in the middle of the ridges, , affect the modes. The dimer width is defined as where represents the single ridge width and is the separation distance between the ridges. For the sake of simplicity, we alter by changing only and keeping , which controls coupling intensity within the dimer, fixed. Also, all remaining parameters of the system are set equivalent to Figure 1a (as mentioned above). Figure 4a presents the scattering cross-section as a function of wavelength and . We note a near-linear redshift in the resonance wavelengths as is increased, which is similar to what we observed above in case of the monomer (Figure 2a) width increasing effect. This hints at the fact that modes D1–D4 of the dimer could be considered as plasmonic MIM-type standing waves confined in an effective plasmonic cavity. The latter is made of either the thin layers in the middle of the ridges plus the small space in between (like for mode D3) or of the gap layer underneath the dimer, where mode D4, for instance, is primarily localized. Let us call the latter cavity the lower cavity and the former the upper cavity. Note that some modes (D1, D2, and D4) are confined in both the lower and upper cavities (with a different rate) as well as in between the dimer. To confirm this, we consider that the MIM-type plasmonic standing waves corresponding to the modes are localized in either the lower or upper cavities (or both) of the nominal length, , and hence, the resonance wavelength is given as follows:
Here, all the parameters are defined in an equivalent manner as in Equation (2) for the monomer. It should be stressed that the nominal length is replaced by , where the latter parameter is a fitting parameter. Such a parameter is meant to account for the dimer mode extension off its outer edges as already explained.
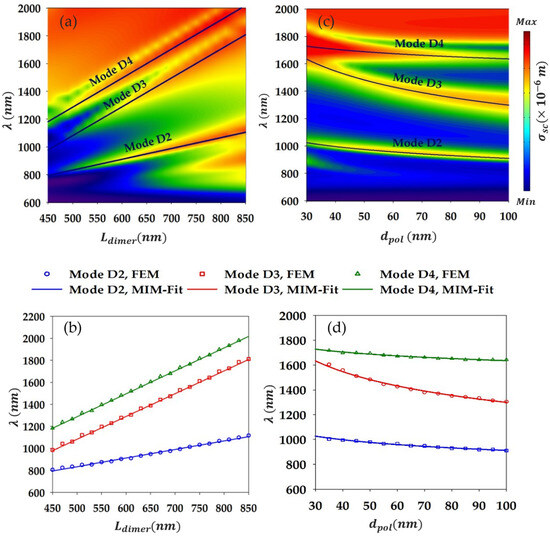
Figure 4.
(a) Scattering cross-section of the dimer-based system (Figure 3a) as a function of the wavelength and . (b) Plot of the resonance wavelengths of modes D2, D3, and D4 as a function of (open symbols). The plot for each mode is fitted (solid lines) with Equation (4), giving the resonance wavelength of the effective (lower or upper) plasmonic cavity. Note that mode D3 is confined in the upper cavity while D4 is mostly trapped in the lower cavity and D2 is localized in the upper cavity and in the lower to a lesser extent. (c) Similar to (a), but as a function of the polymer layers thickness, . (d) Same as in (b), but as a function of and using Equation (5) as for the provided fitting to the modes.
As for the mode order, m, it is determined based on the localized field in the effective plasmonic cavity (lower or upper). From Figure 3d–g, we estimate m = 4 for the mode D2 and m = 2 for both modes D3 and D4. We should mention that because mode D1 has complex features like antenna-like components, with no neat/simple localization features in either the lower or upper cavity, we do not consider fitting its resonance wavelength. Figure 4b shows the fitting provided by Equation (4) (solid lines) to the positions of the modes D2, D3, and D4, resonance wavelengths (indicated by symbols) as functions of . The fitting parameter has been determined for each mode as follows: 58.35 nm for mode D2, 11 nm for mode D3, and 286.76 nm for mode D4. We note that the fitting agrees perfectly with the FEM results for all the three modes, which clearly underscores the MIM character of such modes and that they correspond to MIM-type plasmon standing waves trapped in the effective lower/upper cavities.
We also explored the effect of varying the thickness of the polymer layers inserted in the middle of the ridges . Figure 4c shows the scattering cross-section as a function of wavelength and . This plot indicates that all modes are affected by changes in , but the impact is significantly more pronounced for mode D3, which is understandable since mode D3 is primarily localized within such layers. Following mode D3, we see that mode D2 is the most affected as compared to mode D4, which is consistent with their field localization as the latter is more confined beneath the ridges than in their middle while for the former it is the opposite. Note that for mode D1, due to its complex features, it is difficult to analyze its behavior versus changes in ; however, it can be remarked that for , the mode is nearly cut off as its scattering section becomes quite weak. For , nevertheless, the mode shows a sensitivity with an increase in as its wavelength drops with a non-negligeable magnitude, reflecting its localization in the (middle) layers. Using a similar equation to Equation (4) and the same reasoning as in the case of the monomer, one can capture the modes’ (D3, D2, and D4) behavior as is changed. Equation (3) can be written in case of the dimer as follows:
Here, the ridge width is simply replaced by the dimer effective width, , and is a fitting parameter. Based on such equation, we provide the fitting of the three modes resonance wavelengths as a function of in Figure 4d, where we can observe the excellent agreement with the FEM results. Hence, we can be quite confident that modes D3, D2, and D4 arise out of the trapping of the MIM-type surface-plasmon-guided mode in the lower/upper effective cavity, giving rise to resonating MIM plasmonic standing waves.
4. Effective Volume of the Dimer Localized Plasmon Modes and Prospective Optomechanical Coupling
Here, we focus on the analysis of the effective mode volume of the localized surface plasmon modes of the dimer, aiming to classify these modes for an optimal enhanced optomechanical coupling with localized mechanical vibrations supported by the dimer. As a matter of fact, the present paper, which is about a thorough analysis of the plasmonic properties of the dimer-based device, comes after a previous study about the mechanical characteristics of the system [33]. The general objective is to achieve enhanced acousto-plasmonic coupling using surface acoustic waves (Figure 5a). In this framework, we would like to provide, in this last paragraph, a prospective qualitative analysis of enhanced optomechanical coupling harnessing the dimer plasmonic modes’ effective volume. Note that the optical mode volume is one of the key parameters that govern light–matter interactions in general as it is related to field enhancement and spatial localization [38]. Having an estimation of the effective mode volume can help quantify the spatial extent of the electromagnetic energy confinement, directly impacting the strength of the interaction between light and matter. To get an estimate of the effective mode volumes , we use the quasi-static approximation to calculate the mode volume integral for a leaky plasmonic cavity given [39,40,41] the following:
Here, the integral is performed over of the volume (surface times unit length) of both nano-ridges, is the electromagnetic energy density, and max is its maximum value in the simulation domain. For a dielectric medium, the energy density takes the simple form while, in the case of a dispersive and lossy medium like a metal, an appropriate relation is as follows [37]:
Here, is the complex dielectric function of the metal. In our case, the latter is given by the Lorentz–Drude model (Equation (1)). , on the other hand, is the mode damping taken as the linewidth of the respective LSP mode. As already mentioned, the simulation is performed in 2D due to symmetry along the y-axis, so to calculate the mode volume, one should perform surface integrals in the 2D cross-section system, and then multiply the result by a unit length along the y-direction. Figure 5b, shows the normalized effective mode volume calculated for each mode of the dimer (D1, D2, D3, and D4), where () is the volume occupied by the associated resonance wavelength of the mode in the polymer layer. As can be seen, the effective volumes of modes are well below , reflecting the strong confinement of the dimer plasmonic modes far below the diffraction limit of light. From the values of the mode volumes, we observe that mode D1 has the largest value of , indicating a relatively lower field localization rate compared to the other modes. This relates to such mode localization features like its tendency to radiate energy due to its antenna-like components associated with multipolar localizations at the edges. In contrast, mode D4, with the lowest value of , is relatively the most strongly confined mode. Modes D2 and D3 fall in between with values and , respectively. This result shows that for enhanced light–matter coupling purposes, mode D4 should offer the highest interaction rate as the coherent coupling rate between light and matter scales as [41].
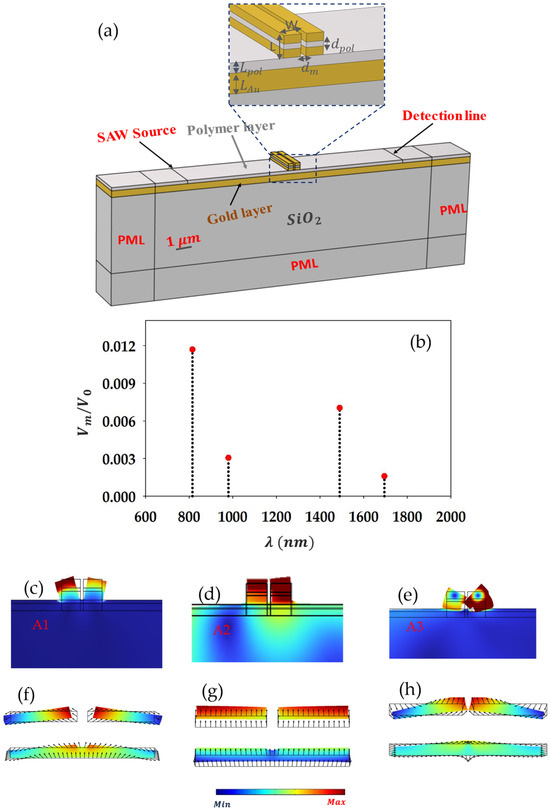
Figure 5.
(a) Sketch of the system design used to excite confined localized mechanical vibrations in the dimer by means of surface acoustic waves (SAWs). The device consists of the dimer structure of Figure 3a deposited above an SiO2 substrate. (b) Effective mode volume of the dimer LSP modes normalized to , representing the volume occupied by the associated resonance wavelengths in the polymer layer. (c–e) Zoom-in view on the mechanical displacement field in and around the dimer at its localized mechanical vibrations resonance frequencies, namely at for the symmetric flexural mode, for the in-phase compression mode, and for the high-order symmetric flexural mode. (f–h) Plots of the displacement field in the polymer layers, both underneath and in the middle of the ridges, associated with the mechanical vibration modes in (c–e), respectively.
Regarding the optomechanical coupling specifically, we can affirm that the acousto-plasmonic interaction is qualitatively related to the overlap degree between the plasmon and the mechanical vibration in a given cavity. This is estimated quantitively via the so-called optomechanical coefficient, whose expression is determined based on the photoelastic volume and the surface moving-boundary effects [16,42]. Given that the dimer plasmonic modes with the lowest volume magnitude are the most highly trapped plasmons, they should manifest the higher overlap rate with a given mechanical vibration localized in the dimer. As a result, such modes should lead to an optimal optomechanical coupling intensity. In Figure 5c–h, we recall the localized mechanical vibrations of the dimer that we deemed to be optomechanically active based on symmetry arguments in a previous work [33] and the design, enabling us to use surface acoustic waves to excite such mechanical vibrations. Considering, for instance, the in-phase compression mode A2 (Figure 5d), which deforms the polymer layers both under and in the middle of the ridges (see Figure 5g), where modes D2, D3, and D4 are localized, we can roughly classify such modes (based on their volume) in terms of the optomechanical coupling rate as follows:
The same reasoning approximately applies if we consider another mechanical vibration of the dimer to classify the LSP modes in terms of acousto-plasmonic coupling magnitude. Obviously, a thorough study based on the rigorous simulations of the optomechanical coefficient is needed to determine the best localized mechanical vibrations and plasmons that yield the highest coupling magnitude. However, this qualitative argument based on the modes volume already gives a good hint regarding the most promising plasmonic mode for the enhanced optomechanical purpose, namely mode D4, which shows the lowest volume or equivalently the highest confinement rate.
In summary, we investigated LSP modes in gold nano-ridges within a dimer-on-mirror structure, with nano-ridges sized at 320 nm in width and 300 nm in height. Previous studies on LSP resonances have predominantly focused on nanoparticles ranging from 1 to ~100 nm [9,17,21,22,23,24,25], with larger particle sizes remaining underexplored due to their experimental challenges and complex behavior [43]. While different shapes of nanoparticles, whether in monomer or dimer configurations, have been studied before, these studies have typically involved homogeneous nanoparticles with uniform material composition. These investigations have provided critical insights into how particle geometry and separation influence plasmonic behavior. In our work, we have explored the effect of introducing a thin dielectric layer at the center of the nano-ridges. This simple modification has been shown to significantly enhance the quality factor and field localization of the plasmonic modes compared to previous systems without such a layer [16]. Furthermore, our findings indicate that optical coupling in dimers leads to strongly confined plasmons with narrower linewidths and higher field localization than in monomers. Specifically, the dimer configuration yields LSP resonances with a quality factor of approximately threefold enhancement relative to a single nano-ridge.
Additionally, we have qualitatively classified the plasmonic modes of the dimer design in terms of optomechanical coupling intensity based on their effective volume. This classification provides valuable insights into the potential applications of these modes in optomechanical systems. Moreover, the further optimization and tuning of the design parameters, such as the thickness of the polymer layer and the dimensions of the nano-ridges, could lead to optimized enhancements in plasmonic performance.
5. Conclusions
In this paper, thorough finite-element-based numerical calculations have been carried-out to investigate localized surface plasmon resonances in a film-coupled nanoparticles system. The proposed design is made of two gold nano-ridges forming a dimer atop a metal plate in between which a thin polymer film acting as a spacer is inserted. We have first studied the optical scattering properties of a monomer ridge and found three MIM-type localized surface plasmons in the frequency ranges of interest, namely the visible and near-infrared domains. Our results indicate that the presence of the polymer layer in the middle of the ridge gives rise to additional LSP modes confined within. In the dimer structure composed of two identical nano-ridges, we have observed that the plasmonic modes exhibit narrower linewidths and enhanced field localization compared to the monomer configuration. The enhanced localization is attributed to the strong coupling between the ridges leading to a higher rate of mode trapping. We have also shown that the inserted polymer layers within the ridges, in their middle, further enhance the modes’ quality factor as compared to the ridges with no layers. The former case adds means to confine, even more, the dimer LSP modes (in the middle layers), which results in narrower linewidths. Also, in that case, a richer plasmonic spectrum based on the dimer is found as additional modes trapped in the ridges’ middle layers show up. We have successfully demonstrated that the dimer/monomer modes arise out of the trapping of MIM-type guided modes in the polymer layers beneath or in the middle of the ridges, acting as plasmonic effective cavities.
Furthermore, based on the simulation of the LSP modes’ effective volume of the dimer, we have been able to roughly class the modes in terms of their optomechanical coupling magnitude with a given mechanical vibration of the dimer. Specifically, mode D4, with its smallest normalized mode volume, stands out as the most promising LSP mode for enhanced acousto-plasmonic interaction. The showcased dimer device in this work could help design new acousto-optic components for high-frequency nanomechanical sensing or optical switching or to perform infrared/visible-light modulation operations.
Author Contributions
Conceptualization, A.N., E.H.E.B. and M.E.G.; methodology, M.E.G., M.A. and M.M.; validation, A.N., E.H.E.B. and M.E.G.; investigation, M.E.G., M.A. and M.M.; data curation, M.E.G. and A.N.; writing—original draft preparation, M.E.G. and A.N.; writing—review and editing, A.N., E.H.E.B. and M.E.G.; funding acquisition, E.H.E.B. and A.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We would like to acknowledge the financial support under the framework of the Research Excellence Grants Program from the Moroccan National Center for Scientific and Technical Research (CNRST).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Stockman, M.I.; Kneipp, K.; Bozhevolnyi, S.I.; Saha, S.; Dutta, A.; Ndukaife, J.; Kinsey, N.; Reddy, H.; Guler, U.; Shalaev, V.M. Roadmap on plasmonics. J. Opt. 2018, 20, 043001. [Google Scholar] [CrossRef]
- Amrani, M.; Khattou, S.; Rezzouk, Y.; Mouadili, A.; Noual, A.; El Boudouti, E.H.; Djafari-Rouhani, B. Analytical and numerical study of T-shaped plasmonic demultiplexer based on Fano and induced transparency resonances. J. Phys. D Appl. Phys. 2021, 55, 075106. [Google Scholar] [CrossRef]
- Duan, Q.; Liu, Y.; Chang, S.; Chen, H.; Chen, J.H. Surface plasmonic sensors: Sensing mechanism and recent applications. Sensors 2021, 21, 5262. [Google Scholar] [CrossRef] [PubMed]
- Noual, A.; Akiki, R.; Pennec, Y.; El Boudouti, E.H.; Djafari-Rouhani, B. Surface acoustic waves-localized plasmon interaction in pillared phononic crystals. Phys. Rev. Appl. 2020, 13, 024077. [Google Scholar] [CrossRef]
- Vasileiadis, T.; Noual, A.; Wang, Y.; Graczykowski, B.; Djafari-Rouhani, B.; Yang, S.; Fytas, G. Optomechanical hot-spots in metallic nanorod-polymer nanocomposites. ACS Nano 2022, 16, 20419–20429. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.; Zhai, X.; Wang, L.; Xiang, Y.; Wen, S. Plasmonically induced transparency in phase-coupled graphene nanoribbons. Phys. Rev. B 2022, 106, 075401. [Google Scholar] [CrossRef]
- Xia, S.-X.; Zhai, X.; Wang, L.-L.; Wen, S.-C. Plasmonically induced transparency in double-layered graphene nanoribbons. Photonics Res. 2018, 6, 692–702. [Google Scholar] [CrossRef]
- Zhang, D.; Xia, S.; Xu, W.; Zhai, X.; Wang, L. Topological plasmonically induced transparency in a graphene waveguide system. Phys. Rev. B 2024, 109, 245420. [Google Scholar] [CrossRef]
- Koya, A.N.; Cunha, J.; Guerrero-Becerra, K.A.; Garoli, D.; Wang, T.; Juodkazis, S.; Proietti Zaccaria, R. Plasmomechanical systems: Principles and applications. Adv. Funct. Mater. 2021, 31, 2103706. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Xuereb, A.; Gröblacher, S.; Paternostro, M.; Regal, C.A.; Weig, E.M. Optomechanics for quantum technologies. Nat. Phys. 2022, 18, 15–24. [Google Scholar] [CrossRef]
- Liu, X.; Liu, W.; Ren, Z.; Ma, Y.; Dong, B.; Zhou, G.; Lee, C. Progress of optomechanical micro/nano sensors: A review. Int. J. Optomechatronics 2021, 15, 120–159. [Google Scholar] [CrossRef]
- Sansa, M.; Defoort, M.; Brenac, A.; Hermouet, M.; Banniard, L.; Fafin, A.; Gely, M.; Masselon, C.; Favero, I.; Jourdan, G. Optomechanical mass spectrometry. Nat. Commun. 2020, 11, 3781. [Google Scholar] [CrossRef]
- Amendola, V.; Pilot, R.; Frasconi, M.; Maragò, O.M.; Iatì, M.A. Surface plasmon resonance in gold nanoparticles: A review. J. Phys. Condens. Matter 2017, 29, 203002. [Google Scholar] [CrossRef]
- Ramos, D.; Malvar, O.; Davis, Z.J.; Tamayo, J.; Calleja, M. Nanomechanical plasmon spectroscopy of single gold nanoparticles. Nano Lett. 2018, 18, 7165–7170. [Google Scholar] [CrossRef] [PubMed]
- Simone, G. Strong plasmon-mechanical coupling through standing acoustic waves and antenna enhancement, toward mass transduction. J. Appl. Phys. 2024, 135, 053152. [Google Scholar] [CrossRef]
- Noual, A.; Akiki, R.; Lévêque, G.; Pennec, Y.; Djafari-Rouhani, B. Enhanced phonon-plasmon interaction in film-coupled dimer nanoridges mediated by surface acoustic waves. Opt. Express 2021, 29, 43104–43123. [Google Scholar] [CrossRef]
- Ahmidayi, N.; d’Orsonnens, W.; Maurer, T.; Lévêque, G. Mechanical Enhancement of the Strain-Sensor Response in Dimers of Strongly Coupled Plasmonic Nanoparticles. Ann. Der Phys. 2023, 535, 2300319. [Google Scholar] [CrossRef]
- Metcalfe, M. Applications of cavity optomechanics. Appl. Phys. Rev. 2014, 1, 031105. [Google Scholar] [CrossRef]
- Firmansyah, T.; Wibisono, G.; Tjipto Rahardjo, E.; Kondoh, J. Reconfigurable localized surface plasmon resonance spectrum based on acousto-dynamic coupling in arrays gold nanoparticles induced by shear horizontal vibration. Appl. Surf. Sci. 2022, 571, 151331. [Google Scholar] [CrossRef]
- Tsukanov, A.V. Optomechanical systems and quantum computing. Russ. Microelectron. 2011, 40, 333–342. [Google Scholar] [CrossRef]
- Li, G.-C.; Zhang, Q.; Maier, S.A.; Lei, D. Plasmonic particle-on-film nanocavities: A versatile platform for plasmon-enhanced spectroscopy and photochemistry. Nanophotonics 2018, 7, 1865–1889. [Google Scholar] [CrossRef]
- Maurer, T.; Adam, P.-M.; Lévêque, G. Coupling between plasmonic films and nanostructures: From basics to applications. Nanophotonics 2015, 4, 363–382. [Google Scholar] [CrossRef]
- Goncalves, M.R. Plasmonic nanoparticles: Fabrication, simulation and experiments. J. Phys. D Appl. Phys. 2014, 47, 213001. [Google Scholar] [CrossRef]
- Charchi, N.; Li, Y.; Huber, M.; Kwizera, E.A.; Huang, X.; Argyropoulos, C.; Hoang, T. Small mode volume plasmonic film-coupled nanostar resonators. Nanoscale Adv. 2020, 2, 2397–2403. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Ming, T.; Lin, Y.; Ling, X.; Ruan, Q.; Palacios, T.; Wang, J.; Dresselhaus, M.; Kong, J. Ultrasmall mode volumes in plasmonic cavities of nanoparticle-on-mirror structures. Small 2016, 12, 5190–5199. [Google Scholar] [CrossRef]
- Deacon, W.M.; Lombardi, A.; Benz, F.; del Valle-Inclan Redondo, Y.; Chikkaraddy, R.; de Nijs, B.; Kleemann, M.-E.; Mertens, J.; Baumberg, J.J. Interrogating nanojunctions using ultraconfined acoustoplasmonic coupling. Phys. Rev. Lett. 2017, 119, 023901. [Google Scholar] [CrossRef]
- Yeshchenko, O.A.; Kozachenko, V.V.; Naumenko, A.P.; Berezovska, N.I.; Kutsevol, N.V.; Chumachenko, V.A.; Haftel, M.; Pinchuk, A.O. Gold nanoparticle plasmon resonance in near-field coupled Au NPs layer/Al film nanostructure: Dependence on metal film thickness. Photonics Nanostruct.-Fundam. Appl. 2018, 29, 1–7. [Google Scholar] [CrossRef]
- Armstrong, R.E.; Van Liempt, J.C.; Zijlstra, P. Effect of film thickness on the far-and near-field optical response of nanoparticle-on-film systems. J. Phys. Chem. C 2019, 123, 25801–25808. [Google Scholar] [CrossRef]
- Mock, J.J.; Hill, R.T.; Degiron, A.; Zauscher, S.; Chilkoti, A.; Smith, D.R. Distance-dependent plasmon resonant coupling between a gold nanoparticle and gold film. Nano Lett. 2008, 8, 2245–2252. [Google Scholar] [CrossRef]
- Lee, H.-Y.; Seong, H.K.; Yoo, J. Optimal shape design of the film-coupled nanoparticle using the phase field design method. Int. J. Precis. Eng. Manuf. 2016, 17, 453–460. [Google Scholar] [CrossRef]
- Li, G.-C.; Zhang, Y.-L.; Lei, D.Y. Hybrid plasmonic gap modes in metal film-coupled dimers and their physical origins revealed by polarization resolved dark field spectroscopy. Nanoscale 2016, 8, 7119–7126. [Google Scholar] [CrossRef] [PubMed]
- Kunert, B.; Guo, W.; Mols, Y.; Tian, B.; Wang, Z.; Shi, Y.; Van Thourhout, D.; Pantouvaki, M.; Van Campenhout, J.; Langer, R. III/V nano ridge structures for optical applications on patterned 300 mm silicon substrate. Appl. Phys. Lett. 2016, 109, 091101. [Google Scholar] [CrossRef]
- El Ghafiani, M.; Noual, A.; Rezzouk, Y.; Moutaouekkil, M.; El Boudouti, E.H. Surface acoustic waves interaction with confined acoustic phonons in a coupled nanoridges dimer set atop of a multilayer design. Arab J. Basic Appl. Sci. 2023, 30, 593–600. [Google Scholar] [CrossRef]
- Raman, A.; Fan, S. Photonic Band Structure of Dispersive Metamaterials Formulated as a Hermitian Eigenvalue Problem. Phys. Rev. Lett. 2010, 104, 087401. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998; Volume 3. [Google Scholar]
- Dorfmüller, J.; Vogelgesang, R.; Weitz, R.T.; Rockstuhl, C.; Etrich, C.; Pertsch, T.; Lederer, F.; Kern, K. Fabry-Pérot resonances in one-dimensional plasmonic nanostructures. Nano Lett. 2009, 9, 2372–2377. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2007; Volume 1. [Google Scholar]
- Baumberg, J.J.; Aizpurua, J.; Mikkelsen, M.H.; Smith, D.R. Extreme nanophotonics from ultrathin metallic gaps. Nat. Mater. 2019, 18, 668–678. [Google Scholar] [CrossRef]
- Koenderink, A.F. On the use of Purcell factors for plasmon antennas. Opt. Lett. 2010, 35, 4208–4210. [Google Scholar] [CrossRef]
- Derom, S.; Vincent, R.; Bouhelier, A.; des Francs, G.C. Resonance quality, radiative/ohmic losses and modal volume of Mie plasmons. Europhys. Lett. 2012, 98, 47008. [Google Scholar] [CrossRef]
- Srinivasan, K.; Borselli, M.; Painter, O.; Stintz, A.; Krishna, S. Cavity Q, mode volume, and lasing threshold in small diameter AlGaAs microdisks with embedded quantum dots. Opt. Express 2006, 14, 1094–1105. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.; Pelton, M.; Guest, J.R. Understanding how acoustic vibrations modulate the optical response of plasmonic metal nanoparticles. ACS Nano 2017, 11, 9360–9369. [Google Scholar] [CrossRef]
- Kolwas, K. Optimization of Coherent Dynamics of Localized Surface Plasmons in Gold and Silver Nanospheres; Large Size Effects. Materials 2023, 16, 1801. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).