Numerical Study on Minor Leak for Pressure-Driven Flow in Straight Pipe and 90° Elbow Transporting Different Media
Abstract
1. Introduction
2. Computational Model and Methodology
2.1. Computational Model
2.2. Governing Equations
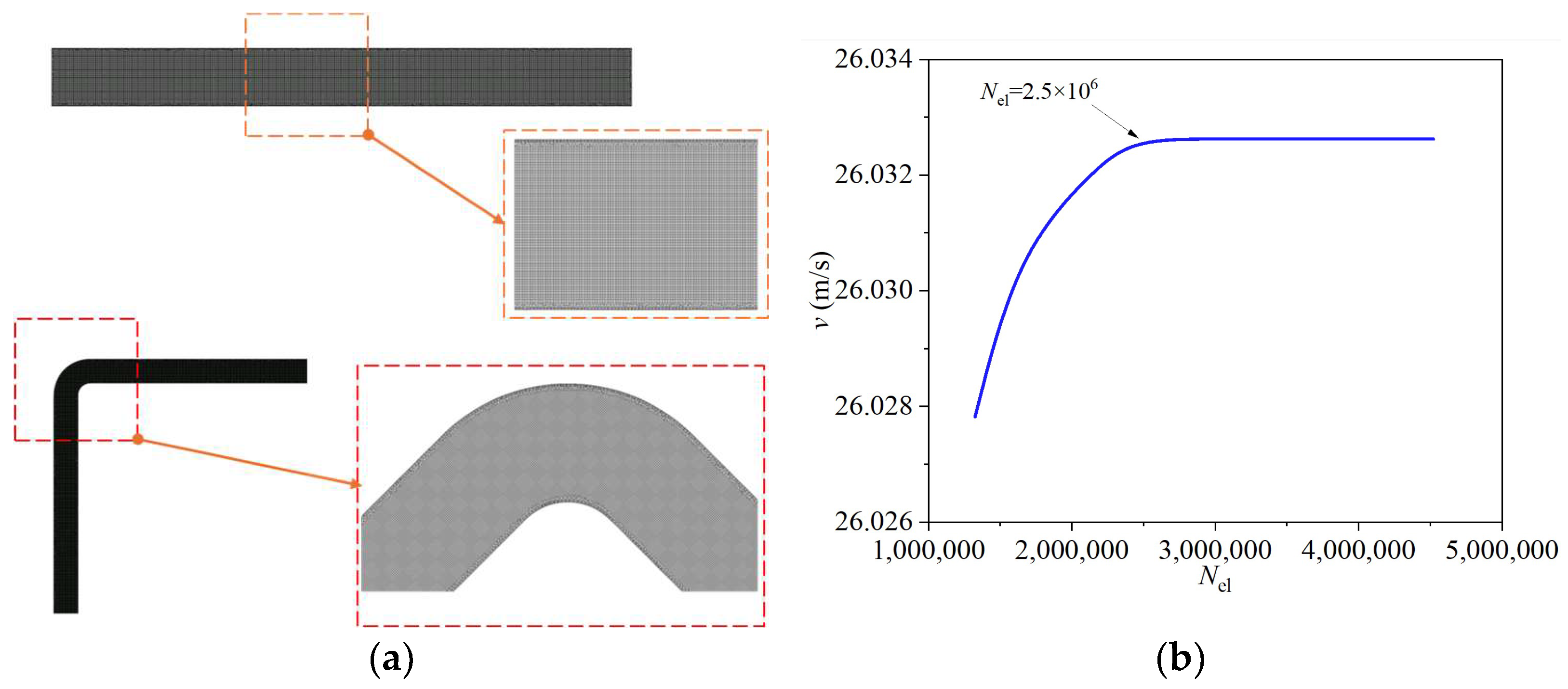
2.3. Mesh Generation
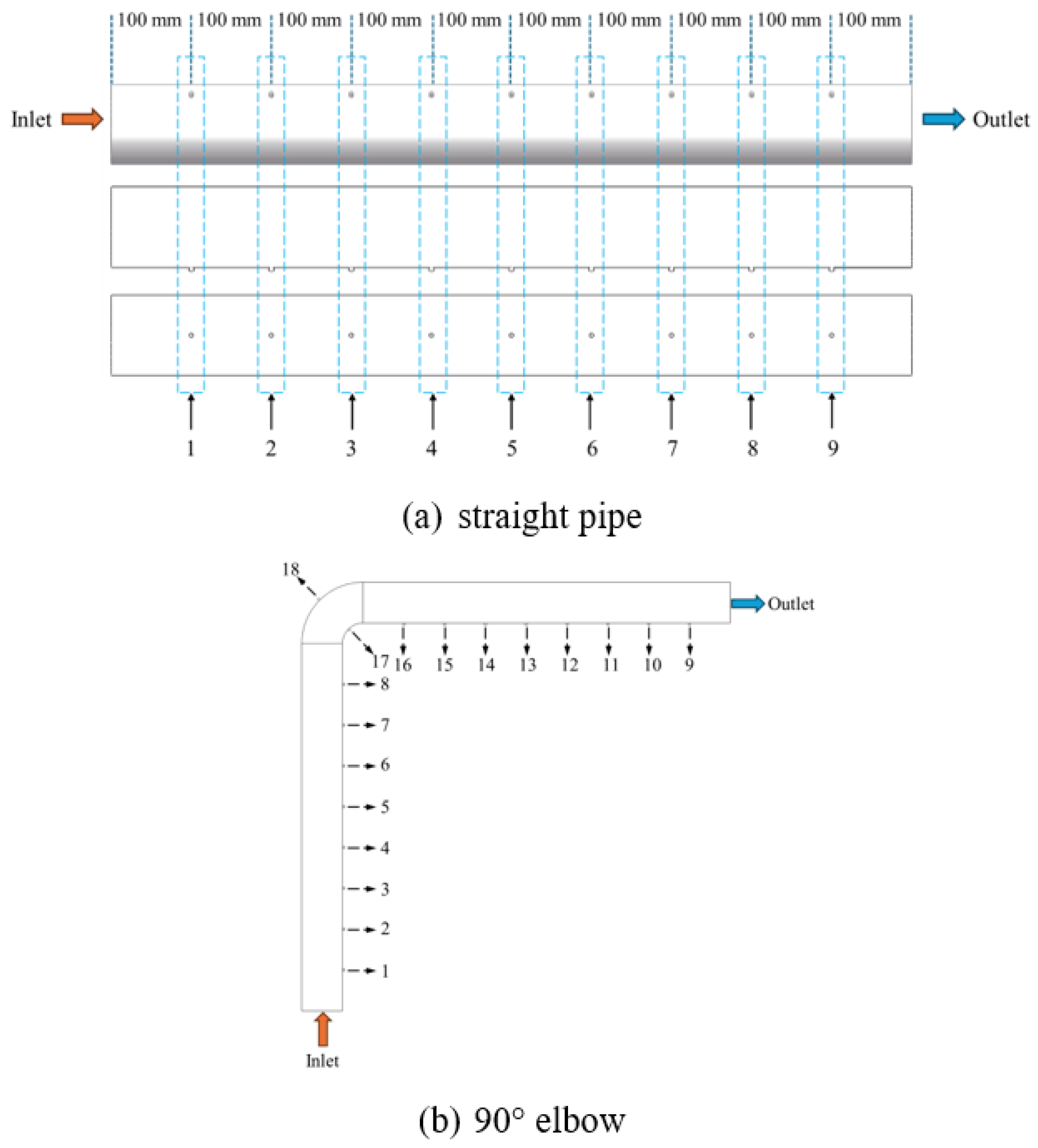
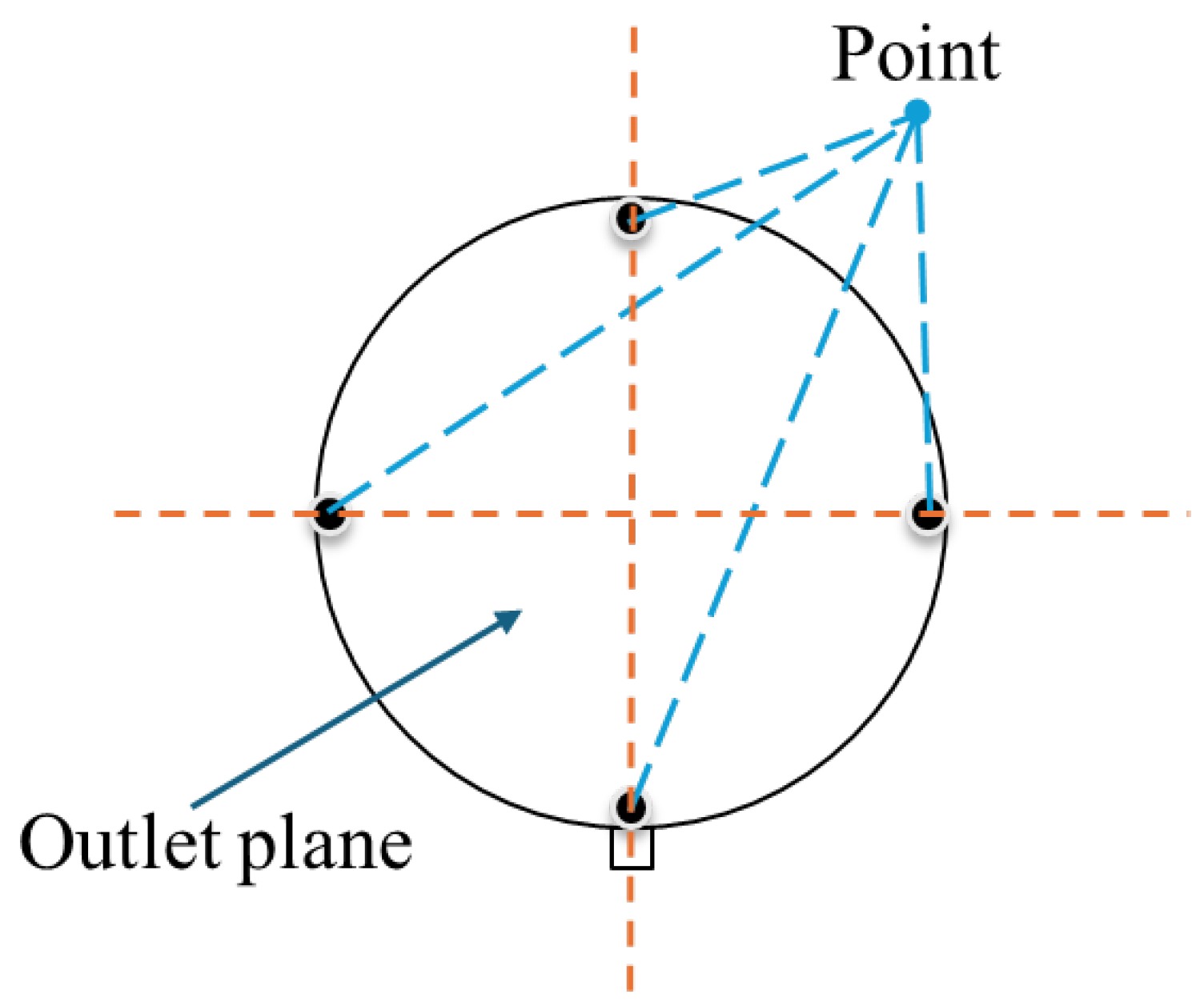
2.4. Boundary Conditions
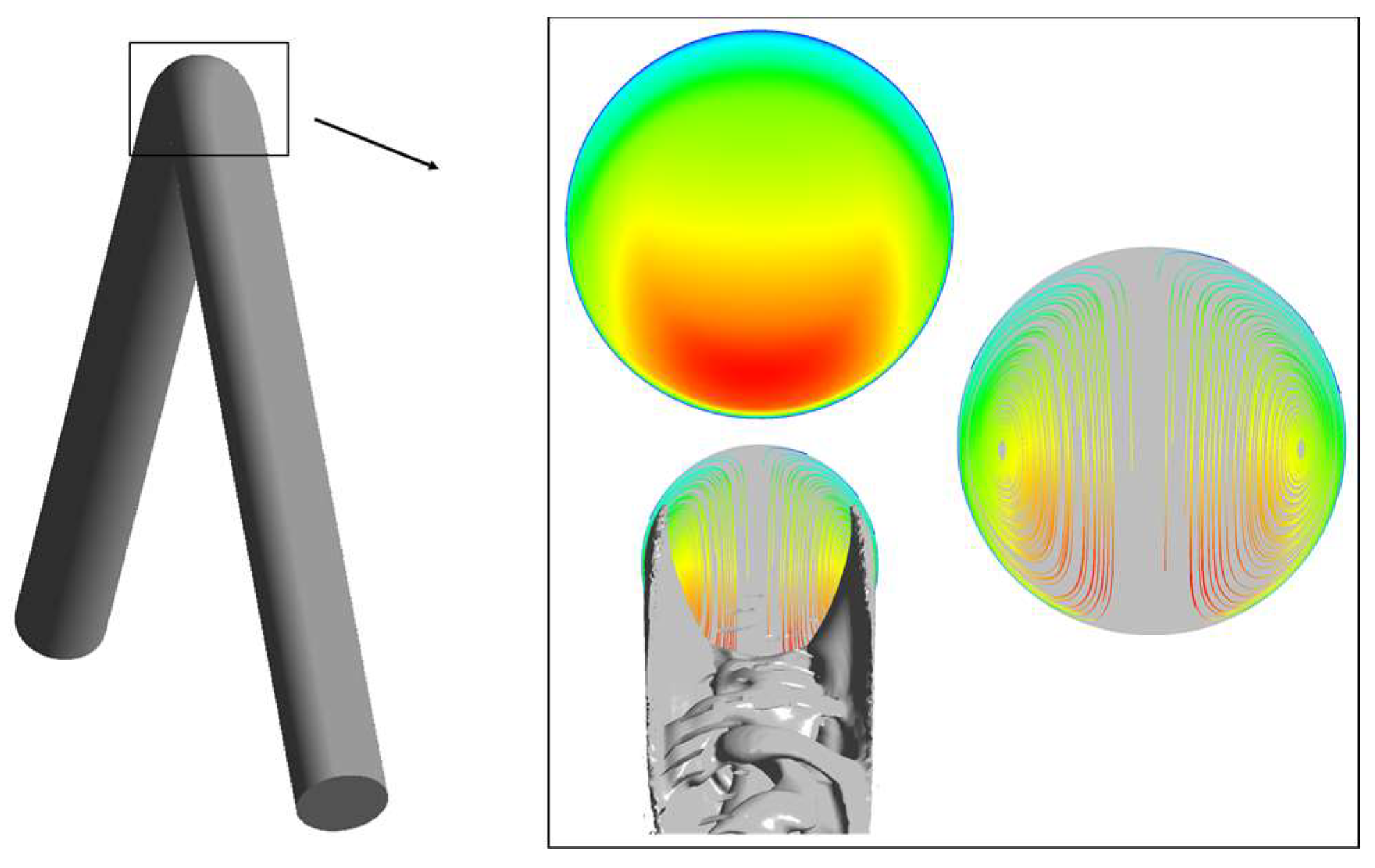
2.5. Vortex Identification
3. Straight Pipe
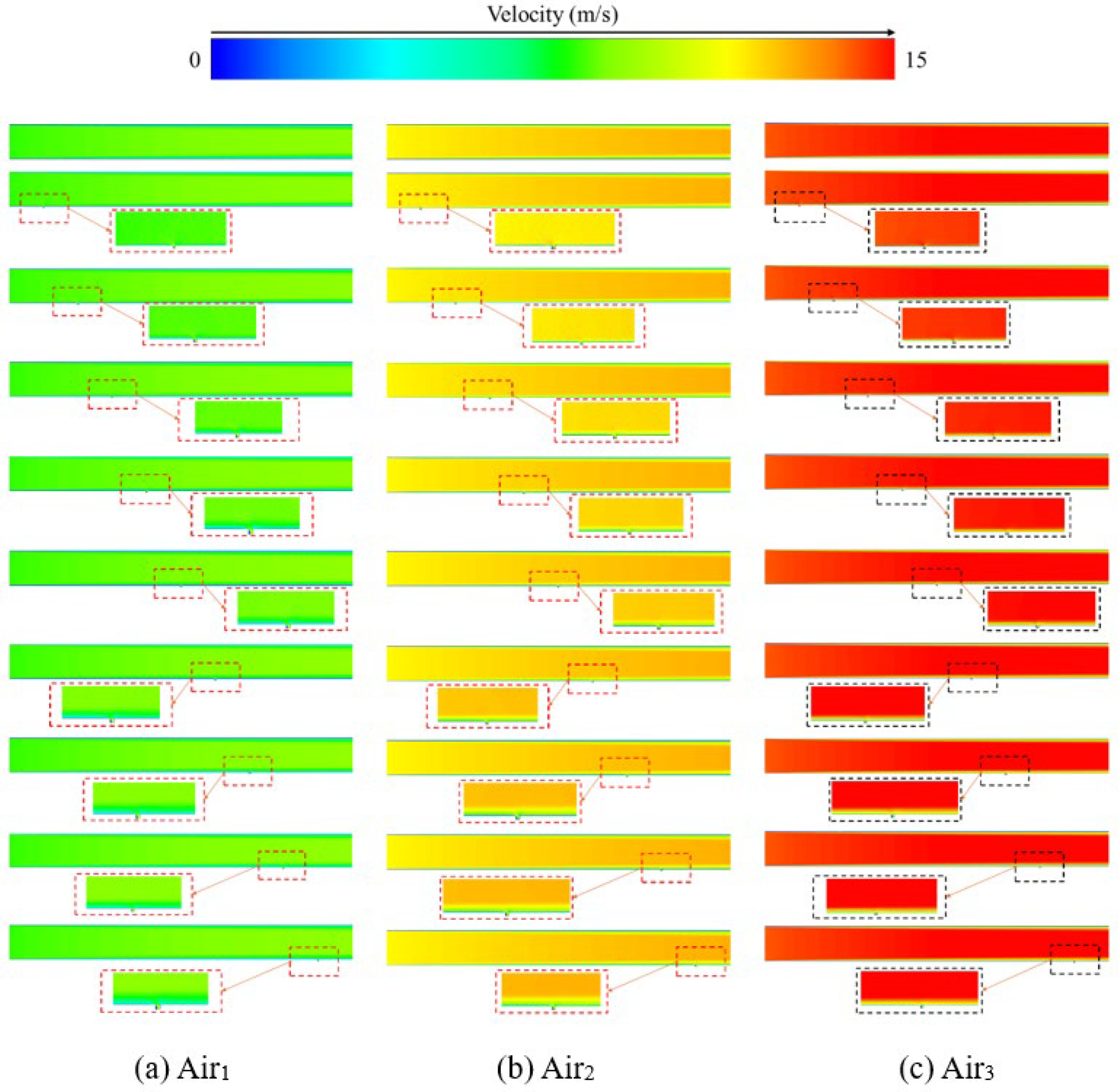
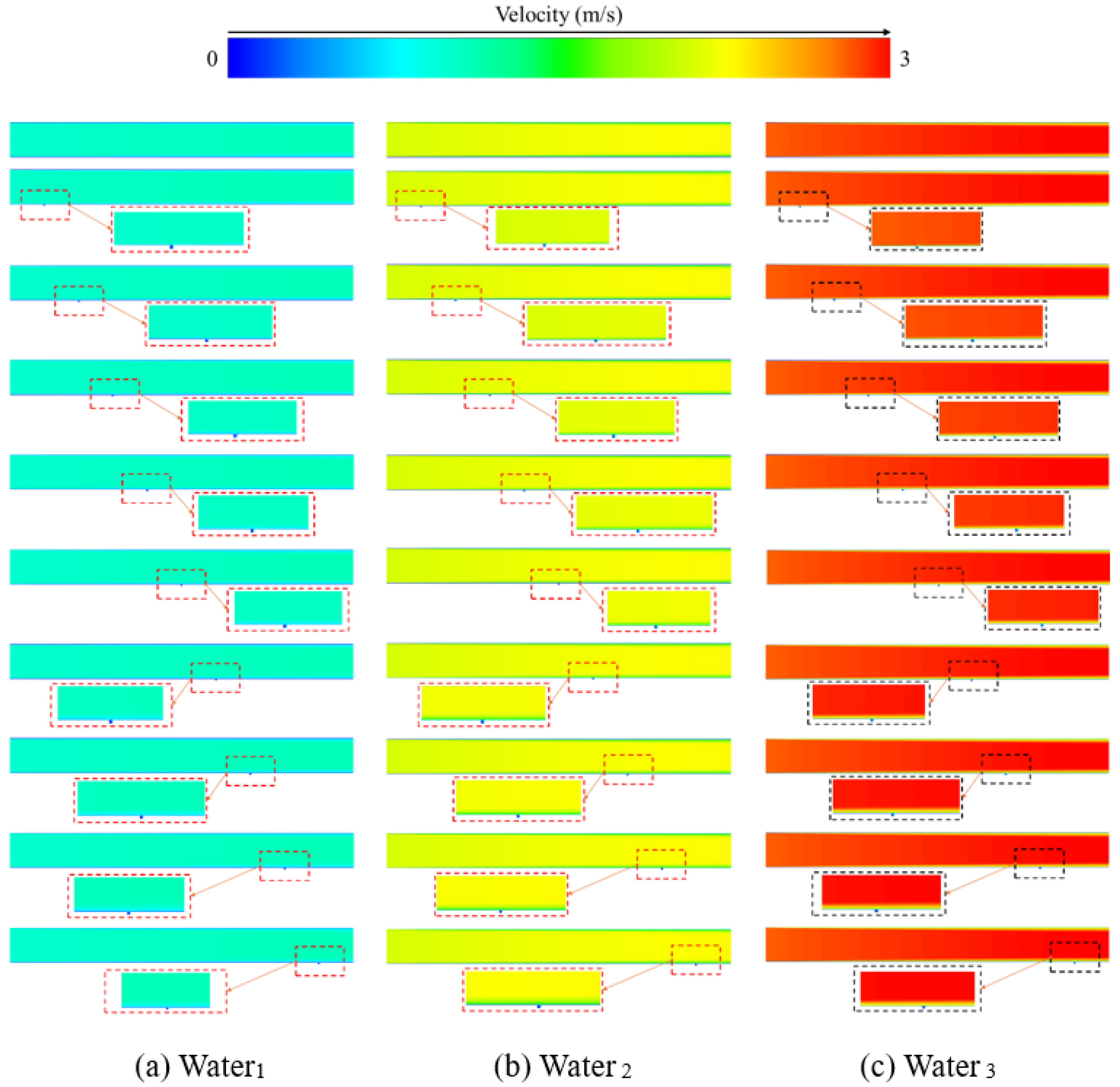
3.1. Internal Flow Field
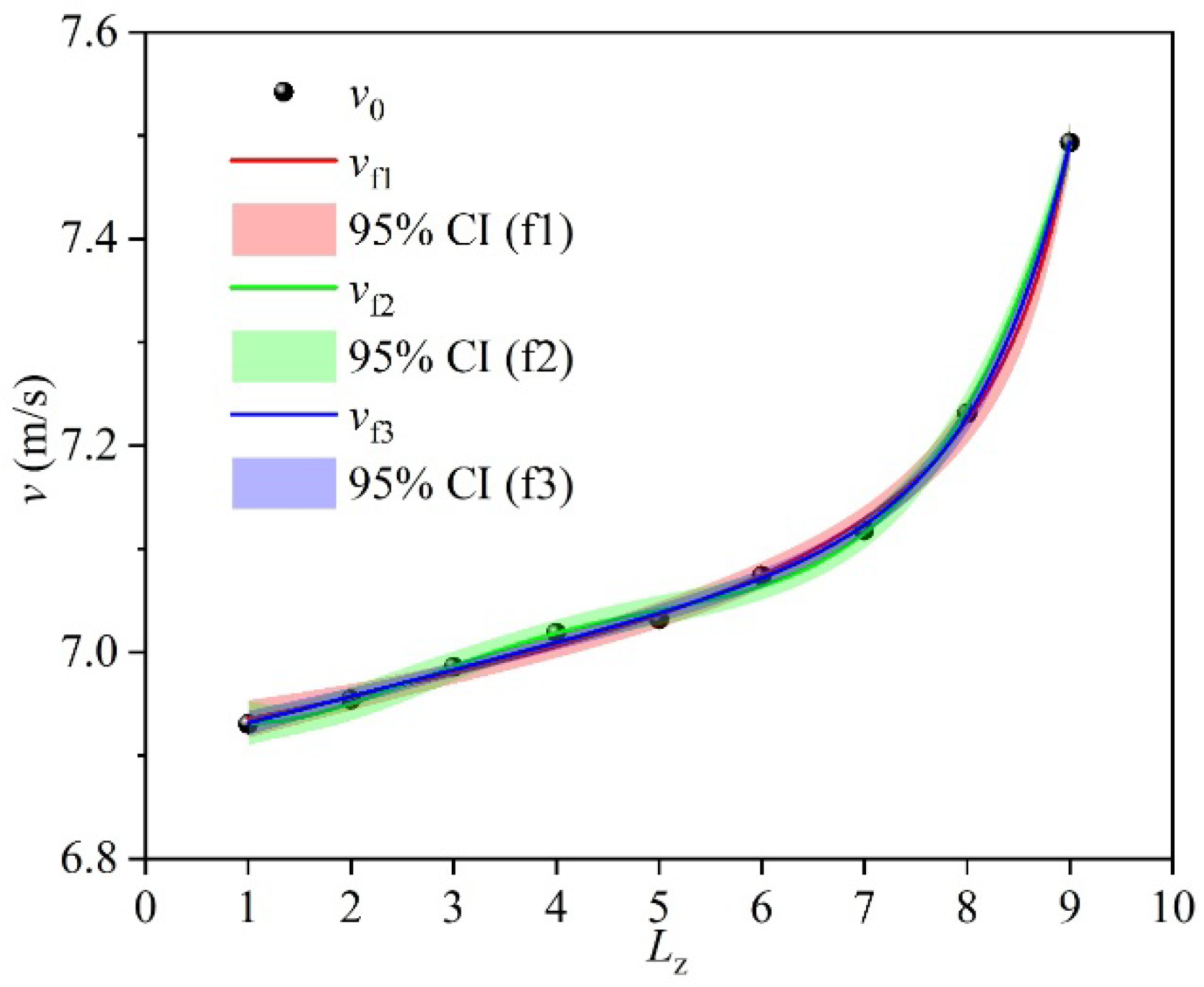
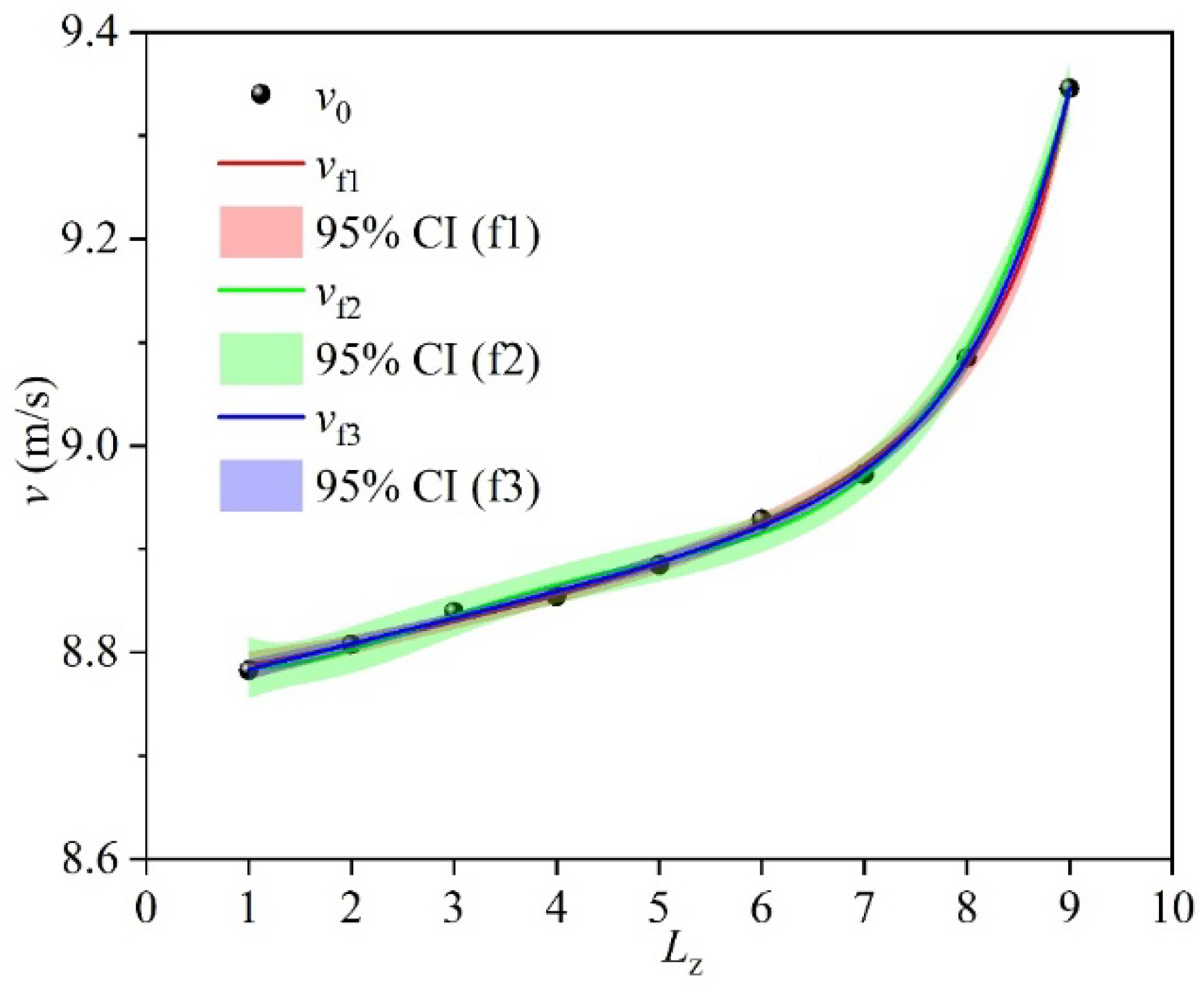
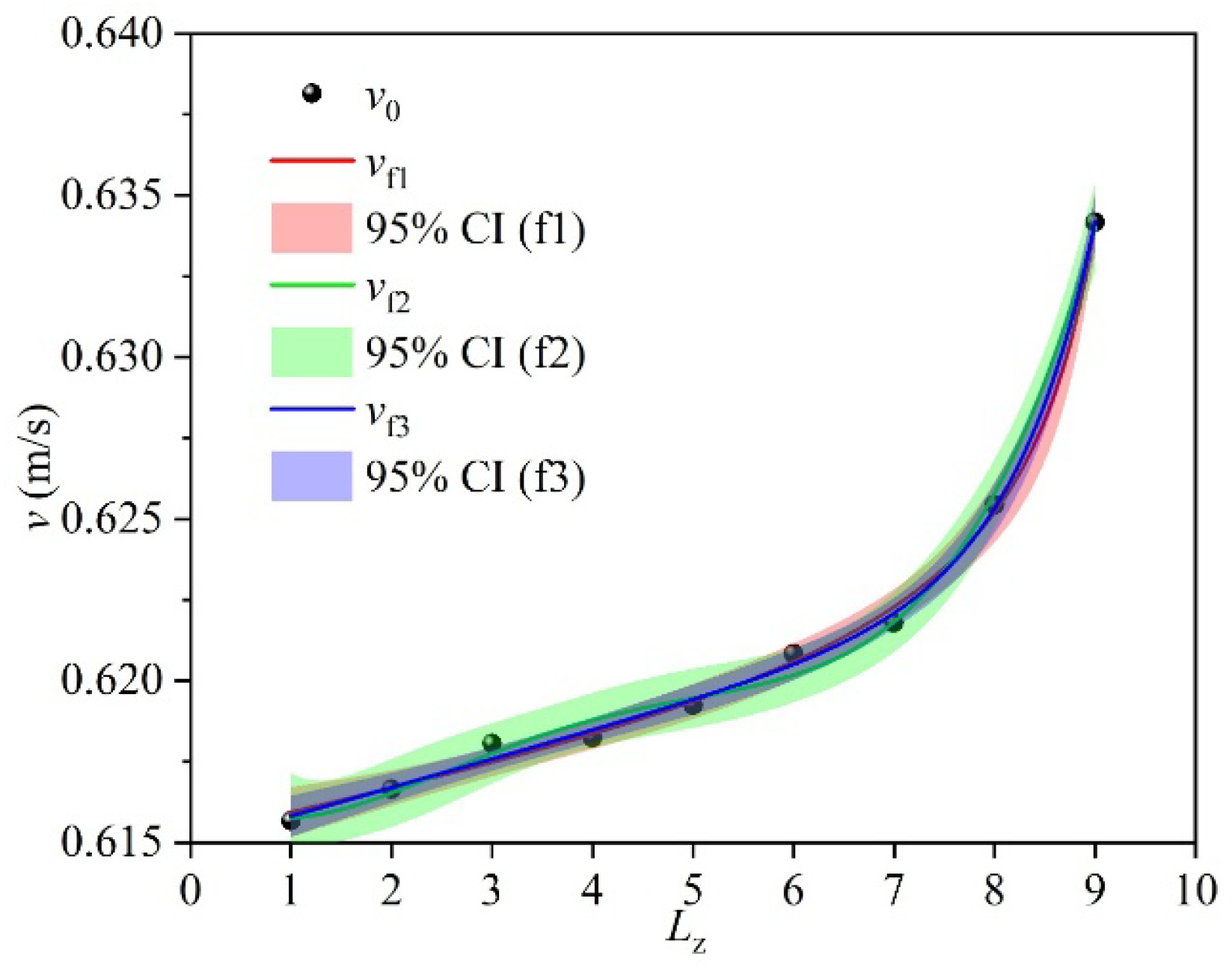
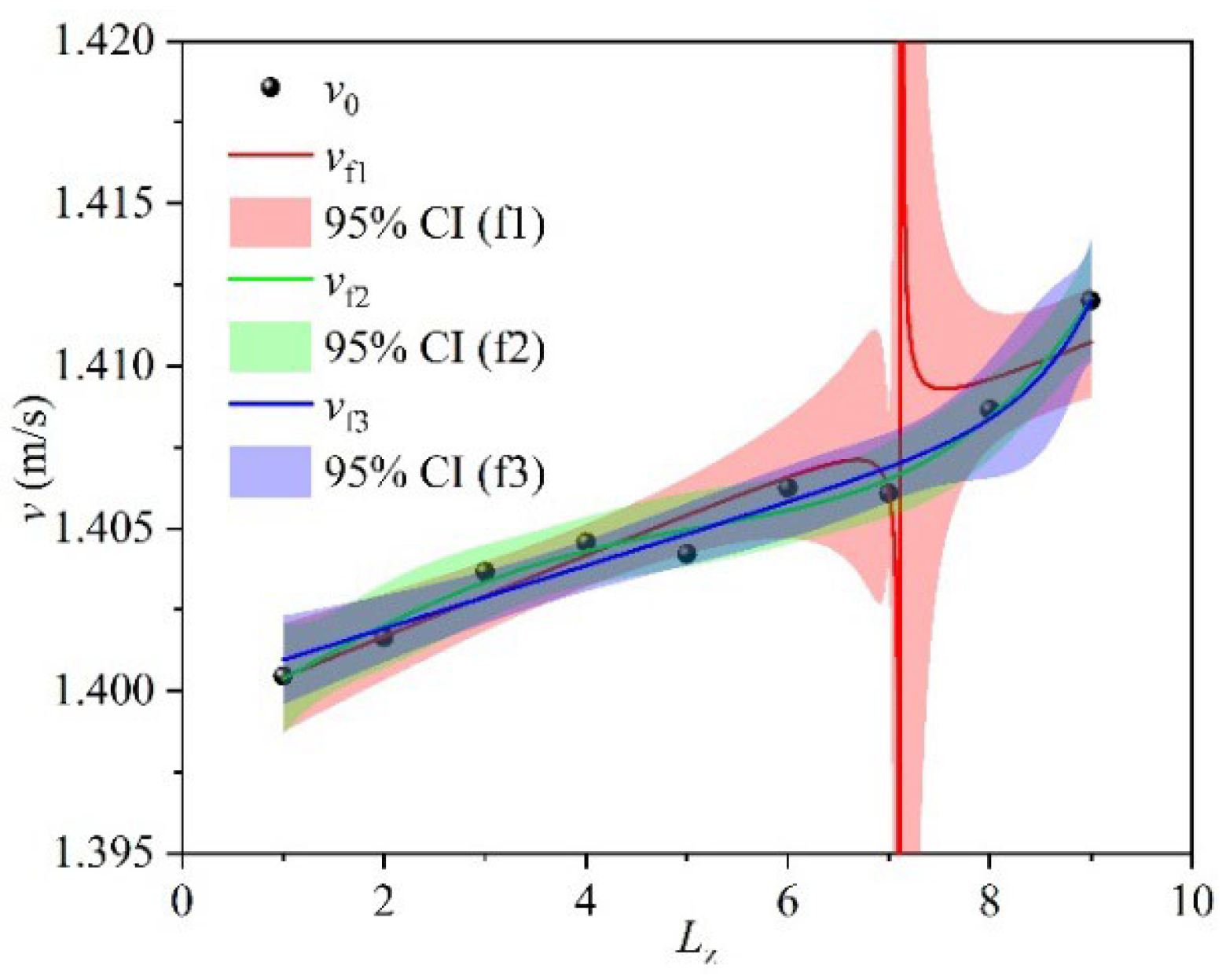
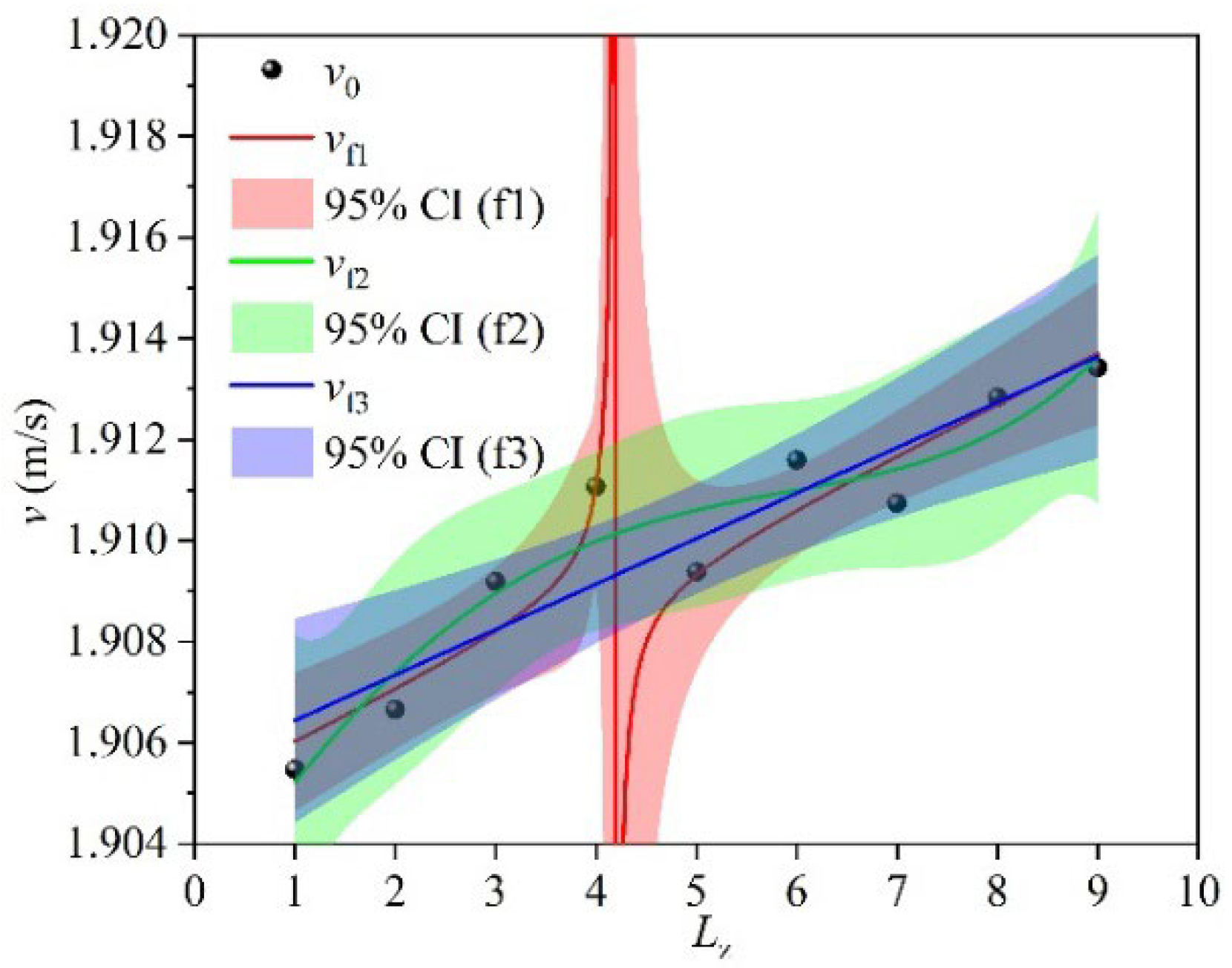
3.2. Prediction Functions
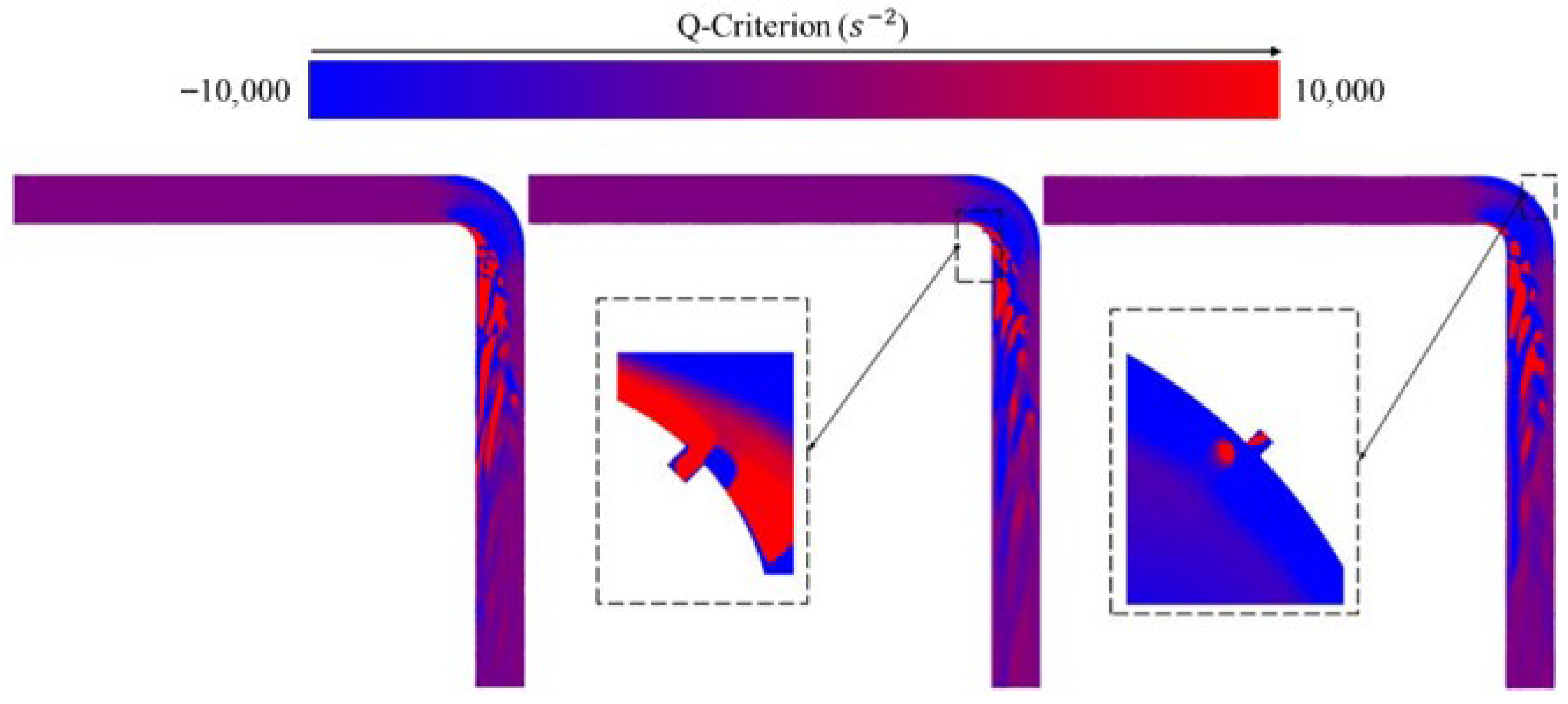
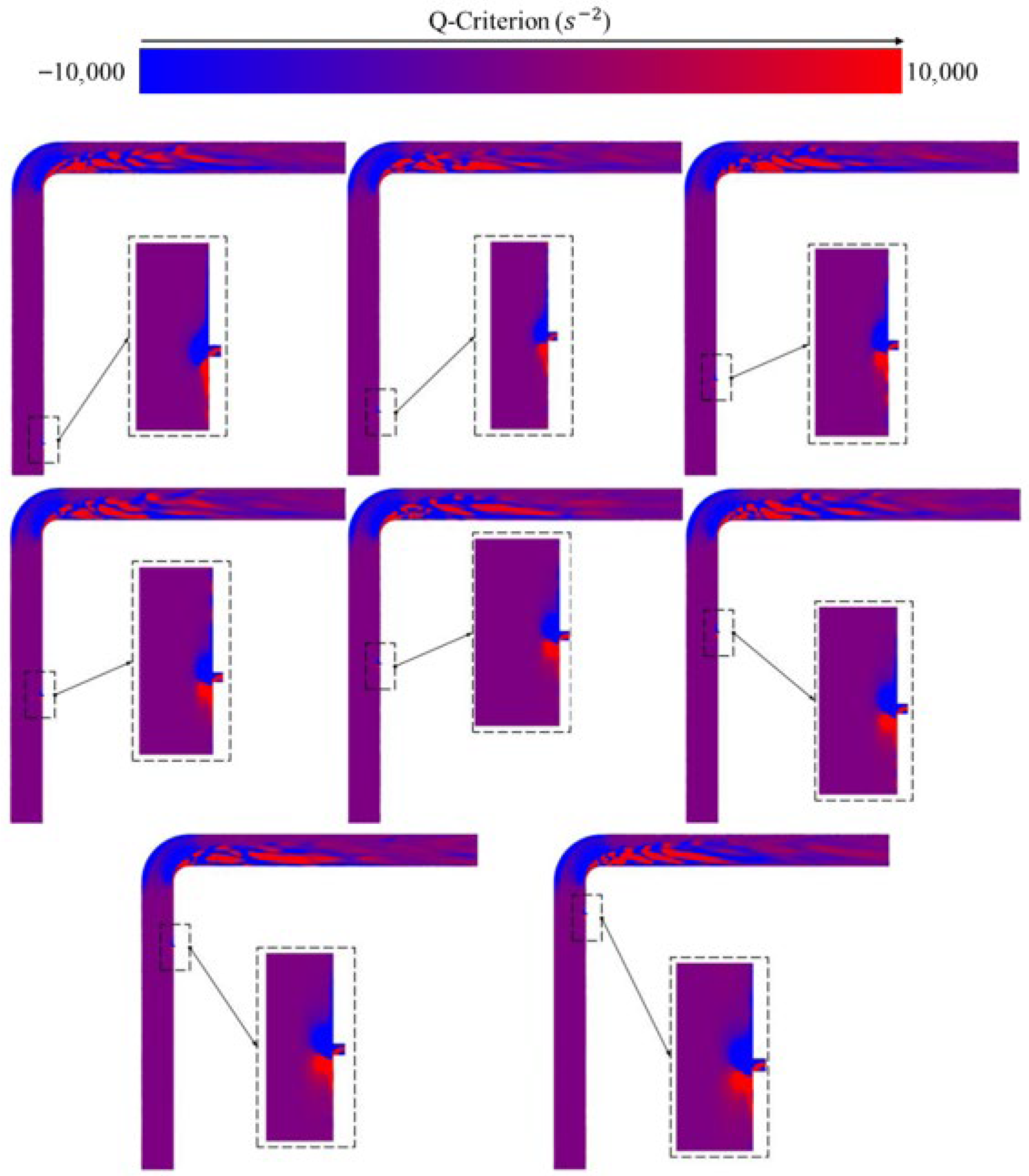
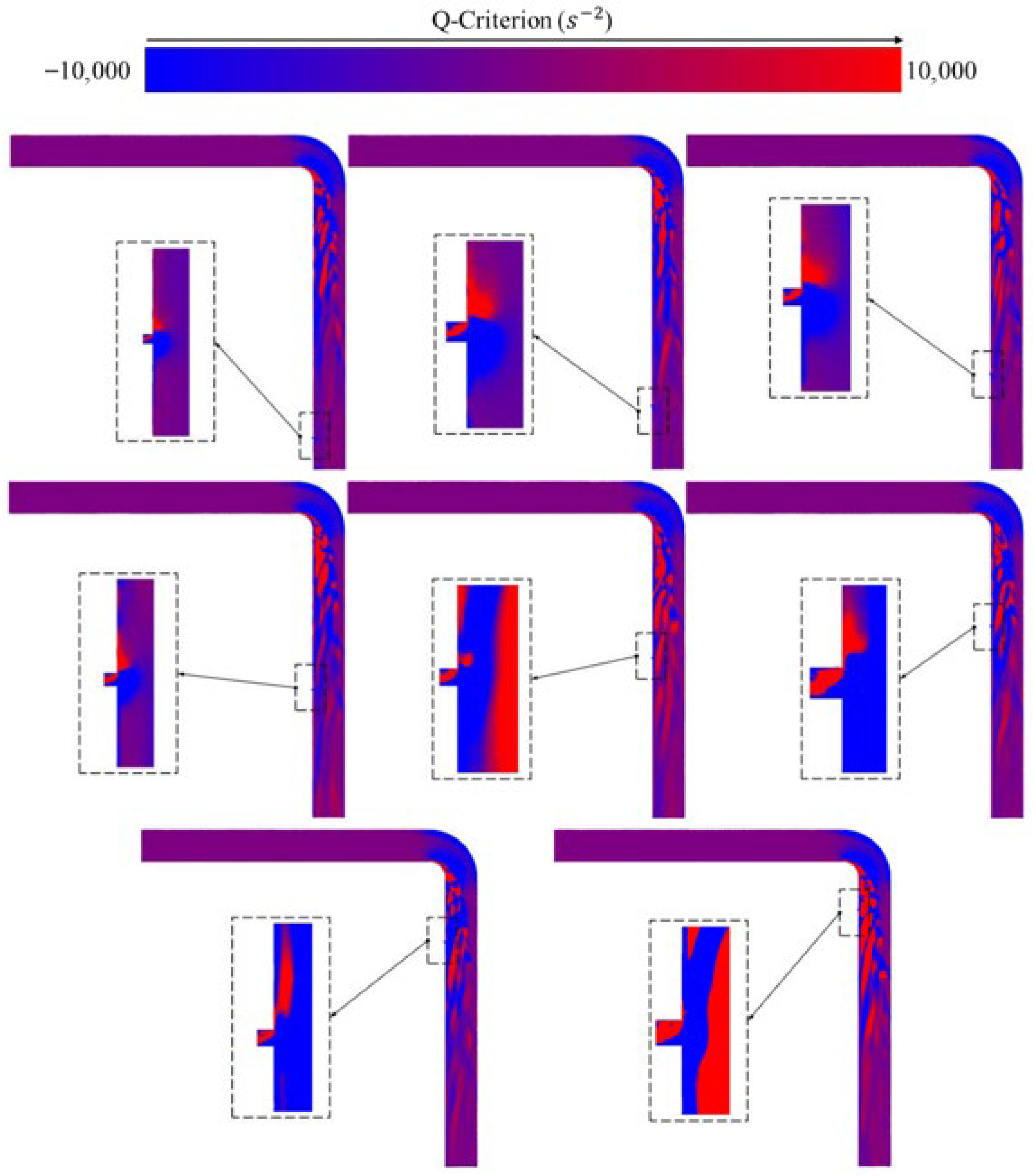
4. 90° Elbow
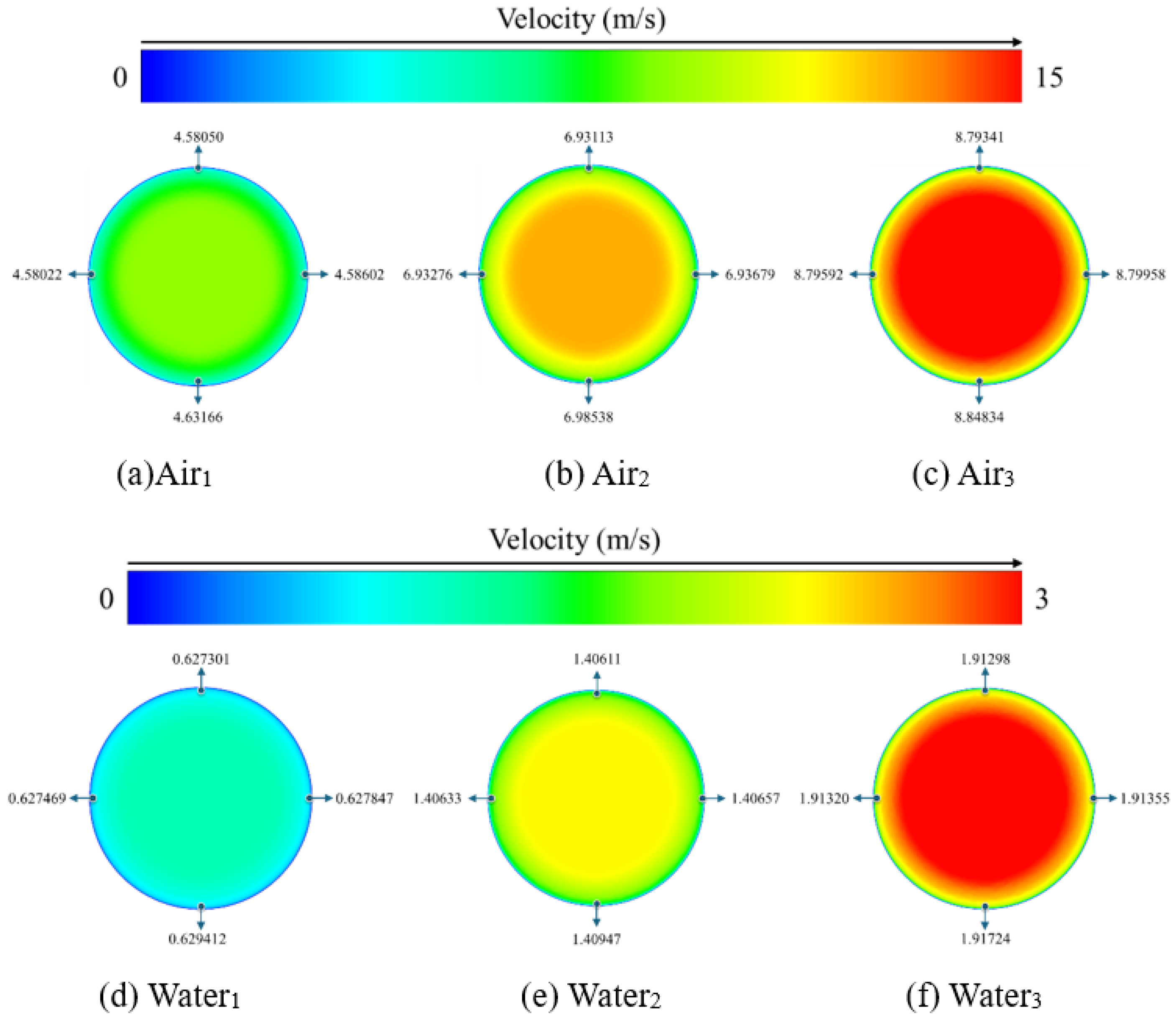
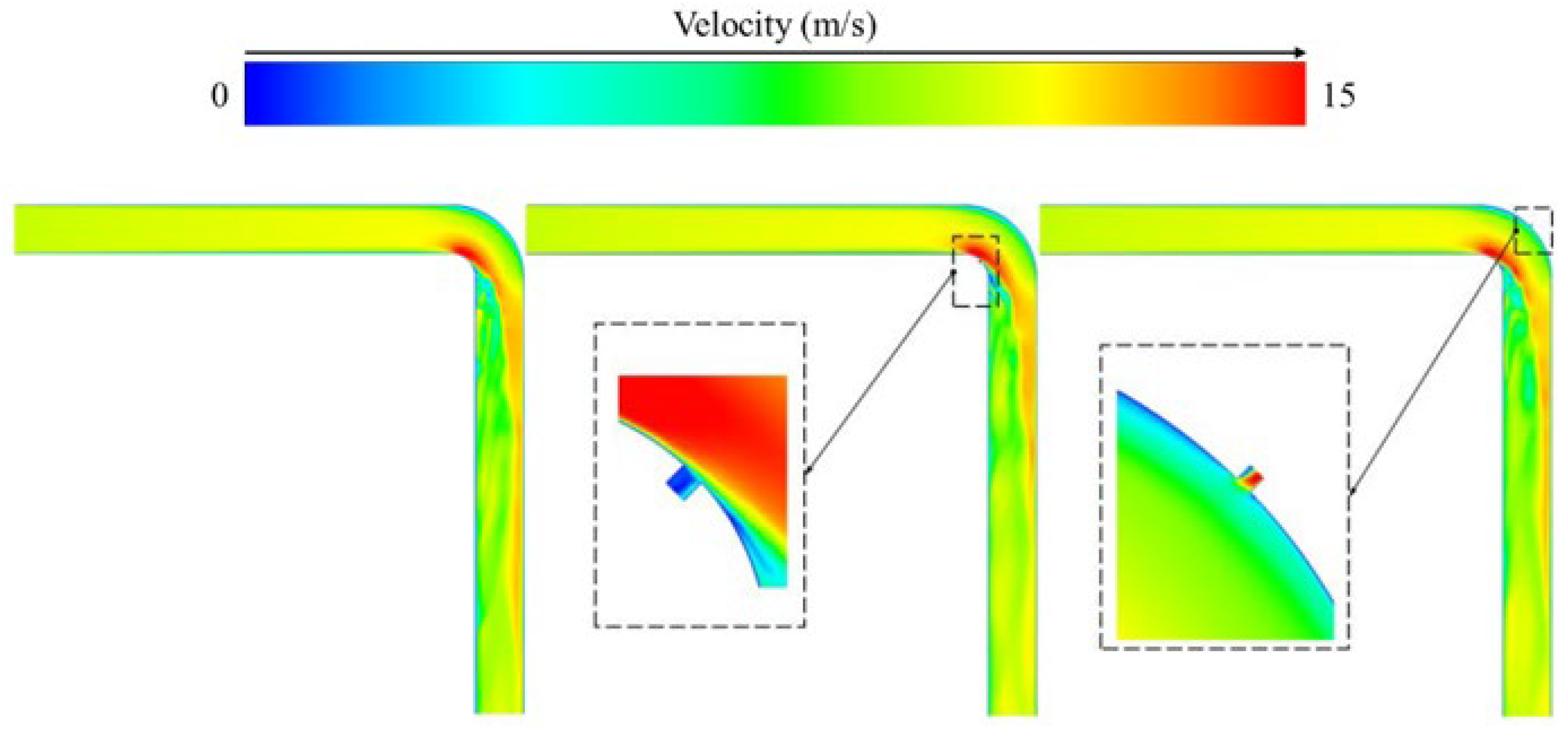
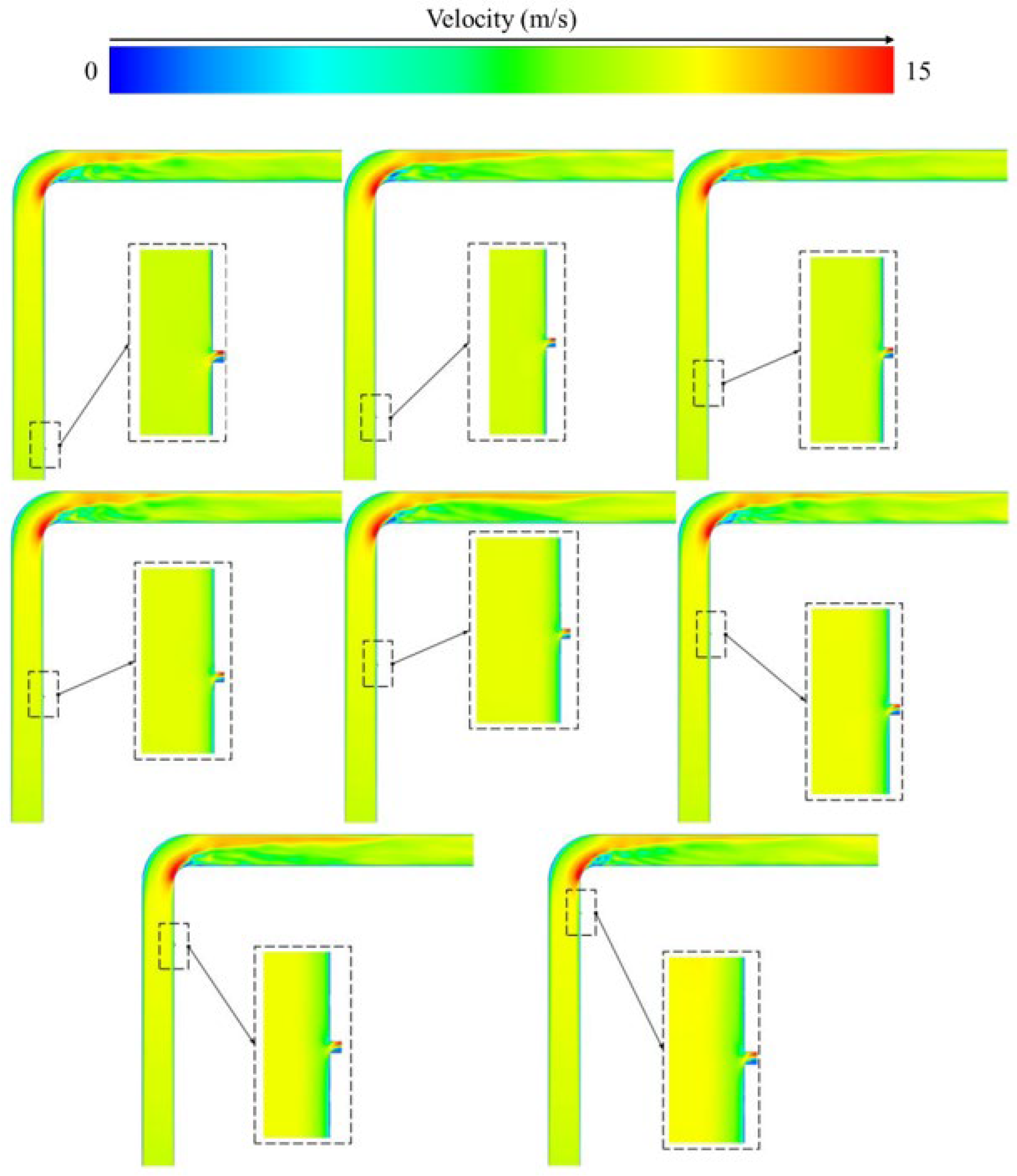
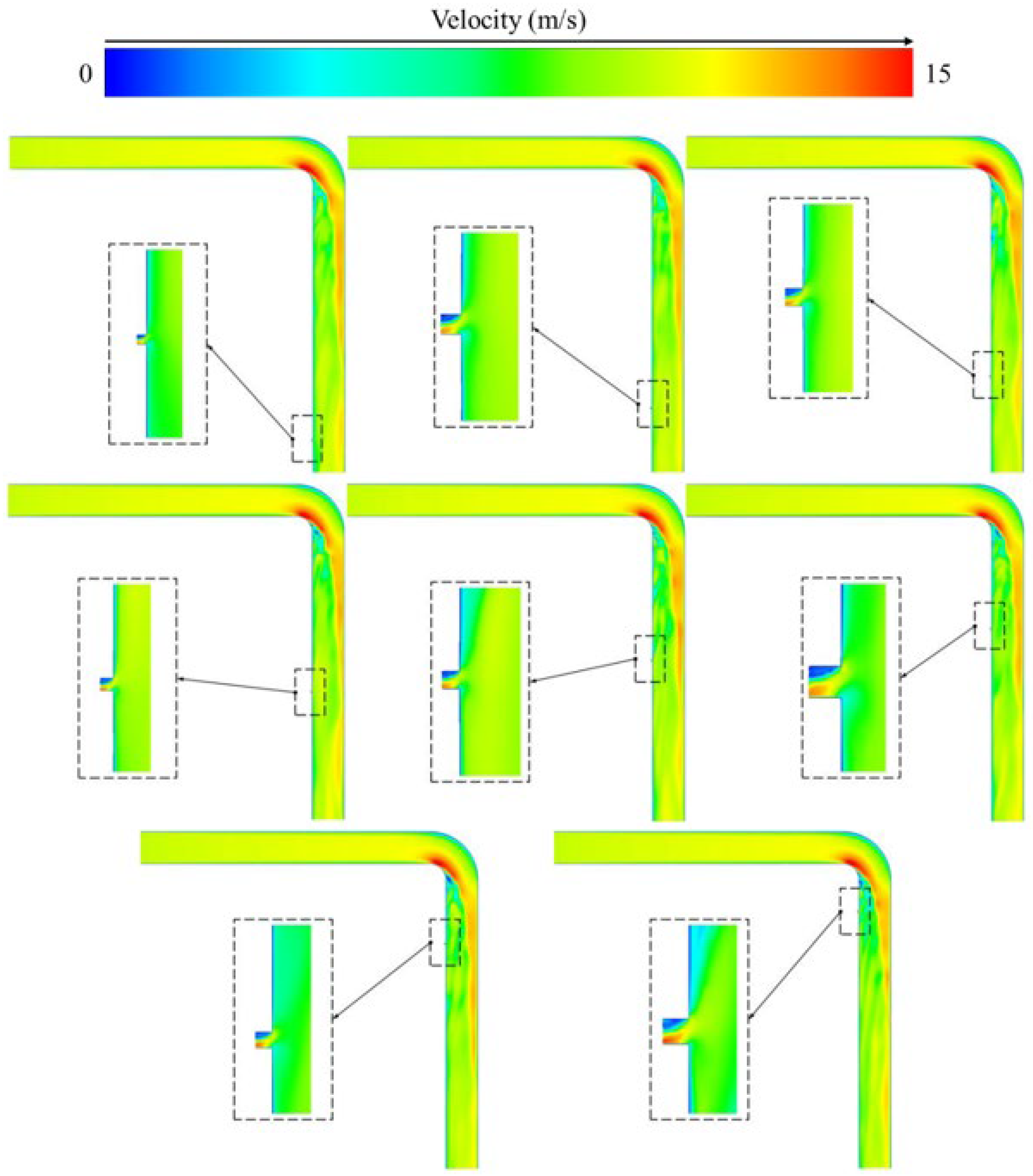
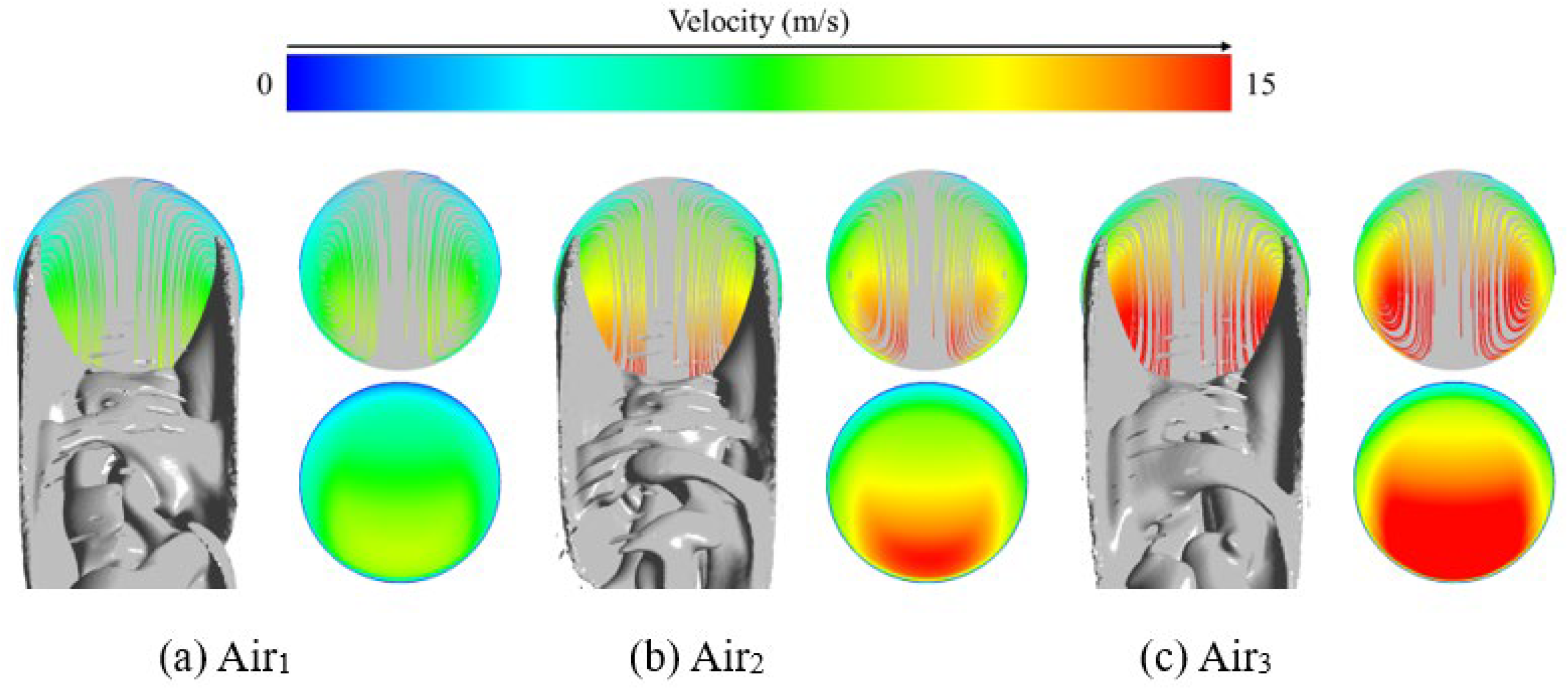
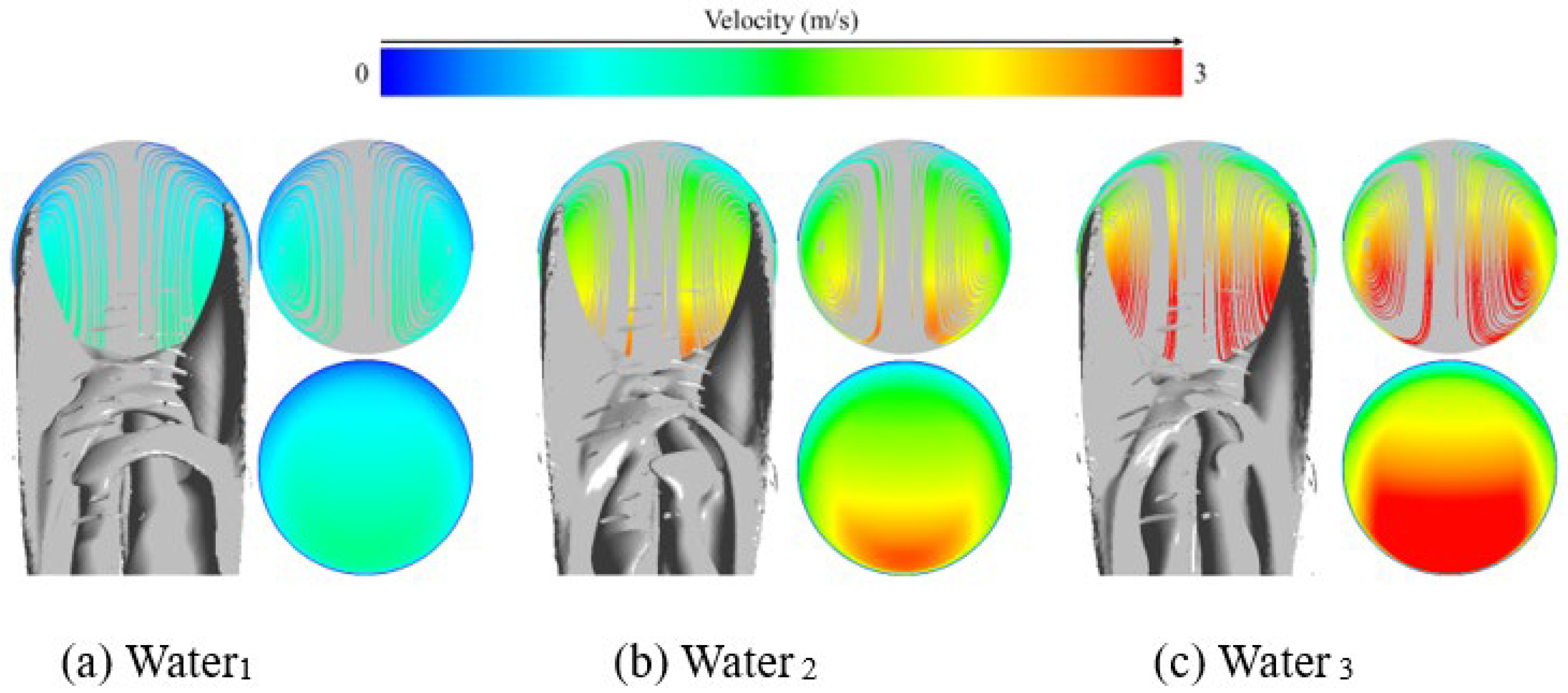
4.1. Velocity Contour
4.2. Vortex Distribution
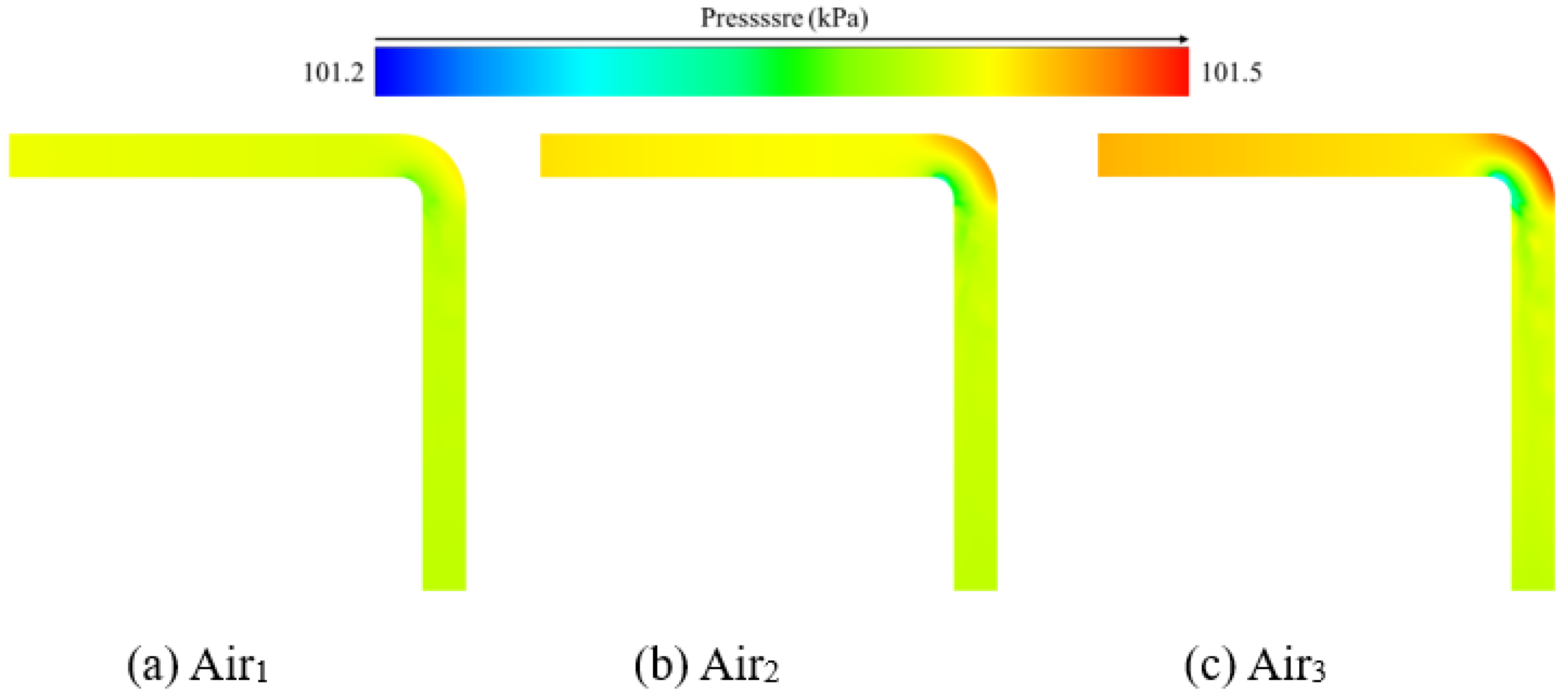
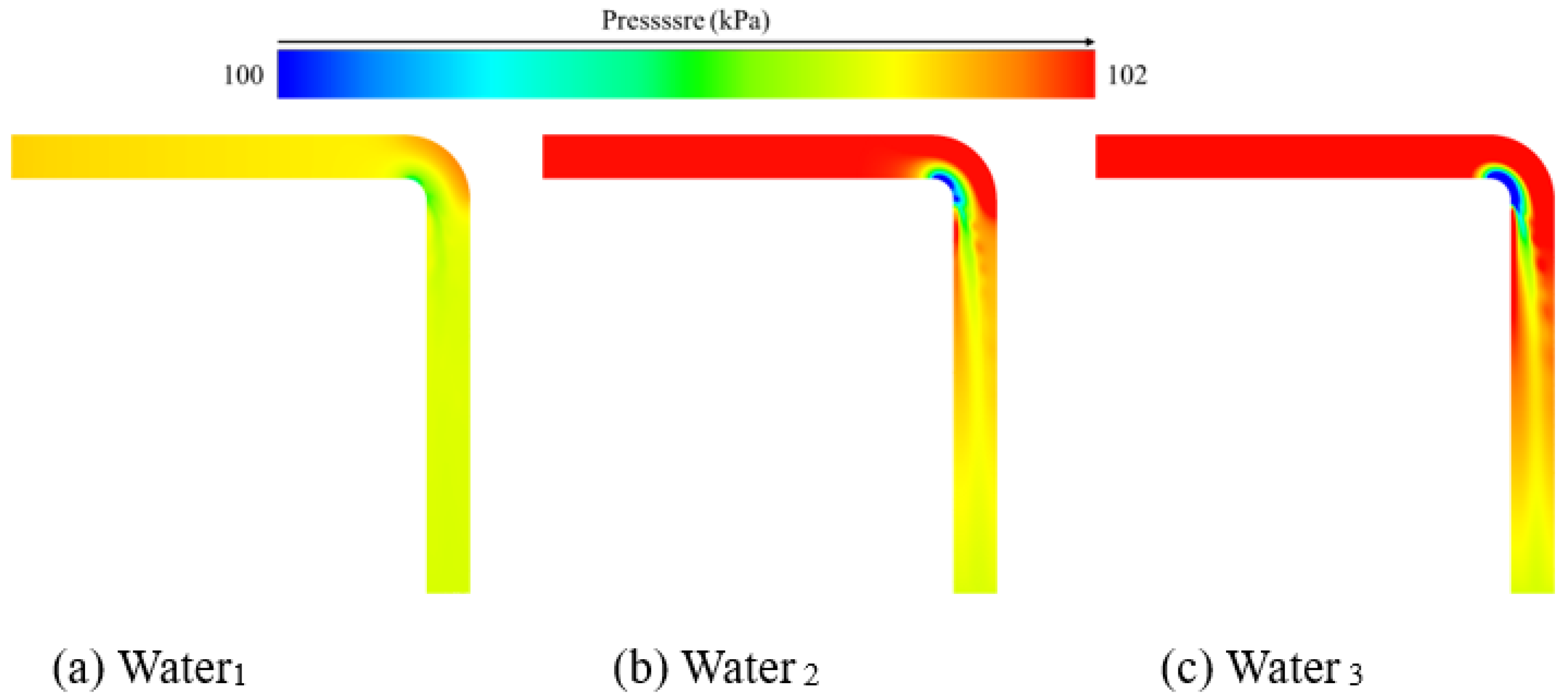
4.3. Pressure Distribution Without Leakage Points
4.4. Discussion
5. Conclusions
- (1)
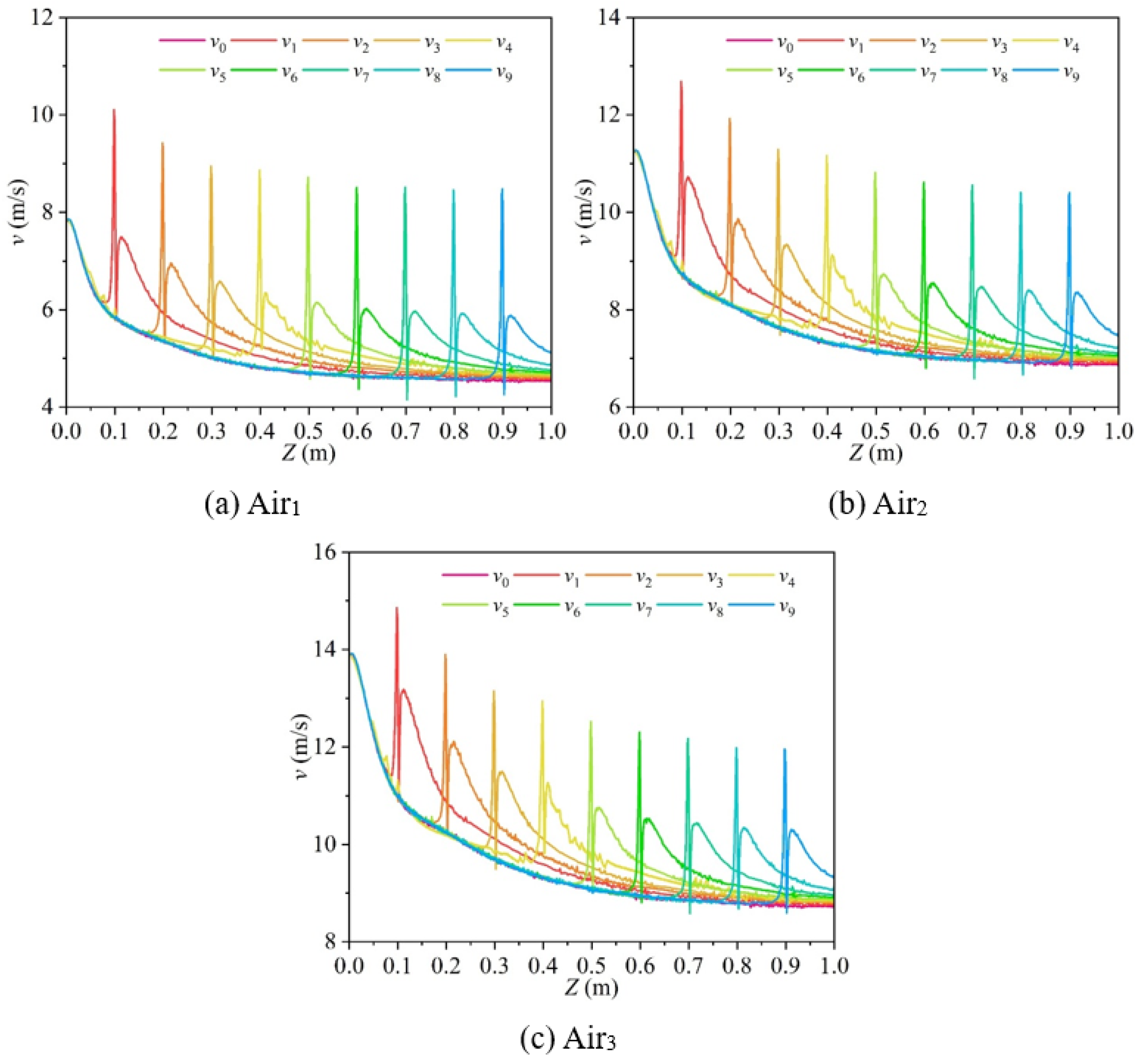
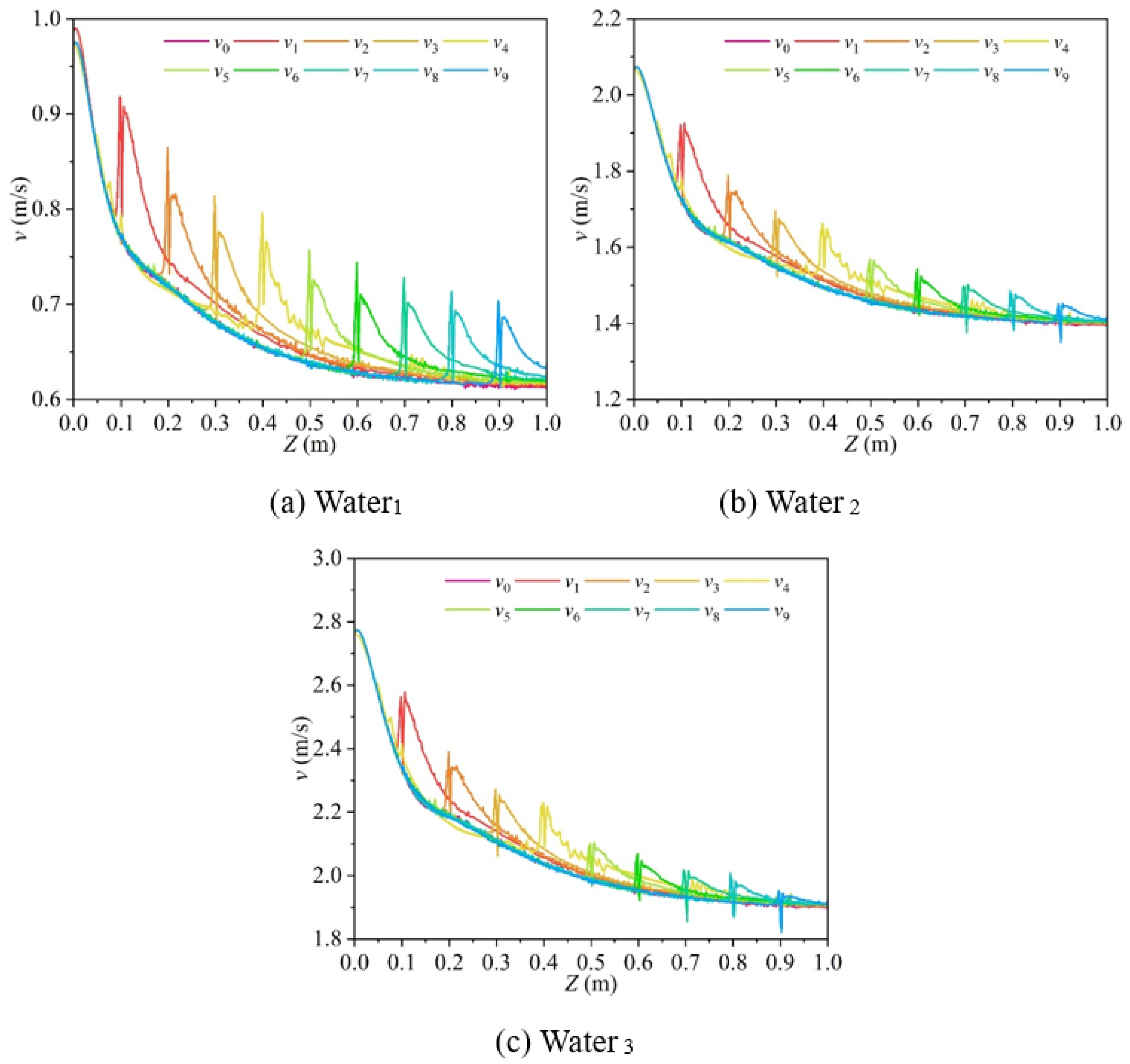
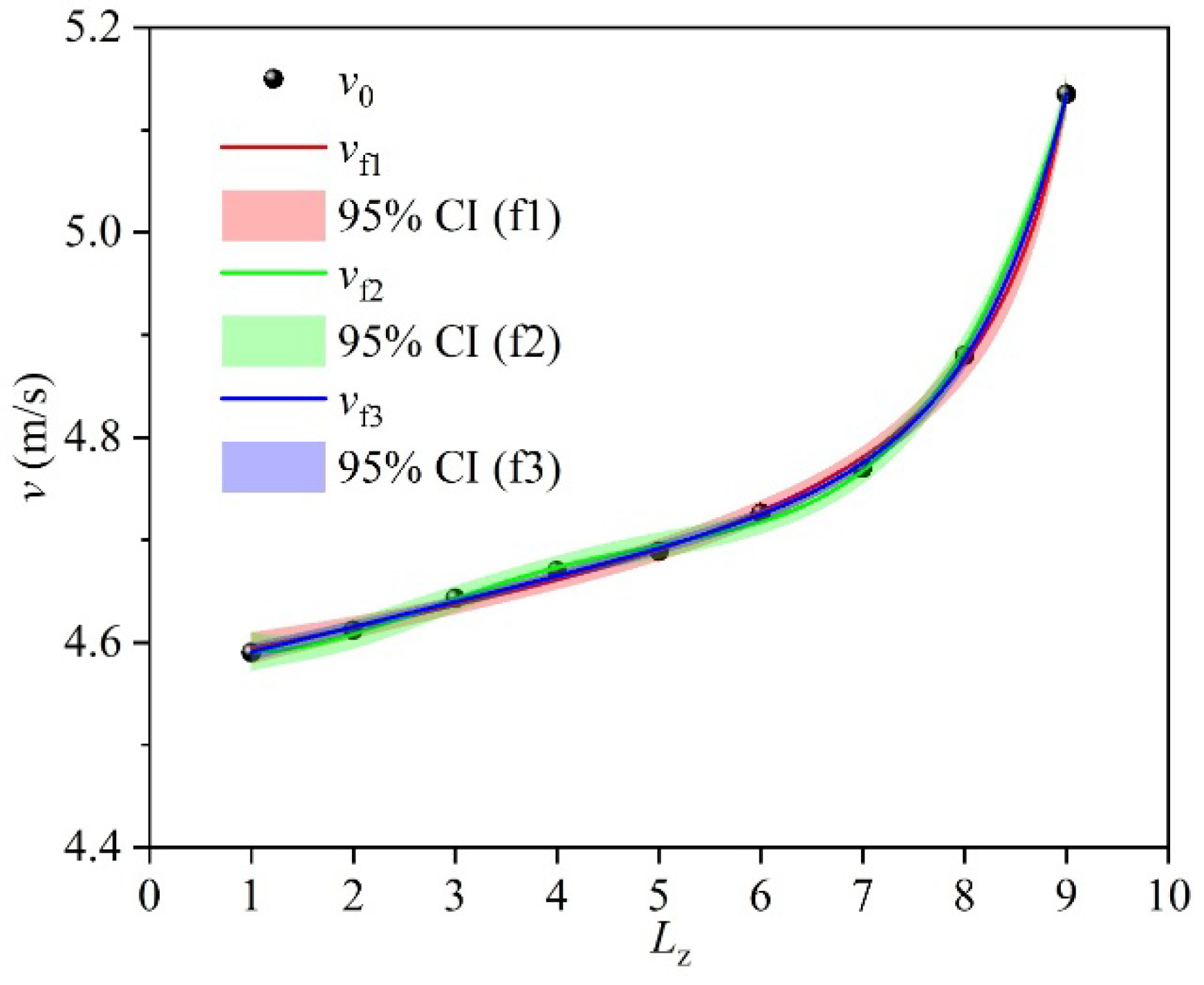
- Regarding the fitting ability of the straight pipeline leakage location monitoring model, the nonlinear function models exhibit excellent prediction accuracy under the air medium (R2 > 0.99), while the fitting effect of the models under the water medium gradually weakens with the increase in inlet pressure (R2 decreases to 0.77 under Water3 condition), mainly limited by the damping effect of the liquid’s high viscosity on velocity field diffusion. Therefore, from a practical application perspective, under the air medium, there remains a one-to-one correspondence between the outlet flow velocity and the leakage hole location, allowing the leakage position to be reliably inferred directly from the outlet flow velocity. Under the water medium, it is necessary to control the inlet pressure below 1.04 × 105 Pa (Water2 condition), while for high-pressure conditions, additional monitoring methods should be integrated to ensure positioning accuracy.
- (2)
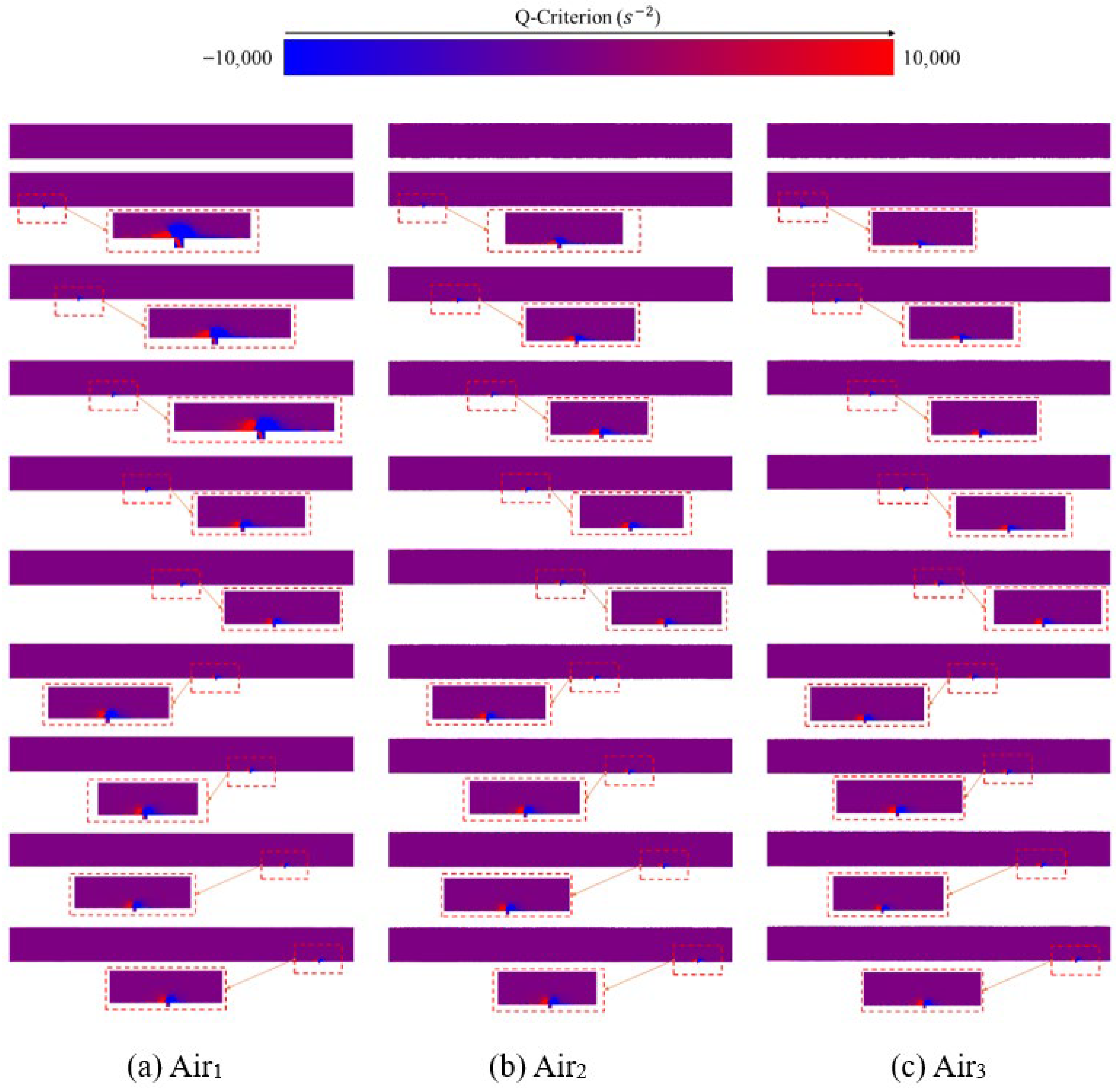
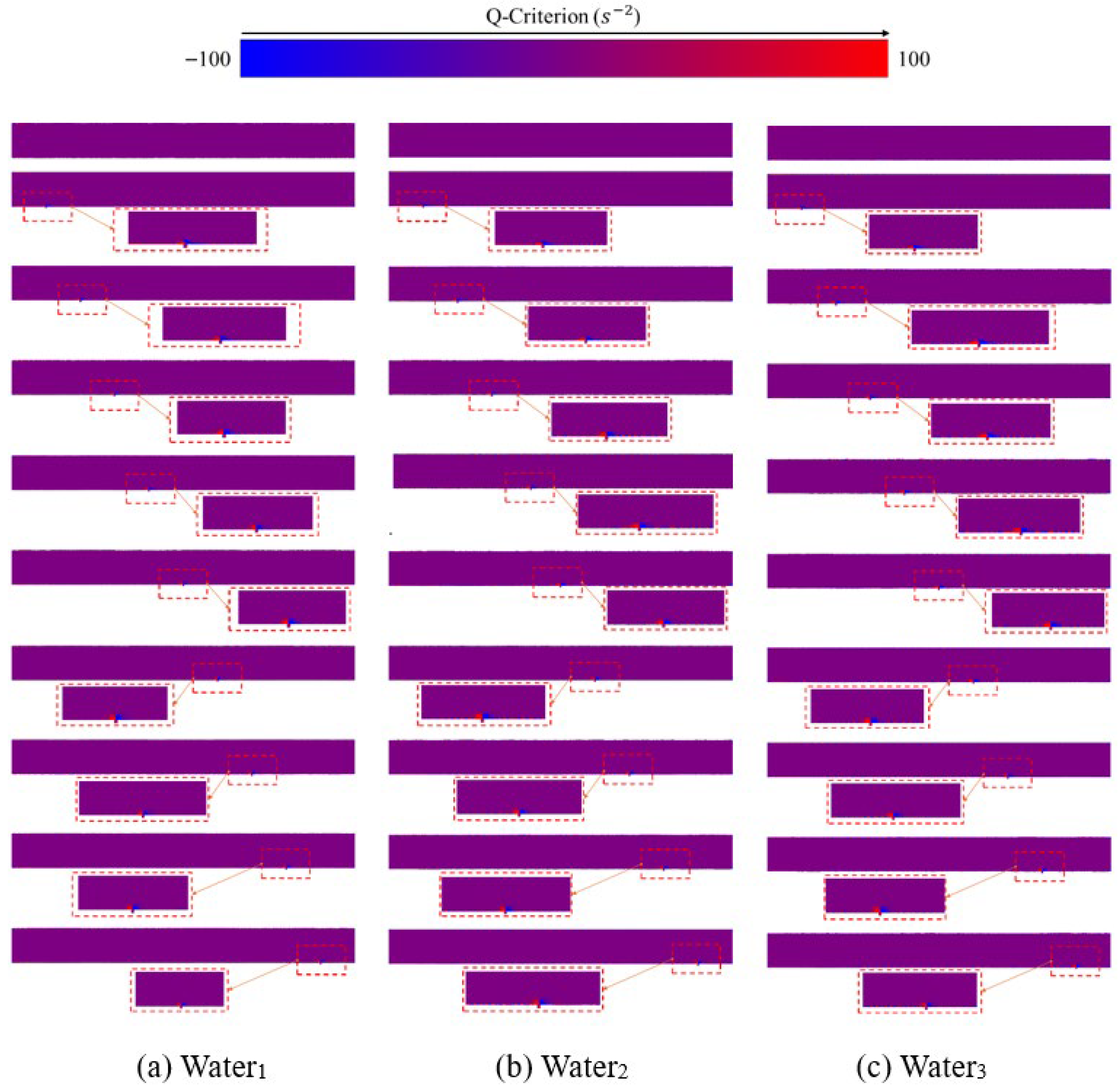
- In terms of vorticity field evolution, the vorticity magnitude at the leakage hole under the air medium in the straight pipeline can reach more than 6 × 105 s−2. In contrast, due to the high viscosity coefficient of the water medium, the vortex structures are rapidly dissipated, with a vorticity magnitude of only 1 × 105 s−2 and showing asymmetric attenuation characteristics.
- (3)
- The migration of the leakage hole position leads to an increase in the density of local velocity contours. In a straight pipeline, the flow velocity in the central region is consistently higher than that in the edge region, and the flow velocity in the lower part of the edge region is significantly enhanced. The root cause can be attributed to the local pressure gradient disturbance and mass flux redistribution induced by the leakage hole.
- (4)
- For curved pipes, the analysis of pressure distribution characteristics reveals that an increase in the inlet pressure gradient directly elevates the overall pressure level within the pipeline and intensifies localized pressure disturbances in the bend region. In the air medium, the peak pressure at the larger bend under high inlet pressure increases significantly. In the water medium, the localized pressure restructuring effect in the curved pipe exhibits a linearly strengthening trend as the inlet pressure rises.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Physical Meaning | Unit |
| k | Turbulent kinetic energy | m2/s2 |
| μt | Turbulent viscosity | Pa·s |
| σω | Turbulent Prandtl number | |
| Pk | Turbulent kinetic energy production term | Pa/s |
| β* | Model constant | |
| ω | Specific dissipation rate | 1/s |
| γ | Model coefficient | |
| β | Model constant | |
| F1 | Blending function | |
| R2 | Coefficient of determination | |
| Original efficiency data | ||
| Average value of the original efficiency data | ||
| Fitted data value |
References
- Lee, M.-R.; Lee, J.-H. A Study on Characteristics of Leak Signals of Pipeline Using Acoustic Emission Technique. Solid State Phenom. 2006, 110, 79–88. [Google Scholar] [CrossRef]
- Yao, L.; Zhang, L.; Wang, L.; Li, R.; Luo, H. A Spatiotemporal Data-Driven Framework for Acoustic Signal-Based Natural Gas Pipeline Leak Detection. IEEE Trans. Instrum. Meas. 2025, 74, 3527512. [Google Scholar] [CrossRef]
- Nguyen, D.-T.; Kim, J.-M. Trustworthy Pipeline Leak Localization Based on Acoustic Emission Event Monitoring. IEEE Trans. Instrum. Meas. 2025, 74, 3514311. [Google Scholar] [CrossRef]
- Saleem, F.; Ahmad, Z.; Kim, J.-M. Real-Time Pipeline Leak Detection: A Hybrid Deep Learning Approach Using Acoustic Emission Signals. Appl. Sci. 2025, 15, 185. [Google Scholar] [CrossRef]
- Yuan, Y.; Cui, X.; Han, X.; Gao, Y.; Lu, F.; Liu, X. Multi-condition pipeline leak diagnosis based on acoustic image fusion and whale-optimized evolutionary convolutional neural network. Eng. Appl. Artif. Intell. 2025, 153, 110886. [Google Scholar] [CrossRef]
- Duan, H.-F. Uncertainty Analysis of Transient Flow Modeling and Transient-Based Leak Detection in Elastic Water Pipeline Systems. Water Resour. Manag. 2015, 29, 5413–5427. [Google Scholar] [CrossRef]
- Adegboye, M.A.; Karnik, A.; Fung, W.-K. Numerical study of pipeline leak detection for gas-liquid stratified flow. J. Nat. Gas Sci. Eng. 2021, 94, 104054. [Google Scholar] [CrossRef]
- Roy, U. Leak Detection in Pipe Networks Using Hybrid ANN Method. Water Conserv. Sci. Eng. 2017, 2, 145–152. [Google Scholar] [CrossRef]
- Rajasekaran, U.; Kothandaraman, M.; Pua, C.H. Water Pipeline Leak Detection and Localization With an Integrated AI Technique. IEEE Access 2025, 13, 2736–2745. [Google Scholar] [CrossRef]
- Behari, N.; Sheriff, M.Z.; Rahman, M.A.; Nounou, M.; Hassan, I.; Nounou, H. Chronic leak detection for single and multiphase flow: A critical review on onshore and offshore subsea and arctic conditions. J. Nat. Gas Sci. Eng. 2020, 81, 103460. [Google Scholar] [CrossRef]
- Al-Ammari, W.A.; Sleiti, A.K.; Rahman, M.A.; Rezaei-Gomari, S.; Hassan, I.; Hassan, R. Digital twin for leak detection and fault diagnostics in gas pipelines: A systematic review, model development, and case study. Alex. Eng. J. 2025, 123, 91–111. [Google Scholar] [CrossRef]
- Xie, J.; Xu, X.; Dubljevic, S. Long range pipeline leak detection and localization using discrete observer and support vector machine. AIChE J. 2019, 65, e16532. [Google Scholar] [CrossRef]
- Asada, Y.; Hagiwara, T.; Tsubota, T.; Kurasawa, T.S.K.; Kimura, M.; Azechi, I.; Iida, T. Field verification of single leak detection method based on transient pressures using optimization technique in in-situ irrigation pipeline system including branch junctions and diameter changes. Paddy Water Environ. 2025, 23, 243–262. [Google Scholar] [CrossRef]
- Delgado-Aguiñaga, J.A.; Besançon, G. EKF-based leak diagnosis schemes for pipeline networks. IFAC-PapersOnLine 2018, 51, 723–729. [Google Scholar] [CrossRef]
- Ahmad, S.; Ahmad, Z.; Kim, C.-H.; Kim, J.-M. A Method for Pipeline Leak Detection Based on Acoustic Imaging and Deep Learning. Sensors 2022, 22, 1562. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, M.; Qu, X.; Zhang, J.; Chen, L. An Improved Identification Method of Pipeline Leak Using Acoustic Emission Signal. J. Mar. Sci. Eng. 2024, 12, 625. [Google Scholar] [CrossRef]
- Kam, S.I. Mechanistic modeling of pipeline leak detection at fixed inlet rate. J. Pet. Sci. Eng. 2010, 70, 145–156. [Google Scholar] [CrossRef]
- Li, W.; Fu, Q.; Gao, H. Pipeline leak detection and localization based on the flow balance and negative pressure wave methods. AIP Adv. 2024, 14, 115203. [Google Scholar] [CrossRef]
- Han, B.; Liu, X.; Liu, B.; Bao, H.; Jiang, X. Study on acoustic source characteristics of gas pipeline leakage. Noise Vib. Worldw. 2019, 50, 67–77. [Google Scholar] [CrossRef]
- Feng, Y.; Gao, J.; Yin, X.; Chen, J.; Wu, X. Risk assessment and simulation of gas pipeline leakage based on Markov chain theory. J. Loss Prev. Process Ind. 2024, 91, 105370. [Google Scholar] [CrossRef]
- Rui, Z.; Han, Q.; Zhang, H.; Wang, S.; Pu, H.; Ling, K. A new model to evaluate two leak points in a gas pipeline. J. Nat. Gas Sci. Eng. 2017, 46, 491–497. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, Y.; Ma, Y.; Chen, X.; Yang, J. Application of the differentiation process into the correlation-based leak detection in urban pipeline networks. Mech. Syst. Signal Process. 2018, 112, 251–264. [Google Scholar] [CrossRef]
- Reda, A.; Mahmoud, R.M.A.; Shahin, M.A.; Amaechi, C.V.; Sultan, I.A. Roadmap for Recommended Guidelines of Leak Detection of Subsea Pipelines. J. Mar. Sci. Eng. 2024, 12, 675. [Google Scholar] [CrossRef]
- Vandrangi, S.K.; Lemma, T.A.; Mujtaba, S.M.; Ofei, T.N. Developments of leak detection, diagnostics, and prediction algorithms in multiphase flows. Chem. Eng. Sci. 2022, 248, 117205. [Google Scholar] [CrossRef]
- You, Y.; Seibold, F.; Wang, S.; Weigand, B.; Gross, U. URANS of turbulent flow and heat transfer in divergent swirl tubes using the k-ω SST turbulence model with curvature correction. Int. J. Heat Mass Transf. 2020, 159, 120088. [Google Scholar] [CrossRef]
- Di Piazza, I.; Ciofalo, M. Numerical prediction of turbulent flow and heat transfer in helically coiled pipes. Int. J. Therm. Sci. 2010, 49, 653–663. [Google Scholar] [CrossRef]
- Cabello, R.; Popescu, A.E.P.; Bonet-Ruiz, J.; Cantarell, D.C.; Llorens, J. Heat transfer in pipes with twisted tapes: CFD simulations and validation. Comput. Chem. Eng. 2022, 166, 107971. [Google Scholar] [CrossRef]
- Kato, Y.; Fujimoto, K.; Guo, G.; Kawaguchi, M.; Kamigaki, M.; Koutoku, M.; Hongou, H.; Yanagida, H.; Ogata, Y.Y.; Fujimoto, K.; et al. Heat transfer characteristics of turbulent flow in double-90-bend pipes. Energies 2023, 16, 7314. [Google Scholar] [CrossRef]
- Jinhee, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Liu, C.-Q.; Gao, Y.-S.; Dong, X.-R.; Liu, J.-M.; Zhang, Y.-N.; Cai, X.-S.; Gui, N. Third generation of vortex identification methods: Omega and Liutex/Rortex based systems. J. Hydrodyn. 2019, 31, 205–223. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Tong, L.-H.; Zhu, Y.-F.; Huang, H.-F.; Zhao, Y.-J.; Zhang, Y.-L. Numerical Study on Minor Leak for Pressure-Driven Flow in Straight Pipe and 90° Elbow Transporting Different Media. Processes 2026, 14, 304. https://doi.org/10.3390/pr14020304
Tong L-H, Zhu Y-F, Huang H-F, Zhao Y-J, Zhang Y-L. Numerical Study on Minor Leak for Pressure-Driven Flow in Straight Pipe and 90° Elbow Transporting Different Media. Processes. 2026; 14(2):304. https://doi.org/10.3390/pr14020304
Chicago/Turabian StyleTong, Liang-Huai, Yuan-Fan Zhu, Hui-Fan Huang, Yan-Juan Zhao, and Yu-Liang Zhang. 2026. "Numerical Study on Minor Leak for Pressure-Driven Flow in Straight Pipe and 90° Elbow Transporting Different Media" Processes 14, no. 2: 304. https://doi.org/10.3390/pr14020304
APA StyleTong, L.-H., Zhu, Y.-F., Huang, H.-F., Zhao, Y.-J., & Zhang, Y.-L. (2026). Numerical Study on Minor Leak for Pressure-Driven Flow in Straight Pipe and 90° Elbow Transporting Different Media. Processes, 14(2), 304. https://doi.org/10.3390/pr14020304





