Braking Control of Mobile Robots Using Integral Sliding-Mode Algorithm with Composite Convergence Regulation

Abstract

With the continuous expansion of the application field of mobile robots, the diversification and complexity of the application scenarios have put forward higher requirements for their motion control performance. In order to enhance the ability to brake fast and to prevent slipping when the mobile robot is working, a slipping ratio tracking strategy based on an improved integral sliding mode algorithm regulated by a composite convergence law is proposed. The composite convergence law is proposed by integrating the power law with the exponential convergence law. A mathematical model of a single-wheeled mobile robot is established, a relationship curve between slipping ratio and pavement adhesion coefficient is introduced to estimate the pavement adhesion coefficient, and an improved integral sliding mode controller is designed. The stability is verified using Lyapunov stability theory. The slipping ratio is tracked based on the integral sliding-mode controller, and the slipping ratio is corrected to control the wheel slipping ratio near the ideal optimal slipping ratio. Furthermore, simulation experiments are conducted in MATLAB/Simulink (R2020b) under two typical working conditions to compare the proposed control strategy with conventional sliding-mode control regulated by an exponential convergence law. Finally, the mobile robot slipping ratio tracking experiments are conducted to verify the simulation results, which show that the proposed control strategy enables the mobile robot to reach the ideal braking state more quickly and stably, thereby improving the braking effect of the ABS braking system of the mobile robots.

1. Introduction

Benefiting from continuous breakthroughs in sensor technology and intelligent algorithms [1,2], robotics has advanced significantly toward greater intelligence. The application of robotic technology has not only enhanced the efficiency of task execution and daily operations but has also effectively reduced human exposure to hazardous environments. Among these advancements, mobile robots, as exemplary systems capable of sensing dynamic environments through sensors and achieving autonomous obstacle avoidance, have become a focal point of research [3,4]. The integration of interdisciplinary knowledge, including automation technology, mechatronics, image processing, and big data analytics, has collectively established the theoretical framework for mobile robots, accelerating their intelligent development [5,6].

The anti-lock braking system (ABS) is a critical safety technology designed to prevent wheel lockup during emergency braking [7,8], thereby maintaining vehicle steerability and reducing stopping distances. By dynamically modulating brake pressure through rapid hydraulic or electronic control, ABS ensures that optimal wheel slipping ratios are preserved, even on low-friction surfaces. This system integrates real-time wheel speed sensors, a central control unit, and actuator mechanisms to adaptively adjust braking torque, effectively balancing deceleration efficiency and directional stability. Widely adopted in automotive and robotic applications [9,10]. ABS exemplifies the fusion of vehicle dynamics and control theory, offering enhanced safety and maneuverability in complex operational scenarios.

The ABS is nonlinear, time-varying, and uncertain due to its dynamic characteristics. This requires the ABS control system to be able to respond quickly and have strong anti-interference ability. Sliding mode variable structure control is often used in the design of nonlinear control systems based on the reaching law because of its insensitivity to system parameter variations, ability to effectively suppress external disturbances, and rapid response [11]. Chereji et al. [12] propose a new sliding mode controller based on the reaching law, which relies on fewer tuning parameters and does not bring additional computational complexity to solve the problem of uncertainty in the process model effectively. Rishabh et al. [13] focuses on the use of computationally efficient algorithms to recognize road surface conditions, and its prediction accuracy is very high. Feng and Hu [14] designed a discrete fuzzy adaptive PID control algorithm for automotive antilock braking system, which calculates the coefficient of adhesion of the vehicle and the wheel slipping ratio as inputs and outputs of the PID control algorithm and can control the wheel slipping ratio of about 20%. Wang et al. [15] proposed a new sliding mode controller based on reaching law, which relies on fewer adjustment parameters and does not bring additional computational complexity to effectively solve the problem of uncertainty in the process model.

To address the limitations of traditional sliding mode control in achieving both rapid convergence and high precision in mobile robot slipping ratio tracking, this research introduces a novel composite convergence law. This law synergistically integrates the advantages of power law and exponential convergence approaches. Specifically, the power law component ensures swift initial convergence, rapidly driving the system towards the sliding surface, while the exponential component guarantees high-precision tracking and minimizes steady-state error by providing a faster convergence rate near the desired equilibrium point. In contrast to conventional exponential convergence laws, which may exhibit slower initial responses and sensitivity to initial condition errors, the proposed composite approach demonstrably accelerates the reaching phase and enhances robustness against disturbances. This results in superior slipping ratio control performance, enabling the mobile robot to achieve the ideal braking state more efficiently and stably, ultimately optimizing the ABS braking system’s effectiveness.

At present, the main problems of the sliding mode control remain the estimation of the optimal slipping ratio, since the identification of the pavement adhesion coefficient when encountering different road surfaces, the slow response speed, and the serious vibration shaking phenomenon. Considering the aforementioned limitations of conventional sliding-mode control, this paper investigates the dynamics of a 1/2 mobile robot model. To address these deficiencies, we employ a curve estimation method for identifying pavement adhesion coefficients and propose an improved integral sliding-mode controller regulated by a composite convergence law to achieve both rapid response and reduced chattering. A comparative analysis against a conventional exponential convergence law-based sliding-mode algorithm is conducted to demonstrate the superior performance of the proposed controller in terms of convergence speed and vibration attenuation.

2. Dynamic Model of Mobile Robots

2.1. Wheel Model

In vehicle dynamics modeling, the quarter-vehicle model and half-vehicle model are two commonly used simplified modeling approaches [16,17]. The half-vehicle model is primarily employed to investigate braking force distribution control issues between front and rear wheels caused by load transfer during braking. The single-wheel model offers incomparable advantages in studying vehicle braking characteristics due to its simplicity and convenience [18,19]. Considering that this paper mainly studies the braking control ability and slip control effect of the mobile robot when traveling in a straight line, a 1/2 vehicle model is used.

Assuming that the vehicle travels on a horizontal straight road surface, while not considering its lateral force and resistance during operation, the wheels on both sides of the coaxial bear the same load, and the tires have the same mechanical properties. Then the 1/2 wheel braking model is shown in Figure 1. Under the action of braking force, the speed of the vehicle will gradually be zero, and the kinetic equations satisfied in this process are [20]:

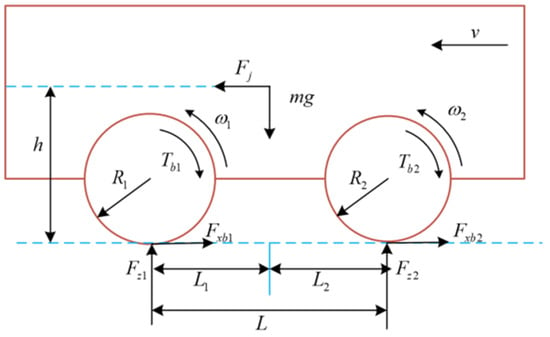
Figure 1. 1/2 Mobile robot force analysis diagram.

To analyze the forces on the wheels, dynamic equations are as follows:

$$m{\displaystyle \frac{dv}{dt}}=-\left(F_{xb1}+F_{xb2}\right),$$

(1)

$$\left\{\begin{array}{l}{J}_1{\displaystyle \frac{d{\omega }_1}{dt}}=F_{xb1}{R}_1-T_{b1}\\ J_2{\displaystyle \frac{d{\omega }_2}{dt}}=F_{xb2}{R}_2-T_{b2}\end{array}\right.,$$

(2)

$$\left\{\begin{array}{l}{F}_{z1}={\displaystyle \frac{m}{2L}}\left(L_{1}g-h{\displaystyle \frac{dv}{dt}}\right)\\ F_{z2}={\displaystyle \frac{m}{2L}}\left(L_{2}g-h{\displaystyle \frac{dv}{dt}}\right)\end{array}\right.,$$

(3)

where m is the 1/2 mobile robot mass, v represents the travel speed of the mobile robot, $F_{xbi}$ (i = 1, 2) is the longitudinal braking force of the wheels, $J_i$ (i = 1, 2) is the wheel moment of inertia, ${\omega }_i$ (i = 1, 2) is the angular velocity of the wheels, $R_i$ (i = 1, 2) is the rolling radius of the tires, T_bi (i = 1, 2) represents the braking torque generated when the brake is applied, $F_{zi}$ (i = 1, 2) represents the dynamic load of vertical weight transfer, $L$ is the wheelbase, h is the center of mass height, and v is the vehicle velocity.

The slipping ratio is defined as [21]:

$$\left\{\begin{array}{l}{\lambda }_1={\displaystyle \frac{v-{\omega }_1{R}_1}{v}}\times 100\%\\ {\lambda }_2={\displaystyle \frac{v-{\omega }_2{R}_2}{v}}\times 100\%\end{array}\right.,$$

(4)

where λ_i (i = 1, 2) is the slipping ratio.

2.2. Tire Model

As the sole force transmission medium between mobile robots and road surfaces, tires’ dynamic characteristics directly affect the robot’s handling stability, braking performance, and driving safety. The primary objective of tire modeling is to accurately characterize the nonlinear relationships between tire forces (longitudinal force, lateral force, vertical force) and parameters such as slipping ratio and slip angle [22,23].

The Burckhardt tire model proposed by Burckhardt et al. [24,25] provides relevant expressions under the assumptions of constant vehicle speed and negligible tire load effects:

$$\mu \left(\lambda \right)=c_1\left[1-\exp \left(-c_2\lambda \right)\right]-c_3\lambda ,$$

(5)

where $c_1$, $c_2$ and $c_3$ represent the fitting parameters derived from experimental data, whose values vary depending on the road surface conditions. The Burckhardt tire model exhibits the following distinctive characteristics: (1) Minimal fitting parameters, resulting in relatively low computational complexity; (2) High fitting accuracy without dependence on vehicle speed; (3) Simple structural form, facilitating parameter identification and application [26]. Based on Equation (5), the optimal slipping ratio ${\lambda }_d$ and peak adhesion coefficient ${\mu }_{\max }$ for typical road surfaces can be determined as:

$${\lambda }_d={\displaystyle \frac{1}{c_2}}\log {\displaystyle \frac{c_1{c}_2}{c_3}}$$

(6)

$${\mu }_{\max }=c_1-{\displaystyle \frac{c_3}{c_2}}\left[1+\log {\displaystyle \frac{c_1{c}_2}{c_3}}\right]$$

(7)

Table 1 presents typical values of ${\lambda }_d$ and ${\mu }_{\max }$ for several common road surfaces [27,28]. Figure 2 illustrates the relationship curve between wheel angular deceleration and the utilization coefficient of adhesion.

Table 1. Fitting parameter values of several common road surfaces.

Pavement Type	${\mathit{\lambda }}_{\mathit{d}}$	${\mathit{\mu }}_{\mathbf{max}}$
Dry asphalt	0.193	1.170
Dry cement	0.1599	1.089
Wet asphalt	0.1308	0.801
Pebble	0.4004	1.002
Snow	0.0779	0.210
Ice	0.0314	0.023

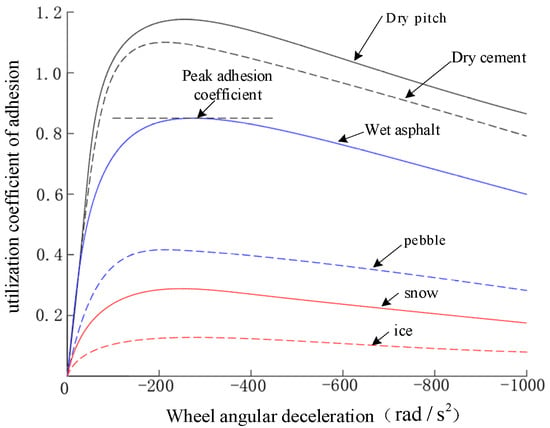
Figure 2. Curve depicting the relationship between slipping ratio and pavement adhesion coefficient.

3. Design of Integral Sliding-Mode Controller

3.1. Estimation of Pavement Adhesion Coefficient

In the motion control system of mobile robots, tires serve as the dynamic interface between the system and the road surface, where slipping behavior directly affects longitudinal force transfer characteristics. During braking, the nonlinear friction properties in the tire-road contact patch leads to slipping-ratio-dependent variations in tangential force transmission capacity [29]. By analyzing the dynamic characteristics of the μ-λ curve, key tire performance parameters can be extracted to determine both the optimal slipping ratio and pavement adhesion coefficient [30]. These parameters are directly related to the maximum value of the longitudinal braking force, F_xbmax:

$$F_{xb\max }={\mu }_{\max }{F}_z,$$

(8)

where $F_z$ is the vertical load.

From the above single wheel dynamics model, the pavement adhesion coefficient can be introduced as [31]:

$$\mu ={\displaystyle \frac{J_i{\dot{\omega }}_i+T_{bi}}{F_{zi}{R}_i}},$$

(9)

Figure 3 shows the μ-λ curve of the tire. In the small slipping ratio range (0–10%), the slopes of the μ-λ curves vary across different road surfaces. By fitting the slope within this small-slip region, the pavement adhesion coefficient can be estimated.

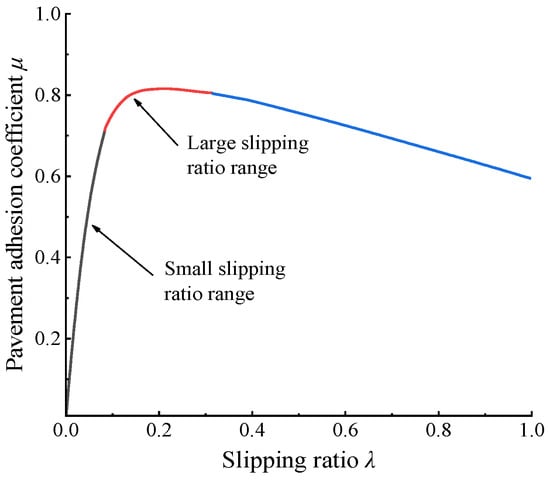
Figure 3. Correlation Curve between μ and λ.

In the large slipping ratio range, the adhesion coefficient first increases and then decreases, so the peak adhesion coefficient must correspond to the zero-slope point. By computing du/dλ in real time, the adhesion coefficient near the zero-slope region can be identified as the pavement adhesion coefficient.

It should be noted that when using the above-mentioned road surface adhesion coefficient method, it is necessary to calculate the slipping ratio, adhesion rate, that is, wheel speed, vehicle speed, ground force, etc., as accurately as possible. The collection or estimation accuracy of these signals has an extremely important impact on the estimation of the road surface adhesion coefficient.

3.2. Design of Integral Sliding-Mode Surface

Based on the relationship between slipping ratio and adhesion coefficient, the design objective of the sliding surface is to ensure system stability while satisfying the dynamic performance requirements. The goal is to maintain the mobile robot’s actual slipping ratio ($\lambda$) near the desired slipping ratio (${\lambda }_d$) [31], thereby minimizing the tracking error (e). This control problem can be formulated as finding a control input ($u\left(t\right)$) that drives the tracking error (e) to converge to zero. Thus, the tracking error is defined as:

$$e=\lambda -{\lambda }_d.$$

(10)

The sliding mode function is defined as:

$$s=e\left(t\right)+c{\displaystyle \int e\left(t\right)}dt,$$

(11)

where c is the integral coefficient and must satisfy the Hurwitz condition [32,33], that is, c > 0; t is time. When the system state moves on the sliding mode surface, s = 0, that is:

$$e\left(t\right)+c{\displaystyle \int e\left(t\right)}dt=0$$

(12)

The convergence result is $e\left(t\right)=e\left(0\right)e^{-et}$; that is, when $t\to \infty$, the error index converges to 0. A derivation on s yields:

$$s^{\prime }=e^{\prime }+ce={\left(\lambda -{\lambda }_d\right)}^{\prime }+c\left(\lambda -{\lambda }_d\right)$$

(13)

Here, the left front wheel is selected for analysis, and substituting Equations (1) and (2) into Equation (4) yields that

$${\lambda }^{\prime }={\left({\displaystyle \frac{v-\omega r}{v}}\right)}^{\prime }={\displaystyle \frac{1}{v}}\left[-r{\omega }^{\prime }+\left(1-\lambda \right)v^{\prime }\right]=-{\displaystyle \frac{R_1\left(F_{xb1}{R}_1-T_{b1}\right)}{J_{1}v}}-{\displaystyle \frac{\omega R_1\left(F_{xb1}+F_{xb2}\right)}{m{v}^2}}$$

(14)

It can be obtained by combining Equation (13) and Equation (15) simultaneously:

$${s_1}^{\prime }=-{\displaystyle \frac{R_1\left(F_{xb1}{R}_1-T_{b1}\right)}{J_{1}v}}-{\displaystyle \frac{\omega R_1\left(F_{xb1}+F_{xb2}\right)}{m{v}^2}}+c{\left(\lambda \right.}_1-\left.{\lambda }_d\right).$$

(15)

3.3. Design of the Composite Convergence Law

For sliding mode variable structure control, it is necessary to ensure that any point in the space can reach the sliding mode surface within a finite time. If the arrival condition is met, the Lyapunov function is constructed. If it is met, it can ensure that the system state continuously moves towards the sliding-mode surface and eventually reaches the sliding mode surface. The condition is guaranteed to be satisfied through the selection of the convergence law.

To meet the control requirements, the expressions of the exponential convergence law and the power convergence law are introduced [34]:

$$s^{\prime }=-\epsilon \mathrm{sgn}\left(s\right)-ks,$$

(16)

where $\epsilon$ > 0, $k$ > 0, $s^{\prime }=-ks$ is the exponential term, in which

$$s^{\prime }=-k{\left|s\right|}^{\alpha }\mathrm{sgn}\left(s\right),$$

(17)

where the convergence coefficient meets 0 < a < 1.

In order to enable the system state to reach the sliding-mode surface in the shortest time and minimize the buffeting generated when the system state reaches the sliding mode surface as much as possible, an improved convergence law is proposed by combining the power approach law and the exponential convergence law as follows [35]:

$$s^{\prime }=-\left(\epsilon \right.{\left|s\right|}^{\alpha }\mathrm{sgn}\left(s\right)+\left.ks\right)$$

(18)

where $\epsilon$ is the switching gain, k is the gain coefficient, and sgn(s) is the sign function. For case $\epsilon$ > 0, k > 0, and 1 > $\alpha$ > 0, its solution is $s=s\left(0\right)e^{-kt}$ exponentially converging to 0, where the convergence rate depends on the value of k. When |s| is large, the combined effect of |s|^α and the ks term provides an extremely strong acceleration effect; when |s| is small, the values of both terms naturally decay, thereby naturally and efficiently suppressing chattering without requiring additional switching functions or complex adjustment mechanisms. By adjusting the parameter $\alpha$, the system can rapidly approach the ideal stable state (sliding mode) when far from equilibrium, ensuring fast convergence. When the system state is close to the desired stable state, reducing $\alpha$ appropriately helps decrease control gain, effectively mitigating potential chattering phenomena and improving control smoothness and stability. In short, this paper not only proposes yet another “composite” approach law, but also introduces a novel combination approach law featuring smooth transition characteristics and superior control performance. It further provides new insights into its dynamic properties and parameter tuning strategies.

3.4. Design of Integral Sliding-Mode Algorithm Regulated by a Composite Convergence Law

In Equation (2), the torque $T_{bi}$ (i = 1, 2) corresponds to the control variable u that the system needs to design. By considering the two scenarios of the sliding mode surface, $s=0$ and $s\ne 0$, the sliding mode equivalent control variable $u_1$ and the compensatory discontinuity control variable $u_2$ are designed accordingly [36]:

$$u=u_1+u_2.$$

(19)

Let $s^{\prime }=0$, the equivalent control quantity $u_1$ can be obtained from Equation (15).

$$u_1=T_{b1}=F_{xb1}{R}_1+{\displaystyle \frac{J_1\omega \left(F_{xb1}+F_{xb2}\right)}{mv}}-{\displaystyle \frac{J_{1}v\cdot c\left({\lambda }_1-{\lambda }_d\right)}{R_1}}.$$

(20)

Meanwhile, if the state of the system moves from a certain initial state towards the sliding mode surface, by combining Equations (15) and (18), we obtain:

$${s_1}^{\prime }=-{\displaystyle \frac{R_1\left(F_{xb1}{R}_1-T_{b1}\right)}{J_{1}v}}-{\displaystyle \frac{\omega R_1\left(F_{xb1}+F_{xb2}\right)}{m{v}^2}}+c{\left(\lambda \right.}_1-\left.{\lambda }_d\right)=-\left(\epsilon \right.{\left|s\right|}^{\alpha }\mathrm{sgn}\left(s\right)+\left.ks\right).$$

(21)

Substituting Equation (21) into the above equation, the overall control law of the integral sliding-mode variable structure controller can be obtained as:

$$u=F_{xb1}{R}_1+{\displaystyle \frac{J_1\omega \left(F_{xb1}+F_{xb2}\right)}{mv}}-{\displaystyle \frac{J_{1}v\cdot c\left({\lambda }_1-{\lambda }_d\right)}{R_1}}-{\displaystyle \frac{\left(\epsilon \right.{\left|s\right|}^{\alpha }\mathrm{sgn}\left(s\right)+\left.ks\right)}{R_1}}{J}_{1}v=u_1-{\displaystyle \frac{\left(\epsilon \right.{\left|s\right|}^{\alpha }\mathrm{sgn}\left(s\right)+\left.ks\right)}{R_1}}{J}_{1}v.$$

(22)

According to the Lyapunov stability criterion [37] the Lyapunov function is defined as:

$$V={\displaystyle \frac{1}{2}}{s}^2.$$

(23)

Taking the derivative of Equation (23) and substituting Equation (21), we obtain:

$$\begin{array}{l}{V}^{\prime }=s\cdot s^{\prime }\\ =s\cdot ({\displaystyle \frac{R_1\left(F_{xb1}{R}_1-T_{b1}\right)}{J_{1}v}}-{\displaystyle \frac{\omega R_1\left(F_{xb1}+F_{xb2}\right)}{m{v}^2}}+c{\left(\lambda \right.}_1-\left.{\lambda }_d\right))\\ =s\cdot (-{\left(\epsilon \left(\left|s\right|\right.\right.}^{\alpha }\mathrm{sgn}\left(s\right)+\left.ks\right))\\ =-\epsilon |s{|}^{\alpha +1}\mathrm{sgn}(s)-k{s}^2.\end{array}$$

(24)

Obviously, $V^{\prime }\left(0\right)=0$, and $V^{\prime }\left(x\right)\le 0$ for cases $s>0$, $s^{\prime }<0$ and $s<0$, $s^{\prime }>0$. Therefore, it can be proved that the system is asymptotically stable.

4. Simulation Verification

4.1. Simulation Model

In this section, in order to verify whether the proposed integral sliding mode control algorithm can better converge the error and weaken the buffeting of the system, based on the designed dynamic model of the mobile robot and the improved approach law integral sliding mode controller model, the anti-lock control system model of the mobile robot is built in Matlab/simulink (R2020b). In the braking simulation, the mobile robot’s initial speed was specified as 20 m/s. Figure 4 is the block diagram of the control system.

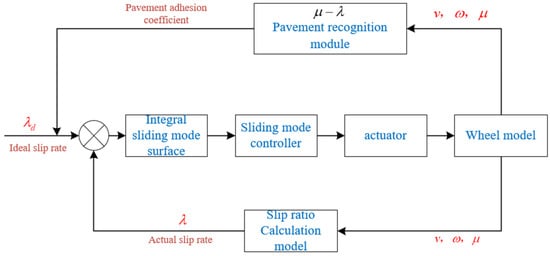
Figure 4. Control system frame diagram.

In the following, simulation experiments will be carried out in the simulation model constructed based on this system block diagram to verify and analyze the proposed ABS control strategy. Simulation experiments are carried out under two different road conditions, low adhesion road surface and high adhesion road surface, and in order to reflect the advantages of the improved convergence law integral sliding mode algorithm, the sliding mode control algorithm is compared with that of the exponential convergence law integral sliding mode surface.

Equation (8) necessitates the optimized selection of four parameters: the convergence coefficient α (0 < α < 1), the integral coefficient c, the switching gain ε, and the gain coefficient k. The convergence coefficient α primarily governs the approach dynamics when the system state is distant from the sliding surface. A smaller α value results in a more pronounced nonlinear acceleration term, thereby enhancing the convergence speed during the initial phase. Conversely, the integral coefficient c predominantly influences the approach dynamics near the sliding surface. The switching gain ε and gain coefficient k, acting in concert, dictate the overall convergence speed, with ε amplifying the nonlinear acceleration term’s influence and k amplifying the linear term’s influence. Given the actuator’s physical output limitations, the optimization objectives are to minimize the braking distance. The optimization of four parameters influencing braking on dry asphalt at an initial velocity of 20 m/s was achieved using a genetic algorithm. The search intervals for these parameters were: α ∈ (0, 1), c ∈ [0, 20], ε ∈ [0, 1], and k ∈ [0, 100]. Figure 5 illustrates the parameter optimization process of the genetic algorithm, aimed at minimizing braking distance. Figure 5a demonstrates a consistently decreasing trend in braking distance (S) throughout the optimization, indicating the algorithm’s success in finding solutions leading to shorter stopping distances. Figure 5b–e depict the behavior of four other parameters: the convergence coefficient (α), integral coefficient (c), switching gain (ε), and gain coefficient (k). These parameters initially exhibit fluctuations, suggesting exploration of the parameter space. Subsequently, they converge to stable values, signifying the algorithm’s identification of optimal or near-optimal settings for these parameters within the context of minimizing braking distance. This convergence highlights the algorithm’s ability to adapt and refine its parameter selection to achieve the desired objective. Table 2 shows the parameters of the mobile robot for the simulation experiments.

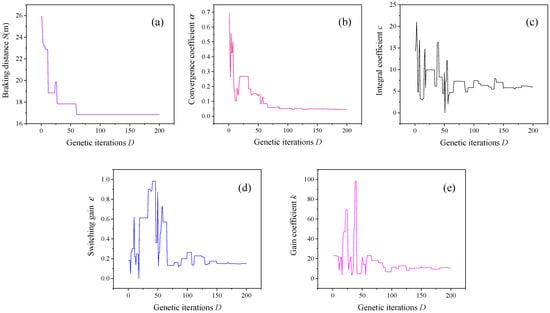
Figure 5. Changes in parameters during genetic algorithm optimization process: (a) braking distance S, (b) convergence coefficient α, (c) integral coefficient c, (d) switching gain ε and (e) gain coefficient k.

Table 2. Mobile robot related simulation parameters.

Parameter Name	Value
One quarter of the mass of the mobile robot m (kg)	150
Tire moment of inertia Ji (kg⋅m2)	1.8
Tire radius Ri (m)	0.3
Adhesion coefficient μ1 (wet asphalt)	0.45
Adhesion coefficient μ2 (dry asphalt)	0.91
Convergence coefficient α	0.05
Integral coefficient c	6
Switching gain ε	0.15
Gain coefficient k	10

4.2. Simulation Results

When the mobile robot is braking, the simulation working condition is set as follows: the mobile robot is traveling on the high adhesion road surface, the initial speed is 15 m/s, the emergency braking starts at the initial moment, and the anti-lock braking system (ABS) starts to work until the mobile robot stops, and the ABS fails to stop working. The simulation results of vehicle speed, wheel speed, braking distance, and slipping ratio changes on dry asphalt pavement are shown in Figure 6.

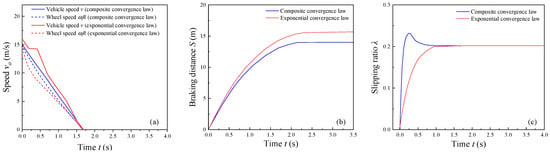
Figure 6. Simulation results of high adhesion pavement (dry asphalt): (a) vehicle speed and wheel speed curves, (b) braking distance curve, and (c) slippage ratio tracking curve.

As can be seen from Figure 6, when the ABS adopts the exponential convergence law integral sliding-mode control algorithm, the wheel speed changes in the early stage are large, and the maximum error rate is 21.2%. When the composite convergence law integral sliding-mode control algorithm is used, the wheel speed change is smooth, and the actual slipping ratio can follow the desired value better, and the maximum error rate is 9.1%. Moreover, the difference between the two in terms of the time required and the distance driven from the start of braking to stopping is not significant. Therefore, compared with the exponential convergence law sliding-mode algorithm, the integral sliding mode algorithm regulated by a composite convergence law has a better control speed, improves the system jitter problem, and has a good control effect.

In order to explore and comparatively analyze the adaptability as well as the advantages and disadvantages of the two control algorithms to the working conditions, wet asphalt pavement is selected for simulation analysis in this part. The simulation conditions are the same as before, and the simulation results are shown in Figure 7 when the ABS adopts the two control algorithms designed above, respectively.

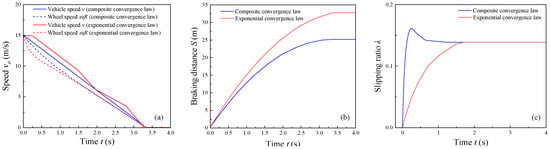
Figure 7. Simulation results of low adhesion pavement (wet asphalt): (a) vehicle speed and wheel speed curves, (b) braking distance curve, and (c) slippage rate tracking curve.

As can be seen from Figure 7, when the exponential convergence law sliding-mode control algorithm is used, the mobile robot travels on the low adhesion road surface, the wheel speed of mobile robot changes are more drastic, and the maximum error rate reaches 32.5%, and it takes a longer control time to control the slipping ratio to the desired value. Moreover, the error between the actual value and the desired value in the whole operation cycle is large, and the control effect is general. When the integral sliding mode algorithm regulated by the composite convergence law is used, the slipping ratio of the mobile robot can converge to the desired value in a shorter time, and the system requires shorter reaction time, and in the whole operation cycle, the actual value can track the desired value better, and the maximum error rate is 13.8%, so the control effect is good. In addition, when the integral sliding mode algorithm regulated by the composite convergence law is used, the braking distance of the mobile robot is reduced by about 7.4 m compared with the sliding-mode control algorithm regulated by the exponential convergence law, which will further improve the driver’s driving safety.

4.3. Experimental Verification

Based on the mobile robot braking platform shown in Figure 8, a mobile robot test system including industrial control machine, brake, controller, sensors and other components is constructed. The wireless remote control device controls the trolley traveling in the test. The Ubuntu system (20.04 version) is used to remotely carry out the unified observation and recording of the mobile robot status, the online rectification of the control parameters, and so on.

Figure 8. Mobile robot control platform.

The mobile robot system can be summarized as a motion unit, a perception unit, human–computer interaction, and the schematic diagram of the mobile robot system is shown in Figure 9. The motion unit is the motor, which provides power for each moving part of the mobile robot. In the perception unit, the gyroscope detects the robot speed information and provides data for the mobile robot traveling speed and attitude control, the speed sensor detects the wheel angular speed change and provides data for slipping ratio calculation, and the motor encoder records the motor speed. The STM32F1 is used to receive data and transmit commands to the controller.

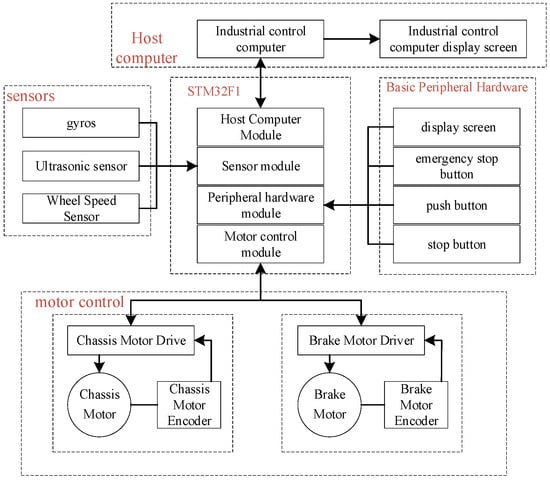
Figure 9. Mobile robot system components.

According to the experimental conditions, since the mass of the mobile robot is lower than that of a conventional vehicle, only braking the rear wheels can meet the expected braking performance requirements. In this experiment, the braking system applies braking force to the two rear wheels of the mobile robot through a hydraulic transmission. Two sets of test conditions, dry and wet road surfaces, are selected as the target road surfaces for the ABS emergency braking test. The mobile robot is accelerated to 15 m/s along a straight line and starts emergency braking until the vehicle stops, and the results are observed.

The real vehicle working condition of emergency braking under a dry road surface is shown in Figure 10. Figure 10a shows the curve of vehicle speed and wheel speed with time, Figure 10b shows the change in braking distance during braking, and Figure 10c shows the change in slipping ratio during braking. From Figure 10, it can be seen that when braking, the longitudinal velocity at the initial moment is consistent with the wheel speed, and the car does not perform a deceleration operation because the brake actuator is eliminating the braking gap at that moment without generating the corresponding braking force. With the intervention of the composite convergence law integral sliding-mode controller, the change in the vehicle wheel speed is smoother compared to the exponential convergence law sliding mode controller, and the wheels of the mobile robot are almost free of locking when it is about to stop. In terms of tracking the slipping ratio, the tire slipping ratio based on the composite convergent law integral sliding-mode control tends to be stable at t = 0.33 s, and the vibration phenomenon is controlled more smoothly, while the exponential convergent law sliding-mode control has a longer response time and the slip value fluctuates more near the target value. The composite convergent law integral sliding-mode strategy is more effective than the exponential convergent law sliding-mode strategy in the braking condition of dry asphalt pavement.

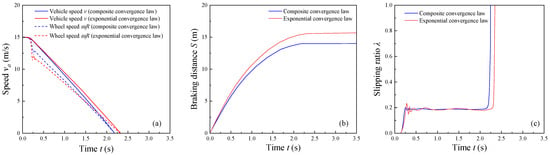
Figure 10. Test results of dry cement pavement: (a) vehicle speed and wheel speed curves, (b) braking distance curve, and (c) slipping ratio tracking curve.

The real vehicle condition of emergency braking under a wet road surface is shown in Figure 11. Figure 11a shows the variation curve of vehicle speed and wheel speed with time, Figure 11b shows the variation in braking distance in the braking process, and Figure 11c shows the variation in slipping ratio in the braking process. Under this condition, in the early stage of braking, the exponential convergence law sliding-mode control wheel speed change fluctuates greatly. And the fluctuation of wheel speed change in the composite convergence law integral sliding-mode control is relatively smaller. In terms of tracking the slipping ratio, in 0~0.45 s, the tire slipping ratio based on the composite convergence law integral sliding-mode control quickly tends to be stable, and in 0.45~3.2 s, the vibration phenomenon is controlled more smoothly, and the slipping ratio is tracked quickly and accurately. While the exponential convergence law sliding-mode control in t = 0.75 s when the slipping ratio converges to the target value, the response time is longer, and the slip value fluctuates more near the target value. Compared with the exponential convergence law sliding-mode control, the composite convergence law sliding-mode control strategy has better safety under the braking condition of a wet asphalt road. In conclusion, the proposed ABS control strategy is robust enough to work in different conditions.

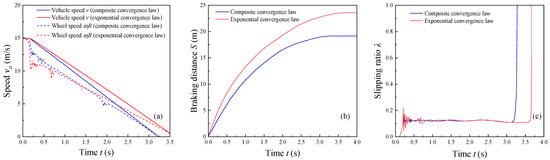
Figure 11. Test results of wet cement pavement: (a) vehicle speed and wheel speed curves, (b) braking distance curve, and (c) slipping ratio tracking curve.

5. Conclusions

In this paper, for the problem of slow and unstable response of ABS control in the braking process of mobile robot, a slipping ratio tracking control system based on the integral sliding-mode control regulated by a composite convergence law is established, and the experimental results show that, in the braking conditions of different adhesion surfaces, the ABS with the integral sliding mode control can make the slipping ratio converge to the vicinity of the ideal slipping ratio quickly, and realize good tracking of the ideal slipping ratio. It has smaller jitters and vibration, better control accuracy and higher braking stability compared with the sliding mode control algorithm based on the exponential convergence law. Under different braking conditions, the ABS with improved convergence law sliding mode control can quickly converge the slipping ratio to the neighborhood of ideal slipping ratio, realize the good tracking of ideal slipping ratio and effectively improve the braking stability; compared with sliding mode control algorithm regulated by the exponential convergence law, it has smaller vibration, better control accuracy and higher braking stability, which improves the braking safety performance.

The integral sliding-mode control algorithm with composite convergence law demonstrates superior performance over the exponential convergence law. It achieves smoother wheel speed transitions, lower maximum slipping ratio errors (9.1% on dry and 13.8% on wet asphalt), faster convergence to desired slip ratios, and reduces braking distance by approximately 7.4 m on low adhesion surfaces, enhancing overall braking safety and system stability.

The proposed composite convergence law integral sliding-mode control demonstrates superior performance in emergency braking on both dry and wet pavements. Compared to the exponential convergence law controller, it achieves faster slip ratio stabilization (0.33 s dry, 0.45 s wet), smoother wheel speed response, and reduced slip fluctuations, resulting in improved braking safety and robustness across varying conditions.

In recent years, the development of intelligent sliding mode controllers using deep learning algorithms has become a research hotspot in the field of automatic control [38,39]. Its main success is reflected in the combination of deep neural networks (DNN) and traditional sliding mode control (SMC), which achieves robust and efficient control of complex nonlinear systems, uncertainties, and external disturbances [40,41]. For example, in systems such as robotic arms, drones, and autonomous vehicles, researchers use deep learning models to estimate the system state and dynamics online and use them to adaptively adjust sliding surfaces or switch control laws, effectively improving the robustness and adaptive performance of the system [42,43,44].