Characteristics of CO2–Formation Water–Rock Reaction and Simulation of CO2 Burial Efficiency in Tight Sandstone Reservoirs
Abstract
1. Introduction
2. Experimental Preparation
2.1. Preparation of Sandstone and Formation Water Samples
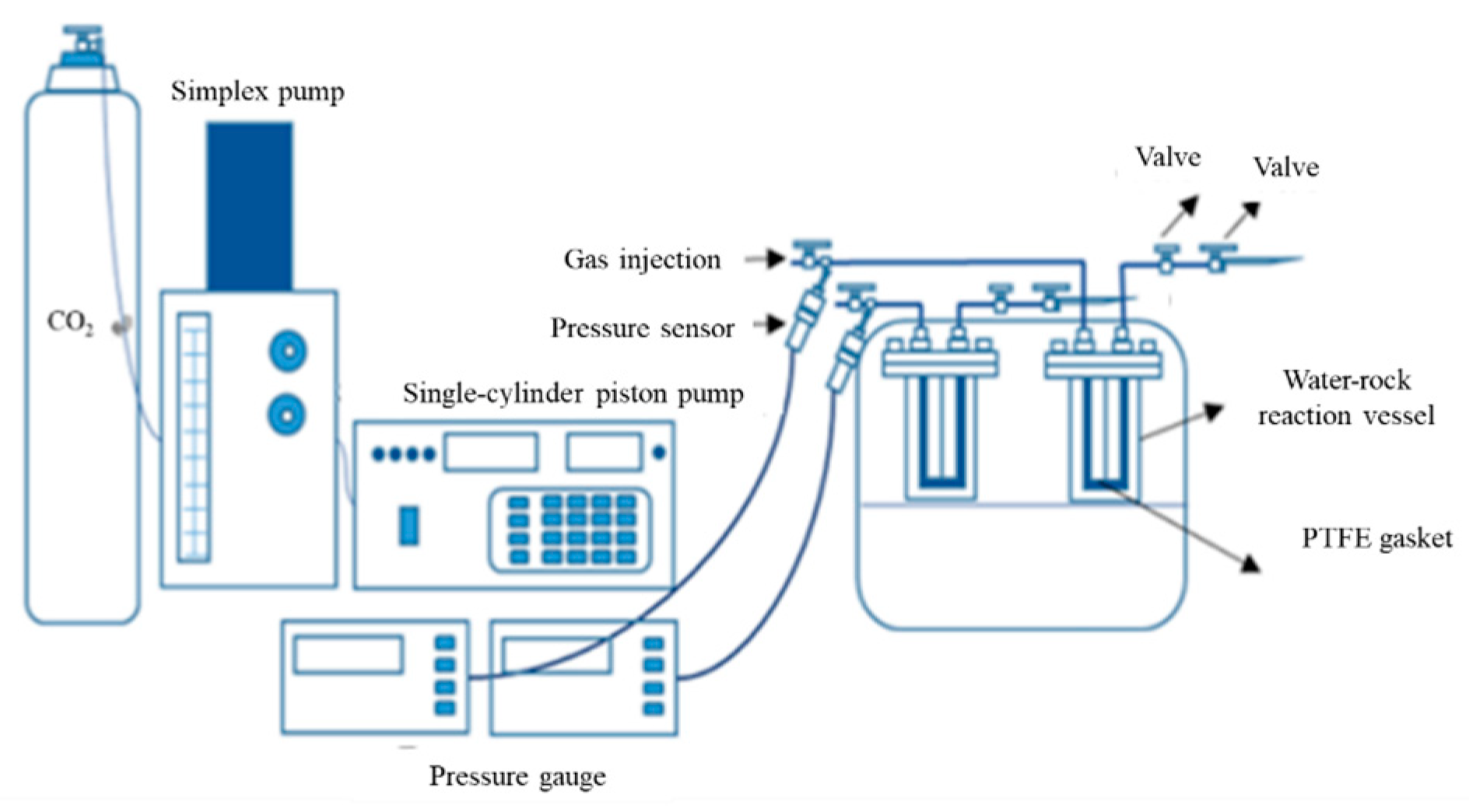
2.2. CO2–Water–Rock Experimental Apparatus and Procedure
- (1)
- First, accurately weigh 1.0 g of sandstone powder with a particle size ranging from 0.075 to 0.6 mm.
- (2)
- Then, add the weighed sandstone powder and the prepared formation water solution into the reactor vessel at a ratio of 1 g sandstone powder to 20 mL formation water.
- (3)
- Seal the reactor, raise the temperature, and increase the pressure to the desired experimental conditions.
- (4)
- Once the temperature and pressure inside the reactor stabilize, record the start time of the reaction.
- (5)
- During the reaction, maintain stable temperature and pressure conditions throughout the experimental duration.
- (6)
- After the reaction completes, release the pressure from the reactor and retrieve the sample.
- (7)
- Filter the aqueous phase from the reactor, transfer it into centrifuge tubes, add 1–2 drops of approximately 2% nitric acid for acidification to prevent the precipitation of metal hydroxides and preserve the sample for analysis, then refrigerate and dilute the samples. Measure cation concentrations in the solution using inductively coupled plasma optical emission spectrometry (ICP-OES). Specifically, for each sample, prepare two parallel solutions diluted 10 times for the measurement of major elements K, Na, Ca, and Mg. Subsequently, take aliquots from these diluted solutions and dilute further by 25 times (i.e., 250 times total dilution relative to the original solution) to measure trace elements such as Al and Si. Four sets of tests are conducted under specific temperature, pressure, and time conditions to cover both major and trace element measurements in parallel. Calibration for major elements uses mixed standards of Na, K, Mg, and Ca, while trace elements are calibrated using mixed standards containing multiple trace elements. During measurement, sample injection intervals are controlled to avoid interference from high chloride concentrations.
- (8)
- Dry the powder samples, then analyze the mineralogical composition before and after reaction using X-ray diffraction (XRD), and characterize the rock surface micro-morphology by scanning electron microscopy (SEM). The procedure includes washing the samples three times with ultrapure water at a ratio of 1 g powder to 40 mL water. After discarding the wash water, place the wet solids in a vacuum drying oven at 40 °C for approximately 2 days to ensure complete drying of the sandstone powder. After drying, grind approximately 0.5 g of the sample in an agate mortar to pass through a 200-mesh sieve. During XRD testing, use a copper target as the X-ray source at 30 kV and 10 mA. The scanning angle range is set from 5° to 70°, covering the main diffraction peaks of the minerals, with a step size of 0.02°.
3. Experimental Results and Analysis
3.1. Analysis of ICP-OES Results
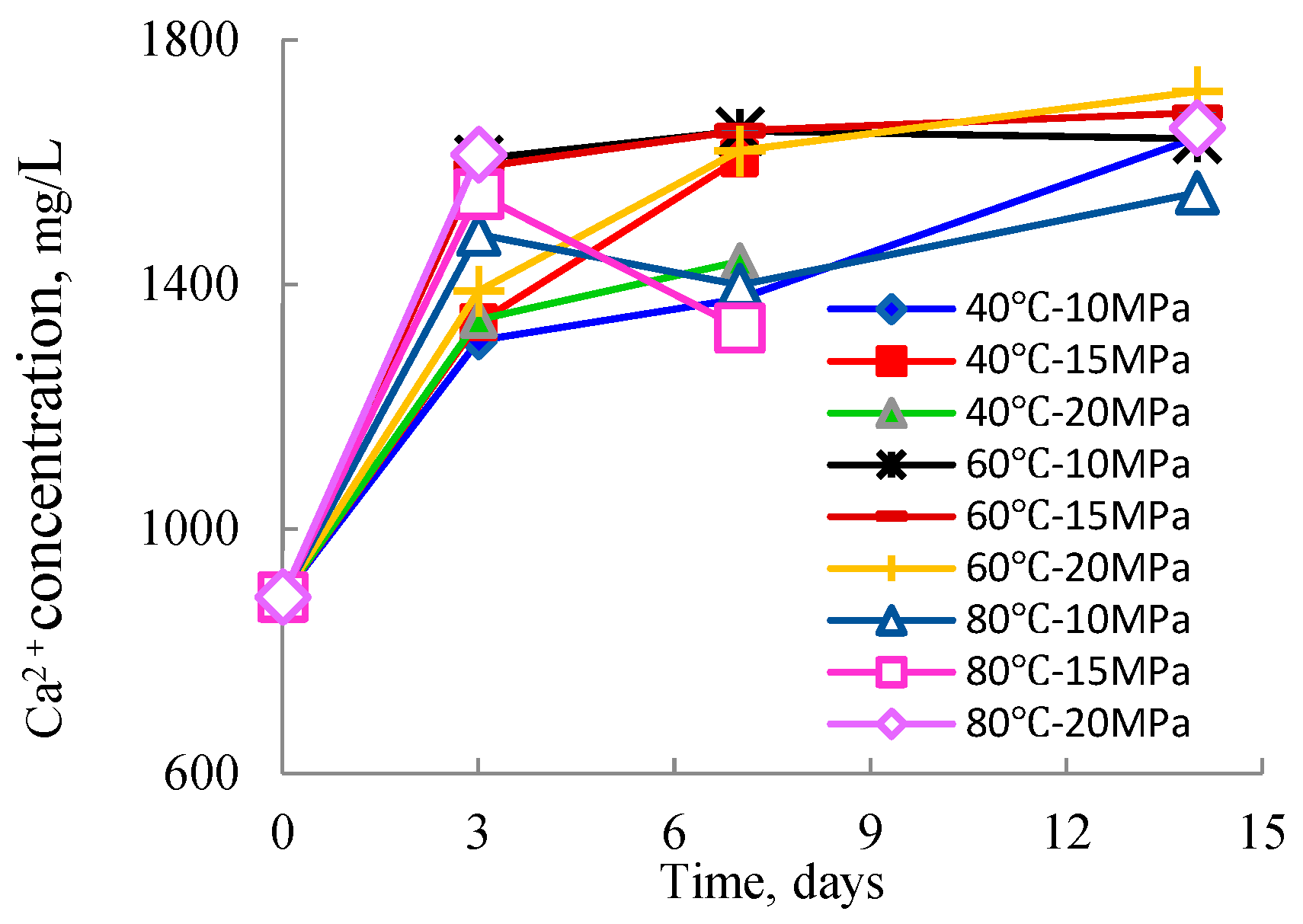
3.1.1. Changes and Reactions of Major Elements
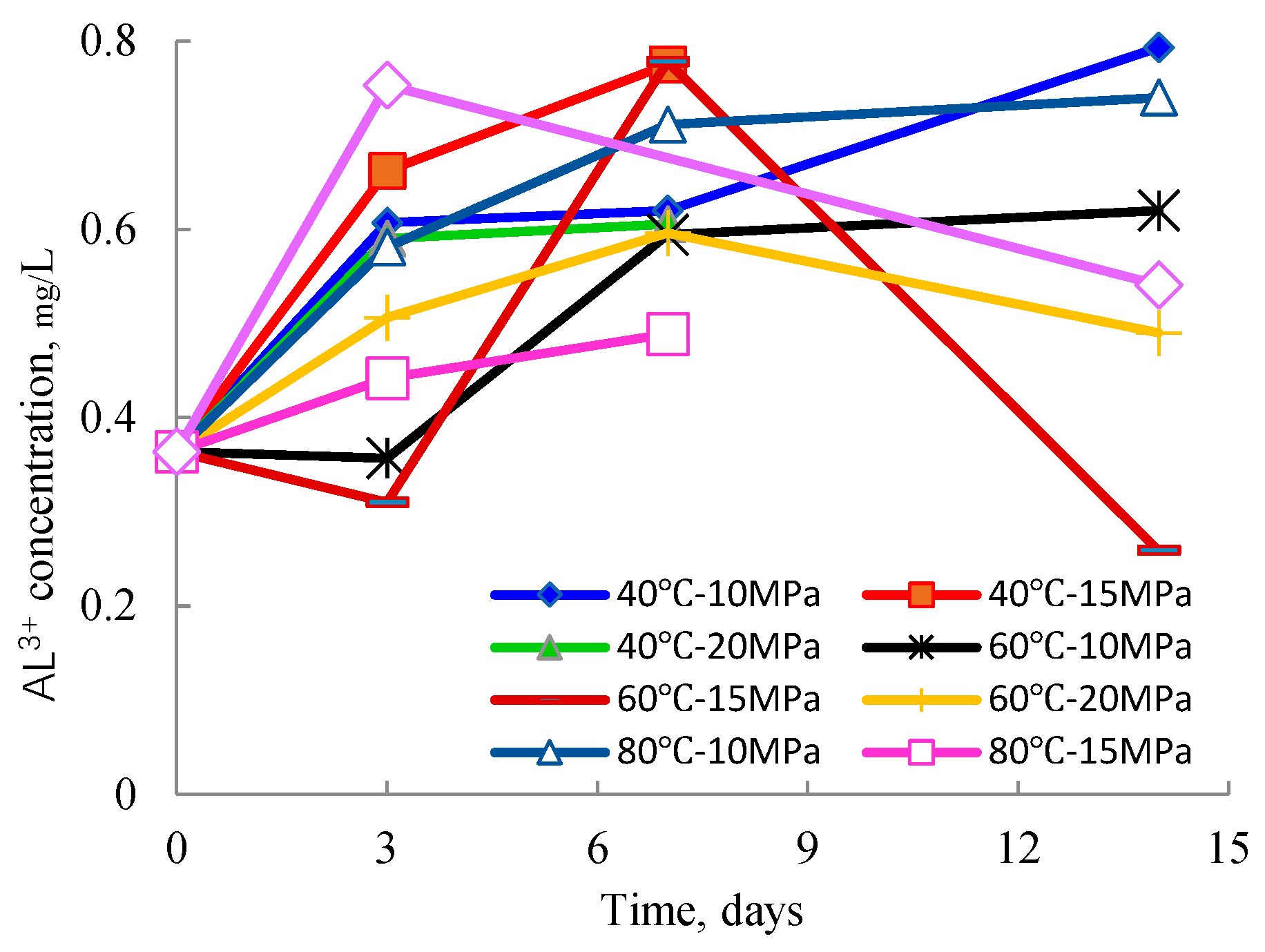
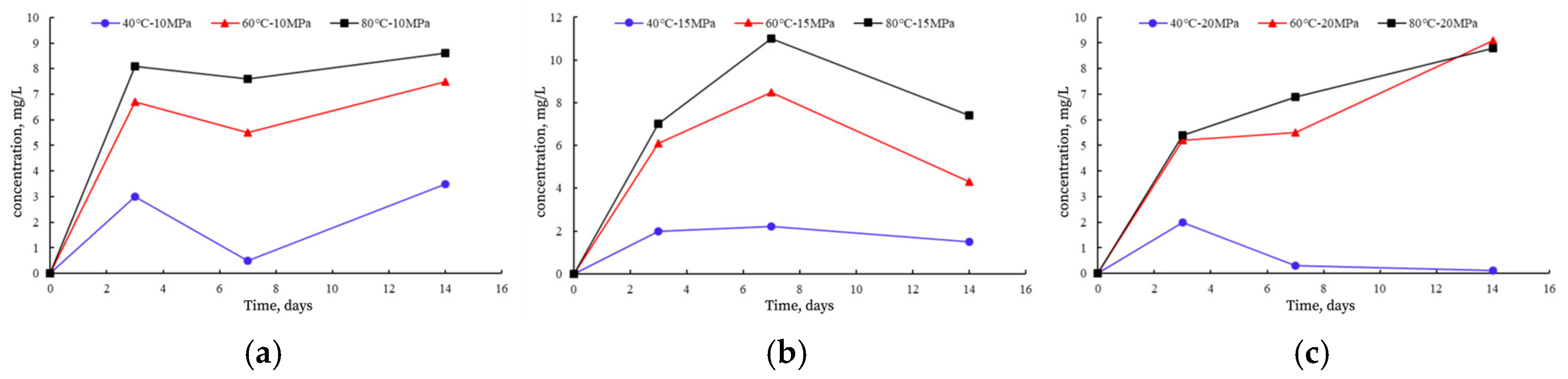
3.1.2. Changes in Al and Si Concentrations and Their Reactions
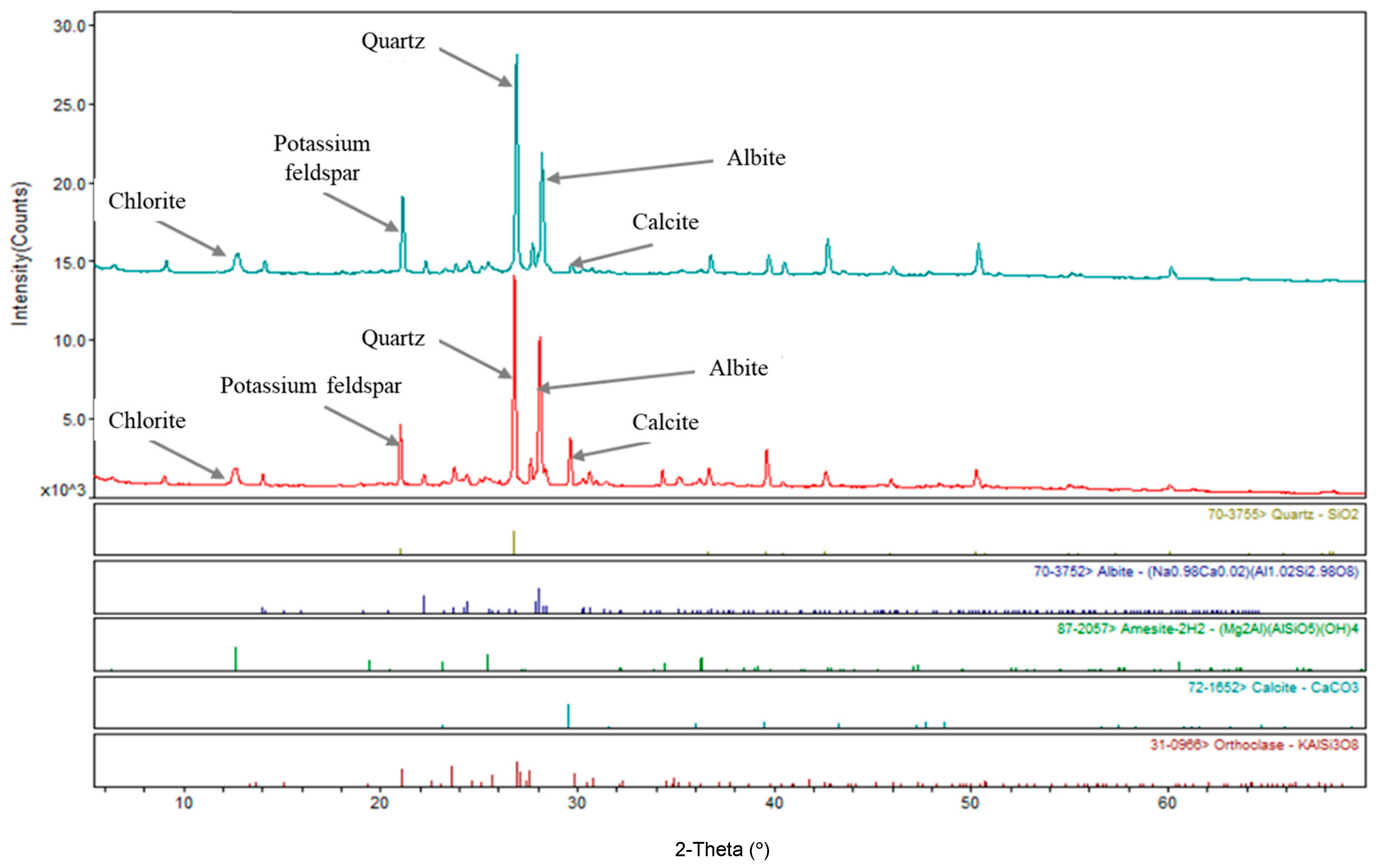
3.2. Powder X-Ray Diffraction (XRD) Analysis
3.3. Scanning Electron Microscope (SEM) Analysis
4. Coupled Numerical Simulation of CO2 EOR and Sequestration
4.1. Water–Rock Reaction Mechanism
4.2. CO2 Geochemical Reaction Model
4.3. Porosity-Permeability Mode
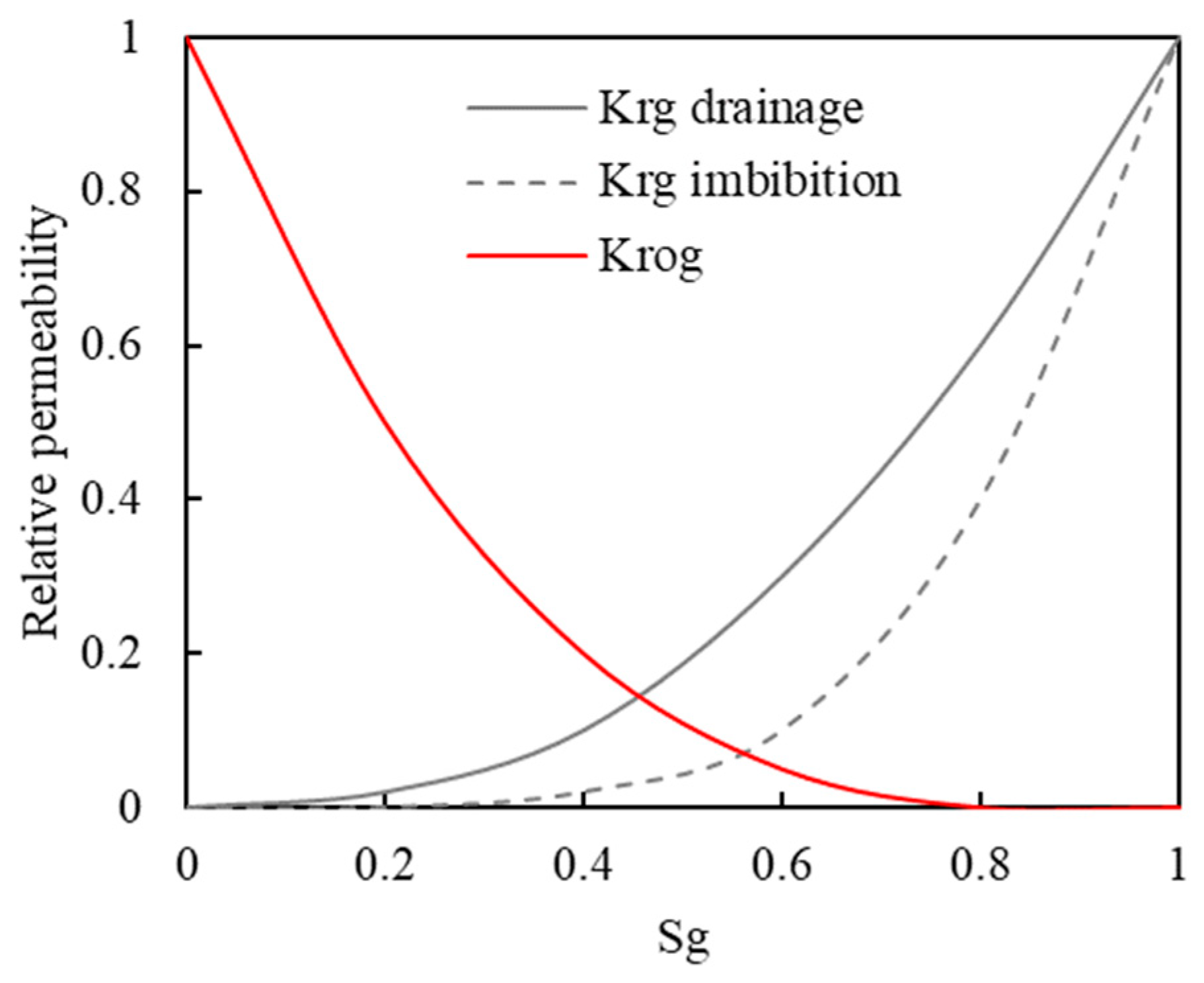
4.4. Relative Permeability Hysteresis Model
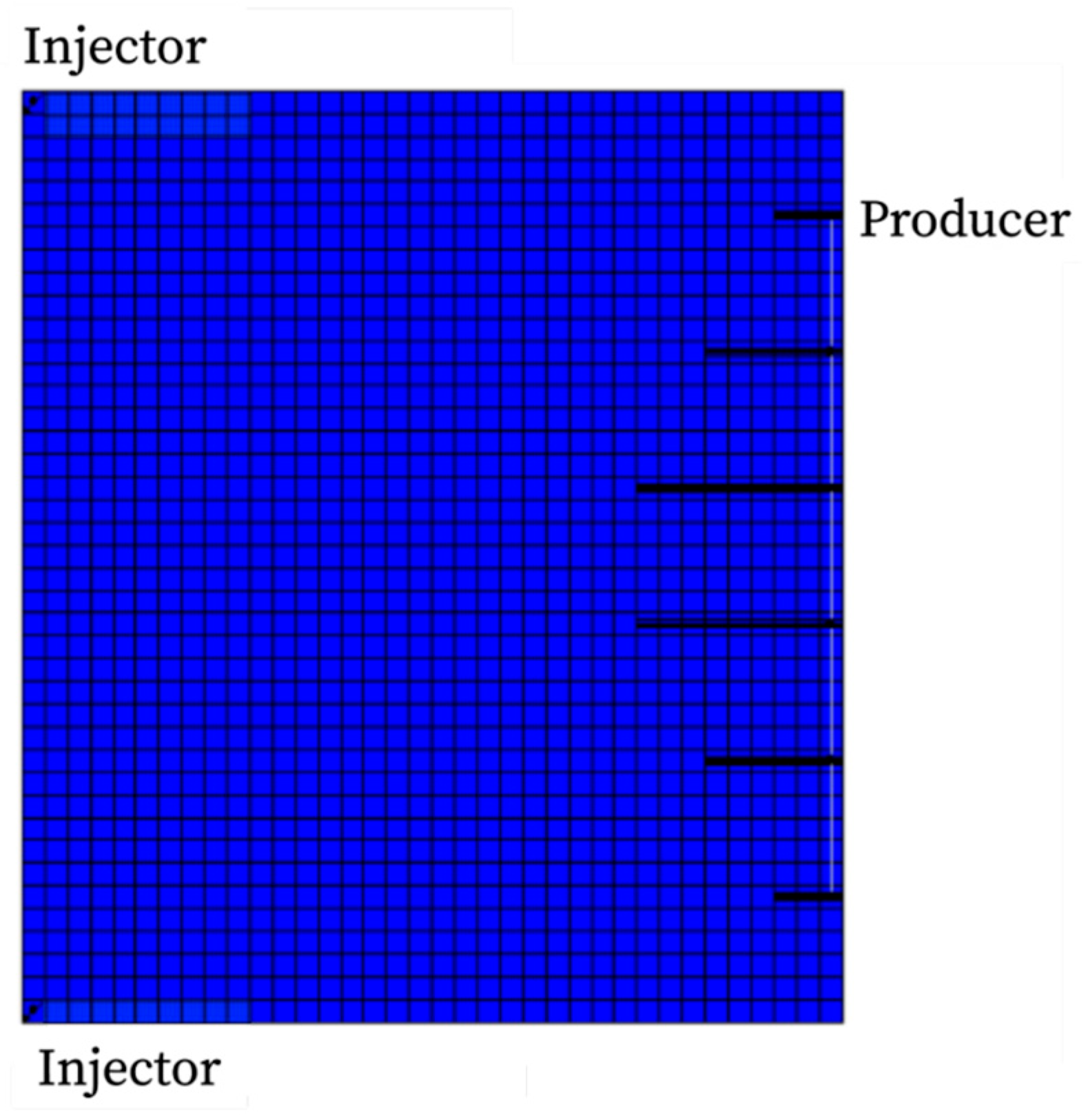
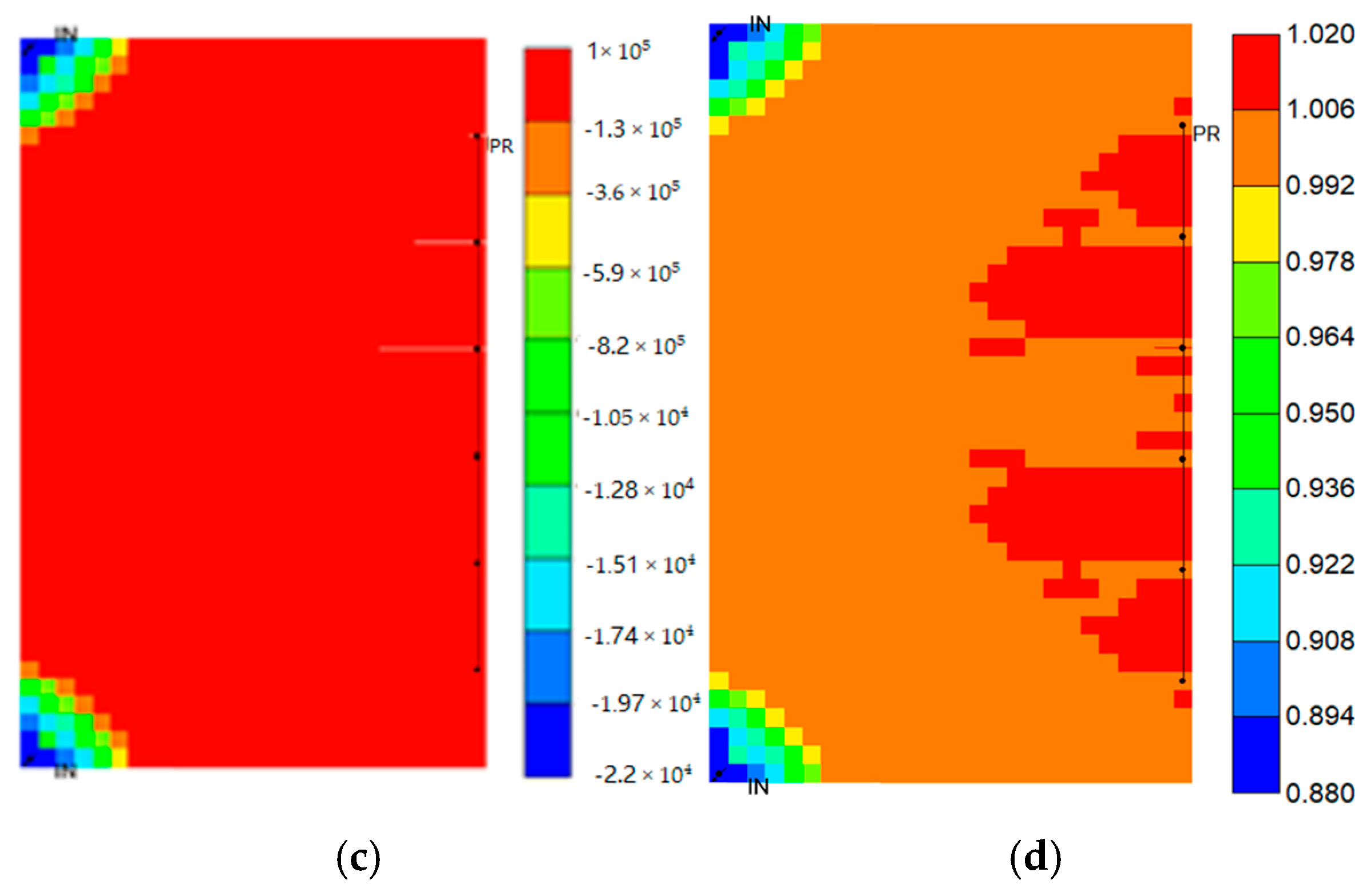
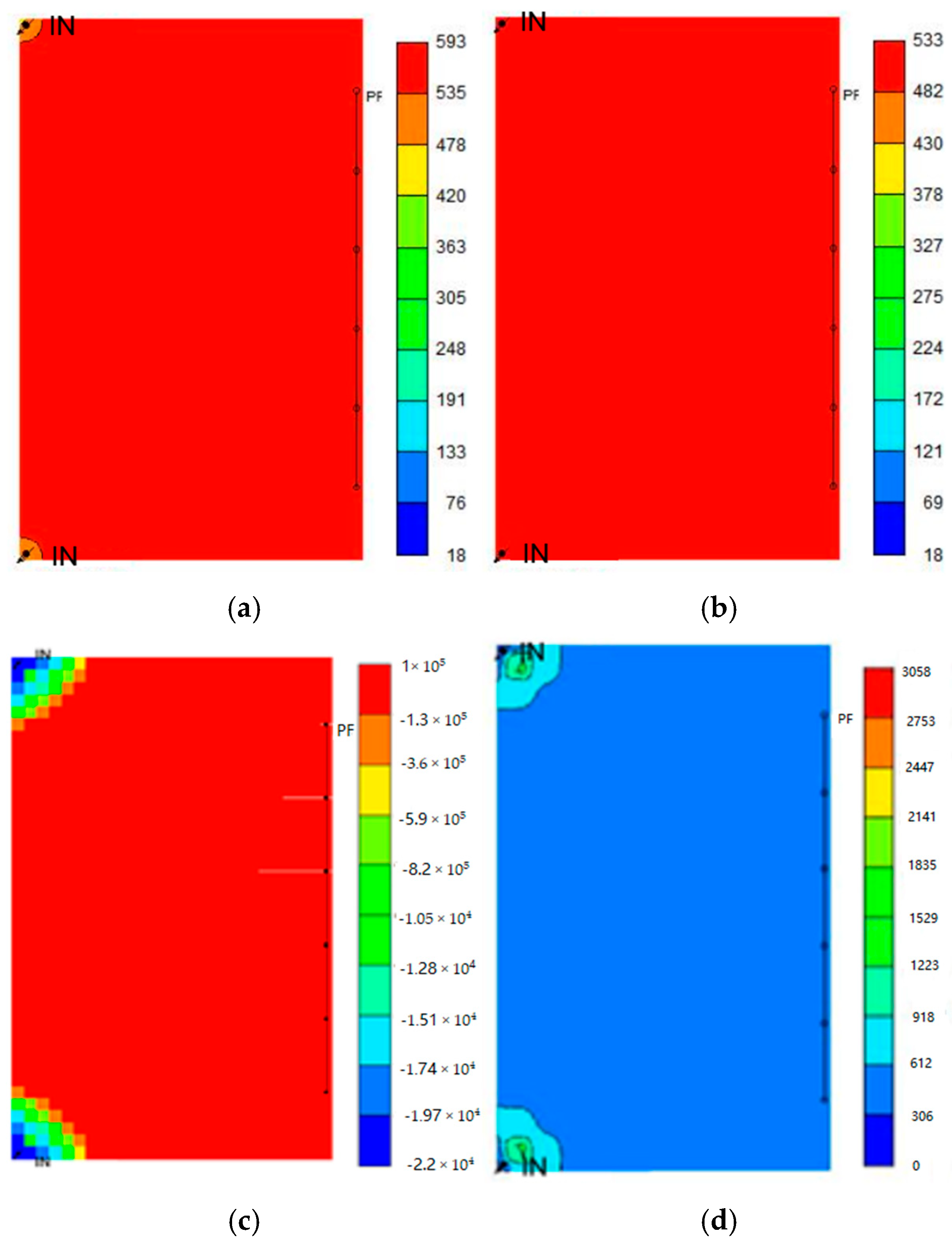
4.5. Field Model Application
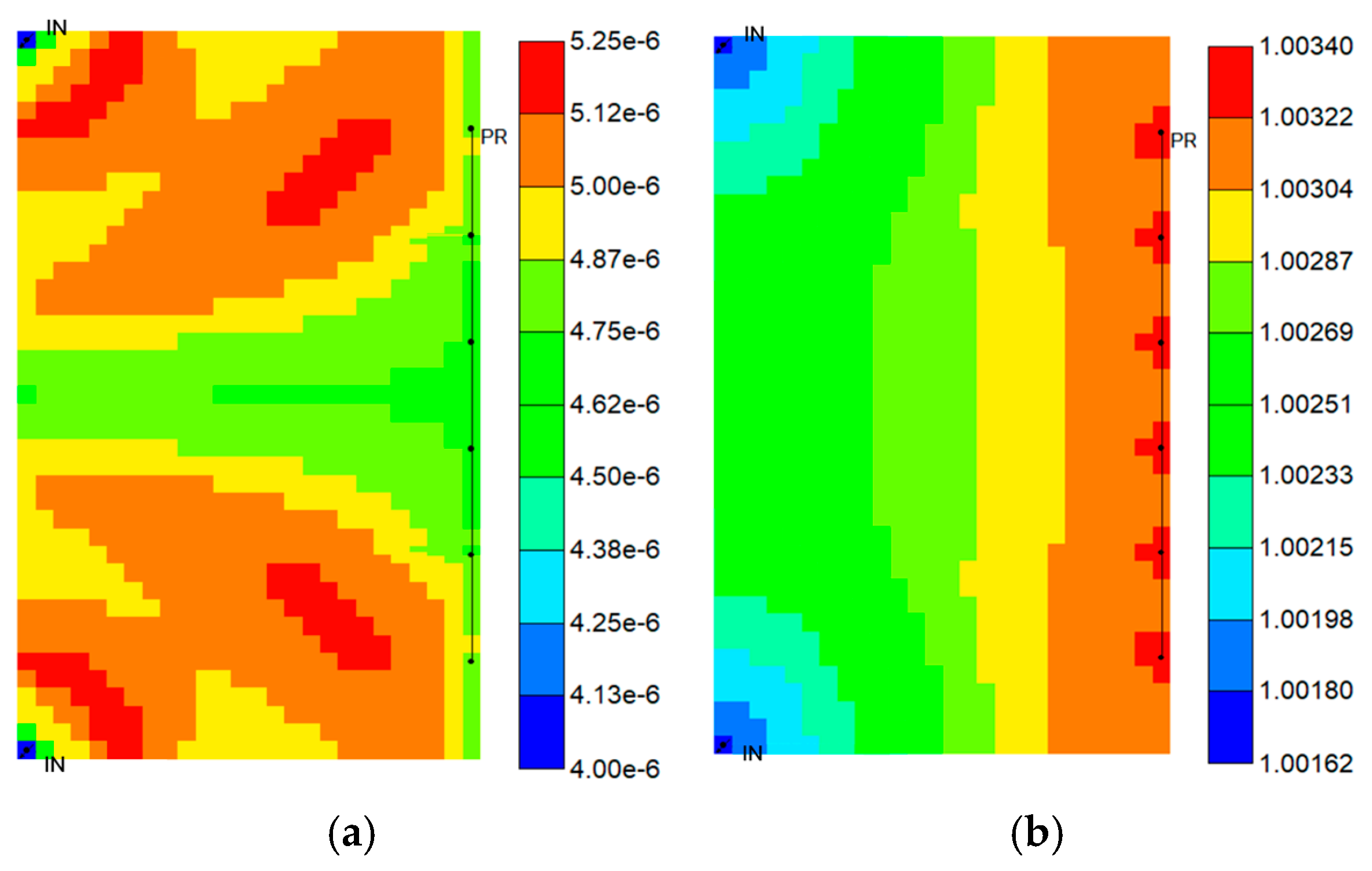
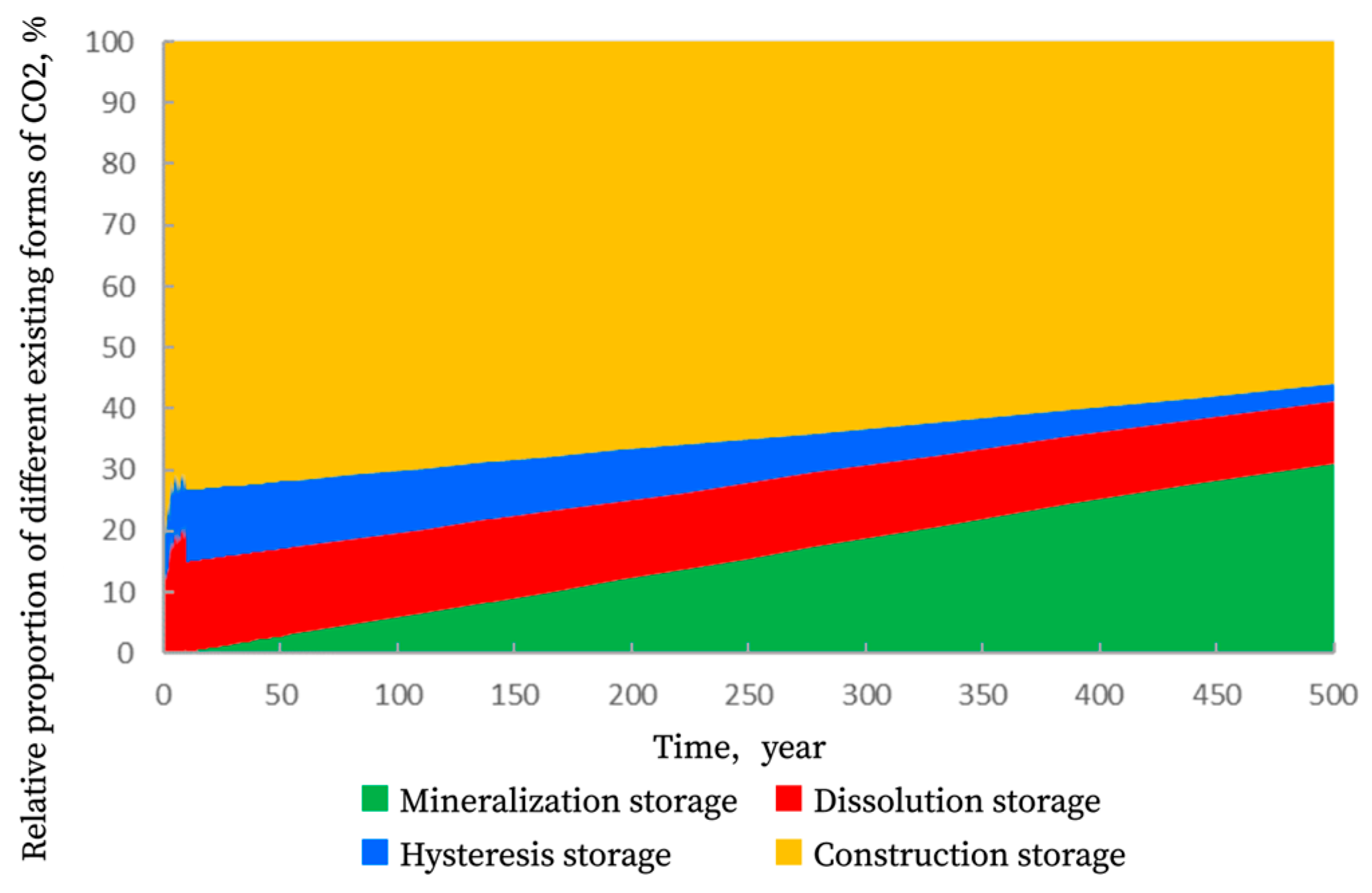
4.6. Time-Dependent Analysis of Different Trapping Mechanisms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, S.; Wang, Y.; Deng, X.; Sun, D.; Yang, Z. Study on water displacement and imbibition features of Chang 6 & Chang 8 tight oil reservoir in Ordos Basin. Unconv. OilGas 2024, 11, 80–91. [Google Scholar] [CrossRef]
- Wei, Y.; Hamidreza, L.; Kamy, S. Simulation study of CO2 huff-n-puff process in Bakken tight oil reservoirs. In SPE Western Regional Meeting; SPE Denver: Denver, CO, USA, 2014; p. SPE-169575. [Google Scholar]
- Qian, Q.; Lu, M.; Zhong, A. Study on fracture morphology of CO2 energized fracturing of continental shale oil in Dongying Sag. Pet. Drill. Tech. 2023, 51, 42–48. [Google Scholar] [CrossRef]
- Zhang, K.; Qi, Y.; Xue, X.; Tao, L.; Chen, W.; Wu, A. CO2 regional enhanced volumetric fracturing technology for shale oil horizontal wells in Ordos Basin. Pet. Drill. Tech. 2023, 51, 15–22. [Google Scholar] [CrossRef]
- He, T.; Xu, Z.; Liu, X.; Cai, X.; Zhang, D.; Zhang, W.; Li, X. Wenjian Zhu Research and Application of Pre-CO2 Energy Storage Fracturing Technology in Ultra-Low Permeability Reservoirs. In Proceedings of the International Field Exploration and Development Conference 2024, IFEDC 2024, Xi’an, China, 12–14 September 2024; Springer: Singapore, 2025; pp. 1665–1684. [Google Scholar] [CrossRef]
- Bertier, P.; Swennen, R.; Laenen, B.; Lagrou, D.; Dreesen, R. Experimental identification of CO2-water-rock interactions caused by equestration of CO2 in Westphalian and Buntsandstein sandstones of the Campine Basin (N E-Belgium). Geochem. Explor. 2006, 89, 10–14. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Xie, J. Influencing factors and application prospects of CO2 flooding in heterogeneous glutenite reservoirs. Sci. Rep. 2020, 10, 1839. [Google Scholar] [CrossRef]
- Peter, A.; Yang, D.; Eshiet, K.I.I.I.; Sheng, Y. A review of the studies on CO2–brine–rock interaction in geological storage process. Geosciences 2022, 12, 168. [Google Scholar] [CrossRef]
- Gaus, I. Role and impact of CO2-rock interactions during CO2 storage in sedimentary rocks. Int. J. Greenh. Gas Control 2010, 4, 73–89. [Google Scholar] [CrossRef]
- Li, Y. Technical advancement and prospect for CO2 flooding enhanced oil recovery in low permeability reservoirs. Pet. Geol. Recovery Effic. 2020, 27, 1–10. [Google Scholar] [CrossRef]
- Bachu, S.; Gunter, W.D.; Perkins, E.H. Aquifer disposal of CO2: Hydrodynamic and mineral trapping. Energy Convers. Manag. 1994, 35, 269–279. [Google Scholar] [CrossRef]
- Hao, Y.; Bo, Q.; Chen, Y. Laboratory investigation of CO2 flooding. Pet. Explor. Dev. 2005, 32, 110–112. [Google Scholar]
- Gao, Y.; Liu, L.; Qu, X. Mechanism of CO2-sandstone interaction and formative authigenic mineral assemblage. Xinjiang Pet. Geol. 2007, 28, 579–584. [Google Scholar]
- Wang, C.; Li, T.; Gao, H.; Gao, Y.; Zhao, J.; Dou, L. Study on influencing mechanism of asphaltene precipitation on oil recovery during CO2 flooding in tight sandstone reservoirs. Pet. Geol. Recovery Effic. 2018, 25, 107–111. [Google Scholar] [CrossRef]
- Wegner, L.; Pohlmeier, A.; Wang, Y.; Klinkenberg, M.; Bosbach, D.; Poonoosamy, J. In Situ Study of Coupled Mineral Dissolution and Precipitation Processes With Gas Production in Porous Media Using Magnetic Resonance Imaging. Water Resour. Res. 2025, 61, e2025WR040035. [Google Scholar] [CrossRef]
- Shang, Q.; Wang, Y.; Wei, D.; Chen, L. Mechanism Analysis and Evaluation of Formation Physical Property Damage in CO2 Flooding in Tight Sandstone Reservoirs of Ordos Basin, China. Processes 2025, 13, 2320. [Google Scholar] [CrossRef]
- Tang, R.; Ou, C.; Lyu, D.; Liu, C.; Wu, H. Effect of isomorphic substitution of clay mineral layers on CO2 hydrate formation: Insights from molecular dynamics simulation study. Geoenergy Sci. Eng. 2025, 250, 213843. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, X.; Kang, Y.; Guo, C.; He, Q.; Li, C. Characterization of Stages of CO2-Enhanced Oil Recovery Process in Low-Permeability Oil Reservoirs Based on Core Flooding Experiments. Energies 2024, 17, 5469. [Google Scholar] [CrossRef]
- Ozório, B.M.J.; Rosset, S.J.; Carvalho, D.A.L.; Concalves, S.D.A.; Santos, D.V.W.; Souza, S.D.B.C.; Farias, S.D.G.P. Influence of Agricultural Systems on the Physical-Granulometric Fractions of Soil Organic Matter and CO2 Emission in the Subtropical Region of Brazil. Commun. Soil Sci. Plant Anal. 2025, 56, 2459–2474. [Google Scholar] [CrossRef]
- Gunter, W.D.; Perkins, E.H.; Hutcheon, I. Aquifer disposal of acid gases: Modelling of water-rock reactions for trapping of acid wastes. J. Geochem. Explor. 2000, 69, 509–513. [Google Scholar] [CrossRef]
- Nghiem, L.; Sammon, P.; Grabenstetter, J.; Ohkuma, H. Modeling CO2 storage in aquifers with a fully-coupled geochemical EOS compositional simulator. In Proceedings of the SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK, USA, 17–21 April 2004. [Google Scholar]
- Lzgec, O.; Demiral, B.; Bertin, H.; Akin, S. Experimental and numerical modeling of direct injection of CO2 into carbonate formations. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Li, Z.; Zhang, Q.; Zhang, T.; Cui, C. Method for determining potential of dissolved CO2 storage in brine layers. Pet. Geol. Recovery Effic. 2023, 30, 174–180. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Xu, C.; Zhang, C. CO2 sequestration morphology and distribution characteristics based on NMR technology and microscopic numerical simulation. Pet. Reserv. Eval. Dev. 2023, 13, 296–304. [Google Scholar] [CrossRef]
- Krevor, S.C.M.; Pini, R.; Zuo, L.; Benson, S.M. Relative permeability and trapping of CO2 and water in sandstone rocks at reservoir conditions. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Cui, G.; Zhang, L.; Ren, S.; Zhang, Y. Geochemical reactions and CO2 storage efficiency during CO2 EOR process and subsequent storage. J. China Univ. Pet. (Ed. Nat. Sci.) 2017, 41, 123–131. [Google Scholar] [CrossRef]
- Chen, Z.; Li, R.; Yang, S.; Qin, Y.; Gong, L.; Zhang, D. A novel algorithm for asphaltene precipitation modeling in shale reservoirs with the consideration of capillary pressure during the CCUS processes. Appl. Therm. Eng. 2024, 248, 123217. [Google Scholar] [CrossRef]


| Ion Classification | Na+ | K+ | Ca2+ | Mg2+ | Cl− | HCO3− |
|---|---|---|---|---|---|---|
| Concentration (mmol/L) | 305.13 | 1.13 | 24.15 | 9.75 | 366.54 | 7.52 |
| Mineral | Quartz | Potassium Feldspar | Albite | Calcite | Chlorite | Illite | Kaolinite | Mica | Others |
|---|---|---|---|---|---|---|---|---|---|
| % | 58.3 | 10.7 | 7.9 | 5.6 | 4.2 | 6.1 | 2.4 | 1.6 | 3.2 |
| Mineral | Log(K25°C) (mol·m−2·s−1) | Activation Energy (J·mol−1) | Initial Reactive Specific Surface Area (m2·m−3) |
|---|---|---|---|
| Calcite | −8.8 | 41,870 | 33 |
| Kaolinite | −13 | 62,760 | 660 |
| Feldspar | −12 | 67,830 | 33 |
| Component Name | Mole Fraction | Molecular Weight (g/mol) | Critical Pressure (bar) | Critical Temperature (K) | Critical Volume (m3/kmol) | Acentric Factor | OMEGA | OMEGB |
|---|---|---|---|---|---|---|---|---|
| CO2 | 0.005 | 44.01 | 72.80 | 304.20 | 0.094 | 0.225 | 0.366 | 0.062 |
| N2-C1 | 0.168 | 17.93 | 43.60 | 180.02 | 0.097 | 0.013 | 0.457 | 0.078 |
| C2-C3 | 0.098 | 39.45 | 44.08 | 350.22 | 0.184 | 0.134 | 0.457 | 0.078 |
| IC4-NC5 | 0.088 | 64.55 | 35.36 | 442.26 | 0.278 | 0.213 | 0.457 | 0.078 |
| C6-C9 | 0.101 | 124.49 | 27.60 | 592.91 | 0.457 | 0.330 | 0.457 | 0.078 |
| C10-C19 | 0.261 | 217.81 | 18.69 | 730.49 | 0.766 | 0.569 | 0.457 | 0.078 |
| C20-C29 | 0.207 | 364.17 | 13.07 | 865.42 | 1.174 | 0.886 | 0.457 | 0.078 |
| C30A+ | 0.048 | 622.54 | 8.73 | 1033.03 | 1.728 | 1.255 | 0.457 | 0.078 |
| C30B+ | 0.024 | 622.54 | 8.73 | 1033.03 | 1.728 | 1.255 | 0.457 | 0.078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J.; Fan, W.; Lu, Y.; Qu, M. Characteristics of CO2–Formation Water–Rock Reaction and Simulation of CO2 Burial Efficiency in Tight Sandstone Reservoirs. Processes 2025, 13, 3644. https://doi.org/10.3390/pr13113644
Jia J, Fan W, Lu Y, Qu M. Characteristics of CO2–Formation Water–Rock Reaction and Simulation of CO2 Burial Efficiency in Tight Sandstone Reservoirs. Processes. 2025; 13(11):3644. https://doi.org/10.3390/pr13113644
Chicago/Turabian StyleJia, Junhong, Wei Fan, Yao Lu, and Ming Qu. 2025. "Characteristics of CO2–Formation Water–Rock Reaction and Simulation of CO2 Burial Efficiency in Tight Sandstone Reservoirs" Processes 13, no. 11: 3644. https://doi.org/10.3390/pr13113644
APA StyleJia, J., Fan, W., Lu, Y., & Qu, M. (2025). Characteristics of CO2–Formation Water–Rock Reaction and Simulation of CO2 Burial Efficiency in Tight Sandstone Reservoirs. Processes, 13(11), 3644. https://doi.org/10.3390/pr13113644







