Microscale Flow Mechanism of Gas Displacement in Heterogeneous Pore Structures

Abstract

As oilfield development enters the mid-to-late stages, conventional water flooding techniques face increasing challenges such as high water cut and limited improvement in recovery efficiency. Gas flooding has gradually become a critical method for enhancing oil recovery (EOR). However, significant heterogeneity in pore structures within complex reservoirs severely affects flow capacity and development performance during gas flooding processes. To elucidate the microscale flow mechanisms influenced by heterogeneity, this study constructs a series of two-dimensional pore network models with varying degrees of heterogeneity based on an improved Quartet Structure Generation Set algorithm. Gas-oil two-phase flow simulations were conducted using the multiphase flow module of COMSOL Multiphysics® 6.2. By adjusting the bimodal pore size ratio and pore distribution parameters, the heterogeneity level of the reservoir was systematically controlled, and relative permeability curves were extracted to inform macro-scale development strategy design. Simulation results indicate that (1) strong heterogeneity reduces the stability of the displacement front, leading to pronounced gas channeling; (2) in strongly heterogeneous pore structures, residual oil saturation significantly increases, with small pore regions forming residual oil-enriched zones that are difficult to mobilize; (3) relative permeability curves vary markedly under different heterogeneity conditions—oil-phase permeability declines rapidly during displacement, while gas-phase permeability rises sharply at high gas saturation levels. This study systematically investigates, for the first time, the microscale impact of pore structure heterogeneity on gas flooding behavior and applies pore-scale simulation outcomes to optimize macro-scale development strategies. The findings offer theoretical support and a technical pathway for gas injection design in complex heterogeneous reservoirs. While two-dimensional pore-network models enable controlled mechanistic and sensitivity analyses of heterogeneity, they do not fully capture three-dimensional connectivity and tortuosity. Accordingly, our results are positioned as mechanistic priors that are calibrated to field data during upscaling.

1. Introduction

As oilfields enter the mid-to-late stages of development, traditional water flooding faces critical challenges, including high water cut and low recovery efficiency. Gas flooding has emerged as an effective enhanced oil recovery (EOR) technique and is widely applied in reservoir development. However, the inherent heterogeneity of reservoir formations has a significant impact on flow mechanisms and overall development outcomes in gas flooding processes. Complex internal pore structures, uneven pore size distributions, and highly variable pore-throat connectivity often lead to unstable displacement fronts, severe gas channeling, and poor volumetric sweep efficiency—factors that severely restrict the overall effectiveness of gas flooding.

In recent years, pore network modeling (PNM) combined with multi-scale digital rock-based direct numerical simulation has been increasingly adopted to overcome the limitations of traditional continuum models in representing pore-scale heterogeneity. These techniques provide an effective approach to investigating multiphase flow mechanisms in complex heterogeneous reservoirs [1,2,3,4,5,6]. Substantial progress has been made in this field. For example, Yang et al. (2023) reconstructed multi-scale digital rocks and applied the PNM method to simulate flow in shale gas reservoirs across nano- to micrometer scales, revealing how heterogeneous pore structures influence flow dynamics [7]. Ruspini et al. (2021) improved the accuracy of relative permeability prediction in complex cores through multi-scale analysis [8]. Feng et al. (2022) systematically reviewed the development of PNM for shale reservoir simulation under multi-scale, multiphase, and multi-physics conditions [9]. Zhang et al. (2024) proposed a hybrid model combining PNM with continuum-scale simulation to better capture multiphase flow behavior in 3D digital rock images [10]. Meanwhile, recent advances in machine learning have brought new perspectives to this field; Telvari et al. (2023) integrated machine learning into PNM frameworks to enhance predictive efficiency and accuracy in highly heterogeneous porous media [11].

Currently, the primary approaches for generating porous media models include simulated annealing, hard-sphere Monte Carlo methods, sphere packing, fractional Brownian motion, and stochastic growth techniques. Among these, the stochastic four-parameter growth method—Improved Quartet Structure Generation Set (Imp-QSGS)—has been widely used due to its high controllability and modeling flexibility. This method is effective in characterizing the pore structures and simulating flow behavior in tight sandstones, shales, and carbonates. It also addresses the limitations of traditional experimental techniques in capturing pore-scale geometries, laying the foundation for simulating multiphase flow in heterogeneous reservoirs.

While the applications of PNM and digital rock physics have expanded to fields such as oil and gas recovery, carbon sequestration, and groundwater remediation, few studies have systematically explored the impact of pore structure heterogeneity on the gas flooding process. Li et al. (2018) performed core displacement experiments and PNM simulations using four rock samples with different pore structure types [12]. Their results demonstrated that significant heterogeneity exists at the microscale even when macroscopic porosity and permeability are similar, and that this heterogeneity strongly influences the distribution of residual oil. In 2019, Raeini et al. employed high-resolution micro-CT scanning to characterize the pore-throat structures of Bentheimer sandstone and Ketton limestone [13]. PNM-based gas flooding simulations revealed that bimodal pore size distributions severely reduced displacement front stability. The presence of large pores increased the residual oil saturation in small-pore regions, highlighting the effects of pore connectivity and throat size on oil displacement. In a related study, Zhang et al. (2023) developed a bimodal pore-size distribution model and used both PNM simulation and core flooding experiments to analyze how pore surface wettability and capillary forces affect flow paths and residual oil distribution under different displacement conditions [14].

On the other hand, deep learning is emerging rapidly in pore-scale digital-rock workflows and pore-network modeling. Applications of convolutional neural networks (including 3D-CNNs) in micro-CT volumes for pore/mineral segmentation, super-resolution, and denoising, and directly regress effective properties such as permeability and relative-permeability endpoints have been reported. Such regression substantially reduces the dependence on expensive lattice-Boltzmann (LBM) or Stokes solvers while retaining geometric fidelity [15,16,17]. Furthermore, generative models, including GANs and diffusion models, are applied in digital-rock reconstruction and pore–throat statistics domain transfer to enhance the cross-lithofacies and cross-resolution data coverage and model generalization [18,19]. Graph neural networks (GNNs) consider the pore–throat network as a natural graph and encode connectivity and tortuosity into message passing to rapidly predict effective permeability and related flow properties from micro-CT data while establishing an interpretable mapping from topological features to effective responses [20]. Physics-informed neural networks (PINNs) embed the governing equations and boundary/initial conditions into the loss function to provide physically constrained surrogates and inversion tools for two-phase transport by supporting fast upscaling and sensitivity analysis under limited labels [21]. Previous studies have suggested that CNN/GNN/PINN methods are being taken up into reservoir-engineering practice at a pace and that, in combination with well logs and field measurements, they can be used to enhance the prediction of permeability and relative permeability [15,16].

Although these studies provide theoretical foundations and technical support for understanding the role of heterogeneity in gas flooding, most existing research still focuses on homogeneous or unimodal pore structures. Systematic studies on gas flooding behavior in complex heterogeneous reservoirs—specifically under bimodal pore size distributions—remain scarce. Moreover, most current work is based on single-core samples and lacks broader investigations into gas flooding performance under varying degrees of heterogeneity. Key flow mechanisms such as dominant channel formation, displacement front evolution, and residual oil distribution under different heterogeneity conditions remain insufficiently understood. Additionally, systematic and quantitative analysis of relative permeability behavior and its relationship with structural heterogeneity is lacking.

To address these gaps, this study proposes an improved version of the classical Imp-QSGS algorithm, incorporating a dual-nucleation growth mechanism and a stepwise propagation strategy. A Euclidean-distance-based connectivity enhancement algorithm is also implemented to improve pore network continuity. Based on the enhanced modeling framework, this study constructs a series of two-dimensional heterogeneous pore network models to investigate the microscale flow mechanisms of gas flooding under different degrees of heterogeneity. Using the multiphase flow module of COMSOL Multiphysics, gas-oil two-phase flow simulations are conducted for multiple heterogeneous conditions. The effects of heterogeneity on front stability, dominant channel development, residual oil distribution, and sweep efficiency are systematically analyzed. Furthermore, relative permeability curves are extracted under each heterogeneity condition to quantitatively evaluate the influence of pore structure on gas flooding efficiency. The results provide theoretical insights and technical references for improving the predictive accuracy of macro-scale reservoir models and optimizing gas injection strategies in heterogeneous reservoirs. This study enriches the understanding of microscale flow mechanisms in complex pore structures and offers practical guidance for enhancing gas flooding recovery and development performance in real-world reservoir applications.

2. Construction of Heterogeneous Pore Network Models

2.1. Methodology for Constructing Heterogeneous Pore Networks

To accurately capture the complex heterogeneity characteristics of the sandstone reservoir in Field D, this study proposes an improved version of the traditional Quartet Structure Generation Set (QSGS) algorithm to generate pore network models with varying degrees of heterogeneity. The generation process is governed by four key parameters: distribution probability p_c, growth probability P_d, directional probability density $p_i^{rs}$, and porosity n, which, respectively, control the spatial distribution of solid-phase elements, the direction and speed of pore growth, directional anisotropy in growth, and the overall porosity level [22,23,24,25,26,27,28,29,30].

While the traditional QSGS algorithm is typically used to generate homogeneous porous media, this study innovatively adapts it to create heterogeneous pore network structures representative of complex reservoir conditions. The reconstruction process includes the following key steps (illustrated in Figure 1):

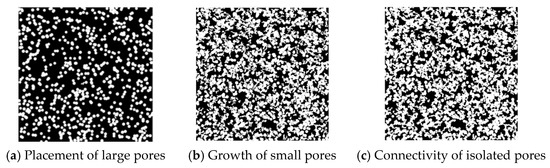
Figure 1. Generation steps of the heterogeneous pore network model.

Generation of Primary (Large) Pore Regions: Within a two-dimensional domain, primary pore nuclei are randomly distributed using a preset size range (e.g., 20–24 μm) and target porosity (e.g., 25%), controlled by the distribution probability p_c The system continuously monitors actual porosity to ensure that the distribution of pore nuclei is both representative and balanced (Figure 1a).

Growth of Secondary (Small) Pore Regions: Upon reaching the target porosity for the large pore regions, additional small pores (e.g., 5–6 μm) are generated through a modified QSGS growth process. Based on the growth probability p_d, pore units are allowed to expand into the eight neighboring directions. The pore image is iteratively updated to form a bimodal pore size distribution while gradually increasing the total porosity to the global target (e.g., 50%), as shown in Figure 1b.

Connectivity Enhancement of Isolated Pores: To address potential disconnected regions within the pore structure, a region-labeling algorithm is first used to identify isolated pore clusters. Then, the Euclidean distance transform is applied to calculate the shortest paths between adjacent isolated pores. New growth nuclei are introduced along these paths, and morphological dilation operations are used to connect boundaries, eventually forming a fully connected pore network (Figure 1c).

Compared with the canonical QSGS, our implementation introduces two independently tunable controls—(i) a dual-nucleation seeding ratio to realize prescribed pore-size bimodality and (ii) a probabilistic throat-bridging rule to raise connectivity (coordination number) while keeping the target size histogram fixed—thereby decoupling ‘size’ from ‘connectivity’ to enable reproducible sensitivity analysis and field-calibrated upscaling.

This approach ensures the accurate construction of heterogeneous pore network models that reflect the complex spatial characteristics of real reservoir rocks and serves as a solid foundation for subsequent flow simulation and displacement studies.

2.2. Pore Network Model Construction and Characterization

Based on the improved Imp-QSGS algorithm, a series of two-dimensional heterogeneous pore network models with bimodal pore size distributions were constructed. Five bimodal ratios were selected (1:2, 1:3, 1:4, 1:5, 1:6) to simulate reservoir conditions ranging from weak to strong heterogeneity. The large pore sizes were set to 10–12 μm, 15–18 μm, 20–24 μm, 25–30 μm, and 30–36 μm, respectively, with a constant porosity of 25% assigned to the large-pore regions.

Subsequently, based on the designated bimodal ratios and a fixed growth probability p_d1−8 = 0.1, small pores with diameters of 5–6 μm were randomly generated within the matrix. This process achieved a distinct bimodal distribution of pore sizes, thereby introducing notable heterogeneity into the model. Across all heterogeneity scenarios, the total porosity was maintained at 0.5 to ensure comparability of flow and permeability performance under different structural conditions. The resulting 2000 × 2000 μm pore network models are shown in Figure 2.

Figure 2. Pore network models with different levels of heterogeneity.

To ensure the generated pore network models reflected the intended structural characteristics and heterogeneity, statistical analysis of pore size distributions was performed. The target parameters were compared with the actual distributions, and adjustments were made as necessary:

Optimization of Small Pore Growth: The growth probability P_g and distribution probability P_d were tuned to regulate the spatial distribution and rate of small pore growth, preventing excessive local accumulation.

Ratio Adjustment Between Large and Small Pores: The number of large and small pores was balanced for each bimodal configuration to maintain the overall porosity within the predefined range.

Morphological Filtering: Morphological filters were applied to balance boundary connectivity between large and small pore regions, enhancing the structural uniformity and overall connectivity of the model.

After correction, the pore size distributions (shown in Figure 3) closely approximated the intended bimodal configurations, and deviations were significantly reduced.

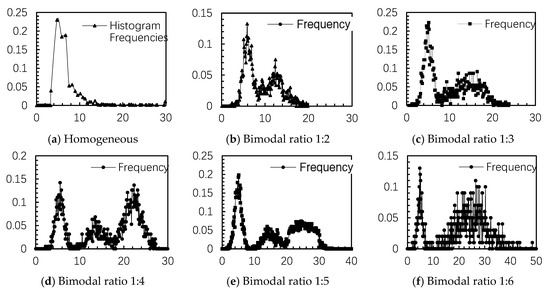
Figure 3. Size distribution of pore network models with different levels of heterogeneity.

This methodology provides a robust and flexible modeling framework for simulating pore-scale heterogeneity in complex reservoirs, laying the groundwork for accurate and meaningful multiphase flow simulations in later stages of the study.

3. Microscopic Pore Network Simulation

3.1. Simulation Results Based on Heterogeneous Pore Network Models

Pore structure heterogeneity plays a critical role in determining displacement efficiency and the spatial distribution of oil and gas phases during gas flooding. To investigate this effect, this study adopts weakly oil-wet pore network models with a contact angle of 60°, a capillary number of 4.687 × 10⁻³, and an oil–gas interfacial tension of 2 × 10⁻⁴ N/m (These values come from reservoir measurements and operating data and were used as priors for field-calibrated history matching). Simulations were performed under varying heterogeneity conditions, including a homogeneous pore network and a series of bimodal pore size distributions with ratios of 1:2, 1:3, 1:4, 1:5, and 1:6. The results are illustrated in Figure 4.

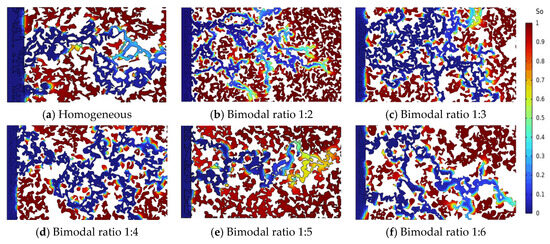
Figure 4. Pore network simulation under varying degrees of pore structure heterogeneity.

The simulation results demonstrate that pore structure heterogeneity significantly alters the displacement behavior and spatial distribution of the oil–gas phases. In the homogeneous network (Figure 4a), pore sizes and throat connectivity are uniform, resulting in minimal flow resistance during gas injection. The displacement front advances in a continuous and regular fashion. Under such conditions, the competition between capillary and viscous forces is relatively balanced, facilitating a stable displacement front and enhancing sweep efficiency, thereby reducing residual oil saturation.

In contrast, increasing structural heterogeneity (Figure 4b–f) leads to bimodal pore size distributions where large and small pores coexist and are unevenly distributed. Large pores tend to form low-resistance channels that allow gas to preferentially penetrate these regions, leading to pronounced gas channeling. Meanwhile, smaller pores, due to stronger capillary resistance, are less likely to be swept effectively, resulting in localized accumulations of residual oil and the formation of isolated oil-rich zones.

Moreover, the complex pore–throat structure at the microscale causes instability in the displacement front, often resulting in finger-like or tongue-shaped invasion patterns. These flow features cause the gas phase to bypass oil-bearing regions, further exacerbating the heterogeneity of residual oil distribution. Under high-heterogeneity conditions (e.g., bimodal ratios 1:5 and 1:6), displacement paths become highly irregular, with some areas nearly unaffected by gas, significantly lowering sweep efficiency (Figure 4e,f).

The heterogeneity of pore structures affects capillary pressure distribution, flow path selection, and front stability, all of which play a decisive role in gas displacement. The results confirm that increasing heterogeneity severely impairs displacement efficiency and highlights the dominant control of pore-scale structural features on macroscopic gas flooding performance. This underscores the importance of pore-scale modeling in accurately evaluating and optimizing injection schemes for heterogeneous reservoirs.

3.2. Relative Permeability Calculation

3.2.1. Unsteady-State Method

The unsteady-state method, also known as the externally driven method, is commonly used to determine relative permeability curves based on dynamic injection processes in porous media. This approach is grounded in Buckley–Leverett theory, which assumes that saturation varies with both time and spatial position during displacement [31]. Given that the saturation of oil and gas changes continuously in time and space, the gas flooding process is inherently unsteady, justifying the use of this method.

By tracking the time-dependent changes in fluid flow at constant pressure, the relative permeability curves can be obtained. The governing equations are as follows:

$$\begin{array}{c}{\mathrm{K}}_{\mathrm{r}\mathrm{o}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)={\displaystyle \frac{{\mathrm{f}}_0\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)\mathrm{d}\left(\frac{1}{\mathrm{V}\left(\mathrm{t}\right)}\right)}{\mathrm{d}\left(\frac{1}{\mathrm{I}·\mathrm{V}\left(\mathrm{t}\right)}\right)}}\end{array}$$

(1)

$${\mathrm{K}}_{\mathrm{r}\mathrm{g}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)={\mathrm{K}}_{\mathrm{r}\mathrm{o}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right){\displaystyle \frac{{\mathrm{\mu }}_{\mathrm{g}}}{{\mathrm{\mu }}_{\mathrm{o}}}}\cdot {\displaystyle \frac{{\mathrm{f}}_{\mathrm{g}}}{{\mathrm{f}}_{\mathrm{o}}}}$$

(2)

$$\begin{array}{c}{\mathrm{S}}_{\mathrm{g}\mathrm{e}}={\mathrm{S}}_{\mathrm{g}\mathrm{i}}+{\overline{\mathrm{V}}}_{\mathrm{o}}\left(\mathrm{t}\right)-{\mathrm{f}}_{\mathrm{o}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)·\overline{\mathrm{V}}\left(\mathrm{t}\right)\end{array}$$

(3)

$$\mathrm{I}={\displaystyle \frac{{\mathrm{\mu }}_{\mathrm{o}}\mathrm{u}\mathrm{L}}{\mathrm{K}·∆\mathrm{p}\left(\mathrm{t}\right)}}={\displaystyle \frac{{\mathrm{\mu }}_{\mathrm{o}}\mathrm{Q}\left(\mathrm{t}\right)\mathrm{L}}{\mathrm{K}\mathrm{A}∆\mathrm{p}\left(\mathrm{t}\right)}}$$

(4)

The relative permeabilities of the oil and gas phases at the outlet-end saturation are represented by ${\mathrm{K}}_{\mathrm{r}\mathrm{o}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)$ and ${\mathrm{K}}_{\mathrm{r}\mathrm{g}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)$. The dimensionless cumulative gas injection, $\overline{\mathrm{V}}\left(\mathrm{t}\right)$, is defined as ${\mathrm{V}}_{\mathrm{t}}/{\mathrm{V}}_{\mathrm{p}}$, where ${\mathrm{V}}_{\mathrm{t}}$ is the cumulative gas injection and ${\mathrm{V}}_{\mathrm{p}}$ is the pore volume of the rock sample. Similarly, ${\overline{\mathrm{V}}}_{\mathrm{o}}\left(\mathrm{t}\right)$=${\mathrm{V}}_{\mathrm{o}}/{\mathrm{V}}_{\mathrm{p}}$ represents the dimensionless cumulative oil production, with ${\mathrm{V}}_{\mathrm{o}}$ being the total oil produced. The oil and gas fractions at the outlet, ${\mathrm{f}}_{\mathrm{o}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)$ and ${\mathrm{f}}_{\mathrm{g}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)$, correspond to the volume percentages of oil and gas in total production. ${\mathrm{S}}_{\mathrm{g}\mathrm{e}}$ is the gas saturation at the outlet, and ${\mathrm{S}}_{\mathrm{g}\mathrm{i}}$ is the irreducible gas saturation of the core. ${\mathrm{\mu }}_{\mathrm{o}}$ and ${\mathrm{\mu }}_{\mathrm{g}}$ are the viscosities of oil and gas, respectively, while K is the core’s absolute permeability. Other variables include the cross-sectional area of the rock sample A, the length of the core L, and the production rate at the outlet Q(t). Finally, $\mathrm{△}\mathrm{p}\left(\mathrm{t}\right)$ is the pressure difference across the core at time t, and u is the flow velocity.

3.2.2. Variation Trends and Plotting of Relative Permeability

Simulations were conducted using a homogeneous pore network with the following parameters:

Length L = 129.42 μm, height H = 83.87 μm, permeability K = 0.04 μm², and viscosity ratio ${\mathrm{\mu }}_{\mathrm{o}}$/${\mathrm{\mu }}_{\mathrm{g}}$= 1.85/0.058.

The simulation and data processing steps are summarized as follows:

Record the initial oil and gas flow data, including pressure drop ΔP, cumulative oil production ${\mathrm{V}}_{\mathrm{o}}$, cumulative gas injection ${\mathrm{V}}_{\mathrm{t}}$, and the gas fraction at the outlet ${\mathrm{f}}_{\mathrm{g}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)$. The dimensionless gas injection volume $\overline{\mathrm{V}}\left(\mathrm{t}\right)$=${\mathrm{V}}_{\mathrm{t}}/{\mathrm{V}}_{\mathrm{p}}$ is calculated, where ${\mathrm{V}}_{\mathrm{p}}$ is the pore volume of the rock sample. Similarly, the dimensionless cumulative oil production ${\overline{\mathrm{V}}}_{\mathrm{o}}\left(\mathrm{t}\right) = {\mathrm{V}}_{\mathrm{o}}/{\mathrm{V}}_{\mathrm{p}}$ is determined. The gas saturation at the outlet, ${\mathrm{S}}_{\mathrm{g}\mathrm{e}}$, is calculated using Equation (3). The injection index $\mathrm{I}$ is then computed from Equation (4). Finally, the relative permeabilities ${\mathrm{K}}_{\mathrm{r}\mathrm{o}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)$ and ${\mathrm{K}}_{\mathrm{r}\mathrm{g}}\left({\mathrm{S}}_{\mathrm{g}\mathrm{e}}\right)$ are obtained using Equations (1) and (2), respectively. The calculation process and results are shown in Table 1.

Table 1. Unsteady-state simulation data for oil–gas relative permeability.

Data Point	$∆\mathbf{P}$, MPa	${\mathbf{V}}_{\mathbf{o}}$, mL	${\mathbf{V}}_{\mathbf{t}}$, mL	${\mathbf{f}}_{\mathbf{g}}$(${\mathbf{S}}_{\mathbf{g}\mathbf{e}}$), %	I	${\mathbf{K}}_{\mathbf{r}\mathbf{o}}$, %	${\mathbf{K}}_{\mathbf{r}\mathbf{g}}$, %
1	1.00	2.41 × 10−3	9.96 × 10−4	29.24	1.00	89.66	0.43
2	1.00	3.36 × 10−3	2.64 × 10−3	44.00	5.74	12.53	6.70
3	1.00	8.14 × 10−3	9.54 × 10−3	53.96	10.53	5.45	15.00
4	1.00	1.84 × 10−2	2.87 × 10−2	60.88	11.48	3.65	26.53
5	1.00	2.09 × 10−2	3.73 × 10−2	64.05	12.07	2.46	36.31
6	1.00	2.14 × 10−2	4.48 × 10−2	67.62	12.65	1.67	44.43
7	1.00	2.70 × 10−2	6.36 × 10−2	70.23	13.21	1.14	51.91

The relative permeability curves under different heterogeneity levels are shown in Figure 5.

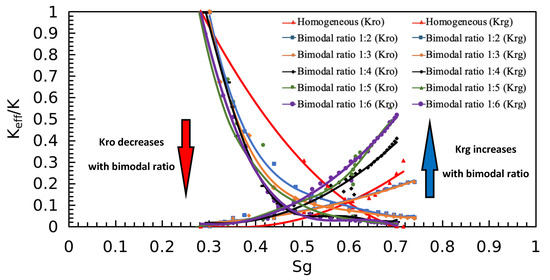
Figure 5. Comparison of oil and gas phase relative permeability curves under varying degrees of pore structure heterogeneity.

The results show that pore structure heterogeneity significantly affects the relative permeability during gas flooding. In homogeneous networks, gas flows uniformly, and gas-phase permeability increases steadily with saturation. As heterogeneity increases, large flow channels dominate, allowing gas to channel through high-permeability paths, leading to rapid increases in gas-phase permeability at high saturations.

Meanwhile, small pores are prone to gas trapping, making the residual oil difficult to recover. This results in higher residual oil saturation and a leftward shift in the oil-phase relative permeability curve. Moreover, oil permeability declines more sharply at low gas saturations, and the displacement front becomes increasingly unstable. Gas intermittency and flow interruption occur more frequently, reducing the overall gas flooding efficiency.

These variations in relative permeability curves under different heterogeneity levels confirm the strong influence of microscale structural characteristics on macroscopic flow behavior. The findings provide quantitative support for constructing parameter models for gas injection development in heterogeneous reservoirs.

4. Field Application

To address the aforementioned challenges, macro-scale reservoir simulation must account for microscopic pore network characteristics and the geological evolution of the reservoir. In this section, both geological features and pore-scale structural heterogeneity are integrated into a numerical simulation framework using tNavigator 24.2, combined with relative permeability templates derived from previous simulations. Time–space partitioning of the relative permeability model is implemented to accurately characterize reservoir development behavior, capture the dynamic variations in reservoir properties and fluid flow during gas injection, and determine optimal injection–production parameters under varying degrees of heterogeneity.

The target formation for development is the 01–04 sublayers within the 1C ΙΙΙ upper member, with a thickness of approximately 25 m, and the reservoir exhibits pronounced planar displacement features.

To accurately characterize the influence of injection stages and reservoir types on relative permeability and recovery performance, a time–space segmentation approach was employed. Specifically, the oil–gas relative permeability curves were defined separately for different injection periods and spatial reservoir partitions.

Time Partitioning

The injection history and production performance of the selected well group were used to divide the development period into three distinct stages:

1

Initial Injection Stage (2014–2017):

2

Gas injection began in 2014, with injected gas mainly distributed around the injection well. Due to higher flow velocities and a larger capillary number (Ca = 6.339 × 10⁻²), the system operated in a miscible or near-miscible state, characterized by extremely low interfacial tension (σ = 1.0 × N/m, Figure 6a). Interfacial tension refers to the contractive tendency of the interface between two immiscible fluids, such as oil and gas, which resists their mixing.

3

Early Stable Injection Stage (2017–2021):

4

As injection volumes increased, the displacement front stabilized. The capillary number decreased to Ca = 4.687 × 10⁻², and the interfacial tension rose to σ = 1.0 × N/m (Figure 6b).

5

Late Injection Stage (2021–2025):

From 2021 onwards, production performance deteriorated, with a sharp rise in the gas–oil ratio. Breakthrough occurred in three production wells, marking the mid- to late stages of gas injection. The capillary number dropped further to Ca = 3.125 × 10⁻², with a higher interfacial tension of σ = 8.0 × N/m (Figure 6c).

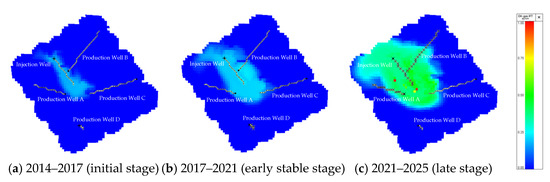
Figure 6. Interfacial tension distribution during different gas injection stages in the D sandstone reservoir.

Next, spatial partitioning was carried out. The injection–production well group mainly develops the 01–04 sublayers, and the gas injection development is characterized by planar displacement, with significant interlayer heterogeneity. As shown in Figure 7, the upper layers 01–02 showed better gas sweep compared to the lower layers 03–04 (Figure 7b). The D sandstone reservoir exhibits obvious vertical heterogeneity, and the gas displacement profile from the injection well to the production wells is uneven, with evident fingering phenomenon.

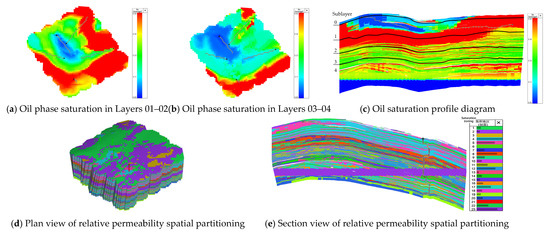
Figure 7. Oil phase saturation profile around gas injection wells in a typical development unit and relative permeability spatial partitioning.

Based on reservoir physical property data and historical gas flooding performance, relative permeability curves are partitioned vertically (Figure 7d,e), and curves are assigned based on the heterogeneity degree of the sublayer zones defined in previous sections. For example, for reservoirs in zone 4 during the mid-to-late stage of gas injection, the relative permeability curve simulated under bimodal pore ratio 1:3, capillary number Ca = 3.125 × 10⁻², and interfacial tension σ = 8.0 × 10⁻⁴ N/m is used.

The advantage of time–space partitioning lies in its ability to more finely characterize the impact of reservoir heterogeneity, injection–production parameters, and fluid phase changes on relative permeability. This helps more accurately predict future production and implement more reliable development strategies.

A comparison of the production matching before and after partitioning of the relative permeability model is shown in Figure 8, which presents daily oil, gas, and water production simulated by the original model and the partitioned model. It can be seen that whether the model uses time–space partitioning of relative permeability curves has a significant impact on development performance in both early and mid-to-late gas injection stages. The model with partitioning performs better in history matching and is more consistent with actual production performance. This indicates that the proposed modeling method of time–space relative permeability segmentation based on reservoir heterogeneity and fluid phase evolution is more reliable for gas injection reservoir simulation.

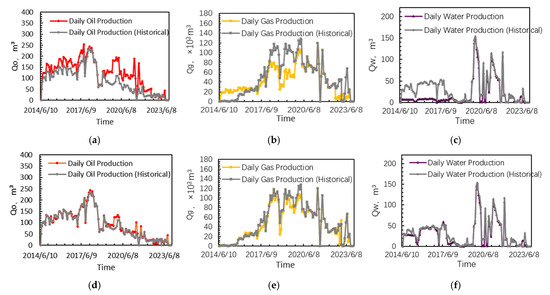
Figure 8. Daily production rates for a representative development unit. (a–c) Oil, gas, and water production from the base (non-partitioned) model. (d–f) Corresponding production rates from the relative permeability partitioned model.

In this section, the simulation results using the partitioned relative permeability model are more consistent with field production data. Figure 9a,b show the oil saturation distributions for the models without and with relative permeability partitioning, respectively, while Figure 9c,d show the gas saturation distributions for the two models. By examining these figures, it is evident that the partitioned model (Figure 9b,d) shows a larger gas sweep range and a wider oil–gas transition zone, which is more in line with actual oil–gas distribution during gas flooding. Specifically, by observing the oil and gas saturation distributions in Figure 9, we can see that in the early stage of injection, the injected gas interacts with residual oil to form a miscible zone, enhancing the permeability of the oil phase and reducing viscosity. This allows the injected gas to penetrate deeper and cover a wider area in the reservoir. This change is particularly noticeable in Figure 9b,d, where the distribution of gas saturation and the variation in oil saturation demonstrate the differences in displacement efficiency between the models.

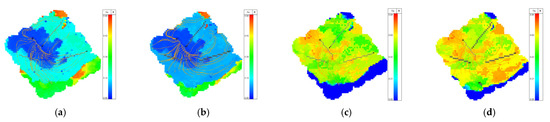
Figure 9. Oil (a,b) and gas (c,d) saturation distribution during gas flooding, comparing the base (a,c) and partitioned (b,d) models.

It is worth noting that in this study, reservoir heterogeneity is parameterized primarily by the pore/throat size statistics to isolate the pore-size effect on displacement mechanisms. Connectivity-related attributes (e.g., coordination number and tortuosity) are kept within a controlled range by the growth rules to avoid confounding factors in the sensitivity analysis. The pore-scale trends and relative-permeability templates derived from the 2D networks are then used as priors in the reservoir simulator and re-calibrated via history matching to production and well-test data, yielding field-consistent parameterization.

5. Conclusions

In this study, a two-dimensional heterogeneous pore network model with bimodal pore size distribution was successfully constructed based on the improved four-parameter stochastic growth method. By controlling the bimodal ratio and pore structure parameters, pore structure characteristics under different degrees of heterogeneity were systematically characterized. Furthermore, the COMSOL Multiphysics multiphase flow module was used to conduct gas–oil two-phase flow simulations under varying heterogeneity conditions, and the effects of heterogeneity on front stability, the dominant channel formation, and residual oil distribution during gas flooding were thoroughly analyzed. The main conclusions are as follows:

• The Imp-QSGS algorithm can effectively reconstruct heterogeneous pore structures with bimodal pore size distributions, enabling digital core modeling under different reservoir heterogeneity conditions and enhancing the structural realism and representativeness of the pore network models.
• As pore structure heterogeneity increases, the front stability during gas flooding significantly decreases, leading to the formation of high-permeability channels and aggravated gas channeling, which in turn reduces the overall sweep volume and oil displacement efficiency.
• In highly heterogeneous pore structures, residual oil tends to accumulate in small pore–throat regions, forming oil-rich zones that are difficult to mobilize. This results in lower oil-phase relative permeability and degraded displacement performance.
• The relative permeability curves under different heterogeneity levels indicate that heterogeneity has a significant impact on oil–gas phase flow behavior. Increased heterogeneity causes an earlier drop in oil-phase relative permeability and a rapid increase in gas-phase relative permeability at high gas saturation.
• The proposed heterogeneous pore network modeling method and the microscopic flow mechanism analysis of gas flooding provide theoretical support and technical guidance for optimizing gas injection development parameters in complex reservoirs and show good engineering application potential.

This study enriches the theoretical framework of microscopic flow mechanisms for gas flooding under complex heterogeneous reservoir conditions and provides an effective method for enhancing recovery and optimizing gas injection strategies in such reservoirs. However, the current study adopts a two-dimensional pore network model, which is primarily used to investigate the influence mechanism of bimodal pore size heterogeneity on gas–oil flow behavior. Because 2D networks cannot fully reproduce 3D connectivity and tortuosity, the quantitative values should be viewed as indicative and are anchored by field calibration in our upscaling workflow. Future research will aim to extend the Imp-QSGS algorithm to 3D pore structure reconstruction based on high-resolution 3D digital core data and conduct multiphysics simulations and cross-validation with experimental data.