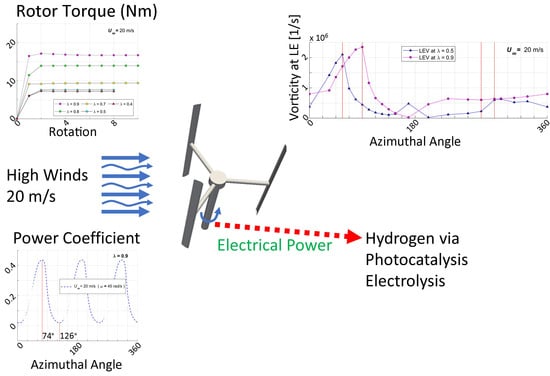
CFD Modeling of an H-Type Darrieus VAWT under High Winds: The Vorticity Index and the Imminent Vortex Separation Condition
Abstract
1. Introduction
- To implement a Vorticity Index (VI), defined as the ratio between the leading-edge vorticity (LEV) and the trailing-edge vorticity (TEV), to quantify vorticity in the VAWTs.
- To develop this study using a 2D model validated with experimental data reported in the literature [22].
- To establish a relationship between the Vorticity Index (VI) and the Imminent Vortex Separation Condition (IVSC) with the VAWT extracted energy, for a VAWT functioning at 8 m/s and 20 m/s.
2. Numerical Simulation
2.1. Physical Model
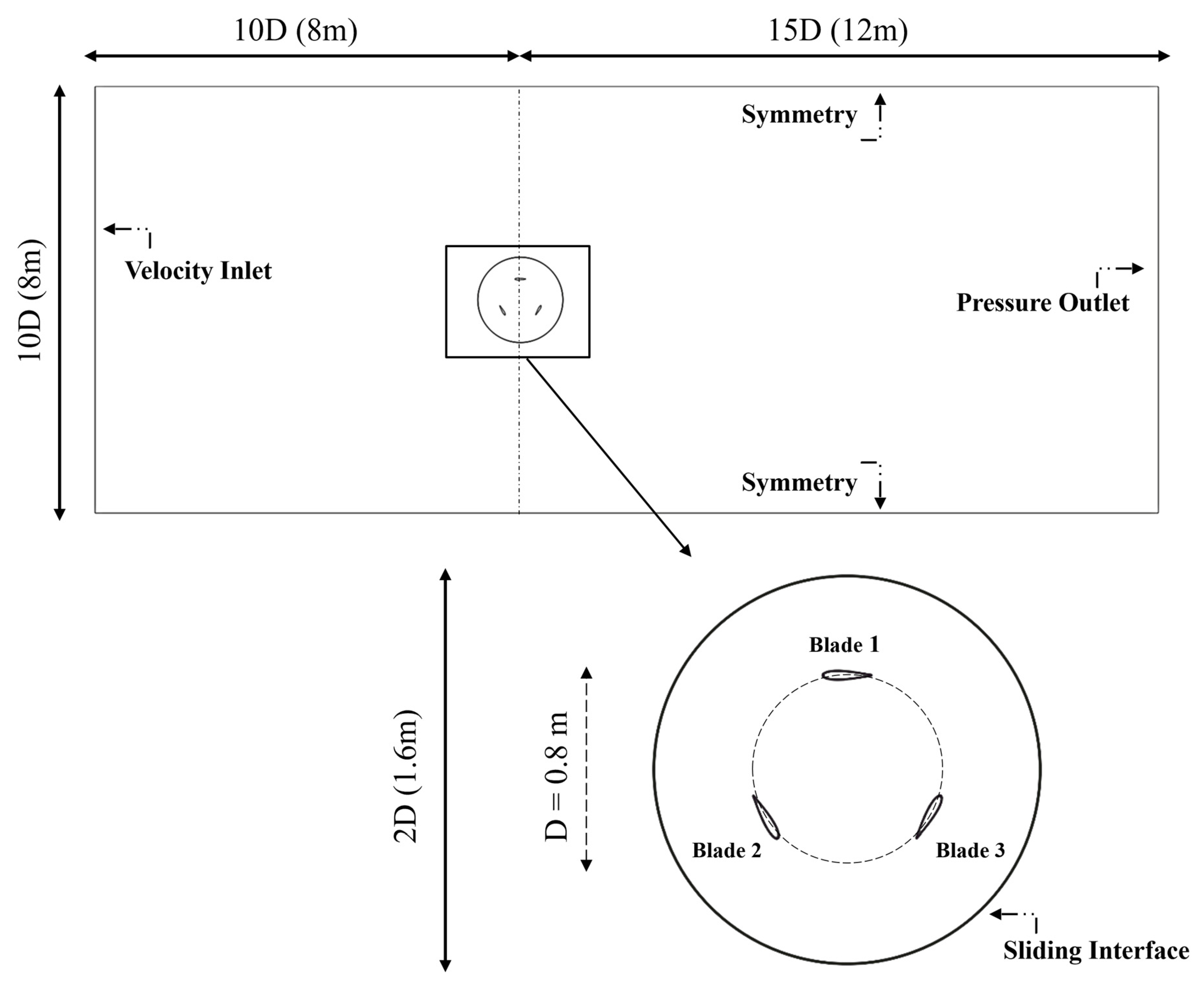
2.2. Computational Domain
2.3. Setting Up
Turbulence Model
2.4. Meshing
2.5. Angular Marching Step
3. Results and Discussion
3.1. Model Validation
3.2. Influence of High Winds
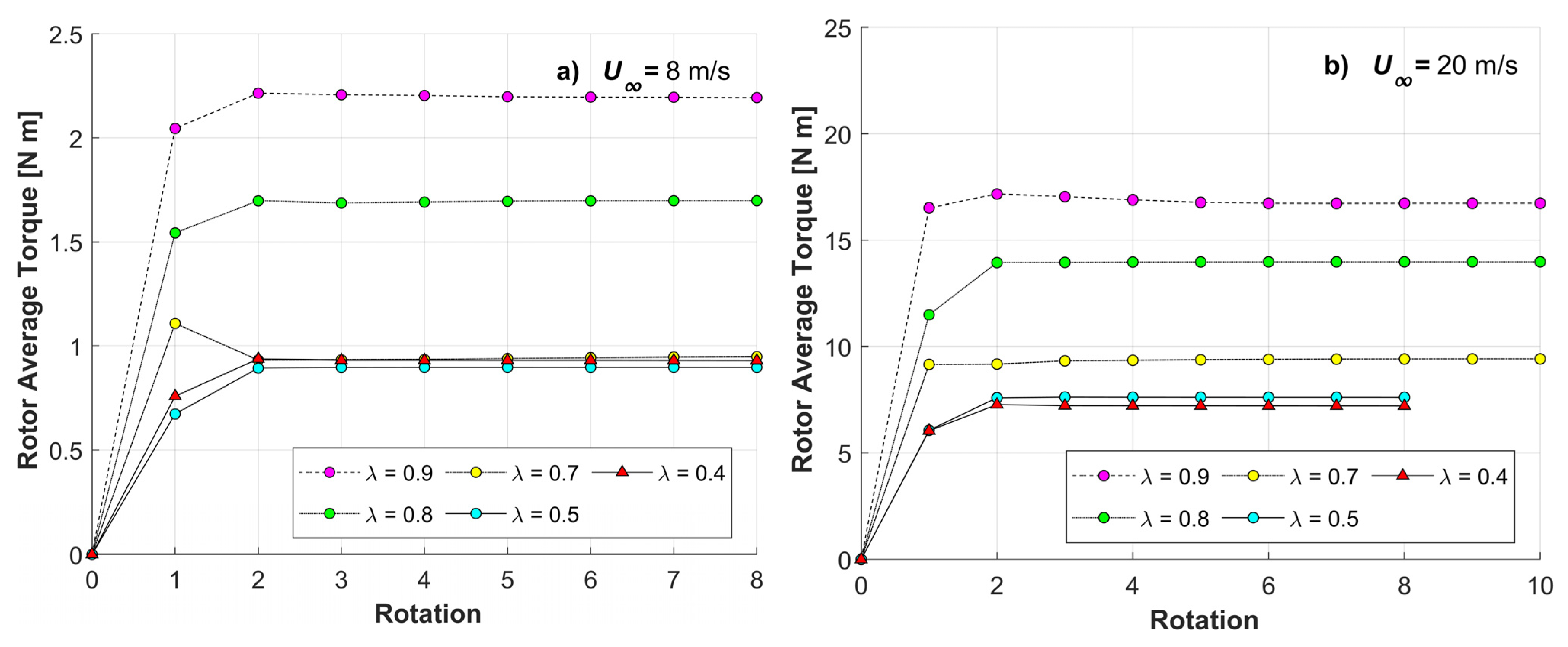
3.2.1. Wind Speed Effect on Overall Torque—Convergence Criteria
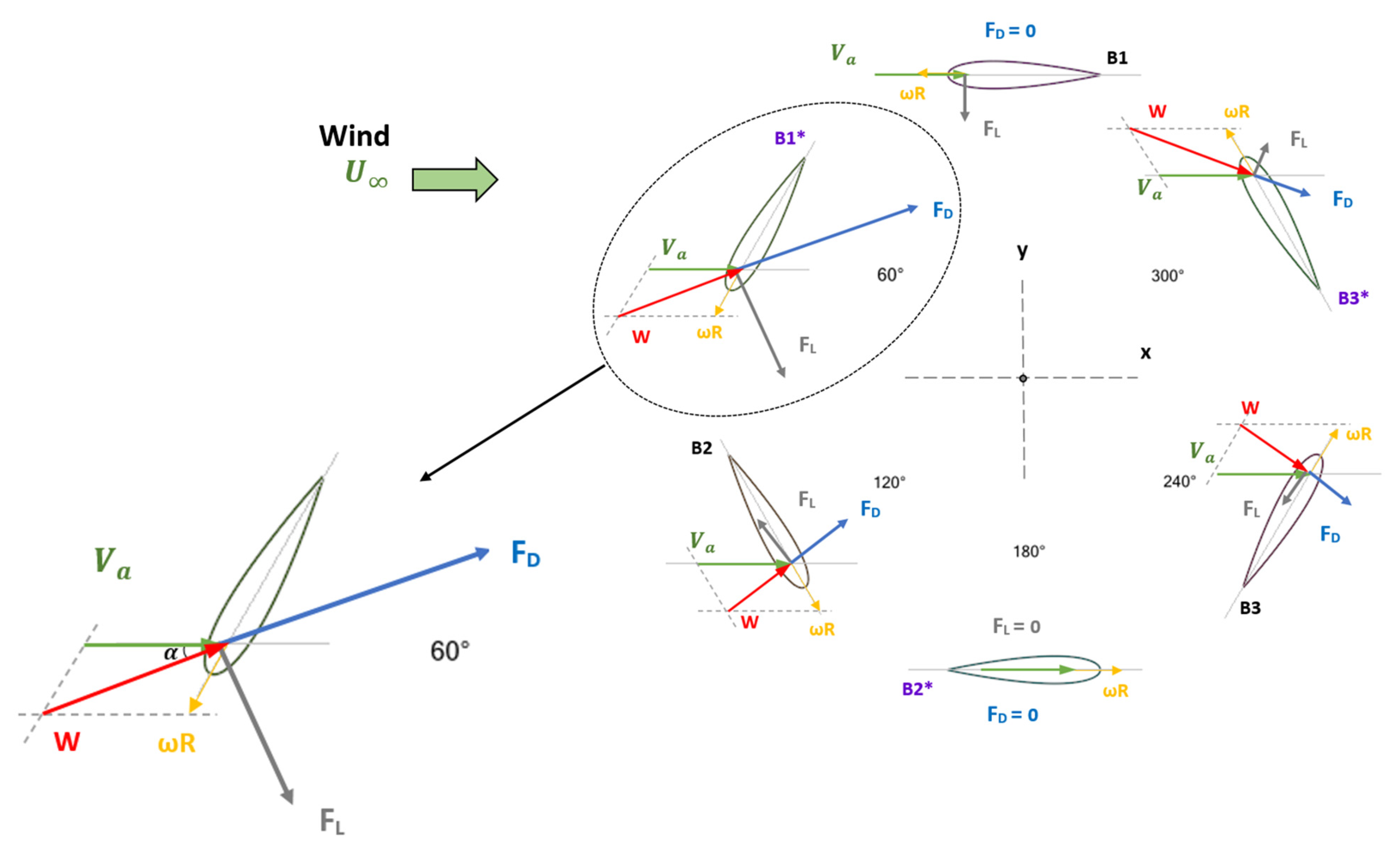
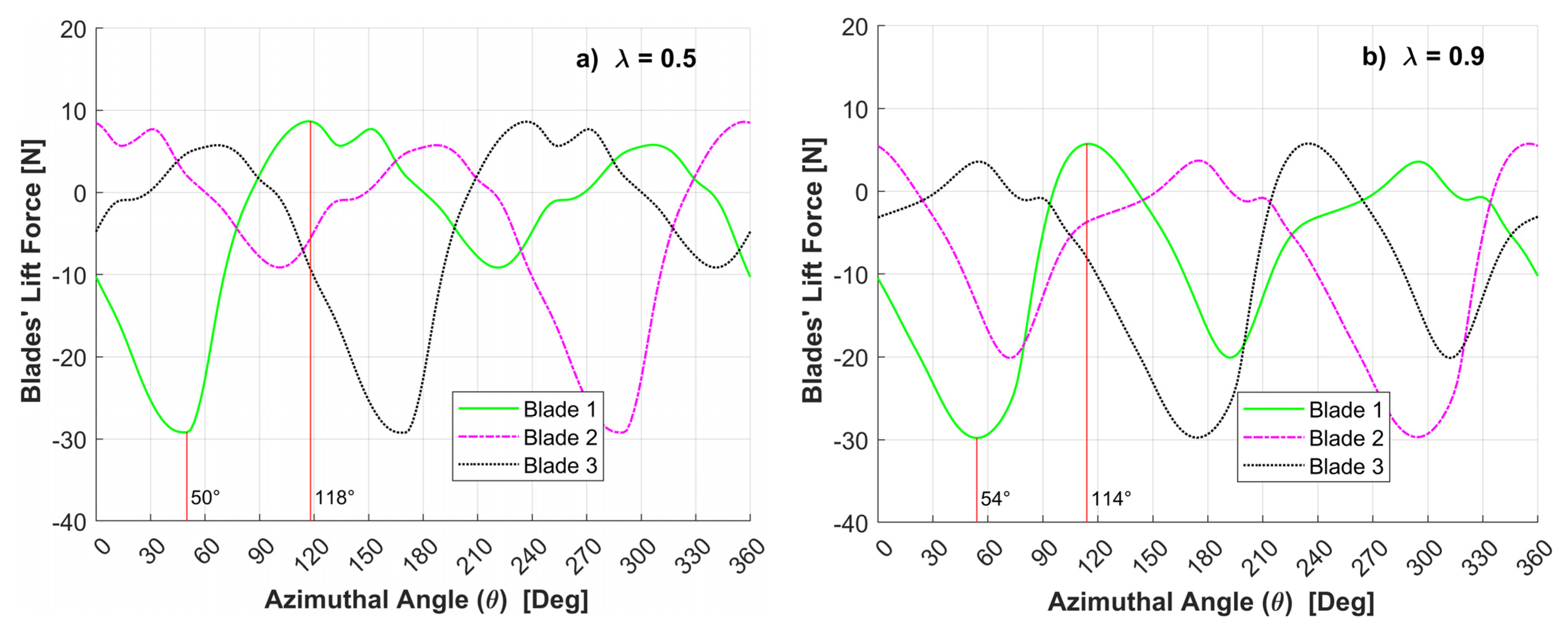
3.2.2. Wind Speed Effect on Drag and Lift Forces
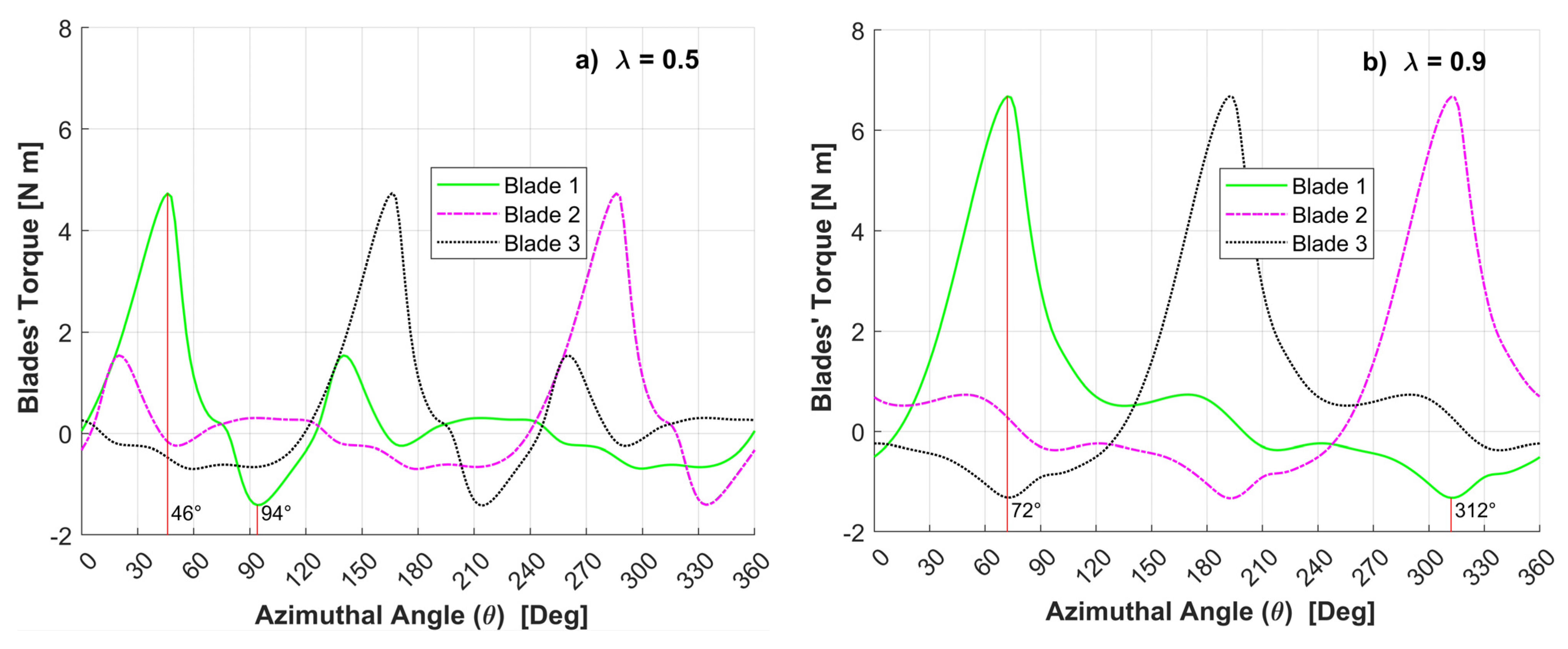
3.2.3. Wind Speed Effect on Individual Torque
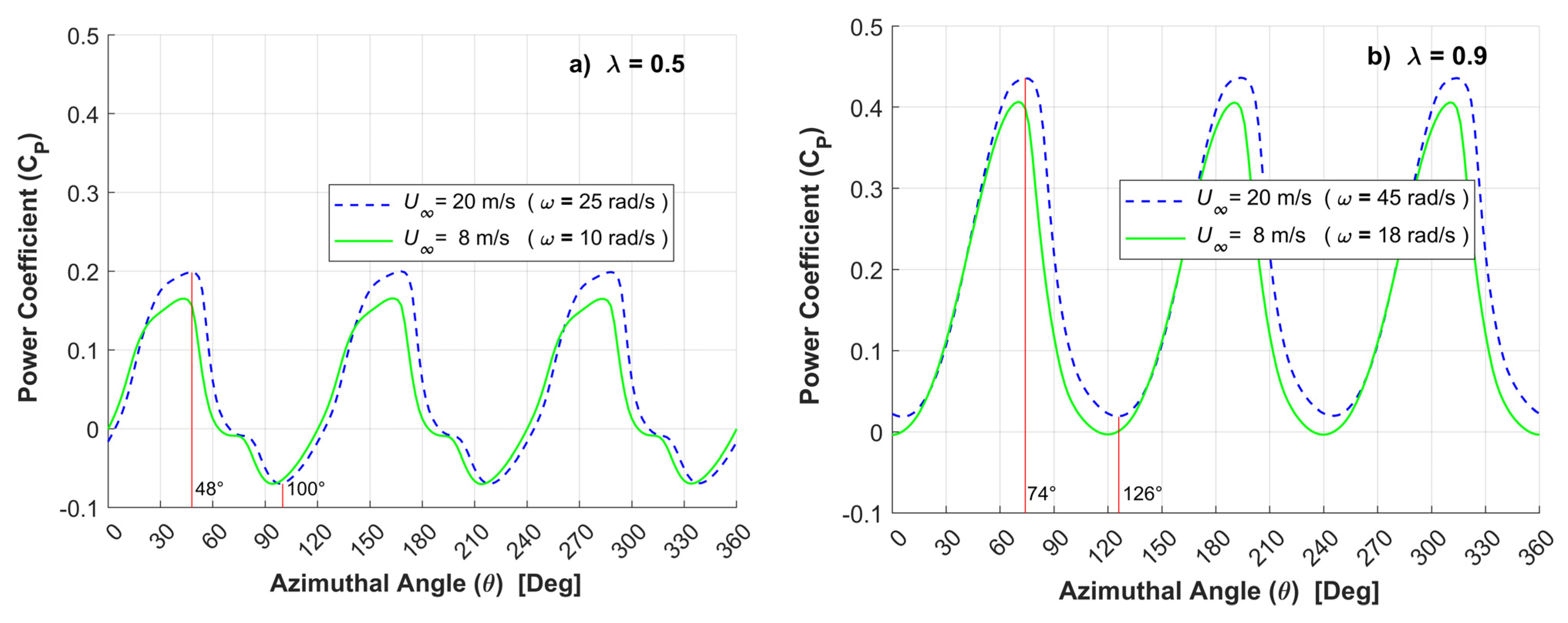
3.2.4. Wind Speed Effect on the Power Coefficient
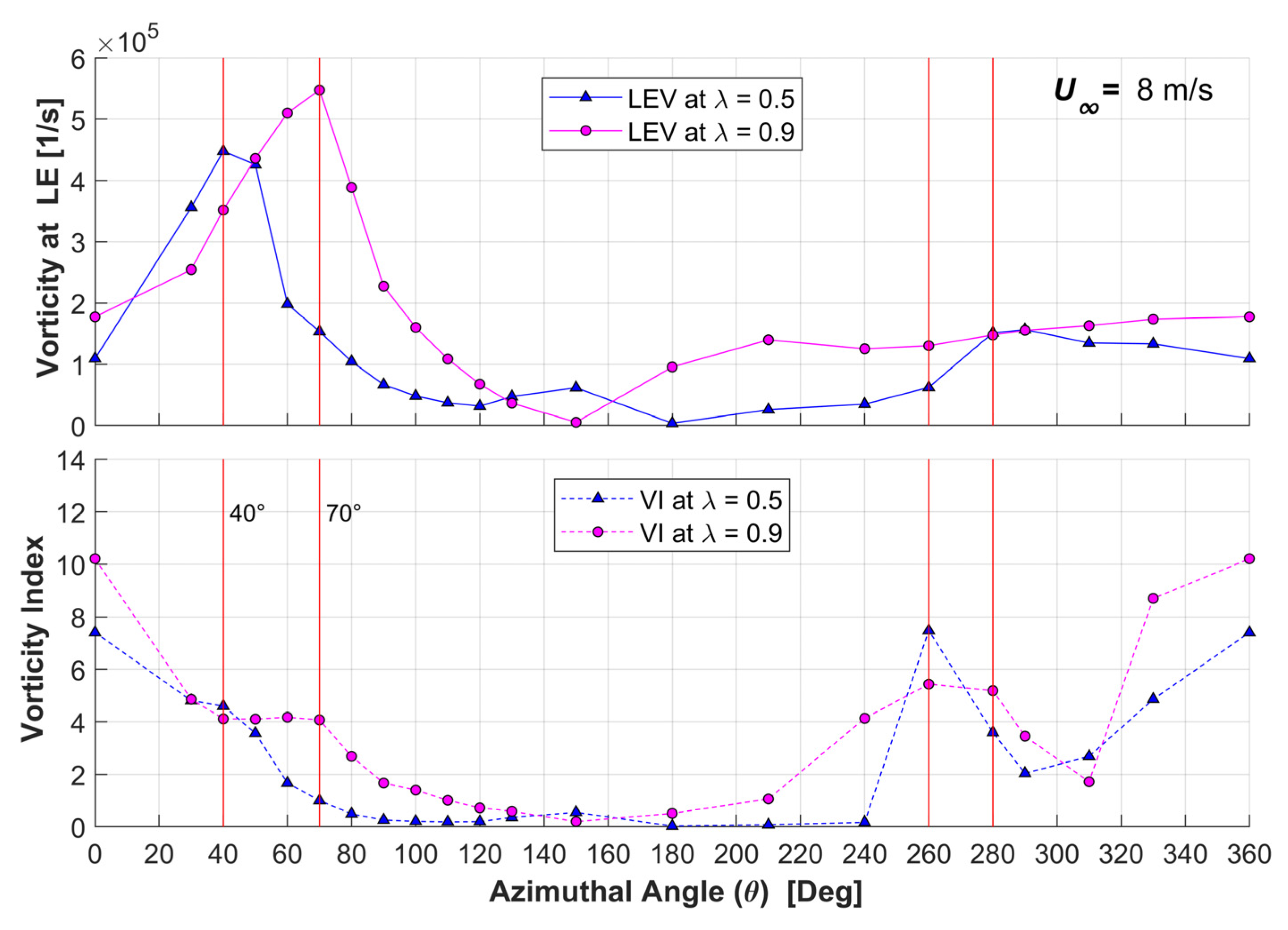
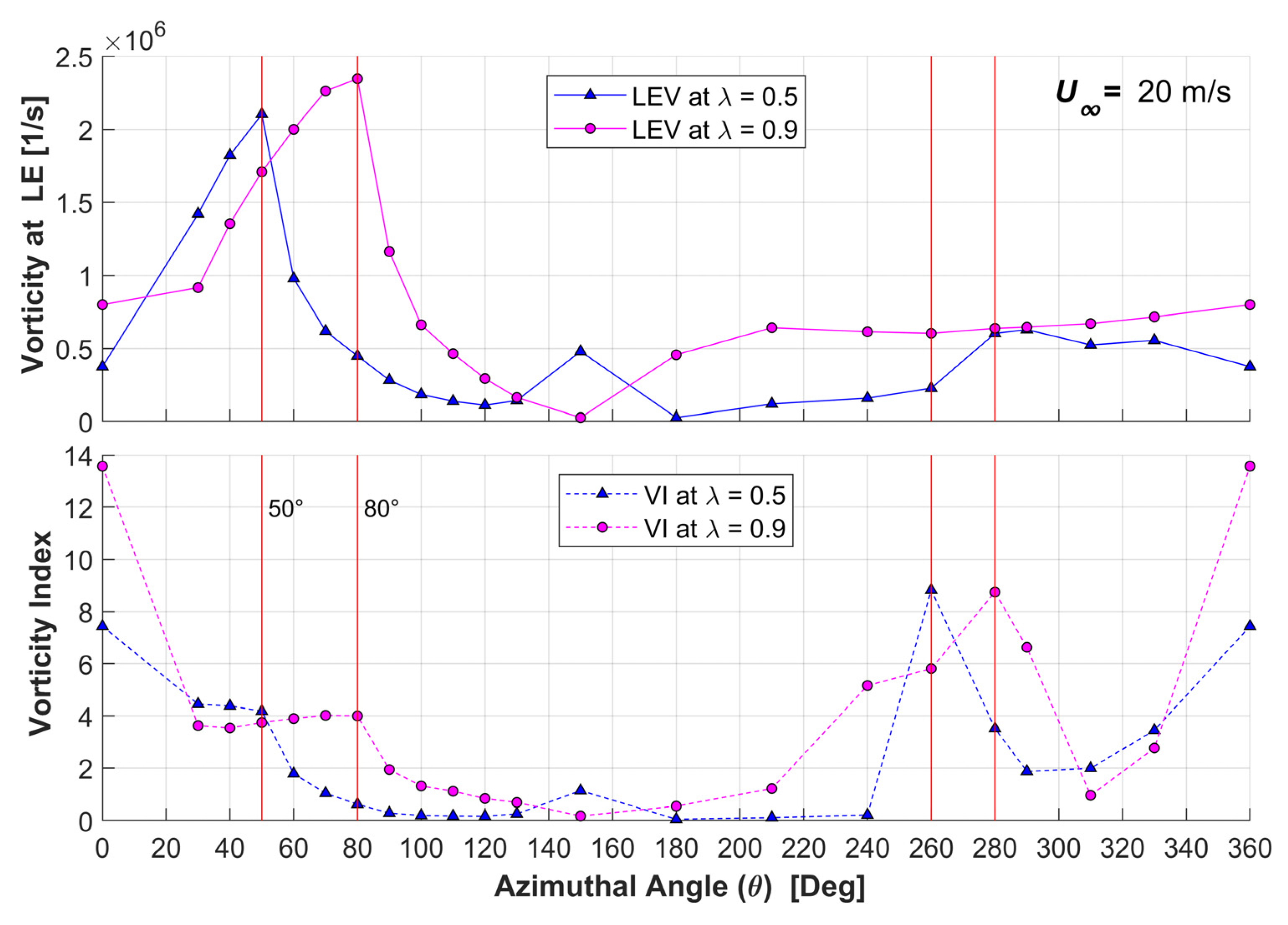
3.3. Vorticity Index Results
4. Conclusions
- The average overall torque values for a complete rotor rotation period are found to provide good numerical convergence criteria [20] for high (20 m/s) wind speeds.
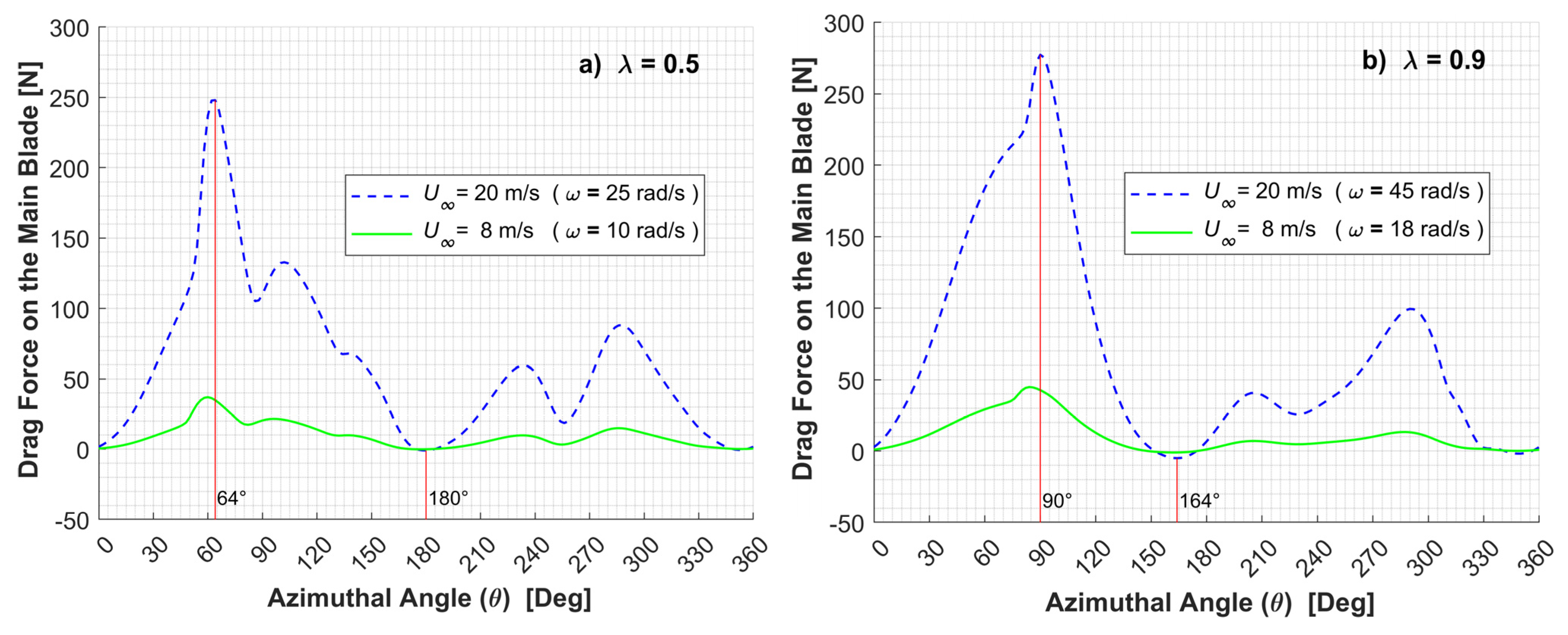
- The maximum drag forces for 8 and 20 m/s wind speeds, are obtained for an azimuthal angle (θ) range of 65° to 85°. This corresponds to an angle of attack (α) close to 45°.
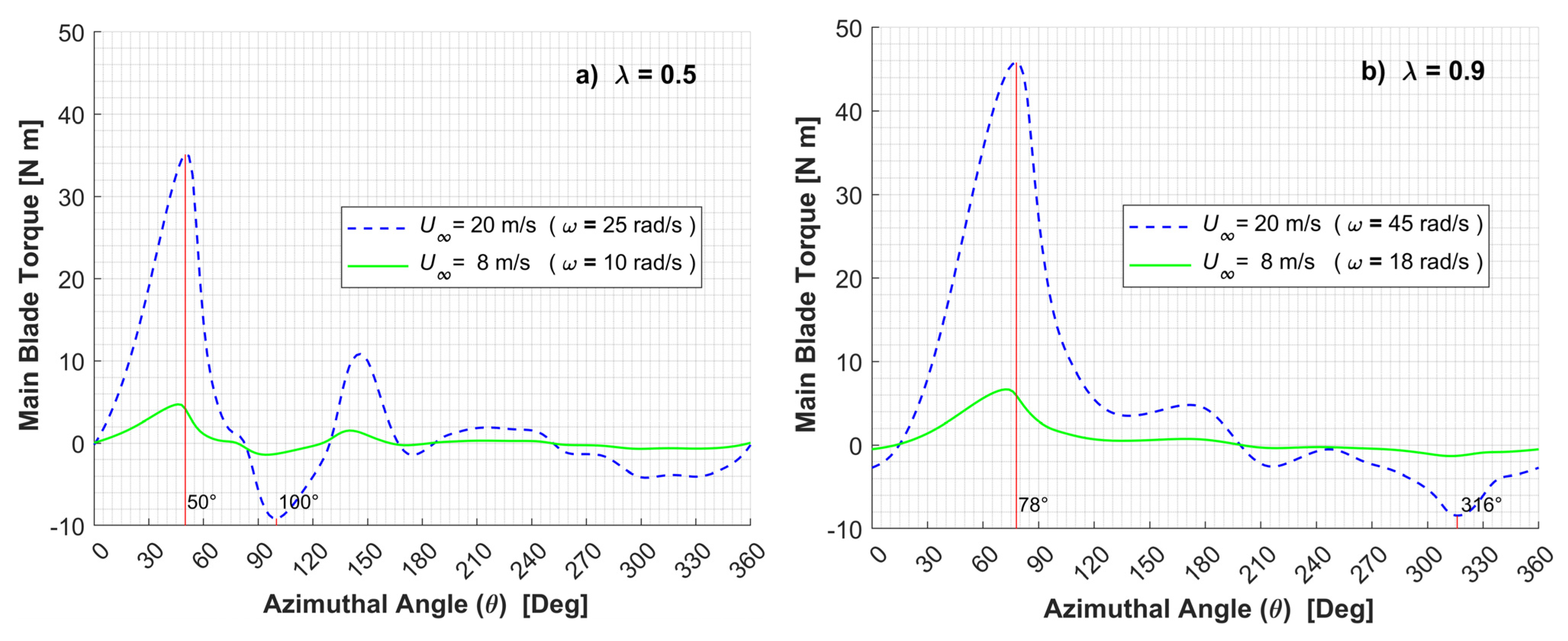
- The maximum torque on the main blade, for 8 and 20 m/s wind speeds is delivered at the following azimuthal positions: between θ = 45° and θ = 50° (α = 31.1–33.8°) for λ = 0.5, and between θ = 72° and θ = 78° (α = 38.2–41.4°) for λ = 0.9.
- Much higher torques are delivered at 20m/s, versus the ones produced at 8m/s. Nonetheless, high wind speeds showed just a moderate influence on the final average power coefficient value of a 3-bladed H-Darrieus VAWT. The overall gains are lessened by the increased turbulence and vorticity, which reduce the energy extraction by the rotor during the wind turbine operation, within the same range of tip speed ratios. This matter may require further studies.
- The torque is significantly reduced for blade azimuthal angles θ > 90°. This even yielded negative torque values, which are attributed to flow separation and strong vorticity interactions with the blades.
- The flow vorticity has a noticeable relation with the turbine performance. The leading edge vorticity (LEV) increases until the blade rotation reaches the azimuthal angle of maximum torque. The proposed vorticity index (VI) displays a constant value around 4 before reaching this maximum torque.
- The VI can be used to quantitatively assess vortex separation conditions. After the maximum torque azimuthal position, VI starts decreasing rapidly until minimum values reached because of vortex generation at the LE of the blade and vorticity accumulation at its TE. Furthermore, when the VI attains a value of 1, the Imminent Vortex Separation Condition (IVSC) takes place with the vortex formed by dynamic stall condition almost detaching from the LE of the blade. This occurs at comparable azimuthal angles for equal tip speed ratios, with this being independent of the wind speed.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| Chord Length [m] | |
| Power Coefficient | |
| Rotor diameter [m] | |
| FD | Drag force [N] |
| FL | Lift force [N] |
| Blade span [m] | |
| Reduced frequency | |
| Number of blades | |
| Power [W] | |
| Mean pressure [Pa] | |
| Dynamic pressure [Pa] | |
| Rotor Radius [m] | |
| Time [s] | |
| Torque [N m] | |
| Mean fluid velocity [m s−1] | |
| Fluctuating fluid velocity [m s−1] | |
| Wind speed [m s−1] | |
| Wind induced velocity [m s−1] | |
| W | Wind relative flow velocity [m s−1] |
| + | Non-dimensional first cell wall distance |
| Greek Symbols | |
| Angle of attack [deg] | |
| Angular marching step [deg] | |
| Azimuthal angle [deg] | |
| Tip speed ratio = [-] | |
| Fluid viscosity [Pa s] | |
| Kinematic viscosity [m2/s] | |
| Fluid density [kg m−3] | |
| Solidity = [-] | |
| Angular velocity [rad s−1] | |
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| DVS | Dynamic Stall Vortex |
| HAWT | Horizontal Axis Wind Turbine |
| IVSC | Imminent Vortex Separation Condition |
| LE | Leading Edge |
| LEV | Leading Edge Vorticity |
| RANS | Reynolds Averaged Navier-Stokes method |
| SRS | Scale Resolving Simulation |
| SST | Shear Stress Transport |
| TE | Trailing Edge |
| TEV | Trailing Edge Vorticity |
| TSR | Tip Speed Ratio |
| URANS | Unsteady Reynolds Averaged Navier–Stokes |
| VAWT | Vertical Axis Wind Turbine |
| VI | Vorticity Index |
Appendix A
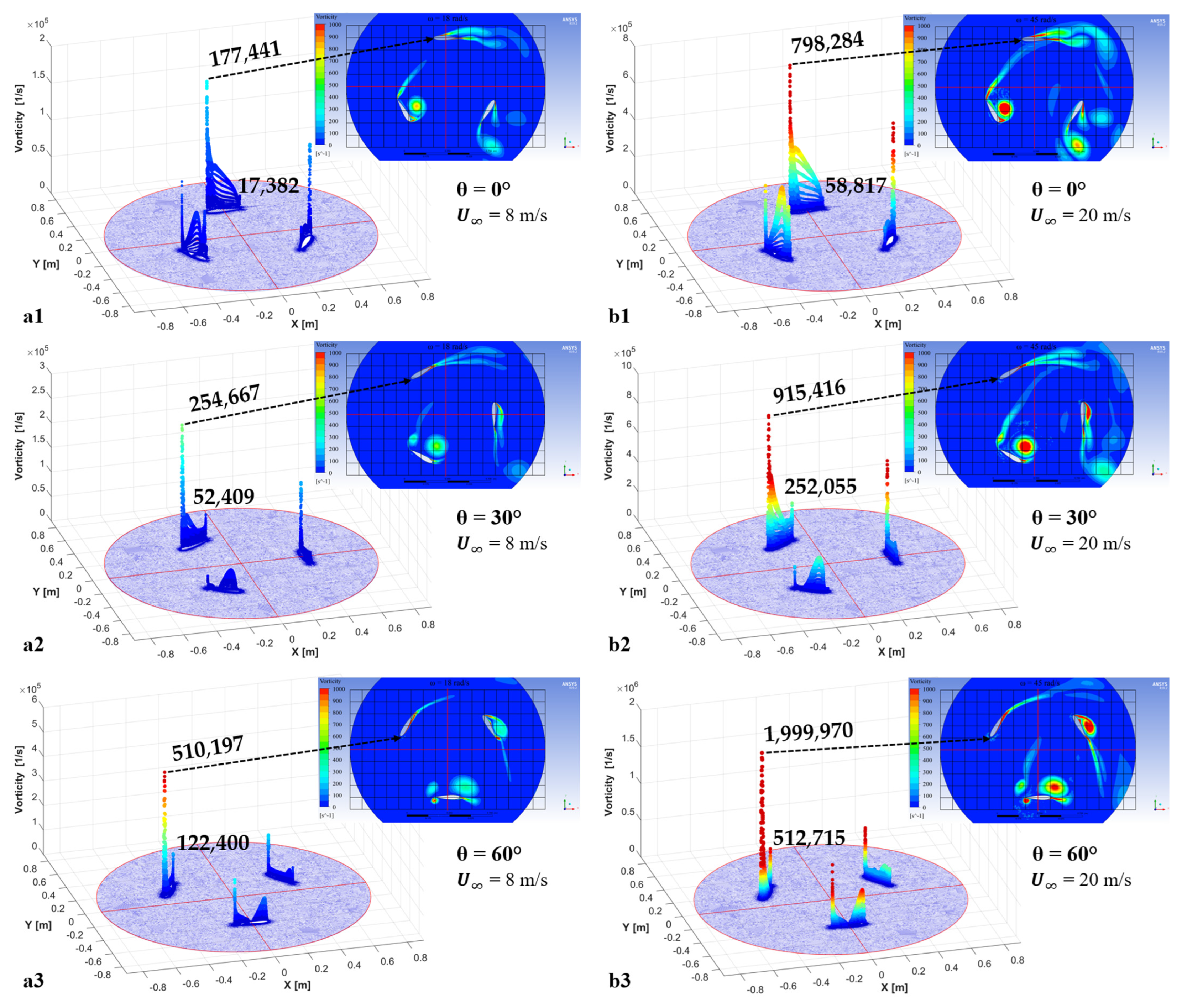
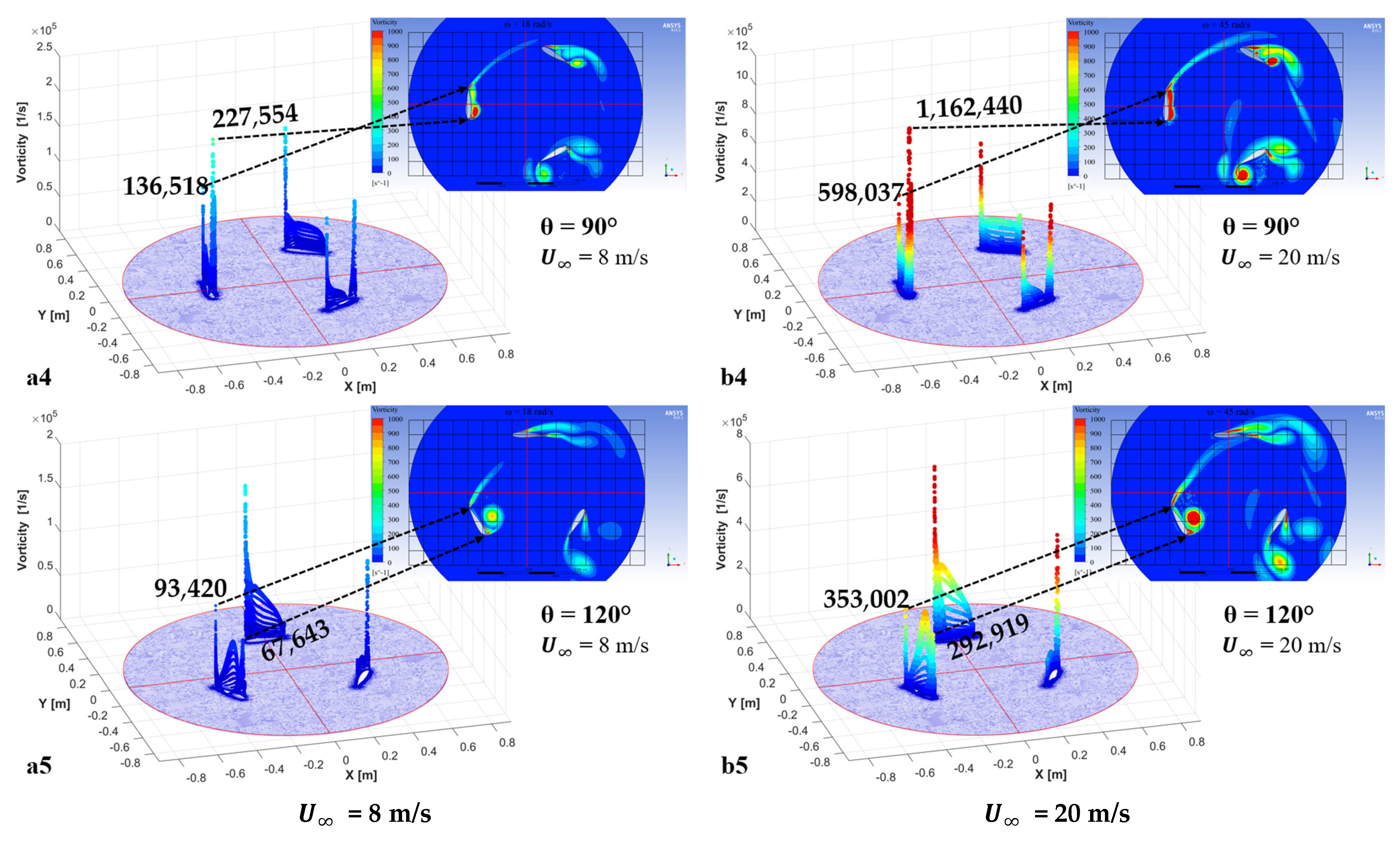
Appendix B
| = 0.5 | = 0.9 | |||||
|---|---|---|---|---|---|---|
| θ (Deg) | LEV (1/s) | TEV (1/s) | VI | LEV (1/s) | TEV (1/s) | VI |
| 0 | 109,113 | 14,749 | 7.40 | 177,441 | 17,382 | 10.21 |
| 30 | 356,125 | 74,080 | 4.81 | 254,667 | 52,409 | 4.86 |
| 40 | 447,702 | 97,372 | 4.60 | 351,808 | 85,683 | 4.11 |
| 50 | 425,774 | 119,716 | 3.56 | 435,962 | 106,290 | 4.10 |
| 60 | 198,316 | 118,434 | 1.67 | 510,197 | 122,400 | 4.17 |
| 70 | 153,440 | 152,854 | 1.00 | 547,857 | 134,543 | 4.07 |
| 80 | 104,366 | 214,936 | 0.49 | 388,710 | 144,981 | 2.68 |
| 90 | 66,788 | 260,797 | 0.26 | 227,554 | 136,518 | 1.67 |
| 100 | 48,225 | 229,827 | 0.21 | 160,139 | 114,489 | 1.40 |
| 110 | 37,120 | 197,066 | 0.19 | 108,520 | 107,670 | 1.01 |
| 120 | 31,700 | 159,208 | 0.20 | 67,643 | 93,420 | 0.72 |
| 130 | 47,272 | 131,531 | 0.36 | 36,521 | 62,172 | 0.59 |
| 150 | 61,833 | 112,285 | 0.55 | 5273 | 26,617 | 0.20 |
| 180 | 3525 | 109,692 | 0.03 | 95,543 | 186,638 | 0.51 |
| 210 | 25,936 | 305,729 | 0.08 | 139,748 | 132,173 | 1.06 |
| 240 | 34,814 | 199,575 | 0.17 | 125,114 | 30,306 | 4.13 |
| 260 | 62,373 | 8341 | 7.48 | 130,162 | 23,938 | 5.44 |
| 280 | 151,299 | 42,150 | 3.59 | 147,775 | 28,452 | 5.19 |
| 290 | 156,562 | 76,667 | 2.04 | 155,332 | 44,992 | 3.45 |
| 310 | 134,699 | 50,313 | 2.68 | 163,063 | 94,642 | 1.72 |
| 330 | 133,190 | 27,380 | 4.86 | 173,659 | 19,959 | 8.70 |
| 360 | 109,113 | 14,749 | 7.40 | 177,441 | 17,382 | 10.21 |
Appendix C
| = 0.5 | 0.9 | |||||
|---|---|---|---|---|---|---|
| θ (Deg) | LEV (1/s) | TEV (1/s) | VI | LEV (1/s) | TEV (1/s) | VI |
| 0 | 374,621 | 50371 | 7.44 | 798,284 | 58,817 | 13.57 |
| 30 | 1,420,000 | 319,441 | 4.45 | 915,416 | 252,055 | 3.63 |
| 40 | 1,822,510 | 415,671 | 4.38 | 1,354,560 | 382,740 | 3.54 |
| 50 | 2,102,810 | 503,018 | 4.18 | 1,708,160 | 455,701 | 3.75 |
| 60 | 977,838 | 550,173 | 1.78 | 1,999,970 | 512,715 | 3.90 |
| 70 | 618,315 | 602,600 | 1.03 | 2,261,180 | 561,845 | 4.02 |
| 80 | 448,167 | 740,703 | 0.61 | 2,345,430 | 586,044 | 4.00 |
| 90 | 282,028 | 1,014,620 | 0.28 | 1,162,440 | 598,037 | 1.94 |
| 100 | 183,997 | 972,682 | 0.19 | 661,746 | 504,683 | 1.31 |
| 110 | 137,458 | 830,830 | 0.17 | 463,944 | 416,734 | 1.11 |
| 120 | 110,174 | 696,534 | 0.16 | 292,919 | 353,002 | 0.83 |
| 130 | 142,477 | 564,754 | 0.25 | 163,461 | 240,015 | 0.68 |
| 150 | 479,418 | 422,522 | 1.13 | 25,712 | 147,822 | 0.17 |
| 180 | 25,802 | 505,638 | 0.05 | 456,111 | 851,410 | 0.54 |
| 210 | 119,269 | 1,124,200 | 0.11 | 642,122 | 532,874 | 1.21 |
| 240 | 158,636 | 766,737 | 0.21 | 614,202 | 119,143 | 5.16 |
| 260 | 226,673 | 25,705 | 8.82 | 603,590 | 103,893 | 5.81 |
| 280 | 603,043 | 171,088 | 3.52 | 637,702 | 72,947 | 8.74 |
| 290 | 628,803 | 336,567 | 1.87 | 646,205 | 97,522 | 6.63 |
| 310 | 523,672 | 263,367 | 1.99 | 669,941 | 705,871 | 0.95 |
| 330 | 555,391 | 160,771 | 3.45 | 715,332 | 258,413 | 2.77 |
| 360 | 374,621 | 50,371 | 7.44 | 798,284 | 58,817 | 13.57 |
References
- Zayats, I. The historical aspect of windmills architectural forms transformation. Procedia Eng. 2015, 117, 685–695. [Google Scholar] [CrossRef]
- BP plc. bp Energy Outlook 2022 Edition. 2022. Available online: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/energy-outlook/bp-energy-outlook-2022.pdf (accessed on 30 June 2022).
- Zhao, D.; Han, N.; Goh, E.; Cater, J.; Reinecke, A. Wind Turbines and Aerodynamics Energy Harvesters, 1st ed.; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Dai, K.; Bergot, A.; Liang, C.; Xiang, W.-N.; Huang, Z. Environmental issues associated with wind energy—A review. Renew Energy 2015, 75, 911–921. [Google Scholar] [CrossRef]
- Maalouly, M.; Souaiby, M.; ElCheikh, A.; Issa, J.; Elkhoury, M. Transient analysis of H-type Vertical Axis Wind Turbines using CFD. Energy Rep. 2022, 8, 4570–4588. [Google Scholar] [CrossRef]
- He, J.; Jin, X.; Xie, S.; Cao, L.; Wang, Y.; Lin, Y.; Wang, N. CFD modeling of varying complexity for aerodynamic analysis of H-vertical axis wind turbines. Renew Energy 2020, 145, 2658–2670. [Google Scholar] [CrossRef]
- Hossain, M.; Ali, M.H. Future research directions for the wind turbine generator system. Renew. Sustain. Energy Rev. 2015, 49, 481–489. [Google Scholar] [CrossRef]
- Al-Sharafi, A.; Sahin, A.Z.; Ayar, T.; Yilbas, B.S. Techno-economic analysis and optimization of solar and wind energy systems for power generation and hydrogen production in Saudi Arabia. Renew. Sustain. Energy Rev. 2017, 69, 33–49. [Google Scholar] [CrossRef]
- Aiche-Hamane, L.; Belhamel, M.; Benyoucef, B.; Hamane, M. Feasibility study of hydrogen production from wind power in the region of Ghardaia. Int. J. Hydrogen Energy 2009, 34, 4947–4952. [Google Scholar] [CrossRef]
- Benghanem, M.; Mellit, A.; Almohamadi, H.; Haddad, S.; Chettibi, N.; Alanazi, A.M.; Dasalla, D.; Alzahrani, A. Hydrogen Production Methods Based on Solar and Wind Energy: A Review. Energies 2023, 16, 757. [Google Scholar] [CrossRef]
- Etemadeasl, V.; Esmaelnajad, R.; Dizaji, F.F.; Farzaneh, B. A novel configuration for improving the aerodynamic performance of Savonius rotors. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233, 751–761. [Google Scholar] [CrossRef]
- Borg, M.; Shires, A.; Collu, M. Offshore floating vertical axis wind turbines, dynamics modelling state of the art. part I: Aerodynamics. Renew. Sustain. Energy Rev. 2014, 39, 1214–1225. [Google Scholar] [CrossRef]
- Schubel, P.J.; Crossley, R.J. Wind turbine blade design. Energies 2012, 5, 3425–3449. [Google Scholar] [CrossRef]
- Souaissa, K.; Ghiss, M.; Chrigui, M.; Bentaher, H.; Maalej, A. A comprehensive analysis of aerodynamic flow around H-Darrieus rotor with camber-bladed profile. Wind Eng. 2019, 43, 459–475. [Google Scholar] [CrossRef]
- Ferreira, C.J.S.; Bijl, H.; Van Bussel, G.; Van Kuik, G. Simulating Dynamic Stall in a 2D VAWT: Modeling strategy, verification and validation with Particle Image Velocimetry data. J. Phys. Conf. Ser. 2007, 75, 012023. [Google Scholar] [CrossRef]
- Sridhar, S.; Zuber, M.; Shenoy B., S.; Kumar, A.; Ng, E.Y.K.; Radhakrishnan, J. Aerodynamic comparison of slotted and non-slotted diffuser casings for Diffuser Augmented Wind Turbines (DAWT). Renew. Sustain. Energy Rev. 2022, 161, 112316. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. On the accuracy of turbulence models for CFD simulations of vertical axis wind turbines. Energy 2019, 180, 838–857. [Google Scholar] [CrossRef]
- Kanyako, F.; Janajreh, I. Vertical Axis Wind Turbine performance prediction for low wind speed environment. In Proceedings of the 2014 IEEE Innovations in Technology Conference, Warwick, RI, USA, 16 May 2014. [Google Scholar] [CrossRef]
- Lanzafame, R.; Mauro, S.; Messina, M. 2D CFD modeling of H-Darrieus Wind Turbines using a transition turbulence model. Energy Procedia 2014, 45, 131–140. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Critical issues in the CFD simulation of Darrieus wind turbines. Renew Energy 2016, 85, 419–435. [Google Scholar] [CrossRef]
- Michna, J.; Rogowski, K. Numerical Study of the Effect of the Reynolds Number and the Turbulence Intensity on the Performance of the NACA 0018 Airfoil at the Low Reynolds Number Regime. Processes 2022, 10, 1004. [Google Scholar] [CrossRef]
- Elkhoury, M.; Kiwata, T.; Aoun, E. Experimental and numerical investigation of a three-dimensional vertical-axis wind turbine with variable-pitch. J. Wind Eng. Ind. Aerodyn. 2015, 139, 111–123. [Google Scholar] [CrossRef]
- EMöllerström, E.; Gipe, P.; Beurskens, J.; Ottermo, F. A historical review of vertical axis wind turbines rated 100 kW and above. Renew. Sustain. Energy Rev. 2019, 105, 1–13. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Ibrahim, A.A.; Etman, A.K.; Abdelfatah, A.A.; Elbaz, A.M. Numerical investigation of Darrieus wind turbine with slotted airfoil blades. Energy Convers. Manag. X 2020, 5, 100026. [Google Scholar] [CrossRef]
- Ahmedov, A.; Ebrahimi, K.M. Numerical Modelling of an H-type Darrieus Wind Turbine Performance under Turbulent Wind. Am. J. Energy Res. 2017, 5, 63–78. [Google Scholar] [CrossRef]
- Trivellato, F.; Castelli, M.R. On the Courant-Friedrichs-Lewy criterion of rotating grids in 2D vertical-axis wind turbine analysis. Renew Energy 2014, 62, 53–62. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Balduzzi, F.; Bianchini, A.; Ferrara, G.; Goude, A. Evaluation of the unsteady aerodynamic forces acting on a vertical-axis turbine by means of numerical simulations and open site experiments. J. Wind. Eng. Ind. Aerodyn. 2020, 198, 104093. [Google Scholar] [CrossRef]
- Alaimo, A.; Esposito, A.; Messineo, A.; Orlando, C.; Tumino, D. 3D CFD analysis of a vertical axis wind turbine. Energies 2015, 8, 3013–3033. [Google Scholar] [CrossRef]
- Orlandi, A.; Collu, M.; Zanforlin, S.; Shires, A. 3D URANS analysis of a vertical axis wind turbine in skewed flows. J. Wind Eng. Ind. Aerodyn. 2015, 147, 77–84. [Google Scholar] [CrossRef]
- Lam, H.; Peng, H. Study of wake characteristics of a vertical axis wind turbine by two- and three-dimensional computational fluid dynamics simulations. Renew Energy 2016, 90, 386–398. [Google Scholar] [CrossRef]
- Hosseini, A.; Goudarzi, N. Design and CFD study of a hybrid vertical-axis wind turbine by employing a combined Bach-type and H-Darrieus rotor systems. Energy Convers. Manag. 2019, 189, 49–59. [Google Scholar] [CrossRef]
- Lee, J.-H.; Lee, Y.-T.; Lim, H.-C. Effect of twist angle on the performance of Savonius wind turbine. Renew Energy 2016, 89, 231–244. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds-averaged Navier-Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]
- Geng, F.; Kalkman, I.; Suiker, A.; Blocken, B. Sensitivity analysis of airfoil aerodynamics during pitching motion at a Reynolds number of 1.35×105. J. Wind Eng. Ind. Aerodyn. 2018, 183, 315–332. [Google Scholar] [CrossRef]
- Ghasemian, M.; Ashrafi, Z.N.; Sedaghat, A. A review on computational fluid dynamic simulation techniques for Darrieus vertical axis wind turbines. Energy Convers. Manag. 2017, 149, 87–100. [Google Scholar] [CrossRef]
- Barnes, A.; Marshall-Cross, D.; Hughes, B.R. Validation and comparison of turbulence models for predicting wakes of vertical axis wind turbines. J. Ocean Eng. Mar. Energy 2021, 7, 339–362. [Google Scholar] [CrossRef]
- Ma, N.; Lei, H.; Han, Z.; Zhou, D.; Bao, Y.; Zhang, K.; Zhou, L.; Chen, C. Airfoil optimization to improve power performance of a high-solidity vertical axis wind turbine at a moderate tip speed ratio. Energy 2018, 150, 236–252. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent Theory Guide 15; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Celik, Y.; Ma, L.; Ingham, D.; Pourkashanian, M. Aerodynamic investigation of the start-up process of H-type vertical axis wind turbines using CFD. J. Wind. Eng. Ind. Aerodyn. 2020, 204, 104252. [Google Scholar] [CrossRef]
- Song, C.; Wu, G.; Zhu, W.; Zhang, X.; Zhao, J. Numerical investigation on the effects of airfoil leading edge radius on the aerodynamic performance of H-rotor Darrieus vertical axis wind turbine. Energies 2019, 12, 3794. [Google Scholar] [CrossRef]
- AlQurashi, F.; Mohamed, M.H. Aerodynamic forces affecting the H-rotor darrieus wind turbine. Model. Simul. Eng. 2020, 2020, 1368369. [Google Scholar] [CrossRef]
- Laneville, A.; Vittecoq, P. Dynamic Stall: The Case of the Vertical Axis Wind Turbine. J. Sol. Energy Eng. 1986, 108, 140–145. Available online: http://solarenergyengineering.asmedigitalcollection.asme.org/ (accessed on 9 July 2022). [CrossRef]
- Dessoky, A.; Bangga, G.; Lutz, T.; Krämer, E. Aerodynamic and aeroacoustic performance assessment of H-rotor darrieus VAWT equipped with wind-lens technology. Energy 2019, 175, 76–97. [Google Scholar] [CrossRef]
- Choudhry, A.; Arjomandi, M.; Kelso, R. Methods to control dynamic stall for wind turbine applications. Renew Energy 2016, 86, 26–37. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Yang, K.; Xu, J.; Li, X. Aerodynamic performance of wind turbine airfoil DU 91-W2-250 under dynamic stall. Appl. Sci. 2018, 8, 1111. [Google Scholar] [CrossRef]
- Menter, F.R. Best Practice: Scale-Resolving Simulations in ANSYS CFD. 2015. Available online: www.ansys.com (accessed on 29 October 2022).

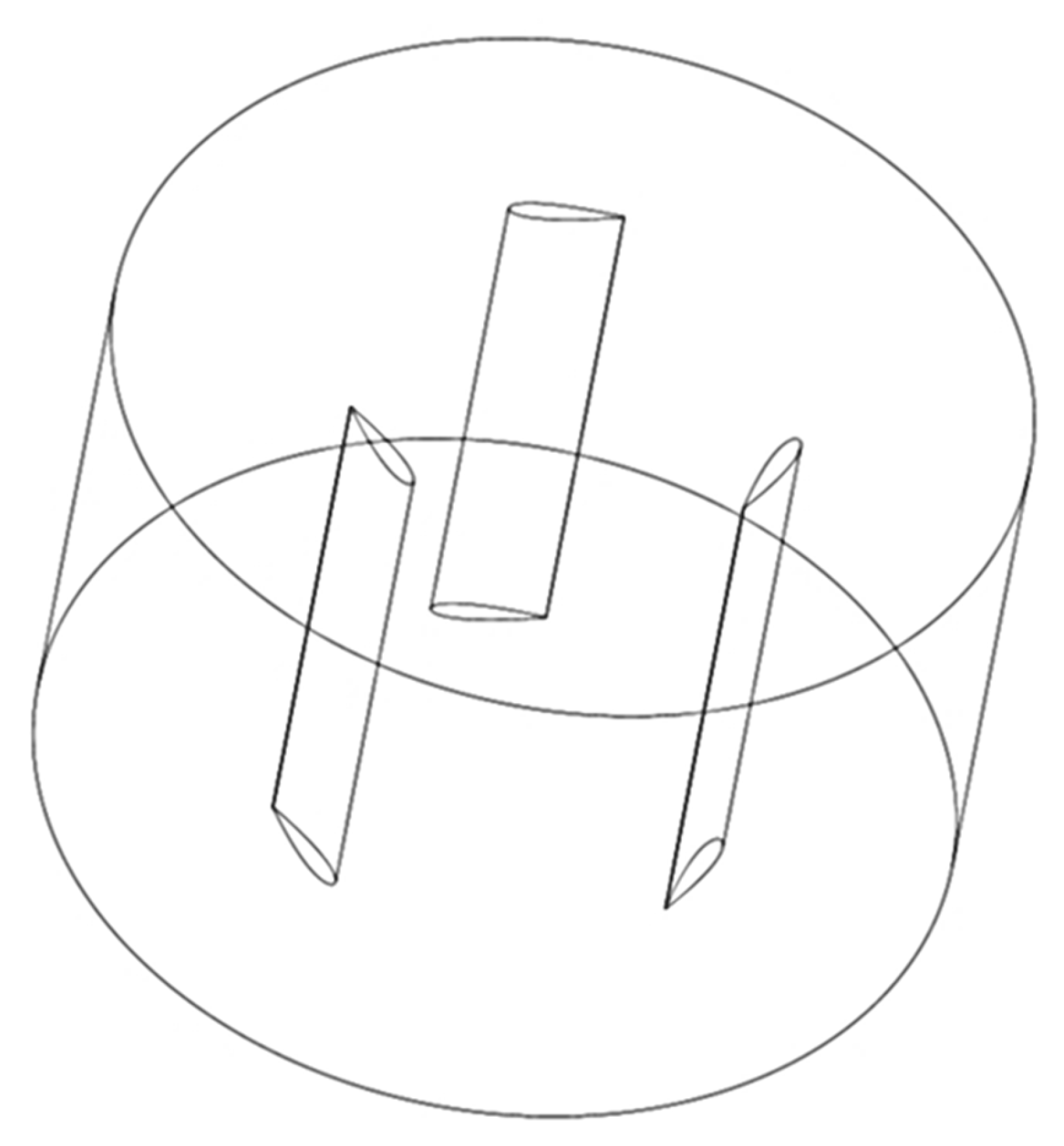











| Vertical Axis Wind Turbine (VAWT) | Horizontal Axis Wind Turbine (HAWT) | |
|---|---|---|
| Efficiency | Lower | Higher |
| Space Efficiency a,b | Higher | Lower |
| Wind Direction a,b | Independent | Dependent |
| Yaw mechanism b | No | Yes |
| Self-Starting b | No | Yes |
| Height from ground b | Small | Large |
| Tower Sway b | Small | Large |
| Generator location b | Ground Level | Not Ground Level Required |
| Installation Cost a,b | Lower | Higher |
| Maintenance Cost a,b | Lower | Higher |
| Shadow Flickering b | Less | More |
| Noise a,b | Low | High |
| Bird/bat safety a,b | High | Low |
| Parameter | Symbol | Value |
|---|---|---|
| Rotor Diameter [m] | 0.8 | |
| Blade Airfoil | - | NACA 0018 |
| Blade Shape | - | Straight |
| Chord Length [m] | 0.2 | |
| Rotor Height [m] | 0.8 m (1 m adopted for 2D simulation) | |
| Blades Number | 3 | |
| Solidity | 0.75 |
| Parameter | Symbol | Value |
|---|---|---|
| Viscous Model | SST k- | k- Shear Stress Transport |
| Air Density | 1.225 kg/m3 | |
| Air Viscosity | 1.79 × 10−5 Pa s | |
| Air Velocity | 8 m/s, 20 m/s | |
| Turbulent Intensity | 1% | |
| Tip Speed Ratio | λ | 0.5–1.5 |
| Solver Type | Pressure-Based | |
| Calculation algorithm | Coupled | |
| Spatial Discretization | 2nd | |
| Time discretization | According to λ, calculated to achieve 2° of rotation per time step | |
| Residuals | 1 × 10−4 |
| Mesh Set | ||||
|---|---|---|---|---|
| Coarse | Medium | Fine | ||
| Face Sizing | Fixed Domain Element Size [m] | 0.120 | 0.080 | 0.060 |
| Rotor Domain Element Size [m] | 0.012 | 0.0073 | 0.0053 | |
| Edge Sizing | Interface Element Size [m] | 0.011 | 0.0069 | 0.0049 |
| Number of Divisions around Blades Surface | 480 | 600 | 600 | |
| Elements Number | Fixed Domain | 29,008 | 75,226 | 143,289 |
| Rotor Domain | 62,416 | 125,564 | 216,843 | |
| Total | 91,424 | 200,790 | 360,132 | |
| Power Coefficient | 0.196 | 0.200 | 0.202 | |
| %Difference of with respect to the Fine Mesh | −3.06% | −1.23% | / | |
| Time Step | with Respect to Smallest Time Step | |||
|---|---|---|---|---|
| 0.003491 s | 4° | 0.200 | 0.200 | −12% |
| 0.001745 s | 2° | 0.220 | 0.220 | −3% |
| 0.000873 s | 1° | 0.227 | 0.227 | <0.1% |
| Experimental Results [37] | 2D SST k- (This Work) | Relative Error 2D vs. Exp | 3D SST k- [37] | Relative Error 3D vs. Exp | |
|---|---|---|---|---|---|
| 0.4 | 0.028 | 0.030 | 5.9% | 0.030 | 5.5% |
| 0.5 | 0.040 | 0.036 | −10.6% | 0.048 | 19.6% |
| 0.7 | 0.073 | 0.053 | −27.5% | 0.079 | 8.6% |
| 0.8 | 0.101 | 0.108 | 7.2% | 0.105 | 4.7% |
| 0.9 | 0.128 | 0.157 | 22.9% | 0.132 | 3.1% |
| 1.0 | 0.167 | 0.220 | 31.5% | 0.159 | −4.7% |
| 1.2 | 0.190 | 0.326 | 71.4% | 0.184 | −3.3% |
| 1.3 | 0.195 | 0.355 | 81.9% | 0.191 | −2.0% |
| 1.4 | 0.186 | 0.375 | 101.5% | 0.191 | 2.5% |
| 1.5 | 0.169 | 0.385 | 128.0% | 0.180 | 6.0% |
| λ | θ [Degrees] | α [Degrees] | ||
|---|---|---|---|---|
| Figure 9 Drag Forces = 8 m/s | 0.5 | 60 | 40.9 | Max. Drag |
| 176 | −8.0 | Min. Drag | ||
| 0.9 | 84 | 44.7 | Max. Drag | |
| 162 | −80.6 | Min. Drag | ||
| Figure 10 Lift Forces = 8 m/s | 0.5 | 50 | 33.8 | Min. Lift |
| 118 | 88.0 | Max. Lift | ||
| 0.9 | 54 | 28.5 | Min. Lift | |
| 114 | 61.6 | Max. Lift | ||
| Figure 11 Drag Forces = 20 m/s | 0.5 | 64 | 43.8 | Max. Drag |
| 180 | 0.0 | Min. Drag | ||
| 0.9 | 90 | 48 | Max. Drag | |
| 164 | −77.5 | Min. Drag | ||
| Figure 12 Lift Forces = 20 m/s | 0.5 | 50 | 33.8 | Min. Lift |
| 120 | 90 | Max. Lift | ||
| 0.9 | 54 | 28.5 | Min. Lift | |
| 116 | 62.8 | Max. Lift |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acosta-López, J.G.; Blasetti, A.P.; Lopez-Zamora, S.; de Lasa, H. CFD Modeling of an H-Type Darrieus VAWT under High Winds: The Vorticity Index and the Imminent Vortex Separation Condition. Processes 2023, 11, 644. https://doi.org/10.3390/pr11020644
Acosta-López JG, Blasetti AP, Lopez-Zamora S, de Lasa H. CFD Modeling of an H-Type Darrieus VAWT under High Winds: The Vorticity Index and the Imminent Vortex Separation Condition. Processes. 2023; 11(2):644. https://doi.org/10.3390/pr11020644
Chicago/Turabian StyleAcosta-López, Jansen Gabriel, Alberto Pedro Blasetti, Sandra Lopez-Zamora, and Hugo de Lasa. 2023. "CFD Modeling of an H-Type Darrieus VAWT under High Winds: The Vorticity Index and the Imminent Vortex Separation Condition" Processes 11, no. 2: 644. https://doi.org/10.3390/pr11020644
APA StyleAcosta-López, J. G., Blasetti, A. P., Lopez-Zamora, S., & de Lasa, H. (2023). CFD Modeling of an H-Type Darrieus VAWT under High Winds: The Vorticity Index and the Imminent Vortex Separation Condition. Processes, 11(2), 644. https://doi.org/10.3390/pr11020644