The Hopf Bifurcation Analysis of the Boissonade Model with Time Delay and Diffusion

Abstract

This paper investigates the dynamical characteristics of the Boissonade model in a class of reaction–diffusion chemical systems with time delays, analyzing the system’s Hopf bifurcation with time delay as the parameter under both diffusion-free and diffusion-included conditions. First, the stability of the positive equilibrium solution is examined in the absence of diffusion, with stability criteria derived for different parameter ranges. This analysis confirms that a Hopf bifurcation occurs near the positive equilibrium, revealing that the system exhibits periodic oscillations once the time delay exceeds a critical threshold. Subsequently, the impact of the diffusion term on the Hopf bifurcation is investigated, and the critical threshold for its occurrence is determined. Finally, numerical simulations are conducted, providing comprehensive numerical validation for the theoretical findings.

1. Introduction

In the mid-20th century, the experimental results of the Belousov–Zhabotinsky reaction demonstrated that, under conditions far from equilibrium, specific chemical reaction systems can exhibit periodic concentration oscillations. This phenomenon challenged the traditional thermodynamic framework, which posits that “chemical reactions are inherently irreversible and invariably approach equilibrium”. Identifying such nonequilibrium oscillatory systems elevated chemical dynamics to a crucial position in the study of complex systems and self-organization phenomena, thus laying a robust groundwork for advancing nonlinear science.

To elucidate the fundamental mechanisms governing chemical oscillatory phenomena [1,2] in chemical reactions, researchers have introduced a variety of theoretical models, such as the Brusselator model [3,4,5], the Oregonator model [6,7], and the Boissonade model [8,9,10], among others. Under plausible dynamical postulates, these chemical reaction models not only reproduce the experimentally observed Hopf bifurcation and limit cycle oscillations [11,12,13,14] but also exhibit chaotic dynamics [15,16,17] under suitably selected parameter regimes. Furthermore, when diffusion phenomena are considered, these chemical models are capable of generating Turing patterns [18,19,20], thereby offering a theoretical framework for exploring the emergence of patterns and non-equilibrium steady states. Chemical reaction models hold considerable significance not only within the domain of physical chemistry but also in mathematical investigations, with particular emphasis on the Boissonade model, which epitomizes a quintessential example of low-dimensional nonlinear ordinary differential equations. Due to its concise equation form and well-defined dynamic characteristics, this model is often extended to account for stochastic noise and unbounded domains [21]. Additionally, the spatial patterns demonstrated by the reaction–diffusion framework of the Boissonade model provide mathematical support for self-organization within intricate systems [22].

The Boissonade model has been proposed by French scholars V. Duffet and J. Boissonade [8]:

$$\begin{array}{l}\left\{\begin{array}{l}{\displaystyle \frac{du}{dt}}=u-av+ruv-u^3\hfill \\ {\displaystyle \frac{dv}{dt}}=u-bv\hfill \end{array}\right.\end{array}$$

(1)

Here, u and v represent the concentrations of two substances in the chemical reaction. Specifically, u is the activator, while v is the inhibitor. The parameters $a,b,r$ are strictly positive control parameters that characterize the intensity of the reaction between the two chemical substances. In the context of this dynamical system, the parameter a is typically associated with the rate of reaction or the strength of inhibition. Parameter b characterizes the self-consumption or natural decay rate of the variable v, while the parameter r generally corresponds to the intensity of positive feedback within the reaction. The first governing equation, which is outlined in the reference model, u represents the linear self-proliferation term, while $-av$ denotes the linear suppression term, the term $ruv$ breaks the symmetry of $\left(u,v\right)\to \left(-u,-v\right)$ in the chemical system, which is atypical in chemical systems. The term $-u^3$ serves to restrict the exponential growth of disturbances and allows for the saturation of instability.The second governing equation, which is outlined in the reference model, u constitutes the linear excitation term, whereas $-bv$ signifies the linear autodegradation term.

Due to the phenomenon of diffusion between molecules of chemical substances during chemical reactions, Zhang investigated the following reaction–diffusion Boissonade model [23]

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{\partial u\left(t\right)}{\partial t}}=d_1\Delta u+u-\alpha v+\gamma uv-u^3,(x\in \Omega ,t>0)\hfill \\ {\displaystyle \frac{\partial v\left(t\right)}{\partial t}}=d_2\Delta v+u-\beta v,(x\in \Omega ,t>0)\hfill \\ u(x,0)=u_0\left(x\right)>0,v(x,0)=v_0\left(x\right)>0,(x\in \Omega )\hfill \\ {\partial }_{\nu }u={\partial }_{\nu }v=0,(x\in \partial \Omega ,t>0)\hfill \end{array}\right.\end{array}$$

(2)

The author employed center manifold theory and the method of normal forms to investigate the pattern formation mechanisms of the model (2), as well as dynamic behaviors such as Hopf bifurcation and Turing bifurcation.

Liu investigated the invariant manifolds of the following non-autonomous Boissonade system defined on a three-dimensional torus [24]

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{\partial u\left(t\right)}{\partial t}}=d\Delta u+u-av+\gamma uv-u^3+f(x,t)\hfill \\ {\displaystyle \frac{\partial v\left(t\right)}{\partial t}}=\Delta v+u-\beta v+g(x,t)\hfill \end{array}\right.\end{array}$$

(3)

This model exhibits a Turing structure, functioning as an activation-inhibition model that delineates the relationship between the real homogeneous two-dimensional system and its corresponding three-dimensional monolayer configuration.

Furthermore, academics have conducted an in-depth analysis of a simplified Boissonade–De Kepper model incorporating time-delayed feedback [25].

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{dx\left(t\right)}{\partial t}}=-(x^3\left(t\right)-\mu x\left(t\right)+\Lambda )-kx(t-\tau )\hfill \\ {\displaystyle \frac{dy\left(t\right)}{\partial t}}=(x-y)/T\hfill \end{array}\right.\end{array}$$

(4)

This investigation reveals that the quadratic term consistently induces a subcritical Hopf bifurcation, while the cubic term facilitates a transition of the model between subcritical and supercritical bifurcations. This research uncovers the subtle interplay between the nonlinear terms and the resulting system dynamics.

The Boissonade model has found broader applications across various fields of research, including chemical reactions [26], pattern formation [27], and chaotic dynamics [28], enabling the model to describe more intricate nonlinear system behaviors.

This study principally explores the Boissonade model with time delay effects:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{\partial u(x,t)}{\partial t}}=u(x,t)-av(x,t-{\tau }_1)+ru(x,t)v(x,t)-u^3(x,t)+d_1\Delta u,x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial v(x,t)}{\partial t}}=u(x,t)-bv(x,t-{\tau }_2)+d_2\Delta v,x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial u(x,t)}{\partial x}}=0,{\displaystyle \frac{\partial v(x,t)}{\partial x}}=0,x\in \partial \Omega ,t>0,\hfill \\ u(x,t)=u_0(x,t)\ge 0,v(x,t)=v_0(x,t)\ge 0,(t,x)\in \left[-\tau ,0\right]\times \overline{\Omega }.\hfill \end{array}\right.\end{array}$$

(5)

From this set, $\Omega =\left[0,\pi \right]$ is a bounded open domain in $R^1$, and $\Delta$ is a Laplacian operator in $R^1$. u and v are the concentrations of the two chemical compounds within the chemical process, $a,b,$ and r are positive parameters used to characterize the intensity of the interaction dynamics of the two chemical compounds, and $d_1$ and $d_2$ correspond to the diffusivity parameters of u and v, respectively.

Through computation, it is determined that System (5) possesses three equilibrium points: $E_0=\left(0,0\right)$, $E_1=\left(u_1,v_1\right)$, and $E_2=\left(u_2,v_2\right)$.

Among these, $u_1={\displaystyle \frac{r+\sqrt{r^2-4b(a-b)}}{2b}}$, $v_1={\displaystyle \frac{r+\sqrt{r^2-4b(a-b)}}{2b^2}}$, $u_2={\displaystyle \frac{r-\sqrt{r^2-4b(a-b)}}{2b}}$, and $v_2={\displaystyle \frac{r-\sqrt{r^2-4b(a-b)}}{2b^2}}$.

When the condition $r^2-4b(a-b)>0$ is satisfied, $E_1$ represents the positive equilibrium point. When condition $r^2-4b(a-b)>0$ and $a-b>0$, system (5) admits two positive equilibrium points, $E_1$ and $E_2$.

This manuscript’s research predominantly examines the Hopf bifurcation at the positive equilibrium point $E_1$ of system (5) with time delay as a parameter.

2. Existence of Hopf Bifurcation in the Model Without Diffusion

The structure of system (5) without diffusion is specified as

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{du}{dt}}=u-av\left(t-{\tau }_1\right)+ruv-u^3\hfill \\ {\displaystyle \frac{dv}{dt}}=u-bv(t-{\tau }_2)\hfill \end{array}\right.\end{array}$$

(6)

This section investigates the stability and Hopf bifurcation of the system based on the methodology established in reference [29]. The linearized equation of system (6) at the equilibrium point $E_1$ is given by

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{du}{dt}}=mu-nv-av(t-{\tau }_1)\hfill \\ {\displaystyle \frac{dv}{dt}}=u-bv(t-{\tau }_2)\hfill \end{array}\right.\end{array}$$

(7)

in which $m=1+r{v}_1-3u_1^2$, $n=-r{u}_1$.

The fundamental equation governing system (7) is

$$\begin{array}{c}{\lambda }^2+(b{e}^{-\lambda {\tau }_2}-m)\lambda -m·b{e}^{-\lambda {\tau }_2}+n+a{e}^{-\lambda {\tau }_1}=0.\end{array}$$

(8)

$\lambda =0$ is not an eigenvalue of the characteristic Equation (8).

In the case that ${\tau }_1={\tau }_2=0$, Equation (8) undergoes a transformation to

$$\begin{array}{c}{\lambda }^2+(b-m)\lambda -bm+n+a=0.\end{array}$$

(9)

Assuming that ${\lambda }_1$ and ${\lambda }_2$ are the two solutions of Equation (9), the calculations yield ${\lambda }_1+{\lambda }_2=-(b-m)<0$ and ${\lambda }_1·{\lambda }_2=-bm+n+a>0$. Thus, the solutions of Equation (9) are characterized by negative real components.

Case 1: ${\tau }_1>0$, ${\tau }_2=0.$

As long as ${\tau }_1>0$, ${\tau }_2=0$, the characteristic Equation (8) is reformulated as

$$\begin{array}{c}{\lambda }^2+(b-m)\lambda -mb+n+a{e}^{-\lambda {\tau }_1}=0.\end{array}$$

(10)

Assuming that $\lambda =\pm i{\omega }_1$$({\omega }_1>0)$ constitutes a pair of purely imaginary eigenvalues of the characteristic Equation (10) and substituting $\lambda =i{\omega }_1$ into the characteristic Equation (10) to separate the real part and the imaginary part, we obtain

$$\begin{array}{c}\left\{\begin{array}{c}-{\omega }_1^2-bm+n+acos{\omega }_1{\tau }_1=0\hfill \\ (b-m){\omega }_1-asin{\omega }_1{\tau }_1=0.\hfill \end{array}\right.\end{array}$$

(11)

This calculation yields

$$\begin{array}{c}{\omega }_1^4+p_1{\omega }_1^2+q_1=0,\end{array}$$

(12)

wherein $p_1=b^2-2n+m^2$ and $q_1=-2bmn+b^2{m}^2+n^2-a^2$.

By reflecting this on the line $z_1={\omega }_1^2$, Equation (12) emerges as

$$\begin{array}{c}{z}_1^2+p_1{z}_1+q_1=0.\end{array}$$

(13)

It has been demonstrated that when $p_1>0$ and $q_1<0$, $p_1^2-4q_1>0$ and Equation (13) yields a positive real solution. The positive solution of Equation (13) is formulated as $v_1$; concretely, ${\omega }_1^{*}=\sqrt{v_1}$. From Equation (11),

$$\begin{array}{c}\left\{\begin{array}{c}cos{\omega }_1^{*}{\tau }_1={\displaystyle \frac{{\left({\omega }_1^{*}\right)}^2+bm-n}{a}}\hfill \\ sin{\omega }_1^{*}{\tau }_1={\displaystyle \frac{(b-m){\omega }_1^{*}}{a}}\hfill \end{array}\right.\end{array}$$

It is established that $b-m>0$; the pivotal threshold of the time delay is

$$\begin{array}{c}{\tau }_1^j={\displaystyle \frac{1}{{\omega }_1^{*}}}arccos{\displaystyle \frac{{\left({\omega }_1^{*}\right)}^2+bm-n}{a}}+2j\pi (j=0,1,2,\dots )\end{array}$$

(14)

We postulate that ${\tau }_1^0=min\left\{{\tau }_1^j\right\}$ and differentiate both sides of Equation (10) with respect to ${\tau }_1$ to ascertain

$$\begin{array}{c}{\left({\displaystyle \frac{d\lambda }{d{\tau }_1}}\right)}^{-1}={\displaystyle \frac{2}{-{\lambda }^2-(b-m)\lambda +mb-n}}+{\displaystyle \frac{b-m}{\lambda \left[-{\lambda }^2-(b-m)\lambda +mb-n\right]}}-{\displaystyle \frac{{\tau }_1}{\lambda .}}\end{array}$$

(15)

Accordingly,

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d{\tau }_1}}\right)}_{\lambda =i{\omega }_1^{*}}^{-1}={\displaystyle \frac{2{\left({\omega }_1^{*}\right)}^2-2n+b^2+m^2}{{\left[{\left({\omega }_1^{*}\right)}^2+bm-n\right]}^2+{(b-m)}^2{\left({\omega }_1^{*}\right)}^2}}.\end{array}$$

(16)

It is established that when $2{\left({\omega }_1^{*}\right)}^2-2n+b^2+m^2\ne 0$ holds, $Re{\left({\displaystyle \frac{d\lambda }{d{\tau }_1}}\right)}_{\lambda =i{\omega }_1^{*}}^{-1}\ne 0$.

We assume that

(Q1):

$$q_1<0,p_1^2-4q_1>0;$$

(Q2):

$$2{\left({\omega }_1^{*}\right)}^2-2n+b^2+m^2\ne 0.$$

Theorem 1.

Regarding model (6), when ${\tau }_1>0$, ${\tau }_2=0$, and conditions $\left(Q1\right)$ and $\left(Q2\right)$ are met, then the positive equilibrium point $E_1=\left(u_1,v_1\right)$ of the model exhibits local asymptotic stability at ${\tau }_1\in [0,{\tau }_1^0)$. When ${\tau }_1>{\tau }_1^0$, the positive equilibrium state of the model exhibits instability, and a Hopf bifurcation appears at ${\tau }_1={\tau }_1^0$.

Case 2: ${\tau }_1=0$ and ${\tau }_2>0$

Given that ${\tau }_1=0$ and ${\tau }_2>0$, the characteristic Equation (8) is represented as

$$\begin{array}{c}{\lambda }^2+(b{e}^{-\lambda {\tau }_2}-m)\lambda -mb{e}^{-\lambda {\tau }_2}+n+a=0\end{array}$$

(17)

We suppose that $\lambda =\pm i{\omega }_2$$({\omega }_2>0)$ represents a pair of purely imaginary solutions of the characteristic Equation (17), and $\lambda =i{\omega }_2$ is plugged into the characteristic Formula (17) to distinguish between the real and imaginary components:

$$\begin{array}{c}\left\{\begin{array}{c}mbcos{\omega }_2{\tau }_2=-{\omega }_2^2+b{\omega }_{2}sin{\omega }_2{\tau }_2+a+n\hfill \\ (bcos{\omega }_2{\tau }_2-m){\omega }_2=-mbsin{\omega }_2{\tau }_2.\hfill \end{array}\right.\end{array}$$

(18)

Then, through calculation, we obtain

$$\begin{array}{c}{z}_2^2+p_2{z}_2+q_2=0\end{array}$$

(19)

in which $z_2={\omega }_2^2$, $p_2=-2a-2n+{(1+r{v}_1)}^2-6u_1^2+9u_1^4+6n{v}_1{u}_1-b^2$, and $q_2=a^2+n^2-b^2+2an$.

On the condition that $p_2<0$, $p_2^2-4q_2>0$, Equation (19) contains at least one positive real zero. Without compromising generality, the two eigenvalues of Equation (19) are characterized as $v_{21}$ and $v_{22}$; specifically, ${\omega }_2^{*}=\sqrt{v_{21}}$ or $\sqrt{v_{22}}$. Equation (18) is solvable:

$$\begin{array}{c}\left\{\begin{array}{c}sin{\omega }_2^{*}{\tau }_2={\displaystyle \frac{{\omega }_2^{*}{m}^2+{\omega }_2^{*}\left[{\left({\omega }_2^{*}\right)}^2-a-n\right]}{b{\left({\omega }_2^{*}\right)}^2+b{m}^2}}\hfill \\ cos{\omega }_2^{*}{\tau }_2={\displaystyle \frac{(a+n)m}{b{\left({\omega }_2^{*}\right)}^2+b{m}^2}}.\hfill \end{array}\right.\end{array}$$

(a):

When $a+n<0$; $a+n>0$, ${\left({\omega }_2^{*}\right)}^2-a-n>0$ or $a+n>0$, ${\left({\omega }_2^{*}\right)}^2-a-n<0$, and $m^2+{\left({\omega }_2^{*}\right)}^2-a-n>0$,

$$\begin{array}{c}{\tau }_{21}^j={\displaystyle \frac{1}{{\omega }_2^{*}}}arccos{\displaystyle \frac{(a+n)m}{b{\left({\omega }_2^{*}\right)}^2+b{m}^2}}+2j\pi (j=0,1,2,\dots );\end{array}$$

(20)

(b):

When $a+n>0$, ${\left({\omega }_2^{*}\right)}^2-a-n<0$, and $m^2+{\left({\omega }_2^{*}\right)}^2-a-n<0$,

$$\begin{array}{c}{\tau }_{22}^j={\displaystyle \frac{1}{{\omega }_2^{*}}}\left[arccos\left(-{\displaystyle \frac{(a+n)m}{b{\left({\omega }_2^{*}\right)}^2+b{m}^2}}\right)+\pi \right]+2j\pi (j=0,1,2,\dots ).\end{array}$$

(21)

Consider the condition ${\tau }_2^j={\tau }_{21}^j$ or ${\tau }_{22}^j$ and ${\tau }_2^0=min\left\{{\tau }_2^j\right\}$; then, Equation (17) is computed by differentiating at both boundaries with respect to ${\tau }_2$:

$$\begin{array}{c}{\left({\displaystyle \frac{d\lambda }{d{\tau }_2}}\right)}^{-1}={\displaystyle \frac{2\lambda -m}{\lambda [-{\lambda }^2+m\lambda -(a+n)]}}+{\displaystyle \frac{1-\lambda {\tau }_2}{(\lambda -m)\lambda }}+{\displaystyle \frac{m}{\lambda -m}}.\end{array}$$

(22)

We can then obtain

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d{\tau }_2}}\right)}_{\lambda =i{\omega }_2^{*}}^{-1}={\displaystyle \frac{2{\left({\omega }_2^{*}\right)}^2[{\left({\omega }_2^{*}\right)}^2-(a+n)]+m^2{\left({\omega }_2^{*}\right)}^2}{{[{\left({\omega }_2^{*}\right)}^2-(a+n)]}^2-{\left({\omega }_2^{*}\right)}^4{m}^2}}+{\displaystyle \frac{-1+m{\tau }_2^j-m^2}{{\left({\omega }_2^{*}\right)}^2+m^2}}.\end{array}$$

Additionally, it follows that

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d{\tau }_2}}\right)}_{\lambda =i{\omega }_2^{*}}^{-1}={\displaystyle \frac{T_{21}{T}_{24}+T_{22}{T}_{23}}{T_{22}{T}_{24}}},\end{array}$$

(23)

such that $T_{21}=2{\left({\omega }_2^{*}\right)}^2[{\left({\omega }_2^{*}\right)}^2-(a+n)]+m^2{\left({\omega }_2^{*}\right)}^2,T_{22}={[{\left({\omega }_2^{*}\right)}^2-(a+n)]}^2-{\left({\omega }_2^{*}\right)}^4{m}^2,T_{23}=-1+m{\tau }_2^j-m^2,$ and $T_{24}={\left({\omega }_2^{*}\right)}^2+m^2.$

Therefore, when $T_{21}{T}_{24}+T_{22}{T}_{23}\ne 0$ is satisfied, there exists $Re{\left({\displaystyle \frac{d\lambda }{d{\tau }_2}}\right)}_{\lambda =i{\omega }_2^{*}}^{-1}\ne 0$.

We assume that

(Q3):

$$p_2<0,p_2^2-4q_2>0;$$

(Q4):

$$T_{21}{T}_{24}+T_{22}{T}_{23}\ne 0.$$

Theorem 2.

In the case of model (6), when ${\tau }_1=0$, ${\tau }_2>0$, and conditions $\left(Q3\right)$ and $\left(Q4\right)$ are satisfied, then the positive equilibrium point $E_1=\left(u_1,v_1\right)$ of the model is locally asymptotically stable at $\tau \in [0,{\tau }_2^0)$. When ${\tau }_2>{\tau }_2^0$, the positive equilibrium point of the model is unstable, and a Hopf bifurcation is observed at ${\tau }_2={\tau }_2^0$.

Case 3: ${\tau }_1={\tau }_2=\tau$.

In the event that ${\tau }_1={\tau }_2=\tau$, the characteristic Equation (8) is reinterpreted as

$$\begin{array}{c}{\lambda }^2+(b{e}^{-\lambda \tau }-m)\lambda +(a-mb)e^{-\lambda \tau }+n=0.\end{array}$$

(24)

We postulate that $\lambda =\pm i{\omega }_3$$({\omega }_3>0)$ denotes a pair of purely imaginary values of the characteristic Equation (24) and substitute $\lambda =i{\omega }_3$ into Equation (24). After decomposing it into real and imaginary components, the equation becomes

$$\begin{array}{c}\left\{\begin{array}{c}-{\omega }_3^2+b{\omega }_{3}sin{\omega }_3\tau +(a-mb)cos{\omega }_3\tau +n=0\hfill \\ (bcos{\omega }_3\tau -m){\omega }_3-(a-mb)sin{\omega }_3\tau =0.\hfill \end{array}\right.\end{array}$$

(25)

Rearranged, it yields

$$\begin{array}{c}{z}_3^2+p_3{z}_3+q_3=0,\end{array}$$

(26)

for which $z_3={\omega }_3^2,p_3=-(2n+b^2-m^2),$ and $q_3=n^2-{(a-mb)}^2$.

In the situation where $p_3<0$, $p_3^2-4q_3>0$, Equation (26) possesses at least one positive real solution. Without narrowing the scope of generality, the two eigenvalues of Equation (26) are specified as $v_{31}$ and $v_{32}$, which means that ${\omega }_3^{*}=\sqrt{v_{31}}$ or $\sqrt{v_{32}}$. From Equation (25), we obtain

$$\begin{array}{c}\left\{\begin{array}{c}cos{\omega }_3^{*}\tau ={\displaystyle \frac{a{\left({\omega }_3^{*}\right)}^2+(mb-a)}{{(a-mb)}^2+b^2{\left({\omega }_3^{*}\right)}^2}}\hfill \\ sin{\omega }_3^{*}\tau ={\displaystyle \frac{{\omega }_3^{*}\left[m(mb-a)+b\left[{\left({\omega }_3^{*}\right)}^2-n\right]\right]}{{(a-mb)}^2+b^2{\left({\omega }_3^{*}\right)}^2}}.\hfill \end{array}\right.\end{array}$$

From this, we can calculate the following:

(a):

When $m(mb-a)>0$ or $m(mb-a)<0$ and $m(mb-a)+b\left[{\left({\omega }_3^{*}\right)}^2-n\right]>0$,

$$\begin{array}{c}{\tau }_{31}^j={\displaystyle \frac{1}{{\omega }_3^{*}}}arccos{\displaystyle \frac{a{\left({\omega }_3^{*}\right)}^2+(mb-a)}{{(a-mb)}^2+b^2{\left({\omega }_3^{*}\right)}^2}}+2j\pi (j=0,1,2,\dots );\end{array}$$

(27)

(b):

When $m(mb-a)<0$ and $m(mb-a)+b\left[{\left({\omega }_3^{*}\right)}^2-n\right]<0$,

$$\begin{array}{c}{\tau }_{32}^j={\displaystyle \frac{1}{{\omega }_3^{*}}}\left[arccos\left(-{\displaystyle \frac{a{\left({\omega }_3^{*}\right)}^2+(mb-a)}{{(a-mb)}^2+b^2{\left({\omega }_3^{*}\right)}^2}}\right)+\pi \right]+2j\pi (j=0,1,2,\dots ).\end{array}$$

(28)

We define ${\tau }^j={\tau }_{31}^j$ or ${\tau }_{32}^j$, ${\tau }^0=min\left\{{\tau }^j\right\}$ and derive the derivative of Equation (24) with respect to $\tau$ at both boundaries:

$$\begin{array}{c}{\left({\displaystyle \frac{d\lambda }{d\tau }}\right)}^{-1}={\displaystyle \frac{2\lambda -m}{\lambda (-\lambda +m\lambda -n)}}+{\displaystyle \frac{b}{(b\lambda +a-mb)\lambda }}-{\displaystyle \frac{\tau }{\lambda }}.\end{array}$$

(29)

Hence,

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d\tau }}\right)}_{\lambda =i{\omega }_3^{*}}^{-1}={\displaystyle \frac{2\left[{\left({\omega }_3^{*}\right)}^2-n\right]+m^2}{{\left[{\left({\omega }_3^{*}\right)}^2-n\right]}^2+m^2{\left({\omega }_3^{*}\right)}^2}}-{\displaystyle \frac{b^2}{{\left({\omega }_3^{*}\right)}^2{b}^2+{(a-mb)}^2}}.\end{array}$$

Subsequently,

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d\tau }}\right)}_{\lambda =i{\omega }_3^{*}}^{-1}={\displaystyle \frac{T_{31}{T}_{34}-T_{32}{T}_{33}}{T_{32}{T}_{34}}}.\end{array}$$

(30)

In this case, $T_{31}=2\left[{\left({\omega }_3^{*}\right)}^2-n\right]+m^2$, $T_{32}={\left[{\left({\omega }_3^{*}\right)}^2-n\right]}^2+m^2{\left({\omega }_3^{*}\right)}^2$, $T_{33}=b^2$, and $T_{34}={\left({\omega }_3^{*}\right)}^2{b}^2+{(a-mb)}^2$.

Evidently, assuming that $T_{31}{T}_{34}-T_{32}{T}_{33}\ne 0$ holds, it follows that there exists $Re{\left({\displaystyle \frac{d\lambda }{d\tau }}\right)}_{\lambda =i{\omega }_3^{*}}^{-1}\ne 0$.

We assume that

(Q5):

$$p_3<0,p_3^2-4q_3>0;$$

(Q6):

$$T_{31}{T}_{34}-T_{32}{T}_{33}\ne 0.$$

Theorem 3.

In terms of model (6), if ${\tau }_1={\tau }_2=\tau$ and conditions $\left(Q5\right)$ and $\left(Q6\right)$ are satisfied, the positive equilibrium point $E_1=\left(u_1,v_1\right)$ of the model is asymptotically stable in the vicinity of $\tau \in [0,{\tau }^0)$. If $\tau >{\tau }^0$, the positive equilibrium point of the model is unstable, and a Hopf bifurcation is observed at $\tau ={\tau }^0$.

3. Existence of Hopf Bifurcation in the Model with Diffusion

Case 1: ${\tau }_1>0$, ${\tau }_2=0$.

In the case where ${\tau }_1>0$ and ${\tau }_2=0$, model (5) undergoes linearization at the positive equilibrium point $E_1=\left(u_1,v_1\right)$:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{\partial U(x,t)}{\partial t}}=mU(x,t)-nV(x,t)-aV(x,t-{\tau }_1)+d_1\Delta U(x,t);\hfill \\ {\displaystyle \frac{\partial V(x,t)}{\partial t}}=U(x,t)-bV(x,t)+d_2\Delta V(x,t).\hfill \end{array}\right.\end{array}$$

(31)

In accordance with (31), the characteristic equation is deduced:

$$\begin{array}{c}{\lambda }^2+T_{k1}\lambda +h_{k1}{e}^{-\lambda {\tau }_1}+D_{k1}=0.\end{array}$$

(32)

under which

$$\begin{array}{cc}{T}_{k1}& =d_1{k}^2+d_2{k}^2-m+b;\hfill \\ h_{k1}& =a;\hfill \\ D_{k1}& =(d_1{k}^2-m)(d_2{k}^2+b)+n.\hfill \end{array}$$

(33)

It is straightforward to demonstrate that $\lambda =0$ is not a solution to the characteristic Equation (32).

Under the condition that ${\tau }_1=0$, Equation (32) simplifies to

$$\begin{array}{c}{\lambda }^2+T_{k1}\lambda +(h_{k1}+D_{k1})=0.\end{array}$$

(34)

Let ${\lambda }_1$ and ${\lambda }_2$ represent any two roots of Equation (34), a fact that can be readily demonstrated:

$$\begin{array}{cc}{\lambda }_1+{\lambda }_2& =-T_{k1}<0;\hfill \\ {\lambda }_1·{\lambda }_2& =h_{k1}+D_{k1}>0.\hfill \end{array}$$

(35)

Lemma 1.

When ${\tau }_1=0$, the positive equilibrium point $E_1$ of the system exhibits local asymptotic stability.

We assume that $\lambda =i\omega$$(\omega >0)$ is the characteristic root of Equation (32) and substitute it into Equation (32) to decompose it into real and imaginary parts:

$$\begin{array}{c}\left\{\begin{array}{c}-{\omega }^2+h_{k1}cos\omega {\tau }_1+D_{k1}=0;\hfill \\ T_{k1}\omega -h_{k1}sin\omega {\tau }_1=0.\hfill \end{array}\right.\end{array}$$

(36)

The calculation of Equation (36) yields

$$\begin{array}{c}{\omega }^4+(T_{k1}^2-2D_{k1}){\omega }^2+D_{k1}^2-h_{k1}^2=0.\end{array}$$

(37)

This simplifies to

$$\begin{array}{c}{z}^2+M_1\left(k\right)z+N_1\left(k\right)=0.\end{array}$$

(38)

At the point where $z={\omega }^2$, $M_1\left(k\right)={T_{k1}}^2-2D_{k1}$, $N_1\left(k\right)={D_{k1}}^2-{h_{k1}}^2$.

It is straightforward to demonstrate that $M_1\left(k\right)>0$ and $D_{k1}+h_{k1}>0$.

(A1):

For an arbitrary value of $k\in N$, ${\left[M_1\left(k\right)\right]}^2>4N_1\left(k\right)$ and $D_{k1}-h_{k1}>0$. In the case that $\left(A1\right)$ holds, Equation (38) does not admit any positive roots. Consequently, Equation (32) has no purely imaginary roots.

(A2):

There exists a $k_0^1\in N$ such that ${\left[M_1\left(k_0^1\right)\right]}^2>4N_1\left(k_0^1\right)$ and $D_{k_0^{1}1}-h_{k_0^{1}1}<0$. Provided that condition $\left(A2\right)$ is satisfied, Equation (32) possesses a pair of purely imaginary roots, $\pm i{\omega }_{k_0^1}=\pm i\sqrt{z_{k_0^1}}$.

Given that

$$\begin{array}{c}{z}_{k_0^1}={\left({\omega }_{k_0^1}\right)}^2={\displaystyle \frac{-M_1\left(k_0^1\right)+\sqrt{M_1{\left(k_0^1\right)}^2-4N_1\left(k_0^1\right)}}{2}},\end{array}$$

(39)

by inserting ${\omega }_{k_0^1}$ into Equation (36), we obtain

$$\begin{array}{c}\left\{\begin{array}{c}cos\left({\omega }_{k_0^1}{\tau }_1\right)={\displaystyle \frac{{\left({\omega }_{k_0^1}\right)}^2-D_{k_0^{1}1}}{h_{k_0^{1}1}}}\hfill \\ sin\left({\omega }_{k_0^1}{\tau }_1\right)={\displaystyle \frac{T_{k_0^{1}1}{\omega }_{k_0^1}}{h_{k_0^{1}1}}}\hfill \end{array}\right.\end{array}$$

(40)

The computation reveals that $sin\left({\omega }_{k_0^1}{\tau }_1\right)>0$.

Consequently,

$$\begin{array}{c}{\tau }_{k_0^1}^j={\displaystyle \frac{arccos\left(C_1\left({\omega }_{k_0^1}{\tau }_1\right)\right)+2j\pi }{{\omega }_{k_0^1}}}(j=0,1,2,\dots ).\end{array}$$

(41)

As is apparent, $\left\{{\tau }_{k_0^1}^j\right\}$ constitutes a monotonically increasing sequence, and $\underset{j\to \infty }{lim}{\tau }_{k_0^1}^j=+\infty$, represented as ${\tau }_{k_0^1}^0=min\left\{{\tau }_{k_0^1}^j\right\}$.

Lemma 2.

Assume that $\lambda \left({\tau }_1\right)=r\left({\tau }_1\right)+i\omega \left({\tau }_1\right)$ is the characteristic root of Equation (32) near ${\tau }_1={\tau }_{k_0^1}^j$, fulfilling the conditions $r\left({\tau }_{k_0^1}^j\right)=0$, $\omega \left({\tau }_{k_0^1}^j\right)={\omega }_{k_0^1}$, and $j=0,1,2,\dots$. If condition $\left(A2\right)$ is satisfied, then

$$\begin{array}{c}Re\left({\displaystyle \frac{d\lambda }{d{\tau }_1}}{|}_{{\tau }_1={\tau }_{k_0^1}^j}\right)>0,j=0,1,2,\dots \end{array}$$

Proof. 

Take the derivative of both sides of Equation (32) with respect to ${\tau }_1$:

$$\begin{array}{c}{\left({\displaystyle \frac{d\lambda }{d{\tau }_1}}\right)}^{-1}={\displaystyle \frac{2}{-{\lambda }^2-T_{k1}\lambda -D_{k1}}}+{\displaystyle \frac{T_{k1}}{\lambda [-{\lambda }^2-T_{k1}\lambda -D_{k1}]}}-{\displaystyle \frac{{\tau }_1}{\lambda }}.\end{array}$$

Compute the real component:

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d{\tau }_1}}\right)}^{-1}{|}_{{\tau }_1={\tau }_{k_0^1}^j}={\displaystyle \frac{2\left[{\left({\omega }_{k_0^1}\right)}^2-D_{k_0^{1}1}\right]+{\left(T_{k_0^{1}1}\right)}^2}{{\left(T_{k_0^{1}1}\right)}^2{\left({\omega }_{k_0^1}\right)}^2+{\left[{\left({\omega }_{k_0^1}\right)}^2-D_{k_0^{1}1}\right]}^2}}.\end{array}$$

Insert (39) into the preceding equation:

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d{\tau }_1}}\right)}^{-1}{|}_{{\tau }_1={\tau }_{k_0^1}^j}={\displaystyle \frac{\sqrt{M_1{\left(k_0^1\right)}^2-4N_1\left(k_0^1\right)}}{{\left(T_{k_0^{1}1}\right)}^2{\left({\omega }_{k_0^1}\right)}^2+{\left[{\left({\omega }_{k_0^1}\right)}^2-D_{k_0^{1}1}\right]}^2}}>0.\end{array}$$

According to Lemmas 1 and 2, the following results are derived. □

Theorem 4.

Assuming that ${\tau }_2=0$, the following conclusion holds:

(i) 

If condition $\left(A1\right)$ holds, then when ${\tau }_1>0$, the positive equilibrium point $E_1$ of system (5) is locally asymptotically stable;

(ii) 

When condition $\left(A2\right)$ is satisfied and ${\tau }_1\in [0,{\tau }_{k_0^1}^0)$, the positive equilibrium point $E_1$ of system (5) is locally asymptotically stable. When ${\tau }_1>{\tau }_{k_0^1}^0$, the positive equilibrium point $E_1$ of the system is unstable. When ${\tau }_1={\tau }_{k_0^1}^j$, with $j=0,1,2,\dots$, Hopf bifurcation occurs at the positive equilibrium point $E_1$; that is, near ${\tau }_1={\tau }_{k_0^1}^j$, the system generates a periodic solution from the positive equilibrium point $E_1$.

Case 2: ${\tau }_1=0$, ${\tau }_2>0$.

When ${\tau }_1=0$ and ${\tau }_2>0$, the linearized system of model (5) at the positive equilibrium point $E_1=\left(u_1,v_1\right)$ is given by

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{\partial U(x,t)}{\partial t}}=mU(x,t)+(-a-n)V(x,t)+d_1\Delta U(x,t)\hfill \\ {\displaystyle \frac{\partial V(x,t)}{\partial t}}=U(x,t)-bV(x,t-{\tau }_2)+d_2\Delta V(x,t)\hfill \end{array}\right.\end{array}$$

(42)

The characteristic Equation (42) is given by

$$\begin{array}{c}{\lambda }^2+T_{k2}\lambda +h_{k2}{e}^{-\lambda {\tau }_2}+D_{k2}=0.\end{array}$$

(43)

Considering that

$$\begin{array}{cc}{T}_{k2}& =d_2{k}^2+d_1{k}^2-m;\hfill \\ h_{k2}& =b\lambda +d_1{k}^{2}b-mb;\hfill \\ D_{k2}& =d_1{d}_2{k}^4-m{d}_2{k}^2+n+a;\hfill \end{array}$$

(44)

for ${\tau }_2=0$, Equation (43) takes the form

$$\begin{array}{c}{\lambda }^2+(T_{k2}+b)\lambda +(d_1{k}^{2}b-mb+D_{k2})=0.\end{array}$$

(45)

Let ${\lambda }_1$ and ${\lambda }_2$ denote any two roots of Equation (45), which are permitted to be easily established:

$$\begin{array}{cc}{\lambda }_1+{\lambda }_2& =-(T_{k2}+b)<0;\hfill \\ {\lambda }_1·{\lambda }_2& =d_1{k}^{2}b-mb+D_{k2}>0.\hfill \end{array}$$

(46)

Lemma 3.

When ${\tau }_2=0$, the positive equilibrium point $E_1$ of the system demonstrates local asymptotic stability.

We let $\lambda =i\omega$$(\omega >0)$ represent the characteristic root of Equation (43) and insert it into Equation (43) to distinguish between the real and imaginary components:

$$\begin{array}{c}\left\{\begin{array}{c}-{\omega }^2+b\omega sin\omega {\tau }_2+(d_1{k}^{2}b-mb)cos\omega {\tau }_2+D_{k2}=0\hfill \\ T_{k2}\omega +b\omega cos\omega {\tau }_2-(d_1{k}^{2}b-mb)sin\omega {\tau }_2=0\hfill \end{array}\right.\end{array}$$

(47)

Then, we can calculate

$$\begin{array}{c}{z}^2+M_2\left(k\right)z+N_2\left(k\right)=0,\end{array}$$

(48)

as defined by $z={\omega }^2$, $M_2\left(k\right)={T_{k2}}^2-b^2-2D_{k2}$, and $N_2\left(k\right)={D_{k2}}^2-{(d_1{k}^{2}b-mb)}^2$.

It is trivial to show that $D_{k2}+(d_1{k}^{2}b-mb)>0$.

(B1):

For an arbitrary value of $k\in N,{\left[M_2\left(k\right)\right]}^2>4N_2\left(k\right),$$M_2\left(k\right)>0$ and $D_{k2}-(d_1{k}^{2}b-mb)>0$.

(B2):

There exists a $k_0^{21}\in N$ such that ${\left[M_2\left(k_0^{21}\right)\right]}^2>4N_2\left(k_0^{21}\right)$ and $D_{k_0^{21}2}-\left[d_1{\left(k_0^{21}\right)}^{2}b-mb\right]<0$.

Given that condition $\left(B2\right)$ is satisfied, Equation (48) exhibits a pair of pure imaginary roots, $\pm i{\omega }_{k_0^{21}}=\pm i\sqrt{z_{k_0^{21}}}$.

In the case of

$$\begin{array}{c}{z}_{k_0^{21}}={\left({\omega }_{k_0^{21}}\right)}^2={\displaystyle \frac{-M_2\left(k_0^{21}\right)+\sqrt{M_2{\left(k_0^{21}\right)}^2-4N_2\left(k_0^{21}\right)}}{2}},\end{array}$$

(49)

substituting the value of ${\omega }_{k_0^{21}}$ into Equation (47) produces

$$\begin{array}{c}\left\{\begin{array}{c}sin\left({\omega }_{k_0^{21}}{\tau }_2\right)={\displaystyle \frac{b{\omega }_{k_0^{21}}\left[{\left({\omega }_{k_0^{21}}\right)}^2-D_{k_0^{21}2}\right]+T_{k_0^{21}2}{\omega }_{k_0^{21}}\left[d_1{\left(k_0^{21}\right)}^{2}b-mb\right]}{b^2{\left({\omega }_{k_0^{21}}\right)}^2+{\left[d_1{\left(k_0^{21}\right)}^{2}b-mb\right]}^2}}\hfill \\ cos\left({\omega }_{k_0^{21}}{\tau }_2\right)={\displaystyle \frac{\left[{\left({\omega }_{k_0^{21}}\right)}^2-D_{k_0^{21}2}\right]\left[d_1{\left(k_0^{21}\right)}^{2}b-mb\right]-T_{k_0^{21}2}b{\left({\omega }_{k_0^{21}}\right)}^2}{b^2{\left({\omega }_{k_0^{21}}\right)}^2+{\left[d_1{\left(k_0^{21}\right)}^{2}b-mb\right]}^2}}\hfill \end{array}\right.\end{array}$$

(50)

From Equation (50), it is inferred that

$$\begin{array}{c}{\tau }_{k_0^{21}}^j=\left\{\begin{array}{c}{\displaystyle \frac{arccos\left[C_{21}\left({\omega }_{k_0^{21}}{\tau }_2\right)\right]+2j\pi }{{\omega }_{k_0^{21}}}},sin\left({\omega }_{k_0^{21}}{\tau }_2\right)>0,j=0,1,2,\dots \hfill \\ {\displaystyle \frac{\pi +arccos\left[-C_{21}\left({\omega }_{k_0^{21}}{\tau }_2\right)\right]+2j\pi }{{\omega }_{k_0^{21}}}},sin\left({\omega }_{k_0^{21}}{\tau }_2\right)<0,j=0,1,2,\dots \hfill \end{array}\right.\end{array}$$

(51)

It is evident that $\left\{{\tau }_{k_0^{21}}^j\right\}$ defines a strictly increasing sequence and $\underset{j\to \infty }{lim}{\tau }_{k_0^{21}}^j=+\infty$, denoted by ${\tau }_{k_0^{21}}^0=min\left\{{\tau }_{k_0^{21}}^j\right\}$.

Lemma 4.

We consider $\lambda \left({\tau }_2\right)=r\left({\tau }_2\right)+i\omega \left({\tau }_2\right)$ as the characteristic root of Equation (43) close to ${\tau }_2={\tau }_{k_0^{21}}^j$, satisfying conditions $r\left({\tau }_{k_0^{21}}^j\right)=0$, $\omega \left({\tau }_{k_0^{21}}^j\right)={\omega }_{k_0^{21}}$, and $j=0,1,2,\dots$. If condition $\left(B2\right)$ holds true, then

$$\begin{array}{c}Re\left({\displaystyle \frac{d\lambda }{d{\tau }_2}}{|}_{{\tau }_2={\tau }_{k_0^{21}}^j}\right)>0,j=0,1,2,\dots \end{array}$$

Proof. 

We apply differentiation to both sides of Equation (43) with respect to ${\tau }_2$:

$$\begin{array}{c}{\left({\displaystyle \frac{d\lambda }{d{\tau }_2}}\right)}^{-1}={\displaystyle \frac{2}{-{\lambda }^2-T_{k2}\lambda -D_{k2}}}+{\displaystyle \frac{T_{k2}}{\lambda (-{\lambda }^2-T_{k2}\lambda -D_{k2})}}+{\displaystyle \frac{b}{\lambda h_{k2}}}-{\displaystyle \frac{{\tau }_2}{\lambda }}.\end{array}$$

Then, we assess the real component:

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d{\tau }_2}}\right)}^{-1}{|}_{{\tau }_2={\tau }_{k_0^{21}}^j}={\displaystyle \frac{2\left[{\left({\omega }_{k_0^{21}}\right)}^2-D_{k_0^{21}2}\right]+{\left(T_{k_0^{21}2}\right)}^2}{{\left(T_{k_0^{21}2}\right)}^2{\left({\omega }_{k_0^{21}}\right)}^2+{\left[{\left({\omega }_{k_0^{21}}\right)}^2-D_{k_0^{21}2}\right]}^2}}-{\displaystyle \frac{1}{\left[{\left({\omega }_{k_0^{21}}\right)}^2+{\left[d_1{\left(k_0^{21}\right)}^2-m\right]}^2\right]}}.\end{array}$$

This gives the following numerical results:

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d{\tau }_2}}\right)}^{-1}{|}_{{\tau }_2={\tau }_{k_0^{21}}^j}={\displaystyle \frac{\sqrt{M_2{\left(k_0^{21}\right)}^2-4N_2\left(k_0^{21}\right)}}{b^2\left[{\left({\omega }_{k_0^{21}}\right)}^2+{\left[d_1{\left(k_0^{21}\right)}^2-m\right]}^2\right]}}>0.\end{array}$$

(B3):

There exists a $k_0^{22}\in N$ such that ${\left[M_2\left(k_0^{22}\right)\right]}^2>4N_2\left(k_0^{22}\right)$, $M_2\left(k_0^{22}\right)<0$, and $D_{k_0^{22}2}-\left[d_1{\left(k_0^{22}\right)}^{2}b-mb\right]>0$.

Given that condition $\left(B3\right)$ is satisfied, Equation (43) exhibits a pair of pure imaginary roots, $\pm i{\omega }_{k_0^{22},\iota }=\pm i\sqrt{z_{k_0^{22},\iota }}$, $(\iota =1,2)$.

For the condition that

$$\begin{array}{c}{z}_{k_0^{22},1}={\left({\omega }_{k_0^{22},1}\right)}^2={\displaystyle \frac{-M_2\left(k_0^{22}\right)+\sqrt{{\left[M_2\left(k_0^{22}\right)\right]}^2-4N_2\left(k_0^{22}\right)}}{2}}\\ z_{k_0^{22},2}={\left({\omega }_{k_0^{22},2}\right)}^2={\displaystyle \frac{-M_2\left(k_0^{22}\right)-\sqrt{{\left[M_2\left(k_0^{22}\right)\right]}^2-4N_2\left(k_0^{22}\right)}}{2}}\end{array}$$

plug ${\omega }_{k_0^{22},\iota }$$(\iota =1,2)$ into Equation (47):

$$\begin{array}{c}\left\{\begin{array}{c}sin\left({\omega }_{k_0^{22},\iota }{\tau }_2\right)={\displaystyle \frac{b{\omega }_{k_0^{22},\iota }\left[{\left({\omega }_{k_0^{22},\iota }\right)}^2-D_{k_0^{22}2}\right]+T_{k_0^{22}2}{\omega }_{k_0^{22},\iota }\left[d_1{\left(k_0^{22}\right)}^{2}b-mb\right]}{b^2{\left({\omega }_{k_0^{22},\iota }\right)}^2+{\left[d_1{\left(k_0^{22}\right)}^{2}b-mb\right]}^2}}\hfill \\ cos\left({\omega }_{k_0^{22},\iota }{\tau }_2\right)={\displaystyle \frac{\left[{\left({\omega }_{k_0^{22},\iota }\right)}^2-D_{k_0^{22}2}\right]\left[d_1{\left(k_0^{22}\right)}^{2}b-mb\right]-T_{k_0^{22}2}b{\left({\omega }_{k_0^{22},\iota }\right)}^2}{b^2{\left({\omega }_{k_0^{22},\iota }\right)}^2+{\left[d_1{\left(k_0^{22}\right)}^{2}b-mb\right]}^2}}\hfill \end{array}\right.\end{array}$$

(52)

Based on Equation (52),

$$\begin{array}{c}{\tau }_{k_0^{22},\iota }^j=\left\{\begin{array}{c}{\displaystyle \frac{arccos\left[C_{22}\left({\omega }_{k_0^{22},\iota }{\tau }_2\right)\right]+2j\pi }{{\omega }_{k_0^{22},\iota }}},sin\left({\omega }_{k_0^{22},\iota }{\tau }_2\right)>0,j=0,1,2,\dots \hfill \\ {\displaystyle \frac{\pi +arccos\left[-C_{22}\left({\omega }_{k_0^{22},\iota }{\tau }_2\right)\right]+2j\pi }{{\omega }_{k_0^{22},\iota }}},sin\left({\omega }_{k_0^{22},\iota }{\tau }_2\right)<0,j=0,1,2,\dots \hfill \end{array}\right.\end{array}$$

(53)

□

Utilizing a proof method comparable to Lemma 4, the following inferences are subject to being drawn:

Lemma 5.

Let $\lambda \left({\tau }_2\right)=r\left({\tau }_2\right)+i\omega \left({\tau }_2\right)$ be the characteristic root of Equation (43) close to ${\tau }_2={\tau }_{k_0^{22},\iota }^j$, $\iota =1,2$, $j=0,1,2,\dots$, and the conditions $r\left({\tau }_{k_0^{22},\iota }^j\right)=0$ and $\omega \left({\tau }_{k_0^{22},\iota }^j\right)={\omega }_{k_0^{22},\iota }$, $\iota =1,2$, $j=0,1,2,\dots$, be met. Assuming condition $\left(B3\right)$ is satisfied,

$$\begin{array}{c}Re\left({\displaystyle \frac{d\lambda }{d{\tau }_2}}{|}_{{\tau }_2={\tau }_{k_0^{22},1}^j}\right)>0,Re\left({\displaystyle \frac{d\lambda }{d{\tau }_2}}{|}_{{\tau }_2={\tau }_{k_0^{22},2}^j}\right)<0,j=0,1,2,\dots \end{array}$$

(54)

As established by Lemmas 3–5, the following conclusions hold.

Theorem 5.

Assuming ${\tau }_1=0$, the following conclusions are valid:

(i) 

If condition $\left(B1\right)$ holds and ${\tau }_2>0$, the positive equilibrium point $E_1$ of system (5) is locally asymptotically stable;

(ii) 

If condition $\left(B2\right)$ is satisfied, assuming that ${\tau }_2\in [0,{\tau }_{k_0^{21}}^0)$, the positive equilibrium point $E_1$ of system (5) is locally asymptotically stable. If ${\tau }_2>{\tau }_{k_0^{21}}^0$, the positive equilibrium point $E_1$ of the system is unstable. As long as ${\tau }_2={\tau }_{k_0^{21}}^j$, $j=0,1,2,\dots$, Hopf bifurcation occurs at the positive equilibrium point $E_1$; that is, near ${\tau }_2={\tau }_{k_0^{21}}^j$, the system generates a periodic solution from the positive equilibrium point $E_1$.

(iii) 

If condition $\left(B3\right)$ is satisfied, then

(a) 

The system undergoes stability switching with the increase τ and the number of switching times is limited; that is, there is a positive integer Q. If and only if ${\tau }_2\in [0,{\tau }_{k_0^{22},1}^0)\bigcup \left({\tau }_{k_0^{22},2}^0,{\tau }_{k_0^{22},1}^1\right)\bigcup \left({\tau }_{k_0^{22},2}^1,{\tau }_{k_0^{22},1}^2\right)\bigcup \cdots \bigcup \left({\tau }_{k_0^{22},2}^{Q-1},{\tau }_{k_0^{22},1}^Q\right)$, the positive equilibrium point $E_1$ of the system is locally asymptotically stable.

(b) 

If ${\tau }_2\in \left({\tau }_{k_0^{22},1}^0,{\tau }_{k_0^{22},2}^0\right)\bigcup \left({\tau }_{k_0^{22},1}^1,{\tau }_{k_0^{22},2}^1\right)\bigcup \left({\tau }_{k_0^{22},1}^2,{\tau }_{k_0^{22},2}^2\right)\bigcup \cdots \bigcup \left({\tau }_{k_0^{22},1}^{Q-1},{\tau }_{k_0^{22},2}^{Q-1}\right)\bigcup$$\left({\tau }_{k_0^{22},1}^Q,\infty \right)$, the positive equilibrium point $E_1$ of the system is unstable. In the event that ${\tau }_2={\tau }_{k_0^{22},\iota }^j$, $\iota =1,2$, $j=0,1,2,\dots$, the system undergoes Hopf bifurcation at the positive equilibrium point $E_1$; that is, the system produces periodic solutions at $E_1$.

Case 3: ${\tau }_1={\tau }_2=\tau$.

Contingent upon ${\tau }_1={\tau }_2=\tau$, model (5) is approximated through linearization at the positive equilibrium point $E_1=\left(u_1,v_1\right)$:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{\partial U(x,t)}{\partial t}}=mU(x,t)-nV(x,t)-aV(x,t-\tau )+d_1\Delta U(x,t)\hfill \\ {\displaystyle \frac{\partial V(x,t)}{\partial t}}=U(x,t)-bV(x,t-\tau )+d_2\Delta V(x,t)\hfill \end{array}\right.\end{array}$$

(55)

Referring to Equation (55), one can obtain the characteristic equation

$$\begin{array}{c}{\lambda }^2+T_{k3}\lambda +h_{k3}{e}^{-\lambda \tau }+D_{k3}=0.\end{array}$$

(56)

At the point where

$$\begin{array}{cc}{T}_{k3}& =d_1{k}^2+d_2{k}^2-m+b{e}^{-\lambda \tau }\hfill \\ h_{k3}& =d_1{k}^{2}b-mb+a\hfill \\ D_{k3}& =d_1{d}_2{k}^4-m{d}_2{k}^2+n,\hfill \end{array}$$

(57)

substituting $\tau =0$ into Equation (57) yields

$$\begin{array}{c}{\lambda }^2+(d_1{k}^2+d_2{k}^2-m+b)\lambda +(h_{k3}+D_{k3})=0.\end{array}$$

(58)

Let ${\lambda }_1$ and ${\lambda }_2$ be two arbitrary roots of Equation (58), which can be readily proven:

$$\begin{array}{cc}{\lambda }_1+{\lambda }_2& =-(d_1{k}^2+d_2{k}^2-m+b)<0;\hfill \\ {\lambda }_1·{\lambda }_2& =h_{k3}+D_{k3}>0.\hfill \end{array}$$

(59)

Lemma 6.

When $\tau =0$, the positive equilibrium point $E_1$ of the system is locally asymptotically stable.

We consider $\lambda =i\omega$$(\omega >0)$ as the characteristic root of Equation (56) and plug it into Equation (56) to separate the real and imaginary terms:

$$\begin{array}{c}\left\{\begin{array}{c}-{\omega }^2+b\omega sin\omega \tau +h_{k3}cos\omega \tau +D_{k3}=0\hfill \\ d_1{k}^2\omega +d_2{k}^2\omega -m\omega +b\omega cos\omega \tau -h_{k3}sin\omega \tau =0.\hfill \end{array}\right.\end{array}$$

(60)

We can then calculate the following:

$$\begin{array}{c}{z}^2+M_3\left(k\right)z+N_3\left(k\right)=0\end{array}$$

(61)

at the point where $z={\omega }^2$, $M_3\left(k\right)={\left(-d_1{k}^2-d_2{k}^2+m\right)}^2-b^2-2D_{k3}$, and $N_3\left(k\right)={D_{k3}}^2-{h_{k3}}^2$.

It is deemed to be easily confirmed that $D_{k3}+h_{k3}>0$.

(C1):

For an arbitrary value of $k\in N,{\left[M_3\left(k\right)\right]}^2>4N_3\left(k\right)$ and $M_3\left(k\right)>0,D_{k3}-h_{k3}>0$.

(C2):

There exists a $k_0^{31}\in N$ such that ${\left[M_3\left(k_0^{31}\right)\right]}^2>4N_3\left(k_0^{31}\right)$, $D_{k_0^{31}3}-h_{k_0^{31}3}<0$, and $E_1^{*}{E}_4+E_2^{*}{E}_3>0$.

From this, we have

$$\begin{array}{cc}{E}_1^{*}& =h_{k_0^{31}3}b{\omega }_{k_0^{31}}\left[T_{k_0^{31}3}-{\left({\omega }_{k_0^{31}}\right)}^2+D_{k_0^{31}3}\right]+2h_{k_0^{31}3}\left\{\left[{\left({\omega }_{k_0^{31}}\right)}^2-D_{k_0^{31}3}\right]h_{k_0^{31}3}+T_{k_0^{31}3}{\left({\omega }_{k_0^{31}}\right)}^{2}b\right\}\hfill \\ E_2^{*}& =b^2\hfill \\ E_3& ={\left({\omega }_{k_0^{31}}\right)}^2{\left\{T_{k_0^{31}3}{h}_{k_0^{31}3}-\left[{\left({\omega }_{k_0^{31}}\right)}^2-D_{k_0^{31}3}\right]b\right\}}^2+{\left\{\left[{\left({\omega }_{k_0^{31}}\right)}^2-D_{k_0^{31}3}\right]h_{k_0^{31}3}+T_{k_0^{31}3}{\left({\omega }_{k_0^{31}}\right)}^{2}b\right\}}^2\hfill \\ E_4& ={\left({\omega }_{k_0^{31}}\right)}^2{b}^2+h_{k_0^{31}3}^2\hfill \end{array}$$

As long as condition $\left(C2\right)$ is met, Equation (56) admits a pair of purely imaginary solutions, $\pm i{\omega }_{k_0^{31}}=\pm i\sqrt{z_{k_0^{31}}}$:

$$\begin{array}{c}{z}_{k_0^{31}}={\left({\omega }_{k_0^{31}}\right)}^2={\displaystyle \frac{-M_3\left(k_0^{31}\right)+\sqrt{M_3{\left(k_0^{31}\right)}^2-4N_3\left(k_0^{31}\right)}}{2}}.\end{array}$$

(62)

Provided that ${\omega }_{k_0^{31}}$ is substituted into Equation (60), it results in

$$\begin{array}{c}\left\{\begin{array}{c}cos\left({\omega }_{k_0^{31}}\tau \right)={\displaystyle \frac{h_{k_0^{31}3}\left[{\left({\omega }_{k_0^{31}}\right)}^2-D_{k_0^{31}3}\right]+(-d_1{k}^2-d_2{k}^2+m)b{\left({\omega }_{k_0^{31}}\right)}^2}{h_{k_0^{31}3}^2+b^2{\left({\omega }_{k_0^{31}}\right)}^2}}\hfill \\ sin\left({\omega }_{k_0^{31}}\tau \right)={\displaystyle \frac{b{\omega }_{k_0^{31}}\left[{\left({\omega }_{k_0^{31}}\right)}^2-D_{k_0^{31}3}\right]+(d_1{k}^2+d_2{k}^2-m)h_{k_0^{31}3}{\omega }_{k_0^{31}}}{h_{k_0^{31}3}^2+b^2{\left({\omega }_{k_0^{31}}\right)}^2}}.\hfill \end{array}\right.\end{array}$$

(63)

Invoking Equation (63), it is easily concluded that

$$\begin{array}{c}{\tau }_{k_0^{31}}^j=\left\{\begin{array}{c}{\displaystyle \frac{arccos\left[C_{31}\left({\omega }_{k_0^{31}}\tau \right)\right]+2j\pi }{{\omega }_{k_0^{31}}}},sin\left({\omega }_{k_0^{31}}\tau \right)>0,j=0,1,2,\dots \hfill \\ {\displaystyle \frac{\pi +arccos\left[-C_{31}\left({\omega }_{k_0^{31}}\tau \right)\right]+2j\pi }{{\omega }_{k_0^{31}}}},sin\left({\omega }_{k_0^{31}}\tau \right)<0,j=0,1,2,\dots \hfill \end{array}\right.\end{array}$$

(64)

Obviously, $\left\{{\tau }_{k_0^{31}}^j\right\}$ is a sequence that exhibits an increase and $\underset{j\to \infty }{lim}{\tau }_{k_0^{31}}^j=+\infty$, symbolized as ${\tau }_{k_0^{31}}^0=min\left\{{\tau }_{k_0^{31}}^j\right\}$.

Lemma 7.

Let $\lambda \left(\tau \right)=r\left(\tau \right)+i\omega \left(\tau \right)$ represent the characteristic root of Equation (56) near $\tau ={\tau }_{k_0^{31}}^j$, satisfying $r\left({\tau }_{k_0^{31}}^j\right)=0$ and $\omega \left({\tau }_{k_0^{31}}^j\right)={\omega }_{k_0^{31}}$, $j=0,1,2,\dots$. Provided that condition $\left(C2\right)$ is satisfied,

$$\begin{array}{c}Re\left({\displaystyle \frac{d\lambda }{d\tau }}{|}_{\tau ={\tau }_{k_0^{31}}^j}\right)>0,j=0,1,2,\dots \end{array}$$

Proof. 

We differentiate both sides of Equation (56) with respect to $\tau$:

$$\begin{array}{c}{\left({\displaystyle \frac{d\lambda }{d\tau }}\right)}^{-1}={\displaystyle \frac{2}{(h_{k3}-\lambda b)e^{-\lambda \tau }}}+{\displaystyle \frac{\tau b}{(h_{k3}-\lambda b)}}+{\displaystyle \frac{d_2{k}^2+d_1{k}^2-m}{(\lambda h_{k3}-{\lambda }^{2}b)e^{-\lambda \tau }}}+{\displaystyle \frac{b-\tau h_{k3}}{\lambda h_{k3}-{\lambda }^{2}b}}.\end{array}$$

Then, we evaluate the real part

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d\tau }}\right)}^{-1}{|}_{\tau ={\tau }_{k_0^{31}}^j}={\displaystyle \frac{E_1^{*}{E}_4+E_2^{*}{E}_3}{E_3{E}_4}}.\end{array}$$

As condition $\left(C2\right)$ is met, specifically $E_1^{*}{E}_4+E_2^{*}{E}_3>0$, it follows that

$$\begin{array}{c}Re{\left({\displaystyle \frac{d\lambda }{d\tau }}\right)}^{-1}{|}_{\tau ={\tau }_{k_0^{31}}^j}={\displaystyle \frac{E_1^{*}{E}_4+E_2^{*}{E}_3}{E_3{E}_4}}>0.\end{array}$$

(C3):

There exists a $k_0^{32}\in N$ such that ${\left[M_3\left(k_0^{32}\right)\right]}^2>4N_3\left(k_0^{32}\right)$, $M_3\left(k_0^{32}\right)<0$, $D_{k_0^{32}3}-h_{k_0^{32}3}>0$, and $E_5{E}_7+E_2^{*}{E}_6>0,$$E_8{E}_{10}+E_2^{*}{E}_9<0$.

From this, we have

$$\begin{array}{cc}{E}_5& =h_{k_0^{32}3}b\left[d_2{\left(k_0^{32}\right)}^2+d_1{\left(k_0^{32}\right)}^2-m\right]\left[T_{k_0^{32}3}-{\left({\omega }_{k_0^{32},1}\right)}^2+D_{k_0^{32}3}\right]+2h_{k_0^{32}3}\left\{\left[{\left({\omega }_{k_0^{32},1}\right)}^2-D_{k_0^{32}3}\right]h_{k_0^{32}3}+T_{k_0^{32}3}{\left({\omega }_{k_0^{32},1}\right)}^{2}b\right\}\hfill \\ E_6& ={\left({\omega }_{k_0^{32},1}\right)}^2{\left\{T_{k_0^{32}3}{h}_{k_0^{32}3}-\left[{\left({\omega }_{k_0^{32},1}\right)}^2-D_{k_0^{32}3}\right]b\right\}}^2+{\left\{\left[{\left({\omega }_{k_0^{32},1}\right)}^2-D_{k_0^{32}3}\right]h_{k_0^{32}3}+T_{k_0^{32}3}{\left({\omega }_{k_0^{32},1}\right)}^{2}b\right\}}^2\hfill \\ E_7& ={\left({\omega }_{k_0^{32},1}\right)}^2{b}^2+h_{k_0^{32}3}^2\hfill \\ E_8& =h_{k_0^{32}3}b\left[d_2{\left(k_0^{32}\right)}^2+d_1{\left(k_0^{32}\right)}^2-m\right]\left[T_{k_0^{32}3}-{\left({\omega }_{k_0^{32},2}\right)}^2+D_{k_0^{32}3}\right]+2h_{k_0^{32}3}\left\{\left[{\left({\omega }_{k_0^{32},2}\right)}^2-D_{k_0^{32}3}\right]h_{k_0^{32}3}+T_{k_0^{32}3}{\left({\omega }_{k_0^{32},2}\right)}^{2}b\right\}\hfill \\ E_9& ={\left({\omega }_{k_0^{32},2}\right)}^2{\left\{T_{k_0^{32}3}{h}_{k_0^{32}3}-\left[{\left({\omega }_{k_0^{32},2}\right)}^2-D_{k_0^{32}3}\right]b\right\}}^2+{\left\{\left[{\left({\omega }_{k_0^{32},2}\right)}^2-D_{k_0^{32}3}\right]h_{k_0^{32}3}+T_{k_0^{32}3}{\left({\omega }_{k_0^{32},2}\right)}^{2}b\right\}}^2\hfill \\ E_{10}& ={\left({\omega }_{k_0^{32},2}\right)}^2{b}^2+h_{k_0^{32}3}^2\hfill \end{array}$$

Under the assumption that condition $\left(C3\right)$ is fulfilled, Equation (56) has a pair of purely imaginary roots, $\pm i{\omega }_{k_0^{32},\iota }=\pm i\sqrt{z_{k_0^{32},\iota }}$, $(\iota =1,2)$.

For the conditions that

$$\begin{array}{c}{z}_{k_0^{32},1}={\left({\omega }_{k_0^{32},1}\right)}^2={\displaystyle \frac{-M_3\left(k_0^{32}\right)+\sqrt{{\left[M_3\left(k_0^{32}\right)\right]}^2-4N_3\left(k_0^{32}\right)}}{2}}\\ z_{k_0^{32},2}={\left({\omega }_{k_0^{32},2}\right)}^2={\displaystyle \frac{-M_3\left(k_0^{32}\right)-\sqrt{{\left[M_3\left(k_0^{32}\right)\right]}^2-4N_3\left(k_0^{32}\right)}}{2}}\end{array}$$

upon substituting ${\omega }_{k_0^{32},\iota }$ into Equation (60), the result is

$$\begin{array}{c}\left\{\begin{array}{c}cos\left({\omega }_{k_0^{32},\iota }\tau \right)={\displaystyle \frac{h_{k_0^{32}3}\left[{\left({\omega }_{k_0^{32},\iota }\right)}^2-D_{k_0^{32}3}\right]+\left[-d_1{\left(k_0^{32}\right)}^2-d_2{\left(k_0^{32}\right)}^2+m\right]b{\left({\omega }_{k_0^{32},\iota }\right)}^2}{{\left(h_{k_0^{32}3}\right)}^2+b^2{\left({\omega }_{k_0^{32},\iota }\right)}^2}}\hfill \\ sin\left({\omega }_{k_0^{32},\iota }\tau \right)={\displaystyle \frac{b{\omega }_{k_0^{32},\iota }\left[{\left({\omega }_{k_0^{32},\iota }\right)}^2-D_{k_0^{32}3}\right]+\left[d_1{\left(k_0^{32}\right)}^2+d_2{\left(k_0^{32}\right)}^2-m\right]h_{k_0^{32}3}{\omega }_{k_0^{32},\iota }}{{\left(h_{k_0^{32}3}\right)}^2+b^2{\left({\omega }_{k_0^{32},\iota }\right)}^2}}\hfill \end{array}\right.\end{array}$$

(65)

The following is derived from (65):

$$\begin{array}{c}{\tau }_{k_0^{32},\iota }^j=\left\{\begin{array}{c}{\displaystyle \frac{arccos\left[C_{32}\left({\omega }_{k_0^{32},\iota }\tau \right)\right]+2j\pi }{{\omega }_{k_0^{32},\iota }}},sin\left({\omega }_{k_0^{32},\iota }\tau \right)>0,j=0,1,2,\dots \hfill \\ {\displaystyle \frac{\pi +arccos\left[-C_{32}\left({\omega }_{k_0^{32},\iota }\tau \right)\right]+2j\pi }{{\omega }_{k_0^{32},\iota }}},sin\left({\omega }_{k_0^{32},\iota }\tau \right)<0,j=0,1,2,\dots \hfill \end{array}\right.\end{array}$$

(66)

□

By applying a proof approach comparable to Lemma 7, the following conclusions are reached.

Lemma 8.

Let $\lambda \left(\tau \right)=r\left(\tau \right)+i\omega \left(\tau \right)$ be the characteristic root of Equation (56) near $\tau ={\tau }_{k_0^{32},\iota }^j$, $\iota =1,2$, $j=0,1,2,\dots$, and the conditions $r\left({\tau }_{k_0^{32},\iota }^j\right)=0$ and $\omega \left({\tau }_{k_0^{32},\iota }^j\right)={\omega }_{k_0^{32},\iota }$, $\iota =1,2$, $j=0,1,2,\dots$, be satisfied. If condition $\left(C3\right)$ is satisfied, then

$$\begin{array}{cc}Re\left({\displaystyle \frac{d\lambda }{d\tau }}{|}_{\tau ={\tau }_{k_0^{32},1}^j}\right)& ={\displaystyle \frac{E_5{E}_7+E_2^{*}{E}_6}{E_6{E}_7}}>0\hfill \\ Re\left({\displaystyle \frac{d\lambda }{d\tau }}{|}_{\tau ={\tau }_{k_0^{32},2}^j}\right)& ={\displaystyle \frac{E_8{E}_{10}+E_2^{*}{E}_9}{E_9{E}_{10}}}<0j=0,1,2,\dots \hfill \end{array}$$

(67)

Based on Lemmas 6–8, the following conclusions are derived.

Theorem 6.

Supposing that ${\tau }_1={\tau }_2=\tau$, the following conclusions hold:

(i) 

Assuming that condition $\left(C1\right)$ is satisfied, when $\tau >0$, the positive equilibrium point $E_1$ of system (5) is locally asymptotically stable;

(ii) 

Assuming that condition $\left(C2\right)$ is satisfied, if $\tau \in [0,{\tau }_{k_0^{31}}^0)$, the positive equilibrium point $E_1$ of system (5) is locally asymptotically stable. When $\tau >{\tau }_{k_0^{31}}^0$, the positive equilibrium point of the system is unstable. If $\tau ={\tau }_{k_0^{31}}^j$ and $j=0,1,2,\dots$, Hopf bifurcation occurs at the positive equilibrium point $E_1$; that is, near $\tau ={\tau }_{k_0^{31}}^j$, the system generates a periodic solution from the positive equilibrium point $E_1$.

(iii) 

Assuming that condition $\left(C3\right)$ is satisfied, then

(a) 

The stability switching of the system occurs with the increase in τ, and the number of switching times is limited; that is, there is a positive integer K. If $\tau \in [0,{\tau }_{k_0^{32},1}^0)\bigcup \left({\tau }_{k_0^{32},2}^0,{\tau }_{k_0^{32},1}^1\right)\bigcup \left({\tau }_{k_0^{32},2}^1,{\tau }_{k_0^{32},1}^2\right)\bigcup \cdots \bigcup \left({\tau }_{k_0^{32},2}^{K-1},{\tau }_{k_0^{32},1}^K\right)$, the positive equilibrium point $E_1$ of the system is locally asymptotically stable.

(b) 

If $\tau \in \left({\tau }_{k_0^{32},1}^0,{\tau }_{k_0^{32},2}^0\right)\bigcup \left({\tau }_{k_0^{32},1}^1,{\tau }_{k_0^{32},2}^1\right)\bigcup \left({\tau }_{k_0^{32},1}^2,{\tau }_{k_0^{32},2}^2\right)\bigcup \cdots \bigcup \left({\tau }_{k_0^{32},1}^{K-1},{\tau }_{k_0^{32},2}^{K-1}\right)\bigcup$$\left({\tau }_{k_0^{32},1}^K,\infty \right)$, the positive equilibrium point $E_1$ of the system is unstable. And if one of the assumptions $\tau ={\tau }_{k_0^{32},\iota }^j$, $\iota =1,2$, $j=0,1,2,\dots$, holds, the system undergoes Hopf bifurcation at the positive equilibrium point $E_1$; that is, the system produces periodic solutions at $E_1$.

4. Numerical Simulation

Building upon the aforementioned research findings, this section will present specific numerical examples to conduct numerical verification of previous research outcomes using MATLAB (R2023a) as the computational tool. The finite difference method is employed to numerically solve the reaction–diffusion Equations (5), with the bounded domain $\Omega =\left[0,\pi \right]$ subject to homogeneous Neumann boundary conditions. The temporal step size is set as $\Delta t={\displaystyle \frac{\tau }{20}}$, $\tau$ represents the time delay parameter, the spatial discretization adopts a step size of $\Delta x=0.03$, and the tolerance criteria are generally configured within the range of ${10}^{-6}$ to ${10}^{-8}$.

(i)

For model (6), in the case that ${\tau }_1=0$ and ${\tau }_2>0$, $a=0.5$, $b=1.2$, and $r=0.1$ are chosen. The calculation yields the positive equilibrium point $E_1=(0.806,0.672)$ and the critical value of the Hopf bifurcation ${\tau }_2^0=1.16$, which satisfies assumptions $\left(Q_3\right)$ and $\left(Q_4\right)$. By calculating equation ${\omega }_2$, the result ${\omega }_2\approx 1.45$ is obtained. According to Theorem 2, when ${\tau }_2=1.10<{\tau }_2^0$ is less than the critical value, the positive equilibrium point $E_1$ of model (6) is locally asymptotically stable (Figure 1). However, assuming that $\tau =1.30>{\tau }_2^0$ exceeds this critical value, the positive equilibrium point $E_1$ of model (6) becomes unstable (Figure 2).

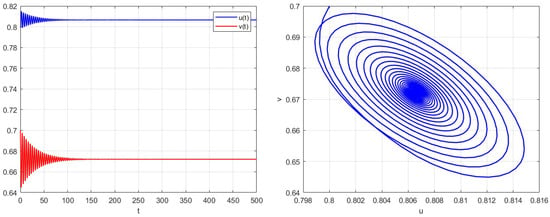Figure 1. Trajectory plot and phase diagram of model (6) when ${\tau }_1=0$ and ${\tau }_2=1.10$.

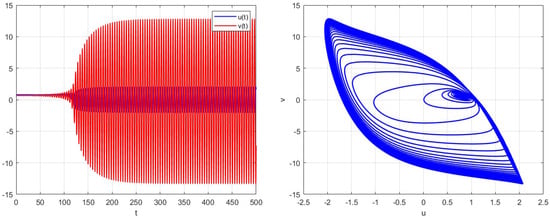Figure 2. Trajectory plot and phase diagram of model (6) when ${\tau }_1=0$ and ${\tau }_2=1.30$.

(ii)

Given that ${\tau }_1>0$ and ${\tau }_2=0$, for system (5), we take $a=0.6$, $b=0.8$, $r=0.2$, $k_0^1=1$, $d_1=0.001$, and $d_2=0.06$. We then compute the equilibrium point $E_1=(0.640,0.801)$ and the critical value of the delay parameter ${\tau }_{k_0^1}^0=1.81$. Moreover, $M_1\left(k_0^1\right)=1.001$ and $N_1\left(k_0^1\right)=-0.356$ satisfy ${\left[M_1\left(k_0^1\right)\right]}^2>4N_1\left(k_0^1\right)$, and $D_{k_0^{1}1}=-0.067$ and $h_{k_0^{1}1}=0.6$ satisfy $D_{k_0^{1}1}-h_{k_0^{1}1}<0$. Hence, condition $\left(A2\right)$ is necessarily satisfied and Theorem 4 is valid. If ${\tau }_1\in [0,{\tau }_{k_0^1}^0)$, the positive equilibrium point $E_1$ of the system is locally asymptotically stable (Figure 3). If ${\tau }_1>{\tau }_{k_0^1}^0$, the positive equilibrium point $E_1$ is unstable, and the system generates periodic solutions from the positive equilibrium point $E_1$ (Figure 4). The time delay effect induced by the inhibition of the reactant v on u in the reaction–diffusion system (5) leads to a spatially uniform variation in the concentrations of u and v when the delay does not exceed the critical threshold. However, when the reaction delay surpasses the critical value, the concentrations of the reactants exhibit periodic oscillations in space.

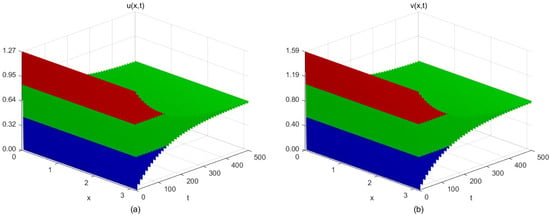Figure 3. The space–time steady-state solution of system (5) when ${\tau }_1=1.60$ and ${\tau }_2=0$. (a) Spatiotemporal steady-state solution of reactant u; (b) Spatiotemporal steady-state solution of reactant v.

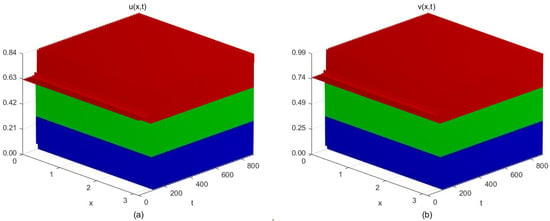Figure 4. The periodic solutions of system (5) when ${\tau }_1=3.00$ and ${\tau }_2=0$. (a) Periodic solution of reactant u; (b) Periodic solution of reactant v.

(iii)

In the event that ${\tau }_1=0$, ${\tau }_2>0$, for system (5), we take $a=1.3$, $b=1.1$, $r=1.5$, $k_0^{21}=1$, and $d_1=0.002$, $d_2=0.05$. Determining the equilibrium point $E_1=(1.213,1.103)$, the threshold value of the time delay parameter ${\tau }_{k_0^{21}}^0=1.46$. Moreover, $M_2\left(k_0^{21}\right)=3.064$ and $N_2\left(k_0^{21}\right)=-3.791$ satisfy ${\left[M_2\left(k_0^{21}\right)\right]}^2>4N_2\left(k_0^{21}\right)$, $D_{k_0^{21}2}=-0.410$, and $D_{k_0^{21}2}-\left[d_1{\left(k_0^{21}\right)}^{2}b-mb\right]=-2.400<0$. Hence, condition $\left(B2\right)$ is necessarily satisfied and Theorem 5 is established. When ${\tau }_2\in [0,{\tau }_{k_0^{21}}^0)$, the positive equilibrium point $E_1$ of the system is locally asymptotically stable (Figure 5). When ${\tau }_2>{\tau }_{k_0^{21}}^0$, the system generates periodic solutions from the positive equilibrium point $E_1$ (Figure 6). It is demonstrated that when the time delay effect induced by the linear self-decay term of the reactant v in the reaction–diffusion system (5) does not exceed the critical value, the concentrations of the reactants u and v tend to vary uniformly in space. However, when the reaction time delay surpasses the critical value, the concentrations of the reactants exhibit periodic oscillations in space.

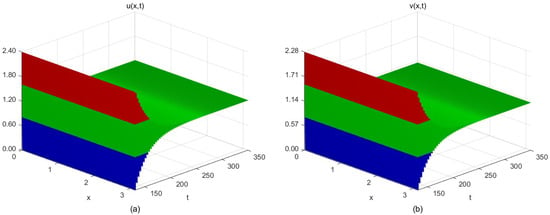Figure 5. The space–time steady-state solution of system (5) when ${\tau }_1=0$ and ${\tau }_2=1.40$. (a) Spatiotemporal steady-state solution of reactant u; (b) Spatiotemporal steady-state solution of reactant v.

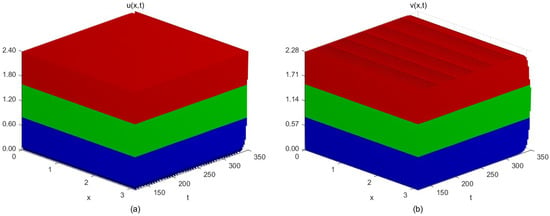Figure 6. The periodic solutions of system (5) when ${\tau }_1=0$ and ${\tau }_2=1.50$. (a) Periodic solution of reactant u; (b) Periodic solution of reactant v.

(iv)

In the instance that ${\tau }_1={\tau }_2=\tau$, for system (5), we take $a=0.8$, $b=1.2$, $r=0.4$, $k_0^{31}=1$, $d_1=0.002$, and $d_2=0.03$. We evaluate the equilibrium point $E_1=(0.767,0.640)$ and the threshold of the delay parameter ${\tau }_{k_0^{31}}^0=0.67$. Additionally, $M_3\left(k_0^{31}\right)=-0.561$ and $N_3\left(k_0^{31}\right)=-1.921$ satisfy ${\left[M_3\left(k_0^{31}\right)\right]}^2>4N_3\left(k_0^{31}\right)$, and $D_{k_0^{31}3}=-0.291$ and $h_{k_0^{31}3}=1.416$ satisfy $D_{k_0^{31}3}-h_{k_0^{31}3}<0$, $E_1{E}_4+E_2{E}_3>0$. Hence, condition $\left(C3\right)$ is necessarily satisfied, and Theorem 3 remains true. As soon as $\tau \in [0,{\tau }_{k_0^{31}}^0)$, the positive equilibrium point $E_1$ of the system is locally asymptotically stable (Figure 7). As soon as $\tau >{\tau }_{k_0^{31}}^0$, the system generates periodic solutions from the positive equilibrium point $E_1$ (Figure 8). Furthermore, it is elucidated that when the time delay effects induced by the inhibition of reactant v on u and the linear self-decay term of reactant v in system (5) are identical, these time delay effects exert a certain influence on the stability of the system. When the time delay does not exceed the critical threshold, the concentrations of reactants u and v change uniformly, whereas when the time delay surpasses the critical value, the concentrations of the reactants exhibit periodic oscillations.

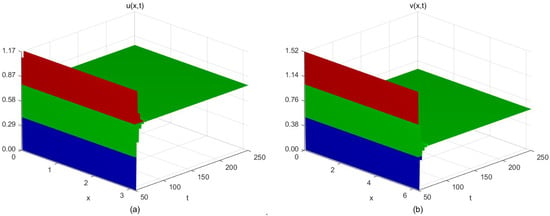Figure 7. The space–time steady-state solution of system (5) when ${\tau }_1={\tau }_2=\tau =0.60$. (a) Spatiotemporal steady-state solution of reactant u; (b) Spatiotemporal steady-state solution of reactant v.

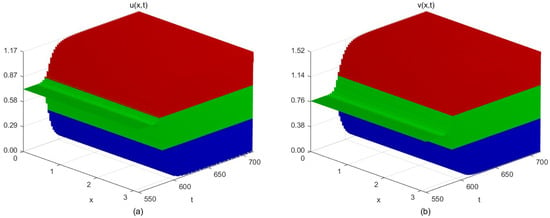Figure 8. The periodic solutions of system (5) when ${\tau }_1={\tau }_2=\tau =1.10$. (a) Periodic solution of reactant u; (b) Periodic solution of reactant v.

5. Conclusions

This study investigates a class of Boissonade reaction-diffusion models with time delays, specifically examining the delayed effects arising from the inhibition of reactant u by reactant v , the delay induced by the linear self-decay term of v , and the dynamical behavior of the system when both delays are identical. Using time delay as a key parameter, the stability of the system at equilibrium points and the existence of Hopf bifurcations under the aforementioned three scenarios are analyzed. The results indicate that when the time delay remains below a critical threshold, the positive equilibrium point exhibits local asymptotic stability, and reactant concentrations vary uniformly in space. However, once the delay exceeds the critical value, the positive equilibrium loses stability, and the system exhibits periodic oscillations, demonstrating typical characteristics of Hopf bifurcation. These findings provide a theoretical foundation for understanding and controlling chemical reaction processes with time delays. Nevertheless, the types of delays considered in this study are relatively limited. Future research could extend to nonlinear delays, multiple delays, or delays with saturation effects to further enrich the understanding of system dynamics. Moreover, since time delays are often closely related to physical conditions such as temperature and pressure, incorporating more practical factors would enhance the model’s real-world applicability. Additionally, the Hopf bifurcation analysis method employed in this study is not only applicable to chemical reaction systems but can also be extended to other nonlinear systems, particularly in control systems where input saturation, time-delay effects, or extreme solution behaviors are significant. This method can effectively predict critical conditions and reveal periodic oscillatory behaviors in such systems. Furthermore, observer design based on partial differential equations and predictive control strategies offer effective means for managing these complex systems. Future research may further explore the application of low-gain control in scenarios where delays and diffusion coexist, integrating nonlinear control theory and stability analysis methods to develop more precise control strategies. Such advancements would provide theoretical support for regulating complex reaction-diffusion systems and promote their interdisciplinary applications in chemistry, physics, biology, and beyond.