Abstract
This paper introduces the Reverse Poisson Counting Process (RPCP), a stochastic model derived from the Poisson counting process with limited and random capacity, characterized by counting backward from a defined maximum level. Explicit analytical formulas are developed for key stochastic properties, including the probability mass function and mean, specifically for scenarios involving random capacity. The model is shown to represent extreme cases of established stochastic processes, such as the M/M/1 queue with instant service completion and the death-only process. Practical applications are discussed, focusing on enhancing streaming service availability and modeling transaction validation in decentralized networks with dynamic node populations on lightweight devices. Analysis under Binomial random capacity demonstrates the impact of node accountability on MSER and network reliability, highlighting the value of incorporating stochastic variations for optimizing system performance. The explicit formulas facilitate straightforward analysis and optimization of system functionals.
Keywords:
Reverse Poisson counting process; blockchain approval system; blockchain network; accountability; duality MSC:
60C55; 60K10; 90B15; 90B50; 91A35; 93C10; 93E03
1. Introduction
In response to recent acts of terrorism and cyberterrorism, it is increasingly critical to provide robust security measures and implement an effective disaster recovery system [1]. This system must be adaptable to various vulnerable targets, including, but not limited to, stock markets, postal services, nuclear facilities, human resource centers, military installations, computer networks, and government agencies. Given the inherent limitations in achieving absolute security, a focus on resilient recovery paradigms becomes essential to mitigate damage and ensure operational continuity across diverse sectors. To enhance global security, three primary aspects merit administration, with prevention as the foremost concern. Cybersecurity represents a critical issue within computer industries, encompassing the Internet, software engineering, and e-commerce. While the conventional notion of security involves strategies to prevent attacks from adversaries, cybersecurity entails three distinct elements: secrecy (confidentiality), accuracy (integrity), and availability (reliability) [2]. Addressing these factors is crucial for maintaining robust and resilient systems against evolving threats in the digital domain. A secure network architecture mandates that information not be disclosed to unauthorized entities. Accuracy requires that the system maintain data integrity, preventing any corruption of stored information. Availability ensures that the network system operates efficiently and possesses the capacity to recover in the event of a disaster [2]. These tenets are essential for establishing a resilient and trustworthy network environment capable of safeguarding sensitive data and sustaining operations under adverse conditions.
Blockchain technology provides a distributed public digital ledger maintained through consensus across a peer-to-peer network, finding application in various services beyond cryptocurrencies [3,4]. Traditional decentralized networks offer advantages over centralized systems by mitigating numerous security risks [5]. The decentralized architecture enhances resilience and trust, making blockchain a foundational technology for secure and transparent operations in diverse applications. Blockchain Governance Game (BGG) offers a theoretical stochastic game framework for determining optimal strategies to prevent network failures [6]. This model combines mixed strategy game and fluctuation theories to yield analytically tractable results for enhancing decentralized network security. Strategic Alliance for Blockchain Governance Game (SABGG) presents an alternative method for reserving real nodes [7], while a novel secure blockchain network framework aims to prevent damages. By applying the alliance concept from a strategic management perspective atop a general BGG, a hybrid mathematical model is created to determine strategies for protecting a network through strategic alliances, or it can perform a security operation to protect entire multi-layered networks from attackers [8]. This study provides a comprehensive analysis of network security, employing explicit mathematical formulations to predict optimal times for security operations. Recent research integrates BGG with machine learning systems to defend against cyberattacks [9]. Furthermore, BGG and its variants have been applied to enhance security in real-world applications, including smart cars [10,11] and AI-enabled robot swarms [12,13,14,15]. These applications underscore the versatility and practical utility of BGG in bolstering the security of blockchain-based networks.
Classic system reliability and network availability models, adapting closed queuing systems (finite sources) with or without reserve backups, have undergone extensive study [16,17]. Various stochastic analysis techniques, including semi-regenerative analysis with additional results for semi-Markov processes, have been explored to derive analytical solutions for practical stochastic models, proving particularly useful in optimization [1,18]. The present stochastic modeling methodology builds upon the foundations laid in [1,18] and further developed in [6,7]. The duality principle, prominent in fields such as set theory, electrical engineering, and mathematical optimization, posits that if a statement is valid, its dual statement is also valid [19]. This principle involves interchanging specific elements within the original statement to generate its dual. For instance, set theory might swap unions with intersections or replace a set with its complement. The duality principle is particularly relevant in servicing machines with double control [19]. This research firstly includes a simple stochastic model, which is a monotone increased counting process referred to as Model-1. Model-2 is similar to Model-1, except that it has the limited capacity (i.e, the counting number is limited up to the full capacity M). Since the model is monotone increase, the counts start from 0 to M (i.e., ). Model-2 is directly connected with yet another model, which we will call Model-3, and Model-3 is called the reverse counting process, which means that the counting number in the system starts from the full capacity (i.e., M) and monotone decreased to the ground (i.e., ). The Poisson point process is a type of mathematical object that consists of points randomly located on a mathematical space with the essential feature that the points occur independently of one another [20]. The process derives from the fact that the number of points in any given finite region follows a Poisson distribution. The process itself was discovered independently and repeatedly in several settings. This process is one of the popular counting processes which has Markov properties. The Poisson counting process has been discovered in several settings, including experiments on radioactive decay, telephone call arrivals, and actuarial science [21,22].
The Reverse Poisson Counting Process (RPCP) represents a stochastic model which focuses on counting possibilities under conditions where the capacity or the number of available opportunities is random. The framework allows for the derivation of key stochastic properties, such as the probability mass function and the mean, specifically tailored to scenarios involving this random capacity element. Its utility lies in providing a tractable approach for analyzing and optimizing systems where such random constraints are significant. Direct observation of this reverse counting process has proven difficult, potentially limiting its discovery due to challenges in identifying systems or models where it explicitly manifests. Nevertheless, this process can effectively characterize the extreme behaviors of established stochastic models. These include the M/M/1 queueing system operating under instantaneous service completion (zero service time or infinite service rate) or the death-only process, which is an extreme case derived from general birth–death processes. One recent study indicates the potential adaptation of this process for enhancing the availability of streaming services, specifically in maintaining a target number of subscribers during broadcasts. In this context, each subscriber or terminal device can be viewed as a network node. Furthermore, the RPCP framework might be applicable to transaction validation systems within decentralized networks (e.g., blockchain networks). This is particularly relevant for handling frequent state transitions of nodes between online and offline states, a critical aspect for systems deployed on lightweight, portable personal devices [23]. Such networks are designed to accommodate frequent user joins and departures. Nevertheless, the assumption is made that user nodes persist online for a minimum duration equivalent to one complete transaction approval time (TAT). This presumption is justified, as user presence for at least one TAT is requisite for transaction finalization via consensus among other nodes [23]. The primary contributions of this research involve the formal definition and analysis of the RPCP. Explicit mathematical derivations were provided for key stochastic characteristics, including the probability mass function and mean, under conditions of random capacity. The relevance of the RPCP to networks allowing for dynamic node participation, while assuming a minimum online duration equivalent to the transaction approval time, was established. The explicit formulas derived provide a direct method for applying functionals of the fundamental stochastic characteristics and optimizing the relevant objective function.
Following this introduction, the paper is organized into four sections. Section 2 presents the theoretical foundation of the basic stochastic process, specifically the Poisson counting process with memoryless observation, along with its capacity-limited variants. Section 3 details the mathematical formulation and analytical proofs underpinning the RPCP. Furthermore, it analyzes an extension incorporating random capacity. Section 4 presents two potential applications of the RPCP, accompanied by analytical results evaluating the effectiveness of the models. Lastly, Section 5 provides a summary of the contributions and outlines potential avenues for future research.
2. Preliminaries
This section extends the classical process to encompass scenarios with capacity constraints, providing a foundational understanding for subsequent analyses. This background is critical for understanding the deviations and novel aspects of the RPCP. The variations in the Poisson counting process, particularly those incorporating limitations on capacity, are thoroughly examined to set the stage for the introduction and analysis of the RPCP in the next section.
2.1. Poisson Counting Process
A counting process is a stochastic process characterized by a sequence of random variables that quantify the number of events occurring within a specified time interval [20] which is represented as Model-1. The number of counting events within a time interval could be defined as , with the initial condition that . The Poisson counting process is a stochastic process wherein the inter-arrival times follow independent exponential distributions, all characterized by the same rate . The probability of observing k counting events within the time interval could be determined as follows:
and the probability generating function (PGF) for (1) is given by:
2.2. Memoryless Observation Process
This subsection establishes the observation process with the memoryless properties for detailing the Poisson counting process [6]. The counting process is observed at random time instances, consistent with a point process equivalent to one transaction approval time (TAT) [23].
and the duration between observation points is stochastically equivalent (i.e., ). Let us consider the number of counts within each observation interval . The duration of each observation interval is treated as a random variable from (3). The functional of Poisson counting measure within the random observation interval has been defined as follows:
which could be calculated from (2) and (4) as follows:
where
Given that the observation duration possesses a memoryless property [6], the random variable representing this duration follows an exponential distribution. From (4) and (5), the following relationships are derived:
where a is the mean of the observation duration (i.e., ). From (6), the PGF of simplifies to , which is expressed as follows:
Based on (7), the probability (denoted as ) of the Poisson counting process given an exponentially distributed observation time can be expressed as:
where
Let represent the counting number with a limited capacity M at each observation at time (i.e., ) as represented by Model-2. It is noted that each observation process resets upon reaching time from the starting moment , and only the duration between these observation moments is considered (i.e., ; ). Compared to the original Poisson counting process (i.e., Model-1), counts exceeding M are considered losses and the loss probability could be calculated as follows:
where
3. Reverse Poisson Counting Process
This section presents detailed proofs and formulations that define the behavior of the RPCP, which is referred to as Model-3. Additionally, the analysis extends to a variant of the RPCP that incorporates random capacity, providing a more flexible and realistic model for various applications. The RPCP is fundamentally a Poisson counting process with both a limited capacity and a memoryless observation process. However, unlike typical counting processes, the RPCP counts backward from a defined maximum level M, representing the full capacity. Let be the number of negative counting from the full capacity M at the observation time (i.e., ). Each observation process shall be reset once the duration reaches from the starting moment and the capacity is fully restored to M.
Theorem 1.
The probability of the RPCP with the exponential observation time could be found as follows:
and
The meaning of Reverse in the RPCP mathematically manifests as a probabilistic reflection of the truncated Poisson counting process from Model-2, where the probability mass function for the RPCP equates , with normalized to ensure summation to unity from (15). This mirrors the cumulative distribution from the upper bound M downward, effectively inverting the directionality: whereas Model-2 accumulates counts upward from zero to a capped M (losses beyond M), the RPCP depletes from full capacity M to zero, interpreting decrements as negative counts or failures. The duality principle allows to swap accumulation with depletion, akin to birth–death process extremes where births vanish, yielding a pure death process; explicit derivation from Theorem 1. It is observed that all parameters and their relationships with the models are detailed in Appendix A.
From (15)–(18), the probability of the RPCP with the exponential observation duration finally determined as follows:
where
The functional of this truncated counting process could be defined as follows:
and the PGF of RPCP with the exponential observation duration becomes which could be calculated as follows:
and the mean of the RPCP is as follows:
which yields
The concept of random capacity is targeted for extend extending the RPCP model to accommodate scenarios where the capacity M is not fixed but rather varies randomly. This enhancement allows the model to better represent real-world systems with fluctuating resources or capacities, adding a layer of complexity and realism to the analysis. Let denote the number of counts from the random capacity representing the random full capacity at the initial moment (i.e., ). The probability mass function (PMF) of (representing the system’s full capacity or the number of full network nodes) is given by . The mean of is denoted as and is the maximum capacity of system or the number of maximum nodes on the network security. From (19), the probability of the RPCP under the random capacity could be as follows:
where
and
which is assumed that . Regarding this matter, robust experiments have been conducted to validate the approximation of the original form by evaluating the mean square error rate (MSER) with the simpler form . The relationship between node accountability and the mean square error rate (MSER) has been illustrated on Figure 1.
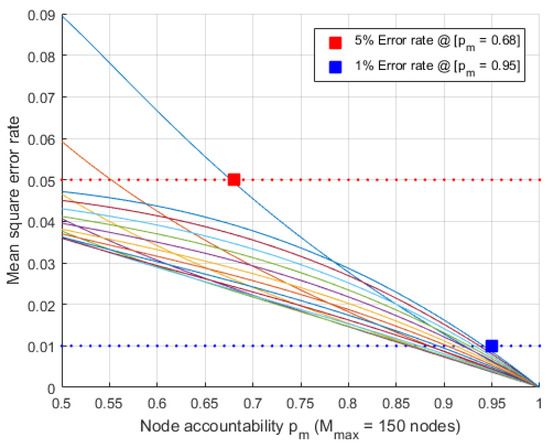
Figure 1.
The MSER comparison between and .
This figure presents the simulated accountability of each node for parameters , , and which offer a gap analysis between two different calculation. This evaluation quantifies the discrepancy between the expected value of the function applied to the random variable and the function applied to the expected value of the random variable. The results demonstrate that the approximation holds with acceptable accuracy under the tested conditions, supporting the use of as a computationally simpler surrogate for in relevant stochastic modeling scenarios. In this scenario, the random capacity follows a Binomial distribution with parameters n and success probability p (i.e., ). The graph shows how MSER decreases as node accountability increases, reflecting improved system reliability with higher accountability . Two key points are highlighted: higher node accountability correlates with improved system performance due to more reliable nodes. Key highlights include a 5% error rate when the average node accountability exceeds approximately 68% (i.e., ), and a further reduction to a 1% error rate when node accountability reaches 95% or higher (i.e., ). Higher node accountability substantially reduces the MSER. The graph demonstrates that accounting for variations in node behavior using closely approximates the original function . This underscores the importance of considering stochastic variations in network nodes to effectively optimize error rates.
4. Case Studies
This section presents case studies applying the RPCP framework to practical scenarios. Additionally, the special case of random capacity (i.e., binomial random capacity) has also been demonstrated. The mathematical formulations for the expected value and the probability mass function of the RPCP are derived for demonstrating how the model can quantify key stochastic characteristics under randomly distributed capacity. These case studies serve to illustrate the utility and analytical tractability of the proposed RPCP model in relevant application domains, evaluating its performance and effectiveness through analytical results.
4.1. Network Availability Optimization
The application of the presented stochastic framework to enhance the availability of network nodes has been demonstrated. It focuses on leveraging the analytical models to determine strategies for maximizing network uptime and resilience. The network of multiple nodes M required to maintain the threshold of the nodes between the evaluation moment (i.e., , , ) to keep up the level of availability of the network. Let be the total number of nodes in the multiple node network and the availability level of the multiple node network is defined as follows:
and
where is the threshold of availability level. This case illustrates how network availability varies with the number of network nodes (see Figure 2). This figure presents the network availability simulation based on the number of network nodes for parameters , and . If the network has more than 35 nodes (i.e., ), the availability of this network is guaranteed 99% (i.e., from (27) which meets the target availability threshold (i.e., ). This visualization emphasizes the balance between network size and availability, demonstrating that beyond a certain number of nodes, further increases do not significantly enhance availability, thereby guiding efficient resource allocation for network design and optimization.
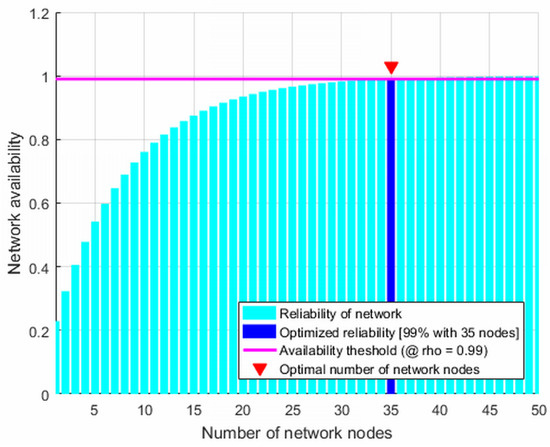
Figure 2.
Network node availability optimization where .
While the specific methodologies and findings are not provided, this case study indicates the practical relevance of the theoretical work for improving the operational reliability of network systems by optimizing node availability.
4.2. Binomial Random Capacity
This case explores the application of the RPCP model when the system capacity is modeled as a binomial random variable. This approach captures the variability in the number of active nodes, reflecting realistic network conditions where node availability fluctuates. Mathematical expressions for the probability mass function and expected values are derived under this assumption, enabling precise quantification of stochastic characteristics. Let us consider that the PMF of the random variable M as the binomial distribution with the accountability of each node and is a maximum capacity of the system. From (21), we have:
and the probability of the RPCP under the binomial random capacity could be determined as follows:
where
The analysis demonstrates how the RPCP framework adapts to random capacity scenarios, providing insights into system performance and reliability. This subsection highlights the flexibility of RPCP and its potential for practical use in networks with dynamic node populations. The relationship between node accountability and the reliability of the network under a binomial random capacity model with total 75 network nodes (i.e., , ) has been demonstrated on Figure 3. The figure presents the simulated probabilities of availability which related with random accountability of each node for parameters , and which offer a comprehensive view of availability performance across the average accountability of each node.
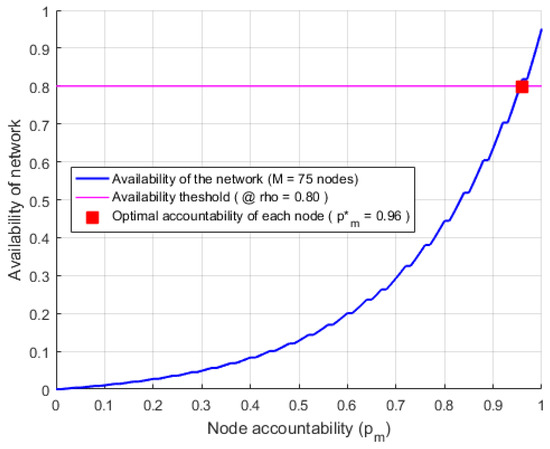
Figure 3.
Binomial random capacity analysis.
The availability threshold is set at 0.80 (i.e, ), which indicates the minimum acceptable network availability level. In this scenario, comprising 75 network nodes (i.e., ), the optimal accountability per node attains 0.96 (i.e., ), yielding a network availability that satisfies or surpasses the designated threshold. This visualization demonstrates how increasing node accountability significantly enhances overall network reliability, especially when the capacity is subject to binomial randomness. The figure underscores the importance of maintaining high node accountability to achieve desired reliability levels in networks with fluctuating node availability, providing practical insights for designing robust decentralized systems.
5. Conclusions
An explicit analysis of the Random Possibility Counting Process (RPCP) has been presented for fundamental stochastic characteristics, including the probability mass function and the mean when considering random capacity. These derived expressions offer a relatively effortless approach to utilizing functionals and optimizing objective functions pertinent to the RPCP. The adaptability of this innovative model has been underscored by demonstrating its capability to represent limiting cases of well-known stochastic models, specifically the M/M/1 queueing system with zero service time and the death-only process derived from birth–death models. Practical applications have been discussed, highlighting the potential of the RPCP in improving the availability of streaming services and modeling transaction validation within decentralized networks populated by frequently changing nodes on handheld devices. Extending the RPCP model to encompass more intricate system behaviors or alternative distributions for random capacity constitutes a viable direction for subsequent research. Exploring the applicability of this framework to other fields characterized by dynamic node populations and capacity constraints also presents valuable opportunities for investigation.
Funding
This work was supported in part by the Macao Polytechnic University (MPU), under Grant RP/FCA-05/2024.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
This paper was revised using AI/ML-assisted tools. Special thanks to the reviewers who provide valuable advice for improving this paper.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
This Appendix provides the summary table to delineates the principal parameters and their mathematical formulations alongside interpretive descriptions for the three foundational stochastic models. Model-1 embodies the unrestricted Poisson counting process, Model-2 imposes a finite capacity M on upward accumulation, and Model-3 inverts this via the reverse counting mechanism.

Table A1.
Description of Parameters.
Table A1.
Description of Parameters.
| Parameter | Formula | Model-1 | Model-2 | Model-3 |
|---|---|---|---|---|
| – | Rate of input counting | Same as Model-1 | Rate of broken nodes | |
| – | – | Observation Process | Same as Model-2 | |
| a | – | Average duration of each observation | Same as Model-2 | |
| Average counting during the duration a | Same as Model-1 | Average counting of broken node during the one observation | ||
| – | Same as Model-3 | Same as Model-2 | ||
| – | Number of counting in the system (i.e., Model-1) during the duration | – | – | |
| (8) | Probabilities of Model-1 (i.e., ) | – | – | |
| – | – | Number of counting for limited capacity system (i.e., Model-2) during the duration | – | |
| (13) | – | Probabilities of Model-2 | – | |
| – | – | – | Number of counting for remaining nodes in the system (i.e., Model-3) during the duration | |
| (15) | – | – | Probabilities of Model-3 |
References
- Kim, S.K.; Dshalalow, J. Stochastic disaster recovery systems with external resources. Math. Comput. Model. 2002, 36, 1235–1257. [Google Scholar] [CrossRef]
- Stallings, W. Cryptography And Network Security, 7th ed.; Pearson: New York, NY, USA, 2017. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 16 November 2023).
- Wood, G. Ethereum: A Secure Decentralised Generalised Transaction Ledger. 2008. Available online: https://ethereum.github.io/yellowpaper/paper.pdf (accessed on 16 November 2023).
- Choudhary, G.; Sharma, V.; You, I. Sustainable and secure trajectories for the military Internet of Drones (IoD) through an efficient Medium Access Control (MAC) protocol. Comput. Electr. Eng. 2019, 74, 59–73. [Google Scholar] [CrossRef]
- Kim, S.K. Blockchain Governance Game. Comput. Ind. Eng. 2019, 136, 373–380. [Google Scholar] [CrossRef]
- Kim, S.K. Strategic Alliance for Blockchain Governance Game. Probab. Eng. Inf. Sci. 2022, 36, 184–200. [Google Scholar] [CrossRef]
- Kim, S.K. Multi-Layered Blockchain Governance Game. Axioms 2022, 11, 27. [Google Scholar] [CrossRef]
- Kim, S.K. Enhanced Blockchain-Based Data Poisoning Defense Mechanism. Appl. Sci. 2025, 15, 4069. [Google Scholar] [CrossRef]
- Cheema, M.A.; Shehzad, M.K.; Qureshi, H.K.; Hassan, S.A.; Jung, H. A Drone-Aided Blockchain-Based Smart Vehicular Network. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4160–4170. [Google Scholar] [CrossRef]
- He, D.; Chan, S.; Guizani, M. Communication Security of Unmanned Aerial Vehicles. Wirel. Commun. 2017, 24, 134–139. [Google Scholar] [CrossRef]
- Strobel, V.; Castelló Ferrer, E.; Dorigo, M. Managing Byzantine Robots via Blockchain Technology in a Swarm Robotics Collective Decision Making Scenario. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; Richland, SC, USA, 2018; pp. 541–549. [Google Scholar]
- Strobel, V.; Castelló Ferrer, E.; Dorigo, M. Blockchain Technology Secures Robot Swarms: A Comparison of Consensus Protocols and Their Resilience to Byzantine Robots. Front. Robot. AI 2020, 7. [Google Scholar] [CrossRef] [PubMed]
- Millard, A.G.; Timmis, J.; Winfield, A.F.T. Towards Exogenous Fault Detection in Swarm Robotic Systems. In Proceedings of the Towards Autonomous Robotic Systems, Oxford, UK, 28–30 August 2013; Springer: Berlin/Heidelberg, Germany, 2014; pp. 429–430. [Google Scholar]
- Pinciroli, C.; Trianni, V.; O’Grady, R.; Pini, G.; Brutschy, A.; Brambilla, M.; Mathews, N.; Ferrante, E.; Caro, G.D.; Ducatelle, F.; et al. ARGoS: A modular, parallel, multi-engine simulator for multi-robot systems. Swarm Intell. 2012, 6, 271–295. [Google Scholar] [CrossRef]
- Srinivasa Rao, T.; Gupta, U. Performance modelling of the M/G/1 machine repairman problem with cold-, warm- and hot-standbys. Comput. Ind. Eng. 2000, 38, 251–267. [Google Scholar] [CrossRef]
- Takcas, L. Introduction to the Theory of Queues; Oxford Press: Oxford, UK, 1962. [Google Scholar]
- Kim, S.K.; Dshalalow, J. A Versatile Stochastic Maintenance Model with Reserve and Super-Reserve Machines. Methodol. Comput. Appl. Probab. 2003, 5, 59–84. [Google Scholar] [CrossRef]
- Dshalalow, J. On A Duality Principle In Processes Of Serving Machines with Double Control. J. Appl. Math. Simul. 1988, 1, 245–252. [Google Scholar]
- Bas, E. A Brief Introduction to Point Process, Counting Process, Renewal Process, Regenerative Process, Poisson Process. In Basics of Probability and Stochastic Processes; Springers: Berlin, Germany, 2019; pp. 131–147. [Google Scholar]
- Stirzaker, D. Advice to hedgehogs, or, constants can vary. Math. Gaz. 2000, 84, 197–210. [Google Scholar] [CrossRef]
- Guttorp, P.; Thorarinsdottir, T.L. What Happened to Discrete Chaos, the Quenouille Process, and the Sharp Markov Property? Some History of Stochastic Point Processes. Int. Stat. Rev. 2012, 80, 253–268. [Google Scholar] [CrossRef]
- Gong, Y.; Kim, S.K. A Novel Private Blockchain Based Multimedia Verification Systems. 2025. Available online: https://github.com/neodark152/bmvs (accessed on 30 October 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).