Dynamic Event-Triggered Adaptive Broad Learning for a Two-Degree-of-Freedom Helicopter System with Prescribed Performance

Abstract

This study proposes an adaptive broad learning strategy for a two-degree-of-freedom helicopter system based on specified performance and dynamic event-triggered. First, broad learning is employed to approximate system uncertainties. Compared to radial basis function neural networks, broad learning achieves this by increasing the number of nodes, enabling it to approximate system uncertainties with smaller tracking errors. At the same time, an error transformation method is employed to guarantee that the tracking error adheres to a predefined performance function. Furthermore, a dynamic event-triggering mechanism reduces communication overhead and prevents the Zeno effect. Subsequent Lyapunov-based stability analysis confirms that the system exhibits semi-global consistency, stability, and boundedness. In addition, simulation results verify the proposed control strategy’s effectiveness and robustness.

1. Introduction

Compared to fixed-wing aircraft, helicopters offer distinct advantages, particularly in their ability to hover, perform vertical takeoffs and landings, and operate in less restrictive environments. Owing to these features, helicopters have been widely employed in military missions, cargo transport, and logistical support [1]. However, helicopters are inherently nonlinear multiple-input multiple-output (MIMO) systems, exhibiting strong inter-axis coupling, time-varying parameters, and system uncertainties [2,3]. These characteristics present major challenges in the design of robust stability controllers. In response, researchers have conducted extensive investigations into helicopter flight control system stability.

In recent years, a variety of advanced control techniques have been introduced for helicopter system regulation. For example, ref. [4] presents a reduced-order output feedback scheme designed to stabilize the attitude of a two-degree-of-freedom (2-DOF) helicopter. This method simplifies the system order to reduce computational complexity while achieving accurate attitude stabilization solely through output feedback, without requiring complete state information. In [5], the authors proposed a sliding mode control method based on a higher-order disturbance observer and validates it on a 2-DOF helicopter. The only requirement regarding uncertainty is knowledge of its boundary conditions, which greatly reduces dependence on prior system modeling. In order to achieve accurate trajectory tracking in uncertain 2-DOF helicopter systems, a preset-time adaptive control strategy was proposed in [6], which guarantees precise regulation of pitch and yaw angles within a predetermined time horizon. In recent years, radial basis function neural networks (RBFNN) have been widely adopted in nonlinear control applications, owing to their excellent function approximation capabilities and fast learning characteristics. For instance, to address control challenges in uncertain 2-DOF helicopter systems experiencing actuator faults, an adaptive NN-based constrained control framework was introduced in [7]. By incorporating input saturation and prescribed performance requirements, the proposed method enhances both robustness and practical feasibility. Additionally, in [8], the authors proposed an adaptive neural network control algorithm for an uncertain 2-DOF helicopter system with input dead zones and output constraints. Meanwhile, the Broad Learning (BL) method has recently garnered increasing attention due to its outstanding approximation performance and enhanced learning capabilities, finding application in helicopter stability control. To compensate for unstructured uncertainties/disturbances in a 2-DOF helicopter system under online conditions, we employ a BL approximator. Compared to classical RBF networks, BL achieves high approximation accuracy through width expansion, and its online adaptation mechanism is more streamlined. This not only facilitates stability analysis but also yields smaller tracking errors. For instance, in [9], the authors proposed a fault-tolerant control algorithm for helicopter systems based on an adaptive broad learning neural network (BLNN). In [10], to tackle the control difficulties caused by unknown dead zone effects in a 2-DOF helicopter, a broad reinforcement learning adaptive control strategy was designed. Despite substantial progress in NN-based helicopter control and unmanned aerial system applications, studies on communication constraints in 2-DOF helicopter systems remain relatively scarce, indicating a critical avenue for future research.

Additionally, 2-DOF helicopter systems are typically implemented using embedded/networked hardware, where periodic sampling continuously updates control signals. This approach wastes communication and computational resources even when errors are minimal. In contrast, event-triggered mechanisms refresh inputs only when beneficial, thereby reducing the average update frequency [11,12]. An event-triggered (ET) fuzzy flight control system was developed in [13] for a 2-DOF helicopter, aiming to reduce the communication load. In [14], the authors designed an ET strategy for a 2-DOF helicopter system under denial-of-service attacks. To handle external disturbances and input saturation in quadrotor UAVs, ref. [15] presented an ET discrete-time neural control approach. Furthermore, ref. [16] addressed the trajectory tracking problem for a 6-DOF quadcopter under time-varying and asymmetric output constraints. In this work, ET control was applied in the attitude loop design to reduce communication demands without relying on prior knowledge of the trigger threshold’s upper bound. Although the aforementioned studies on ET control for helicopters and UAVs are relatively mature, research specifically focusing on dynamic event-triggered (DET) control for 2-DOF helicopters remains limited, highlighting the need for further exploration.

Event-triggered mechanisms (ETMs) effectively reduce communication overhead but may compromise tracking accuracy and even affect system stability. Simultaneously, a two-degree-of-freedom helicopter constitutes a nonlinear, strongly coupled MIMO system with time-varying parameters and uncertainties. Beyond minor steady-state errors, safety and mission requirements necessitate explicit specifications for transient and steady-state performance metrics, such as overshoot, convergence rate, and residual limits. Therefore, integrating a prescribed performance function (PPF) is crucial for enhancing system tracking performance [17,18]. Currently, extensive research has been conducted on PPFs for nonlinear systems. For instance, to address control challenges in vehicle active suspension systems, ref. [19] introduced a novel control scheme based on a specified performance function. This approach efficiently characterizes both the convergence rate of the tracking error and the peak overshoot. In [20], the authors proposed an adaptive saturated command performance control problem for air-breathing hypersonic vehicles subject to parameter uncertainties and unknown external disturbances. In [21], the author proposed a sliding mode control scheme for uncertain nonlinear systems, which exhibits precise convergence time characteristics. To address the challenge of robust attitude control for a 2-DOF helicopter under fixed-time constraints, the authors in [22] proposed a control strategy that integrates a sliding mode switching mechanism with an innovative arrival law. This approach ensures effective attitude control under input saturation while satisfying prescribed performance (PP) requirements. Additionally, to meet the practical control needs of coaxial composite helicopters, ref. [23] presented a performance-based envelope protection control strategy to enhance flight safety. By defining PP boundaries, the proposed scheme achieves the desired transient response. Despite the significant progress made in PP control, no existing research has yet addressed the control of 2-DOF helicopter systems based on both DET and PP, which motivates further investigation.

To address the nonlinear, strongly coupled, and time-varying characteristics of a 2-DOF helicopter system, we employ a control architecture that integrates Preset Performance Control (PPC), DET, and BL. To compensate for uncertainties in the 2-DOF helicopter system, we utilize adaptive broad-learning, which achieves high-precision fitting through width expansion and possesses efficient online update capabilities. PPC explicitly encodes transient and steady-state errors through performance functions. Leveraging an error transformation mechanism ensures tracking errors remain within specified performance boundaries under uncertainty. Considering bandwidth and computational constraints in networked implementations, we further designed a dynamic event-triggered mechanism that updates control strategies only when necessary. This mechanism, controlled by dynamic thresholds, avoids Zeno behavior. This control strategy designs a controller that ensures predetermined performance while significantly reducing the communication load. The system’s semi-global asymptotic stability is proven via Lyapunov stability analysis, and the effectiveness and robustness of the proposed strategy are validated through simulations. The key contributions of this study are outlined below:

(i) Unlike [3,11], the dynamic event-triggering (DET) strategy proposed in this work not only markedly reduces communication and computation load, but also enhances the closed-loop stability and operational reliability of the helicopter system by preventing unnecessary control updates and actuator wear.

(ii) To ensure that both the transient and steady-state tracking errors of the 2-DOF helicopter remain within predefined bounds, a prescribed performance constraint (PPC) is integrated into the control design. In addition, an appropriate error-transformation technique is introduced to simplify controller synthesis and reduce computational complexity.

(iii) Under the conditions where DET and PPF constraints coexist and are mutually coupled, this paper constructs an adaptive broad learning control with a dynamic threshold triggering mechanism. It is proven that the closed-loop system is semi-globally asymptotically stable, simultaneously satisfying error constraints imposed by PPF and avoiding Zeno phenomena.

2. Problem Formulation

2.1. 2-DOF Helicopter System

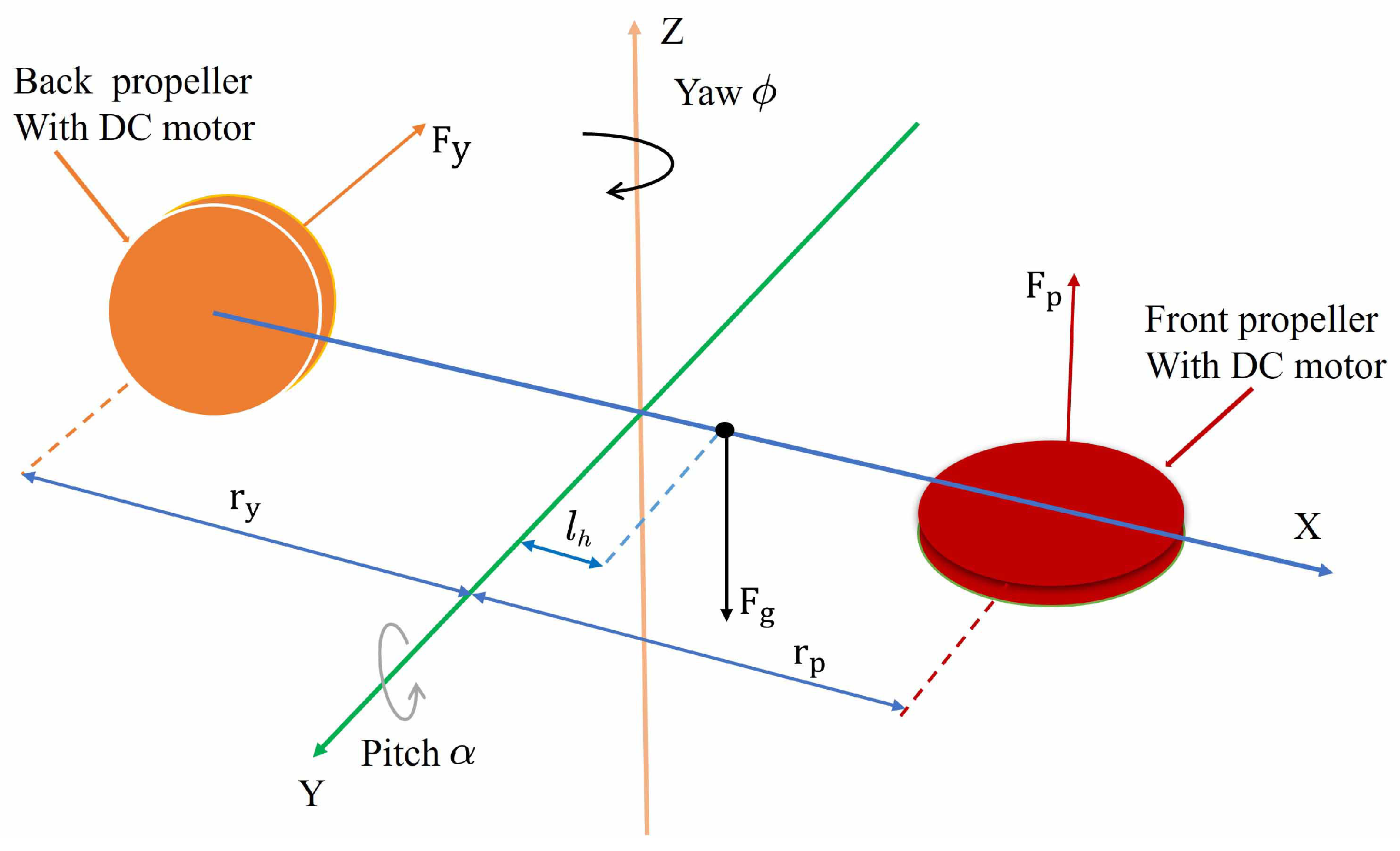
Figure 1 shows the model diagram of a 2-DOF helicopter system. As stated in [9], the dynamic model of the 2-DOF helicopter system is given by:

$$\begin{array}{ll}\ddot{\alpha }& ={\displaystyle \frac{-M_h{g}_h{l}_{h}cos\alpha -D_{hpp}\dot{\alpha }-M_h{l}_h^2{\dot{\varphi }}^{2}sin\alpha cos\alpha }{(J_{hpp}+M_h{l}_h^2)}}\\ & +{\displaystyle \frac{K_{hpp}{V}_p+K_{hpy}{V}_y}{(J_{hpp}+M_h{l}_h^2)}},\end{array}$$

(1)

$$\begin{array}{ll}\ddot{\varphi }& ={\displaystyle \frac{-D_{hyy}\dot{\varphi }+2M_h{l}_h^2\dot{\varphi }\dot{\alpha }sin\alpha cos\alpha }{(J_{hyy}+M_h{l}_h^2{cos}^2\alpha )}}\\ & +{\displaystyle \frac{K_{hyp}{V}_p+K_{hyy}{V}_y}{(J_{hyy}+M_h{l}_h^2{cos}^2\alpha )}},\end{array}$$

(2)

where $\alpha$ and $\varphi$ represent the pitch and yaw angles, respectively, and also serve as the system states. $V_p$ and $V_y$ denote the system inputs. $M_h$ is the mass of the system, and $l_h$ denotes the distance from the helicopter’s center of gravity to the coordinate origin. $g_h$ represents gravitational acceleration. $D_{hpp}$ and $D_{hyy}$ are the moments of inertia about the pitch and yaw axes, respectively. $K_{hpp}$, $K_{hpy}$, $K_{hyp}$, and $K_{hyy}$ represent the thrust torques acting on the system [24].

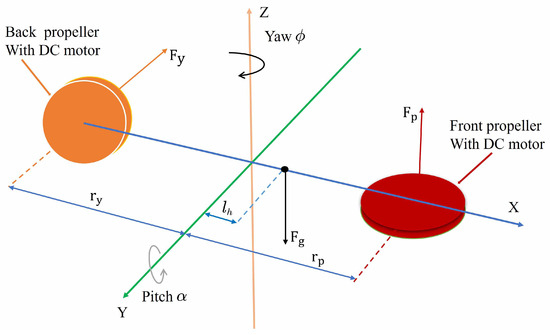
Figure 1. Model diagram of a 2-DOF helicopter system [24].

Define $\psi ={[{\psi }_1,{\psi }_2]}^T$, where ${\psi }_1={[\alpha ,\varphi ]}^T$ and ${\psi }_2={[\dot{\alpha },\dot{\varphi }]}^T$. Considering the uncertainties in the system, the helicopter models (1) and (2) are reformulated into a standard MIMO system.

$$\begin{array}{cc}\hfill {\dot{\psi }}_1& ={\psi }_2\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\dot{\psi }}_2& =X\left(\psi \right)+\Delta X\left(\psi \right)+Y\left(\psi \right)v\hfill \end{array}$$

(4)

where $v={[V_p,V_y]}^T$ is the system input, and $\Delta X$ indicates an unknown smooth nonlinear function. X and Y expressed as follows:

$$\begin{array}{cc}\hfill X\left(\psi \right)& =\left[\begin{array}{c}{\displaystyle \frac{-M_h{g}_h{l}_{h}cos\left({\psi }_{11}\right)-D_{hpp}{\psi }_{21}-M_h{l}_h^2{\psi }_{22}^{2}sin\left({\psi }_{11}\right)cos\left({\psi }_{11}\right)}{J_{hpp}+M_h{l}_h^2}}\\ {\displaystyle \frac{-D_{hyy}{\psi }_{22}+2M_h{l}_h^2{\psi }_{22}{\psi }_{21}sin\left({\psi }_{11}\right)cos\left({\psi }_{11}\right)}{J_{hyy}+M_h{l}_h^2{cos}^2\left({\psi }_{11}\right)}}\end{array}\right],\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill Y\left(\psi \right)& =\left[\begin{array}{cc}{\displaystyle \frac{K_{hpp}}{J_{hpp}+M_h{l}_h^2}}& {\displaystyle \frac{K_{hpy}}{J_{hpp}+M_h{l}_h^2}}\\ {\displaystyle \frac{K_{hyp}}{J_{hyy}+M_h{l}_h^2{cos}^2\left({\psi }_{11}\right)}}& {\displaystyle \frac{K_{hyy}}{J_{hyy}+M_h{l}_h^2{cos}^2\left({\psi }_{11}\right)}}\end{array}\right].\hfill \end{array}$$

(6)

2.2. Broad Learning

When used as a function approximation tool, RBFNN can approximate any continuous function $f(·)$ with arbitrary precision if it has enough nodes. Its expression is as follows:

$$\begin{array}{c}\hfill f\left(Z\right)=W^{\ast T}S\left(Z\right)+\eta ,\end{array}$$

(7)

where $W\in R^n$ and $Z={[z_1,z_2,\cdots ,z_g]}^T$ represent the updated weights and input vector of the NN, and $\left|\right|\eta \left|\right|\le \overline{\eta }$. $S\left(Z\right)=[s_1,\cdots ,s_n]$ is the NN basis function expressed as:

$$\begin{array}{c}\hfill s_i\left(Z\right)=\exp \left[{\displaystyle \frac{-{(Z-{\mu }_i)}^T(Z-{\mu }_i)}{{\iota }_i^2}}\right],i=1,2,\cdots ,m\end{array}$$

(8)

where ${\mu }_i={[{\mu }_{i1},{\mu }_{i2},\cdots ,{\mu }_{iq}]}^T$ denotes the center of the receptive field, and q denotes the dimension of the input space. The parameters ${\iota }_i$ and $m>1$ are defined as the width of the Gaussian function and the number of nodes in the RBFNN, respectively. To improve the generalization ability of NN, the number and range of hidden nodes need to be reasonably planned. To meet this requirement, we designed BLNN based on RBFNN to enhance the generalization ability and performance of NNs. The main difference between BLNN and RBFNN is that it can selectively add incremental nodes based on the new input vector. Given the current n center vectors, $\mu =[{\mu }_1,{\mu }_2,\cdots ,{\mu }_n]$, we first calculate the distance between the input vector and each ${\mu }_i$, and select the $n_1$ closest vectors from $\mu$ to form a matrix called $c=c_1,\cdots ,c_{n_1}\subseteq \mu$. We then define the mean of these $n_1$ vectors as ${\mu }_{avg}={\sum }_{i=1}^{n_1}{c}_i/n_1$ (where $n_1<n$ is a design parameter). The new incremental vector ${\mu }_{new}$ is then generated as follows [9]:

$$\begin{array}{c}\hfill {\mu }_{new}={\mu }_{avg}+a_o(Z-{\mu }_{avg})\end{array}$$

(9)

where $a_o$ is an adjustable parameter. The condition that triggers the addition of an incremental node is formulated as follows:

$$\begin{array}{c}\hfill \mu (t+T)=\left\{\begin{array}{cc}\left[\mu \left(t\right){\mu }_{\mathrm{new}}\right],\hfill & \mathrm{if}\mathrm{dis}(Z,{\mu }_{\mathrm{avg}})>\Theta \hfill \\ \mu \left(t\right),\hfill & \mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(10)

where T denotes the calculation interval, and $c(t+T)$ is the center vector of the BLNN at the subsequent calculation step. $\mathrm{dis}(Z,{\mu }_{\mathrm{avg}})$ stands for the norm distance between Z and ${\mu }_{\mathrm{avg}}$, while $\Theta$ is a threshold. When the trigger condition $\mathrm{dis}(Z,{\mu }_{\mathrm{avg}})>\Theta$ is met, an incremental node is added; otherwise, the center vector remains unchanged. In view of practical real-time performance, a trigonometric expansion method is integrated into the BLNN to mitigate computational overhead by creating corresponding enhancement nodes, which can be formulated as:

$$\begin{array}{c}\hfill P\left(t\right)=[P_1,\cdots ,P_i],i=1,\cdots ,n\end{array}$$

(11)

where $P_i=[cos\left(s_i\left(Z\right)\right),sin\left(s_i\left(Z\right)\right)]$. Subsequently, the hidden layer of the BLNN is defined as $H\left(t\right)=\left[S\right(\Phi \left)\right|P]$. The revised network structure can be outlined as follows:

$$\begin{array}{cc}\hfill S_B(t+T)& =\left[S(\Phi )\right|S_{ex}\left(Z\right)]\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill P_B(t+T)& =\left[P\right|cos\left(S_{ex}\left(Z\right)\right),sin\left(S_{ex}\left(Z\right)\right)]\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill W_B(t+T)& =\left[W\right|W_{ex}]\hfill \end{array}$$

(14)

Here, $S_{ex}$ represents the Gaussian function associated with the new center ${\mu }_{\mathrm{new}}$ of the incremental node, and $W_{ex}$ denotes the weight of $S_{ex}$. Consequently, the output of the BLNN is expressed as

$$\begin{array}{c}\hfill Y\left(Z\right)=\left[S(t+T)\right|P(t+T)]W^T=H\ast W^T\end{array}$$

(15)

2.3. Some Assumptions and Lemmas

Assumption 1

([3]). The nonlinear function $Y\left(\psi \right)$ satisfies $\left|Y\left(\psi \right)\right|\le \overline{Y}$, where $\overline{Y}$ is a positive constant.

Assumption 2

([25]). The system state vector ${\overline{x}}_i$ is measurable and available. Moreover, the desired trajectory ${\psi }_d$ is a function of $t>0$, and ${\psi }_d$, ${\dot{\psi }}_d$, and ${\ddot{\psi }}_d$ are all bounded. Therefore, there exists an unknown constant $\overline{\Lambda }$ such that:

$$\begin{array}{c}\hfill \Lambda :=\{({\psi }_d,{\dot{\psi }}_d,{\ddot{\psi }}_d):\parallel {\psi }_d{\parallel }^2+\parallel {\dot{\psi }}_d{\parallel }^2+\parallel {\ddot{\psi }}_d{\parallel }^2\le \overline{\Lambda }\}\end{array}$$

(16)

Lemma 1

([26]). Considering that the Lyapunov function $V\left(\psi \right)$ is continuous and positive definite, and its initial value $V\left(0\right)$ falls within a limited range, one can infer that $V\left(\psi \right)$ remains bounded and fulfills the conditions below:

$$\begin{array}{c}\hfill \dot{V}\left(\psi \right)\le aV\left(\psi \right)+B\end{array}$$

(17)

where $a>0$ and $B>0$

3. Controller Design

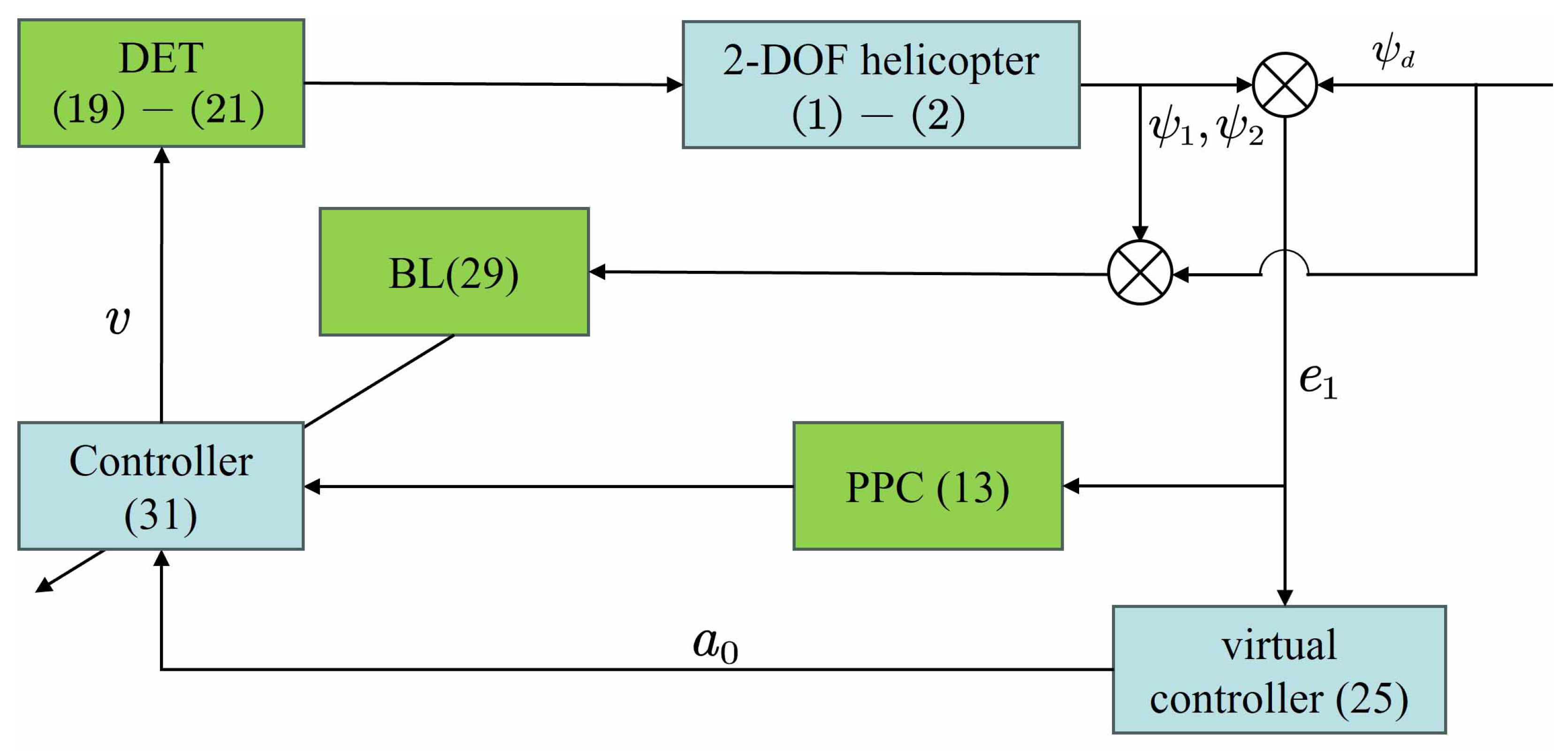
This section first proposes a performance function designed to confine tracking errors within a predefined region throughout the system’s operation. An error transformation method is simultaneously employed to ensure compliance with required tracking specifications. Subsequently, a DET mechanism is introduced to enhance network resource utilization efficiency and minimize communication overhead. Finally, theoretical analysis verifies the stability of the proposed control framework. The system flowchart is illustrated in Figure 2.

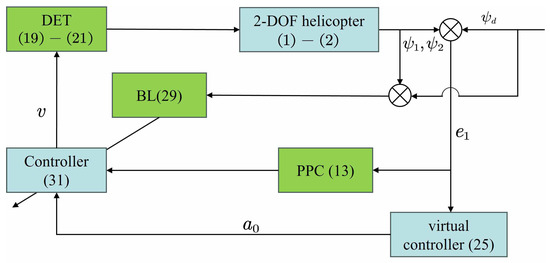
Figure 2. System control solution block diagram.

3.1. Prescribed Performance Function

First, the tracking error of the helicopter system is defined as $e_1={\psi }_1-{\psi }_d$, where $e_1={[e_{11},e_{12}]}^T$ and ${\psi }_d$ denotes the desired trajectory. When the tracking error $e_1$ remains within the specified bounds, the corresponding performance requirements can be effectively satisfied. To ensure that the control performance meets expectations, the following inequality is introduced to constrain the tracking error [27].

$$\begin{array}{c}\hfill {\zeta }_{1i}<e_{1i}<{\zeta }_{2i},\end{array}$$

(18)

where

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\zeta }_{1i}\left(t\right)=-c_{1i}{m}_{1i}{\rho }_{1i}\left(t\right)+(c_{1i}-1){\rho }_{2i}\left(t\right),\hfill \\ {\zeta }_{2i}\left(t\right)=(1-c_{1i})m_{1i}{\rho }_{1i}\left(t\right)+c_{1i}{\rho }_{2i}\left(t\right),i=1,2\hfill \end{array}\right.\end{array}$$

(19)

For Equation (19), the parameters $c_{1i}$ are design variables defined as $c_{1i}=0$ if $e_{1i}\left(0\right)<0$, and $c_{1i}=1$ if $e_{1i}\left(0\right)\ge 0$. The parameter $m_{1i}$ is also a design variable and satisfies the non-negativity condition. ${\rho }_{ji}$ (where $j=1,2$) possesses the properties of strict positivity, monotonic decrease, smoothness, and boundary constraints. In this paper, the selected performance function is an exponential decay function given as follows:

$$\begin{array}{c}\hfill {\rho }_{ji}=({\rho }_{ji}\left(0\right)-{\rho }_{ji}(\infty ))e^{-r_{ji}t}+{\rho }_{ji}(\infty )\end{array}$$

(20)

where ${\rho }_{ji}\left(0\right)$, ${\rho }_{ji}(\infty )$, and $r_{ji}$ are all positive constants, and satisfy ${\rho }_{ji}\left(0\right)>{\rho }_{ji}(\infty )>0$.

3.2. Error Transformation

It is worth noting that satisfying the performance constraints described in Equation (18) is highly challenging. Therefore, a novel error transformation method is proposed in this study to ensure the desired tracking performance is achieved.

$$\begin{array}{c}\hfill {\pi }_i\left(t\right)={\displaystyle \frac{c_0{e}_{1i}\left(t\right)-{\zeta }_{1i}\left(t\right)-{\zeta }_{2i}\left(t\right)}{{\zeta }_{2i}\left(t\right)-{\zeta }_{1i}\left(t\right)}}\end{array}$$

(21)

where $c_0$ is a design parameter.

From Equation (21), it can be inferred that under the constraint $|{\pi }_i\left(t\right)|<1$$(i=1,2)$, the performance boundary defined for the tracking error in (18) remains valid for all $t>0$. This indicates that achieving the PP objectives can be reformulated as the following core task: ensuring that the transformation error ${\pi }_i\left(t\right)$ satisfies the boundary condition $|{\pi }_i\left(t\right)|<1$$(i=1,2)$. This objective can be realized through the appropriate design of the control scheme.

Based on the previous definitions of ${\zeta }_{1i}\left(t\right)$ and ${\zeta }_{2i}\left(t\right)$, it can be directly concluded that ${\zeta }_{2i}-{\zeta }_{1i}>0$. Furthermore, by combining this with Equation (21), the time derivative of the transformation error $\pi$ can be expressed as:

$$\begin{array}{c}\hfill {\dot{\pi }}_i\left(t\right)={\displaystyle \frac{c_0{\dot{e}}_{1i}\left(t\right)}{{\zeta }_{2i}\left(t\right)-{\zeta }_{1i}\left(t\right)}}+{\displaystyle \frac{-c_0({\dot{\zeta }}_{2i}\left(t\right)-{\dot{\zeta }}_{1i}\left(t\right))e_{1i}\left(t\right)}{{({\zeta }_{2i}\left(t\right)-{\zeta }_{1i}\left(t\right))}^2}}+{\displaystyle \frac{c_0({\zeta }_{1i}\left(t\right){\dot{\zeta }}_{2i}\left(t\right)-{\zeta }_{2i}\left(t\right){\dot{\zeta }}_{1i}\left(t\right))}{{({\zeta }_{2i}\left(t\right)-{\zeta }_{1i}\left(t\right))}^2}}.\end{array}$$

(22)

We define $\pi ={[{\pi }_1,{\pi }_2]}^T$, so (22) can be rewritten as

$$\begin{array}{c}\hfill \dot{\pi }=R_1{\dot{e}}_1+R_2{e}_1+R_3\end{array}$$

(23)

where $R_1=diag\{{\displaystyle \frac{c_0}{{\zeta }_{21}-{\zeta }_{11}}},{\displaystyle \frac{c_0}{{\zeta }_{22}-{\zeta }_{12}}}\}$, $R_2=diag\{{\displaystyle \frac{c_0({\dot{\zeta }}_{21}\left(t\right)-{\dot{\zeta }}_{11}\left(t\right))}{{({\zeta }_{21}-{\zeta }_{11})}^2}},{\displaystyle \frac{-c_0({\dot{\zeta }}_{22}\left(t\right)-{\dot{\zeta }}_{12}\left(t\right))}{({\zeta }_{22}-{\zeta }_{12}^2)}}\}$, and $R_3=[{\displaystyle \frac{c_0({\zeta }_{11}\left(t\right){\dot{\zeta }}_{21}\left(t\right)-{\zeta }_{21}\left(t\right){\dot{\zeta }}_{11}\left(t\right))}{{({\zeta }_{21}\left(t\right)-{\zeta }_{11}\left(t\right))}^2}},{\displaystyle \frac{c_0({\zeta }_{12}\left(t\right){\dot{\zeta }}_{22}\left(t\right)-{\zeta }_{22}\left(t\right){\dot{\zeta }}_{12}\left(t\right))}{{({\zeta }_{22}\left(t\right)-{\zeta }_{12}\left(t\right))}^2}}]$.

3.3. Dynamic Event-Triggered

In practical network systems, communication channel bandwidth is typically subject to strict limitations, and multicast communication among multiple nodes often requires sharing the same channel. This directly results in bandwidth contention among system nodes. Given this situation, improving the resource utilization efficiency of networked control systems has significant theoretical and engineering importance. Inspired by earlier studies, ET control has gradually emerged as an effective approach to reduce network load in NCSs due to its non-periodic communication nature. To this end, a DET strategy is developed in this section, incorporating an external auxiliary variable, and is mathematically described as follows [28]:

$$\begin{array}{cc}\hfill v_i\left(t\right)& ={\widehat{v}}_i\left(t_{\kappa }\right),\forall t\in [t_{\kappa },t_{\kappa +1}),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill t_{\kappa +1}& =sup\left\{t>t_{\kappa }\mid \theta \left(\parallel {\Delta }_v{\parallel }^2-\sigma \sum _{i=1}^2{k}_i{e}_{1i}^2\right)\le \eta \right\},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\dot{\eta }}_i& =-m\eta +\chi \left(\sigma \sum _{i=1}^2{k}_i{e}_{1i}^2-{\parallel {\Delta }_v\parallel }^2\right),\hfill \end{array}$$

(26)

where ${\Delta }_v={[{\Delta }_{v1},{\Delta }_{v2}]}^T$. For any $\kappa \in \mathbb{Z}+$, the parameters $k_i>0$, $\theta >0$, $m>0$, $\sigma \in (0,1)$, and $\chi \in (0,1]$ are all positive definite constants. Here, $\Delta vi=v_i-\widehat{v}i$ denotes the control signal deviation caused by the ETM, and $t\kappa$ represents the controller update time, with the initial time $t_0=0$. Specifically, when the triggering condition in Equation (25) is satisfied, the current time is marked as $t_{\kappa +1}$, and the control input $v_i$ is updated to $\widehat{v}i\left(t\kappa +1\right)$. During the interval $t\in [t_{\kappa },t_{\kappa +1})$, the control signal remains unchanged, i.e., $v_i\left(t\right)={\widehat{v}}_i$.

3.4. Design of DET Adaptive BLNN Controller

The second error is defined as:

$$\begin{array}{c}\hfill e_2={\psi }_2-a_0\end{array}$$

(27)

where $a_0$ is a virtual controller.

The Lyapunov candidate function is selected as

$$\begin{array}{c}\hfill V_1={\displaystyle \frac{1}{2}}{\pi }_1^T{\pi }_1\end{array}$$

(28)

Substitute (28) into the time derivative of $V_1$ to yield

$$\begin{array}{c}\hfill {\dot{V}}_1={\pi }^T(R_1(e_2+a_0-{\psi }_d)+R_2{e}_1+R_3)\end{array}$$

(29)

We define $a_0$ as

$$\begin{array}{c}\hfill a_0=R_1^{-1}(-q_1\pi -R_2{e}_1-R_3)+{\dot{\psi }}_d\end{array}$$

(30)

where $q_1\in R^{2\times 2}$ is the design parameter.

Substituting (30) into (29) yields

$$\begin{array}{c}\hfill {\dot{V}}_1=-{\pi }^T{q}_1\pi +{\pi }^T{R}_1{e}_2\end{array}$$

(31)

Directly computing the multivariable error term $a_0$ is the main source of increased computational complexity and burden. To address this problem, a first-order filter $\omega$ is introduced in this paper to process $a_0$, thereby optimizing the subsequent controller design and reducing computational cost. The expression of the filter is given as follows:

$$\begin{array}{c}\hfill \tau \dot{\omega }+\omega =a_0,\omega \left(0\right)=a_0\left(0\right)\end{array}$$

(32)

where $\tau$ is the time constant of this first-order filter. By defining the error variable $p=\omega -a_0$, substituting into (32) and (30), we derive

$$\begin{array}{cc}\hfill \dot{p}=& =\dot{\omega }-{\dot{a}}_0\hfill \\ \hfill & =-{\displaystyle \frac{p}{\tau }}+\left(-{\displaystyle \frac{\partial a_0}{\partial R_1}}{\dot{R}}_1-{\displaystyle \frac{\partial a_0}{\partial e_1}}{\dot{e}}_1-{\displaystyle \frac{\partial a_0}{\partial \pi }}\dot{\theta }-{\displaystyle \frac{\partial a_0}{\partial R_2}}{\dot{R}}_2\right.\hfill \\ \hfill & \left.-{\displaystyle \frac{\partial a_0}{\partial R_3}}{\dot{R}}_3-{\displaystyle \frac{\partial a_0}{\partial {\psi }_d}}{\dot{\psi }}_d\right)\hfill \\ \hfill & =-{\displaystyle \frac{p}{\tau }}+Q(R_1,e_1,\pi ,R_2,R_3,{\psi }_d),\hfill \end{array}$$

(33)

where $Q(R_1,e_1,\pi ,R_2,R_3,{\psi }_d)$ indicates a vector of continuous functions defined on the compact set $B=(R_1,e_1,\pi ,R_2,R_3,{\psi }_d)$. Given the initial state conditions, the fundamental properties of compact sets imply that Q attains a maximum value $\overline{Q}$ on $B(·)$, satisfying $\left|Q\right|\le \overline{Q}$.

To design a reliable and efficient controller, it is first necessary to address the uncertainty associated with the unknown smooth nonlinear function $\Delta X$ in Equation (4). To this end, a BLNN is introduced in this paper as an estimator to approximate $\Delta X$.

$$\begin{array}{c}\hfill \Delta X=W_b^{\ast }{S}_b\left(L\right)+\iota \left(L\right)\end{array}$$

(34)

where the BLNN input vector L is defined as $L={[{\psi }_1^T,{\psi }_2^T,{\psi }_d^T,{\dot{\psi }}_d^T]}^T$. The term $\iota$ denotes the approximation error, which is bounded. Specifically, $\iota \left(L\right)$ represents the approximation error associated with L, and there exists a constant ${\iota }^{\ast }>0$ such that the inequality $\parallel \iota \left(L\right)\parallel \le {\iota }^{\ast }$ holds, where ${\iota }^{\ast }$ is a sufficiently small positive constant.

According to the above equation, the second error variable’s time derivative is

$$\begin{array}{cc}\hfill {\dot{e}}_2& =X\left(\psi \right)+\Delta X\left(\psi \right)+Y\left(\psi \right)v-{\dot{a}}_0\hfill \\ \hfill & =X\left(\psi \right)+W_b^{\ast }{S}_b\left(L\right)+\iota \left(L\right)+Y\left(\psi \right)(\widehat{v}+{\Delta }_v)-{\dot{a}}_0\hfill \end{array}$$

(35)

Therefore, a DET adaptive broad learning controller is designed as

$$\begin{array}{c}\hfill \widehat{v}=Y^{-1}(-X-{\widehat{W}}_b^T{S}_b\left(L\right)-R_1\pi -q_2{e}_2+\dot{\omega })\end{array}$$

(36)

where $q_2\in R^{2\times 2}$ indicates the design parameter.

Next, we present the weight update law for BLNN as follows

$$\begin{array}{c}\hfill {\dot{\widehat{W}}}_b={\Gamma }_b(S_b\left(L\right)e_2^T-\epsilon {\widehat{W}}_b)\end{array}$$

(37)

where ${\Gamma }_b={\Gamma }_b^T$ is a positive definite diagonal matrix, and $\epsilon$ represents a positive constant.

Theorem 1.

Consider the helicopter systems (1) and (2), the adaptive broad–learning controller (36) with the update law (37), and the dynamic event–triggered (DET) mechanism (24)–(26). If design parameters are selected appropriately, the following can be ensured: (1) all signals of the closed–loop system are bounded; (2) the tracking error strictly satisfies the prescribed–performance constraint specified in (18) for all $t\ge 0$; and (3) the Zeno behavior is avoided, and equivalently, there exists a strictly positive lower bound on the inter–event times.

Proof. 

Consider the following second Lyapunov candidate function:

$$\begin{array}{c}\hfill V_2=V_1+{\displaystyle \frac{1}{2}}{e}_2^T{e}_2+{\displaystyle \frac{1}{2}}\mathrm{tr}\left\{{\tilde{W}}_b^T{\Gamma }_b^{-1}{\tilde{W}}_b\right\}+{\displaystyle \frac{1}{2}}{p}^{T}p\end{array}$$

(38)

Substituting (31), (33), and (35)–(37) into the time derivative of $V_2$, we derive

$$\begin{array}{cc}\hfill {\dot{V}}_2& =-{\pi }^T{q}_1\pi +{\pi }^T{R}_1{e}_2+e_2^T(X\left(\psi \right)+W_b^{\ast }{S}_b\left(L\right)+\iota \left(L\right)+Y\left(\psi \right)\left(Y^{-1}\right(-X\left(\psi \right)-{\widehat{W}}_b^T{S}_b\left(L\right)\hfill \\ & -R_1\pi -q_2{e}_2+\dot{\omega }\left)\right)+Y\left(\psi \right){\Delta }_v-{\dot{a}}_0)+\mathrm{tr}\left\{{\tilde{W}}_b^T(S_b\left(L\right)e_2^T-\epsilon {\widehat{W}}_b)\right\}+p^T(-{\displaystyle \frac{p}{\tau }}+Q)\hfill \\ \hfill & =-{\pi }^T{q}_1\pi -e_2^T{q}_2{e}_2-e_2^T{\tilde{W}}_b{S}_b\left(L\right)-{\displaystyle \frac{1}{2}}{e}_2^T{e}_2+{\displaystyle \frac{1}{2}}{{\iota }^{\ast }}^2+e_2^{T}Y{\Delta }_v-e_2^T{\displaystyle \frac{p}{\tau }}+e_2^{T}Q\hfill \\ & +\mathrm{tr}\left\{{\tilde{W}}_b{S}_b\left(L\right)e_2^T\right\}-\epsilon \mathrm{tr}\left\{{\tilde{W}}_b{\widehat{W}}_b\right\}-{\displaystyle \frac{p^{T}p}{\tau }}+p^{T}Q\hfill \end{array}$$

(39)

where $e_2^T\iota \left(L\right)\le -{\displaystyle \frac{1}{2}}{e}_2^T{e}_2+{\displaystyle \frac{1}{2}}{{\iota }^{\ast }}^2$.

According to Young’s inequality, we get

$$\begin{array}{cc}\hfill -\mathrm{tr}\left\{{\tilde{W}}_b{\widehat{W}}_b\right\}& \le -{\displaystyle \frac{1}{2}}\parallel {\tilde{W}}_b{\parallel }_F^2+{\displaystyle \frac{1}{2}}{\parallel {\tilde{W}}^{\ast }\parallel }_F^2,\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill -e_2^T{\displaystyle \frac{p}{\tau }}& \le -{\displaystyle \frac{1}{2\tau }}{e}_2^T{e}_2+{\displaystyle \frac{1}{2\tau }}{p}^{T}p,\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill e_2^{T}Q& \le {\displaystyle \frac{1}{2}}{e}_2^T{e}_2+{\displaystyle \frac{1}{2}}\overline{Q},\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill p^{T}Q& \le {\displaystyle \frac{1}{2}}{p}^{T}p+{\displaystyle \frac{1}{2}}\overline{Q},\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill e_2^{T}Y{\Delta }_v& \le {\displaystyle \frac{1}{2}}{e}_2^T{e}_2+{\displaystyle \frac{{\overline{Y}}^2}{2}}{\parallel {\Delta }_v\parallel }^2\hfill \end{array}$$

(44)

Substitute (40) through (44) into (39) to yield

$$\begin{array}{cc}\hfill {\dot{V}}_2& =-{\pi }^T{q}_1\pi -e_2^T(q_2+({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2\tau }}))e_2-{\displaystyle \frac{\epsilon }{2}}\parallel {\tilde{W}}_b{\parallel }_F^2-({\displaystyle \frac{1}{2\tau }}-{\displaystyle \frac{1}{2}})p^{T}p+{\displaystyle \frac{1}{2}}{{\iota }^{\ast }}^2+{\displaystyle \frac{\epsilon }{2}}{\parallel {\tilde{W}}^{\ast }\parallel }_F^2\hfill \\ & +\overline{Q}+{\displaystyle \frac{{\overline{Y}}^2}{2}}{\parallel {\Delta }_v\parallel }^2\hfill \\ & \le -c_o{V}_2+B_o\hfill \end{array}$$

(45)

where

$$\begin{array}{c}\hfill c_o=min\{2\left(q_1\right),2(q_2+({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2\tau }})),{\displaystyle \frac{2\epsilon }{{\lambda }_{max}\left({\Gamma }_b^{-1}\right)}},2({\displaystyle \frac{1}{2\tau }}-{\displaystyle \frac{1}{2}})\}\end{array}$$

(46)

and

$$\begin{array}{c}\hfill B_o={\displaystyle \frac{1}{2}}{{\iota }^{\ast }}^2+{\displaystyle \frac{\epsilon }{2}}\parallel {\tilde{W}}^{\ast }{\parallel }_F^2+\overline{Q}+{\displaystyle \frac{{\overline{Y}}^2}{2}}{\parallel {\Delta }_v\parallel }^2\end{array}$$

(47)

To guarantee the stability of the closed-loop system, the parameters $q_1$, $q_2$, and $\tau$ must satisfy the following conditions:

$$\begin{array}{c}\hfill 2\left(q_1\right)>0,2(q_2+({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2\tau }}))>0,2({\displaystyle \frac{1}{2\tau }}-{\displaystyle \frac{1}{2}})>0\end{array}$$

(48)

Based on the analysis of Equation (45), the boundedness of the parameters $\pi$, $e_2$, W, and p is ensured. Furthermore, by continuing the application and derivation of (45), we obtain:

$$\begin{array}{c}\hfill 0\le V_2\le {\displaystyle \frac{B_o}{c_o}}+\left[V_2\left(0\right)-{\displaystyle \frac{B_o}{c_o}}\right]e^{-c_{o}t}.\end{array}$$

(49)

First, by invoking Equation (49), we compute the limit ${lim}_{t\to \infty }{V}_2={\displaystyle \frac{B_o}{c_o}}$, which mathematically confirms the boundedness of the Lyapunov function $V_2$. Second, based on the key assumption that $V_2$ is bounded, it can be inferred that the transformation error $\pi$, the tracking error $e_2$, and the BLNN weight approximation error $\tilde{W}$ in the system are all bounded. Finally, given the boundedness of $\pi$, analysis of Equation (21) reveals that the dynamic behavior of the tracking error $e_1$, as defined by Equation (18), remains strictly within the PP bounds.

Furthermore, this paper demonstrates that the proposed DET mechanism can effectively circumvent the Zeno paradox. Within the interval $[t_{\kappa },t_{\kappa +1})$ defined by two consecutive ET times $t_{\kappa }$ and $t_{\kappa +1}$, the control variable v remains constant. From the definition ${\Delta }_{vi}=v_i-{\widehat{v}}_i$, it follows that ${\dot{\Delta }}_{vi}=-{\dot{\widehat{v}}}_i$. Within this interval, $|{\Delta }_{vi}|$ starts at zero and may return to zero multiple times. Let $\overline{t}$ denote the time of the last zero crossing of $|{\Delta }_{vi}|$, satisfying $t_{\kappa }\le \overline{t}<t_{\kappa +1}$. Furthermore, within the time interval $(\overline{t},t_{\kappa +1})$, $|{\Delta }_{vi}|$ remains strictly positive. Based on this, the derivative of $|{\Delta }_{vi}|$ within this interval can be computed as follows:

$$\begin{array}{c}\hfill {\displaystyle \frac{d|{\Delta }_{vi}|}{dt}}={\displaystyle \frac{d\sqrt{{\Delta }_{vi}^2}}{dt}}={\displaystyle \frac{{\Delta }_{vi}\dot{{\Delta }_{vi}}}{|{\Delta }_{vi}|}}\le {\displaystyle \frac{|{\Delta }_{vi}\left|\right|\dot{{\Delta }_{vi}}|}{|{\Delta }_{vi}|}}=\left|{\dot{\widehat{v}}}_i\right|.\end{array}$$

(50)

Since all variables $\dot{u}$ are bounded, it follows that $\dot{\widehat{u}}$ is also bounded. Thus, there exists a positive constant $\kappa$ such that ${\displaystyle \frac{d}{dt}}|{\Delta }_{vi}|\le |{\dot{\widehat{v}}}_i|\le \kappa$. Combining the condition ${\Delta }_{vi}\left(\overline{t}\right)=0$ with the fact that ${\Delta }_{vi}\left(t\right)\in L_{\infty }$, there exists a positive constant l such that $t_{\kappa +1}-t_{\kappa }\ge t_{\kappa +1}-\overline{t}\ge {\displaystyle \frac{l}{\kappa }}$, thereby ruling out the Zeno phenomenon. □

Remark 1.

From the control objective of this study, it is required that the tracking error $e_1$ of the 2-DOF helicopter strictly satisfy the PP bounds and converge to a small neighborhood of zero. During the control process, if the PPC parameters ${\rho }_{\theta 0},{\rho }_{\psi 0}$ or the adaptive gains ${\Gamma }_b$ is chosen excessively large, the transient response may become oscillatory or even unstable. Therefore, smaller initial bounds ${\rho }_{1i}\left(0\right),{\rho }_{2i}\left(0\right)$ and appropriate steady-state limits ${\rho }_{1i}(\infty ),{\rho }_{2i}(\infty )$ should be selected. Meanwhile, the control gains $q_1,q_2$, the learning rates ${\Gamma }_b$ and the event-triggering parameters $k_i$, θ, and σ, and m should be carefully tuned to satisfy the stability inequalities derived in Theorem 1 and Equations (45)–(49). In practice, the tuning procedure is as follows. First, choose suitable PPC parameters ${\rho }_{ji}\left(0\right),{\rho }_{ji}(\infty ),r_{ji}$ to determine the desired transient speed and steady-state accuracy. Next, select the adaptive gains ${\Gamma }_b$ to guarantee adequate learning capability of the BL network while avoiding over-adaptation. Then, determine the DET parameters $k_i$, θ, and σ, and m to balance tracking performance and communication frequency.

Remark 2.

Unlike [3,11], the proposed DET strategy not only significantly reduces the communication computational load and improves closed-loop stability and hardware reliability, but also outperforms the relative threshold ETM. The relative threshold ETM is also a static triggering mechanism. Its core concept is to design trigger conditions in the form of inequalities and continuously monitor them, updating and transmitting the signal only when the trigger conditions are violated. However, it should be noted that due to the existence of this mechanism, redundant terms are inevitably included in the stability analysis, and the designed controller cannot compensate for this. Therefore, even if the system adopts a parameterized uncertain system form, it can only guarantee the final global boundedness result, not the asymptotic tracking result. The advantages of the dynamic event triggering (DET) proposed in this paper over the static ETM with relative thresholds are as follows: the threshold $\eta \left(t\right)$ is adaptively driven by the error term $\sum k_e{e}_i^2$ and the input variation ${\parallel \Delta v\parallel }^2$. It is automatically “relaxed” and updated in a timely manner during fast-changing phases and “tightened” during steady-state phases to suppress redundant transmissions, significantly reducing the average trigger rate while converging. Furthermore, the first-order filtering and bleeding term of $\dot{\eta }=-m\eta +\chi (·)$ provides a strict minimum event interval, suppresses noise-induced chattering, and eliminates Zeno. This reduces the conservative redundancy introduced by static triggering in Lyapunov analysis, thereby achieving higher event efficiency and more robust closed-loop performance.

4. Simulation Experiment Validation

This section demonstrates the performance of the proposed DET-based adaptive BLNN scheme through simulation studies, followed by a comprehensive analysis of the obtained results. The parameter settings of the 2-DOF helicopter model employed in the simulations are listed in Table 1.

Table 1. System Parameters [24].

Symbol	Value	Unit
$J_{hpp}$	0.0215	kg · m2
$J_{hyy}$	0.0237	kg · m2
$M_h$	1.0750	kg
$D_{hpp}$	0.0071	N/V
$D_{hyy}$	0.0220	N/V
$l_h$	0.002	m
$K_{hpp}$	0.022	N·m/V
$K_{hpy}$	0.0221	N·m/V
$K_{hyp}$	−0.0227	N·m/V
$K_{hyy}$	0.0022	N·m/V
$g_h$	9.8	m/s2

The helicopter is assigned an initial state of ${\psi }_1\left(0\right)={[0.05,0]}^T$ and a desired trajectory defined as ${\psi }_d={[\pi sin\left(t\right)/10,\pi cos\left(t\right)/15]}^T$. The PPF are set as follows: $m_{1i}=0.1$, ${\rho }_{1i}\left(0\right)=2$, ${\rho }_{2i}\left(0\right)=0.09$, ${\rho }_{1i}(\infty )=0.05$, ${\rho }_{2i}(\infty )=0.05$, $r_{1i}=0.5$, and $r_{2i}=0.3$, for $i=1,2$. The DET parameters are chosen as: $\theta =0.1$, $k_1=k_2=1$, $\chi =0.01$, and $\sigma =0.1$.

In the control algorithm design, the initial parameter settings of the Gaussian RBFNN and the BLNN are related. The former contains $\iota$ nodes, the radial basis function variance $\iota =1$, and the center vector is $\mu =[-1,-0.5,0,0.5,1]$. The latter also has an initial number of nodes set to 5, the weights initialized to 0, and the variance and initial center parameters completely follow the RBFNN configuration. In addition, the weight matrix $a_o$ in (9) is fixed to $0.7$, and its initial weight is 0; the threshold design refers to the size range of the input vector $n_1=2$.

4.1. DET-ABLNN

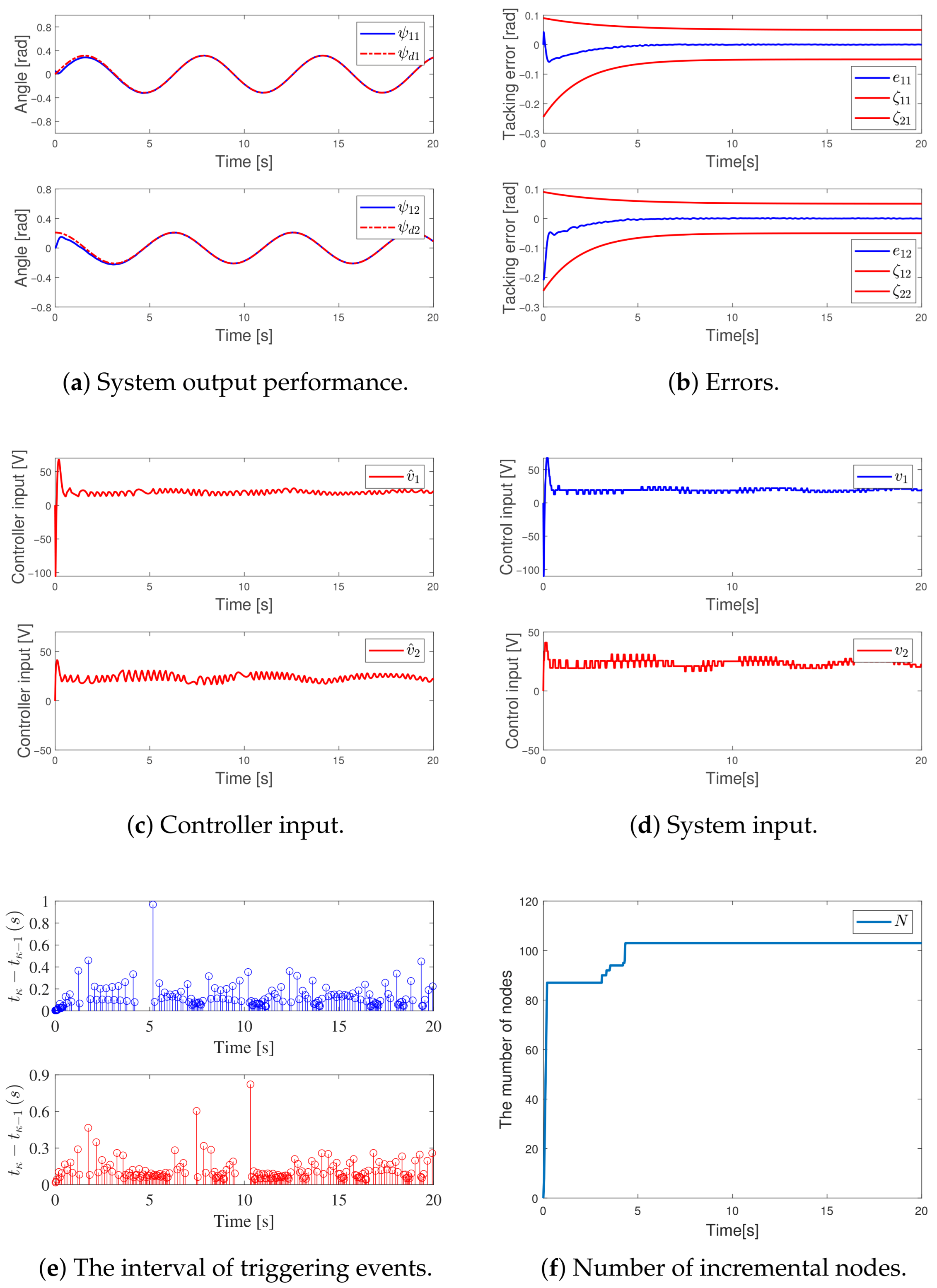
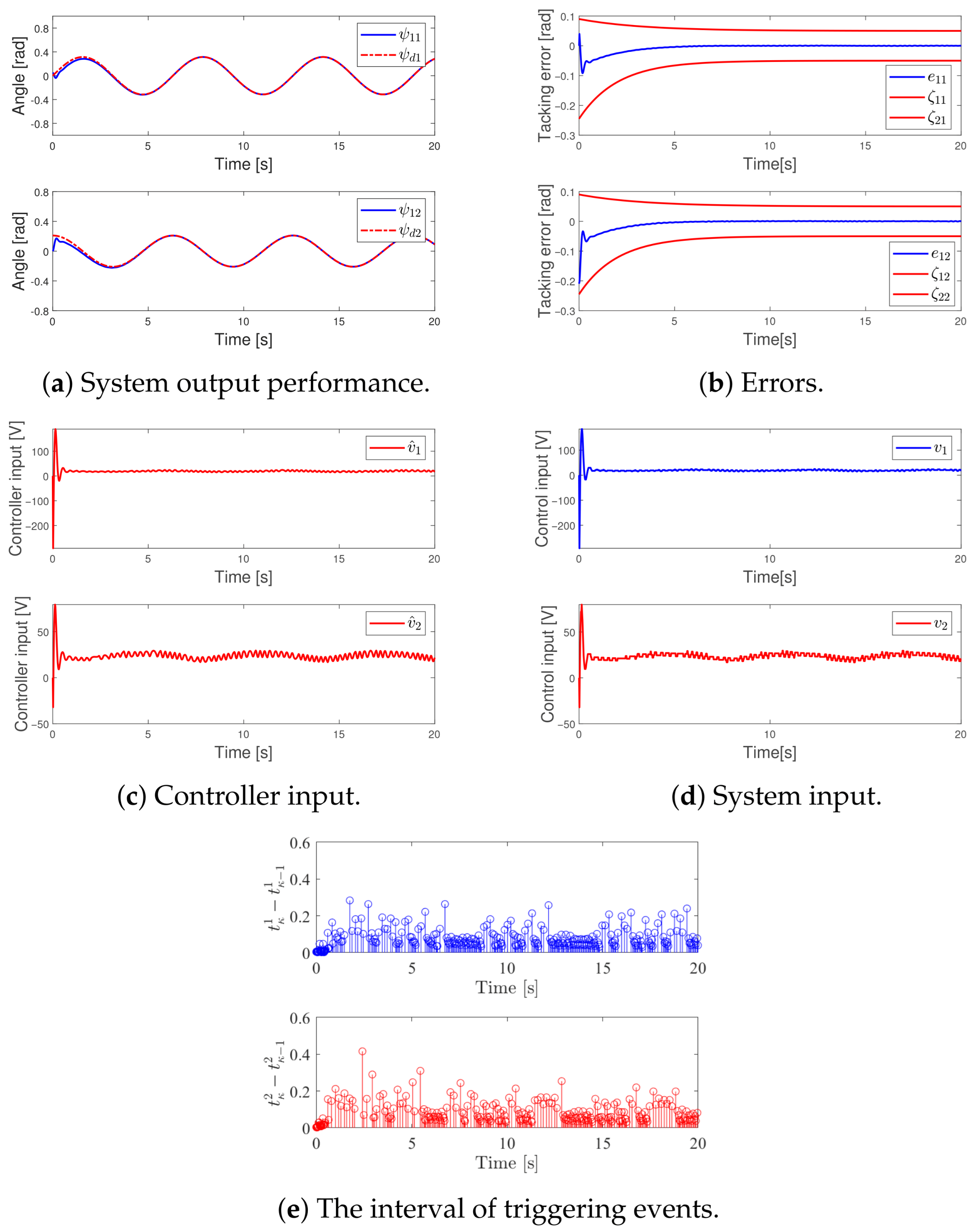
The system output is capable of accurately following the reference trajectory, with the tracking error initially exhibiting a large deviation that gradually diminishes under the regulation of the PPC, eventually approaching zero. These behaviors are illustrated in Figure 3a,b, which depict the tracking response and the evolution of the tracking error, respectively. Throughout the process, the error consistently remains within the PP bounds. Figure 3c,d depict the dynamic variations of the controller output and the control input, respectively. Figure 3e presents the triggering interval characteristics of the controller. In this simulation, the controller was triggered 173 and 175 times, respectively, with a minimum sampling interval of 0.002 s. Figure 3f shows the incremental growth in the number of nodes in the BLNN. Based on these simulation results, the proposed control strategy effectively achieves the system control objectives and demonstrates strong performance.

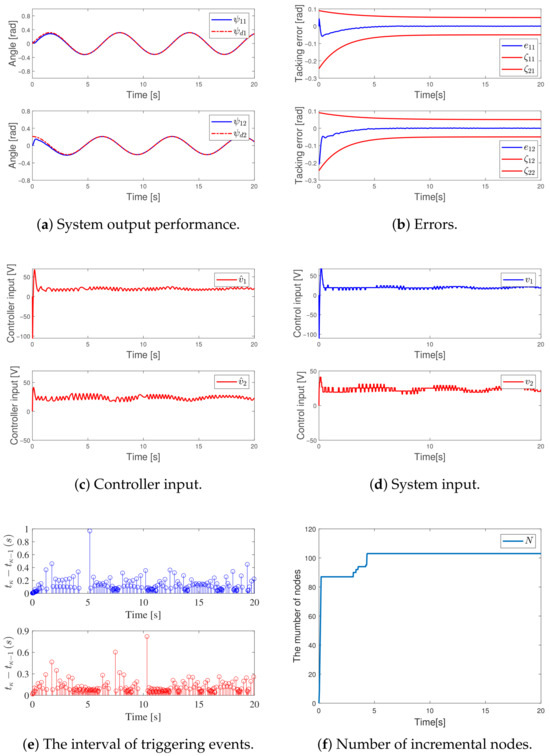
Figure 3. The control performance of DET- adaptive BLNN.

4.2. Compared with Adaptive NN Control Based on PPC

In this section, to further validate the reliability of the control strategy proposed in this study, a comparison is conducted with the PPC scheme from [29]. The key advantage of the proposed method lies in its ability to keep the system tracking error within the predefined permissible range throughout the entire process, using a constraint mechanism based on PP boundaries. This comparison provides additional evidence supporting the reliability of the proposed control approach.

$$\begin{array}{c}\hfill c_{1i}{\xi }_i<e_{1i}<c_{2i}{\xi }_i,i=1,2\end{array}$$

(51)

where $c_{1i}>0$ and $c_{2i}>0$ denote the performance constants. Additionally, the performance function is selected as: ${\xi }_i\left(t\right)=({\xi }_i\left(o\right)-{\xi }_i(\infty ))e^{-r_{i}t}+{\xi }_i(\infty )$, $i=1,2$.

For the aforementioned performance function, the selected parameters are as follows: ${\xi }_i\left(0\right)=0.3$, ${\xi }_i(\infty )=0.05$, $r_i=0.5$, $c_{1i}=-0.97$, and $c_{2i}=0.97$. All other parameters are kept consistent with those used in the DET-adaptive BLNN algorithm.

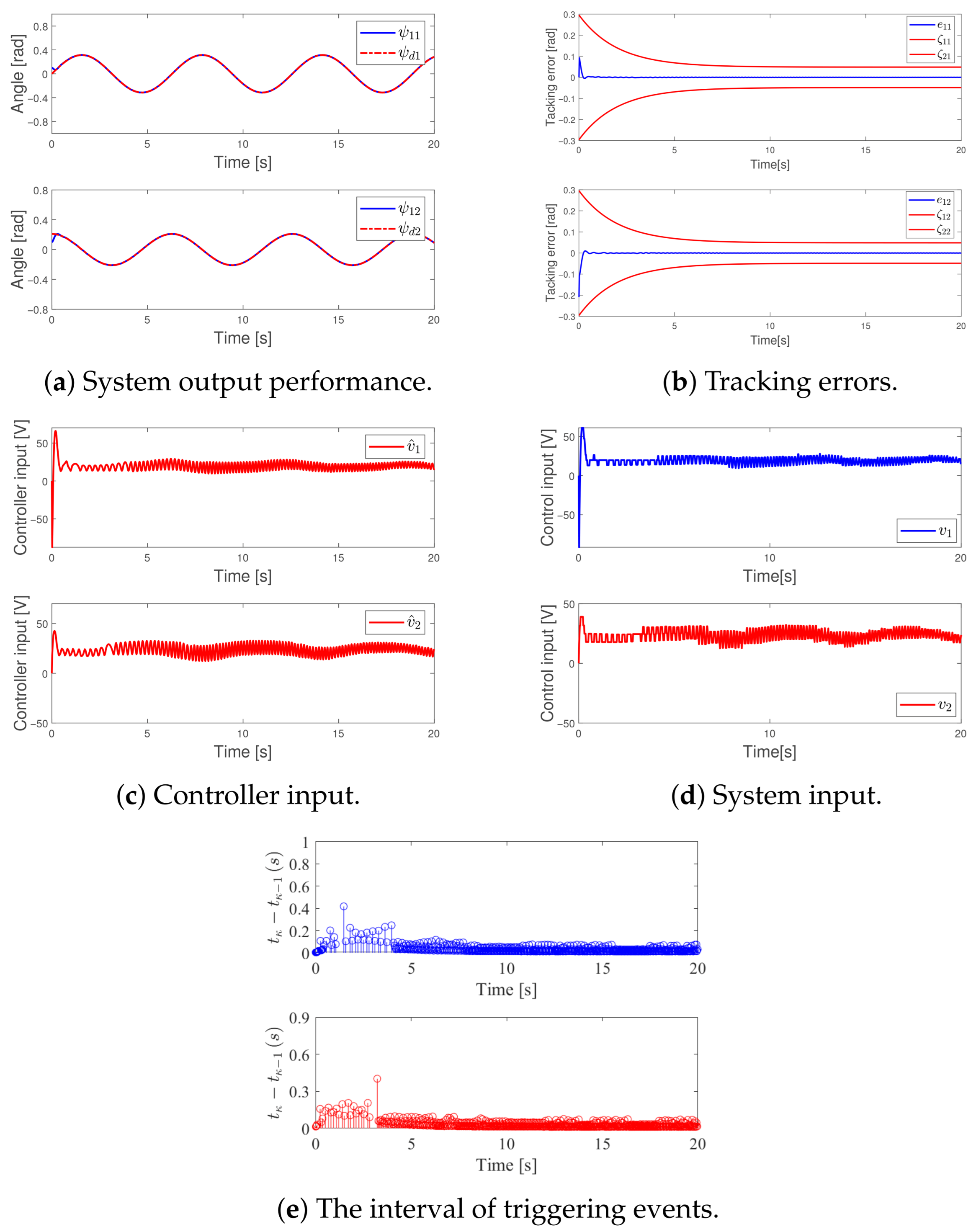
Figure 4a depicts the system output’s dynamic characteristics, whereas Figure 4b demonstrates the progression of the tracking error. Meanwhile, Figure 4c,d illustrate the changes in the controller signal and the corresponding input response behavior, respectively. Figure 4e depicts the temporal distribution of trigger events, with a total of 631 and 632 occurrences, respectively.

Figure 4. The control performance of the adaptive NN control based on PPC.

Compared to the DET-adaptive BLNN algorithm proposed in this study, although the tracking error in that research also remains within the specified performance range, the controller input and system input exhibit poorer performance. The resulting fluctuations can easily lead to system instability.

4.3. Comparing Different ETM

To verify the superiority of the proposed DET, we compared our algorithm with the relative threshold ETM [11]. Figure 5a shows the tracking response of the system output. Figure 5b shows the tracking error of the system. Figure 5c,d represent the controller input and control input of the system, respectively. Figure 5e shows the trigger interval of the controller, where the number of controller triggers is 328 and 265, respectively.

Figure 5. The control performance based on ETM adaptive NN control [11].

To intuitively evaluate the tracking performance in the two scenarios, we selected tracking error, input control, and event triggering as key metrics for quantitative comparison. The results are detailed in Table 2. A total of 100 data samples were collected over a 0–20 s experimental period. The data in Table 2 shows that compared to the comparison scenario, the proposed control strategy performs better in tracking accuracy and control efficiency, while also resulting in fewer event triggerings. This demonstrates that the proposed strategy not only offers enhanced robustness and stability, but also effectively alleviates system communication pressure and provides reliable protection for system components.

Table 2. Comparison of performance and number of events.

Comparative Performance	DET-ABLNN	Comparing Different ETM
${\sum }_{t=1}^{1000}{\left[e_{11}\left(t\right)\right]}^2$	0.00032	0.00075
${\sum }_{t=1}^{1000}{\left[e_{12}\left(t\right)\right]}^2$	0.00634	0.0092
${\displaystyle \frac{|{\sum }_{t=1}^{1000}\left[v_1\left(t\right)\right]|}{1000}}$	322.104	654.023
${\displaystyle \frac{|{\sum }_{t=1}^{1000}\left[v_2\left(t\right)\right]|}{1000}}$	567.885	682.769
Interval of triggering events	173 and 175	328 and 265

5. Conclusions

In this study, a DET adaptive BL algorithm based on PP was proposed to address communication constraints, performance limitations, and system uncertainties in 2-DOF helicopter systems. The system’s uncertainties were estimated using a BLNN. In addition, a novel error transformation strategy was designed to ensure that the tracking error remained within predefined performance bounds. Subsequently, a dynamic threshold strategy incorporating external auxiliary variables was introduced as the triggering mechanism. This approach not only reduced communication overhead but also effectively avoided the occurrence of the Zeno phenomenon. Theoretical analysis demonstrated that all signals within the closed-loop framework remain bounded when governed by the proposed control method. Finally, by comparing the simulation results with those reported in [11], it can be seen that the sum of squared tracking errors and the average control-input amplitude are smaller in this study. This indicates that our control strategy offers significant advantages in tracking accuracy and control efficiency, and remains within the PPF boundaries throughout. Furthermore, the number of event triggers is low, with only 173 and 175 triggers (for the two channels), thereby reducing communication and execution burden while ensuring convergence and robustness. In summary, this study strikes a balance among meeting the specified performance, reducing communication overhead, and improving closed-loop robustness.