Qualitative Analysis of Delay Stochastic Systems with Generalized Memory Effects

Abstract

Fractional stochastic differential equations (FSDEs) are powerful tools for modeling real-world phenomena, as they incorporate both memory effects and stochastic noise. A central focus in their analysis is establishing the well-posedness and regularity of solutions. Moreover, the averaging principle offers a systematic approach to simplify complex dynamical systems by approximating their behavior through time-averaged models. In this paper, we develop a theoretical framework for a class of FSDEs involving the Hilfer–Katugampola derivative. Our main contributions include proving the well-posedness and regularity of solutions, establishing a generalized averaging principle, and demonstrating real-life applications solved via the Euler–Maruyama method. All numerical simulations were conducted using the Python programming language (version 3.11). These results are formulated for the $\tilde{\mathcal{P}}$th moment, providing a unified analysis that extends existing findings.

1. Introduction

The literature includes discussions on various types of fractional operators [1,2,3,4,5]. In recent years, many researchers have adopted the Hilfer–Katugampola fractional derivative (HKFD) in their work, as it serves as an interpolation between several fractional operators, including the Riemann–Liouville (R-L), Caputo, Hadamard, Hilfer, Caputo–Hadamard, Hilfer–Hadamard, Weyl, and Liouville derivatives. The authors in [6] established the existence and uniqueness (Ex-Un) of a fractional model involving the HKFD. In [7], several theoretical results were derived for fractional-order systems involving the HKFD. The study in [8] presented important findings concerning solutions to fractional-order models with the HKFD. The authors of [9] derived solutions for the fractional radial diffusion model with respect to the HKFD. Additionally, in [10], the authors obtained solutions to space-time fractional models using the Mellin transform.

Before introducing the HKFD, we first need to define the Katugampola fractional integral and derivative. The Katugampola fractional integral of order $0<\vartheta <1$ and $\kappa >0$ for the function ℷ is given as follows [11]:

$${}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }\gimel \left(\mathfrak{b}\right)={\displaystyle \frac{{\kappa }^{1-\vartheta }}{\Gamma \left(\vartheta \right)}}{\int }_{\mathrm{u}}^{\mathfrak{b}}{\mathfrak{c}}^{\kappa -1}{\left({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa }\right)}^{\vartheta -1}\gimel \left(\mathfrak{c}\right)\mathrm{d}\mathfrak{c}.$$

(1)

The Katugampola fractional derivative is given as follows [11]:

$$\begin{array}{c}\hfill {}^{\kappa }\mathcal{T}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }\gimel \left(\mathfrak{b}\right)={\displaystyle \frac{{\kappa }^{\vartheta }}{\Gamma (1-\vartheta )}}\left({\mathfrak{b}}^{1-\kappa }{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{b}}}\right){\int }_{\mathrm{u}}^{\mathfrak{b}}{\displaystyle \frac{{\mathfrak{c}}^{\kappa -1}}{{\left({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa }\right)}^{\vartheta }}}\gimel \left(\mathfrak{c}\right)\mathrm{d}\mathfrak{c}.\end{array}$$

The HKFD of order $0<\vartheta <1$ and $0\le \varpi \le 1$ with $\kappa >0$, with respect to $\mathfrak{b}$, is defined as follows [12]:

$$\begin{array}{c}\hfill {}^{\kappa }\mathcal{T}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel \left(\mathfrak{b}\right)={}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\varpi (1-\vartheta )}{}^{\kappa }\mathcal{T}_{{\mathrm{u}}^{\mathrm{+}}}^{\lambda }\gimel \left(\mathfrak{b}\right),\lambda =\vartheta +\varpi -\vartheta \varpi .\end{array}$$

(2)

The subsequent fractional derivatives can be interpolated using the HKFD: Caputo–Hadamard ($\varpi =1,\kappa \to 0^{+}$) [13], Caputo-kind ($\varpi =1$) [14], Hilfer–Hadamard ($\kappa \to 0^{+}$) [15], generalized ($\varpi =0$) [16], Hilfer ($\kappa \to 1$) [17], R-L ($\varpi =0,\kappa \to 1$) [18], Hadamard ($\varpi =1,\kappa \to 0^{+}$) [18], Caputo ($\varpi \to 1,\kappa \to 1$) [18], Liouville ($\varpi =0,\kappa \to 1,\mathrm{u}=0$) [18], and Weyl ($\varpi =0,\kappa \to 1,\mathrm{u}=-\infty$) [19].

Implementing HKFD in large-scale systems poses significant computational challenges due to the memory effect, where the current state relies on all previous states. This reliance leads to a considerable increase in computational costs and memory usage as both the system size and simulation time expand. The complicated interactions among subsystems further complicate matters, resulting in more complex equations that are challenging to solve. Additionally, numerical methods for HKFD necessitate small time steps to effectively manage singularities, which exacerbates the computational burden. The nonlocal and high-dimensional characteristics of fractional models also complicate the identification of system parameters and the development of appropriate controllers.

Fractional delay stochastic differential equations (FDSDEs) are mathematical models that incorporate fractional derivatives to account for memory effects, time delays in dynamic interactions, and stochastic processes to represent random or noisy events. These equations are particularly well-suited for systems in which past states, delay effects, and random fluctuations significantly influence the system’s dynamics. FDSDEs find applications in various real-world scenarios, such as finance (e.g., asset pricing with time-lagged market responses) and physics (e.g., viscoelastic materials with delayed stress-strain relationships). By integrating these complex factors, FDSDEs provide a robust framework for analyzing and predicting the behavior of time-dependent and unstable systems.

Numerous scholars have contributed diverse findings to the field of FSDEs. For instance, Kahouli et al. [20] established stability criteria for such systems. Subsequent work has focused on various analytical and practical aspects: the Ex-Un of solutions was confirmed for coupled systems using Picard’s iteration method [21], and controllability was examined for FSDEs with Hilfer fractional derivatives via sectorial operators [22]. Further foundational results in this area were established in [23,24].

Building on this, the authors of [25] proved various qualitative results for FSDEs, while studies concerning specific derivatives, such as the CHFD, have also been explored [26]. Moualkia and Xu [27] extended the analysis to variable-order FSDEs, deriving novel sufficient conditions and obtaining solutions via Picard’s method. Applications of FSDEs are also emerging; for example, a financial chaotic model incorporating an Atangana–Baleanu operator was investigated in [28], complete with numerical solutions and graphical interpretations. Finally, the theory for more complex systems has been advanced by research into Ex-Un for impulsive FSDEs [29] and into the finite-time stability of specific FSDE categories [30].

This research provides substantial new findings for FDSDEs involving the HKFD. The Banach contraction principle (BCP) is utilized to confirm the Ex-Un of solutions. The work further derives the continuous dependence and regularity properties of the solutions to FDSDEs. Interval translation and inequality techniques are employed to validate the averaging principle (Av-Pr).

The validation of our theoretical findings is contingent upon the pivotal application of fundamental inequalities, most notably Jensen’s (Jen-Ineq), the Burkholder–Davis–Gundy (Bu-Da-Gu-Ineq), and Hölder’s (Höl-Ineq). The Bu-Da-Gu-Ineq mostly affects the system’s stochastic part, and it becomes more sensitive as higher moments are used. On the other hand, the Höl-Ineq affects how product terms are separated and can create wider boundaries if the exponents are not set carefully. The Jen-Ineq may also make the bound less strict when expectations are changed between nonlinear terms. Therefore, the overall error bound depends on how these inequalities interact with each other. To obtain more accurate and tighter predictions, one needs to choose the right moment orders and exponents very carefully.

The main contributions of this work are summarized as follows:

• We present a novel analysis of FDSDEs, establishing, for the first time, the existence of unique solutions that depend continuously on initial conditions and the fractional derivative order, alongside the Av-Pr for the HKFD in the $\tilde{\mathcal{P}}$th moment sense.
• Our findings are broadly applicable due to the HKFD’s generality, which incorporates many specific fractional derivatives as special cases.
• A key advancement of our work is the generalization of standard well-posedness and regularity results from the conventional ${\mathrm{L}}^2$ setting to the more comprehensive ${\mathrm{L}}^{\tilde{\mathcal{P}}}$ space.

We consider the following Hilfer–Katugampola FDSDEs:

$$\{\begin{array}{cc}{}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel \left(\mathfrak{b}\right)=\mathfrak{g}(\mathfrak{b},\gimel \left(\mathfrak{b}\right),\gimel \left(\mathfrak{b}-\varrho \right))+\mathfrak{r}(\mathfrak{b},\gimel \left(\mathfrak{b}\right),\gimel \left(\mathfrak{b}-\varrho \right)){\displaystyle \frac{\mathrm{d}\mathcal{W}\left(\mathfrak{b}\right)}{\mathrm{d}\mathfrak{b}}},\hfill & \\ \gimel \left(0\right)=\nu ,\hfill \end{array}$$

(3)

where ${}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }$ is the HKFD, with its parameters defined by $\vartheta \in \left({\displaystyle \frac{1}{2}},1\right)$, $0<\kappa \le 1$, and $0\le \varpi \le 1$. The term $\varrho \in \mathbb{R}$ represents a constant delay. The functions $\mathfrak{g}:[0,\varsigma ]\times {\mathbb{R}}^{\mathfrak{e}}\times {\mathbb{R}}^{\mathfrak{e}}\to {\mathbb{R}}^{\mathfrak{e}}$ and $\mathfrak{r}:[0,\varsigma ]\times {\mathbb{R}}^{\mathfrak{e}}\times {\mathbb{R}}^{\mathfrak{e}}\to {\mathbb{R}}^{\mathfrak{e}\times \sigma }$ are measurable and continuous. All these elements are defined with respect to a $\sigma$-dimensional Brownian motion $\left({\mathcal{W}}_{\mathfrak{b}}\right)\mathfrak{b}\ge 0$, which itself is defined on a complete filtered probability space $(\Omega ,\mathrm{F},\mathbb{F}={\left({\mathrm{F}}_{\mathfrak{b}}\right)}_{\mathfrak{b}\ge 0},\mathrm{P})$.

The following Section 2 introduces key definitions and outlines the assumptions underpinning the analysis of Hilfer–Katugampola FDSDEs. Section 3.1 establishes the well-posedness of the Hilfer–Katugampola FDSDEs, while Section 3.2 addresses their regularity properties. Section 4 presents results related to Av-Pr. Section 5 illustrates the theoretical findings through two examples. Section 6 summarizes the main conclusions of the study. Finally, we outline directions for future work.

2. Preliminaries

This section presents lemmas, definitions, and assumptions essential for deriving key results.

 Lemma 1 

([31]). Assume that $0<\vartheta <1$, $0\le \varpi \le$1, $\kappa >0$. Then, for a continuously differentiable function $\gimel \left(\mathfrak{b}\right)$, we have the following:

$$\begin{array}{c}\hfill \left({}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }{}^{\kappa }\mathcal{T}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }\gimel \right)\left(\mathfrak{b}\right)=\gimel \left(\mathfrak{b}\right)-{\displaystyle \frac{{}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{1-\vartheta }\gimel \left(0\right)}{\Gamma \left(\vartheta \right)}}{\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}}{{\kappa }^{\vartheta -1}}},\end{array}$$

where ${}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }$ and ${}^{\kappa }\mathcal{T}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }$ are the Katugampola fractional integral and derivative, respectively.

 Lemma 2 

([31]). Suppose $0<\vartheta <1$, $0\le \varpi \le 1$, $\kappa >0$, and $\lambda =\vartheta +\varpi -\vartheta \varpi$, then

$$\begin{array}{c}\hfill \left({}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\lambda }{}^{\kappa }\mathcal{T}_{{\mathrm{u}}^{\mathrm{+}}}^{\lambda }\gimel \right)\left(\mathfrak{b}\right)=\left({}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }{}^{\kappa }\mathcal{T}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel \right)\left(\mathfrak{b}\right),\end{array}$$

and

$$\begin{array}{c}\hfill \left({}^{\kappa }\mathcal{T}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta ,\varpi }{}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }\gimel \right)\left(\mathfrak{b}\right)=\gimel \left(\mathfrak{b}\right).\end{array}$$

The following semigroup property holds:

$$\begin{array}{c}\hfill \left({}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }{}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\varpi }\gimel \right)\left(\mathfrak{b}\right)=\left({}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta +\varpi }\gimel \right)\mathfrak{b},\end{array}$$

and

$$\begin{array}{c}\hfill \left({}^{\kappa }\mathcal{T}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }{}^{\kappa }\mathcal{I}_{{\mathrm{u}}^{\mathrm{+}}}^{\vartheta }\right)\gimel \left(\mathfrak{b}\right)=\gimel \left(\mathfrak{b}\right).\end{array}$$

 Lemma 3. 

Assume that ${\gimel }_1\left(\mathfrak{b}\right)\in {\mathrm{L}}^{\tilde{\mathcal{P}}}$ and ${\gimel }_2\left(\mathfrak{b}\right)\in {\mathrm{L}}^{\mathrm{q}}$. Thus, Höl-Ineq is given below:

$$\parallel {\gimel }_1{\gimel }_2{\parallel }_1\le \parallel {\gimel }_1{\parallel }_{\tilde{\mathcal{P}}}{\parallel {\gimel }_2\parallel }_{\mathrm{q}},$$

where ${\displaystyle \frac{1}{\tilde{\mathcal{P}}}}+{\displaystyle \frac{1}{\mathrm{q}}}=1$.

 Definition 1. 

Let ${\mathcal{Z}}_{\mathfrak{b}}^{\tilde{\mathcal{P}}}={\mathrm{L}}^{\tilde{\mathcal{P}}}(\Omega ,{\mathrm{F}}_{\mathfrak{b}},\mathrm{P})$ be the space of ${\mathrm{F}}_{\mathfrak{b}}$-measurable and $\tilde{\mathcal{P}}$th-integrable functions $\gimel ={({\gimel }_1,{\gimel }_2,\dots ,{\gimel }_{\mathfrak{e}})}^{\mathbb{T}}$: $\Omega \to {\mathbb{R}}^{\mathfrak{e}}$, which satisfy

$${\parallel \gimel \parallel }_{\tilde{\mathcal{P}}}={\left({\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }{\left|{\gimel }_{ı}\right|}^{\tilde{\mathcal{P}}}\right)}^{{\displaystyle \frac{1}{\tilde{\mathcal{P}}}}}.$$

A stochastic process $\gimel :[0,\varsigma ]\to {\mathrm{L}}^{\tilde{\mathcal{P}}}(\Omega ,{\mathrm{F}}_{\mathfrak{b}},\mathrm{P})$ satisfying the requisite measurability conditions is said to be $\mathbb{F}$-adapted provided that $\gimel \left(\mathfrak{b}\right)\in {\mathcal{Z}}_{\mathfrak{b}}^{\tilde{\mathcal{P}}}$ for every $\mathfrak{b}\ge 0$. For any initial value $\nu \in {\mathcal{Z}}_0^{\tilde{\mathcal{P}}}$, such an $\mathbb{F}$-adapted process ℷ constitutes a solution to Equation (3) under the initial condition $\gimel \left(0\right)=\nu$ whenever condition (4) is satisfied. The derivation of this solution proceeds by applying the fractional integral operator ${}^{\kappa }\mathcal{I}_{0^{\mathrm{+}}}^{\vartheta }$ to (3) and subsequently leveraging the results of Lemmas 1 and 2

$$\begin{array}{cc}\hfill \gimel \left(\mathfrak{b}\right)& ={\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}+{\displaystyle \frac{{\kappa }^{1-\vartheta }}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}{\mathfrak{c}}^{\kappa -1}\mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)\mathrm{d}\mathfrak{c}\hfill \\ & +{\displaystyle \frac{{\kappa }^{1-\vartheta }}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}{\mathfrak{c}}^{\kappa -1}\mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right).\hfill \end{array}$$

(4)

For $\mathfrak{g} \mathrm{and} \mathfrak{r}$, assume the following:

• $\left({\daleth }_1\right)$$\forall {\Lambda }_1,{\Lambda }_2,{{\rm Y}}_1,{{\rm Y}}_2\in {\mathbb{R}}^{\mathfrak{e}}$. There are ${\delta }_1$ and ${\delta }_2$, such as

  $$\parallel \mathfrak{g}(\mathfrak{b},{\Lambda }_1,{\Lambda }_2)-\mathfrak{g}(\mathfrak{b},{{\rm Y}}_1,{{\rm Y}}_2){\parallel }_{\tilde{\mathcal{P}}}\le {\delta }_1\left(\parallel {\Lambda }_1-{{\rm Y}}_1{\parallel }_{\tilde{\mathcal{P}}}+{\parallel {\Lambda }_2-{{\rm Y}}_2\parallel }_{\tilde{\mathcal{P}}}\right).$$

  $$\parallel \mathfrak{r}(\mathfrak{b},{\Lambda }_1,{\Lambda }_2)-\mathfrak{r}(\mathfrak{b},{{\rm Y}}_1,{{\rm Y}}_2){\parallel }_{\tilde{\mathcal{P}}}\le {\delta }_2\left(\parallel {\Lambda }_1-{{\rm Y}}_1{\parallel }_{\tilde{\mathcal{P}}}+{\parallel {\Lambda }_2-{{\rm Y}}_2\parallel }_{\tilde{\mathcal{P}}}\right).$$
• $\left({\daleth }_2\right)$$\mathfrak{g}(\mathfrak{b},0,0)$ and $\mathfrak{r}(\mathfrak{b},0,0)$ are essential-bounded, so

  $$\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }{\parallel \mathfrak{g}(\mathfrak{b},0,0)\parallel }_{\tilde{\mathcal{P}}}<\mathfrak{a},\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }{\parallel \mathfrak{r}(\mathfrak{b},0,0)\parallel }_{\tilde{\mathcal{P}}}<\mathfrak{a}.$$

  (5)

Now assume the following:

• $\left({\daleth }_3\right):$$\forall {\Lambda }_1,{\Lambda }_2,{{\rm Y}}_1,{{\rm Y}}_2,\Lambda ,{\rm Y}\in {\mathbb{R}}^{\mathfrak{e}}$, $\mathfrak{b}\in [0,\varsigma ]$; there exists a ${\delta }_3>0$, ensuring that

  $$\begin{array}{cc}\hfill \parallel \mathfrak{g}(\mathfrak{b},{\Lambda }_1,{\Lambda }_2)-& \mathfrak{g}(\mathfrak{b},{{\rm Y}}_1,{{\rm Y}}_2)\parallel \vee \parallel \mathfrak{r}(\mathfrak{b},{\Lambda }_1,{\Lambda }_2)-\mathfrak{r}(\mathfrak{b},{{\rm Y}}_1,{{\rm Y}}_2)\parallel \hfill \\ & \le {\delta }_3\left(\parallel {\Lambda }_1-{{\rm Y}}_1\parallel +\parallel {\Lambda }_2-{{\rm Y}}_2\parallel \right).\hfill \end{array}$$
• $\left({\daleth }_4\right):$$\forall {\Lambda }_1,{\Lambda }_2$,${{\rm Y}}_1$,${{\rm Y}}_2$,$\Lambda ,$${\rm Y}\in {\mathbb{R}}^{\mathfrak{e}}$, $\mathfrak{b}\in [0,\varsigma ]$; there is ${\delta }_4>0$, satisfying the following:

  $$\begin{array}{c}\hfill \parallel \mathfrak{g}(\mathfrak{b},\Lambda ,{\rm Y})\parallel \vee \parallel \mathfrak{r}(\mathfrak{b},\Lambda ,{\rm Y})\parallel \le {\delta }_4\left(1+\parallel \Lambda \parallel +\parallel {\rm Y}\parallel \right).\end{array}$$
• $\left({\daleth }_5\right):$ For ${\varsigma }_1\in [0,\varsigma ]$, $\mathfrak{b}\in [0,\varsigma ]$, and $\tilde{\mathcal{P}}\ge 2$, we have

  $$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\varsigma }_1}}{\int }_0^{{\varsigma }_1}\parallel \mathfrak{g}(\mathfrak{b},\Lambda ,{\rm Y})& - \tilde{\mathfrak{g}}{(\mathfrak{b},\Lambda )\parallel }^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{b}\le {\xi }_1\left({\varsigma }_1\right)\left(1+{\parallel \Lambda \parallel }^{\tilde{\mathcal{P}}}+{\parallel {\rm Y}\parallel }^{\tilde{\mathcal{P}}}\right),\hfill \end{array}$$
  $$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\varsigma }_1}}{\int }_0^{{\varsigma }_1}\parallel \mathfrak{r}(\mathfrak{b},\Lambda ,{\rm Y})& - \tilde{\mathfrak{r}}{(\mathfrak{b},\Lambda )\parallel }^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{b}\le {\xi }_2\left({\varsigma }_1\right)\left(1+{\parallel \Lambda \parallel }^{\tilde{\mathcal{P}}}+{\parallel {\rm Y}\parallel }^{\tilde{\mathcal{P}}}\right),\hfill \end{array}$$

where ${lim}_{{\varsigma }_1\to \infty }{\xi }_1\left({\varsigma }_1\right)=0$ and ${lim}_{{\varsigma }_1\to \infty }{\xi }_2\left({\varsigma }_1\right)=0$.

3. Generalized Results

This section contains generalized results for the Hilfer–Katugampola FDSDEs.

3.1. Well-Posedness

Within the ${\mathrm{L}}^{\tilde{\mathcal{P}}}$ space, we derive generalized results regarding the Ex-Un and the continuous dependence of solutions to Hilfer–Katugampola FDSDEs.

By applying the BCP, we initially derive the Ex-Un results for the solutions of Hilfer–Katugampola FDSDEs.

The space ${\mathcal{H}}^{\tilde{\mathcal{P}}}\left([0,\varsigma ]\right)$ is defined as the collection of all measurable and $\mathbb{F}\left(\mathfrak{b}\right)$-adapted processes ℷ with ${\parallel \gimel \parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}=\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}$ finite.

It is easy to verify that $\left({\mathcal{H}}^{\tilde{\mathcal{P}}}\left([0,\varsigma ]\right),{\parallel ·\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}\right)$ forms a Banach space.

The next step is to establish an operator ${\psi }_{\nu }:{\mathcal{H}}^{\tilde{\mathcal{P}}}\left([0,\varsigma ]\right)\to {\mathcal{H}}^{\tilde{\mathcal{P}}}\left([0,\varsigma ]\right)$ where ${\psi }_{\nu }(\gimel \left(0\right))=\nu$ and

$$\begin{array}{cc}\hfill {\psi }_{\nu }(\gimel \left(\mathfrak{b}\right))& ={\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}+{\displaystyle \frac{{\kappa }^{1-\vartheta }}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}{\mathfrak{c}}^{\kappa -1}\mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)\mathrm{d}\mathfrak{c}\hfill \\ & +{\displaystyle \frac{{\kappa }^{1-\vartheta }}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}{\mathfrak{c}}^{\kappa -1}\mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right).\hfill \end{array}$$

(6)

The following lemma is essential for proving the main results of this paper.

$$\parallel {\gimel }_1+{\gimel }_2{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le 2^{\tilde{\mathcal{P}}-1}({\parallel {\gimel }_1\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+(\parallel {\gimel }_2{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}),\forall {\gimel }_1,{\gimel }_2\in {\mathbb{R}}^{\mathfrak{e}}.$$

(7)

 Lemma 4. 

Let ${\daleth }_1$ and ${\daleth }_2$ hold. Then, ${\psi }_{\nu }$ is well-defined.

Proof. 

Suppose $\gimel \left(\mathfrak{b}\right)\in {\mathcal{H}}^{\tilde{\mathcal{P}}}[0,\varsigma ]$ and $\forall \mathfrak{b}\in [0,\varsigma ]$. From (6) and (7), we have

$$\begin{array}{cc}\hfill & \parallel {\psi }_{\nu }(\gimel \left(\mathfrak{b}\right)){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le 2^{\tilde{\mathcal{P}}-1}\parallel {\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill +& {\displaystyle \frac{2^{2\tilde{\mathcal{P}}-2}{\left({\kappa }^{1-\vartheta }\right)}^{\tilde{\mathcal{P}}}}{{(\Gamma \left(\vartheta \right))}^{\tilde{\mathcal{P}}}}}\parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill +& {\displaystyle \frac{2^{2\tilde{\mathcal{P}}-2}{\left({\kappa }^{1-\vartheta }\right)}^{\tilde{\mathcal{P}}}}{{(\Gamma \left(\vartheta \right))}^{\tilde{\mathcal{P}}}}}\parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}.\hfill \end{array}$$

(8)

Using Höl-Ineq, we have

$$\begin{array}{cc}\hfill & {∥{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}=\hfill \\ & {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }|{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}|{\mathfrak{g}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)|{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{|}^{\tilde{\mathcal{P}}}\hfill \\ & \le {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }\left({\left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{{\displaystyle \frac{(\vartheta -1)\tilde{\mathcal{P}}}{(\tilde{\mathcal{P}}-1)}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{\tilde{\mathcal{P}}-1}}}\mathrm{d}\mathfrak{c}\right)}^{\tilde{\mathcal{P}}-1}{\int }_0^{\mathfrak{b}}\right|{\mathfrak{g}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){|}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c})\hfill \\ & \le {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }\left({\left\{\left(\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{1}{\tilde{\mathcal{P}}-1}}}\right)\left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{{\displaystyle \frac{(\vartheta -1)\tilde{\mathcal{P}}}{(\tilde{\mathcal{P}}-1)}}}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right)\right\}}^{\tilde{\mathcal{P}}-1}{\int }_0^{\mathfrak{b}}\right|{\mathfrak{g}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){|}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c})\hfill \\ & \le {\mathfrak{M}}^{\tilde{\mathcal{P}}-1}{\left({\left({\varsigma }^{\kappa }\right)}^{{\displaystyle \frac{\vartheta \tilde{\mathcal{P}}-1}{\tilde{\mathcal{P}}-1}}}\right)}^{\tilde{\mathcal{P}}-1}\mathfrak{U}{\int }_0^{\mathfrak{b}}{\left(\parallel \mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\parallel }_{\tilde{\mathcal{P}}}\right)}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c},\hfill \end{array}$$

(9)

where $\mathfrak{M}=\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{1}{\tilde{\mathcal{P}}-1}}}$ and $\mathfrak{U}={\left({\displaystyle \frac{\tilde{\mathcal{P}}-1}{\vartheta \tilde{\mathcal{P}}-1}}\right)}^{\tilde{\mathcal{P}}-1}$.

Now from $\left({\daleth }_1\right)$, we have

$$\begin{array}{cc}\hfill \parallel \mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le & 2^{\tilde{\mathcal{P}}-1}\left(\parallel \mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-\mathfrak{g}(\mathfrak{c},0,0){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel \mathfrak{g}(\mathfrak{c},0,0){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right)\hfill \\ \hfill \le & 2^{\tilde{\mathcal{P}}-1}(2^{\tilde{\mathcal{P}}-1}{\delta }_1^{\tilde{\mathcal{P}}}\left(\parallel \gimel \left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel \gimel (\mathfrak{c}-\varrho ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right)+\parallel \mathfrak{g}(\mathfrak{c},0,0){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}).\hfill \end{array}$$

(10)

Therefore, we obtain

$$\begin{array}{cc}\hfill {\int }_0^{\mathfrak{b}}\parallel \mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}& \le 2^{2\tilde{\mathcal{P}}-2}{\delta }_1^{\tilde{\mathcal{P}}}({\left(\underset{\mathfrak{c}\in [0,\varsigma ]}{\mathrm{ess}\sup }{\parallel \gimel \left(\mathfrak{c}\right)\parallel }_{\tilde{\mathcal{P}}}\right)}^{\tilde{\mathcal{P}}}+{\left(\underset{\mathfrak{c}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel \gimel \left(\mathfrak{c}-\varrho \right){\parallel }_{\tilde{\mathcal{P}}}\right)}^{\tilde{\mathcal{P}}})\hfill \\ & {\int }_0^{\mathfrak{b}}1\mathrm{d}\mathfrak{c}+2^{\tilde{\mathcal{P}}-1}{\int }_0^{\mathfrak{b}}\parallel \mathfrak{g}(\mathfrak{c},0,0){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\hfill \\ & \le 2^{2\tilde{\mathcal{P}}-2}\varsigma {\delta }_1^{\tilde{\mathcal{P}}}(\parallel \gimel \left(\mathfrak{c}\right){\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}}+\parallel \gimel (\mathfrak{c}-\varrho ){\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}})\hfill \\ & +2^{\tilde{\mathcal{P}}-1}{\int }_0^{\mathfrak{b}}\parallel \mathfrak{g}(\mathfrak{c},0,0){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

(11)

From (9) and (11), we obtain

$$\begin{array}{cc}\hfill & {∥{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le {\mathfrak{M}}^{\tilde{\mathcal{P}}-1}{\left({\left({\varsigma }^{\kappa }\right)}^{{\displaystyle \frac{(\vartheta \tilde{\mathcal{P}}-1)}{\tilde{\mathcal{P}}-1}}}\right)}^{\tilde{\mathcal{P}}-1}\hfill \\ & \mathfrak{U}{2}^{\tilde{\mathcal{P}}-1}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_1^{\tilde{\mathcal{P}}}\varsigma \right(\parallel \gimel \left(\mathfrak{c}\right){\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}}+\parallel \gimel (\mathfrak{c}-\varrho ){\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}})+{\int }_0^{\mathfrak{b}}\parallel \mathfrak{g}(\mathfrak{c},0,0){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}).\hfill \end{array}$$

(12)

Using $\left({\daleth }_2\right)$, we obtain the following from (12):

$$\begin{array}{cc}\hfill & {∥{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le {\mathfrak{M}}^{\tilde{\mathcal{P}}-1}\hfill \\ & {\left({\left({\varsigma }^{\kappa }\right)}^{{\displaystyle \frac{(\vartheta \tilde{\mathcal{P}}-1)}{\tilde{\mathcal{P}}-1}}}\right)}^{\tilde{\mathcal{P}}-1}{2}^{\tilde{\mathcal{P}}-1}\mathfrak{U}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_1^{\tilde{\mathcal{P}}}\varsigma \right(\parallel \gimel \left(\mathfrak{c}\right){\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}}+\parallel \gimel (\mathfrak{c}-\varrho ){\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}})+\varsigma {\mathfrak{a}}^{\tilde{\mathcal{P}}}).\hfill \end{array}$$

(13)

Using Bu-Da-Gu-Ineq, we obtain

$$\begin{array}{cc}\hfill & \parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ & ={\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }|{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left({\mathfrak{r}}_{ı}(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){|}^{\tilde{\mathcal{P}}}\hfill \\ & \le {\sum }_{ı=1}^{\mathfrak{e}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }\left|{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\right|{\mathfrak{r}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){|}^2{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}{|}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ & \le {\sum }_{ı=1}^{\mathfrak{e}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}|{\mathfrak{r}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){|}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ & {\left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ & \le {\sum }_{ı=1}^{\mathfrak{e}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}|{\mathfrak{r}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){|}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ & {\left(\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ & \le {\mathbf{G}}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}{\left({\displaystyle \frac{{\left({\varsigma }^{\kappa }\right)}^{2\vartheta -1}}{2\vartheta -1}}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ & {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\parallel \mathfrak{r}\left(\mathfrak{c},\gimel (\mathfrak{c},\gimel (\mathfrak{c}-\varrho )\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c},\hfill \end{array}$$

(14)

where $\mathbf{G}=\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}$ and ${\mathcal{C}}_{\tilde{\mathcal{P}}}={\left({\displaystyle \frac{{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}+1}}{2{(\tilde{\mathcal{P}}-1)}^{\tilde{\mathcal{P}}-1}}}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}$.

Using $\left({\daleth }_1\right)$ and $\left({\daleth }_2\right)$, we have

$$\begin{array}{cc}\hfill \parallel \mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le & 2^{2\tilde{\mathcal{P}}-2}{\delta }_2^{\tilde{\mathcal{P}}}\left(\parallel \gimel \left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel \gimel (\mathfrak{c}-\varrho ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right)+2^{\tilde{\mathcal{P}}-1}\parallel \mathfrak{r}(\mathfrak{c},0,0){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill \le & 2^{2\tilde{\mathcal{P}}-2}{\delta }_2^{\tilde{\mathcal{P}}}\left(\parallel \gimel \left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel \gimel (\mathfrak{c}-\varrho ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right)+2^{\tilde{\mathcal{P}}-1}{\mathfrak{a}}^{\tilde{\mathcal{P}}}.\hfill \end{array}$$

(15)

So with $\forall \mathfrak{b}\in [0,\varsigma ]$, we have

$$\begin{array}{cc}\hfill & {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\parallel \mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\le 2^{2\tilde{\mathcal{P}}-2}{\delta }_2^{\tilde{\mathcal{P}}}\hfill \\ & {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}({\left(\underset{\mathfrak{c}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel \gimel \left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}\right)}^{\tilde{\mathcal{P}}}+{\left(\underset{\mathfrak{c}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel \gimel (\mathfrak{c}-\varrho ){\parallel }_{\tilde{\mathcal{P}}}\right)}^{\tilde{\mathcal{P}}}){\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ \hfill +& 2^{\tilde{\mathcal{P}}-1}{\mathfrak{a}}^{\tilde{\mathcal{P}}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ \hfill \le & 2^{2\tilde{\mathcal{P}}-2}{\delta }_2^{\tilde{\mathcal{P}}}\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}({\left(\underset{\mathfrak{c}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel \gimel \left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}\right)}^{\tilde{\mathcal{P}}}\hfill \\ \hfill +& {\left(\underset{\mathfrak{c}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel \gimel (\mathfrak{c}-\varrho ){\parallel }_{\tilde{\mathcal{P}}}\right)}^{\tilde{\mathcal{P}}}){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}+2^{\tilde{\mathcal{P}}-1}{\mathfrak{a}}^{\tilde{\mathcal{P}}}\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill =& \mathbf{G}{\displaystyle \frac{2^{\tilde{\mathcal{P}}-1}{\left({\varsigma }^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}(2^{\tilde{\mathcal{P}}-1}{\delta }_2^{\tilde{\mathcal{P}}}\left({\parallel \gimel \left(\mathfrak{c}\right)\parallel }_{{\mathcal{H}}_{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}}+{\parallel \gimel (\mathfrak{c}-\varrho )\parallel }_{{\mathcal{H}}_{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}}\right)+{\mathfrak{a}}^{\tilde{\mathcal{P}}}).\hfill \end{array}$$

(16)

Now the above yields

$$\begin{array}{cc}\hfill {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}& {∥\mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\le {\displaystyle \frac{2^{\tilde{\mathcal{P}}-1}{\left({\varsigma }^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\mathbf{G}\hfill \\ & (2^{\tilde{\mathcal{P}}-1}{\delta }_2^{\tilde{\mathcal{P}}}\left({\parallel \gimel \left(\mathfrak{c}\right)\parallel }_{{\mathcal{H}}_{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}}+{\parallel \gimel (\mathfrak{c}-\varrho )\parallel }_{{\mathcal{H}}_{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}}\right)+{\mathfrak{a}}^{\tilde{\mathcal{P}}}).\hfill \end{array}$$

(17)

Using (17) in (14), we obtain

$$\begin{array}{cc}\hfill & {∥{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right)∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le {\mathbf{G}}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ & {\mathcal{C}}_{\tilde{\mathcal{P}}}{\left({\displaystyle \frac{{\left({\varsigma }^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\displaystyle \frac{2^{\tilde{\mathcal{P}}-1}{\left({\varsigma }^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\hfill \\ & \mathbf{G}(2^{\tilde{\mathcal{P}}-1}{\delta }_2^{\tilde{\mathcal{P}}}\left({\parallel \gimel \left(\mathfrak{c}\right)\parallel }_{{\mathcal{H}}_{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}}+{\parallel \gimel (\mathfrak{c}-\varrho )\parallel }_{{\mathcal{H}}_{\tilde{\mathcal{P}}}}^{\tilde{\mathcal{P}}}\right)+{\mathfrak{a}}^{\tilde{\mathcal{P}}}).\hfill \end{array}$$

(18)

Hence, ${\parallel \psi (\gimel \left(\mathfrak{b}\right))\parallel }_{\mathcal{H}\tilde{\mathcal{P}}}$ is finite. □

The next lemma is important for proving the Ex-Un of the solution to Hilfer–Katugampola FDSDEs.

 Lemma 5. 

Let $\vartheta ,\mathfrak{B}>0$, and $\forall \mathfrak{b}\in [0,\varsigma ]$; thus,

$${}^{\kappa }\mathcal{I}_{0^{\mathrm{+}}}^{\vartheta }{\mathfrak{e}}^{\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)}\le {\displaystyle \frac{{\mathfrak{e}}^{\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)}}{{\mathfrak{B}}^{\vartheta }}}.$$

Proof. 

From (1), we obtain the following:

$$\begin{array}{cc}\hfill {}^{\kappa }\mathcal{I}_{0^{\mathrm{+}}}^{\vartheta }exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)& ={\displaystyle \frac{{\kappa }^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}exp\left(\mathfrak{B}\left({\mathfrak{c}}^{\kappa }\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

Using $\mathbb{K}={\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa }$, we have

$${}^{\kappa }\mathcal{I}_{0^{\mathrm{+}}}^{\vartheta }exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)={\kappa }^{\vartheta }{\displaystyle \frac{exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)}{\Gamma \left(\vartheta \right)}}{\int }_0^{{\mathfrak{b}}^{\kappa }}{\mathbb{K}}^{\vartheta -1}exp(-\mathfrak{B}\mathbb{K})\mathrm{d}\mathbb{K}.$$

(19)

Applying $\mathcal{W}=\mathfrak{B}\mathbb{K}$ in (19), we obtain

$$\begin{array}{cc}\hfill {}^{\kappa }\mathcal{I}_{0^{\mathrm{+}}}^{\vartheta }exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)& ={\kappa }^{\vartheta }{\displaystyle \frac{exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)}{{\mathfrak{B}}^{\vartheta }\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{B}\left({\mathfrak{b}}^{\kappa }\right)}{\mathcal{W}}^{\vartheta -1}exp(-\mathcal{W})\mathrm{d}\mathcal{W}\hfill \\ & \le {\kappa }^{\vartheta }{\displaystyle \frac{exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)}{{\mathfrak{B}}^{\vartheta }\Gamma \left(\vartheta \right)}}{\int }_0^{\infty }{\mathcal{W}}^{\vartheta -1}exp(-\mathcal{W})\mathrm{d}\mathcal{W}\hfill \\ & ={\kappa }^{\vartheta }{\displaystyle \frac{exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)}{{\mathfrak{B}}^{\vartheta }}}.\hfill \end{array}$$

Thus, we have

$${\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\le {\displaystyle \frac{\Gamma \left(\vartheta \right)}{\kappa }}{\displaystyle \frac{exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)}{{\mathfrak{B}}^{\vartheta }}}.$$

(20)

□

The following lemma concerns the Ex-Un of solutions to the Hilfer–Katugampola FDSDEs.

 Theorem 1. 

 Let $\left({\daleth }_1\right)$ and $\left({\daleth }_2\right)$ be valid; afterward, Hilfer–Katugampola FDSDEs (3) ensures a unique solution. 

Proof. 

Considering $\mathfrak{B}$ under the condition that

$${\mathfrak{B}}^{2\vartheta -1}>{\displaystyle \frac{2\mathbb{Z}\Gamma (2\vartheta -1)}{\kappa }},$$

(21)

where

$$\begin{array}{cc}\hfill \mathbb{Z}& ={\displaystyle \frac{2^{\tilde{\mathcal{P}}-1}{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{(\Gamma \left(\vartheta \right))}^{\tilde{\mathcal{P}}}}}\left(2^{\tilde{\mathcal{P}}-1}{\mathfrak{f}}^{\tilde{\mathcal{P}}-1}{\displaystyle \frac{{\delta }_1^{\tilde{\mathcal{P}}}{\left({\varsigma }^{\kappa }\right)}^{(\tilde{\mathcal{P}}\vartheta -2\vartheta +1)}{(\tilde{\mathcal{P}}-1)}^{\tilde{\mathcal{P}}-1}}{{\left(\tilde{\mathcal{P}}\vartheta -2\vartheta +1\right)}^{\tilde{\mathcal{P}}-1}}}\mathbf{G}+2^{\tilde{\mathcal{P}}-1}{\mathbf{G}}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\left({\displaystyle \frac{{\left({\varsigma }^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\mathbf{G}\right).\hfill \end{array}$$

(22)

${\parallel ·\parallel }_{\mathfrak{B}}$ is

$${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\mathfrak{B}}=\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }{\left({\displaystyle \frac{{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)}}\right)}^{{\displaystyle \frac{1}{\tilde{\mathcal{P}}}}},\forall \gimel \left(\mathfrak{b}\right)\in {\mathcal{H}}^{\tilde{\mathcal{P}}}\left([0,\varsigma ]\right),$$

(23)

where $\mu \left(\mathfrak{b}\right)=exp\left(\mathfrak{B}{\mathfrak{b}}^{\kappa }\right)$.

First we will prove that ${\parallel ·\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}$ and ${\parallel ·\parallel }_{\mathfrak{B}}$ are equivalent norms.

Let ${\mathcal{H}}^{\tilde{\mathcal{P}}}\left([0,\varsigma ]\right)$ be a space of functions $\gimel \left(\mathfrak{b}\right):[0,\varsigma ]\to {\mathbb{R}}^{\mathfrak{e}}$ with the following norms:

$${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}=\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}},$$

$${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\mathfrak{B}}={\left[\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\left({\displaystyle \frac{{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{{\mathfrak{e}}^{\mathfrak{B}{\mathfrak{b}}^{\kappa }}}}\right)\right]}^{{\displaystyle \frac{1}{\tilde{\mathcal{P}}}}}.$$

Since $\mathfrak{b}\in [0,\varsigma ]$, we have ${\mathfrak{b}}^{\kappa }\in [0,{\varsigma }^{\kappa }]$ and

$$1\le \mu \left(\mathfrak{b}\right)\le {\mathfrak{e}}^{\mathfrak{B}{\varsigma }^{\kappa }}.$$

Define $\mathrm{M}={\mathfrak{e}}^{\mathfrak{B}{\varsigma }^{\kappa }}\ge 1$.

First inequality ${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\mathfrak{B}}\le {\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}$.

Assume $\mathrm{U}={\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}$, then for $\mathfrak{b}\in [0,\varsigma ]$, we have

$${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}\le \mathrm{U}.$$

Taking $\tilde{\mathcal{P}}$,

$${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le {\mathrm{U}}^{\tilde{\mathcal{P}}}.$$

Since $\mu \left(\mathfrak{b}\right)\ge 1$, we obtain the following:

$${\displaystyle \frac{{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{b}\right)}}\le {\mathrm{U}}^{\tilde{\mathcal{P}}}.$$

Taking the essential supremum over $\mathfrak{b}$,

$$\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }{\displaystyle \frac{{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{b}\right)}}\le {\mathrm{U}}^{\tilde{\mathcal{P}}}.$$

By taking $1/\tilde{\mathcal{P}}$, we obtain

$${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\mathfrak{B}}\le \mathrm{U}={\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}.$$

By considering the second inequality ${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}\le {\mathrm{M}}^{1/\tilde{\mathcal{P}}}{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\mathfrak{B}}$.

Let $\mathrm{V}={\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\mathfrak{B}}$; then, we have

$${\mathrm{V}}^{\tilde{\mathcal{P}}}=\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }{\displaystyle \frac{{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{b}\right)}}.$$

Hence, for $\mathfrak{b}$

$${\displaystyle \frac{{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{b}\right)}}\le {\mathrm{V}}^{\tilde{\mathcal{P}}}.$$

Multiplying by $\mu \left(\mathfrak{b}\right)$,

$${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le {\mathrm{V}}^{\tilde{\mathcal{P}}}·\mu \left(\mathfrak{b}\right)\le {\mathrm{V}}^{\tilde{\mathcal{P}}}·\mathrm{M}.$$

Taking $1/\tilde{\mathcal{P}}$ power,

$${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\tilde{\mathcal{P}}}\le \mathrm{V}·{\mathrm{M}}^{1/\tilde{\mathcal{P}}}.$$

Taking essential supremum over $\mathfrak{b}$,

$${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}\le {\mathrm{M}}^{1/\tilde{\mathcal{P}}}\mathrm{V}={\mathfrak{e}}^{{\displaystyle \frac{\mathfrak{B}{\varsigma }^{\kappa }}{\tilde{\mathcal{P}}}}}{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\mathfrak{B}}.$$

We have shown

$${\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\mathfrak{B}}\le {\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}\le {\mathfrak{e}}^{{\displaystyle \frac{\mathfrak{B}{\varsigma }^{\kappa }}{\tilde{\mathcal{P}}}}}{\parallel \gimel \left(\mathfrak{b}\right)\parallel }_{\mathfrak{B}},$$

which proves that the norms ${\parallel ·\parallel }_{{\mathcal{H}}^{\tilde{\mathcal{P}}}}$ and ${\parallel ·\parallel }_{\mathfrak{B}}$ are equivalent. Thus, the space $\left({\mathcal{H}}^{\tilde{\mathcal{P}}}\left([0,\varsigma ]\right),{\parallel ·\parallel }_{\mathfrak{B}}\right)$ remains complete and normed.

For $\gimel \left(\mathfrak{b}\right)$, $\tilde{\gimel }\left(\mathfrak{b}\right)\in {\mathcal{H}}^{\tilde{\mathcal{P}}}\left([0,\varsigma ]\right)$, we obtain

$$\begin{array}{cc}\hfill & {∥{\psi }_{\nu }(\gimel \left(\mathfrak{b}\right))-{\psi }_{\nu }(\tilde{\gimel }\left(\mathfrak{b}\right))∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le \hfill \\ & {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{2^{1-\tilde{\mathcal{P}}}{(\Gamma \left(\vartheta \right))}^{\tilde{\mathcal{P}}}}}{∥{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-\mathfrak{g}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\hfill \\ & {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{2^{1-\tilde{\mathcal{P}}}{(\Gamma \left(\vartheta \right))}^{\tilde{\mathcal{P}}}}}{∥{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-\mathfrak{r}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right)∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}.\hfill \end{array}$$

(24)

Applying Höl-Ineq and $\left({\daleth }_1\right)$, we achieve

$$\begin{array}{cc}\hfill & \parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-\mathfrak{g}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill =& {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }|{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left({\mathfrak{g}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-{\mathfrak{g}}_{ı}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{|}^{\tilde{\mathcal{P}}}\hfill \\ \hfill \le & {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }({\left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{{\displaystyle \frac{(\vartheta -1)(\tilde{\mathcal{P}}-2)}{\tilde{\mathcal{P}}-1}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{\tilde{\mathcal{P}}-1}}}\mathrm{d}\mathfrak{c}\right)}^{\tilde{\mathcal{P}}-1}\hfill \\ & \left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\right|{\mathfrak{g}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-{\mathfrak{g}}_{ı}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\left)\right|{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right))\hfill \\ \hfill \le & {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }({\left(\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{1}{1-\tilde{\mathcal{P}}}}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{{\displaystyle \frac{(\vartheta -1)(\tilde{\mathcal{P}}-2)}{\tilde{\mathcal{P}}-1}}}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right)}^{\tilde{\mathcal{P}}-1}\hfill \\ & \left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\right|{\mathfrak{g}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-{\mathfrak{g}}_{ı}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\left)\right|{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right))\hfill \\ \hfill \le & 2^{\tilde{\mathcal{P}}-1}{\mathfrak{f}}^{\tilde{\mathcal{P}}-1}{\displaystyle \frac{{\delta }_1^{\tilde{\mathcal{P}}}{\left({\varsigma }^{\kappa }\right)}^{(\tilde{\mathcal{P}}\vartheta -2\vartheta +1)}{(\tilde{\mathcal{P}}-1)}^{\tilde{\mathcal{P}}-1}}{{\left(\tilde{\mathcal{P}}\vartheta -2\vartheta +1\right)}^{\tilde{\mathcal{P}}-1}}}\hfill \\ & \underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }\left(\mathfrak{c}\right)){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel \gimel (\mathfrak{c}-\varrho )-\tilde{\gimel }(\mathfrak{c}-\varrho )){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c},\hfill \end{array}$$

(25)

here, $\mathfrak{f}=\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{1}{1-\tilde{\mathcal{P}}}}}$.

Therefore, we have

$$\begin{array}{cc}\hfill & \parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-\mathfrak{g}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill \le & 2^{\tilde{\mathcal{P}}-1}\mathbf{G}{\mathfrak{f}}^{\tilde{\mathcal{P}}-1}{\displaystyle \frac{{\delta }_1^{\tilde{\mathcal{P}}}{\left({\varsigma }^{\kappa }\right)}^{(\tilde{\mathcal{P}}\vartheta -2\vartheta +1)}{(\tilde{\mathcal{P}}-1)}^{\tilde{\mathcal{P}}-1}}{{\left(\tilde{\mathcal{P}}\vartheta -2\vartheta +1\right)}^{\tilde{\mathcal{P}}-1}}}\hfill \\ & {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }\left(\mathfrak{c}\right)){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel \gimel (\mathfrak{c}-\varrho )-\tilde{\gimel }(\mathfrak{c}-\varrho )){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

(26)

Now, using $\left({\daleth }_1\right)$ and the Bu-Da-Gu-Ineq, we have

$$\begin{array}{cc}\hfill & \parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-\mathfrak{r}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill =& {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }|{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left({\mathfrak{r}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-{\mathfrak{r}}_{ı}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){|}^{\tilde{\mathcal{P}}}\hfill \\ \hfill \le & {\sum }_{ı=1}^{\mathfrak{e}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }\left|{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\right|{\mathfrak{r}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-{\mathfrak{r}}_{ı}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right){|}^2{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}{|}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill \le & {\sum }_{ı=1}^{\mathfrak{e}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}|{\mathfrak{r}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-{\mathfrak{r}}_{ı}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right){|}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ & {\left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ \hfill \le & {\sum }_{ı=1}^{\mathfrak{e}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}|{\mathfrak{r}}_{ı}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-{\mathfrak{r}}_{ı}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right){|}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ & {\left(\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}\left({\mathfrak{c}}^{\kappa -1}\right){\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ \hfill \le & 2^{\tilde{\mathcal{P}}-1}{\mathbf{G}}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\left({\displaystyle \frac{{\left({\varsigma }^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }\left(\mathfrak{c}\right){{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel \gimel (\mathfrak{c}-\varrho )-\tilde{\gimel }(\mathfrak{c}-\varrho )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}.\hfill \\ \hfill \le & 2^{\tilde{\mathcal{P}}-1}{\mathbf{G}}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\left({\displaystyle \frac{({\varsigma }^{\kappa }{)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\hfill \\ \hfill & \left(\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }\left(\mathfrak{c}\right){{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel \gimel (\mathfrak{c}-\varrho )-\tilde{\gimel }(\mathfrak{c}-\varrho )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

From the above, we have

$$\begin{array}{cc}\hfill & \parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{r}\left(\mathfrak{c},\gimel \left(\mathfrak{c}\right),\gimel (\mathfrak{c}-\varrho )\right)-\mathfrak{r}\left(\mathfrak{c},\tilde{\gimel }\left(\mathfrak{c}\right),\tilde{\gimel }(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill \le & 2^{\tilde{\mathcal{P}}-1}{\mathbf{G}}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\left({\displaystyle \frac{{\left({\varsigma }^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\mathbf{G}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }{\left(\mathfrak{c}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+{\parallel \gimel (\mathfrak{c}-\varrho )-\tilde{\gimel }(\mathfrak{c}-\varrho )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

(27)

Thus, with $\forall \mathfrak{b}\in [0,\varsigma ]$, we have

$$\begin{array}{c}\hfill \parallel {\psi }_{\nu }\left(\gimel \left(\mathfrak{b}\right)\right)-{\psi }_{\nu }\left(\tilde{\gimel }\left(\mathfrak{b}\right)\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le \mathbb{Z}{\int }_0^{\mathfrak{b}}\left(\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }{\left(\mathfrak{c}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+{\parallel \gimel (\mathfrak{c}-\varrho )-\tilde{\gimel }(\mathfrak{c}-\varrho )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}.\end{array}$$

(28)

Therefore, we acquire

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\parallel {\psi }_{\nu }(\gimel \left(\mathfrak{b}\right))-{\psi }_{\nu }\left(\tilde{\gimel }\left(\mathfrak{b}\right)\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{b}\right)}}\le {\displaystyle \frac{1}{\mu \left(\mathfrak{b}\right)}}\mathbb{Z}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\hfill \\ & \left(\mu \left(\mathfrak{c}\right){\displaystyle \frac{\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }{\left(\mathfrak{c}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{c}\right)}}+\mu (\mathfrak{c}-\varrho ){\displaystyle \frac{\parallel \gimel (\mathfrak{c}-\varrho )-\tilde{\gimel }{(\mathfrak{c}-\varrho )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu (\mathfrak{c}-\varrho )}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill \le & {\displaystyle \frac{1}{\mu \left(\mathfrak{b}\right)}}\mathbb{Z}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}(\mu \left(\mathfrak{c}\right)\underset{\mathfrak{c}\in [0,\varsigma ]}{\mathrm{ess}\sup }\left({\displaystyle \frac{\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }{\left(\mathfrak{c}\right)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{c}\right)}}\right)\hfill \\ \hfill +& \mu (\mathfrak{c}-\varrho )\underset{\mathfrak{c}\in [0,\varsigma ]}{\mathrm{ess}\sup }\left({\displaystyle \frac{\parallel \gimel (\mathfrak{c}-\varrho )-\tilde{\gimel }{(\mathfrak{c}-\varrho )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu (\mathfrak{c}-\varrho )}}\right)){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill \le & {\displaystyle \frac{\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }{\left(\mathfrak{c}\right)\parallel }_{\mathfrak{B}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{b}\right)}}\mathbb{Z}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\mu \left(\mathfrak{c}\right)+\mu (\mathfrak{c}-\varrho )\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill \le & {\displaystyle \frac{2\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }{\left(\mathfrak{c}\right)\parallel }_{\mathfrak{B}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{b}\right)}}\mathbb{Z}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\mu \left(\mathfrak{c}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

(29)

Now, replace $\vartheta$ by $2\vartheta -1$ in (20).

$${\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\mu \left(\mathfrak{c}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\le {\displaystyle \frac{\Gamma (2\vartheta -1)}{\kappa }}{\displaystyle \frac{\mu \left(\mathfrak{b}\right)}{{\mathfrak{B}}^{2\vartheta -1}}}.$$

As a result, we obtain

$$\begin{array}{c}\hfill {\parallel {\psi }_{\nu }\left(\gimel \left(\mathfrak{b}\right)\right)-{\psi }_{\nu }\left(\tilde{\gimel }\left(\mathfrak{b}\right)\right){\parallel }_{\mathfrak{B}}\le {\left({\displaystyle \frac{2\mathbb{Z}\Gamma (2\vartheta -1)}{\kappa {\mathfrak{B}}^{2\vartheta -1}}}\right)}^{{\displaystyle \frac{1}{\tilde{\mathcal{P}}}}}\parallel \gimel \left(\mathfrak{c}\right)-\tilde{\gimel }\left(\mathfrak{c}\right)\parallel }_{\mathfrak{B}}.\end{array}$$

(30)

From (21), we have ${\displaystyle \frac{2\mathbb{Z}\Gamma (2\vartheta -1)}{\kappa {\mathfrak{B}}^{2\vartheta -1}}}<1$. Accordingly, the desired outcome is achieved. □

 Theorem 2. 

 Suppose ${\daleth }_1$ and ${\daleth }_2$ hold; then, 

$$\underset{\vartheta \to \tilde{\vartheta }}{lim}\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }{\parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\tilde{\vartheta }}(\mathfrak{b},\nu )\parallel }_{\tilde{\mathcal{P}}}=0,$$

(31)

where ${\varkappa }_{\vartheta }(\mathfrak{b},\nu )$ is the solution.

Proof. 

For $\vartheta$, $\tilde{\vartheta }\in ({\displaystyle \frac{1}{2}},1)$, we have

$$\begin{array}{cc}\hfill & {\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\tilde{\vartheta }}(\nu ,\mathfrak{b})={\displaystyle \frac{{\kappa }^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-\mathfrak{g}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ))\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill +& {\int }_0^{\mathfrak{b}}\left({\displaystyle \frac{{\kappa }^{\vartheta -1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}-{\displaystyle \frac{{\kappa }^{\tilde{\vartheta }-1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\tilde{\vartheta }-1}}{\Gamma \left(\tilde{\vartheta }\right)}}\right)\mathfrak{g}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu )){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill +& {\displaystyle \frac{{\kappa }^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{r}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-\mathfrak{r}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ))\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right)\hfill \\ \hfill +& {\int }_0^{\mathfrak{b}}\left({\displaystyle \frac{{\kappa }^{\vartheta -1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}-{\displaystyle \frac{{\kappa }^{\tilde{\vartheta }-1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\tilde{\vartheta }-1}}{\Gamma \left(\tilde{\vartheta }\right)}}\right)\mathfrak{r}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu )){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right).\hfill \end{array}$$

(32)

The subsequent result is inferred from (32) with the aid of (7):

$$\begin{array}{cc}\hfill & {∥{\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\tilde{\vartheta }}(\mathfrak{b},\nu )∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le 2^{\tilde{\mathcal{P}}}\mathbb{Z}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{∥{\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\tilde{\vartheta }}(\nu ,\mathfrak{b})∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\hfill \\ \hfill +& 2^{2\tilde{\mathcal{P}}-2}{∥{\int }_0^{\mathfrak{b}}\left({\displaystyle \frac{{\kappa }^{\vartheta -1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}-{\displaystyle \frac{{\kappa }^{\tilde{\vartheta }-1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\tilde{\vartheta }-1}}{\Gamma \left(\tilde{\vartheta }\right)}}\right)\mathfrak{g}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu )){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill +& 2^{2\tilde{\mathcal{P}}-2}{∥{\int }_0^{\mathfrak{b}}\left({\displaystyle \frac{{\kappa }^{\vartheta -1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}-{\displaystyle \frac{{\kappa }^{\tilde{\vartheta }-1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\tilde{\vartheta }-1}}{\Gamma \left(\tilde{\vartheta }\right)}}\right)\mathfrak{r}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu )){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right)∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}.\hfill \end{array}$$

(33)

Assume the following:

$$\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )=|{\displaystyle \frac{{\kappa }^{\vartheta -1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}-{\displaystyle \frac{{\kappa }^{\tilde{\vartheta }-1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\tilde{\vartheta }-1}}{\Gamma \left(\tilde{\vartheta }\right)}}|{\mathfrak{c}}^{\kappa -1}.$$

(34)

Using Höl-Ineq, $\left({\daleth }_1\right)$, $\left({\daleth }_2\right)$, and (7), we have

$$\begin{array}{cc}\hfill & \parallel {\int }_0^{\mathfrak{b}}\left({\displaystyle \frac{{\kappa }^{\vartheta -1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}-{\displaystyle \frac{{\kappa }^{\tilde{\vartheta }-1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\tilde{\vartheta }-1}}{\Gamma \left(\tilde{\vartheta }\right)}}\right)\mathfrak{g}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu )){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill =& {\sum }_{\iota =1}^m\tilde{\Xi }|{\int }_0^{\mathfrak{b}}\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa ){\mathfrak{g}}_{ı}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ))\mathrm{d}\mathfrak{c}{|}^{\tilde{\mathcal{P}}}\hfill \\ \hfill \le & {\sum }_{\iota =1}^m\tilde{\Xi }({\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta })\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{\tilde{\mathcal{P}}-1}}}\right)}^{\tilde{\mathcal{P}}-1}{\int }_0^{\mathfrak{b}}\left|{\mathfrak{g}}_{ı}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu )){|}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\right)\hfill \\ \hfill \le & {\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}{\left({\int }_0^{\mathfrak{b}}1\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\int }_0^{\mathfrak{b}}{\parallel \mathfrak{g}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ))\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\hfill \\ \hfill \le & {\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}{\varsigma }^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\int }_0^{\mathfrak{b}}{2}^{\tilde{\mathcal{P}}-1}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_1^{\tilde{\mathcal{P}}}(\parallel {\varkappa }_{\tilde{\vartheta }}{(\mathfrak{c},\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel {\varkappa }_{\tilde{\vartheta }}{(\mathfrak{c}-\varrho ,\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}{)+\parallel \mathfrak{g}(\mathfrak{c},0,0)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right)\hfill \\ \hfill \le & {\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}{\varsigma }^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}{2}^{\tilde{\mathcal{P}}-1}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_1^{\tilde{\mathcal{P}}}(\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}{(\mathfrak{c},\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}})+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right).\hfill \end{array}$$

(35)

Utilizing (34), $\left({\daleth }_1\right)$, and $\left({\daleth }_2\right)$ in (33),

$$\begin{array}{cc}\hfill & \parallel {\int }_0^{\mathfrak{b}}\left({\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}-{\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\tilde{\vartheta }-1}}{\Gamma \left(\tilde{\vartheta }\right)}}\right)\mathfrak{r}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu )){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill =& {\sum }_{\iota =1}^m\tilde{\Xi }|{\int }_0^{\mathfrak{b}}\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa ){\mathfrak{r}}_{ı}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ))\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){|}^{\tilde{\mathcal{P}}}\hfill \\ \hfill \le & {\sum }_{\iota =1}^m{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }\left|{\int }_0^{\mathfrak{b}}\zeta {(\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )}^2\right|{\mathfrak{r}}_{ı}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu )){|}^2\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){|}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill \le & {\sum }_{\iota =1}^m{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }{\left[{\left({\int }_0^{\mathfrak{b}}\zeta {(\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )}^2|{\mathfrak{r}}_{ı}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu )){|}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{2}{\tilde{\mathcal{P}}}}}{\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{\tilde{\mathcal{P}}}}}\right]}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill =& {\mathcal{C}}_{\tilde{\mathcal{P}}}{\int }_0^{\mathfrak{b}}\zeta {(\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )}^2{\parallel \mathfrak{r}(\mathfrak{c},{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu ),{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ))\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}{\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{\tilde{\mathcal{P}}}}}\hfill \\ \hfill \le & {\mathcal{C}}_{\tilde{\mathcal{P}}}{\left({\int }_0^{\mathfrak{b}}\zeta {(\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}{2}^{\tilde{\mathcal{P}}-1}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_2^{\tilde{\mathcal{P}}}(\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}{(\mathfrak{c},\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}})+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right).\hfill \end{array}$$

(36)

Thus, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{∥{\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\tilde{\vartheta }}(\mathfrak{b},\nu )∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{b}\right)}}\hfill \\ \hfill \le & {\displaystyle \frac{\mathbb{Z}{2}^{\tilde{\mathcal{P}}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\frac{{∥{\varkappa }_{\vartheta }(\mathfrak{c},\nu )-{\varkappa }_{\tilde{\vartheta }}(\mathfrak{c},\nu )\parallel ∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}}{\mu \left(\mathfrak{c}\right)}\mu \left(\mathfrak{c}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}}{\mu \left(\mathfrak{b}\right)}}\hfill \\ \hfill +& 2^{3\tilde{\mathcal{P}}-3}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_1^{\tilde{\mathcal{P}}}(\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}{(\mathfrak{c},\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}})+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right){\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}{\varsigma }^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill +& 2^{3\tilde{\mathcal{P}}-3}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_2^{\tilde{\mathcal{P}}}(\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}{(\mathfrak{c},\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}})+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right){\mathcal{C}}_{\tilde{\mathcal{P}}}{\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill \le & {\displaystyle \frac{\mathbb{Z}{2}^{\tilde{\mathcal{P}}}\Gamma (2\vartheta -1)}{\kappa {\mathfrak{B}}^{2\vartheta -1}}}{∥{\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\tilde{\vartheta }}(\mathfrak{b},\nu )∥}_{\mathfrak{B}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill +& 2^{3\tilde{\mathcal{P}}-3}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_1^{\tilde{\mathcal{P}}}(\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}{(\mathfrak{c},\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}})+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right){\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}{\varsigma }^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill +& 2^{3\tilde{\mathcal{P}}-3}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_2^{\tilde{\mathcal{P}}}(\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}{(\mathfrak{c},\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}})+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right){\mathcal{C}}_{\tilde{\mathcal{P}}}{\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}.\hfill \end{array}$$

(37)

Hence, we derive

$$\begin{array}{cc}\hfill & \left(1-{\displaystyle \frac{\mathbb{Z}{2}^{\tilde{\mathcal{P}}-1}\Gamma (2\vartheta -1)}{\kappa {\mathfrak{B}}^{2\vartheta -1}}}\right)\parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\tilde{\vartheta }}(\mathfrak{b},\nu ){\parallel }_{\mathfrak{B}}^{\tilde{\mathcal{P}}}\le 2^{3\tilde{\mathcal{P}}-3}\hfill \\ \hfill & \left(2^{\tilde{\mathcal{P}}-1}{\delta }_1^{\tilde{\mathcal{P}}}(\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}{(\mathfrak{c},\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}})+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right)\hfill \\ & {\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}{\varsigma }^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}+2^{3\tilde{\mathcal{P}}-3}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_2^{\tilde{\mathcal{P}}}(\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}{(\mathfrak{c},\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\underset{\mathfrak{b}\in [0,\varsigma ]}{\mathrm{ess}\sup }\parallel {\varkappa }_{\tilde{\vartheta }}(\mathfrak{c}-\varrho ,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}})+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right)\hfill \\ & {\mathcal{C}}_{\tilde{\mathcal{P}}}{\left({\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}.\hfill \end{array}$$

(38)

Next, we demonstrate

$$\underset{\tilde{\vartheta }\to \vartheta }{lim}\underset{\mathfrak{b}\in [0,\varsigma ]}{s\mathfrak{u}p}{\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\mathrm{d}\mathfrak{c}=0.$$

To see this note,

$$\begin{array}{cc}\hfill & {\int }_0^{\mathfrak{b}}{\left(\zeta (\mathfrak{b},\mathfrak{c},\vartheta ,\tilde{\vartheta },\kappa )\right)}^2\mathrm{d}\mathfrak{c}={\int }_0^{\mathfrak{b}}{\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}}{{\Gamma }^2\left(\vartheta \right)}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}+{\int }_0^{\mathfrak{b}}{\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\tilde{\vartheta }-2}}{{\Gamma }^2\left(\tilde{\vartheta }\right)}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ \hfill -& 2{\int }_0^{\mathfrak{b}}{\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta +\tilde{\vartheta }-2}}{\Gamma \left(\vartheta \right)\Gamma \left(\tilde{\vartheta }\right)}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ \hfill \le & \underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}}{{\Gamma }^2\left(\vartheta \right)}}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}+\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\tilde{\vartheta }-2}}{{\Gamma }^2\left(\tilde{\vartheta }\right)}}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill -& 2\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta +\tilde{\vartheta }-2}}{\Gamma \left(\vartheta \right)\Gamma \left(\tilde{\vartheta }\right)}}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill =& \mathbf{G}\left({\displaystyle \frac{{\left({\mathfrak{b}}^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\right){\displaystyle \frac{1}{{\Gamma }^2\left(\vartheta \right)}}+\mathbf{G}\left({\displaystyle \frac{{\left({\mathfrak{b}}^{\kappa }\right)}^{(2\tilde{\vartheta }-1)}}{(2\tilde{\vartheta }-1)}}\right){\displaystyle \frac{1}{{\Gamma }^2\left(\tilde{\vartheta }\right)}}-\mathbf{G}{\displaystyle \frac{2{\left({\mathfrak{b}}^{\kappa }\right)}^{(\vartheta +\tilde{\vartheta }-1)}}{(\vartheta +\tilde{\vartheta }-1)\Gamma \left(\vartheta \right)\Gamma \left(\tilde{\vartheta }\right)}}.\hfill \end{array}$$

(39)

Hence, the proof is complete. □

 Theorem 3. 

Assume $\nu ,\mathfrak{u}$, then

$${∥{\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\vartheta }{(\mathfrak{b},\mathfrak{u})|}_{\tilde{\mathcal{P}}}\le \delta \parallel \nu -\mathfrak{u}∥}_{\tilde{\mathcal{P}}},\forall \mathfrak{b}\in [0,\varsigma ],$$

(40)

where ${\varkappa }_{\vartheta }(\mathfrak{b},\nu )$ is the solution.

Proof. 

We have

$$\begin{array}{cc}\hfill & {\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\vartheta }(\mathfrak{b},\mathfrak{u})={\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}-{\displaystyle \frac{\mathfrak{u}}{\Gamma (\aleph )\Gamma (2-\aleph )}}\hfill \\ & +{\displaystyle \frac{{\kappa }^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-\mathfrak{g}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}))\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ & +{\displaystyle \frac{{\kappa }^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{r}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-\mathfrak{r}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}))\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right).\hfill \end{array}$$

(41)

Utilizing (7) in the above, we obtain

$$\begin{array}{cc}\hfill & \parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\vartheta }(\mathfrak{b},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le 2^{\tilde{\mathcal{P}}-1}\parallel {\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}-{\displaystyle \frac{\mathfrak{u}}{\Gamma (\aleph )\Gamma (2-\aleph )}}{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill +& {\displaystyle \frac{2^{2\tilde{\mathcal{P}}-2}{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{(\Gamma \left(\vartheta \right))}^{\tilde{\mathcal{P}}}}}{∥{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\right(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-\mathfrak{g}\left(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}))\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill +& {\displaystyle \frac{2^{2\tilde{\mathcal{P}}-2}{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{(\Gamma \left(\vartheta \right))}^{\tilde{\mathcal{P}}}}}{∥{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}(\mathfrak{r}\left(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))\right)-\mathfrak{r}\left(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right)∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}.\hfill \end{array}$$

(42)

Using Höl-Ineq and $\left({\daleth }_1\right)$, we extract

$$\begin{array}{cc}\hfill & \parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\right(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-\mathfrak{g}\left(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}))\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill =& {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }\left|{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\right({\mathfrak{g}}_{ı}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-{\mathfrak{g}}_{ı}\left(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}))\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{|}^{\tilde{\mathcal{P}}}\hfill \\ \hfill \le & {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }({\left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{{\displaystyle \frac{(\vartheta -1)(\tilde{\mathcal{P}}-2)}{\tilde{\mathcal{P}}-1}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{\tilde{\mathcal{P}}-1}}}\mathrm{d}\mathfrak{c}\right)}^{\tilde{\mathcal{P}}-1}\hfill \\ & \left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\right|{\mathfrak{g}}_{ı}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-{\mathfrak{g}}_{ı}\left(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u})\left)\right|{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right))\hfill \\ \hfill \le & {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }({\left(\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{1}{1-\tilde{\mathcal{P}}}}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{{\displaystyle \frac{(\vartheta -1)(\tilde{\mathcal{P}}-2)}{\tilde{\mathcal{P}}-1}}}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right)}^{\tilde{\mathcal{P}}-1}\hfill \\ \hfill & \left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\right|{\mathfrak{g}}_{ı}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-{\mathfrak{g}}_{ı}\left(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u})\left)\right|{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right))\hfill \\ \hfill \le & 2^{\tilde{\mathcal{P}}-1}{\mathfrak{f}}^{\tilde{\mathcal{P}}-1}\left({\displaystyle \frac{{\delta }_1^{\tilde{\mathcal{P}}}{\left({\varsigma }^{\kappa }\right)}^{(\tilde{\mathcal{P}}\vartheta -2\vartheta +1)}{(\tilde{\mathcal{P}}-1)}^{\tilde{\mathcal{P}}-1}}{{\left(\tilde{\mathcal{P}}\vartheta -2\vartheta +1\right)}^{\tilde{\mathcal{P}}-1}}}\right){\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\hfill \\ & \left(\parallel {\varkappa }_{\vartheta }(\mathfrak{c},\nu )-{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel {\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )-{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}.\hfill \\ \hfill \le & 2^{\tilde{\mathcal{P}}-1}{\mathfrak{f}}^{\tilde{\mathcal{P}}-1}\left({\displaystyle \frac{{\delta }_1^{\tilde{\mathcal{P}}}{\left({\varsigma }^{\kappa }\right)}^{(\tilde{\mathcal{P}}\vartheta -2\vartheta +1)}{(\tilde{\mathcal{P}}-1)}^{\tilde{\mathcal{P}}-1}}{{\left(\tilde{\mathcal{P}}\vartheta -2\vartheta +1\right)}^{\tilde{\mathcal{P}}-1}}}\right)\hfill \\ & \underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\parallel {\varkappa }_{\vartheta }(\mathfrak{c},\nu )-{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel {\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )-{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill =& 2^{\tilde{\mathcal{P}}-1}{\mathfrak{f}}^{\tilde{\mathcal{P}}-1}\left({\displaystyle \frac{{\delta }_1^{\tilde{\mathcal{P}}}{\left({\varsigma }^{\kappa }\right)}^{(\tilde{\mathcal{P}}\vartheta -2\vartheta +1)}{(\tilde{\mathcal{P}}-1)}^{\tilde{\mathcal{P}}-1}}{{\left(\tilde{\mathcal{P}}\vartheta -2\vartheta +1\right)}^{\tilde{\mathcal{P}}-1}}}\right)\mathbf{G}\hfill \\ & {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\parallel {\varkappa }_{\vartheta }(\mathfrak{c},\nu )-{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel {\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )-{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

(43)

Through $\left({\daleth }_1\right)$, Höl-Ineq, and Bu-Da-Gu-Ineq, we have

$$\begin{array}{cc}\hfill & \parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{r}\right(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-\mathfrak{r}\left(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}))\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ \hfill =& {\sum }_{ı=1}^{\mathfrak{e}}\tilde{\Xi }\left|{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\right({\mathfrak{r}}_{ı}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-{\mathfrak{r}}_{ı}\left(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}))\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){|}^{\tilde{\mathcal{P}}}\hfill \\ \hfill \le & {\sum }_{ı=1}^{\mathfrak{e}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }\left|{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\right|{\mathfrak{r}}_{ı}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-{\mathfrak{r}}_{ı}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u})){|}^2{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}{|}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill \le & {\sum }_{ı=1}^{\mathfrak{e}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left|{\mathfrak{r}}_{ı}\right(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-{\mathfrak{r}}_{ı}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u})){|}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ & {\left({\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ \hfill \le & {\sum }_{ı=1}^{\mathfrak{e}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left|{\mathfrak{r}}_{ı}\right(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))-{\mathfrak{r}}_{ı}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u})){|}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ & {\left(\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ \hfill \le & 2^{\tilde{\mathcal{P}}-1}{\mathbf{G}}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}{\left({\displaystyle \frac{{\left({\varsigma }^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ \hfill & {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\parallel {\varkappa }_{\vartheta }(\mathfrak{c},\nu )-{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel {\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )-{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}.\hfill \\ \hfill \le & 2^{\tilde{\mathcal{P}}-1}{\mathbf{G}}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}{\left({\displaystyle \frac{{\left({\varsigma }^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ \hfill & \underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\parallel {\varkappa }_{\vartheta }(\mathfrak{c},\nu )-{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel {\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )-{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}.\hfill \\ \hfill =& 2^{\tilde{\mathcal{P}}-1}{\mathbf{G}}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}{\left({\displaystyle \frac{{\left({\varsigma }^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\mathbf{G}\hfill \\ & {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\parallel {\varkappa }_{\vartheta }(\mathfrak{c},\nu )-{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel {\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )-{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

(44)

From (42), using (43) and (44), we obtain

$$\begin{array}{cc}\hfill \parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )& -{\varkappa }_{\vartheta }(\mathfrak{b},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le 2^{\tilde{\mathcal{P}}-1}{∥{\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}-{\displaystyle \frac{\mathfrak{u}}{\Gamma (\aleph )\Gamma (2-\aleph )}}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ & +2^{\tilde{\mathcal{P}}}\mathbb{Z}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\left(\parallel {\varkappa }_{\vartheta }(\mathfrak{c},\nu )-{\varkappa }_{\vartheta }(\mathfrak{c},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

(45)

With the Grönwall inequality, we achieve

$$\begin{array}{cc}\hfill \parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )& -{\varkappa }_{\vartheta }(\mathfrak{b},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le 2^{\tilde{\mathcal{P}}-1}exp\left(2^{\tilde{\mathcal{P}}-1}\mathbb{Z}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right)\hfill \\ & {∥{\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}-{\displaystyle \frac{\mathfrak{u}}{\Gamma (\aleph )\Gamma (2-\aleph )}}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}.\hfill \end{array}$$

From above

$$\begin{array}{cc}\hfill \parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )& -{\varkappa }_{\vartheta }(\mathfrak{b},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le 2^{\tilde{\mathcal{P}}-1}{\mathbb{E}}_{2\vartheta -1}\left(2^{\tilde{\mathcal{P}}-1}\mathbb{Z}\Gamma (2\vartheta -1){\left({\mathfrak{b}}^{\kappa }\right)}^{(2\vartheta -1)}\right)\hfill \\ & {∥{\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}-{\displaystyle \frac{\mathfrak{u}}{\Gamma (\aleph )\Gamma (2-\aleph )}}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}.\hfill \end{array}$$

Hence,

$$\begin{array}{c}\hfill \underset{\nu \to \mathfrak{u}}{lim}\parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\vartheta }(\mathfrak{b},\mathfrak{u}){\parallel }_{\tilde{\mathcal{P}}}=0.\end{array}$$

□

3.2. Regularity

Next, we prove the most important characteristic of the solution of Hilfer–Katugampola FDSDEs, known as regularity.

 Theorem 4. 

Assume $\left({\daleth }_1\right)$ and $\left({\daleth }_2\right)$ are valid. Afterward, for $\mathcal{U}>0$, which relies on $\vartheta ,\delta ,\mathfrak{a},\tilde{\mathcal{P}},$ and ς, we obtain

$${∥{\varkappa }_{\vartheta }(\nu ,\mathfrak{b})-{\varkappa }_{\vartheta }(\nu ,{\mathfrak{b}}_1)∥}_{\tilde{\mathcal{P}}}\le \mathcal{U}{|\mathfrak{b}-{\mathfrak{b}}_1|}^{\vartheta -{\displaystyle \frac{1}{2}}},\forall \mathfrak{b},{\mathfrak{b}}_1\in [0,\varsigma ].$$

(46)

Proof. 

For $\mathfrak{b}>{\mathfrak{b}}_1$, we achieve

$$\begin{array}{cc}\hfill & {∥{\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\vartheta }({\mathfrak{b}}_1,\nu )∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)2^{2-2\tilde{\mathcal{P}}}}}{∥{\int }_{{\mathfrak{b}}_1}^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\mathfrak{g}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ & +{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)2^{2-2\tilde{\mathcal{P}}}}}{∥{\int }_{{\mathfrak{b}}_1}^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\mathfrak{r}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right)∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ & +{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)2^{2-2\tilde{\mathcal{P}}}}}{∥{\int }_0^{{\mathfrak{b}}_1}|{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}-{({\mathfrak{b}}_1^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}|\mathfrak{g}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\hfill \\ & +{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)2^{2-2\tilde{\mathcal{P}}}}}{∥{\int }_0^{{\mathfrak{b}}_1}|{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}-{({\mathfrak{b}}_1^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}|\mathfrak{r}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right)∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}.\hfill \end{array}$$

(47)

Through Höl-Ineq and Bu-Da-Gu-Ineq,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)2^{2-2\tilde{\mathcal{P}}}}{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}}\parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\vartheta }({\mathfrak{b}}_1,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le {\displaystyle \frac{{(\tilde{\mathcal{P}}-1)}^{\tilde{\mathcal{P}}-1}}{{(\tilde{\mathcal{P}}\vartheta -1)}^{\tilde{\mathcal{P}}-1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{b}}_1^{\kappa })}^{1-\vartheta \tilde{\mathcal{P}}}}}{\int }_{{\mathfrak{b}}_1}^{\mathfrak{b}}\parallel \mathfrak{g}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\hfill \\ \hfill +& {\mathcal{C}}_{\tilde{\mathcal{P}}}\left({\int }_{{\mathfrak{b}}_1}^{\mathfrak{b}}\parallel \mathfrak{r}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu )){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right){\left({\int }_{{\mathfrak{b}}_1}^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}\hfill \\ \hfill +& {\displaystyle \frac{1}{{\left({\varsigma }^{\kappa }\right)}^{\frac{2-\tilde{\mathcal{P}}}{2}}}}{\int }_0^{{\mathfrak{b}}_1}{\parallel \mathfrak{g}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}{\left({\int }_0^{{\mathfrak{b}}_1}|{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}-{({\mathfrak{b}}_1^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}{|}^2{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill +& {\mathcal{C}}_{\tilde{\mathcal{P}}}{\int }_0^{{\mathfrak{b}}_1}{\left({({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}-{({\mathfrak{b}}_1^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\right)}^2{\parallel \mathfrak{r}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ),{\varkappa }_{\vartheta }(\mathfrak{c}-\varrho ,\nu ))\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ \hfill \times & {\left({\int }_0^{{\mathfrak{b}}_1}{\left({({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}-{({\mathfrak{b}}_1^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\right)}^2{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}-2}{2}}}.\hfill \end{array}$$

We obtain the following:

$${∥\mathfrak{g}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ))∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le 2^{\tilde{\mathcal{P}}-1}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_1^{\tilde{\mathcal{P}}}(\parallel {\varkappa }_{\vartheta }(\mathfrak{c},\nu )){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel {\varkappa }_{\vartheta }{(\mathfrak{c}-\varrho ,\nu ))\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}{)+\parallel \mathfrak{g}(\mathfrak{c},0)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right)\le 2^{\tilde{\mathcal{P}}-1}\left(2^{\tilde{\mathcal{P}}}{\delta }_1^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right).$$

$${∥\mathfrak{r}(\mathfrak{c},{\varkappa }_{\vartheta }(\mathfrak{c},\nu ))∥}_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le 2^{\tilde{\mathcal{P}}-1}\left(2^{\tilde{\mathcal{P}}-1}{\delta }_2^{\tilde{\mathcal{P}}}(\parallel {\varkappa }_{\vartheta }{(\mathfrak{c},\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}+\parallel {\varkappa }_{\vartheta }{(\mathfrak{c}-\varrho ,\nu )\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}{)+\parallel \mathfrak{r}(\mathfrak{c},0)\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\right)\le 2^{\tilde{\mathcal{P}}-1}\left(2^{\tilde{\mathcal{P}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right).$$

Furthermore, we have

$$\begin{array}{ll}\hfill {\int }_0^{{\mathfrak{b}}_1}& {\left({({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}-{({\mathfrak{b}}_1^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\right)}^2{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\hfill \\ \hfill & \le \underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\mathfrak{c}}^{\kappa -1}{\int }_0^{{\mathfrak{b}}_1}{\left({({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}-{\left({\mathfrak{b}}_1^{\kappa }-{\mathfrak{c}}^{\kappa }\right)}^{\vartheta -1}\right)}^2{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill & \le \mathbf{G}{\int }_0^{{\mathfrak{b}}_1}\left({({\mathfrak{b}}_1^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}-{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{2\vartheta -2}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ \hfill & ={\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{b}}_1^{\kappa })}^{(2\vartheta -1)}}{(2\vartheta -1)}}+{\displaystyle \frac{{\left({\mathfrak{b}}_1^{\kappa }\right)}^{(2\vartheta -1)}-{\left({\mathfrak{b}}^{\kappa }\right)}^{(2\vartheta -1)}}{(2\vartheta -1)}}\hfill \\ \hfill & \le {\displaystyle \frac{{({\mathfrak{b}}^{\kappa }-{\mathfrak{b}}_1^{\kappa })}^{(2\vartheta -1)}}{(2\vartheta -1)}}.\hfill \end{array}$$

(48)

So, we extract

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)2^{2-2\tilde{\mathcal{P}}}}{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}}\parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )-& {\varkappa }_{\vartheta }({\mathfrak{b}}_1,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le {\displaystyle \frac{{(2\tilde{\mathcal{P}}-2)}^{\tilde{\mathcal{P}}-1}}{{(\tilde{\mathcal{P}}\vartheta -1)}^{\tilde{\mathcal{P}}-1}}}{\left({\mathfrak{b}}^{\kappa }-{\mathfrak{b}}_1^{\kappa }\right)}^{{\displaystyle \frac{(2\vartheta -1)\tilde{\mathcal{P}}}{2}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_1^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right){\left({\varsigma }^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill +& {\displaystyle \frac{1}{{(2\vartheta -1)}^{\frac{\tilde{\mathcal{P}}}{2}}}}{\left({\mathfrak{b}}^{\kappa }-{\mathfrak{b}}_1^{\kappa }\right)}^{{\displaystyle \frac{(2\vartheta -1)\tilde{\mathcal{P}}}{2}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right)2^{\tilde{\mathcal{P}}-1}{\mathcal{C}}_{\tilde{\mathcal{P}}}\hfill \\ \hfill +& {\displaystyle \frac{2^{\tilde{\mathcal{P}}-1}}{{(2\vartheta -1)}^{\tilde{\mathcal{P}}-1}}}{\left({\mathfrak{b}}^{\kappa }-{\mathfrak{b}}_1^{\kappa }\right)}^{{\displaystyle \frac{(2\vartheta -1)\tilde{\mathcal{P}}}{2}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_1^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right){\left({\varsigma }^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill +& {\displaystyle \frac{1}{{(2\vartheta -1)}^{\frac{\tilde{\mathcal{P}}}{2}}}}{\left({\mathfrak{b}}^{\kappa }-{\mathfrak{b}}_1^{\kappa }\right)}^{{\displaystyle \frac{(2\vartheta -1)\tilde{\mathcal{P}}}{2}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right)2^{\tilde{\mathcal{P}}-1}{\mathcal{C}}_{\tilde{\mathcal{P}}}.\hfill \end{array}$$

It follows from the above that

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)2^{2-2\tilde{\mathcal{P}}}}{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}}\parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )-& {\varkappa }_{\vartheta }({\mathfrak{b}}_1,\nu ){\parallel }_{\tilde{\mathcal{P}}}^{\tilde{\mathcal{P}}}\le ({\displaystyle \frac{{(2\tilde{\mathcal{P}}-2)}^{\tilde{\mathcal{P}}-1}}{{(\tilde{\mathcal{P}}\vartheta -1)}^{\tilde{\mathcal{P}}-1}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_1^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right){\left({\varsigma }^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill +& {\displaystyle \frac{1}{{(2\vartheta -1)}^{\frac{\tilde{\mathcal{P}}}{2}}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right)2^{\tilde{\mathcal{P}}-1}{\mathcal{C}}_{\tilde{\mathcal{P}}}\hfill \\ \hfill +& {\displaystyle \frac{2^{\tilde{\mathcal{P}}-1}}{{(2\vartheta -1)}^{\tilde{\mathcal{P}}-1}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_1^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right){\left({\varsigma }^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill +& {\displaystyle \frac{1}{{(2\vartheta -1)}^{\frac{\tilde{\mathcal{P}}}{2}}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right)2^{\tilde{\mathcal{P}}-1}{\mathcal{C}}_{\tilde{\mathcal{P}}}){\left({\mathfrak{b}}^{\kappa }-{\mathfrak{b}}_1^{\kappa }\right)}^{{\displaystyle \frac{(2\vartheta -1)\tilde{\mathcal{P}}}{2}}}.\hfill \end{array}$$

Therefore, we obtain

$${∥{\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\vartheta }({\mathfrak{b}}_1,\nu )∥}_{\tilde{\mathcal{P}}}\le \mathcal{U}{\left({\mathfrak{b}}^{\kappa }-{\mathfrak{b}}_1^{\kappa }\right)}^{\tilde{\mathcal{P}}\vartheta -{\displaystyle \frac{1}{2}}\tilde{\mathcal{P}}}.$$

where,

$$\begin{array}{cc}\hfill \mathcal{U}=& {\displaystyle \frac{{(2\tilde{\mathcal{P}}-2)}^{\tilde{\mathcal{P}}-1}}{{(\tilde{\mathcal{P}}\vartheta -1)}^{\tilde{\mathcal{P}}-1}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_1^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right){\left({\varsigma }^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}+{\displaystyle \frac{1}{{(2\vartheta -1)}^{\frac{\tilde{\mathcal{P}}}{2}}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right)2^{\tilde{\mathcal{P}}-1}{\mathcal{C}}_{\tilde{\mathcal{P}}}\hfill \\ \hfill +& {\displaystyle \frac{2^{\tilde{\mathcal{P}}-1}}{{(2\vartheta -1)}^{\tilde{\mathcal{P}}-1}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_1^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right){\left({\varsigma }^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}+{\displaystyle \frac{1}{{(2\vartheta -1)}^{\frac{\tilde{\mathcal{P}}}{2}}}}\left(2^{\tilde{\mathcal{P}}}{\delta }_2^{\tilde{\mathcal{P}}}{\mathfrak{a}}_1+{\mathfrak{a}}^{\tilde{\mathcal{P}}}\right)2^{\tilde{\mathcal{P}}-1}{\mathcal{C}}_{\tilde{\mathcal{P}}}.\hfill \end{array}$$

Thus, we obtain the following:

$$\underset{{\mathfrak{b}}_1\to \mathfrak{b}}{lim}\parallel {\varkappa }_{\vartheta }(\mathfrak{b},\nu )-{\varkappa }_{\vartheta }({\mathfrak{b}}_1,\nu ){\parallel }_{\tilde{\mathcal{P}}}=0.$$

□

4. Averaging Principle

This section includes the Av-Pr.

 Lemma 6. 

With $\left({\daleth }_4\right)$ and $\left({\daleth }_5\right)$, we obtain

$${∥\tilde{\mathfrak{r}}(\Lambda ,{\rm Y})∥}^{\tilde{\mathcal{P}}}\le {\delta }_6\left(1+{\parallel \Lambda \parallel }^{\tilde{\mathcal{P}}}+{\parallel {\rm Y}\parallel }^{\tilde{\mathcal{P}}}\right),$$

where ${\delta }_6=\left(2^{\tilde{\mathcal{P}}-1}{\xi }_2\left({\varsigma }_1\right)+6^{\tilde{\mathcal{P}}-1}{\delta }_4^{\tilde{\mathcal{P}}}\right)$.

Proof. 

With $\left({\daleth }_4\right),\left({\daleth }_5\right)$ and (7), we obtain

$$\begin{array}{cc}\hfill {∥\tilde{\mathfrak{r}}(\Lambda ,{\rm Y})∥}^{\tilde{\mathcal{P}}}& \le \parallel \mathfrak{r}(\mathfrak{b},\Lambda ,{\rm Y})-\tilde{\mathfrak{r}}{(\Lambda ,{\rm Y})\parallel }^{\tilde{\mathcal{P}}}+2^{\tilde{\mathcal{P}}-1}{\parallel \mathfrak{r}(\mathfrak{b},\Lambda ,{\rm Y})\parallel }^{\tilde{\mathcal{P}}}{2}^{\tilde{\mathcal{P}}-1}\hfill \\ & \le 2^{\tilde{\mathcal{P}}-1}{\xi }_2\left({\varsigma }_1\right)\left(1+{\parallel \Lambda \parallel }^{\tilde{\mathcal{P}}}+{\parallel {\rm Y}\parallel }^{\tilde{\mathcal{P}}}\right)+2^{\tilde{\mathcal{P}}-1}{\delta }_4^{\tilde{\mathcal{P}}}{(1+\parallel \Lambda \parallel +\parallel {\rm Y}\parallel )}^{\tilde{\mathcal{P}}}\hfill \\ & \le \left({\xi }_2\left({\varsigma }_1{2}^{\tilde{\mathcal{P}}-1}\right)+6^{\tilde{\mathcal{P}}-1}{\delta }_4^{\tilde{\mathcal{P}}}\right)\left(1+{\parallel \Lambda \parallel }^{\tilde{\mathcal{P}}}+{\parallel {\rm Y}\parallel }^{\tilde{\mathcal{P}}}\right).\hfill \end{array}$$

Now, we deal with the important lemma, which is useful for proving Av-Pr. □

 Lemma 7. 

Suppose $\mathfrak{b}=\phi \hslash$. Afterward,

$${}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel (\phi \hslash )={\phi }^{\kappa \vartheta }{}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel \left(\mathfrak{b}\right).$$

Proof. 

From (2), we have

$$\begin{array}{c}\hfill {}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel \left(\mathfrak{b}\right)={}^{\kappa }\mathcal{I}_{0^{\mathrm{+}}}^{\varpi (1-\vartheta )}{}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\lambda }\gimel \left(\mathfrak{b}\right),\lambda =\vartheta +\varpi -\vartheta \varpi .\end{array}$$

From the above, we have

$$\begin{array}{cc}\hfill {}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel (\phi \hslash )& ={\displaystyle \frac{{\kappa }^{1-\varpi (1-\vartheta )}}{\Gamma \left(\varpi \right(1-\vartheta \left)\right)}}{\int }_{\mathfrak{a}}^{\hslash }{({\hslash }^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\varpi (1-\vartheta )-1}{\mathfrak{c}}^{\kappa -1}\hfill \\ & {\displaystyle \frac{{\kappa }^{\lambda }}{\Gamma (1-\lambda )}}\left({\hslash }^{1-\kappa }{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\hslash }}\right){\int }_0^{\hslash }{\displaystyle \frac{{\mathfrak{c}}^{\kappa -1}}{{({\hslash }^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\lambda }}}\gimel (\phi \mathfrak{c})\mathrm{d}\mathfrak{c}\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

Let $\phi \mathfrak{c}=\theta$ and $\mathfrak{c}={\displaystyle \frac{\theta }{\phi }}$.

$$\begin{array}{cc}\hfill {}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel (\phi \hslash )& ={\displaystyle \frac{{\kappa }^{1-\varpi (1-\vartheta )}}{\Gamma \left(\varpi \right(1-\vartheta \left)\right)}}{\int }_0^{\phi \hslash }{\left({\hslash }^{\kappa }-{\left({\displaystyle \frac{\theta }{\phi }}\right)}^{\kappa }\right)}^{\varpi (1-\vartheta )-1}{\left({\displaystyle \frac{\theta }{\phi }}\right)}^{\kappa -1}\hfill \\ & {\displaystyle \frac{{\kappa }^{\lambda }}{\Gamma (1-\lambda )}}\left({\hslash }^{1-\kappa }{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\hslash }}\right){\int }_{\mathfrak{a}}^{\phi \hslash }{\displaystyle \frac{{\left(\frac{\theta }{\phi }\right)}^{\kappa -1}}{{\left({\hslash }^{\kappa }-{\left(\frac{\theta }{\phi }\right)}^{\kappa }\right)}^{\lambda }}}\gimel \left(\theta \right){\displaystyle \frac{\mathrm{d}\theta }{\phi }}{\displaystyle \frac{\mathrm{d}\theta }{\phi }},\hfill \end{array}$$

or

$$\begin{array}{cc}\hfill {}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel (\phi \hslash )& ={\displaystyle \frac{{\kappa }^{1-\varpi (1-\vartheta )}}{\Gamma \left(\varpi \right(1-\vartheta \left)\right)}}{\int }_0^{\phi \hslash }{\left({\displaystyle \frac{{\phi }^{\kappa }{\hslash }^{\kappa }-{\theta }^{\kappa }}{{\phi }^{\kappa }}}\right)}^{\varpi (1-\vartheta )-1}{\left({\displaystyle \frac{\theta }{\phi }}\right)}^{\kappa -1}\hfill \\ & {\displaystyle \frac{{\kappa }^{\lambda }}{\Gamma (1-\lambda )}}\left({\hslash }^{1-\kappa }{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\hslash }}\right){\int }_{\mathfrak{a}}^{\phi \hslash }{\phi }^{\kappa \lambda }{\displaystyle \frac{{\left(\frac{\theta }{\phi }\right)}^{\kappa -1}}{{\left({\phi }^{\kappa }{\hslash }^{\kappa }-{\theta }^{\kappa }\right)}^{\lambda }}}\gimel \left(\theta \right){\displaystyle \frac{\mathrm{d}\theta }{\phi }}{\displaystyle \frac{\mathrm{d}\theta }{\phi }}.\hfill \end{array}$$

Taking $\phi \hslash =\mathfrak{b}$, $\hslash ={\displaystyle \frac{\mathfrak{b}}{\phi }}$, and ${\displaystyle \frac{d}{d\hslash }}={\displaystyle \frac{d}{\mathrm{d}\mathfrak{b}}}.{\displaystyle \frac{\mathrm{d}\mathfrak{b}}{d\hslash }}=\phi {\displaystyle \frac{d}{\mathrm{d}\mathfrak{b}}}$, we have

$$\begin{array}{cc}\hfill {}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel (\phi \hslash )& ={\displaystyle \frac{{\kappa }^{1-\varpi (1-\vartheta )}}{\Gamma \left(\varpi \right(1-\vartheta \left)\right)}}{\int }_0^{\phi \hslash }{\left({\displaystyle \frac{{\mathfrak{b}}^{\kappa }-{\theta }^{\kappa }}{{\phi }^{\kappa }}}\right)}^{\varpi (1-\vartheta )-1}{\left({\displaystyle \frac{\theta }{\phi }}\right)}^{\kappa -1}\hfill \\ & {\displaystyle \frac{\phi {\kappa }^{\lambda }}{\Gamma (1-\lambda )}}\left({\displaystyle \frac{{\mathfrak{b}}^{1-\kappa }}{{\phi }^{1-\kappa }}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{b}}}\right){\int }_{\mathfrak{a}}^{\phi \hslash }{\phi }^{\kappa \lambda }{\displaystyle \frac{{\left(\frac{\theta }{\phi }\right)}^{\kappa -1}}{{\left({\mathfrak{b}}^{\kappa }-{\theta }^{\kappa }\right)}^{\lambda }}}\gimel \left(\theta \right){\displaystyle \frac{\mathrm{d}\theta }{\phi }}{\displaystyle \frac{\mathrm{d}\theta }{\phi }}\hfill \end{array}$$

So, we have the following result:

$${}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel (\phi \hslash )={\phi }^{\kappa \vartheta }{}^{\kappa }\mathcal{T}_{\mathrm{a+}}^{\vartheta ,\varpi }\gimel \left(\mathfrak{b}\right).$$

Now, consider the following system for the Av-Pr:

$$\{\begin{array}{cc}{}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel \left(\mathfrak{b}\right)=\mathfrak{g}({\displaystyle \frac{\mathfrak{b}}{\epsilon }},\gimel \left(\mathfrak{b}\right),\gimel (\mathfrak{b}-\varrho ))+\mathfrak{r}({\displaystyle \frac{\mathfrak{b}}{\epsilon }},\gimel \left(\mathfrak{b}\right),\gimel \left(\mathfrak{b}-\varrho \right)){\displaystyle \frac{\mathrm{d}\mathcal{W}\left(\mathfrak{b}\right)}{d\mathfrak{b}}},\hfill & \\ \gimel \left(0\right)=\nu .\hfill \end{array}$$

(49)

Utilizing ${\displaystyle \frac{\mathfrak{b}}{\epsilon }}=\Theta$, Lemma 7 in (49),

$$\begin{array}{cc}\hfill & {}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel \left(\epsilon \Theta \right)=\mathfrak{g}(\Theta ,\gimel (\epsilon \Theta ),\gimel \left(\epsilon (\Theta -\varrho )\right))+\mathfrak{r}(\Theta ,\gimel \left(\epsilon \Theta \right),\gimel \left(\epsilon (\Theta -\varrho )\right)){\displaystyle \frac{\mathrm{d}\mathcal{W}(\epsilon \Theta )}{\epsilon d\Theta }}.\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill & {\epsilon }^{-\kappa \vartheta }{}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }{\gimel }_{\epsilon }(\Theta )=\mathfrak{g}(\Theta ,{\gimel }_{\epsilon }(\Theta ),{\gimel }_{\epsilon }(\varrho \Theta ))+{\epsilon }^{-{\displaystyle \frac{1}{2}}}\mathfrak{r}(\Theta ,{\gimel }_{\epsilon }(\Theta ),{\gimel }_{\epsilon }\left(\varrho \Theta \right)){\displaystyle \frac{\mathrm{d}\mathcal{W}(\Theta )}{d\Theta }}.\hfill \end{array}$$

Therefore, we obtain

$$\left\{\begin{array}{cc}\hfill & {}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }{\gimel }_{\epsilon }\left(\mathfrak{b}\right)={\epsilon }^{\kappa \vartheta }\mathfrak{g}\left(\mathfrak{b},{\gimel }_{\epsilon }\left(\mathfrak{b}\right),{\gimel }_{\epsilon }(\mathfrak{b}-\varrho )\right)+{\epsilon }^{\kappa \vartheta -{\displaystyle \frac{1}{2}}}\mathfrak{r}\left(\mathfrak{b},{\gimel }_{\epsilon }\left(\mathfrak{b}\right),{\gimel }_{\epsilon }(\mathfrak{b}-\varrho )\right){\displaystyle \frac{\mathrm{d}\mathcal{W}\left(\mathfrak{b}\right)}{\mathrm{d}\mathfrak{b}}},\hfill \\ & {\gimel }_{\epsilon }\left(0\right)=\nu .\hfill \end{array}\right.$$

(50)

Thus, (50) can be expressed integrally as

$$\begin{array}{cc}\hfill {\gimel }_{\epsilon }\left(\mathfrak{b}\right)& ={\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}\hfill \\ & +{\epsilon }^{\vartheta \kappa }{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{\mathfrak{c}}^{\kappa -1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{1-\vartheta }\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)\mathrm{d}\mathfrak{c}\hfill \\ & +{\epsilon }^{\vartheta \kappa -{\displaystyle \frac{1}{2}}}{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{\mathfrak{c}}^{\kappa -1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{1-\vartheta }\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right),\hfill \end{array}$$

(51)

and as $\epsilon \in (0,{\epsilon }_0]$ possessing a stationary point ${\epsilon }_0$. As a consequence of (51), we find

$$\begin{array}{cc}\hfill {\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right)& ={\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}\hfill \\ & +{\epsilon }^{\vartheta \kappa }{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{\mathfrak{c}}^{\kappa -1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{1-\vartheta }\tilde{\mathfrak{g}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\mathrm{d}\mathfrak{c}\hfill \\ & +{\epsilon }^{\vartheta \kappa -{\displaystyle \frac{1}{2}}}{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{\mathfrak{c}}^{\kappa -1}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{1-\vartheta }\tilde{\mathfrak{r}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right),\hfill \end{array}$$

(52)

here, $\tilde{\mathfrak{g}}:{\mathbb{R}}^{\mathfrak{e}}\times {\mathbb{R}}^{\mathfrak{e}}\to {\mathbb{R}}^{\mathfrak{e}},\tilde{\mathfrak{r}}:{\mathbb{R}}^{\mathfrak{e}}\times {\mathbb{R}}^{\mathfrak{e}}\to {\mathbb{R}}^{\mathfrak{e}\times \sigma }$. □

 Theorem 5. 

When $\left({\daleth }_3\right)$ to $\left({\daleth }_5\right)$ are valid, for $\mho >0$, $\alpha >0$, and ${\epsilon }_1\in \left(0,{\epsilon }_0\right]$ accompanied by $\upsilon \in (0,\vartheta \tilde{\mathcal{P}}-{\displaystyle \frac{\tilde{\mathcal{P}}}{2}})$, we have the following

$$\tilde{\Xi }\left[\underset{\mathfrak{b}\in [0,\alpha {\epsilon }^{-\upsilon }]}{sup}\parallel {\gimel }_{\epsilon }\left(\mathfrak{b}\right)-{\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right){\parallel }^{\tilde{\mathcal{P}}}\right]\le \mho ,\epsilon \in (0,{\epsilon }_1].$$

(53)

Proof. 

Using (51) and (52), we obtain

$$\begin{array}{cc}\hfill & {\gimel }_{\epsilon }\left(\mathfrak{b}\right)-{\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right)\hfill \\ & ={\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}-{\displaystyle \frac{\nu }{\Gamma (\aleph )\Gamma (2-\aleph )}}\hfill \\ & +{\epsilon }^{\vartheta \kappa }{\displaystyle \frac{{\kappa }^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{g}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ & +{\epsilon }^{\vartheta \kappa -{\displaystyle \frac{1}{2}}}{\displaystyle \frac{{\kappa }^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{r}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right)\hfill \\ & {\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right).\hfill \end{array}$$

(54)

Via Jen-Ineq, we have

$$\begin{array}{cc}\hfill & {∥{\gimel }_{\epsilon }\left(\mathfrak{b}\right)-{\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right)∥}^{\tilde{\mathcal{P}}}\le 2^{\tilde{\mathcal{P}}-1}\hfill \\ & \parallel {\epsilon }^{\vartheta \kappa }{\displaystyle \frac{{\kappa }^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{g}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{\parallel }^{\tilde{\mathcal{P}}}\hfill \\ & +2^{\tilde{\mathcal{P}}-1}\hfill \\ & \parallel {\epsilon }^{\vartheta \kappa -{\displaystyle \frac{1}{2}}}{\displaystyle \frac{{\kappa }^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{r}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){\parallel }^{\tilde{\mathcal{P}}}\hfill \\ & \le {\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{\tilde{\mathcal{P}}-1}\hfill \\ & \parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{g}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{\parallel }^{\tilde{\mathcal{P}}}\hfill \\ & +{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{\tilde{\mathcal{P}}-1}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}\hfill \\ & {∥{\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{r}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right)∥}^{\tilde{\mathcal{P}}}.\hfill \end{array}$$

(55)

Utilizing (55) in (53),

$$\begin{array}{cc}\hfill \tilde{\Xi }[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}& {∥{\gimel }_{\epsilon }\left(\mathfrak{b}\right)-{\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right)∥}^{\tilde{\mathcal{P}}}]\hfill \\ & \le {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{\tilde{\mathcal{P}}-1}{\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}\hfill \\ & \tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}\parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{g}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{\parallel }^{\tilde{\mathcal{P}}}\right]\hfill \\ & +{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{\tilde{\mathcal{P}}-1}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}\hfill \\ & \tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}\parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{r}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){\parallel }^{\tilde{\mathcal{P}}}\right]\hfill \\ & ={\chi }_1+{\chi }_2.\hfill \end{array}$$

(56)

From ${\chi }_1$, we extract

$$\begin{array}{cc}\hfill {\chi }_1\le & {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}\hfill \\ & \tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}\parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{\parallel }^{\tilde{\mathcal{P}}}\right]\hfill \\ & +{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}\hfill \\ & \tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}\parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left(\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{g}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}{\parallel }^{\tilde{\mathcal{P}}}\right]\hfill \\ & ={\chi }_{11}+{\chi }_{12}.\hfill \end{array}$$

(57)

By utilizing Höl-Ineq, Jen-Ineq, and $\left({\daleth }_3\right)$ on ${\chi }_{11}$,

$$\begin{array}{cc}\hfill & {\chi }_{11}\le {\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\left({\int }_0^{\mathfrak{n}}{({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{{\displaystyle \frac{(\vartheta -1)\tilde{\mathcal{P}}}{\tilde{\mathcal{P}}-1}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{\tilde{\mathcal{P}}-1}}}\mathrm{d}\mathfrak{c}\right)}^{\tilde{\mathcal{P}}-1}\hfill \\ & \tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}{\int }_0^{\mathfrak{b}}{∥\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)∥}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\right]\hfill \\ \hfill \le & {\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\left(\underset{0<\mathfrak{c}\le \mathfrak{n}}{sup}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{1}{\tilde{\mathcal{P}}-1}}}{\int }_0^{\mathfrak{n}}{({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{{\displaystyle \frac{(\vartheta -1)\tilde{\mathcal{P}}}{\tilde{\mathcal{P}}-1}}}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right)}^{\tilde{\mathcal{P}}-1}\hfill \\ & \tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}{\int }_0^{\mathfrak{b}}{∥\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)∥}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\right]\hfill \\ \hfill \le & {\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{3\tilde{\mathcal{P}}-3}{\mathfrak{M}}^{\tilde{\mathcal{P}}-1}{\delta }_3^{\tilde{\mathcal{P}}}{\left({\left({\mathfrak{n}}^{\kappa }\right)}^{{\displaystyle \frac{(\vartheta \tilde{\mathcal{P}}-1)}{\tilde{\mathcal{P}}-1}}}\right)}^{\tilde{\mathcal{P}}-1}\mathfrak{U}\hfill \\ & \left(\tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}{\int }_0^{\mathfrak{b}}{∥{\gimel }_{\epsilon }\left(\mathfrak{c}\right)-{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right)∥}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\right]+\tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}{\int }_0^{\mathfrak{b}}{∥{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )-{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )∥}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\right]\right)\hfill \\ \hfill =& {\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\Psi }_{11}{\left({\mathfrak{n}}^{\kappa }\right)}^{(\vartheta \tilde{\mathcal{P}}-1)}({\int }_0^{\mathfrak{n}}\tilde{\Xi }\left[\underset{0\le \Phi \le \mathfrak{c}}{sup}{∥{\gimel }_{\epsilon }(\Phi )-{\gimel }_{\epsilon }^{*}(\Phi )∥}^{\tilde{\mathcal{P}}}\right]\mathrm{d}\mathfrak{c}\hfill \\ & +{\int }_0^{\mathfrak{n}}\tilde{\Xi }\left[\underset{0\le \Phi \le \mathfrak{c}}{sup}{\parallel {\gimel }_{\epsilon }(\Phi -\varrho )-{\gimel }_{\epsilon }^{*}(\Phi -\varrho )\parallel }^{\tilde{\mathcal{P}}}\right]\mathrm{d}\mathfrak{c}),\hfill \end{array}$$

(58)

where ${\Psi }_{11}={\displaystyle \frac{1}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{3\tilde{\mathcal{P}}-3}{\delta }_3^{\tilde{\mathcal{P}}}\mathfrak{U}{\mathfrak{M}}^{\tilde{\mathcal{P}}-1}$.

From ${\chi }_{12}$, by applying Höl-Ineq, Jen-Ineq, and $\left({\daleth }_5\right)$,

$$\begin{array}{cc}\hfill & {\chi }_{12}\le {\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\left({\int }_0^{\mathfrak{n}}{({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{{\displaystyle \frac{(\vartheta -1)\tilde{\mathcal{P}}}{\tilde{\mathcal{P}}-1}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{\tilde{\mathcal{P}}-1}}}\mathrm{d}\mathfrak{c}\right)}^{\tilde{\mathcal{P}}-1}\hfill \\ & \tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}{\int }_0^{\mathfrak{b}}\parallel \mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{g}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right){\parallel }^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\right]\hfill \\ \hfill \le & {\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\left(\underset{0<\mathfrak{c}\le \mathfrak{b}}{sup}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{{\displaystyle \frac{1}{\tilde{\mathcal{P}}-1}}}{\int }_0^{\mathfrak{n}}{({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{{\displaystyle \frac{(\vartheta -1)\tilde{\mathcal{P}}}{\tilde{\mathcal{P}}-1}}}{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right)}^{\tilde{\mathcal{P}}-1}\hfill \\ & \tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}{\int }_0^{\mathfrak{b}}\parallel \mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{g}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right){\parallel }^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\right]\hfill \\ \hfill \le & {\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\mathfrak{M}}^{\tilde{\mathcal{P}}-1}{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\left({\left({\mathfrak{n}}^{\kappa }\right)}^{{\displaystyle \frac{(\vartheta \tilde{\mathcal{P}}-1)}{\tilde{\mathcal{P}}-1}}}\right)}^{\tilde{\mathcal{P}}-1}\mathfrak{U}{\xi }_1\left(\mathfrak{n}\right)\hfill \\ & \mathfrak{n}\left(1+\tilde{\Xi }\parallel {\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right){\parallel }^{\tilde{\mathcal{P}}}+\tilde{\Xi }\parallel {\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho ){\parallel }^{\tilde{\mathcal{P}}}\right)\hfill \\ \hfill =& {\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\Psi }_{12}{\left({\mathfrak{n}}^{\kappa }\right)}^{(\vartheta \tilde{\mathcal{P}}-1)},\hfill \end{array}$$

(59)

Here, ${\Psi }_{12}=\mathfrak{n}{\mathfrak{M}}^{\tilde{\mathcal{P}}-1}{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}\mathfrak{U}{\xi }_1\left(\mathfrak{n}\right)\left(1+\tilde{\Xi }\parallel {\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right){\parallel }^{\tilde{\mathcal{P}}}+\tilde{\Xi }\parallel {\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho ){\parallel }^{\tilde{\mathcal{P}}}\right)$.

From ${\chi }_2$ via Jen-Ineq, we have

$$\begin{array}{cc}\hfill & {\chi }_2\le {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}\hfill \\ & \left(\tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}\parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left[\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right]{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){\parallel }^{\tilde{\mathcal{P}}}\right]\right)\hfill \\ \hfill +& {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}\hfill \\ & \left(\tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}\parallel {\int }_0^{\mathfrak{b}}{({\mathfrak{b}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{\vartheta -1}\left[\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{r}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)\right]{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathcal{W}\left(\mathfrak{c}\right){\parallel }^{\tilde{\mathcal{P}}}\right]\right)\hfill \\ \hfill =& {\chi }_{21}+{\chi }_{22}.\hfill \end{array}$$

(60)

By employing $\left({\daleth }_3\right)$, Höl-Ineq, and Bu-Da-Gu-Ineq on ${\chi }_{21}$,

$$\begin{array}{cc}\hfill & {\chi }_{21}\le {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\mathcal{C}}_{\tilde{\mathcal{P}}}\hfill \\ & \tilde{\Xi }{\left[{\int }_0^{\mathfrak{n}}{\left({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa }\right)}^{2\vartheta -2}{∥\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)∥}^2{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right]}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ & \le {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}{\mathcal{C}}_{\tilde{\mathcal{P}}}\hfill \\ & \tilde{\Xi }\left[{\int }_0^{\mathfrak{n}}{\left({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa }\right)}^{(\vartheta -1)\tilde{\mathcal{P}}}{∥\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }\left(\mathfrak{c}\right),{\gimel }_{\epsilon }(\mathfrak{c}-\varrho )\right)-\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)∥}^{\tilde{\mathcal{P}}}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\right]\hfill \\ & \le {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{3\tilde{\mathcal{P}}-3}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}{\delta }_3^{\tilde{\mathcal{P}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}{\int }_0^{\mathfrak{n}}{({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa })}^{(\vartheta -1)\tilde{\mathcal{P}}}\hfill \\ & \tilde{\Xi }\left[\underset{0\le \Phi \le \mathfrak{c}}{sup}\left[{∥{\gimel }_{\epsilon }(\Phi )-{\gimel }_{\epsilon }^{*}(\Phi )∥}^{\tilde{\mathcal{P}}}+{∥{\gimel }_{\epsilon }(\Phi -\varrho )-{\gimel }_{\epsilon }^{*}(\Phi -\varrho )∥}^{\tilde{\mathcal{P}}}\right]{\left({\mathfrak{c}}^{\kappa -1}\right)}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}\right]\hfill \\ & \le {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{3\tilde{\mathcal{P}}-3}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}{\delta }_3^{\tilde{\mathcal{P}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}\underset{0<\mathfrak{c}\le \mathfrak{n}}{sup}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{\tilde{\mathcal{P}}-1}{\int }_0^{\mathfrak{n}}{\left({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa }\right)}^{(\vartheta -1)\tilde{\mathcal{P}}}\hfill \\ & \tilde{\Xi }\left[\underset{0\le \Phi \le \mathfrak{c}}{sup}\left[{∥{\gimel }_{\epsilon }(\Phi )-{\gimel }_{\epsilon }^{*}(\Phi )∥}^{\tilde{\mathcal{P}}}+{∥{\gimel }_{\epsilon }(\Phi -\varrho )-{\gimel }_{\epsilon }^{*}(\Phi -\varrho )∥}^{\tilde{\mathcal{P}}}\right]{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right]\hfill \\ & ={\Psi }_{21}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}\left({\int }_0^{\mathfrak{n}}\right({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa }{)}^{(\vartheta -1)\tilde{\mathcal{P}}}\tilde{\Xi }\left[\underset{0\le \Phi \le \mathfrak{c}}{sup}{∥{\gimel }_{\epsilon }(\Phi )-{\gimel }_{\epsilon }^{*}(\Phi )∥}^{\tilde{\mathcal{P}}}\right]{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\hfill \\ & +{\int }_0^{\mathfrak{n}}\left({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa }{)}^{(\vartheta -1)\tilde{\mathcal{P}}}\tilde{\Xi }\left[\underset{0\le \Phi \le \mathfrak{c}}{sup}{∥{\gimel }_{\epsilon }(\Phi -\varrho )-{\gimel }_{\epsilon }^{*}(\Phi -\varrho )∥}^{\tilde{\mathcal{P}}}\right]{\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right),\hfill \end{array}$$

(61)

where ${\Psi }_{21}=2^{3\tilde{\mathcal{P}}-3}{\delta }_3^{\tilde{\mathcal{P}}}{\mathcal{C}}_{\tilde{\mathcal{P}}}{\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}\mathcal{Y}$ and $\mathcal{Y}=\underset{0<\mathfrak{c}\le \mathfrak{n}}{sup}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{(\tilde{\mathcal{P}}-1)}$.

By utilizing Höl-Ineq and Bu-Da-Gu-Ineq on ${\chi }_{22}$,

$$\begin{array}{cc}\hfill & {\chi }_{22}\le {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{2}^{2\tilde{\mathcal{P}}-2}{\mathcal{C}}_{\tilde{\mathcal{P}}}\hfill \\ & \tilde{\Xi }{\left[{\int }_0^{\mathfrak{n}}{∥\mathfrak{g}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)-\tilde{\mathfrak{r}}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)∥}^2{\left({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa }\right)}^{2\vartheta -2}{\left({\mathfrak{c}}^{\kappa -1}\right)}^2\mathrm{d}\mathfrak{c}\right]}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}}\hfill \\ \hfill \le & {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }\left[{\int }_0^{\mathfrak{n}}\right({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa }{)}^{(\vartheta -1)\tilde{\mathcal{P}}}\hfill \\ & \left({∥\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)∥}^{\tilde{\mathcal{P}}}+\parallel \tilde{\mathfrak{r}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right){\parallel }^{\tilde{\mathcal{P}}}\right){\left({\mathfrak{c}}^{\kappa -1}\right)}^{\tilde{\mathcal{P}}}\mathrm{d}\mathfrak{c}]\hfill \\ \hfill \le & {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{2}^{2\tilde{\mathcal{P}}-2}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}{\mathcal{C}}_{\tilde{\mathcal{P}}}\tilde{\Xi }[\underset{0<\mathfrak{c}\le \mathfrak{n}}{sup}{\left({\mathfrak{c}}^{\kappa -1}\right)}^{(\tilde{\mathcal{P}}-1)}\hfill \\ & {\int }_0^{\mathfrak{n}}\left({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa }{)}^{(\vartheta -1)\tilde{\mathcal{P}}}\left({∥\mathfrak{r}\left(\mathfrak{c},{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right)∥}^{\tilde{\mathcal{P}}}+\parallel \tilde{\mathfrak{r}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )\right){\parallel }^{\tilde{\mathcal{P}}}\right){\mathfrak{c}}^{\kappa -1}\mathrm{d}\mathfrak{c}\right]\hfill \\ \hfill \le & {\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}{\displaystyle \frac{2^{3\tilde{\mathcal{P}}-3}{3}^{\tilde{\mathcal{P}}-1}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -\frac{1}{2})}{\left({\mathfrak{n}}^{\kappa }\right)}^{((\vartheta -1)\tilde{\mathcal{P}}+1)+\frac{\tilde{\mathcal{P}}}{2}-1}{\delta }_4^{\tilde{\mathcal{P}}}{\left({\delta }_4^{\tilde{\mathcal{P}}}+{\delta }_6\right)}^{\tilde{\mathcal{P}}}}{((\vartheta -1)\tilde{\mathcal{P}}+1)}}\hfill \\ & \mathcal{Y}{\mathcal{C}}_{\tilde{\mathcal{P}}}\left(1+\tilde{\Xi }\left[{∥{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right)∥}^{\tilde{\mathcal{P}}}\right]+\tilde{\Xi }\left[{∥{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )∥}^{\tilde{\mathcal{P}}}\right]\right)\hfill \\ \hfill =& {\Psi }_{22}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{((\vartheta -1)\tilde{\mathcal{P}}+1)+{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1},\hfill \end{array}$$

(62)

here,

$$\begin{array}{cc}\hfill & {\Psi }_{22}=2^{3\tilde{\mathcal{P}}-3}{3}^{\tilde{\mathcal{P}}-1}{\delta }_4^{\tilde{\mathcal{P}}}{\left({\delta }_4^{\tilde{\mathcal{P}}}+{\delta }_6\right)}^{\tilde{\mathcal{P}}}{\displaystyle \frac{1}{((\vartheta -1)\tilde{\mathcal{P}}+1)}}\mathcal{Y}{\mathcal{C}}_{\tilde{\mathcal{P}}}\left(1+\tilde{\Xi }\left[{∥{\gimel }_{\epsilon }^{*}\left(\mathfrak{c}\right)∥}^{\tilde{\mathcal{P}}}\right]+\tilde{\Xi }\left[{∥{\gimel }_{\epsilon }^{*}(\mathfrak{c}-\varrho )∥}^{\tilde{\mathcal{P}}}\right]\right){\displaystyle \frac{{\left({\kappa }^{\vartheta -1}\right)}^{\tilde{\mathcal{P}}}}{{\Gamma }^{\tilde{\mathcal{P}}}\left(\vartheta \right)}}.\hfill \end{array}$$

From (57), (62), and (56),

$$\begin{array}{cc}\hfill & \tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}{∥{\gimel }_{\epsilon }\left(\mathfrak{b}\right)-{\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right)∥}^{\tilde{\mathcal{P}}}\right]\le {\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\Psi }_{12}{\left({\mathfrak{n}}^{\kappa }\right)}^{(\vartheta \tilde{\mathcal{P}}-1)}+{\Psi }_{22}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{((\vartheta -1)\tilde{\mathcal{P}}+1)+{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}\hfill \\ \hfill & +{\int }_0^{\mathfrak{n}}({\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\Psi }_{11}{\left({\mathfrak{n}}^{\kappa }\right)}^{(\vartheta \tilde{\mathcal{P}}-1)}+{\Psi }_{21}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}\left({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa }{)}^{(\vartheta -1)\tilde{\mathcal{P}}}{\mathfrak{c}}^{\kappa -1}\right)\hfill \\ \hfill & \tilde{\Xi }\left[\underset{0\le \Phi \le \mathfrak{c}}{sup}{∥{\gimel }_{\epsilon }(\Phi )-{\gimel }_{\epsilon }^{*}(\Phi )∥}^{\tilde{\mathcal{P}}}\right]\mathrm{d}\mathfrak{c}+{\int }_0^{\mathfrak{n}}({\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\Psi }_{11}{\left({\mathfrak{n}}^{\kappa }\right)}^{(\vartheta \tilde{\mathcal{P}}-1)}+{\Psi }_{21}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}\hfill \\ & \left({\mathfrak{n}}^{\kappa }-{\mathfrak{c}}^{\kappa }{)}^{(\vartheta -1)\tilde{\mathcal{P}}}{\mathfrak{c}}^{\kappa -1}\right)\tilde{\Xi }\left[\underset{0\le \Phi \le \mathfrak{c}}{sup}{∥{\gimel }_{\epsilon }(\Phi -\varrho )-{\gimel }_{\epsilon }^{*}(\Phi -\varrho )∥}^{\tilde{\mathcal{P}}}\right]\mathrm{d}\mathfrak{c}.\hfill \end{array}$$

(63)

From (63), we have

$$\begin{array}{cc}\hfill & \tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \mathfrak{n}}{sup}\parallel {\gimel }_{\epsilon }\left(\mathfrak{b}\right)-{\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right){\parallel }^{\tilde{\mathcal{P}}}\right]\le \left({\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\Psi }_{12}{\left({\mathfrak{n}}^{\kappa }\right)}^{(\vartheta \tilde{\mathcal{P}}-1)}+{\Psi }_{22}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{((\vartheta -1)\tilde{\mathcal{P}}+1)+{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}\right)\hfill \\ & exp\left(2{\left({\epsilon }^{\vartheta \kappa }\right)}^{\tilde{\mathcal{P}}}{\Psi }_{11}{\left({\mathfrak{n}}^{\kappa }\right)}^{(\vartheta \tilde{\mathcal{P}}-1)}\mathfrak{n}+{\displaystyle \frac{2{\Psi }_{21}}{((\vartheta -1)\tilde{\mathcal{P}}+1)}}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\mathfrak{n}}^{\kappa }\right)}^{((\vartheta -1)\tilde{\mathcal{P}}+1)+{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}\right).\hfill \end{array}$$

Therefore, in order to reach $\alpha >0$, $\upsilon \in (0,\vartheta \tilde{\mathcal{P}}-{\displaystyle \frac{\tilde{\mathcal{P}}}{2}})$, and $\mathfrak{b}\in \left[0,\alpha {\epsilon }^{-\upsilon }\right]\subseteq [0,\varsigma ]$, we conclude that

$$\tilde{\Xi }\left[\underset{0\le \mathfrak{b}\le \alpha {\epsilon }^{-\upsilon }}{sup}{∥{\gimel }_{\epsilon }\left(\mathfrak{b}\right)-{\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right)∥}^{\tilde{\mathcal{P}}}\right]\le \mathbb{A}{\epsilon }^{1-\upsilon },$$

(64)

here,

$$\begin{array}{cc}\hfill \mathbb{A}=& {\epsilon }^{\upsilon -1}\left({\Psi }_{12}{\left({\left(\alpha {\epsilon }^{-\upsilon }\right)}^{\kappa }\right)}^{(\vartheta \tilde{\mathcal{P}}-1)}+{\Psi }_{22}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\left(\alpha {\epsilon }^{-\upsilon }\right)}^{\kappa }\right)}^{((\vartheta -1)\tilde{\mathcal{P}}+1)+{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}\right)\hfill \\ & exp\left(2{\Psi }_{11}{\left({\left(\alpha {\epsilon }^{-\upsilon }\right)}^{\kappa }\right)}^{(\vartheta \tilde{\mathcal{P}}-1)}\alpha {\epsilon }^{-\upsilon }+{\displaystyle \frac{2{\Psi }_{21}}{((\vartheta -1)\tilde{\mathcal{P}}+1)}}{\epsilon }^{\tilde{\mathcal{P}}(\vartheta \kappa -{\displaystyle \frac{1}{2}})}{\left({\left(\alpha {\epsilon }^{-\upsilon }\right)}^{\kappa }\right)}^{((\vartheta -1)\tilde{\mathcal{P}}+1)+{\displaystyle \frac{\tilde{\mathcal{P}}}{2}}-1}\right).\hfill \end{array}$$

This concludes the proof. □

 Remark 1. 

The parameter $\upsilon \in (0,\vartheta \tilde{\mathcal{P}}-{\displaystyle \frac{\tilde{\mathcal{P}}}{2}})$ determines the time interval over which the averaged model remains a good representation of the original stochastic system. It specifies the scale $[0,\alpha {\epsilon }^{-\upsilon }]$ within which the two solutions stay close to each other. When υ is smaller, convergence is quicker but valid only for shorter periods; a larger υ extends the comparison to longer intervals, although the accuracy may gradually decrease. In essence, υ regulates the balance between precision and duration, and an appropriate choice of its value ensures that the Av-Pr yields a stable and dependable approximation for practical stochastic systems.

5. Applications

To facilitate a clearer understanding of the results presented in this study, several applications are provided along with graphical analyses comparing the original and estimated solutions. Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 illustrate these comparisons, supporting and validating the theoretical findings. All applications are solved using the Euler–Maruyama method [32].

 Application 1. 

We examine the following fractional stochastic delay logistic equation to account for the combined effects of memory, time delay, stochastic perturbations, and harvesting on population dynamics:

$${}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel \left(\mathfrak{b}\right)=\mathfrak{r}\gimel \left(\mathfrak{b}\right)\left(1-{\displaystyle \frac{\gimel (\mathfrak{b}-\varrho )}{K}}\right)-h\gimel \left(\mathfrak{b}\right)+\sigma \gimel \left(\mathfrak{b}\right){\displaystyle \frac{\mathrm{d}\mathcal{W}\left(\mathfrak{b}\right)}{\mathrm{d}\mathfrak{b}}},$$

(65)

The parameters are as follows: $\gimel \left(\mathfrak{b}\right)$: the population; $\mathfrak{r}>0$: the growth rate; $K>0$: the carrying capacity; $\varrho >0$: the time delay for maturation; $h>0$: the harvesting rate; and $\sigma >0$: the strength of environmental noise.

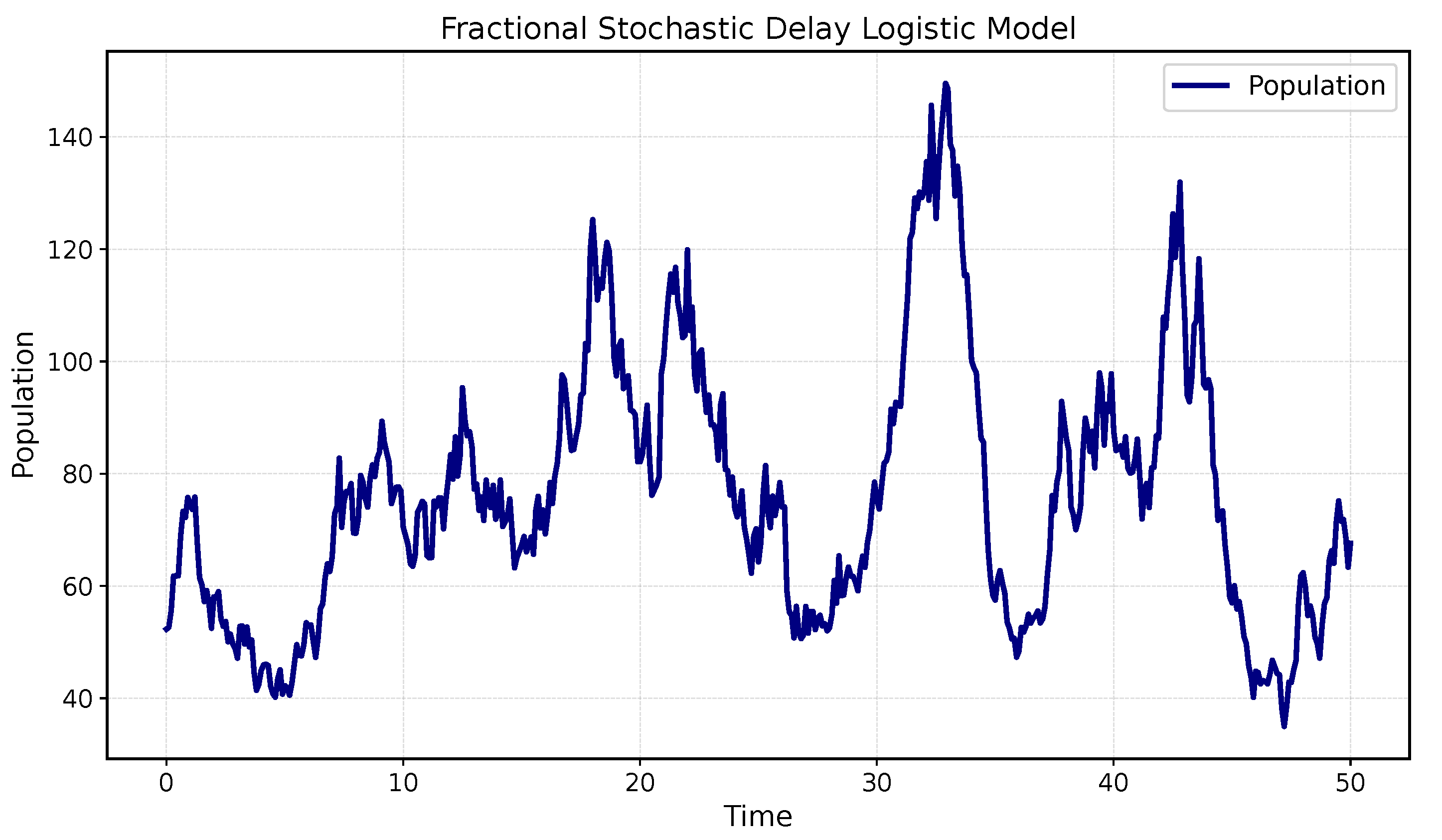
Since the Ex–Un criteria are satisfied by system (65), the model (65) is solved using the EMM. The following figure shows the solution of system (65):

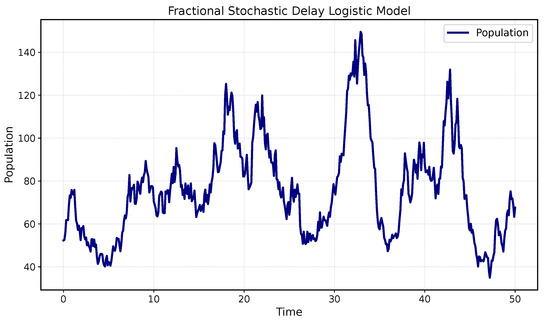
Figure 1. Representation of the solution for Application 1.

Figure 1. Representation of the solution for Application 1.

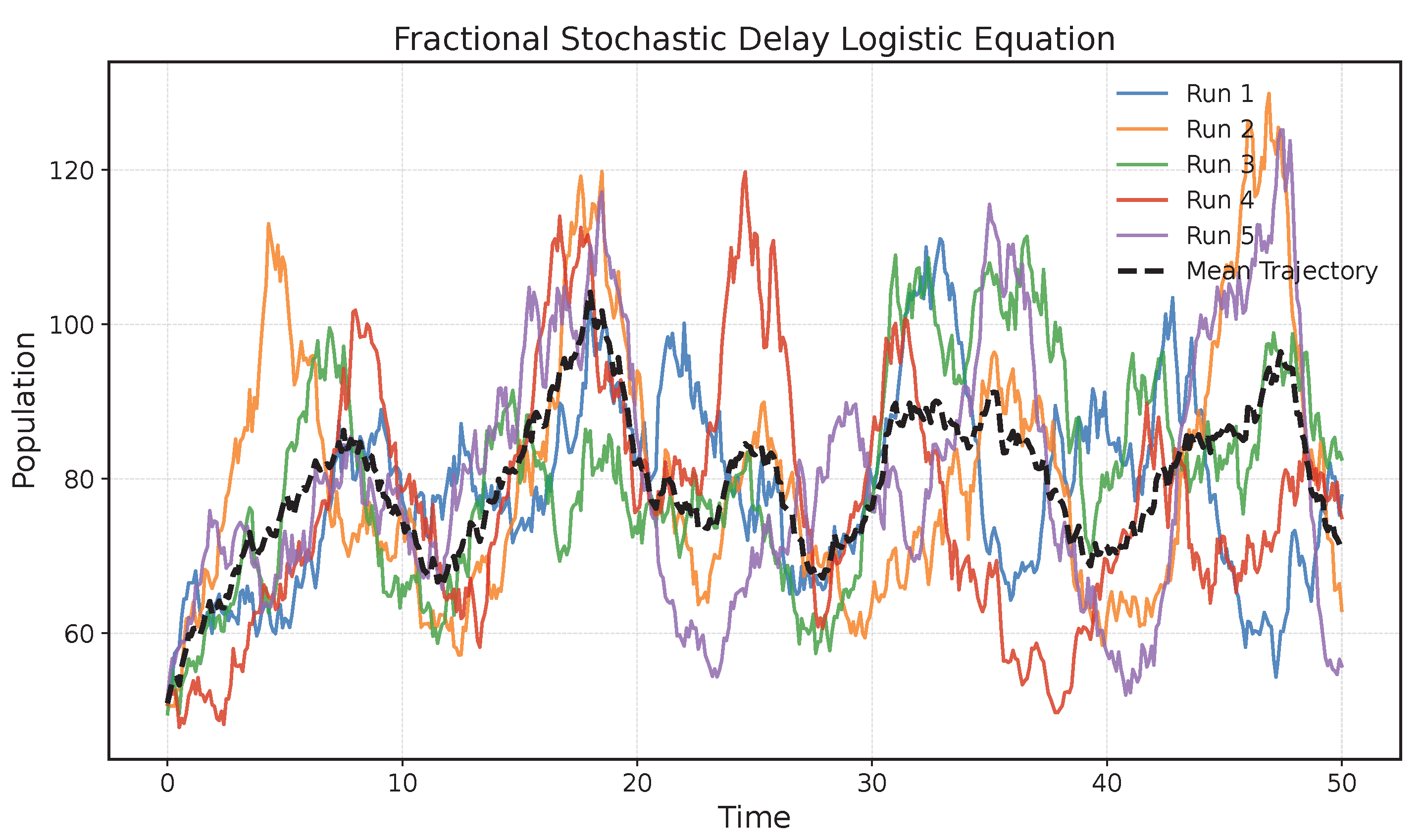
The following graph depicts five simulated trajectories of the system along with their corresponding mean trajectory.

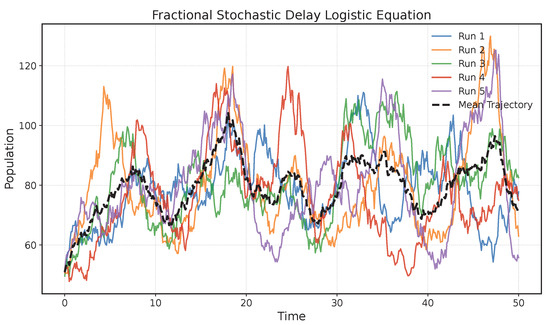
Figure 2. Five simulated trajectories of the system along with their mean trajectory.

Figure 2. Five simulated trajectories of the system along with their mean trajectory.

The main parameters and their corresponding descriptions used in the simulation of Application (1) are presented in Table 1.

Table 1. Parameter values used for the simulation of the fractional stochastic delay logistic model with harvesting.

Symbol	Parameter	Value
$\vartheta ,\varpi ,\kappa$	Fractional order	$\vartheta =0.8$, $\varpi \to 1,\kappa \to 1$
r	Growth rate	$0.5$
K	Carrying capacity	100
$\varrho$	Time delay	$2.0$
h	Harvesting rate	$0.1$
$\sigma$	Noise intensity	$0.2$
$\varsigma$	Simulation time	50
$\Delta \mathfrak{b}$	Time step	$0.1$
$\gimel \left(\mathfrak{b}\right)$	Initial condition	$50.0$

 Application 2. 

Nicholson’s fractional stochastic blowflies model is formulated as follows:

$${}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }\gimel \left(\mathfrak{b}\right)=-\delta \gimel \left(\mathfrak{b}\right)+p\gimel (\mathfrak{b}-\varrho )e^{-\mathfrak{a}\gimel (\mathfrak{b}-\varrho )}+\sigma \gimel \left(\mathfrak{b}\right){\displaystyle \frac{\mathrm{d}\mathcal{W}\left(\mathfrak{b}\right)}{\mathrm{d}\mathfrak{b}}}.$$

(66)

here, δ denotes the natural death rate, p is the maximum reproduction rate, a measures the strength of density dependence, ϱ represents the maturation delay, and $\sigma \gimel \left(\mathfrak{b}\right){\displaystyle \frac{\mathrm{d}\mathcal{W}\left(\mathfrak{b}\right)}{\mathrm{d}\mathfrak{b}}}$ accounts for stochastic perturbations representing environmental fluctuations.

Since system (66) satisfies the Ex–Un criteria, the EMM is employed to solve model (66). The following figure illustrates the solution of system (66):

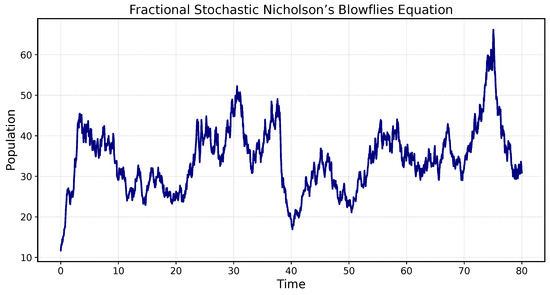
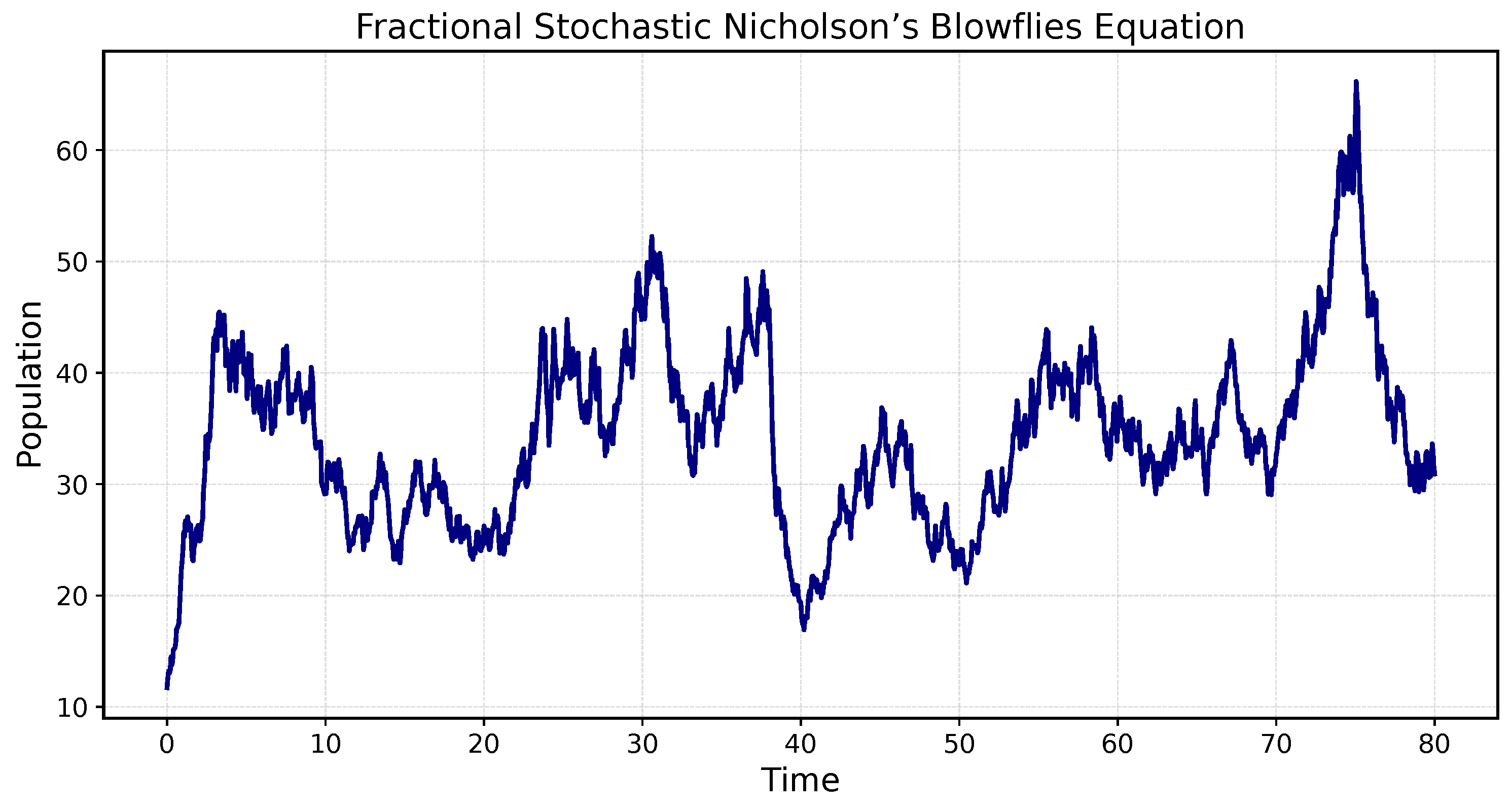
Figure 3. Solution trajectory of Nicholson’s fractional stochastic blowflies equation.

Figure 3. Solution trajectory of Nicholson’s fractional stochastic blowflies equation.

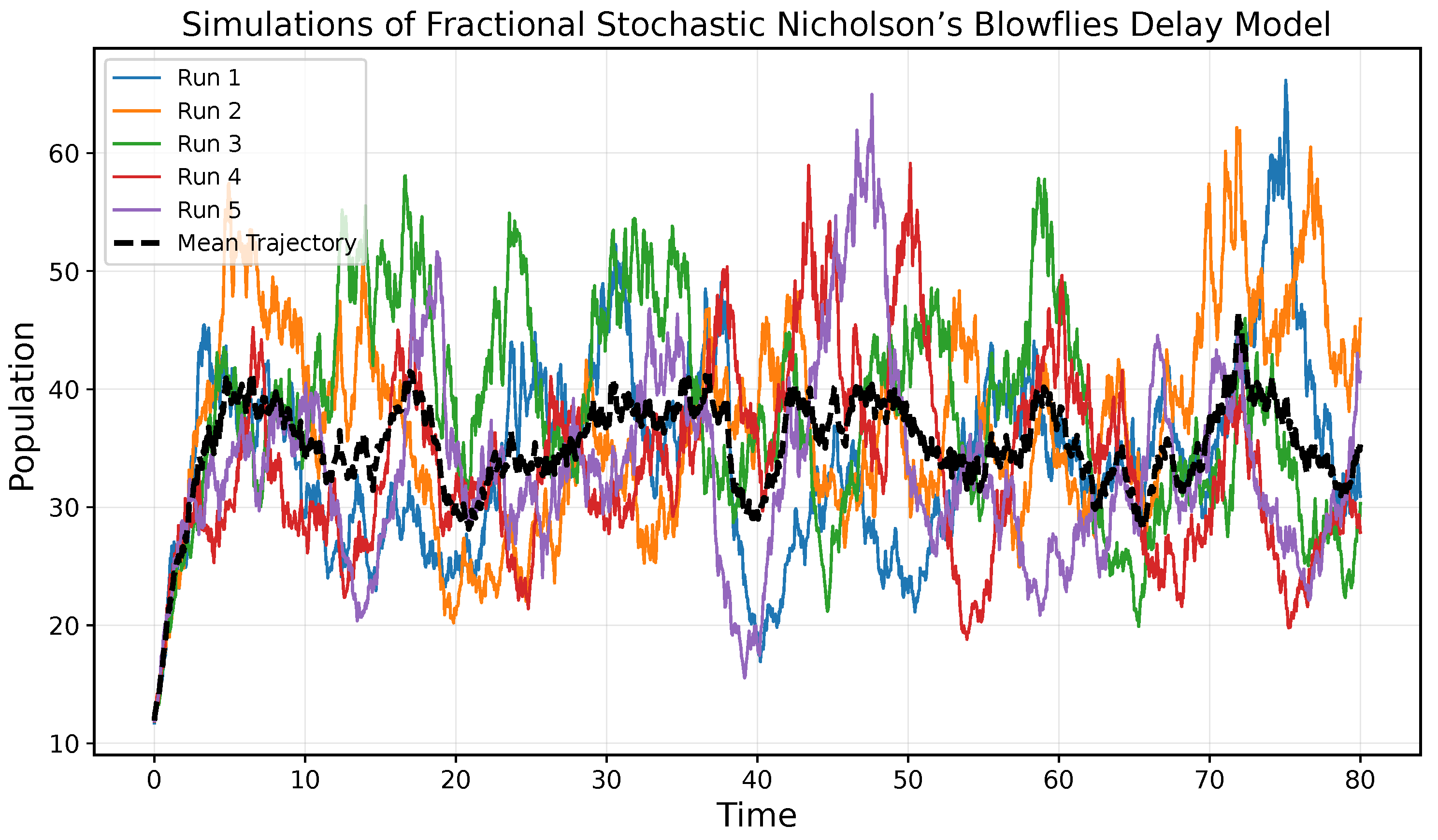
The following graph illustrates five simulated trajectories of the system along with their corresponding mean trajectory.

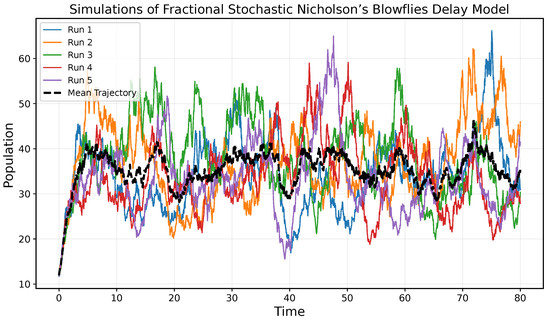
Figure 4. Five simulated trajectories of Nicholson’s fractional stochastic blowflies equation.

Figure 4. Five simulated trajectories of Nicholson’s fractional stochastic blowflies equation.

The parameter values and their corresponding descriptions used in the simulation of Nicholson’s fractional stochastic blowflies model are summarized in Table 2.

Table 2. Parameter values used in the simulation of Nicholson’s fractional stochastic blowflies model.

Parameter	Symbol	Value
Fractional order	$\vartheta ,\varpi ,\kappa$	0.9
Death rate	$\delta$	0.1
Reproduction coefficient	p	3.0
Density effect coefficient	a	0.1
Time delay	$\varrho$	2.0
Noise intensity	$\sigma$	0.15
Total simulation time	$\varsigma$	80.0
Time step size	$\Delta \mathfrak{b}$	0.05
Initial history function	$\gimel \left(\mathfrak{b}\right)$, $\mathfrak{b}\in [-\varrho ,0]$	$10+2sin\left(0.5(\mathfrak{b}+\varrho )\right)$

 Application 3. 

 Consider the following, 

$${}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }{\gimel }_{\epsilon }\left(\mathfrak{b}\right)={\epsilon }^{\vartheta \kappa }\mathfrak{g}(\mathfrak{b},{\gimel }_{\epsilon }\left(\mathfrak{b}\right),{\gimel }_{\epsilon }(\mathfrak{b}-\tau ))+{\epsilon }^{\vartheta \kappa -{\displaystyle \frac{1}{2}}}\mathfrak{r}(\mathfrak{b},{\gimel }_{\epsilon }\left(\mathfrak{b}\right),{\gimel }_{\epsilon }(\mathfrak{b}-\varrho )){\displaystyle \frac{\mathrm{d}\mathcal{W}\left(\mathfrak{b}\right)}{\mathrm{d}\mathfrak{b}}},$$

(67)

where, $\epsilon >0$ is a small perturbation parameter, $\varrho >0$ represents the delay, and $\mathcal{W}\left(\mathfrak{b}\right)$ is a standard Brownian motion.

The drift and diffusion functions are defined as

$$\mathfrak{g}(\mathfrak{b},{\gimel }_{\epsilon }\left(\mathfrak{b}\right),{\gimel }_{\epsilon }(\mathfrak{b}-\varrho ))=1.5-0.8{\gimel }_{\epsilon }\left(\mathfrak{b}\right)+0.3sin\left(\mathfrak{b}\right)-0.4{\gimel }_{\epsilon }(\mathfrak{b}-\varrho ),$$

and

$$\mathfrak{r}(\mathfrak{b},{\gimel }_{\epsilon }\left(\mathfrak{b}\right),{\gimel }_{\epsilon }(\mathfrak{b}-\varrho ))=0.5+0.2cos\left(\mathfrak{b}\right).$$

By applying the Av-Pr, the oscillatory terms with respect to b can be replaced by their mean values. Hence, the averaged system is given by

$${}^{\kappa }\mathcal{T}_{0^{\mathrm{+}}}^{\vartheta ,\varpi }{\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right)={\epsilon }^{\vartheta \kappa }\tilde{\mathfrak{g}}({\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{b}-\varrho ))+{\epsilon }^{\vartheta \kappa -{\displaystyle \frac{1}{2}}}\tilde{\mathfrak{r}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{b}-\varrho )\right){\displaystyle \frac{\mathrm{d}\mathcal{W}\left(\mathfrak{b}\right)}{\mathrm{d}\mathfrak{b}}},$$

where

$$\tilde{\mathfrak{g}}({\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{b}-\varrho ))=1.5-0.8{\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right)-0.4{\gimel }_{\epsilon }^{*}(\mathfrak{b}-\varrho ),\tilde{\mathfrak{r}}\left({\gimel }_{\epsilon }^{*}\left(\mathfrak{b}\right),{\gimel }_{\epsilon }^{*}(\mathfrak{b}-\varrho )\right)=0.5.$$

The absolute error values between the original and averaged systems are summarized in Table 3. This table demonstrates the reliability of the results established regarding the Av–Pr.

Table 3. Absolute error between original and averaged systems.

Time	Original	Averaged	Absolute Error
0	1.000000	1.000000	0.000000
1	1.023456	1.021789	0.001667
2	1.045678	1.043210	0.002468
3	1.067890	1.064321	0.003569
4	1.089012	1.085432	0.003580
5	1.110234	1.106543	0.003691
6	1.131456	1.127654	0.003802
7	1.152678	1.148765	0.003913
8	1.173890	1.169876	0.004014
9	1.195012	1.190987	0.004025
10	1.216234	1.212098	0.004136
11	1.237456	1.233209	0.004247
12	1.258678	1.254320	0.004358
13	1.279890	1.275431	0.004459
14	1.301012	1.296542	0.004470
15	1.322234	1.317653	0.004581
16	1.343456	1.338764	0.004692
17	1.364678	1.359875	0.004803
18	1.385890	1.380986	0.004904
19	1.407012	1.402097	0.004915
20	1.428234	1.423208	0.005026

The figure below illustrates the behavior of the original and averaged systems, both solved using the EMM. The results show that the behaviors of both systems are nearly identical, thereby validating the reliability of our theoretical results.

Figure 5. Numerical solutions of the original and averaged systems. Green: original system; red: averaged system.

Figure 5. Numerical solutions of the original and averaged systems. Green: original system; red: averaged system.

A detailed summary of the error statistics, illustrating the accuracy of the averaging results, is provided in Table 4.

Table 4. Error statistics summary.

Statistic	Value
Mean Absolute Error	0.003876
Maximum Absolute Error	0.005026
Minimum Absolute Error	0.000000
Root Mean Square Error	0.003941

6. Conclusions

This study presents several novel findings regarding the Ex-Un of solutions and their continuous dependence on Hilfer–Katugampola FDSDEs. We also establish results for the regularity of the solution and Av-Pr, presenting all findings in the $\tilde{\mathcal{P}}$th moment. In this way, contribute meaningfully to the existing body of literature. The application of several pivotal inequalities, including the Bu-Da-Gu-Ineq, Höl-Ineq, and Jen-Ineq, plays a key role in proving theorems and lemmas.

7. Future Directions

Looking forward, we plan to extend our Av-Pr results to two-time-scale SFDEs driven by fractional Brownian motion.