Abstract
Tourism demand forecasting has evolved into a wide variety of models, including time-series models that incorporate economic, environmental, and behavioral factors. Macao, one of the world’s most profitable gaming destinations, finds that gaming revenue is highly related to tourist arrivals. A forecast model for gaming tourism is essential for accurately predicting tourist arrivals. The challenge with ARIMA-type models is optimizing parameter selection in order to improve the accuracy of tourism demand forecasts. In this study, an enhanced version of SARIMAX, called SARIMAX-E, was developed to identify the most effective parameter combinations. By integrating data related to gaming revenue, weather, transportation, currency exchange rate, holidays, and seasonality into a single forecast model, this study examined the performance of different forecasting models, including the proposed SARIMAX-E model; ARIMA-type models (ARIMA, SARIMA, ARIMAX); and machine learning models (Transformer, LTSM, Random Forests, XGBoost). The results showed that the ARIMA family of models, including SARIMAX-E, ARIMAX, and SARIMA, was particularly well suited to tourism demand forecasting, as its members consistently ranked among the top performers in terms of error metrics. By applying multi-step predictions, LSTM outperforms most conventional approaches. Compared with all other models, the SARIMAX-E performed the best after applying the additional parameter grid.
MSC:
91B84
1. Introduction
As the tourism industry has developed through the years, a large number of data-rich models have evolved to forecast tourism demand, from simple time-series forecasts to sophisticated models that include economic, environmental, and behavioral factors in the forecasting process (Song & Zhang, 2025; Wu et al., 2024) [1,2]. In the case of Macao, one of the world’s most profitable gaming destinations, gaming revenue has been found to be highly correlated with tourist arrivals (Lim & To, 2022) [3]. It is essential to develop a forecast model that can accurately predict the tourist arrivals in such a specialized tourism environment as gaming tourism. Therefore, it is considered appropriate to incorporate gaming revenue data into the forecast model as part of the big data approach. In addition, taking historical weather data into account is an important component of forecasting tourism demand, as it affects motivation, attraction, and selection of destinations (Bi et al., 2020; Matthews et al., 2021) [4,5]. Apart from weather temperature data, transportation data and currency exchange rates can also be used to forecast tourism demand. Estimating tourist transportation is crucial to forecasting tourism demand and tourism planning (Hussain, 2023) [6]. Similarly, currency exchange rates also affect tourism demand (Opstad et al., 2021) [7]. Therefore, this research uses the big data approach to include key data sources related to the gaming tourism industry, including gaming revenue, weather temperature data, transport data (incoming vehicles), currency exchange rate, holidays, and seasonality.
Apart from the use of big data, there are still uncertainties regarding the choice of models in tourism forecasting. The complexity of forecasting time series data has led scholars to use a variety of methods (Liu et al., 2021) [8]. Time series models, such as autoregressive integrated moving averages (ARIMAs) and seasonal ARIMAs (SARIMAs), are popular models in tourism demand forecasting research because of their ability to capture a wide range of features in time series data, including long-term dependence, trends, seasonality, and fluctuations (Song et al., 2019) [9]. These models have been widely used over the past five decades to predict tourism demand, especially autoregressive integrated moving average (ARIMA-type) models (Craig, 2024; Huang et al., 2017; Korinth, 2022; Kumar & Ekka, 2025; Lim & To, 2022; Peng et al., 2021; Perles-Ribes et al., 2023) [3,10,11,12,13,14,15]. In recent years, however, the use of artificial intelligence (AI)-based models has been emerging as an innovative method for forecasting tourism demand (Wu et al., 2024) [2], despite the difficulties in proving its theoretical and methodological foundations (Song et al., 2019) [9]. For instance, the machine learning model known as Long Short-Term Memory (LSTM) has been widely adopted for forecasting tourism demand in recent studies (Bi et al., 2020; Binesh et al., 2024; Han et al., 2024; Law et al., 2019) [4,16,17,18]. Since each model has its own limitations to some degree, there is no single forecasting model considered to be optimal for all forecasting tasks (Law et al., 2019) [18]. Therefore, researchers in this field have been making changes to existing models in order to improve the accuracy of tourism demand forecasts (Wu et al., 2024) [2].
When comparing ARIMA-type models with machine learning models, the existing literature demonstrates inconsistent results in forecasting studies. While the use of machine learning and deep learning models for forecasting studies has become increasingly popular because of the ability of these models to learn complex and nonlinear temporal dependencies (Kişmiroğlu & Isik, 2025) [19], Kontopoulou et al. (2023) [20] pointed out that when faced with a limited dataset or limited timeframes, ARIMA also outperforms its machine learning counterparts. Machine learning, and especially deep learning, requires large amounts of information to train effectively. Likewise, Lee et al. (2025) [21] also stated that the Seasonal Autoregressive Integrated Moving-Average with Exogenous Regressors (SARIMAX) is best suited to short-term forecasting due to its limited training data, but LSTM shows greater potential in long-term forecasting due to its ability to learn complex temporal patterns from historical data.
In particular, the Seasonal Autoregressive Integrated Moving-Average with Exogenous Regressors (SARIMAX), a modified version of ARIMA that captures seasonality and trend components in structured data effectively, was shown to demonstrate greater accuracy in temperature forecasting in the short term than LSTM (Kişmiroğlu & Isik, 2025) [19]. Moreover, similar results have been found in other forecasting studies that compared the SARIMAX model with machine learning and deep leaning models. For instance, Lee et al. (2025) [21] found that SARIMAX demonstrated higher Probability of Detection (POD) and higher accuracy than LSTM for all statistical metrics, particularly in detecting air pollution related to high PM2.5 concentrations in Republic of Korea. Baloch et al. (2024) [22] found that SARIMAX performs better than other competitive models, such as LSTM and Prophet, when forecasting solar irradiance for Muscat, Oman. In addition, based on one-year data from three solar photovoltaic (PV) installations in the Philippines, Benitez et al. (2023) [23] found that SARIMAX outperforms LSTM, XGBoost, and their combinations. It is well established by existing literature that SARIMAX continues to be an effective tool for forecasting studies. The present research follows the same approach and applies SARIMAX to forecasting the demand for gaming tourism destinations. However, setting up a SARIMAX model can be complex because of the need to identify the right parameters and integrate external data (Shah et al., 2024) [24]. Specifying the correct model order (p, d, q, P, D, Q) can be difficult due to this complexity.
In order to contribute to the development of tourism demand forecasting research, the present study developed an enhanced SARIMAX model named SARIMAX-E that incorporated additional parameter selection grids. Parameter grids represent multidimensional spaces in which each dimension represents a parameter of the model. Since there are seasonal autoregressive orders (P), seasonal difference orders (D), and seasonal moving average orders (Q) included in the SARIMAX model, a set of possible values is assigned to each parameter, and the values selected are generally determined by prior experience and knowledge. Parameter grids are Cartesian products, and each grid point represents a different parameter combination, making the parameter space exploration systematic. The model aims to find the most appropriate parameter combinations to provide optimal model performance. As a result, this study has two objectives. First, different forecasting models will be compared to see which model is the most effective in forecasting tourism demand, including the newly proposed SARIMAX-E model; ARIMA-type models (ARIMA, SARIMA, ARIMAX); and machine learning models (Transformer, LTSM, Random Forests, XGBoost). Second, by integrating data related to gaming revenue, weather, transportation, currency exchange rate, holidays, and seasonality into a single forecast model, this study aims to forecast tourism demand with a big data approach.
2. Literature Review
2.1. The Use of ARIMA-Type Models to Forecast Tourism Demand
Forecasting tourism demand has been largely based on time series models over the past 50 years (Song et al., 2019) [9], particularly the autoregressive integrated moving average (ARIMA-type) models such as ARIMA (Craig, 2024; Huang et al., 2017; Korinth, 2022; Kumar & Ekka, 2025; Lim & To, 2022; Peng et al., 2021; Perles-Ribes et al., 2023) [3,10,11,12,13,14,15], and Seasonal Autoregressive Integrated Moving Average (SARIMA) (Abellana et al., 2021; Chu, 2009) [25,26]. In statistics, ARIMA is useful for analysis and forecasting time series data (Box, 1976) [27]. Time series data can be captured in ARIMA models in a variety of ways, including long-term dependence, seasonality, and trends. When the parameters of the model (p, d, q) are appropriately chosen, ARIMA models can be adapted to a variety of different types of time series data and used for forecasting short-term trends. Further, the Seasonal Autoregressive Integrated Moving Average (SARIMA) and Seasonal Autoregressive Integrated Moving Average with External Variables (SARIMAX) models are extended ARIMA models, in which all ARIMA model properties are included along with seasonal components and external variables (Box, 1976) [27]. The ARIMA model has been widely applied by researchers in different tourism forecasting contexts including climate impact on tourism (Craig, 2024; Pan & Yang, 2017) [10,28]; COVID-19 impact on tourism and employment (Korinth, 2022; Perles-Ribes et al., 2023) [12,15]; hotel demand (Kumar & Ekka, 2025; Pan & Yang, 2017) [13,28]; gaming revenue and tourism demand (Lim & To, 2022) [3]; tourism demand across different countries (Abellana et al., 2021; Chu, 2009) [25,26] and tourist attraction demand (Huang et al., 2017) [11].
In general, there has been extensive use of the ARIMA model to forecast tourism demand in different countries and visitors’ arrivals at tourist attractions. According to Chu (2009) [26], tourism demand was forecasted in nine Asian-Pacific destinations, including Hong Kong, Japan, Korea, Taiwan, Singapore, Thailand, the Philippines, Australia, and New Zealand, using three univariate ARMA-based models (ARFIMA, ARAR, and SARIMA). Similarly, tourism demand in the Philippines can be predicted using a hybrid support vector regression (SVR) model with seasonal autoregressive integrated moving averages (SARIMA) (Abellana et al., 2021) [25]. Additionally, Huang et al. (2017) [11] developed an ARIMA model based on time series data regarding visitors to the Forbidden City. In addition, other aspects of tourism have also been explored by researchers by using ARIMA-type models. For instance, Craig (2024) [10] found climate indices in four of Australia’s most populous cities to be a powerful predictor on marine and urban tourism. Likewise, an ARMAX model was used by Pan and Yang (2017) [28] to forecast weekly hotel occupancy for a destination based on weather data as one of the key big data sources. In the same way as hotel demand forecasts, Kumar and Ekka (2025) [13] propose an integrated system that takes into account the interconnectedness of data from Property Management Systems (PMSs), staff productivity, and procurement efficiency, with a particular emphasis on the ARIMA model’s efficiency in predicting hotel demand (Kumar & Ekka, 2025) [13]. Moreover, scholars also applied ARIMA models to forecast the impact of COVID-19 on tourism, including the impact of COVID-19 on tourist and non-tourist employment in Spain, which was explored by Perles-Ribes et al. (2023) [15] using the ARIMA model, and Korinth (2022) [12] investigated the impact of COVID-19 on Poland’s tourism industry. Additionally, the ARIMA model has also been used on longitudinal data in Lim and To’s (2022) [3] study to demonstrate that Macao’s gambling revenue is greatly dependent on tourist arrivals, and the industry is experiencing unprecedented revenue declines based on predicted and actual values.
However, optimizing parameter selection is one of the challenges associated with implementing ARIMA-type models. As one of the objectives in the present study, a modified version of SARIMAX named SARIMAX-E was developed that incorporates additional parameter selection grids in order to contribute to the development of tourism demand forecasting research. Parameter grids are multidimensional spaces in which each dimension represents a parameter within the model. As the SARIMAX model includes seasonal autoregressive orders (P), seasonal difference orders (D), seasonal moving average orders (Q), and seasonal periods (s), a number of possible values are assigned to each of these parameters, and the values selected depend on prior experience and knowledge. It is a Cartesian product that shows a series of parameters with each grid point representing a different parameter combination, thus allowing systematic exploration of the parameter space. The purpose of the SARIMAX-E model is to find the most appropriate parameter combination to give the model the best performance.
2.2. Artificial Intelligence-Based Forecasting of Tourism Demand
As an alternative to ARIMA-type models, AI-based models have become increasingly popular for forecasting tourism demand in recent years (Wu et al., 2024) [2]. The use of artificial intelligence does not require models to consider input-output relationships or distributions of data when predicting future tourism demand because they enable nonlinear data prediction (Song & Zhang, 2025) [1]. Despite the theoretical and methodological foundations remaining relatively unclear (Song et al., 2019) [9], there has been a claim that AI-based models have proven to be a novel approach to tourism forecasting since they outperformed advanced time series models on a performance basis (Hewapathirana, 2023; Li et al., 2023) [29,30]. Studies related to tourism forecasting have identified the Long Short-Term Memory (LSTM) model as one of the most commonly used AI-based forecasting models in this field (Bi et al., 2020; Binesh et al., 2024; Han et al., 2024; Law et al., 2019) [4,16,17,18].
The LSTM model was originally introduced to address the problem of vanishing and exploding gradients encountered by traditional RNNs when dealing with long-sequence data (Han et al., 2024) [17]. This model excels at processing time-series data and is widely used in forecasting tasks, including the prediction of tourism numbers (Wu et al., 2022) [31]. An LSTM model is composed of multiple layers, each containing memory cells that are gated by three structures: input gates, forget gates, and output gates. Using these gates, long-term dependencies can be captured by determining the type of information stored and output in each cell (Law et al., 2019) [18]. As an example, using Macao’s monthly tourist arrival data and search query data, LSTM model with attention mechanism was used by Law et al. (2019) [18] to forecast tourist arrivals in Macao. The LSTM model showed superior results with lower MAPE, MAE, and RMSE in comparison with other baseline models, proving that an AI-based model was more effective than time series models. Likewise, two famous tourist attractions in China (Jiuzhaigou and Huangshan mountain) were also forecasted with the LSTM model in the study conducted by Bi et al. (2020) [4], and the results were better than those of the ARIMAX model. In light of the superior performance of LSTM found in the existing literature, the present study will compare a variety of forecast models including the newly proposed SARIMAX-E model; ARIMA-type models (ARIMA, SARIMA, ARIMAX); and machine learning models (Transformer, LTSM, Random Forests, XGBoost).
3. Methodology
In this model, SARIMA serves as a baseline for capturing trends and seasonal variations within time series, in addition to incorporating a number of exogenous variables related to economic, climatic, and policy factors. In order to mitigate cointegration issues, exogenous variables undergo lag processing, while holiday windows are created in order to capture the impact of specific events on the data. Variables are standardized to eliminate dimensional effects, and rolling cross-validation is used to select parameters under conditions of small sample sizes. The parameter search is confined within a finite grid to prevent overfitting, and the optimization is aimed at minimizing the Mean Absolute Error (MAE). A number of parameters undergo full-sample retraining to ensure they meet the requirements of the tourism industry for controlling ‘visitor count bias’. During the final evaluation, a rolling zero-point single-step forecasting method is used to simulate operational scenarios, with updates being made to the model on a monthly basis.
The research experiment will compare different forecasting models and determine which is the most effective in forecasting tourism demand, including the newly proposed SARIMAX-E model; ARIMA-type models (ARIMA, SARIMA, ARIMAX); and machine learning models (Transformer, LTSM, Random Forests, XGBoost). The datasets will cover a number of key data sources related to the tourism industry, including gaming revenue, weather temperature data, transportation data (incoming vehicles), currency exchange rates, holidays and seasonality. The overall methodological design of this study is illustrated in Figure 1.
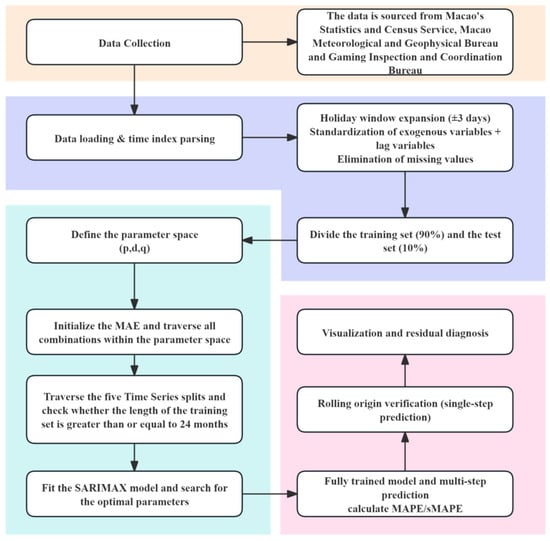
Figure 1.
Methodological design of the present research. Source: Authors own work.
3.1. Data Collection
The context of this study is to forecast tourist arrivals for Macao Special Administrative Region (Macao SAR). The datasets used are time series data pertaining to gaming revenue, weather temperature, incoming vehicles, exchange rates between Macao Pataca (MOP) and Chinese Yuan (RMB), as well as tourist arrivals from July 2010 to December 2019. All the data used in this study are available online from a variety of sources. Macao’s Statistics and Census Service website provides visitor arrival, exchange rates, and incoming vehicle data at https://www.dsec.gov.mo/zh-MO (accessed on 14 July 2025) [32]; weather temperature data can be found on the website of the Macao Meteorological and Geophysical Bureau https://www.smg.gov.mo/zh (accessed on 14 July 2025) [33], and Macao’s gaming revenue data can be found on the website of the Gaming Inspection and Coordination Bureau https://www.dicj.gov.mo/web/en/frontpage/index.html (accessed on 14 July 2025) [34]. The present research did not take into account unexpected external events, such as the COVID-19 pandemic and economic downturns. In view of the significant impact of pandemic control measures on Macao’s tourism industry, this study excludes the years following the start of the COVID-19 pandemic in 2020 due to a sudden decline in tourist arrivals following that time. Moreover, economic downturns are difficult to quantify in advance, and based on such rare events as external factors, the dataset may not generalize to a large extent.
In order to provide an overview of the overall dataset, Table 1 summarizes the central tendency (mean and median), variability (standard deviation), and range for every key variable. In addition, as the dependent variable in the tourism demand forecasting model, Figure 2 shows the number of mainland tourists who have traveled to Macao between 2010 and 2019. Thus, as illustrated in Figure 3, gaming revenue, a major economic driver in Macao, can be used as a key variable to demonstrate the relationship between visitor arrivals and spending patterns. Moreover, mainland visitors’ travel affordability may be affected by currency fluctuations between MOP and RMB, and cross-border transportation flows can serve as a leading indicator of tourist arrivals. Lastly, seasonal climate variations may explain seasonal peaks in arrivals. Initially, a coefficient analysis was performed to evaluate how the influence of each exogenous variable affected forecasting performance (See Figure 4).

Table 1.
Descriptive statistics on gaming revenue, weather temperatures, incoming vehicles, exchange rates between Macao Pataca (MOP) and Chinese Yuan (RMB), and tourist arrivals. Source: (Gaming Inspection and Coordination Bureau; Macao Meteorological and Geophysical Bureau; Macao’s Statistics and Census Service).
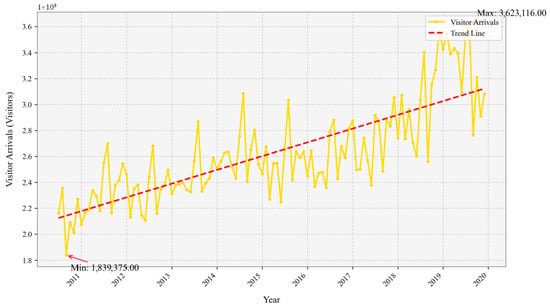
Figure 2.
An overview of the visitor arrivals dataset. The line graph illustrates tourist arrivals to Macao from 2010 to 2019. Source: (Macao’s Statistics and Census Service).
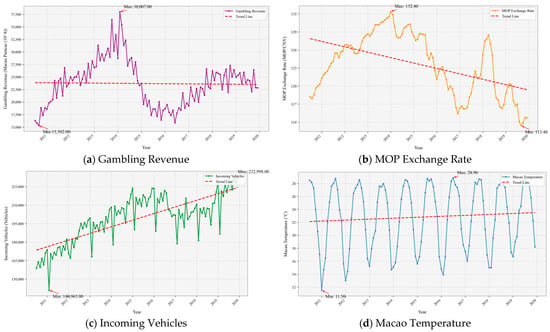
Figure 3.
Variable time series diagram. The line graph illustrates the monthly gaming revenue of Macao, the monthly exchange rate between MOP and RMB, the number of vehicles entering Macao per month and the monthly temperature of Macao from 2010 to 2019. Source: (Gaming Inspection and Coordination Bureau, Macao’s Statistics and Census Service, Macao Meteorological and Geophysical Bureau).
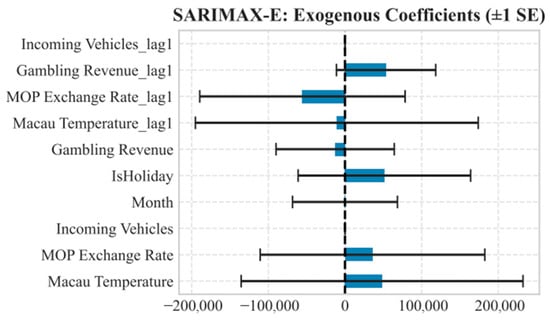
Figure 4.
Variable coefficients. Source: Authors own work.
In addition, for the purpose of understanding how potential correlations might interact and affect predictions before implementing the different forecast models, statistical tests including the variance inflation factor (VIF) and correlation coefficients were conducted. According to the VIF analysis, multicollinearity among the selected predictors is low across the model. The MOP exchange rate shows the highest VIF at approximately 1.41, followed closely by gambling revenue at approximately 1.37. Incoming vehicles have a VIF of 1.07, while Macao’s temperature is the lowest at approximately 1.02. The VIF scores are all well below the common threshold of 5, so each variable contributes unique information to the model. Along with the VIF results, the correlation matrix provides an additional insight into the relationship between the variables (See Figure 5). Generally, the pairwise correlations are weak, which explains why VIF scores are low.
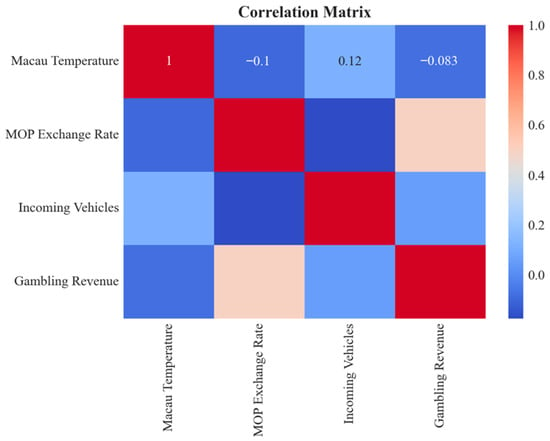
Figure 5.
Variable correlation matrix. Source: Authors own work.
3.2. SARIMAX-E Model Implementation
The present research proposes the SARIMAX-E model presenting a Seasonal AutoRegressive Integrated Moving Average with eXogenous variables—Enhanced forecasting framework for Macao visitor arrivals during 2010 to 2019. By embedding a discrete parameter grid and rolling cross-validation in the classical SARIMAX specification, the proposed model selection approach turns the problem of model selection into a countable, finite parameter space that can be optimized explicitly. Another key aspect of this algorithm is the use of holiday window expansion and the addition of lagged variables during the data preprocessing phase. In the hyperparameter optimization phase, small-scale time series dataset limitations are taken into consideration, and rolling cross-validation is used in conjunction with grid parameter search space techniques to select parameter combinations that produce the smallest Mean Absolute Error (MAE). Mathematically, this can be viewed as an optimization method where the goal is to minimize MAE. At present, the commonly used parameter selection method of ARIMA is to use the autoarima library in the Python environment. However, the autoarima library cannot select the corresponding evaluation indicators according to the actual business to achieve the best prediction effect when selecting parameters.
The SARIMAX-E model can be described as:
where
- : Tourist arrivals in period (t) (target variable).
- (xt): Vector of exogenous variables, including gaming revenue, temperature, inbound vehicles, exchange rate, and public holidays.
- (β): Vector of coefficients associated with the exogenous variables.
- (L): Lag operator, where .
- : Non seasonal autoregressive polynomial of order .
- : Non seasonal moving average polynomial of order .
- : Seasonal autoregressive polynomial of order (P) and period .
- : Seasonal moving average polynomial of order and period .
- (d): Non seasonal differencing order.
- (D): Seasonal differencing order.
- (s = 12): Seasonal period (monthly data).
- : White noise error term with zero mean and variance .
In this study, the non-seasonal orders to and were restricted, while the seasonal orders are taken as with and , yielding a finite grid of cardinality . For each candidate tuple , a five-fold rolling-origin cross-validation was performed. Specifically, and denoted the training and evaluation windows of the kth fold, . Within each fold the model was re-estimated on , where was the augmented exogenous matrix containing contemporaneous and lagged covariates as well as holiday indicators, and a one-step-ahead forecast was produced for the earliest observation in . The mean absolute error was then recorded, ignoring any folds that fail to converge.
The optimal configuration was illustrated as follows:
where the range of parameters used are:
- p (Non-seasonal AR order): 0, 1, 2
- d (Non-seasonal differencing order): 0, 1, 2
- q (Non-seasonal MA order): 0, 1, 2, 3, 4
- P (Seasonal AR order): 0, 1, 2
- D (Seasonal differencing order): 1 (fixed)
- Q (Seasonal MA order): 0, 1, 2
Once the optimal orders were identified, the final model was re-fitted on the full training sample and was used to generate an -step-ahead forecast for the hold-out period. Exogenous variables comprised Macao temperature, MOP exchange rate, gross gaming revenue, and inbound vehicle counts; official holidays were expanded to a seven-day window centered on each public holiday and encoded as a binary indicator; continuous covariates were standardized via the Z-score transformation; model estimation employed the L-BFGS optimizer with a maximum of 600 iterations.
3.3. Machine Learning Models Implementation
The hardware configuration for this study includes an AMD 7800X3D processor, a Windows 11 operating system, 32 GB of RAM, and an NVIDIA 4070 graphics card with 12 GB of dedicated video memory. Python 3.9.12 was used in the development environment with the following libraries: TensorFlow 2.10.0 (for the LSTM model), XGBoost 1.7.0, PyTorch 2.0.1 (for the Transformer model), and scikit-learn 1.1.3 as the primary libraries.
In terms of data preprocessing, the LSTM and XGBoost models utilized MinMaxScaler (feature_range = (0, 1)) for standardization, while the Transformer model utilized RobustScaler to enhance robustness against outliers. All models used a holiday list that included Macao public holidays as part of their holiday handling. The holiday variable was converted to a binary type (is_holiday), along with temporal features such as the month and day of the week. For the lag feature configuration, LSTM used look_back = 1 (i.e., the preceding one period), while Transformer used seq_len = 12 (i.e., the preceding 12 periods). During dataset partitioning, all models were trained on 80% of the dataset and tested on 20%, with a fixed random seed of ‘random_state = 42’ or ‘torch.manual_seed (42)’ to ensure reproducibility.
The experimental parameters are as follows: The LSTM model consists of two layers of 50 LSTM units, followed by a Dense (1) layer, with Adam serving as the optimiser and MSE serving as the loss function. Training is conducted over 100 epochs with a batch size of 32; XGBoost is set with n_estimators = 100, learning_rate = 0.1, and random_state = 42; Transformer employs an encoder architecture with d_model = 64, n_heads = 4, and n_layers = 3, using a batch size of 64. The training was conducted over 200 epochs with early stopping applied.
To ensure randomization control and experimental replication, the LSTM and XGBoost models were run ten times with MAE, MAPE, and SMAPE being recorded for each iteration. Based on the mean values and standard deviations, the presented results reflect the mean. The Transformer model employed a fixed random seed (<code>torch.manual_seed (42)</code>), saved the optimal model weights, and evaluated each run individually. Furthermore, the mean and standard deviation from 10 runs were included, with the final mean result being presented.
3.4. Model Evaluation
The model evaluation parameters used in this study are MAPE (Mean Absolute Percentage Error), SMAPE (Symmetric Mean Absolute Percentage Error) and Mean Absolute Error (MAE). MAPE is the mean absolute percentage error between the predicted and actual values (Sun et al., 2019) [35]. The value of MAPE is usually expressed as a percentage, ranging from 0% to infinity. 0% indicates a perfect prediction, while higher values indicate a larger prediction error. Moreover, SMAPE is a variant of MAPE designed to address the instability of MAPE when the actual value is very small (close to zero) (Li et al., 2023) [30]. SMAPE is expressed as a percentage and also has a range of values from 0% to infinity. In addition, Mean Absolute Error (MAE) is a regression prediction model evaluation metric used to measure the difference between predicted and actual values (Zhang et al., 2021) [36]. It has the same value as the target variable and a range of 0 to positive infinity. 0 indicates an accurate prediction; the greater the value, the greater the error. Mathematically, the model evaluation parameters can be expressed as:
3.5. Multi-Step Predictions
As part of the tourism demand forecasting process, the prediction horizon refers to the period of time into the future for forecasting tourist arrival numbers, and this parameter determines how far in advance one can predict tourist arrivals (Kumar et al., 2025) [37]. Depending on the prediction horizon, models can be classified as single-step or multi-step. Multi-step prediction models predict more than one future point in a sequence, while single-step prediction models are developed to predict one future point at a time. (Green et al., 2025) [38]. Moreover, multi-step predictions have been used as a method to assess the accuracy of models in forecasting studies. For instance, a study by Liu et al. (2025) [39] compared Informer, LSTM, and CNN models in time steps of 1, 3, 5, and 10 for forecasting gas concentration and discovered that the proposed model had smaller error metrics. Furthermore, Wang et al. (2024) [40] compared up to 5-step predictions among six different models in a study focused on wind speed forecasting and found that with increasing forecasting steps, error metrics generally increase.
In order to better compare and evaluate the overall performance of each model in the current study, multi-step prediction experiments have been conducted by comparing machine learning models including LSTM, Random Forest, XGBoost, Transformer with SARIMAX and SARIMAX-E models in the time steps of 1, 3, 6, and 12 that correspond with the seasonal characteristics of tourism demand. The results shown in Table 2 demonstrated that SARIMAX-E consistently outperformed the majority of other models in terms of MAE, MAPE, and SMAPE across the one-step, three-step, and six-step predictions. In the twelve-step prediction, however, LSTM overtook SARIMAX-E slightly, resulting in lower MAE, MAPE and SMAPE, suggesting that deep sequence models may capture long-range dependencies more effectively.

Table 2.
Summary of multi-step prediction experiments. Source: Authors own work.
4. Results
In this study, a dynamic seasonal regression model SARIMAX-E (p, d, q) (P, D, Q, 12) was used as the primary methodology for developing an algorithm for forecasting visitor arrivals in Macao during the period 2010 to 2019. After loading the data, a 10-dimensional feature vector was constructed using a ±3-day sliding holiday window, lag 1-period exogenous variables (temperature, exchange rate, incoming vehicles, gambling revenue), and Z-score standardization. Among 64 parameter grids, 5-fold rolling cross-validation (re-training and predicting one step per fold) was used to finalize the combination as (0, 1, 0) (1, 1, 1, 12). Using a fixed 90/10 split, the model was trained to accurately predict the entire year of 2019, achieving MAE 171,042, MAPE 5.7% and SMAPE 5.6% by rolling the origin monthly in one-step validation. Therefore, Figure 6 and Figure 7 illustrated the visual representation of the predicted outcome and residual distribution from the SARIMAX-E model. Further to that, additional time series forecasting models were compared in this study including Autoregressive integrated moving average (ARIMA), Seasonal Auto-Regressive Integrated Moving Average (SARIMA), Auto-Regressive Integrated Moving Average with Explanatory variables (ARIMAX), long short-term memory (LSTM), random forests, XGBoost and Transformer (See Table 3).
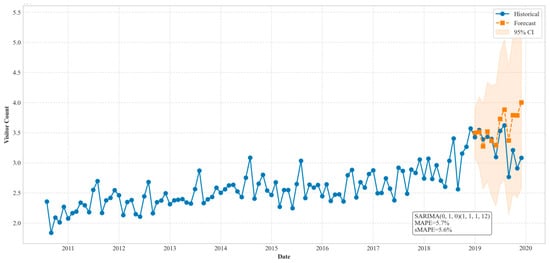
Figure 6.
SARIMAX-E prediction visual representation. The line graph illustrates the actual and forecasted tourist arrivals. The blue line indicates actual tourist numbers, and the orange line indicates the predicted values of SARIMAX-E model. Source: Authors own work.
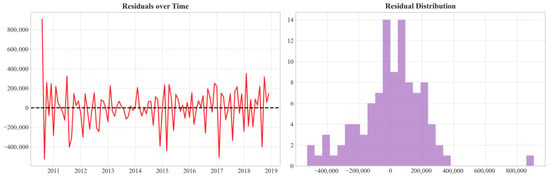
Figure 7.
SARIMAX-E residuals. The graphs illustrate the details and distribution of SARIMAX-E model residuals over time. Source: Authors own work.

Table 3.
An overview of forecasting results MAPE (Mean Absolute Percentage Error), SMAPE (Symmetric Mean Absolute Percentage Error) and Mean Absolute Error (MAE). Source: Authors own work.
The results indicated that the ARIMA family of models (SARIMAX-E, ARIMAX, and SARIMA) was particularly well suited for this forecasting task, as its members consistently ranked among the top performers in terms of error percentages. SARIMAX-E achieved the best overall performance with MAE 171,042, MAPE 5.7% and SMAPE 5.6%, which highlights the importance of incorporating exogenous variables into models. While ARIMAX was closely followed with MAE 273,880, MAPE 8.4% and SMAPE 8.8%, SARIMA also delivered excellent results by capturing seasonality effectively with MAE 279,837, MAPE 8.5% and SMAPE 9.0%. In contrast, the machine learning models yielded more mixed results. It is worth noting that LSTM presented a balanced and competitive performance with MAE 166,782, MAPE 6.6% and SMAPE 6.3%, outperforming most conventional approaches with the exception of SARIMAX-E. Both Random Forest and XGBoost underperformed, with high error rates. The Transformer model performs slightly better than Random Forest and XGBoost but fails to outperform SARIMA, ARIMAX, LSTM, and SARIMAX-E.
5. Discussion
Time series forecasting relies on a variety of methods due to its complexity, and tourism demand has been forecasted mostly using autoregressive integrated moving average (ARIMA-type) models over the past five decades (Craig, 2024; Huang et al., 2017; Korinth, 2022; Kumar & Ekka, 2025; Lim & To, 2022; Peng et al., 2021; Perles-Ribes et al., 2023) [3,10,11,12,13,14,15]. While machine learning models have emerged as an innovative method for forecasting tourism demand (Wu et al., 2024) [2], a comparison of ARIMA-type models with machine learning models in the existing literature indicates inconsistent results. In some studies, researchers have demonstrated that ARIMA-type models perform better than their machine learning counterparts (Kontopoulou et al., 2023) [20], and this situation is particularly pertinent to SARIMAX models (Baloch et al., 2024; Benitez et al., 2023; Kişmiroğlu & Isik, 2025; Lee et al., 2025) [19,21,22,23]. Therefore, this study developed an enhanced SARIMAX model named SARIMAX-E that incorporated additional parameter selection grids to find the parameter combinations that will provide the best performance for the model. Based on the enhanced SARIMAX-E model presented in this study, it is possible to predict small-scale time series datasets and time series datasets with special labels, such as holidays. A key aspect of this algorithm is the use of holiday window expansion and the addition of lagged variables during the data preprocessing phase. During the hyperparameter optimization stage, consideration is given to the limitations of small-scale time series datasets, and rolling cross-validation is used in conjunction with grid parameter search space methods to select the parameter combinations that provide the smallest average mean absolute error (MAE). Following the training of the SARIMAX model on the full dataset, the model is retrained using rolling origin validation, single-step predictions are made, and results are recorded. The rolling origin metrics are then computed.
Furthermore, this study examined the performance of different forecasting models, including the newly proposed SARIMAX-E model; ARIMA-type models (ARIMA, SARIMA, ARIMAX); and machine learning models (Transformer, LTSM, Random Forests, XGBoost). It was found that the ARIMA family of models, including SARIMAX-E, ARIMAX, and SARIMA, was particularly well suited to tourism demand forecasting, as its members consistently ranked among the top performers in terms of error rates. By applying the additional parameter grid, the combination (0, 1, 0) (1, 1, 1, 12) was optimized for SARIMAX-E (p, d, q) (P, D, Q, 12), resulting in MAE 171,042, MAPE 5.7%, and SMAPE 5.6% with the best overall performance. Machine learning models, on the other hand, produced mixed results. Aside from SARIMAX-E, LSTM displayed a balanced and competitive performance with MAE 166,782, MAPE 6.6%, and SMAPE 6.3%, outperforming most conventional approaches after applying multi-step predictions. XGBoost and Random Forest both underperformed, with high error rates. In comparison with Random Forest and XGBoost, Transformer performed somewhat better, but it fell short of SARIMA, ARIMAX, LSTM, and SARIMAX-E. This study confirmed that SARIMAX continues to be an effective tool for forecasting studies in the tourism field, particularly for limited datasets or short time periods (Kontopoulou et al., 2023) [20]. The proposed SARIMAX-E model optimized the parameter selection and resulting the best performance under the condition where training data was limited, whereas machine learning and deep learning models require a great deal of information to train effectively and to learn complex temporal patterns from historical data (Lee et al., 2025) [21]. Lastly, in addition to introducing the SARIMAX-E model, this research follows a big data approach and incorporates multiple key data sources relating to Macao’s tourism industry, including gaming revenue, weather conditions, transportation data (incoming vehicles), currency exchange rates, holidays, and seasonality. The present research emphasizes the importance of multi-source big data in tourism demand forecasting.
6. Conclusions
In conclusion, an enhanced SARIMAX model, SARIMAX-E, was developed that included additional parameter selection grids to find the optimal parameter combinations. In addition, this study examined different forecasting models, including the newly proposed SARIMAX-E model, ARIMA-type models (ARIMA, SARIMA, ARIMAX), and machine learning models (Transformer, LTSM, Random Forests, XGBoost). Models such as SARIMAX-E, ARIMAX, and SARIMA are especially suited to tourism demand forecasting, as they consistently rank among the best models in terms of error percentages. Additionally, LSTM outperformed most conventional approaches except for SARIMAX-E when multi-step predictions were applied. Furthermore, this study incorporates a number of key data sources relating to Macao’s tourism industry through the use of big data and examines the importance of multi-source big data when forecasting tourism demand.
However, it is important to note that this study has several limitations. Considering the inability to obtain monthly time series data in other aspects of this study, it was limited to datasets that are publicly accessible from the websites of the Statistics and Census Service (DSEC), the Macao Meteorological and Geophysical Bureau, and the Gaming Inspection and Coordination Bureau. Due to this limitation, the datasets examined only involve time-series data pertaining to gaming revenue, weather temperature, incoming vehicles, and the exchange rate between Macao Pataca (MOP) and Chinese Yuan (RMB). Additional data sources that are deemed relevant to Macao’s tourism demand may be incorporated into future research. In addition, this study compared four ARIMA-type models (ARIMA, SARIMA, ARIMAX, SARIMAX-E) with machine learning and deep learning models (Transformer, LTSM, Random Forests, XGBoost). Further research could compare more AI-based models and explore the possibility of implementing hybrid models. Lastly, despite its high accuracy on small datasets, the SARIMAX-E model still requires further testing in order to be evaluated on longer-term time series data.
Author Contributions
Conceptualization, C.F.L.; Writing—original draft, C.F.L.; Visualization, C.F.L.; Data curation, F.C.; Methodology, F.C.; Validation, F.C.; Writing—review and editing, C.W.C.; Supervision, C.W.C.; Funding acquisition, C.W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the City University of Macau and the Shenzhen Great Bay Technology Joint Laboratory of Artificial Intelligence and Big Data.
Data Availability Statement
Data available in a publicly accessible repository. The combined dataset supporting the findings of this study is available at https://github.com/492579299Chen/Tourism-Forcasting (data accessed on 14 July 2025 and uploaded on 29 August 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Song, H.; Zhang, H. Tourism demand modelling and forecasting: A Horizon 2050 paper. Tour. Rev. 2025, 80, 8–27. [Google Scholar] [CrossRef]
- Wu, D.C.; Zhong, S.; Wu, J.; Song, H. Tourism and Hospitality Forecasting with Big Data: A Systematic Review of the Literature. J. Hosp. Tour. Res. 2024, 49, 615–634. [Google Scholar] [CrossRef]
- Lim, W.M.; To, W.-M. The economic impact of a global pandemic on the tourism economy: The case of COVID-19 and Macao’s destination- and gambling-dependent economy. Curr. Issues Tour. 2022, 25, 1258–1269. [Google Scholar] [CrossRef]
- Bi, J.-W.; Liu, Y.; Li, H. Daily tourism volume forecasting for tourist attractions. Ann. Tour. Res. 2020, 83, 102923. [Google Scholar] [CrossRef]
- Matthews, L.; Scott, D.; Andrey, J.; Mahon, R.; Trotman, A.; Burrowes, R.; Charles, A. Developing climate services for Caribbean tourism: A comparative analysis of climate push and pull influences using climate indices. Curr. Issues Tour. 2021, 24, 1576–1594. [Google Scholar] [CrossRef]
- Hussain, M.N. Evaluating the impact of air transportation, railway transportation, and trade openness on inbound and outbound tourism in BRI countries. J. Air Transp. Manag. 2023, 106, 102307. [Google Scholar] [CrossRef]
- Opstad, L.; Hammervold, R.; Idsø, J. The Influence of Income and Currency Changes on Tourist Inflow to Norwegian Campsites: The Case of Swedish and German Visitors. Economies 2021, 9, 104. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, Z.; Gao, J.; Xu, C. Forecast Methods for Time Series Data: A Survey. IEEE Access 2021, 9, 91896–91912. [Google Scholar] [CrossRef]
- Song, H.; Qiu, R.T.; Park, J. A review of research on tourism demand forecasting: Launching the Annals of Tourism Research Curated Collection on tourism demand forecasting. Ann. Tour. Res. 2019, 75, 338–362. [Google Scholar] [CrossRef]
- Craig, C.A. Forecasting Australia’s international arrivals with climate indices. Int. J. Tour. Cities 2024, 10, 1098–1108. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Ding, Y. The Baidu Index: Uses in predicting tourism flows—A case study of the Forbidden City. Tour. Manag. 2017, 58, 301–306. [Google Scholar] [CrossRef]
- Korinth, B. Implications of COVID-19 on tourism sector in Poland: Its current state and perspectives for the future. Tour. Recreat. Res. 2022, 47, 636–640. [Google Scholar] [CrossRef]
- Kumar, P.; Ekka, P. Demand Forecasting for Ensuring Safety and Boosting Operational Efficiency in Hotel Hospitality Using ARIMA Model. J. Hosp. Tour. Educ. 2025, 1–15. [Google Scholar] [CrossRef]
- Peng, T.; Chen, J.; Wang, C.; Cao, Y. A Forecast Model of Tourism Demand Driven by Social Network Data. IEEE Access 2021, 9, 109488–109496. [Google Scholar] [CrossRef]
- Perles-Ribes, J.F.; Ramón-Rodríguez, A.B.; Jesús-Such-Devesa, M.; Aranda-Cuéllar, P. The Immediate Impact of Covid19 on Tourism Employment in Spain: Debunking the Myth of Job Precariousness? Tour. Plan. Dev. 2023, 20, 1–11. [Google Scholar] [CrossRef]
- Binesh, F.; Belarmino, A.M.; van der Rest, J.-P.; Singh, A.K.; Raab, C. Forecasting hotel room prices when entering turbulent times: A game-theoretic artificial neural network model. Int. J. Contemp. Hosp. Manag. 2024, 36, 1044–1065. [Google Scholar] [CrossRef]
- Han, W.; Li, Y.; Li, Y.; Huang, T. A deep learning model based on multi-source data for daily tourist volume forecasting. Curr. Issues Tour. 2024, 27, 768–786. [Google Scholar] [CrossRef]
- Law, R.; Li, G.; Fong, D.K.C.; Han, X. Tourism demand forecasting: A deep learning approach. Ann. Tour. Res. 2019, 75, 410–423. [Google Scholar] [CrossRef]
- Kişmiroğlu, C.; Isik, O. Temperature Prediction Using Transformer–LSTM Deep Learning Models and Sarimax from a Signal Processing Perspective. Appl. Sci. 2025, 15, 9372. [Google Scholar] [CrossRef]
- Kontopoulou, V.I.; Panagopoulos, A.D.; Kakkos, I.; Matsopoulos, G.K. A Review of ARIMA vs. Machine Learning Approaches for Time Series Forecasting in Data Driven Networks. Future Internet 2023, 15, 255. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Lee, J.-Y.; Han, S.-H.; Kang, J.-G.; Lee, J.-B.; Choi, D.-R. Performance Evaluation of PM2.5 Forecasting Using SARIMAX and LSTM in the Korean Peninsula. Atmosphere 2025, 16, 524. [Google Scholar] [CrossRef]
- Baloch, M.; Honnurvali, M.S.; Kabbani, A.; Jumani, T.A.; Chauhdary, S.T. An Intelligent SARI-MAX-Based Machine Learning Framework for Long-Term Solar Irradiance Forecasting at Muscat, Oman. Energies 2024, 17, 6118. [Google Scholar] [CrossRef]
- Benitez, I.B.; Ibañez, J.A.; Lumabad, C.D., III; Cañete, J.M.; Principe, J.A. Day-Ahead Hourly Solar Photovoltaic Output Forecasting Using SARIMAX, Long Short-Term Memory, and Extreme Gradient Boosting: Case of the Philippines. Energies 2023, 16, 7823. [Google Scholar] [CrossRef]
- Shah, V.; Patel, N.; Shah, D.; Swain, D.; Mohanty, M.; Acharya, B.; Gerogiannis, V.C.; Kanavos, A. Fore-casting Maximum Temperature Trends with SARIMAX: A Case Study from Ahmedabad, India. Sustainability 2024, 16, 7183. [Google Scholar] [CrossRef]
- Abellana, D.P.M.; Rivero, D.M.C.; Aparente, M.E.; Rivero, A. Hybrid SVR-SARIMA model for tourism forecasting using PROMETHEE II as a selection methodology: A Philippine scenario. J. Tour. Futures 2021, 7, 78–97. [Google Scholar] [CrossRef]
- Chu, F.-L. Forecasting tourism demand with ARMA-based methods. Tour. Manag. 2009, 30, 740–751. [Google Scholar] [CrossRef]
- Box, G.E.P. Time Series Analysis, Forecasting and Control, 2nd ed.; Wiley and Sons Inc.: Hoboken, NJ, USA, 1976. [Google Scholar]
- Pan, B.; Yang, Y. Forecasting Destination Weekly Hotel Occupancy with Big Data. J. Travel Res. 2017, 56, 957–970. [Google Scholar] [CrossRef]
- Hewapathirana, I.U. Advancing tourism demand forecasting in Sri Lanka: Evaluating the performance of machine learning models and the impact of social media data integration. J. Tour. Futures 2023, 11, 261–285. [Google Scholar] [CrossRef]
- Li, M.; Zhang, C.; Sun, S.; Wang, S. A novel deep learning approach for tourism volume forecasting with tourist search data. Int. J. Tour. Res. 2023, 25, 183–197. [Google Scholar] [CrossRef]
- Wu, D.C.; Zhong, S.; Qiu, R.T.R.; Wu, J. Are customer reviews just reviews? Hotel forecasting using sentiment analysis. Tour. Econ. 2022, 28, 795–816. [Google Scholar] [CrossRef]
- Macao’s Statistics and Census Service. Statistics. Available online: https://www.dsec.gov.mo/zh-MO (accessed on 14 July 2025).
- Macao Meteorological and Geophysical Bureau. Macao Clim. Available online: https://www.smg.gov.mo/zh (accessed on 14 July 2025).
- Gaming Inspection and Coordination Bureau. Information. Available online: https://www.dicj.gov.mo/web/en/frontpage/index.html (accessed on 14 July 2025).
- Sun, S.; Wei, Y.; Tsui, K.-L.; Wang, S. Forecasting tourist arrivals with machine learning and internet search index. Tour. Manag. 2019, 70, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, G.; Muskat, B.; Law, R. Tourism Demand Forecasting: A Decomposed Deep Learning Approach. J. Travel Res. 2021, 60, 981–997. [Google Scholar] [CrossRef]
- Kumar, B.A.; Singh, R.; Shaji, H.E.; Vanajakshi, L. Bus Arrival Time Prediction: A Comprehensive Review. IEEE Trans. Intell. Transp. Syst. 2025, 26, 7362–7379. [Google Scholar] [CrossRef]
- Green, R.; Stevens, G.; Abdallah, Z.S.; Silva Filho, T.M. Stratify: Unifying multi-step forecasting strategies. Data Min. Knowl. Discov. 2025, 39, 64. [Google Scholar] [CrossRef]
- Liu, B.; Li, Z.; Zang, Z.; Yin, S.; Niu, Y.; Cai, M. Multi-information Fusion Gas Concentration Prediction of Working Face Based on Informer. Min. Metall. Explor. 2025, 42, 597–613. [Google Scholar] [CrossRef]
- Wang, K.; Tang, X.-Y.; Zhao, S. Robust multi-step wind speed forecasting based on a graph-based data reconstruction deep learning method. Expert Syst. Appl. 2024, 238, 121886. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).