1. Introduction
Information diffusion becomes a concerning public issue nowadays as the rapid and vast adoption of online social media, like Facebook, Twitter, Whatsapp, Weibo, Wechat, etc. For example during the outbreak of Covid-19, various information on the virus is widespread through the online social media platforms quickly, and has a significant impact on the whole society. Therefore, it is of great importance to investigate the process of information diffusion. There are lots of research trying to explore the mechanism underlying how information spreads over social network [
1,
2,
3].
Up to now, a large body of research has demonstrated that network structure plays a crucial role in the process of information diffusion, with studies examining its influence from multiple scales. For example, Duffy et al. [
4] experimentally explored the influence of network structure on financial contagion in interbank networks, and showed that contagions are more likely to occur in incomplete network structures than in complete ones. Montanari and Saberi [
5] investigated the network structure favoring rapid spread of innovations, finding that diffusion is significantly slower on well-connected network structures dominated by long range links. In contrast, Bakshy et al. [
6] argued that weak ties in the social network play a dominant role in the information diffusion online. Similarly, Qiao et al. in [
7] demonstrated that scale-free network or the existence of hubs can facilitate knowledge diffusion better than other network structures, such as small-world network and regular network. Furthermore, an optimal network topology is presented in [
8] based on link structure to increase spreading prevalence. Pan et al. in [
9] further explored the interplay between network topology and spreading dynamics, showing that the degree distribution of an optimal network topology for spreading prevalence relies on the infection rate, where strong degree heterogeneity can facilitate the spreading only for small infection rate.
While the above studies focus primarily on macro-level features such as degree distribution and overall network connectivity, other research has examined diffusion dynamics from a meso-scale perspective. For example, Stegehuis et al. [
10] analyzed epidemic spreading on networks with community structures and found that such structures can either facilitate or hinder the diffusion process, depending on their configuration. Similarly, Lin et al. [
11] also investigated the community effect on information diffusion and demonstrated evident homophily in both actions and influence, as individuals within the same community tend to behave similarly and exert stronger mutual influence during the diffusion process.
Core-periphery (CP) is another typical mesoscale property of network structure. It is first formalized by Borgatti and Everett [
12], and described by two qualitatively distinct components: densely connected nodes in the core component and loosely connected nodes in the periphery component. The core size is typically much smaller than the entire network [
13]. CP structure appears widely in the real world networks, such as trade network [
14], financial network [
15], brain networks [
16], transportation networks [
17], as well as World Wide Web and social networks [
18,
19], etc. However, unlike the community structure, the role of CP structure in diffusion processes has not yet been extensively explored.
Most of the prior research has concentrated either on detecting core-periphery structure more efficiently [
13,
20,
21,
22,
23] or on understanding how core-periphery structure can emergence [
24,
25,
26]. More recently, some attentions have been paid to their impact on the dynamics on networks, such as cascading failure and information diffusion over networks. For example, Ref. [
27] investigated the impact of CP structure on cascading failures in interdependent networks, and demonstrated that the networks with weak core-periphery structure will be more robust. In [
28], the influence of CP network on Ising model was examined by numerical simulations, revealing that a strong core-periphery structure leads to an intermediate phase and a double phase transition, the nature of which depends on whether the connections between the core and periphery nodes scale sub-linearly or linearly with the network size. Similarly, Ref. [
29] explored the dynamics of epidemics over weighted core-periphery networks and derived the upper bound of critical threshold for epidemic spreading, but they did not further indicate the influence of core-periphery structure on epidemic prevalence. These works reveal that CP structure can significantly alter the robustness and dynamical behavior of networks.
Overall, despite these advances, there are still relatively few work into the influence of CP structure on the diffusion dynamics, and the specific role of CP structure in shaping information propagation over networks remained insufficiently understood. There are still several gaps to be addressed.
Firstly, existing studies predominantly considered the scenario of simple contagion, which required a single exposure for adoption. However, empirical evidence [
30] indicated that many real-world behaviors spread through complex contagion, in which adoption requires multiple exposures due to social reinforcement. Therefore, it is necessary to further examine the impact of CP structure under different contagion scenarios, including both simple and complex contagion.
Secondly, most existing studies employed epidemic models like SIS in [
29] to investigate the diffusion dynamics over networks, while the impact of CP periphery structure on diffusion dynamics under Maki–Thompson (MT) model [
31] is still lacking. MT model, a representative rumor spreading model, differs from epidemic models in the removal mechanism [
32], leading to different dynamic behavior. MT model assumes that a spreader ceases spreading only when contacting another spreader or stifler, whereas in epidemic models an infected individual can recover spontaneously at a given recovering rate. Consequently, MT model is generally much more vulnerable to the network structure compared to epidemic model [
32]. Therefore, it would make the investigation of CP effects particularly relevant.
In order to bridge the aforementioned gaps, this paper would focus on the role of core-periphery structure playing in the process of information diffusion within the framework of Maki–Thompson model, from both simple contagion and complex contagion perspectives. To this end, a tunable CP network is constructed to generate networks with different strength of CP structure. We then analyze the information diffusion dynamics across these networks with different strength of CP structure, and further examine the impact of CP structure on information intervention under different intervention strategies.
The remainder of this paper is organized as follows.
Section 2 introduces the construction of networks with different strength of core-periphery structure, and provides a description of Maki-Thompson model.
Section 3 and
Section 4 present the main results on the influence of core-periphery structure on information diffusion and information intervention. Finally, some discussions and conclusions are drawn in
Section 5.
3. Information Diffusion with Different Core-Periphery Structure
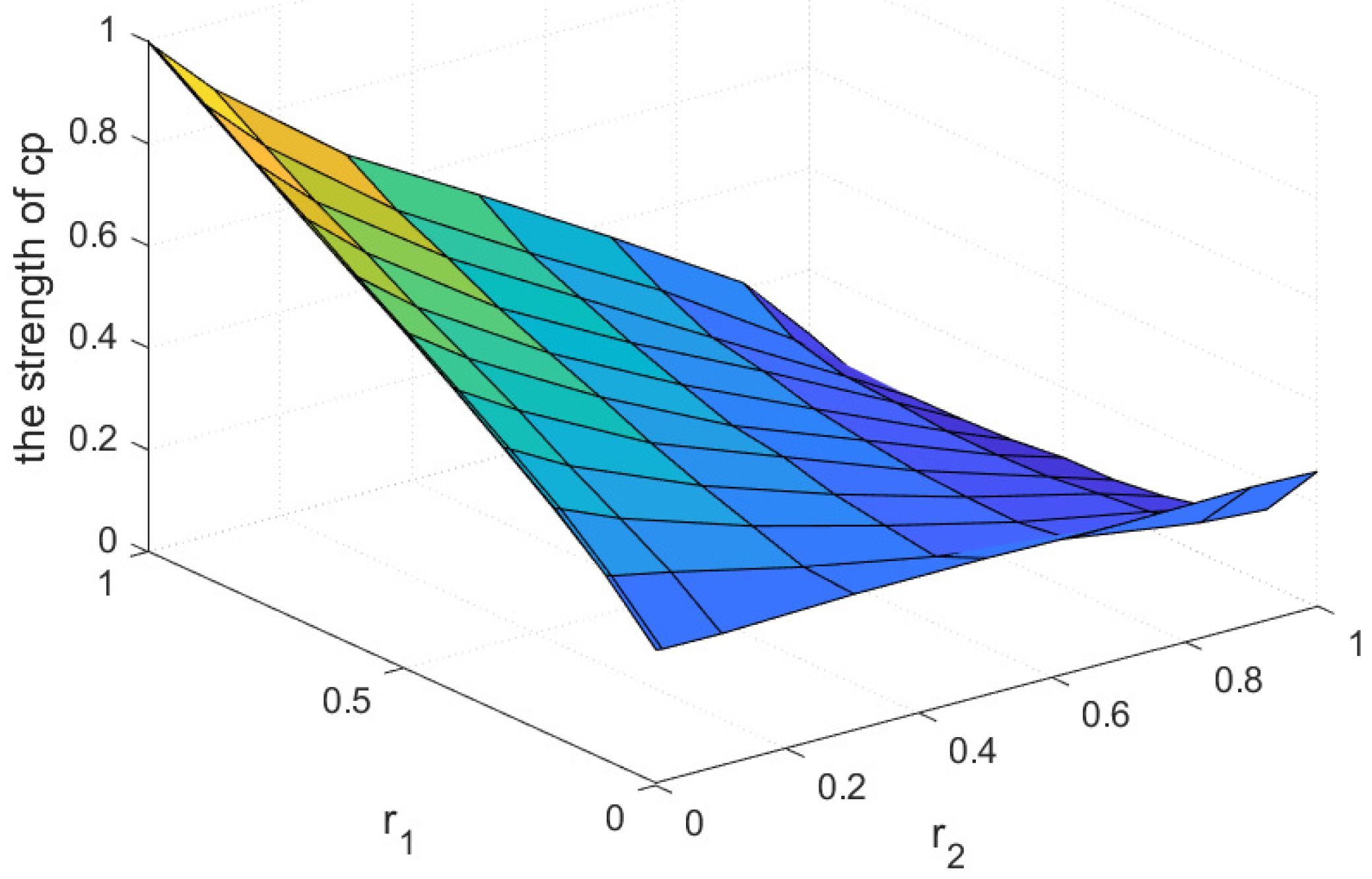
In this section we will analyze the influence of core-periphery structure on information diffusion from the perspective of the relationship between different core-periphery structure and the final percentage of the population adopting the information. To this end, different CP networks will be constructed by tuning the parameters
and
and fixing the other parameters based on the description in the previous section. We consider the network size
, and assume the percentage of core nodes is 20%, i.e., there are 200 core individuals, while the connectivity probability of core-core nodes
. Inspired by
Figure 2, the parameters
and
would be chosen as 1 and
, 1 and 1,
and
,
and
,
and 1,
and
, respectively. So that the strength of core-periphery for these networks can vary from small to large. The statistics for these networks is shown in
Table 1, where
is the average degree,
l is the average shortest path length and
is the clustering coefficient.
In what follows, we will present the results of information diffusion over the networks with CP structure shown in
Table 1 through numerical simulations, considering both simple contagion process and complex contagion process. Without loss of generality, we assume
and the initial number of spreaders is 3, which are chosen randomly from the whole population. The detailed parameters used are provided in
Table 2, and the methodology for implementing the numerical simulations is described in
Appendix C. All the results are obtained through 100 independent realizations.
3.1. Simple Contagion Process
Simple contagion in MT model means that only one successful interaction between ignorant individual and spreader is required before the ignorant can be transferred to a spreader. As is shown in
Appendix A, based on MT model as the ratio
is large enough, the information will go virus among the population, i.e., all of the individuals will finally become stiflers. Thus in this subsection we will analyze the influence of core-periphery with different ratio
. We assume the initial number of seed is 3, which are randomly selected from the whole population.
Figure 3,
Figure 4 and
Figure 5 are the numerical simulation results for the simple contagion.
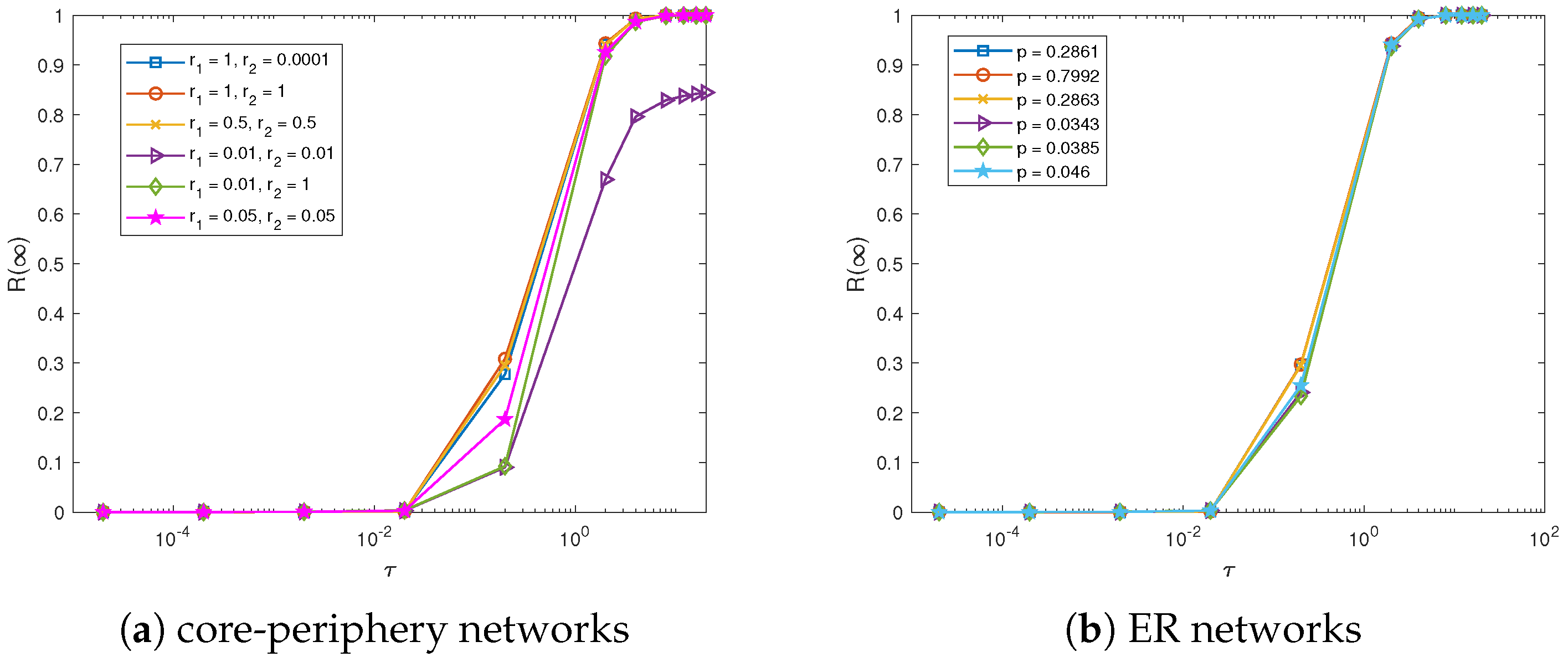
Figure 3 is the final percentage of stiflers with different ratio
over the networks in
Table 1. As can be seen in
Figure 3a, the final percentage of stiflers is almost 0 when
is small, and then increases quickly until it approaches its stable value when
is larger than a threshold value
. The threshold value
is almost the same, about 0.02, for different core-periphery strength, which indicates the core-periphery structure has little impact on the threshold value
in this case. But the value of final percentage of stiflers is different under different core-periphery structure. It can be seen in
Figure 3a that
increases much slower than others, when
and
, and its final percentage of
is also much smaller than others. That is partly due to the fact that the network is quite sparse when
and
and the average length of the path is relative large compared with other networks. Since according to
Figure 2, the strength of core-periphery structure for
and
is much larger than that for
and
, while the final percentage of stiflers for
and
still approaches 1.
In order to further demonstrate the influence of core-periphery structure, we also compare with the corresponding results over ER random networks, as is shown in
Figure 3b. By the corresponding ER random networks, it is actually zero order null model of the corresponding CP network, i.e., the average degree of the network is reserved, while every two nodes are connected with a predefined probability
, where
m and
n are the number of links and the number of nodes in the CP network, respectively. Obviously
p can be regarded as the network density. Thus in this paper we just assume
p as the network density of the CP network.
It is obvious from
Figure 3b that the final percentage of the stiflers keeps almost the same with different ER random networks, and the shape is quite similar to cases when the strength of core-periphery is relatively large. In addition, we can also see in the
Figure 3 that the final percentage of stiflers
will converge to stable level when
is larger than about 8 for all of CP networks, which is quite the same for random networks. Therefore, it can be indicated that the structure of core-periphery has little impact on the dynamics of information diffusion for simple contagion in this case.
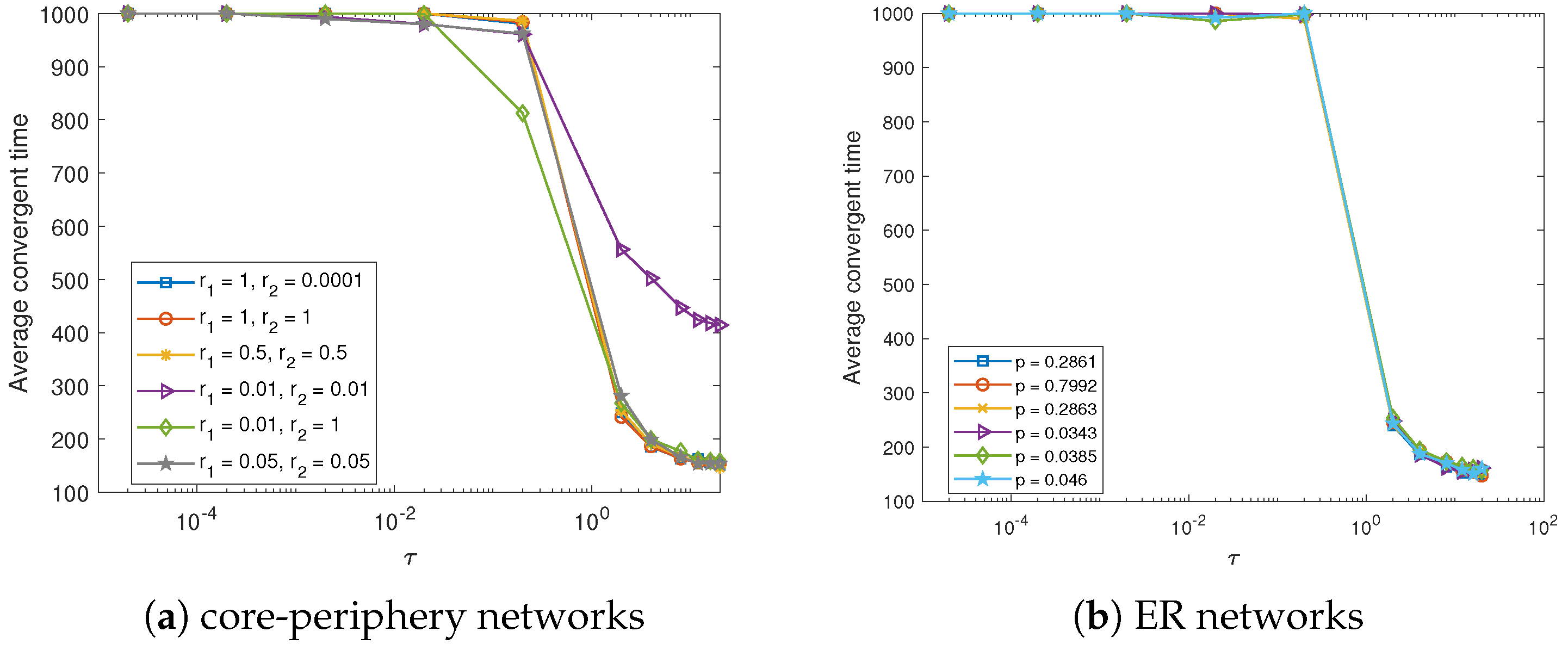
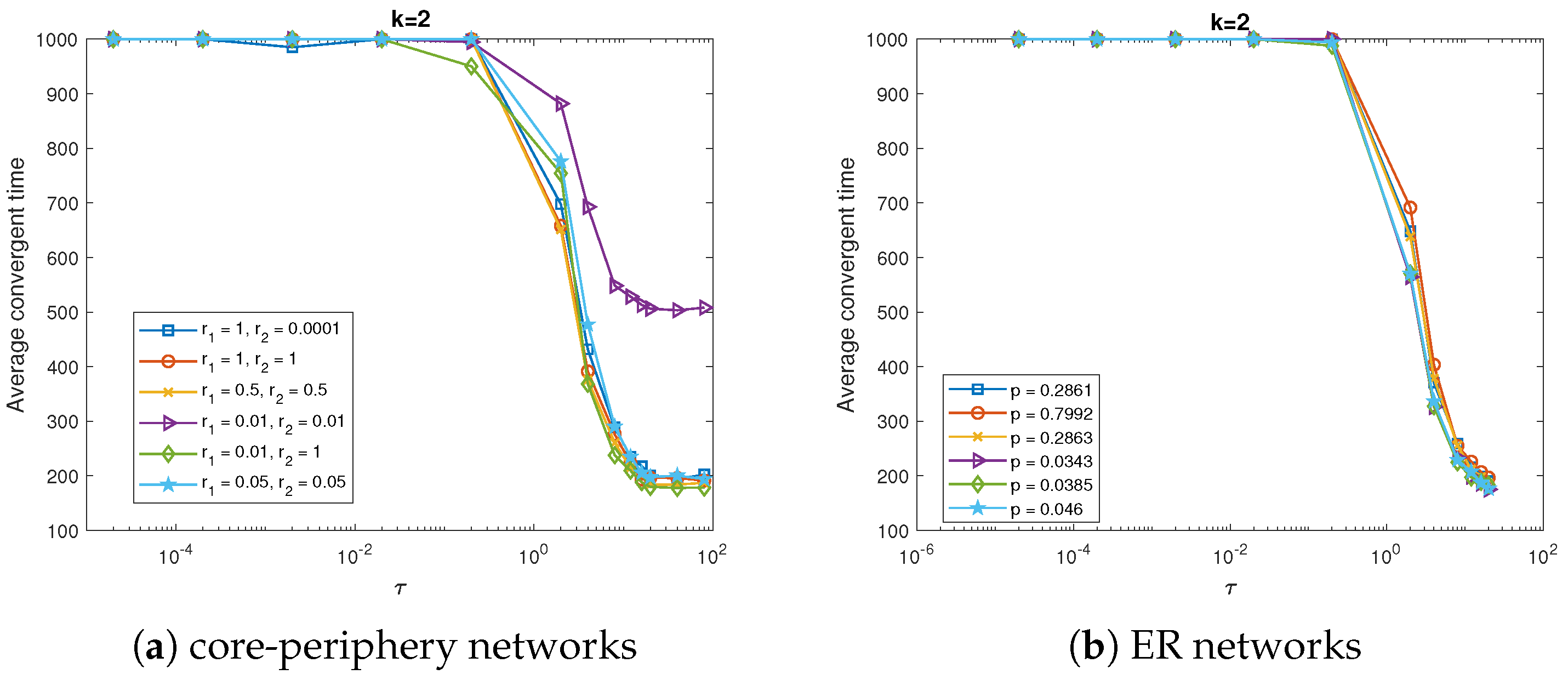
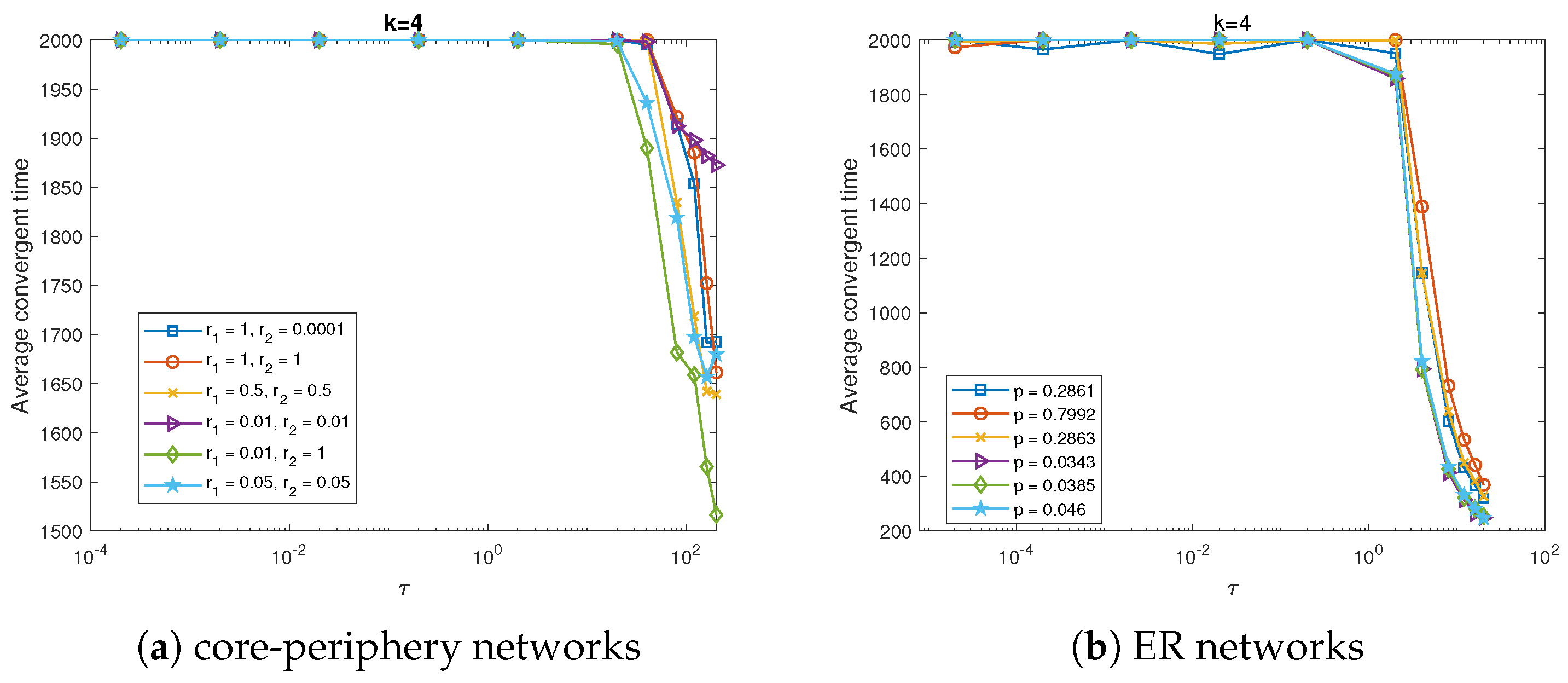
The convergence speed is also considered under different strength of CP structure in
Figure 4. According to the theoretical analysis in the
Appendix A, it is known that when the spreader is extinct, the population will reach a stable equilibrium. Thus the convergent time can refer to the number of time steps it takes until either the number of spreader is zero or it reaches the maximum number of time steps. It can be seen from
Figure 4 that for both the core-periphery networks and ER random network the average convergence time decrease sharply when
is near
. Specifically, for the CP networks it makes little difference among different strength of core-periphery structure except the case when
, whose average convergence time is much larger than others. At the meanwhile, the average convergence time exhibits the same trend for all the corresponding ER random networks. These results coincide with that of the final percentage of stiflers. Thus it can further confirm that it makes no difference for the dynamics of information diffusion in this scenario by core-periphery structure.
3.2. Complex Contagion Process
Inspired by the empirical studies [
30,
38,
39], which show that the process of information diffusion exhibits complex contagion, thus we will further look into the influence of core-periphery structure on the dynamics of information diffusion in the scenario of complex contagion. By complex contagion in MT model, it means multiple successful interactions between ignorant individual and spreader are required before the ignorant can switch to a spreader. In what follows we denote
k-complex contagion where
k is the required number of successful interactions. When
, it becomes simple contagion. In this paper we will consider the cases when
respectively.
Before we demonstrate the results through numerical simulations, a proposition would be proposed based on heterogeneous mean-field theory.
Proposition 1. Consider a complex contagion process on a core–periphery (CP) network. Let the threshold value , then the critical threshold on a CP network, , satisfieswhere is the corresponding threshold for the equivalent Erdős–Rényi (ER) network with the same average degree. Regarding the proof of the proposition, please refer to
Appendix B.
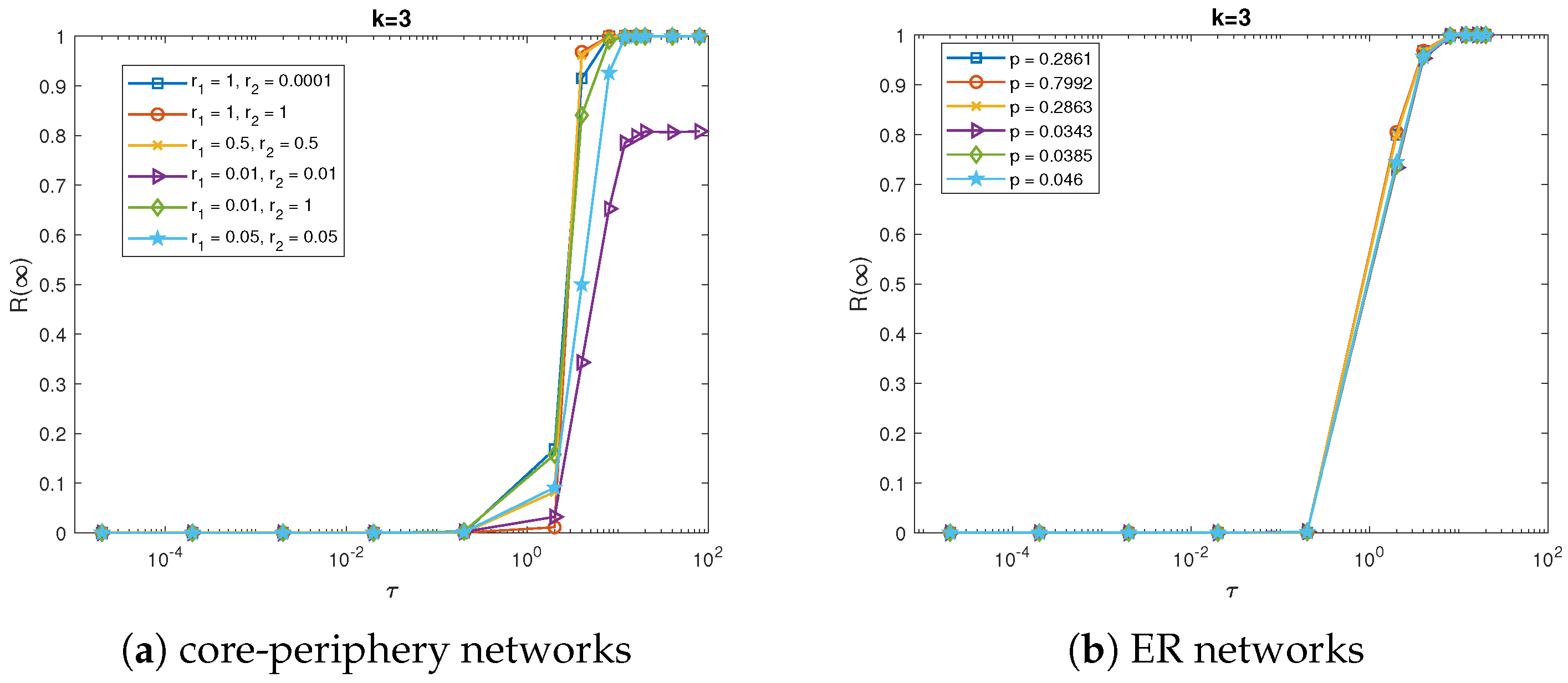
In what follows, numerical simulations will be carried out to further verify Proposition 1. Likewise, we will investigate the relationship between final percentage of stiflers and the threshold value under different strength of core-periphery structure, as well as the convergence speed.
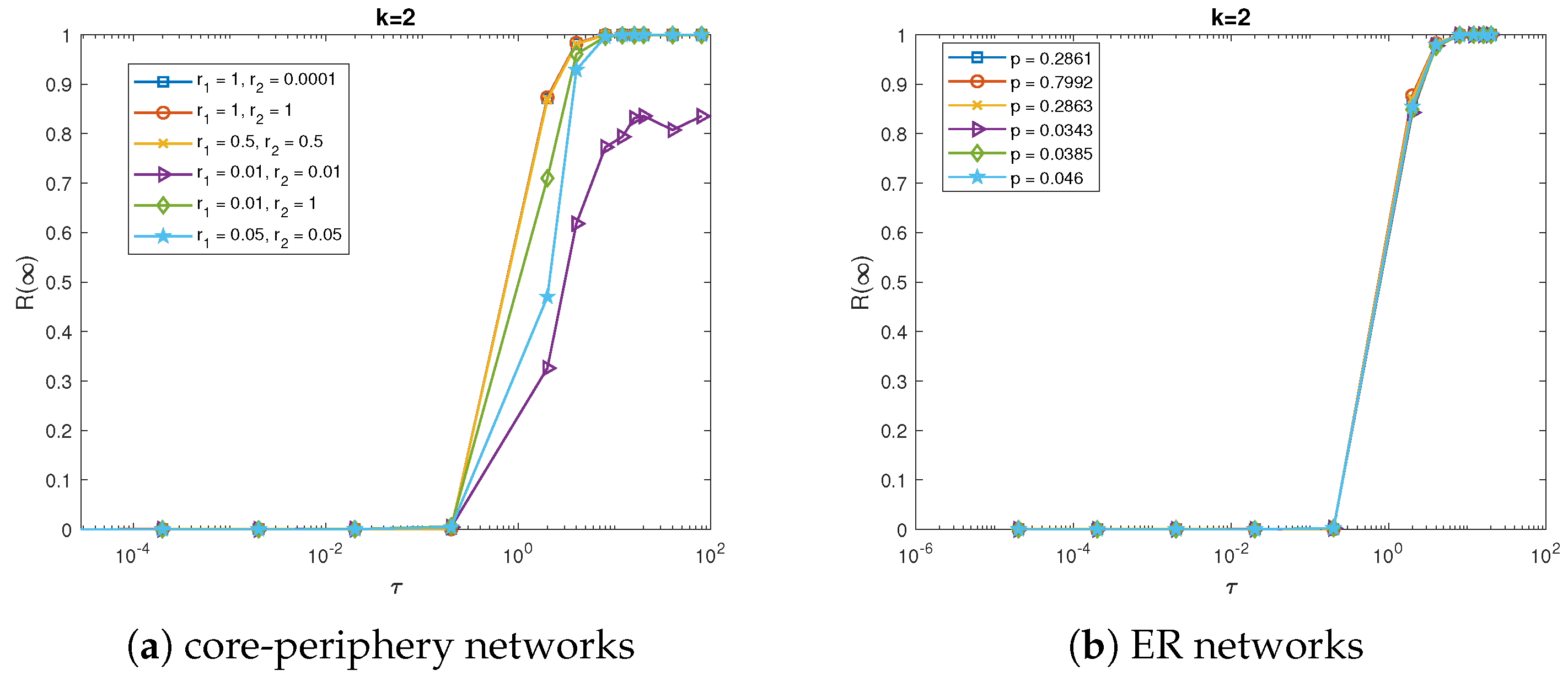
Figure 5 shows that the final percentage of stiflers increases with large
until it reaches its stable value over different CP networks when
. It can be seen from
Figure 5a that there is also a phase transition which occurs at the critical threshold value
in the simulation results for all the CP networks. Thus it can be indicated that the CP structure has no impact on the critical threshold value in this complex contagion. As is the same with simple contagion, the final percentage of stiflers varies with
in almost the same way for different CP networks except the network with
, whose
is much smaller. That is because the network is much sparser and its average shortest path length is much larger. Likewise, we also compare the results with the corresponding ER random networks, shown in
Figure 5b. It can be seen that the final percentage of stiflers increases with large
on all different ER random networks in the same way, which is a little bit different from that on CP networks. It can be partly due to the fact that there is not much difference for the average shortest path length among all the ER random networks.
Figure 6 is the average convergence time for both the CP networks and the corresponding ER networks. It can be found that the shapes are quite the same with simple contagion. It further implies that the dynamics of information diffusion is almost unaffected by the structure of core-periphery.
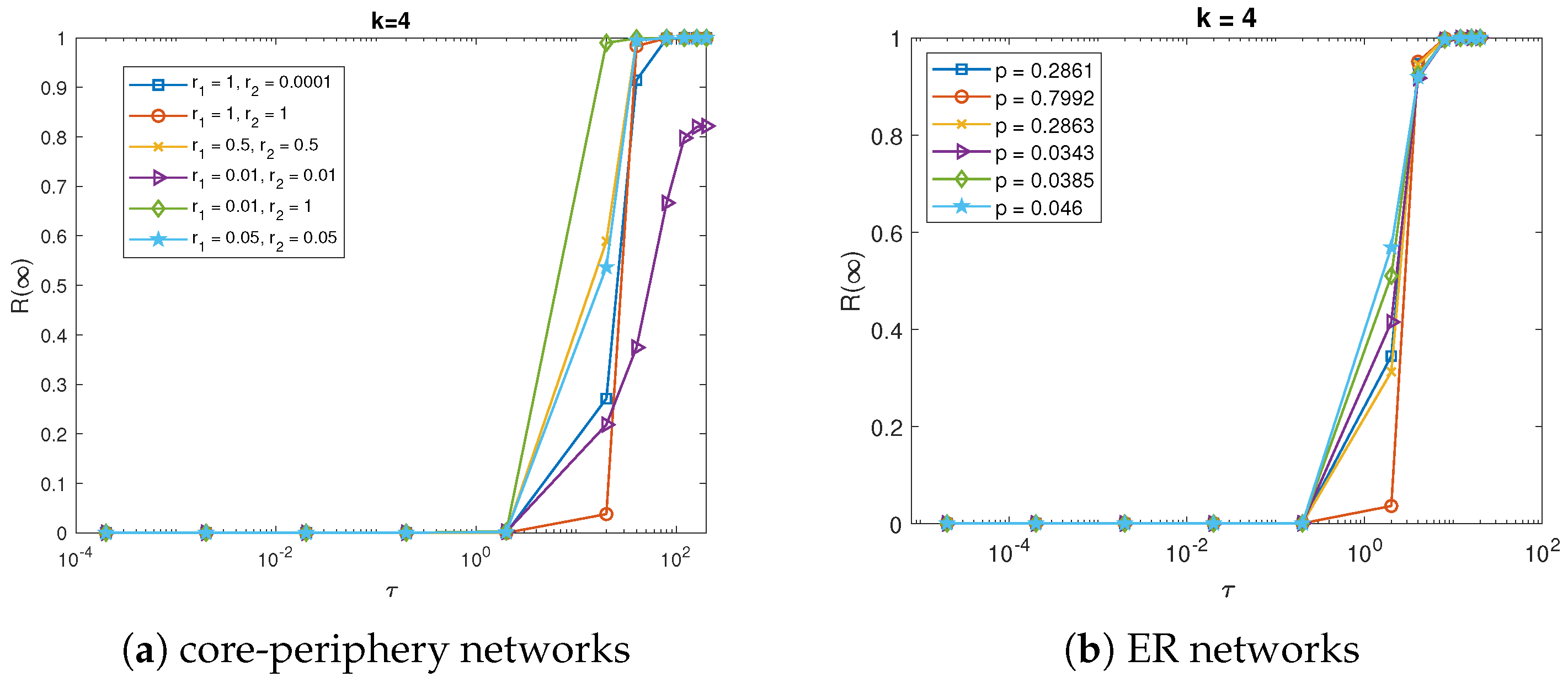
We also presented the results when
and
respectively in
Figure 7,
Figure 8,
Figure 9 and
Figure 10. The final percentage of stiflers over CP networks and ER random networks increases with
in the similar way as in the previous results. The only difference lies in the value of critical threshold
. As
k becomes large,
increases too. In these simulation results, for CP networks it can be seen that
when
, and
when
, while the value is 2 when
. This is mainly due to the fact more successful interactions are required for larger
k. Therefore it is much more difficult for the ignorant individuals to change their states to a spreader. In order to realize such transformation it should have higher probability to be successful for each interaction
. As a result the threshold value
is much larger with larger
k. Meanwhile the critical threshold value for the corresponding ER random networks is a little bit smaller. For example when
, the value is about
, as is shown in
Figure 8b. It implies that core-periphery structure may even diminish the ability for the network to disperse the information extensively.
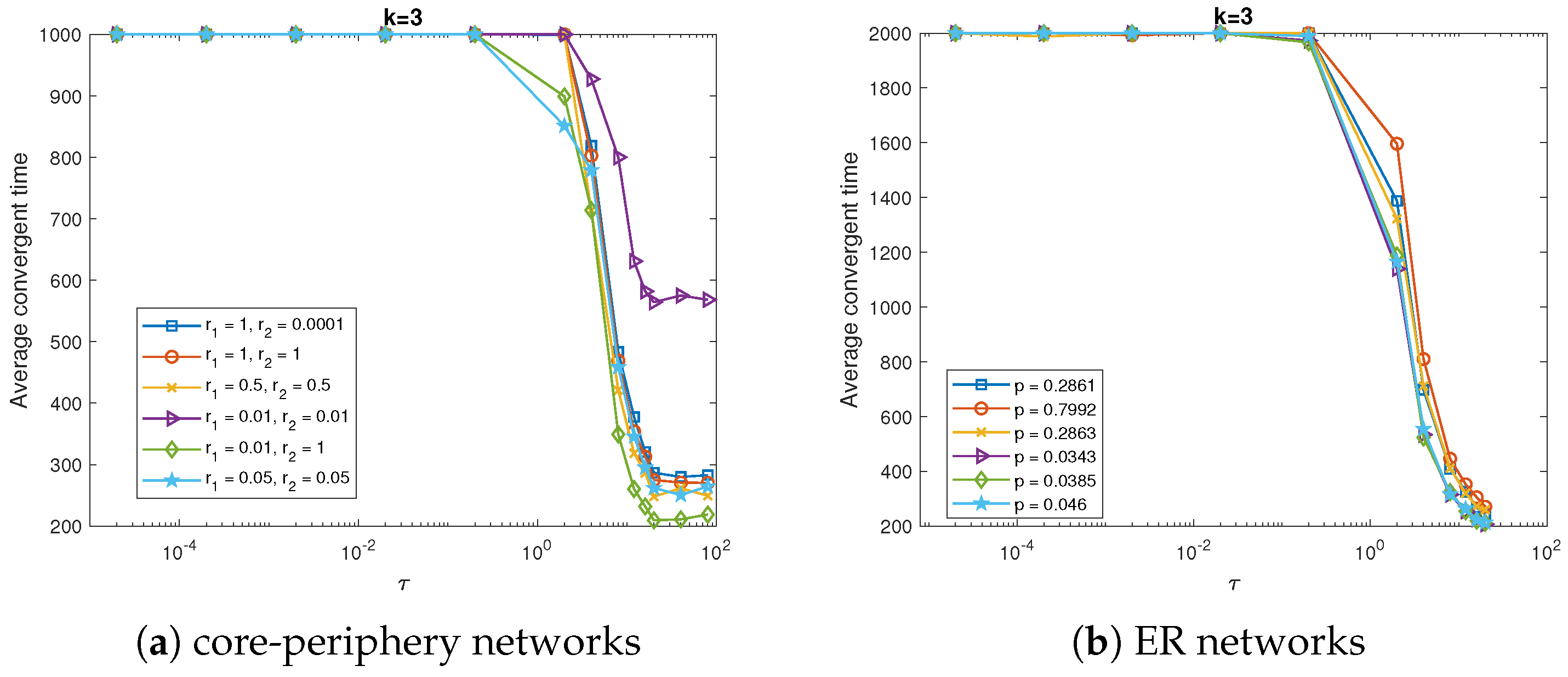
As for the average convergence time shown in
Figure 9 and
Figure 10, it is interested to find that the network with
and
can converge to the equilibrium much faster than the other networks when
. For the CP network with
and
in this paper, it means that the individuals other than the core individuals will connect to any individual randomly with the same probability. Therefore it is somehow much closer to a random network, whose clustering coefficient is quite small, as is shown in the
Table 1. By comparing with ER random networks, it is obviously that the random networks require much less time steps under the same threshold
. Thus the network akin to ER random network can converge to the stable equilibrium with less time steps. Meanwhile, when
k is small, the difference between CP networks and ER random networks is quite few, as is shown in
Figure 4, so that most of the CP networks converge to the stable equilibrium at similar speed.
4. Immunization-Based Information Diffusion Control
In the previous section, it is found that the CP structure has little impact on information diffusion. We will further investigate the influence of the CP structure on fighting fake news and preventing information diffusion in this section. Inspired by the immunization strategy proposed by [
40], the random immunization and target immunization will be analyzed respectively. By random immunization it means a random selected individual would become a stifler at a predefined probability no matter what kind of state he is, while by target immunization it refers to a targeted individual, which was set as core individual in the network in this paper. We assume the rate
and
, so that
can be guaranteed. The diffusion dynamics will be examined and compared under varying immunization rates, i.e., the proportion of nodes immunized, thereby capturing the range of available intervention capacity.
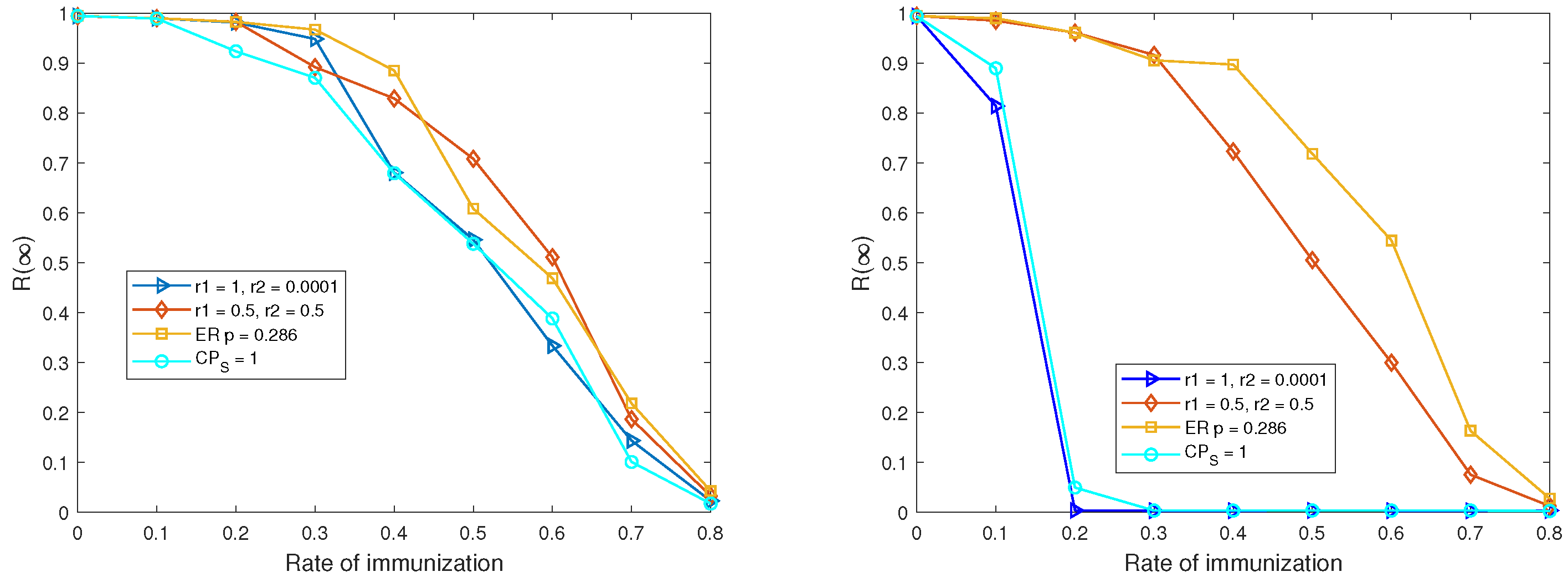
Figure 11 is the final percentage of stifler with different rates of immunization over different networks. The results for both the CP networks and the corresponding ER random networks are presented. It can be seen from
Figure 11a that with the strategy of random immunization, the final percentage of stiflers decreases in a similar way as the rate of immunization increases for all the networks. Thus the network structure has little impact on the performance of the information intervention under the strategy of random immunization. Meanwhile,
Figure 11b is the final percentage of stiflers with increasing rate of immunization over different networks when the target immunization is taken. It can be seen that there are phase transition for the networks with strong core-periphery structure, while for the other two networks the final percentage of stiflers declines much more smoothly as the rate of immunization increases, which is much more similar to the case of random immunization. It can be thus indicated that the structure of core-periphery has a significant impact on the information diffusion in this case. That is mainly due to the fact that the core nodes can be regarded as hubs to some extent.
Figure 12 is the average convergent time with different rates of immunization over different networks under the strategy of random immunization and targeted immunization respectively. It can be seen from
Figure 12a that the average convergent time keeps almost the same when the rate of individuals being immunized is relatively small, and then declines much more quickly when the rate is larger than about
in this case. The two networks with strong the core-periphery structure can converge to the stable equilibrium a little bit faster than the other two networks, especially when the rate of immunization is large, but the difference is quite tiny. Thus it can be indicated that under the strategy of random immunization the structure of core-periphery can hardly accelerate the convergence speed. As for the case of target immunization, it can be observed from
Figure 12b that there is a sharp decline for the two networks with strong core-periphery structure compared to the other two networks, when the rate of immunization reaches a threshold about 0.2 in these cases. The trend is quite similar to the results for the average final percentage of stiflers shown in
Figure 11b. Thus it can be obviously indicated that the structure of core-periphery may help speed up the convergence in the case of targeted immunization. That may be due to the fact that in strong CP networks, core nodes can act as critical bridges between dense core and sparse periphery. Thus targeting these core nodes can essentially fragment the network and sever the main pathways for information spread to the majority of nodes in the periphery.
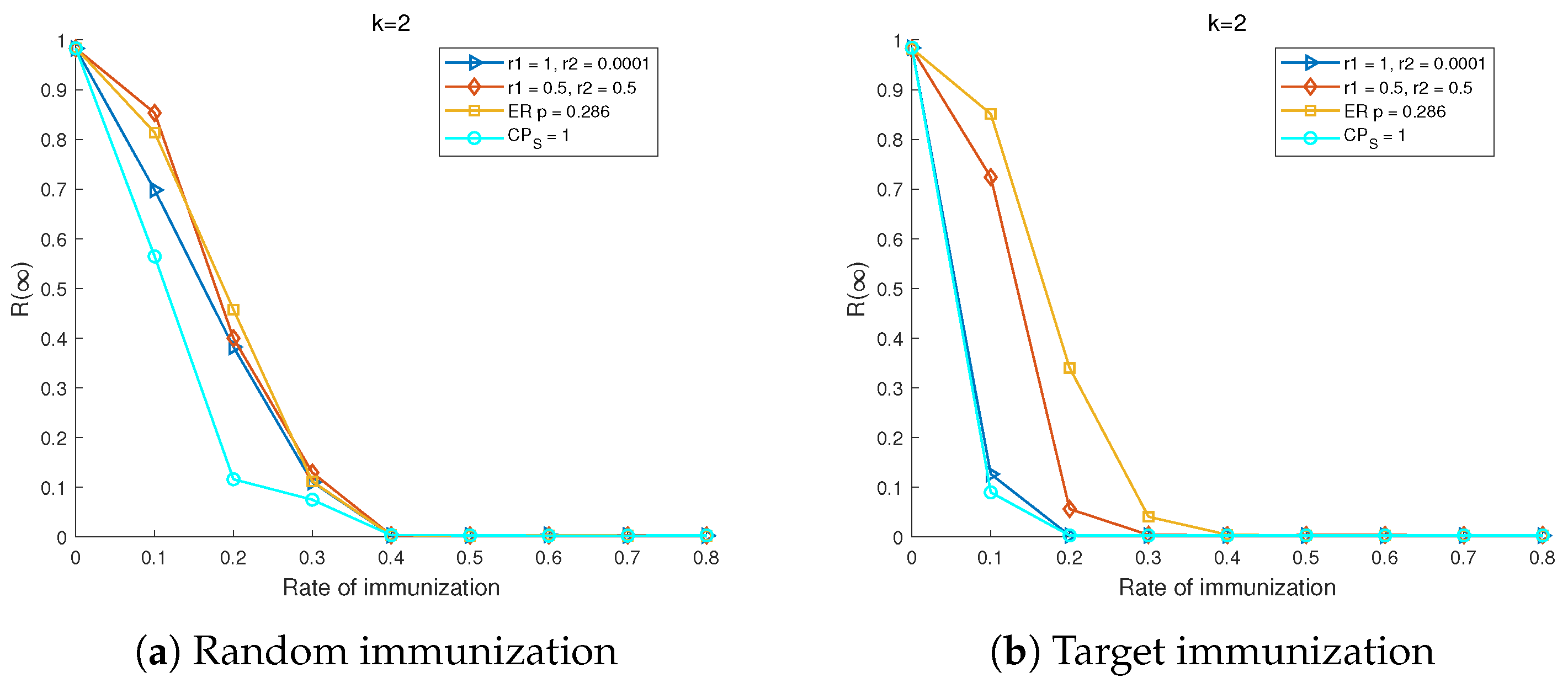
While the above results are concerned with simple contagion, we further investigate the case of complex contagion. The corresponding results when
are presented in
Figure 13 and
Figure 14. As can be seen in
Figure 13a, under the strategy of random immunization, there is little impact from core-periphery structure as well. The final percentage of stiflers decreases at almost the same speed, irrespective of different strength of core-periphery structure. Meanwhile, it can be found from
Figure 13b that under the strategy of target immunization, the influence by core-periphery becomes slighter compared to the case of simple contagion. We also investigate the scenario with different
k, and find when
k increases, the influence is gradually diminishing. That is partly because when
k increases, it is much more difficult for the individual to change his state. As a result, the impact by immunizing the core individual is fading, especially when the threshold
is not large.
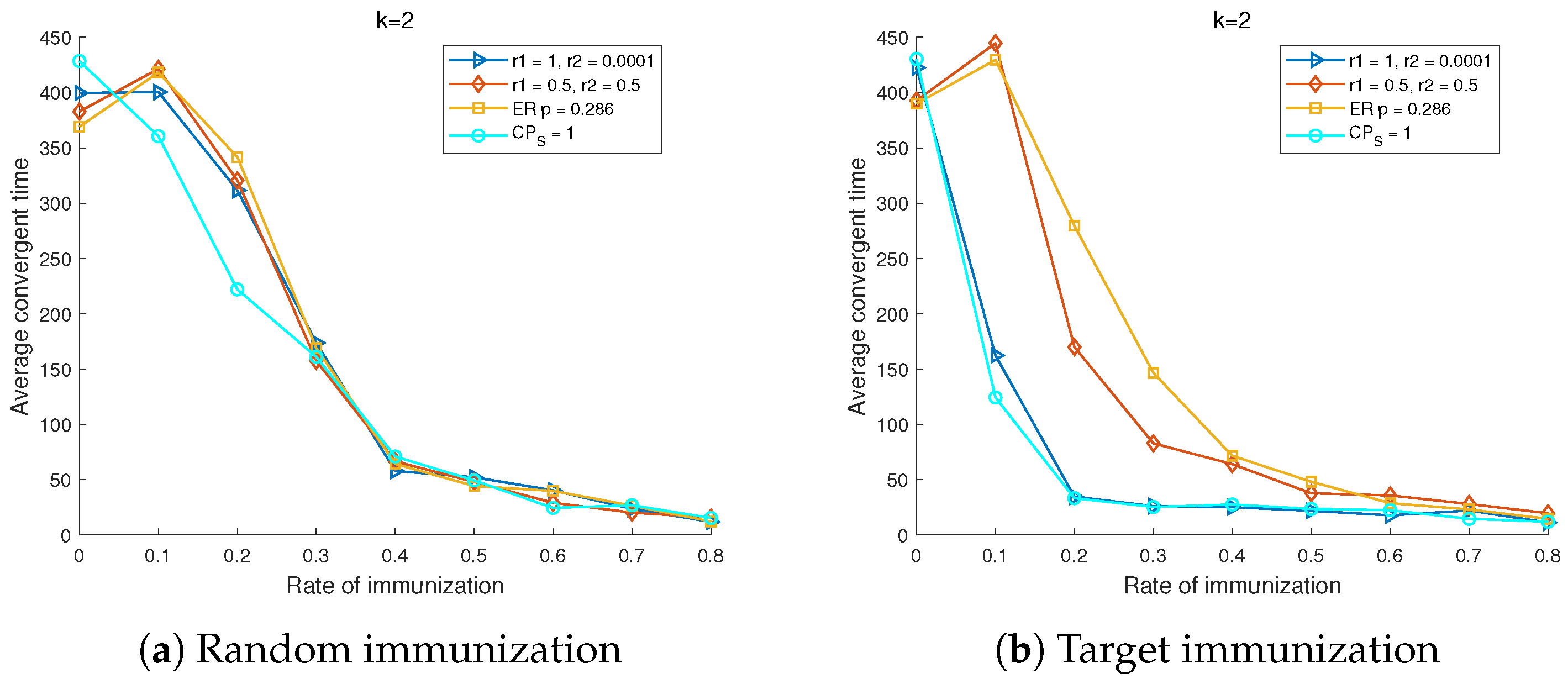
Likewise the average convergence time over different networks is also presented in
Figure 14. It can be observed that the average convergent time decreases as the rate of immunization becomes large for both the random immunization and target immunization. Moreover, the average convergent time goes down a little bit more sharply over the networks with stronger core-periphery structure than weak core-periphery structure under the strategy of target immunization. However as
k increases, such difference is diminishing as well. Thus it can be indicated the structure of core-periphery cannot accelerate convergence for target immunization as well when the adoption threshold for complex contagion increases.
5. Conclusions
In this paper, we conducted a comprehensive investigation into the influence of core-periphery (CP) structure on information diffusion over social networks, utilizing the Maki-Thompson (MT) model. By constructing networks with tunable CP strength and employing numerical simulations supported by theoretical analysis, we systematically examined the dynamics under both simple and complex contagion scenarios. The main contributions and findings can be summarized as follows.
Firstly, it is found that CP structure plays a nuanced, dual role in diffusion. While a stronger CP structure facilitates broader dissemination of information across the population compared to a weaker one, it simultaneously hinders the onset of complex contagions. Counterintuitively, CP networks require a significantly higher critical threshold for a global cascade of complex behaviors than equivalent random networks, due to the lack of local social reinforcement in the sparse periphery.
Secondly, the results demonstrate that networks with a strong CP structure are highly susceptible to targeted immunization strategies. Intervening in the densely connected core nodes is remarkably effective at curbing information spread, whereas random interventions show little dependence on the network structure. This underscores the practical importance of identifying and targeting structural cores for efficient information control.
Moreover, the advantage of targeted immunization diminishes as the complexity of the contagion, k, increases. This suggests that controlling the spread of behaviors requiring strong social reinforcement may necessitate more sophisticated strategies beyond simply targeting central nodes.
These findings offer crucial insights into how network structure governs diffusion dynamics. Since core–periphery structures are prevalent across diverse domains, such as financial, trade, and transportation networks, these results extend beyond social media contexts. In particular, the distinction between how CP structures affect simple versus complex contagion is especially relevant for understanding systemic risk in interbank networks, where multiple shocks may be required to trigger failures (analogous to complex contagion), in contrast to the rapid spread of financial panic (akin to simple contagion). This realization highlights that such a prevalent network topology can both facilitate and hinder diffusion depending on the contagion type, carrying significant implications for public opinion management, viral marketing, and epidemic control.
While this study provides a solid foundation, it also has several limitations opening up several avenues for future research. First, all the simulation results are based on synthetic networks with fixed size. Validating these findings on large-scale, real-world network data and exploring the model’s robustness across different network sizes and core proportions could be an important extension. Second, comparing the effects of CP structure with other mesoscale topologies, such as community or small-world structures, would also be a valuable extension. Furthermore, promising future directions include investigating diffusion on adaptive CP networks where the structure co-evolves with the spreading process, as well as incorporating more complex real-world factors such as multi-source information fusion [
41] and negative user emotions [
42].