Abstract
In RNA-seq data analysis, a primary objective is the identification of differentially expressed genes, which are genes that exhibit varying expression levels across different conditions of interest. It is widely known that hidden factors, such as batch effects, can substantially influence the differential expression analysis. Furthermore, apart from the primary factor of interest and unforeseen artifacts, an RNA-seq experiment typically contains multiple measured covariates, some of which may significantly affect gene expression levels, while others may not. Existing methods either address the covariate selection or the unknown artifacts separately. In this study, we investigate two integrated strategies, FSR_sva and SVAall_FSR, for jointly addressing covariate selection and hidden factors through simulations based on a real RNA-seq dataset. Our results show that when no available relevant covariates are strongly associated with the main factor of interest, FSR_sva performs comparably to existing methods. However, when some available relevant covariates are strongly correlated with the primary factor of interest–SVAall_FSR achieves the best performance among the compared methods.
Keywords:
RNA-seq; false discovery rate; variable selection; differential expression analysis; hidden factors; batch effects; surrograte variable analysis MSC:
62-08; 62F03; 62F07; 62F40; 62P10
1. Introduction
Differential expression analysis is a central task in analyzing RNA-seq data. Its primary goal is to identify genes whose expression levels differ across levels of a factor of interest. Differential expression analysis is typically carried out within a regression model framework, where the response variables are gene expression levels, and the explanatory variables include the primary factor of interest along with other measured covariates and potentially unobserved hidden factors. A gene is considered differentially expressed (DE) with respect to the factor of interest if its regression coefficients for that factor are significantly different from zero, usually determined via statistical hypothesis testing. Otherwise, the gene is classified as equivalently expressed (EE). Given that RNA-seq datasets often contain thousands of genes, differential expression analysis must address the multiple testing problem. Techniques such as false discovery rate (FDR) control are employed to limit the proportion of false positives—genes incorrectly identified as differentially expressed.
As in any experiment, additional significant factors beyond the main variable of interest must be considered. RNA-seq studies frequently involve measured variables related to genetic background, environmental conditions, demographic factors, experimental design, or technical aspects of RNA sequencing. Some covariates may strongly influence gene expression, while others may have little or no effect. Therefore, selecting the most relevant variables for inclusion in the model is critical for robust differential expression analysis. Nguyen and Nettleton [1] introduced a variable selection approach that extends the method of Wu et al. [2] from a single-response to a multi-response setting for differential expression analysis in RNA-seq data. Their method uses pseudo variables to control the expected proportion of irrelevant covariates selected (false selection rate, FSR). In practice, this is implemented in the FSRAnalysisBS function of the R package csrnaseq, which applies FSR-controlled variable selection to RNA-seq datasets.
In addition to measured covariates, hidden factors such as batch effects can substantially influence differential expression analysis results [3]. Batch effects are unintended variations in experimental data that arise from factors unrelated to the primary scientific question. To address this, our study incorporated a method for removing hidden factors. A widely used approach is surrogate variable analysis (SVA) [4,5,6], which estimates hidden factors directly from gene expression data. In particular, the Iteratively Re-weighted Surrogate Variable Analysis (IRW-SVA) method can estimate these factors without prior knowledge of variable selection among available covariates. IRW-SVA is implemented via the sva function in the R package sva (version 3.56.0) for log-transformed RNA-seq count data.
To the best of our knowledge, no existing method simultaneously addresses both variable selection and hidden factor adjustment when determining explanatory variables for differential expression analysis. We explore two strategies for combining these tasks: in the first, we use the FSR method to identify the most relevant covariates before estimating surrogate variables based on those covariates, with the final model including both the selected covariates and the estimated surrogate variables; in the second, we first estimate surrogate variables using all available covariates, then apply the FSR method to the combined set of original covariates and surrogate variables, with the final model including the covariates selected in this process. We assess the performance of these strategies through a simulation study based on a real RNA-seq dataset.
The remainder of this paper is organized as follows: Section 2 reviews RNA-seq data preliminaries, the FSR method for variable selection, SVA techniques, and our proposed integration of the two. Section 3 applies the combined methods to the RFI RNA-seq dataset, which includes 13 measured covariates in addition to the primary variable of interest. Section 4 presents a data-driven simulation study assessing (1) the accuracy of variable selection and (2) the effectiveness in identifying DE genes. Section 5 concludes with a summary and discussion of findings.
2. Methods
2.1. Notation and Preliminaries
In this section, we introduce the notation used throughout the paper, review the variable selection method FSR [1] and surrogate variable analysis sva [4,5,6], and describe our proposed integrated strategies for simultaneously accounting for variable selection and hidden factors in RNA-seq differential expression analysis.
Consider RNA-seq data with G genes and n samples where index genes and index samples. Let denote the read count for gene g in sample i.
Suppose we have k known measured variables for each sample, denoted by , , where the prime symbol “′” denotes the transpose operator. Let be the set of n-dimensional column vectors corresponding to the j-th variable, . For continuous variable j, is a single column, whereas for a categorical j, it is represented by a set of dummy variables with one fewer column than the number of categories.
We denote by the primary variables—those always included in the model—and by the candidate covariates subject to variable selection.
The library size for sample i, , is computed as the 75-th percentile of its counts [7]. Following Law et al. [8], we define the log-counts values as follows:
For gene g, the count vector is , and the corresponding log-count vector is .
2.2. FSR Variable Selection Method
2.2.1. voom R packageProcedure
Nguyen and Nettleton [1] applied the voom-limma method [8] for RNA-seq differential expression analysis. This method adapts linear modeling to log-count data by assigning precision weights that account for the mean–variance relationship, enabling the computation of p-values for regression coefficients. The steps are as follows:
- Let denote the index set of covariates in the model, including all primary variables . For each gene g, fit the linear modelIn vector form:where contains an intercept column and all covariate columns with , and denotes the vector of regression coefficients containing both the intercept and all covariate coefficients for . As a consequence of (2), .
- Let and be the ML and REML estimates of and , respectively. Let .
- Let be the mean log-count value for each gene g.
- The predictor, let , is obtained by fitting a LOWESS regression [9] of on . For each gene , the precision weight is then calculated by
The weighted log count data were then analyzed using limma’s moderated testing pipeline, yielding q-values for differential expression declaration. Hereafter, the subscript is omitted for brevity.
2.2.2. Measure of Covariate Relevance
For covariate j, define the relevance measure
where is the indicator function. This ratio increases when covariate j shows a significant association with many genes and decreases when its effects are mostly weak.
Nguyen and Nettleton [1] combined this measure with the FSR variable selection method of Wu et al. [2], applying a backward selection procedure to retain only the most relevant covariates. Note that other implementations of the FSR method using different selection procedures, such as MaxR or forward selection, are possible and represent an area for future work.
2.2.3. Backward Selection to Control FSR
The backward selection procedure operates on the covariates of using the relevance measure . Let denote the largest subset of for which each variable satisfies r-value . The size of this subset is
where and are the number of relevant and irrelevant selected covariates, respectively.
The FSR is defined as
Then, the tuning parameter that controls FSR at a target level is estimated by
This choice of maximizes the number of included covariates while ensuring the FSR does not exceed .
To estimate in practice, pseudo-variables are introduced. For an integer and each , define as a set of pseudo-variables. Following Nguyen and Nettleton [1], define
where is the number of pseudo-variables selected from , and
is the total number of selected covariates (: relevant, : irrelevant, and : pseudo).
Following Wu et al. [2], the estimation of relies on two key assumptions:
- (A1)
- , where is the unknown number of irrelevant covariates.
- (A2)
- .
Combining (A1) and (A2) yields
which can be estimated by
where
2.2.4. Pseudo-Variable Generation
The pseudo-variables are generated according to the conditions (A1 and A2) described above. In our analysis, we used one of the four pseudo-variable generation methods proposed by Wu et al. [2]—specifically, the variant that combines orthogonal white noise with the FSR (ratio of expectations) approach. This method constructs pseudo-variables as the columns of , where is the hat matrix and is an matrix with entries independently and identically distributed as .
2.3. Surrogate Variable Analysis
2.3.1. SVA Method
Unmodeled artifacts—such as genetic, environmental, technical, and demographic factors—are collectively known as batch effects. These effects can have a widespread and detrimental impact on differential expression analysis, introducing systematic bias and compromising the accuracy of statistical inference.
Surrogate Variable Analysis (SVA), introduced by Leek and Storey [4], provides a framework for modeling omics data when batch effects are unmeasured or unknown. The method identifies genes whose variation patterns suggest influence from unmeasured artifacts, then uses these genes to estimate artifact signals through data decomposition techniques such as factor analysis. The resulting artifact profiles are incorporated as covariates in downstream models, removing confounding effects while preserving biological signals. By treating estimated artifacts as observed variables in statistical models, SVA systematically accounts for unmeasured variation, improving the robustness and accuracy of downstream analyses.
For sequencing data, Leek et al. [6] extended the SVA framework with specialized algorithms. In this paper, we focus on estimating the number of surrogate variables using the be algorithm from Leek and Storey [4] and estimating the surrogate variables themselves using the Iteratively Re-weighted SVA (IRW-SVA) algorithm from Leek and Storey [5].
Our analysis begins with a log-transformed count matrix where genes are rows and samples as columns. For each gene g and sample i, is modeled as
where is the gene-specific intercept term, and denotes either a one-dimensional column vector for continuous covariate, or for categorical variables, a set of indicator vectors with one fewer column than the number of levels (). These k covariates include ℓ primary variables and additional covariates , each associated with coefficient vector . The term represents h unobserved artifact vectors () with corresponding coefficients , and is the residual term.
Originally, Leek and Storey [4] described this model for a single primary variable, but also noted that it naturally extends to include all available covariates, as shown here.
In matrix form, the model can be written as
where is the gene expression matrix, is the design matrix containing the intercept, the main factor of interest, and the measured covariates, and () is the matrix of unobserved artifacts. The function denotes the log transformation applied to the counts, as defined in Section 2.1. The matrices and have dimensions and , respectively, and contain the regression coefficients for the measured covariates and the surrogate variables.
The SVA procedure consists of two main steps: (1) detection of unmodeled factors, and (2) construction of surrogate variables. We first describe the algorithm for estimating the number of surrogate variables following the approach of Leek and Storey [4]:
- Fit a model including the primary variable and all known covariates, omitting the hidden factors :The residuals are computed asThen, residual matrix (genes × samples) is constructed with entries .
- Perform singular value decomposition (SVD) of residuals
- Let be the s-th diagonal entry of (). If is the degrees of freedom for the model in Step 1, the last eigenvalues are zero and excluded form the analysis. For each eigengene ,representing the proportion of variance explained by the m-th eigengene.
- Independently permute each row of to obtain (entries ). Fit the model in Step 1 to , i.e., , and substract the fitted values to obtain the null residual matrix , i.e., .
- Perform SVD on :and compute for :where is the sth diagonal element of .
- Repeat Steps 4 and 5 for B times to obtain null statistics for and .
- Compute the p-value for each eigengene m:Under the assumption that eigengene significance is non-increasing with respect to m, we enforce monotonicity through recursive p-value correction:
- Estimate the number of surrogate variables given a user-specified significance level :
While Leek and Storey [4] first introduced the SVA framework, their work primarily focused on a two-step approach. The iteratively re-weighted (IRW) algorithm, which is the default method in the current sva package, was later formally described in Leek and Storey [5]. This iterative approach refines the original method by continuously re-weighting genes during surrogate variable estimation, leading to more robust adjustment for hidden factors. The IRW procedure can be summarized as follows:
- Let denote the estimated number of statistically significant right singular vectors () obtained from the singular value decomposition (SDV) of the residual matrix . The residuals ’s are the -th element of , derived from the fitted model: .
- Initialize as an matrix whose m-th row is , for
- Iterative procedure (for ):
- (a)
- Compute the empirical posterior probabilitiesusing the method of [10].
- (b)
- Perform a weighted SVD of , weighting each gene g by .
- (c)
- Update to be the matrix containing the first right singular vectors from the weighted SVD.
- After the final iteration (), re-compute the weightsand perform a weighted SVD of .
- Identify right singular vectors from the final weighted SVD that are highly correlated with the initial from Step 1.
- Construct an matrix whose m-th row is .
- Fit the final linear modelwhere are the estimated hidden factors, included as fixed covariates, and conduct significance testing for .
For our analysis, we employed the default settings of the sva function in the sva R package to estimate both the number of surrogate variables and their values.
2.3.2. Strategies to Handle Variable Selection and Surrogate Variable Analysis
In this study, we examined two integrated strategies that combine the FSR variable selection method with surrogate variable analysis (SVA) to construct the explanatory variable set for differential expression analysis.
- FSR_sva: Performs FSR-based variable selection first, followed by surrogate variable estimation using only the selected covariates and the primary factor of interest.
- SVAall_FSR: Estimates surrogate variables using all available covariates first, then applies FSR variable selection to the combined set of surrogate variables and all covariates.
The details of the algorithms for the two integrated strategies, FSR_sva and SVAall_FSR, are provided in Sections S4 and S5 of the Supplementary Materials, respectively.
For comparison, we also evaluated SVA0, a conventional SVA approach that estimates surrogate variables using only the primary factor of interest. We assessed the performance of all three methods in recovering relevant variables and identifying differentially expressed genes through a simulation study based on real RNA-seq data.
3. Data Analysis
We applied the two integrated strategies—FSR_sva, and SVAall_FSR—along with the existing strategy SVA0 to the RFI RNA-seq dataset, previously described in Nguyen and Nettleton [1] and Liu et al. [11], and available from the ArrayExpress database (accession E-MTAB-4179). The dataset contains 12,280 genes with average read counts of at least 8 and no more than 27 zeros across 31 pigs.
The primary variable of interest, Line (high-RFI vs. low-RFI), represents two pig lines created through divergent selection. Remaining variables—Diet (2 levels), Order (8 levels), Block (4 levels), Concb, RINb, Conca, RINa, Baso, Eosi, Lymp, Mono, Neut, and RFI (continuous covariates)—were subject to variable selection. Notably, Line and RFI are strongly positively correlated, as the lines were defined based on RFI values. A detailed description of the covariates, along with their correlation structure, is provided in Sections S1 and S2 of the Supplementary Materials, respectively. Our analysis systematically evaluated how covariate combinations and surrogate variables jointly influence the detection of DE genes, aiming to ensure robust biological interpretation while controlling for technical and environmental artifacts.
In surrogate variable estimation, FSR_sva and SVA0 each identified six surrogate variables. SVAall_FSR first estimated two surrogate variables, after which FSR selection on the thirteen available covariates, plus these two variables, retained five covariates (Baso, Lymp, Mono, Neut, Block) along with the two surrogate variables. At a 5% false discovery rate, the voom-limma model with the explanatory variables from FSR_sva identified 751 DE genes. A model with only Line detected 238 DE genes, whereas combining Line with SVA0 surrogate variables yielded 744 DE genes. The SVAall_FSR approach, incorporating FSR selection on all covariates and surrogate variables estimated from them, identified 293 DE genes.
4. Simulation Study
4.1. Simulation Description
4.1.1. Aims
Our simulation study has two main goals. First, we aim to evaluate the ability of two integrated approaches—combining variable selection with surrogate variable analysis—to correctly identify the most relevant covariates. Second, we assess their performance in terms of statistical power while ensuring control of the false discovery rate (FDR) in differential expression analysis.
4.1.2. Data-Generating Mechanisms
To achieve these goals, we simulated RNA-seq datasets containing both truly relevant covariates and a mixture of DE and EE genes with respect to the primary variable of interest and the relevant covariates. The RFI RNA-seq dataset was used as the basis for these simulations due to its complexity and the presence of multiple covariates. Sets of truly relevant covariates are defined in Table 1.

Table 1.
Simulation scenarios corresponding to eigth sets of truly relevant covariates (Nguyen and Nettleton [1]).
For each set of truly relevant covariates, we first obtained parameter vectors—comprising scaled error variance, precision weights, and partial regression coefficients—for all 12,280 genes from the voom-limma fit of the RFI RNA-seq data using the primary variable (Line) and the relevant covariates. To simulate EE genes, for each variable j (including Line and the covariates), we set the least significant regression coefficients to zero, where is the estimated number of true null genes for variable j according to the histogram-based method of Nettleton et al. [12].
We then randomly sampled 2000 parameter vectors (by default) and combined them with the observed values of Line and the relevant covariates from the 31 pigs. Gene counts were generated via inverse transformation of the linear model described in Equations (1) and (2), resulting in a 2000 × 31 count matrix. The simulated count matrix was then processed through the analysis pipeline described in Section 2 and repeated in Section 4.1.4. This procedure was repeated 100 times.
To explore how the proposed strategies handle hidden factors and variable selection, we considered two scenarios:
- Scenario 1: No hidden covariates (S1)—All relevant and irrelevant covariates are available: Diet, RFI, Block, Order, RINa, RINb, Conca, Concb, Baso, Eosi, Lymp, Mono, Neut.
- Scenario 2: Hidden covariates (S2)—Some truly relevant covariates are unobserved: only Diet, RFI, Block, Order, RINa, RINb, Conca, Concb are available, while all complete blood count variables (Baso, Eosi, Lymp, Mono, Neut) are missing.
4.1.3. Estimands
For variable selection, our primary estimands are the false selection rate (FSR) and the number of selected covariates that are truly relevant (R). In differential expression analysis, we assess the false discovery rate (FDR), the number of correctly identified differentially expressed genes (NTP), and the partial area under the ROC curve (PAUC) for false positive rates less than or equal to 0.05. We also examine the proportion of surrogate variables selected across both integrated SVA-variable selection strategies as well as the SVA0 approach, and we compute the mean and standard deviation of the coefficient of determination () when modeling surrogate variables as responses with hidden relevant covariates as predictors. This latter measure provides insight into each method’s ability to capture hidden factors.
4.1.4. Methods
In this study, variable selection was performed using the FSR method with default settings [1], and surrogate variables were estimated using the sva method with default options [4]. Differential expression analysis was conducted using the voom-limma pipeline, incorporating the explanatory variables constructed by the proposed approaches, as well as those from SVA0.
4.1.5. Performance Measure
Evaluation metrics for both variable selection and differential expression analysis were computed over 100 replications for each scenario and for eight values of relevant covariates. For variable selection, we report the average FSR and the average number of selected relevant covariates R across replications. For differential expression analysis, we focus on the empirical FDR, the average number of true positives NTP, and the average partial area under the ROC curve PAUC. The nominal levels for both FSR in variable selection and FDR in differential expression analysis were set at 0.05.
4.2. Simulation Results
We first evaluated the two proposed strategies in terms of their ability to control the FSR. As illustrated in Figure 1, we compared the FSR and the number of truly relevant covariates R selected by the FSR_sva and SVAall_FSR methods. In Scenario 1, both strategies exhibited similar performance. In Scenario 2, however, their performance was less consistent: when the number of relevant covariates was small (), neither method adequately controlled the FSR. For larger numbers of relevant covariates (), FSR_sva effectively controlled the FSR and was more conservative than SVAall_FSR.
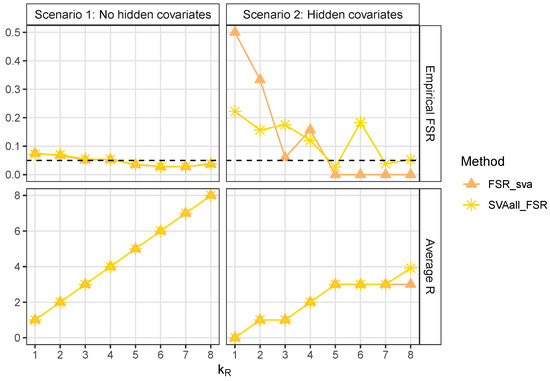
Figure 1.
This plot presents a line graph showing the empirical FSR and the average R across two different scenarios, evaluated for various values over 100 replications.
For reference, we also included an Oracle method, which incorporates all truly relevant covariates. As shown in Figure 2, in Scenario 1 the two integrated strategies performed similarly, controlled the FDR well, and achieved higher power than SVA0. As expected, the Oracle method outperformed all other approaches across all metrics. SVA0 slightly failed to control the FDR and was particularly liberal in the case where , in which the variable RFI is one of the relevant covariates. This result is likely due to RFI being highly positively correlated with the primary variable Line, as discussed earlier.
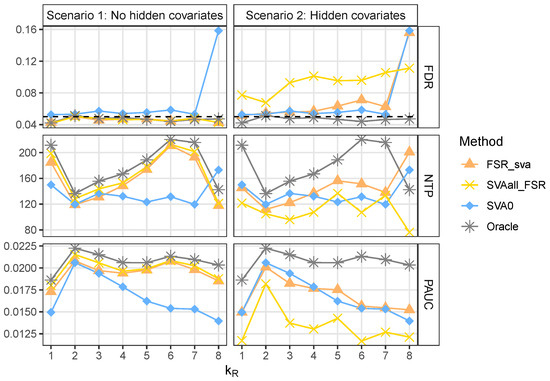
Figure 2.
The figure illustrates the performance of four differential expression analysis methods, evaluated under sixteen simulated scenarios—eight with hidden covariates and eight without. The nominal false selection rate was set at . Each scenario consisted of 100 replications, with simulated count data comprising 2000 genes across 31 samples. Performance was compared using three metrics: the empirical false discovery rate (FDR), the average number of true DE genes detected (NTP), and the average partial area under the ROC curve (PAUC) for false positive rates below 0.05.
In Scenario 2, where hidden relevant covariates were present, the performance of the two integrated strategies was less optimal. The performance of SVA0 and Oracle was similar to that in Scenario 1, as these methods do not rely on the availability of observed explanatory variables. For , although both integrated strategies failed to control the FDR, FSR_sva was less liberal than SVAall_FSR. In contrast, for , SVAall_FSR outperformed both FSR_sva and SVA0. In terms of PAUC, FSR_sva showed the best overall performance among the three non-Oracle methods.
Figure 3 shows the frequency distribution of the number of surrogate variables estimated by different methods across two scenarios and eight values of . In Scenario 1, where all relevant covariates are observed, the FSR variable selection step effectively identifies them, resulting in an expected pattern: the number of estimated surrogate variables is consistently zero (or near zero) across all over 100 replicates. This stability confirms that the variable selection step in FSR_sva and SVAall_FSR is functioning as intended.

Figure 3.
The figure shows the frequency distribution of the estimated number of surrogate variables for each of the three strategies across two simulation scenarios, based on 100 replications and eight different values of the number of relevant covariates .
In Scenario 2, with hidden relevant covariates, both integrated strategies estimate a number of surrogate variables that closely matches the number of unobserved relevant covariates. This pattern is evident in the frequency plots, with peaks aligning with the true count of hidden variables. Moreover, estimation accuracy improves as model size increases, with the number of estimated surrogates converging to the true number of hidden covariates. This trend is consistent with the factor estimation framework of Bai and Ng [13], which provides theoretical guarantees for consistent factor number estimation in high-dimensional settings, as both the number of variables and the sample size grow at specific rates.
The SVA0 method shows similar behavior across both scenarios for all values of , as it relies solely on the primary variable Line to estimate surrogate variables, without using additional covariate information. Consequently, its frequency distributions remain identical between scenarios.
Table 2 reports the average values and their standard errors from linear regression models in which the estimated surrogate variables serve as responses and the unselected hidden relevant covariates serve as explanatory variables for the three strategies, FSR_sva, FSRall_sva, and SVA0. The results indicate that, when combined with FSR variable selection, surrogate variables estimated by FSR_sva and FSRall_sva achieve higher —and thus better accuracy—than those obtained from SVA0.

Table 2.
Average values with corresponding standard errors across 100 replications.
4.3. Additional Simulation Study
We also conducted additional analyses and simulation studies using another RNA-seq dataset derived from a Zebrafish embryo experiment [14]. The results, provided in Section S6 of the accompanying Supplementary Materials, demonstrate similar performance of the considered strategies to those observed for the RFI RNA-seq data under the considered context.
5. Conclusions and Discussion
The data we analyze are RNA-seq gene expression counts, which are discrete and can range from zero to infinity. Many differential expression analysis methods have been proposed for RNA-seq data. Broadly, these methods can be classified into two groups: (i) count-based methods that directly model the counts using distributions such as the negative binomial (e.g., DESeq2 [15], edgeR [16,17]), and (ii) linear model-based methods such as voom-limma (described in Section 2.2.1 of the main text). In our study, we use the voom-limma approach because it is computationally efficient and has been shown in most studies to perform as well as, or better than, count-based methods. By applying a logarithmic transformation, this approach converts discrete counts into a continuous scale, making them suitable for analysis within the linear regression framework.
We propose a statistical framework for selecting biologically relevant covariates in RNA-seq differential expression analysis while accounting for noise and unknown artifacts (e.g., batch effects). This framework builds on the FSR covariate selection method of Nguyen and Nettleton [1] and the surrogate variable analysis (SVA) method of Leek and Storey [4]. By explicitly modeling and removing these artifacts while retaining only biologically relevant covariates, our approach enhances the performance of differential expression analysis.
Simulation results show that proper variable selection, combined with controlling unwanted latent variation, can substantially improve RNA-seq differential expression analysis. When all relevant covariates are included, the need for surrogate variables is minimal. Conversely, when important covariates are omitted, SVA compensates by estimating a number of surrogate variables that often matches the number of missing covariates, suggesting these variables act as proxies for unmeasured biological factors.
Although performance differences between the integrated approaches and SVA0 are not uniform across all settings, FSR_sva achieved the highest PAUC in our simulations. For FDR control, SVAall_FSR outperformed other methods when some hidden covariates were strongly associated with the primary factor of interest. Overall, when all relevant covariates were available, both integrated approaches (FSR_sva and SVAall_FSR) outperformed SVA0. In contrast, when some relevant covariates were hidden and none of the available covariates were strongly correlated with the primary factor of interest, SVA0 performed best, followed by FSR_sva and then SVAall_FSR. However, in scenarios where hidden relevant covariates existed and some of the available covariates were strongly correlated with the primary factor of interest (i.e., under strong multicollinearity), SVAall_FSR achieved the best performance among the compared methods.
It is worth noting that other methods exist for addressing hidden factors in RNA-seq data, such as Remove Unwanted Variation (RUV) [18]. However, this approach does not provide a way to estimate the number of unknown hidden factors, and its effective application requires a set of negative control genes, which are not available in our setting. Therefore, we excluded RUV methods from consideration.
Our study represents an initial step toward integrated approaches that address both variable selection and hidden factors. Future work will focus on refining these methods to better account for unobserved variables and further improve the robustness of differential expression analysis.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/math13183047/s1.
Author Contributions
Conceptualization, F.N., H.J. and Y.N.; formal analysis, F.N.; methodology, F.N., H.J. and Y.N.; supervision, Y.N.; writing—original draft, F.N.; writing—review and editing, F.N., H.J. and Y.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The R codes are available in the GitHub repository folder https://github.com/Farzana001-Noorzahan/covariate-selection-hidden-factor-rnaseq, accessed on 18 September 2025.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DE | differentially expressed |
| EE | equivalently expressed |
| FSR | false selection rate |
| FDR | false discovery rate |
| NTP | number of correctly identified differentially expressed genes |
| PAUC | partial area under the ROC curve |
| SVA | surrogate variable analysis |
| IRW-SVA | Iteratively Re-weighted Surrogate Variable Analysis |
References
- Nguyen, Y.; Nettleton, D. relevant covariates in RNA-seq analysis by pseudo-variable augmentation. In Journal of Agricultural, Biological and Environmental Statistics; Springer Nature: Berlin/Heidelberg, Germany, 2024; Available online: https://link.springer.com/content/pdf/10.1007/s13253-024-00665-3.pdf (accessed on 4 November 2024). [CrossRef]
- Wu, Y.; Boos, D.D.; Stefanski, L.A. Controlling Variable Selection by the Addition of Pseudovariables. J. Am. Stat. Assoc. 2007, 102, 235–243. [Google Scholar] [CrossRef]
- Leek, J.T.; Scharpf, R.B.; Bravo, H.C.; Simcha, D.; Langmead, B.; Johnson, W.E.; Geman, D.; Baggerly, K.; Irizarry, R.A. Tackling the widespread and critical impact of batch effects in high-throughput data. Nat. Rev. Genet. 2010, 11, 733–739. [Google Scholar] [CrossRef] [PubMed]
- Leek, J.T.; Storey, J.D. Capturing Heterogeneity in Gene Expression Studies by Surrogate Variable Analysis. PLoS Genet. 2007, 3, e161. [Google Scholar] [CrossRef] [PubMed]
- Leek, J.T.; Storey, J.D. A general framework for multiple testing dependence. Proc. Natl. Acad. Sci. USA 2008, 105, 18718–18723. [Google Scholar] [CrossRef] [PubMed]
- Leek, J.T.; Johnson, W.E.; Parker, H.S.; Jaffe, A.E.; Storey, J.D. The sva package for removing batch effects and other unwanted variation in high-throughput experiments. Bioinformatics 2012, 28, 882–883. [Google Scholar] [CrossRef] [PubMed]
- Bullard, J.H.; Purdom, E.; Hansen, K.D.; Dudoit, S. Evaluation of statistical methods for normalization and differential expression in mRNA-seq experiments. BMC Bioinform. 2010, 11, 94. [Google Scholar] [CrossRef] [PubMed]
- Law, C.W.; Chen, Y.; Shi, W.; Smyth, G.K. voom: Precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biol. 2014, 15, R29. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, W.S. Robust Locally Weighted Regression and Smoothing Scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Storey, J.D.; Akey, J.M.; Kruglyak, L. Multiple locus linkage analysis of genomewide expression in yeast. PLoS Biol. 2005, 3, e267. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Nguyen, Y.T.; Nettleton, D.; Dekkers, J.C.M.; Tuggle, C.K. Post-weaning blood transcriptomic differences between Yorkshire pigs divergently selected for residual feed intake. BMC Genom. 2016, 17, 73. [Google Scholar] [CrossRef] [PubMed]
- Nettleton, D.; Hwang, J.T.G.; Caldo, R.A.; Wise, R.P. Estimating the Number of True Null Hypotheses from a Histogram of p Values. J. Agric. Biol. Environ. Stat. 2006, 11, 337–356. [Google Scholar] [CrossRef]
- Bai, J.; Ng, S. Determining the number of factors in approximate factor models. Econometrica 2002, 70, 191–221. [Google Scholar] [CrossRef]
- Reinwald, H.; Alvincz, J.; Salinas, G.; Schäfers, C.; Hollert, H.; Eilebrecht, S. Toxicogenomic profiling after sublethal exposure to nerve- and muscle-targeting insecticides reveals cardiac and neuronal developmental effects in zebrafish embryos. Chemosphere 2022, 291, 132746. [Google Scholar] [CrossRef]
- Love, M.I.; Huber, W.; Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014, 15, 550. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, D.J.; Chen, Y.; Smyth, G.K. Differential expression analysis of multifactor RNA-Seq experiments with respect to biological variation. Nucleic Acids Res. 2012, 40, 4288–4297. [Google Scholar] [CrossRef] [PubMed]
- Lun, A.T.L.; Chen, Y.; Smyth, G.K. It’s DE-licious: A Recipe for Differential Expression Analyses of RNA-seq Experiments Using Quasi-Likelihood Methods in edgeR. In Statistical Genomics: Methods and Protocols; Mathé, E., Davis, S., Eds.; Springer: New York, NY, USA, 2016; pp. 391–416. [Google Scholar] [CrossRef]
- Risso, D.; Ngai, J.; Speed, T.P.; Dudoit, S. Normalization of RNA-seq data using factor analysis of control genes or samples. Nat. Biotechnol. 2014, 32, 896–902. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).