Abstract
A problem of modeling radiation patterns of wave sources in two-dimensional acoustic tomography is considered. Each source has its own radiation patterns, and their modeling will be used to improve the solvability of inverse problems of recovering the acoustic parameters of human soft tissues and come closer to building a digital twin of acoustic tomography. The problem is considered as a control problem of the right side for the velocities by spatial variables. Two statements are investigated—control by time or space functions. A numerical solution method is implemented. The results of numerical calculations are presented.
Keywords:
acoustic; tomography; first-order hyperbolic system; inverse problem; control problem; gradient descent method; acoustic radiation pattern MSC:
35L40; 35R30
1. Introduction
This article considers a problem of modeling radiation patterns of wave sources in two-dimensional acoustic tomography. One of the important applications of acoustic tomography is ultrasound tomography in medicine [1,2,3,4,5,6,7,8,9,10,11,12]. Inverse problems of ultrasound tomography can be considered as coefficient-inverse problems [13,14,15,16,17,18,19,20,21]. A radiation pattern (or antenna pattern or far-field pattern) refers to the directional (angular) dependence of the strength of waves from an antenna [22,23].
A mathematical model of acoustic tomography based on a hyperbolic system of PDE and numerical methods of its solution are presented in [24,25]. The well-posedness of direct problems for hyperbolic systems of equations are presented in [26,27]. Inverse problems for hyperbolic systems are investigated theoretically in [28].
Each source has its own radiation patterns [29], and their modeling will increase the solvability of inverse problems of restoring the acoustic parameters of human soft tissues and come closer to building a digital twin of acoustic tomography.
A possibility of designing the radiation pattern of a structural–acoustic communication system by predicting the pressure distribution was demonstrated in [30].
A finite element method (FEM) was implemented for calculating the far field directivity pattern of individual array elements in phased-array antennas [31].
In [32], the influence of a cross-coupling lattice caused by the filling material on radiation patterns was investigated.
To represent the essence of cross-coupling, the radiation pattern of an individual array element was calculated in pulse mode directly using FEM [33]. Several array design options have been studied to reduce the level of crosstalk.
A method proposed in [34] made it possible to weaken the influence of reflected signals and obtain frequency characteristics that practically coincide with those measured in free-field conditions.
A differential evolution algorithm was applied to synthesize unequally spaced linear antenna arrays [35]. Position-only, position-phase synthesis, and effect of angle resolution have been studied.
A full wave-equation reverse-time, prestack migration algorithm was used to investigate the potential to correct the multi-offset, ground-penetrating radar amplitudes for antenna radiation pattern effects [36].
The concept of directional patterns appeared in marine acoustics when modeling tsunami waves. The initial disturbance may have oscillations in some direction, then the main part of the wave will propagate in this direction [37]. An asymptotically numerical description of the propagation of tsunami waves in an area with an inhomogeneous depth in the vicinity of wave fronts, which may have caustics, has been proposed [38]. A long-wave approximation was used. It was assumed that the size of the initial disturbance area is small compared to the characteristic length of the interval of change in the depth of the bottom and with the distance from the observation point. The description was based on the Maslov canonical operator approach [39]. A potential tsunami model with a simple piston-type source was used, and estimates of the geographical coordinates of two characteristic parameters of the tsunami source and the epicenter were given [40,41].
A parametric approach for classifying the radiation pattern of an acoustic source taking into account the signals captured by several microphones was developed in [42].
A cuckoo search optimisation algorithm was applied to model electromagnetic antennas [43].
To control the radiation pattern, an observation of dipole radiation of sound with a wide bandwidth through a decorated plate with periodic two-dimensional Helmholtz resonators was used [44].
A radiation pattern method of the characteristic basis function was presented as a general modeling method for obtaining high-precision approximations of antenna radiation patterns using a very small number of measurements in [45].
The results of a proposed source centering algorithm [46], which works on plane sections and is aimed at achieving a convex objective function on each plane section, turned out to be more accurate than the previous algorithms for sources with a higher-order radiation pattern, usually at higher frequencies.
A backtracking search optimization algorithm was applied to synthesize the directional pattern [47] of a linear antenna array with specified nulls in the interference directions by controlling only the amplitude, position and phase of the antenna array elements.
A developed new radiation pattern model, in which part of the energy is radiated inside and behind the lobes, the program and output files can be easily implemented to analyze the phenomenon of radio wave propagation in any algorithms and numerical calculations [48].
The results of experimental studies of linear arrays for hydroacoustic applications with a low level of acoustic coupling between elements through the supporting structure of the lattice and a strong coupling of elements with an acoustic load and modeling of the angular and frequency behavior of linear arrays were presented in [49].
A database of acoustic radiation patterns was recorded, modeled and analyzed for musical instruments in [50]. A centering algorithm was used to analyze the complexity of the acoustic radiation pattern in terms of the number of excitation points.
In [51], a comparative analysis of an equivalent source method and a boundary element method was carried out. The equivalent source method is also known as the method of fundamental solutions, the method of superposition of waves, the method of equivalent source, etc.
A signal modeling method was presented that allows measurements to be made at acoustic frequencies below the limits set by time, without echo [52]. The signals received during calibration were modeled, first using a simple model of a stationary response of a transducer and then using an extended model consisting of terms that were used to describe both the stationary and resonant behaviors of the device.
An optimization method based on a flower pollination algorithm was presented [53] for designing a linear antenna array to reduce the maximum level of side lobes by controlling the amplitudes or positions of the array elements.
A simple electrical method for analyzing the physical behavior of piezoelectric transducer arrays has been proposed [54].
A fairly general methodology was proposed for evaluating the radiation pattern of acoustic sources for a wide range of sources without the need for anechoic operating conditions [55].
It was shown [56] that using an equivalent source method makes it possible to reconstruct the sound field from measurements of the sound field excited by this emitter in a tank with reflecting boundaries.
Reconstruction of the radiation pattern of a sound source in free space from measurements of the field excited by this source in a pool was discussed [57]. The reconstruction procedure was based on the use of a reference acoustic monopole.
The modelling of the radiation pattern of acoustic sources was proposed in [58]. The problem was formulated as a control problem of finding arbitrary functions in the right-hand side of the equations for velocities, assuming that the pressure has a given shape.
In this article, we will consider a problem of modeling the radiation pattern of an acoustic wave source, which is formulated as a problem of controlling the right part of a system of equations for the velocities by spacial variables for a hyperbolic system of 2D first-order PDE, which is connected directly with conservation laws of continuum mechanics. Two statements are investigated: in time and in space. Hölder stability and global Carleman estimates for an inverse boundary value problem for dynamic hyperbolic equations were considered [59].
The structure of this paper is as follows. Section 2 contains statements of two inverse problems under consideration. In this section, we reduce the inverse problems to minimizing of a cost functional by a gradient method. Section 3 demonstrates numerical results of the solution of both inverse problems. In the Conclusion, some numerical results are discussed.
2. Problem Formulation
Let us consider the following 2D direct problem of acoustic wave propagation in the form of a first-order system of hyperbolic equations [60]:
Here, , and , are the components of the velocity vector with respect to x and y; is the acoustic pressure; is the density of the medium; is the speed of the wave propagation; is the source location; and is a Ricker wavelet ( is a frequency):
Let us denote as inverse problem I the problem of the reconstruction of and from the inverse problem data:
Stability and global uniqueness for source and coefficients problems for wave equations were investigated in [61,62,63,64].
We should also mention [65,66], where the authors considered the problem of detecting the source of acoustical noise in the Helmholtz equation from measurements of the acoustical pressure field inside the domain, proved the uniqueness of the reconstruction and obtained a sharp stability estimate.
In addition, in [67], the authors proposed a general framework to study uniqueness, stability and reconstruction for infinite-dimensional inverse problems when only a finite-dimensional approximation of the measurements is available. It is shown that the same estimate holds for a large class of inverse problems satisfying a Lipschitz stability, even with a finite number of measurements. The authors also derived a globally convergent reconstruction algorithm based on the Landweber iteration.
We reduce the inverse problem (1)–(5), (7) to the problem of minimization of the cost functional:
by a gradient method.
The gradient of the cost functional is calculated as follows [68]:
Here, the functions , solve the following adjoint problem:
Let inverse problem II be the problem of reconstruction of and in (1)–(5) from the known inverse problem data (7).
Note that if the inverse problem data (7) are used in Equations (1)–(3) and all functions are smooth enough, we obtain the following equation:
In inverse problem I, we find the functions and ; in inverse problem II, the functions and are unknowns. So far, no theoretical results on the uniqueness and stability of the solution have been obtained.
We reduce the inverse problem (1)–(5), (7) to the problem of minimization of the following cost functional:
by a gradient method.
The gradient is calculated as follows:
At each iteration of the gradient method, we solve both the direct and adjoint problems. A comparative analysis of two gradient calculation strategies has been carried out [68]. It was shown that calculating the gradient from all sources and receivers gives the best approximate solution at the next iteration, in contrast to the case when the gradient is calculated from a single source. A new approach to calculating the gradient of the functional has been developed and implemented [69]. It saves almost twice the RAM and speeds up the inverse problem solving code by up to 25%, depending on the number of CPU cores used. The convergence of the gradient methods for hyperbolic equations is investigated in [70]. It has been shown [71] that adding a priori information about the inverse problem solution to the gradient method can significantly decrease the number of iterations. In [72], a stopping criterion for the gradient method, consistent with the accumulation of machine round-off errors, is it presented.
3. Numerical Results
We apply the MUSCL–Hancock method for the direct and adjoint problem solution. This method was introduced in [73] as a variant of the MUSCL scheme. This scheme is full time and space second-order accurate. It differs from the other MUSCL variants [74,75,76,77] in its second-order time accuracy. Indeed, the time accuracy rises when using a step based on a central-differencing scheme [78,79]. The -stability of the MUSCL–Hancock scheme is considered in [80]. The influence of the method of solving the direct and adjoint problem on the solution of the inverse problem was investigated in [81]. The accuracy of the numerical simulation of nonlinear acoustic wave propagation in a liquid medium based on the Navier–Stokes equations is investigated in [82].
We use a homogeneous medium with acoustic parameters of the medium corresponding to water: kg/m, m/s. The computational domain is m. The grid parameters are chosen as follows: , the CFL number is equal to 0.5. The initial guess is zero.
We conducted two tests for the two inverse problem statements. In Test 1, we know the exact solution for some model data. In Test 2, no exact solution is known. The data of the inverse problem are obtained from solving the direct problem after zeroing the pressure outside the desired sector.
For inverse problem 1 (Test 1 and Test 2), the functions are . For Test 1, , are as follows:
Figure 1 presents the exact solution (green line) and inverse problem solution after 2000 iterations (using exact data). Figure 2 presents the inverse problem solution after 2000 iteration using noisy data with and .
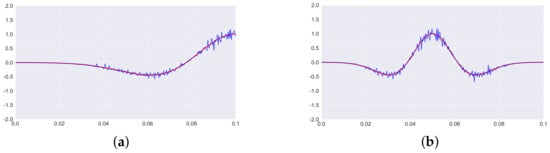
Figure 1.
Test 1. Inverse problem I. Reconstruction result after 2000 iterations (Exact data). (a)—function ; (b)—function . Green lines—true solution, red lines—computed solution.
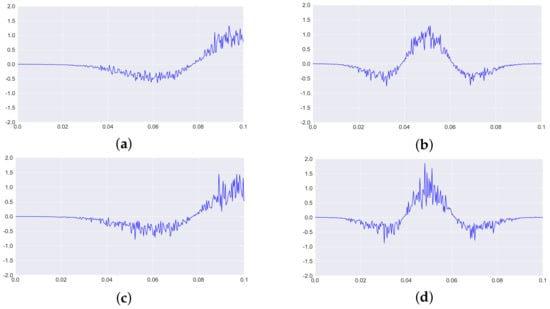
Figure 2.
Test 1. Inverse problem I. Reconstruction result after 2000 iterations (noisy data). Level of noise is 5% (graphs (a,b)) and 10% (graphs (c,d)). Graphs (a,c)—reconstruction of the function ; Graphs (b,d)—reconstruction of the function . Green lines—true solution, red lines—computed solution.
Let us consider the results of numerical calculations for a sector with additional information on the pressure obtained as a solution to the direct problem (1)–(5) and then set to zero outside the specified sector.
Let us present the results of numerical calculations for inverse problem II. In order to make dimensions of the equations coincide, we consider the following:
We also studied the dependence of the algorithm in the cases of exact and noisy data. We added some noise to the inverse problem data as follows:
Here, are the exact data, is the percentage of noise level in the data and is a random variable uniformly distributed on the interval for each variable x, y and t.
Figure 3 presents the exact solution and approximate solution of the inverse problem functions and after 1500 iterations. Figure 4 presents the exact solution and approximate solution of the inverse problem with noise in data and , respectively. The inverse problem is quite stable, even for noisy data, due to the following consideration: We recover two functions of two spatial variables, and , from the known inverse problem data of a function of three variables (two spatial variables and one time variable) .
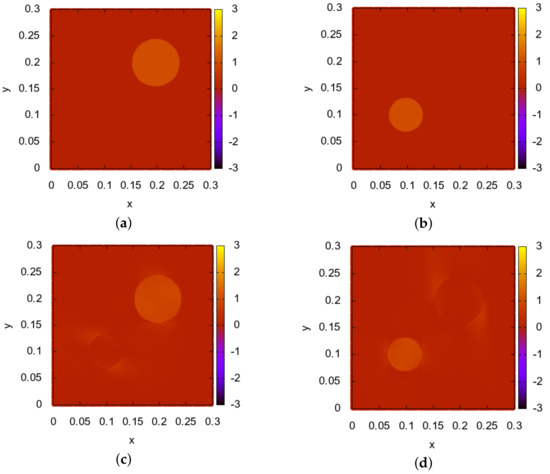
Figure 3.
Test 1. Inverse problem 2. Numerical solution. 1500 iterations. Exact data: (a)—true solution , (b)—true solution , (c)—-computed solution , (d)—computed solution .
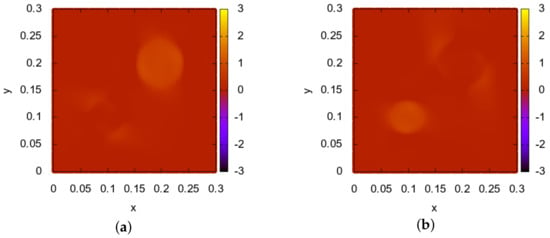
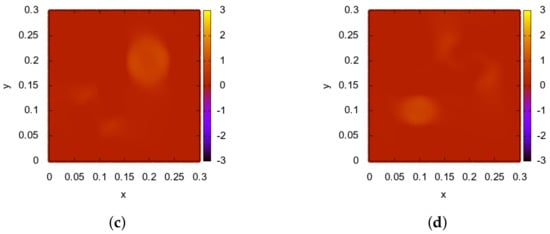
Figure 4.
Test 1. Inverse problem 2. Reconstruction result after 1500 iterations (noisy data). Level of noise is 5% (graphs (a,b)) and 10% (graphs (c,d)). Graphs (a,c)—result of the reconstruction of the function ; Graphs (b,d)—reconstruction of the function .
Next, we consider the results of two numerical calculations for wide and narrow sectors. In this case, for some arbitrary data, no inverse problem solution may exist.
Figure 5 shows additional information (a sector of 90 degrees). The top of the sector is located on the right boundary.
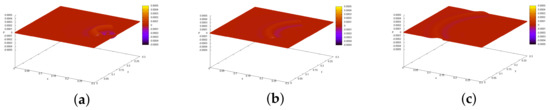
Figure 5.
Test 2. Inverse problem 2. Additional information (function ). (a)—pressure distribution at ms, (b)—pressure distribution at ms, (c)—pressure distribution at ms.
The left column of Figure 6 presents the pressure with functions . The right column of the Figure 6 presents the pressure with restored functions , (see Figure 7) after 900 iterations.
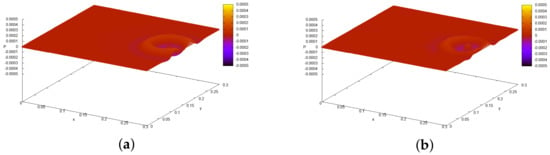
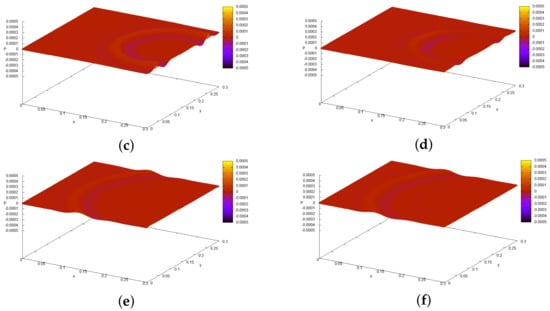
Figure 6.
Test 2. Inverse problem 2. Numerical solution. 900 iterations. (a)—direct problem solution (1)–(5) with . Pressure ms). (b)—direct problem solution (1)–(5) with approximate solution , . Pressure ms). (c)—direct problem solution (1)–(5) with . Pressure ms). (d)—direct problem solution (1)–(5) with approximate solution , . Pressure ms). (e)—direct problem solution (1)–(5) with . Pressure ms). (f)—Direct problem solution (1)–(5) with approximate solution , . Pressure ms).
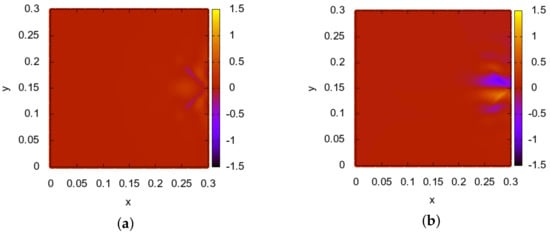
Figure 7.
Test 2. Inverse problem 2. Numerical solution. 900 iterations. (a)—computed solution . (b)—computed solution .
Figure 8 considers the inverse problem data for a narrow sector. The sector moves from the middle of the side to the corners of the opposite one. The top of the sector is right on the border.

Figure 8.
Test 3. Inverse problem 2. Numerical solution. (a)—Additional information (pressure) . (b)—additional information (pressure) . (c)—additional information (pressure) .
In the right column of Figure 9, the pressure is presented with the restored functions and (see Figure 10). Figure 10 presents functions , obtained from the additional information (narrow sector) when solving the inverse problem. On Figure 11 on nth iteration is presented (green line is for Test 3, red line is for Test 2).
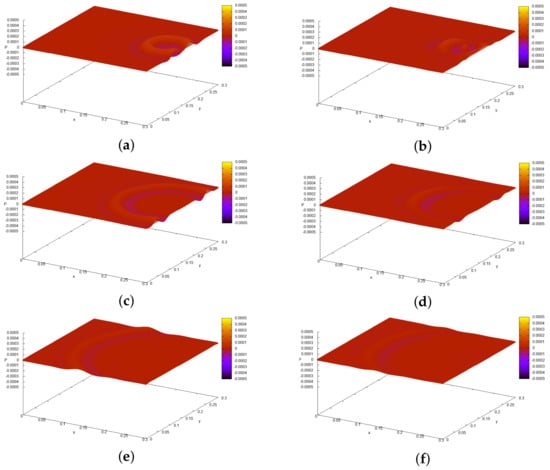
Figure 9.
Test 3. Inverse problem 2. Numerical solution. 900 iterations. Left column (a,c,e)—solution of the direct problem (1)–(5) with (pressure distribution ). Right column (b,d,f)—solution of the direct problem (1)–(5) with reconstructed functions , (pressure distribution ). 1),2)—pressure distribution at ms; (c,d)—pressure distribution at ms; (e,f)—pressure distribution at ms.
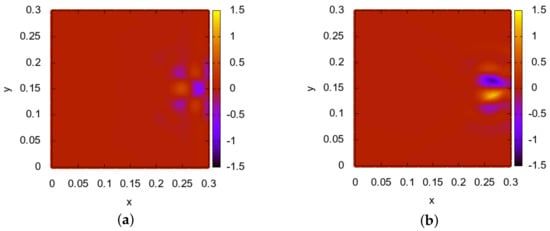
Figure 10.
Test 3. Inverse problem 2. Numerical solution. 900 iterations. (a)—computed solution . (b)—computed solution .
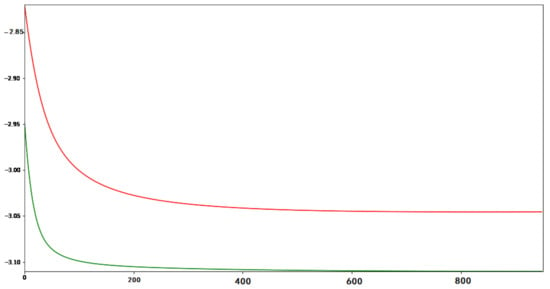
Figure 11.
Inverse problem 2. Numerical solution. on nth iteration. Red line is Test 2. Green line is Test 3.
4. Concluding Remarks
Two ways to simulate radiation patterns have been presented. The modelling of radiation patterns is formulated as control problems, which are solved by a gradient method. A numerical method for solving the inverse problems was implemented, and the results of numerical experiments were presented.
The numerical experiments have shown that if we simulate the radiation patterns by controlling and we may not obtain suitable results because the solution of the inverse problem of finding and may not exist. For the case of control by , it is possible to reduce the pressure outside the sector by 15–20%, which is considered to be a good result.
5. Discussion
This work aimed to investigate some aspects of mathematical models of ultrasound tomography related to the radiation pattern of a sounding pulse and study a way to bring the model closer to the physical process. Naturally, the physical structure of the source of a sounding wave provides the direction in which the main part of sounding impulse propagates. The goal is to reflect such behaviour when considering an acoustic approximation based on a first order system of equations in time domain. This leads us to the control problem considered in this paper. One formulation was aimed to find a suitable wave time form that would provide the desired behaviour. The other, when we use functions of the spatial variables as means of control, changes the properties of the medium in the area, which corresponds to the source location. A natural way to continue this study is to try to use several sources and to try to control the radiation pattern by using the locations of these sources. In addition, the spatial functions of the second inverse problem can be considered as changes of the absorption properties in the area of the source. This connection will be studied as the next step of our research by introducing absorption parameters into the model.
Author Contributions
Conceptualization, M.S.; methodology, D.K., N.N. and M.S.; software, D.K. and N.N.; formal analysis, N.N. and N.S.; writing—original draft preparation, N.S.; writing—review and editing, N.N., N.S. and M.S.; project administration, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by Russian Science Foundation, grant 19-11-00154 “Developing of new mathematical models of acoustic tomography in medicine. Numerical methods, HPC and software”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article.
Acknowledgments
The authors kindly thank the reviewers for their remarks and comments which helped us to improve the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jirik, R.; Peterlik, I.; Ruiter, N.; Fousek, J.; Dapp, R.; Zapf, M.; Jan, J. Sound-speed image reconstruction in sparse-aperture 3D ultrasound transmission tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 254–264. [Google Scholar] [CrossRef] [PubMed]
- Burov, V.A.; Voloshinov, V.B.; Dmitriev, K.V.; Polikarpova, N.V. Acoustic waves in metamaterials, crystals, and anomalously refracting structures. Adv. Phys. Sci. 2011, 54, 1165–1170. [Google Scholar]
- Duric, N.; Littrup, P.; Poulo, L.; Babkin, A.; Pevzner, R.; Holsapple, E.; Rama, O.; Glide, C. Detection of breast cancer with ultrasound tomography: First results with the computed ultrasound risk evaluation (CURE) prototype. Med. Phys. 2007, 34, 773–785. [Google Scholar] [CrossRef] [PubMed]
- Wiskin, J.; Borup, D.; Andre, M.; Johnson, S.; Greenleaf, J.; Parisky, Y.; Klock, J. Three dimensional nonlinear inverse scattering: Quantitative transmission algorithms, refraction corrected reflection, scanner design, and clinical results. Proc. Meet. Acoust. 2013, 19, 075001. [Google Scholar]
- Wiskin, J.; Borup, D.; Iuanow, E.; Klock, J.; Lenox, M. 3-D nonlinear acoustic inverse scattering: Algorithm and quantitative results. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 1161–1174. [Google Scholar] [CrossRef]
- Wiskin, J.; Malik, B.; Natesan, R.; Borup, D.; Pirshafiey, N.; Lenox, M.; Klock, J. Full Wave 3D Inverse Scattering Transmission Ultrasound Tomography: Breast and Whole Body Imaging. In Proceedings of the IUS—IEEE International Ultrasonics Symposium, Glasgow, UK, 6–9 October 2019; pp. 951–958. [Google Scholar] [CrossRef]
- Filatova, V.; Danilin, A.; Nosikova, V.; Pestov, L. Supercomputer Simulations of the Medical Ultrasound Tomography Problem. Commun. Comput. Inf. Sci. 2019, 1063, 297–308. [Google Scholar]
- Klibanov, M.V. Travel time tomography with formally determined incomplete data in 3D. Inverse Probl. Imaging 2019, 13, 1367–1393. [Google Scholar] [CrossRef]
- Klibanov, M.V. On the travel time tomography problem in 3D. J. Inverse Ill-Posed Probl. 2019, 27, 591–607. [Google Scholar] [CrossRef]
- Burov, V.A.; Zotov, D.I.; Rumyantseva, O.D. Reconstruction of the sound velocity and absorption spatial distributions in soft biological tissue phantoms from experimental ultrasound tomography data. Acoust. Phys. 2015, 61, 231–248. [Google Scholar] [CrossRef]
- Duric, N.; Littrup, P.; Li, C.; Roy, O.; Schmidt, S.; Janer, R.; Cheng, X.; Goll, J.; Rama, O.; Bey-Knight, L.; et al. Breast ultrasound tomography: Bridging the gap to clinical practice. Proc. SPIE 2012, 8320, 832000. [Google Scholar]
- Wiskin, J.; Malik, B.; Natesan, R.; Lenox, M. Quantitative assessment of breast density using transmission ultrasound tomography. Med. Phys. 2019, 46, 2610–2620. [Google Scholar] [CrossRef]
- Beilina, L.; Klibanov, M.V. Synthesis of global convergence and adaptivity for a hyperbolic coefficient inverse problem in 3D. J. Inverse Ill-Posed Probl. 2010, 18, 85–132. [Google Scholar] [CrossRef]
- He, S.; Kabanikhin, S.I. An optimization approach to a three-dimensional acoustic inverse problem in the time domain. J. Math. Phys. 1995, 36, 4028–4043. [Google Scholar] [CrossRef]
- Beilina, L.; Hosseinzadegan, S. An adaptive finite element method in reconstruction of coefficients in Maxwell’s equations from limited observations. Appl. Math. 2016, 61, 253–286. [Google Scholar] [CrossRef]
- Beilina, L. Adaptive Finite Element Method for a coefficient inverse problem for the Maxwell’s system. Appl. Anal. 2011, 90, 1461–1479. [Google Scholar] [CrossRef]
- Beilina, L.; Klibanov, M.V. A posteriori error estimates for the adaptivity technique for the Tikhonov functional and global convergence for a coefficient inverse problem. Inverse Probl. 2010, 26, 045012. [Google Scholar] [CrossRef][Green Version]
- Xin, J.; Beilina, L.; Klibanov, M. Globally convergent numerical methods for some coefficient inverse problems. Comput. Sci. Eng. 2010, 12, 64–76. [Google Scholar]
- Beilina, L.; Klibanov, M.V. Globally strongly convex cost functional for a coefficient inverse problem. Nonlinear Anal. Real World Appl. 2015, 22, 272–288. [Google Scholar] [CrossRef]
- Klibanov, M.V. Carleman estimates for global uniqueness, stability and numerical methods for coefficient inverse problems. J. Inverse Ill-Posed Probl. 2013, 21, 477–560. [Google Scholar] [CrossRef]
- Shishlenin, M.A.; Novikov, N.S.; Klyuchinskiy, D.V. On the recovering of acoustic attenuation in 2D acoustic tomography. J. Phys. Conf. Ser. 2021, 2099, 012046. [Google Scholar] [CrossRef]
- Cheng, D.K. Field and Wave Electromagnetics, 2nd ed.; Pearson: Boston, MA, USA, 1998. [Google Scholar]
- Isaev, A.E.; Nikolaenko, A.S.; Chernikov, I.V. Suppression of reverberation distortions of a receiver signal using the water tank transfer function. Acoust. Phys. 2017, 63, 175–184. [Google Scholar] [CrossRef]
- Klyuchinskiy, D.; Novikov, N.; Shishlenin, M. Recovering Density and Speed of Sound Coefficients in the 2D Hyperbolic System of Acoustic Equations of the First Order by a Finite Number of Observations. Mathematics 2021, 9, 199. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Klyuchinskiy, D.V.; Novikov, N.S.; Shishlenin, M.A. Numerics of acoustical 2D tomography based on the conservation laws. J. Inverse Ill-Posed Probl. 2020, 28, 287–297. [Google Scholar] [CrossRef]
- Bastin, G.; Coron, J.-M. Stability and Boundary Stabilization of 1-D Hyperbolic Systems. In Progress in Nonlinear Differential Equations and Their Applications; Birkhauser: Boston, MA, USA, 2016. [Google Scholar]
- Blokhin, A.M.; Trakhinin, Y.L. Well-Posedness of Linear Hyperbolic Problems: Theory and Applications; Nova Publishers: Hauppauge, NY, USA, 2006. [Google Scholar]
- Romanov, V.G.; Kabanikhin, S.I. Inverse Problems for Maxwell’s Equations; VSP: Utrecht, The Netherlands, 1994. [Google Scholar]
- Butler, J.L.; Sherman, C.H. Transducers and Arrays for Underwater Sound; Springer: Berlin, Germany, 2016. [Google Scholar]
- Seo, H.-S.; Kim, Y.-H. Directional radiation pattern in structural–acoustic coupled system. J. Acoust. Soc. Am. 2005, 118, 92–103. [Google Scholar] [CrossRef]
- Friedrich, W.; Kaarmann, H.; Lerch, R. Finite element modeling of acoustic radiation from piezoelectric phased array antennas. IEEE Symp. Ultrason. 1990, 2, 763–767. [Google Scholar]
- Gori, P.; Iula, A.; Pappalardo, M.; Lamberti, N.; Montero de Espinosa, F. Influence of the inter-element coupling on ultrasound array radiation patterns. J. Comput. Acoust. 2001, 9, 773–788. [Google Scholar] [CrossRef]
- Caronti, A.; Carotenuto, R.; Caliano, G.; Pappalardo, M. Finite element study of cross coupling in 1-D capacitive micromachined ultrasonic transducer arrays. In Proceedings of the Ultrasonics Symposium 2002, Munich, Germany, 8–11 October 2002; Volume 2, pp. 1059–1062. [Google Scholar]
- Isaev, A.E.; Matveev, A.N. Calibration of hydrophones in a field with continuous radiation in a reverberating pool. Acoust. Phys. 2009, 55, 762. [Google Scholar] [CrossRef]
- Lin, C.; Qing, A.; Feng, Q. Synthesis of Unequally Spaced Antenna Arrays by Using Differential Evolution. IEEE Trans. Antennas Propag. 2010, 58, 2553–2561. [Google Scholar]
- Bradford, J.H. GPR prestack amplitude recovery for radiation patterns using a full wave-equation, reverse-time migration algorithm. In SEG Technical Program Expanded Abstracts; SEG: Houston, TX, USA, 2012; pp. 1–5. [Google Scholar]
- Dobrokhotov, S.Y.; Sekerzh-Zenkovich, S.Y. A class of exact algebraic localized solutions of the multidimensional wave equation. Math. Notes 2010, 88, 894–897. [Google Scholar] [CrossRef]
- Dobrokhotov, S.Y.; Sekerzh-Zenkovich, S.Y.; Tirozzi, B.; Volkov, B. Explicit asymptotics for tsunami waves in framework of the piston model. Russ. J. Earth. Sci. 2006, 8, ES4003. [Google Scholar] [CrossRef]
- Dobrokhotov, S.Y.; Nazaikinskii, V.E.; Shafarevich, A.I. Maslov’s canonical operator in arbitrary coordinates on the Lagrangian manifold. Dokl. Math. 2016, 93, 99–102. [Google Scholar] [CrossRef]
- Sekerzh-Zenkovich, S.Y. Analytical Study of the Tsunami Potential Model with a Simple Piston-Like Source. 2. Asymptotic Formula for the Height of Tsunami in the Far Field. Russ. J. Math. Phys. 2013, 20, 342–346. [Google Scholar]
- Dobrokhotov, S.Y.; Nazaikinskii, V.E. Asymptotic localized solutions of the shallow water equations over a nonuniform bottom. AIP Conf. Proc. 2018, 2048, 040026. [Google Scholar]
- Brutti, A.; Omologo, M.; Svaizer, P. An environment aware ML estimation of acoustic radiation pattern with distributed microphone pairs. Signal Process. 2013, 93, 784–796. [Google Scholar] [CrossRef]
- Khodier, M. Optimisation of antenna arrays using the cuckoo search algorithm. IET Microw. Antennas Propag. 2013, 7, 458–464. [Google Scholar]
- Quan, L.; Zhong, X.; Liu, X.; Gong, X.; Johnson, P.A. Effective impedance boundary optimization and its contribution to dipole radiation and radiation pattern control. Nat. Commun. 2014, 5, 3188. [Google Scholar] [CrossRef]
- Young, A.; Maaskant, R.; Ivashina, M. Radiation Pattern Modeling with Characteristic Basis Function Patterns. FERMAT J. 2014, 2, 1–12. [Google Scholar]
- Shabtai, N.R.; Vorländer, M. Acoustic centering of sources with high-order radiation patterns. J. Acoust. Soc. Am. 2015, 137, 1947–1961. [Google Scholar] [CrossRef]
- Guney, K.; Durmus, A. Pattern Nulling of Linear Antenna Arrays Using Backtracking Search Optimization Algorithm. Int. J. Antennas Propag. 2015, 2015, 713080. [Google Scholar] [CrossRef]
- Jankowski-Mihulowicz, P.; Lichon, W.; Weglarski, M. Numerical Model of Directional Radiation Pattern Based on Primary Antenna Parameters. Int. J. Electron. Telecommun. 2015, 61, 191–197. [Google Scholar] [CrossRef]
- Stytsenko, E.; Scott, N.L.; Meijer, M. Acoustic coupling in linear arrays. In Proceedings of the OCEANS 2016, Shanghai, China, 10–13 April 2016; pp. 1–7. [Google Scholar]
- Shabtai, N.R.; Behler, G.; Vorländer, M.; Weinzierl, S. Generation and analysis of an acoustic radiation pattern database for forty-one musical instruments. J. Acoust. Soc. Am. 2017, 141, 1246–1256. [Google Scholar] [CrossRef]
- Lee, S. Review: The Use of Equivalent Source Method in Computational Acoustics. J. Comput. Acoust. 2017, 25, 1630001. [Google Scholar] [CrossRef]
- Robinson, S.P.; Hayman, G.; Harris, P.M.; Beamiss, G.A. Signal-modelling methods applied to the free-field calibration of hydrophones and projectors in laboratory test tanks. Sci. Technol. 2018, 29, 085001. [Google Scholar] [CrossRef]
- Singh, U.; Salgotra, R. Synthesis of linear antenna array using flower pollination algorithm. Neural Comput. Appl. 2018, 29, 435–448. [Google Scholar] [CrossRef]
- Bybi, A.; Mouhat, O.; Garoum, M.; Drissi, H.; Grondel, S. One-dimensional equivalent circuit for ultrasonic transducer arrays. Appl. Acoust. 2019, 156, 246–257. [Google Scholar] [CrossRef]
- Canclini, A.; Antonacci, F.; Tubaro, S.; Sarti, A. A Methodology for the Robust Estimation of the Radiation Pattern of Acoustic Sources. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 28, 211–224. [Google Scholar] [CrossRef]
- Virovlyansky, A.L.; Deryabin, M.S. On the use of the equivalent source method for free-field calibration of an acoustic radiator in a reverberant tank. J. Sound Vib. 2019, 455, 69–81. [Google Scholar] [CrossRef]
- Virovlyansky, A.L.; Kazarova, A.Y.; Lyubavin, L.Y. Reconstructing the directivity pattern of a sound source in free space by measuring its field in a tank. Acoust. Phys. 2020, 66, 501–507. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Klyuchinskiy, D.V.; Novikov, N.S.; Shishlenin, M.A. On the problem of modeling the acoustic radiation pattern of source for the 2D first-order system of hyperbolic equations. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 1715, p. 012038. [Google Scholar]
- Bellassoued, M.; Cristofol, M.; Soccorsi, E. Inverse boundary value problem for the dynamical heterogeneous Maxwell’s system. Inverse Probl. 2012, 28, 095009. [Google Scholar] [CrossRef]
- Godunov, S.K.; Zabrodin, A.V.; Ivanov, M.Y.; Kraikov, A.N.; Prokopov, G.P. Numerical Solution for Multidimensional Problems of Gas Mechanics; Nauka: Moscow, Russia, 1976. [Google Scholar]
- Isakov, V.; Yamamoto, M. Stability in a wave source problem by Dirichlet data on subboundary. J. Inverse Ill-Posed Probl. 2003, 11, 399–409. [Google Scholar] [CrossRef]
- Imanuvilov, O.Y.; Yamamoto, M. Global uniqueness and stability in determining coefficients of wave equations. Commun. Partial. Differ. Equ. 2001, 26, 1409–1425. [Google Scholar] [CrossRef]
- Bruckner, G.; Yamamoto, M. Determination of point wave sources by pointwise observations: Stability and reconstruction. Inverse Probl. 2000, 16, 723–748. [Google Scholar] [CrossRef]
- Yamamoto, M.; Zhang, X. Global uniqueness and stability for an inverse wave source problem for less regular data. J. Math. Anal. Appl. 2001, 263, 479–500. [Google Scholar] [CrossRef]
- Delillo, T.; Isakov, V.; Valdivia, N.; Wang, L. The detection of the source of acoustical noise in two dimensions. SIAM J. Appl. Math. 2001, 61, 2104–2121. [Google Scholar] [CrossRef]
- DeLillo, T.; Isakov, V.; Valdivia, N.; Wang, L. The detection of surface vibrations from interior acoustical pressure. Inverse Problem. 2003, 19, 507–524. [Google Scholar] [CrossRef]
- Alberti, G.S.; Santacesaria, M. Infinite-Dimensional Inverse Problems with Finite Measurements. Arch. Ration. Mech. Anal. 2022, 243, 1–31. [Google Scholar] [CrossRef]
- Klyuchinskiy, D.; Novikov, N.; Shishlenin, M. A Modification of gradient descent method for solving coefficient inverse problem for acoustics equations. Computation 2020, 8, 73. [Google Scholar] [CrossRef]
- Klyuchinskiy, D.V.; Novikov, N.S.; Shishlenin, M.A. CPU-time and RAM memory optimization for solving dynamic inverse problems using gradient-based approach. J. Comput. Phys. 2021, 439, 110374. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Scherzer, O.; Shishlenin, M.A. Iteration methods for solving a two dimensional inverse problem for a hyperbolic equation. J. Inverse Ill-Posed Probl. 2003, 11, 87–109. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Shishlenin, M.A. Quasi-solution in inverse coefficient problems. J. Inverse Ill-Posed Probl. 2008, 16, 705–713. [Google Scholar] [CrossRef]
- Wang, Y.; Lukyanenko, D.V.; Yagola, A.G. Regularized Inversion of Full Tensor Magnetic Gradient Data. Numer. Methods Program. (Vychislitel’Nye Metod. Program.) 2016, 17, 13–20. [Google Scholar]
- van Leer, B. On the relation between the upwind-differencing schemes of Godunov, Engquist-Osher and Roe. SIAM J. Sci. Stat. Comput. 1984, 5, 1–20. [Google Scholar] [CrossRef]
- van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Khobalatte, B.; Perthame, B. Maximum principle on the entropy and second-order kinetic schemes. Math. Comput. 1994, 62, 119–131. [Google Scholar] [CrossRef]
- Perthame, B.; Qiu, Y. A variant of Van Leer’s method for multidimensional systems of conservation laws. J. Comput. Phys. 1994, 112, 370–381. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. A Practical Introduction, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1999. [Google Scholar]
- Nessyahu, H.; Tadmor, E. Nonoscillatory central differencing for hyperbolic conservation laws. J. Comput. Phys. 1990, 87, 408–463. [Google Scholar] [CrossRef]
- Bianco, F.; Puppo, G.; Russo, G. High-order central schemes for hyperbolic systems of conservation laws. SIAM J. Sci. Comput. 1999, 21, 294–322. [Google Scholar] [CrossRef][Green Version]
- Berthon, C. Why the MUSCL-Hancock scheme is L1-stable. Numer. Math. 2006, 104, 27–46. [Google Scholar] [CrossRef]
- Novikov, N.S.; Klyuchinskiy, D.V.; Shishlenin, M.A.; Kabanikhin, S.I. On the modeling of ultrasound wave propagation in the frame of inverse problem solution. J. Phys. Conf. Ser. 2021, 2099, 012044. [Google Scholar] [CrossRef]
- Kozelkov, A.S.; Krutyakova, O.L.; Kurulin, V.V.; Strelets, D.Y.; Shishlenin, M.A. The accuracy of numerical simulation of the acoustic wave propagations in a liquid medium based on Navier-Stokes equations. Sib. Electron. Math. Rep. 2021, 18, 1238–1250. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).