An Efficient Approach to Approximate Fuzzy Ideals of Semirings Using Bipolar Techniques

Abstract

The bipolar fuzzy (BF) set is an extension of the fuzzy set used to solve the uncertainty of having two poles, positive and negative. The rough set is a useful mathematical technique to handle vagueness and impreciseness. The major objective of this paper is to analyze the notion of approximation of BF ideals of semirings by combining the theories of the rough and BF sets. Then, the idea of rough approximation of BF subsemirings (ideals, bi-ideals and interior ideals) of semirings is developed. In addition, semirings are characterized by upper and lower rough approximations using BF ideals. Further, it is seen that congruence relations (CRs) and complete congruence relations (CCRs) play fundamental roles for rough approximations of bipolar fuzzy ideals. Therefore, their associated properties are investigated by means of CRs and CCRs.

1. Introduction and Motivation

The implementation of traditional fuzzy sets presented by Zadeh [1] in the field of algebraic structures has brought great success to the study of fuzzy algebra. A few mathematical researchers, such as Rosenfeld [2], Mordeson and Malik [3], Akram et al. [4], Mandal [5], Shabir and Mahmood [6] and Zhan [7], have obtained many wonderful and useful results on fuzzy sets. Nevertheless, the membership degrees of elements in conventional fuzzy sets are all limited to the interval [0,1], which leads to a great difficulty in explaining the distinction between the irrelevant elements and the opposite elements in fuzzy sets. Zhang [8] presented the theory of the bipolar fuzzy (BF) set, which has a range of $[-1,1]$, to avoid this problem. Recently, keeping the results of BF sets under consideration, many researchers have been using BF sets to represent algebraic structures [9,10,11,12]. This theory provides the difference between positive and negative aspects of the same situation. In real life, we observe many bipolar concepts, good and bad effects of medicines, thickness and thinness of fluid, honesty and dishonesty. For more applications, see [13,14,15,16,17,18].

Pawlak, in 1982 [19], initiated the theory of rough sets. Based on the known attributes, a rough set contains all the information. Rough sets are characterized by means of upper and lower approximation. This theory is a useful tool in the areas of artificial intelligence, such as pattern recognition, learning algorithms, inductive reasoning, automatic classification, etc. In addition, it has many applications in measurement theory, classification theory, taxonomy, cluster analysis, etc. In the medical field, a serious challenge is abdominal pain in children. There are many reasons for this disease and it is hard to detect the main cause. This theory helps the doctors to detect the cause through discharge observations.

In 1934, Vandiver studied the structure of semirings [20]. A large amount of work has been conducted on this mathematical algebraic structure in the fields of medical science, social science, engineering, arts, economics and environmental science. From an algebraic point of view, semirings provide the most natural common generalization of the theories of rings and bounded distributive lattices, and the techniques used in analyzing them are taken from both areas.

Fuzzy semirings, introduced by Ahsan et al. [21], have drawn widespread interest from scholars. In addition, a large amount of related findings have emerged by Ahsan et al. [22]. Many experts have investigated roughness in algebra and fuzzy algebraic structures [23,24,25,26]. Hosseini et al. studied the generalizations of roughness or T-roughness in fuzzy algebra [27]. In 2020, Bashir et al. studied the roughness of fuzzy ideals with three-dimensional congruence relations of ternary semigroups [28]. In 2019, Shabir et al. [29] worked on BF ideals of regular semigroups. Moreover, Bashir et al. extended the work of [29] to regular ordered ternary semigroups [30] and regular ternary semirings [31]. However, approximation of BF sets has not been commonly used in semirings so far, to our knowledge. Therefore, consideration of a new framework of approximation of BF subsemirings (resp. ideals) is reasonable and necessary. We address the principles of RBF subsemirings (resp. ideals) in this article and analyze related properties by extending [29,32].

This paper is arranged as follows. In Section 1, we introduce all of the terms used in this paper. In Section 2, we discuss the ideas of rough sets and BF sets and present some basic definitions. The main section of this paper is Section 3, where we will present RBF ideals, bi-ideals and interior ideals of semirings and their related theorems on the basis of CRs and CCRs. In the last section, a comparative study and conclusions are given.

The list of acronyms used in the research article is given in Table 1.

Table 1. List of acronyms.

Acronyms	Representation
BF	Bipolar fuzzy
RBF	Rough bipolar fuzzy
BF$(\mathfrak{S})$	A set of all bipolar fuzzy subsets of a semiring $\mathfrak{S}$
CR	Congruence relation
CCR	Complete congruence relation

2. Preliminaries

A nonempty set $(\mathfrak{S},+,·)$ is known as a semiring if $(\mathfrak{S},+)$ is a commutative semigroup, $(\mathfrak{S},·)$ is a semigroup and $s.(p+q)=s.p+s.q,$$(p+q).s=p.s+q.s$for every $s,p,q\in \mathfrak{S}$. By a subset, we always mean a nonempty one. A subset P of a semiring $\mathfrak{S}$ is known as a subsemiring of $\mathfrak{S}$ if P is itself a semiring under addition and multiplication as defined in $\mathfrak{S}$. A subset P of a semiring $\mathfrak{S}$ is known as a left (resp. right) ideal of $\mathfrak{S}$ if $(P,+)$ is a groupoid and $sp\in P(ps\in P)\mathrm{for}\mathrm{every}s\in \mathfrak{S},p\in P.$ If P is both a right and left ideal, then it is said to be an ideal of $\mathfrak{S}$. A subset P of a semiring $\mathfrak{S}$ is called a bi-ideal if P is a subsemiring of $\mathfrak{S}$ and $P\mathfrak{S}P\subseteq P.$ A subset P of a semiring $\mathfrak{S}$ is known as an interior ideal if P is a subsemiring and $\mathfrak{S}P\mathfrak{S}\subseteq P.$

In BF subset $\rho =(\mathfrak{S},{\rho }^p,{\rho }^n)$ of $\mathfrak{S}$, ${\rho }^p(z)$ presents the satisfaction degree of z to the correlated characteristic of $\rho$ and ${\rho }^n(z)$ is the satisfaction degree of z to the somewhat opposite characteristic of $\rho$. The fuzzy set presents only positive aspects of a situation with membership function $[0,1]$. The difference between the fuzzy set and the BF set is shown by the following example. Let $A=\{u,v,w,x,y,z\}$ be a set of workers of a company. Define a fuzzy set on A with fuzzy property “honesty”, the workers $v,x$ and y having property “honesty” mapped to $[0,1]$, as shown by the bar graph in Figure 1.

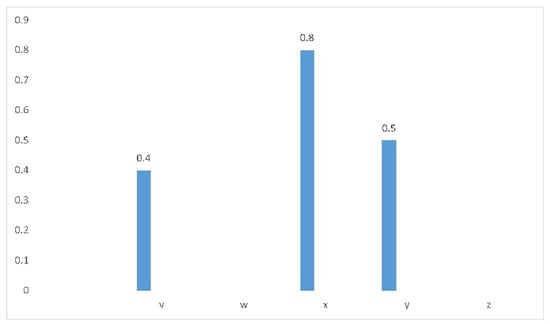
Figure 1. Graph of fuzzy set.

Other workers have no membership degree in range $[0,1]$, as they are not honest. In the fuzzy set, we can cover only positive aspects of any situation. We cannot deal with negative aspects of situations. To facilitate, we deal with such problems with the BF set. The property “dishonesty” is opposite to “honesty”. The workers $u,w$ and z are mapped to $[-1,0]$ with property “dishonesty”. In such a way, the BF set gives information about all elements, as shown in Figure 2.

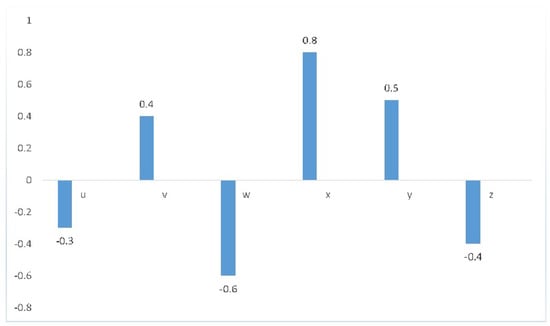
Figure 2. Graph of bipolar fuzzy set.

Throughout this article, $\mathfrak{S}$ represents a semiring. Let $\lambda ,\rho$$\in BF(\mathfrak{S})$. Then, $\lambda \subseteq \rho$ if and only if ${\lambda }^p(z)\le {\rho }^p(z)$ and ${\lambda }^n(z)\ge {\rho }^n(z)$ for every $z\in \mathfrak{S}$, and $\lambda =\rho$ if and only if $\lambda \subseteq \rho$ and $\rho \subseteq \lambda$. Let $\lambda ,\rho$$\in BF(\mathfrak{S})$. Then, $\lambda +\rho =(\mathfrak{S},{\lambda }^p+{\rho }^p,{\lambda }^n+{\rho }^n)$, the sum of $\lambda$ and $\rho$, is defined as

$$({\lambda }^p+{\rho }^p)(z)=\underset{z=a+c}{\bigvee }\{{\lambda }^p(a)\wedge {\rho }^p(c)\}$$

and

$$({\lambda }^n+{\rho }^n)(z)=\underset{z=a+c}{\bigwedge }\{{\lambda }^n(a)\vee {\rho }^n(c)\}$$

for $a,c,z\in \mathfrak{S}$. For $\lambda ,\rho$$\in BF(\mathfrak{S})$, define the BF subset $\lambda \circ \rho =(\mathfrak{S},{\lambda }^p\circ {\rho }^p,{\lambda }^n\circ {\rho }^n)$ of $\mathfrak{S}$ as

$$({\lambda }^p\circ {\rho }^p)(z)=\left\{\begin{array}{c}\underset{z={\Sigma }_{i=1}^n{a}_i{b}_i}{\bigvee }\left\{\underset{i=1}{\overset{n}{\bigwedge }}({\lambda }^p(a_i)\wedge {\rho }^p(b_i))\right\},\hfill \\ 0\mathrm{if}z\mathrm{is}\mathrm{not}\mathrm{expressible}\mathrm{as}z={\Sigma }_{i=1}^n{a}_i{b}_i\hfill \end{array}\right.$$

and

$$({\lambda }^n\circ {\rho }^n)(z)=\left\{\begin{array}{c}\underset{z={\Sigma }_{i=1}^n{a}_i{b}_i}{\bigwedge }\left\{\underset{i=1}{\overset{n}{\bigvee }}({\lambda }^p(a_i)\vee {\rho }^p(b_i))\right\},\hfill \\ 0\mathrm{if}z\mathrm{is}\mathrm{not}\mathrm{expressible}\mathrm{as}z={\Sigma }_{i=1}^n{a}_i{b}_i\hfill \end{array}\right.$$

for $z,a_i,b_i\in \mathfrak{S}.$

Definition 1

([29]). Let ρ$\in BF(\mathfrak{S}).$ Then, ρ is known as a BF subsemiring of $\mathfrak{S}$ if for every $a,z\in \mathfrak{S}:$

(i) 

${\rho }^p(0)\ge {\rho }^p(z)$, ${\rho }^n(0)\le {\rho }^n(z)$;

(ii) 

${\rho }^p(a+z)\ge min\{{\rho }^p(a),{\rho }^p(z)\}$, ${\rho }^n(a+z)\le max\{{\rho }^n(a),{\rho }^n(z)\}$;

(iii) 

${\rho }^p(az)\ge min\{{\rho }^p(a),{\rho }^p(z)\}$, ${\rho }^n(az)\le max\{{\rho }^n(a),{\rho }^n(z)\}$.

Definition 2

([29]). Let ρ$\in BF(\mathfrak{S})$. Then, ρ is known as a BF left (resp. right) ideal of $\mathfrak{S}$ if for every $a,z\in \mathfrak{S}:$

(i) 

${\rho }^p(a+z)\ge min\{{\rho }^p(a),{\rho }^p(z)\}$, ${\rho }^n(a+z)\le max\{{\rho }^n(a),{\rho }^n(z)\}$;

(ii) 

$({\rho }^p(az)\ge {\rho }^p(z)$, ${\rho }^n(az)\le {\rho }^n(z))($resp. ${\rho }^p(az)\ge {\rho }^p(a)$, ${\rho }^n(az)\le {\rho }^n(a)).$

If ρ is both a BF left and right ideal, then it is known as a BF ideal of $\mathfrak{S}$.

Definition 3

([29]). Let ρ$\in BF(\mathfrak{S})$. Then ρ is known as a BF bi-ideal of $\mathfrak{S}$ if for every $a,c,z\in \mathfrak{S}$:

(i) 

${\rho }^p(a+z)\ge min\{{\rho }^p(a),{\rho }^p(z)\}$, ${\rho }^n(a+z)\le max\{{\rho }^n(a),{\rho }^n(z)\}$;

(ii) 

${\rho }^p(az)\ge min\{{\rho }^p(a),{\rho }^p(z)\}$, ${\rho }^n(az)\le max\{{\rho }^n(a),{\rho }^n(z)\}$;

(iii) 

${\rho }^p(azc)\ge min\{{\rho }^p(a),{\rho }^p(c)\}$, ${\rho }^n(azc)\le max\{{\rho }^n(a),{\rho }^n(c)\}$.

Definition 4.

Let ρ$\in BF(\mathfrak{S}).$ Then, ρ is known as a BF interior ideal of $\mathfrak{S}$ if for every $a,c,z\in \mathfrak{S}$:

(i) 

${\rho }^p(a+z)\ge min\{{\rho }^p(a),{\rho }^p(z)\}$, ${\rho }^n(a+z)\le max\{{\rho }^n(a),{\rho }^n(z)\}$;

(ii) 

${\rho }^p(az)\ge min\{{\rho }^p(a),{\rho }^p(z)\}$, ${\rho }^n(az)\le max\{{\rho }^n(a),{\rho }^n(z)\}$;

(iii) 

${\rho }^p(acz)\ge {\rho }^p(c)$, ${\rho }^n(azc)\le {\rho }^n(c)$.

Let W be a universe and $\widehat{\Theta }$ an equivalence relation on W. Then $E=(W,\widehat{\Theta })$ is known as an approximation space. The equivalence classes of $\widehat{\Theta }$ are the main constituents of the rough sets. Let $Y(\ne \phi )\subseteq W$. The set Y is called a definable subset of W if it is the collection of some equivalence classes of the universal set W; otherwise, it is not definable. The set Y is approximated in the form of upper and lower approximations, which are given as:

$$\overline{Apr}(Y)=\left\{w\in W:{\left[w\right]}_{\widehat{\Theta }}\cap Y\ne \phi \right\},$$

$$\underline{Apr}(Y)=\left\{w\in W:{\left[w\right]}_{\widehat{\Theta }}\subseteq Y\right\},$$

where ${\left[w\right]}_{\widehat{\Theta }}$ is the equivalence class of w for $w\in W.$

The rough set is a pair $(\overline{Apr}(Y),\underline{Apr}(Y))$ if $\overline{Apr}(Y)\ne \underline{Apr}(Y).$ The set Y is a definable set if $\overline{Apr}(Y)=\underline{Apr}(Y).$

3. Approximations of Bipolar Fuzzy Ideals in Semirings

This is the main section of our paper in which we present the concepts of RBF subsets of semirings and concentrate on their key properties. RBF subsemirings, RBF ideals, RBF bi-ideals and RBF interior ideals of the semirings are additionally discussed in this section. The lower and upper RBF approximations of $\xi$ under the relation $\widehat{\Theta }$ are the BF subsets $\underline{\widehat{\Theta }}(\xi )$ and $\overline{\widehat{\Theta }}(\xi )$ of $\mathfrak{S}$, respectively, defined as:

$$\begin{array}{ccc}\hfill \underline{\widehat{\Theta }}(\xi )& =& \{(s,\underline{\widehat{\Theta }}{\xi }^p(s),\underline{\widehat{\Theta }}{\xi }^n(s)):s\in \mathfrak{S}\};\hfill \\ \hfill \overline{\widehat{\Theta }}(\xi )& =& \{(s,\overline{\widehat{\Theta }}{\xi }^p(s),\overline{\widehat{\Theta }}{\xi }^n(s)):s\in \mathfrak{S}\},\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill \underline{\widehat{\Theta }}{\xi }^p(s)& =& \underset{b\in {\left[s\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(b),\underline{\widehat{\Theta }}{\xi }^n(s)=\underset{b\in {\left[s\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(b);\hfill \\ \hfill \overline{\widehat{\Theta }}{\xi }^p(s)& =& \underset{b\in {\left[s\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(b),\overline{\widehat{\Theta }}{\xi }^n(s)=\underset{b\in {\left[s\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(b).\hfill \end{array}$$

If $\overline{\widehat{\Theta }}(\xi )=\underline{\widehat{\Theta }}(\xi )$, then $\xi$ is $\widehat{\Theta }$-definable; else, $\xi$ is an RBF subset of $\mathfrak{S}$ [33]. An equivalence relation $\widehat{\Theta }$ on $\mathfrak{S}$ which satisfies the additional condition that if $(i,j)$ and $(k,l)\in \widehat{\Theta }$ then $(i+k,j+l)\in \widehat{\Theta }$ and $(ik,jl)\in \widehat{\Theta }$ is known as a congruence relation (CR) on $\mathfrak{S}$. A CR $\widehat{\Theta }$ on $\mathfrak{S}$ is complete if for every$j,k\in \mathfrak{S},$${\left[j\right]}_{\widehat{\Theta }}+{\left[k\right]}_{\widehat{\Theta }}={[j+k]}_{\widehat{\Theta }}$and${\left[j\right]}_{\widehat{\Theta }}{\left[k\right]}_{\widehat{\Theta }}={\left[jk\right]}_{\widehat{\Theta }}$ [32]. Some authors used the term full congruence instead of complete congruence in their research.

Theorem 1.

If $\widehat{\Theta }$ is a CCR on $\mathfrak{S}$, then $\underline{\widehat{\Theta }}(\xi )\circ \underline{\widehat{\Theta }}(\rho )\subseteq \underline{\widehat{\Theta }}(\xi \circ \rho )$ for any ξ, $\rho \in BF(\mathfrak{S}).$

Proof. 

Since the CR $\widehat{\Theta }$ is complete on $\mathfrak{S}$, ${\left[u\right]}_{\widehat{\Theta }}{\left[v\right]}_{\widehat{\Theta }}={\left[uv\right]}_{\widehat{\Theta }}$for all$u,v\in \mathfrak{S}.$ Let $\xi ,\rho \in BF(\mathfrak{S})$. The following two cases arise for $z\in \mathfrak{S}$:

Case (i): If $z\ne {\sum }_{i=1}^n{a}_i{b}_i$ for $a_i,b_i\in \mathfrak{S},$ then $(\underline{\widehat{\Theta }}{\xi }^p\circ \underline{\widehat{\Theta }}{\rho }^p)(z)=0=(\underline{\widehat{\Theta }}{\xi }^n\circ \underline{\widehat{\Theta }}{\rho }^n)(z)$. Thus, $(\underline{\widehat{\Theta }}{\xi }^p\circ \underline{\widehat{\Theta }}{\rho }^p)(z)=0\le \underline{\widehat{\Theta }}({\xi }^p\circ {\rho }^p)(z)$ and $(\underline{\widehat{\Theta }}{\xi }^n\circ \underline{\widehat{\Theta }}{\rho }^n)(z)=0\ge \underline{\widehat{\Theta }}({\xi }^n\circ {\rho }^n)(z).$

Case (ii): If $z={\sum }_{i=1}^n{a}_i{b}_i$ for $a_i,b_i\in \mathfrak{S},$ then

$$\begin{array}{cc}\hfill (\underline{\widehat{\Theta }}{\xi }^p\circ \underline{\widehat{\Theta }}{\rho }^p)(z)& =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left\{\underset{i=1}{\overset{n}{\bigwedge }}\left(\underline{\widehat{\Theta }}{\xi }^p(a)\wedge \underline{\widehat{\Theta }}{\rho }^p(b)\right)\right\}\hfill \\ \hfill & =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left[\underset{i=1}{\overset{n}{\bigwedge }}\{(\underset{s\in {\left[a_i\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(s))\wedge (\underset{t\in {\left[b_i\right]}_{\widehat{\Theta }}}{\bigwedge }{\rho }^p(t))\}\right]\hfill \\ \hfill & =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left[\underset{i=1}{\overset{n}{\bigwedge }}\{\underset{s\in {\left[a_i\right]}_{\widehat{\Theta }}}{\bigwedge }\underset{t\in {\left[b_i\right]}_{\widehat{\Theta }}}{\bigwedge }({\xi }^p(s)\wedge {\rho }^p(t))\}\right]\hfill \\ \hfill & \le \underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left[\underset{i=1}{\overset{n}{\bigwedge }}\{\underset{st\in {\left[a_i{b}_i\right]}_{\widehat{\Theta }}}{\bigwedge }\underset{st={\sum }_{i=1}^n{s}_i{t}_i}{\bigvee }\left({\xi }^p(s_i)\wedge {\rho }^p(t_i)\right)\}\right]\hfill \end{array}$$

where $st\in {\left[a_i\right]}_{\widehat{\Theta }}{\left[b_i\right]}_{\widehat{\Theta }}={\left[a_i{b}_i\right]}_{\widehat{\Theta }}$ and

$$\begin{array}{cc}\hfill (\underline{\widehat{\Theta }}{\xi }^p\circ \underline{\widehat{\Theta }}{\rho }^p)(z)& =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left[\underset{st\in {\left[a_i{b}_i\right]}_{\widehat{\Theta }}}{\bigwedge }\underset{st={\sum }_{i=1}^n{s}_i{t}_i}{\bigvee }\{\underset{i=1}{\overset{n}{\bigwedge }}\left({\xi }^p(s_i)\wedge {\rho }^p(t_i)\right)\}\right]\hfill \\ \hfill & =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left\{\underset{st\in {\left[a_i{b}_i\right]}_{\widehat{\Theta }}}{\bigwedge }\left({\xi }^p\circ {\rho }^p\right)(st)\right\}\hfill \\ \hfill & =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\underline{\widehat{\Theta }}\left({\xi }^p\circ {\rho }^p\right)(a_i{b}_i)\hfill \\ \hfill & \le \underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\underline{\widehat{\Theta }}\left({\xi }^p\circ {\rho }^p\right)({\Sigma }_{i=1}^n{a}_i{b}_i)\hfill \\ \hfill & =\underline{\widehat{\Theta }}\left({\xi }^p\circ {\rho }^p\right)(z).\hfill \end{array}$$

Similarly, $(\underline{\widehat{\Theta }}{\xi }^n\circ \underline{\widehat{\Theta }}{\rho }^n)(z)\ge \underline{\widehat{\Theta }}\left({\xi }^n\circ {\rho }^n\right)(z)$. Hence, $\underline{\widehat{\Theta }}(\xi )\circ \underline{\widehat{\Theta }}(\rho )\subseteq \underline{\widehat{\Theta }}(\xi \circ \rho ).$ □

Theorem 2.

If $\widehat{\Theta }$ is a CR on $\mathfrak{S}$, then $\overline{\widehat{\Theta }}(\xi )\circ \overline{\widehat{\Theta }}(\rho )\subseteq \overline{\widehat{\Theta }}(\xi \circ \rho )$ for any ξ, $\rho \in BF(\mathfrak{S}).$

Proof. 

As $\widehat{\Theta }$ is a CR on $\mathfrak{S}$, ${\left[u\right]}_{\widehat{\Theta }}{\left[v\right]}_{\widehat{\Theta }}\subseteq {\left[uv\right]}_{\widehat{\Theta }}$for all$u,v\in \mathfrak{S}.$ Let $\xi ,\rho \in BF(\mathfrak{S})$. The following two cases arise for $z\in \mathfrak{S}$:

Case (i): If $z\ne {\sum }_{i=1}^n{a}_i{b}_i$ for $a_i,b_i\in \mathfrak{S},$ then it is obvious.

Case (ii): If $z={\sum }_{i=1}^n{a}_i{b}_i$ for $a_i,b_i\in \mathfrak{S},$ then we have

$$\begin{array}{cc}\hfill (\overline{\widehat{\Theta }}{\xi }^p\circ \overline{\widehat{\Theta }}{\rho }^p)(z)& =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left\{\underset{i=1}{\overset{n}{\bigwedge }}(\overline{\widehat{\Theta }}{\xi }^p(a)\wedge \overline{\widehat{\Theta }}{\rho }^p(b))\right\}\hfill \\ \hfill & =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left[\underset{i=1}{\overset{n}{\bigwedge }}\{(\underset{s\in {\left[a_i\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(s))\wedge (\underset{t\in {\left[b_i\right]}_{\widehat{\Theta }}}{\bigvee }{\rho }^p(t))\}\right]\hfill \\ \hfill & =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left[\underset{i=1}{\overset{n}{\bigwedge }}\{\underset{s\in {\left[a_i\right]}_{\widehat{\Theta }}}{\bigvee }\underset{t\in {\left[b_i\right]}_{\widehat{\Theta }}}{\bigvee }\left({\xi }^p(s)\wedge {\rho }^p(t)\right)\}\right]\hfill \\ \hfill & \le \underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left[\underset{i=1}{\overset{n}{\bigwedge }}\{\underset{st\in {\left[a_i{b}_i\right]}_{\widehat{\Theta }}}{\bigvee }\underset{st={\sum }_{i=1}^n{s}_i{t}_i}{\bigvee }\left({\xi }^p(s_i)\wedge {\rho }^p(t_i)\right)\}\right]\hfill \\ \hfill \mathrm{where},st& \in {\left[a_i\right]}_{\widehat{\Theta }}{\left[b_i\right]}_{\widehat{\Theta }}\subseteq {\left[a_i{b}_i\right]}_{\widehat{\Theta }}\hfill \\ \hfill & =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left[\underset{st\in {\left[a_i{b}_i\right]}_{\widehat{\Theta }}}{\bigvee }\underset{st={\sum }_{i=1}^n{s}_i{t}_i}{\bigvee }\{\underset{i=1}{\overset{n}{\bigwedge }}\left({\xi }^p(s_i)\wedge {\rho }^p(t_i)\right)\}\right]\hfill \\ \hfill & =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\left\{\underset{st\in {\left[a_i{b}_i\right]}_{\widehat{\Theta }}}{\bigvee }\left({\xi }^p\circ {\rho }^p\right)(st)\right\}\hfill \\ \hfill & =\underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\overline{\widehat{\Theta }}\left({\xi }^p\circ {\rho }^p\right)(a_i{b}_i)\hfill \\ \hfill & \le \underset{z={\sum }_{i=1}^n{a}_i{b}_i}{\bigvee }\overline{\widehat{\Theta }}\left({\xi }^p\circ {\rho }^p\right)({\Sigma }_{i=1}^n{a}_i{b}_i)\hfill \\ \hfill & =\overline{\widehat{\Theta }}\left({\xi }^p\circ {\rho }^p\right)(z).\hfill \end{array}$$

Similarly, $(\overline{\widehat{\Theta }}{\xi }^n\circ \overline{\widehat{\Theta }}{\rho }^n)(z)\ge \overline{\widehat{\Theta }}\left({\xi }^n\circ {\rho }^n\right)(z).$ Hence, $\overline{\widehat{\Theta }}(\xi )\circ \overline{\widehat{\Theta }}(\rho )\subseteq \overline{\widehat{\Theta }}(\xi \circ \rho ).$ □

Theorem 3.

If $\widehat{\Theta }$ is a CCR on $\mathfrak{S}$, then $\underline{\widehat{\Theta }}(\xi )+\underline{\widehat{\Theta }}(\rho )\subseteq \underline{\widehat{\Theta }}(\xi +\rho )$ for any ξ, $\rho \in BF(\mathfrak{S}).$

Proof. 

Since the CR $\widehat{\Theta }$ is complete on $\mathfrak{S}$, ${\left[u\right]}_{\widehat{\Theta }}+{\left[v\right]}_{\widehat{\Theta }}={[u+v]}_{\widehat{\Theta }}$for all$u,v\in \mathfrak{S}.$ Let $\xi ,\rho \in BF(\mathfrak{S})$ and $z\in \mathfrak{S}$. Consider

$$\begin{array}{ccc}\hfill (\underline{\widehat{\Theta }}{\xi }^p+\underline{\widehat{\Theta }}{\rho }^p)(z)& =& \underset{z=u+x}{\bigvee }\left(\underline{\widehat{\Theta }}{\xi }^p(u)\wedge \underline{\widehat{\Theta }}{\rho }^p(x)\right)\hfill \\ & =& \underset{z=u+x}{\bigvee }\left\{(\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(b))\wedge (\underset{c\in {\left[x\right]}_{\Theta }}{\bigwedge }{\rho }^p(c))\right\}\hfill \\ & =& \underset{z=u+x}{\bigvee }\left\{\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigwedge }\underset{c\in {\left[x\right]}_{\widehat{\Theta }}}{\bigwedge }\left({\xi }^p(b)\wedge {\rho }^p(c)\right)\right\}\hfill \\ & =& \underset{z=u+x}{\bigvee }\left\{\underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[x\right]}_{\widehat{\Theta }}}{\bigwedge }\left({\xi }^p(b)\wedge {\rho }^p(c)\right)\right\}\hfill \\ & \le & \underset{z=u+x}{\bigvee }\left\{\underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[x\right]}_{\widehat{\Theta }}}{\bigwedge }\underset{b+c=m+n}{\bigvee }\left({\xi }^p(m)\wedge {\rho }^p(n)\right)\right\}\hfill \\ & =& \underset{z=u+x}{\bigvee }\left\{\underset{(b+c)\in {[u+x]}_{\widehat{\Theta }}}{\bigwedge }\left({\xi }^p+{\rho }^p\right)(b+c)\right\}\hfill \\ & =& \underset{z=b+c}{\bigvee }\left(\underline{\widehat{\Theta }}\left({\xi }^p+{\rho }^p\right)(b+c)\right)\hfill \\ & =& \underline{\widehat{\Theta }}\left({\xi }^p+{\rho }^p\right)(z).\hfill \end{array}$$

Similarly, $(\underline{\widehat{\Theta }}{\xi }^n+\underline{\widehat{\Theta }}{\rho }^n)(z)\ge \underline{\widehat{\Theta }}\left({\xi }^n+{\rho }^n\right)(z).$ Thus, $\underline{\widehat{\Theta }}(\xi )+\underline{\widehat{\Theta }}(\rho )\subseteq \underline{\widehat{\Theta }}(\xi +\rho ).$ □

Theorem 4.

If $\widehat{\Theta }$ is a CR on $\mathfrak{S}$, then $\overline{\widehat{\Theta }}(\xi )+\overline{\widehat{\Theta }}(\rho )\subseteq \overline{\widehat{\Theta }}(\xi +\rho )$ for any ξ, $\rho \in BF(\mathfrak{S}).$

Proof. 

As $\widehat{\Theta }$ is a CR on $\mathfrak{S}$, ${\left[u\right]}_{\widehat{\Theta }}+{\left[v\right]}_{\widehat{\Theta }}\subseteq {[u+v]}_{\widehat{\Theta }}$ for all $u,v\in \mathfrak{S}.$ Let $\xi ,\rho \in BF(\mathfrak{S}).$ Then, for any $z\in \mathfrak{S}$, consider

$$\begin{array}{ccc}\hfill (\overline{\widehat{\Theta }}{\xi }^p+\overline{\widehat{\Theta }}{\rho }^p)(z)& =& \underset{z=u+x}{\bigvee }\left(\overline{\widehat{\Theta }}{\xi }^p(u)\wedge \overline{\widehat{\Theta }}{\rho }^p(x)\right)\hfill \\ & =& \underset{z=u+x}{\bigvee }\left\{(\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(b))\wedge (\underset{c\in {\left[x\right]}_{\widehat{\Theta }}}{\bigvee }{\rho }^p(c))\right\}\hfill \\ & =& \underset{z=u+x}{\bigvee }\left\{\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigvee }\underset{c\in {\left[x\right]}_{\widehat{\Theta }}}{\bigvee }\left({\xi }^p(b)\wedge {\rho }^p(c)\right)\right\}\hfill \\ & =& \underset{z=u+x}{\bigvee }\left\{\underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[x\right]}_{\widehat{\Theta }}}{\bigvee }\left({\xi }^p(b)\wedge {\rho }^p(c)\right)\right\}\hfill \\ & \le & \underset{z=u+x}{\bigvee }\left\{\underset{b+c\in {[u+x]}_{\widehat{\Theta }}}{\bigvee }\left({\xi }^p(b)\wedge {\rho }^p(c)\right)\right\}\hfill \\ & =& \underset{b+c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }\left({\xi }^p(b)\wedge {\rho }^p(c)\right)\hfill \\ & =& \underset{r\in {\left[z\right]}_{\widehat{\Theta }},r=b+c}{\bigvee }\left({\xi }^p(b)\wedge {\rho }^p(c)\right)\hfill \\ & =& \underset{r\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }\left(\underset{r=b+c}{\bigvee }({\xi }^p(b)\wedge {\rho }^p(c))\right)\hfill \\ & =& \underset{r\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }({\xi }^p+{\rho }^p)(r)\hfill \\ & =& \overline{\widehat{\Theta }}\left({\xi }^p+{\rho }^p\right)(z).\hfill \end{array}$$

Similarly, $(\overline{\widehat{\Theta }}{\xi }^n+\overline{\widehat{\Theta }}{\rho }^n)(z)\ge \overline{\widehat{\Theta }}\left({\xi }^n+{\rho }^n\right)(z).$ Hence, $\overline{\widehat{\Theta }}(\xi )+\overline{\widehat{\Theta }}(\rho )\subseteq \overline{\widehat{\Theta }}(\xi +\rho ).$ □

Definition 5.

Let $\widehat{\Theta }$ be a CR on $\mathfrak{S}$ and $\xi \in BF(\mathfrak{S})$. Then, ξ is a lower (resp. upper) RBF subsemiring of $\mathfrak{S}$ if $\underline{\widehat{\Theta }}(\xi )(\overline{\widehat{\Theta }}(\xi ))$ is a BF subsemiring of $\mathfrak{S}$.

A BF subset ξ of $\mathfrak{S}$ which is both a lower and upper RBF subsemiring of $\mathfrak{S}$ is known as an RBF subsemiring of $\mathfrak{S}$.

Theorem 5.

If $\widehat{\Theta }$ is a CR on $\mathfrak{S}$, then each BF subsemiring $\xi =(\mathfrak{S};{\xi }^p,{\xi }^n)$ of $\mathfrak{S}$ is an upper RBF subsemiring of $\mathfrak{S}$.

Proof. 

For all $u,z\in \mathfrak{S}$, consider

$$\begin{array}{ccc}\hfill \overline{\widehat{\Theta }}{\xi }^p(u+z)& =& \underset{s\in {[u+z]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(s)\hfill \\ & \ge & \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }}\subseteq {[u+z]}_{\widehat{\Theta }}\hfill \\ & =& \underset{(b+c)\in ({\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(b+c)\hfill \\ & \ge & \underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }({\xi }^p(b)\wedge {\xi }^p(c))\hfill \\ & =& \left(\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(b)\right)\wedge \left(\underset{c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(c)\right)\hfill \\ & =& \overline{\widehat{\Theta }}{\xi }^p(u)\wedge \overline{\widehat{\Theta }}{\xi }^p(z).\hfill \end{array}$$

Similarly, $\overline{\widehat{\Theta }}{\xi }^n(u+z)\le \overline{\widehat{\Theta }}{\xi }^n(u)\vee \overline{\widehat{\Theta }}{\xi }^n(z).$ In addition,

$$\begin{array}{ccc}\hfill \overline{\widehat{\Theta }}{\xi }^p(uz)& =& \underset{s\in {\left[uz\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(s)\hfill \\ & \ge & \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }}\subseteq {\left[uz\right]}_{\widehat{\Theta }}\hfill \\ & =& \underset{bc\in ({\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(bc)\hfill \\ & \ge & \underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }({\xi }^p(b)\wedge {\xi }^p(c))\hfill \\ & =& \left(\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(b)\right)\wedge \left(\underset{c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(c)\right)\hfill \\ & =& \overline{\widehat{\Theta }}{\xi }^p(u)\wedge \overline{\widehat{\Theta }}{\xi }^p(z).\hfill \end{array}$$

Similarly, $\overline{\widehat{\Theta }}{\xi }^n(uz)\le \overline{\widehat{\Theta }}{\xi }^n(u)\vee \overline{\widehat{\Theta }}{\xi }^n(z).$ Thus, $\overline{\widehat{\Theta }}(\xi )$ is a BF subsemiring of $\mathfrak{S}$. Therefore, $\xi$ is an upper RBF subsemiring of $\mathfrak{S}$. □

Theorem 6.

If $\widehat{\Theta }$ is a CCR on $\mathfrak{S}$, then each BF subsemiring $\xi =(\mathfrak{S};{\xi }^p,{\xi }^n)$ of $\mathfrak{S}$ is a lower RBF subsemiring of $\mathfrak{S}$.

Proof. 

Let $\xi =(\mathfrak{S};{\xi }^p,{\xi }^n)$ be a BF subsemiring of $\mathfrak{S}$. Now, for all $u,z\in \mathfrak{S}$, consider

$$\begin{array}{ccc}\hfill \underline{\widehat{\Theta }}{\xi }^p(u+z)& =& \underset{s\in {[u+z]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(s)\hfill \\ & =& \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }}={[u+z]}_{\widehat{\Theta }}\hfill \\ & =& \underset{(b+c)\in ({\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(b+c)\hfill \\ & \ge & \underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigwedge }({\xi }^p(b)\wedge {\xi }^p(c))\hfill \\ & =& \left(\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(b)\right)\wedge \left(\underset{c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(c)\right)\hfill \\ & =& \underline{\widehat{\Theta }}{\xi }^p(u)\wedge \underline{\widehat{\Theta }}{\xi }^p(z).\hfill \end{array}$$

Similarly, $\underline{\widehat{\Theta }}{\xi }^n(u+z)\le \underline{\widehat{\Theta }}{\xi }^n(u)\vee \underline{\widehat{\Theta }}{\xi }^n(z).$ In addition,

$$\begin{array}{ccc}\hfill \underline{\widehat{\Theta }}{\xi }^p(uz)& =& \underset{s\in {\left[uz\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(s)\hfill \\ & =& \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }}={\left[uz\right]}_{\widehat{\Theta }}\hfill \\ & =& \underset{bc\in ({\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(bc)\hfill \\ & \ge & \underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigwedge }({\xi }^p(b)\wedge {\xi }^p(c))\hfill \\ & =& \left(\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(b)\right)\wedge \left(\underset{c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(c)\right)\hfill \\ & =& \underline{\widehat{\Theta }}{\xi }^p(u)\wedge \underline{\widehat{\Theta }}{\xi }^p(z).\hfill \end{array}$$

Similarly, $\underline{\widehat{\Theta }}{\xi }^n(uz)\le \underline{\widehat{\Theta }}{\xi }^n(u)\vee \underline{\widehat{\Theta }}{\xi }^n(z).$ Thus, $\underline{\widehat{\Theta }}(\xi )$ is a BF subsemiring of $\mathfrak{S}$. Therefore, $\xi$ is a lower RBF subsemiring of $\mathfrak{S}$. □

The example defined below illustrates that Theorem 6 does not hold if the CR $\widehat{\Theta }$ is not complete.

Example 1.

Let $\mathfrak{S}=\{0,1,\iota ,\kappa ,\nu \}$ be a semiring with the addition “+” and multiplication “· ” given in Table 2 and Table 3.

Table 2. Table of binary addition. ($\mathfrak{S}=\{0,1,\iota ,\kappa ,\nu \}$).

+	0	1	$\iota$	$\kappa$	$\nu$
0	0	1	$\iota$	$\kappa$	$\nu$
1	1	$\kappa$	1	$\iota$	1
$\iota$	$\iota$	1	$\iota$	$\kappa$	$\iota$
$\kappa$	$\kappa$	$\iota$	$\kappa$	1	$\kappa$
$\nu$	$\nu$	1	$\iota$	$\kappa$	$\nu$

Table 3. Table of binary multiplication. ($\mathfrak{S}=\{0,1,\iota ,\kappa ,\nu \}$).

·	0	1	$\iota$	$\kappa$	$\nu$
0	0	0	0	0	0
1	0	1	$\iota$	$\kappa$	$\nu$
$\iota$	0	$\iota$	$\iota$	$\iota$	$\nu$
$\kappa$	0	$\kappa$	$\iota$	1	$\nu$
$\nu$	0	$\nu$	$\nu$	$\nu$	$\nu$

Consider a binary relation $\widehat{\Theta }=\{(0,0),(1,1),(\iota ,\iota ),(\kappa ,\kappa ),(\nu ,\nu ),(\iota ,\nu ),(\nu ,\iota )\}$ on $\mathfrak{S}$. Then, $\widehat{\Theta }$ is a CR on $\mathfrak{S}$, defining the congruence classes $\{0\}$, $\{1\}$, $\{\iota ,\nu \}$ and $\{\kappa \}$, and $\widehat{\Theta }$ is not complete, since $\{1\}+\{\kappa \}=\{\iota \}\subseteq \{\iota ,\nu \}$. We take a BF subset $\xi$ of $\mathfrak{S}$, as below.

$$\xi =\{(0,0.6,-0.7),(1,0.6,-0.4),(\iota ,0.6,-0.5),(\kappa ,0.6,-0.4),(\nu ,0.5,-0.2)\}.$$

Then, $\xi$ is a BF subsemiring of $\mathfrak{S}$. Now,

$$\begin{array}{ccc}\hfill \overline{\widehat{\Theta }}(\xi )& =& \{(0,0.6,-0.7),(1,0.6,-0.4),(\iota ,0.6,-0.5),(\kappa ,0.6,-0.4),(\nu ,0.6,-0.5)\},\hfill \\ \hfill \underline{\widehat{\Theta }}(\xi )& =& \{(0,0.6,-0.7),(1,0.6,-0.4),(\iota ,0.5,-0.2),(\kappa ,0.6,-0.4),(\nu ,0.5,-0.2)\}.\hfill \end{array}$$

It can be vindicated by simple calculations that $\overline{\widehat{\Theta }}(\xi )$ is also a BF subsemiring of $\mathfrak{S}$, whereas $\underline{\widehat{\Theta }}(\xi )$ is not, as $\underline{\widehat{\Theta }}({\xi }^p)(1+\kappa )\ngeqq \underline{\widehat{\Theta }}({\xi }^p)(1)\wedge \underline{\widehat{\Theta }}({\xi }^p)(\kappa ).$

Definition 6.

If $\widehat{\Theta }$ is a CR on $\mathfrak{S}$ and $\xi \in BF(\mathfrak{S})$, then ξ is a lower (resp. upper) RBF left (resp. right) ideal of $\mathfrak{S}$ if $\underline{\widehat{\Theta }}(\xi )($resp. $\overline{\widehat{\Theta }}(\xi ))$ is a BF left (resp. right) ideal of $\mathfrak{S}$.

Theorem 7.

If $\widehat{\Theta }$ is a CR on $\mathfrak{S}$, then each BF left (resp. right) ideal $\xi =(\mathfrak{S};{\xi }^p,{\xi }^n)$ of $\mathfrak{S}$ is an upper RBF left (resp. right) ideal of $\mathfrak{S}$.

Proof. 

For $u,z\in \mathfrak{S},$ consider

$$\begin{array}{ccc}\hfill \overline{\widehat{\Theta }}{\xi }^p(u+z)& =& \underset{s\in {[u+z]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(s)\hfill \\ & \ge & \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }}\subseteq {[u+z]}_{\widehat{\Theta }}\hfill \\ & =& \underset{(b+c)\in ({\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(b+c)\hfill \\ & \ge & \underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }\left({\xi }^p(b)\wedge {\xi }^p(c)\right)\hfill \\ & =& \left(\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(b)\right)\wedge \left(\underset{c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(c)\right)\hfill \\ & =& \overline{\widehat{\Theta }}{\xi }^p(u)\wedge \overline{\widehat{\Theta }}{\xi }^p(z).\hfill \end{array}$$

Similarly, $\overline{\widehat{\Theta }}{\xi }^n(u+z)\le \overline{\widehat{\Theta }}{\xi }^n(u)\vee \overline{\widehat{\Theta }}{\xi }^n(z).$ In addition,

$$\begin{array}{ccc}\hfill \overline{\widehat{\Theta }}{\xi }^p(uz)& =& \underset{s\in {\left[uz\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(s)\hfill \\ & \ge & \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }}\subseteq {\left[uz\right]}_{\widehat{\Theta }}\hfill \\ & =& \underset{bc\in ({\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(bc)\hfill \\ & =& \underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(bc)\hfill \\ & \ge & \underset{c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(c)\hfill \\ & =& \overline{\widehat{\Theta }}{\xi }^p(z).\hfill \end{array}$$

Similarly, $\overline{\widehat{\Theta }}{\xi }^n(uz)\le \overline{\widehat{\Theta }}{\xi }^n(z).$ This implies that $\overline{\widehat{\Theta }}(\xi )$ is a BF left ideal. Therefore, $\xi$ is an upper RBF left ideal of $\mathfrak{S}$. Similarly, the case of a BF right ideal can be verified. □

Theorem 8.

Let $\widehat{\Theta }$ be a CCR on $\mathfrak{S}$. Then, each BF left (resp. right) ideal $\xi =(\mathfrak{S};{\xi }^p,{\xi }^n)$ of $\mathfrak{S}$ is a lower RBF left (resp. right) ideal of $\mathfrak{S}$.

Proof. 

For $u,z\in \mathfrak{S},$ consider

$$\begin{array}{ccc}\hfill \underline{\widehat{\Theta }}{\xi }^p(u+z)& =& \underset{s\in {[u+z]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(s)\hfill \\ & =& \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }}={[u+z]}_{\widehat{\Theta }}\hfill \\ & =& \underset{(b+c)\in ({\left[u\right]}_{\widehat{\Theta }}+{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(b+c)\hfill \\ & \ge & \underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigwedge }\left({\xi }^p(b)\wedge {\xi }^p(c)\right)\hfill \\ & =& \left(\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(b)\right)\wedge \left(\underset{c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(c)\right)\hfill \\ & =& \underline{\widehat{\Theta }}{\xi }^p(u)\wedge \underline{\widehat{\Theta }}{\xi }^p(z).\hfill \end{array}$$

Similarly, $\underline{\widehat{\Theta }}{\xi }^n(u+z)\le \underline{\widehat{\Theta }}{\xi }^n(u)\vee \underline{\widehat{\Theta }}{\xi }^n(z).$ In addition,

$$\begin{array}{ccc}\hfill \underline{\widehat{\Theta }}{\xi }^p(uz)& =& \underset{s\in {\left[uz\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(s)\hfill \\ & =& \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }}={\left[uz\right]}_{\widehat{\Theta }}\hfill \\ & =& \underset{bc\in ({\left[u\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(bc)\hfill \\ & =& \underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(bc)\hfill \\ & \ge & \underset{c\in {\left[z\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(c)\hfill \\ & =& \underline{\widehat{\Theta }}{\xi }^p(z).\hfill \end{array}$$

Similarly, $\underline{\widehat{\Theta }}{\xi }^n(uz)\le \underline{\widehat{\Theta }}{\xi }^n(z).$ Thus, $\underline{\widehat{\Theta }}(\xi )$ is a BF left ideal. Therefore, $\xi$ is a lower RBF left ideal of $\mathfrak{S}$. Similarly, the case of a BF right ideal of $\mathfrak{S}$ can be verified. □

The example defined below illustrates that Theorem 8 does not hold if the CR $\widehat{\Theta }$ is not complete.

Example 2.

Let $\mathfrak{S}=\{\iota ,\kappa ,\nu \}$ be a semiring with the addition “+” and multiplication “·” defined in Table 4 and Table 5.

Table 4. Table of binary addition. ($\mathfrak{S}=\{\iota ,\kappa ,\nu \}$).

+	$\iota$	$\kappa$	$\nu$
$\iota$	$\iota$	$\kappa$	$\nu$
$\kappa$	$\kappa$	$\kappa$	$\kappa$
$\nu$	$\nu$	$\kappa$	$\nu$

Table 5. Table of binary multiplication. ($\mathfrak{S}=\{\iota ,\kappa ,\nu \}$).

·	$\iota$	$\kappa$	$\nu$
$\iota$	$\iota$	$\iota$	$\iota$
$\kappa$	$\iota$	$\iota$	$\iota$
$\nu$	$\iota$	$\iota$	$\iota$

Consider a binary relation $\widehat{\Theta }=\{(\iota ,\iota ),(\kappa ,\kappa ),(\nu ,\nu ),(\iota ,\nu ),(\nu ,\iota )\}$ on $\mathfrak{S}$. Then, $\widehat{\Theta }$ is a CR on $\mathfrak{S}$. Defining the congruence classes $\{\kappa \}$ and $\{\iota ,\nu \}$, $\widehat{\Theta }$ is not complete. Therefore, $\{\kappa \}\{\iota ,\nu \}=\{\iota \}\subseteq \{\iota ,\nu \}$.

We take a BF subset $\xi$ of $\mathfrak{S}$, as below.

$$\xi =\{(\iota ,0.8,-0.45),(\kappa ,0.7,-0.4),(\nu ,0.5,-0.4)\}.$$

Then, $\xi$ is a BF left ideal of $\mathfrak{S}$. Now,

$$\begin{array}{ccc}\hfill \overline{\widehat{\Theta }}(\xi )& =& \{(\iota ,0.8,-0.45),(\kappa ,0.7,-0.4),(\nu ,0.8,-0.45)\},\hfill \\ \hfill \underline{\widehat{\Theta }}(\xi )& =& \{(\iota ,0.5,-0.4),(\kappa ,0.7,-0.4),(\nu ,0.5,-0.4)\}.\hfill \end{array}$$

It can be vindicated by simple calculations that $\overline{\widehat{\Theta }}(\xi )$ is also a BF left ideal of $\mathfrak{S}$, whereas $\underline{\widehat{\Theta }}(\xi )$ is not, as $\underline{\widehat{\Theta }}({\xi }^p)(\iota .\kappa )=0.5\ngeqq 0.7=\underline{\widehat{\Theta }}({\xi }^p)(\kappa ).$

Definition 7.

If $\widehat{\Theta }$ is a CR on $\mathfrak{S}$ and $\xi \in BF(\mathfrak{S})$, then ξ is a lower (resp. upper) RBF bi-ideal of $\mathfrak{S}$ if $\underline{\widehat{\Theta }}(\xi )(\overline{\widehat{\Theta }}(\xi ))$ is a BF bi-ideal of $\mathfrak{S}$.

A BF subset ξ of $\mathfrak{S}$ which is both a lower and upper RBF bi-ideal is called an RBF bi-ideal of $\mathfrak{S}$.

Theorem 9.

For a CR $\widehat{\Theta }$ on $\mathfrak{S}$, each BF bi-ideal $\xi =(\mathfrak{S};{\xi }^p,{\xi }^n)$ is an upper RBF bi-ideal of $\mathfrak{S}$.

Proof. 

A BF bi-ideal $\xi$ is also a BF subsemiring of $\mathfrak{S}$. We have by Theorem 5 that $\overline{\widehat{\Theta }}(\xi )$ is a BF subsemiring of $\mathfrak{S}$. Now, for $u,x,z\in \mathfrak{S}$, consider

$$\begin{array}{ccc}\hfill \overline{\widehat{\Theta }}{\xi }^p(uxz)& =& \underset{s\in {\left[uxz\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(s)\hfill \\ & \ge & \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }}\subseteq {\left[uxz\right]}_{\widehat{\Theta }}\hfill \\ & =& \underset{bcd\in ({\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(bcd)\hfill \\ & \ge & \underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[x\right]}_{\widehat{\Theta }},d\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }({\xi }^p(b)\wedge {\xi }^p(d))\hfill \\ & =& \left(\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(b)\right)\wedge \left(\underset{d\in {\left[z\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(d)\right)\hfill \\ & =& \overline{\widehat{\Theta }}{\xi }^p(u)\wedge \overline{\widehat{\Theta }}{\xi }^p(z).\hfill \end{array}$$

and $\overline{\widehat{\Theta }}{\xi }^n(uxz)\le \overline{\widehat{\Theta }}{\xi }^n(u)\vee \overline{\widehat{\Theta }}{\xi }^n(z).$ Thus, $\overline{\widehat{\Theta }}(\xi )$ is a BF bi-ideal of $\mathfrak{S}$. Therefore, $\xi$ is an upper RBF bi-ideal of $\mathfrak{S}$. □

Theorem 10.

For a CCR $\widehat{\Theta }$ on $\mathfrak{S}$, each BF bi-ideal $\xi =(\mathfrak{S};{\xi }^p,{\xi }^n)$ is a lower RBF bi-ideal of $\mathfrak{S}$.

Proof. 

A BF bi-ideal $\xi$ is also a BF subsemiring of $\mathfrak{S}$. In addition, by Theorem 6, $\underline{\widehat{\Theta }}(\xi )$ is a BF subsemiring of $\mathfrak{S}$. Now, for $u,x,z\in \mathfrak{S}$, consider

$$\begin{array}{ccc}\hfill \underline{\widehat{\Theta }}{\xi }^p(uxz)& =& \underset{s\in {\left[uxz\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(s)\hfill \\ & =& \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }}={\left[uxz\right]}_{\widehat{\Theta }}\hfill \\ & =& \underset{bcd\in ({\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(bcd)\hfill \\ & \ge & \underset{b\in {\left[u\right]}_{\widehat{\Theta }},c\in {\left[x\right]}_{\widehat{\Theta }},d\in {\left[z\right]}_{\widehat{\Theta }}}{\bigwedge }({\xi }^p(b)\wedge {\xi }^p(d))\hfill \\ & =& \left(\underset{b\in {\left[u\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(b)\right)\wedge \left(\underset{d\in {\left[z\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(d)\right)\hfill \\ & =& \underline{\widehat{\Theta }}{\xi }^p(u)\wedge \underline{\widehat{\Theta }}{\xi }^p(z).\hfill \end{array}$$

and $\underline{\widehat{\Theta }}{\xi }^n(uxz)\le \underline{\widehat{\Theta }}{\xi }^n(u)\vee \underline{\widehat{\Theta }}{\xi }^n(z).$ This implies $\underline{\widehat{\Theta }}(\xi )$ is a BF bi-ideal of $\mathfrak{S}$. Therefore, $\xi$ is a lower RBF bi-ideal of $\mathfrak{S}$. □

The example defined below illustrates that Theorem 10 does not hold if CR $\widehat{\Theta }$ is not complete.

Example 3.

Let $\mathfrak{S}=\{\iota ,\kappa ,\nu \}$ be the semiring and $\widehat{\Theta }$ be the CR on $\mathfrak{S}$, as defined in Example$2$, which is not complete, and define the congruence classes $\{\kappa \},\{\iota ,\nu \}$.

We take a BF subset ξ of $\mathfrak{S}$, as below.

$$\xi =\{(\iota ,0.6,-0.5),(\kappa ,0.4,-0.2),(\nu ,0.2,-0.2)\}.$$

Then, ξ is a BF bi-ideal of $\mathfrak{S}$. Then,

$$\begin{array}{ccc}\hfill \overline{\widehat{\Theta }}(\xi )& =& \{(\iota ,0.6,-0.5),(\kappa ,0.4,-0.2),(\nu ,0.6,-0.5)\},\hfill \\ \hfill \underline{\widehat{\Theta }}(\xi )& =& \{(\iota ,0.2,-0.2),(\kappa ,0.4,-0.4),(\nu ,0.2,-0.2)\}.\hfill \end{array}$$

It can be seen by simple calculations that $\overline{\widehat{\Theta }}(\xi )$ is also a BF bi-ideal, whereas $\underline{\widehat{\Theta }}(\xi )$ is not, as

$$\underline{\widehat{\Theta }}({\xi }^p)(\kappa \iota \kappa )=0.2\ngeqq 0.4=\underline{\widehat{\Theta }}({\xi }^p)(\kappa )\wedge \underline{\widehat{\Theta }}({\xi }^p)(\kappa ).$$

Definition 8.

For a CR $\widehat{\Theta }$ on $\mathfrak{S}$ and $\xi \in BF(\mathfrak{S})$, ξ is a lower (resp. upper) RBF interior ideal of $\mathfrak{S}$ if $\underline{\widehat{\Theta }}(\xi )(\overline{\widehat{\Theta }}(\xi ))$ is a BF interior ideal of $\mathfrak{S}$.

If ξ is both a lower and upper RBF interior ideal, then it is called an RBF interior ideal of $\mathfrak{S}$.

Theorem 11.

For a CR $\widehat{\Theta }$ on $\mathfrak{S}$, each BF interior ideal, $\xi =(\mathfrak{S};{\xi }^p,{\xi }^n)$ is an upper RBF interior ideal of $\mathfrak{S}$.

Proof. 

Since a BF interior ideal $\xi$ is also a BF subsemiring of $\mathfrak{S}$, by Theorem 5, $\overline{\widehat{\Theta }}(\xi )$ is a BF subsemiring of $\mathfrak{S}$. Now, for all $u,x,z\in \mathfrak{S}$,

$$\begin{array}{ccc}\hfill \overline{\widehat{\Theta }}{\xi }^p(uxz)& =& \underset{s\in {\left[uxz\right]}_{\widehat{\Theta }}}{\bigvee }{\xi }^p(s)\hfill \\ & \ge & \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }}\subseteq {\left[uxz\right]}_{\widehat{\Theta }}\hfill \\ & =& \underset{bcd\in ({\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigvee }{\xi }^p(bcd)\hfill \\ & \ge & \underset{c\in {\left[x\right]}_{\widehat{\Theta }}}{\bigvee }({\xi }^p(c))\hfill \\ & =& \overline{\widehat{\Theta }}{\xi }^p(x).\hfill \end{array}$$

Similarly, $\overline{\widehat{\Theta }}{\xi }^n(uxz)\le \overline{\widehat{\Theta }}{\xi }^n(x).$ This implies $\overline{\widehat{\Theta }}(\xi )$ is a BF interior ideal of $\mathfrak{S}$. Therefore, $\xi$ is an upper RBF interior ideal of $\mathfrak{S}$. □

Theorem 12.

Consider a CCR $\widehat{\Theta }$ on $\mathfrak{S}$. Then, each BF interior ideal $\xi =(\mathfrak{S};{\xi }^p,{\xi }^n)$ is a lower RBF interior ideal of $\mathfrak{S}$.

Proof. 

We have by Theorem 6 that $\underline{\widehat{\Theta }}(\xi )$ is a BF subsemiring of $\mathfrak{S}$. Consider, for every $u,x,z\in \mathfrak{S}$,

$$\begin{array}{ccc}\hfill \underline{\widehat{\Theta }}{\xi }^p(uxz)& =& \underset{s\in {\left[uxz\right]}_{\widehat{\Theta }}}{\bigwedge }{\xi }^p(s)\hfill \\ & =& \underset{s\in ({\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(s),\sin \mathrm{ce}{\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }}={\left[uxz\right]}_{\widehat{\Theta }}\hfill \\ & =& \underset{bcd\in ({\left[u\right]}_{\widehat{\Theta }}{\left[x\right]}_{\widehat{\Theta }}{\left[z\right]}_{\widehat{\Theta }})}{\bigwedge }{\xi }^p(bcd)\hfill \\ & \ge & \underset{c\in {\left[x\right]}_{\widehat{\Theta }}}{\bigwedge }({\xi }^p(c))\hfill \\ & =& \underline{\widehat{\Theta }}{\xi }^p(x).\hfill \end{array}$$

Similarly, $\underline{\widehat{\Theta }}{\xi }^n(uxz)\le \underline{\widehat{\Theta }}{\xi }^n(x).$ Thus, $\underline{\widehat{\Theta }}(\xi )$ is a BF interior ideal of $\mathfrak{S}$. Therefore, $\xi$ is a lower RBF interior ideal of $\mathfrak{S}$. □

The example defined below illustrates that Theorem 12 does not hold if the CR $\widehat{\Theta }$ is not complete.

Example 4.

Let $\mathfrak{S}=\{\iota ,\kappa ,\nu \}$ be the semiring and $\widehat{\Theta }$ be the CR on $\mathfrak{S}$, as defined in Example$2$, which is not complete, and define the congruence classes $\{\kappa \}and\{\iota ,\nu \}$.

We take a BF subset $\xi$ of $\mathfrak{S}$, as below.

$$\xi =\{(\iota ,0.6,-0.6),(\kappa ,0.5,-0.2),(\nu ,0.1,-0.5)\}.$$

Thus, $\xi$ is a BF interior ideal of $\mathfrak{S}$. Now,

$$\begin{array}{ccc}\hfill \overline{\widehat{\Theta }}(\xi )& =& \{(\iota ,0.6,-0.6),(\kappa ,0.5,-0.2),(\nu ,0.6,-0.6)\},\hfill \\ \hfill \underline{\widehat{\Theta }}(\xi )& =& \{(\iota ,0.1,-0.5),(\kappa ,0.5,-0.2),(\nu ,0.1,-0.5)\}.\hfill \end{array}$$

It can be seen by simple calculations that $\overline{\widehat{\Theta }}(\xi )$ is also a BF interior ideal of $\mathfrak{S}$, whereas $\underline{\widehat{\Theta }}(\xi )$ is not, because

$$\underline{\widehat{\Theta }}({\xi }^p)(\iota \kappa \nu )=0.1\ngeqq 0.5=\underline{\widehat{\Theta }}({\xi }^p)(\kappa ).$$

4. Comparative Study and Discussion

In this section, a connection between this paper and previous papers [29,32] is described. In [32], Ali et al. conducted work on approximations of hemirings (semirings with additive identity), and in [29], Shabir et al. characterized BF ideals and BF bi-ideals in semirings. In this paper, we give a new model of approximations of BF subsemirings (resp. ideals, bi-ideals and interior ideals). Our approach is better than previous approaches because this tackles the vague and complicated problems in both positive and negative aspects. Approximation of BF sets has not been commonly used in semirings so far, to our knowledge. Therefore, consideration of a new framework of approximation of BF subsemirings (resp. ideals) is reasonable and necessary.

5. Conclusions

In this paper, concepts from [29,32] are combined. The CRs and CCRs are used to evaluate rough approximations. These relations help us in a fruitful way to consider roughness in BF ideals of semirings. However, it is probably visible that during the case of lower approximation, the CR fails to obtain the favored result. To tackle this complication, CCRs are being taken into consideration. Furthermore, the idea of approximations is applied to BF subsemirings, BF bi-ideals and BF interior ideals by using CRs and CCRs in semirings.

In the future, we will study the roughness of BF ideals of ternary semigroups and ternary semirings. We will also give attention to the roughness of multipolar fuzzy ideals and multipolar fuzzy hyperideals of semihypergroups.