Homogeneous Banach Spaces as Banach Convolution Modules over M(G)

Abstract

This paper is supposed to form a keystone towards a new and alternative approach to Fourier analysis over LCA (locally compact Abelian) groups G. In an earlier paper the author has already shown that one can introduce convolution and the Fourier–Stieltjes transform on $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$, the space of bounded measures (viewed as a space of linear functionals) in an elementary fashion over ${\mathbb{R}}^d$. Bounded uniform partitions of unity (BUPUs) are easily constructed in the Euclidean setting (by dilation). Moving on to general LCA groups, it becomes an interesting challenge to find ways to construct arbitrary fine BUPUs, ideally without the use of structure theory, the existence of a Haar measure and even Lebesgue integration. This article provides such a construction and demonstrates how it can be used in order to show that any so-called homogeneous Banach space $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$ on G, such as $({\mathit{L}}^p\left(G\right),{\parallel ·\parallel }_p)$, for $1\le p<\infty$, or the Fourier–Stieltjes algebra $\mathcal{F}\mathit{M}\left(G\right)$, and in particular any Segal algebra is a Banach convolution module over $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$ in a natural way. Via the Haar measure we can then identify $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ with the closure (of the embedded version) of ${\mathit{C}}_c\left(G\right)$, the space of continuous functions with compact support, in $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$, and show that these homogeneous Banach spaces are essential ${\mathit{L}}^1\left(G\right)$-modules. Thus, in particular, the approximate units act properly as one might expect and converge strongly to the identity operator. The approach is in the spirit of Hans Reiter, avoiding the use of structure theory for LCA groups and the usual techniques of vector-valued integration via duality. The ultimate (still distant) goal of this approach is to provide a new and elementary approach towards the (extended) Fourier transform in the setting of the so-called Banach–Gelfand triple $({\mathit{S}}_0,{\mathit{L}}^2,{\mathit{S}}_0^{\prime })\left(G\right)$, based on the Segal algebra ${\mathit{S}}_0\left(G\right)$. This direction will be pursued in subsequent papers.

1. Introduction

Let us begin with the observation that the usual approach to harmonic analysis over locally compact Abelian (LCA) groups G (see for example [1,2,3,4]) starts with a description of the Lebesgue space $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$, which turns out to be a Banach algebra with respect to convolution. Based on the description of the Fourier transform as an integral transform, the traditional approach continues with the demonstration of the fact that the Fourier transform turns convolution into pointwise multiplication (the so-called convolution theorem). This result describes one of the crucial properties of the Fourier transform, and Lebesgue space appears to be a very natural and the best possible domain, because it allows one to describe the convolution product of two functions (more precisely of equivalence classes of measurable functions) in the pointwise sense (almost everywhere), combined with the corresponding norm estimate

$${\parallel f\ast g\parallel }_{{\mathit{L}}^1}\le {\parallel f\parallel }_{{\mathit{L}}^1}{\parallel g\parallel }_{{\mathit{L}}^1},f,g\in {\mathit{L}}^1\left(G\right).$$

It is also plausible that $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ is considered the natural domain for the Fourier transform, because for any character $\chi \in \widehat{G}$ the integral

$$\widehat{f}\left(\chi \right)={\int }_{G}f\left(x\right)\overline{\chi \left(x\right)}dx$$

(1)

exists in the Lebesgue sense (for one and then for any $\chi \in \widehat{G}$) if and only if $f\in {\mathit{L}}^1\left(G\right)$. In a similar way, it appears as a natural restriction to assume that $\widehat{f}$ belongs to ${\mathit{L}}^1(\widehat{G})$ if one wants to obtain $f\left(x\right)$ back (again via the usual integral formula describing the inverse Fourier transform) from $\widehat{f}$. The range of the Fourier transform is denoted by $\left(\mathcal{F}{\mathit{L}}^1\left({\mathbb{R}}^d\right),{\parallel ·\parallel }_{\mathcal{F}{\mathit{L}}^1}\right)$. It is a Banach algebra with respect to pointwise multiplication, hence called the Fourier algebra, with respect to the norm $\parallel \widehat{f}{\parallel }_{\mathcal{F}{\mathit{L}}^1}:={\parallel f\parallel }_{{\mathit{L}}^1}$.

Although technically demanding, this approach based on measure theory allows one to formulate and answer interesting mathematical questions (e.g., about the almost-everywhere convergence of Fourier series), but it does not reveal the relevance of convolution for applications. The situation is different when moving on to tempered distributions, which have become the key tool for the treatment of PDEs. However, in order to make use of these tools it is necessary to first study to some extent the Schwartz space $\mathcal{S}\left({\mathbb{R}}^d\right)$, a nuclear Fréchet space with a countable system of seminorms involving differentiation. For general LCA groups one can define the Schwartz–Bruhat space via structure theory, but it is even more complicated and very difficult to use.

Recalling the fact that engineers learn about the concept of convolution in their introductory courses on translation-invariant linear systems (TILS), this author has so far developed an approach to convolution (for bounded measures) which is based on the isometric one-to-one correspondence between linear functionals on $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$ (we call them bounded measures and use the symbol $(\mathit{M}\left(G\right),\parallel \hspace{0.17em}·\hspace{0.17em}{\parallel }_{\mathit{M}})$) and bounded linear operators commuting with translations. Obviously, the space $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$ of continuous, complex-valued functions vanishing at infinity forms a Banach space (even a pointwise algebra) if endowed with the sup-norm, and ${\mathit{C}}_c\left(G\right)$ (compactly supported functions) are dense in $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$. It is also invariant under translations, defined as usual by

$$\left[T_{z}f\right]\left(y\right)=f(y-z),y,z\in G.$$

(2)

Any such TILS can be identified with a moving average resp. a convolution operator by a uniquely determined bounded measure $\mu \in (\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})=({\mathit{C}}_0^{\prime }\left(G\right),{\parallel ·\parallel }_{{\mathit{C}}_0^{\prime }})$. This isometric identification allows us to transfer the composition structure of linear operators to the corresponding bounded measures, and call it convolution. Of course, this viewpoint is compatible with the usual approach (see [2], p.46). It turns out that it is the unique $w^{\ast }$—continuous extension of the identification of translation operators $T_x$ with the corresponding Dirac measures ${\delta }_x\in \mathit{M}\left(G\right)$. In this way $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$ is a Banach module over $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$ with respect to convolution. Details are given in [5] (and in the Lecture Notes for the ETH course, see www.nuhag.eu/ETH20, accessed on 3 January 2021).

The realization of this correspondence makes use of so-called BUPUs, i.e., bounded uniform partitions of unity. They allow one to decompose every $\mu \in \mathit{M}\left(G\right)$ into an absolutely convergent sum of well-localized measures, which, among other approaches, allows the extension of the action of $\mu \in {\mathit{C}}_0^{\prime }\left(G\right)$ to all of ${\mathit{C}}_b\left(G\right)$, the continuous, bounded functions on G (also endowed with the sup-norm). In this way it is possible to define the Fourier–Stieltjes transform of bounded measures and derive the convolution theorem before even discussing the existence of a Haar measure or the necessary Lebesgue integration theory required in order to study everything in the ${\mathit{L}}^1$-context.

The goal of the present manuscript is to provide an important step towards a description of the (generalized) Fourier transform over LCA groups along the lines of the approach described above. This author is convinced that the appropriate setting is that of the Banach–Gelfand triple $({\mathit{S}}_0,{\mathit{L}}^2,{\mathit{S}}_0^{\prime })\left(G\right)$, consisting of the Segal algebra ${\mathit{S}}_0\left(G\right)$, which can be defined on arbitrary LCA groups, its dual space ${\mathit{S}}_0^{\prime }\left(G\right)$, the space of so-called mild distributions, and in the middle the Hilbert space ${\mathit{L}}^2\left(G\right)$ (defined as the completion of ${\mathit{S}}_0\left(G\right)$ with respect to the usual scalar product).

Although such an approach can be realized easily in the context of $G={\mathbb{R}}^d$, the Euclidean setting, making use of the special ingredients available in this context, notably the existence of a Fourier-invariant Gaussian function and dilation operators, which among other uses, allow one to create arbitrary fine BUPUs in a natural fashion, it is not so obvious whether and how one can obtain such BUPUs in the context of an abstract LCA group. Moreover, many important convolution relations make use of the fact that convolution operators induced by bounded measures act also boundedly on a large variety of Banach spaces of functions over the group G, e.g., on the usual spaces $({\mathit{L}}^p\left(G\right),{\parallel ·\parallel }_p)$, or the Fourier algebra $\mathcal{F}{\mathit{L}}^1\left(G\right)$ and (hence) on $\left({\mathit{S}}_0\left(G\right),{\parallel ·\parallel }_{{\mathit{S}}_0}\right)$. We will provide a relatively simple construction of such arbitrary fine BUPUs, avoiding the use of structure theory of LCA groups, and derive similar results making use of these BUPUs.

The natural setting for the realization of such a general statement is the setting of homogeneous Banach spaces (HBS) (in the sense of Y. Katznelson), which are isometrically translation invariant by assumption. The family of Segal algebras (in the sense of H. Reiter) is an interesting subfamily of this class of Banach spaces of locally integrable functions over G. The second main result of this paper will deal with such Banach spaces and will demonstrate that any such HBS $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$ is actually a Banach module over $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$ (hence over $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$) with respect to convolution.

The paper is organized in the following way. First we discuss several variations of the concept of a bounded uniform partition of unity (BUPU) in Section 2, and explain their mutual relationship. We also provide a few historical comments on their use in the literature.

In Section 3 the existence of arbitrary fine BUPUs is established as our first main result. Instead of the Haar measure, we use a kind of coarse measurement of the size of sets, called a capacity (with respect to a sufficiently small reference set). This provides the basis for our key results, without making use of the structure theory for LCA groups. Subsequently it is shown in Section 4 how to make use of such BUPUs. In Section 5 we also discuss various characterizations of the Wiener algebra $\mathit{W}=\mathit{W}({\mathit{C}}_0,{\ell }^1)\left(G\right)$ and its dual via BUPUs.

In Section 6 our second main result is shown: any homogeneous Banach space (in the sense of Y. Katznelson) is a Banach module over $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$ with respect to convolution. In fact, we formulate an even more general abstract approach based on isometric, strongly continuous representations of the group G on an arbitrary Banach space $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$. This approach is based on the methods developed in [5] and makes use of a constructive way of approximating bounded measures by discrete measures in the $w^{\ast }-$ sense. The technical realization of this second main result is based on the completeness of Banach spaces, which also implies that (bounded) Cauchy nets are actually convergent in any Banach space. The necessary background is described in Section 7. This approach also permits us to demonstrate that the $w^{\ast }$—convergence of bounded and tight nets leads to strong operator convergence of the corresponding convolution operators (Theorem 5).

Only then is the existence of the Haar measure invoked in order to define $\left({\mathit{L}}^1\left(G\right),{\parallel \hspace{0.17em}·\hspace{0.17em}\parallel }_1\right)$ as a subspace of $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$, namely, as a closure of ${\mathit{C}}_c\left(G\right)$. In this sense, Section 6 characterizes the usual integrated group representation as the restriction of the established module structure over $\mathit{M}\left(G\right)$. In particular it is shown that any homogeneous Banach space is also an essential Banach module over $\left({\mathit{L}}^1\left(G\right),{\parallel \hspace{0.17em}·\hspace{0.17em}\parallel }_1\right)$.

2. Different Types of Uniform Partitions

It is the purpose of this section to compare various notions of uniform partitions of unity in the context of harmonic analysis over LCA groups. It is easy to construct arbitrary fine BUPUs of a given degree of smoothness on $\mathbb{R}$ merely by applying appropriate dilations to the basis of B-splines of sufficiently high order (or even infinitely differentiable) which are obtained as translations along the integer lattice $\mathbb{Z}$ of the convolution powers of the indicator function ${\mathbf{1}}_{[-1/2,1/2]}$. For B-splines of order 3 (four-fold convolution power) one obtains a Riesz basis for the cubic spline function in $\left({\mathit{L}}^2\left(\mathbb{R}\right),{\parallel \hspace{0.17em}·\hspace{0.17em}\parallel }_2\right)$. Via tensor products, the same can be achieved on ${\mathbb{R}}^d$ for $d\ge 2$.

In contrast, it is not at all clear how to provide similar families of functions in a situation where there is a lack of fine lattices (and corresponding fundamental domains) and without having an appropriate automorphism group on the underlying group (replacing dilations).

It is our main goal in this section to demonstrate that the existence of such BUPUs (using a suitable version of the BUPU concept) can be guaranteed, using relatively elementary arguments. Thus, we will not rely on the existence of a Haar measure on such a group G, although that would make the proof a little bit shorter.

The notion of uniform partitions of unity appears in different papers, which are usually similar in spirit and which mostly refer to the uniform size of the constituents of the partition of unity. In order to compare the different possible concepts, let us recall the corresponding definitions. The concept of choice for this article is that of BUPUs as introduced in [6] (i.e., Definition 2 below). It has been used regularly since then (e.g., in [7], Section 3.2.2 and in many other papers by the author).

The following situation will be the most simple and still the most useful for our purpose. It is a simplification of the concept of BUPUs as introduced in [6] (given below). Since it is natural to formulate these results in the context of locally compact groups G, we formulate the next definition by writing the group operation in a multiplicative way.

Definition 1.

Given some neighborhood $U\in \mathcal{U}\left(e\right)$ of the identity of a locally compact group G, a non-negative U-BUPU, a so-called (left) bounded uniform partition of unity of size U is a family $\mathsf{\Psi }={\left({\psi }_i\right)}_{i\in I}$ of continuous, non-negative functions on G satisfying the following conditions (we write the group law multiplicatively here):

1. 

For some family ${\left(x_i\right)}_{i\in I}$ in G one has: $supp\left({\psi }_i\right)\subseteq x_{i}U$ for all $i\in I$;

2. 

The family ${\left(x_{i}U\right)}_{i\in I}$ satisfies the bounded overlap property (BOP); the number of intersecting neighbors is uniformly bounded (with respect to $i\in I$):

$$\underset{i\in I}{sup}\#\{j|x_{i}U\cap x_{j}U\ne \varnothing \}\le B_0<\infty ;$$

3. 

${\sum }_{i\in I}{\psi }_i\left(x\right)\equiv 1$ on G.

Remark 1. 

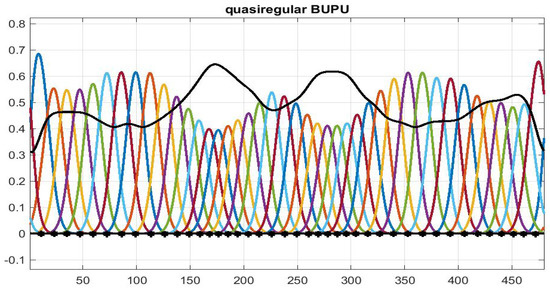
The continuity of the constituents ${\psi }_i$ of the BUPU requires some overlap of their supports, which is illustrated in Figure 1. On the other hand, we can apply bounded measures (i.e., linear functionals on $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$) only on continuous functions with compact support, and not on the indicator functions of compact sets. Although one might think of a fine partition of the group (e.g., translates of a fundamental domain), we do not want to make use of this more measure-theoretic setting.

Remark 2. 

Observe that the bounded overlap property implies that the sum in (3) is a finite sum (with at most $B_0$ non-zero terms for each $x\in G$). We call $B_0$ the “overlap bound” of the family $\left(x_{i}U\right)$.

The non-negativity of the functions ${\psi }_i$ implies by (3) that ${sup}_{i\in I}{\parallel {\psi }_i\parallel }_{\infty }\le 1$, i.e., the family Ψ is bounded in $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$ (the space of continuous complex-valued functions vanishing at infinity, endowed with the sup-norm).

For the characterization of general Wiener amalgam spaces of the form $\mathit{W}(\mathit{B},{\ell }^q)$, for example, (with a local component $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$, which are more general than being just another ${\mathit{L}}^p$-space, but something like ${(\mathit{B},\parallel ·\hspace{0.17em}\parallel }_{\mathit{B}})=\left(\mathcal{F}{\mathit{L}}^1\left({\mathbb{R}}^d\right),{\parallel \hspace{0.17em}·\hspace{0.17em}\parallel }_{\mathcal{F}{\mathit{L}}^1}\right)$ or $\mathcal{F}{\mathit{L}}^p$), it is important to assume the boundedness of the family $\mathsf{\Psi }$ in some Banach algebra (with respect to pointwise multiplication), contained in the multiplier algebra of $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$. We assume in that case that ${(\mathit{A},\parallel ·\hspace{0.17em}\parallel }_{\mathit{A}})\hookrightarrow \left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$ (continuous embedding). On the other hand, non-negativity is not required in this case. The subsequent definition of BUPUs goes back to [6].

Definition 2.

Given $U\in \mathcal{U}\left(e\right)$, a family $\mathsf{\Psi }={\left({\psi }_i\right)}_{i\in I}$ is a BUPU, a bounded uniform partition of unity (of size U) in the Banach algebra $(\mathit{A},\parallel ·{\parallel }_{\mathit{A}})$ if one has:

1. 

There exists a family ${\left(x_i\right)}_{i\in I}$ in G such that $supp\left({\psi }_i\right)\subseteq x_{i}U$ for all $i\in I$;

2. 

The family Ψ is bounded in $(\mathit{A},\parallel ·{\parallel }_{\mathit{A}})$, i.e., $su{p}_{i\in I}{\parallel {\psi }_i\parallel }_{\mathit{A}}\le C_{\mathsf{\Psi }}<\infty$;

3. 

There exists $B_0>0$ such that $\#\{j|x_{i}U\cap x_{j}U\ne \varnothing \}\le B_0;$

4. 

${\sum }_{i\in I}{\psi }_i\left(x\right)\equiv 1$ on G.

The constant $C_{\mathsf{\Psi }}=C(\mathsf{\Psi },\mathit{A})$ is called the norm of the family $\mathsf{\Psi }$ in $(\mathit{A},\parallel \hspace{0.17em}·\hspace{0.17em}{\parallel }_{\mathit{A}})$, and $B_0$ is the overlapping constant of the family. The family $X={\left(x_i\right)}_{i\in I}$ is called the family of centers of the BUPU $\mathsf{\Psi }={\left({\psi }_i\right)}_{i\in I}$.

For the case of a metric group G we can use balls of radius $\delta >0$ as a basis of neighborhoods and thus it is natural to write $\left|\mathsf{\Psi }\right|\le \delta$ if one has $supp\left({\psi }_i\right)\subseteq B_{\delta }\left(x_i\right)$ for $i\in I$. In this case we call $\mathsf{\Psi }$ a $\delta -BUPU$, or a BUPU of size $\delta$.

Remark3. 

The usefulness of BUPUs with different specific properties arises in various contexts. Let us mention only a few of them here.

Sometimes it is enough to have some BUPUs, which may be bounded in a suitable Banach algebra $(\mathit{A},\parallel ·{\parallel }_{\mathit{A}})$, e.g., for the construction of Wiener amalgam spaces, such as $(\mathit{W}(\mathcal{F}{\mathit{L}}^1,{\ell }^1)\left({\mathbb{R}}^d\right),\parallel ·{\parallel }_{\mathit{W}(\mathcal{F}{\mathit{L}}^1,{\ell }^1)})$. In fact, for such spaces one can show that different BUPUs define the same Wiener amalgam spaces with equivalent norms. However, BUPUs are not only helpful in defining new function spaces, they also play an important role in the alternative approach to convolution for the measure algebra $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$, as presented in [5]. The decomposition of $\mu \in \mathit{M}\left(G\right)$ as an absolutely convergent sum of measures with small support allows us to take a crucial step in the isometric isomorphism between $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$ and the Banach algebra (under composition) of bounded linear operators on $\left({\mathit{C}}_0\left(G\right),{\parallel \hspace{0.17em}·\hspace{0.17em}\parallel }_{\infty }\right)$ which commute with translation, the so-called TILS (translation-invariant linear systems, as they are called in engineering books).

For the work on coorbit theory developed jointly with K. Gröchenig, as well as the closely related work on irregular sampling, it is important to be able to have BUPUs which are centered at a given $\delta$—dense subset of ${\mathbb{R}}^d$ (or a LCA group); see [8] or [9]; see also [10,11,12].

For the current paper the existence of arbitrary fine BUPUs over general LC groups will be crucial. Currently it is not clear whether one can find UPUs (in the sense of [13]) of size U (meaning with $supp\left(\phi \right)\subseteq U$, for a given neighborhood of the identity) in the case of general groups. Fortunately, the concept of BUPUs is more flexible, and it will be the first main result of this paper to demonstrate that one can derive the existence of arbitrary fine non-negative BUPUs over any given locally compact group G using elementary considerations (reminding perhaps some readers of the construction of a Haar measure on G, see [14]).

For most applications, so-called regular BUPUs will be sufficient (and in fact easier to handle), and these are obtained as translates of a (smooth) function with compact support along some lattice $\mathsf{\Lambda }⊲G$. Especially over $G={\mathbb{R}}^d$ it would be natural to make use of smooth BUPUs with respect to some lattice of the form $\mathsf{\Lambda }=\mathit{A}{\mathbb{Z}}^d$, for some non-singular $d\times d$ matrix $\mathit{A}$. Note that in the Euclidean case (or, for example, also for stratified Lie groups) one can obtain “arbitrary fine BUPUs” by applying a simple dilation (or rather compression) routine to a given BUPU. If one only needs some BUPU over ${\mathbb{R}}^d$ it is quite natural to obtain BUPUs as translates of a single function:

Definition 3.

A family $\mathsf{\Psi }={\left({\psi }_{\lambda }\right)}_{\lambda \in \mathsf{\Lambda }}={\left(T_{\lambda }{\psi }_0\right)}_{\lambda \in \mathsf{\Lambda }}$ is called a regular (smooth) uniform partition of unity on ${\mathbb{R}}^d$ in $\left(\mathcal{F}{\mathit{L}}^1\left({\mathbb{R}}^d\right),{\parallel ·\parallel }_{\mathcal{F}{\mathit{L}}^1}\right)$ if it satisfies:

1. 

${\psi }_0$ is compactly supported and ${\widehat{\psi }}_0\in {\mathit{L}}^1\left({\mathbb{R}}^d\right)$, (resp. ${\psi }_0\in D\left({\mathbb{R}}^d\right)$);

2. 

${\sum }_{\lambda \in \mathsf{\Lambda }}{\psi }_{\lambda }\left(x\right)={\sum }_{\lambda \in \mathsf{\Lambda }}{\psi }_O(x-\lambda )\equiv 1$ on ${\mathbb{R}}^d$.

Note that the finite overlap condition of support easily follows from the properties of a lattice, and that furthermore the boundedness of the family $\mathsf{\Psi }$ is an easy consequence of the isometric translation invariance of the algebra $(\mathit{A},\parallel ·{\parallel }_{\mathit{A}})$ under consideration (here $\left(\mathcal{F}{\mathit{L}}^1\left({\mathbb{R}}^d\right),{\parallel \hspace{0.17em}·\hspace{0.17em}\parallel }_{\mathcal{F}{\mathit{L}}^1}\right)$).

Historical note: BUPUs were introduced (although not first used) by this name by the author in [6] for the “discrete” characterization of Wiener amalgam spaces.

A slightly different approach has been taken in [13], based on earlier work of [15].

Definition 4.

Let G be a locally compact group. A family Ψ in ${\mathit{C}}_c\left(G\right)$ is called a UPU (a uniform partition of unity) if there exists some function $\phi \in {\mathit{C}}_c\left(G\right)$ (i.e., continuous and compactly supported, perhaps satisfying some smoothness conditions) such that, for a suitable family ${\left(y_i\right)}_{i\in I}$ in G one has

$$\sum _{i\in I}{T}_{y_i}\phi \left(x\right)=\sum _{i\in I}\phi \left(y_i^{-1}x\right)\equiv 1onG.$$

(3)

Although formally there is no BOP property required in this case it is shown in [13] that the family of shift parameters ${\left(y_i\right)}_{i\in I}$ is relatively separated, or equivalently, that such an UPU is in fact a BUPU of size $supp\left(\phi \right)$.

We can give the following characterization of relatively separated families ${\left(x_i\right)}_{i\in I}$ as they appear in the above definitions. For details see e.g., Theorem 22 in [12].

Lemma 1.

For a discrete family ${\left(x_i\right)}_{i\in I}$ in G the following properties are equivalent:

1. 

The family is relatively separated, i.e., a finite union of separated sets, i.e., of subfamilies ${\left(x_j\right)}_{j\in J}$ with the property that $x_{j}V\cap x_{l}V=\varnothing$ for $j\ne l\in J$, for some open set V in G;

2. 

For any relatively compact set W the family ${\left(x_{i}W\right)}_{i\in I}$ has the uniformly controlled neighbors property;

3. 

For any compact set $Q\subset G$ the number of points in $zQ$ is controlled as follows:

$$\underset{z\in G}{sup}\#\{i|x_i\in zQ\}=B\left(Q\right)<\infty .$$

Remark 4. 

The latter property can be equivalently described as the property that the (irregular) Dirac comb ${\bigsqcup \bigsqcup }_X:={\sum }_{i\in I}{\delta }_{x_i}$ belongs to the Wiener amalgam space $\mathit{W}(\mathit{M},{\ell }^{\infty })$, which is the dual of the Wiener algebra $\left(\mathit{W}({\mathit{C}}_0,{\ell }^1)\left(G\right),{\parallel ·\parallel }_{\mathit{W}}\right)$. We will not pursue this connection any further as it might confuse readers who are not familiar with the theory of Wiener amalgam spaces.

Let us next recall that the main result of [13] describes (making use of the structure theory of locally compact groups) the existence of UPUs for arbitrary LC groups G. However, it is not claimed that one can find arbitrary fine UPUs in that paper. Still, for further reference, let us formulate their main result as follows:

Proposition 1

(Leptin/Müller). For any locally compact group G there exist UPUs.

Remark 5. 

Using a simple compactness argument one can even rewrite the function φ as a finite sum $\phi ={\sum }_{k=1}^K{\phi }_k$ of functions with arbitrary small support and thus derive the existence of BUPUs by translating each of them using the same family of shift-parameters $\left(y_j\right)$. However, the disadvantage (from our perspective) of this approach is the fact that it is heavily based on structure theory.

Remark 6. 

Note that of course one even can obtain a situation where the indicator function of a relatively compact set covers the group by translates along a discrete family ${\left(y_j\right)}_{j\in J}$, without having any group structure, i.e., not using a lattice (discrete subgroup) as the parameter set of the shift operators. Such a situation is known from wavelet theory, where one obtains such coverings on the “$ax+b$”-group. Although the translation parameters (taken from $\mathbb{Z}$) and the dilation parameters of the form $2^k,k\in \mathbb{Z}$ form discrete subgroups of Abelian subgroups; the combined “geometric lattice” is not a discrete subgroup of the affine group.

Historical Notes

There are several situations in which BUPUs have played an important role in the past. The first of these was the paper which introduced the general Wiener amalgams (originally called Wiener-type spaces) [6].

Of course, various forms of smooth BUPUs, such as B-spline systems had already been used early on, e.g., in the theory of numerical integration. In fact, any BUPU allows one to define a so-called quasi-interpolation operator of the form ${Sp}_{\mathsf{\Psi }}f\left(x\right):={\sum }_{i\in I}f\left(x_i\right){\psi }_i$. Sometimes (e.g., for the BUPU obtained by B-splines of order one, which are triangular functions), these operators interpolate the function f at the node points, but in most other cases they just approximate a given smooth function. Integration formulas thus allow us to calculate the integral of ${Sp}_{\mathsf{\Psi }}$ in a closed form, based on the knowledge of the sampling values $\left(f\left(x_i\right)\right)$ only.

BUPUs over LC groups play a prominent role in the development of coorbit theory, which was put in place by the author together with K. Gröchenig (see [16]).

At the heart of coorbit theory are reconstruction methods which allow us to reconstruct an abstract wavelet transform $V_{g}f$ defined over a locally compact group G (such as the Heisenberg group, the “$ax+b$”-group, or the shearlet group, to mention concrete examples) from samples, taken over a sufficiently dense, discrete family ${\left(x_i\right)}_{i\in I}$ in G. The first step here is to establish a quasi-interpolation for $V_{g}f$, using the given sampling values only. However, one then observes that the resulting function may not belong to the range of the transform $f\mapsto V_{g}f$, and thus one has to project back to the range, which can be realized by means of a convolution with $V_{g}g$. The details are found in [8] and related papers. Of course, one has to estimate the guaranteed approximation quality for this kind of approximation, in order to have a basis for an iterative method of reconstruction (at a geometric rate).

The intuitive similarity of the properties of those wavelet transforms $V_{g}f$ with band-limited functions of two variables (as well as the existence of a reproducing convolution relation in both cases) then inspired the authors to deal with the “irregular sampling problem”, i.e., the problem of reconstructing a band-limited function from irregular samples. Recall that the regular case, i.e., the reconstruction of a band-limited function in ${\mathit{L}}^2\left({\mathbb{R}}^d\right)$ (with compact support $supp(\widehat{f})\subseteq B_R\left(0\right)$) from samples along some lattice $\mathsf{\Lambda }$ can be guaranteed if the lattice $\mathsf{\Lambda }$ is fine enough, essentially making use of Poisson’s formula. In the irregular case the first generation of iterative algorithms was based on the use of BUPUs, which are fine enough and are centered at the given sampling points (see [10,12]).

3. Arbitrary Fine BUPUs over LC Groups

In this section we establish our first main result, in the context of general locally compact groups. Since this includes many non-commutative groups, we choose the usual multiplicative notation for the group law.

Definition 5.

For any fixed and relatively compact subset $S\subset G$ the mapping $M\mapsto {cap}_S\left(M\right)$ is defined on the collection of (relatively) compact sets M according to the following rule

$${cap}_S\left(M\right):=min\{\#F|M\subseteq \bigcup _{i\in F}{x}_{i}S\}$$

(4)

where the minimum is taken over all finite subsets of possible translation parameters.

Note that, based on the fact that the interior of S is non-empty and M is supposed to be compact, the minimum is taken over a non-empty subset of $\mathbb{N}$.

Remark 7. 

The term “capacity” originates from a similar construction, where one measures the size of an indicator function by minimizing over all the (typically non-negative) functions in a given function’s spaces, typically a Sobolev space ${\mathcal{H}}_s\left({\mathbb{R}}^d\right)$, which dominate the indicator function ${\mathbf{1}}_M$ of the set M.

Such an interpretation is in fact also possible here: Given a set S, ${cap}_S\left(M\right)$ can be interpreted as the infimum over all norms in $\mathit{W}({\mathit{L}}^{\infty },{\ell }^1)\left(G\right)$ of functions, dominating the indicator function ${\mathbf{1}}_M$. We leave it to the interested reader to check the details.

Lemma 2.

For any fixed and relatively compact subset $S\subset G$ the mapping $M\mapsto {cap}_S\left(M\right)$, defined on the collection of compact sets M, has the following properties:

1. 

${cap}_S\left(S\right)=1$

2. 

${cap}_S\left(zM\right)={cap}_S\left(M\right),\forall z\in G$

3. 

The mapping $M\mapsto {cap}_S\left(M\right)$ is subadditive in the sense that we have for finite unions of compact sets:

$${cap}_S\left(\bigcup _{k=1}^K{M}_k\right)\le \sum _{k=1}^K{cap}_S\left(M_k\right)$$

4. 

Given any finite collection of compact sets $M_k,k=1,...,K$ which are S-separated, i.e., satisfying the condition that $M_{k}S\cap M_{j}S=\varnothing$ for $k\ne j$, one has

$${cap}_S\left(\bigcup _{k=1}^K{M}_k\right)=\sum _{k=1}^K{cap}_S\left(M_k\right).$$

Proof. 

Claim (1) is obvious, and the translation invariance (2) follows from

$$M\subseteq \bigcup _{i\in F}{x}_{i}S\iff zM\subseteq \bigcup _{i\in F}\left(z{x}_i\right)S,\forall z\in G.$$

Thus, any covering of M has a corresponding covering of equal cardinality for $zM$.

The subadditivity property (3) is easy to check, since the combination of all the translates needed to cover all the sets $M_i,i\in F$, obviously constitutes a covering of their union.

Finally, we check for the additivity property (4). Given a minimal covering of ${\bigcup }_{k=1}^K{M}_k$, using a set of translates of the form $y_{i}S,i=1,\dots L$, we argue that each of the translates will be relevant for exactly one of the constituting sets $M_k$, $1\le k\le K$, since due to the minimality we can limit our consideration to translates of the form $zS$ which intersect at least one of the sets $M_k$.

Using an indirect argument we assume that $zS$ has non-trivial intersection with, for instance, $x_{1}S$ and $x_{2}S$. Then we have $zs=x_1{s}_1=x_2{s}_2$ for some elements $s,s_1,s_2\in S$. However, we then have $z\in M_{1}S\cap M_{2}S=\varnothing$, in contradiction to the assumption. Thus, for every index k the collection of sets $s_{i}S$ with $i\in I_k$ given by

$$I_k:=\{i\in F|M_k\cap s_{i}S\ne \varnothing \}$$

describes a covering of the set $M_k$.

This is a minimal covering, because if there was another covering of the set $M_k$ with fewer terms, it could be used to obtain an even better covering of their union (by simply leaving the other contributions fixed), in contradiction to the assumed minimality of the covering and property (3) in Lemma 2. □

Remark 8. 

Note that up to this point we have only used a few topological properties of locally compact groups G. The use of the simple expression of a capacity (which should be seen as a simplified or coarse form of a measure) will allow us to derive the existence of arbitrary fine BUPUs on any locally compact group G.

Note that similar expressions appear in the construction of the Haar measure on a given locally compact group. We leave it to the reader to check this similarity. For us it is only important to mention that the use of this “coarse form of a measure” precedes the construction of a Haar measure and thus allows us to derive the validity of the integrated group action (as described in Section 3.2 of [2]) without any measure theory, as it does not make use of Lebesgue integration theory nor the existence of the Haar measure.

Theorem 1.

Let G be any locally compact group and $U\in \mathcal{U}\left(e\right)$ be any neighborhood of the neutral element $e\in G$. Then there exist (plenty of) BUPUs $\mathsf{\Psi }={\left({\psi }_i\right)}_{i\in I}$ of non-negative functions of size U, meaning that

$$supp\left({\psi }_i\right)\subseteq x_{i}U,\forall i\in I,$$

(5)

for a suitable discrete (in fact uniformly separated) family $X={\left(x_i\right)}_{i\in I}$ in G, and

$$\sum _{i\in I}{\psi }_i\left(x\right)\equiv 1.$$

(6)

Proof. 

Given U we choose some compact neighborhood $V\in \mathcal{U}\left(e\right)$ such that $V^3\subseteq U$, and an even smaller neighborhood $S\in \mathcal{U}\left(e\right)$ with $S^2\subseteq V$. Without the loss of generality, we will assume that all these neighborhoods are symmetric (with respect to the group action), i.e., that $z\in U$ if and only if $z^{-1}\in U$ (and the same for the other neighborhoods).

We then select a maximal family ${\left(x_i\right)}_{i\in I}$ with respect to the property that $\{x_{i}V|i\in I\}$ forms a pavement in G, i.e., such that the sets $x_{i}V$ do not intersect in a non-trivial way, but that there is no $z\in G$ such that $zV$ could be added to the family without destroying this property. Consequently, any translate $zV$ intersects at least one of the sets $x_{i}V$, or $zV\cap x_{i}V\ne \varnothing$ for some index $i\in I$. Due to the symmetry assumption, this implies that the family $\left(x_i{V}^2\right)$ covers the group G.

Due to the regularity of a locally compact group there exists $\phi \in {\mathit{C}}_c\left(G\right)$ with $\phi \left(y\right)=1$ on $V^2$, $supp\left(\phi \right)\subseteq V^3$ and ${\parallel \phi \parallel }_{\infty }=1$. Thus (by setting $L_x\phi \left(y\right)=\phi \left(x^{-1}y\right)$) the sum

$$\mathsf{\Phi }\left(x\right):=\sum _{i\in I}{L}_{x_i}\phi \left(x\right)=\sum _{i\in I}\phi \left({x_i}^{-1}x\right)$$

is well defined and satisfies $\mathsf{\Phi }\left(x\right)\ge 1$ for all $x\in G$. In order to show that the sum is finite (in a uniform sense) for each $x\in G$, let us fix $i\in I$ and consider $I_i:=\{j|{\psi }_i{\psi }_j\ne 0\}.$ Since $I_i\subseteq \{j|x_i{V}^3\cap x_j{V}^3\ne \varnothing \}$ we have to count the indices $j\in I$ with $x_j\in x_i{V}^6$, or

$$x_{j}S\subseteq x_i{V}^{6}S\subset x_i{V}^7.$$

Since the family of sets $x_{j}S,i\in I$ is an S-separated family of translates of S, thanks to the assumption $S^2\subseteq V$ and the pavement conditions stated at the beginning of the proof we can apply property (4) of Lemma 2 in order to finish our proof.

Hence for any fixed $i\in I$ the number of possible indices such that ${\psi }_i·{\psi }_j\ne 0$ is at most ${cap}_S\left(V^7\right)$ (because we have ${cap}_S\left(x_{j}S\right)={cap}_S\left(S\right)=1$, using properties (1) and (2) from Lemma 2 above).

Overall, we have established that the sum defining $\mathsf{\Phi }\left(x\right)$ is pointwise a finite sum and the resulting function $\mathsf{\Phi }$ satisfies

$$1\le \mathsf{\Phi }\left(x\right)\le {cap}_S\left(V^7\right),x\in G.$$

(7)

Consequently, we observe that the family defined by

$${\psi }_i\left(x\right):={\mathsf{Ł}}_{x_i}\phi \left(x\right)/\mathsf{\Phi }\left(x\right),i\in I,$$

defines a partition of unity of size U, since $V^3\subseteq U$ and

$$supp\left({\psi }_i\right)=supp\left(L_{x_i}\phi \right)=x_{i}supp\left(\phi \right)\subset x_i{V}^3\subset x_{i}U.$$

□

4. Towards Integrated Group Representations

To some extent the usefulness of BUPUs is based on the fact that they allow us to define natural operators. Any non-negative BUPU $\mathsf{\Psi }={\left({\psi }_i\right)}_{i\in I}$ induces two operators, namely, the spline quasi-interpolation operator ${Sp}_{\mathsf{\Psi }}$ on $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$, given by

$${Sp}_{\mathsf{\Psi }}f:=\sum _{i\in I}f\left(x_i\right){\psi }_i,$$

(8)

and its adjoint operator, the so-called discretization operator $D_{\mathsf{\Psi }}$ on $(\mathit{M}\left(G\right),\parallel \hspace{0.17em}·\hspace{0.17em}{\parallel }_{\mathit{M}})=\left({\mathit{C}}_0^{\prime }\left(G\right),{\parallel \hspace{0.17em}·\hspace{0.17em}\parallel }_{{\mathit{C}}_0^{\prime }}\right)$, which takes the form

$$D_{\mathsf{\Psi }}\mu =\sum _{i\in I}\mu \left({\psi }_i\right){\delta }_{x_i}.$$

(9)

Since any ${Sp}_{\mathsf{\Psi }}$ is obviously a nonexpansive operator on $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$ it is also clear that its adjoint is nonexpansive on $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$ as well.

Let us first recall a few facts concerning the discretized measures for the case of $G={\mathbb{R}}^d$.

In [5] the following facts were derived:

Proposition 2.

Given $\mu \in \mathit{M}\left({\mathbb{R}}^d\right)$ the net (the reader is definitely familiar with such a concept, recalling the concept of convergence of Riemann sums, which approach the limit ${\int }_a^{b}f\left(x\right)dx$, given that $f\in \mathit{C}\left(\right[a,b\left]\right)$.) ${\left(D_{\mathsf{\Psi }}\mu \right)}_{\left|\mathsf{\Psi }\right|\to 0}$ is $w^{\ast }$-convergent:

$$D_{\mathsf{\Psi }}\mu \left(f\right)\to \mu \left(f\right),\forall f\in {\mathit{C}}_0,\left|\mathsf{\Psi }\right|\to 0.$$

(10)

In fact, we have for any BUPU Ψ:

$$\parallel D_{\mathsf{\Psi }}\mu {\parallel }_{\mathit{M}}\le {\parallel \mu \parallel }_{\mathit{M}},\mu \in \mathit{M}\left({\mathbb{R}}^d\right).$$

(11)

Moreover, the family ${\left(D_{\mathsf{\Psi }}\mu \right)}_{\left|\mathsf{\Psi }\right|\le 1}$ is uniformly tight in $(\mathit{M}\left({\mathbb{R}}^d\right),\parallel ·{\parallel }_{\mathit{M}})$ (a bounded set $S\subset \mathit{M}\left({\mathbb{R}}^d\right)$ is called tight if for every $\epsilon >0$ there exists $p\in {\mathit{C}}_c\left(G\right)$ such that ${\parallel p\mu -\mu \parallel }_{\mathit{M}}\le \epsilon ,\forall \mu \in S$).

We do not go into a discussion of tightness combined with $w^{\ast }$-convergence, but recall that we have established strong operator norm convergence for the corresponding convolution operators (by [5]), given pointwise by $\mu \ast f\left(x\right)=\mu \left(T_x{f}^{✓}\right),x\in {\mathbb{R}}^d$:

$$\underset{\left|\mathsf{\Psi }\right|\to 0}{lim}{\parallel D_{\mathsf{\Psi }}\mu \ast f-\mu \ast f\parallel }_{\infty }=0,f\in {\mathit{C}}_0\left({\mathbb{R}}^d\right).$$

(12)

Our next goal is to verify that a corresponding behaviour remains valid for general (isometric) group representations on Banach spaces. In a sense, this shows that the Banach algebra $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$, with the composition rule being internal convolution), provides a universal algebra which can be embedded into the Banach algebra of all operators on a variety of Banach spaces. Note that in addition to the crucial estimate (controlling the operator norm of the convolution operator $f\mapsto \mu \ast f$ by ${\parallel \mu \parallel }_{\mathit{M}}$) we have to ensure the validity of the associative law, i.e., that we have for ${\mu }_1,{\mu }_2\in \mathit{M}\left(G\right)$:

$$({\mu }_1\star {\mu }_2)\ast f={\mu }_1\ast ({\mu }_2\ast f),f\in \mathit{B}.$$

(13)

This is non-trivial and authors often neglect to mention it, but it is obvious for Dirac measures, and hence for discrete measures, and thus can be obtained by taking limits.

Since our goal is mostly application for LCA groups, we have formulated the next definition for the Abelian setting, thus making use of additive notation for the group law.

Definition 6.

A mapping $\rho :G\to \mathcal{L}\left(\mathit{B}\right)$, the bounded, linear operators on a Banach spaces $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$, is called an isometric representation of a group G on the Banach space $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$ if the mapping ρ is a group homomorphism, i.e., satisfies

$$\rho (x+y)=\rho \left(x\right)\circ \rho \left(y\right),x,y\in G,$$

and if each of the operators are isometric on $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$, i.e., if one has

$${\parallel \rho \left(x\right)f\parallel }_{\mathit{B}}={\parallel f\parallel }_{\mathit{B}},f\in \mathit{B},x\in G.$$

(14)

Moreover, if the mapping $x\mapsto \rho \left(x\right)f$ is continuous from G to $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$, i.e.,

$$\underset{x\to 0}{lim}{\parallel \rho \left(x\right)f-f\parallel }_{\mathit{B}}=0,f\in \mathit{B}.$$

(15)

we say that the representation ρ is strongly continuous.

An important family of examples arises from the so-called regular representation of G, i.e., the action of the group by (left or right) translation on functions or distributions over G, i.e., $\rho \left(x\right)=T_x$ the integrated action corresponds to the usual convolution (see [2], p. 73). In this case the notation of homogeneous Banach spaces is used, which suggests calling Banach spaces endowed with an isometric, strongly continuous group representation of an LC group G an abstract homogeneous Banach space (cf. [17], Chap. 9).

The main result of this paper is the observation that we can establish the fact that every strongly continuous, isometric representation of ${\mathbb{R}}^d$ on a Banach space $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$ gives rise to an extended representation (the so-called integrated group representation) of the Banach convolution algebra $(\mathit{M}\left({\mathbb{R}}^d\right),\parallel ·{\parallel }_{\mathit{M}})$. In fact, this extension is unique among all those who respect tight, $w^{\ast }$-convergence of nets (or just sequences), with the understanding that $\rho \left(x\right)$ is of course identified with $\rho \left({\delta }_x\right)$ (we avoid the use of a different symbol for the integrated representation).

Remark 9. 

Usually, in the standard literature on the subject, the integrated group representation describes the action of $f\in {\mathit{L}}^1\left(G\right)$ on $f\in \mathit{B}$, and is thus not immediately visible as a natural extension of the group representation. Aside from technical arguments (and there are many such considerations, involving abstract measure theory and a lot of functional analysis) the focus on ${\mathit{L}}^1\left(G\right)$ appears to come from a similar situation, where the group representation of a discrete group G can be extended naturally to ${\ell }^1\left(G\right)$, which has the “unit vectors” ${\delta }_x,x\in G$ as a natural (unconditional) basis. In other words, in this case any $f\in {\ell }^1\left(G\right)$ can be written (uniquely) as

$$f=\sum _{x\in G}f\left(x\right){\delta }_{x}with{\parallel f\parallel }_1:=\sum _{x\in G}\left|f\left(x\right)\right|<\infty .$$

(16)

However, for a discrete group we have of course ${\ell }^1\left(G\right)=\mathit{M}\left(G\right)$ and the finite, discrete measures are dense in $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$ (see [18], Example 6.1.7). In contrast, for non-discrete groups the subspace ${\mathit{M}}_d\left(G\right)$ of discrete measures (of the form $\mu ={\sum }_{k=1}^{\infty }{c}_k{\delta }_{x_k}$ with ${\sum }_{k=1}^{\infty }\left|c_k\right|<\infty$) forms a proper closed subalgebra of $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$. However, fortunately ${\mathit{M}}_d\left(G\right)$ is $w^{\ast }$—dense in $\mathit{M}\left(G\right)$ and the constructive way of proving this fact (described in [5]) serves as the basis for the results presented in this paper.

Remark 10. 

Using the terminology of Banach modules we can state that any strongly continuous, isometric representation of G on $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$ turns $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$ into a Banach module over the (commutative, unital) Banach convolution algebra $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$ (we use the symbol ⋆ for internal convolution).

Later (see Section 6) we will see that the restriction of the module action to ${\mathit{L}}^1\left(G\right)$ makes $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$ an essential Banach (convolution) module over $\left({\mathit{L}}^1\left(G\right),{\parallel \hspace{0.17em}·\hspace{0.17em}\parallel }_1\right)$.

Next we will show that the convolution action of bounded discrete measures on a homogenous Banach space can be extended to all of the measures in order to generate an action of $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$ on such a Banach space $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$.

Theorem 2.

Any abstract homogeneous Banach space $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$ with respect to a given, strongly continuous and isometric representation ρ of a locally compact group G is also a Banach module over the Banach algebra $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$ (with respect to convolution). This claim includes the validity of the following associativity law:

$$\rho ({\mu }_1\star {\mu }_2)=\rho \left({\mu }_1\right)\circ \rho \left({\mu }_2\right),{\mu }_1,{\mu }_2\in \mathit{M}\left(G\right).$$

(17)

The mapping $(\mu ,f)\mapsto \mu {•}_{\rho }f=\rho \left(\mu \right)f$ is the natural extension of the action of discrete measure given by ${\delta }_x{•}_{\rho }f=\rho \left(x\right)f$ and satisfies the norm estimate

$$\parallel \mu {•}_{\rho }{f\parallel }_{\mathit{B}}\le {\parallel \mu \parallel }_{\mathit{M}}{\parallel f\parallel }_{\mathit{B}},\mu \in \mathit{M}\left(G\right),f\in \mathit{B}.$$

(18)

Proof. 

We start from the expected action of Dirac measures via

$${\delta }_x{•}_{\rho }f=:\rho \left(x\right)f,f\in \mathit{B}.$$

(19)

Since discrete measures are absolutely convergent sums of Dirac measures it is then clear that we have for a discrete measure $\mu ={\sum }_{k=1}^{\infty }{c}_k{\delta }_{x_k}$, with ${\sum }_{k=1}^{\infty }\left|c_k\right|={\parallel \mu \parallel }_{\mathit{M}}<\infty$:

$$\mu {•}_{\rho }f=\sum _{n=1}^{\infty }{c}_k\rho \left(x_k\right)f,$$

(20)

the sum being absolutely convergent for each f and $\mu \in {\mathit{M}}_d\left(G\right)$, since we have

$$\parallel \mu {•}_{\rho }{f\parallel }_{\mathit{B}}\le \sum _{n=1}^{\infty }|c_k|\parallel \rho \left(x_k\right){f\parallel }_{\mathit{B}}\le {\parallel f\parallel }_{\mathit{B}}\sum _{n=1}^{\infty }\left|c_k\right|={\parallel \mu \parallel }_{\mathit{M}}{\parallel f\parallel }_{\mathit{B}}.$$

(21)

Observe also that the assumptions concerning $\rho$ imply that this action of ${\mathit{M}}_d\left(G\right)$ is not only an individual action (given for each $\mu \in {\mathit{M}}_d\left(G\right)$) but it in fact defines a representation of the Banach convolution algebra $({\mathit{M}}_d\left(G\right),\parallel ·{\parallel }_{{\mathit{M}}_b})$, since we have

$$({\mu }_1\star {\mu }_2){•}_{\rho }f={\mu }_1{•}_{\rho }\left({\mu }_2{•}_{\rho }f\right),{\mu }_1,{\mu }_2\in {\mathit{M}}_d\left(G\right),f\in \mathit{B}$$

(22)

as a consequence of the validity of

$$({\delta }_x\star {\delta }_y){•}_{\rho }f={\delta }_{x+y}{•}_{\rho }f=\rho (x+y)f=\rho \left(x\right)\left(\rho \left(y\right)f\right)={\delta }_x{•}_{\rho }\left({\delta }_y{•}_{\rho }f\right).$$

(23)

Consequently, for a given $\mu \in \mathit{M}\left(G\right)$ and $f\in \mathit{B}$ we set

$$D_{\mathsf{\Psi }}\mu {•}_{\rho }f=\sum _{i\in I}\mu \left({\psi }_i\right)\rho \left(x_i\right)f.$$

(24)

Based on (21) and (11) we have for any $\mathsf{\Psi }$:

$$\parallel D_{\mathsf{\Psi }}\mu {•}_{\rho }{f\parallel }_{\mathit{B}}\le {\parallel f\parallel }_{\mathit{B}}\sum _{i\in I}\left|\mu \left({\psi }_i\right)\right|={\parallel f\parallel }_{\mathit{B}}\parallel D_{\mathsf{\Psi }}\mu {\parallel }_{\mathit{M}}\le {\parallel \mu \parallel }_{\mathit{M}}{\parallel f\parallel }_{\mathit{B}}.$$

(25)

We will show next that it is convergent, as $\left|\mathsf{\Psi }\right|\to 0$ or $diam\left(\mathsf{\Psi }\right)\to 0$. The motivation for this approach becomes plausible once one understands $D_{\mathsf{\Psi }}\mu$ on f as a Riemann-type sum for the Banach-space-valued integral of $x\to \rho \left(x\right)f$, usually written as ${\int }_G\rho (x)f(x)d\mu (x)$.

Given two families $\mathsf{\Psi }={\left({\psi }_i\right)}_{i\in I}$ and $\mathsf{\Phi }={\left({\varphi }_j\right)}_{j\in J}$, with their centers ${\left(x_i\right)}_{i\in I}$ and ${\left(y_j\right)}_{j\in J}$ respectively, we define their joint refinement $\mathsf{\Psi }-\mathsf{\Phi }$ as the family ${\left({\psi }_i{\varphi }_j\right)}_{(i,j)\in I\diamond J}$. It is natural to take $I\diamond J$, the family of all index pairs such that ${\psi }_i·{\varphi }_j\ne 0$ (because all the other products are trivial and should be neglected) as the new index set. In fact, if both $\mathsf{\Psi }$ and $\mathsf{\Phi }$ are sufficiently “fine” BUPUs, one has: (using the fact that ${\psi }_i={\sum }_{j\in j}{\psi }_i{\varphi }_j$, hence ${\sum }_{(i,j)\in I\diamond J}{\psi }_i{\varphi }_j\equiv 1$ and ${\sum }_{(i,j)\in I\diamond J}\parallel \left({\psi }_i{\varphi }_j\right){\mu \parallel }_{\mathit{M}}={\parallel \mu \parallel }_{\mathit{M}}$).

$$\parallel D_{\mathsf{\Psi }}\mu {•}_{\rho }f-D_{\mathsf{\Phi }}\mu {•}_{\rho }{f\parallel }_{\mathit{B}}=\sum _{(i,j)\in I\diamond J}\parallel \rho \left(x_i\right)f-\rho \left(y_j\right){f\parallel }_{\mathit{B}}\left|\mu \left({\psi }_i{\varphi }_j\right)\right|\le$$

(26)

$$\underset{(i,j)\in I\diamond J}{sup}\parallel \rho \left(x_i\right)[f-\rho (y_j-x_i)f]{\parallel }_{\mathit{B}}\sum _{(i,j)\in I\diamond J}\parallel \left({\psi }_i{\varphi }_j\right){\mu \parallel }_{\mathit{M}}\le \epsilon {\parallel \mu \parallel }_{\mathit{M}},$$

if only $\mathsf{\Psi }$ resp. $\mathsf{\Phi }$ are fine enough. Due to the completeness of $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$ one finds that there is a uniquely determined limit, which we will call $\mu {•}_{\rho }f$. It is then obvious that

$$\parallel \mu {•}_{\rho }{f\parallel }_{\mathit{B}}=\underset{\left|\mathsf{\Psi }\right|\to 0}{lim}\parallel D_{\mathsf{\Psi }}\mu {•}_{\rho }{f\parallel }_{\mathit{B}}\le \underset{\left|\mathsf{\Psi }\right|\to 0}{lim\; sup}\parallel D_{\mathsf{\Psi }}\mu {\parallel }_{\mathit{M}}{\parallel f\parallel }_{\mathit{B}}={\parallel \mu \parallel }_{\mathit{M}}{\parallel f\parallel }_{\mathit{B}}.$$

(27)

Of course, it remains to be shown that the action defined in this way is associative, i.e., that

$$({\mu }_1\star {\mu }_2){•}_{\rho }f={\mu }_1{•}_{\rho }\left({\mu }_2{•}_{\rho }f\right),\forall {\mu }_1,{\mu }_2\in \mathit{M}\left(G\right),f\in \mathit{B},$$

(28)

but this follows from the associativity for the discrete measures $D_{\mathsf{\Psi }}\mu$ and $D_{\mathsf{\Phi }}\mu$. Note that H. S. Shapiro (cf. [17]) makes this associativity an extra axiom, apparently because he could not prove it directly for technical reasons, based on the way in which he defines the action of bounded measures on an “abstract homogeneous Banach space”. H.C. Wang exhibits in [19] an example of what he calls a semi-homogeneous Banach space (without strong continuity of the action of G on $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$, which does not allow the extension to all of the bounded measures. Indeed, it is a Banach space of measurable and bounded functions on $\mathbb{R}$ which is non-trivial, but which does not contain any non-zero continuous function. The example was suggested to him in a correspondence by the author of this note. □

Remark 11. 

In the derivation above we have used the isometric property and the fact that $\rho \left(x_1{x}_2\right)=\rho \left(x_1\right)\circ \rho \left(x_2\right)$. It would have been no problem if this identity was only true “up to some constant of absolute value one”, i.e., if one has a projective representation of G only, such as the mapping $\lambda =(t,\omega )\mapsto \rho \left(\lambda \right)=M_{\omega }{T}_t$ from ${\mathbb{R}}^d\times {\widehat{\mathbb{R}}}^d$ into the unitary operators on the Hilbert space $\left({\mathit{L}}^2\left({\mathbb{R}}^d\right),{\parallel ·\parallel }_2\right)$, which is one of the key players in time-frequency analysis. This direction will also be explored further in subsequent notes.

Remark 12. 

Another possible and powerful extension of the above result will involve cases where the group action is not isometric anymore, but still bounded by some weight function, i.e., the case where each $\rho \left(x\right)$ is a bounded operator and one has control over the operator norms of these operators on $(\mathit{B},\parallel ·{\parallel }_{\mathit{B}})$. In this case, one has to replace the algebra $(\mathit{M}\left(G\right),\parallel ·{\parallel }_{\mathit{M}})$ by weighted versions, and $\left({\mathit{L}}^1\left(G\right),{\parallel \hspace{0.17em}·\hspace{0.17em}\parallel }_1\right)$ by Beurling algebras (see [3]). This direction will also be pursued elsewhere in more detail. This is a crucial starting point for the analysis of TMIBs, i.e., translation- and modulation-invariant function spaces (see e.g., [20,21]).

5. The Wiener Algebra W(C${}_{\mathbf{0}}$,ℓ${}^{\mathbf{1}}$)

The purpose of this section is to demonstrate that the concept of homogeneous Banach spaces over LCA groups, originally introduced in a book by Y. Katznelson [22] (see Remark 14 below), can be introduced without making use of the Haar integral. For this purpose we will make use of Wiener’s algebra (as described in [23]), which is found already in Reiter’s book [3,4] for $G={\mathbb{R}}^d$, as a prototypical example of a Segal algebra. It was the model case for many characterizations of minimal spaces (a pointwise ${\mathit{C}}_0\left({\mathbb{R}}^d\right)$-module in this case); see [23] and the subsequent papers [24,25].

Obviously, BUPUs play an important role in the description of Wiener amalgam spaces (such as Wiener’s algebra, which is of the form $\mathit{W}({\mathit{C}}_0,{\ell }^1)\left({\mathbb{R}}^d\right)$, or the Segal algebra ${\mathit{S}}_0\left({\mathbb{R}}^d\right)=\mathit{W}(\mathcal{F}{\mathit{L}}^1,{\ell }^1)\left({\mathbb{R}}^d\right)$). The justification for characterizing Wiener amalgam spaces via BUPUs comes from the main results of [6]. Leaving out the details, let us summarize a few properties of Wiener’s algebra on a general LCA group G:

Definition 7.

$$\mathit{W}\left(G\right):=\mathit{W}({\mathit{C}}_0,{\ell }^1)\left(G\right):=\{f\in {\mathit{C}}_0\left(G\right)|{\parallel f\parallel }_{\mathit{W}}:=\sum _{i\in I}{\parallel f{\psi }_i\parallel }_{\infty }<\infty \}.$$

We have the following general facts, which are easily proved without making use of the existence of a Haar measure on G:

Proposition 3. 

1. 

$(\mathit{W},\parallel ·{\parallel }_{\mathit{W}})$ is a Banach space, for any BUPU Ψ, and continuously embedded into $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$.

2. 

$(\mathit{W},\parallel ·{\parallel }_{\mathit{W}})$ is a Banach ideal in $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$, i.e., pointwise products are in $\mathit{W}$; in particular, it is a Banach algebra under pointwise multiplication;

3. 

The space does not depend on the particular choice of Ψ, i.e., different BUPUs define the same space and equivalent norms;

4. 

The decomposition of $f\in \mathit{W}$ as $f={\sum }_{i\in I}f{\psi }_i$ is not only valid absolutely in $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$, but even in $\left({\mathit{W},\parallel ·\hspace{0.17em}\parallel }_{\mathit{W}}\right)$. Hence, ${\mathit{C}}_c\left(G\right)$ is dense in $\left({\mathit{W},\parallel ·\hspace{0.17em}\parallel }_{\mathit{W}}\right)$ and $\mathit{W}$ is dense in $\left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$;

5. 

For any open, relatively compact neighborhood Q of the identity we have the following atomic characterization of $\mathit{W}$, via the absolutely convergent series:

$${\mathit{W}}_{at}:=\{f\in {\mathit{C}}_0\left(G\right)|f=\sum _{k=1}^{\infty }{f}_k,with\sum _{k=1}^{\infty }{\parallel f_k\parallel }_{\infty }<\infty ,\exists x_k\in G:supp\left(f_k\right)\subseteq x_k+Q\}.$$

6. 

The corresponding (equivalent)inf-norm (infimum over all admissible sums) is isometrically translation-invariant, with continuous translation, i.e.,

$$\parallel T_{x}f{\parallel }_{\mathit{W}}={\parallel f\parallel }_{\mathit{W}},x\in G,and\underset{x\to e}{lim}\parallel T_{x}f-f{\parallel }_{\mathit{W}}=0,\forall f\in \mathit{W}.$$

(29)

Remark 13. 

As a matter of fact, the functions in $\mathit{W}\left({\mathbb{R}}^d\right)$ are (even absolutely Riemann) integrable and thus $\mathit{W}$ is a dense subspace of $\left({\mathit{L}}^1\left({\mathbb{R}}^d\right),{\parallel ·\parallel }_1\right)$. Combined with property (29), this implies that $\mathit{W}({\mathit{C}}_0,{\ell }^1)\left({\mathbb{R}}^d\right)$ is in fact a Segal algebra on ${\mathbb{R}}^d$ (see [3,4]). Similar comments apply for general LCA groups based on Proposition 3, once the existence of a Haar measure is established (in order to characterize $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ as a closed ideal of $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$; see Section 6).

Since ${(\mathit{W},\parallel ·\parallel }_{\mathit{W}})\hookrightarrow \left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$ as a dense subspace, the dual space ${\mathit{W}}^{\ast }$ (which can be characterized as the subspace $\mathit{W}(\mathit{M},{\ell }^{\infty })\left(G\right)$ of all Radon measures) is known in the literature as the space of translation-bounded measures.

First we give a characterization of ${\mathit{W}}^{\ast }$ as a subspace of all tempered distributions (for the case $G={\mathbb{R}}^d$). Note that in this case $\mathcal{S}\left({\mathbb{R}}^d\right)$ is a dense subspace of $\mathit{W}$.

Lemma 3.

A tempered distribution $\sigma \in {\mathcal{S}}^{\prime }$ extends to a bounded linear functional on $(\mathit{W},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{W}})$ if and only if one has the following estimate:

Fixing a compact set Q (with non-void interior) there exists a constant $B\left(Q\right)$ such that one has: For any $\phi \in \mathcal{D}\left({\mathbb{R}}^d\right)=\mathcal{S}\left({\mathbb{R}}^d\right)\cap {\mathit{C}}_c\left({\mathbb{R}}^d\right)$ (the space of infinitely smooth functions with compact support) with $supp\left(\phi \right)\subseteq x+Q$ for some $x\in G$:

$$\left|\sigma \left(\phi \right)\right|\le B\left(Q\right){\parallel \phi \parallel }_{\infty }.$$

(30)

Equivalently one has: A tempered distribution defines a translation-bounded measure if and only if for any $p\in \mathcal{D}\left({\mathbb{R}}^d\right)$ the family $(T_{x}p·\sigma )$ constitutes a bounded family in $(\mathit{M}\left({\mathbb{R}}^d\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$.

Dueto the atomic characterization of $\mathit{W}\left(G\right)$, we can also provide a kind of atomic representation of ${\mathit{W}}^{\ast }$, which works as follows:

Lemma 4.

Given any well-spread family ${\left(x_i\right)}_{i\in I}$ in G, the elements $\sigma \in {\mathit{W}}^{\ast }$ can be characterized as the $w^{\ast }$—convergent series of the following form (recall that $(\sigma ·h):=\sigma (h·f)$ by definition.)

$$\sigma =\sum _{i\in I}{\mu }_i·T_{x_i}p,$$

(31)

for some fixed, non-zero $p\in {\mathit{C}}_c\left(G\right)$ and some bounded family ${\left({\mu }_i\right)}_{i\in I}$ in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$.

Proof. 

The proof has two directions. First of all we fix some U-BUPU $\mathsf{\Psi }={\left({\psi }_i\right)}_{i\in I}$ and some $p\in {\mathit{C}}_c\left(G\right)$ with ${\parallel p\parallel }_{\infty }=1$, $p\left(x\right)\equiv 1$ on U, and hence ${\psi }_i={\psi }_i·T_{x_i}p$ for $i\in I$.

This allows us to decompose any linear functional $\sigma \in {\mathit{W}}^{\ast }$ in the usual way as a $w^{\ast }$—convergent series of the form

$$\sigma =\sum _{i\in I}\sigma ·{\psi }_i=\sum _{i\in I}(\sigma ·{\psi }_i)·T_{x_i}p.$$

(32)

We will check that the functionals ${\mu }_i:=\sigma ·{\psi }_i$ define a bounded family in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$. In fact, we have, thanks to the atomic characterization

$$\parallel {\mu }_i{\parallel }_{\mathit{M}}=\parallel \sigma {\psi }_i{\parallel }_{\mathit{M}}\le {\parallel {\psi }_i\parallel }_{\infty }\parallel \sigma ·\left(T_{x_i}p\right){\parallel }_{\mathit{M}}\le C{\parallel \sigma \parallel }_{{\mathit{W}}^{\ast }},i\in I.$$

(33)

In order to prove the converse, let ${\left({\mu }_i\right)}_{i\in I}$ be a bounded family in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$. We have to control the norm of the functional $\sigma$ given by Equation (32). Due to the atomic characterization it is enough to present an estimate for the atoms, i.e., a uniform estimate (with respect to the sup-norm) for functions $f\in {\mathit{C}}_c\left(G\right)$ with $supp\left(f\right)\subset z+Q$, for some $z\in G$. The assumptions concerning the family ${\left(x_i\right)}_{i\in I}$ then imply that one has for the compact set $K=supp\left(p\right)$ the following uniform bound (independent of z):

$$\#F=\#\{i\in I,(x_i+I)\cap (z+K)\ne \varnothing \}\le C\left(X\right)<\infty .$$

Using $supp(T_{x_i}p·f)\subseteq supp\left(T_{x_i}p\right)=x_i+K$ and ${\parallel T_{x_i}p·f\parallel }_{\infty }\le {\parallel f\parallel }_{\infty }$ we conclude

$$\left|\sigma \left(f\right)\right|\le \sum _{i\in I}|({\mu }_i·T_{x_i}p)\left(f\right)|=\sum _{i\in F}\left|{\mu }_i(T_{x_i}p·f)\right|\le C\left(X\right)\underset{i\in I}{sup}\parallel {\mu }_i{\parallel }_{\mathit{M}}{\parallel f\parallel }_{\infty }.$$

(34)

□

Remark 14. 

This definition appears to be different from the setting chosen in Katznelson’s book [22], p. 127. He assumes only instead of condition (1) that one has a continuous embedding ${(\mathit{B},\parallel ·\hspace{0.17em}\parallel }_{\mathit{B}})\hookrightarrow {\mathit{L}}_{\mathit{loc}}^1\left({\mathbb{R}}^d\right)$. However, due to the translation invariance property (2) imposed on the norm of $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$, this implies immediately that one has ${(\mathit{B},\parallel ·\hspace{0.17em}\parallel }_{\mathit{B}})\hookrightarrow \mathit{W}({\mathit{L}}^1,{\ell }^{\infty })$, which is a closed subspace of $\mathit{W}(\mathit{M},{\ell }^{\infty })$ (the usual characterization of the dual of $\mathit{W}({\mathit{C}}_0,{\ell }^1)$ in the context of Wiener amalgam spaces).

Conversely, one can show that the continuous shift property implies that in the case that $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ is defined in the usual way with the help of Lebesgue integration combined with the existence of a Haar measure on G, the continuous shift property (3), in conjunction with (1) and (2), actually implies that $\mathit{B}$ is contained in the subspace $\mathit{W}({\mathit{L}}^1,{\ell }^{\infty })\subset \mathit{W}(\mathit{M},{\ell }^{\infty })$.

Equipped with these spaces, which can be described now for any LCA group G without the use of the Haar measure or structure theory, we can provide a definition of a homogeneous Banach space on G (HBSG).

Definition 8.

A Banach space $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$ is called a homogeneous Banach space on an LCA group G (HBSG) given that

1. 

${(\mathit{B},\parallel ·\hspace{0.17em}\parallel }_{\mathit{B}})\hookrightarrow {\mathit{W}}^{\ast }$;

2. 

Translation is isometric on $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$, i.e.,

$$\parallel T_x{f\parallel }_{\mathit{B}}={\parallel f\parallel }_{\mathit{B}},\forall f\in \mathit{B},x\in G;$$

3. 

Translation is strongly continuous on $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$, i.e.,

$$\underset{x\to 0}{lim}\parallel T_x{f-f\parallel }_{\mathit{B}}=0,\forall f\in \mathit{B}.$$

The following lemma provides a connection between the different notions. For simplicity we formulate the result for $G={\mathbb{R}}^d$, endowed with the Lebesgue integral. It is valid for general LCA groups.

Lemma 5.

For any HSBG on $G={\mathbb{R}}^d$, we have ${(\mathit{B},\parallel ·\hspace{0.17em}\parallel }_{\mathit{B}})\hookrightarrow {\mathit{L}}_{\mathit{loc}}^1\left({\mathbb{R}}^d\right)$.

Proof. 

In the current situation the abstract results imply that $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$ is an essential Banach module over ${\mathit{L}}^1\left({\mathbb{R}}^d\right)$ with respect to convolution. By means of the Cohen–Hewitt factorization theorem (see [26]) any $f\in \mathit{B}$ can be written as $f=g\ast h$, for some $g\in {\mathit{L}}^1\left({\mathbb{R}}^d\right)$ and some $h\in \mathit{B}\subset \mathit{W}(\mathit{M},{\ell }^{\infty })\left({\mathbb{R}}^d\right)$. However, the convolution relations for Wiener amalgams established in [6] imply (altogether) that

$$\mathit{B}={\mathit{L}}^1\left({\mathbb{R}}^d\right)\ast \mathit{B}\subset {\mathit{L}}^1\left(G\right)\ast \mathit{W}(\mathit{M},{\ell }^{\infty })\left({\mathbb{R}}^d\right)\subset \mathit{W}({\mathit{L}}^1,{\ell }^{\infty })\left({\mathbb{R}}^d\right)\subset {\mathit{L}}_{\mathit{loc}}^1\left({\mathbb{R}}^d\right).$$

(35)

□

6. Homogeneous Banach Spaces as Essential L${}^{\mathbf{1}}$-Modules

Let us start with the comment that the so-called regular representation of a group G, i.e., the mapping which assigns to any $x\in \mathit{C}\left(G\right)$ the (left) translation operator $T_x$ (this operator is denoted by $L_x$ in [3]) is of course one of the most important cases for the application of the abstract principle developed in Section 6.

It is also clear that the general assumptions which allow us to invoke Theorem 2 are satisfied for any homogeneous Banach space on G. Since such Banach spaces usually contain many functions from ${\mathit{C}}_c\left(G\right)$ and since in this case it is clear that the abstract form of the convolution coincides with the pointwise action as defined via the pairing of ${\mathit{C}}_0\left(G\right)$ and $\mathit{M}\left(G\right)$ it is justified to still call the mapping $\mu {•}_{\rho }f$ convolution in this case and simply write $\mu \ast f$. In view of density considerations, it is possible to verify, in case there are different possible interpretations of the symbol “*”, that the result does not depend on the context.

This seemingly harmless, but nevertheless highly non-trivial use of this symbol in situations which are generated by different technical considerations is well justified in all the cases which are considered here. Occasionally a strict verification of such a claim has to be undertaken. However, unlike the approach taken occasionally by experts in distribution theory, we take care in regard to the “existence of the convolution product” at an individual level (in such a situation even the associative law may fail!) and we emphasize module actions and bilinear pairings for Banach spaces, which are obtained via an extension of standard operations.

We can thus summarize our findings so far in the following theorem:

Theorem 3.

Let $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$ be a homogeneous Banach space of an LCA group G. Then $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$ is a Banach module over $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$ with respect to convolution. In fact, the action of μ on $f\in \mathit{B}$ is defined as the limit of expressions of the form $D_{\mathsf{\Psi }}\mu \ast f$, in the norm of $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$.

Although it is enough to know the Riemann integral (on ${\mathit{C}}_c\left({\mathbb{R}}^d\right)$) for the case $G={\mathbb{R}}^d$ (or similar elementary LCA groups), we have to invoke to the existence of the Haar measure on G, which is a translation-invariant linear functional on ${\mathit{C}}_c\left(G\right)$ (in fact on $\mathit{W}({\mathit{C}}_0,{\ell }^1)\left(G\right)$). This allows us to endow ${\mathit{C}}_c\left(G\right)$ with the ${\mathit{L}}^1$-norm, and establish that ${\mathit{C}}_c\left(G\right)$ with this norm is a normed space. With a little bit of extra work, one then goes on to show that the bounded measure ${\mu }_k$ induced by $k\in {\mathit{C}}_c\left(G\right)$ via the mapping $f\mapsto {\int }_{G}f\left(x\right)k\left(x\right)dx$, or better $f\mapsto H(f·k)$ (here we write H for the Haar functional, i.e., the linear functional arising in the construction of the so-called Haar measure (see e.g., [1])) is in fact an isometric embedding from ${\mathit{C}}_c\left(G\right)$ into $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$. Consequently, it makes sense to define the space $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ simply as the closure of ${\mathit{C}}_c\left(G\right)$, more precisely of $\{{\mu }_k|k\in {\mathit{C}}_c\left(G\right)\}$ in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$.

Continuing our efforts to develop the foundations of harmonic analysis without the use of measure theory, we have to establish a few basic properties:

Lemma 6. 

1. 

$\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ is a Banach space;

2. 

$\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ is a homogeneous Banach space;

3. 

In fact, $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ is a closed ideal in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$.

4. 

${\mathit{L}}^1\left(G\right)$ is $w^{\ast }$—dense in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$.

Proof. 

By definition $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ is a closed subspace subspace of $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$ and hence complete, and thus a Banach space. The uniform continuity of any $k\in {\mathit{C}}_c\left(G\right)$ implies that ${\parallel T_{x}k-k\parallel }_{\infty }\to 0$ for $x\to 0$. Due to the(joint) compact support of all these translates (for x near 0, resp. the neutral element $e\in G$) one also has ${lim}_{x\to 0}{\parallel T_{x}f-f\parallel }_1=0$ for $f\in {\mathit{L}}^1\left(G\right)$ by approximation. Due to the continuous embedding $\left(\mathit{W}({\mathit{C}}_0,{\ell }^1)\left(G\right),{\parallel \hspace{0.17em}·\hspace{0.17em}\parallel }_{\mathit{W}}\right)\hookrightarrow \left({\mathit{C}}_0\left(G\right),{\parallel ·\parallel }_{\infty }\right)$ it is clear that ${\mathit{L}}^1\left(G\right)$ is contained in ${\mathit{W}}^{\ast }$, and thus the formal axioms for an HBSG are satisfied.

As a consequence of Theorem 3 it is also an $\mathit{M}\left(G\right)$-module with respect to convolution and thus a closed ideal in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$, once it is verified that the external action of $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$ on $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ is compatible with the internal (e.g., obtained by a pointwise definition of $f\ast g\left(x\right)$ for $f,g\in {\mathit{C}}_c\left(G\right)$, or using Lebesgue integration). Observe that the convolution of a compactly supported measure $\mu \in (\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$ with $k\in {\mathit{C}}_c\left(G\right)$ is a continuous function in ${\mathit{C}}_c\left(G\right)$ and thus, by taking limits, ${\mathit{L}}^1\left(G\right)$ is a closed ideal of $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$. The pointwise relation $\mu \ast k\left(x\right)=\mu \left(T_x{k}^{✓}\right)$ implies

$$supp(\mu \ast k)\subset supp\left(\mu \right)+supp\left(k\right).$$

(36)

Since any measure $\mu \in (\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$ can be approximated by finite sums of the form ${\sum }_{i\in F}\mu {\psi }_i$ (in the norm of $\mathit{M}\left(G\right)$) the obvious estimate

$${\parallel \mu \ast k\parallel }_1=\parallel \mu \star {\mu }_k{\parallel }_{\mathit{M}}\le {\parallel \mu \parallel }_{\mathit{M}}\parallel {\mu }_k{\parallel }_{\mathit{M}}={\parallel \mu \parallel }_{\mathit{M}}{\parallel k\parallel }_1,\mu \in \mathit{M}\left(G\right),k\in {\mathit{C}}_c\left(G\right),$$

(37)

we see that $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ is a closed ideal in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$.

In order to verify the $w^{\ast }$—density of ${\mathit{L}}^1\left(G\right)$ in $\mathit{M}\left(G\right)$ it is enough to check that it is possible to find an approximation of Dirac measures in the $w^{\ast }$—sense, because this implies the possibility of approximating discrete measures by elements of ${\mathit{L}}^1\left(G\right)$ (in fact by elements in ${\mathit{C}}_c\left(G\right)$) by means of transitivity.

In fact, given $h\in {\mathit{C}}_0\left(G\right)$ and $x\in G$, the uniform continuity of h implies that ${\delta }_x$ can be approximated well by non-negative functions $k\in {\mathit{C}}_c\left(G\right)$ with small support U centered around x. In fact, assuming ${\int }_{G}k\left(x\right)dx=1$ (just a normalization) it is easy to estimate the difference

$$|{\delta }_x\left(f\right)-{\mu }_k\left(f\right)|=|1·f\left(x\right)-{\int }_{G}f\left(y\right)g\left(y\right)dy|\le {\int }_U|f\left(x\right)-f\left(y\right)|\left|k\left(x\right)\right|dx<\epsilon .$$

(38)

□

Next, we can also recall the definition of a Segal algebra:

Definition 9.

A Banach space $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$, which is continuously and densely embedded into $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$, and which is also a homogeneous Banach space, is called a Segal algebra (in Reiter’s sense; see [3,4]).

Our knowledge so far implies immediately the following claim:

Lemma 7.

Any Segal algebra $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$ is a so-called Banach ideal in $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$, i.e., it is a Banach space with its own right, and an (left) ideal in $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$, satisfying the estimate

$${\parallel g\ast f\parallel }_{\mathit{B}}\le {\parallel g\parallel }_1{\parallel f\parallel }_{\mathit{B}},g\in {\mathit{L}}^1\left(G\right),f\in \mathit{B}.$$

(39)

In order to check that any homogeneous Banach space is an essential Banach module over $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ we will prove the third main result of this article. We start from the same situation as in Theorem 2. The following theorem is inspired by the results in [27], in particular Theorem 2.2, in which such a result was shown using different arguments.

Theorem 4.

Given a HBSG and a bounded and tight net ${\left({\mu }_{\alpha }\right)}_{\alpha \in I}$ in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$ with

$${\mu }_0={w^{\ast }-lim}_{\alpha \to \infty }{\mu }_{\alpha }$$

then one has norm convergence

$$\underset{\alpha \to \infty }{lim}\parallel {\mu }_{\alpha }\ast f-{\mu }_0\ast {f\parallel }_{\mathit{B}}=0,f\in \mathit{B}.$$

The result will be realized in the abstract setting of Theorem 2. This is our third main result. It shows that in the current context for bounded and tight nets in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$, the $w^{\ast }$-convergence of measures results in strong operator norm convergence of the corresponding convolution operators.

Theorem 5.

Let ρ be a strongly continuous, isometric representation of the locally compact group G on the Banach space $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$ and ${\left({\mu }_{\alpha }\right)}_{\alpha \in I}$ a bounded and tight net in $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$ with ${\mu }_0={w^{\ast }-lim}_{\alpha \to \infty }{\mu }_{\alpha }$. Then one has

$$\underset{\alpha \to \infty }{lim}\parallel {\mu }_{\alpha }{•}_{\rho }f-{\mu }_0{•}_{\rho }{f\parallel }_{\mathit{B}}=0,\forall f\in \mathit{B}.$$

(40)

Proof. 

Given $\epsilon >0$ and $f\in \mathit{B}$ we have to find ${\alpha }_0$ such that $\alpha ⪰{\alpha }_0$ implies

$$\parallel {\mu }_{\alpha }{•}_{\rho }f-{\mu }_0{•}_{\rho }{f\parallel }_{\mathit{B}}\le \epsilon .$$

(41)

For convenience we assume that ${\parallel f\parallel }_{\mathit{B}}$ = 1.

According to Theorem 2 we can find $U\in \mathcal{U}\left(e\right)$ such that for any $U-BUPU\mathsf{\Psi }$ one has

$$\parallel (D_{\mathsf{\Psi }}{\mu }_{\alpha }-{\mu }_{\alpha }){•}_{\rho }{f\parallel }_{\mathit{B}}=\parallel {\mu }_{\alpha }{•}_{\rho }f-D_{\mathsf{\Psi }}{\mu }_{\alpha }{•}_{\rho }{f\parallel }_{\mathit{B}}\le \epsilon /4\forall \alpha \in \{I,0\}.$$

(42)

Let us now fix one such BUPU $\mathsf{\Psi }={\left({\psi }_i\right)}_{i\in I}$. Based on the definition of tightness, we find that there exist compactly supported functions $p\in {\mathit{C}}_c\left(G\right)$ (one should think of plateaus as similar to functions, as they arise, e.g., as finite partial sums of the form ${\sum }_{i\in F}{\psi }_i$ from any BUPU $\mathsf{\Psi }$ on G.) such that

$$\parallel {\mu }_{\alpha }·p-{\mu }_{\alpha }{\parallel }_{\mathit{M}}\le \epsilon /4,\forall \alpha \in I.$$

(43)

By taking limits, the estimate (43) will be also valid for $\alpha =0$ (the limit measure ${\mu }_0$).

Thus, up to a controllable error we may assume that the measures ${\left({\mu }_{\alpha }\right)}_{\alpha \in I}$ (and their limit ${\mu }_0$) have joint compact support, and consequently there exists some finite set $F\subset I$ such that ${\mu }_{\alpha }\left({\psi }_i\right)=0$ for $i\in I\backslash F$, for all $\alpha \in I$ and $\alpha =0$.

Based on the assumed $w^{\ast }$—convergence of the net ${\left({\mu }_{\alpha }\right)}_{\alpha \in I}$, we can find some index ${\alpha }_0$ with

$$\sum _{i\in F}|{\mu }_{\alpha }\left({\psi }_i\right)-{\mu }_0\left({\psi }_i\right)|\le \epsilon /4,\forall \alpha ⪰{\alpha }_0,$$

(44)

which in turn implies that we have for $\alpha ⪰{\alpha }_0$:

$$\parallel D_{\mathsf{\Psi }}{\mu }_{\alpha }{•}_{\rho }f-D_{\mathsf{\Psi }}{\mu }_0{•}_{\rho }{f\parallel }_{\mathit{B}}\le \sum _{i\in F}|{\mu }_{\alpha }\left({\psi }_i\right)-{\mu }_0\left({\psi }_i\right)|\parallel \rho \left(x_i\right){f\parallel }_{\mathit{B}}\le \epsilon /4.$$

(45)

By combining the estimates (42), (44) and (45) we have verified (41), i.e., we can estimate $\parallel ({\mu }_{\alpha }-{\mu }_0){•}_{\rho }{f\parallel }_{\mathit{B}}$ in the following way:

$$\le \parallel ({\mu }_{\alpha }-D_{\mathsf{\Psi }}{\mu }_{\alpha }){•}_{\rho }{f\parallel }_{\mathit{B}}+\parallel (D_{\mathsf{\Psi }}{\mu }_{\alpha }-D_{\mathsf{\Psi }}{\mu }_0){•}_{\rho }{f\parallel }_{\mathit{B}}+\parallel (D_{\mathsf{\Psi }}{\mu }_0-{\mu }_0){•}_{\rho }{f\parallel }_{\mathit{B}}\le 3\epsilon /4.$$

□

There are many applications of this rather strong statement, so we present only a striking one. As is well known, bounded approximate units in $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ are obtained by taking a sequence (or net) of non-negative (for simplicity) functions ${\left(k_{\alpha }\right)}_{\alpha \in I}$ with shrinking support and with ${\int }_G{k}_{\alpha }\left(x\right)=1$ for all $\alpha \in I$. Such a sequence is often called a Dirac sequence in the literature, and it is obviously tight and bounded in $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$. It is a simple exercise to verify that ${\mu }_{\alpha }:={\mu }_{k_{\alpha }}$ is then a $w^{\ast }$—convergent net with

$${w^{\ast }-lim}_{\alpha \to \infty }{\mu }_{\alpha }={\delta }_0.$$

(46)

As a consequence we thus have:

Corollary 1.

Given the situation of Theorem 4, and a bounded approximate unit ${\left(g_{\alpha }\right)}_{\alpha \in I}$ in $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$, then one has

$$\underset{\alpha \to \infty }{lim}\parallel g_{\alpha }{•}_{\rho }{f-f\parallel }_{\mathit{B}}=0,\forall f\in \mathit{B}.$$

(47)

As pointed out in Section 5.2 of [5] the net $D_{\mathsf{\Psi }}\mu$ provides a tight $w^{\ast }$—approximation to $\mu$. Combining this fact with the iteration principle (see [28], p. 69) for convergent nets, we come up with a verification of the associativity law which is required for Banach modules.

Corollary 2.

In the situation of Theorem 5 let ${\mu }_1,{\mu }_2\in \mathit{M}\left(G\right)$ be given. Then

$$\underset{\left|\mathsf{\Psi }\right|\to 0}{lim}\parallel D_{\mathsf{\Psi }}{\mu }_1{•}_{\rho }\left(D_{\mathsf{\Psi }}{\mu }_2{•}_{\rho }f\right)-({\mu }_1\star {\mu }_2){•}_{\rho }{f\parallel }_{\mathit{B}}=0,f\in \mathit{B}.$$

(48)

Combining the observations made so far we come to the following final result, which shows that the notion of the integrated group representation arises as a consequence of the approach presented in this paper:

Theorem 6.

Given an isometric, strongly continuous representation of a locally compact group G on a Banach space $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$, the restriction of the Banach module action of $(\mathit{M}\left(G\right),\parallel ·\hspace{0.17em}{\parallel }_{\mathit{M}})$ to the closed ideal $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ turns $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$ into an essential Banach module over $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$.

Conversely, the $w^{\ast }$—continuity of the action of $\mathit{M}\left(G\right)$ for bounded and tight families implies that the action of all of $\mathit{M}\left(G\right)$ is uniquely determined by the integrated group action, i.e., the ${\mathit{L}}^1\left(G\right)$-module properties.

Remark 15. 

We think that it is easier to obtain the integrated group representation of $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ on $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$ by way of restriction, instead of going the more cumbersome way of extending the representation of $\left({\mathit{L}}^1\left(G\right),{\parallel ·\parallel }_1\right)$ by taking (vague) limits.

7. Some Basic Functional Analysis

An important tool from functional analysis is the fact that any Banach space is complete with respect to convergence of the Cauchy net, not just Cauchy sequences.

Although Cauchy nets (implicitly) appear in many places, e.g., in the definition of the Riemann integral, they are typically not discussed as such. The reader could consult Bourbaki ([29]) for details on nets, or [30] (Prop. 2.1.40), but in order to make this note more self-contained, let us collect some relevant facts.

Definition 10.

A set $(I,⪰)$ is called a directed set with respect to the orientation (given by ⪰), if it satisfies the following properties:

1. 

one has transitivity, i.e., if $\alpha ⪰\beta$ and $\beta ⪰\gamma$ then $\alpha ⪰\gamma$;

2. 

Given $\alpha ,\beta \in I$ there exists $\gamma \in I$ such that $\gamma ⪰\alpha$ and $\gamma ⪰\beta$.

Of course, in many cases one can have a partially ordered set and choose $\gamma =max(\alpha ,\beta )$ in the above setting, but this operation need not be meaningful in the general case.

Definition 11.

A net in a set X is a mapping from a directed set $(I,⪰)$, usually described as an indexed family ${\left(x_{\alpha }\right)}_{\alpha \in I}$.

A net in a metric space $(X,d)$ is called convergent if there exists some $x_0\in X$ such that one has: Given $\epsilon >0$ there exists ${\alpha }_0$ such that

$$\alpha ⪰{\alpha }_0\Rightarrow d(x_0,x_{\alpha })<\epsilon .$$

In this case we also write: ${lim}_{\alpha \to \infty }{x}_{\alpha }=x_0.$

Nets are natural generalizations of sequences (and are thus often just called generalized sequences). The analogue of a Cauchy sequence is of course a Cauchy net.

Definition 12.

A net ${\left(x_{\alpha }\right)}_{\alpha \in I}$ is a Cauchy net if for any $\epsilon >0$$\exists {\alpha }_0\in I$ such that

$$\alpha ,\beta ⪰{\alpha }_0\Rightarrow d(x_{\alpha },x_{\beta })<\epsilon .$$

Remark 16. 

Typical nets relevant for our discussion are the nets of the form ${\left({St}_{\rho }g\right)}_{\rho \to 0}$, with $\left[{St}_{\rho }g\right]\left(x\right)={\rho }^{-d}g(x/\rho )$, with ${\rho }_1⪰{\rho }_2$ if ${\rho }_2\le {\rho }_1$, which are used to generate Dirac nets (bounded approximate units) in $\left({\mathit{L}}^1\left({\mathbb{R}}^d\right),{\parallel ·\parallel }_1\right)$.

Other nets occur naturally, such as the index set to the Riemann sums for an integral of the form ${\int }_a^{b}f\left(x\right)dx$, given by some finite decomposition of the interval $[a,b]$ and the choice of a family of points $\left({\xi }_i\right)$ in the corresponding intervals. As we all know, a Riemannian sum is considered good if the maximal length appearing in the corresponding decomposition is controlled by a positive value $\delta >0$. Furthermore, given two decompositions, one can generate the joint refinement as a decomposition which is “better” than both of the decompositions generating it.

Theorem 7.

A normed space $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$ is complete if and only if any Cauchy net is convergent in $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$.

Note: it is well known that a Banach space is complete if and only if every Cauchy sequence is convergent, or equivalently, if every absolutely convergent series is convergent in $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$. It is also clear that any Cauchy sequence is a Cauchy net (using the index set $\mathbb{N}$ with natural ordering as index set). Thus, it is clear that we only have to verify that any Cauchy sequence ${\left(x_{\alpha }\right)}_{\alpha \in I}$ is convergent in $(\mathit{B},\parallel ·\hspace{0.17em}{\parallel }_{\mathit{B}})$.

Proof. 

First we determine a sequence ${\epsilon }_n$, e.g., $\epsilon =2^{-n}$ for $n\ge 1$, and, following the definition of a Cauchy net, a sequence ${\alpha }_n$ such that $\alpha ,\beta ⪰{\alpha }_n$

$$\alpha ,\beta ⪰{\alpha }_n\Rightarrow \parallel x_{\alpha }-x_{\beta }{\parallel }_{\mathit{B}}<{\epsilon }_n.$$

(49)

Without the loss of generality (due to the majorization property) we can determine the sequence ${\alpha }_n$ inductively with ${\alpha }_{n+1}⪰{\alpha }_n$. Formally we choose $x_{{\alpha }_0}=0\in \mathit{B}$.

The series ${\sum }_{n\ge 1}\left(x_{{\alpha }_n}-x_{{\alpha }_{n-1}}\right)$ is then absolutely convergent, because

$$\sum _{n\ge 1}\parallel x_{{\alpha }_n}-x_{{\alpha }_{n-1}}{\parallel }_{\mathit{B}}\le \sum _{n\ge 1}{\epsilon }_n\le 1<\infty .$$

Hence the partial sums are

$$\sum _{n=1}^N\left(x_{{\alpha }_n}-x_{{\alpha }_{n-1}}\right)=x_{{\alpha }_N}(!)$$

are convergent, i.e., there exists some $x_0\in \mathit{B}$ with

$$\underset{n\to \infty }{lim}{x}_{{\alpha }_n}=x_0{in(\mathit{B},\parallel ·\hspace{0.17em}\parallel }_{\mathit{B}}).$$

Invoking the initial Cauchy net condition, we complete the argument by showing (once a limit has been identified) that we indeed have

$$\underset{\alpha \to \infty }{lim}{x}_{\alpha }=x_0{in(\mathit{B},\parallel ·\hspace{0.17em}\parallel }_{\mathit{B}}).$$

□

Remark 17. 

It should be noted as a delicate point that the convergent Cauchy sequence obtained in the proof does not have to be a subnet of the original Cauchy net, because the notation of a subnet (which we do not need here) is more complex than just the idea of a subsequence of a given sequence. At least, it does not just mean reducing the index set (which for sequences has a natural order) to a subset of the original index set with strictly increasing enumeration of the elements of the subsequence.