When Is a Graded Free Complex Exact?

Abstract

Minimal free resolutions of a finitely generated module over a polynomial ring $S=k\left[\mathbf{x}\right]$, with variables $\mathbf{x}=\{x_1,\dots ,x_n\}$ and a field k have been extensively studied. Almost all the results in the literature about minimal free resolutions give their Betti numbers, that is, the ranks of the free modules in the resolution at each degree. Several techniques have been developed to compute Betti numbers, making this a manageable problem in many cases. However, a description of the differentials in the resolution is rarely given, as this turns out to be a more difficult problem. The main purpose of this article is to give a criterion to check when a graded free complex of an S-module is exact. Unlike previous similar criteria, this one allows us to give a description of the differentials using the combinatorics of the S-module. The criterion is given in terms of the Betti numbers of the resolutions in each degree and the set of columns of the matrix representation of the differentials. In the last section, and with the aim of illustrating how to use the criterion, we apply it to one of the first better-understood cases, the edge ideal of the complete graph. However, this criterion can be used to give an explicit description of the differentials of a resolution of several monomial ideals such as the duplication of an ideal, the edge ideal of a cograph, etc.

1. Introduction

In the early 1960s, Irving Kaplansky raised the problem of constructing a minimal free resolution of a monomial ideal I in a polynomial ring $S=k\left[\mathbf{x}\right]$ over a field k in a nonrecursive way. Giving an explicit description of a minimal free resolution of a monomial ideal has been a central problem of combinatorial commutative algebra since then. See, for instance, Refs. [1,2,3,4,5] and the references contained there. Almost all the results about minimal free resolutions give their graded Betti numbers, that is, the ranks of the free module in the resolution at each degree. Since the 1970s, Hochster’s formula [6] has given us a way to calculate the graded Betti numbers of a minimal free resolution of $S/I$, but it is rare to find a good description of its differentials.

In contrast, it is not strange to guess what a resolution of a monomial ideal looks like, in which case it is not so difficult to check that it is a complex. However, in general, to prove that a complex is exact and minimal is the difficult part. There are various tools which can be used to establish exactness, but in general, they are not easy to apply. For instance, in [4] (Theorem 6.4), there is a homotopic criterion for a graded complex to be exact, and in [7], a criterion for exactness in a more general setting is given.

On the other hand, it is common to assume that modules and their free resolutions are graded, which offers some advantages. There are many possible graded structures in S and its modules. For instance, the standard grading on S given by

$$\mathrm{deg}\left(c{\mathbf{x}}^{\mathbf{g}}\right)={\mathbf{g}}_1+\cdots +{\mathbf{g}}_n\mathrm{for}\mathrm{all}\mathbf{g}\in {\mathbb{N}}^n\mathrm{and}c\in k$$

is one of the most used. A little bit less common is to consider the polynomial ring S with the so-called standard multigrading induced by $\mathrm{mdeg}\left(c{\mathbf{x}}^{\mathbf{g}}\right)=\mathbf{g}$ for all $\mathbf{g}\in {\mathbb{N}}^n$ and $c\in k$.

The main purpose of this article is to give a more manageable (at least in the monomial case) criterion to check when a free complex of a graded S-module is exact and minimal. The criterion is given in terms of the ranks of the free modules in a free resolution (which can be obtained by Hochster’s formula) in each degree and the set of columns of the matrix representation of the differentials. Usually, the hardest and nontrivial part of finding a minimal free resolution of a module M is to show that a given free complex is indeed exact and minimal, but using this criterion, it becomes a manageable problem.

The article is organized as follows: In the first section, we review how a ring can be graded and its modules. Then we discuss some of the properties that must be satisfied in order to obtain a good grading for our purposes. Briefly speaking, we require the base monoid of the grading to be noncancellative, reduced and torsion-free. Moreover, by the Grillet Theorem (see [8] Theorem 3.11), such a monoid is a positive affine monoid. We put emphasis on the properties of the natural order induced over the monoid, then we finish by presenting the concepts of non-negative and positive gradings.

The criterion is given in the second section, in which we begin with the following lemma that can be applied in a slightly more general setting.

Lemma 2.Let N be a positively graded finitely generated S-module. If Γ is a homogeneous minimal generating set of N and Λ is an irredundant homogeneous subset of N with $|{\mathsf{\Gamma }}_{\mathbf{c}}|=|{\mathsf{\Lambda }}_{\mathbf{c}}|$ for all $\mathbf{c}\in \mathbb{M}$, then there exists an automorphism φ of N such that

$$\phi \left({\mathsf{\Lambda }}_{\mathbf{c}}\right)={\mathsf{\Gamma }}_{\mathbf{c}}$$

and whose restriction on ${\mathsf{\Lambda }}_{\mathbf{c}}$ is a k-linear map for all $\mathbf{c}\in \mathbb{M}$. Moreover, if M is a matrix representation of φ where Λ and Γ are ordered by their multidegrees in a non-decreasing way, then it is an upper triangular block matrix.

Above, a set of vectors $\mathsf{\Gamma }=\{{\gamma }_1,\cdots ,{\gamma }_s\}$ in an S-module N is called irredundant whenever ${\gamma }_i\notin ⟨{\gamma }_1,\cdots ,\widehat{{\gamma }_i},\cdots ,{\gamma }_s⟩$ for all $1\le i\le s$. Lemma 2 is similar to the foundational Theorem 2.12 given in [4]. However, there exists a crucial difference between them, Lemma 2 does not assume that $\mathsf{\Gamma }$ and $\mathsf{\Lambda }$ are both minimal homogeneous generators of N as in [4] (foundational Theorem 2.12). Actually, we deduce that an irredundant homogeneous subset of N is a minimal homogeneous generator of N just by comparing the ranks at each degree with a minimal homogeneous generator set of N. As a consequence, we obtain the following criterion to check when a complex is indeed exact.

Theorem 2.If M is a finitely generated positively graded S-module,

$${\mathbf{F}}_{•}:0\leftarrow M\stackrel{d_0}{\leftarrow }{F}_0\stackrel{d_1}{\leftarrow }{F}_1\leftarrow \cdots \stackrel{d_p}{\leftarrow }{F}_p\leftarrow 0$$

is a graded minimal free resolution of M and

$${\mathbf{C}}_{•}:0\leftarrow M\stackrel{{\delta }_0}{\leftarrow }{C}_0\stackrel{{\delta }_1}{\leftarrow }{C}_1\leftarrow \cdots \stackrel{{\delta }_p}{\leftarrow }{C}_p\leftarrow 0$$

is a graded free complex of M such that

$$F_i=\underset{\mathbf{a}\in A_i\subset \mathbb{M}}{⨁}S(-\mathbf{a})=C_i$$

as free graded S-modules and the column sets, $C\left(D_i\right)$ of the matrix representations $D_i$ of the differentials ${\delta }_i$ are irredundant for all $0⩽i⩽p$, then ${\mathbf{C}}_{•}$ is isomorphic to ${\mathbf{F}}_{•}$.

In the third section, we construct a complex for the edge ideal of the complete graph in terms of some of its induced subgraphs as those given in [9] which is equivalent to the given in [10]. We use the criterion to prove that this complex is indeed exact.

2. Graded Rings and Modules

Before talking about graded complexes, we must first define what it means for a ring and module to be graded. Briefly, a grading of a ring or module consists of a decomposition of its additive structure indexed by a monoid. In the first subsection, we define, in the most general setting, a grading over a ring and a module.

On the other hand, any monoid is naturally endowed with a preorder, which becomes an order whenever the monoid is commutative, cancellative, and reduced. Furthermore, this order induces an order on its homogeneous components and, therefore, also on the elements of the ring or module which we are grading. This order plays an important role in the study of grading rings or modules. In the second subsection, we establish the conditions that must be satisfies the base monoid with the purpose that this natural order will be a partial well order.

In the third subsection, we concentrate on gradings over the polynomial ring $S=k\left[\mathbf{x}\right]$ and their free modules. We finish this section by introducing shifted gradings and homogeneous homomorphisms between grading modules.

2.1. Graded Rings and Modules

A grading over a ring R is a pair $\mathsf{\Omega }=(\mathbb{M},{\left\{R_{\mathbf{a}}\right\}}_{\mathbf{a}\in \mathbb{M}})$, which consists of a monoid $\mathbb{M}=(M,·)$ and a sequence ${\left\{R_{\mathbf{a}}\right\}}_{\mathbf{a}\in \mathbb{M}}$ of subgroups of the additive group of R such that

$$R=\underset{\mathbf{a}\in \mathbb{M}}{⨁}{R}_{\mathbf{a}}\mathrm{as}\mathrm{additive}\mathrm{groups}\mathrm{and}{R}_{\mathbf{a}}{R}_{\mathbf{b}}\subseteq R_{\mathbf{a}·\mathbf{b}}\mathrm{for}\mathrm{all}\mathbf{a},\mathbf{b}\in \mathbb{M}.$$

That is, a ring is endowed with a grading whenever it can be decomposed into a direct sum of some of its additive subgroups in such a way that the multiplicative structure of the ring is compatible with the monoid operation. We say that $\mathbb{M}$ is the base monoid of the grading. If the ring is commutative, then the monoid which we graded it with must also be commutative. Therefore, since we only deal with commutative rings, from here on out, all the base monoids will be commutative and the monoid operation will be denoted by +. Although two different gradings can have the same base monoid (see Section 2.3 for an example), we simply say that a ring R is $\mathbb{M}$-graded.

In a similar way, a module N over an $\mathbb{M}$-graded ring R is $\mathbb{M}$-graded whenever we have a sequence ${\left\{N_{\mathbf{a}}\right\}}_{\mathbf{a}\in \mathbb{M}}$ of subgroups of the additive group of N such that

$$N=\underset{\mathbf{a}\in \mathbb{M}}{⨁}{N}_{\mathbf{a}}\mathrm{as}\mathrm{additive}\mathrm{groups}\mathrm{and}{R}_{\mathbf{a}}{N}_{\mathbf{b}}\subseteq N_{\mathbf{a}+\mathbf{b}}\mathrm{for}\mathrm{all}\mathbf{a},\mathbf{b}\in \mathbb{M}.$$

That is, in a similar way that with a ring, a module is endowed with a grading whenever its additive group can be decomposed as a direct sum of some of its subgroups in such a way that the multiplicative structure of the components of the decomposition of the module and the base ring is compatible with the monoid operation. We recall that when we say that an R-module is $\mathbb{M}$-graded, we are necessarily assuming that the base ring R is also $\mathbb{M}$-graded.

Remark 1.

The multiplicative condition $R_{\mathbf{a}}{N}_{\mathbf{b}}\subseteq N_{\mathbf{a}+\mathbf{b}}$ for graded modules corresponds to the multiplicative condition for rings when it is considered as a module over itself.

Definition 1.

The additive subgroups $N_{\mathbf{a}}$ in the decomposition of a grading are its homogeneous components and their elements are called homogeneous of degree $\mathbf{a}$. We write ${\mathrm{mdeg}}_{\mathsf{\Omega }}\left(m\right)=\mathbf{a}$ for $m\in N$ when $m\in N_{\mathbf{a}}$.

In a similar way, a subset A is homogeneous whenever its elements are homogeneous. A grading allows decomposing each element of the ring or module on its homogeneous parts, which in many cases makes it more manageable. Several ring and module concepts can be specialized to take advantage of the fact that they are endowed with a grading. For instance, it is not difficult to check that any graded R-module has a homogeneous minimal set of generators, see Proposition 2.1 [4]. Thus, homogeneity is a key concept in graded rings and modules.

Remark 2.

We recall that the zero (additive identity) of the ring or module belongs to all the homogeneous components of a grading. Thus, the zero is considered of undetermined degree.

Any ring can be graded in a trivial way over the zero monoid by taking $R_0=R$. Thus not just any graduation contributes with an interesting additional structure over a ring or a module. In general, it is not required that the homogeneous components of a grading be non zero.

To avoid the uncorrespondence between the base monoid and the grading, we introduce the concept of a faithful grading. A grading is called faithful whenever all its homogeneous components are not equal to zero. We would like to note that every grading $\mathsf{\Omega }=(\mathbb{M},{\left\{R_{\mathbf{a}}\right\}}_{\mathbf{a}\in \mathbb{M}})$ over a ring is equivalent to the faithful grading ${\mathsf{\Omega }}^{\prime }=({\mathbb{M}}^{\prime },{\left\{R_{\mathbf{a}}\right\}}_{\mathbf{a}\in {\mathbb{M}}^{\prime }})$ where ${\mathbb{M}}^{\prime }$ is the submonoid of $\mathbb{M}$ given by ${\mathbb{M}}^{\prime }=\{\mathbf{a}\in \mathbb{M}:R_{\mathbf{a}}\ne 0\}$. Unfortunately, ${\mathbb{M}}^{\prime }$ as defined is not a monoid. Still, we can find a monoid that serves this purpose.

Definition 2.

A grading ${\mathsf{\Omega }}^{\prime }=({\mathbb{M}}^{\prime },{\left\{R_{\mathbf{a}}^{\prime }\right\}}_{\mathbf{a}\in {\mathbb{M}}^{\prime }})$ is said to be a corefinement of $\mathsf{\Omega }=(\mathbb{M},{\left\{R_{\mathbf{a}}\right\}}_{\mathbf{a}\in \mathbb{M}})$ whenever there exists a monoid homomorphism $\psi :\mathbb{M}\to {\mathbb{M}}^{\prime }$ such that

$$R_{\mathbf{a}}\simeq R_{\psi \left(\mathbf{a}\right)}^{\prime }\mathit{as}\mathit{additive}\mathit{groups}\mathit{for}\mathit{all}\mathbf{a}\in \mathbb{M}\mathit{such}\mathit{that}{R}_{\mathbf{a}}\ne 0$$

and ${\psi |}_{\{\mathbf{a}\in M:R_{\mathbf{a}}\ne 0\}}$ is a bijection onto $\{\mathbf{b}\in M^{\prime }:R_{\mathbf{b}}\ne 0\}$.

Example 1.

The induced $\mathbb{Z}-$grading Ω on $R=k\left[x\right]/⟨x^2⟩$ is given by $R_0=k$, $R_1={⟨x⟩}_k$ and $R_n=0$ for $n\in \mathbb{Z}\setminus \{0,1\}$. We can consider a ${\mathbb{Z}}_2-$grading ${\mathsf{\Omega }}^{\prime }$ on R given by $R_{\left[0\right]}=k,R_{\left[1\right]}={⟨x⟩}_k$. Then, the canonical projection $\pi :\mathbb{Z}\to {\mathbb{Z}}_2$ satisfies the conditions for ${\mathsf{\Omega }}^{\prime }$ to be a corefinement of Ω.

Example 2.

We can also define a ${\mathbb{Z}}_4$-grading on $R=k\left[x\right]/⟨x^2⟩$ by $R_{\left[0\right]}=k$, $R_{\left[1\right]}={⟨x⟩}_k$, $R_{\left[2\right]}=R_{\left[3\right]}=0$. This one is also a corefinement of Ω, although it still has null components.

Proposition 1.

Every $\mathbb{M}$-grading of a ring has a faithful corefinement.

Proof. 

Let $\mathsf{\Omega }$ be a $\mathbb{M}$-grading of a ring R. Define $\mathbf{a}\sim \mathbf{b}$ if $R_{\mathbf{a}}=R_{\mathbf{b}}$. Then, ∼ is a congruence over M. Indeed, if $\mathbf{a}\sim \mathbf{b}$ and $\mathbf{c}\sim \mathbf{d}$, then

$$R_{\mathbf{a}+\mathbf{c}}=R_{\mathbf{a}}{R}_{\mathbf{c}}=R_{\mathbf{b}}{R}_{\mathbf{d}}=R_{\mathbf{b}+\mathbf{d}}$$

which means $\mathbf{a}+\mathbf{c}\sim \mathbf{b}+\mathbf{d}$. This means that we can define a quotient monoid ${\mathbb{M}}^{\prime }=\mathbb{M}/$∼, and the induced grading given by $R_{\left[\mathbf{a}\right]}=R_{\mathbf{a}}$ is faithful. □

From here on out, all the gradings are assumed to be faithful.

Remark 3.

Not any ring can be graded in a non-trivial way. For instance, the ring of the integers $\mathbb{Z}$ cannot be graded in a non-trivial way because its proper subgroups are of the form $k\mathbb{Z}$ for some $2\le k\in {\mathbb{N}}_{+}$ and therefore cannot be the direct sum of some of these subgroups.

When either the ring or module that we are grading is finitely generated, then the base monoid that we can use to grade it must also be finitely generated. Thus, since we deal with finitely generated modules, it is desirable that the base monoid be finitely generated.

Grading imposes some structural restrictions on rings and their modules. For instance, if N is a graded R-module, then $R_{\mathbf{0}}{N}_{\mathbf{a}}\subseteq N_{\mathbf{a}}$ and therefore, $N_{\mathbf{a}}$ is not only an additive group, but an $R_{\mathbf{0}}$-module for all $\mathbf{a}\in \mathbb{M}$. In particular, when $R_{\mathbf{0}}$ is a field k, we find that homogeneous components are actually k-vector spaces. Moreover, if, additionally, N is a finitely generated R-module, then the homogeneous components are finitely dimensional k-vector spaces. Thus, we can briefly think a finitely generated graded R-module with $R_{\mathbf{0}}$ a field, as a kind of a sheaf of finitely dimensional space vectors over a monoid.

At first sight, there is no big difference between the structure imposed by different gradings. For instance, there is not an apparent difference when a ring or module is either graded or multigraded. However, as we show after, depending of the base ring and the module, some gradings are more convenient than others.

Here, we are mostly interested in modules with base ring of a polynomial ring over a field. In particular, we are interested in the kernel of a homogeneous homomorphism between free S-modules.

To finish this subsection, we define when two gradings are equivalent.

Definition 3.

Two gradings $\mathsf{\Omega }=(\mathbb{M},{\left\{R_{\mathbf{a}}\right\}}_{\mathbf{a}\in \mathbb{M}})$ and ${\mathsf{\Omega }}^{\prime }=({\mathbb{M}}^{\prime },{\left\{R_{\mathbf{a}}^{\prime }\right\}}_{\mathbf{a}\in {\mathbb{M}}^{\prime }})$ over a ring R are equivalent, denoted by $\mathsf{\Omega }{\sim }_{\psi }{\mathsf{\Omega }}^{\prime }$, whenever there exists a monoid isomorphism $\psi :\mathbb{M}\to {\mathbb{M}}^{\prime }$ such that

$$R_{\mathbf{a}}\simeq R_{\psi \left(\mathbf{a}\right)}^{\prime }\mathit{as}\mathit{additive}\mathit{groups}\mathit{for}\mathit{all}\mathbf{a}\in \mathbb{M}.$$

In a similar way, two gradings $\Pi =(\mathbb{M},{\left\{N_{\mathbf{a}}\right\}}_{\mathbf{a}\in \mathbb{M}})$ and ${\Pi }^{\prime }=({\mathbb{M}}^{\prime },{\left\{N_{\mathbf{a}}^{\prime }\right\}}_{\mathbf{a}\in {\mathbb{M}}^{\prime }})$ over an R-module N with gradings Ω and ${\mathsf{\Omega }}^{\prime }$ over the base ring R are equivalent, denoted by $\Pi {\sim }_{\psi }{\Pi }^{\prime }$, whenever there exists a monoid isomorphism $\psi :\mathbb{M}\to {\mathbb{M}}^{\prime }$ such that $\mathsf{\Omega }{\sim }_{\psi }{\mathsf{\Omega }}^{\prime }$ and $N_{\mathbf{a}}\simeq N_{\psi \left(\mathbf{a}\right)}^{\prime }$ as additive groups for all $\mathbf{a}\in \mathbb{M}$.

The next very simple example illustrates the concept of equivalence between graded rings.

Example 3.

Consider the grading over the polynomial ring $k\left[x\right]$ in one variable given by

$$k{\left[x\right]}_t=\left\{\begin{array}{cc}{⟨x^{t/2}⟩}_k\hfill & \mathit{if}t\mathit{is}\mathit{even},\hfill \\ 0\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

In other words, we are considering the variable x with degree two instead of degree one as in the classical standard grading. It is not difficult to check that it is an $\mathbb{N}$-grading, which is equivalent to the standard grading (see next subsection for the formal definition) over $k\left[x\right]$.

If the base monoid contains an idempotent element, say, $\mathbf{a}$ (that is, an element such that $\mathbf{a}+\mathbf{a}=\mathbf{a}$) and $p\in R_{\mathbf{a}}$, then $p^n\in R_{\mathbf{a}}$ for all $n\in \mathbb{N}$, which is not a desirable property because the grading cannot distinguish the elements on the set $\{p^n:n\in \mathbb{N}\}$. In the next subsection, we conduct a deeper analysis in order to establish which properties of the monoid imply a desirable property on the grading, using the natural order induced on the base monoid as a guide.

2.2. Positive Monotone Partial Well Orders on the Base Monoid

In this subsection, we study the possible orders over a monoid that are compatible with its operation; we place a particular emphasis on the natural order induced by the monoid operation. We are mainly interested when these orders are positive, monotone, and partial well orders.

First, any monoid is naturally endowed with a preorder structure over it. More precisely, let ${\le }_{\mathbb{M}}$ be the binary relation given by

$$\mathbf{a}{\le }_{\mathbb{M}}\mathbf{b}\mathrm{whenever}\mathbf{a}+\mathbf{c}=\mathbf{b}\mathrm{for}\mathrm{some}\mathbf{c}\in \mathbb{M}.$$

It is not difficult to check that this binary relation is indeed a preorder, that is,

• For all $\mathbf{a}\in \mathbb{M}$, $\mathbf{a}{\le }_{\mathbb{M}}\mathbf{a}$ (reflexive) and
• For all $\mathbf{a},\mathbf{b},\mathbf{c}\in \mathbb{M}$, if $\mathbf{a}{\le }_{\mathbb{M}}\mathbf{b}$ and $\mathbf{b}{\le }_{\mathbb{M}}\mathbf{c}$, then $\mathbf{a}{\le }_{\mathbb{M}}\mathbf{c}$ (transitive).

Remark 4.

Reflexivity follows from the fact that $\mathbf{a}+\mathbf{0}=\mathbf{a}$. In a similar way, transitivity follows because if $\mathbf{a}+\mathbf{d}=\mathbf{b}$ for some $\mathbf{d}\in \mathbb{M}$ and $\mathbf{b}+\mathbf{e}=\mathbf{c}$ for some $\mathbf{c}\in \mathbb{M}$, then $\mathbf{a}+\mathbf{d}+\mathbf{e}=\mathbf{b}+\mathbf{e}=\mathbf{c}$.

As we will see next, several properties of the preorder ${\le }_{\mathbb{M}}$ are directly related with properties of the monoid. For instance, an order ≤ on $\mathbb{M}$ is referred to as positive whenever $0_{\mathbb{M}}\le \mathbf{a}$ for all $\mathbf{a}\in M$. That is, the zero of the monoid is a minimum element under ≤ and a monoid is referred to as reduced whenever $\mathbf{a}+\mathbf{b}=0$ if and only if $\mathbf{a}=0$ (that is, a monoid is reduced whenever it has no inverses). The next result shows that these two concepts are equivalent.

Proposition 2.

A monoid is reduced if and only if the natural order ${\le }_{\mathbb{M}}$ is positive.

Proof. 

It follows directly from the definitions of reduced monoid and positive order. □

Now, in order for a preorder ≤ to be an order, we need that additionally to be antisymmetric. That is, if $\mathbf{a}\le \mathbf{b}$ and $\mathbf{b}\le \mathbf{a}$, then $\mathbf{a}=\mathbf{b}$. On the other hand, a monoid is called cancellative whenever $\mathbf{a}+\mathbf{c}=\mathbf{b}+\mathbf{c}$ implies that $\mathbf{a}=\mathbf{b}$. The next result gives us conditions in such a way that ${\le }_{\mathbb{M}}$ be indeed an order.

Proposition 3.

If a monoid $\mathbb{M}$ is cancellative and reduced, then ${\le }_{\mathbb{M}}$ is antisymmetric.

Proof. 

Let $\mathbf{a},\mathbf{b}\in M$ such that $\mathbf{a}{\le }_{\mathbb{M}}\mathbf{b}$ and $\mathbf{b}{\le }_{\mathbb{M}}\mathbf{a}$. Then, there exists $\mathbf{c},\mathbf{d}\in M$ such that $\mathbf{a}+\mathbf{c}=\mathbf{b}$ and $\mathbf{b}+\mathbf{d}=\mathbf{a}$. Thus, $\mathbf{a}+\mathbf{c}+\mathbf{d}=\mathbf{b}+\mathbf{d}=\mathbf{a}$. Since $\mathbb{M}$ is cancellative, then $\mathbf{c}+\mathbf{d}=0$, which means, since $\mathbb{M}$ is reduced, that $\mathbf{c}=0$, therefore $\mathbf{a}=\mathbf{b}$. □

We say that ${\le }_{\mathbb{M}}$ is the natural order in $\mathbb{M}$. We have a partial converse of previous result.

Proposition 4.

Let $\mathbb{M}$ be a cancelative monoid. If ${\le }_{\mathbb{M}}$ is antisymmetric, then $\mathbb{M}$ is reduced.

Proof. 

We will proceed by contradiction. Assume that $\mathbb{M}$ is not reduced, that is, there exist $0\ne \mathbf{b},\mathbf{c}\in M$ such that $\mathbf{b}+\mathbf{c}=0$. Now, let $0\ne \mathbf{a}\in M$, by the definition of ${\le }_{\mathbb{M}}$,

$$\mathbf{a}{\le }_{\mathbb{M}}\mathbf{a}+\mathbf{b}\mathrm{and}(\mathbf{a}+\mathbf{b}){\le }_{\mathbb{M}}(\mathbf{a}+\mathbf{b})+\mathbf{c}=\mathbf{a}+0=\mathbf{a}.$$

On the other hand, since M is cancellative and $\mathbf{b}\ne 0$, then $\mathbf{a}\ne \mathbf{a}+\mathbf{b}$; a contradiction to the fact that ${\le }_{\mathbb{M}}$ is antisymmetric. □

It is not difficult to check that a cancellative monoid does not have idempotents, therefore, for our purposes, it is desirable for the base monoid to be cancellative and reduced.

On the other hand, we say that an order relation ≤ on a monoid $\mathbb{M}$ is monotone (with respect to the monoid operation) whenever $\mathbf{a}\le \mathbf{b}$ implies that $\mathbf{a}+\mathbf{c}\le \mathbf{b}+\mathbf{c}$ for all $\mathbf{a},\mathbf{b},\mathbf{c}\in \mathbb{M}$. By definition, the natural order on $\mathbb{M}$ is monotone.

Corollary 1.

If $\mathbb{M}$ is cancellative and reduced, then ${\le }_{\mathbb{M}}$ is a positive monotone partial order.

Proof. 

It follows from Propositions 3 and 4. □

Remark 5.

Given a monotone order ≤ on the base monoid $\mathbb{M}$ of a grading of a ring R, the binary relation ${\le }_R$ given by

$$r_1{\le }_R{r}_2\mathit{whenever}{r}_1\in R_{{\mathbf{a}}_1},r_2\in R_{{\mathbf{a}}_2}\mathit{and}{\mathbf{a}}_1{\le }_{\mathbb{M}}{\mathbf{a}}_2$$

is a monotone order on $(R,·)$.

On the other hand, we say that an order ${\le }_2$ is a refinement of an another order ${\le }_1$ whenever $\mathbf{a}{\le }_1\mathbf{b}$ implies that $\mathbf{a}{\le }_2\mathbf{b}$. In other words, if $(\le )$ is the subset of $M\times M$ that defines the binary relation ≤, then ${\le }_2$ is a refinement of ${\le }_1$ if and only if $\left({\le }_1\right)\subseteq \left({\le }_2\right)$.

Proposition 5.

If M is a cancellative reduced monoid, then any positive monotone order ≤ is a refinement of the natural order ${\le }_{\mathbb{M}}$.

Proof. 

Let $\mathbf{a},\mathbf{b},\mathbf{c}\in M$ such that $\mathbf{a}+\mathbf{b}=\mathbf{c}$, that is, $\mathbf{a}{\le }_{\mathbb{M}}\mathbf{c}$. Since ≤ is positive, then $0\le \mathbf{b}$. Moreover, since ≤ is monotone, then $\mathbf{a}=\mathbf{a}+0\le \mathbf{a}+\mathbf{b}=\mathbf{c}$ and therefore, ≤ is a refinement of ${\le }_{\mathbb{M}}$. □

Remark 6.

In other words, the natural order ${\le }_{\mathbb{M}}$ of a reduced cancellative monoid $\mathbb{M}$ is the minimum element in the set of all positive monotone orders over $\mathbb{M}$ and, therefore, some of its properties are inherited to any positive monotone order ≤ in $\mathbb{M}$.

Now, we turn our attention to a central concept in order theory: antichains. Elements $\mathbf{a},\mathbf{b}$ in M such that either $\mathbf{a}\le \mathbf{b}$ or $\mathbf{b}\le \mathbf{a}$ are called comparable. Otherwise, they are called incomparable, denoted by $\mathbf{a}\perp \mathbf{b}$. A set of incomparable elements in M is an antichain. It is not difficult to check that if ${\le }_{\mathbb{M}}$ has no infinite antichains, then neither does any positive monotone order ≤ in $\mathbb{M}$.

On the other hand, a finite set $G=\{{\mathbf{g}}_1,\dots ,{\mathbf{g}}_q\}\subseteq M$ generates $\mathbb{M}$ whenever for all $\mathbf{a}\in M$, there exists $\mathbf{r}\in {\mathbb{N}}^q$ such that $\mathbf{a}={\sum }_{i=1}^q{r}_i{\mathbf{g}}_i$. In this case, we say that $\mathbb{M}$ is finitely generated. The next result shows that if $\mathbb{M}$ is a reduced cancellative monoid, then concepts of no infinite antichain and finitely generated ones are equivalent.

Proposition 6.

If $\mathbb{M}$ is a cancellative reduced monoid, then it is finitely generated if and only if ${\le }_{\mathbb{M}}$ does not contain infinite antichains.

Before we proceed with the proof of Proposition 6, we will introduce the concept of a representation of an element of the monoid. Given a finite generating set $G=\{{\mathbf{g}}_1,\dots ,{\mathbf{g}}_q\}$ of $\mathbb{M}$ a G-representation of $\mathbf{a}\in M$ is a vector $\mathbf{r}\in {\mathbb{N}}^q$ such that $\mathbf{a}={\sum }_{i=1}^q{r}_i{\mathbf{g}}_i$. On the other hand, let ${\le }_{{\mathbb{N}}^q}$ be the natural partial order in the monoid ${\mathbb{N}}^q$, that is, $\mathbf{r}\le \mathbf{s}$ if and only if $r_i\le s_i$ for all $1\le i\le q$.

Proof. 

$(\Rightarrow )$ Let $G=\{{\mathbf{g}}_1,\dots ,{\mathbf{g}}_q\}$ be a minimal generating set of $\mathbb{M}$. It is not difficult to check that $\mathbf{a}$ and $\mathbf{b}$ in M are incomparable under ${\le }_{\mathbb{M}}$ if and only if any G-representations of $\mathbf{a}$ are incomparable under ${\le }_{{\mathbb{N}}^q}$ with any G-representations of $\mathbf{b}$. Thus, if A is an antichain in $\mathbb{M}$, then

$$\mathbb{A}=\{{\mathbf{r}}_i:{\mathbf{r}}_i\mathrm{is}\mathrm{a}G-\mathrm{representation}\mathrm{of}{\mathbf{a}}_i\in A\},$$

is also an antichain of ${\mathbb{N}}^q$ and therefore by [11] (Lemma A) $\left|A\right|=\left|\mathbb{A}\right|$ is finite.

$(\Leftarrow )$ We will prove that if G is a minimal generating set for $\mathbb{M}$, then it is an antichain. If ${\mathbf{g}}_i,{\mathbf{g}}_j\in G$ are such that ${\mathbf{g}}_i{\le }_{\mathbb{M}}{\mathbf{g}}_j$, then ${\mathbf{g}}_i+\mathbf{a}={\mathbf{g}}_j$. Since G is a minimal generating of $\mathbb{M}$, then $\mathbf{a}={\sum }_{\mathbf{g}\in G}{r}_{\mathbf{g}}\mathbf{g}$ for some $r_{\mathbf{g}}\in \mathbb{N}$ with $r_{\mathbf{g}}=0$ for all but a finite number of $\mathbf{g}$.

First, $r_{{\mathbf{g}}_j}\ne 0$, otherwise G will not be a minimal generating set. In a similar way $\mathbf{a}\ne {\mathbf{g}}_j$, otherwise ${\mathbf{g}}_i+{\mathbf{g}}_j={\mathbf{g}}_j$ and since $\mathbb{M}$ is cancellative, then ${\mathbf{g}}_i=0$; a contradiction to the fact that G is a minimal generating set. On the other hand, since $\mathbb{M}$ is cancellative, then ${\mathbf{g}}_i+{\sum }_{{\mathbf{g}}_j\ne \mathbf{g}\in G}{r}_{\mathbf{g}}\mathbf{g}+(r_{{\mathbf{g}}_j}-1){\mathbf{g}}_j=0$ with ${\sum }_{{\mathbf{g}}_j\ne \mathbf{g}\in G}{r}_{\mathbf{g}}\mathbf{g}+(r_{{\mathbf{g}}_j}-1){\mathbf{g}}_j\ne 0$; which is a contradiction to the fact that $\mathbb{M}$ is reduced. Thus, all the elements of G are incomparable for ${\le }_{\mathbb{M}}$ and therefore, it is an antichain. Since $\mathbb{M}$ has no infinite antichains, it means G is finite too, which means that G is finitely generated. □

Remark 7.

In general, the G-representation of an element in $\mathbb{M}$ is not necessarily unique. For instance, a set $G=\{{\mathbf{g}}_1,\dots ,{\mathbf{g}}_q\}$ of a monoid $\mathbb{M}$ is a minimal generating set if and only if G generates $\mathbb{M}$ and the G-representation of each ${\mathbf{g}}_i\in G$ is unique.

Next, we will show that under some assumptions, many properties of the natural induced order of a monoid are inherited from natural order ${\le }_{{\mathbb{N}}^q}$ of ${\mathbb{N}}^q$.

Lemma 1.

Let $\mathbb{M}$ be a cancellative reduced finitely generated monoid and $G=\{{\mathbf{g}}_1,\dots ,{\mathbf{g}}_q\}$ be a subset of $\mathbb{M}$ such that ${\mathbf{g}}_i\ne 0$ for all $1\le i\le q$. If $\mathbf{r}$ and $\mathbf{s}$ are two different G-representations of $\mathbf{a}\in M$, then they are incomparable in $({\mathbb{N}}^q,{\le }_{{\mathbb{N}}^q})$.

Proof. 

We will proceed by contradiction. Assume that $\mathbf{r}{\le }_{{\mathbb{N}}^q}\mathbf{s}$. Thus, since $\mathbb{M}$ is cancellative and ${\sum }_{i=1}^q{r}_i{\mathbf{g}}_i={\sum }_{i=1}^q{s}_i{\mathbf{g}}_i$, we obtain that ${\sum }_{i=1}^q(s_i-r_i){\mathbf{g}}_i=0$. Moreover, since $\mathbf{r}\ne \mathbf{s}$, then $s_j-r_j\ne 0$ for at least some $1\le j\le q$, which is a contradiction to the fact that $\mathbb{M}$ is reduced. □

Now, we turn our attention to descending sequences. A descending chain of ≤ is a sequence ${\left\{{\mathbf{a}}_i\right\}}_{i\in \mathbb{N}}$ of elements such that ${\mathbf{a}}_{i+1}\le {\mathbf{a}}_i$. An order is called a well order whenever it has no infinite descending sequences and infinite antichains.

Proposition 7.

If $\mathbb{M}$ is a finitely generated monoid, then the natural order ${\le }_{\mathbb{M}}$ does not contain infinite descending sequences.

Proof. 

Let ${\left\{{\mathbf{a}}_i\right\}}_{i\in \mathbb{N}}$ be a descending sequence for ${\le }_{\mathbb{M}}$ and $G=\{{\mathbf{g}}_1,\dots ,{\mathbf{g}}_q\}$ be a minimal generating set of $\mathbb{M}$. Thus, ${\mathbf{a}}_0={\sum }_{j=1}^q{r}_i{\mathbf{g}}_i$ for some $r_i\in \mathbb{N}$ for all $1\le j\le q$.

On the other hand, if $\mathbf{a}{\le }_{\mathbb{M}}\mathbf{b}$, then there exists a G-representation ${\mathbf{r}}_{\mathbf{a}}$ of $\mathbf{a}$ and a G-representation ${\mathbf{r}}_{\mathbf{b}}$ of $\mathbf{b}$ such that ${\mathbf{r}}_{\mathbf{a}}{\le }_{{\mathbb{N}}^q}{\mathbf{r}}_{\mathbf{b}}$. Thus, since any two representations of ${\mathbf{a}}_0$ are incomparable and ${\mathbb{N}}^q$ has no infinite antichains, then there exist only a finite number of elements in $\mathbb{M}$ such that are less or equal to ${\mathbf{a}}_0$ under ${\le }_{\mathbb{M}}$ and we obtain the result. □

Using previous results, we obtain that the natural order of a cancellative reduced finitely generated monoid is a partial well order.

Corollary 2.

Let $\mathbb{M}$ be a cancellative reduced monoid. If $\mathbb{M}$ is finitely generated, then ${\le }_{\mathbb{M}}$ is a partial well order.

Proof. 

It follows from Propositions 6 and 7. □

Moreover, we have that any positive monotone order over a cancellative reduced finitely generated monoid is a partial well order.

Proposition 8.

Let $\mathbb{M}$ be a cancellative reduced monoid. If $\mathbb{M}$ is finitely generated, then any positive monotone order ≤ over $\mathbb{M}$ is a partial well order.

Proof. 

By Proposition 5, ≤ is a refinement of ${\le }_{\mathbb{M}}$. Thus, if $A={\left\{{\mathbf{a}}_i\right\}}_{i\in I}$ is an antichain of ≤, then it is also an antichain of ${\le }_{\mathbb{M}}$ and, therefore, A must be finite.

Now, let $A={\left\{{\mathbf{a}}_i\right\}}_{i\in I\subseteq \mathbb{N}}$ be a descending sequence in $\mathbb{M}$ with respect to ≤. It only remains to prove that A must be finite. Let $B_0=\{i\in I:{\mathbf{a}}_i{\le }_{\mathbb{M}}{\mathbf{a}}_0\}$ and $C_1=I-B_0$ and, in general,

$$B_j=\{i\in C_j:{\mathbf{a}}_i{\le }_{\mathbb{M}}{\mathbf{a}}_{s_j}\}\mathrm{where}{s}_j=\min \{i:i\in C_j\}\mathrm{and}{C}_{j+1}=C_j-B_j.$$

Additionally, let $J=\{k_j:k_j=\min \{i:i\in B_j\}\}$ and $A^{\prime }=\{{\mathbf{a}}_j:j\in J\}$ be a subsequence of A.

By construction, the subsequence $A^{\prime }$ of A is an antichain with respect to ${\le }_{\mathbb{M}}$ and, therefore, finite. Using similar arguments to those given in Proposition 7 we obtain that all the sets $B_j$’s are finite. Finally, since $I={\bigsqcup }_{j\in J}{B}_j$, then I is finite and, therefore, so is A. □

Thus, from here on out, we will assume that the base monoid which we use to grade as well as commutative is cancellative, reduced and finitely generated.

Now, we discuss the effect of torsion on gradings. Torsion on monoids generalizes the classical notion of torsion on groups.

Definition 4.

We say that a monoid $\mathbb{M}$ is torsion-free if $k\mathbf{a}=k\mathbf{b}$ for some $\mathbf{a},\mathbf{b}\in M$ and $k\in {\mathbb{N}}_{+}$ implies $\mathbf{a}=\mathbf{b}$. Otherwise, we say that $\mathbb{M}$ has torsion.

Remark 8.

We say a monoid is cyclic torsion-free whenever $k\mathbf{a}=0$ for some $k\in {\mathbb{N}}_{+}$ with $\mathbf{a}\in M$ implies that $\mathbf{a}=0$. It is not difficult to check that reduced implies cyclic torsion-free. We recall that a group is torsion-free when it is cyclic torsion-free.

As we mentioned before, a desirable property of a grading is that its zero homogeneous component would be a field. Gradings with a base monoid with torsion have the disadvantage that we cannot guarantee that the zero homogeneous component is a field. For instance, consider the ${\mathbb{Z}}_2$-grading over S given by

$$S_0={⟨\{{\mathbf{x}}^{\mathbf{b}}:{\mathbf{b}}_1+\cdots +{\mathbf{b}}_n\equiv 0\left(\mathrm{mod}2\right)\}⟩}_k\mathrm{and}{S}_1={⟨\{{\mathbf{x}}^{\mathbf{b}}:{\mathbf{b}}_1+\cdots +{\mathbf{b}}_n\equiv 1\left(\mathrm{mod}2\right)\}⟩}_k.$$

Even more, in this case, the zero homogeneous component is a vector space of infinite dimension. In some sense, this example results in being a little bit pathological in part because the binary relation ${\le }_{{\mathbb{Z}}_2}$ is not even an order. In general, the torsion in the base monoid does not imply this behaviour, but it is still not good enough for our purposes.

The most studied gradings are ones in which their base monoids are positive affine monoids, that is, finitely generated submonoids of ${\mathbb{N}}^q$ for some $q\in \mathbb{N}$. The next result shows that any positive affine monoid is isomorphic to a commutative, cancellative, reduced, finitely generated and torsion-free monoid. If we drop the condition of being reduced, we obtain affine monoids which are finitely generated submonoids of ${\mathbb{Z}}^q$ for some $q\in \mathbb{N}$.

Theorem 1

(Grillet’s Theorem, see [8] Theorem 3.11). Let $\mathbb{M}$ be a finitely generated monoid. Then, $\mathbb{M}$ is commutative, cancellative, reduced and torsion-free if and only if it is isomorphic to a positive affine monoid.

Remark 9.

Any monomial order corresponds to an order induced by gradings of the polynomial ring S with the natural numbers as base monoid and k-vector space ${⟨{\mathbf{x}}^{\mathbf{a}}⟩}_k$ for all $\mathbf{a}\in {\mathbb{N}}^n$ as homogeneous components.

We finish this subsection by presenting the main concept of this section. First, a $\mathbb{M}$-grading over a module N is called non-negative whenever there is a partial well order. $\mathbb{M}$ can be endowed with a monotone positive partial well order. Next, we show an example of a non-negative grading. Let $S=k\left[\mathbf{x}\right]$ be the polynomial ring over a field k and consider the $\mathbb{N}$-grading defined by the decomposition $S={⨁}_{d\in \mathbb{N}}{T}_d$ where $T_d={⟨\{{\mathbf{x}}^{\mathbf{a}}:{\mathbf{a}}_n=d\}⟩}_k$. It is not difficult to confirm that it is a faithful non-negative grading. However, it still has the disadvantage that it cannot distinguish between polynomials in the first $n-1$ variables.

Definition 5.

A non-negative grading over a polynomial ring over a field is called positive whenever the zero homogeneous component is equal to the field.

When S is graded by a positive grading, we say that it is positively graded. Next, we present an example of a positive grading where the base monoid has torsion. Let $\mathbb{M}$ be the commutative monoid generated by a and b subject to $2a=2b$. It is not difficult to check that it can be described as the set $M=\{sa:s\in \mathbb{N}\}\bigsqcup \{sa+b:s\in \mathbb{N}\}$ with an operation given by

$$(s_{1}a+t_{1}b)+(s_{2}a+t_{2}b)=(s_1+s_2+w)a+(t_1+t_2)\left(\mathrm{mod}2\right)b\mathrm{where}w=⌊\frac{t_1+t_2}{2}⌋.$$

Now, if $S_{sa+tb}={⟨\{x^u{y}^v:u+v=s+t\mathrm{and}u,v\in \mathbb{N}\}⟩}_k$, then $\mathsf{\Omega }=(\mathbb{M},{\left\{S_{\mathbf{m}}\right\}}_{\mathbf{m}\in \mathbb{M}})$ is an $\mathbb{M}$-grading of the polynomial ring $S=k[x,y]$ over a field k.

In [2] (Chapter 8), there is a similar discussion concerning which gradings have some desirable properties. Our approach is different to these in the sense that we use the natural order on the base monoid as a guide to deduce which properties must satisfy the base monoid in order to achieve a partial well order, which is good for our purposes.

Once we have discussed what it means to be graded and their positive monotone partial well orders, we turn our attention to the particular case of how to grade the polynomial ring S.

2.3. Grading the Polynomial Ring S and Their Free Modules

Now, we will focus on gradings over the polynomial ring $S=k\left[\mathbf{x}\right]$ and their free modules. The most common grading over the polynomial ring S is the $\mathbb{N}$-grading defined by the decomposition

$$S=\underset{d\in \mathbb{N}}{⨁}{S}_d\mathrm{where}{S}_d={⟨\{{\mathbf{x}}^{\mathbf{a}}:{\mathbf{a}}_1+\cdots +{\mathbf{a}}_n=d\}⟩}_k,$$

which is called the standard grading. We recall that, given a subset $\mathbf{A}$ of ${\mathbb{N}}^n$, ${⟨\{{\mathbf{x}}^{\mathbf{a}}:\mathbf{a}\in \mathbf{A}\}⟩}_k$ denotes the additive subgroup of $S=k\left[\mathbf{x}\right]$ generated by $\{{\mathbf{x}}^{\mathbf{a}}:\mathbf{a}\in \mathbf{A}\}$. Since $S_{\mathbf{0}}=k$, then in a natural way, ${⟨\{{\mathbf{x}}^{\mathbf{a}}:\mathbf{a}\in \mathbf{A}\}⟩}_k$ is also endowed with the structure of k-vector space.

Another grading over S is the ${\mathbb{N}}^n$-grading defined by the decomposition

$$S=\underset{\mathbf{a}\in {\mathbb{N}}^n}{⨁}{S}_{\mathbf{a}}\mathrm{where}{S}_{\mathbf{a}}={⟨{\mathbf{x}}^{\mathbf{a}}⟩}_k,$$

which is called standard multigrading over S. It is not difficult to see that when $n=1$, these two gradings are equivalent. By contrast, when $n\ge 2$, it can be seen that they are not equivalent.

Moreover, the dimension of the k-vector spaces $S_d$ and $T_d$ from the grading defined in the previous subsection are different and, therefore, they cannot be equivalent. Thus, a module can have non-equivalent gradings with the same base monoid. Additionally, S has the following different gradings.

Given a multiset $\mathbf{D}=\{{\mathbf{d}}_1,\dots ,{\mathbf{d}}_t\}$ of ${\mathbb{Z}}^m$, let ${\mathbb{M}}_{\mathbf{D}}$ be the affine monoid of ${\mathbb{Z}}^m$ generated by $\mathbf{D}$ and $T_{\mathbf{m}}^{\mathbf{D}}={⟨\{{\mathbf{x}}^{\mathbf{a}}:D\mathbf{a}=\mathbf{m}\}⟩}_k$, where D is the matrix whose columns are the vectors in $\mathbf{D}$. It is not difficult to check that ${\mathsf{\Gamma }}_{\mathbf{D}}=({\mathbb{M}}_{\mathbf{D}},{\left\{T_{\mathbf{m}}^{\mathbf{D}}\right\}}_{\mathbf{m}\in {\mathbb{M}}_{\mathbf{D}}})$ is a grading of S.

Proposition 9.

Two gradings ${\mathsf{\Gamma }}_{\mathbf{D}}$ and ${\mathsf{\Gamma }}_{{\mathbf{D}}^{\prime }}$ are equivalent if and only if the base monoids ${\mathbb{M}}_{\mathbf{D}}$ and ${\mathbb{M}}_{{\mathbf{D}}^{\prime }}$ are isomorphic.

Proof. 

If ${\mathbb{M}}_{\mathbf{D}}$ and ${\mathbb{M}}_{{\mathbf{D}}^{\prime }}$ are isormophic, then there exists an isomorphism $\psi :{\mathbb{M}}_{\mathbf{D}}\to {\mathbb{M}}_{{\mathbf{D}}^{\prime }}$ such that $\psi \left({\mathbf{d}}_{\mathbf{i}}\right)={\mathbf{d}}_{\mathbf{i}}^{\prime }$. Take ${\mathbf{x}}^{\mathbf{a}}$ in $T_m^{\mathbf{D}}$, it means, $D\mathbf{a}=m$, which is the same as $a_1{\mathbf{d}}_1+\not\equiv a_t{\mathbf{d}}_t=m$. Applying $\psi$ on both sides, we obtain that $a_1{{\mathbf{d}}^{\prime }}_1+\not\equiv a_t{{\mathbf{d}}^{\prime }}_t=\psi \left(m\right)$, that is, $D^{\prime }\mathbf{a}=\psi \left(m\right)$, and thus ${\mathbf{x}}^{\mathbf{a}}$ is in $T_{\psi \left(m\right)}^{{\mathbf{D}}^{\prime }}$. Therefore, $T_m^{\mathbf{D}}\simeq T_{\psi \left(m\right)}^{{\mathbf{D}}^{\prime }}$ and ${\mathsf{\Gamma }}_{\mathbf{D}}$ and ${\mathsf{\Gamma }}_{{\mathbf{D}}^{\prime }}$ are equivalent. The converse is clear from the definition. □

Remark 10.

The standard degree is the grading induced by the row matrix $\mathbf{D}=(1\cdots 1)$ and the standard multigrading is the grading induced by the identity matrix $I_n$.

In a more general setting, as the next two results show any grading of S, this comes from a monoid homomorphism.

Proposition 10.

If $\mathsf{\Gamma }=(\mathbb{M},{\left\{S_{\mathbf{m}}\right\}}_{\mathbf{m}\in \mathbb{M}})$ is a faithful grading of S, then ${\varphi }_{\mathsf{\Gamma }}:{\mathbb{N}}^n\to \mathbb{M}$ given by ${\varphi }_{\mathsf{\Gamma }}\left(\mathbf{a}\right)=\mathbf{m}$ whenever ${\mathbf{x}}^{\mathbf{a}}\in S_{\mathbf{m}}$ and ${\varphi }_{\mathsf{\Gamma }}\left(\mathbf{0}\right)=0_{\mathbb{M}}$, is a surjective monoid homomorphism.

Proof. 

First, ${\varphi }_{\mathsf{\Gamma }}$ is well defined because $S_{\mathbf{m}}\cap S_{{\mathbf{m}}^{\prime }}=0$ for all $\mathbf{m},{\mathbf{m}}^{\prime }\in \mathbb{M}$. Now, let $\mathbf{a},\mathbf{b}\in {\mathbb{N}}^n$ and $\mathbf{m},\mathbf{n}\in \mathbb{M}$ such that ${\varphi }_{\mathsf{\Gamma }}\left(\mathbf{a}\right)=\mathbf{m}$ and ${\varphi }_{\mathsf{\Gamma }}\left(\mathbf{b}\right)=\mathbf{n}$. That is, ${\mathbf{x}}^{\mathbf{a}}\in S_{\mathbf{m}}$ and ${\mathbf{x}}^{\mathbf{b}}\in S_{\mathbf{n}}$. Thus, ${\mathbf{x}}^{\mathbf{a}+\mathbf{b}}={\mathbf{x}}^{\mathbf{a}}{\mathbf{x}}^{\mathbf{b}}\in S_{\mathbf{m}}{S}_{\mathbf{n}}\subseteq S_{\mathbf{m}+\mathbf{n}}$ and, therefore, ${\varphi }_{\mathsf{\Gamma }}(\mathbf{a}+\mathbf{b})=\mathbf{m}+\mathbf{n}={\varphi }_{\mathsf{\Gamma }}\left(\mathbf{a}\right)+{\varphi }_{\mathsf{\Gamma }}\left(\mathbf{b}\right)$. Finally, it is clear that ${\varphi }_{\mathsf{\Gamma }}$ is surjective if and only if $\mathsf{\Gamma }$ is faithful. □

The next result is, in a way, the converse of the previous one.

Proposition 11.

If $\varphi :{\mathbb{N}}^n\to \mathbb{M}$ is a surjective monoid homomorphism and

$$S_{\mathbf{a}}={⟨\{{\mathbf{x}}^{\mathbf{b}}:\mathbf{b}\in {\varphi }^{-1}\left(\mathbf{a}\right)\}⟩}_k\mathrm{for}\mathrm{all}\mathbf{a}\in \mathbb{M},$$

then the pair $\Phi =(\mathbb{M},{\left\{S_{\mathbf{a}}\right\}}_{\mathbf{a}\in \mathbb{M}})$ is a faithful $\mathbb{M}$-grading over S.

Proof. 

Since $\varphi$ is a function, it is easy to see that $S_a\cap S_b=0$. Then, from the definition of $\varphi$, we have that $S={⨁}_{\mathbf{a}\in \mathbb{M}}{S}_{\mathbf{a}}.$ On the other hand, since $\varphi$ is a monoid homomorphism, then $\varphi (\mathbf{c}+\mathbf{d})=\mathbf{a}+\mathbf{b}$ for all $\mathbf{c}\in {\varphi }^{-1}\left(\mathbf{a}\right)$ and $\mathbf{d}\in {\varphi }^{-1}\left(\mathbf{b}\right)$ and therefore

$${\varphi }^{-1}\left(\mathbf{a}\right)+{\varphi }^{-1}\left(\mathbf{b}\right)=\{\mathbf{c}+\mathbf{d}:\mathbf{c}\in {\varphi }^{-1}\left(\mathbf{a}\right)\mathrm{and}\mathbf{d}\in {\varphi }^{-1}\left(\mathbf{b}\right)\}\subseteq {\varphi }^{-1}(\mathbf{a}+\mathbf{b}).$$

Thus, $S_{\mathbf{a}}{S}_{\mathbf{b}}\subseteq S_{\mathbf{a}+\mathbf{b}}$ and, therefore, $\Phi$ is an $\mathbb{M}$-grading over S. □

Remark 11.

The standard grading is induced by the map $\varphi :{\mathbb{N}}^n\to \mathbb{N}$ given by $\varphi \left(\mathbf{a}\right)={\mathbf{a}}_1+\cdots +{\mathbf{a}}_n$ and the standard multigrading is induced by the identity map.

Now, we turn our attention to the gradings over free S-modules. First, we define the classical standard multigrading of $S^r$.

Definition 6.

The standard multigrading over $S^r$ is the ${\mathbb{N}}^n$-grading defined by the decomposition

$$S^r=\underset{\mathbf{a}\in {\mathbb{N}}^n}{⨁}{\left(S_{\mathbf{a}}\right)}^r=\underset{\mathbf{a}\in {\mathbb{N}}^n}{⨁}(S_{\mathbf{a}}\oplus \cdots \oplus S_{\mathbf{a}}),$$

where $S_{\mathbf{a}}$ is the homogeneous component in multidegree $\mathbf{a}$ in the standard multigrading over S.

In other words, the standard multigrading over $S^r$ decomposes it into the k-vector spaces ${\left(S_{\mathbf{a}}\right)}^r$ of dimension r over the field k. Its homogeneous elements are vectors with a term of the form $c{\mathbf{x}}^{\mathbf{a}}$ in all its entries. For instance, consider $S=k[x,y]$ and $S^2$ be the free S-module of rank two. In this case, the vector $v_1=(2xy,x)\in S^2$ is not homogeneous because $v_1=(2xy,0)+(0,x)\mathrm{and}(2xy,0)\in S_{xy}\oplus S_{xy}\mathrm{while}(0,x)\in S_x\oplus S_x$. For simplicity, sometimes $S_{(a,b)}$ will be denoted by $S_{x^a{y}^b}$.

The standard multigrading over $S^r$ can be easily generalized by replacing the standard grading on each copy of S.

Definition 7.

Given a sequence $\Phi ={\left\{(\mathbb{M},{\left\{S_{\mathbf{a},i}\right\}}_{\mathbf{a}\in \mathbb{M}})\right\}}_{i=1}^r$ of $\mathbb{M}$-gradings over the polynomial ring S, let ${\mathsf{\Gamma }}_{\Phi }$ be the $\mathbb{M}$-grading over $S^r$ defined by the decomposition

$$S^r=\underset{\mathbf{a}\in \mathbb{M}}{⨁}(S_{\mathbf{a},1}\oplus \cdots \oplus S_{\mathbf{a},r}).$$

Moreover, the $\mathbb{M}$-grading ${\mathsf{\Gamma }}_{\Phi }$ is a positive $\mathbb{M}$-grading over $S^r$ whenever all the M-gradings in Φ over S are positive.

To finish, we introduce shifted gradings and homogeneous homomorphisms between them.

2.4. Homogeneous Homomorphisms and Shifted Gradings

We begin by introducing the shifted grading of a module.

Definition 8.

Given an $\mathbb{M}$-graded R-module N the R-module N shifted by $\mathbf{a}\in \mathbb{M}$, denoted by $N(-\mathbf{a})$, is the R-module N, but generated in the degree $\mathbf{a}$. In other words, $N{(-\mathbf{a})}_{\mathbf{a}+\mathbf{b}}=N_{\mathbf{b}}$ for all $\mathbf{b}\in \mathbb{M}$.

For simplicity, sometimes, $S(-\mathbf{a})$ will be denoted by $S(-{\mathbf{x}}^{\mathbf{a}})$. For instance, if $S=k[x,y]$ is the S-module with the standard multidegree shifted by $(1,2)$, then $1\in S{(-x{y}^2)}_{x{y}^2}$ and $xy\in S{(-x{y}^2)}_{x^2{y}^3}$.

In a similar way, given a finite multiset $\mathbf{A}=\{{\mathbf{a}}_1,\cdots ,{\mathbf{a}}_r\}$ in $\mathbb{M}$, the free R-module $R^r$ shifted by $\mathbf{A}$, denoted by $R(-\mathbf{A})$, is the direct sum ${⨁}_{{\mathbf{a}}_i\in \mathbf{A}}R(-{\mathbf{a}}_i)$ of R-modules shifted by each element in $\mathbf{A}$. That is, $R(-\mathbf{A})$ is the free R-module minimally generated by elements of degrees ${\mathbf{a}}_1,\cdots ,{\mathbf{a}}_r$ and its grading is given by

$$R(-\mathbf{A})=\underset{\mathbf{b}\in \mathbb{M}}{⨁}\left(\underset{1\le i\le r}{⨁}R{(-{\mathbf{a}}_i)}_{\mathbf{b}}\right)=\underset{\mathbf{b}\in \mathbb{M}}{⨁}(R{(-{\mathbf{a}}_1)}_{\mathbf{b}}\oplus \cdots \oplus R{(-{\mathbf{a}}_r)}_{\mathbf{b}}).$$

Now, we are ready to define homogeneous homomorphisms between graded free S-modules.

Definition 9.

A homomorphism $\varphi :M\to N$ of $\mathbb{M}$-graded R-modules is called graded or homogeneous whenever there exists $\mathbf{c}\in \mathbb{M}$ such that for all $\mathbf{a}\in \mathbb{M}$,

$$\varphi \left(M_{\mathbf{a}}\right)\subseteq N_{\mathbf{a}+\mathbf{c}}.$$

For instance, if $\mathbf{A}=\{{\mathbf{a}}_1,\cdots ,{\mathbf{a}}_s\}$ and $\mathbf{B}=\{{\mathbf{b}}_1,\cdots ,{\mathbf{b}}_t\}$ are finite multisets in $\mathbb{M}$, then a homomorphism of R-modules

$$d:R(-\mathbf{A})\to R(-\mathbf{B})$$

is homogeneous if and only if the columns of its matrix representation matrix $\Delta$ are homogeneous in the standard shifted $\mathbb{M}$-grading of $R(-\mathbf{B})$. For instance, if S is graded with the standard multigrading, then the entries of the matrix representation of a homogeneous homomorphism $d:S(-\mathbf{A})\to S(-\mathbf{B})$ are terms. That is, if $\delta =({\delta }_1,\dots ,{\delta }_r)$ is a column of $\Delta$, then each ${\delta }_i$ is a term $e{\mathbf{x}}^{{\mathbf{c}}_i}$ with $e\in k$ and ${\mathbf{c}}_i+{\mathbf{b}}_i={\mathbf{c}}_j+{\mathbf{b}}_j$ for all $1\le i,j\le r$. By contrast, this is not necessarily true if we use the standard degree to grade S. Which is a slight, but important difference between these two gradings.

3. The Criterion

Once we have defined what it means for a free S-module to be graded, we are almost ready to establish a criterion to check when a set of elements of a finitely generated graded free S-module is indeed a minimal generating set. However, we first need to introduce the concept of irredundancy, which plays a central role in the criterion.

Definition 10.

A set of vectors $\mathsf{\Gamma }=\{{\gamma }_1,\not\equiv ,{\gamma }_s\}$ in an S-module is called irredundant whenever

$${\gamma }_i\notin ⟨{\gamma }_1,\not\equiv ,\widehat{{\gamma }_i},\not\equiv ,{\gamma }_s⟩\mathit{for}\mathit{all}1\le i\le s.$$

We recall that if $\mathsf{\Gamma }$ is a generating set, then, being irredundant is equivalent to being minimal. Furthermore, irredundancy shares some of the spirit of the condition of being linearly independent in linear algebra. For instance, if $\mathsf{\Gamma }$ is irredundant, then

$$\sum _{j\in J}{r}_j{\gamma }_j\ne 0\mathrm{for}\mathrm{all}{r}_j\in k\setminus 0\mathrm{and}J\subseteq \left[s\right]=\{1,\dots ,s\}.$$

Checking irredundancy is more complicated than checking linear independence. Ho-wever, it is simpler than checking that it is a minimal generating set of a S-module. Especially when the entries of the vectors in $\mathsf{\Gamma }$ are monomials, checking irredundancy is a manageable problem, see, for instance, Theorem 4.

From here on out, we assume that any S-module is endowed with a non-negative $\mathbb{M}$-grading $\mathsf{\Omega }$ and ${\le }_{\mathsf{\Omega }}$ is the corresponding monotone positive partial well order in $\mathbb{M}$. Now, given any set $\mathsf{\Gamma }$ of a graded S-module N, let

$${\mathbb{M}}_{\mathsf{\Gamma }}:=\{\mathbf{c}:{\mathsf{\Gamma }}_{\mathbf{c}}\ne \varnothing \}\subseteq \mathbb{M},$$

${\mathrm{Min}}_{{\le }_{\mathsf{\Omega }}}\left({\mathbb{M}}_{\mathsf{\Gamma }}\right)$ be its minimal set of elements under ${\le }_{\mathsf{\Omega }}$ and ${\mathrm{Min}}_{{\le }_{\mathsf{\Omega }}}\left(\mathsf{\Gamma }\right):={⨆}_{\mathbf{c}\in {\mathrm{Min}}_{{\le }_{\mathsf{\Omega }}}\left({\mathbb{M}}_{\mathsf{\Gamma }}\right)}{\mathsf{\Gamma }}_{\mathbf{c}}$, see the next commutative diagram

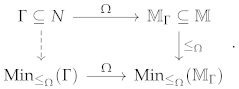We recall that ${\mathrm{Min}}_{{\le }_{\mathsf{\Omega }}}\left({\mathbb{M}}_{\mathsf{\Gamma }}\right)$ is well defined and finite because ${\le }_{\mathsf{\Omega }}$ has neither infinite descending chains, nor infinite antichains. Thus, let

$${\mathsf{\Gamma }}^i=\left\{\begin{array}{cc}{\mathrm{Min}}_{{\le }_{\mathsf{\Omega }}}\left(\mathsf{\Gamma }\right)\hfill & \mathrm{if}i=1,\hfill \\ {\mathrm{Min}}_{{\le }_{\mathsf{\Omega }}}(\mathsf{\Gamma }\setminus {\mathsf{\Gamma }}^1\cup \cdots \cup {\mathsf{\Gamma }}^{i-1})\hfill & \mathrm{if}i\ge 2.\hfill \end{array}\right.$$

Since ${\mathrm{Min}}_{{\le }_{\mathsf{\Omega }}}\left(\mathsf{\Gamma }\right)\ne \varnothing$ for all $\mathsf{\Gamma }\ne \varnothing$, then, if $\mathsf{\Gamma }$ is finite, then there exists a natural number $c\left(\mathsf{\Gamma }\right)<\infty$ such that

$$\mathsf{\Gamma }=\bigcup _{1\le i\le c\left(\mathsf{\Gamma }\right)}{\mathsf{\Gamma }}^i\mathrm{with}{\mathsf{\Gamma }}^i\ne \varnothing \mathrm{for}\mathrm{all}1\le i\le c\left(\mathsf{\Gamma }\right).$$

We call the number $c\left(\mathsf{\Gamma }\right)$ as the complexity number of $\mathsf{\Gamma }$ with respect to the grading $\mathsf{\Omega }$. Finally, we are ready to present the main result of this section. From here on out, we assume that all the free S-modules are positively graded by a $\mathbb{M}$-grading $\mathsf{\Omega }$.

Lemma 2.

Let N be a positively graded finitely generated S-module. If Γ is a homogeneous minimal generating set of N and Λ is an irredundant homogeneous subset of N with $|{\mathsf{\Gamma }}_{\mathbf{c}}|=|{\mathsf{\Lambda }}_{\mathbf{c}}|$ for all $\mathbf{c}\in \mathbb{M}$, then there exists an automorphism φ of N such that

$$\phi \left({\mathsf{\Lambda }}_{\mathbf{c}}\right)={\mathsf{\Gamma }}_{\mathbf{c}}$$

and whose restriction on ${\mathsf{\Lambda }}_{\mathbf{c}}$ is a k-linear map for all $\mathbf{c}\in \mathbb{M}$. Moreover, if M is a matrix representation of φ where Λ and Γ are ordered by its multidegree on a nondecreasing way, then it is an upper triangular block matrix.

Proof. 

Firstly, given $\lambda \in \mathsf{\Lambda }$, let ${\mathsf{\Gamma }}_{<\lambda }=\{\gamma \in \mathsf{\Gamma }:{\mathrm{mdeg}}_{\mathsf{\Omega }}\left(\gamma \right)<{\mathrm{mdeg}}_{\mathsf{\Omega }}\left(\lambda \right)\}$, ${\mathsf{\Gamma }}_{>\lambda }=\{\gamma \in \mathsf{\Gamma }:{\mathrm{mdeg}}_{\mathsf{\Omega }}\left(\gamma \right)>{\mathrm{mdeg}}_{\mathsf{\Omega }}\left(\lambda \right)\}$, ${\mathsf{\Gamma }}_{=\lambda }=\{\gamma \in \mathsf{\Gamma }:{\mathrm{mdeg}}_{\mathsf{\Omega }}\left(\gamma \right)={\mathrm{mdeg}}_{\mathsf{\Omega }}\left(\lambda \right)\}$ and ${\mathsf{\Gamma }}_{\perp \lambda }=\mathsf{\Gamma }\setminus ({\mathsf{\Gamma }}_{<\lambda }\cup {\mathsf{\Gamma }}_{>\lambda }\cup {\mathsf{\Gamma }}_{=\lambda })$. That is, ${\mathsf{\Gamma }}_{\perp \lambda }$ are the elements in $\mathsf{\Gamma }$ that are not comparable with $\lambda$.

Since $\mathsf{\Gamma }$ is a generating set of N, then for all $\lambda \in \mathsf{\Lambda }\subset N$, there exists $r_{\gamma }$’s in S such that

$$\lambda =\sum _{\gamma \in \mathsf{\Gamma }}{r}_{\gamma }\gamma =\sum _{\gamma \in {\mathsf{\Gamma }}_{<\lambda }}{r}_{\gamma }\gamma +\sum _{\gamma \in {\mathsf{\Gamma }}_{=\lambda }}{r}_{\gamma }\gamma +\sum _{\gamma \in {\mathsf{\Gamma }}_{\perp \lambda }}{r}_{\gamma }\gamma +\sum _{\gamma \in {\mathsf{\Gamma }}_{>\lambda }}{r}_{\gamma }\gamma .$$

Note that the $r_{\gamma }$’s are not necessarily different from zero and the $r_{\gamma }$’s are not necessarily unique. Now, let $h_1,\dots ,h_r$ be the homogeneous components of ${\sum }_{\gamma \in {\mathsf{\Gamma }}_{>\lambda }}{r}_{\gamma }\gamma$. That is, ${\sum }_{\gamma \in {\mathsf{\Gamma }}_{>\lambda }}{r}_{\gamma }\gamma ={\sum }_{i=1}^r{h}_i$ where the $h_i$s are homogeneous and different from zero. Since the $\gamma$’s are homogeneous, then

$${\mathrm{mdeg}}_{\mathsf{\Omega }}\left(h_i\right)>{\mathrm{mdeg}}_{\mathsf{\Omega }}\left(\lambda \right)\mathrm{for}\mathrm{all}1\le i\le r.$$

Thus, $h_i$ must be equal to zero for all $1\le i\le r$ and, therefore, ${\sum }_{\gamma \in {\mathsf{\Gamma }}_{>\lambda }}{r}_{\gamma }\gamma$ is equal to zero. We remark that if we not assume that the $\gamma$’s are homogeneous, then this is not necessarily true.

Using similar arguments, we also obtain that ${\sum }_{\gamma \in {\mathsf{\Gamma }}_{\perp \lambda }}{r}_{\gamma }\gamma =0$ and since $S^r(-\mathbf{A})$ is positively graded, $r_{\gamma }\in k$ for all $\gamma \in {\mathsf{\Gamma }}_{=\lambda }$. That is, for all $\lambda \in \mathsf{\Lambda }$ there exists ${\gamma }_1,\dots {\gamma }_{s+t}\in \mathsf{\Gamma }$ with ${\mathrm{mdeg}}_{\mathsf{\Omega }}\left({\gamma }_i\right)<{\mathrm{mdeg}}_{\mathsf{\Omega }}\left(\lambda \right)$ for all $1\le i\le s$ and ${\mathrm{mdeg}}_{\mathsf{\Omega }}\left({\gamma }_{s+i}\right)={\mathrm{mdeg}}_{\mathsf{\Omega }}\left(\lambda \right)$ for all $1\le i\le t$, $r_i\in S$ for all $1\le i\le s$ and $r_{s+i}\in k$ for all $1\le i\le t$ such that

$$\lambda =\sum _{i=1}^s{r}_i{\gamma }_i+\sum _{i=1}^t{r}_{s+i}{\gamma }_{s+i}\mathrm{with}\sum _{i\in I}{r}_i{\gamma }_i\ne 0\mathrm{for}\mathrm{all}I\subseteq [s+t].$$

We recall that this representation is not necessarily unique. Given one of these representations of $\lambda \in \mathsf{\Lambda }$, let $r_{\mathsf{\Gamma },\lambda }\in S^{\mathsf{\Gamma }}$ given by

$${\left(r_{\mathsf{\Gamma },\lambda }\right)}_{\gamma }=\left\{\begin{array}{cc}{r}_i\hfill & \mathrm{if}\gamma ={\gamma }_i\mathrm{for}\mathrm{some}1\le i\le s+t,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Furthermore, let $M_{\phi }$ be the matrix whose columns are indexed by the elements of $\mathsf{\Lambda }$, whose rows are indexed by the elements of $\mathsf{\Gamma }$ and whose columns are the vectors $r_{\mathsf{\Gamma },\lambda }$. It is not difficult to check that if $\mathsf{\Lambda }$ and $\mathsf{\Gamma }$ are ordered by their multidegree on a nondecreasing way by ${\le }_{\mathsf{\Omega }}$, then $M_{\phi }$ is a square upper triangular block matrix with diagonal blocks for each $\mathbf{c}\in \mathbb{M}$ such that ${\mathsf{\Gamma }}_{\mathbf{c}}\ne \varnothing$. The matrix $M_{\phi }$ can also be seen as an upper triangular block matrix with diagonal blocks for each pair $({\mathsf{\Gamma }}^i,{\mathsf{\Lambda }}^i)$ and this diagonal block with entries in the field k.

Now, let $\phi$ be the endomorphism of N given by $\phi \left(\gamma \right)=M_{\phi }{\mathbf{e}}_{\gamma }$ for all $\gamma \in \mathsf{\Gamma }$ where ${\mathbf{e}}_{\gamma }\in S^{\mathsf{\Gamma }}$ is the canonical vector given by

$${\left({\mathbf{e}}_{\gamma }\right)}_{{\gamma }^{\prime }}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{\gamma }^{\prime }=\gamma ,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

That is, $\phi \left({\mathsf{\Lambda }}_{\mathbf{c}}\right)={\mathsf{\Gamma }}_{\mathbf{c}}$ and its restriction on ${\mathsf{\Lambda }}_{\mathbf{c}}$ is a k-linear map for all $\mathbf{c}\in \mathbb{M}$. When the diagonal blocks of an upper triangular block matrix $\left(\begin{array}{cc}A& C\\ 0& B\end{array}\right)$ are invertible, its inverse is equal to $\left(\begin{array}{cc}{A}^{-1}& -A^{-1}C{B}^{-1}\\ 0& B^{-1}\end{array}\right)$. Thus, using induction on the number of diagonal blocks, we have that an upper triangular block matrix is invertible if and only if each of its diagonal blocks are invertible. Thus, to prove that $\phi$ is an automorphism only remains to prove that the diagonal blocks of $M_{\phi }$ are invertible. In order to do that, we will use induction on the complexity of $\mathsf{\Gamma }$. If $c\left(\mathsf{\Gamma }\right)=1$, then the entries of $M_{\phi }$ are in the field k. Thus, if $M_{\phi }$ is not invertible, then there exists $0\ne \mathbf{r}\in k^{\mathsf{\Lambda }}$ such that $M_{\phi }\mathbf{r}=\mathbf{0}$. That is, ${\sum }_{\lambda \in \mathsf{\Lambda }}{\mathbf{r}}_{\lambda }\lambda =0$ and, therefore, $\mathsf{\Lambda }$ is not irredundant, which is a contradiction. Now, assume that $M_{\phi }$ is invertible for all the finitely generated submodules N of a shifted free S-module $S^r(-\mathbf{A})$ with $c\left(\mathsf{\Gamma }\right)\le i-1$.

Now, we will prove the result when $c\left(\mathsf{\Gamma }\right)=i$. For all $\lambda \in {\mathsf{\Lambda }}^i$, let

$${\mathbf{r}}_{\mathsf{\Gamma },\lambda }^{\prime }=\left\{\begin{array}{cc}{\mathbf{r}}_{\mathsf{\Gamma },\lambda }\hfill & \mathrm{if}\lambda \notin {\mathsf{\Lambda }}^i,\hfill \\ 0\hfill & \mathrm{if}\lambda \in {\mathsf{\Lambda }}^i,\hfill \end{array}\right.$$

where ${\mathbf{r}}_{\mathsf{\Gamma },\lambda }$ is the column of $M_{\phi }$ corresponding to $\lambda$ and let ${\lambda }^{\prime }={\sum }_{\gamma \in \mathsf{\Gamma }}{({\mathbf{r}}_{\mathsf{\Gamma },\lambda }-{\mathbf{r}}_{\mathsf{\Gamma },\lambda }^{\prime })}_{\gamma }\gamma =\lambda -{\sum }_{\gamma \in \mathsf{\Gamma }}{\left({\mathbf{r}}_{\mathsf{\Gamma },\lambda }^{\prime }\right)}_{\gamma }\gamma$. Let ${\mathsf{\Lambda }}^{<i}={\cup }_{j=1}^{i-1}{\mathsf{\Lambda }}^i$, ${\mathsf{\Gamma }}^{<i}={\cup }_{j=1}^{i-1}{\mathsf{\Gamma }}^i$ and $M_{\phi }^{<i}$ be the submatrix of $M_{\phi }$ obtained by deleting the columns not indexed by the elements in ${\mathsf{\Lambda }}^{<i}$ and the rows not indexed by the elements in ${\mathsf{\Gamma }}^{<i}$. By induction, hypothesis $M_{\phi }^{<i}$ is invertible. Thus,

$$\sum _{\gamma \in \mathsf{\Gamma }}{\left({\mathbf{r}}_{\mathsf{\Gamma },\lambda }^{\prime }\right)}_{\gamma }\gamma =\sum _{\lambda \in {\mathsf{\Lambda }}^{<i}}{s}_{\lambda }\lambda \mathrm{for}\mathrm{some}{s}_{\lambda }\prime \mathrm{s}\mathrm{in}S.$$

Now, let $M_{\phi }^i$ be the diagonal block of $M_{\phi }$ whose columns are indexed by ${\mathsf{\Lambda }}^i$ and whose rows are indexed by ${\mathsf{\Gamma }}^i$. If $M_{\phi }^i$ is not invertible, then there exists $0\ne \mathbf{r}\in k^{{\mathsf{\Lambda }}^i}$ such that $M_{\phi }^i\mathbf{r}=\mathbf{0}$, that is, ${\sum }_{\lambda \in {\mathsf{\Lambda }}^i}{\mathbf{r}}_{\lambda }{\lambda }^{\prime }=0$. Thus,

$$\begin{array}{ccc}\hfill 0=\sum _{\lambda \in {\mathsf{\Lambda }}^i}{\mathbf{r}}_{\lambda }{\lambda }^{\prime }& =& \sum _{\lambda \in {\mathsf{\Lambda }}^i}{\mathbf{r}}_{\lambda }(\lambda -\sum _{\gamma \in \mathsf{\Gamma }}{\left({\mathbf{r}}_{\mathsf{\Gamma },\lambda }^{\prime }\right)}_{\gamma }\gamma )\hfill \\ & =& \sum _{\lambda \in {\mathsf{\Lambda }}^i}{\mathbf{r}}_{\lambda }(\lambda -\sum _{\lambda \in {\mathsf{\Lambda }}^{<i}}{s}_{\lambda }\lambda )=\sum _{\lambda \in {\mathsf{\Lambda }}^i}{\mathbf{r}}_{\lambda }\lambda -\sum _{\lambda \in {\mathsf{\Lambda }}^i}{\mathbf{r}}_{\lambda }\sum _{\lambda \in {\mathsf{\Lambda }}^{<i}}{s}_{\lambda }\lambda .\hfill \end{array}$$

That is, $\mathsf{\Lambda }$ is not irredundant, which is a contradiction and, therefore, we find that $M_{\phi }$ is invertible and $\phi$ an automorphism of N. □

Remark 12.

Lemma 2 is similar to the Foundational Theorem given in [4] (Theorem 2.12). However, there exists a crucial difference between them, Lemma 2 does not assume that Γ and Λ are both minimal homogeneous generators of N as in [4] (foundational Theorem 2.12). Actually, we deduce that an irredundant homogeneous subset of N is a minimal homogeneous generator of N by comparing the ranks at each degree with a minimal homogeneous generator of N. The first part of the proof of Lemma 2 uses similar ideas to the ones used in the graded Nakayama’s Lemma.

We are mostly interested in cases when the S-submodule N is the kernel of a homogeneous homomorphism between graded free S-modules. In this case, applying Lemma 2, we obtain a criterion to check when a set of elements in the kernel is indeed a minimal generating set.

Corollary 3.

Let $\mathbf{A}$ and $\mathbf{B}$ be multisets in $\mathbb{M}$ and $d:S^r(-\mathbf{A})\to S^t(-\mathbf{B})$ be a homogeneous homomorphism of S-modules. If Γ is a homogeneous minimal generating set of $ker\left(d\right)$ and Λ is an irredundant homogeneous subset of $ker\left(d\right)$ such that

$$|{\mathsf{\Gamma }}_{\mathbf{c}}|=|{\mathsf{\Lambda }}_{\mathbf{c}}|\mathrm{for}\mathrm{all}\mathbf{c}\in \mathbb{M},$$

then there exists an automorphism φ of $ker\left(d\right)$ such that $\phi \left({\mathsf{\Lambda }}_{\mathbf{c}}\right)={\mathsf{\Gamma }}_{\mathbf{c}}$ for all $\mathbf{c}\in \mathbb{M}$ and whose restriction on each ${\mathsf{\Lambda }}_{\mathbf{c}}$ is a k-linear map. Moreover, if M is the matrix representation of φ with respect to Λ and Γ ordered by their multidegrees on a nondecreasing way, then it is an upper triangular block matrix.

Proof. 

It follows directly from Lemma 2 because $\ker \left(d\right)$ is a finitely generated S-submodule of $S^r(-\mathbf{A})$. □

The next example illustrates the previous result is obtained.

Example 4.

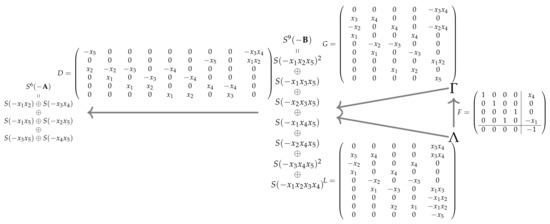
Let $d:S^9(-\mathbf{B})\to S^6(-\mathbf{A})$ be the homogeneous (under the standard multidegree) homomorphism whose matrix representation is the matrix D given in Figure 1.

Figure 1. The matrix representation of the first differential $d:S^9(-\mathbf{B})\to S^6(-\mathbf{A})$ of a minimal free resolution of the edge ideal of the bowtie graph $I_G=⟨x_1{x}_2,x_2{x}_5,x_5{x}_1,x_5{x}_3,x_3{x}_4,x_4{x}_5⟩$ and two possible minimal generating set for its kernel.

Let Γ and Λ be the columns of the matrices G and L, respectively. It is not difficult to check, using, for instance, Macaulay2 [12], that Γ and Λ are homogeneous minimal generator sets of $ker\left(d\right)$ with $|G_{\mathbf{a}}|=|L_{\mathbf{a}}|$ for all $\mathbf{a}\in {\mathbb{N}}^n$. We recall that the multidegrees of the columns of G are $x_1{x}_2{x}_3{x}_5$, $x_1{x}_2{x}_4{x}_5$, $x_1{x}_3{x}_4{x}_5$, $x_2{x}_3{x}_4{x}_5$ and $x_1{x}_2{x}_3{x}_4{x}_5$, respectively. The multidegrees of the columns of L are $x_1{x}_2{x}_3{x}_5$, $x_1{x}_2{x}_4{x}_5$, $x_2{x}_3{x}_4{x}_5$, $x_1{x}_3{x}_4{x}_5$ and $x_1{x}_2{x}_3{x}_4{x}_5$, respectively.

It is not difficult to check that F is the matrix representation of an automorphism as in Corollary 3. The first diagonal block of F is clearly invertible because it is a permutation. The second diagonal block is equal to the matrix $(-1)$. Additionally, ${\lambda }_5=x_4{\gamma }_1-x_1{\gamma }_4-{\gamma }_5$ and ${\lambda }_5^{\prime }={\lambda }_5-(x_4{\lambda }_1-x_1{\lambda }_3)=-{\gamma }_5$.

Now, we apply Corollary 3 to obtain a criterion for a graded free complex being exact and minimal. Before doing this, we introduce the concept of complex.

A free complex of F is a sequence of homomorphisms ${\mathbf{F}}_{•}={\{F_i,d_i\}}_{i=-1}^p$ between free S-modules, which are called differentials,

$${\mathbf{F}}_{•}:0\leftarrow F\stackrel{\pi =d_0}{\leftarrow }{F}_0\stackrel{d_1}{\leftarrow }{F}_1\stackrel{d_2}{\leftarrow }\cdots \stackrel{d_p}{\leftarrow }{F}_p\leftarrow 0$$

such that $d_{i-1}{d}_i=0$ for all $1⩽i⩽p$. We say that it is graded whenever the modules $F_i$ are graded and the $d_i$’s are homogeneous. Moreover, it is exact whenever $\mathrm{im}\left(d_i\right)=\ker \left(d_{i-1}\right)$ for all $1⩽i⩽p$ in which case it is a free resolution of $F_{-1}$. We say that two complexes ${\mathbf{F}}_{•}$ and ${\mathbf{C}}_{•}$ are isomorphic whenever there exists a series of homogeneous isomomorphisms $T_i:F_i\to C_i$ for all $-1\le i\le p$ such that the following diagram commutes.

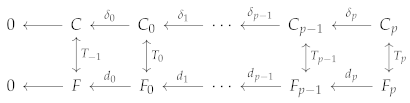
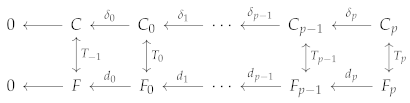
Theorem 2.

If M is a finitely generated positively graded S-module,

$${\mathbf{F}}_{•}:0\leftarrow M\stackrel{d_0}{\leftarrow }{F}_0\stackrel{d_1}{\leftarrow }{F}_1\leftarrow \cdots \stackrel{d_p}{\leftarrow }{F}_p\leftarrow 0$$

is a graded minimal free resolution of M and

$${\mathbf{C}}_{•}:0\leftarrow M\stackrel{{\delta }_0}{\leftarrow }{C}_0\stackrel{{\delta }_1}{\leftarrow }{C}_1\leftarrow \cdots \stackrel{{\delta }_p}{\leftarrow }{C}_p\leftarrow 0$$

is a graded free complex of M such that

$$F_i=\underset{\mathbf{a}\in A_i\subset \mathbb{M}}{⨁}S(-\mathbf{a})=C_i$$

as free graded S-modules and the column sets $C\left(D_i\right)$ of the matrix representations $D_i$ of the differentials ${\delta }_i$ are irredundant for all $0⩽i⩽p$, then ${\mathbf{C}}_{•}$ is isomorphic to ${\mathbf{F}}_{•}$.

Proof. 

We will use induction on the homological degree of ${\mathbf{F}}_{•}$. Note that $T_{-1}$ is the identity map on M. We begin by proving that $T_0$ is an isomorphism. Let q be the rank of the free modules $F_0$ and $C_0$ and ${\left\{{\mathbf{e}}_j\right\}}_{1⩽j⩽q}$ its canonical basis. Let $\mathbf{G}={\left\{d_0\left({\mathbf{e}}_j\right)\right\}}_{1⩽j⩽q}:={\left\{g_j\right\}}_{1⩽j⩽q}$ and $\mathbf{H}={\left\{{\delta }_0\left({\mathbf{e}}_j\right)\right\}}_{1⩽j⩽q}:={\left\{h_j\right\}}_{1⩽j⩽q}$. That is, $\mathbf{G}$ and $\mathbf{H}$ are the columns of the matrix representation of $d_0$ and ${\delta }_0$, respectively. Since $d_0$ and ${\delta }_0$ are homogeneous maps, $\mathbf{H}$ and $\mathbf{G}$ are homogeneous of the same multidegrees. Thus, by Lemma 2, there exists an isomorphism $\phi$ between $\mathbf{G}$ and $\mathbf{H}$ such that ${\left\{\phi \left(g_j\right)\right\}}_{1⩽j⩽q}={\left\{h_j\right\}}_{1⩽j⩽q}$ and $T_0$ given by

$$T_0\left({\mathbf{e}}_j\right)=\sum _{l=1}^q{r}_l{\mathbf{e}}_l\mathrm{where}\phi \left(g_j\right)=\sum _{l=1}^q{r}_l{g}_l\mathrm{with}{r}_l\in S\mathrm{for}\mathrm{all}1\le j\le q$$

is an isomorphism between $C_0$ and $F_0$.

Now, let us assume that there exist homogeneous isomomorphisms $T_j$ for all $0\le j\le i$ such that the previous diagram commutes up to that point. Thus, we need to prove that there exists a homogeneous isomomorphism $T_{i+1}$ such that the diagram commutes

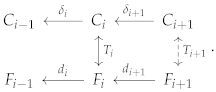
Since $F_{i+1}$ and $C_{i+1}$ are equal as free graded S-modules, they have the same rank q. Let ${\left\{{\mathbf{e}}_j\right\}}_{1\le j\le q}$ be their canonical basis. Now, let

$$\mathbf{G}={\left\{d_{i+1}\left({\mathbf{e}}_j\right)\right\}}_{1\le j\le q}:={\left\{{\mathbf{g}}_j\right\}}_{1\le j\le q}\mathrm{and}\mathbf{H}={\left\{{\delta }_{i+1}\left({\mathbf{e}}_j\right)\right\}}_{1\le j\le q}:={\left\{{\mathbf{h}}_j\right\}}_{1\le j\le q}.$$

That is, $\mathbf{G}$ and $\mathbf{H}$ are the columns of the matrix representations of $d_{i+1}$ and ${\delta }_{i+1}$, respectively, which are homogeneous. Since ${\mathbf{F}}_{•}$ and ${\mathbf{C}}_{•}$ are complexes, then ${\mathbf{g}}_j\in \ker \left(d_i\right)$ and ${\mathbf{h}}_j\in \ker \left({\delta }_i\right)$ for all $1\le j\le q$. Moreover, since ${\mathbf{F}}_{•}$ is exact, then $\mathbf{G}$ is a minimal generator of $\ker \left(d_i\right)$.

On the other hand, since $d_i{T}_i=T_{i-1}{\delta }_i$, then $d_i{T}_i\left({\mathbf{h}}_j\right)=T_{i-1}{\delta }_i\left({\mathbf{h}}_j\right)=T_{i-1}\left(0\right)=0$ and, therefore, $T_i\left({\mathbf{h}}_j\right)\in \ker \left(d_i\right)$ for all $1\le j\le q$. Moreover, since $T_i$ is an automorphism and $\mathbf{H}$ is irredundant, then ${\left\{T_i\left({\mathbf{h}}_j\right)\right\}}_{1\le i\le q}$ is irredundant and homogeneous. Thus, by Corollary 3, there exists a homogeneous isomorphism $\phi$ such that ${\left\{T_i\left({\mathbf{h}}_j\right)\right\}}_{1\le j\le q}={\left\{\phi \left({\mathbf{g}}_j\right)\right\}}_{1\le j\le q}$. Finally, $\phi$ induces an isomorphism $T_{i+1}$ between $C_{i+1}$ and $F_{i+1}$ given by

$$T_{i+1}\left({\mathbf{e}}_j\right)=\sum _{l=1}^q{r}_l{\mathbf{e}}_l\mathrm{where}\phi \left({\mathbf{g}}_j\right)=\sum _{l=1}^q{r}_l{\mathbf{g}}_l\mathrm{with}{r}_l\in S\mathrm{for}\mathrm{all}1\le j\le q.$$

□

This criterion simplifies the highly nontrivial part of showing that a free complex is exact and minimal, that is, a minimal free resolution of a module. Now, instead of showing that the equality $ker\left(d_i\right)=\mathrm{im}\left(d_{i+1}\right)$ holds, we only have to show that a free complex has the correct Betti numbers and each column set of any differential is an irredundant set.

Resolutions in the noncommutative case have also been studied, see, for instance, the second and seventh article in [13]. However, this criterion cannot be applied there because of multiple issues, in particular, not every projective resolution is free, resolutions may have infinite length, or infinite ranks.

We finish this section with an example of how Theorem 2 works for a non-monomial ideal.

Example 5.

Let $I=⟨x_1+x_2,x_2^2+x_1{x}_3,x_4^3⟩$ be a homogeneous non-monomial ideal of the polynomial ring $S=k[x_1,x_2,x_3,x_4]$ with the standard grading. Using Macaulay2 [12] we get the minimal free resolution of I in the top line of Figure 2. In the bottom line of Figure 2, we show a free complex ${\mathbf{C}}_{•}$ of I with the columns of its differentials irredundant.

By Theorem 2, ${\mathbf{C}}_{•}$ is also a minimal free resolution of I as shown in the isomorphisms between ${\mathbf{F}}_{•}$ and ${\mathbf{C}}_{•}$ given in Figure 2.

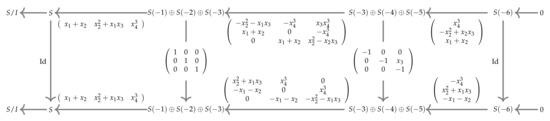
Figure 2. Two minimal free resolutions of the ideal $I=⟨x_1+x_2,x_2^2+x_1{x}_3,x_4^3⟩$ and isomorphism between them.

4. Multigraded Minimal Free Resolution of the Complete Graph

One way to prove that a sequence of free S-modules and homomorphisms between them is actually a minimal free resolution is to break it down into two steps: we first prove that it is a complex and then prove that it is exact. Usually, the second step is the more complicated of the two. In this section, we present the case of the edge ideal of the complete graph to show how Theorem 2 can be used to accomplish this second step. Finding a minimal free resolution of the edge ideal of the complete graph is one better-understood case. However, in almost all cases only are given their graded Betti numbers. Here, we present an explicit way to calculate its differentials.

To the authors’ knowledge, an explicit minimal free resolution of the edge ideal of the complete graph has been proposed at least twice before. The first one was by Reiner in Welker in 2001. More precisely, in [14], there is a description of a graded minimal free resolution of a matroidal ideal. The second one was proposed in 2020 by Galetto in [10], using standard Young tableaux with a hook shape; this resolution is exactly the same as the one given here. However, unlike these two previous approaches, our method is of general purpose, that is, it is applicable to any monomial ideal for which we have a guess about a minimal free resolution. For instance, in [15], the criterion given in Theorem 2 is used to prove that a given complex is indeed a minimal free resolution of the duplication of a monomial ideal.

Briefly, our approach consists of introducing some subsets of subgraphs of the complete graph, which we called basis graphs. Then, we use them to construct a sequence of free S-modules and homomorphism between them. After that, we prove, using the combinatorics of these basis graphs, that it is indeed a complex. Finally, we use Theorem 2 to prove that this complex is exact and, therefore, a minimal free resolution. The minimal free resolution presented is as those given in [9].

The complete graph, denoted by $K_n$, is the graph with vertex set $V\left(K_n\right)=\{v_1,\dots ,v_n\}$ and edge set $E\left(K_n\right)=\{v_i{v}_j:1\le i\ne j\le n\}$. We recall that its edge ideal is the monomial ideal

$$I_{K_n}=⟨\{x_i{x}_j:v_i{v}_j\in E\left(K_n\right)\}⟩\subset S.$$

Recall also that we are considering that the variables in S inherit the ordering of their indices. More precisely, $x_i<x_j$ if and only if $i<j$. Now, let us define basis graphs of the complete graph.

Definition 11.

Given $A=(i_1,\dots ,i_a)\subseteq \left[n\right]$ with $i_1<i_2<\cdots <i_a$ and $i_1\ne i\in A$, the basis graph ${\mathrm{B}}_A^i$ of $K_n$ with support A and order a is the subgraph of $K_n$ with edge set

$$E\left({\mathrm{B}}_A^i\right)=\{v_i{v}_a:a\in A\}\cup \{v_a{v}_{a^{\prime }}:i<a,a^{\prime }\in A\}.$$

In other words, if $A_{\le j}=\{a\in A:a\le j\}$ and $A_{\ge j}=\{a\in A:a\ge j\}$ for all $j\in A$, then ${\mathrm{B}}_A^i$ is such that its induced subgraphs in $A_{\le i}$ and $A_{\ge i}$ are a star with center in $v_i$ and a complete graph, respectively. Thus, we say that ${\mathrm{B}}_A^i$ is rooted in $v_i$. In the next example, we illustrate this concept by presenting basis graphs of $K_4$ of order four.

Example 6.

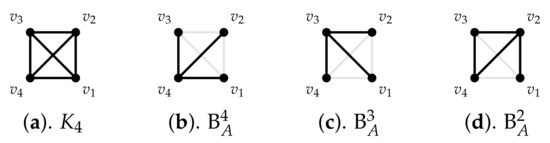
The complete graph with four vertices has three basis graphs with support $A=\{1,2,3,4\}$, see Figure 3b–d.

Figure 3. The complete graph $K_4$ and its three possible basis graphs with support $A=\{1,2,3,4\}$.

Remark 13.

It is not difficult to check that there are $\left|A\right|-1$ basis graphs with support $A\subseteq \left[n\right]$ and there are $\left(\genfrac{}{}{0pt}{}{n}{j}\right)(j-1)$ basis graphs of the complete graph with n vertices of order j.

The poset of basis graphs of the complete graph under the subgraph relation will play the role of a type of skeleton of a minimal free resolution for its edge ideal. Thus, we turn our attention to establishing when a basis graph is a subgraph of another one.

Lemma 3.

If $i\in A\subseteq \left[n\right]$ and $j\in C\subseteq \left[n\right]$, then

$${\mathrm{B}}_A^i\subseteq {\mathrm{B}}_C^j\mathit{if}\mathit{and}\mathit{only}\mathit{if}\mathit{either}\left\{\begin{array}{cc}A\subseteq C\hfill & \mathit{when}i=j,\mathit{or}\hfill \\ A\subseteq C_{\ge j}\hfill & \mathit{when}i\ne j.\hfill \end{array}\right.$$

Proof. 

When $i=j$, the result follows directly from the definition of the basis graphs of $K_n$. On the other hand, when $i\ne j$ we have the following: $(\Rightarrow )$ If there exists $k\in A$ such that $k<j$, then $v_i{v}_k\in E\left({\mathrm{B}}_A^i\right)$ and $v_i{v}_k\notin E\left({\mathrm{B}}_C^j\right)$, which is a contradiction. $(\Leftarrow )$ It follows because ${\mathrm{B}}_C^j\left[C_{\ge j}\right]$ is a complete graph. □

Now, let ${\mathcal{B}}_j$ be the set of basis graphs of $K_n$ of order j, ${\mathbf{x}}^A={\prod }_{a\in A}{\mathbf{x}}^a$ and

$$F_i=\left\{\begin{array}{cc}S/I_n\hfill & \mathrm{if}i=-1,\hfill \\ S\hfill & \mathrm{if}i=0,\hfill \\ F_i=\underset{{\mathrm{B}}_A^k\in {\mathcal{B}}_{i+1}}{⨁}S(-{\mathbf{x}}^A)\hfill & \mathrm{if}1\le i\le n-1,\hfill \end{array}\right.$$

be a sequence of free S-modules. That is, we have a shifted copy of S in $F_i$ for each basis graph of $K_n$ of order i.

The next ingredient that we need to define the homogeneous homomorphism between the free S-modules $F_i$ and $F_{i-1}$ is a scalar function between the basis graphs of $K_n$.

Definition 12.

If ${\mathrm{B}}_A^i$ and ${\mathrm{B}}_C^j$ are basis graphs of $K_n$ with $C=A\cup \left\{l\right\}$, then the scalar function between them is given by

$$\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_C^j)=\left\{\begin{array}{cc}{(-1)}^{|A_{\le l}\setminus i|}\hfill & \mathit{if} i=j,\hfill \\ {(-1)}^{|A_{\le i}|}\hfill & \mathit{if} l<j<i.\hfill \end{array}\right.$$

Note that the scalar function is only defined whenever ${\mathrm{B}}_A^i$ is a proper subgraph of ${\mathrm{B}}_C^j$ of order one plus. However, it is convenient to think that scalar function is equal to zero in the other cases. In this case, it only takes the values either of zero, one or minus one, but in general, takes any value in the field k. Moreover, it is not difficult to check that the basis graph ${\mathrm{B}}_A^i$ has $a-1$ basis graphs as subgraphs whenever $i\ne i_2$ and $2(a-2)$ whenever $i=i_2$. In the next example, we illustrate this property of basis graphs of $K_n$.

Example 7.

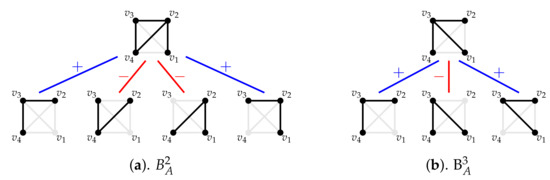
Let $A=(1,2,3,4)$ and consider the basis graphs $B_A^2$ and $B_A^3$. It is not difficult to check that $B_A^2$ has $4=2\left(\right|A|-2)$ basis graphs and $B_A^3$ has only $3=\left|A\right|-1$ basis subgraphs, see Figure 4.

Figure 4. Basis subgraphs $B_A^2$ and $B_A^3$ and their basis subgraphs. Arrows code the scalar function between them.

Now, let $d_k:F_k\to F_{k-1}$ whose matrix representation is given by

$${\left(d_k\right)}_{{\mathrm{B}}_A^i,{\mathrm{B}}_C^j}=\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_C^j){\mathbf{x}}^{C\setminus A}.$$

That is, the columns and rows of $d_k$ correspond to elements in ${\mathcal{B}}_{k+1}$ and ${\mathcal{B}}_k$ respectively. For instance, the first column of the matrix $d_3$, given in Example 8, corresponds to the basis graph $K_{(1,2,3,4)}^3$ whose entries different from zero correspond to its basis subgraphs $K_{(2,3,4)}^3$, $K_{(2,3,4)}^4$, $K_{(1,2,4)}^2$ and $K_{(1,2,3)}^2$, as in Example 7. For simplicity, we say that the column (row) associated to the basis graph $B_A^i$ is the $B_A^i$ column (row). Finally, taking $d_0=\pi$ as the projection of $F_0$ over the quotient module $F_{-1}$, we obtain the sequence

$${\mathrm{K}}_{•}\left(n\right):0\leftarrow S/I\stackrel{\pi =d_0}{\leftarrow }S\stackrel{d_1}{\leftarrow }{F}_1\stackrel{d_2}{\leftarrow }\cdots \stackrel{d_{n-1}}{\leftarrow }{F}_{n-1}\leftarrow 0$$

of free S-modules and the graded homomorphism between them.

The next example illustrates the construction of ${\mathrm{K}}_{•}\left(4\right)$.

Example 8.

For $n=4$, the sequence of free modules ${\mathrm{K}}_{•}\left(n\right)$ is given by:

$${\mathrm{K}}_{•}\left(4\right):0\leftarrow S/I\stackrel{\pi =d_0}{\leftarrow }S\stackrel{d_1}{\leftarrow }{F}_1\stackrel{d_2}{\leftarrow }{F}_2\stackrel{d_3}{\leftarrow }{F}_3\leftarrow 0,$$

where $F_1=S(-x_1{x}_3)\oplus S(-x_2{x}_3)\oplus S(-x_1{x}_2)\oplus S(-x_1{x}_4)\oplus S(-x_2{x}_4)\oplus S(-x_3{x}_4)$, $F_2=S{(-x_1{x}_2{x}_3)}^2\oplus S{(-x_1{x}_2{x}_4)}^2\oplus S{(-x_1{x}_3{x}_4)}^2\oplus S{(-x_2{x}_3{x}_4)}^2,F_3=S{(-x_1{x}_2{x}_3{x}_4)}^3$ and the differentials are given by:

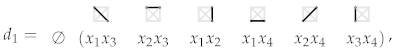
and

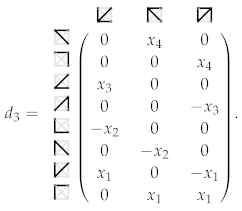
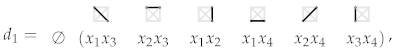
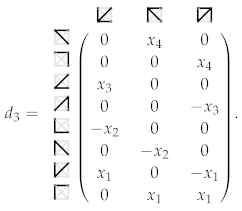
Once we have a candidate to a minimal free resolution, the next step is to prove that it is indeed a complex, that is, the products $d_k{d}_{k+1}$ are equal to zero. In general, this part it is not that difficult to check. When, as in our case, the sequence of free S-modules and differentials is given in terms of the combinatorics of the monomial ideal, the fact of being a complex relies significantly on this.

Next, we present some basic properties of basis graphs of $K_n$, which rely on the fact that the sequence of free S-modules and differentials is a complex.

Next, the lemma tells us that between two basis graphs $B_A^i⊊B_C^j$ of $K_n$ whose respective orders differ by two, there are exactly two basis subgraphs.

Lemma 4.

Let $i\in A\subseteq \left[n\right]$, $r\in F\subseteq \left[n\right]$ and $j\in C=(j_1,j_2,\dots ,j_c)\subseteq \left[n\right]$ with $j_1<j_2<\cdots <j_c$. If $C=A\cup \{g,h\}$ with $g<h$ and ${\mathrm{B}}_A^i⊊{\mathrm{B}}_F^r⊊{\mathrm{B}}_C^j$, then

$${\mathrm{B}}_F^r\mathit{equals}\mathit{one}\mathit{of}\left\{\begin{array}{cc}{\mathrm{B}}_{A\cup \left\{g\right\}}^i\mathit{or}{\mathrm{B}}_{A\cup \left\{h\right\}}^i\hfill & \mathit{if}i=j,\hfill \\ {\mathrm{B}}_{A\cup \left\{j_2\right\}}^i\mathit{or}{\mathrm{B}}_{A\cup \left\{j_2\right\}}^{j_3}\hfill & \mathit{if}i>j=j_2\mathit{and}A=\{j_3,\dots ,j_c\},\hfill \\ {\mathrm{B}}_{A\cup \left\{j_1\right\}}^j\mathit{or}{\mathrm{B}}_{A\cup \left\{j_2\right\}}^j\hfill & \mathit{if}i>j=j_3\mathit{and}A=\{j_3,\dots ,j_c\},\hfill \\ {\mathrm{B}}_{A\cup \left\{j_1\right\}}^j\mathit{or}{\mathrm{B}}_{A\cup \left\{h\right\}}^i\hfill & \mathit{if}i>j=j_2\in A.\hfill \end{array}\right.$$

Proof. 

First, by Lemma 3, $A⊊F⊊C$ and $j\le r\le i$. Thus, since $C=A\cup \{g,h\}$ we get that F equals $A\cup \left\{g\right\}$ or $A\cup \left\{h\right\}$. Now, if $i=j$, then $r=i$ and by Lemma 3, we obtain that ${\mathrm{B}}_F^r$ equals ${\mathrm{B}}_{A\cup \left\{g\right\}}^i$ or ${\mathrm{B}}_{A\cup \left\{h\right\}}^i$. Thus, from here, we assume that $i>j$. We divide the prove in two cases: when $j\in A$ and when $j\notin A$.

First, if $j\notin A$, we have that $g=j_1$, $h=j_2=j$ and $i\ge j_4$. Now, if $F=A\cup \left\{j_1\right\}$, then $j_{1}r\in E\left({\mathrm{B}}_F^r\right)$ and $j_{1}r\notin E\left({\mathrm{B}}_C^j\right)$, a contradiction to the fact that ${\mathrm{B}}_F^r⊊{\mathrm{B}}_C^j$. Thus, $F=A\cup \left\{j_2\right\}$ and therefore, $r\ne j_2$. In a similar way, if $j_3<r<i$, then $j_{3}i\in E\left({\mathrm{B}}_A^i\right)$ and $j_{3}i\notin E\left({\mathrm{B}}_F^r\right)$, a contradiction to the fact that ${\mathrm{B}}_A^i⊊{\mathrm{B}}_F^r$. Thus, r equals i or $j_3$ and by Lemma 3 we get that ${\mathrm{B}}_F^r$ equals ${\mathrm{B}}_{A\cup \left\{j_2\right\}}^i$ or ${\mathrm{B}}_{A\cup \left\{j_2\right\}}^{j_3}$.

If $j\in A$, we need to consider two additional cases: when either $j=j_3$ or $j=j_2$. In the first case, it is not difficult to check that $g=j_1$ and $h=j_2$. Moreover, if $r\ne j$ and $j_1\in F$, then $j_{1}r\in {\mathrm{B}}_F^r$ and $j_{1}r\notin {\mathrm{B}}_C^j$, a contradiction to the fact that ${\mathrm{B}}_F^r⊊{\mathrm{B}}_C^j$. A similar argument can be used when $r\ne j$ and $j_2\in F$. Since $\{j_1,j_2\}\cap F\ne \varnothing$, $j=r$ and by Lemma 3, we obtain that ${\mathrm{B}}_F^r$ equals ${\mathrm{B}}_{A\cup \left\{j_1\right\}}^j$ or ${\mathrm{B}}_{A\cup \left\{j_2\right\}}^j$.

Finally, if $j=j_2$, then $g=j_1$. Moreover, if $r\ne j$, then $j_1\notin F$, otherwise, $j_{1}r\in {\mathrm{B}}_F^r$ and $j_{1}r\notin {\mathrm{B}}_C^j$, a contradiction to the fact that ${\mathrm{B}}_F^r⊊{\mathrm{B}}_C^j$. Moreover, $r=i$, otherwise, $ij\in {\mathrm{B}}_A^i$ and $ij\notin {\mathrm{B}}_F^r$, a contradiction to the fact that ${\mathrm{B}}_A^i⊊{\mathrm{B}}_F^r$. Thus, r can only be either i or j and by Lemma 3, we obtain that ${\mathrm{B}}_F^r$ equals ${\mathrm{B}}_{A\cup \left\{j_1\right\}}^j$ or ${\mathrm{B}}_{A\cup \left\{h\right\}}^i$. □

The fact that ${\mathrm{K}}_{•}\left(n\right)$ is indeed a complex relies on the previous property of the basis graphs of $K_n$.

Proposition 12.

The sequence ${\mathrm{K}}_{•}\left(n\right)$ of free S-modules and differentials is a complex.

Proof. 

To prove that ${\mathrm{K}}_{•}\left(n\right)$ is a complex, we need to prove that the product of two consecutive differentials $d_k{d}_{k+1}$ is always equal to zero. Indeed, the product of the matrices $d_k$ and $d_{k+1}$ is equal to zero if and only if the dot product of each row of $d_k$ with each column of $d_{k+1}$ is equal to zero.

We recall that the entries in $d_k$ are determined by pairs of basis graphs. More precisely, the entries of the column (row) ${\mathrm{B}}_A^i$ are determined by the basis subgraph of ${\mathrm{B}}_A^i$ and the scalar function between them. Thus, the dot product of rows and columns is also determined by the relation between basis graphs.

For instance, let ${\mathrm{B}}_A^i$ be the basis graph associated to a row of the differential $d_k$ and ${\mathrm{B}}_C^j$ be the basis graph associated to a column of the differential $d_{k+1}$. An entry of the column ${\mathrm{B}}_C^j$ of $d_{k+1}$ is different from zero if and only if there exists basis a subgraph ${\mathrm{B}}_F^r$ such that ${\mathrm{B}}_F^r⊊{\mathrm{B}}_C^j$ and an entry of the row ${\mathrm{B}}_A^i$ of $d_k$ is different from zero if and only if there exists a basis subgraph ${\mathrm{B}}_F^r$ such that ${\mathrm{B}}_A^i⊊{\mathrm{B}}_F^r$. Thus, if ${\mathrm{B}}_A^i\neg \subset {\mathrm{B}}_C^j$, then its dot product is zero because the intersection between the support of the column ${\mathrm{B}}_C^j$ and the support of the row ${\mathrm{B}}_A^i$ is empty. That is, there does not exist ${\mathrm{B}}_F^r$ such that ${\mathrm{B}}_A^i⊊{\mathrm{B}}_F^r⊊{\mathrm{B}}_C^j$.

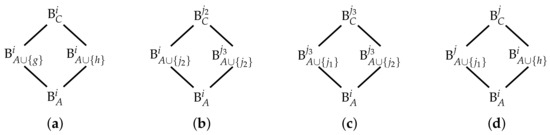
Now, we calculate the dot product of the column ${\mathrm{B}}_C^j$ with row ${\mathrm{B}}_A^i$ with ${\mathrm{B}}_A^i⊊{\mathrm{B}}_C^j$ and $|C\setminus A|=2$. Lemma 4 establishes that there exist four possible cases all of them with only two products in the dot product which are different form zero. Following the notation in Lemma 4, the diagrams given in Figure 5 describe the four possible cases and the associated basis graphs to the entries which yield products different from zero.

Figure 5. The four possible cases of products different from zero in the dot product of a row of $d_k$ with a column of $d_{k+1}$.

Thus, if ${\mathrm{B}}_{F_1}^{r_1}$ and ${\mathrm{B}}_{F_2}^{r_2}$ are the unique basis graphs such that ${\mathrm{B}}_A^i⊊{\mathrm{B}}_{F_1}^{r_1},{\mathrm{B}}_{F_2}^{r_2}⊊{\mathrm{B}}_C^j$, then the dot product of the row ${\mathrm{B}}_A^i$ and column ${\mathrm{B}}_C^j$ is zero if and only if $r({\mathrm{B}}_A^i,{\mathrm{B}}_{F_1}^{r_1})c({\mathrm{B}}_{F_1}^{r_1},{\mathrm{B}}_C^j)+r({\mathrm{B}}_A^i,{\mathrm{B}}_{F_2}^{r_2})c({\mathrm{B}}_{F_2}^{r_2},{\mathrm{B}}_C^j)=0$, where $c({\mathrm{B}}_A^i,{\mathrm{B}}_C^j)$ is the entry of the column ${\mathrm{B}}_C^j$ corresponding to ${\mathrm{B}}_A^i$ and $r({\mathrm{B}}_A^i,{\mathrm{B}}_C^j)$ is the entry of the row ${\mathrm{B}}_A^i$ corresponding to ${\mathrm{B}}_C^j$. For instance, for the first case

$$\sigma ({\mathrm{B}}_{A\cup \left\{g\right\}}^i,{\mathrm{B}}_C^i)\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{g\right\}}^i)x_g{x}_h+\sigma ({\mathrm{B}}_{A\cup \left\{h\right\}}^i,{\mathrm{B}}_C^i)\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{h\right\}}^i)x_g{x}_h=0$$

if and only if $\sigma ({\mathrm{B}}_{A\cup \left\{g\right\}}^i,{\mathrm{B}}_C^i)\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{g\right\}}^i)+\sigma ({\mathrm{B}}_{A\cup \left\{h\right\}}^i,{\mathrm{B}}_C^i)\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{h\right\}}^i)=0$ and, therefore, we only need to check that the scalar function on the edges of each square in Figure 5 has an odd number of minus signs. Using a similar argument, it is not difficult to see that in the other cases, it is also only necessary to verify the same condition on the scalar function. This condition is what is called an unbalanced scalar function in [9]. Now, by the definition of the scalar function, we have that

$$\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{h\right\}}^i)\sigma ({\mathrm{B}}_{A\cup \left\{g\right\}}^i,{\mathrm{B}}_C^i)={(-1)}^{|A_{\le h}\setminus i|}{(-1)}^{{|(A\cup \left\{g\right\})}_{\le h}\setminus i|}=-1$$

and

$$\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{g\right\}}^i)\sigma ({\mathrm{B}}_{A\cup \left\{h\right\}}^i,{\mathrm{B}}_C^i)={(-1)}^{|A_{\le g}\setminus i|}{(-1)}^{{|(A\cup \left\{h\right\})}_{\le g}\setminus i|}=1$$

because $g<h$. For the second case, we have that

$$\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{j_2\right\}}^i)\sigma ({\mathrm{B}}_{A\cup \left\{j_2\right\}}^{j_3},{\mathrm{B}}_C^{j_2})={(-1)}^{|A_{\le j_2}\setminus i|}{(-1)}^{|{(A\cup \left\{j_2\right\})}_{\le j_3}|}={(-1)}^0{(-1)}^2=1$$

and

$$\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{j_2\right\}}^{j_3})\sigma ({\mathrm{B}}_{A\cup \left\{j_2\right\}}^i,{\mathrm{B}}_C^{j_2})={(-1)}^{|A_{\le i}|}{(-1)}^{|{(A\cup \left\{j_2\right\})}_{\le i}|}=-1$$

because $j_2<j_3<i$ and $A=\{j_3,\dots ,j_c\}$. For the third case, we have that

$$\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{j_2\right\}}^{j_3})\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{j_1\right\}}^{j_3})={(-1)}^{|A_{\le i}|}{(-1)}^{|A_{\le i}|}=1$$

and

$$\begin{array}{ccc}\hfill \sigma ({\mathrm{B}}_{A\cup \left\{j_1\right\}}^{j_3},{\mathrm{B}}_C^{j_3})\sigma ({\mathrm{B}}_{A\cup \left\{j_2\right\}}^{j_3},{\mathrm{B}}_C^{j_3})& =& {(-1)}^{|{(A\cup \left\{j_1\right\})}_{\le j_2}\setminus j_3|}{(-1)}^{|{(A\cup \left\{j_2\right\})}_{\le j_1}\setminus j_3|}\hfill \\ & =& {(-1)}^1{(-1)}^0=-1\hfill \end{array}$$

because $A=\{j_3,\dots ,j_c\}$. Finally, for the fourth case, we have that

$$\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{j_1\right\}}^j)\sigma ({\mathrm{B}}_{A\cup \left\{h\right\}}^i,{\mathrm{B}}_C^j)={(-1)}^{|A_{\le i}|}{(-1)}^{{|(A\cup \left\{h\right\})}_{\le i}|}=\left\{\begin{array}{cc}-1\hfill & \mathrm{if}h<i,\hfill \\ 1\hfill & \mathrm{if}h>i,\hfill \end{array}\right.$$

and

$$\sigma ({\mathrm{B}}_A^i,{\mathrm{B}}_{A\cup \left\{h\right\}}^i)\sigma ({\mathrm{B}}_{A\cup \left\{j_1\right\}}^j,{\mathrm{B}}_C^j)={(-1)}^{|A_{\le h}\setminus i|}{(-1)}^{|{(A\cup \left\{j_1\right\})}_{\le h}\setminus j|}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}h<i,\hfill \\ -1\hfill & \mathrm{if}h>i.\hfill \end{array}\right.$$

□

The next step is to prove that the complex ${\mathrm{K}}_{•}\left(n\right)$ is exact. In order to apply Theorem 2, we first need to calculate the Betti numbers of the edge ideal of the complete graph. We recall the definition of Betti numbers of an ideal.

Definition 13.

The i-th Betti number in multidegree $\mathbf{b}$ of an ideal I, denoted as ${\beta }_{i,\mathbf{a}}\left(I\right)$, is the number of summands equal to $S(-\mathbf{a})$ in the i-th free module $F_i$ of a minimal free resolution ${\mathrm{F}}_{•}={\{F_i,{\delta }_i\}}_{i=-1}^p$ of I.

We will calculate the Betti numbers by using Hochster’s formula, that is, by computing the reduced homology of the lower Koszul simplicial complex.

Definition 14.

Given a monomial ideal I and $\mathbf{a}\in {\mathbb{N}}^n$, the lower and upper Koszul simplicial complex are given by

$$\begin{array}{ccc}\hfill K_{\mathbf{a}}\left(I\right)& =& \{\mathit{squarefree}\mathit{vectors}\tau ⩽\mathbf{a}:{\mathbf{x}}^{\mathbf{a}-\mathbf{1}+\tau }\notin I\}\mathit{and}{K}^{\mathbf{a}}\left(I\right)\hfill \\ & =& \{\mathit{squarefree}\mathit{vectors}\tau :{\mathbf{x}}^{\mathbf{a}-\tau }\in I\}.\hfill \end{array}$$

Theorem 3

(Hochster’s formula). If ${\beta }_{i,\mathbf{g}}\left(I\right)$ is the i-th Betti number of a monomial ideal I in multidegree $\mathbf{a}$, then

$${\beta }_{i,\mathbf{a}}\left(I\right)=\left\{\begin{array}{c}{dim}_k{\tilde{H}}_{i-1}(K^{\mathbf{a}}\left(I\right);k),\hfill \\ {dim}_k{\tilde{H}}^{n-i-2}(K_{\mathbf{a}}\left(I\right);k),\hfill \\ {dim}_k{\tilde{H}}^{i-1}(K^{\mathbf{a}}\left(I\right);k),\hfill \\ {dim}_k{\tilde{H}}_{n-i-2}(K_{\mathbf{a}}\left(I\right);k).\hfill \end{array}\right.$$

Proof. 

A version of this classical formula appeared for the first time in [6]. Several of these versions can be found in the literature, for instance, the first two can be found in [2] (Theorems 1.34 and 5.11). The last two versions apply the Universal Coefficient Theorem for cohomology to the first two. □

Before we calculate the Betti numbers, we will state some notation. Given a vector $\mathbf{a}\in {\mathbb{N}}^n$, we set $\mathrm{supp}\left(\mathbf{a}\right)=\{i\in \left[n\right]:{\mathbf{a}}_i\ne 0\}$ and given $A\subseteq \left[n\right]$ and a monomial ideal I, we set $I\left(A\right)=⟨{\mathbf{x}}^{\mathbf{a}}\in I:\mathrm{supp}\left(\mathbf{a}\right)\subseteq A⟩$. Finally, let $e_i$ be the i-th vector in the canonical basis of ${\mathbb{R}}^n$, that is, the vector with a 1 in position i and 0 in the other positions.

Proposition 13.

If $\mathbf{a}\in {\{0,1\}}^n$ and ${\mathcal{B}}_{\mathbf{a}}$ is the set of basis graphs of $K_n$ with base $A=\mathrm{supp}\left(\mathbf{a}\right)$, then

$${\beta }_{\left|A\right|-1,\mathbf{a}}\left(I_{K_n}\right)=\left|A\right|-1=|{\mathcal{B}}_{\mathbf{a}}|.$$

Proof. 

It is not difficult to see that $K_{\mathbf{a}}\left(I_{K_n}\right)=K_{\mathbf{a}}\left(I_{K_n}\left(A\right)\right)$ and

$$K_{\mathbf{b}}\left(I_{K_n}\left(A\right)\right)=\left\{\begin{array}{cc}\{e_i:i\in A\}\hfill & \mathrm{if}\mathbf{b}=\mathbf{a},\hfill \\ \left\{\mathbf{0}\right\}\hfill & \mathrm{if}\mathbf{b}\ne \mathbf{a}.\hfill \end{array}\right.$$

Thus, ${\tilde{H}}_i(K_{\mathbf{a}}\left(I\right);k)$ is equal to zero with the exception of $i=0$ where its dimension is equal to the number of connected components of $K_{\mathbf{a}}$ minus one. Therefore, using Hochster’s formula, we conclude the result. □

Remark 14.

The Betti numbers of the ideal edge of a complete graph are very easy to calculate and this has been done several times before.

Now, we prove that the set of columns of the differentials of ${\mathrm{K}}_{•}\left(n\right)$ are irredundant.

Theorem 4.

The columns of the differentials of the complex ${\mathrm{K}}_{•}\left(n\right)$ are irredundant.

Proof. 

We will proceed by contradiction, that is, we will assume that the columns $\{c_1,\cdots ,c_r\}$ of a differential $d_i$ in ${\mathrm{K}}_{•}\left(n\right)$ are redundant. Without loss of generality, we can assume that $c_1=s_2{c}_2+\cdots +s_r{c}_r$ with $s_i\in S$ for all $2⩽j⩽r$. Let $h_1,\dots ,h_t$ homogeneous such that ${\sum }_{i=2}^r{s}_i{c}_i={\sum }_{i=1}^l{h}_i$. Since the $c_i$’s are homogeneous of multidegree ${\mathbf{x}}^A$ with $\left|A\right|=i+1$ for some $A\subseteq \left[n\right]$, then $h_i=0$ whenever $\mathrm{mdeg}\left(h_i\right)\ne \mathrm{mdeg}\left(c_1\right)$ and if $\mathrm{mdeg}\left(h_i\right)=\mathrm{mdeg}\left(c_1\right)$, then $\mathrm{mdeg}\left(h_i\right)={\sum }_{j=1}^t{s}_{i_j}{c}_{i_j}$ with $\mathrm{mdeg}\left(c_{i_j}\right)=\mathrm{mdeg}\left(c_1\right)$ and $s_{i_j}\in k$ for all $1\le j\le t$.

Thus, without loss of generality, we can assume that $c_1=s_2{c}_2+\cdots s_t{c}_t$ where $s_j\in k$ and $\mathrm{mdeg}\left(c_j\right)=\mathrm{mdeg}\left(c_1\right)$ for all $2⩽j⩽t$. Now, let $i_u\in A$ and $i_u\ne min\left(A\right)$ and ${\mathrm{B}}_A^{i_1},\cdots ,{\mathrm{B}}_A^{i_t}$ be the basis graphs associated to the columns $c_1,\cdots ,c_t$, respectively. By Lemma 3, ${\mathrm{B}}_{A\setminus i_u}^{i_1}$ is a subgraph of ${\mathrm{B}}_A^{i_1}$ and not a subgraph of ${\mathrm{B}}_{A\setminus i_u}^{i_j}$ for $2⩽j⩽t$. Therefore, ${\left(c_1\right)}_{{\mathrm{B}}_{A\setminus i_u}^{i_1}}\ne 0$ and ${\left(c_i\right)}_{{\mathrm{B}}_{A\setminus i_u}^{i_1}}=0$ for all $2⩽j⩽t$, which is a contradiction to the fact that $c_1=s_2{c}_2+\cdots s_t{c}_t$. □

Finally, considering everything, we can conclude that the complex ${\mathrm{K}}_{•}\left(n\right)$ is exact.

Corollary 4.

The complex ${\mathrm{K}}_{•}\left(n\right)$ is a minimal free resolution of the edge ideal of the complete graph with n vertices.

Proof. 

It follows from Theorems 2, 4 and Proposition 13. □