On Lemniscate Starlikeness of the Solution of General Differential Equations

Abstract

In this article, we derived conditions on the coefficient functions $a\left(z\right)$ and $b\left(z\right)$ of the differential equations $y^{″}\left(z\right)+a\left(z\right)y^{\prime }\left(z\right)+b\left(z\right)y\left(z\right)=0$ and $z^2{y}^{″}\left(z\right)+a\left(z\right)z{y}^{\prime }\left(z\right)+b\left(z\right)y\left(z\right)=0,$ such their solution $f\left(z\right)$ with normalization $f\left(0\right)=0=f^{\prime }\left(0\right)-1$ is starlike in the lemniscate domain, equivalently $z{f}^{\prime }\left(z\right)/f\left(z\right)\prec \sqrt{1+z}$. We provide several examples with graphical presentations for a clear view of the obtained results.

1. Introduction

Let $\mathcal{A}$ denote the class of functions f in the open unit disk $\mathbb{D}=\{z:|z|<1\}$, and normalized by the conditions $f\left(0\right)=0=f^{\prime }\left(0\right)-1$. If f and g are analytic in $\mathbb{D}$, then f is subordinate [1] to g, written $f\prec g,$ or $f\left(z\right)\prec g\left(z\right),$ $z\in \mathbb{D}$, if there is an analytic self-map $\omega$ of $\mathbb{D}$ satisfying $w\left(0\right)=0$ and $\left|w\right(z\left)\right|<1$ such that $f\left(z\right)=g\left(\omega \right(z\left)\right)$, $z\in \mathbb{D}$. In particular, if g is univalent and $g\left(0\right)=f\left(0\right)$, then $f\left(D\right)\subset g\left(D\right)$.

Denote by ${\mathcal{S}}^{\ast }$ and $\mathcal{C}$, respectively, the important subclasses of $\mathcal{A}$ consisting of univalent starlike and convex functions. Geometrically $f\in {\mathcal{S}}^{\ast }$ if the linear segment $tw$, $0\le t\le 1,$ lies completely in $f\left(\mathbb{D}\right)$ whenever $w\in f\left(\mathbb{D}\right)$, while $f\in \mathcal{C}$ if $f\left(\mathbb{D}\right)$ is a convex domain. Related to these subclasses is the Cárathèodory class $\mathcal{P}$ consisting of analytic functions p satisfying $p\left(0\right)=1$ and $\mathrm{Re}p\left(z\right)>0$ in $\mathbb{D}$. Analytically, $f\in {\mathcal{S}}^{\ast }$ if $z{f}^{\prime }\left(z\right)/f\left(z\right)\in \mathcal{P}$, while $f\in \mathcal{C}$ if $1+z{f}^{″}\left(z\right)/f^{\prime }\left(z\right)\in \mathcal{P}$.

A function $f\in \mathcal{A}$ is lemniscate convex if $1+(z{f}^{″}\left(z\right)/f^{\prime }\left(z\right))$ lies in the region bounded by right half of lemniscate of Bernoulli given by $\{w:|w^2-1|=1\}$, which is equivalent to the subordination $1+(z{f}^{\prime \prime }\left(z\right)/f^{\prime }\left(z\right))\prec \sqrt{1+z}$. Similarly, the function f is lemniscate starlike if $z{f}^{\prime }\left(z\right)/f\left(z\right)\prec \sqrt{1+z}$. On the other hand, the function $f\in \mathcal{A}$ is lemniscate Carathéodory if $f^{\prime }\left(z\right))\prec \sqrt{1+z}$. Clearly, lemniscate Carathéodory function is a Carathéodory function and hence is univalent.

For studying different classes of analytical functions, the principle of differential subordination [2,3] is a vital tool. Following Lemma 1, derived by using the principle of differential subordination is useful in sequence to study geometric properties related to the lemniscate.

Lemma 1

([4]). Let $p\in \mathcal{H}[1,n]$ with $p\left(z\right)\not\equiv 1$ and $n\ge 1$. Let $\Omega \subset \mathbb{C}$, and $\Psi :{\mathbb{C}}^3\times \mathbb{D}\to \mathbb{C}$ satisfy

$$\Psi (r,s,t;z)\notin \Omega$$

(1)

whenever $z\in \mathbb{D},$ and for $m\ge n\ge 1$, $-\pi /4\le \theta \le \pi /4$,

$$\begin{array}{c}\hfill r=\sqrt{2cos\left(2\theta \right)}{e}^{i\theta },s=\frac{m{e}^{3i\theta }}{2\sqrt{2cos\left(2\theta \right)}}\mathrm{and}\left((t+s)e^{-3i\theta }\right)\ge \frac{3m^2}{8\sqrt{2cos\left(2\theta \right)}}.\end{array}$$

(2)

If $\Psi (p\left(z\right),z{p}^{\prime }\left(z\right),z^2{p}^{″}\left(z\right);z)\in \Omega$ for $z\in \mathbb{D}$, then $p\left(z\right)\prec \sqrt{1+z}$ in $\mathbb{D}$.

The following inequalities are true for r and s as given in (2):

$$\begin{array}{c}\hfill |s+r^2-1|\ge \frac{1}{2\sqrt{2}}+1\mathrm{and}|r-1|\le \sqrt{2}-1.\end{array}$$

(3)

In Section 2, we consider a set of differential equations

$$y^{″}\left(z\right)+a\left(z\right)y^{\prime }\left(z\right)+b\left(z\right)y\left(z\right)=0$$

and

$$z^2{y}^{″}\left(z\right)+a\left(z\right)z{y}^{\prime }\left(z\right)+b\left(z\right)y\left(z\right)=0.$$

Using Lemma 1, we derived conditions on $a\left(z\right)$ and $b\left(z\right)$ for which the solution of the above differential equations are lemniscate starlike. The work is motivated by the articles [5,6] where several geometric properties of the solution of general ordinary differential equations are considered. In Section 3, we demonstrate the special cases by choosing $a\left(z\right)$ and $b\left(z\right)$ which leads to several well known special differential Equations [7] like as confluent hypergeometric, Bessel, etc,. We also provide some graphical demonstrations and highlight open problems.

2. Lemniscate Starlike Functions

In this section, we state and prove our main results. We consider two ordinary differential equations and derived the conditions by which the solution of those differential equations is lemniscate starlike. It is worth noting here that the existence of the solution of those differential equations is altogether a different case of study. Here, with examples we show that there are functions that are the solution of considered differential equations.

Theorem 1.

Suppose that $\mathtt{F}$ is the solution of the differential equation

$$\begin{array}{c}\hfill y^{″}\left(z\right)+a\left(z\right)y^{\prime }\left(z\right)+b\left(z\right)y\left(z\right)=0\end{array}$$

(4)

with the normalization $\mathtt{F}\left(0\right)=0$, ${\mathtt{F}}^{\prime }\left(0\right)=1$. Suppose that $F\left(z\right)\ne 0$ for all $z\in \mathbb{D}\setminus \left\{0\right\}$. If the analytic functions a and b satisfy the inequality

$$\begin{array}{c}\hfill 4(\sqrt{2}-1)|za\left(z\right)-1|+4|zb\left(z\right)+a\left(z\right)|<4+\sqrt{2},\end{array}$$

(5)

then $\mathtt{F}$ is lemniscate starlike in $\mathbb{D}$.

Proof. 

Suppose that $\mathtt{F}\left(z\right)\ne 0$ ($\forall z\in \mathbb{D}\setminus \left\{0\right\}$) is a solution of the differential Equation (4) with the condition $\mathtt{F}\left(0\right)=0$ and ${\mathtt{F}}^{\prime }\left(0\right)=1$. Define

$$p\left(z\right):=\frac{z{\mathtt{F}}^{\prime }\left(z\right)}{\mathtt{F}\left(z\right)}.$$

A computation yield

$$\begin{array}{cc}\hfill z{\mathtt{F}}^{\prime }\left(z\right)& =p\left(z\right)\mathtt{F}\left(z\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill z^2{\mathtt{F}}^{″}\left(z\right)& =\left(z{p}^{\prime }\left(z\right)+(p\left(z\right)-1)p\left(z\right)\right)\mathtt{F}\left(z\right).\hfill \end{array}$$

(7)

Since, $\mathtt{F}$ is the solution of (4), it follows

$$\begin{array}{c}\hfill z^2{\mathtt{F}}^{″}\left(z\right)+a\left(z\right)z^2{\mathtt{F}}^{\prime }\left(z\right)+b\left(z\right)z^2\mathtt{F}\left(z\right)=0.\end{array}$$

This along with (6) and (7) gives

$$\begin{array}{c}\hfill z{p}^{\prime }\left(z\right)+(p\left(z\right)-1)p\left(z\right)+za\left(z\right)p\left(z\right)+z^{2}b\left(z\right)=0.\end{array}$$

(8)

Let $\Omega :=\left\{0\right\}$, and the function $\Psi :{\mathbb{C}}^2\times \mathbb{D}\to \mathbb{C}$ is defined by

$$\begin{array}{c}\hfill \Psi (r,s;z)=s+(r-1)r+za\left(z\right)r+z^{2}b\left(z\right)\end{array}$$

(9)

Then, from (8), it follows $\Psi (p,z{p}^{\prime };z)\in \Omega .$ By considering r and s as mention in Lemma 1 along with (9) and inequalities in (3) gives

$$\begin{array}{cc}\hfill |\Psi (r,s;z\left)\right|& =|(s+r^2-1)+(za\left(z\right)-1)(r-1)+z^{2}b\left(z\right)+za\left(z\right)|\hfill \\ \hfill & \ge |s+r^2-1|-|za\left(z\right)-1\left|\right|r-1|-|zb\left(z\right)+a\left(z\right)|\hfill \\ \hfill & \ge \left(\frac{1}{2\sqrt{2}}+1\right)-(\sqrt{2}-1)|za\left(z\right)-1|-|zb\left(z\right)+a\left(z\right)|>0.\hfill \end{array}$$

This implies that $\Psi (r,s;z)\notin \Omega$. From Lemma 1, it follows that $p\left(z\right)=z{\mathtt{F}}^{\prime }\left(z\right)/\mathtt{F}\left(z\right)\prec \sqrt{1+z}$. □

Theorem 2 (Lemniscate Starlike functions).

Let a and b be two analytic functions defined in $\mathbb{D}$ for which the differential equation

$$\begin{array}{c}\hfill z^2{y}^{″}\left(z\right)+a\left(z\right)z{y}^{\prime }\left(z\right)+b\left(z\right)y\left(z\right)=0\end{array}$$

(10)

has the solution $\mathtt{F}$ satisfying $\mathtt{F}\left(0\right)=0={\mathtt{F}}^{\prime }\left(0\right)-1$, and $\mathtt{F}\left(z\right)\ne 0$ for all $z\in \mathbb{D}\setminus \left\{0\right\}$. Suppose that

$$\begin{array}{c}\hfill 4(\sqrt{2}-1)|a\left(z\right)-1|+4|a\left(z\right)+b\left(z\right)|<4+\sqrt{2}.\end{array}$$

(11)

Then, $\mathtt{F}$ is lemniscate starlike in $\mathbb{D}$.

Proof. 

The proof is simlar to the proof of Theorem 1, we omit the details. In this case, the function $\Psi :{\mathbb{C}}^2\times \mathbb{D}\to \mathbb{C}$ is defined by

$$\begin{array}{c}\hfill \Psi (r,s;z)=s+(r-1)r+a\left(z\right)r+b\left(z\right)\end{array}$$

(12)

and

$$\begin{array}{cc}\hfill |\Psi (r,s;z\left)\right|& \ge |s+r^2-1|-|a\left(z\right)-1\left|\right|r-1|-|a\left(z\right)+b\left(z\right)|\hfill \\ \hfill & \ge \left(\frac{1}{2\sqrt{2}}+1\right)-(\sqrt{2}-1)|a\left(z\right)-1|-|a\left(z\right)+b\left(z\right)|>0.\hfill \end{array}$$

The rest of the explanation as given in the proof of Theorem 1. □

3. Examples of Leminscate Starlike Functions

In this section, we present some examples involving special functions which prove that the solution set of the differential Equations (4) and (10) is non-empty. Further, we provide conditions for which those solutions are lemniscate starlike.

3.1. Example Involving Error Function

Our first example involves the error function. The error function, denoted by erf [8] is defined as

$$\begin{array}{c}\hfill \mathit{erf}\left(z\right):=\frac{2}{\sqrt{\pi }}{\int }_0^z{e}^{-t^2}dt=\frac{2}{\sqrt{\pi }}\sum _{n=0}^{\infty }\frac{{(-1)}^n}{n!\left(2n+1\right)}{z}^{2n+1}.\end{array}$$

The error function can also be expressed by the confluent hypergeometric functions through $\sqrt{\pi }\mathit{erf}\left(z\right)=2z{}_1{F}_1(1/2;3/2;-z^2)$. Functional inequalities involving the real error functions can be found in [9]. In [10], Coman determined the radius of starlikeness of the error function. Now, we state and prove our first Theorem involving the error function.

The function

$$\begin{array}{c}\hfill f_1\left(z\right):=\sqrt{\frac{\pi \alpha }{2}}{e}^{z^2/\left(2\alpha \right)}\mathit{erf}\left(\frac{z}{\sqrt{2\alpha }}\right),\alpha >0\end{array}$$

(13)

is lemniscate starlike for $\alpha >4(\sqrt{2}+1)/(8-3\sqrt{2})$.

Since $\mathit{erf}\left(0\right)=0$, it follows that $f_1\left(0\right)=0$. Taking derivative of both side of (13), it follows

$$\begin{array}{c}\hfill f_1^{\prime }\left(z\right)=\sqrt{\frac{\pi }{2\alpha }}z{e}^{\frac{z^2}{2\alpha }}\mathrm{erf}\left(\frac{z}{\sqrt{2\alpha }}\right)+1\end{array}$$

(14)

Clearly, $f_1^{\prime }\left(0\right)=1$. Further, a derivative of (14) yields

$$\begin{array}{c}\hfill f_1^{″}\left(z\right)=\sqrt{\frac{\pi }{2\alpha }}z{e}^{\frac{z^2}{2\alpha }}\mathrm{erf}\left(\frac{z}{\sqrt{2\alpha }}\right)+1\end{array}$$

(15)

A computation gives

$$\begin{array}{cc}\hfill & \alpha f_1^{″}\left(z\right)-z{f}_1^{\prime }\left(z\right)-f_1\left(z\right)\hfill \\ & =\frac{\alpha \left(\sqrt{2\pi }{e}^{\frac{z^2}{2\alpha }}\left(\alpha +z^2\right)\mathrm{erf}\left(\frac{z}{\sqrt{2\alpha }}\right)+2\sqrt{\alpha }z\right)}{2{\alpha }^{3/2}}-z\left(\frac{\sqrt{\frac{\pi }{2}}z{e}^{\frac{z^2}{2\alpha }}\mathrm{erf}\left(\frac{z}{\sqrt{2\alpha }}\right)}{\sqrt{\alpha }}+1\right)-\sqrt{\frac{\pi \alpha }{2}}\mathrm{erf}\left(\frac{z}{\sqrt{2\alpha }}\right)exp\left(\frac{z^2}{2\alpha }\right)=0.\hfill \end{array}$$

Thus, $f_1$ is a solution of the differential equation $\alpha y^{″}\left(z\right)-z{y}^{\prime }\left(z\right)-y\left(z\right)=0.$.

Let $a\left(z\right)=-z/\alpha$ and $b\left(z\right)=-1/\alpha$ in (5). Then

$$\begin{array}{c}\hfill 4(\sqrt{2}-1)\left|-\frac{z^2}{\alpha }-1\right|+4\left|-\frac{z}{\alpha }-\frac{z}{\alpha }\right|-4-\sqrt{2}\le \frac{4(\sqrt{2}+1)}{\left|\alpha \right|}-(8-3\sqrt{2})<0,\end{array}$$

provided $\left|\alpha \right|>4(\sqrt{2}+1)/(8-3\sqrt{2})$.

Clearly for $\alpha >{\alpha }_0=4(\sqrt{2}+1)/(8-3\sqrt{2})=2.57012$, the function

$$\begin{array}{c}\hfill {\mathcal{H}}_{\alpha }\left(z\right):={\displaystyle \frac{z\frac{d}{dz}\left(\sqrt{\frac{\pi \alpha }{2}}{e}^{z^2/\left(2\alpha \right)}\mathit{erf}\left(\frac{z}{\sqrt{2\alpha }}\right)\right)}{\sqrt{\frac{\pi \alpha }{2}}{e}^{z^2/\left(2\alpha \right)}\mathit{erf}\left(\frac{z}{\sqrt{2\alpha }}\right)}}={\displaystyle \frac{z\frac{d}{dz}\left(e^{z^2/\left(2\alpha \right)}\mathit{erf}\left(\frac{z}{\sqrt{2\alpha }}\right)\right)}{e^{z^2/\left(2\alpha \right)}\mathit{erf}\left(\frac{z}{\sqrt{2\alpha }}\right)}}\prec \sqrt{1+z}.\end{array}$$

To investigate the minimum value of ${\alpha }_0$, we experiment graphically for various values of $\alpha$. From Figure 1, it is certain that ${\mathcal{H}}_{\alpha }\left(z\right)\prec \sqrt{1+z}$ for $\alpha >{\alpha }_0=2.57012$, however, it is also evident that ${\alpha }_0$ can be lower down to a number between $(1.67,1.7)$. Based on this fact, we state an open PB as below:

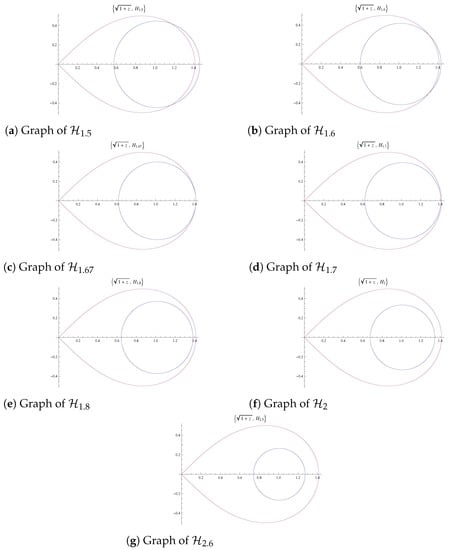
Figure 1. ${\mathcal{H}}_{\alpha }$ for $\alpha =1.5,1.6,1.67,1.7,1.8,2,2.6.$.

Open Problem 1.

There exist a ${\alpha }_0\in (1.67,1.7)$, such that $\sqrt{\frac{\pi \alpha }{2}}{e}^{z^2/\left(2\alpha \right)}\mathit{erf}\left(\frac{z}{\sqrt{2\alpha }}\right)$ is lemniscate starlike for $\alpha \ge {\alpha }_0$.

3.2. Example Involving Classical Bessel Function

The Bessel function $J_{\nu }$ of order $\nu$ is the solution of the differential equation

$$\begin{array}{c}\hfill z^2{y}^{″}\left(z\right)+z{y}^{\prime }\left(z\right)+(z^2-{\nu }^2)y\left(z\right)=0.\end{array}$$

(16)

Several results related to the geometric properties of the Bessel function and its generalizations can be seen in [11,12,13,14,15,16,17,18,19,20,21,22] and references therein.

Here, we consider the function

$$\begin{array}{c}\hfill f_2\left(z\right)=\frac{\pi }{sin\left(\frac{2\pi \nu }{\sqrt{\beta }}\right)}\left(J_{-\frac{2\nu }{\sqrt{\beta }}}\left(\frac{2}{\sqrt{\beta }}\right)J_{\frac{2\nu }{\sqrt{\beta }}}\left(2\sqrt{\frac{e^z}{\beta }}\right)-J_{\frac{2\nu }{\sqrt{\beta }}}\left(\frac{2}{\sqrt{\beta }}\right)J_{-\frac{2\nu }{\sqrt{\beta }}}\left(2\sqrt{\frac{e^z}{\beta }}\right)\right),\nu \notin \mathbb{Z},\beta >0.\end{array}$$

Clearly,

$$f_2\left(0\right)=\frac{\pi }{sin\left(\frac{2\pi \nu }{\sqrt{\beta }}\right)}\left(J_{-\frac{2\nu }{\sqrt{\beta }}}\left(\frac{2}{\sqrt{\beta }}\right)J_{\frac{2\nu }{\sqrt{\beta }}}\left(\frac{2}{\sqrt{\beta }}\right)-J_{\frac{2\nu }{\sqrt{\beta }}}\left(\frac{2}{\sqrt{\beta }}\right)J_{-\frac{2\nu }{\sqrt{\beta }}}\left(\frac{2}{\sqrt{\beta }}\right)\right)=0.$$

A careful computation as in [5] (Example 3, Page 561), it follows that $f_2^{\prime }\left(0\right)=1$ and $f_2$ is the solution of the differential equation

$$\beta F^{″}\left(z\right)+(e^z-{\nu }^2)F\left(z\right)=0.$$

For $a\left(z\right)=0$ and $b\left(z\right)=(e^z-{\nu }^2)/\beta$, (5) implies

$$\begin{array}{cc}\hfill & 4(\sqrt{2}-1)|za\left(z\right)-1|+4|zb\left(z\right)+a\left(z\right)|-4-\sqrt{2}\hfill \\ \hfill & <\frac{4}{\beta }\left|e^z-{\nu }^2\right|-8+3\sqrt{2}\hfill \\ \hfill & \le \frac{4}{\beta }\left(e^2-2{\nu }^{2}ecos\left(1\right)+{\nu }^4\right)-8+3\sqrt{2}\hfill \end{array}$$

Thus, an application of Theorem 1 conclude that for fixed $\beta >0$, if there exist a $\nu$ for which

$$\begin{array}{c}\hfill 4({\nu }^4-2{\nu }^{2}ecos\left(1\right)+e^2)\le (8-3\sqrt{2})\beta ,\end{array}$$

(17)

then $f_2$ is Lemniscate starlike in $\mathbb{D}$.

To investigate about the existence of $\beta$ and corresponding $\nu$ for which the inequality (17) holds, we found that it is possible only when $\beta >{\beta }_0\approx 5.56986$.

3.3. Example Involving Airy Functions

In this example, we consider the function

$$f_3\left(z\right)={\displaystyle \frac{\Gamma \left(\frac{1}{3}\right)\left(3^{5/6}Bi\left(\sqrt[3]{a}z\right)-3^{4/3}Ai\left(\sqrt[3]{a}z\right)\right)}{6\sqrt[3]{a}}},a\ne 0.$$

Here, $Ai$ and $Bi$ are well-known Airy functions [8] which are independent solutions of the differential equation $y^{″}\left(z\right)-zy\left(z\right)=0$ with initial value

$$Ai\left(0\right)=\frac{1}{3^{2/3}\Gamma \left(\frac{2}{3}\right)},A{i}^{\prime }\left(0\right)=-\frac{1}{3^{1/3}\Gamma \left(\frac{1}{3}\right)},Bi\left(0\right)=\frac{1}{3^{1/6}\Gamma \left(\frac{2}{3}\right)},B{i}^{\prime }\left(0\right)=\frac{3^{1/6}}{\Gamma \left(\frac{1}{3}\right)}.$$

Thus,

$$f_3\left(0\right)={\displaystyle \frac{\Gamma \left(\frac{1}{3}\right)\left(3^{5/6}Bi\left(0\right)-3^{4/3}Ai\left(0\right)\right)}{6\sqrt[3]{a}}}={\displaystyle \frac{\Gamma \left(\frac{1}{3}\right)}{6\sqrt[3]{a}}}\left(\frac{3^{5/6}}{3^{1/6}\Gamma \left(\frac{2}{3}\right)}-\frac{3^{4/3}}{3^{2/3}\Gamma \left(\frac{2}{3}\right)}\right)=0$$

and

$$f_3^{\prime }\left(0\right)={\displaystyle \frac{\Gamma \left(\frac{1}{3}\right)\left(3^{5/6}\sqrt[3]{a}B{i}^{\prime }\left(0\right)-3^{4/3}\sqrt[3]{a}A{i}^{\prime }\left(0\right)\right)}{6\sqrt[3]{a}}}={\displaystyle \frac{\Gamma \left(\frac{1}{3}\right)}{6}}\left(\frac{3}{\Gamma \left(\frac{1}{3}\right)}+\frac{3^{4/3}}{3^{1/3}\Gamma \left(\frac{1}{3}\right)}\right)=1$$

Further computation yields that $f_3$ is the solution of the differential equation

$${\mathtt{F}}^{″}\left(z\right)-az\mathtt{F}\left(z\right)=0.$$

Thus, by (5), $f_3$ is lemniscate starlike for $\left|a\right|<(8-3\sqrt{2})/4\approx 0.93934$.

3.4. Example Involving Generalized Bessel Functions

One of the most significant functions included in the literature of geometric functions theory is the generalized and normalized Bessel functions of the form

$$\begin{array}{c}\hfill {\mathtt{U}}_p\left(z\right)=\sum _{n=0}^{\infty }\frac{{(-1)}^n{c}^n}{4^n{\left(\kappa \right)}_n}\frac{z^n}{n!},2\kappa =2p+b+1\ne 0,-2,-4,-6,\dots ;\end{array}$$

which is the solution of

$$\begin{array}{c}\hfill 4z^2{\mathtt{U}}^{″}\left(z\right)+4\kappa z{\mathtt{U}}^{\prime }\left(z\right)+cz\mathtt{U}\left(z\right)=0.\end{array}$$

(18)

For $b=c=1$, the function ${\mathtt{U}}_p$ represents the normalized Bessel function of order p, while for $b=-c=1$, the function ${\mathtt{U}}_p$ represents the normalized modified Bessel function of order p. The Spherical Bessel function can also be obtain by using $b=2$, $c=1$.

The inclusion of ${\mathtt{U}}_p$ in various subclasses of univalent functions theory is extensively studied by many authors [11,12,13,14,15,17,19,23,24] and some references therein. Recently, the lemniscate convexity and other properties of ${\mathtt{U}}_p$ is studied in [24].

Now consider

$$\begin{array}{c}\hfill f_4\left(z\right)=z{\mathtt{U}}_p\left(z\right).\end{array}$$

A differentiation gives

$$\begin{array}{cc}\hfill z{f}_4^{\prime }\left(z\right)& =z^2{\mathtt{U}}_p^{\prime }\left(z\right)+z{\mathtt{U}}_p\left(z\right)\Rightarrow z^2{\mathtt{U}}_p^{\prime }\left(z\right)=z{f}_4^{\prime }\left(z\right)-f_4\left(z\right).\hfill \end{array}$$

Differentiate again we have

$$\begin{array}{cc}\hfill & z^2{\mathtt{U}}_p^{″}\left(z\right)+2z{\mathtt{U}}_p^{\prime }\left(z\right)=z{f}_4^{″}\left(z\right)\hfill \\ \hfill \Rightarrow & z^3{\mathtt{U}}_p^{″}\left(z\right)=z{f}_4^{″}\left(z\right)-2(z{f}_4^{\prime }\left(z\right)-f_4\left(z\right))\hfill \end{array}$$

All the above calculation together with (18) implies that $f_4$ is the solution of the differential equation

$$\begin{array}{c}\hfill 4z{f}_4^{″}\left(z\right)+4(\kappa -2)z{f}_4^{\prime }\left(z\right)+(cz-4\kappa +8)f_4\left(z\right)=0.\end{array}$$

(19)

Choosing $a\left(z\right)=\kappa -2$ and $b\left(z\right)=(cz-4\kappa +8)/4$.

$$\begin{array}{cc}4(\sqrt{2}-1)|\kappa -3|+|\frac{cz}{4}|& <4(\sqrt{2}-1)|\kappa -3|+\frac{\left|c\right|}{4}.\end{array}$$

Finally, by (11), the function $f_4$ is lemniscate starlike if

$$16(\sqrt{2}-1)|\kappa -3|+\left|c\right|<4+\sqrt{2}.$$

In particular, the normalized Bessel $z^{1-(p/2)}\Gamma (1+p)2^p{\mathtt{J}}_p\left(\sqrt{z}\right)$$(\kappa =p+1,c=1,b=1)$ and normalized modified Bessel $z^{1-(p/2)}\Gamma (1+p)2^p{\mathtt{I}}_p$$(\kappa =p+1,c=-1,b=1)$ is lemniscate starlike for

$$|p-2|<\frac{3+\sqrt{2}}{16(\sqrt{2}-1)}\Rightarrow 1.33395<p<2.66605.$$

The range of p is slightly better than Corollary [4] (Corollary 2.5). Clearly, this is a very small range of p. By curiosity, we try to understand the possibility of increasing the range of p, through experimenting graphically the image of

$${\mathcal{G}}_p\left(z\right)=\frac{z\frac{d}{dz}\left(z^{1-(p/2)}\Gamma (1+p)2^p{\mathtt{J}}_p\left(\sqrt{z}\right)\right)}{z^{1-(p/2)}\Gamma (1+p)2^p{\mathtt{J}}_p\left(\sqrt{z}\right)}.$$

It is evident that for $p=-0.46$, the image of ${\mathcal{G}}_p\left(D\right)$ lies slightly inside the lemniscate $\sqrt{1+z}$. On the other hand when $p=-0.45$, ${\mathcal{G}}_p\left(D\right)$ lies inside $\sqrt{1+z}$. It is also clear that when p increases, the image of ${\mathcal{G}}_p\left(D\right)$ shrinks and always lies inside the lemniscate $\sqrt{1+z}$. Based on this we can state the following open PB:

Open Problem 2.

There exist a $p_0\in (-0.45,-0.44)$ for which the normalized Bessel function $z^{1-(p/2)}\Gamma (1+p)2^p{\mathtt{J}}_p\left(\sqrt{z}\right)$ is lemniscate starlike for $p\ge p_0$.

3.5. Example Involving Confluent Hypergeometric Functions

The geometric functions theory has a close association with the hypergeometric functions ${}_2{F}_1$ and the confluent hypergeometric functions ${}_1{F}_1$ (refer to the articles [5,25,26,27,28,29,30,31]).

The differential equation

$$z^2{y}^{″}\left(z\right)+(\beta -z)y^{\prime }\left(z\right)-\alpha zy\left(z\right)=0$$

have the solution ${}_1{F}_1(\alpha ,\beta ;z)$.

Now consider the function $f_5\left(z\right):=z{}_1{F}_1(\alpha ,\beta ;z)$. Then, $f_5$ is lemniscate starlike if

$$\begin{array}{c}\hfill 4(\sqrt{2}-1)|\beta -3|+\left|\alpha \right|<8-3\sqrt{2}.\end{array}$$

(20)

Consider a special case by taking $\alpha =1$ and $\beta =3$. Then, we have $f_6\left(z\right)=z{}_1{F}_1(1,3;z)=\left(2(-1+e^z-z)\right)/z$. Clearly, the inequality (20) holds in this case. Figure 2 represents that $z{f}_6^{\prime }\left(z\right)/f_6\left(z\right)\prec \sqrt{1+z}$.

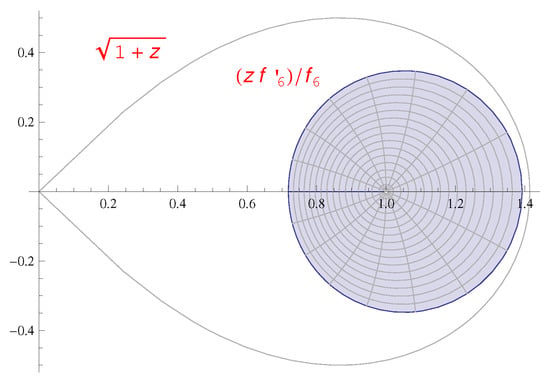
Figure 2. $z{f}_6^{\prime }\left(z\right)/f_6\left(z\right)\prec \sqrt{1+z}$.

Next take $\beta =3+\alpha$ ( for $\alpha >-1$). In this case, the inequality (20) holds for $-1<\alpha <\sqrt{2}$. Thus,

$${\mathcal{F}}_{\alpha }\left(z\right)=\frac{z\frac{d}{dz}\left(z{}_1{F}_1(\alpha ,\alpha +3;z)\right)}{z{}_1{F}_1(\alpha ,\alpha +3;z)}\prec \sqrt{1+z},\mathrm{for}-1<\alpha <\sqrt{2}.$$

However, the graphical experiment in Figure 3 indicates that the subordination may holds for $\alpha \ge \sqrt{2}$. We state the following possible improvement from Figure 3e,f.

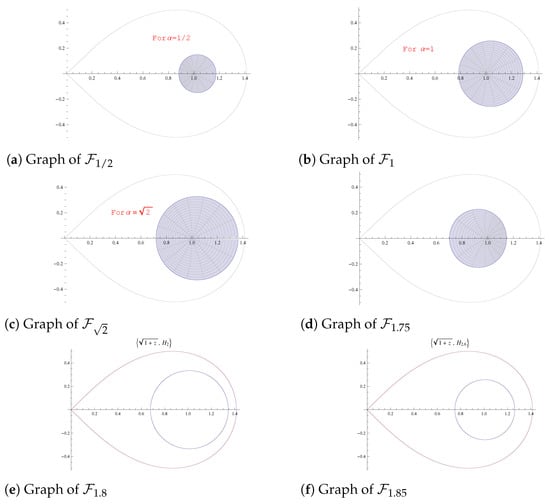
Figure 3. ${\mathcal{F}}_{\alpha }$ for $\alpha =1/2,1,\sqrt{2},1.75,1.8,1.85$.

Open Problem 3.

For $\alpha >-1$, the function $z{}_1{F}_1(\alpha ,\alpha +3;z)$ is lemniscate starlike provided $\alpha \le {\alpha }_0\approx 1.8$.

4. Conclusions

As presented in Section 2, we considered two second-order differential equations. We derived the conditions on the coefficient functions $a\left(z\right)$ and $b\left(z\right)$, respectively, for $y^{\prime }\left(z\right)$ and $y\left(z\right)$ in the differential equation, for which the solution of the differential equations are lemniscate starlike. The judicious choice of $a\left(z\right)$ and $b\left(z\right)$ provides different functions as the solution of the differential equation and that is presented in Section 3. We also highlight some open PBs in Section 3 based on graphical experiment.