Acquisition Performance Analysis of Communication and Ranging Signals in Space-Based Gravitational Wave Detection

Abstract

Space-based gravitational wave detection relies on laser interferometry to measure picometer-level displacements over ${10}^5$–${10}^6$ km baselines. To integrate ranging and communication within the same optical link without degrading the primary scientific measurement, a low modulation index of 0.1 rad is required, resulting in extremely weak signals and challenging acquisition conditions. This study developed mathematical models for signal acquisition, identifying and analyzing key performance-limiting factors for both Binary Phase Shift Keying (BPSK) and Binary Offset Carrier (BOC) schemes. These factors include spreading factor, acquisition step, modulation index, and carrier-to-noise ratio (CNR). Particularly, the acquisition threshold can be directly calculated from these parameters and applied to the acquisition process of communication and ranging signals. Numerical simulations and evaluations, conducted with TianQin mission parameters, demonstrate that, for a data rate of 62.5 kbps and modulation indices of 0.081 rad (BPSK) or 0.036 rad (BOC), respectively, acquisition (probability ≈ 1) is achieved when the CNR is ≥104 dB·Hz under a false alarm rate of ${10}^{-6}$. These results provide critical theoretical support and practical guidance for optimizing the inter-satellite communication and ranging system design for the space-based gravitational wave detection missions.

1. Introduction

As a key prediction of Einstein’s general theory of relativity, gravitational waves have opened up a completely new approach to exploring and understanding the universe. However, due to seismic noise and other unavoidable disturbances, low-frequency gravitational wave signals (mHz–Hz) cannot be detected on the ground, which is precisely the part of the spectrum that holds the greatest research value [1]. To enable in-depth exploration of the universe via low-frequency gravitational waves, several space-based gravitational wave detection missions have been proposed and developed, including LISA [2], TianQin [3], and Taiji [4]. All three missions are designed to detect gravitational waves in the frequency band from 0.1 mHz to 1 Hz [5].

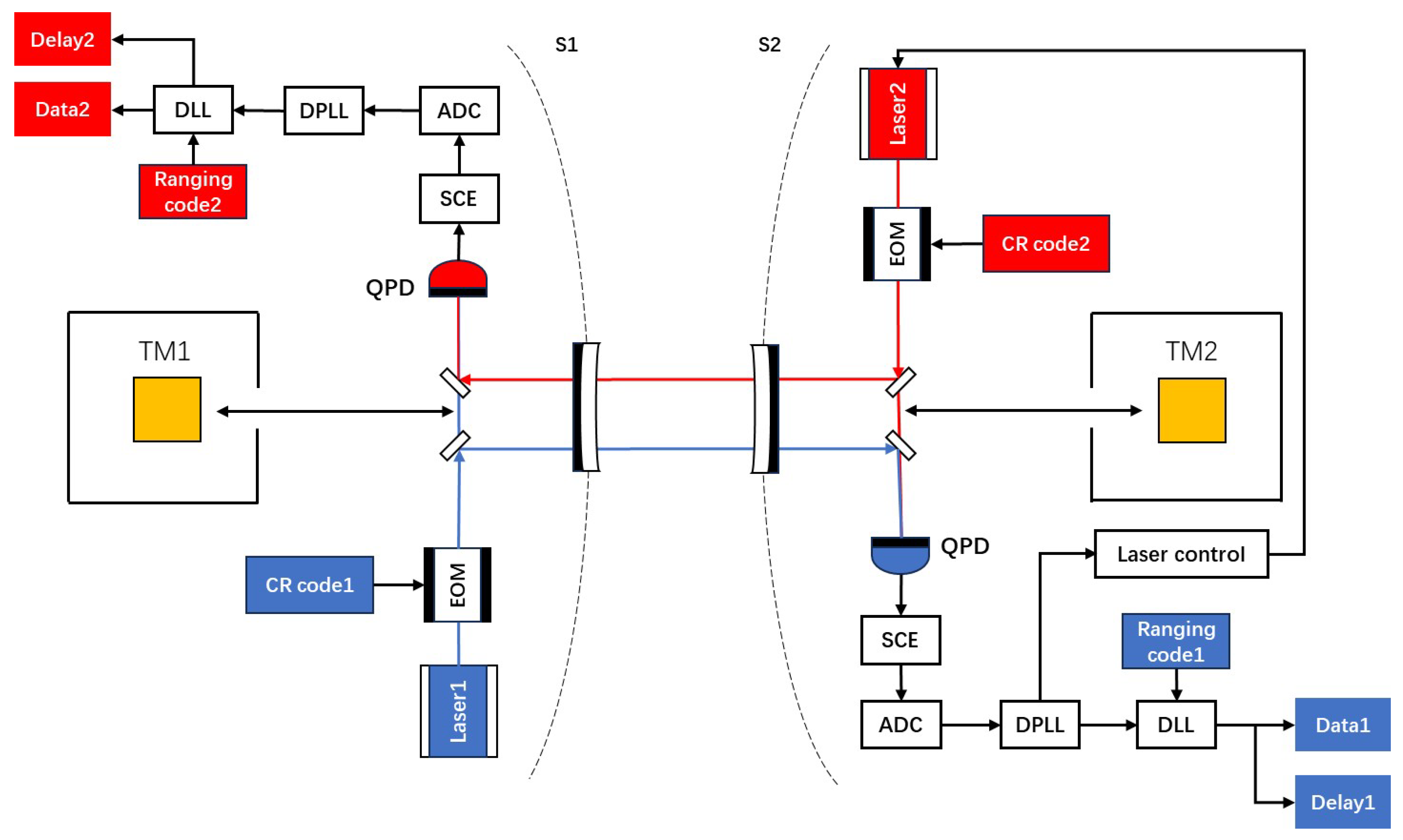
In the gravitational wave detection constellations involved in these missions, each satellite contains a reference object in a fully free-floating state, known as a test mass. During detection, gravitational wave effects are measured by precisely monitoring the displacement between the satellite and the test mass. At the same time, high-precision laser interferometry is employed to record extremely subtle changes in the distance between test masses, thereby extracting information related to gravitational wave signals [6]. However, the relative orbital motion of the satellites leads to variations in the interferometer arm lengths, resulting in unequal arms. In such laser interferometers, laser frequency noise constitutes a dominant noise source, whose residual amplitude is proportional to the arm-length mismatch. To suppress the frequency noise arising from these variations, Time Delay Interferometry (TDI) is employed. This technique processes the measured data through appropriate time delays and linear combinations, effectively reconstructing a virtual equal-arm interferometer and achieving com-mon-mode suppression of laser frequency noise [7,8]. The implementation of TDI during data post-processing requires precise measurement of the absolute inter-satellite distances [9,10]. Meanwhile, to enable the transmission and backup of scientific data, inter-satellite laser communication based on Pseudo-Random Noise (PRN) codes is implemented on the same laser interferometry link [11].

In space-based gravitational wave detection, to minimize the impact on inter-satellite laser interferometric measurements, the functions of inter-satellite laser communication and ranging are integrated into the same laser interferometry link. The communication and ranging signals are phase-modulated onto the laser carrier with a low modulation index. After ultra-long-distance transmission between satellites, the receiving terminal performs demodulation, acquisition, and tracking of these signals, thereby recovering the communication data and the ranging delay [12]. The acquisition of the communication and ranging signals is the key to achieving successful inter-satellite communication and ranging. However, this process faces substantial challenges due to limited bandwidth, weak light conditions with low modulation indices, and ultra-long transmission distances in space-based gravitational wave detection [13,14]. These influences lead to a significant reduction of the received signal’s signal-to-noise ratio (SNR), consequently decreasing the acquisition performance of the communication and ranging signals and even leading to acquisition failures. Therefore, identifying the main factors that influence the acquisition performance of the inter-satellite communication and ranging signals in space-based gravitational wave missions, and establishing accurate mathematical models to describe the quantitative relationship between acquisition performance and these influencing factors, represents critical research questions that must be addressed.

In terms of current space gravitational wave communication and ranging, the LISA project [11] has achieved absolute distance measurements with an accuracy of 2.44 cm using BPSK modulation with a modulation index of 0.1 rad and a PRN code rate of 1.25 MHz. It also demonstrates inter-satellite communication at 78.125 kbps with a bit error rate below ${10}^{-6}$. To further mitigate the impact of communication and ranging signals on laser interferometry, as well as the high-pass filtering effect of the phase-locked loop error signal, the LISA project [15] proposes using BOC modulation for inter-satellite ranging and communication, enabling sub-meter ranging accuracy. The Taiji project [16] initially employs a modulation index of 0.4 rad and a PRN code rate of 1.25 MHz, achieving a data rate of 19.5 kbps with a bit error rate below ${10}^{-6}$. Subsequently, it has reduced the modulation index to 0.1 rad [17], resulting in an absolute distance measurement accuracy of 82.1 cm and a root-mean-square error of 9.14 cm. The TianQin project [9] has achieved an absolute distance measurement accuracy of 1.2 m with a modulation index of 0.1 rad and a PRN code rate of 3.125 MHz, which meets the ranging requirements for TDI [18]. Due to the high CNR of the beat note signal, the TianQin project [19] utilizes a low modulation index of $3.4\times {10}^{-3}$. Simulation results have verified an inter-satellite communication data rate of 62.5 kbps with a bit error rate below ${10}^{-6}$. The communication and ranging signal schemes and system parameters of these missions are summarized in

Table 1. Communication and ranging signaling schemes and system parameters for different space-based gravitational wave detection projects.

Space-Based Gravitational Wave Detection Projects	LISA			Taiji		TianQin
Communication and Ranging Signal	BPSK		BOC	BPSK		BPSK
Modulation Index (rad)	0.1		0.1	0.1	0.4	0.1	0.0034
System Clock Rate (MHz)	80		80	80		100
PRN Code Length	1024	2500	1024	1024		1023	1024
PRN Code Rate (MHz)	1.25	1	1.6	1.25		3.125	1
Data Rate (kbps)	78.125	80	15.625	19.5		/	62.5

.

Current research on communication and ranging for space-based gravitational wave detection shows that the signals employed in such missions primarily adopt BPSK and BOC modulation schemes. Intuitively, the modulation index is a key factor influencing the acquisition performance of communication and ranging signals. Moreover, the communication rate also plays an important role, as it affects the acquisition of PRN codes through the spreading factor. In addition, the design of PRN codes—such as code rate and code length—can further influence acquisition performance. However, due to the absence of accurate mathematical models that describe these relationships, it remains challenging for current studies to quantitatively analyze the acquisition performance of communication and ranging signals.

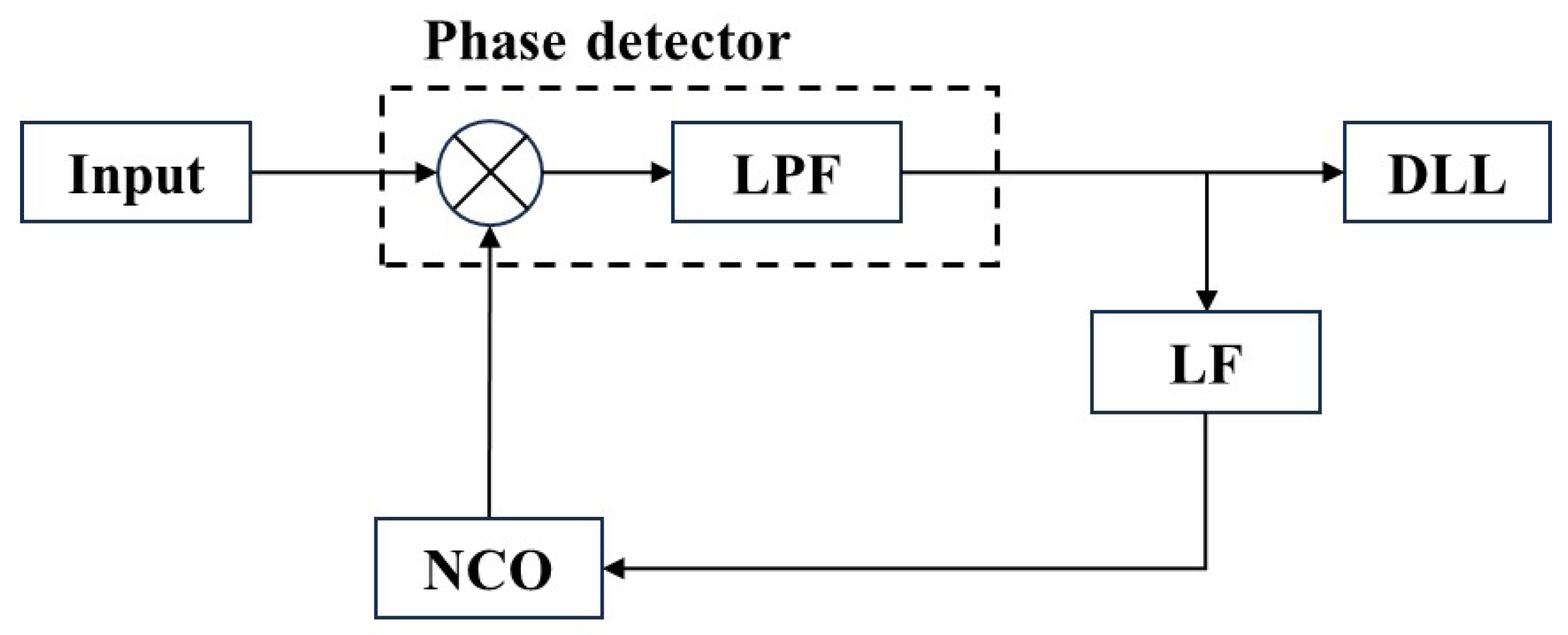
Therefore, the acquisition of ranging and communication signals for space-based gravitational wave detection constitutes a signal synchronization problem under multiple parameter constraints. Conventional satellite navigation signal acquisition typically employs suppressed-carrier synchronization, allocating all signal power to communication and ranging. It faces a high-dynamic, two-dimensional search problem due to high-velocity satellite motion, namely, the unknown and rapidly varying Doppler shift and code phase. Thus, it commonly employs coupled carrier and code tracking loops for joint acquisition [20,21]. However, in space gravitational wave detection, the scientific measurement demands phase stability of the main laser carrier at the picometer level, leaving only 1% of the signal power available for communication and ranging. To minimize the impact of the code loop on the phase measurement of the carrier loop and enable reliable acquisition of the communication and ranging signal, in summary, this study adopted a decoupled architecture described as “DPLL-first carrier locking with Doppler cancellation, followed by DLL-only code-phase acquisition.” Based on this architecture, this study focused on analyzing the acquisition performance of the communication and ranging signals in the gravitational wave detection mission. This study was organized as follows. First, a modulation and demodulation model for the communication and ranging signals was established (Section 2). Second, an acquisition performance model was developed and the key factors influencing acquisition were identified (Section 3). Finally, experimental verification, analysis of the factors influencing acquisition performance, and optimization of the modulation index were carried out (Section 4).

2. Signal Model for Communication and Ranging in Space-Based Gravitational Wave Detection

2.1. Fundamental Principles of Communication and Ranging

For space-based gravitational wave missions, the fundamental principles of the PRN code ranging and communication system [22,23] are illustrated in Figure 1. On the transmitter side of a satellite, a low-rate data code is combined with a high-rate PRN code using the direct-sequence spread spectrum (DS/SS) to generate a BPSK baseband signal. A BOC baseband signal can subsequently be obtained by applying an additional layer of subcarrier modulation to this signal. These two distinct baseband signals are collectively referred to as the communication and ranging codes (CR codes). To minimize the impact of the communication and ranging functions on the primary scientific measurement of the gravitational wave detection, only extremely low optical power is permitted for the laser phase modulation of the communication and ranging codes within an electro-optic modulator (EOM). The modulated laser beam is then transmitted to the remote satellite.

On the receiver side, the incoming laser beam and a local laser beam undergo heterodyne interference. The resulting heterodyned optical signal is then converted into an electrical signal using a quadrant photodetector (QPD). After passing through a series of signal conditioning electronics (SCEs), this electrical signal is digitized by an analog-to-digital converter (ADC). The resulting digital signal is first processed by a digital phase-locked loop (DPLL), which demodulates the communication and ranging codes as an error signal. This signal is then fed into a delay-locked loop (DLL). The DLL subsequently acquires and tracks an identical replica of the PRN code, ultimately calculating the PRN code delay time and recovering the original data code.

2.2. Transmitter Signal Modeling

Let the PRN code signal be

$$a\left(t\right)=\sum _{j=0}^{L-1}{a}_j{g}_{T_c}\left(t-j{T}_c\right)$$

(1)

where $a_j$ is the PRN code sequence with a length of L, taking values of +1 or −1. $g_{T_c}\left(t\right)$ is a rectangular function with a width of $T_c$. The rectangular function with a width of $T_c$ is defined as

$$g_{T_c}\left(t\right)=\left\{\begin{array}{cc}1& 0\le t\le T_c\\ 0& otherwise\end{array}\right.$$

(2)

Let the data code signal be

$$d\left(t\right)=\sum _{i=-\infty }^{+\infty }{d}_i{g}_{T_c}\left(t-iF{T}_c\right)$$

(3)

where $d_i$ is the data code sequence, taking values of +1 or −1. F represents the spreading factor.

When the communication and ranging signal in space-based gravitational wave detection adopts a BPSK baseband signal, its signal model can be expressed as follows:

$$s_{BPSK}\left(t\right)=\sum _{i=-\infty }^{\infty }{d}_i\sum _{j=0}^{L-1}{a}_j{g}_{T_c}\left(t-j{T}_c-iF{T}_c\right)$$

(4)

The BOC baseband signal is generated by applying an additional layer of subcarrier modulation to the BPSK baseband signal. The notation $BOC\left(f_{sc},f_c\right)$ is conventionally used to denote the relationship between the PRN code rate $f_c$ and the subcarrier frequency $f_{sc}$. The subcarrier signal is typically represented as a square wave function:

$$sc\left(t\right)=\left\{\begin{array}{cc}sign\left[sin\left(2\pi f_{sc}t\right)\right]& sinBOC\\ sign\left[cos\left(2\pi f_{sc}t\right)\right]& cosBOC\end{array}\right.$$

(5)

The detailed modulation processes for both the BPSK and BOC baseband signals are illustrated in Figure 2.

When the communication and ranging signal for space-based gravitational wave detection adopts a BOC baseband signal, its signal model can be expressed as follows:

$$\begin{array}{c}\hfill s_{BOC}\left(t\right)=s_{BPSK}\left(t\right)sc\left(t\right)=\sum _{i=-\infty }^{\infty }{d}_i\sum _{j=0}^{L-1}{a}_j{g}_{T_c}\left(t-j{T}_c-iF{T}_c\right)\sum _{l=0}^{S-1}{h}_l{g}_{T_c/S}\left(t-l{T}_c/S\right)\end{array}$$

(6)

where $g_{T_c/S}\left(t\right)$ is a rectangular function with a width of $T_c/S$. $h_l$ is the subcarrier code, taking values of +1 or −1. S is the BOC modulation order. The values of S and $h_l$ are given by

$$\left(S,h_l\right)=\left\{\begin{array}{cc}\left(2{\displaystyle \frac{f_{sc}}{f_c}},{\left(-1\right)}^l\right)& sinBOC\\ \left(4{\displaystyle \frac{f_{sc}}{f_c}},{\left(-1\right)}^{⌈{\displaystyle \frac{l}{2}}⌉}\right)& cosBOC\end{array}\right.$$

(7)

For BOC signals, a higher modulation order introduces more secondary peaks in its autocorrelation function [24], thereby increasing receiver complexity. To satisfy the displacement measurement requirements of laser interferometry [15] while avoiding additional receiver complexity, this study adopted the $sinBOC$ for investigation and selected $f_{sc}=f_c$. In this case, S was 2 and $h_l$ took the values +1 and −1. The BOC signal could thus be expressed as $sinBOC$$\left(1,1\right)$ and its signal model could be simplified to

$$s_{BOC}\left(t\right)=\sum _{i=-\infty }^{\infty }{d}_i\sum _{j=0}^{L-1}{a}_j{g}_2\left(t-j{T}_c-iF{T}_c\right)$$

(8)

where $g_2\left(t\right)$ can be defined as the subcarrier function, with the specific expression being

$$g_2\left(t\right)=\left\{\begin{array}{cc}1& 0\le t<{\displaystyle \frac{T_c}{2}}\\ -1& {\displaystyle \frac{T_c}{2}}<t\le T_c\\ 0& otherwise\end{array}\right.$$

(9)

To minimize the impact of communication and ranging on gravitational wave scientific measurements, the optical power allocated for inter-satellite communication and ranging is typically about 1% of the main carrier power. Since a bipolar non-return-to-zero (NRZ) code was adopted in this study, the relationship between the ratio of the main carrier signal power to the communication and ranging code power and the modulation index was given by [22]

$${\displaystyle \frac{P_{\mathrm{modulation}}}{P_{\mathrm{carrier}}}}={tan}^2\left(m_{prn}\right)$$

(10)

where $P_{\mathrm{modulation}}$ is the communication and ranging code power. $P_{\mathrm{carrier}}$ is the main carrier signal power. $m_{prn}$ is the modulation index.

Within the EOM, the communication and ranging code is modulated onto the phase of the laser carrier for interferometry with a low modulation index. The signal model is expressed as

$$s\left(t\right)=sin\left({\omega }_{c}t+m_{prn}{s}_{CR}\left(t\right)\right)$$

(11)

where ${\omega }_c$ is the angular frequency of the laser carrier. $s_{CR}\left(t\right)$ represents the communication and ranging code.

2.3. Receiver Signal Modeling

After ultra-long-distance transmission, the laser arrives at the receiving end and undergoes heterodyne interference with a local laser. Since inter-satellite communication and ranging utilize a laser link, the dominant noise considered is shot noise [25]. The interference signal is converted from optical to electrical form by a QPD. In the frequency domain, the clock sidebands lie outside the main lobe of the primary beat frequency and thus do not affect the modulation and reception of the PRN code [22]. Therefore, neglecting the influence of sidebands, the output primary beat frequency signal was modeled as

$$p\left(t\right)=\eta {J_0}^2\left(m_{sb}\right)\sqrt{\gamma P_{LO}{P}_S}sin\left({\omega }_{het}\left(t-\tau \right)+m_{prn}{s}_{CR}\left(t-\tau \right)+\phi \right)+n_1\left(t\right)$$

(12)

where $\eta$ is the responsivity of the photodiode in the QPD. $J_0\left(m_{sb}\right)$ represents the $J_0$ term of the Bessel function of the first kind, determined by the modulation index $m_{sb}$ of the clock sidebands. $\gamma$ is the laser interference efficiency. $P_{LO}$ is the power of the local satellite laser. $P_S$ is the power of the received laser. ${\omega }_{het}$ is the angular frequency of the primary beat note signal. $\phi$ represents the phase, which contains scientific information. $\tau$ is the time delay from the transmitter to the receiver. $n_1\left(t\right)$ is additive white Gaussian noise (AWGN) with a mean of 0 and a variance of ${{\sigma }_1}^2$.

The primary beat note signal subsequently passes through a series of SCEs and is digitized by an ADC. The resulting signal input to the DPLL can be modeled as follows:

$$\begin{array}{cc}\hfill & s_{ADC}\left[n{T}_s\right]=sin\left[{\omega }_{het}\left(n-m\right)T_s+m_{prn}{s}_{CR}\left[\left(n-m\right)T_s\right]+\phi \right]+n_2\left[n{T}_s\right]\hfill \end{array}$$

(13)

where $T_s$ is the system sampling period. $m{T}_s$ is the digital time delay obtained after sampling the analog delay. $n_2\left[n{T}_s\right]$ is AWGN with a mean of 0 and a variance of ${{\sigma }_2}^2$.

The DPLL primarily consists of a phase detector, a loop filter (LF), and a numerically controlled oscillator (NCO), with its overall structure shown in Figure 3.

Upon entering the DPLL, the signal is first mixed with the cosine signal output by the NCO. The high-frequency components are then filtered out by a low-pass filter (LPF), generating an error signal which serves as the input for the DLL. This error signal is processed by the LF to produce a feedback control signal for the NCO, thereby achieving loop lock. The DPLL primarily functions to track the slowly varying phase (scientific information $\phi$), allowing the high-speed communication ranging codes to pass through in the form of phase error. The error transfer function of the DPLL exhibits a high-pass characteristic, typically with a bandwidth on the order of kHz, whereas the bandwidth of the communication ranging signal is usually on the order of MHz. Consequently, the DPLL slightly attenuates the low-frequency energy of the communication ranging signal. Therefore, the error signal output of the digital phase-locked loop can be approximated as

$$h\left[n{T}_s\right]=m_{prn}{s}_{CR}\left[n{T}_s-m{T}_s\right]+n_3\left[n{T}_s\right]$$

(14)

where $n_3\left[n{T}_s\right]$ is AWGN with a mean of 0 and a variance of ${{\sigma }_3}^2$. Based on the relationship between phase noise and the carrier-to-noise ratio of the main beat signal [22], it can be derived that

$${{\sigma }_3}^2=B_i{\left({\displaystyle \frac{C}{N_0}}\right)}^{-1}$$

(15)

In phase-locked loop systems, the signal-to-noise ratio is typically used to assess signal quality. According to phase-locked loop theory, the relationship between the loop signal-to-noise ratio of a DPLL and the signal-to-noise ratio of its input signal can be expressed as

$${\left({\displaystyle \frac{S}{N}}\right)}_L={\left({\displaystyle \frac{S}{N}}\right)}_i{\displaystyle \frac{B_i}{B_L}}$$

(16)

where ${\left(S/N\right)}_L$ is the DPLL loop SNR. ${\left(S/N\right)}_i$ is the DPLL input SNR. $B_i$ is the DPLL loop noise bandwidth.

In practice, the DPLL can function properly only when ${\left(S/N\right)}_L\ge 6$ dB. Therefore, it can be concluded that the SNR of the DPLL input signal must satisfy the following requirement:

$${\left({\displaystyle \frac{S}{N}}\right)}_i\ge \left(10\times {log}_{10}\left({\displaystyle \frac{B_L}{B_i}}\times \left({10}^{{\displaystyle \frac{6}{10}}}\right)\right)\right)\mathrm{dB}$$

(17)

Furthermore, based on the relationship between the carrier-to-noise ratio and the signal-to-noise ratio, it can be concluded that the carrier-to-noise ratio of the DPLL input signal must satisfy the condition that

$${\displaystyle \frac{C}{N_0}}\ge \left(10\times {log}_{10}\left(B_L\times \left({10}^{{\displaystyle \frac{6}{10}}}\right)\right)\right)\mathrm{dB}·\mathrm{Hz}$$

(18)

3. Acquisition Performance Modeling

After the DPLL extracts the communication and ranging codes from the main beat signal, the received communication and ranging codes are correlated with the local PRN code in the DLL. This correlation operation completes the acquisition and tracking processes, thereby enabling absolute distance measurement and data communication. This chapter models the acquisition performance based on the communication ranging signal model. This process involves setting the acquisition step size, calculating the acquisition detection metric through the acquisition process for different signals, and, finally, establishing the acquisition performance model. Currently, the communication and ranging signals for space-based gravitational wave detection utilize two modulation schemes: BPSK baseband signals and BOC baseband signals. Their acquisition performance models were thus developed.

3.1. Modeling of Acquisition Step Size

During the acquisition process, the acquisition step size determines the selection of both the maximum acquisition time and the acquisition threshold. Therefore, this chapter begins by describing the modeling of the acquisition step size.

Assuming the acquisition process begins scanning from the position furthest from the correlation peak, the acquisition time is given by

$$t_{acq}={\displaystyle \frac{{\left(L{T}_c\right)}^2}{T_{step}}}$$

(19)

where L represents the PRN code length, $T_c$ denotes the PRN code chip period, and $T_{step}$ is the acquisition step size.

Due to the relative motion between satellites, the actual delay of the PRN code changes during the acquisition process. The maximum variation is

$$\Delta {\tau }_{max}={\displaystyle \frac{v_{max}{t}_{acq}}{c}}$$

(20)

where $v_{max}$ is the maximum relative velocity between satellites and c is the speed of light.

It is optimal that during the acquisition period, the delay variation does not exceed the range of the tracking phase detector. Since the width of the tracking phase detector’s range typically matches the acquisition step size, the following relationship can be established:

$$\Delta {\tau }_{max}<T_{step}$$

(21)

From this, the minimum value for the acquisition step size $T_{step}$ can be derived:

$$L{T}_c\sqrt{{\displaystyle \frac{v_{max}}{c}}}<T_{step}$$

(22)

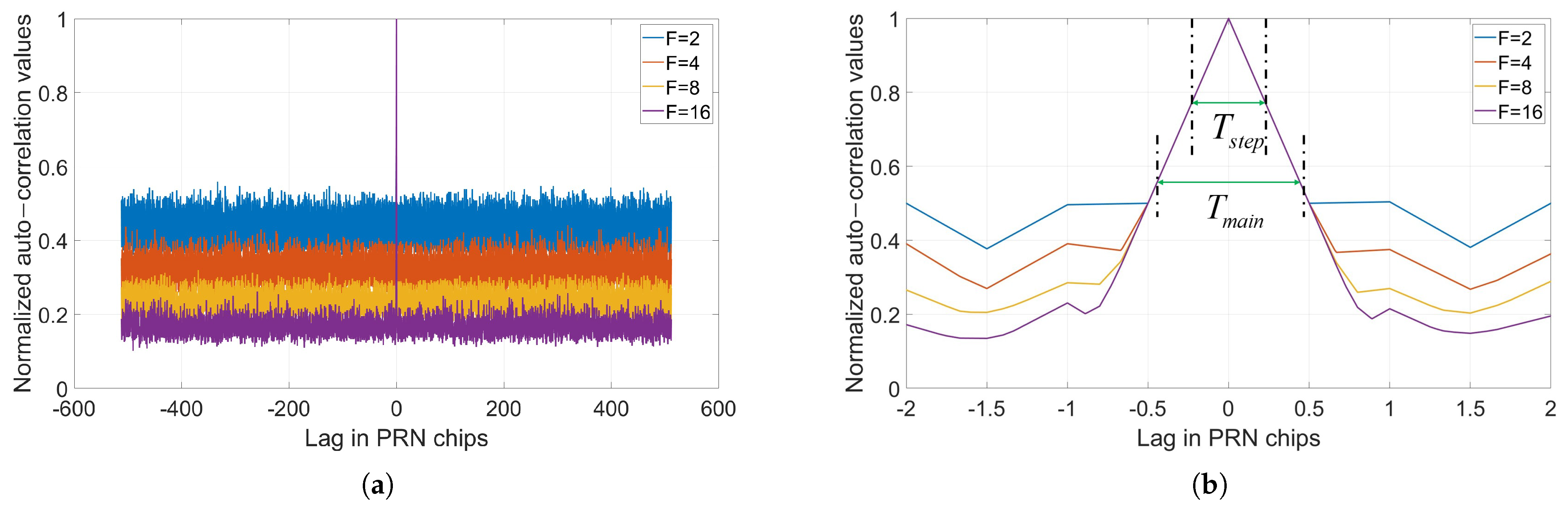
The acquisition process is estimated based on the most conservative scenario, considering that the maximum uncertainty $V_{max}$ requiring scanning when the communication and ranging codes are synchronized is symmetric about the peak of the autocorrelation function. The total symmetric length is the acquisition step size $T_{step}$.

Given that the minimum value within the main peak of the autocorrelation function $T_{main}$ must exceed all sidelobe values, and since the sidelobe magnitude is strongly correlated with (and increases as) the spreading factor F decreases, the size of the main peak $T_{main}$ therefore needed to be designed according to the specific spreading factor F, as illustrated in Figure 4.

The acquisition step size $T_{step}$ could not exceed the width of the main lobe of the autocorrelation function $T_{main}$. Therefore, the valid range for the acquisition step size was

$$L{T}_c\sqrt{{\displaystyle \frac{v_{max}}{c}}}<T_{step}<T_{main}$$

(23)

3.2. Acquisition Performance Modeling for BPSK Baseband Signals

Once the acquisition step size was determined, the acquisition detection metric could be calculated based on the acquisition process. Subsequently, the acquisition performance model could be established according to the acquisition decision criteria.

3.2.1. Acquisition Process

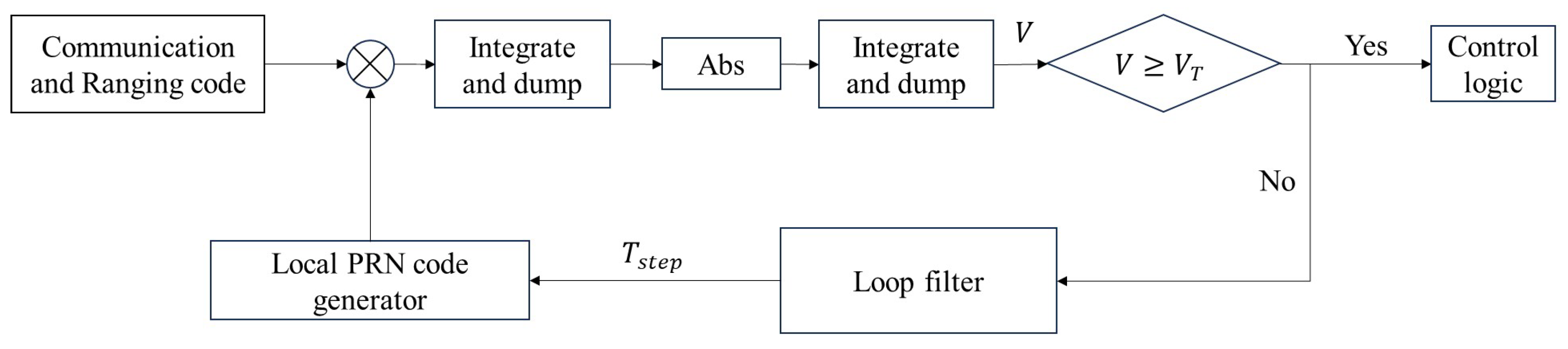
Considering hardware resource constraints, the time-domain serial acquisition process was employed for the BPSK baseband signal in the DLL. The corresponding processing flow is illustrated in Figure 5.

The received communication and ranging signal and the local PRN code first undergo coherent integration over a duration equal to the data code period. The absolute value of the resulting output is then computed, followed by noncoherent integration over the PRN code period to obtain the acquisition detection metric, denoted as V. If the acquisition detection metric V exceeds a predefined acquisition threshold $V_T$, the process is considered successfully acquired. Otherwise, the local PRN code is shifted by the acquisition step size $T_{step}$, and the process is repeated until successful acquisition is achieved.

3.2.2. Acquisition Detection Metric

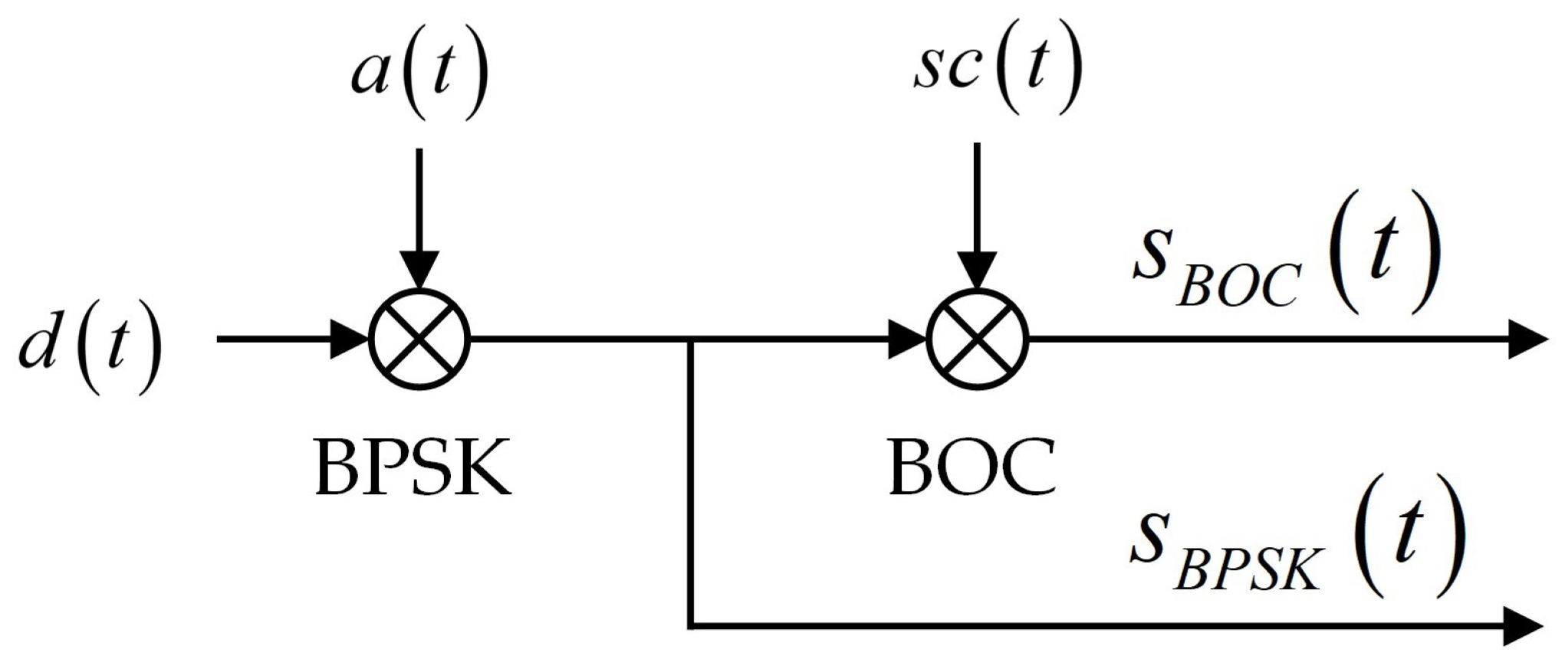
The data code is inherently a random signal. To facilitate quantitative analysis of the acquisition detection metric, this study analyzes the scenario where the data code is assumed to be an all-ones sequence. Based on Equations (4) and (14), the BPSK baseband signal input to the DLL is expressed as

$$\begin{array}{c}\hfill h_{BPSK}\left[n{T}_s\right]=m_{prn}\sum _{j=0}^{L-1}{a}_j{g}_{T_c}\left[n{T}_s-j{T}_c-m{T}_s\right]+n\left[n{T}_s\right]\end{array}$$

(24)

For notational convenience, the noise input to the DLL can be rewritten as $n\left[n{T}_s\right]$, which is AWGN with zero mean and a variance of ${\sigma }^2$ (given by Equation (15)).

The local PRN code generated by the local code generator within the DLL is expressed as

$$r_{BPSK}\left[n{T}_s\right]=\sum _{i=0}^{L-1}{a}_i{g}_{T_c}\left[n{T}_s-i{T}_c\right]$$

(25)

where $a_i$ is the local PRN code sequence of length L, taking values of +1 or −1.

The acquisition detection metric V is calculated as

$$R_{BPSK}\left[m{T}_s\right]=\sum _{k=0}^{L/F-1}\left(\left|m_{prn}{x}_1\left[m\right]+x_2\left[m\right]n\left[n{T}_s\right]\right|\right)$$

(26)

where $x_1\left[m\right]$ represents the autocorrelation value of the PRN codes over one data code length and $x_2\left[m\right]$ denotes the accumulated value of the noise-correlated PRN code over the same interval.

3.2.3. Acquisition Decision Analysis

Based on the preceding analysis, this study considers the signal to be synchronized when the acquisition detection metric V is greater than or equal to the acquisition threshold $V_T$. Otherwise, it is regarded as not synchronized.

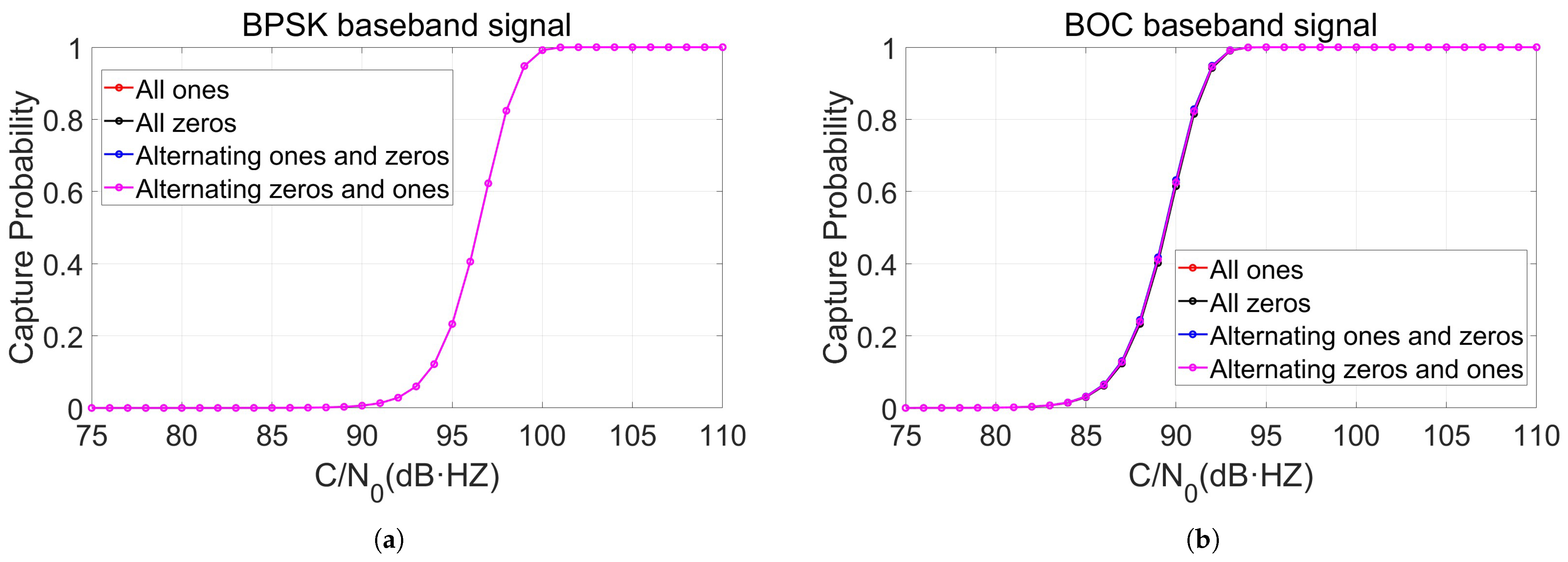
An analysis is conducted for both synchronized and non-synchronized states of the BPSK baseband signal. Let $H_1$ denote the hypothesis that the BPSK baseband signal is synchronized and $H_0$ denote the hypothesis that it is not synchronized. If the acquisition threshold $V_T$ is set too low when the signal is not synchronized, this will lead to a false alarm. Conversely, if the threshold $V_T$ is set too high when the signal is synchronized, this will result in a missed detection. The acquisition threshold value $V_T$ is first calculated based on the required false alarm probability $P_{fa}$. Subsequently, the detection probability $P_d$ is derived using this threshold. The resulting detection probability under a fixed false alarm probability defines the acquisition performance.

This study considered the most conservative scenario. When synchronized, the acquisition detection metric V was assumed to be equal to the acquisition threshold $V_T$. When not synchronized, the acquisition detection metric V was assumed to be the maximum possible value that was still less than the acquisition threshold $V_T$.

The probability distribution of the acquisition detection metric V was then analyzed. For $m_{prn}{x}_1\left[m\right]+x_2\left[m\right]n\left[n{T}_s\right]$, its mean and variance were, respectively,

$$E=m_{prn}{x}_1\left[m\right]$$

(27)

$$D=FN{\sigma }^2$$

(28)

Since $n\left[n{T}_s\right]$ follows a normal distribution, $m_{prn}{x}_1\left[m\right]+x_2\left[m\right]n\left[n{T}_s\right]$ also follows a normal distribution. For $\left|m_{prn}{x}_1\left[m\right]+x_2\left[m\right]n\left[n{T}_s\right]\right|$, this follows a folded normal distribution. By the central limit theorem, ${\displaystyle \sum _{k=0}^{L/F-1}}\left(\left|m_{prn}{x}_1\left[m\right]+x_2\left[m\right]n\left[n{T}_s\right]\right|\right)$ can be approximated as normally distributed. Its mean and variance are given by (see Appendix A)

$$E\left(R_{BPSK}\left[m{T}_s\right]\right)={\displaystyle \frac{L}{F}}\left\{\sqrt{{\displaystyle \frac{2FN{\sigma }^2}{\pi }}}{e}^{-{\displaystyle \frac{{\left(m_{prn}{x}_1\left[m\right]\right)}^2}{2FN{\sigma }^2}}}-m_{prn}{x}_1\left[m\right]\left[erf\left(-{\displaystyle \frac{m_{prn}{x}_1\left[m\right]}{\sqrt{2FN{\sigma }^2}}}\right)\right]\right\}$$

(29)

$$D\left(R_{BPSK}\left[m{T}_s\right]\right)={\displaystyle \frac{L}{F}}\left\{{\left(m_{prn}{x}_1\left[m\right]\right)}^2+FN{\sigma }^2-{\left\{{\left({\displaystyle \frac{2FN{\sigma }^2}{\pi }}\right)}^{{\displaystyle \frac{1}{2}}}{e}^{-{\displaystyle \frac{{\left(m_{prn}{x}_1\left[m\right]\right)}^2}{2FN{\sigma }^2}}}-m_{prn}{x}_1\left[m\right]\left[erf\left(-{\displaystyle \frac{m_{prn}{x}_1\left[m\right]}{\sqrt{2FN{\sigma }^2}}}\right)\right]\right\}}^2\right\}$$

(30)

where $erf\left(·\right)$ represents the error function, defined as

$$erf\left(x\right)={\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_0^x{e}^{-t^2}dt$$

(31)

Its probability density function is given by

$$f\left(x\right)=\sqrt{{\displaystyle \frac{1}{2\pi D\left(R_{BPSK}\left[m{T}_s\right]\right)}}}{e}^{-{\displaystyle \frac{{\left(x-E\left(R_{BPSK}\left[m{T}_s\right]\right)\right)}^2}{2D\left(R_{BPSK}\left[m{T}_s\right]\right)}}}$$

(32)

When the BPSK baseband signal is not synchronized, the mean and variance of $R_{BPSK}\left[m{T}_s\right]$ are $E_{BPSK,H_0}$ and $D_{BPSK,H_0}$, respectively, where the value of $x_1\left[m\right]$ is taken as the average over all non-synchronized cases. A false alarm is considered to occur when the acquisition detection metric V is greater than or equal to the acquisition threshold $V_T$. Therefore, the false alarm probability is

$$\begin{array}{cc}\hfill P_{fa}& =P(V\ge V_T|H_0)={\int }_{V_T}^{\infty }f\left(x\right)dx\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{1}{2\pi D_{BPSK,H_0}}}}{\int }_{V_T}^{\infty }{e}^{-{\displaystyle \frac{{\left(x-E_{BPSK,H_0}\right)}^2}{2D_{BPSK,H_0}}}}dx\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}erfc\left(\left(V_T-E_{BPSK,H_0}\right)\sqrt{{\displaystyle \frac{1}{2D_{BPSK,H_0}}}}\right)\hfill \end{array}$$

(33)

where $erfc\left(·\right)$ represents the complementary error function, defined as

$$erfc\left(x\right)={\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_x^{\infty }{e}^{-t^2}dt$$

(34)

The acquisition threshold $V_T$ can be obtained as

$$V_T=E_{BPSK,H_0}+\sqrt{2D_{BPSK,H_0}}erfcinv\left(2P_{fa}\right)$$

(35)

where $erfcinv\left(·\right)$ represents the inverse function of the complementary error function, defined as

$$erfcinv\left(erfc\left(x\right)\right)=x$$

(36)

When the BPSK baseband signal is synchronized, the mean and variance of $R_{BPSK}\left[m{T}_s\right]$ are $E_{BPSK,H_1}$ and $D_{BPSK,H_1}$, respectively, where the value of $x_1\left[m\right]$ is taken as the average over all synchronized cases. The detection probability is thus

$$\begin{array}{cc}\hfill P_d& =P(V\ge V_T|H_1)={\displaystyle \frac{1}{2}}erfc\left(\left(V_T-E_{BPSK,H_1}\right)\sqrt{{\displaystyle \frac{1}{2D_{BPSK,H_1}}}}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}erfc\left(\left(E_{BPSK,H_0}+\sqrt{2D_{BPSK,H_0}}erfcinv\left(2P_{fa})\right)-E_{BPSK,H_1}\right)\sqrt{{\displaystyle \frac{1}{2D_{BPSK,H_1}}}}\right)\hfill \end{array}$$

(37)

In summary, the acquisition probability for the BPSK baseband signal depends on the PRN code length L, the sampling factor N, the modulation index $m_{prn}$, the CNR $C/N_0$ of the primary beat note signal input to the DPLL, the spreading factor F, the acquisition step size $T_{step}$, the DPLL input noise bandwidth $B_i$. Based on the parameters mentioned above, the acquisition threshold $V_T$ can first be calculated. This threshold $V_T$ is then used to compute the acquisition probability $P_d$. When the acquisition probability $P_d$ reaches 1, the corresponding threshold value can be applied to the practical acquisition process for BPSK baseband signals in communication and ranging.

3.3. Acquisition Performance Modeling for BOC Baseband Signals

3.3.1. Acquisition Process

For the $sinBOC\left(1,1\right)$ signal, this study employs the Autocorrelation Side-Peak Cancellation Technique (ASPeCT) to eliminate the secondary peaks present in the autocorrelation function of the BOC baseband signal. The fundamental principle of the ASPeCT is to use a combined operation of the BOC code autocorrelation function and the BOC/PRN code cross-correlation function to achieve side-peak cancellation. The process is expressed as follows:

$$R\left(\tau \right)=R_{BOC}{\left(\tau \right)}^2-R_{BOC/PRN}{\left(\tau \right)}^2$$

(38)

where $R_{BOC}\left(\tau \right)$ represents the autocorrelation function of the BOC code and $R_{BOC/PRN}\left(\tau \right)$ denotes the cross-correlation function between the BOC code and the PRN code.

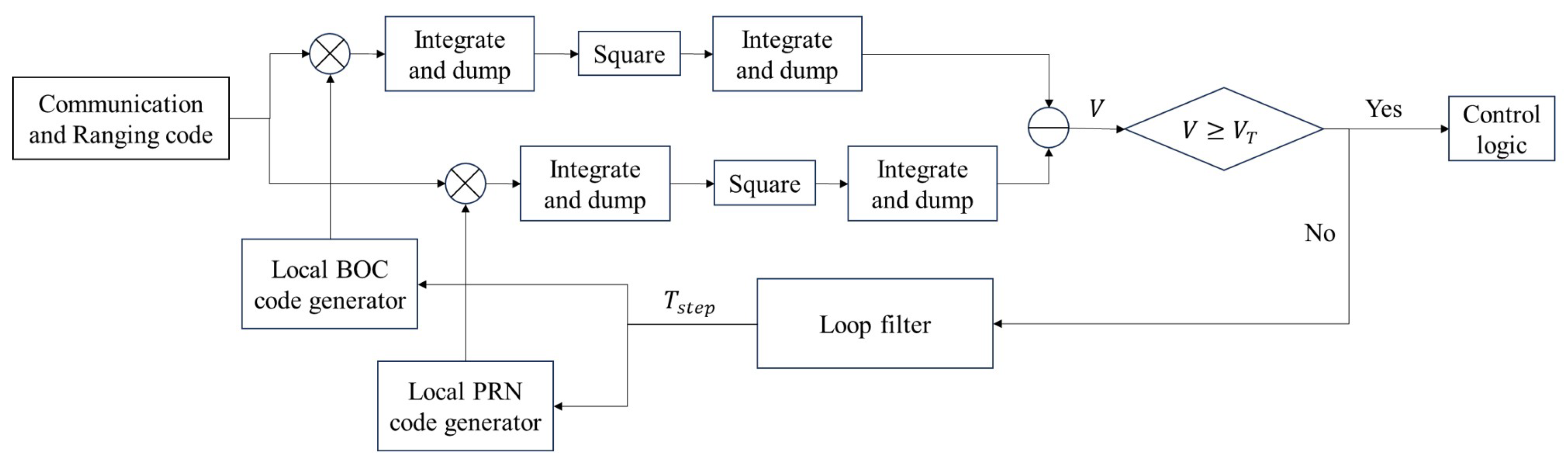
The ASPeCT is implemented in the DLL for the acquisition of the BOC baseband signal. The fundamental workflow is illustrated in Figure 6.

The received communication and ranging signal is separately correlated with the local BOC code and the local PRN code, performing coherent integration over a duration equal to the data code period. The results of this integration are then squared. Subsequently, non-coherent integration is performed over the PRN code period on the squared results to yield the acquisition detection metric V. If the acquisition detection metric V exceeds a pre-defined acquisition threshold $V_T$, the process is deemed successfully acquired. Otherwise, both the local BOC code and the local PRN code are shifted by the acquisition step size $T_{step}$, and the process iterates until successful acquisition is achieved.

3.3.2. Acquisition Detection Metric

Following the same approach as for the BPSK baseband signal, the scenario where the data code is an all-ones sequence is analyzed. According to Equations (6) and (14), the BOC baseband signal input to the DLL is expressed as

$$h_{BOC}\left[n{T}_s\right]=m_{prn}\sum _{j=0}^{L-1}{a}_j{g}_2\left[n{T}_s-j{T}_c+m{T}_s\right]+n\left[n{T}_s\right]$$

(39)

The local BOC code generated by the local BOC code generator and the local PRN code generated by the local PRN code generator in the DLL are respectively expressed as

$$r_{BOC}\left[n{T}_s\right]=\sum _{i=0}^{L-1}{a}_i{g}_2\left[n{T}_s-i{T}_c\right]$$

(40)

$$r_{PRN}\left[n{T}_s\right]=\sum _{i=0}^{L-1}{a}_i{g}_{T_c}\left[n{T}_s-i{T}_c\right]$$

(41)

Using the ASPeCT for acquisition, the acquisition detection metric V is calculated as

$$\begin{array}{c}\hfill R_{BOC}\left[m{T}_s\right]=\sum _{k=0}^{L/F-1}{\left(m_{prn}{y}_1\left[m\right]+y_2\left[m\right]n\left[n{T}_s\right]\right)}^2-\sum _{k=0}^{L/F-1}{\left(m_{prn}{y}_3\left[m\right]+y_4\left[m\right]n\left[n{T}_s\right]\right)}^2\end{array}$$

(42)

where $y_1\left[m\right]$ represents the BOC code autocorrelation value over one data code length, $y_2\left[m\right]$ denotes the accumulated value correlated with the BOC code over the same interval, $y_3\left[m\right]$ represents the BOC-PRN code cross-correlation value over one data code length, and $y_4\left[m\right]$ denotes the accumulated value correlated with the PRN code over the same interval.

3.3.3. Acquisition Decision Analysis

The acquisition decision process for the BOC signal follows the same logical procedure as detailed for the BPSK baseband signal and will not be repeated here. The probability distribution of the acquisition detection metric V is now analyzed. For $m_{prn}{y}_1\left[m\right]+y_2\left[m\right]n\left[n{T}_s\right]$, its mean and variance are, respectively,

$$E=m_{prn}{y}_1\left[m\right]$$

(43)

$$D=FN{\sigma }^2$$

(44)

Since $n\left[n{T}_s\right]$ follow normal distributions, $m_{prn}{y}_1\left[m\right]+y_2\left[m\right]n\left[n{T}_s\right]$ also follows normal distributions. For ${\displaystyle \sum _{k=0}^{L/F-1}}{\left(m_{prn}{y}_1\left[m\right]+y_2\left[m\right]n\left[n{T}_s\right]\right)}^2$, this follows a scaled non-central chi-square distribution. Its mean and variance are, respectively,

$$E_{BOC/BOC}=FN{\sigma }^2{\displaystyle \frac{L}{F}}+\sum _{i=0}^{L/F-1}{\left(m_{prn}{y}_1\left[m\right]\right)}^2$$

(45)

$$D_{BOC/BOC}=2FN{\sigma }^2\left({\displaystyle \frac{L}{F}}FN{\sigma }^2+2\sum _{i=1}^{L/F}{\left(m_{prn}{y}_1\left[m\right]\right)}^2\right)$$

(46)

Similarly, for ${\displaystyle \sum _{k=0}^{L/F-1}}{\left(y_3\left[m\right]+y_4\left[m\right]n\left[n{T}_s\right]\right)}^2$, this also follows a scaled non-central chi-square distribution. Its mean and variance are, respectively,

$$E_{BOC/PRN}=FN{\sigma }^2{\displaystyle \frac{L}{F}}+\sum _{i=1}^{L/F}{\left(m_{prn}{y}_3\left[m\right]\right)}^2$$

(47)

$$D_{BOC/PRN}=2FN{\sigma }^2\left({\displaystyle \frac{L}{F}}FN{\sigma }^2+2\sum _{i=1}^{L/F}{\left(m_{prn}{y}_3\left[m\right]\right)}^2\right)$$

(48)

The probability density function of $R_{BOC}\left[m{T}_s\right]$ is

$$f\left(x\right)=\sqrt{{\displaystyle \frac{1}{2\pi D\left(R_{BOC}\left[m{T}_s\right]\right)}}}{e}^{-{\displaystyle \frac{{\left(x-E\left(R_{BOC}\left[m{T}_s\right]\right)\right)}^2}{2D\left(R_{BOC}\left[m{T}_s\right]\right)}}}$$

(49)

When the BOC baseband signal is not synchronized, the mean and variance of $R_{BOC}\left[m{T}_s\right]$ are $E_{BOC,H_0}$ and $D_{BOC,H_0}$, respectively. Here, the values of ${\left(y_1\left[m\right]\right)}^2-{\left(y_3\left[m\right]\right)}^2$ and ${\left(y_1\left[m\right]\right)}^2+{\left(y_3\left[m\right]\right)}^2$ are taken as their averages over all non-synchronized cases. A false alarm occurs when the acquisition detection metric V is greater than or equal to the threshold $V_T$. Thus, the false alarm probability is

$$\begin{array}{cc}\hfill P_{fa}& =P(V\ge V_T|H_0)={\int }_{V_T}^{\infty }f\left(x\right)dx\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{1}{2\pi D_{BOC,H_0}}}}{\int }_{V_T}^{\infty }{e}^{-{\displaystyle \frac{{\left(x-E_{BOC,H_0}\right)}^2}{2D_{BOC,H_0}}}}dx\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}erfc\left(\left(V_T-E_{BOC,H_0}\right)\sqrt{{\displaystyle \frac{1}{2D_{BOC,H_0}}}}\right)\hfill \end{array}$$

(50)

The acquisition threshold $V_T$ is given by

$$V_T=E_{BOC,H_0}+\sqrt{2D_{BOC,H_0}}erfcinv\left(2P_{fa}\right)$$

(51)

When the BOC baseband signal is synchronized, the mean and variance of $R_{BOC}\left[m{T}_s\right]$ are $E_{BOC,H_1}$ and $D_{BOC,H_1}$, respectively, where ${\left(y_1\left[m\right]\right)}^2-{\left(y_3\left[m\right]\right)}^2$ and ${\left(y_1\left[m\right]\right)}^2+{\left(y_3\left[m\right]\right)}^2$ are taken as their averages over all synchronized cases. The detection probability is

$$\begin{array}{cc}\hfill & P_d=P(V\ge V_T|H_1)={\displaystyle \frac{1}{2}}erfc\left(\left(V_T-E_{BOC,H_1}\right)\sqrt{{\displaystyle \frac{1}{2D_{BOC,H_1}}}}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}erfc\left(\left(E_{BOC,H_0}+\sqrt{2D_{BOC,H_0}}erfcinv\left(2P_{fa}\right)-E_{BOC,H_1}\right)\sqrt{{\displaystyle \frac{1}{2D_{BOC,H_1}}}}\right)\hfill \end{array}$$

(52)

In summary, the acquisition probability for the BOC baseband signal depends on the PRN code length L, the sampling factor N, the modulation index $m_{prn}$, the CNR $C/N_0$ of the primary beat note signal input to the DPLL, the spreading factor F, the acquisition step size $T_{step}$, and the DPLL input noise bandwidth $B_i$. Based on the parameters mentioned above, the acquisition threshold $V_T$ can first be calculated. This threshold $V_T$ is then used to compute the acquisition probability $P_d$. When the acquisition probability $P_d$ reaches 1, the corresponding threshold value can be applied to the practical acquisition process for BOC baseband signals in communication and ranging.

4. Numerical Experimental Verification and Analysis

4.1. Model Parameter Design

Numerical simulations were conducted using the system parameters of the TianQin mission. Considering that the maximum inter-satellite relative velocity $v_{max}$ of the TianQin constellation is 4 m/s, the input noise bandwidth $B_i$ of the DPLL was set to 20 MHz and the loop noise bandwidth $B_L$ was set to 10 kHz. Based on Equation (18), it could be derived that the CNR of the DPLL input signal needed to satisfy

$${\displaystyle \frac{C}{N_0}}\ge 46\mathrm{dB}·\mathrm{Hz}$$

(53)

To ensure the accurate transmission of TianQin’s detection data and its timely delivery to the ground for processing, the required inter-satellite communication data rate needed to be greater than 41.54 kbps [26]. The digital system operated at a sampling rate $f_s$ of 100 MHz, and the PRN code employed for inter-satellite communication and ranging was a length-1024 M-sequence.

For the BPSK baseband signal, the PRN code chip period $T_c$ was 1 $\mathsf{\mu }$s and the spreading factor F was set to 16. This configuration achieved an inter-satellite communication rate of 62.5 kbps. The width $T_{main}$ of the main lobe of the autocorrelation function was approximately $1.6T_c$ (depending on the spreading factor F). Under the 100 MHz sampling rate, the acquisition step size needed to be an integer multiple of 10 ns. Thus, the valid range for the acquisition step size of the BPSK baseband signal was calculated as

$$0.12T_c<T_{step}<1.6T_c$$

(54)

For the BOC baseband signal, to maintain the same occupied bandwidth as the BPSK baseband signal, the PRN code chip period $T_c$ was increased to 2 $\mathsf{\mu }$s and the spreading factor F was set to 8. This configuration also achieved an inter-satellite communication rate of 62.5 kbps. The width of the main lobe of the autocorrelation function for the ASPeCT was approximately $0.4T_c$ (depending on the spreading factor F). Thus, the valid range for the BOC baseband signal acquisition step size was calculated as

$$0.12T_c<T_{step}<0.4T_c$$

(55)

The parameters used in this study are summarized in

Table 2. Simulation parameter.

Parameter (Unit)	Symbol	Value
System Sampling Rate (MHz)	$f_s$	100
PRN Code Length (-)	L	1024
Maximum Inter-Satellite Relative Velocity (m/s)	$v_{max}$	4
Chip Period in BPSK ($\mathsf{\mu }$s)	$T_c$	1
Spreading Factor for BPSK (-)	F	16
Acquisition Step Size for BPSK (-)	$T_{step}$	$0.14T_c$
Chip Period in BOC ($\mathsf{\mu }$s)	$T_c$	2
Spreading Factor for BOC (-)	F	8
Acquisition Step Size for BOC (-)	$T_{step}$	$0.28T_c$
Acquisition False Alarm Probability (-)	$P_{fa}$	${10}^{-6}$
Modulation Index (rad)	$m_{prn}$	0.1
DPLL Input Noise Bandwidth (MHz)	$B_i$	20
DPLL Loop Noise Bandwidth (kHz)	$B_L$	10

.

4.2. Validation of Analytical Model Correctness

Using the parameters listed in Table 2, the acquisition step size, spreading factor, PRN code length, and modulation index for the BPSK baseband signal were set to $0.14T_c$, 16, 1024, and 0.1 rad, respectively. Correspondingly, for the BOC baseband signal, these parameters were set to $0.28T_c$, 8, 1024, and 0.1 rad. Under these conditions, the occupied bandwidth, maximum acquisition time, and inter-satellite communication data rate were identical for both the BPSK and BOC baseband signals. Using MATLAB (R2023b) computational software, the acquisition threshold $V_T$ was first derived theoretically based on the acquisition false alarm probability $P_{fa}$. This theoretical value was then incorporated into the numerical calculation process for acquisition performance to obtain the numerical result of the acquisition probability $P_d$. The calculation was repeated 100 times, and the average of the results was taken. The analytical and numerical results for the acquisition performance model of the space-based gravitational wave detection communication and ranging signals are shown in Figure 7.

As shown in Figure 7, the analytical and numerical results of the acquisition performance model for both the BPSK and BOC baseband signals exhibited close agreement, thereby validating the correctness of the proposed models. Consequently, the derived mathematical framework could be reliably used to analyze the factors influencing acquisition performance.

Based on the analysis in Section 3.2.2, the acquisition performance model was first established in this study under the assumption of an all-ones data code. To further verify the generality of the conclusions, this study was extended to investigate the acquisition performance under different data code sequences. Theoretical analysis shows that the specific content of the data code has a negligible impact on the system’s acquisition performance and can be disregarded in practical applications (see Appendix B).

4.3. Analysis of Acquisition Performance Under Different Acquisition Step Sizes and Spreading Factors

Based on the parameters in Table 2, for the BPSK baseband signal, the acquisition step sizes were set to $0.5T_c$, $1.0T_c$ and $1.5T_c$ and the spreading factors were set to 4, 8, and 16. For the BOC baseband signal, the acquisition step sizes were set to $0.15T_c$, $0.3T_c$, and $0.45T_c$ and the spreading factors were set to 2, 4, and 8. Keeping all other conditions unchanged, the acquisition performance of the communication and ranging signals for space-based gravitational wave detection under different acquisition step sizes and spreading factors was compared. The analytical results for both the BPSK and BOC baseband signals are shown in Figure 8.

As shown in Figure 8, the acquisition performance remained largely stable when the acquisition step size was relatively small or the spreading factor was relatively large. As the acquisition step size increased within a certain range, acquisition performance continued to hold steady. However, once the acquisition step size exceeded this range, performance began to degrade. Notably, if the step size surpassed the width of the autocorrelation main peak, acquisition could fail entirely.

Conversely, as the spreading factor decreased, the sidelobe values of the autocorrelation function gradually increased and approached the acquisition threshold, which also led to performance degradation. If the spreading factor became too small, acquisition failure could likewise occur.

Overall, owing to the sharper main peak of its autocorrelation function compared to that of the BPSK baseband signal, the BOC baseband signal demonstrated superior acquisition performance.

4.4. Modulation Index Optimization

As can be seen from the previous analysis, using the parameters listed in Table 2, the acquisition probability reached 1 at a CNR of 101 dB·Hz for the BPSK baseband signal, while this was achieved at 94 dB·Hz for the BOC baseband signal. Therefore, for the TianQin mission’s scenario with a CNR of 104 dB·Hz, the modulation index could be further reduced.

Based on the parameters configured in Table 2, the modulation indices for the BPSK baseband signal were set to 0.1 rad, 0.09 rad, and 0.081 rad, while, for the BOC baseband signal, they were set to 0.1 rad, 0.06 rad, and 0.036 rad, respectively, with all other conditions held constant. The acquisition performance of the space-based gravitational wave detection communication and ranging signals under these different modulation indices was compared. The analytical and numerical results for both the BPSK and BOC baseband signals are presented in Figure 9.

As observed in Figure 9, the acquisition performance improved as the modulation index increased. When the modulation index was identical for both BPSK and BOC baseband signals, the BOC baseband signal exhibited superior acquisition performance compared to the BPSK baseband signal. For the specific case of the TianQin mission with a CNR $C/N_0$ of 104 dB·Hz, the modulation index for the BPSK baseband signal could be reduced to 0.081 rad, while, for the BOC baseband signal, it could be reduced to 0.036 rad.

By comparing the acquisition performance of BOC and BPSK baseband signals, the following conclusions can be drawn. BOC signals outperform BPSK signals in acquisition performance and allow the modulation index to be reduced to a lower level. However, this advantage comes at the cost of higher implementation complexity—BOC signals require additional cross-correlation operations with the local PRN code, involving multiplication and subtraction operations, thus consuming more computational resources. On the other hand, the BPSK signal’s autocorrelation function has a wider main lobe, which supports the use of a larger acquisition step size, thereby resulting in a shorter acquisition time compared to BOC signals.

Furthermore, for both BPSK and BOC signals, provided that the acquisition step size $T_{step}$ and spreading factor F are properly configured (the sidelobes of the autocorrelation function remain below the acquisition threshold $V_T$), the acquisition probability $P_d$ is highly sensitive to variations in the CNR. Theoretical analysis shows that increasing the CNR $C/N_0$ of the primary beat note signal input to the DPLL by approximately 12 dB·Hz can raise the acquisition probability from near 0 to near 1.

5. Discussion

Achieving ranging and communication using only 1% optical power on the same laser interferometry measurement link poses a significant challenge in space-based gravitational wave detection. In order to achieve the correct acquisition of communication and ranging signals, this study established a comprehensive signal-level communication and ranging mathematical model based on the principle of laser interferometry, including transmitter and receiver subsystems. Subsequently, acquisition performance models were developed for both BPSK and BOC baseband signals, incorporating the acquisition step size, acquisition process, acquisition detection metric, and acquisition decision criteria. The key factors influencing acquisition performance were identified, including the PRN code length, sampling factor, modulation index, CNR of the primary beat note signal input to the DPLL, spreading factor, acquisition step size, and the DPLL input noise bandwidth. Alternatively, the acquisition threshold could be directly derived from the these parameters for use in acquiring communication and ranging signals.

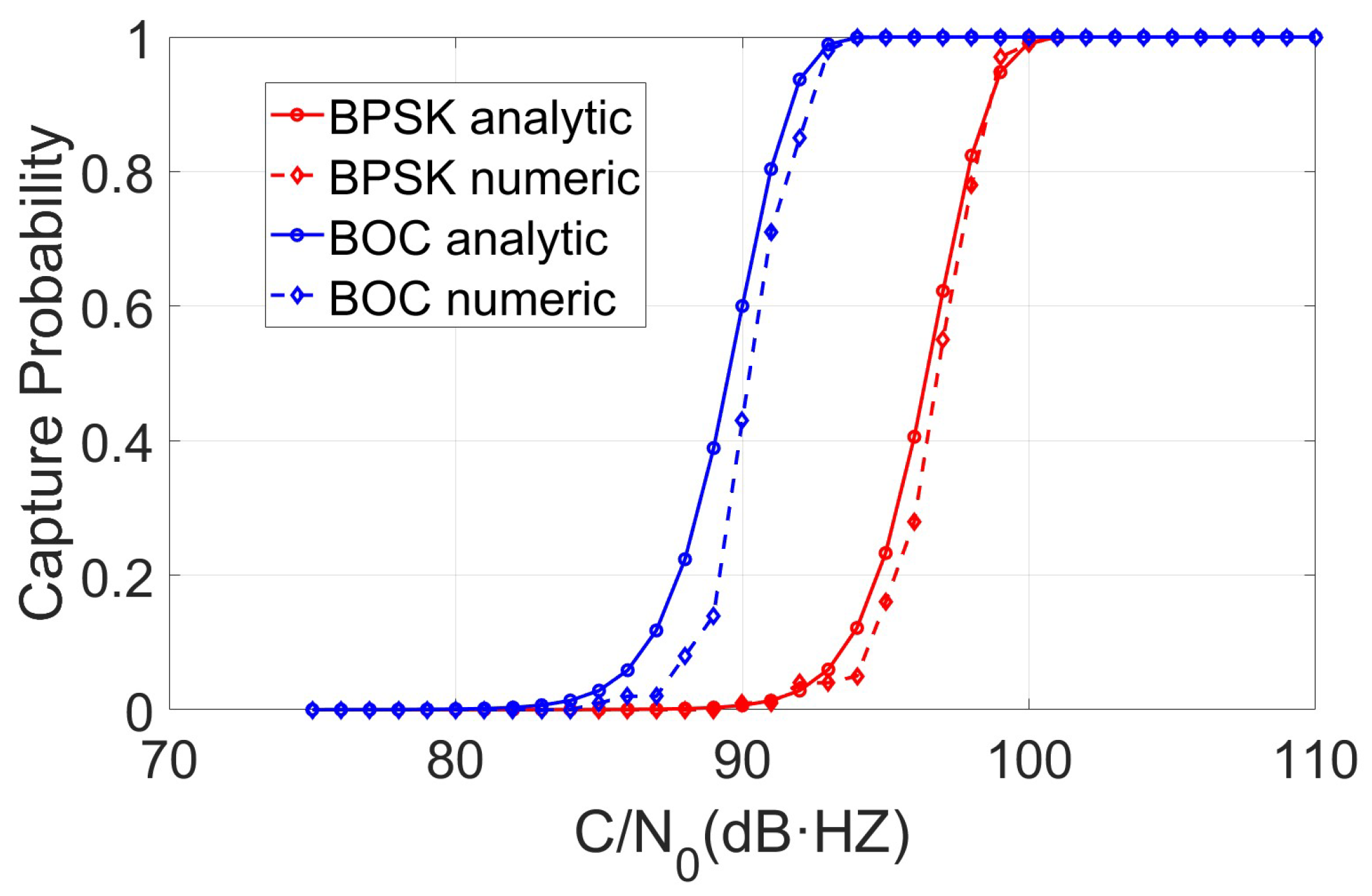
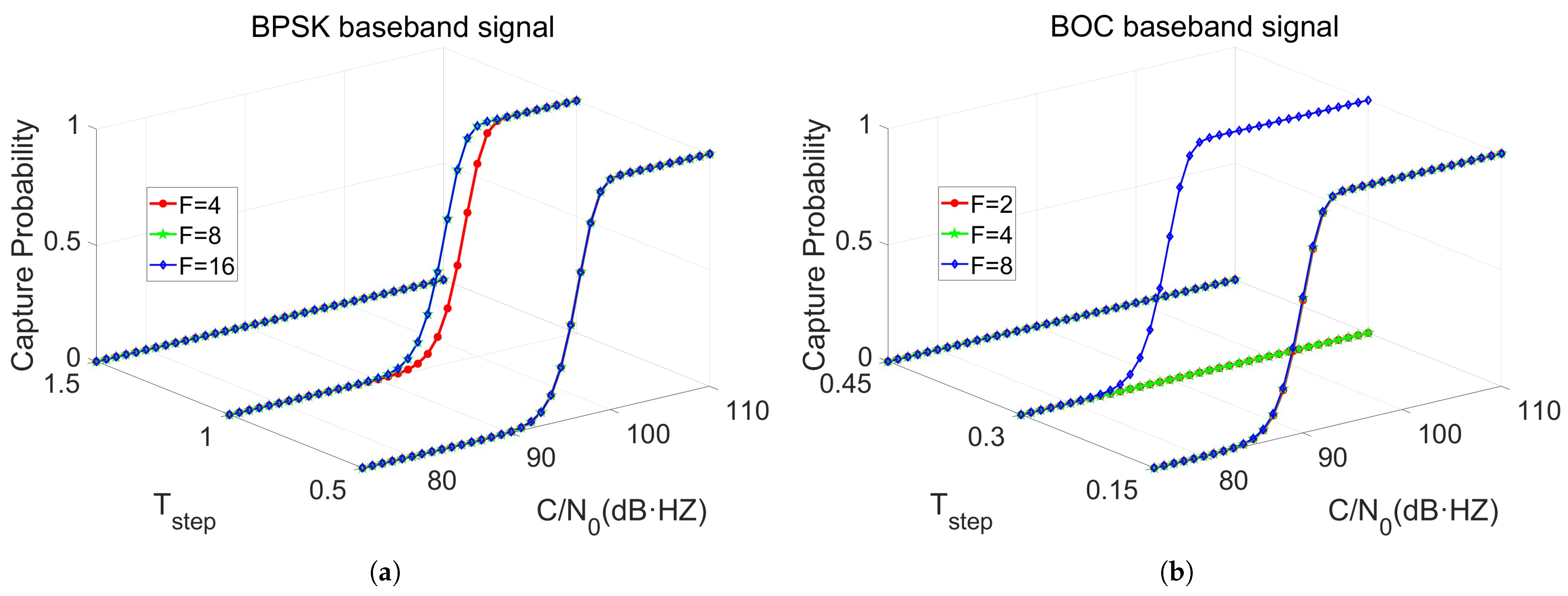
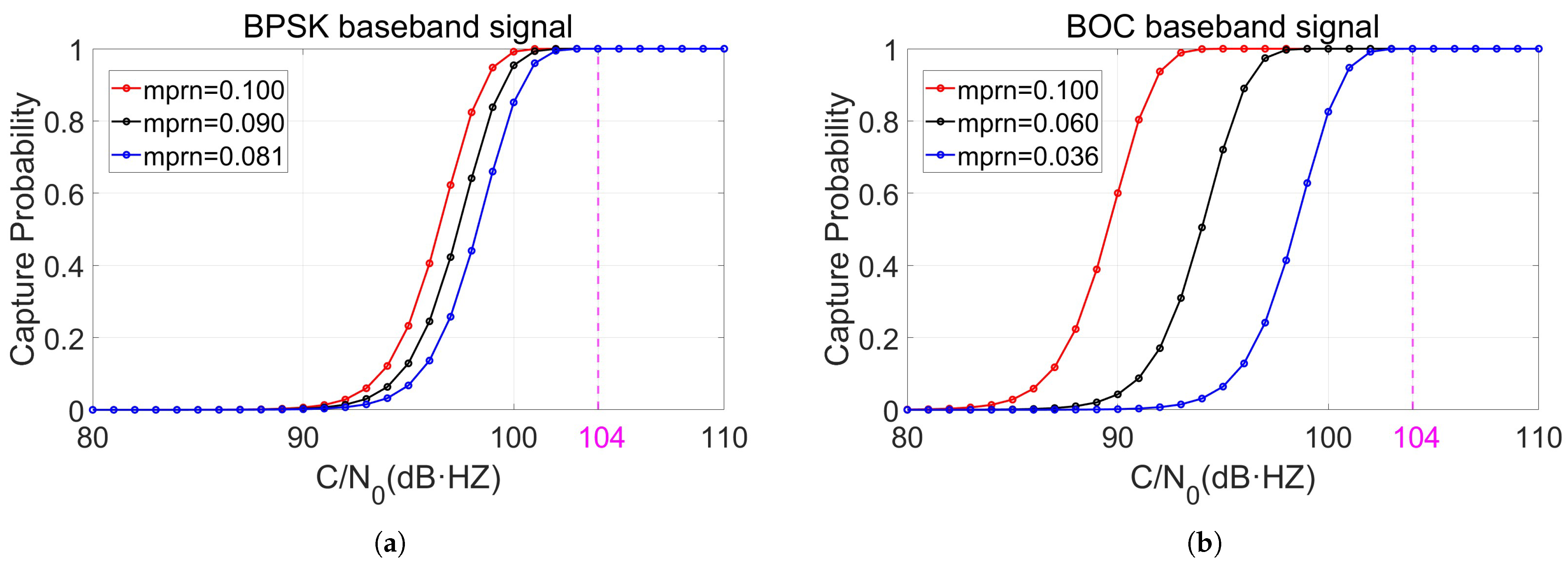
This study validated the proposed mathematical models for the acquisition performance of both BPSK and BOC baseband signals, analyzing comparatively the acquisition performance under different acquisition step sizes, spreading factors, and modulation indices. The results indicate that acquisition performance can be improved by increasing the spreading factor F, the modulation index $m_{prn}$, and the CNR $C/N_0$ of the primary beat note signal input to the DPLL and decreasing the acquisition step size $T_{step}$ and the DPLL input noise bandwidth $B_i$.

However, as a theoretical exploration, the practicality of the proposed model and conclusions require further multidimensional deepening and validation, which also outlines clear directions for future research.

First, regarding noise modeling, this study simplified the analysis by focusing primarily on additive white Gaussian noise dominated by shot noise. However, in practical links, laser intensity noise, frequency noise, and other factors may exhibit non-Gaussian and non-stationary characteristics. Future work should incorporate these noise sources into the model to quantify their impact on acquisition performance, thereby enhancing the model’s predictive accuracy and engineering guidance value in real space environments.

Second, experimental validation oriented toward engineering implementation is needed. The conclusions in this paper are derived from numerical simulations, and their transition to engineering practice requires experimental support. The next research priority will be to validate the theoretical model by building a ground-based prototype or a high-fidelity hardware-in-the-loop simulation platform.

The communication and ranging signal acquisition performance model proposed in this study demonstrates cross-mission applicability. Its starting point is not specific mission parameters but rather addresses the common challenge in space gravitational wave detection of “minimizing interference with the main carrier while achieving reliable communication and ranging”. The core mathematical relationships of the model are independent of specific parameters, allowing it to be directly transferred to similar missions such as LISA and Taiji. By substituting the corresponding mission parameters, performance predictions and design guidance can be obtained, forming a universal theoretical tool.

6. Conclusions

This study focused on the acquisition of communication and ranging signals employing low-depth phase modulation on the primary carrier within the inter-satellite laser interferometry link for space gravitational wave detection. A systematic theoretical analysis model was established, which quantitatively revealed the influence of key parameters—including modulation index, spreading factor, acquisition step size, and loop bandwidth—on acquisition performance.

Numerical simulations confirm that for the BPSK baseband signal, with a PRN code length of 1024 and an acquisition step size of $0.14T_c$, the modulation index can be reduced to 0.081 rad. For the BOC baseband signal, with a PRN code length of 1024 and an acquisition step size $0.28T_c$, the modulation index can be reduced to 0.036 rad. Under this configuration, the system supports an inter-satellite data rate of 62.5 kbps and achieves an acquisition false alarm probability of ${10}^{-6}$ and a perfect acquisition probability of 1, given a CNR $C/N_0$ of 104 dB·Hz for the signal input to the DPLL.

The model developed in this study elucidates the key factors governing the acquisition of communication and ranging signals. The findings provide a theoretical foundation and an engineering reference for the design and optimization of future inter-satellite laser links for space-based gravitational wave detection.