Bayesian Spatio-Temporal Trajectory Prediction and Conflict Alerting in Terminal Area
Abstract
1. Introduction
- (1)
- We propose the BST-Transformer, a Bayesian spatio-temporal deep learning framework. Building upon the multi-dimensional exploration of aircraft trajectory features—including temporal dependencies and spatial positional relationships—the framework incorporates Bayesian inference to characterize model parameter uncertainty, thereby capturing uncertainties arising from limited training data and parameter variability.
- (2)
- We develop a probabilistic conflict alerting mechanism that directly links predicted trajectory distributions with conflict probability estimation. Based on the predicted distribution of aircraft positions, potential conflicts are identified and quantified using Monte Carlo sampling, which improves the accuracy and robustness of conflict detection.
- (3)
- We introduce a two-stage probabilistic framework for TMA trajectory prediction, consisting of a trajectory pre-training stage and a probabilistic conflict alerting stage. These two stages are seamlessly connected, enabling an integrated workflow from trajectory prediction to conflict alerting. The framework outputs multi-step probabilistic trajectory forecasts, providing reliable, real-time decision support for air traffic management.
2. Literature Review
2.1. Deterministic Trajectory Prediction Method
2.2. Probabilistic Trajectory Prediction Method
2.3. Summary
- (1)
- Limited modeling of aircraft interaction, resulting in underutilization of spatial dependence and behavioral correlation;
- (2)
- Inconsistent characterization of trajectory uncertainty affects interpretability and applicability;
- (3)
- The lack of an integrated early warning module failed to meet the closed-loop paradigm requirements advocated by TBO.
3. Methodologies
3.1. Problem Setup
3.2. Spatio-Temporal Prediction
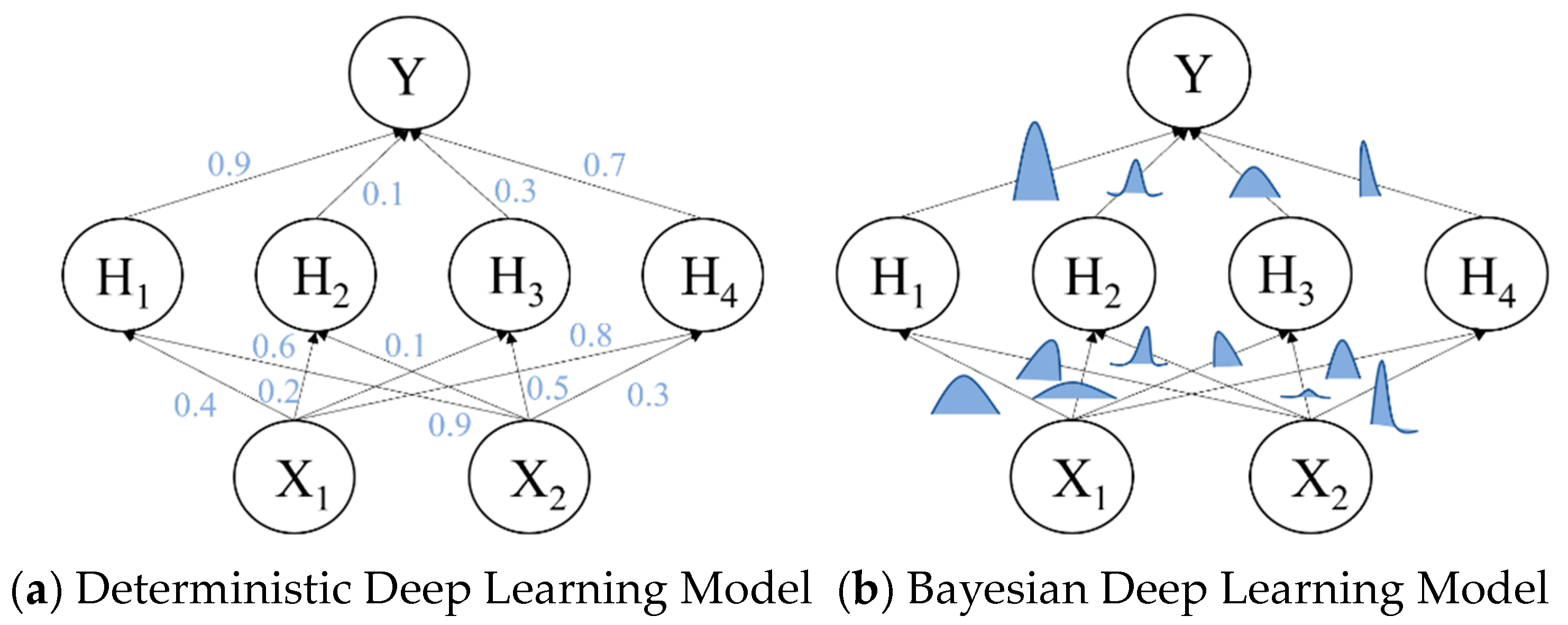
3.3. Bayesian Deep Learning
3.3.1. Bayesian Inference
3.3.2. Variational Inference
3.4. Probabilistic TMA Trajectory Prediction Framework
3.4.1. BST-Transformer
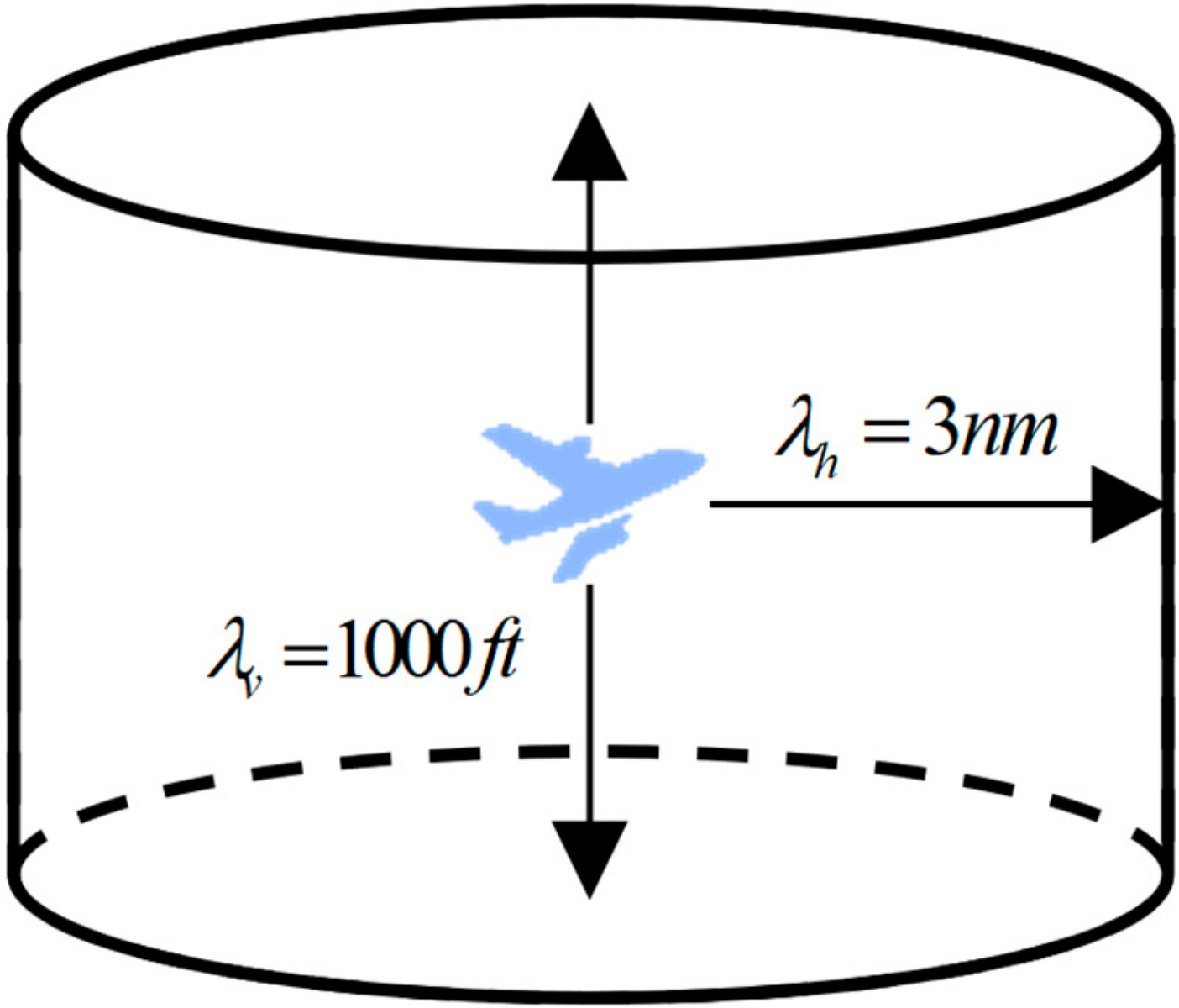
3.4.2. Aircraft Conflict Alerting Module
4. Experiments
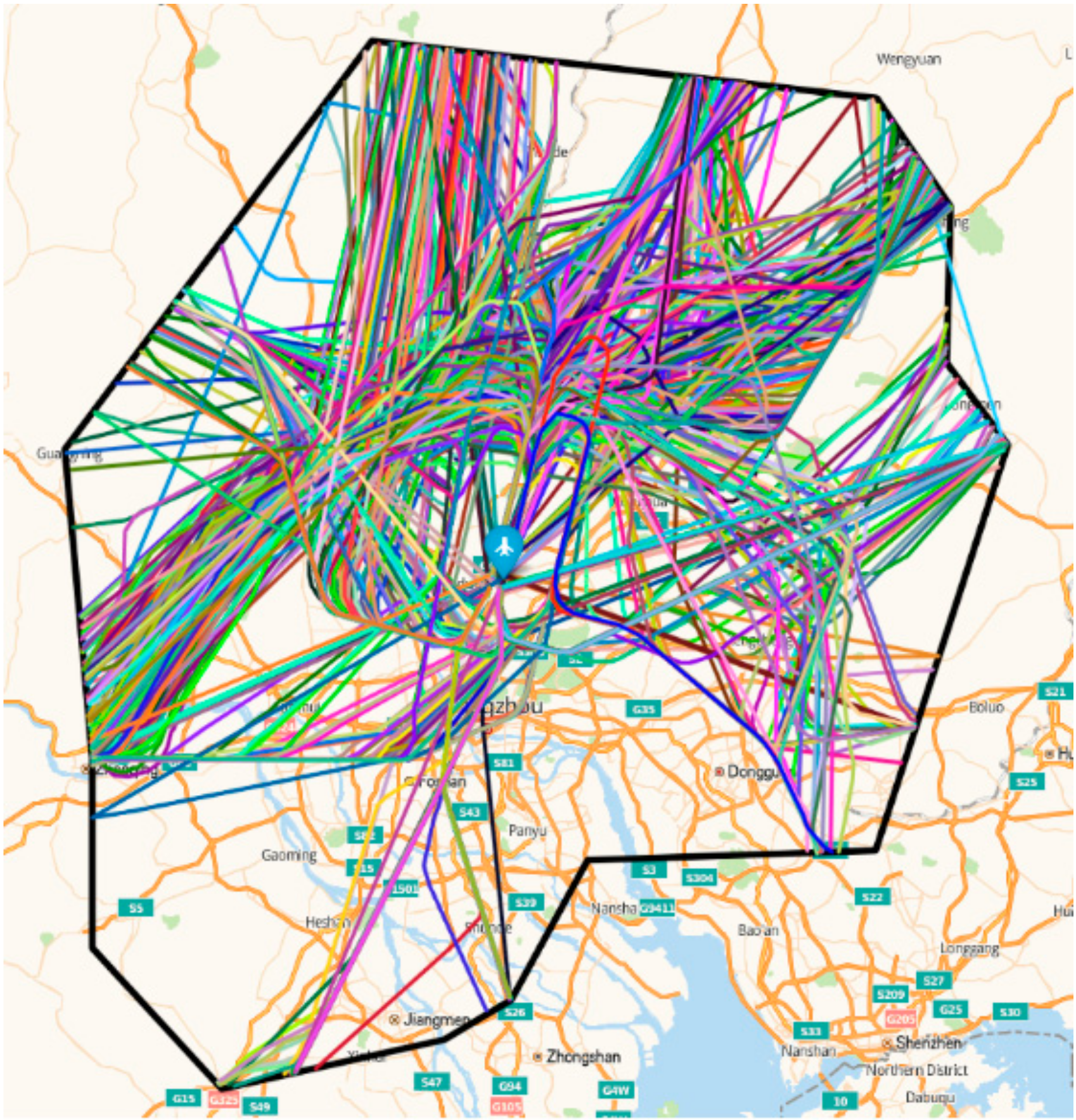
4.1. Datasets
- (1)
- Time resampling is carried out with a fixed step of 5 s. If the trajectory point is missing, fill it by linear interpolation between adjacent time steps.
- (2)
- Perform linear interpolation correction on the trajectory points with incomplete positions.
- (3)
- Convert the timestamp into a relative time difference and label the flight ID to ensure the consistency of the input features.
- (4)
- To meet the requirement of Bayesian network modeling for complete trajectory observation, only complete trajectory fragments covering the entire takeoff or landing stage were selected.
4.2. Evaluation Metrics
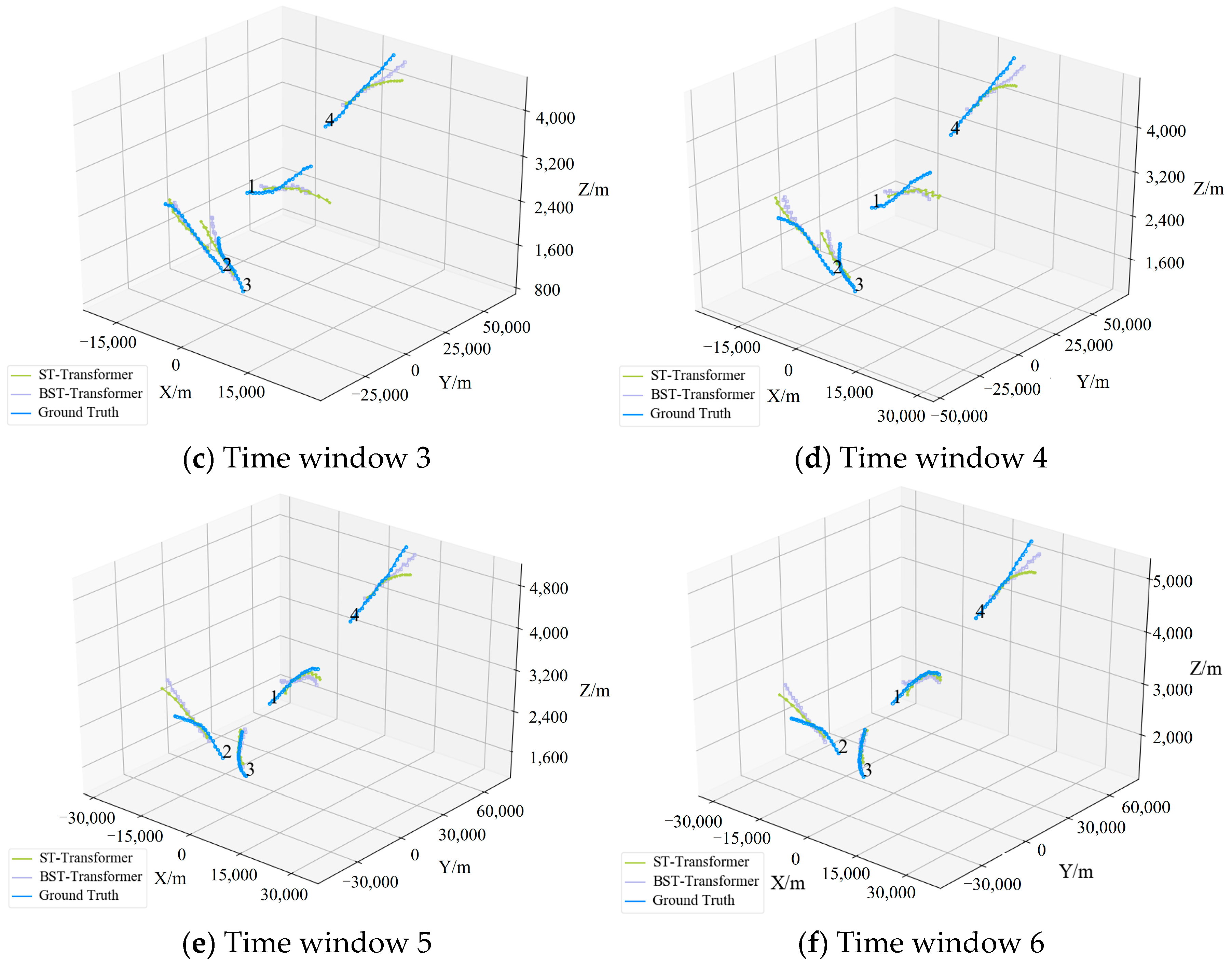
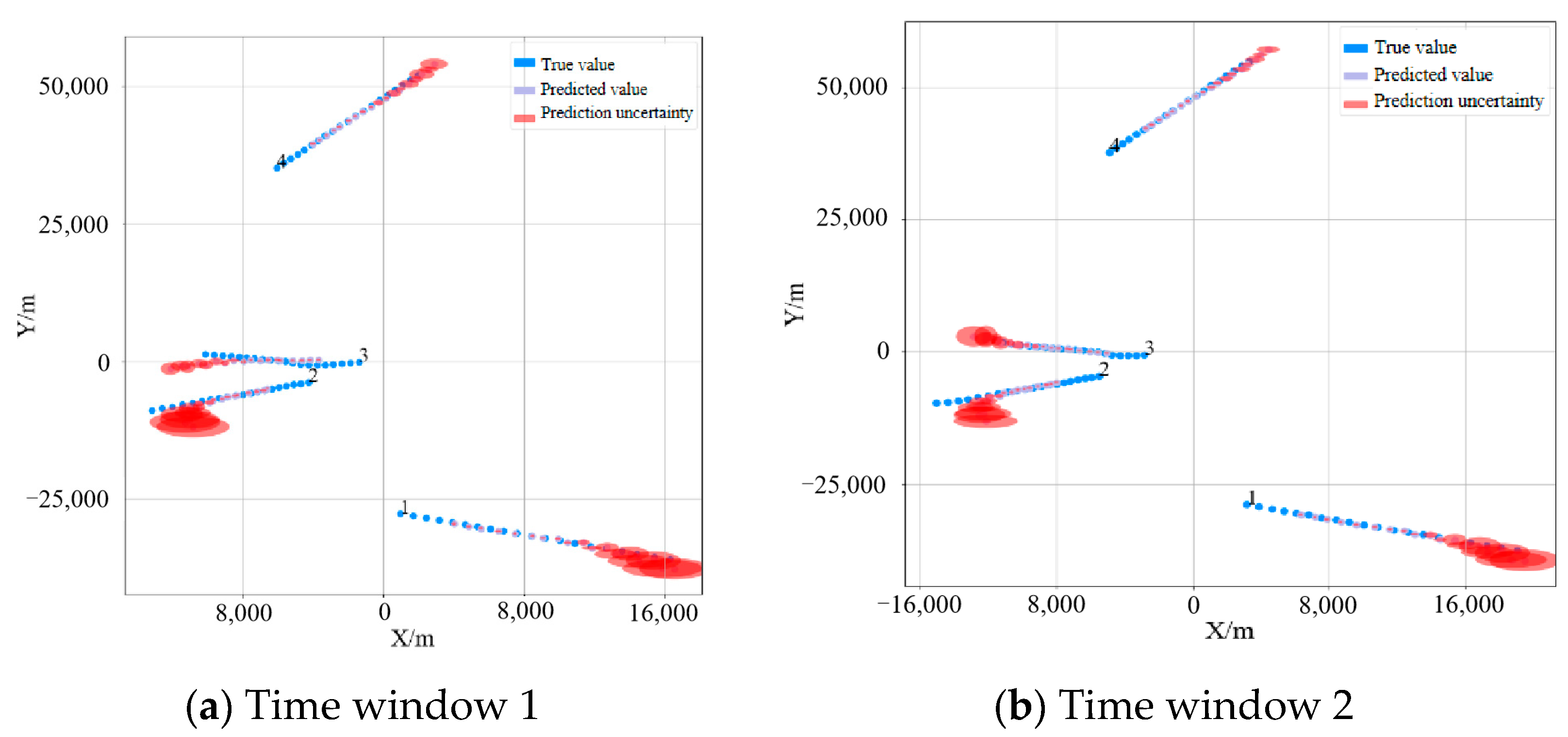
4.3. Trajectory Prediction Results Analysis
- (1)
- Back Propagation (BP) Neural Network: A classic multi-layer feedforward network trained with the backpropagation algorithm, which serves as a fundamental nonlinear function approximator benchmark. The embedding size is set to 32, the number of neurons per hidden layer is 64, the dropout rate is 0.1, the learning rate is 0.0019, and the number of training epochs is 200.
- (2)
- Recurrent Neural Network (RNN): A fundamental neural network architecture designed for sequential data, which utilizes cyclic connections to maintain a hidden state that captures historical information. The loss function converged within 100 training epochs and the number of epochs is 100. The embedding size is 32, number of hidden layers is 2, number of neurons per hidden layer is 64, dropout rate is 0.1, and learning rate is 0.0015.
- (3)
- Long Short-Term Memory (LSTM): An advanced variant of RNN that introduces gating mechanisms to mitigate the vanishing gradient problem and better capture long-range dependencies. The loss function converged within 100 training epochs and the number of epochs is set to 100. The embedding size is 32, number of hidden layers is 2, number of neurons per hidden layer is 64, dropout rate is 0.1, and learning rate is 0.0015.
- (4)
- State Refined LSTM (SR-LSTM): An extension of LSTM that explicitly models the interaction between different temporal states of a single sequence through a state refinement module, enhancing its ability to capture complex temporal patterns. The loss function converged within 100 training epochs and the number of epochs is set to 100. The number of refinement layers is set to 2.
- (5)
- ST-Transformer: The deterministic version of the Spatio-Transformer, which shares the same spatio-temporal attention architecture as our model but without Bayesian uncertainty quantification. This comparison is crucial to isolate the benefit of our Bayesian framework [10]. The training epochs are 100.
- (6)
- ST-Transformer Dropout: The Dropout model of the ST-Transformer approximates the Bayesian inference process by applying Dropout to simulate the posterior distribution. This method is based on the equivalence between Monte Carlo Dropout and ELBO maximization, a principle that has been confirmed by the research of Gal et al. [51].
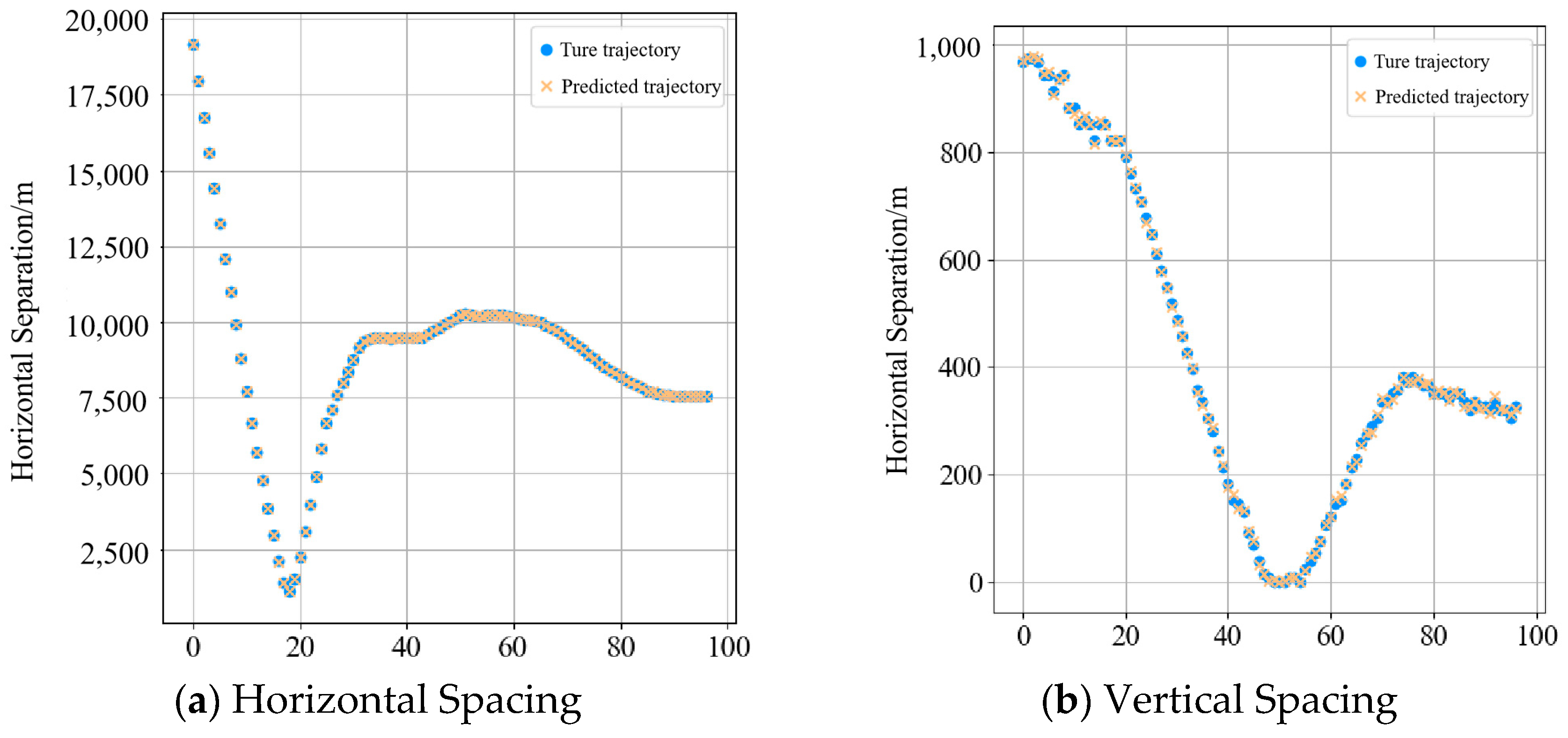
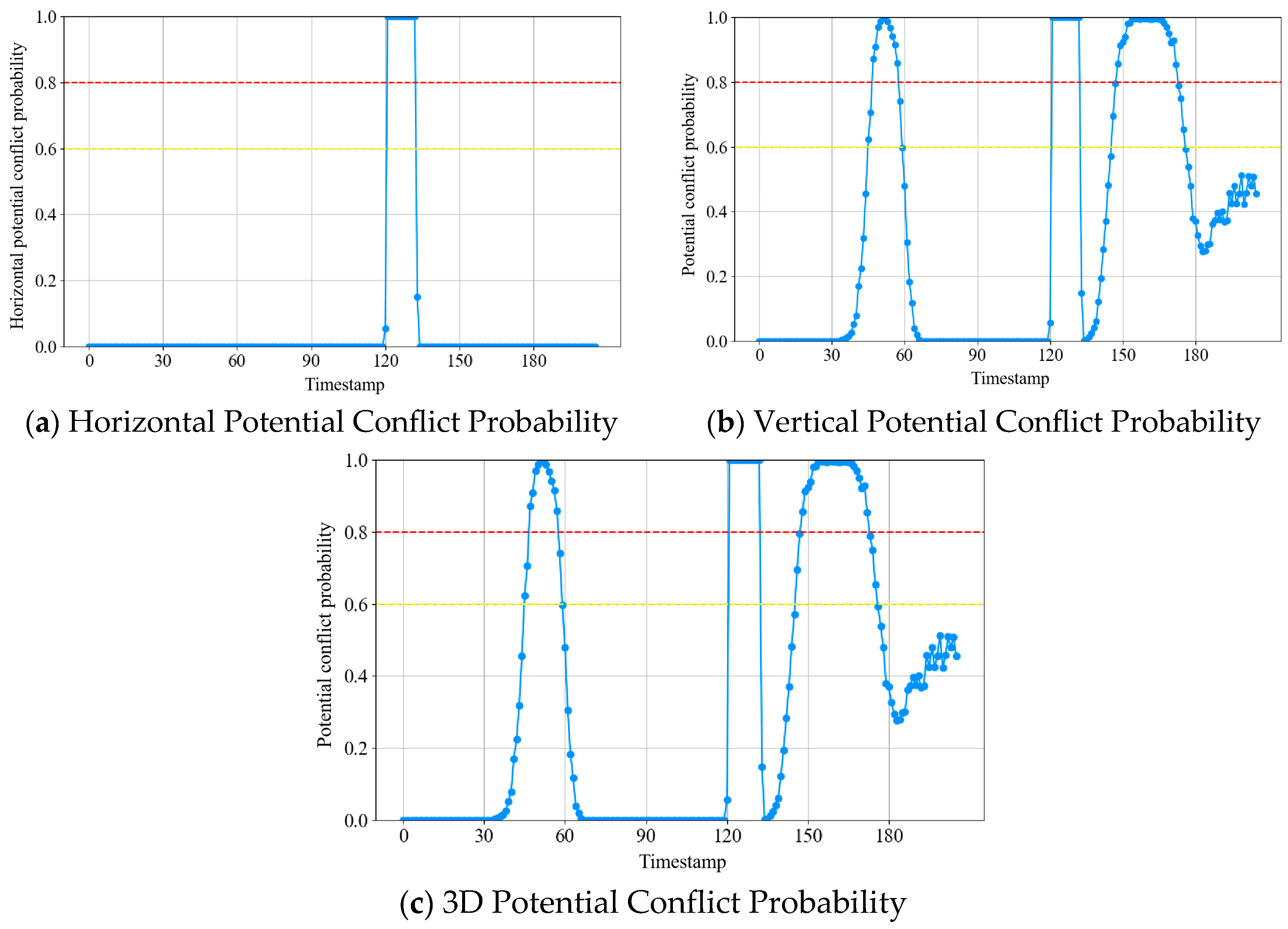
4.4. Conflict Alert Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Definition | Abbreviation | Definition |
| TMA | Terminal Area | TBO | Trajectory Based Operations |
| BST-Transformer | Bayesian Spatio-Temporal Transformer | WATS | World Air Transport Statistics |
| IATA | International Air Transport Association | RPKs | Passenger Revenue Kilometers |
| ICAO | International Civil Aviation Organization | LSTM | Long Short-Term Memory |
| GANs | Generative Adversarial Networks | GNNs | Graph Neural Networks |
| RNNs | Recurrent Neural Networks | GRU | Gated Recurrent Unit |
| CNN | Convolutional Neural Network | GCN | Graph Convolutional Network |
| TCN | Temporal Convolutional Network | GMM | Gaussian Mixture Module |
| BNN | Bayesian Neural Network | VI | Variational Inference |
| KL | Kullback–Leibler | ELBO | Evidence Lower Bound |
| Adam | Adaptive Moment Estimation | GPU | Graphics Processing Unit |
| Q | Query | K | Key |
| V | Value | MSE | Mean Squared Error |
| MADE | Mean Absolute Displacement Error | MADHE | Mean Absolute Displacement Horizontal Error |
| MADVE | Mean Absolute Displacement Vertical Error | ||
| Nomenclature | |||
| Nomenclature | Definition | Nomenclature | Definition |
| Embedded features | Key vector dimension | ||
| Output of the m-th attention head | Output of the multi-head attention layer | ||
| Aircraft distance | Transformed aircraft x axial coordinates | ||
| Transformed aircraft y axial coordinates | Transformed aircraft z axial coordinates | ||
| Weight | Prior distribution | ||
| Posterior distribution | Likelihood function | ||
| Marginal likelihood | Probability distribution of the output | ||
| Approximate probability distribution | Kullback–Leibler divergence | ||
| Weight perturbation matrix | Base perturbation | ||
| Sampled weight matrix | Aircraft horizontal separation | ||
| Aircraft vertical separation | Minimum horizontal separation standard | ||
| Minimum vertical separation standard | Potential conflict probability | ||
| Probability threshold for horizontal conflict alerting | Probability threshold for vertical conflict alerting | ||
| Distance separation distribution function | Sample size | ||
| Number of samples below the safety threshold |
References
- International Air Transport Association. World Air Transport Statistics; IATA: Montreal, QC, Canada, 2023; Available online: https://www.iata.org (accessed on 14 March 2024).
- IATA. World Air Transport Statistics (WATS), 2024 ed.; International Air Transport Association (IATA): Montreal, QC, Canada, 2024; Available online: https://www.iata.org/en/services/data/market-data/world-air-transport-statistics/ (accessed on 7 June 2025).
- Performance Review Commission (PRC), EUROCONTROL. Performance Review Report 2022: An Assessment of Air Traffic Management in Europe; Eurocontrol: Brussels, Belgium, 2023; Available online: https://www.eurocontrol.int/sites/default/files/2023-06/eurocontrol-prr-2022.pdf (accessed on 18 December 2024).
- ICAO. Trajectory Based Operations (TBO)—Global Concept/Operational Guidance; International Civil Aviation Organization (ICAO): Montreal, QC, Canada, 2025; Available online: https://www2023.icao.int/airnavigation/tbo/Pages/Why-Global-TBO-Concept.aspx (accessed on 6 August 2025).
- Guo, P.; Liang, B.; Li, S.; Yang, K.; Li, Q. Research on Trajectory Conflict Detection and Resolution for TBO. In Proceedings of the International Conference on Guidance, Navigation and Control, Changsha, China, 9–11 August 2024; Springer Nature: Singapore, 2024; pp. 381–392. [Google Scholar] [CrossRef]
- FAA/EUROCONTROL. Common TP Structure and Terminology in Support of SESAR & NextGen; FAA/Eurocontrol: Brussels, Belgium, 2010.
- Ma, L.; Tian, S. A Hybrid CNN-LSTM Model for Aircraft 4D Trajectory Prediction. IEEE Access 2020, 8, 134668–134680. [Google Scholar] [CrossRef]
- Song, Y.; Cheng, P.; Mu, C. An Improved Trajectory Prediction Algorithm Based on Trajectory Data Mining for Air Traffic Management. In Proceedings of the 2012 IEEE International Conference on Information and Automation, Chengdu, China, 6–8 June 2012; IEEE: Shenyang, China, 2012; pp. 981–986. [Google Scholar] [CrossRef]
- Chen, H.; Jilkov, V.P.; Li, X.R. On Threshold Optimization for Aircraft Conflict Detection. In Proceedings of the 18th International Conference on Information Fusion, Washington, DC, USA, 6–9 July 2015; IEEE: Washington, DC, USA, 2015; pp. 1198–1204. Available online: https://www.webofscience.com/wos/alldb/full-record/WOS:000389523300157 (accessed on 12 January 2025).
- Dong, X.; Tian, Y.; Dai, L.; Li, J.; Wan, L. A New Accurate Aircraft Trajectory Prediction in Terminal Airspace Based on Spatio-Temporal Attention Mechanism. Aerospace 2024, 11, 718. [Google Scholar] [CrossRef]
- Kuchar, J.K.; Yang, L.C. A Review of Conflict Detection and Resolution Modeling Methods. IEEE Trans. Intell. Transp. Syst. 2000, 1, 179–189. [Google Scholar] [CrossRef]
- Hwang, I.; Seah, C.E. Intent-Based Probabilistic Conflict Detection for the Next Generation Air Transportation System. Proc. IEEE 2009, 96, 2040–2059. [Google Scholar] [CrossRef]
- Lymperopoulos, I.; Lygeros, J.; Lecchini, A. Model Based Aircraft Trajectory Prediction During Takeoff. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006; Aerospace Research Central: Keystone, CO, USA, 2006. [Google Scholar]
- Thipphavong, D.P.; Schultz, C.A.; Lee, A.G.; Chan, S.H. Adaptive Algorithm to Improve Trajectory Prediction Accuracy of Climbing Aircraft. J. Guid. Control Dyn. 2013, 36, 15–24. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.; Hu, R.; Zhu, H. Online Four Dimensional Trajectory Prediction Method Based on Aircraft Intent Updating. Aerosp. Sci. Technol. 2018, 77, 774–787. [Google Scholar] [CrossRef]
- Chatterji, G. Short-Term Trajectory Prediction Methods. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Portland, OR, USA, 9–11 August 1999; AIAA: Portland, OR, USA, 1999; p. 4233. [Google Scholar]
- Zhang, J.; Wang, G.; Xiao, G. Dynamic Trajectory Prediction for Continuous Descend Operations Based on Unscented Kalman Filter. In Proceedings of the 2020 Chinese Intelligent Systems Conference: Volume I., Guilin, China, 25–26 October 2020; Springer: Singapore, 2021; pp. 206–216. [Google Scholar] [CrossRef]
- Ayhan, S.; Samet, H. Aircraft Trajectory Prediction Made Easy with Predictive Analytics. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: San Francisco, CA, USA, 2016; pp. 21–30. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, B.; Zhang, J.; Liu, H. Approach for 4D Trajectory Management Based on HMM and Trajectory Similarity. J. Mar. Sci. Technol. 2019, 27, 7. [Google Scholar] [CrossRef]
- Xu, Z.; Zeng, W.; Chu, X.; Cao, P. Multi-Aircraft Trajectory Collaborative Prediction Based on Social Long Short-Term Memory Network. Aerospace 2021, 8, 115. [Google Scholar] [CrossRef]
- Wu, X.; Yang, H.; Chen, H.; Hu, Q.; Hu, H. Long-Term 4D Trajectory Prediction Using Generative Adversarial Networks. Transp. Res. Part C Emerg. Technol. 2022, 136, 103554. [Google Scholar] [CrossRef]
- Sudarsanan, V.S.; Kostiuk, P.F. Deep-Learning Framework for Terminal Airspace Trajectory Prediction and In-Time Prognostics. J. Aerosp. Inf. Syst. 2024, 21, 628–640. [Google Scholar] [CrossRef]
- Chu, X.; Zeng, W.; Wu, L. Joint Prediction of Multi-Aircraft Trajectories in Terminal Airspace: A Flight Pattern-Guided Social Long-Short Term Memory Network. Eng. Appl. Artif. Intell. 2025, 147, 110325. [Google Scholar] [CrossRef]
- Tran, P.N.; Nguyen, H.Q.; Pham, D.T.; Alam, S. Aircraft Trajectory Prediction with Enriched Intent Using Encoder-Decoder Architecture. IEEE Access 2022, 10, 17881–17896. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, M.; Pan, Q. 4-D Flight Trajectory Prediction with Constrained LSTM Network. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7242–7255. [Google Scholar] [CrossRef]
- Jia, P.; Zhang, H.; Li, Y.; Wang, X.; Chen, J. Attention-LSTM Based Prediction Model for Aircraft 4-D Trajectory. Sci. Rep. 2022, 12, 11345. [Google Scholar] [CrossRef]
- Schimpf, N.; Wang, Z.; Li, S.; Knoblock, E.J.; Li, H.; Apaza, R.D. A Generalized Approach to Aircraft Trajectory Prediction via Supervised Deep Learning. IEEE Access 2023, 11, 116183–116195. [Google Scholar] [CrossRef]
- Tong, Q.; Hu, J.; Chen, Y.; Guo, D.; Liu, X. Long-Term Trajectory Prediction Model Based on Transformer. IEEE Access 2023, 11, 143695–143703. [Google Scholar] [CrossRef]
- Luo, A.; Luo, Y.; Liu, H.; Du, W.; Wu, X.; Chen, H.; Yang, H. An Improved Transformer-Based Model for Long-Term 4D Trajectory Prediction in Civil Aviation. IET Intell. Transp. Syst. 2024, 18, 1588–1598. [Google Scholar] [CrossRef]
- Shafienya, H.; Regan, A.C. 4D Flight Trajectory Prediction Using a Hybrid Deep Learning Prediction Method Based on ADS-B Technology: A Case Study of Hartsfield–Jackson Atlanta International Airport (ATL). Transp. Res. Part C Emerg. Technol. 2022, 144, 103878. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, Y.; Chu, X.; Tan, X.; Zeng, W. Aircraft Trajectory Prediction for Terminal Airspace Employing Social Spatiotemporal Graph Convolutional Network. J. Aerosp. Inf. Syst. 2023, 20, 319–333. [Google Scholar] [CrossRef]
- He, H.; Shi, X.; Liu, H.; Hui, K. Multi-Aircraft Trajectory Prediction Method in Terminal Area Based on Improved Spatio-Temporal Model. J. Beihang Univ. 2025, 51, 1–16. [Google Scholar] [CrossRef]
- Nilim, A.; El Ghaoui, L.; Hansen, M.; Duong, V. Trajectory-Based Air Traffic Management (TB-ATM) under Weather Uncertainty. In Proceedings of the Fourth International Air Traffic Management R&D Seminar (ATM-2001), Santa Fe, NM, USA, 3–7 December 2001. [Google Scholar]
- Pang, Y.; Liu, Y. Conditional Generative Adversarial Networks (CGAN) for Aircraft Trajectory Prediction Considering Weather Effects. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1853. [Google Scholar]
- Barratt, S.T.; Kochenderfer, M.J.; Boyd, S.P. Learning Probabilistic Trajectory Models of Aircraft in Terminal Airspace from Position Data. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3536–3545. [Google Scholar] [CrossRef]
- Franco, A.; Rivas, D.; Valenzuela, A. Probabilistic Aircraft Trajectory Prediction in Cruise Flight Considering Ensemble Wind Forecasts. Aerosp. Sci. Technol. 2018, 82, 350–362. [Google Scholar] [CrossRef]
- Zhang, X.; Mahadevan, S. Bayesian Neural Networks for Flight Trajectory Prediction and Safety Assessment. Decis. Support Syst. 2020, 131, 113246. [Google Scholar] [CrossRef]
- Pang, Y.; Zhao, X.; Yan, H.; Liu, Y. Data-Driven Trajectory Prediction with Weather Uncertainties: A Bayesian Deep Learning Approach. Transp. Res. Part C Emerg. Technol. 2021, 130, 103326. [Google Scholar] [CrossRef]
- Wang, Y.; Pang, Y.; Chen, O.; Iyer, H.N.; Dutta, P.; Menon, P.K.; Liu, Y. Uncertainty Quantification and Reduction in Aircraft Trajectory Prediction Using Bayesian-Entropy Information Fusion. Reliab. Eng. Syst. Saf. 2021, 212, 107650. [Google Scholar] [CrossRef]
- Pang, Y.; Zhao, X.; Hu, J.; Yan, H.; Liu, Y. Bayesian Spatio-Temporal Graph Transformer Network (B-STAR) for Multi-Aircraft Trajectory Prediction. Knowl. Based Syst. 2022, 249, 108998. [Google Scholar] [CrossRef]
- Dong, X. Research on Terminal Area 4D Trajectory Prediction Based on Machine Learning. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2023. [Google Scholar]
- Zeh, T.; Rosenow, J.; Fricke, H. Bayesian Inference of Aircraft Operating Speeds for Stochastic Medium-Term Trajectory Prediction. In Proceedings of the 2023 IEEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1–5 October 2023; IEEE: New York, NY, USA, 2023; pp. 1–10. [Google Scholar] [CrossRef]
- Nghiem, T.L.; Le, T.L.; Le, V.D.; Maréchal, P.; Delahaye, D. Improving Flight Trajectory Predictions with Bayesian-Optimized ConvLSTM Models. In Proceedings of the International Conference on Intelligent Systems & Networks, Hanoi, Vietnam, 22–23 March 2024; pp. 604–614. [Google Scholar] [CrossRef]
- Xiang, J.; Chen, J. Data-Driven Probabilistic Trajectory Learning with High Temporal Resolution in Terminal Airspace. J. Aerosp. Inf. Syst. 2025, 22, 1–11. [Google Scholar] [CrossRef]
- Pepper, N.; De Ath, G.; Carvell, B.; Hodgkin, A.; Dodwell, T.; Thomas, M.; Everson, R. A Sector-Specific Probabilistic Approach for 4D Aircraft Trajectory Generation. Transp. Res. Part C Emerg. Technol. 2025, 179, 105291. [Google Scholar] [CrossRef]
- Hu, H.; Yuan, Y.; Xue, Q. A Deep Learning Approach for General Aviation Trajectory Prediction Based on Stochastic Processes for Uncertainty Handling. Appl. Sci. 2025, 15, 6810. [Google Scholar] [CrossRef]
- Zhang, Y. Research on 4D Trajectory Prediction and Conflict Detection in Terminal Airspace Based on Deep Learning. Master’s Thesis, Civil Aviation Flight University of China, Guanghan, China, 2024. [Google Scholar]
- Worley, B. Scalable Mean-Field Sparse Bayesian Learning. IEEE Trans. Signal Process. 2019, 67, 6314–6326. [Google Scholar] [CrossRef]
- Wen, Y.; Vicol, P.; Ba, J.; Tran, D.; Grosse, R. Flipout: Efficient Pseudo-Independent Weight Perturbations on Mini-Batches. arXiv 2018, arXiv:1803.04386. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Air Traffic Control: FAA Order JO-7110.65; FAA: Washington, DC, USA, 2024.
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning (ICML), New York City, NY, USA, 19–24 June 2016; PMLR: Maastricht, The Netherlands, 2016; pp. 1050–1059. [Google Scholar]









| Parameter | Parameter Value |
|---|---|
| num of heads | 8 |
| num of encoder layers | 2 |
| dimension of model | 32 |
| dropout | 0.05 |
| learning rate | 0.0015 |
| train epoch | 100 |
| num of aircraft stored as one batch | 128 |
| Model | MADE (m) | MADHE (m) | MADVE (m) |
|---|---|---|---|
| BP | 5841.98 | 5834.31 | 242.60 |
| RNN | 3060.21 | 3041.44 | 243.91 |
| LSTM | 2616.54 | 2593.01 | 237.53 |
| SR-LSTM | 2608.83 | 2583.24 | 233.36 |
| ST-Transformer | 1365.27 | 1353.54 | 100.53 |
| ST-Transformer Dropout | 703.45 | 688.78 | 77.25 |
| BST-Transformer | 542.37 | 511.98 | 52.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Tian, Y.; Xie, X.; Zhi, B.; Wan, L. Bayesian Spatio-Temporal Trajectory Prediction and Conflict Alerting in Terminal Area. Aerospace 2025, 12, 855. https://doi.org/10.3390/aerospace12090855
Li Y, Tian Y, Xie X, Zhi B, Wan L. Bayesian Spatio-Temporal Trajectory Prediction and Conflict Alerting in Terminal Area. Aerospace. 2025; 12(9):855. https://doi.org/10.3390/aerospace12090855
Chicago/Turabian StyleLi, Yangyang, Yong Tian, Xiaoxuan Xie, Bo Zhi, and Lili Wan. 2025. "Bayesian Spatio-Temporal Trajectory Prediction and Conflict Alerting in Terminal Area" Aerospace 12, no. 9: 855. https://doi.org/10.3390/aerospace12090855
APA StyleLi, Y., Tian, Y., Xie, X., Zhi, B., & Wan, L. (2025). Bayesian Spatio-Temporal Trajectory Prediction and Conflict Alerting in Terminal Area. Aerospace, 12(9), 855. https://doi.org/10.3390/aerospace12090855






