Research on Congestion Situation Relief in Terminal Area Based on Flight Path Adjustment
Abstract
1. Introduction
2. Congestion Relief Methods in Terminal Area
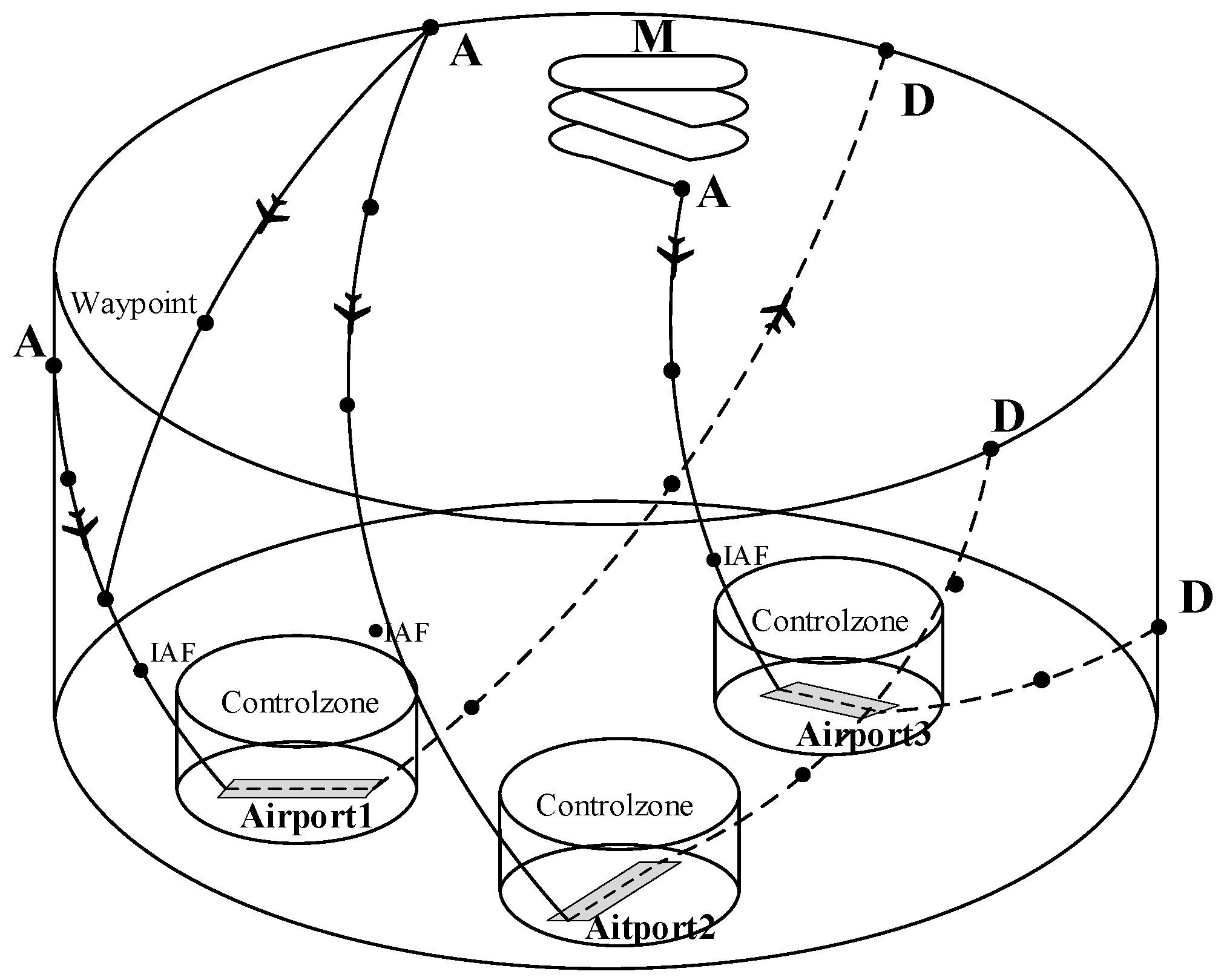
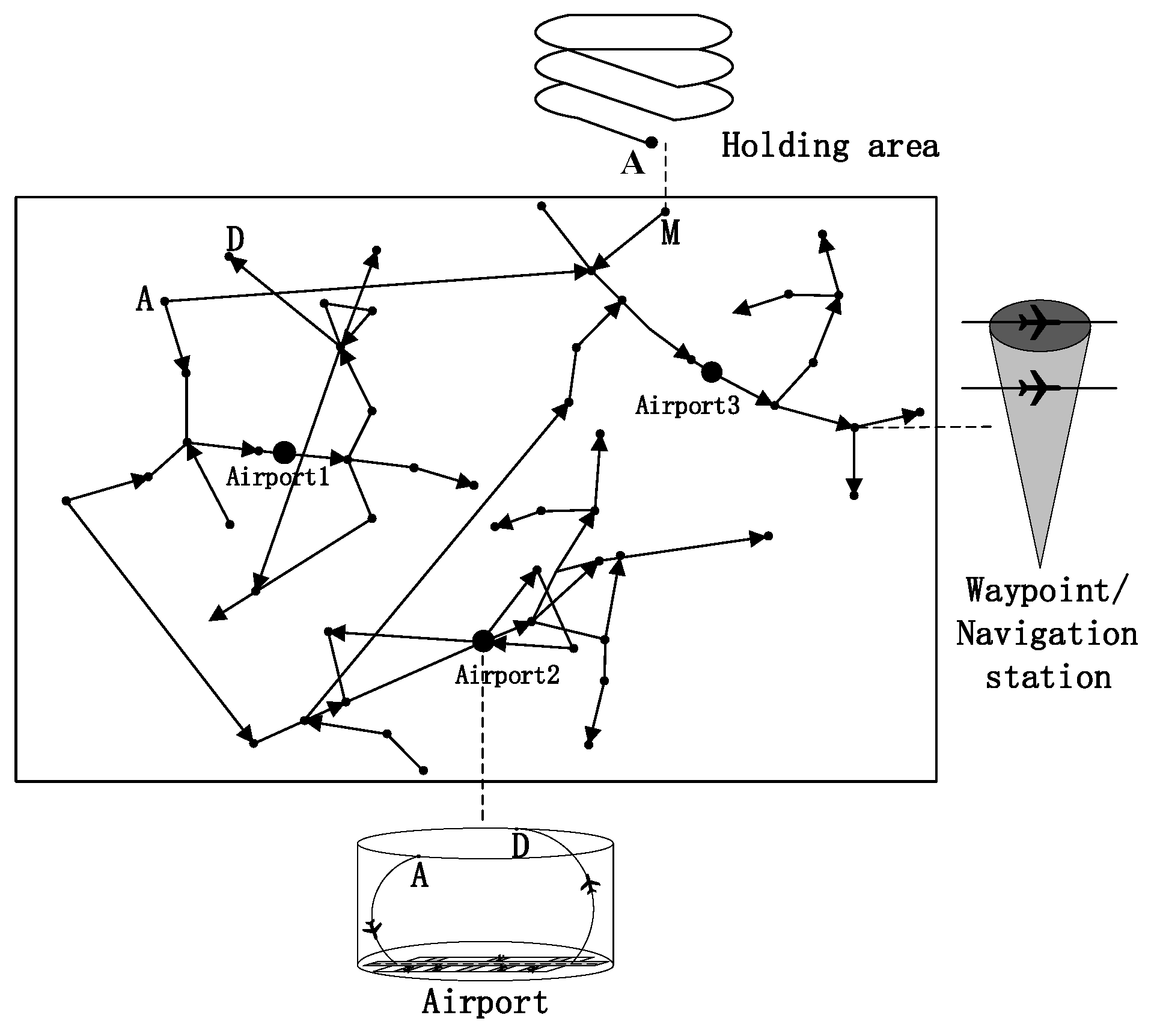
2.1. Establish a Transportation Network Model for the Terminal Area
2.1.1. Advantages Analysis of Constructing Terminal Area Traffic Network by Using Complex Network
2.1.2. Formal Definition of Terminal Area Traffic Network
- Node set ()
- Edge set ()
- Weight set ()
2.2. Establish a Congestion Relief Model for the Terminal Area
2.2.1. Set the Objective Function
2.2.2. Set Constraints
2.3. Solving the Congestion Relief Model for the Terminal Area
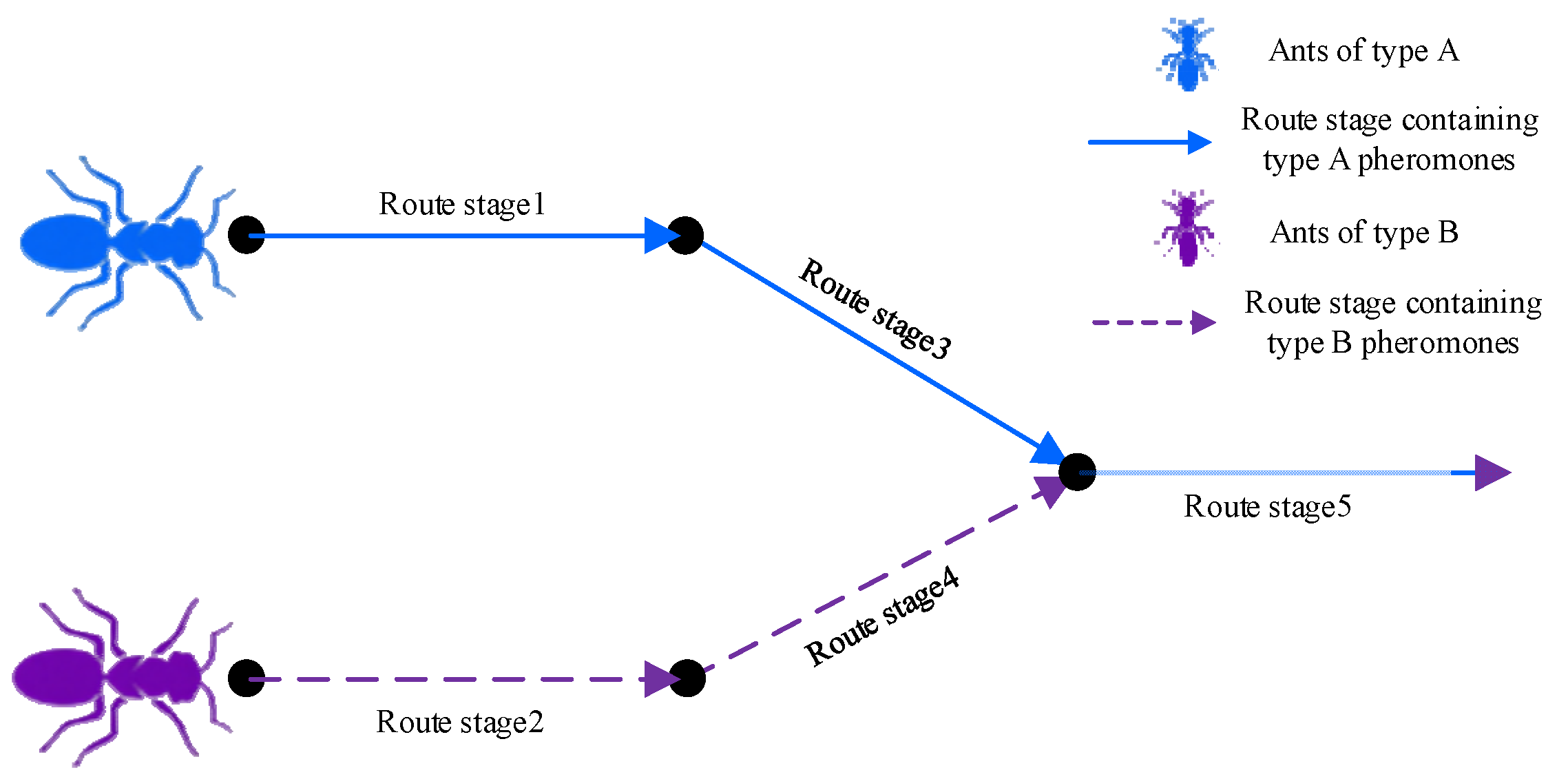
2.3.1. Principles of Improving the Ant Colony Optimization
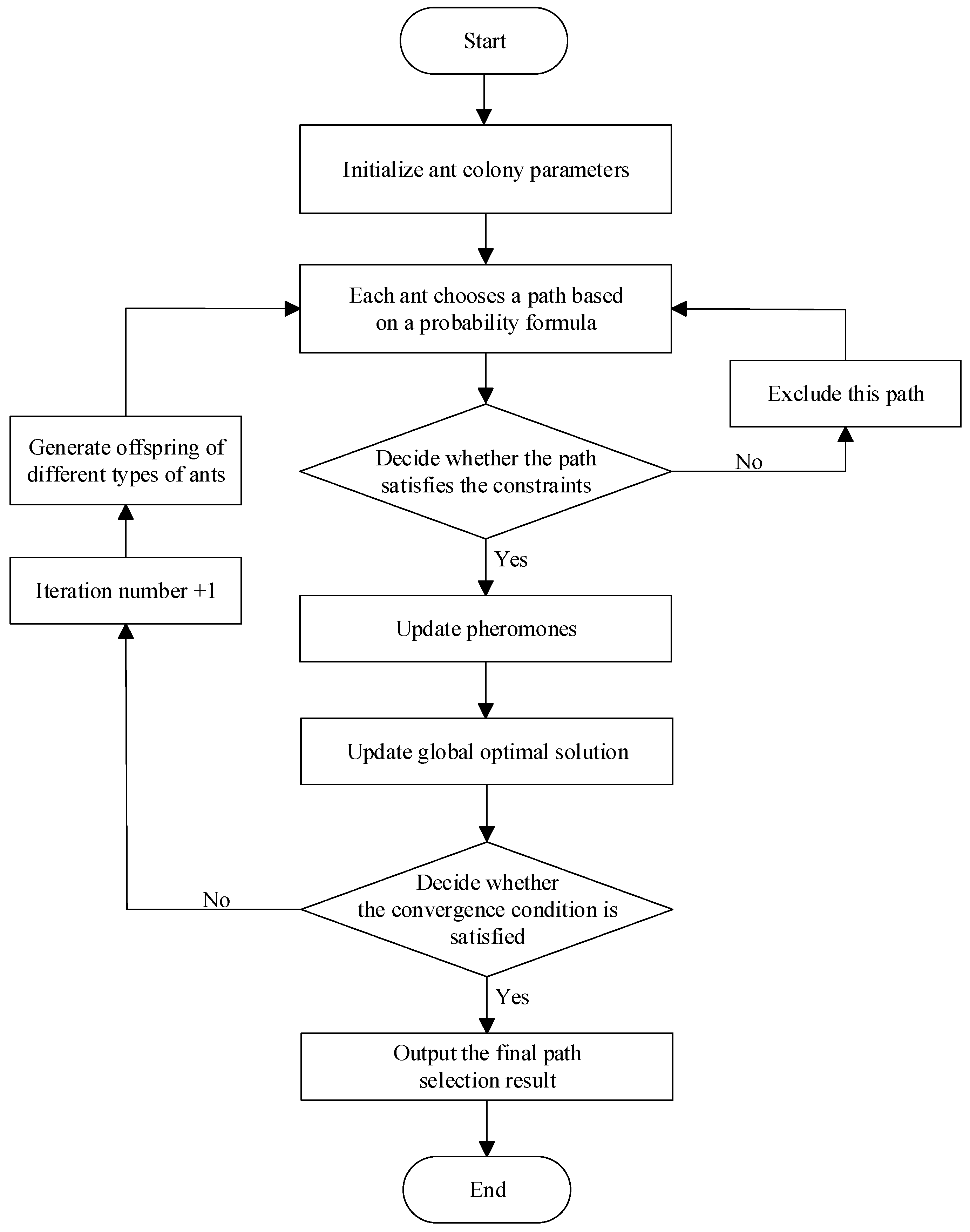
2.3.2. Implementation of Improved Ant Colony Optimization
- 1.
- Initialize ant colony parameters;
- 2.
- Select path;
- 3.
- Determine whether the constraints are satisfied;
- 4.
- Update pheromones;
- 5.
- Iterate the cycle and determine convergence;
- 6.
- Output the final path selection result.
3. Simulation Experiment
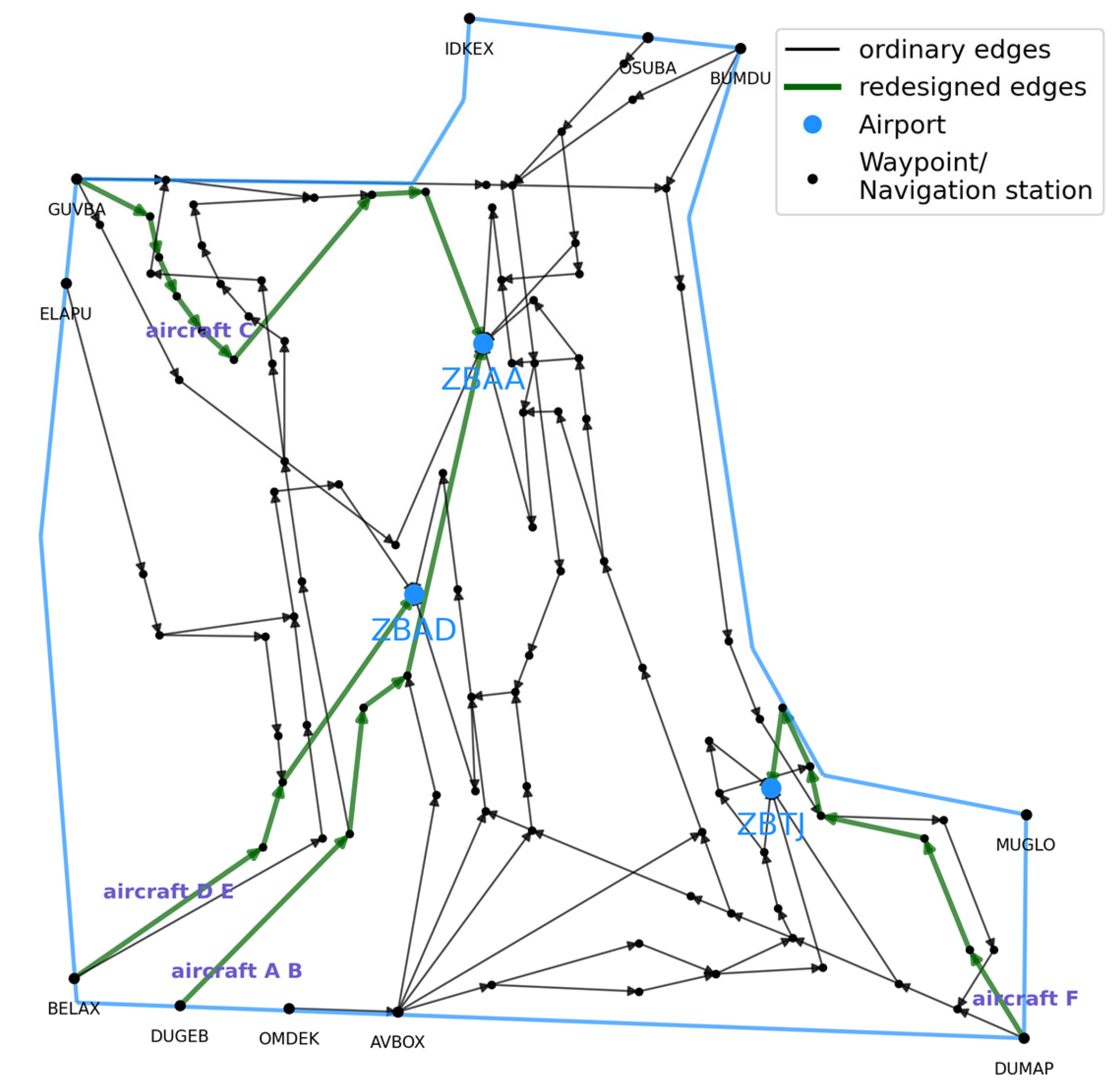
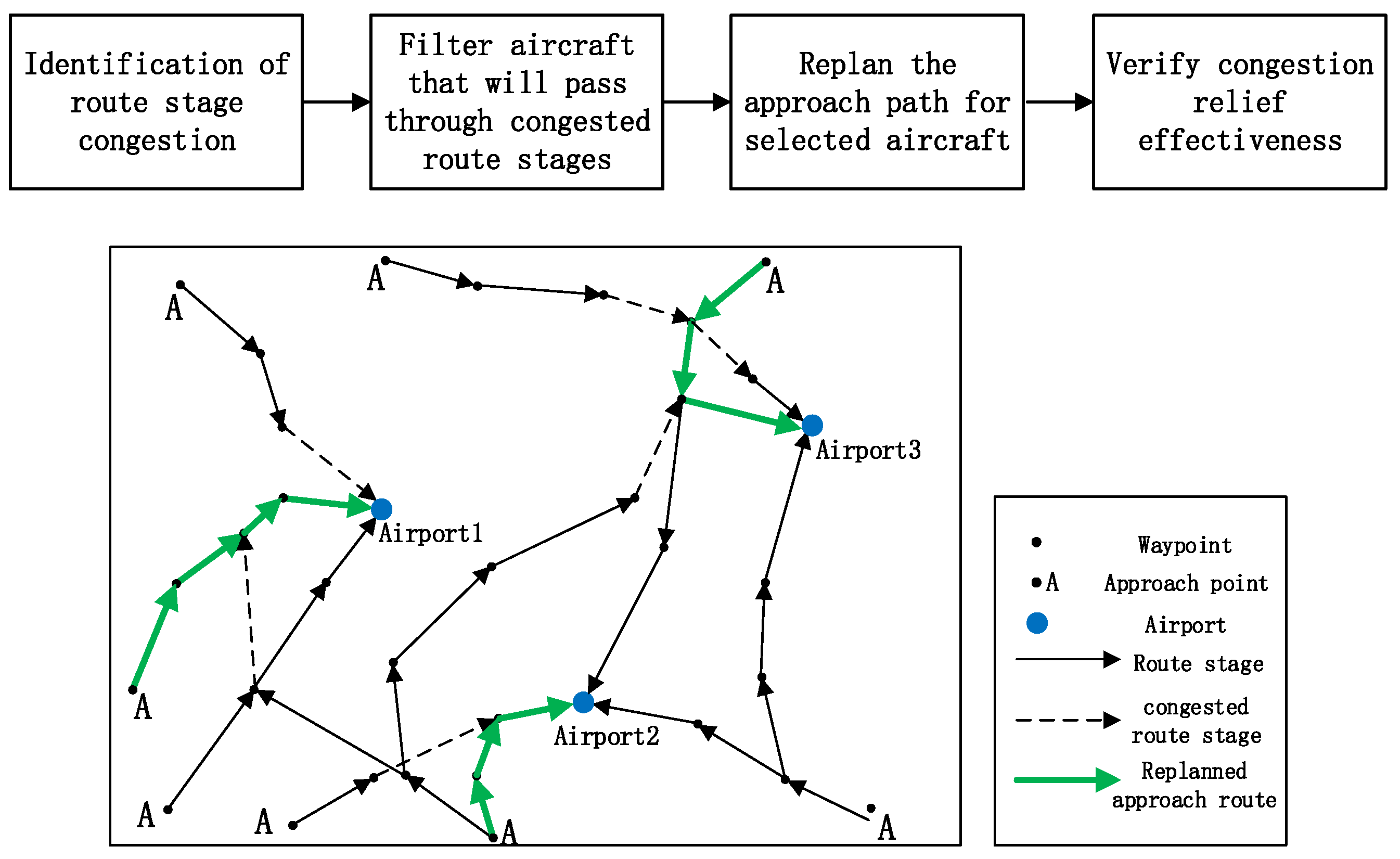
3.1. Identification of Congested Route Stages and Initialization of Ant Colonies
3.2. Select Approach Path
| Number of Iterations | (* 60%) | (* 40%) | |
|---|---|---|---|
| 1 | 0.277 | 0.236 | 0.513 |
| 2 | 0.157 | 0.231 | 0.388 |
| 3 | 0.231 | 0.187 | 0.418 |
| 4 | 0.243 | 0.136 | 0.379 |
| …… | …… | …… | …… |
| 9 | 0.103 | 0.106 | 0.209 |
| 10 | 0.068 | 0.146 | 0.214 |
| 11 | 0.044 | 0.140 | 0.184 |
| 12 | 0.044 | 0.140 | 0.184 |
| Number of Experiments | Optimal MinF | Number of Occurrences | Number of Iterations at Fastest Convergence |
|---|---|---|---|
| 1 | 0.388 | 2 | 14 |
| 3 | 0.418 | 1 | 17 |
| 4 | 0.215 | 4 | 14 |
| 7 | 0.184 | 17 | 11 |
| 16 | 0.412 | 1 | 13 |
| 23 | 0.365 | 3 | 19 |
| 27 | 0.322 | 2 | 15 |
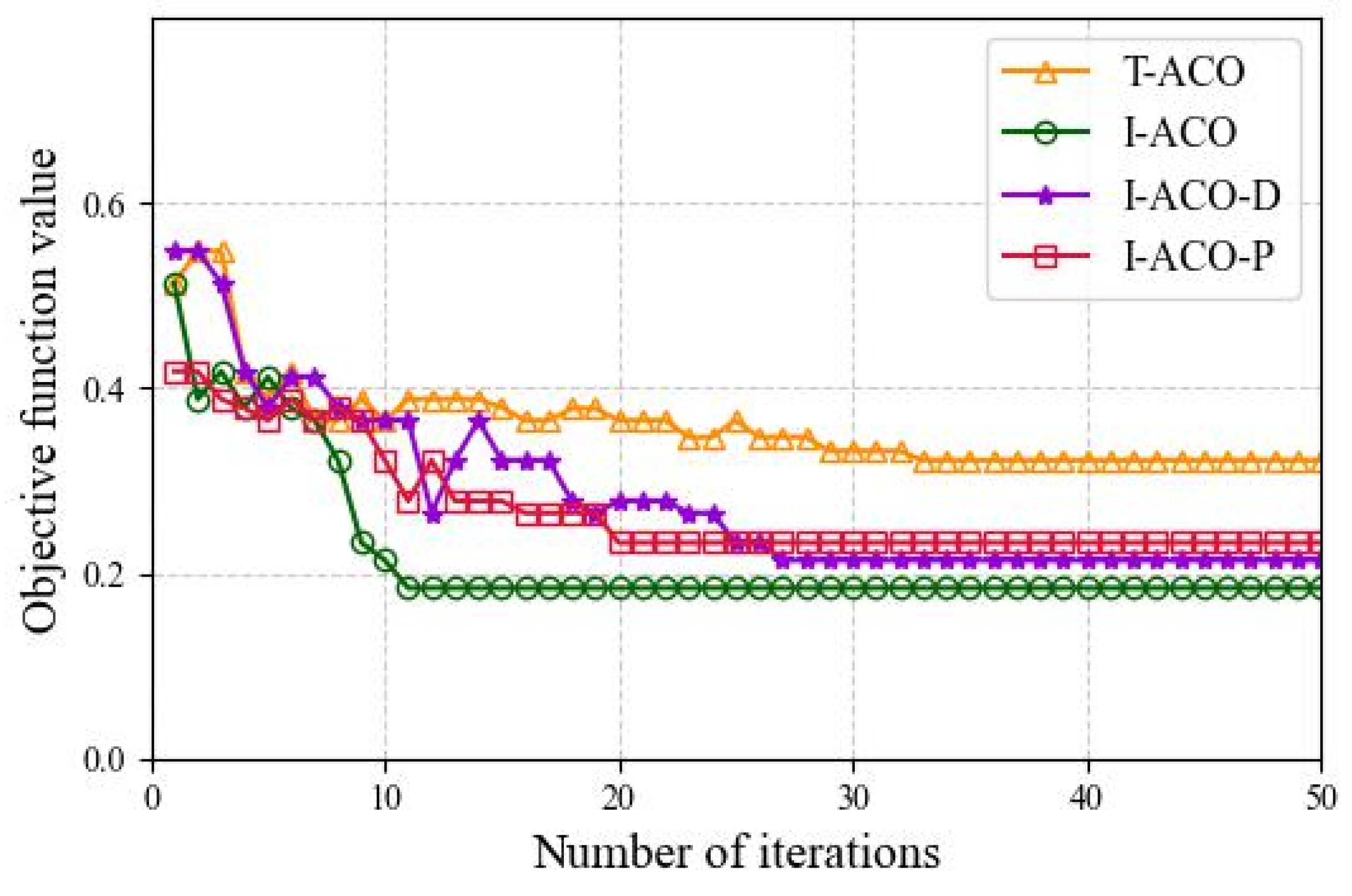
3.3. Comparison of 4 Algorithms Based on Ablation Experiments
- 1.
- Traditional Ant Colony Optimization (T-ACO);
- 2.
- The improved Ant Colony Optimization in this paper (I-ACO);
- 3.
- Ablation Algorithm I (I-ACO-D);
- 4.
- Ablation Algorithm Ⅱ (I-ACO-P).
3.3.1. Comparison of Objective Functions
3.3.2. Comparison of Algorithm Performance
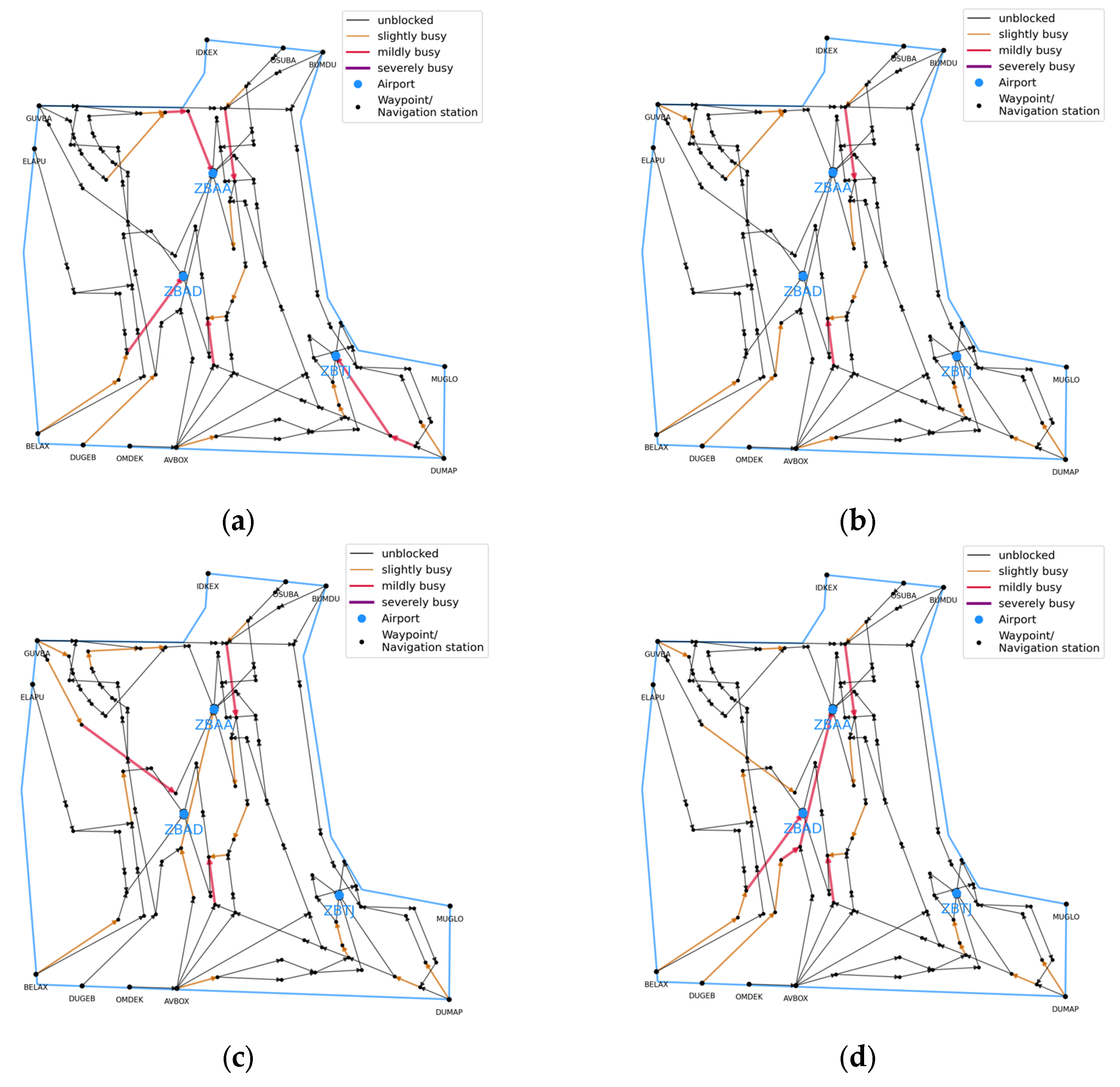
3.3.3. Comparison of Congestion Relief Effects
4. Discussion
4.1. Application Value of Congestion Relief Model
4.2. Prospect of Congestion Relief Model
5. Conclusions
- A traffic network model for the Terminal Area was constructed using a complex network, which can fit the actual situation in the Terminal Area and grasp the overall congestion situation in the Terminal Area from a global perspective.
- This paper proposes a congestion relief strategy model. The optimal objective function value obtained by the model is 0.184, which is significantly lower than other algorithms. At the same time, it can converge in the 11th generation, and the convergence speed is faster than other algorithms. The congestion mitigation effect is also the best.
- The feasibility of integrating a congestion relief model into the air traffic control system is preliminarily conceived in this paper
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wei, M.; Wu, W.; Sun, B. An Optimization Model for Inbound and Outbound Flight Scheduling with Consideration of Potential Risk Levels and Priorities. Ind. Eng. Manag. 2022, 27, 40–45. [Google Scholar]
- Lw, M.L.; Wu, X.S.; Hu, Y.M. Arrival flights optimal sequencing with multi-path selection based on rolling horizon control. J. Beijing Univ. Aeronaut. Astronaut. 2023, 49, 3222–3229. [Google Scholar]
- Yang, L. Studies on Complex Dynamics & Congestion Mitigation Methods of Air Traffic Flow in Terminal Airspace. Doctoral Dissertation, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. [Google Scholar]
- Chen, D.; Tang, C.; Zhang, H.; Ma, Y.; Xu, H. Fine Modeling of Aviation Emissions and Green Trajectory Optimization of Complex En-route Networks. J. Transp. Syst. Eng. Inf. Technol. 2024, 24, 318–326. [Google Scholar]
- Zhu, Y.F.; Sun, Y.; Zhen, Z.Y. Optimization of vertical profile for civil aircraft climbing phase based on improved NSGA-II. Flight Dyn. 2025, 1–7. [Google Scholar] [CrossRef]
- Yang, X.S.; Zhang, C.; Zhu, C.Y. Research on multi-objective optimization of four-dimensional trajectory in the flexible airspace structure. Flight Dyn. 2025, 43, 83–89. [Google Scholar]
- Yang, S.S. Research on Rerouting Strategy Based on Multi-objective Optimization. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2013. [Google Scholar]
- Hao, E.L. Research on Rerouting Tactics in Terminal Area Based on Task Complexity of ATC. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2017. [Google Scholar]
- Zelinski, S.; Xue, M.; Bassett, P. Optimized Route Capability Intelligent Offloading of Congested Arrival Routes; AIAA Aviation: Washington, DC, USA, 2016. [Google Scholar]
- Xue, M.; Zelinski, S. Route Optimization for Offloading Congested Meter Fix. In Proceedings of the 35th Digital Avionics Systems Conference, Sacramento, CA, USA, 25–29 September 2016. [Google Scholar]
- Chen, H.; Zhao, Y.J. Sequential Dynamic Strategies for Real-Time Scheduling of Terminal Traffic. J. Aircr. 2012, 49, 237–249. [Google Scholar] [CrossRef]
- Xiang, Z.; He, Y.Y.; Quan, Z.W. A Rerouting Path Planning Based on Q-Learning Algorithm in Traffic Congestion Airspace. Sci. Technol. Eng. 2022, 22, 14494–14501. [Google Scholar]
- Daganzo, C.F. Urban gridlock: Macroscopic modeling and mitigation approaches. Transp. Res. PART B-Methodol. 2007, 41, 49–62. [Google Scholar] [CrossRef]
- Wu, M.G.; Ye, Z.L.; Wen, X.X.; Jiang, X.R. Air traffic complexity recognition method based on complex networks. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 839–850. [Google Scholar]
- Heng, Y.M.; Wu, M.G.; Wen, X.X.; Lin, F.G.; Yang, T. Controller Workload Evaluation Based on Complex Network. J. Xihua Univ. (Nat. Sci. Ed.) 2022, 41, 52–58. [Google Scholar]
- Peng, Y.T.; Wen, X.X.; Wu, M.G.; Zhu, D.S.; Ding, L. Complex network-based air traffic complexity analysis in TBO. J. Beijing Univ. Aeronaut. Astronaut. 2023, 42, 435–445. [Google Scholar]
- Li, Y.F. Research on Key Techniques of Complex Airport Terminal Airspace Resources Allocation. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2016. [Google Scholar]
- Ji, Y.R.; Yu, F.P.; Shen, D.; Peng, Y.T. Study on the Identification of Terminal Area Traffic Congestion Situation Based on Symmetrical Random Forest. Symmetry 2025, 17, 96. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.C.; Pu, J.X.; Si, Y.N.; Sun, L.F. Survey on Application of Ant Colony Algorithm in Path Planning of Mobile Robot. Comput. Eng. Appl. 2020, 56, 10–19. [Google Scholar]
- Xiao, J.Z.; Yu, X.L.; Zhou, G.; Shun, K.K.; Zhou, Z. An improved ant colony algorithm for indoor AGV path planning. Chin. J. Sci. Instrum. 2022, 43, 277–285. [Google Scholar]
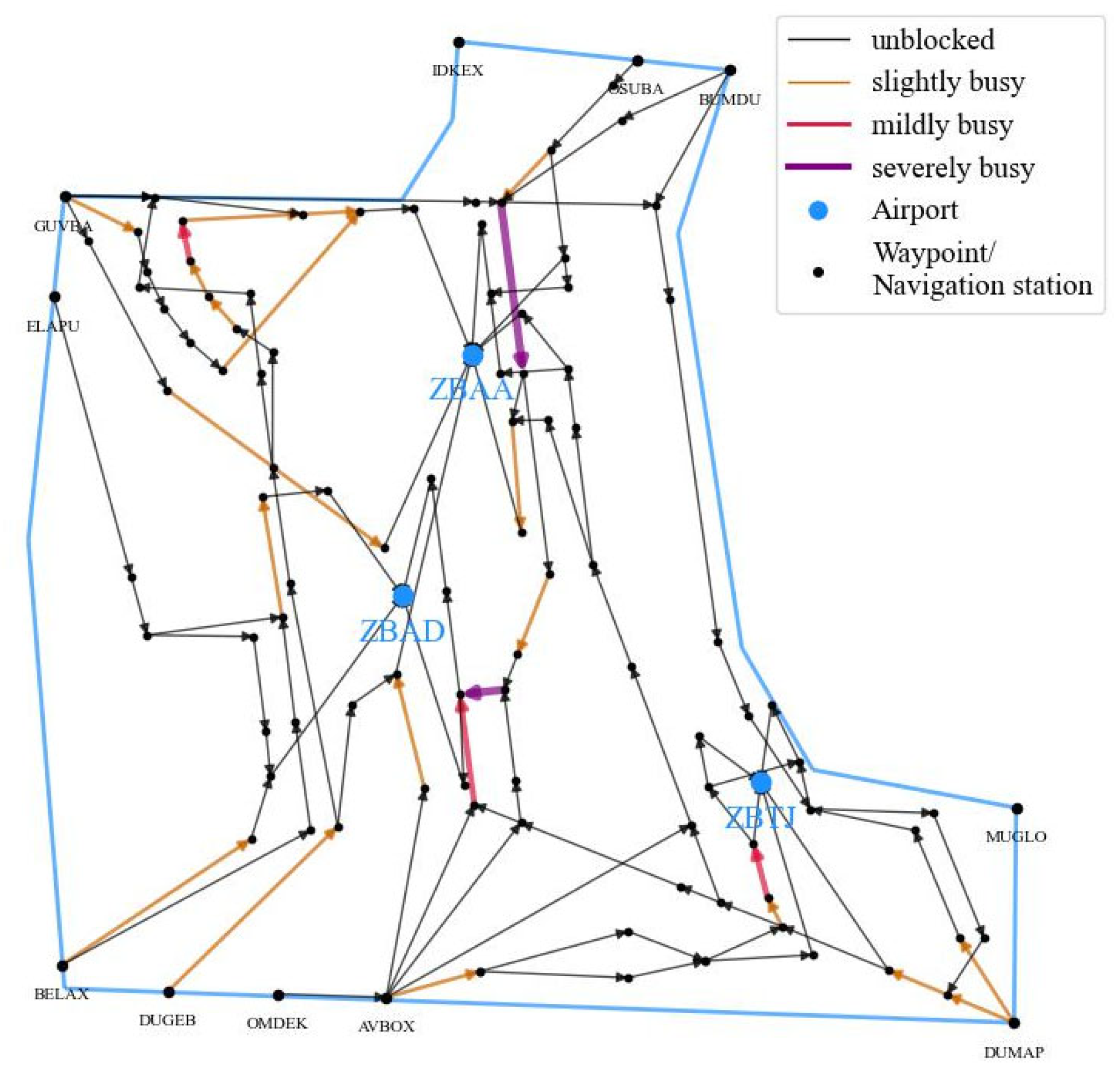

| Aircraft Number | Approach Direction | Ant Type Number | Approach Point Selection Range |
|---|---|---|---|
| aircraft A | southwest | ant A | BELAX; DUGEB; OMDEK; AVBOX |
| aircraft B | southwest | ant B | BELAX; DUGEB; OMDEK; AVBOX |
| aircraft C | west | ant C | GUVBA; ELAPU; BELAX; DUGEB; OMDEK; AVBOX |
| aircraft D | southwest | ant D | BELAX; DUGEB; OMDEK; AVBOX |
| aircraft E | southwest | ant E | BELAX; DUGEB; OMDEK; AVBOX |
| aircraft F | southeast | ant F | DUMAP; MUGLO |
| Types of Algorithms | (* 60%) | (* 40%) | Optimal MinF | Number of Occurrences of the Optimal MinF |
|---|---|---|---|---|
| T-ACO | 0.165 | 0.157 | 0.322 | 8 |
| I-ACO | 0.044 | 0.140 | 0.184 | 17 |
| I-ACO-D | 0.068 | 0.146 | 0.214 | 9 |
| I-ACO-P | 0.102 | 0.131 | 0.233 | 14 |
| Types of Algorithms | Congestion Situation Level | Number of Route Stages with Slight Busyness | Number of Route Stages with Medium Busyness | Number of Route Stages with Severe Busyness |
|---|---|---|---|---|
| T-ACO | medium congestion | 15 | 7 | 0 |
| I-ACO | unblocked situation | 16 | 2 | 0 |
| I-ACO-D | slight congestion | 18 | 3 | 0 |
| I-ACO-P | slight congestion | 16 | 4 | 0 |
| Congestion in the previous period | medium congestion | 19 | 3 | 2 |
| Types of Algorithms | Optimal MinF | Convergence Iteration Number | Number of Occurrences of the Optimal MinF | Congestion Situation Level for the Next Period | p-Value (vs. I-ACO) |
|---|---|---|---|---|---|
| T-ACO | 0.322 | 29 | 8 | medium congestion | <0.001 |
| I-ACO | 0.184 | 11 | 17 | unblocked situation | |
| I-ACO-D | 0.214 | 27 | 9 | slight congestion | <0.001 |
| I-ACO-P | 0.233 | 20 | 14 | slight congestion | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Yu, F.; Shen, D.; Peng, Y. Research on Congestion Situation Relief in Terminal Area Based on Flight Path Adjustment. Aerospace 2025, 12, 856. https://doi.org/10.3390/aerospace12100856
Ji Y, Yu F, Shen D, Peng Y. Research on Congestion Situation Relief in Terminal Area Based on Flight Path Adjustment. Aerospace. 2025; 12(10):856. https://doi.org/10.3390/aerospace12100856
Chicago/Turabian StyleJi, Yuren, Fuping Yu, Di Shen, and Yating Peng. 2025. "Research on Congestion Situation Relief in Terminal Area Based on Flight Path Adjustment" Aerospace 12, no. 10: 856. https://doi.org/10.3390/aerospace12100856
APA StyleJi, Y., Yu, F., Shen, D., & Peng, Y. (2025). Research on Congestion Situation Relief in Terminal Area Based on Flight Path Adjustment. Aerospace, 12(10), 856. https://doi.org/10.3390/aerospace12100856




