A Tether System at the L₁, L₂ Collinear Libration Points of the Mars–Phobos System: Analytical Solutions

Abstract

This paper is dedicated to identifying stable equilibrium positions of the tether systems attached to the L₁ or L₂ libration points of the Mars–Phobos system. The orbiting spacecraft deploying the tether is at the L₁ or L₂ libration point and is held at one of these unstable points by the low thrust of its engines. In this paper, the analysis is performed assuming that the tether length is constant. The equation of motion for the system in the polar reference frame is obtained. The stable equilibrium positions are found and the dependence of the tether angular oscillation period on the tether length is determined. An analytical solution in the vicinity of the stable equilibrium positions for small angles of deflection of the tether from the local vertical is obtained in Jacobi elliptic functions. The comparison of the numerical and analytical solutions for small angles of deflection is performed. The results show that the dependencies of the oscillation period on the length of the tether are fundamentally different for L₁ and L₂ points. Analytical expressions for the tether tension are derived, and the influence of system parameters on this force is investigated for static and dynamic cases.

1. Introduction

The space tether is a type of tether that is made of high-strength fiber used to connect spacecraft to each other or to other masses. The space tether systems allow us to perform missions that are impossible, impractical or unprofitable to accomplish with the help of other space equipment. For example, tether systems can be used for docking between spacecraft [1], as a space elevator [2,3,4,5,6], for payload orbital transfer [7,8], for exploring deep space [9], the atmosphere and the surface of the planets and their moons [10], as well as asteroids. For instance, Mashayekhi and Misra studied the effect of attaching a tether and ballast mass to an asteroid with subsequent cutting of the tether [11]. In recent decades, the use of space tethers near the collinear Lagrangian points has received considerable attention [12,13,14,15]. Ref. [14] focused on the development of a new mission to explore Phobos using a tether system anchored below the L₁ Mars–Phobos libration point and deployed toward Mars at a length slightly greater than the distance from Phobos. Paper [15] showed the maintenance of an L₁-type artificial equilibrium point in the Sun (Earth + Moon) circular restricted three-body problem by means of an electric solar wind sail. The tether capture system is also a promising method for removing space debris [16,17,18,19,20,21]. The topic of dynamics and control of tether systems has received substantial attention [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Huang et al. examined several new applications for the space tether during operation in orbit, focusing on the structure, dynamics and control [23]. Paper [24] discussed the diversity of tether modelling that has been undertaken recently, and showed that dynamics and control are the two fundamentally important aspects of all tether concepts, designs and mission architectures.

In 2017, NASA proposed the PHLOTE mission (Phobos L₁ Operational Tether Experiment) to explore the surface of Phobos using a tether system ‘‘anchored’’ at the L₁ libration point of the Mars–Phobos system [10]. The tether release point was proposed to be an orbiting spacecraft hovering in the vicinity of the L₁ point. Once deployed, the small vehicle with a sensor package attached to the tether was expected to investigate Phobos. This mission concept is a synthesis of new technologies that would provide a unique platform for multiple sensors directed at Phobos as well as at Mars. The PHLOTE ConOps describes the PHLOTE mission and provides a key systems engineering document to support future mission development. However, such a complex innovative mission requires an additional theoretical justification and a variety of analytical models of the system motion. The work of [37] considers a mission similar to the PHLOTE mission, where a detailed study of the behavior of the tether system attached at the L₁ collinear libration point was performed using the classical Nehvil equations.

The purpose of the present work is to find the stable equilibrium positions of the tether system attached at the L₁ or L₂ collinear libration points of the Mars–Phobos system and to study the features of the tether motion near these positions. The system consists of the tether and the end mass attached to its end. The mathematical model is based on the differential equations of the classical circular restricted three-body problem [38,39,40,41,42]. The equation of motion for the tether system of constant length under the action of two gravitational fields (Mars–Phobos) and the centrifugal force associated with the rotation of the frame of the Mars–Phobos system are obtained in polar coordinates. The first integral of this differential equation is found and used to determine the phase trajectories and the stable equilibrium positions. The approximate analytical solutions of the equation of motion for the tether system are obtained using Jacobi elliptic functions. Next, the dependence of the oscillation period on the length of the tether is found. Finally, analytical expressions for the tether tension are derived, and the influence of system parameters on this force is investigated for static and dynamic cases. The results of this work can be used for PHLOTE-like mission design. It is worth noting that the obtained solutions for small tether deflection angles are of interest for the creation of the space elevator at the L₁ and L₂ libration points of the Mars–Phobos system in the future.

2. Mathematical Model: Finding Sustainable Positions

In this section, the behavior of the tether system of constant length attached to the $L_1$ or $L_2$ libration point under the action of two massive attracting bodies, $M_1$ and $M_2$ (Mars and Phobos), is described using the differential equations of the classical circular restricted three-body problem [38,39,40,41,42]. It is assumed that the mass of the body $M$ is much less than the mass of the bodies $M_1$ and $M_2$. As a result, the body $M$ has negligible influence on other bodies. In addition, it is assumed that the eccentricity of the two bodies of the primary orbit is $e=0$ and the distance between them is

$$r=d,$$

(1)

where $d$ is the semilatus rectum. The orbiter is located at the L₁ or L₂ libration points, either of which can be the attachment point for the tether.

In the following subsections, we consider two cases characterized by different values of the tether deflection angle, namely, $\phi$ and $\psi =\phi +\pi$.

2.1. Tether Deflection Angle $\phi$

The equations of motion of the circular restricted three-body problem [42] in the polar reference frame $\left(\mathcal{l},\phi \right)$ (see Figure 1) for the constant length tether $\mathcal{l}=\mathrm{const}$ can be written as

$$\ddot{\phi }-F_i\left(\phi \right)=0,\left(i=1,2\right)$$

(2)

where

$$F_i\left(\phi \right)=-\frac{n^2\mathit{sin}\phi \hspace{0.17em}{a}_i}{\mathcal{l}}+\frac{G\mathit{sin}\phi }{\mathcal{l}}\left(\frac{m_1\left(d\mu +a_i\right)}{r_1{}^3}+\right.\left.\frac{m_2\left(d\hspace{0.17em}\left(\mu -1\right)+a_i\right)}{r_2{}^3}\right)$$

(3)

$n=\sqrt{\frac{G\left(m_1+m_2\right)}{d^3}}$ is the mean motion, $G$ is the Newtonian gravitational constant, $m_1$ and $m_2$ are masses of the bodies $M_1$ and $M_2$, respectively, $a_1\approx d\hspace{0.17em}[ 1-{\left(\frac{\mu }{3}\right)}^{\frac{1}{3}} ],\hspace{0.17em}\hspace{0.17em}{a}_2\approx d\hspace{0.17em}[ 1+{\left(\frac{\mu }{3}\right)}^{\frac{1}{3}} ]$ are the distances from the origin to the $L_1$ and $L_2$ libration points, respectively $\mu =\frac{m_2}{m_1+m_2}$ is the mass ratio,

Figure 1. Frame Oxy and the polar frame $\left(\mathcal{l},\phi \right)$.

$r_1$ is the distance between the primary 1 and the end mass,

$$r_1=\sqrt{{\left(a_i+d\hspace{0.17em}\mu +\mathcal{l}\mathit{cos}\phi \right)}^2+{\left(\mathcal{l}\mathit{sin}\phi \right)}^2}, \left(i=1,2\right),$$

(4)

$r_2$ is the distance between the primary 2 and the end mass,

$$r_2=\sqrt{{\left(a_i+d\hspace{0.17em}\left(\mu -1\right)+\mathcal{l}\mathit{cos}\phi \right)}^2+{\left(\mathcal{l}\mathit{sin}\phi \right)}^2}, \left(i=1,2\right)$$

(5)

Equation (2) has the following energy integral:

$$E=\frac{{\dot{\phi }}^2}{2}+P\left(\phi \right)=h=\mathrm{const}$$

(6)

where $E$ is the total energy. The potential energy can be written as

$$P\left(\phi \right)=-\int F_i\left(\phi \right)\hspace{0.17em}d\phi =-\frac{n^2{a}_i\mathit{cos}\phi }{\mathcal{l}}-\frac{G}{{\mathcal{l}}^2}\left(\frac{m_1}{r_1}+\frac{m_2}{r_2}\right), \left(i=1,2\right)$$

(7)

It follows from the Equations (6) and (7) that the equation of phase trajectories has the form

$$\dot{\phi }=\pm \sqrt{2\left(h-P\left(\phi \right)\right)}.$$

(8)

Figure 2 shows the potential energy (7) and the corresponding phase portrait of the system (2) for the tether length $\mathcal{l}=3000$ m and the following parameters:

$$d=9.4\cdot {10}^6 \mathrm{m}, a_1=9.38\cdot {10}^6 \mathrm{m}, a_2=9.42\cdot {10}^6 \mathrm{m}, \mu =1.67\cdot {10}^{-8}.$$

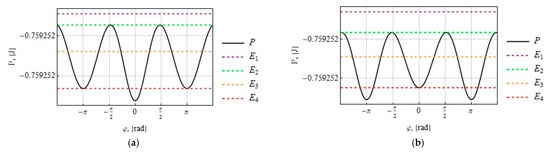
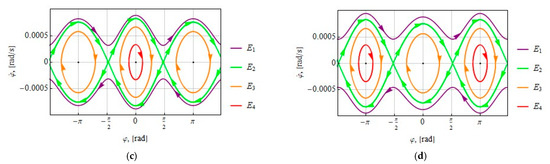
Figure 2. (a) The potential energy $P\left(\phi \right)$ for the tether system attached at the $L_1$ libration point; (b) the potential energy $P\left(\phi \right)$ for the tether system attached at the $L_2$ libration point; (c) phase trajectories $\dot{\phi }\left(\phi \right)$ corresponding to different levels of the total energy $E_j\left(j=1,\hspace{0.17em}2,\hspace{0.17em}3,\hspace{0.17em}4\right)$ for the tether system attached at the $L_1$ libration point; (d) phase trajectories $\dot{\phi }\left(\phi \right)$ corresponding to different levels of the total energy $E_j\left(j=1,\hspace{0.17em}2,\hspace{0.17em}3,\hspace{0.17em}4\right)$ for the tether system attached at the $L_2$ libration point.

The stationary positions for $\phi \in \left[-\pi ,\hspace{0.17em}\pi \right]$ can be found from the equation

$$F_i\left({\phi }_{*}\right)=0.$$

(9)

The stable equilibrium positions are ${\phi }_s=-\pi ,\hspace{0.17em}0,\pi$, and the unstable positions are ${\phi }_{us}=-\frac{\pi }{2},\hspace{0.17em}\frac{\pi }{2}$.

2.2. Tether Deflection Angle $\psi$

To consider this case, let us represent the deflection angle of the tether as

$$\psi =\phi +\hspace{0.17em}\pi .$$

(10)

The equations of motion in polar coordinates for the constant tether length are

$$\ddot{\psi }-Q_i\left(\psi \right)=0, \left(i=1,2\right)$$

(11)

where

$$Q_i\left(\psi \right)=\frac{n^2\mathit{sin}\psi \hspace{0.17em}{a}_i}{\mathcal{l}}-\frac{G\mathit{sin}\psi }{\mathcal{l}}\left(\frac{m_1\left(d\hspace{0.17em}\mu +a_i\right)}{r_1^3}+\frac{m_2\left(d\hspace{0.17em}\left(\mu -1\right)+a_i\right)}{r_2^3}\right)$$

(12)

$r_1$ is the distance between the primary 1 and the end mass,

$$r_1=\sqrt{{\left(a_i-\mathcal{l}\mathit{cos}\psi +d\hspace{0.17em}\mu \right)}^2+{\left(\mathcal{l}\mathit{sin}\psi \right)}^2},$$

(13)

$r_2$ is the distance between the primary 2 and the end mass,

$$r_2=\sqrt{{\left(a_i-\mathcal{l}\mathit{cos}\psi +d\hspace{0.17em}\left(\mu -1\right)\right)}^2+{\left(\mathcal{l}\mathit{sin}\psi \right)}^2}.$$

(14)

Equation (11) has the following energy integral:

$$E=\frac{{\left(\dot{\psi }\right)}^2}{2}+P\left(\psi \right)=h=\mathrm{const}$$

(15)

where $E$ is the total energy. The potential energy is

$$P\left(\psi \right)=-\int Q_i\left(\psi \right)\hspace{0.17em}d\psi =\frac{n^2{a}_i\mathit{cos}\psi }{\mathcal{l}}-\frac{G}{{\mathcal{l}}^2}\left(\frac{m_1}{r_1}+\frac{m_2}{r_2}\right)$$

(16)

It follows from the equations (15) and (16) that the equation of phase trajectories has the form

$$\dot{\psi }=\pm \sqrt{2\left(h-P\left(\psi \right)\right)}$$

(17)

Figure 3 depicts the potential energy (16) and the corresponding phase portrait of the system (11) for the tether length $\mathcal{l}=3000$ m and the following parameters:

$$d=9.4\cdot {10}^6 \mathrm{m}, a_1=9.38\cdot {10}^6 \mathrm{m}, a_2=9.42\cdot {10}^6 \mathrm{m}, \mu =1.67\cdot {10}^{-8}$$

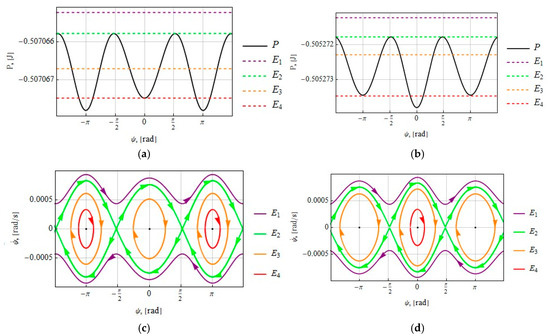
Figure 3. (a) The potential energy $P\left(\psi \right)$ for the tether system attached at the $L_1$ libration point; (b) the potential energy $P\left(\psi \right)$ for the tether system attached at the $L_2$ libration point; (c) the separatrices $\dot{\psi }\left(\psi \right)$ in the phase space corresponding to different levels of the total energy $E_j\left(j=1,\hspace{0.17em}2,\hspace{0.17em}3,\hspace{0.17em}4\right)$ for the tether system attached at the $L_1$ libration point; (d) the separatrices $\dot{\psi }\left(\psi \right)$ in the phase space corresponding to different levels of the total energy $E_j\left(j=1,\hspace{0.17em}2,\hspace{0.17em}3,\hspace{0.17em}4\right)$ for the tether system attached at the $L_2$ libration point.

Equating the generalized force (12) to zero,

$$Q_i\left({\psi }_{*}\right)=0,$$

(18)

leads to two types of stationary positions for $\psi \in \left[-\pi ,\hspace{0.17em}\pi \right]$. The stable equilibrium positions are ${\psi }_s=-\pi ,\hspace{0.17em}0,\pi$, and the unstable positions are ${\psi }_{us}=-\frac{\pi }{2},\hspace{0.17em}\frac{\pi }{2}$.

3. Approximate Analytical Solutions

In this section, the approximate analytical solutions of the equations of motion of the tether system in Jacobi elliptic functions [43] for small deflection angles are found and compared with the numerical solutions.

3.1. Tether Deflection Angle $\phi$

The following notation for the small tether deflection angle is used:

$$\phi \to \alpha .$$

(19)

Let us expand the right hand side of Equation (2), which is an odd periodic function, into a Taylor series and keep the first two terms:

$$\ddot{\alpha }=A\alpha +B{\alpha }^3,$$

(20)

where $A$ and $B$ are coefficients depending on the system parameters

$$A=-\frac{n^2{a}_i}{\mathcal{l}}+\frac{G}{\mathcal{l}}\left(\frac{m_1\left(d\hspace{0.17em}\mu +a_i\right)}{{\mathcal{l}}_1{}^3}+\frac{m_2\left(d\hspace{0.17em}\left(\mu -1\right)+a_i\right)}{{\mathcal{l}}_2{}^3}\right), \left(i=1,2\right)$$

(21)

$$B=\frac{n^2{a}_i}{6\hspace{0.17em}\mathcal{l}}+\frac{3\hspace{0.17em}G}{2\hspace{0.17em}\mathcal{l}}\left(\frac{m_1\mathcal{l}\hspace{0.17em}{\left(d\hspace{0.17em}\mu +a_i\right)}^2}{{\mathcal{l}}_1{}^5}+\frac{m_2\mathcal{l}\hspace{0.17em}{\left(d\hspace{0.17em}\left(\mu -1\right)+a_i\right)}^2}{{\mathcal{l}}_2{}^5}-\right.$$

$$\frac{1}{9}\frac{m_1\left(d\hspace{0.17em}\mu +a_i\right)}{{\mathcal{l}}_1{}^3}-\frac{1}{9}\frac{m_2\left(d\hspace{0.17em}\left(\mu -1\right)+a_i\right)}{{\mathcal{l}}_2{}^3}$$

(22)

$${\mathcal{l}}_1=\mathcal{l}+d\hspace{0.17em}\mu +a_i,{\mathcal{l}}_2=\mathcal{l}+d\hspace{0.17em}\left(\mu -1\right)+a_i$$

The phase trajectory equation for the Equation (20) in this case is

$$\dot{\alpha }=\pm \sqrt{2E_1+A{\alpha }^2+B\frac{{\alpha }^4}{2}}$$

(23)

where $E_1=-A\frac{{\alpha }_0{}^2}{2}-B\frac{{\alpha }_0{}^4}{4}=\mathrm{const}$ and is determined from the initial conditions $t=0,\dot{\alpha }=0,\alpha ={\alpha }_0$, ${\alpha }_0$ being the initial tether deflection angle measured from the x-axis. Separating variables in the Equation (23) leads to

$$\int dt=\pm \int \frac{d\alpha }{\sqrt{2E_1+A{\alpha }^2+B\frac{{\alpha }^4}{2}}}$$

(24)

The polynomial under the root of the expression (24) [$2E_1+A{\alpha }^2+B\frac{{\alpha }^4}{2}$] can be factored as

$$\frac{B}{2}\left(\alpha -c_1\right)\left(\alpha -c_2\right)\left(\alpha -c_3\right)\left(\alpha -c_4\right)$$

(25)

The roots of the polynomial (25) have the form

$$\hspace{0.17em}{c}_{1,4}=\mp \sqrt{-\frac{A-N}{B}},c_{2,3}=\mp \sqrt{-\frac{A+N}{B}}$$

(26)

where $N=\sqrt{A^2-4B{E}_1}$. The right part of expression (24) is an elliptic integral. To reduce it to the canonical form, it is necessary to calculate the modulus, which is determined by [43].

$$k=\frac{z^{\prime }-z^{″}}{z^{\prime }+z^{″}},0<k^2<1$$

(27)

where $z^{\prime }=\sqrt{c_{13}{c}_{24}},\hspace{0.17em}{z}^{″}=\sqrt{c_{12}{c}_{34}},c_{ij}=c_j-c_i$ $\left(i=1,2,3,4;j=1,2,3,4\right)$. Now the expression (24) can be reduced to the form

$$\pm \hspace{0.17em}zt=F\left(\alpha ,k\right)$$

(28)

where $z=\frac{z^{\prime }+z^{″}}{2}\sqrt{\frac{B}{2}}$, $F\left(\alpha ,k\right)$ is the elliptic integral of the first kind,

$$F\left(\alpha ,k\right)=\underset{0}{\overset{\alpha }{{\displaystyle \int }}}\frac{d\alpha }{\sqrt{\left(1-{\alpha }^2\right)\left(1-k^2{\alpha }^2\right)}}$$

(29)

Converting the elliptic integral from the expression (28) and using an elliptic sine $sn\left(u,k\right)$, we obtain the approximate analytical solution:

$$\alpha \left(t\right)={\alpha }_{0}sn\left(u,k\right)$$

(30)

where $u=zt$.

Let us compare the obtained analytical solution Equation (30) with the results of numerical integration of the initial Equation (2). Figure 4 illustrates the simulation results for $\mathcal{l}=3000$ m and the following initial conditions for the tether system attached in the $L_1$ libration point:

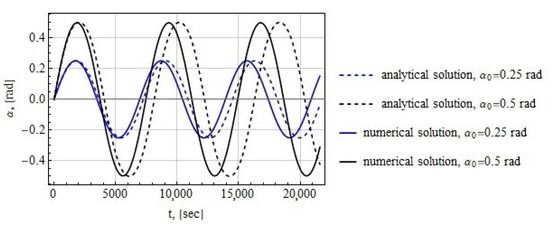
Figure 4. Time history of the tether deflection angle for the tether system attached in the $L_1$ libration point.

${\alpha }_0=0.25$ rad, $\dot{\alpha }=0.00022732$ rad/s

and

${\alpha }_0=0.5$ rad, $\dot{\alpha }=0.00043229$ rad/s.

Figure 5 shows the simulation results for $\mathcal{l}=3000$ m and the following initial conditions for the tether system attached in the $L_2$ libration point:

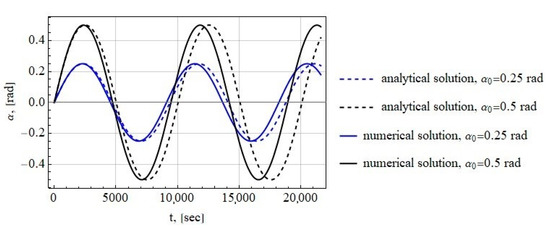
Figure 5. Time history of the tether deflection angle for the tether system attached in the $L_2$ libration point.

${\alpha }_0=0.25$ rad, $\dot{\alpha }=0.00017327$ rad/s

and

${\mathsf{\alpha }}_0=0.5$ rad, $\dot{\alpha }=0.0003377$ rad/s.

3.2. Tether Deflection Angle $\psi$

If the deflection angles are small, one can write, using Equations (10) and (19), that

$$\beta =\alpha +\pi .$$

(31)

In this case, the approximate analytical solution can be written as

$$\beta \left(t\right)={\beta }_{0}sn\left(u,k\right),$$

(32)

where ${\beta }_0$ is the initial deflection angle of the tether measured from the x-axis,

$$\begin{array}{l}u=zt,\\ k=\frac{z^{\prime }-z^{″}}{z^{\prime }+z^{″}}, 0<k^2<1,\\ z=\frac{z^{\prime }+z^{″}}{2}\sqrt{\frac{D}{2}},\\ z^{\prime }=\sqrt{c_{13}{c}_{24}},\hspace{0.17em}{z}^{″}=\sqrt{c_{12}{c}_{34}},c_{ij}=c_j-c_i,\left(i=1,2,3,4;j=1,2,3,4\right)\\ c_{1,4}=\mp \sqrt{-\frac{C-N}{D}},c_{2,3}=\mp \sqrt{-\frac{C+N}{D}},\\ N=\sqrt{C^2-4D{E}_2},\\ E_2=-C\frac{{\beta }_0{}^2}{2}-D\frac{{\beta }_0{}^4}{4}=\mathrm{const},\\ C=\frac{n^2{a}_i}{\mathcal{l}}+\frac{G}{\mathcal{l}}\left(\frac{m_1\left(d\hspace{0.17em}\mu +a_i\right)}{{\mathcal{l}}_3{}^3}-\frac{m_2\left(d\left(\mu -1\right)+a_i\right)}{{\mathcal{l}}_4{}^3}\right),\\ D=-\frac{n^2{a}_i}{6\mathcal{l}}+\frac{3\hspace{0.17em}G}{2\hspace{0.17em}\mathcal{l}}\left(\frac{1}{9}\frac{m_1\left(d\hspace{0.17em}\mu +a_i\right)}{{\mathcal{l}}_3{}^3}+\frac{m_1\mathcal{l}{\left(d\hspace{0.17em}\mu +a_i\right)}^2}{{\mathcal{l}}_3{}^5}+\right.\frac{1}{9}\left.\frac{m_2\left(d\hspace{0.17em}\left(\hspace{0.17em}\mu -1\right)+a_i\right)}{{\mathcal{l}}_4{}^3}+\frac{m_2\mathcal{l}{\left(d\hspace{0.17em}\left(\hspace{0.17em}\mu -1\right)+a_i\right)}^2}{{\mathcal{l}}_4{}^5}\right),\\ {\mathcal{l}}_3=\mathcal{l}-d\hspace{0.17em}\mu -a_i,{\mathcal{l}}_4=\mathcal{l}-d\hspace{0.17em}\left(\mu -1\right)-a_i\end{array}$$

Figure 6 shows the simulation results for $\mathcal{l}=3000$ m and the following initial conditions of the tether system attached in the $L_1$ libration point:

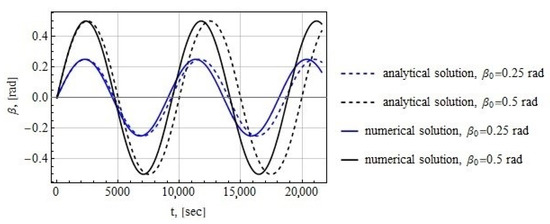
Figure 6. Time history of the tether deflection angle for the tether system attached in the $L_1$ libration point.

${\beta }_0=0.25$ rad, $\dot{\beta }=0.00017414$ rad/s

and

${\beta }_0=0.5$ rad, $\dot{\beta }=0.00033936$ rad/s.

Figure 7 shows the simulation result for $\mathcal{l}=3000$ m and the following initial conditions for the tether system attached in the $L_2$ libration point:

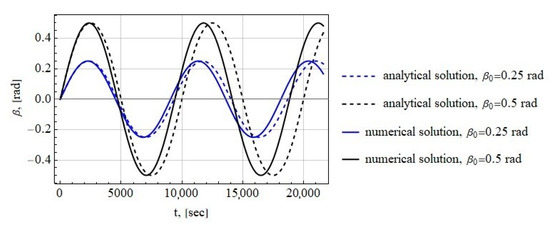
Figure 7. Time history of the tether deflection angle for the tether system attached in the $L_2$ libration point.

${\beta }_0=0.25$ rad, $\dot{\beta }=0.00022753$ rad/s

and

${\beta }_0=0.5$ rad, $\dot{\beta }=0.00043273$ rad/s.

The comparison of the numerical and analytical results shows that the approximate analytical solutions are able to accurately predict the amplitudes of tether angular oscillations, but not the frequencies. However, in the considered case, the amplitudes are much more important for the analysis of tether oscillations, so the approximate analytical solutions are quite consistent with the numerical solutions.

4. Oscillation Period of the Tether near the Stable Position

4.1. Tether Deflection Angle $\phi$

According to Equation (28) and Ref. [43], the oscillation period of Equation (30) is determined by the formula

$${\tau }_1=\frac{4K\left(k\right)}{\hspace{0.17em}z}$$

(33)

where $K\left(\frac{\pi }{2},k\right)={{\displaystyle \int }}_0^{\frac{\pi }{2}}\frac{d\alpha }{\sqrt{\left(1-k^2\sin {\alpha }^2\right)}}$ is the complete elliptic integral of the first kind,

$$\begin{array}{l}k=\frac{z^{\prime }-z^{″}}{z^{\prime }+z^{″}},0<k^2<1,\\ z=\frac{z^{\prime }+z^{″}}{2}\sqrt{\frac{B}{2}},\\ z^{\prime }=\sqrt{c_{13}{c}_{24}},\hspace{0.17em}{z}^{″}=\sqrt{c_{12}{c}_{34}},\hspace{0.17em}{c}_{ij}=c_j-c_i,\left(i=1,2,3,4;j=1,2,3,4\right)\\ \hspace{0.17em}{c}_{1,4}=\mp \sqrt{-\frac{A-N}{B}},c_{2,3}=\mp \sqrt{-\frac{A+N}{B}},\\ A=-\frac{n^2{a}_i}{\mathcal{l}}+\frac{G}{\mathcal{l}}\left(\frac{m_1\left(d\hspace{0.17em}\mu +a_i\right)}{{\mathcal{l}}_1{}^3}+\frac{m_2\left(d\hspace{0.17em}\left(\mu -1\right)+a_i\right)}{{\mathcal{l}}_2{}^3}\right),\\ B=\frac{n^2{a}_i}{6\hspace{0.17em}\mathcal{l}}+\frac{3\hspace{0.17em}G}{2\hspace{0.17em}\mathcal{l}}\left(\frac{m_1\mathcal{l}\hspace{0.17em}{\left(d\hspace{0.17em}\mu +a_i\right)}^2}{{\mathcal{l}}_1{}^5}+\frac{m_2\mathcal{l} {\left(d\hspace{0.17em}\left(\mu -1\right)+a_i\right)}^2}{\mathcal{l}{l}_2{}^5}-\right.\frac{1}{9}\frac{m_1\left(d\hspace{0.17em}\mu +a_i\right)}{{\mathcal{l}}_1{}^3}-\frac{1}{9}\frac{m_2\left(d\hspace{0.17em}\left(\mu -1\right)+a_i\right)}{{\mathcal{l}}_2{}^3},\\ N=\sqrt{A^2-4B{E}_1},\\ E_1=-A\frac{{\alpha }_0{}^2}{2}-B\frac{{\alpha }_0{}^4}{4}=\mathrm{const},\\ {\mathcal{l}}_1=\mathcal{l}+d\hspace{0.17em}\mu +a_i,{\mathcal{l}}_2=\mathcal{l}+d\hspace{0.17em}\left(\mu -1\right)+a_i\end{array}$$

Figure 8 shows the dependence of the oscillation period on the length of the tether attached at the $L_1$ and $L_2$ libration points based on analytical and numerical calculations for the initial deflection angle of the tether ${\alpha }_0=0.25$ rad.

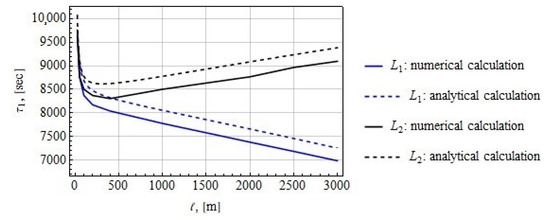
Figure 8. The oscillation periods of the tether systems attached at the $L_1$ and $L_2$ libration points.

The difference between the numerical and analytical calculations is approximately 300 s. As the tether length increases for the case when the tether system is fixed at the libration point $L_1$, the period decreases. If the tether is attached at the $L_2$ libration point, the period of oscillation of the tether decreases at $\mathcal{l}<200$ m, but begins to increase at $\mathcal{l}>200$ m. This change in the character of the dependence of the oscillation period on the tether length requires further study. For the tether length $\mathcal{l}=3000$ m, the analytical calculation gives the oscillation period of about 7000 s ≈ 1.94 h for the tether attached at the $L_1$ point and 9081 s ≈ 2.52 h for the $L_2$ point, while the orbital period of Phobos around Mars is 27,540 s ≈ 7.65 h.

4.2. Tether Deflection Angle $\psi$

According to Ref. [43], the oscillation period of Equation (32) is determined by the formula

$${\tau }_2=\frac{4K\left(k\right)}{\hspace{0.17em}z}$$

(34)

where $K\left(\frac{\pi }{2},k\right)={{\displaystyle \int }}_0^{\frac{\pi }{2}}\frac{d\beta }{\sqrt{\left(1-k^2\sin {\beta }^2\right)}}$ is the complete elliptic integral of the first kind,

$$\begin{array}{l}k=\frac{z^{\prime }-z^{″}}{z^{\prime }+z^{″}},0<k^2<1,\\ z=\frac{z^{\prime }+z^{″}}{2}\sqrt{\frac{D}{2}},\\ z^{\prime }=\sqrt{c_{13}{c}_{24}},\hspace{0.17em}{z}^{″}=\sqrt{c_{12}{c}_{34}},c_{ij}=c_j-c_i,\left(i=1,2,3,4;j=1,2,3,4\right)\\ c_{1,4}=\mp \sqrt{-\frac{C-N}{D}},c_{2,3}=\mp \sqrt{-\frac{C+N}{D}}\\ N=\sqrt{C^2-4D{E}_2},\\ E_2=-C\frac{{\beta }_0{}^2}{2}-D\frac{{\beta }_0{}^4}{4}=\mathrm{const},\\ C=\frac{n^2{a}_i}{\mathcal{l}}+\frac{G}{\mathcal{l}}\left(\frac{m_1\left(d\hspace{0.17em}\mu +a_i\right)}{{\mathcal{l}}_3{}^3}-\frac{m_2\left(d\left(\mu -1\right)+a_i\right)}{{\mathcal{l}}_4{}^3}\right),\\ D=-\frac{n^2{a}_i}{6\mathcal{l}}+\frac{3\hspace{0.17em}G}{2\hspace{0.17em}\mathcal{l}}\left(\frac{1}{9}\frac{m_1\left(d\hspace{0.17em}\mu +a_i\right)}{{\mathcal{l}}_3{}^3}+\frac{m_1\mathcal{l}{\left(d\hspace{0.17em}\mu +a_i\right)}^2}{{\mathcal{l}}_3{}^5}+\right.\frac{1}{9}\left.\frac{m_2\left(d\hspace{0.17em}\left(\hspace{0.17em}\mu -1\right)+a_i\right)}{{\mathcal{l}}_4{}^3}+\frac{m_2\mathcal{l}{\left(d\hspace{0.17em}\left(\hspace{0.17em}\mu -1\right)+a_i\right)}^2}{{\mathcal{l}}_4{}^5}\right)\\ {\mathcal{l}}_3=\mathcal{l}-d\hspace{0.17em}\mu -a_i,{\mathcal{l}}_4=\mathcal{l}-d\hspace{0.17em}\left(\mu -1\right)-a_i\end{array}$$

Figure 9 shows the dependence of the oscillation period on the length of the tether attached in the $L_1$ and $L_2$ libration points based on analytical and numerical calculations for the initial tether deflection angle ${\beta }_0=0.25$ rad.

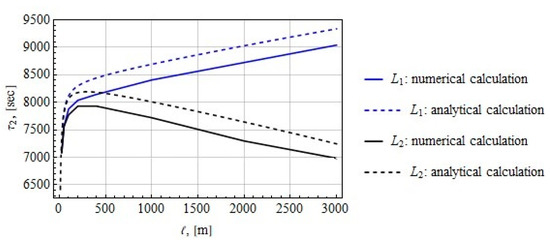
Figure 9. The oscillation periods of the tether systems attached at the $L_1$ and $L_2$ libration points.

The difference between the numerical and analytical calculations is approximately 300 s. As the tether length increases for the case when the tether system is fixed at the libration point $L_2$, the period rises. If the tether is attached at the $L_1$ libration point, the period of oscillation of the tether increases at $\mathcal{l}<200$ m, but begins to decrease at $\mathcal{l}>200$ m. At the tether length of $\mathcal{l}=3000$ m, attached in the $L_1$ or $L_2$ libration point, the oscillation period according to the analytical calculation is equal to, respectively, 6982 s ≈ 1.94 h и 9028 s ≈ 2.51 h.

5. Tether Tension Force

In this section, the equations of motion of the end mass in the polar reference frame are derived for the angle $\phi$, in order to obtain the tension of the tether. Note that the equations will be the same for the angle $\psi$. Analytical expressions for the tether tension force are given and the influence of tether system parameters on this force is investigated in both dynamic and static cases.

Consider the equations of planar motion for the end mass in the Oxy coordinate frame within the scope of the classical restricted three-body problem [42]. In the presence of tether tension, these equations can be written as

$$\ddot{x}-2n\dot{y}-n^{2}x=\frac{\partial U}{\partial x}-\frac{1}{m}{T}_x,$$

(35)

$$\ddot{y}+2n\dot{x}-n^{2}y=\frac{\partial U}{\partial y}-\frac{1}{m}{T}_y,$$

(36)

where $T=\left(T_x,T_y\right)$ is the tether tension force acting on the end mass from the tether. Position of the body $M$ relative to the origin of coordinates in the polar reference frame $\left(\mathcal{l},\phi \right)$ is defined by

$$\begin{array}{l}x=a_i+\mathcal{l}\mathit{cos}\phi , \left(i=1,2\right)\\ y=\mathcal{l}\mathit{sin}\phi .\end{array}$$

(37)

In the polar reference frame $\left(\mathcal{l},\phi \right)$, the Equations (35) and (36) can be written as

$$\ddot{\phi }+F_{\phi }=0$$

(38)

$$\ddot{\mathcal{l}}+F_{\mathcal{l}}=-\frac{1}{m}T$$

(39)

where $T=\sqrt{T_x^2+T_y^2}$ is the magnitude of the tether tension force acting on the end mass from the tether,

$$F_{\phi }=\frac{n^2\mathit{sin}\phi \hspace{0.17em}{a}_i}{\mathcal{l}}-\frac{G\mathit{sin}\phi }{\mathcal{l}}\left(\frac{m_1\left(d\mu +a_i\right)}{r_1^3}+\right.\left.\frac{m_2\left(d\hspace{0.17em}\left(\mu -1\right)+a_i\right)}{r_2^3}\right)+\frac{2\dot{\mathcal{l}}}{\mathcal{l}}\left(n+\dot{\phi }\right), \left(i=1,2\right),$$

(40)

$$F_{\mathcal{l}}=-n^2\mathit{cos}\phi \hspace{0.17em}{a}_i+G\left(\frac{m_1\left(\mathcal{l}+\mathit{cos}\phi \hspace{0.17em}\left(d\mu +a_i\right)\right)}{r_1^3}\right.+\left.\frac{m_2\left(\mathcal{l}+\mathit{cos}\phi \hspace{0.17em}\left(d\left(\mu -1\right)+a_i\right)\right)}{r_2^3}\right)-\mathcal{l}{\left(n+\dot{\phi }\right)}^2,$$

(41)

$r_1$ is the distance between the primary 1 and the end mass,

$$r_1=\sqrt{{\left(a_i+\mathcal{l}\mathit{cos}\phi +d\hspace{0.17em}\mu \right)}^2+{\left(\mathcal{l}\mathit{sin}\phi \right)}^2},$$

(42)

$r_2$ is the distance between the primary 2 and the end mass,

$$r_2=\sqrt{{\left(a_i+\mathcal{l}\mathit{cos}\phi +d\hspace{0.17em}\left(\mu -1\right)\right)}^2+{\left(\mathcal{l}\mathit{sin}\phi \right)}^2}.$$

(43)

5.1. Static Tension

The static tension of the constant length tether can be calculated using Equation (39) according to the following formula:

$$T_{st}=m\hspace{0.17em}{n}^2\left(\mathcal{l}+a_i\right)-mG\left(\frac{m_1}{{\mathcal{l}}_1{}^2}+\frac{m_2}{{\mathcal{l}}_2{}^2}\right)$$

(44)

where ${\mathcal{l}}_1=\mathcal{l}+d\hspace{0.17em}\mu +a_i,{\mathcal{l}}_2=\mathcal{l}+d\hspace{0.17em}\left(\mu -1\right)+a_i$.

Figure 10 shows that the tension force is almost proportional to the length of the tether.

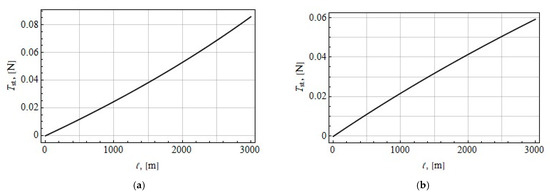
Figure 10. Tension force of the tether, as a function of its length for the end mass of 50 kg: (a) tether attached at the $L_1$ libration point; (b) tether attached at the $L_2$ libration point.

For the 50 kg end mass and the tether length of 3000 m attached in the $L_1$ libration point, Equation (44) gives the tension force of 0.086 N. When considering the $L_2$ libration point, the tension force is 0.059 N.

5.2. Dynamic Tension

The dynamic tether tension force can be found using Equations (39) and (41) as

$$\begin{array}{l}T=-m{F}_{\mathcal{l}}=\\ -m\left(-n^2\mathit{cos}\phi \hspace{0.17em}{a}_i+G\left(\frac{m_1\left(\mathcal{l}+\mathit{cos}\phi \hspace{0.17em}\left(d\mu +a_i\right)\right)}{r_1^3}+\right.\right.\left.\left.\frac{m_2\left(\mathcal{l}+\mathit{cos}\phi \hspace{0.17em}\left(d\hspace{0.17em}\left(\mu -1\right)+a_i\right)\right)}{r_2^3}\right)-\mathcal{l}{\left(n+\dot{\phi }\right)}^2\right),\end{array}$$

(45)

Figure 11 shows the tether tension force and the tether deflection angle from the gravitational vertical for the end mass of 50 kg and the tether length of 3000 m.

Figure 11. (a) Tension force for the tether attached in the $L_1$ libration point; (b) tension force for the tether attached in the $L_2$ libration point; (c) tether deflection angle for the tether attached in the $L_1$ libration point; (d) tether deflection angle for the tether attached in the $L_2$ libration point.

The graphs in Figure 11 allow us to make the following conclusions:

• The tether is stretched $(T>0)$ in all cases considered;
• The greater the amplitude of oscillation of the tether, the greater the period of oscillation.

6. Conclusions

For the tether system attached at the L₁ or L₂ collinear libration points of the Mars–Phobos system, the equations of motion for the system for the case of massless and non-extensible tether with the end mass have been obtained. The first integrals of these differential equations have been found and used to determine the phase trajectories and the stable equilibrium positions. Simplified equations for small tether deflection angles in Jacobi elliptic functions have been obtained. The oscillation period of the system has been analytically found. It has been shown that the dependencies of the oscillation period on the tether length for L₁ and L₂ points are different. The obtained approximate analytical solutions and the results of the numerical integration of the original equations of motion for small angles of deflection of the tether are in good agreement. Analytical expressions have been obtained to determine the tether tension, and it has been shown that for the end mass of 50 kg, this force is small and does not exceed 1 N both for the static and dynamic states of the tether.

The results of this study confirm the possibility of a PHLOTE-like mission and give it some theoretical justification. The prospects of using similar tether systems in the future to create a space elevator anchored at the L₁ or L₂ libration point is a good stimulus for future research, which will also focus on the consideration of an elastic tether.