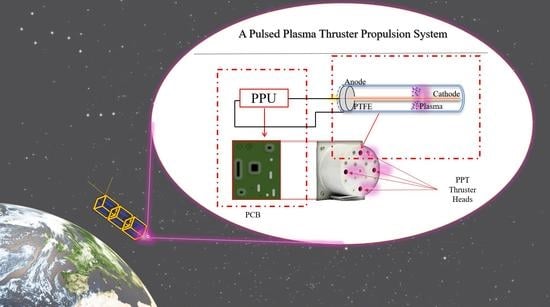
A Coaxial Pulsed Plasma Thruster Model with Efficient Flyback Converter Approaches for Small Satellites
Abstract
1. Introduction
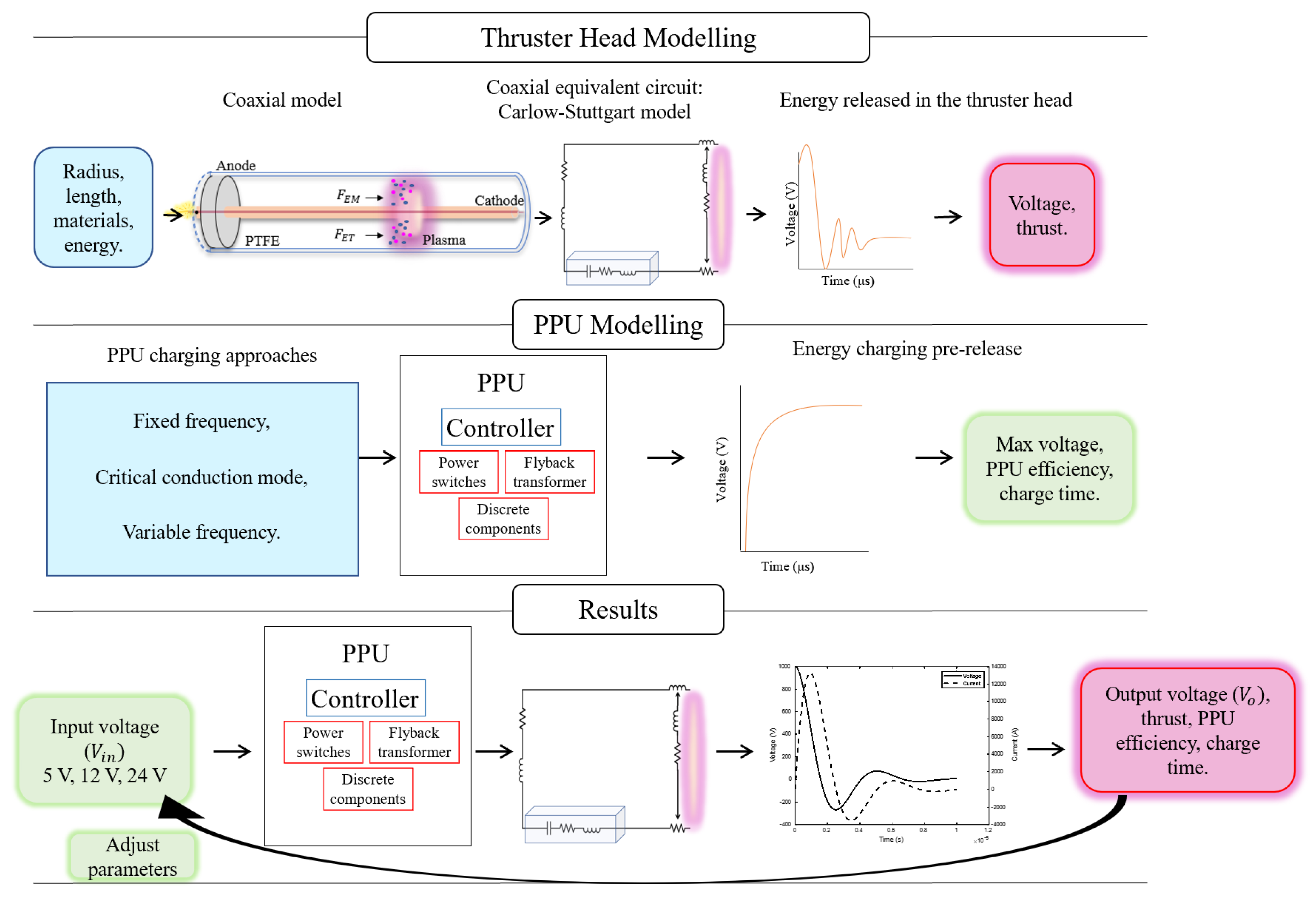
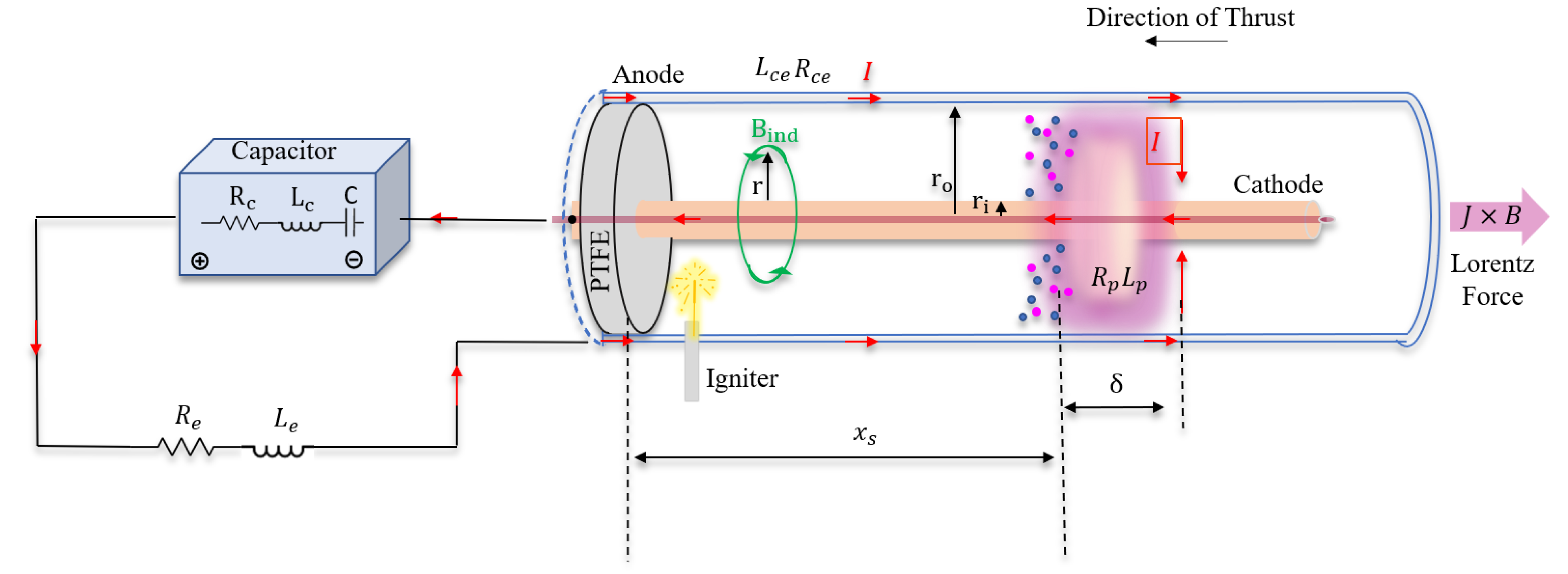
2. Thruster Head Modeling
Coaxial Equivalent Circuit: Carlow–Stuttgart Model
3. Power Processing Unit Modeling (PPU)
3.1. Fixed Frequency Discontinuous Conduction Mode (DCM) Flyback
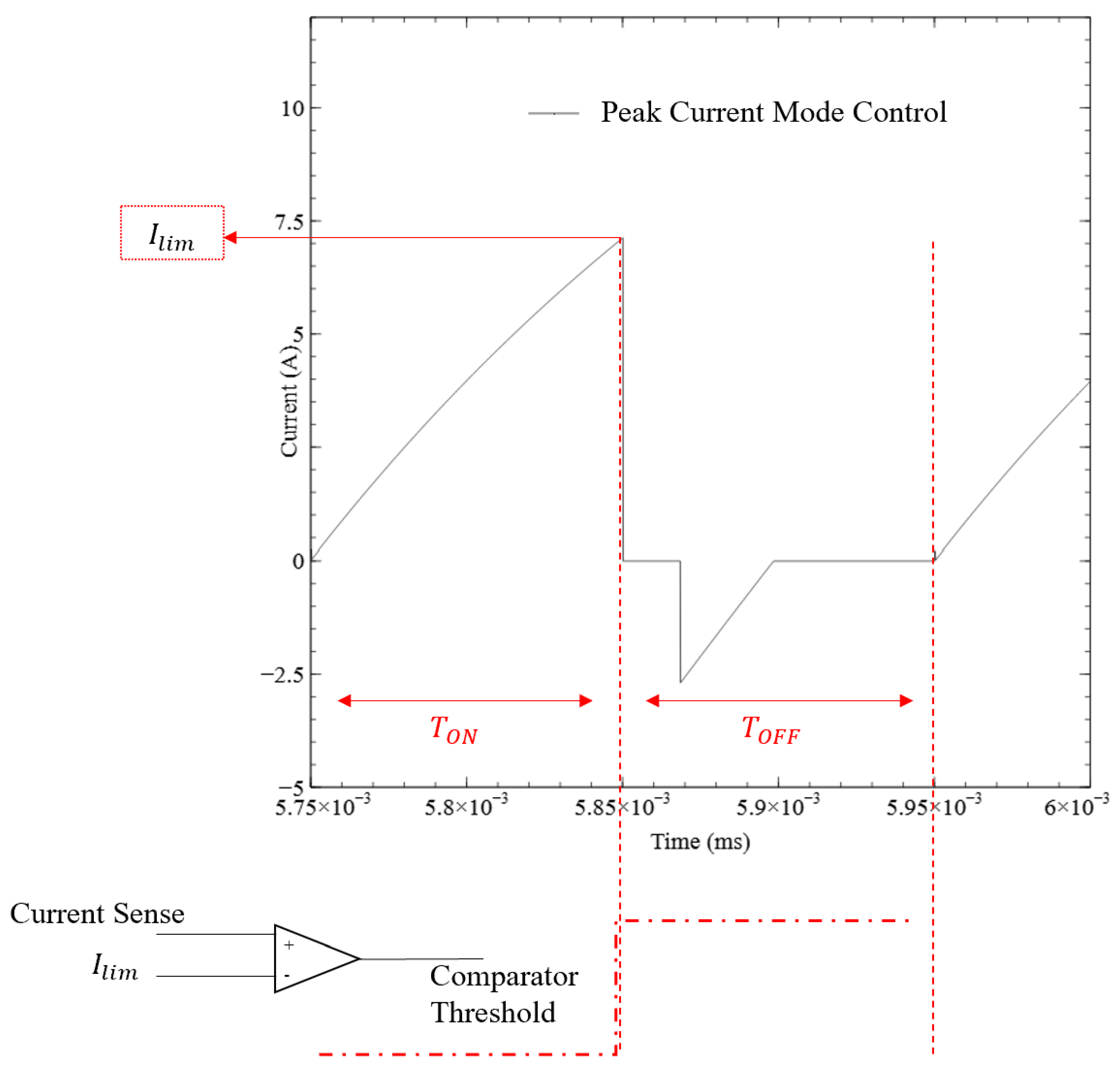
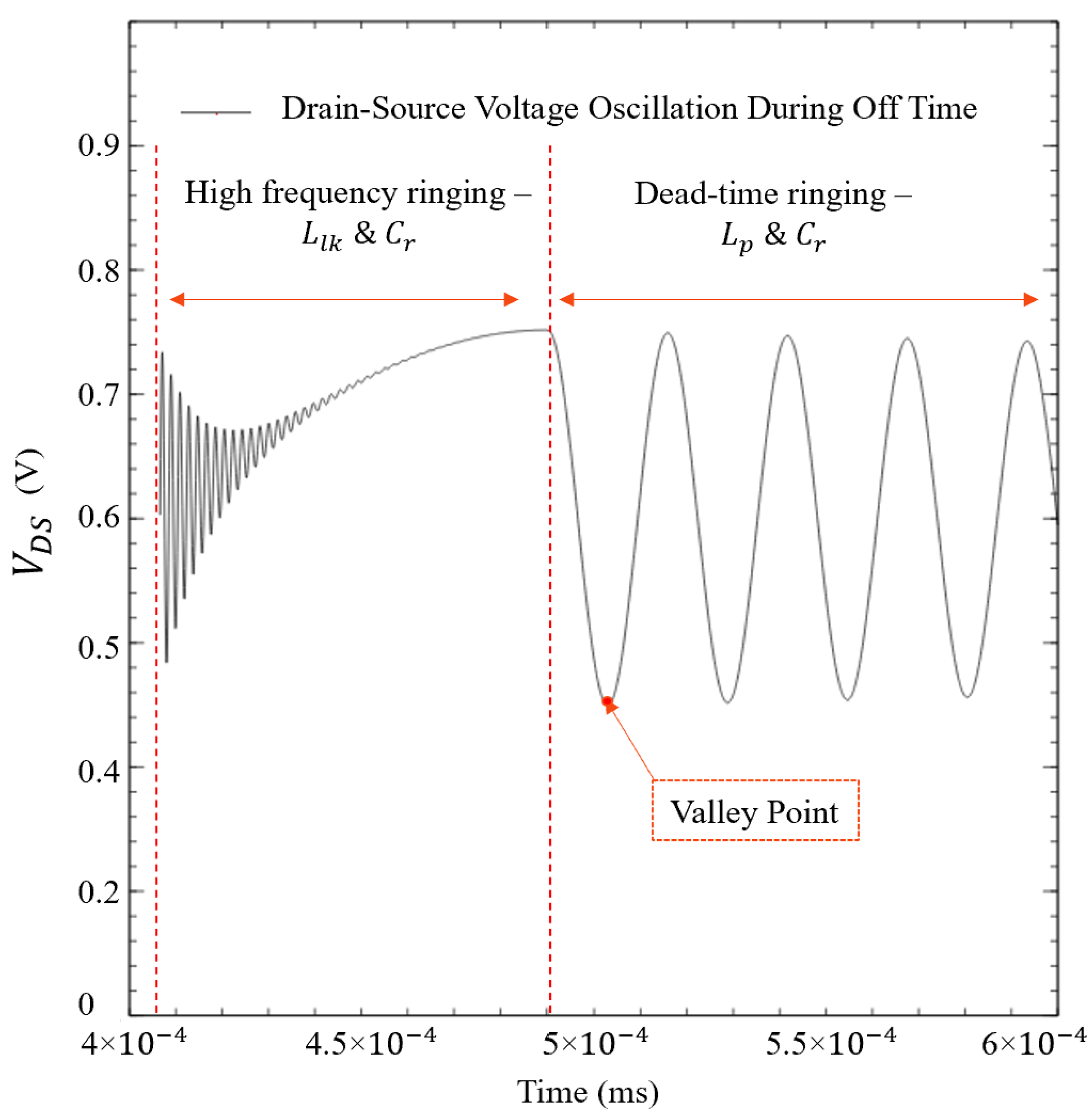
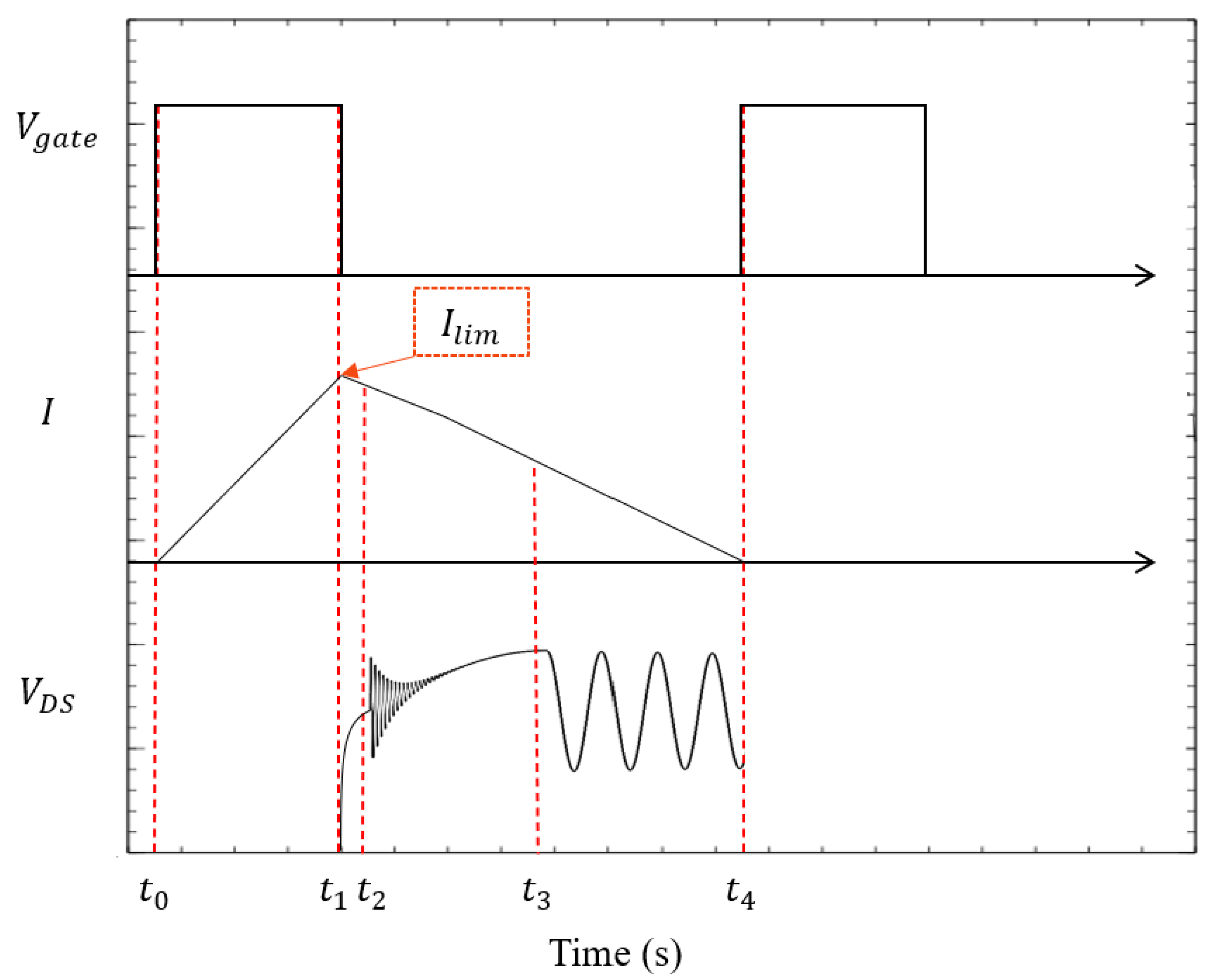
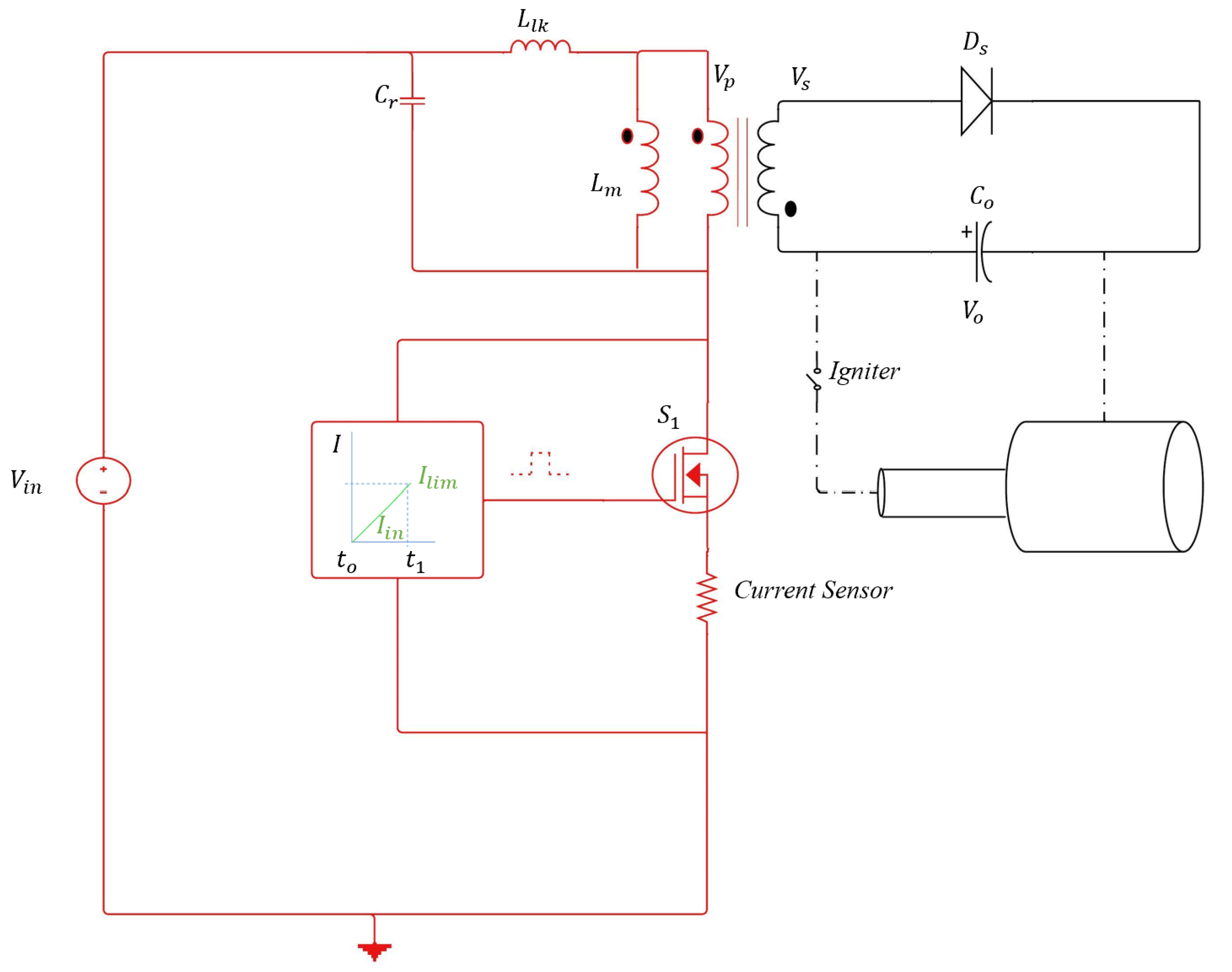
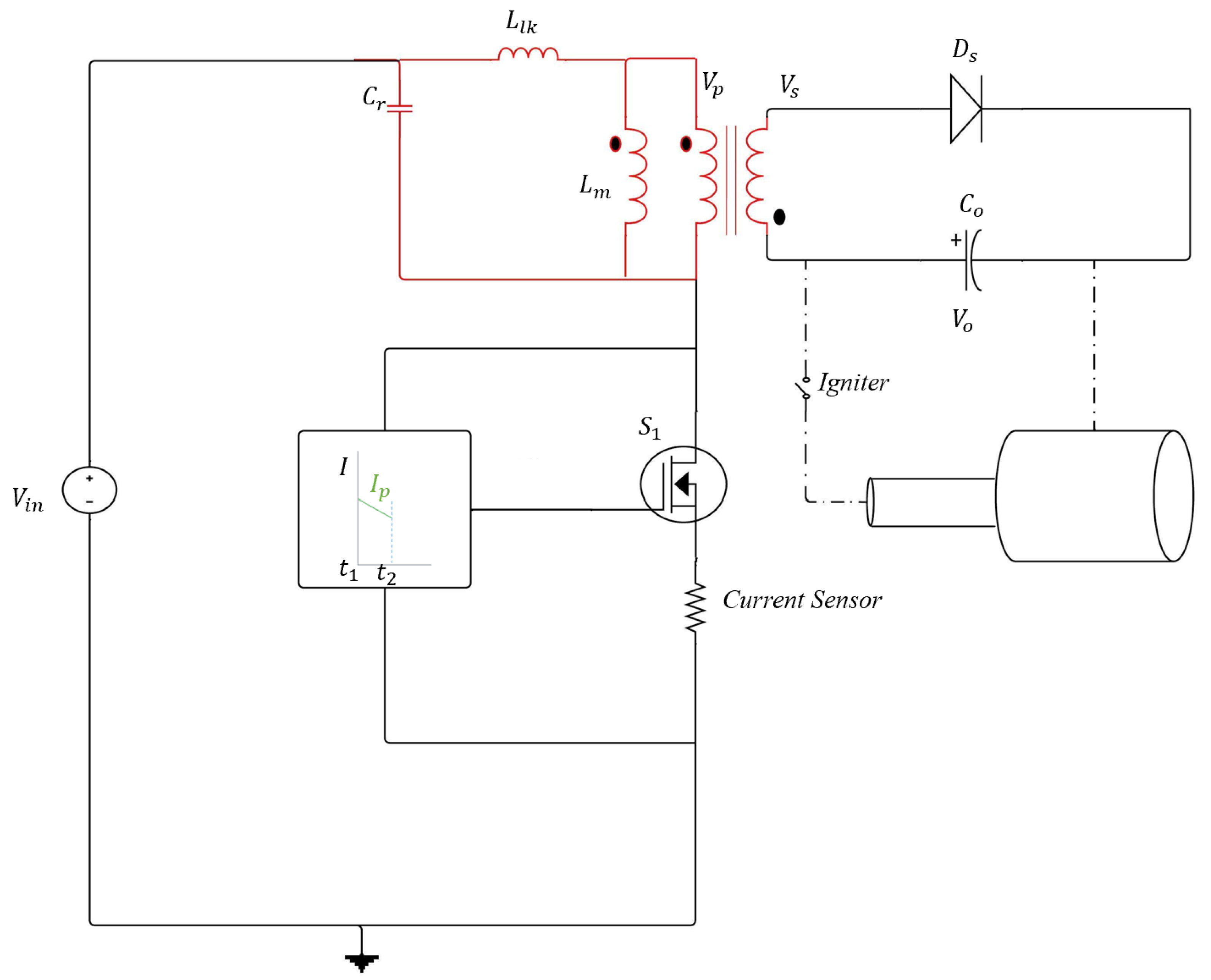
3.2. Critical Conduction Mode (CrCM) Flyback
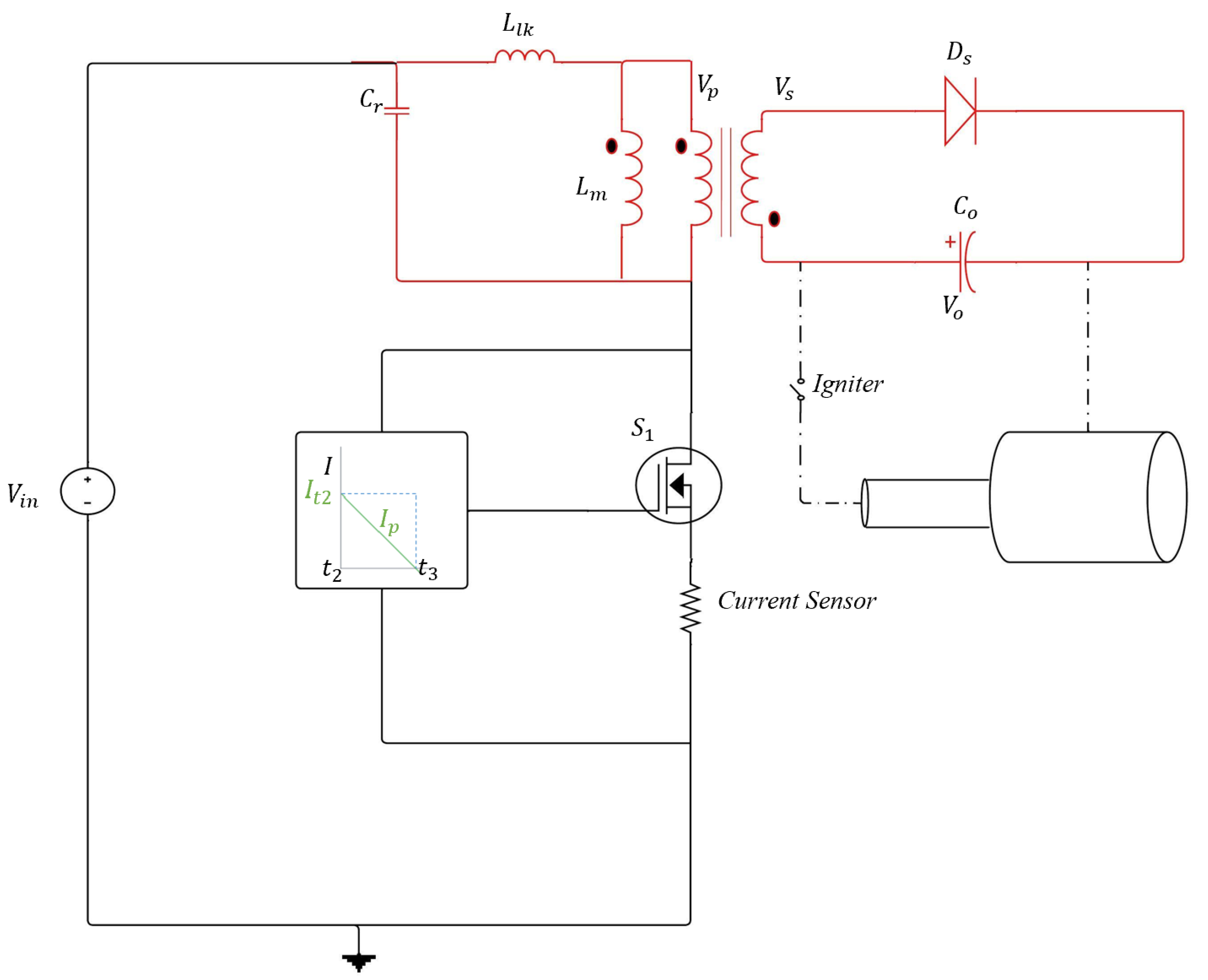
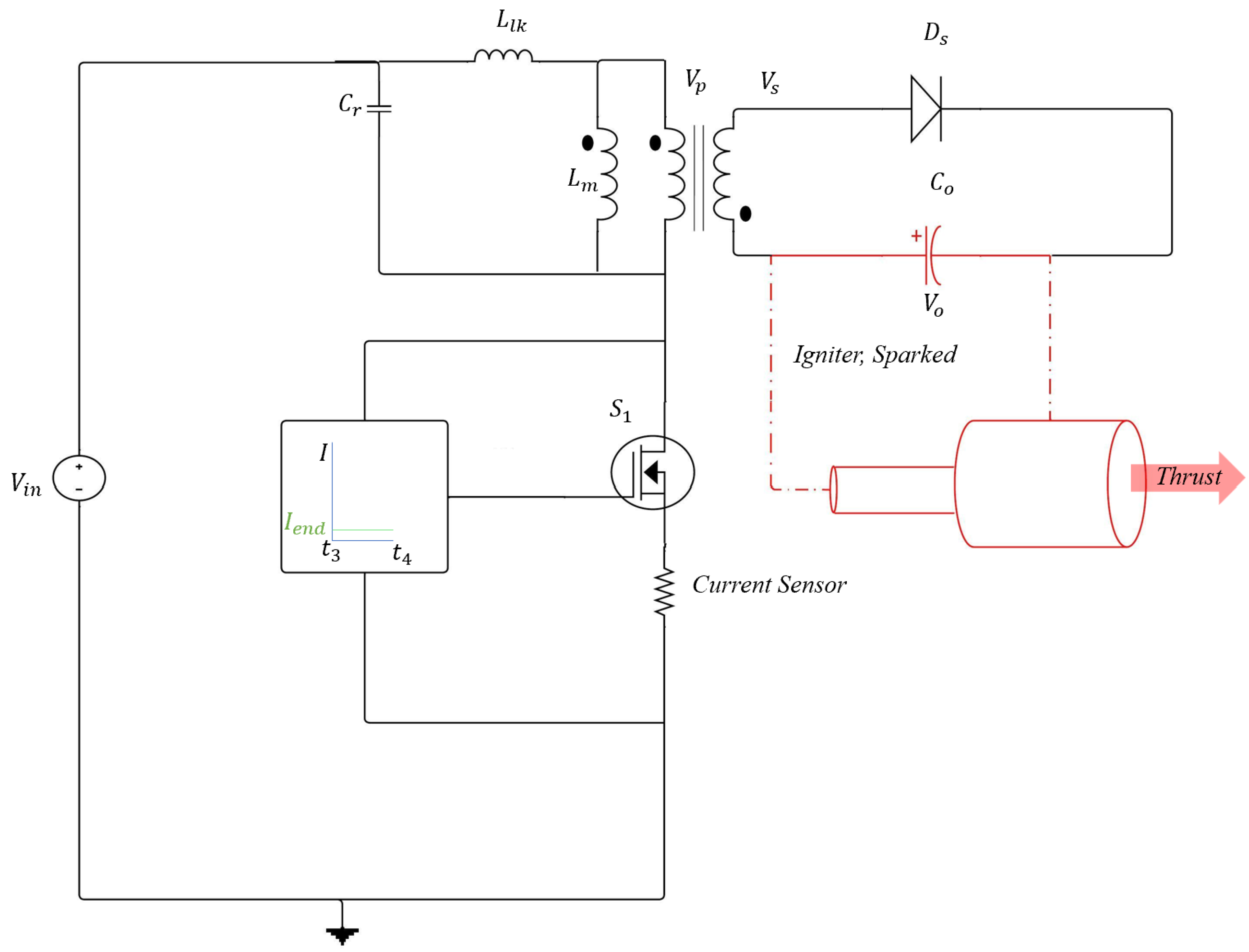
3.2.1. Mode 1 to
3.2.2. Mode 2 ( to )
3.2.3. Mode 3 ( to )
3.2.4. Mode 4 ( to )
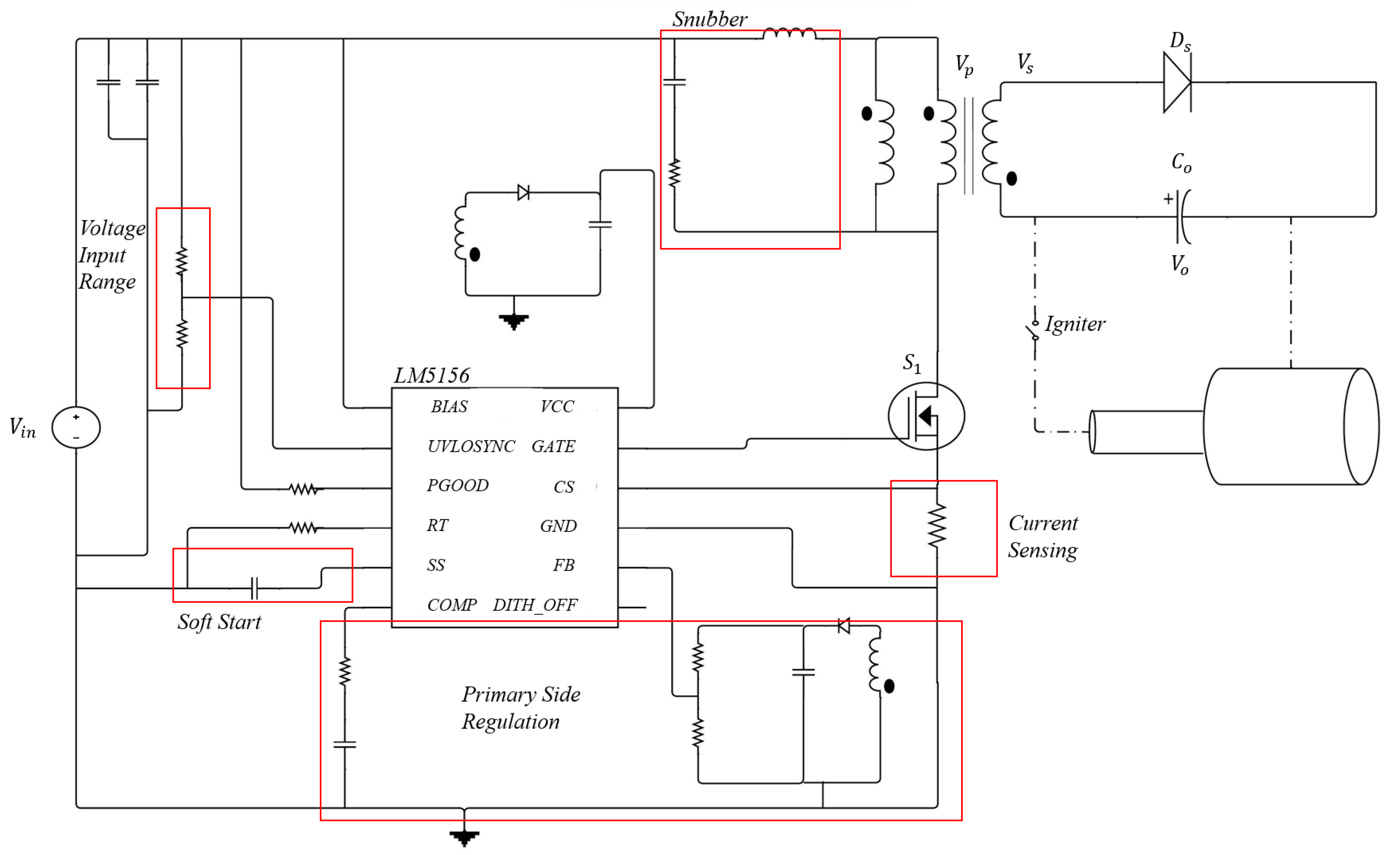
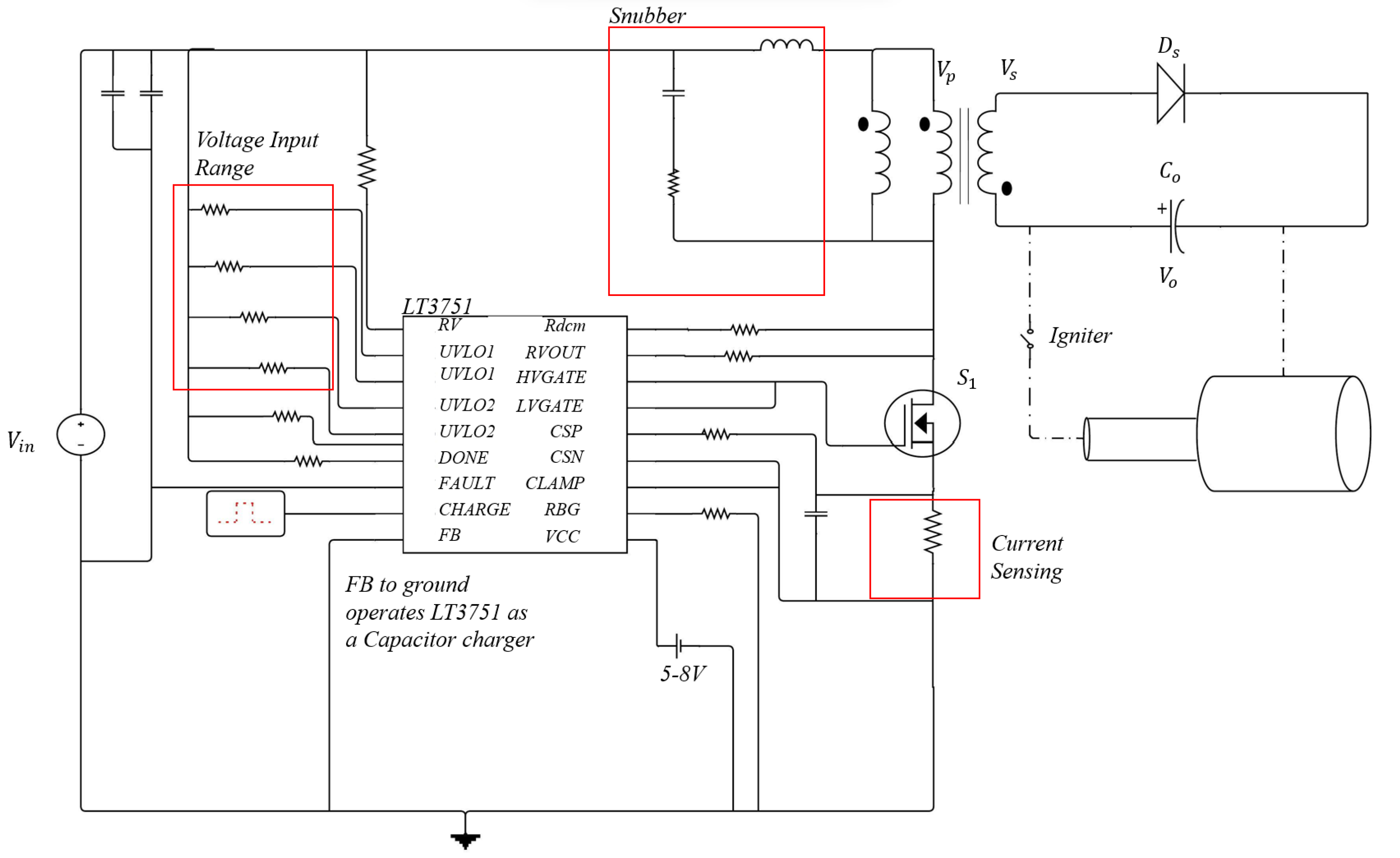
3.3. Variable Frequency DCM Flyback: COTS Solutions
4. Results
4.1. Thruster Head Modeling
4.2. PPU Modeling
5. Discussion
5.1. Thruster Head Modeling
5.2. PPU Modeling
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCM | Boundary Conduction Mode |
| BEO | Beyond Earth Orbit |
| CCM | Continuous Conduction Mode |
| COTS | Commercial Off The Shelf |
| CrCM | Critical Conduction Mode |
| CWVM | Cockroft-Walton Voltage Multiplier |
| DC | Direct Current |
| DCM | Discontinuous Conduction Mode |
| EMI | Electromagnetic Interference |
| EP | Electric Propulsion |
| ESU | Energy Storage Unit |
| FB | Feedback pin |
| FF | Fixed Frequency |
| GaN | Gallium Nitride |
| LEO | Low Earth Orbit |
| MCU | Microcontroller |
| MOSFET | Metal Oxide Semiconductor Field Effect Transistor |
| ODE | Ordinary Differential Solver |
| PCMC | Peak Current Mode Control |
| PETRUS | Pulsed Electrothermal Thruster for the University of Stuttgart |
| PPT | Pulsed Plasma Thruster |
| PPU | Power Processing Unit |
| PSR | Primary Side Regulation |
| PTFE | polytetrafluoroethylene |
| PWM | Pulse Width Modulation |
| QR | Quasi Resonant |
| RLC | Resistor, Inductor, Capacitor |
| SMPS | Switch Mode Power Supply |
| SiC | Silicon Carbide |
| TI | Texas Instruments |
| UVLO | Under-Voltage Lockout |
| VVS | Valley Voltage Switching |
| VF | Variable Frequency |
| WBG | Wide-Band Gap |
| ZVS | Zero Voltage Switching |
References
- O’Reilly, D.; Herdrich, G.; Kavanagh, D.F. Electric Propulsion Methods for Small Satellites: A Review. Aerospace 2022, 8, 22. [Google Scholar] [CrossRef]
- Krejci, D.; Lozano, P. Space Propulsion Technology for Small Spacecraft. IEEE Xplore 2018, 106, 362–376. [Google Scholar] [CrossRef]
- Lev, D.; Myers, R.M.; Lemmer, K.M.; Kolbeck, J.; Koizumi, H.; Polzin, K. The technological and commercial expansion of electric propulsion. Acta Astronaut. 2019, 159, 213–227. [Google Scholar] [CrossRef]
- Kazeev, M.N.; Kozubskiy, K.N.; Popov, G.A. Pioneer of the First Space Electric Propulsion System Development and Space Tests. In Proceedings of the International Electric Propulsion Conference, Ann Arbor, MI, USA, 20–24 September 2009. [Google Scholar]
- Arrington, A.L.; Haag, W.T.; Meckel, J.N. A Performance Comparison of Pulsed Plasma Thruster Electrode Configurations. In Proceedings of the International Electric Propulsion Conference, Cleveland, OH, USA, 24–28 August 1997. [Google Scholar]
- Hansen, J.F.; Wendt, F. History and State of the Art in Commercial Electric Ship Propulsion, Integrated Power Systems, and Future Trends. Proc. IEEE 2015, 103, 2229–2242. [Google Scholar] [CrossRef]
- Shaw, P.V. Pulsed Plasma Thrusters for Small Satellites. Ph.D. Thesis, University of Surrey, Guildford, UK, 2011. [Google Scholar]
- Chan, Y.A.; Montag, C.; Herdrich, G. Review of Thermal Pulsed Plasma Thruster—Design, Characterization, and Application. In Proceedings of the International Electric Propulsion Conference, Kobe, Japan, 4–10 July 2015. [Google Scholar]
- Burton, R.L.; Turchi, P.J. Pulsed Plasma Thruster. J. Propuls. Power 1998, 14, 716–735. [Google Scholar] [CrossRef]
- Northway, P.E.; Aubuchon, C.A.; Mellema, H.P.; Winglee, R.M.; Johnson, I.K. Pulsed Plasma Thruster Gains in Specific Thrust for CubeSat Propulsion. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017. [Google Scholar] [CrossRef]
- Alarcon, J.R.C.; Örger, N.C.; Kim, S.; Vinh, T.Q.; Seng, L.W.; Duy Vu, B.T.; Cho, M. Moon Mission Lifetime Analysis of a 2U CubeSat Equipped with Pulsed Plasma Thrusters; The Aoba-VELOX IV Mission Case. In Proceedings of the 31st International Symposium on Space Technology and Science(ISTS), Dogomachi, Japan, 24–27 October 2017; Available online: https://www.issfd.org/ISSFD_2017/paper/ISTS-2017-d-073__ISSFD-2017-073.pdf (accessed on 21 February 2023).
- Ciaralli, S.; Coletti, M.; Gabriel, S.B. Performance and lifetime testing of a pulsed plasma thruster for Cubesat applications. Aerosp. Sci. Technol. 2015, 47, 291–298. [Google Scholar] [CrossRef]
- Scharlemann, C.; Krejci, D. Analytic Model for the Assessment of the Electrode Configuration of a µPPT. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009; p. 5279. [Google Scholar]
- Shangmin, W.; Licheng, T.; Weiwei, F.; Tianping, Z.; Xinwei, C.; Changwen, C.; Xingda, L.; Jun, G.; Weidong, L. micro-PPT electro-propulsion system Development and First flight Application. In Proceedings of the 35th International Electric Propulsion Conference Georgia Institute of Technology, Atlanta, GA, USA, 8–12 October 2017; Available online: http://electricrocket.org/IEPC/IEPC_2017_179.pdf (accessed on 21 February 2023).
- Kang, B.; Low, K.S.; Soon, J.J.; Tran, Q.V. Single-Switch Quasi-Resonant DC–DC Converter for a Pulsed Plasma Thruster of Satellites. IEEE Trans. Power Electron. 2017, 32, 4503–4513. [Google Scholar] [CrossRef]
- Li, Y.H.; Royer, C. Effect of voltage on second-stage electrodes of dual-stage solid propellant pulsed plasma thruster. Vacuum 2019, 167, 103–112. [Google Scholar] [CrossRef]
- Nawaz, A.; Albertoni, R.; Auweter-Kurtz, M. Thrust efficiency optimization of the pulsed plasma thruster SIMP-LEX. Acta Astronaut. 2010, 67, 440–448. [Google Scholar] [CrossRef]
- Kim, V.; Popov, G.; Arkhipov, B.; Murashko, V.; Gorshkov, O.; Koroteyev, A.; Garkusha, V.; Semenkin, A.; Tverdokhlebov, S. Electric propulsion activity in Russia. In Proceedings of the 27th International Electric Propulsion Conference, Pasadena, CA, USA, 15–19 October 2001. [Google Scholar]
- Cassady, R.J.; Hoskins, W.A.; Campbell, M.; Rayburn, C. A micro pulsed plasma thruster (PPT) for the “Dawgstar” spacecraft. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 18–25 March 2000; Volume 4, pp. 7–14. [Google Scholar] [CrossRef]
- Vondra, R.J. The MIT Lincoln Laboratory Pulsed Plasma Thruster; Massachusetts Inst of Tech Lexington Lincoln Lab, Defense Technical Information Center: Fort Belvoir, VA, USA, 1976. [Google Scholar]
- Rezaeiha, A.; Anbarloui, M.; Farshchi, M. Design, development and operation of a laboratory pulsed plasma thruster for the first time in west Asia. Trans. Jpn. Soc. Aeronaut. Space Sci. 2011, 9, 45–50. [Google Scholar] [CrossRef]
- An, S.M.; Wu, H.J.; Feng, X.Z.; Liu, W.X. Space flight test of electric thruster system MDT-2A. J. Spacecr. Rocket. 1984, 21, 593. [Google Scholar] [CrossRef]
- Ebert, W.; Kowal, S.; Sloan, R. Operational Nova spacecraft teflon pulsed plasma thruster system. In Proceedings of the 25th Joint Propulsion Conference, Monterey, CA, USA, 10–12 July 1989; p. 2497. [Google Scholar]
- Rayburn, C.; Campbell, M.; Hoskins, W.; Cassady, R. Development of a micro pulsed plasma thruster for the Dawgstar nanosatellite. In Proceedings of the 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Las Vegas, NV, USA, 24–28 July 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar]
- Zakrzwski, C.; Benson, S.; Sanneman, P.; Hoskins, A. On-orbit testing of the EO-1 pulsed plasma thruster. In Proceedings of the 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Indianapolis, India, 7–10 July 2002; p. 3973. [Google Scholar] [CrossRef]
- Simon, D.; Land, B. Instrumentation development for micro pulsed plasma thruster experiments. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, AZ, USA, 10–13 July 2005; p. 4264. [Google Scholar] [CrossRef]
- Schönherr, T.; Komurasaki, K.; Kawashima, R.; Arakawa, Y.; Herdrich, G. Effect of Capacitance on Discharge Behavior of Pulsed Plasma Thruster. J. IAPS 2010, 18, 23–28. [Google Scholar]
- Shin, G.H.; Shin, G.S.; Nam, M.R.; Kang, K.I.; Lim, J.T. High Voltage DC-DC Converter of Pulsed Plasma Thruster for Science and Technology Satellite-2 (STSAT-2). In Proceedings of the 2005 International Conference on Power Electronics and Drives Systems, Kuala Lumpur, Malaysia, 28 November–1 December 2005; pp. 926–931. [Google Scholar] [CrossRef]
- Schäfer, F.; Montag, C.; Herdrich, G.; Laufer, R.; Santoni, F.; Piergentili, F.; Marzioli, P.; Amadio, D.; Frezza, L.; Dannenmayer, K.; et al. Flight results of the PETRUS pulsed plasma thruster on the 3u CubeSat GreenCube. In Proceedings of the 73rd International Astronautical Congress (IAC), Paris, France, 18–22 September 2022. [Google Scholar]
- Montag, C.; Herdrich, G.; Gonzalez Del Amo, J.; Bauer, P.; Feyhl, D. PETRUS 2.0 PPT and its CubeSat-size PPU: Testing and Characterization. In Proceedings of the International Electric Propulsion Conference, Vienna, Austria, 15–20 September 2019. [Google Scholar]
- Patel, A.; Frederick, R.A. Overview of Small Satellite Micro-Propulsion Devices, Ground Test Capabilities, and Performance Measurement Techniques. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017; p. 4886. [Google Scholar] [CrossRef]
- Uezu, J.; Iio, J.; Kamishima, Y.; Takegahara, H.; Wakizono, T.; Sugiki, M. Study on pulsed plasma thruster configuration to expand impulse bit range. In Proceedings of the 29th International Electric Propulsion Conference, Princeton, NJ, USA, 31 October–4 November 2005; Volume 234, pp. 1–12. [Google Scholar]
- Jahn, R.G. Physics of Electric Propulsion, 1st ed.; McGraw-Hill Inc.: New York, NY, USA, 1968; Chapter 9. [Google Scholar]
- Burton, R.; Wilson, M.; Bushman, S. Energy balance and efficiency of the pulsed plasma thruster. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998; p. 3808. [Google Scholar]
- Texas Instruments. TMS320F28004x Real-Time Microcontrollers Datasheet; Version January 2023; SPRS945G; Texas Instruments: Dallas, TX, USA, 2023. [Google Scholar]
- Texas Instruments. LM5156x 2.2-MHz Wide VIN 65-V Non-Synchronous Boost/SEPIC/Flyback Controller with Dual Random Spread Spectrum; Version January 2021; SNVSBI6; Texas Instruments: Dallas, TX, USA, 2021. [Google Scholar]
- Linear Technologies Inc. High Voltage Capacitor Charger Controller with Regulation Datasheet; Version REV D 2017; LT 1217; Linear Technologies Inc.: Milpitas, CA, USA, 2017. [Google Scholar]
- Guman, W.J.; Peko, P.E. Solid-propellant pulsed plasma microthruster studies. J. Spacecr. Rocket. 1968, 5, 732–733. [Google Scholar] [CrossRef]
- Laperriere, D. Electromechanical Modelling and Open-Loop Control of Parallel-Plate Pulsed Plasma Microthrusters with Applied Magnetic Fields. Worcester Polytechnic Institute. 2005. Available online: https://digital.wpi.edu/concern/etds/n870zq908?locale=en (accessed on 2 February 2023).
- Coletti, M.; Guarducci, F.; Gabriel, S.B. A micro PPT for Cubesat application: Design and preliminary experimental results. Acta Astronaut. 2011, 69, 200–208. [Google Scholar] [CrossRef]
- Shaw, P.V.; Lappas, V.J. Mathematical Modelling of High Efficiency Pulsed Plasma Thrusters for Microsatellites. In Proceedings of the American Institute of Aeronautics and Astronautics 57th International Astronautical Congress, Valencia, Spain, 2–6 October 2006. [Google Scholar]
- Krejci, D.; Seifert, B.; Scharlemann, C. Endurance testing of a pulsed plasma thruster for nanosatellites. Acta Astronaut. 2013, 91, 187–193. [Google Scholar] [CrossRef]
- Ciaralli, S.; Coletti, M.; Gabriel, S.B. Results of the qualification test campaign of a Pulsed Plasma Thruster for Cubesat Propulsion (PPTCUP). Acta Astronaut. 2016, 121, 314–322. [Google Scholar] [CrossRef]
- Li, H.; Wu, Z.; Sun, G.; Zhu, K.; Huang, T.; Liu, X.; Yeong, W.; Ling, L.; Wang, N. A model for macro-performances applied to low power coaxial pulsed plasma thrusters. Acta Astronaut. 2020, 170, 154–162. [Google Scholar] [CrossRef]
- Ziemer, J.K.; Choueiri, E.Y.; Birx, D. Comparing the performance of co-axial and parallel-plate gas-fed PPTs. In Proceedings of the 26th International Electric Propulsion Conference, Kitakyushu, Japan, 17–21 October 1999; IEPC 99-209. Available online: https://alfven.princeton.edu/publications/pdf/ziemer-iepc-1999-209.pdf (accessed on 22 December 2022).
- Montag, C.; Burghaus, H.; Herdrich, G.; Schönherr, T. Development of a New Pulsed Plasma Thruster and a Brief Introduction of a Planned Test Facility. In Proceedings of the 67th International Astronautical Congress-IAC-16-C4.4.13.x35105, Guadalajara, Mexico, 26–30 September 2016. [Google Scholar]
- Senan, N.A.F. A Brief Introduction to Using ode45 in MATLAB; University of California at Berkeley: Berkeley, CA, USA, 2007. [Google Scholar]
- Kang, B.; Low, K.S.; Ng, K.J. Capacitor Charging by Quasi-Resonant Approach for a Pulsed Plasma Thruster in Nano-Satellite. IEEE Trans. Plasma Sci. 2020, 48, 1271–1278. [Google Scholar] [CrossRef]
- Tseng, K.C.; Chen, J.Z.; Lin, J.T.; Huang, C.C.; Yen, T.H. High step-up interleaved forward-flyback boost converter with three-winding coupled inductors. IEEE Trans. Power Electron. 2014, 30, 4696–4703. [Google Scholar] [CrossRef]
- Hwu, K.I.; Jiang, W.Z. Isolated step-up converter based on flyback converter and charge pumps. IET Power Electron. 2014, 7, 2250–2257. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Li, Y.H.; Palagiri, S.; Chang, P.; Montag, C.; Herdrich, G. Plasma Behavior in a Solid-Fed Pulsed Plasma Thruster. J. Aeronaut. Astronaut. Aviat. 2019, 51, 31–42. [Google Scholar] [CrossRef]
- Keidar, M.; Boyd, I.D.; Antonsen, E.; Spanjers, G.G. Electromagnetic Effects in the Near Field Plume Exhaust of a Micro-Pulsed-Plasma Thruster. J. Propuls. Power 2004, 20, 961–969. [Google Scholar] [CrossRef]
- Promislow, C.; Little, J. Operation and Performance of a Power Processing Unit for Inductive Pulsed Plasma Thrusters Operating at High Repetition Rates. IEEE Trans. Plasma Sci. 2022, 50, 3065–3076. [Google Scholar] [CrossRef]
- Baddipadiga, B.P.; Strathman, S.; Ferdowsi, M.; Kimball, J.W. A High-Voltage-Gain DC-DC Converter for Powering a Multi-mode Monopropellant-Electrospray Propulsion System in Satellites. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1561–1565. [Google Scholar] [CrossRef]
- Quentin, N.; Perrin, R.; Martin, C.; Joubert, C.; Grimaud, L.; Burgos, R.; Boroyevich, D. A Large Input Voltage Range 1 MHz Full Converter with 95% Peak Efficiency for Aircraft Applications. In Proceedings of the PCIM Europe 2016, International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 10–12 May 2016; pp. 1–8. [Google Scholar]


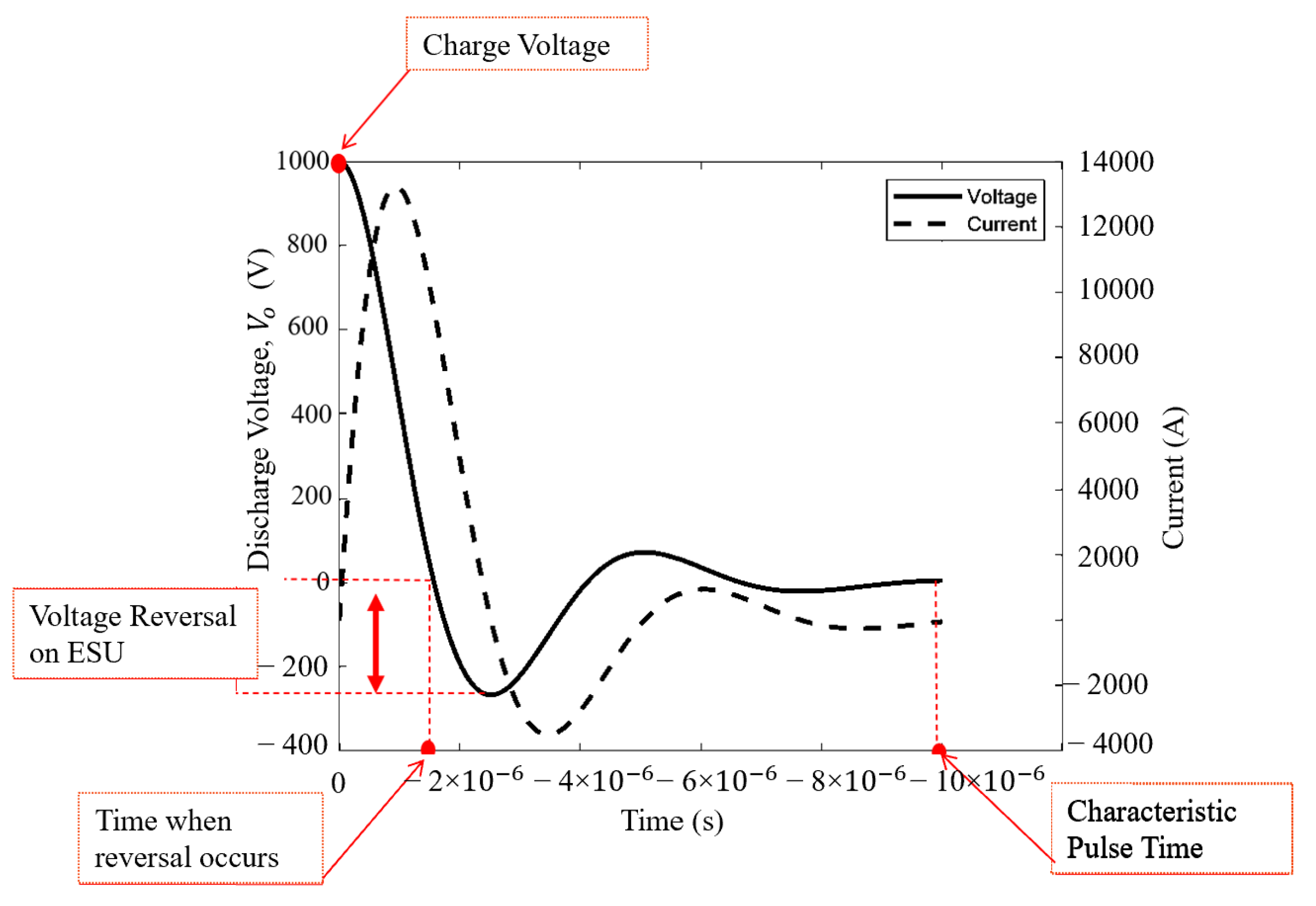
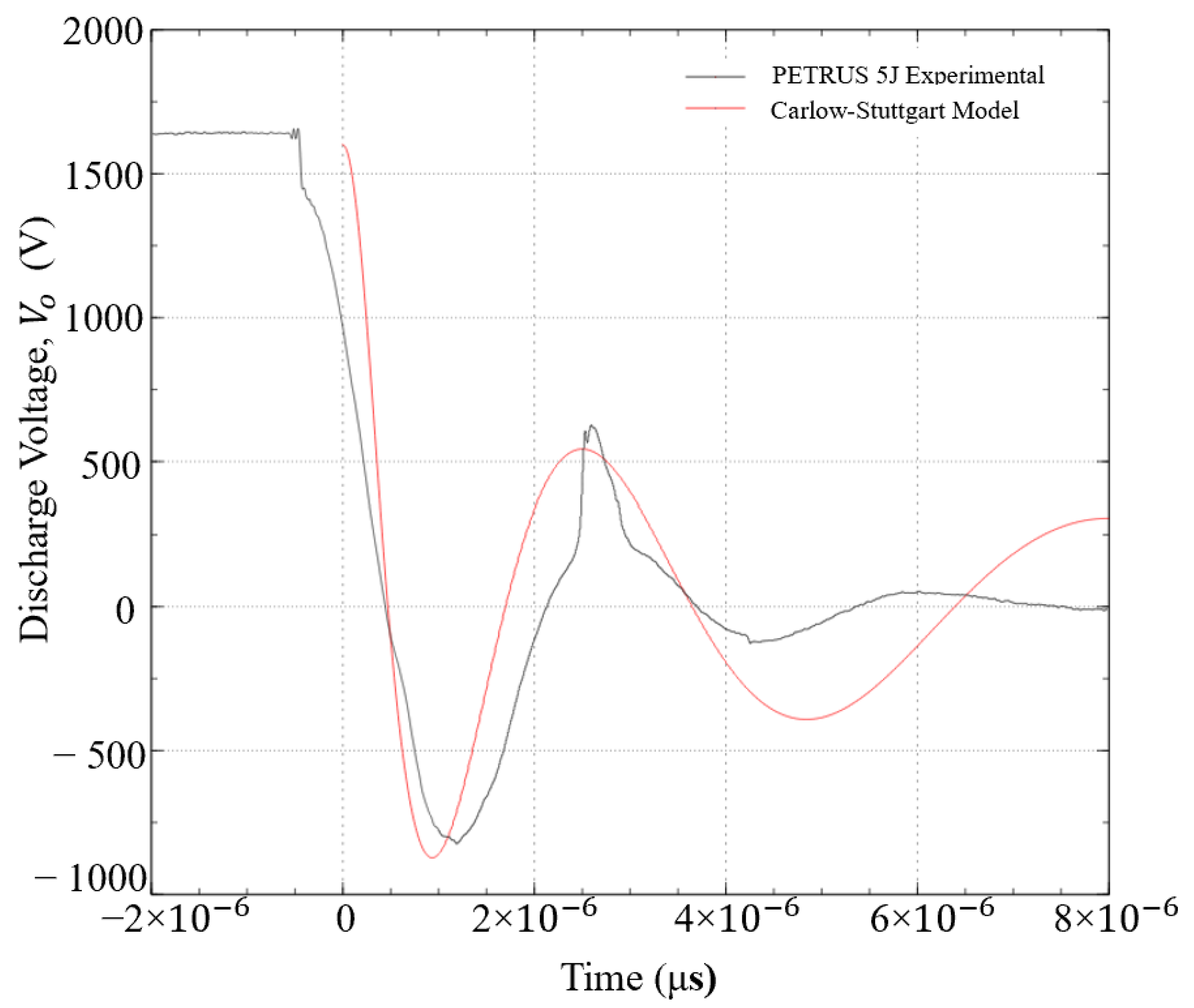

| PPT | ESU, J | Isp, s | Thrust Efficiency % |
|---|---|---|---|
| Add Simplex [17] | 68 | 2700 | 30 |
| Busek MPACS [1] | 2.25 | 827 | 8.4 |
| Zond 2 [4,18] | 50 | 410 | 8 |
| LES-6 [19] | 1.85 | 300 | 2 |
| SMS [19] | 8.4 | 450 | 3.7 |
| LES 8/9 [19] | 20 | 1000 | 7.4 |
| MIT Lab [20] | 20 | 600 | 6.6 |
| Japan Lab [21] | 30.4 | 423 | 3.2 |
| MDT-2A [22] | 4 | 280 | 2 |
| NOVA-1 [23] | 20 | 540 | 5.3 |
| Millipound [20] | 750 | 1210 | 17 |
| Primex NASA Breadboard [24] | 20 | 1136 | 9.8 |
| Mighty-Sat [19] | 40 | 1150 | 9.8 |
| EO-1 min [25] | 8.5 | 678 | 7.6 |
| Micro APPT-Series [26] | 3.8–8.4 | 1140–1800 | 14–40 |
| SIMP-LEX [27] | 68 | 1800 | 12 |
| STSAT-2 [28] | 4.2 | 800 | 2.3 |
| VELOX-3 [11] | 2.25 | 700–1500 | 8 |
| PETRUS 1J [29] | 1 | 724 | 7.8 |
| PETRUS 5J [30] | 5 | 852 | 8.9 |
| IL-PPT-3 Lab [31] | 7.5 | 600 | 5 |
| Dawgstar [19] | 5.23 | 483 | 9 |
| PPT-B20 [32] | 3.38 | 960 | 7.9 |
| Clyde Space [12] | 2 | 590 | 5 |
| UW [10] | 18.1 | 1200 | 22.5 |
| Parameter | Requirement |
|---|---|
| Input Voltage, | 5–24 |
| Output Power, W | ≤20 |
| Max Switching Frequency | Variable |
| Output Voltage, | 1–1.6 kV |
| Cost | Low |
| PPU Efficiency | >70% |
| Size | Small (PC104) |
| EMI Compatibility | Space Grade |
| Safety Requirements | High Voltage |
| Charge Time (upper limit) | <1 s |
| Variable | Value |
|---|---|
| Initial Voltage | 1600 |
| Capacitance, μF | 1–6 |
| Ablation mass, µg | 9.5 |
| Ion Plasma Density, m−3 | |
| Plasma Temperature, eV | 2 |
| Inner Radius, mm | 3 |
| Outer Radius, mm | 12 |
| Length, mm | 50 |
| Pulse time, μs | 2 |
| Circuit Inductance, nH | 130 |
| Circuit Resistance, mΩ | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Reilly, D.; Herdrich, G.; Schäfer, F.; Montag, C.; Worden, S.P.; Meaney, P.; Kavanagh, D.F. A Coaxial Pulsed Plasma Thruster Model with Efficient Flyback Converter Approaches for Small Satellites. Aerospace 2023, 10, 540. https://doi.org/10.3390/aerospace10060540
O’Reilly D, Herdrich G, Schäfer F, Montag C, Worden SP, Meaney P, Kavanagh DF. A Coaxial Pulsed Plasma Thruster Model with Efficient Flyback Converter Approaches for Small Satellites. Aerospace. 2023; 10(6):540. https://doi.org/10.3390/aerospace10060540
Chicago/Turabian StyleO’Reilly, Dillon, Georg Herdrich, Felix Schäfer, Christoph Montag, Simon P. Worden, Peter Meaney, and Darren F. Kavanagh. 2023. "A Coaxial Pulsed Plasma Thruster Model with Efficient Flyback Converter Approaches for Small Satellites" Aerospace 10, no. 6: 540. https://doi.org/10.3390/aerospace10060540
APA StyleO’Reilly, D., Herdrich, G., Schäfer, F., Montag, C., Worden, S. P., Meaney, P., & Kavanagh, D. F. (2023). A Coaxial Pulsed Plasma Thruster Model with Efficient Flyback Converter Approaches for Small Satellites. Aerospace, 10(6), 540. https://doi.org/10.3390/aerospace10060540