Abstract
We find a zero in the positronium formation scattering amplitude and a deep minimum in the logarithm of the corresponding differential cross section for positron–helium collisions for an energy just above the positronium formation threshold. Corresponding to the zero, there is a vortex in the extended velocity field that is associated with this amplitude when one treats both the magnitude of the momentum of the incident positron and the angle of the scattered positronium as independent variables. Using the complex Kohn variational method, we determine accurately two-channel K-matrices for positron–helium collisions in the Ore gap. We fit these K-matrices using both polynomials and the Watanabe and Greene’s multichannel effective range theory taking into account explicitly the polarization potential in the Ps-He+ channel. Using the fitted K-matrices we determine the extended velocity field and show that it rotates anticlockwise around the zero in the positronium formation scattering amplitude. We find that there is a valley in the logarithm of the positronium formation differential cross section that includes the deep minimum and also a minimum in the forward direction.
1. Introduction
Positronium (Ps) formation, a rearrangement process for positron collisions, is of interest in both theoretical and experimental studies [1,2,3,4,5,6]. Recently, we obtained two zeros in the Ps-formation scattering amplitude, , for positron–hydrogen collisions in the Ore gap [7]. We used the Kohn and inverse Kohn variational methods to compute the two-channel K-matrices, and from these we computed , the Ps-formation differential cross section (DCS) and the extended velocity field that is associated with . (The extended velocity field is defined in reference [7].) Corresponding to the zeros in , there are deep minima in the logarithm of the Ps-formation DCS and vortices in that are associated with [7].
Positron–helium collisions are more accessible experimentally than positron–hydrogen collisions. The absolute near-forward direction Ps-formation DCS has recently been measured for positron collisions from helium for an incident positron energy of 24.7 eV to 138 eV [4,6]. In this paper, we report a zero in for positron–helium collisions just above the Ps-formation threshold, a corresponding deep minimum in the logarithm of the Ps-formation DCS, a vortex in that is associated with , and also a minimum in the forward direction Ps-formation DCS [8,9]. We use the complex Kohn variational method to compute two-channel K-matrices for s-, p-, d- and f-wave positron–helium collisions in the Ore gap for a fine grid in k, where k is the magnitude of the momentum of the incoming positron . We optimize the non-linear parameters in the short-range part of the trial wave function in the vicinity of the zero in to obtain accurate K-matrices in this region. For positron–helium collisions the Ore gap is the energy range from the onset of Ps(1s)-formation to the threshold for the excitation of He(). This corresponds to the energy range of the incoming positron of eV to 20.62 eV, or the k range of 1.143 a.u. to 1.231 a.u. [10,11,12]. It also corresponds to a range of 0 a.u. to 0.65 a.u., where is the magnitude of the momentum of the outgoing Ps, . In our calculations, we neglect positron annihilation [13,14].
We fit the complex Kohn K-matrices using polynomials and using the Watanabe and Greene’s multichannel effective range theory (WG MERT) [15], explicitly taking into account the polarization potential in the Ps-He+ channel [8,9]. The polarizability of Ps is significant, 36 a.u., and its effective polarizability in the Ps-He+ channel is 72 a.u. [16]. The WG MERT has previously been applied for positron collisions from hydrogen [16,17,18] and from helium [16,18]. An advantage of fitting the K-matrices is that we can determine that is associated with [7] without having to compute the complex Kohn K-matrices over a fine grid in two components of the momentum of the outgoing Ps, .
For positron–helium collisions, we locate the position of a zero in and thus the position of a deep minimum in the logarithm of the Ps-formation DCS. We determine the Ps-formation DCS as a function of k and , where is the angle of the outgoing Ps with respect to the z-axis, which is taken to be parallel to the momentum of the incident positron . Due to the experimental interest of the near-forward direction Ps-formation DCS for positron–helium collisions [4,5,6], we also compute this cross section using the complex Kohn K-matrices and using different fits for the K-matrices. In the near-forward direction, the Ps-formation DCS for positron collisions from Ne, Ar, Kr and Xe has recently been measured and a dip at a low energy is present in this cross section for each of these target atoms [5]. Fayer et al. [5] raised the question of whether the low-energy features that they obtained for the Ps-formation DCS near 0° are related to quantum vortices. Interestingly, we find that there is a valley in the logarithm of the Ps-formation DCS for positron–helium collisions that contains a minimum in the forward direction and a deep minimum that is connected to a vortex in . We note that a minimum is not seen in the measurements by Shipman et al. of the near-forward direction Ps-formation DCS for positron–helium collisions in the energy range of the experiment, which is above the Ore gap [4,6].
Previously, Van Reeth and Humberston [19] applied the Kohn, inverse Kohn and complex Kohn variational methods for positron–helium collisions to compute accurate K-matrices and cross sections below the He() excitation threshold. They showed the Ps-formation angular distribution as a function of the angle of the outgoing Ps for three different incident energies of Ps. The paper by Shipman et al. [4] shows experimental data of the Ps-formation DCS for positron–helium collisions as a function of with results from theoretical calculations for the forward direction, including those from using the (inverse) Kohn variational method. The Ps-formation DCS for positron–helium collisions in the Ore gap, computed using the (inverse) Kohn variational method, rises steeply from the Ps-formation threshold [4]. Drachman et al. [20] mentioned that minima may be present in the Ps-formation DCS for positron–helium collisions. Using the distorted wave approximation, Mandal et al. [21] and later Sen and Mandal [22], obtained deep minima in the Ps-formation DCS for energies above the Ore gap. A minimum has been obtained theoretically in the elastic differential cross section for positron–hydrogen scattering, which was attributed to destructive interference between partial waves [23].
A deep minimum in the experimental measurements of the triply differential cross section for electron–helium ionization (plotted on a logarithmic scale) [24,25] has been interpreted [26] in terms of a vortex in the velocity field associated with the ionization amplitude. Studies of deep minima and vortices in electron-impact and positron-impact ionization have been made [26,27,28,29,30,31,32,33,34,35].
The outline of the paper is as follows. We present the theory in Section 2. In Section 2.1, we present the scattering theory for Ps-formation in positron–helium scattering in the Ore gap. Specifically, we present equations for and the Ps-formation DCS, and discuss the fits that we perform of the complex Kohn K-matrices. In Section 2.2, we provide an expression for the extended velocity field that is associated with . We present our results in Section 3. We show in Section 3.1 the deep minimum in the logarithm of the Ps-formation DCS and give the position of the zero in . In Section 3.2 we show the minimum in the forward-direction Ps-formation DCS. In both Section 3.1 and Section 3.2, we discuss the convergence of results with respect to the maximum partial wave, , which we use in the sum in the equation of . We show in Section 3.3 that the unit vector of the extended velocity field rotates around the zero in and we present conclusions in Section 4. In Appendix A, we describe the complex Kohn ℓth partial-wave trial functions that we use to compute the K-matrices. In Appendix B, we discuss some numerical investigations that we performed and also the WG MERT and polynomial fits.
2. Theory
2.1. Scattering Theory for Ps-Formation in Positron–Helium Collisions
Using the complex Kohn variational method, we compute partial-wave two channel K-matrices for positron–helium collisions in the Ore gap [1,13,19,36,37,38,39,40]. In Appendix A we describe the complex Kohn trial wave function for the th partial wave. From the partial-wave K-matrices, , we determine the Ps-formation scattering amplitude , using
where I is the identity matrix, is the angle of the outgoing Ps, and are Legendre polynomials [41]. The Ps-formation scattering amplitude, , has azimuthal symmetry. In Equation (1), the number 1 in the subscript refers to the initial channel i which is the positron–helium scattering channel and the number 2 in the subscript refers to the final channel, which is the Ps-He+ channel [1]. Thus, the subscript 12 in Equation (1) refers to Ps formation so that is . The magnitude of the momentum of the incident positron k and of the outgoing Ps atom are related through energy conservation, which is given by
where E is the total energy of the positron–helium system, is the energy of the helium ion, is the energy of the Ps atom, whose mass is 2. We take the ground-state energy of the helium atom to be the variational determined energy that corresponds to the variational wave function given in Refs. [19,36,37,38] (see Appendix A). For this value of , the lowest limit of the Ore gap is 17.79 eV.
In our calculations of , we sum to a finite ℓ, which we call . The highest value of that we consider is three, but we vary from one to three to consider the convergence of the position of the zero in and of the corresponding Ps-formation DCS with respect to the number of partial waves included in Equation (1). We determine the Ps-formation DCS using [41]:
We fit the complex Kohn K-matrices using polynomials and also the WG MERT [15] for which we explicitly take into account the polarization potential in the Ps-He+ channel [15,16,17,18]. Using both the complex Kohn K-matrices and the fitted K-matrices, we determine the position of the zero in and thus in the corresponding Ps-formation DCS.
2.2. Extended Velocity Field Associated with the Ps-Formation Scattering Amplitude
Macek et al. related experimental measurements of a deep minimum in the triply differential cross section of the electron-impact ionization of helium to a vortex in a velocity field associated with the ionization amplitude [26]. A deep minimum in a differential cross section is a quantity that, in principle, is accessible to experimental measurements. While the extended velocity field associated with the Ps-formation scattering amplitude is not experimentally measurable, a zero in the Ps-formation differential cross section means that there is a vortex in this field. A discussion of the standard velocity field that is associated with the wave function in coordinate space is given in reference [42].
In our preceding paper [7] on the deep minima and vortices for Ps formation in positron–hydrogen collisions, we gave an expression for the velocity field associated with the Ps-formation scattering amplitude , namely,
We referred to the velocity field of Equation (4) as the extended velocity field , where we treated k and , and thus and , as independent variables [7]. Here, we determine the extended velocity field that corresponds to for positron–helium collisions.
In the vicinity of a first-order isolated zero in the complex function , this function can be expressed in linear form
where [7,26,27,43,44]. In Equation (5), and are the z- and x-components of the momentum of the outgoing Ps in the z-x plane, where the z-axis is taken to be parallel to the momentum of the incident positron . The position of the zero in is at and . We treat the two components and as independent variables, which is consistent with treating k and as independent variables. Using the linear form of , which is a good approximation in the vicinity of the zero , one can determine the dominant term of in this vicinity. Using this term, one can determine the circulation as [7,27,42,44]:
for a closed contour c, of anticlockwise orientation, enclosing only the isolated first-order zero in .
We determine , the Ps-formation DCS and using the s- and p-wave K-matrices from the WG MERT and the d- and f-wave from the polynomial fits. We refer to this specific set of K-matrices as the hybrid fit. In the vicinity of the zero of we fit , which we obtain using the hybrid fit to the power expansion:
where we take . We substitute Equation (7) into Equation (4) to determine in the vicinity of the zero in .
3. Results
3.1. Deep Minimum in the Logarithm of the Ps-Formation DCS and the Position of the Zero in Ps-Formation Scattering Amplitude
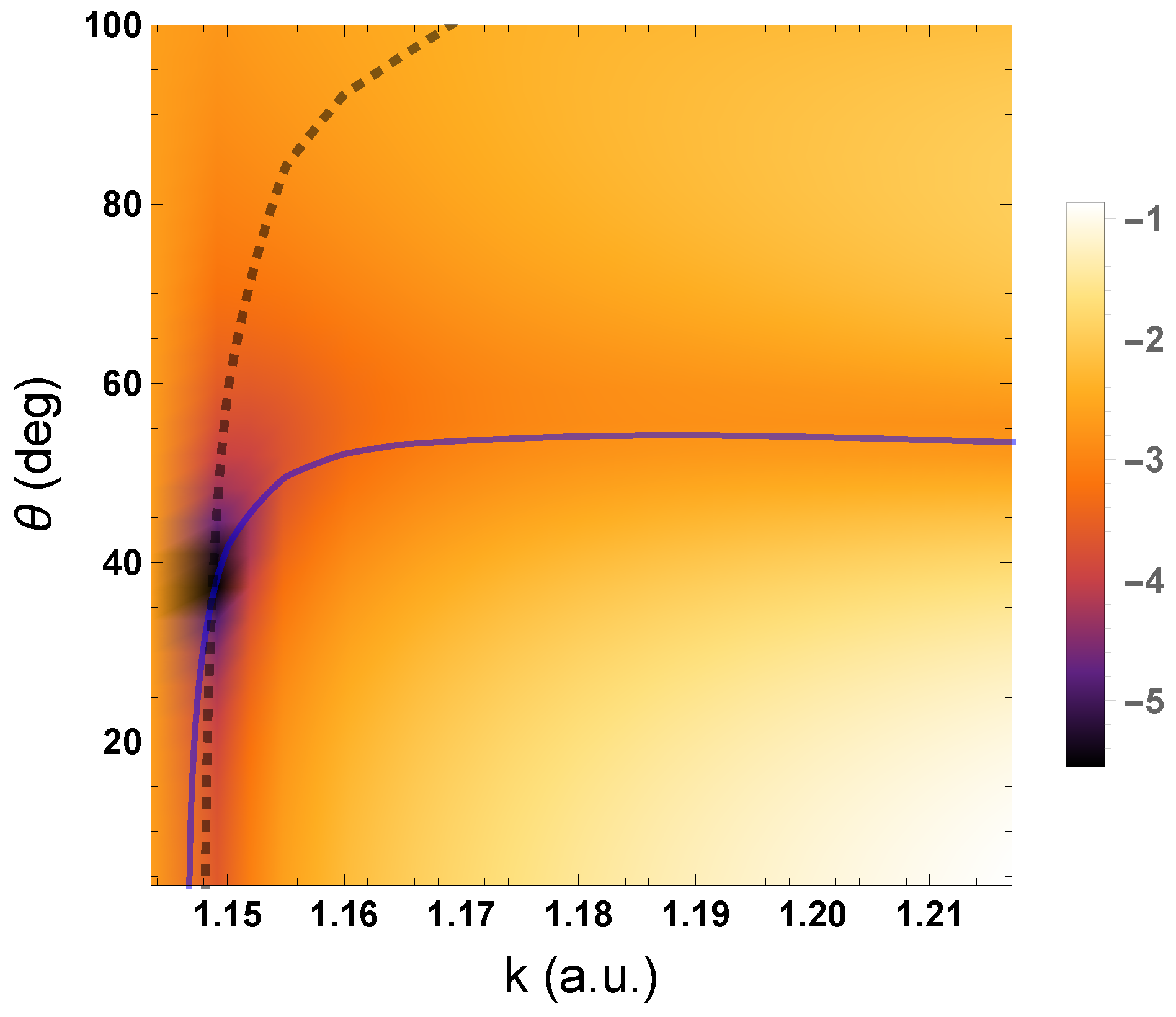
Figure 1 shows a density plot of the common logarithm of the Ps-formation DCS as a function of k and , and also the nodal lines of and . From near the threshold, the nodal lines rise steeply with respect to , become closer together, and then intersect at zero in . After this intersection point, the nodal line continues to rise steeply. However, the nodal line rises less steeply, turns and then becomes almost a constant with respect to for increasing k. The figure shows that there is a region surrounding the zero in where the Ps-formation DCS is very small.
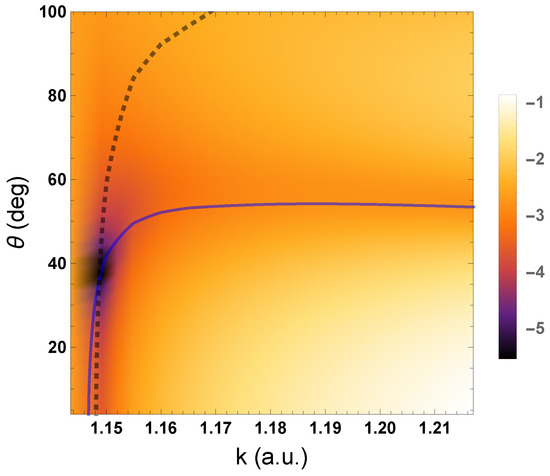
Figure 1.
Density plot of the common logarithm of the Ps-formation differential cross section, , which we compute using the complex Kohn K-matrices as a function of the magnitude of the momentum of the incident positron, k, and the angle of the outgoing Ps, , for positron–helium collisions. The nodal lines of and are represented by the solid blue line and the dashed black line, respectively.
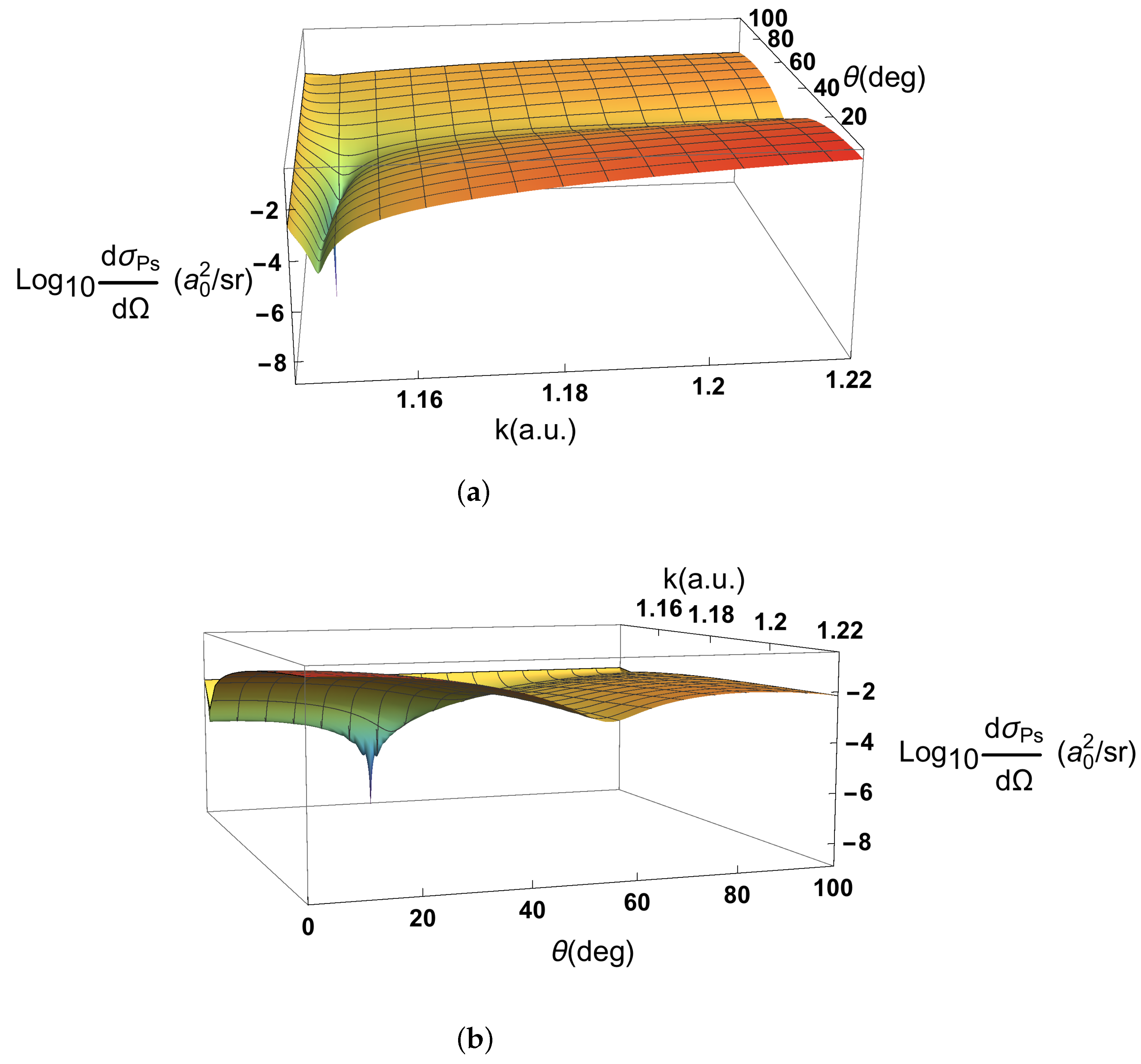
The three-dimensional plots of the common logarithm of the Ps-formation DCS, Figure 2a,b, show a deep minimum that corresponds to the zero in . The deep minimum lies in a valley (Figure 2a). The valley extends to the forward direction so that there is a minimum in the forward direction (Figure 2b), which we discuss in Section 3.2.
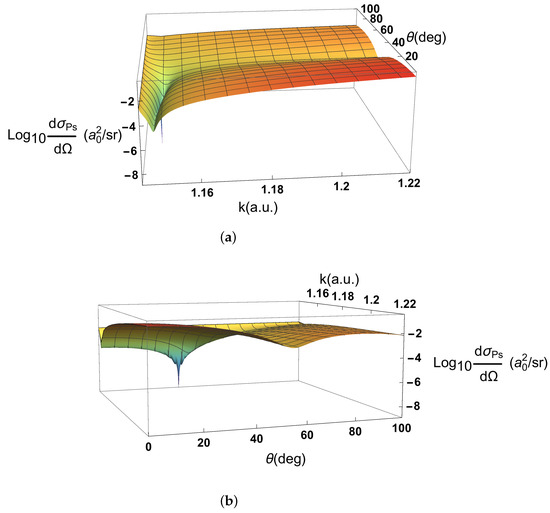
Figure 2.
The common logarithm of the Ps-formation differential cross section, , for positron–helium collisions as a function of k and . (a) Shows the k range of most of the Ore gap and for the range from close to zero to 100°. (b) Shows a different rotation for the same k range and for the range from the 0° to 100°.
Table 1 presents the position of the zero in , &, which we determine using the complex Kohn K-matrices. We show the variation of the position of the zero with , where is the maximum value of that we use in Equation (1). We obtain a zero in with ; thus, only the first two partial waves, = 0 and 1, are needed to obtain a zero. This is also the case for the first zero in for positron–hydrogen collisions [7]. For positron–helium collisions, we note that the value of the position of the zero changes significantly with the inclusion of the d-wave while the k0 value changes only slightly. However, the value of the position of the zero changes only slightly by further adding the f-wave. There is no change in the value up to the fourth decimal figure with the inclusion of the f-wave. We can, thus, conclude that the value of the position of the zero has essentially converged with respect to partial waves by . This is reasonable since the k value of the position of the zero is just slightly higher than the k value for the Ps(1s)-formation threshold. Interestingly, for positron–helium collisions in the Ore gap, we obtain a single zero in ; whereas, for positron–hydrogen collisions in the Ore gap, we obtained two zeros in [7].

Table 1.
Position of the zero in , & , which we compute using the complex Kohn K-matrices. The table shows the convergence of the position of the zero with respect to the maximum partial wave . It also gives the position of the zero in , which we compute using various fits, and taking .
We also give in Table 1 the position of the zero in with , which we obtain using the hybrid, WG MERT and polynomial fits. The result using the WG MERT fits is in better agreement with the complex Kohn result than the result using the polynomial fits. Thus, it is important to explicitly take into account the polarization potential in the Ps-He+ channel in the fitting of the K-matrices [16,18]. This is reasonable since the effective polarizability of Ps in the Ps-He+ channel is significant [16].
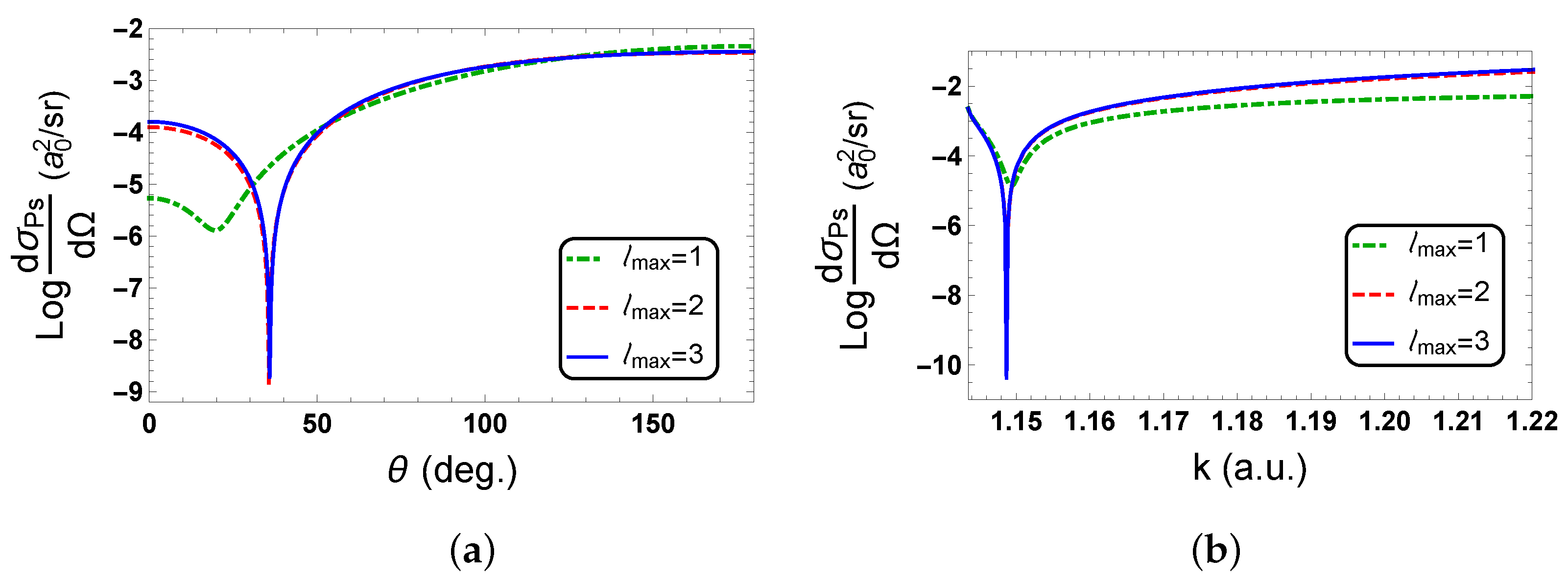
In Figure 3a, we show the logarithm of the Ps-formation DCS as a function of the angle at , the k value of the zero in with . In Figure 3b, we show the logarithm of the Ps-formation DCS as a function of k at 35.9°, the value of the zero in with . We use the complex Kohn K-matrices to compute the Ps-formation DCS, and we compare the Ps-formation DCS for different values of . The minimum in the logarithm of the Ps-formation DCS for in these figures is not deep since the zero in for is at a noticeably different position than for (see Table 1). For the kinematics of the figures, we find that the Ps-formation DCS for and are almost identical. Thus, for these figures, we conclude that the Ps-formation DCS has converged sufficiently with respect to partial waves by . We discuss in Appendix B other numerical investigations that we perform.
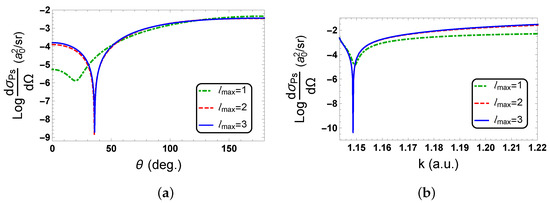
Figure 3.
The common logarithm of Ps-formation DCS, , which we compute using the complex Kohn K-matrices. The figures show the deep minimum in the logarithm of the cross section and the convergence of the cross section with respect to , the maximum value of , which we use in Equation (1). (a) The logarithm of the Ps-formation DCS for as a function of . (b) The logarithm of the Ps-formation DCS for 35.9° as a function of k.
3.2. Minimum in the Ps-Formation DCS in the Forward Direction
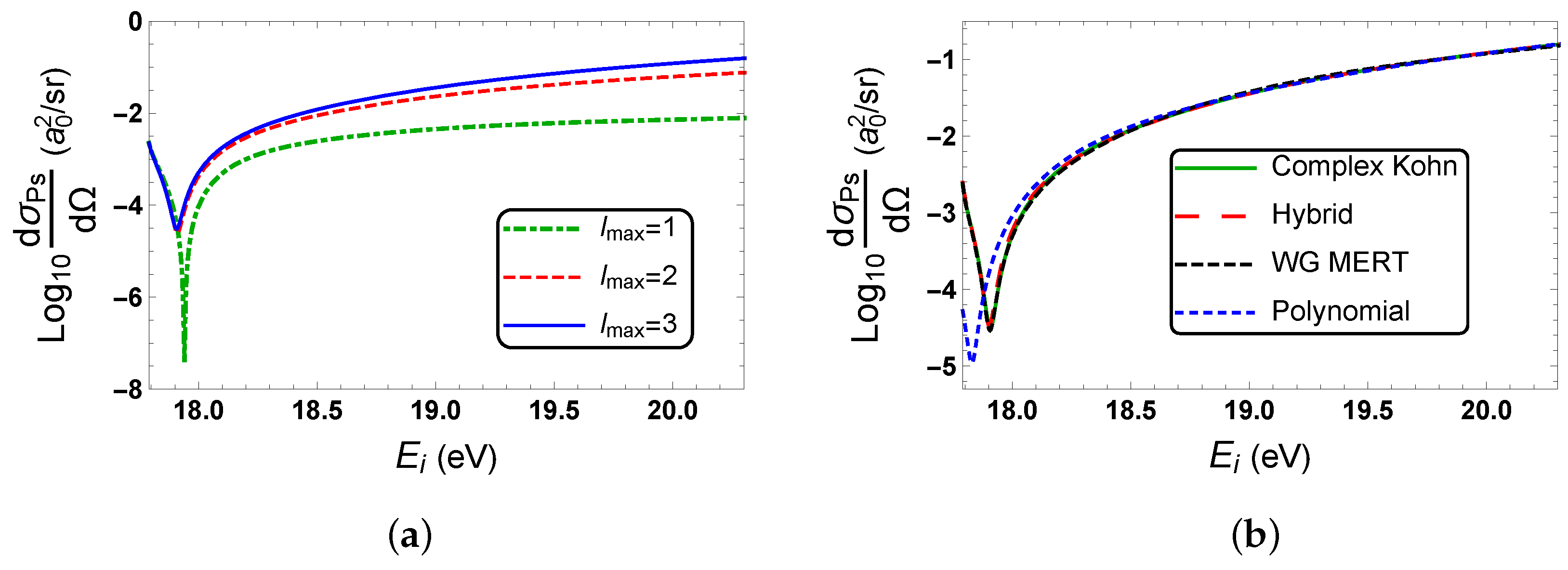
We show in Figure 4 the logarithm of Ps-formation DCS in the forward direction as a function of the energy of the incident positron . There is a minimum in the Ps-formation DCS ( 0°), whose position for the calculation, where we use the complex Kohn K-matrices and take = 3, is at = 17.9 eV (k = 1.1472). The minimum is, therefore, at an energy lower than the lowest energy of 24.7 eV considered in the experimental measurements of the near-forward direction Ps-formation DCS for positron–helium collisions [4,6]. At the k position of the minimum in the Ps-formation DCS ( 0°) is not zero as and . However, the Ps-formation DCS is small since the k value at the minimum is between the k value, where () and where ().
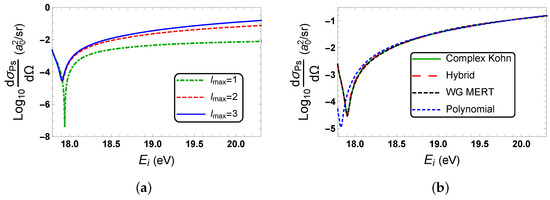
Figure 4.
The common logarithm of the forward direction Ps-formation DCS, , as a function of the energy of the incident positron. (a) Comparing the logarithm of the Ps-formation DCS computed with the complex Kohn K-matrices for different values of . (b) Comparing the logarithm of the Ps-formation DCS computed with the complex Kohn K-matrices and with the hybrid, WG MERT and polynomial fits.
Figure 4a shows the convergence with respect to of the logarithm of the Ps-formation DCS in the forward direction, which we compute using the complex Kohn K-matrices. One can see that the cross sections for = 2 and = 3 are similar, especially in the region of the minimum. The minimum in the logarithm of the Ps-formation DCS is deepest for = 1, which is not surprising since the value for the zero in is significantly closer to the forward direction for = 1 than for the other two values of (see Table 1).
Figure 4b compares the Ps-formation DCS (plotted using a logarithmic scale) in the forward direction, which we compute using the complex Kohn K-matrices with the cross sections that we compute using the WG MERT, hybrid and polynomial fits. The cross sections, which we compute with the WG MERT and hybrid fits, are in excellent agreement with the cross section that we compute directly with the complex Kohn K-matrices. However, the position of the minimum in the Ps-formation DCS ( 0°), which we compute with the polynomial fits, is noticeably different to the position that we compute using the complex Kohn K-matrices or the other fits. These results show that, for energies in the vicinity of the minimum in the Ps-formation DCS ( 0°), it is important in the fittings of the K-matrices to explicitly include the polarization potential in the Ps-He+ channel.
3.3. Extended Velocity Field Associated with the Ps-Formation Scattering Amplitude
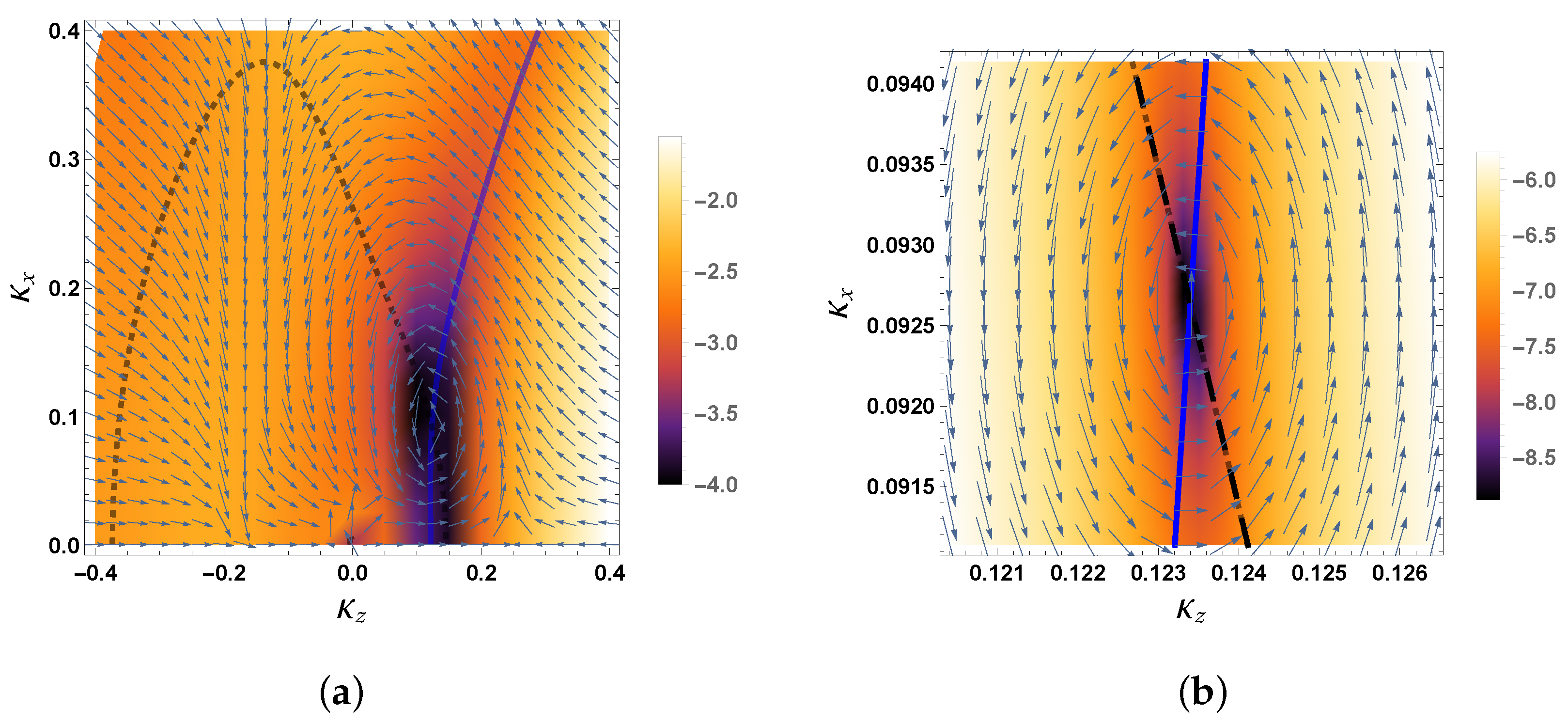
We consider to depend on two independent variables, k and , or alternatively and . We refer to the velocity field Equation (4), associated with this , as the extended velocity field [7]. Using the hybrid fit of the complex Kohn K-matrices, we compute , the Ps-formation DCS, and for a grid. Figure 5a shows a density plot of the common logarithm of the Ps-formation DCS, the nodal lines of and , and . For a small grid that is in the vicinity of the zero in , we fit , which we determine from the hybrid fit of the complex Kohn K-matrices, to Equation (7). We use this fitted to determine the Ps-formation DCS, and . Figure 5b shows the logarithm of the Ps-formation DCS, the nodal lines of and , and that we obtain using the fitted .
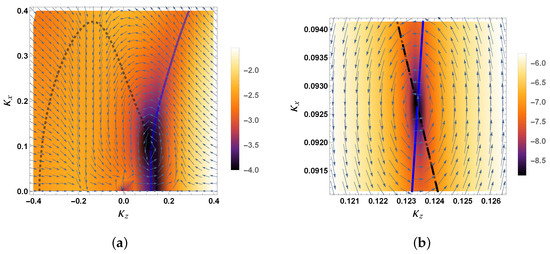
Figure 5.
The density plot of for Ps-formation in positron–helium collisions. The nodal lines of and are denoted by the solid blue line and the dashed black line, respectively, while is represented by the arrows. (a) We use the hybrid fit to compute , the Ps-formation DCS and . (b) A small () grid that is in the vicinity of the zero in . We use Equation (7) to fit that we compute using the hybrid fit, and we use the fitted to compute the Ps-formation DCS and .
The rotation of is anticlockwise around the zero in , which is the same direction of rotation of for the first zero in for positron–hydrogen collisions in the Ore gap [7]. For Ps-formation in positron–hydrogen collisions, we previously found two zeros in in the Ore gap [7]. While the direction of rotation of around the first zero in is anticlockwise, the direction of rotation of is clockwise around the second zero [7]. Recently, for the electron-impact ionization of helium and for a number of different incident energies, it was found that the velocity field associated with the transition matrix element rotates anticlockwise around a zero in the transition matrix element [30]. In contrast, for the positron-impact ionization of helium, it was found that the direction of rotation of the velocity field is clockwise and, thus, in the opposite direction of rotation for electron-impact ionization of the same target [30]. However, one cannot assume that the direction of rotation of the velocity field is projectile dependent for the ionization of a given target, since it was found that, for both electron- and positron-impact ionization of atomic hydrogen, the velocity field associated with the transition matrix element rotates in the same direction (anticlockwise) around a zero [31].
4. Conclusions
Using complex Kohn K-matrices, we have computed the Ps-formation scattering amplitude, , and the corresponding DCS for positron–helium collisions in the energy range of the Ore gap. We found a deep minimum in the logarithm of the Ps-formation DCS that corresponds to a zero in [8,9]. Corresponding to the zero in , there is a vortex in the extended velocity field that is associated with . We showed that rotates anticlockwise around the zero in [8,9], which is the same direction of rotation of around the first zero in for positron–hydrogen collisions in the Ore gap [7].
We saw that, to obtain a position of the zero in that compares well with the complex Kohn result, it is important to explicitly include the polarization potential in the Ps+He+ channel in the fits of the K-matrices. For the minimum in the forward direction Ps-formation DCS, it is important to explicitly include the polarization potential in the fittings of the K-matrices for the s- and p-waves. These findings are consistent with earlier findings that the WG MERT describes well the behaviour of the Ps-formation partial-wave cross sections near the Ps-formation threshold for positron collisions from hydrogen [16,17,18] and from helium [16,18].
The Ps-formation DCS near the forward direction has been recently measured for positron collisions for a number of targets including helium [4,5,6]. While a dip was found in the measured near-forward direction Ps-formation DCS for positron collisions from Ne, Ar, Kr and Xe [5], it was not observed in the cross section for positron–helium collisions for the energy range of the experiment [4,6]. However, we theoretically obtained a minimum in the Ps-formation DCS ( 0°) for positron–helium collisions at 17.9 eV, which is at a lower energy than the energies considered in the experiment for helium [4,6]. Interestingly, both the deep minimum and the minimum in the forward direction lie in a valley in the logarithm of the Ps-formation DCS, which is a function of k and .
We can conclude that, for the particular process of Ps formation in positron–helium collisions in the Ore gap, there is a deep minimum in the logarithm of the Ps-formation DCS, which is connected via the valley to the minimum in the logarithm of the Ps-formation DCS in the forward direction, and that there corresponds to the zero in a vortex in that is associated with .
Author Contributions
All authors were involved in the research and in the preparation of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
S.J.W. gratefully acknowledges support from the NSF under Grant No. PHYS-1707792.
Data Availability Statement
Data is available upon request. Please email S.J.W. to request data. Additional material to that given in this paper may be found in reference [9].
Acknowledgments
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DCS | Differential Cross Section |
| WG MERT | Watanabe and Greene’s Multichannel Effective Range Theory |
Appendix A. Complex Kohn ℓth Partial Wave Trial Functions
We use the complex Kohn variational method to compute K-matrices for positron–helium collisions in the Ore gap. We describe briefly here the complex Kohn trial wave function for the th partial wave. The application of the Kohn-type variational method to positron–helium collisions may be found in Refs. [1,13,19,36,37,38,39,40].
In the Ore gap, if one ignores positron annihilation, the only two open channels are elastic scattering and Ps(1s) formation. The total wave function has two components, and , where represents elastic positron–helium scattering and Ps(1s) formation, whilst represents elastic Ps-He+ scattering and helium formation [1]. In Figure A1, we show the position vectors for the positron–helium system. In this figure, N denotes the nucleus of the helium atom, He2+, which we take to be infinitely massive. The complex Kohn asymptotic form of the two components, and , for the th partial wave may be written in the form [13,19,47,48]
where
and where and are the ground-state wave functions of the helium ion and of the Ps atom, respectively. We take for the ground-state wave function of helium, , the variational wave function given in Refs. [19,37]. This wave function is of Hylleraas form and is symmetric with respect to the two electrons in the helium atom. In Equations (A2)–(A5), is the spherical harmonic function, and are the two spherical Hankel functions that are related to the spherical Bessel function and the spherical Neumann function according to and , respectively [49,50,51]. The operator is the space exchange operator for the two electrons. The in Equation (A1) are the partial wave S-matrix elements, where the S-matrix is related to the K-matrix by [19,41]
In constructing the th partial-wave trial function to use for all distances, we multiply the spherical Neumann functions in the asymptotic form of the two components ( and ) by shielding functions that remove the singularities at the origin and which asymptotically tends to unity. We refer to these two resulting components, ( and ), as the long-range components of the ℓth partial-wave trial functions. For the s-wave, we add to the two long-range components highly correlated Hylleraas-type short-range terms of the form [13,19]
which include all six interparticle distances (see Figure A1). In Equation (A7), and are non-linear parameters, the s are linear parameters, , , , , and are non-negative integer powers and is restricted to even powers only. The sum of these non-linear parameters, , is less than or equal to , where is a non-negative integer [13,19,38]. To avoid the same Hylleraas-type short-range terms being repeated with the operation we require that , but if then [13,19,36,38]. The number of terms N in the sum in Equation (A7) for = 4, 5, 6, 7 and 8 is 84, 172, 330, 588 and 1001, respectively.
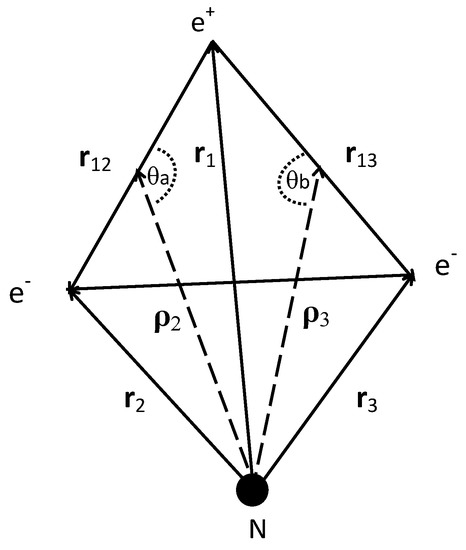
Figure A1.
The positron–helium coordinate system.
Figure A1.
The positron–helium coordinate system.
For the higher partial waves, we add to the two long-range components two sets of Hylleraas-type short-range terms of different symmetries,
where the angular momentum is either on the positron (Equation (A8)) or on one of the electrons (Equation (A9)). In Equations (A8) and (A9), the linear parameters are and , respectively, and () is the number of terms for the first (second) symmetry. We take for all partial waves () and values except the f-wave and , where we take but to avoid linear dependence. For the s-, p-, d- and f-waves, the highest value of we use is = 8, 6, 5 and 4, respectively.
There are rotational harmonics [13,52] terms to consider that include the angular momentum on the incoming positron, angular momentum on one of the electrons and also mixed symmetry terms where the angular momentum is shared. However, following Van Reeth and Humberston [19], we do not explicitly include the mixed symmetry terms. The neglect of the mixed symmetry terms has been discussed in Refs. [19,39,48,53,54].
Following Van Reeth and Humberston [19], as well as adding the Hylleraas-type short-range terms to the two resulting components of the trial wave function, we add for the s-, p- and d-waves polarized-orbital terms of the form [19]
to each component, where is the angle between the vectors and (see Figure A1). For the s-wave we consider four polarized-orbital terms, ( and , and 3), whereas for the p- and d-waves we only consider two polarized-orbital terms, ( and , ). The shielding function removes the singularity at the origin arising from . The polarized-orbital terms represent the configuration of the Ps atom distorted by the He+ ion in the intermediate region. Adding these terms to the trial wave functions significantly improved the convergence of the matrix elements [19].
Appendix B. Numerical Investigations
We examine the convergence of the complex Kohn K-matrix elements at the k position of the zero in ( = 1.1487) by computing the ratio:
where is a K-matrix element for a particular partial wave that we evaluate at a certain value of . The largest value of that we consider for the s-, p-, d- and f-wave is 8, 6, 5 and 4, respectively. We find that for the s-wave , , and . For the p-wave, for all K-matrix elements and for the d-wave, . For the f-wave, the ratio is larger than the above percentages for and is significantly larger for . However, as one can see from Table 1, the f-wave has only a small effect on the position of the zero in .
In Table A1, we show the convergence in the position of the zero in with respect to for the s-wave only. We fix for the p-, d-, and f-wave at 6, 5 and 4, respectively. Both the k and values of the position of the zero, and , in increase with increasing for the s-wave. The zero in is at a k value just above the Ps-formation threshold. We found that the position of the zero , especially the angle , is extremely sensitive to the s-wave value. Thus, it is important to determine the s-wave K-matrix accurately at the k value of the zero in .

Table A1.
Convergence of the position of the zero in with respect to variations in for the s-wave only. For the p-, d- and f-wave, is 6, 5 and 4, respectively.
Table A1.
Convergence of the position of the zero in with respect to variations in for the s-wave only. For the p-, d- and f-wave, is 6, 5 and 4, respectively.
| (deg.) | ||
|---|---|---|
| 8 | 1.1487 | 35.9 |
| 7 | 1.1485 | 34.6 |
| 6 | 1.1482 | 31.7 |
| 5 | 1.1477 | 21.8 |
In Table A2 we show the convergence in the position of the zero in with respect to the p-wave value in which we fix the values for the other partial waves ( = 8 for the s-wave, = 5 for the d-wave and = 4 for the f-wave). Similar to the s-wave case, the angle increases with increasing for the p-wave. However, in contrast, the k value decreases with increasing for the p-wave. The position of the zero is less sensitive to increasing for the p-wave than the s-wave. For the d-wave, we find that increasing from three to five does not change, to five significant figures, the k value of the position of the zero in , but it does change by less than 0.7°. Furthermore, for the f-wave, increasing from zero to four does not change the k value to at least five significant figures, although changes by less than 0.1°.

Table A2.
Convergence of the position of the zero in with respect to variations in for the p-wave only. For the s-, d- and f-wave, the value is 8, 5 and 4, respectively.
Table A2.
Convergence of the position of the zero in with respect to variations in for the p-wave only. For the s-, d- and f-wave, the value is 8, 5 and 4, respectively.
| (deg.) | ||
|---|---|---|
| 6 | 1.1487 | 35.9 |
| 5 | 1.1489 | 34.8 |
| 4 | 1.1491 | 33.7 |
In Table A3, we show the variation in the position of the zero in with respect to the set, where = and i = 0 to 3. The set is the set that we use for our most elaborate calculations in which = 8, 6, 5 and 4 for the s-, p-, d- and f-wave, respectively. The set, for i = 1 to 3, is where the value for each partial wave is decreased by i. We find that, while there is no change in the value to five significant figures when going from the set to the set, the value changes in the second significant figure.

Table A3.
Convergence of the position of the zero in with respect to the set , where to 3, and where for the set = 8, 6, 5, 4 for the s-, p-, d- and f-wave, respectively.
Table A3.
Convergence of the position of the zero in with respect to the set , where to 3, and where for the set = 8, 6, 5, 4 for the s-, p-, d- and f-wave, respectively.
| (deg.) | ||
|---|---|---|
| 1.1487 | 35.9 | |
| 1.1487 | 33.6 | |
| 1.1486 | 30.2 | |
| 1.1481 | 27.3 |
We compare in Figure A2 the logarithm of the Ps-formation DCS in the forward direction, which we compute with different sets of complex Kohn K-matrices, where to 3. One can see in the main figure of Figure A2 that the Ps-formation DCS ( 0°) is very stable with respect to over most of the energy range that we show. For a fine energy mesh in the vicinity of the minimum in the logarithm of the Ps-formation DCS ( 0°), one can clearly see a variation in the cross section for the different sets (see inset of Figure A2).
Figure A2.
The common logarithm of the forward direction Ps-formation DCS, , as a function of the energy of the incident positron. Comparing the logarithm of cross section for different sets, where i = 0, 1, 2 and 3, and where for the set = 8, 6, 5, 4 for the s-, p-, d- and f-wave, respectively. The inset shows for a fine energy mesh in the vicinity of the minimum.
Figure A2.
The common logarithm of the forward direction Ps-formation DCS, , as a function of the energy of the incident positron. Comparing the logarithm of cross section for different sets, where i = 0, 1, 2 and 3, and where for the set = 8, 6, 5, 4 for the s-, p-, d- and f-wave, respectively. The inset shows for a fine energy mesh in the vicinity of the minimum.
We apply the WG MERT [15] in which the polarization potential is explicitly included in the Ps+He+ channel [15,16,17,18] to fit the complex Kohn K-matrices. The WG MERT expansion of a K-matrix is expressed in terms of the quantum defect parameters that vary rapidly with energy and depend on the polarizability of Ps, and on the matrix elements that, in general, vary slowly with the energy and are related to short-range interactions [16]. Using the s-, p-, d- and f-wave complex Kohn variational K-matrices and the polarizability of positronium, we extract the matrix elements [15,16,17,18] at different k values. We fit these elements to polynomials of powers of , which enables us to determine K-matrices at any value of k. For the , and matrix elements we chose cubic polynomials, whereas for the and matrix elements we chose quintic polynomials. We use quartic polynomials for the other matrix elements for the various partial waves. (For the p-wave we just use five values of k [1.16, 1.18, 1.20, 1.22 and 1.24] in obtaining fits for the matrix elements.) For the polynomial fits of the complex Kohn matrix elements , we use for each partial wave the same order of polynomials as we use in the corresponding matrix elements.
References
- Charlton, M.; Humberston, J.W. Positron Physics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Laricchia, G.; Walters, H.R.J. Positronium collision physics. La Rivista Del Nuovo Cimento 2012, 35, 305–351. [Google Scholar]
- Schippers, S.; Sokell, E.; Aumayr, F.; Sadeghpour, H.; Ueda, K.; Bray, I.; Bartschat, K.; Murray, A.; Tennyson, J.; Dorn, A.; et al. Roadmap on photonic, electronic and atomic collision physics: II. electron and antimatter interactions. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 171002-1–171002-49. [Google Scholar] [CrossRef]
- Shipman, M.; Armitage, S.; Beale, J.; Brawley, S.J.; Fayer, S.E.; Garner, A.J.; Leslie, D.E.; Van Reeth, P.; Laricchia, G. Absolute differential positronium-formation cross sections. Phys. Rev. Lett. 2015, 115, 033401-1–033401-5. [Google Scholar] [CrossRef] [Green Version]
- Fayer, S.E.; Newson, D.M.; Brawley, S.J.; Loreti, A.; Kadokura, R.; Babij, T.J.; Lis, J.; Shipman, M.; Laricchia, G. Differential positronium-formation cross sections for Ne, Ar, Kr and Xe. Phys. Rev. A 2019, 100, 062709-1–062709-4. [Google Scholar] [CrossRef]
- Laricchia, G.; University College London, London, UK. Private Communication, 2021.
- Alrowaily, A.W.; Ward, S.J.; Van Reeth, P. Deep minima and vortices for positronium formation in low-energy positron–hydrogen collisions. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 205201-1–205201-11. [Google Scholar] [CrossRef]
- Ward, S.J.; Alrowaily, A.W.; Van Reeth, P. Deep minimum in the Ps-formation differential cross section for positron-helium collisions in the Ore gap. Bull. Am. Phys. Soc. 2020, 65(No. 4), E01.00028. Available online: https://meetings.aps.org/Meeting/DAMOP20/Session/E01.28 (accessed on 12 July 2021).
- Alrowaily, A.W. Deep Minima and Vortices for Positronium Formation in Positron-Hydrogen and Positron-Helium Collisions. Ph.D. Thesis, University of North Texas, Denton, TX, USA, 2021. [Google Scholar]
- Basic Atomic Spectroscopic Data. Available online: https://physics.nist.gov/PhysRefData/Handbook/Tables/heliumtable1.htm (accessed on 18 February 2021).
- Basic Atomic Spectroscopic Data. Available online: https://physics.nist.gov/PhysRefData/Handbook/Tables/heliumtable5.htm (accessed on 18 February 2021).
- The NIST Reference on Constants, Units, and Uncertainity. Available online: https://physics.nist.gov/cuu/Constants/energy.html (accessed on 18 February 2021).
- Armour, E.A.G.; Humberston, J.W. Methods and programs in collisions of positrons with atoms and molecules. Phys. Rep. 1991, 204, 165–251. [Google Scholar] [CrossRef]
- Van Reeth, P.; Humberston, J.W. The energy dependence of the annihilation rate in positron-atom scattering. J. Phys. B At. Mol. Opt. Phys. 1998, 31, L231–L238. [Google Scholar] [CrossRef]
- Watanabe, S.; Greene, C.H. Atomic polarizability in negative-ion photodetachment. Phys. Rev. A 1980, 22, 158–169. [Google Scholar] [CrossRef]
- Ward, S.J.; Hunnell, J.C.; Macek, J.H. The effect of the polarization potential on low energy atomic processes. Nucl. Instr. Methods Phys. Res. B 2002, 192, 54–62. [Google Scholar] [CrossRef]
- Ward, S.J.; Macek, J.H. Effective range analysis of positron–hydrogen collisions. Phys. Rev. A 2000, 62, 052715-1–052715-15. [Google Scholar] [CrossRef]
- Ward, S.J. Positronium formation in low-energy positron collisions with one- and two-electron atoms. Comments Mod. Phys. 2002, 2, D245–D261. [Google Scholar]
- Van Reeth, P.; Humberston, J.W. Elastic scattering and positronium formation in low-energy positron–helium collisions. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 3651–3667. [Google Scholar] [CrossRef]
- Drachman, R.J.; Omidvar, K.; McGuire, J.H. Differential cross section for positronium formation in positron-atomic-hydrogen collisions. Phys. Rev. A 1976, 14, 100–103. [Google Scholar] [CrossRef]
- Mandal, P.; Guha, S.; Sil, N.C. Positronium formation in positron scattering from hydrogen and helium atoms: The distorted-wave approximation. J. Phys. B At. Mol. Phys. 1979, 12, 2913–2924. [Google Scholar] [CrossRef]
- Sen, S.; Mandal, P. Positron-helium collisions: Positronium formation using the distorted-wave approximation. Phys. Rev. A 2009, 80, 062714-1–062714-10. [Google Scholar] [CrossRef]
- Ghoshal, A.; Mandal, P. Elastic differential cross section and critical point for positron–hydrogen collisions. Phys. Rev. A 2005, 72, 042710-1–042710-9. [Google Scholar] [CrossRef]
- Murray, A.J.; Read, F.H. Evolution from the coplanar to the perpendicular plane geometry of helium (e,2e) differential cross sections symmetric in scattering angle and energy. Phys. Rev. A. 1993, 47, 3724–3732. [Google Scholar] [CrossRef]
- Murray, A.J.; Read, F.H. Exploring the helium (e,2e) differential cross section at 64.6 eV with symmetric scattering angles but nonsymmetric energies. J. Phys. B At. Mol. Opt. Phys. 1993, 26, L359–L365. [Google Scholar] [CrossRef]
- Macek, J.H.; Sternberg, J.B.; Ovchinnikov, S.Y. Theory of deep minima in (e,2e) measurements of triply differential cross sections. Phys. Rev. Lett. 2010, 104, 033201-1–033201-4. [Google Scholar] [CrossRef]
- Ward, S.J.; Macek, J.H. Effect of a vortex in the triply differential cross section for electron impact K-shell ionization of carbon. Phys. Rev. A 2014, 90, 062709-1–062709-11. [Google Scholar] [CrossRef] [Green Version]
- Feagin, J.M. Vortex kinematics of a continuum electron pair. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 011001-1–011001-4. [Google Scholar] [CrossRef]
- Colgan, J.; Al-Hagan, O.; Madison, D.H.; Murray, A.J.; Pindzola, M.S. Deep interference minima in non-coplanar triple differential cross sections for the electron-impact ionization of small atoms and molecules. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 171001. [Google Scholar] [CrossRef]
- DeMars, C.M.; Kent, J.B.; Ward, S.J. Deep minima in the Coulomb-Born triply differential cross sections for ionization of helium by electron and positron impact. Eur. Phys. J. D 2020, 74, 48. [Google Scholar] [CrossRef]
- DeMars, C.M.; Ward, S.J.; Colgan, J.; Amami, S.; Madison, D.H. Deep minima in the triply differential cross section for ionization of atomic hydrogen by electron and positron impact. Atoms 2020, 8, 26. [Google Scholar] [CrossRef]
- Navarrete, F.; Della Picca, R.; Fiol, J.; Barrachina, R.O. Vortices in ionization collisions by positron impact. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 115203-1–115203-6. [Google Scholar] [CrossRef] [Green Version]
- Navarrete, F.; Barrachina, R.O. Vortices in the three-body electron-positron-proton continuum system induced by the positron-impact ionization of hydrogen. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 055201-1–055201-6. [Google Scholar] [CrossRef]
- Navarrete, F.; Barrachina, R.O. Vortices in ionization collisions. Nucl. Instrum. Phys. Res. B 2016, 369, 72–76. [Google Scholar] [CrossRef]
- Navarrete, F.; Barrachina, R.O. Vortices rings in the ionization of atoms by positron impact. J. Phys. Conf. Ser. 2017, 857, 012022. [Google Scholar] [CrossRef] [Green Version]
- Van Reeth, P. Theoretical Studies of Positronium Formation in Low Energy Positron-Helium Collisions. Ph.D. Thesis, University College London, London, UK, 1996. [Google Scholar]
- Van Reeth, P.; Humberston, J.W. The use of inexact helium wavefunctions in positron–helium scattering. J. Phys. B At. Mol. Phys. Opt. Phys. 1995, 28, L23–L28. [Google Scholar] [CrossRef]
- Van Reeth, P.; Humberston, J.W. Positronium formation in low energy s-wave positron–helium scattering. J. Phys. B At. Mol. Phys. Opt. Phys. 1995, 28, L511–L517. [Google Scholar] [CrossRef]
- Van Reeth, P.; Humberston, J.W. A partial-wave analysis of positronium formation in positron–helium scattering. J. Phys. B At. Mol. Phys. Opt. Phys. 1997, 30, L95–L100. [Google Scholar] [CrossRef]
- Van Reeth, P.; Humberston, J.W. Theoretical studies of threshold features in the cross-sections for low-energy e+-H and e+-He scattering. Nucl. Instrum. Methods B 2000, 171, 106–112. [Google Scholar] [CrossRef]
- Bransden, B.H. Atomic Collision Theory, Lecture Notes and Supplements in Physics; W. A. Benjamin, Inc.: New York, NY, USA, 1970. [Google Scholar]
- Kan, K.-K.; Griffin, J.J. Single-Particle Schrödinger Fluid. I. Formulation. Phys. Rev. C 1977, 15, 1126–1151. [Google Scholar] [CrossRef]
- Macek, J.H. Peripheral collisions of fast electrons with highly charged ions. AIP Conf. Proc. 2013, 1525, 111–113. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Bialynicka-Birula, Z.; Śliwa, C. Motion of vortex lines in quantum mechanics. Phys. Rev. A 2000, 61, 032110-1–032110-7. [Google Scholar] [CrossRef] [Green Version]
- Mathematica; 10.2; Wolfram Research, Inc.: Champaign, IL, USA, 2015.
- Microsoft® Publisher for Microsoft 365 MSO, version 2011; Microsoft Corporation: Redmond, WA, USA, 2020.
- Cooper, J.N.; Plummer, M.; Armour, E.A.G. Equivalence of the generalized and complex Kohn variational methods. J. Phys. A 2010, 43, 175302. [Google Scholar] [CrossRef]
- Woods, D.; Ward, S.J.; Van Reeth, P. Detailed investigation of low-energy positronium-hydrogen scattering. Phys. Rev. A 2015, 92, 022713-1–022713-17. [Google Scholar] [CrossRef] [Green Version]
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists, 7th ed; Elsevier: Boston, MA, USA; London, UK, 2013. [Google Scholar]
- Wolfram MathWorld. Available online: https://mathworld.wolfram.com/SphericalHankelFunctionoftheFirstKind.html (accessed on 12 July 2021).
- Wolfram MathWorld. Available online: https://mathworld.wolfram.com/SphericalHankelFunctionoftheSecondKind.html (accessed on 12 July 2021).
- Schwartz, C. Lamb shift in the helium atom. Phys. Rev. 1961, 123, 1700–1705. [Google Scholar] [CrossRef]
- Wu, M.-S.; Zhang, J.-Y.; Gao, X.; Qian, Y.; Xie, H.-H.; Varga, K.; Yan, Z.-C.; Schwingenschlögl, U. Confined variational calculation of o-Ps-He scattering properties. Phys. Rev. A 2020, 101, 042705-1–042705-6. [Google Scholar] [CrossRef]
- Wu, M.-S.; Zhang, J.-Y.; Qian, Y.; Varga, K.; Schwingenschlögl, U.; Yan, Z.-C. Confined variational calculation of positronium-hydrogen scattering below the positronium excitation threshold. Phys. Rev. A 2021, 103, 022817-1–022817-7. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).