Deep Minimum and a Vortex for Positronium Formation in Low-Energy Positron-Helium Collisions
Abstract
:1. Introduction
2. Theory
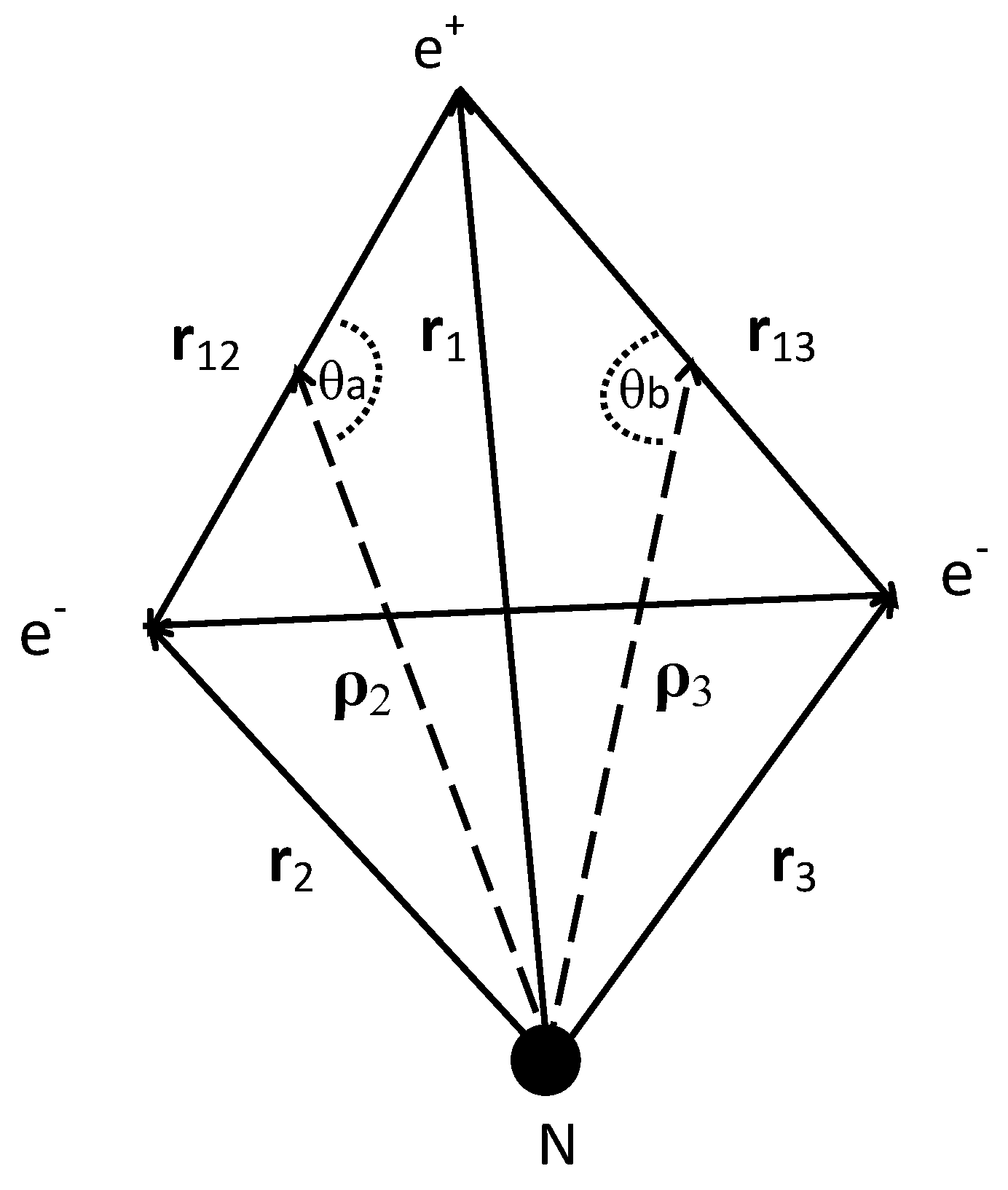
2.1. Scattering Theory for Ps-Formation in Positron–Helium Collisions
2.2. Extended Velocity Field Associated with the Ps-Formation Scattering Amplitude
3. Results
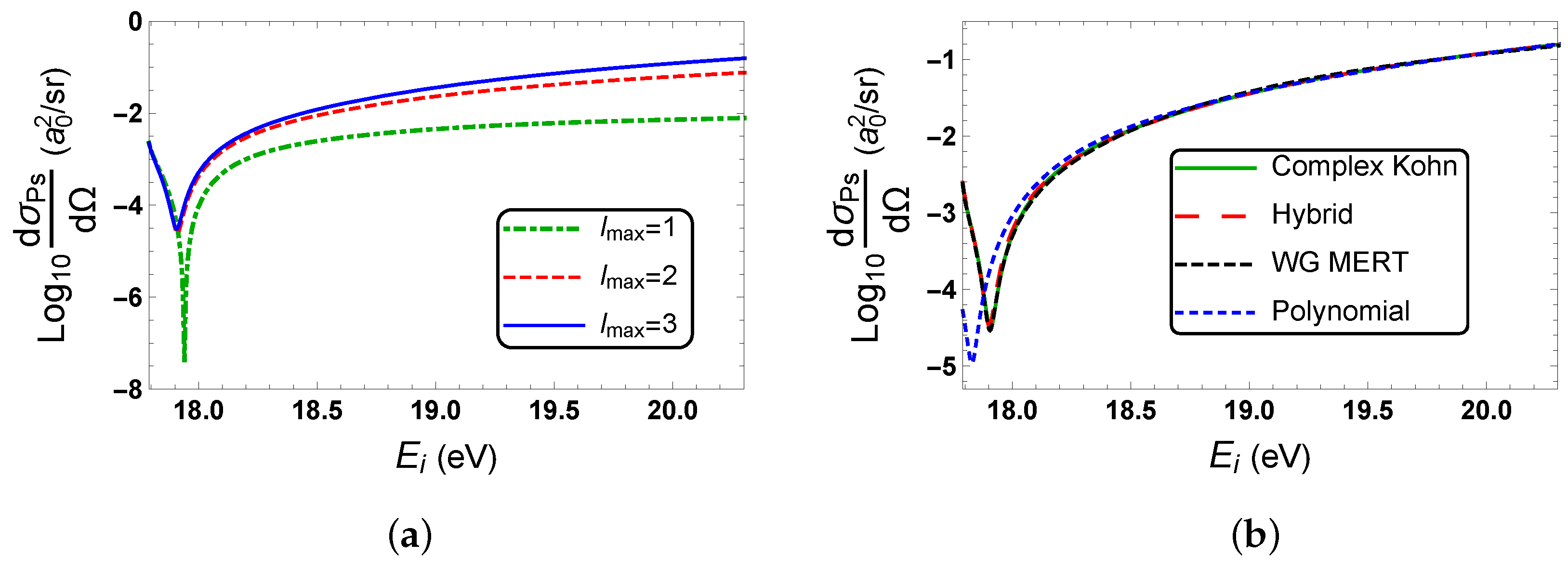
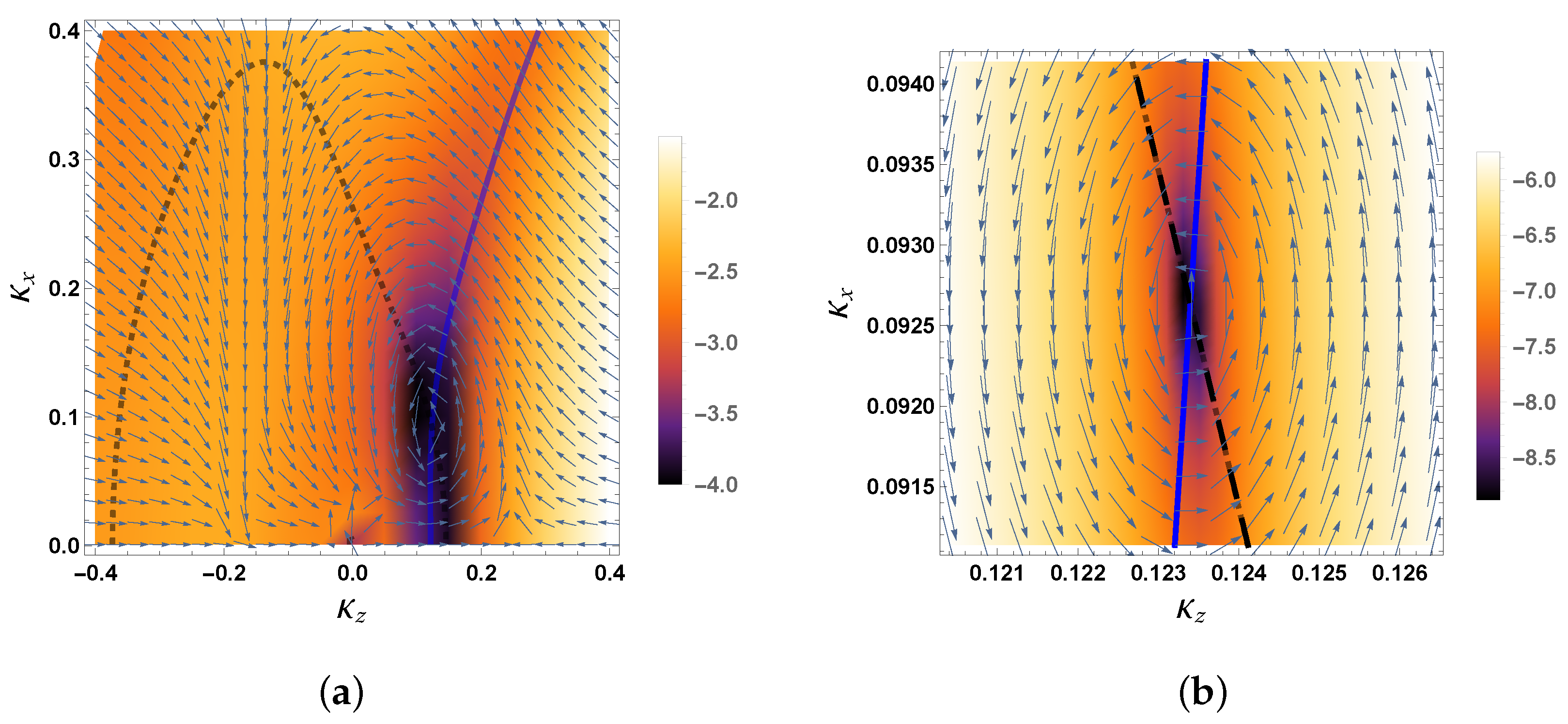
3.1. Deep Minimum in the Logarithm of the Ps-Formation DCS and the Position of the Zero in Ps-Formation Scattering Amplitude
3.2. Minimum in the Ps-Formation DCS in the Forward Direction
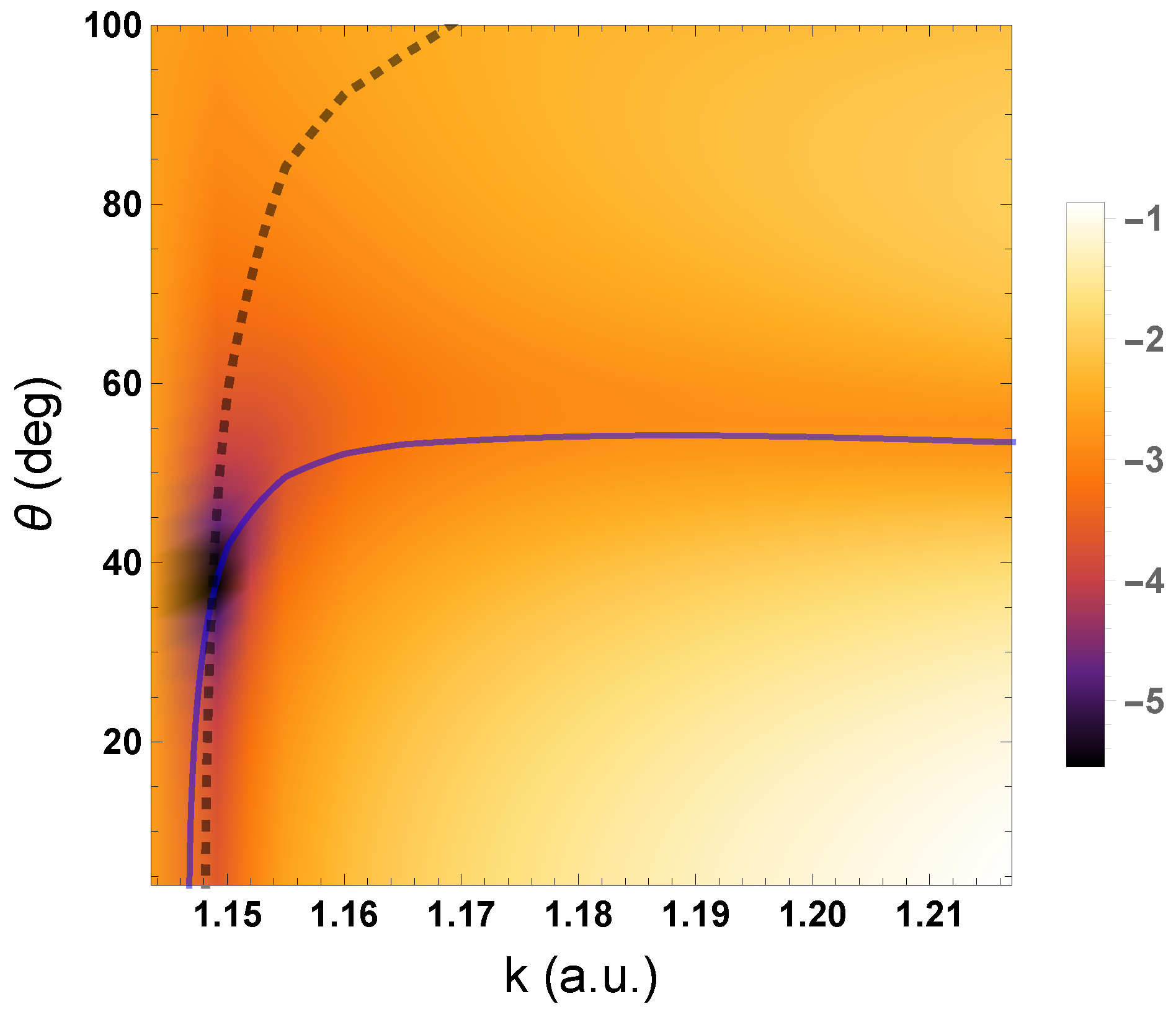
3.3. Extended Velocity Field Associated with the Ps-Formation Scattering Amplitude
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DCS | Differential Cross Section |
| WG MERT | Watanabe and Greene’s Multichannel Effective Range Theory |
Appendix A. Complex Kohn ℓth Partial Wave Trial Functions
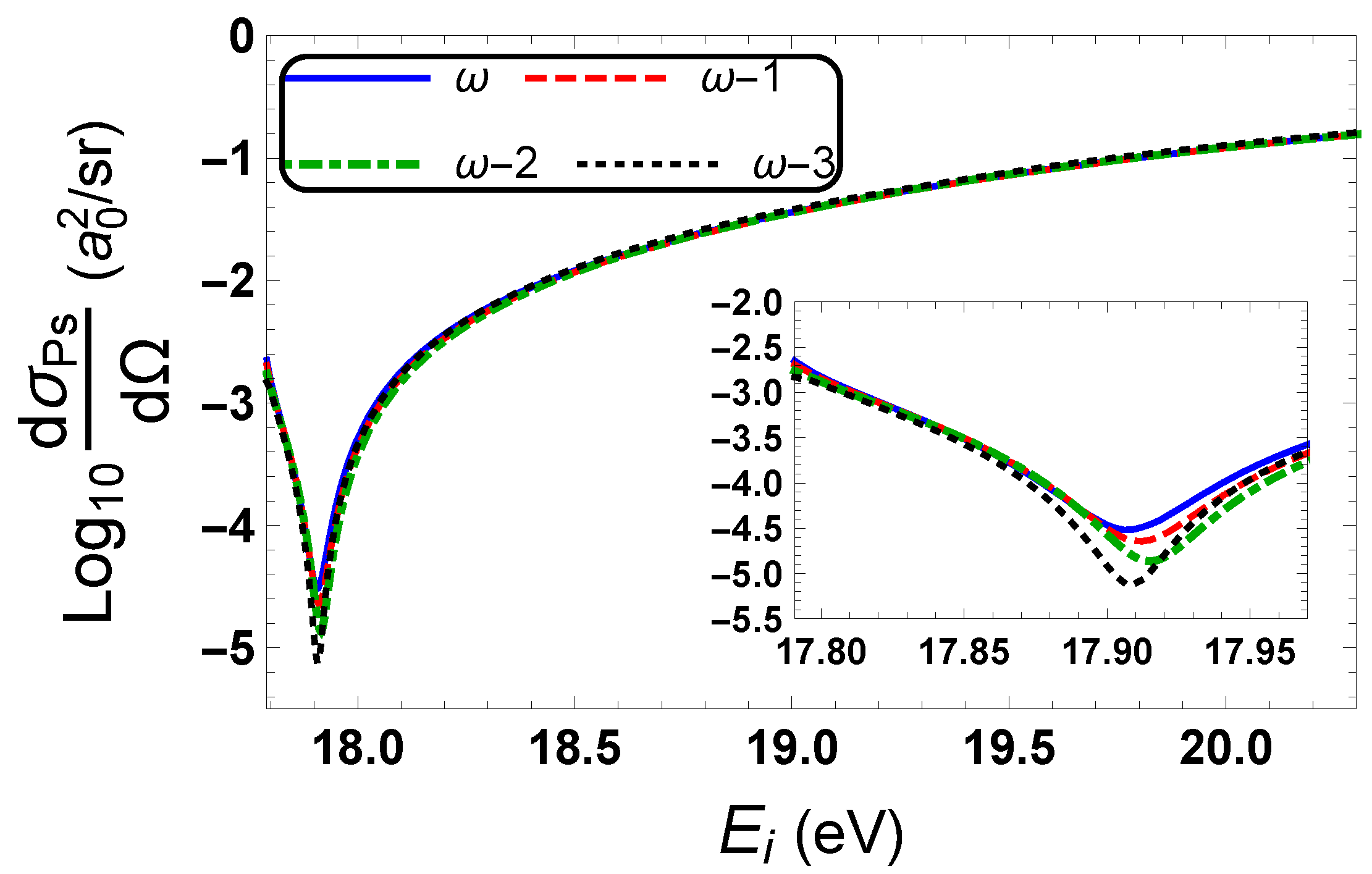
Appendix B. Numerical Investigations
| (deg.) | ||
|---|---|---|
| 8 | 1.1487 | 35.9 |
| 7 | 1.1485 | 34.6 |
| 6 | 1.1482 | 31.7 |
| 5 | 1.1477 | 21.8 |
| (deg.) | ||
|---|---|---|
| 6 | 1.1487 | 35.9 |
| 5 | 1.1489 | 34.8 |
| 4 | 1.1491 | 33.7 |
| (deg.) | ||
|---|---|---|
| 1.1487 | 35.9 | |
| 1.1487 | 33.6 | |
| 1.1486 | 30.2 | |
| 1.1481 | 27.3 |
References
- Charlton, M.; Humberston, J.W. Positron Physics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Laricchia, G.; Walters, H.R.J. Positronium collision physics. La Rivista Del Nuovo Cimento 2012, 35, 305–351. [Google Scholar]
- Schippers, S.; Sokell, E.; Aumayr, F.; Sadeghpour, H.; Ueda, K.; Bray, I.; Bartschat, K.; Murray, A.; Tennyson, J.; Dorn, A.; et al. Roadmap on photonic, electronic and atomic collision physics: II. electron and antimatter interactions. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 171002-1–171002-49. [Google Scholar] [CrossRef]
- Shipman, M.; Armitage, S.; Beale, J.; Brawley, S.J.; Fayer, S.E.; Garner, A.J.; Leslie, D.E.; Van Reeth, P.; Laricchia, G. Absolute differential positronium-formation cross sections. Phys. Rev. Lett. 2015, 115, 033401-1–033401-5. [Google Scholar] [CrossRef] [Green Version]
- Fayer, S.E.; Newson, D.M.; Brawley, S.J.; Loreti, A.; Kadokura, R.; Babij, T.J.; Lis, J.; Shipman, M.; Laricchia, G. Differential positronium-formation cross sections for Ne, Ar, Kr and Xe. Phys. Rev. A 2019, 100, 062709-1–062709-4. [Google Scholar] [CrossRef]
- Laricchia, G.; University College London, London, UK. Private Communication, 2021.
- Alrowaily, A.W.; Ward, S.J.; Van Reeth, P. Deep minima and vortices for positronium formation in low-energy positron–hydrogen collisions. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 205201-1–205201-11. [Google Scholar] [CrossRef]
- Ward, S.J.; Alrowaily, A.W.; Van Reeth, P. Deep minimum in the Ps-formation differential cross section for positron-helium collisions in the Ore gap. Bull. Am. Phys. Soc. 2020, 65(No. 4), E01.00028. Available online: https://meetings.aps.org/Meeting/DAMOP20/Session/E01.28 (accessed on 12 July 2021).
- Alrowaily, A.W. Deep Minima and Vortices for Positronium Formation in Positron-Hydrogen and Positron-Helium Collisions. Ph.D. Thesis, University of North Texas, Denton, TX, USA, 2021. [Google Scholar]
- Basic Atomic Spectroscopic Data. Available online: https://physics.nist.gov/PhysRefData/Handbook/Tables/heliumtable1.htm (accessed on 18 February 2021).
- Basic Atomic Spectroscopic Data. Available online: https://physics.nist.gov/PhysRefData/Handbook/Tables/heliumtable5.htm (accessed on 18 February 2021).
- The NIST Reference on Constants, Units, and Uncertainity. Available online: https://physics.nist.gov/cuu/Constants/energy.html (accessed on 18 February 2021).
- Armour, E.A.G.; Humberston, J.W. Methods and programs in collisions of positrons with atoms and molecules. Phys. Rep. 1991, 204, 165–251. [Google Scholar] [CrossRef]
- Van Reeth, P.; Humberston, J.W. The energy dependence of the annihilation rate in positron-atom scattering. J. Phys. B At. Mol. Opt. Phys. 1998, 31, L231–L238. [Google Scholar] [CrossRef]
- Watanabe, S.; Greene, C.H. Atomic polarizability in negative-ion photodetachment. Phys. Rev. A 1980, 22, 158–169. [Google Scholar] [CrossRef]
- Ward, S.J.; Hunnell, J.C.; Macek, J.H. The effect of the polarization potential on low energy atomic processes. Nucl. Instr. Methods Phys. Res. B 2002, 192, 54–62. [Google Scholar] [CrossRef]
- Ward, S.J.; Macek, J.H. Effective range analysis of positron–hydrogen collisions. Phys. Rev. A 2000, 62, 052715-1–052715-15. [Google Scholar] [CrossRef]
- Ward, S.J. Positronium formation in low-energy positron collisions with one- and two-electron atoms. Comments Mod. Phys. 2002, 2, D245–D261. [Google Scholar]
- Van Reeth, P.; Humberston, J.W. Elastic scattering and positronium formation in low-energy positron–helium collisions. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 3651–3667. [Google Scholar] [CrossRef]
- Drachman, R.J.; Omidvar, K.; McGuire, J.H. Differential cross section for positronium formation in positron-atomic-hydrogen collisions. Phys. Rev. A 1976, 14, 100–103. [Google Scholar] [CrossRef]
- Mandal, P.; Guha, S.; Sil, N.C. Positronium formation in positron scattering from hydrogen and helium atoms: The distorted-wave approximation. J. Phys. B At. Mol. Phys. 1979, 12, 2913–2924. [Google Scholar] [CrossRef]
- Sen, S.; Mandal, P. Positron-helium collisions: Positronium formation using the distorted-wave approximation. Phys. Rev. A 2009, 80, 062714-1–062714-10. [Google Scholar] [CrossRef]
- Ghoshal, A.; Mandal, P. Elastic differential cross section and critical point for positron–hydrogen collisions. Phys. Rev. A 2005, 72, 042710-1–042710-9. [Google Scholar] [CrossRef]
- Murray, A.J.; Read, F.H. Evolution from the coplanar to the perpendicular plane geometry of helium (e,2e) differential cross sections symmetric in scattering angle and energy. Phys. Rev. A. 1993, 47, 3724–3732. [Google Scholar] [CrossRef]
- Murray, A.J.; Read, F.H. Exploring the helium (e,2e) differential cross section at 64.6 eV with symmetric scattering angles but nonsymmetric energies. J. Phys. B At. Mol. Opt. Phys. 1993, 26, L359–L365. [Google Scholar] [CrossRef]
- Macek, J.H.; Sternberg, J.B.; Ovchinnikov, S.Y. Theory of deep minima in (e,2e) measurements of triply differential cross sections. Phys. Rev. Lett. 2010, 104, 033201-1–033201-4. [Google Scholar] [CrossRef]
- Ward, S.J.; Macek, J.H. Effect of a vortex in the triply differential cross section for electron impact K-shell ionization of carbon. Phys. Rev. A 2014, 90, 062709-1–062709-11. [Google Scholar] [CrossRef] [Green Version]
- Feagin, J.M. Vortex kinematics of a continuum electron pair. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 011001-1–011001-4. [Google Scholar] [CrossRef]
- Colgan, J.; Al-Hagan, O.; Madison, D.H.; Murray, A.J.; Pindzola, M.S. Deep interference minima in non-coplanar triple differential cross sections for the electron-impact ionization of small atoms and molecules. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 171001. [Google Scholar] [CrossRef]
- DeMars, C.M.; Kent, J.B.; Ward, S.J. Deep minima in the Coulomb-Born triply differential cross sections for ionization of helium by electron and positron impact. Eur. Phys. J. D 2020, 74, 48. [Google Scholar] [CrossRef]
- DeMars, C.M.; Ward, S.J.; Colgan, J.; Amami, S.; Madison, D.H. Deep minima in the triply differential cross section for ionization of atomic hydrogen by electron and positron impact. Atoms 2020, 8, 26. [Google Scholar] [CrossRef]
- Navarrete, F.; Della Picca, R.; Fiol, J.; Barrachina, R.O. Vortices in ionization collisions by positron impact. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 115203-1–115203-6. [Google Scholar] [CrossRef] [Green Version]
- Navarrete, F.; Barrachina, R.O. Vortices in the three-body electron-positron-proton continuum system induced by the positron-impact ionization of hydrogen. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 055201-1–055201-6. [Google Scholar] [CrossRef]
- Navarrete, F.; Barrachina, R.O. Vortices in ionization collisions. Nucl. Instrum. Phys. Res. B 2016, 369, 72–76. [Google Scholar] [CrossRef]
- Navarrete, F.; Barrachina, R.O. Vortices rings in the ionization of atoms by positron impact. J. Phys. Conf. Ser. 2017, 857, 012022. [Google Scholar] [CrossRef] [Green Version]
- Van Reeth, P. Theoretical Studies of Positronium Formation in Low Energy Positron-Helium Collisions. Ph.D. Thesis, University College London, London, UK, 1996. [Google Scholar]
- Van Reeth, P.; Humberston, J.W. The use of inexact helium wavefunctions in positron–helium scattering. J. Phys. B At. Mol. Phys. Opt. Phys. 1995, 28, L23–L28. [Google Scholar] [CrossRef]
- Van Reeth, P.; Humberston, J.W. Positronium formation in low energy s-wave positron–helium scattering. J. Phys. B At. Mol. Phys. Opt. Phys. 1995, 28, L511–L517. [Google Scholar] [CrossRef]
- Van Reeth, P.; Humberston, J.W. A partial-wave analysis of positronium formation in positron–helium scattering. J. Phys. B At. Mol. Phys. Opt. Phys. 1997, 30, L95–L100. [Google Scholar] [CrossRef]
- Van Reeth, P.; Humberston, J.W. Theoretical studies of threshold features in the cross-sections for low-energy e+-H and e+-He scattering. Nucl. Instrum. Methods B 2000, 171, 106–112. [Google Scholar] [CrossRef]
- Bransden, B.H. Atomic Collision Theory, Lecture Notes and Supplements in Physics; W. A. Benjamin, Inc.: New York, NY, USA, 1970. [Google Scholar]
- Kan, K.-K.; Griffin, J.J. Single-Particle Schrödinger Fluid. I. Formulation. Phys. Rev. C 1977, 15, 1126–1151. [Google Scholar] [CrossRef]
- Macek, J.H. Peripheral collisions of fast electrons with highly charged ions. AIP Conf. Proc. 2013, 1525, 111–113. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Bialynicka-Birula, Z.; Śliwa, C. Motion of vortex lines in quantum mechanics. Phys. Rev. A 2000, 61, 032110-1–032110-7. [Google Scholar] [CrossRef] [Green Version]
- Mathematica; 10.2; Wolfram Research, Inc.: Champaign, IL, USA, 2015.
- Microsoft® Publisher for Microsoft 365 MSO, version 2011; Microsoft Corporation: Redmond, WA, USA, 2020.
- Cooper, J.N.; Plummer, M.; Armour, E.A.G. Equivalence of the generalized and complex Kohn variational methods. J. Phys. A 2010, 43, 175302. [Google Scholar] [CrossRef]
- Woods, D.; Ward, S.J.; Van Reeth, P. Detailed investigation of low-energy positronium-hydrogen scattering. Phys. Rev. A 2015, 92, 022713-1–022713-17. [Google Scholar] [CrossRef] [Green Version]
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists, 7th ed; Elsevier: Boston, MA, USA; London, UK, 2013. [Google Scholar]
- Wolfram MathWorld. Available online: https://mathworld.wolfram.com/SphericalHankelFunctionoftheFirstKind.html (accessed on 12 July 2021).
- Wolfram MathWorld. Available online: https://mathworld.wolfram.com/SphericalHankelFunctionoftheSecondKind.html (accessed on 12 July 2021).
- Schwartz, C. Lamb shift in the helium atom. Phys. Rev. 1961, 123, 1700–1705. [Google Scholar] [CrossRef]
- Wu, M.-S.; Zhang, J.-Y.; Gao, X.; Qian, Y.; Xie, H.-H.; Varga, K.; Yan, Z.-C.; Schwingenschlögl, U. Confined variational calculation of o-Ps-He scattering properties. Phys. Rev. A 2020, 101, 042705-1–042705-6. [Google Scholar] [CrossRef]
- Wu, M.-S.; Zhang, J.-Y.; Qian, Y.; Varga, K.; Schwingenschlögl, U.; Yan, Z.-C. Confined variational calculation of positronium-hydrogen scattering below the positronium excitation threshold. Phys. Rev. A 2021, 103, 022817-1–022817-7. [Google Scholar] [CrossRef]


| K-Matrix | (deg.) | ||||
|---|---|---|---|---|---|
| Complex Kohn | 1 | 1.1483 | 7.9 | 0.1487 | 0.0205 |
| 2 | 1.1487 | 35.5 | 0.1265 | 0.0903 | |
| 3 | 1.1487 | 35.9 | 0.1261 | 0.0912 | |
| Hybrid | 3 | 1.1486 | 36.9 | 0.1234 | 0.0926 |
| WG MERT | 3 | 1.1486 | 35.6 | 0.1251 | 0.0894 |
| Polynomial | 3 | 1.1466 | 35.3 | 0.0991 | 0.0701 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrowaily, A.W.; Ward, S.J.; Van Reeth, P. Deep Minimum and a Vortex for Positronium Formation in Low-Energy Positron-Helium Collisions. Atoms 2021, 9, 56. https://doi.org/10.3390/atoms9030056
Alrowaily AW, Ward SJ, Van Reeth P. Deep Minimum and a Vortex for Positronium Formation in Low-Energy Positron-Helium Collisions. Atoms. 2021; 9(3):56. https://doi.org/10.3390/atoms9030056
Chicago/Turabian StyleAlrowaily, Albandari W., Sandra J. Ward, and Peter Van Reeth. 2021. "Deep Minimum and a Vortex for Positronium Formation in Low-Energy Positron-Helium Collisions" Atoms 9, no. 3: 56. https://doi.org/10.3390/atoms9030056
APA StyleAlrowaily, A. W., Ward, S. J., & Van Reeth, P. (2021). Deep Minimum and a Vortex for Positronium Formation in Low-Energy Positron-Helium Collisions. Atoms, 9(3), 56. https://doi.org/10.3390/atoms9030056






