Abstract
Molecular dynamic simulations of Li+, and Br− ions in acetonitrile were carried out. The simulated structural properties were compared to experimental data. The solvent potentials of Li+-Br−, Li+-Li+, and Br−-Br− were evaluated using constrained molecular dynamics (CMD) simulations, to determine the solvent contribution to the total force acting on the solute and estimate the liquid arrangements according to the potential of mean force (PMF) values. The PMF of friction kernels and the passage across the Li+-Br− barrier was studied using the Grote–Hynes theory. The union-separation development happens in the polarization confining system.
1. Introduction
Understanding ionic association in polar solvents at the molecular level is vital to interpreting many chemical and biological processes [1]. Much research is being carried out based on molecular dynamics simulations of ionic liquids in polar diluents, such as methanol and water [2,3,4]. Constrained molecular dynamics (CMD) [5] simulations are performed while maintaining a fixed interior separation. In this way, the ion–ion potential of mean force (PMF) and coefficients of relative friction can be obtained to determine the association constants. In addition, such simulations can reveal the behavior of ions and adjacent molecules at the microscopic level. A characteristic of the liquids mentioned is that, unlike acetonitrile (MeCN), they form hydrogen bridges.
Equations for deriving PMF values for lithium bromide in acetonitrile through simulations have not yet been established, although theoretical calculations can be performed via the Ornstein–Zernike equation using a hypernetted-chain (HNC) approach [6]. Acetonitrile is a widely used organic solvent whose molecules do not form hydrogen bonds, unlike water (H2O) and methanol (MeOH). In addition, it has a relative permittivity () significantly lower than that of water () and similar to that of methanol (). It can be beneficial to compare the results obtained with different solvents. The ion pair (Li+-Br−) was chosen in this study because data on neutron diffraction [7] and dielectric relaxation [8] are available for comparison. In the last 20 years, a great deal of progress has been made in the study of ions in solution (both aqueous and non-, and both experimental and theoretical). For example, the importance of explicit polarizability in models to describe solvation of anions such as Br− is well established, and certainly new experimental data using neutron scattering or other methods are available. Metal salt solutions in polar aprotic solvents have a wide range of uses, including electrolytes in electrochemical devices (such as lithium batteries with high energy density, capacitors, and so on) and reagents in organometallic chemistry. The details of interactions between dissolved salt ions and organic solvent molecules influence the density, viscosity, volatility, ionic conductivity, and other essential properties of ionic solutions. As a result, ion–solvent interactions appear to be critical for furthering our understanding of ionic solutions. The interaction of solvents with positive and negative ions differs significantly, making it difficult to obtain a thorough knowledge of the anion solvation mechanism. Because of the huge size of anions, their intricate geometry (for polyatomic anions) and charge distribution, anion solvent interactions are weaker than cation solvent interactions. Second, in aprotic solvents, anion solvation is mostly accomplished through hydrogen bonding, which is absent in anionic solvents. For these reasons, it is commonly assumed that metal salt dissolving in polar aprotic solvents occurs solely due to the solvation of metal cations, whereas anions remain uncoordinated by the solvent molecules. Nevertheless, a thorough investigation of monoatomic halide anions using both theoretical and experimental methods has revealed that these notions are oversimplified, and that interactions of the halide anion with polar aprotic solvent molecules is possible. The weak halide–solvent interactions, on the other hand, make theoretical analyses of halide solvation difficult, necessitating a fine balance between ion–solvent and solvent–solvent interactions. For bromide, as well as aprotic and non-polar solvents, this trend becomes very pronounced. When acetonitrile is utilized as the solvent, solvation numbers in the range of 1–9 are discovered in the literature for this anion. Furthermore, the solvent molecules’ molecular organization is not well understood [9,10,11].
The PMF values (W (r)) between particles with electrical charge in liquid perform a crucial part of the analysis of liquefied mixtures. CMD, as a computer simulation technique, is very useful for calculating W (r). CMD simulations can be used to calculate the mean force (MF) exerted on dissolved substance by solvent, whereas the separation between the solute is constrained. We used CMD and non-constrained (non-CMD) simulations to calculate the W(r) of Li+-Br−, Li+-Li+, and Br−-Br− and the dynamics of these particles with electrical charge.
This article is structured as follows. Details of our simulations and interaction potential models are given in Section 2. The ion–solvent structural properties obtained from the non-CMD simulations, the ion–ion MF along with PMF results obtained for all the simulations and the Li+-Br− pair friction kernel and the interconversion process are analyzed in Section 3. The conclusions of this paper are summarized in Section 4.
2. Materials and Methods
The PMF values for Li+-Br−, Li+-Li+, and Br−-Br− in acetonitrile have been evaluated. We carried out CMD simulations of systems built of two ions and 214 solvent molecules located in a cubic box with periodic boundary conditions. The volume of the cubic box (L = 26.58 Å) was selected to give a solvent density of 0.777 g/cm3 and with a temperature of 298 K. Additionally, non-CMD simulations were performed for two systems with free ions: one with Li+ and another with Br−. All code/programs-software used to perform the simulations were developed in-house. Mainly the simulations codes were developed using Fortran 77. The code included routines which evaluated the interaction potential, periodic conditions, integration algorithms, implementation of constraints (SHAKE procedure) and the mean force. See the Appendix A and Appendix B for simulation details.
We used an “acetonitrile rigid molecule pairwise additive potential model” [12,13] and performed calculations for the nitrogen (N), carbon (C) and methyl group (Me) interaction sites. Me is considered to be a unit atom model. The methyl-carbon and carbon-nitrogen distances were 1.458 Å and 1.157 Å, respectively, as shown in Figure 1. The dipole moment of each acetonitrile molecule is equal to 3.96 D.
Figure 1.
Molecular model of acetonitrile.
The ion–ion, ion–solvent and solvent–solvent interactions were evaluated using the following mathematical expression:
in terms of the Lennard–Jones parameters, , and is the charge allocated to the place i.
We used the parameters for Li+ and Br− derived by Chandrasekhar et al. [14] and Lybrand [15] from first principles computations of free ions in . The values of the parameters are summarized in Table 1. By using the same ion’s Lennard–Jones parameters for acetonitrile as for water, we are assuming that ε and σ transfer from one solvent to another.

Table 1.
Lennard–Jones Interaction potential parameters.
Table 2 summarizes the range of the interionic separation for each pair and the total number of simulations performed. Each simulation consisted of a stabilization interval of 25 ps followed by a generation time of 50 ps. For certain interionic separations, CMD simulations of 100 ps were carried out to calculate statistical errors and friction kernels, and for detailed study of the configuration of the solvent over the ion pairs. In the case of acetonitrile, an integration step of 0.005 ps was used. We used the integration algorithm of Berendsen et al. [16] with the SHAKE technique [17] to fix the molecular distances. The Lennard–Jones interactions were cut off at L/2 and the long-range exchanges were calculated by the Ewald sum technique [18].

Table 2.
Range of inter ion distances and total number of CMD simulations conducted for each ion pair.
Radial distribution functions . The number of particles in a volume dr centered at r, provided that one is at the origin is ; we know that depends solely on the modulus r, so we may better consider the number of particles contained in a spherical shell of radius r and r + Δr, given by , from this formula can be calculated as, .
In a practical simulation, a finite Δr is considered. At each time step of the numerical integration, all the pairs separated by a distance (r, r + Δr) would be counted and added to a histogram, then a coarse-grained g(r) is obtained.
Finally, we carried out two unconstrained simulations of Li+ and Br−, with 215 solvent molecules. The information obtained from these ion–solvent structure simulations is compared to the neutron diffraction data in Section 3. In addition, these simulations are representative of an infinitely diluted solution (zero concentration limit). According to Chandrasekhar and Jorgensen [19], the enthalpy of dissolution () can be determined from these simulations by means of the following expression:
where the last two terms are negligible under normal environmental conditions, and is the difference between the interaction energy of the infinite dilution system and the pure solvent ():
although these expressions are commonly used to determine from the simulations, we will use them in reverse to obtain an experimental estimate of from the experimental results of and U*.
Table 3 shows the values corresponding to our simulations, which are compared against the experimental values obtained from the procedure described above.

Table 3.
Comparison between the experimental and simulation results regarding the interaction energy of a solution at infinite dilution .
3. Results and Discussion
3.1. Ion–Acetonitrile Structural Properties
The structural properties obtained from the non-CMD simulations of Li+ and Br− ions in acetonitrile are shown in Figure 2 (left axis) in the form of ion-acetonitrile radial distribution functions . We similarly calculated the running coordination numbers () which is giving by where is the numeric solvent density. The function gives the mean number of molecules within a sphere of radius r centered on the ion. The coordination number is defined as the plateau value of at distances close to the first g(r) minimum (Figure 2, right axis). Table 4 summarizes the positions of the first peaks of , and the coordination numbers obtained from our simulations and neutron diffraction experiments. The most probable distances, Li+-N and Li+-C, are well-reproduced. For Li+ in acetonitrile, we obtain a coordination number slightly higher than the experimental one (5.5 instead of 3).
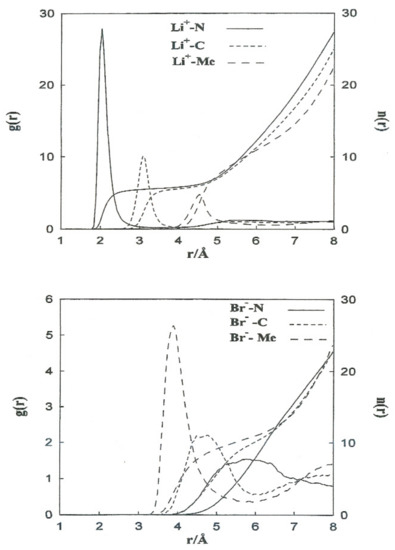
Figure 2.
Free ion–N (__________________), free ion–C (---------------), and free ion–Me (- - - - - - - -) radial distribution functions and running coordination numbers for Li+ (top) and Br− (bottom).

Table 4.
Ion-atom distances and corresponding coordination numbers.
Elastic neutron scattering measurements obtained by applying the first-order difference approach [22,23] yield experimental information about the arrangement of solvent molecules surrounding ions. This procedure establishes a difference function , which is a combination of the partial radial distribution functions corresponding to each solvent atom: , , . The experimental solubility of LiBr in acetonitrile is 0.58 M. We calculated the corresponding to this concentration from the for Li+ as follows:
where the constants A–F depend on the concentration and scattering lengths. The contribution of the first two terms of (4) pertains to distances beyond the first hydration shell, . The shape of the function resulting from the simulations is in agreement with the experimental results (Figure 3). We obtained the contribution to for the last three terms of (4). The results are consistent with the interpretation regarding the principal peaks. The discrepancies in the height of the peaks can be attributed to the deficiency in the interaction potentials used, as well as to experimental inaccuracies and the hydrogen atoms of the methyl group not being taken into account. Nevertheless, nearly all of the computer simulation studies described for acetonitrile and acetonitrile solutions are based on the hypothesis of rigid molecular models that do not explicitly consider the hydrogen atoms of the methyl group. With this assumption, the computing time is substantially decreased, and longer simulations of larger systems can be carried out.
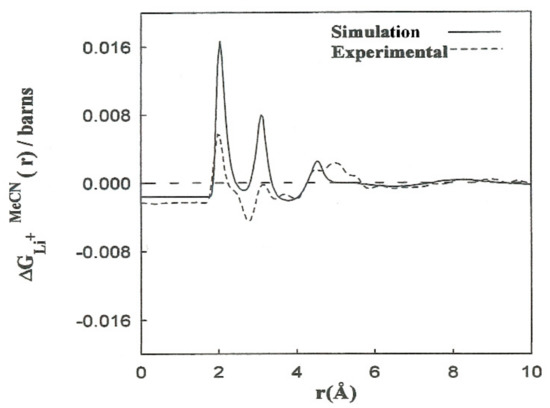
Figure 3.
Comparison between the functions resulting from the CMD simulations (________) and (- - - -) the experiments from Ref. [7].
Table 4 summarizes the positions of the first peaks of , and the coordination numbers obtained from our simulations and neutron diffraction experiments. The most probable distances, Li+-N and Li+-C, are well-reproduced. For Li+ in acetonitrile, we obtain a coordination number slightly higher than the experimental one (5.5 instead of 3). This failure of simulations can be attributed to the deficiency in the interaction potentials used and the hydrogen atoms of the methyl group not being considered explicit.
3.2. Mean Force Potentials
The force (∆F(t;r)) applied by N solvent molecules along the intermolecular axis of two A and B ions is indicated by:
the resultant forces FAS(t; r) and FBS(t; r) acting on the solute caused by the molecular liquid, mA and mB are the masses of the solute, is the unit vector alongside the AB path and is the reduced mass. This expression is calculated at every single time interval and averaged throughout the entire simulation. Where Fd(r) is the direct solute force, and the resultant MF between ions is:
where . W(r) was calculated by integrating the mean force:
W(r0) was calculated so the PMF values matched the macroscopic Coulomb potential at large distances ( and used the experimental acetonitrile relative permittivity (). Table 2 summarizes the range of interionic separation for each pair and the total number of simulations performed.
The statistical errors for W(r) and ΔF were analyzed as stated by the method outlined in the ref. [24]. Table 5 shows the statistical inefficiency (), standard deviation () and estimated statistical errors () values according to several interionic distances and simulation lengths. Simulations beyond 50 ps provided no further benefit. The estimated errors for the mean force potentials for the various ion pairs range between and .

Table 5.
Error estimates: value to the ion–ion PMF ().
The MF acting on every single ion is shown in Figure 4, jointly with the direct (Fd) and solvent (∆F(r)) contributions to the Li+-Br−, Li+-Li+, and Br−-Br− pairs. The contributions of the solvent (∆F(r)) are opposite to the direct ion–ion force in all the systems.
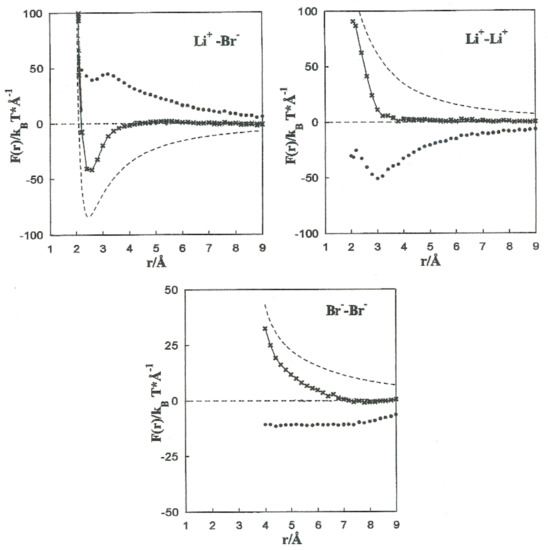
Figure 4.
Contributions to the mean force acting on the Li+-Br−, Li+-Li+, and Br−–Br− ion pairs. -------- Fd, •••••••• ∆F(r), -*-*-*-*-F(r).
This is constant with the trend of polar liquids to produce stable complexes in the case of like-ion pairs, and to separate ions with opposite signs [2,3,4,5]. Equilibrium between the direct and solvent contributions results in a repulsive force acting on the Li+-Li+ pair at all distances. For the Li+-Br− pair, the resultant force is repulsive at extremely small distances and attractive at middle separation. The total force on the Br−-Br− pair has similar tendencies, but the attractive component is considerably less significant.
Figure 5 shows the PMF values for the various ion pairs. Oscillations in the potential corresponding to Li+-Br− occur in association with the structure of the solvent in the vicinity of the ions. W(r) shows a noticeable minimum at 2.2 Å and lower one at 8.0 Å. The contact ion pair (CIP) region corresponding to the first minimum, and for the solvent separated ion pair (SSIP) region the second one. W(r) shows a maximum at r = 4.4 Å. In the CIP region, the ion pairs are enclosed by acetonitrile particles, with the corresponding nitrogen atoms geared to the Li+ and their methyl groups in the direction of Br−, as illustrated in Figure 6. The SSIP region values are attributed to attractive forces produced by solvent molecules between ion pairs.
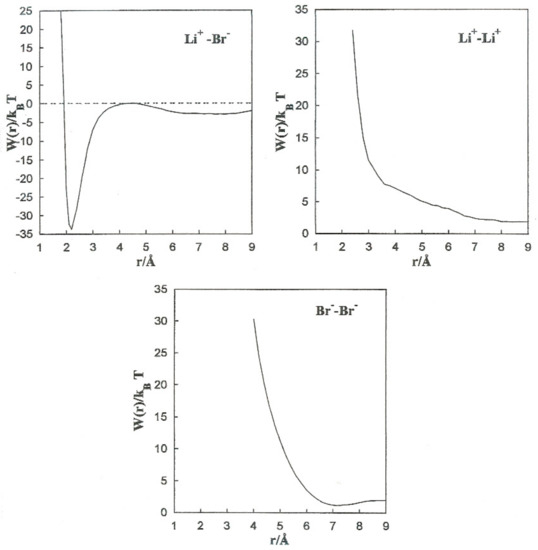
Figure 5.
Mean force potentials for the various ion pairs.
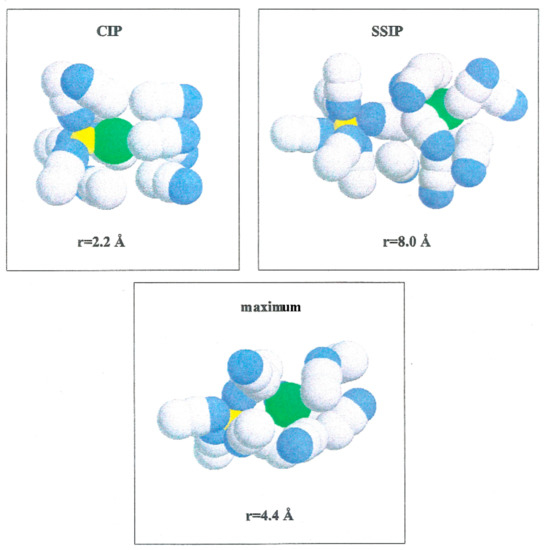
Figure 6.
Configurations of acetonitrile clusters that illustrating the compositions of solvent molecules over ion pairs at various interionic separations. Li+ (yellow color), Br− (green color), N (blue color) and C and Me (gray color).
The stability of the CIP and SSIP regions is indicated by the association constants [25]. For the CIP and SSIP state we have the following expressions
where is the Avogadro’s number and is a cut-off parameter that we have chosen as the position of the first potential of mean force W(r) maximum, and is some value of r for which it is considered that the diffusive motion is a good approximation. Moreover, the equilibrium constant is giving by
we calculate the association constants and and the equilibrium constant, as shown in Table 6. We found that . The value obtained from the equilibrium constant () indicates much less stable configurations in the SSIP region compared to the CIP region.

Table 6.
Li+-Br− association-dissociation barrier heights in and association constants in 1/mol (ion–ion distances are in Å).
W(r) for Li+-Li+ is repulsive and decreases monotonically to zero. Even though the acetonitrile molecules located near the ion pairs have their nitrogen atoms toward Li+, as shown in Figure 7, the electrostatic interaction N-Li+ is less important than Fd.
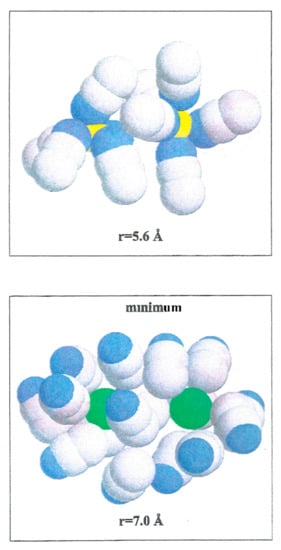
Figure 7.
Configurations of acetonitrile clusters illustrating the arrangements of solvent molecules around Li+-Li+, and Br−-Br− ion pairs at two interionic separations. Li+ (yellow color), Br− (green color), N (blue color) and C and Me (gray color).
The Br−-Br− pair conformation is steadied at a separation corresponding to the minimum (r = 7.0 Å) of W(r) by the acetonitrile molecules enveloping it. Their methyl atoms are oriented toward the Br− ions due to an attractive interaction. The structure is stabilized by the methyl atoms of the liquid molecule in the central area.
To carry out a more quantitative analysis of the distribution of the liquid molecules around the ionic particles, we determined the radial ion–solvent distribution functions (left axis) and their corresponding coordination numbers (right axis) for different interionic separations. Figure 8 and Figure 9 show the radial distribution functions, Ion-Me, Ion-C and Ion-N, obtained in the situation of the Li+-Br− ion pair for the interionic separations corresponding to rCIP, rSIP and the maximum value of W(r). Table 7 summarizes the positions of the maximum and minimum radial distribution functions for the various cases analyzed. The corresponding coordination numbers are given in Table 8. A coordination number () of 23 for a free bromide ion in acetonitrile is large. This value may be attributed to the deficiency in the interaction potentials used. Nevertheless, other studies indicate that the solvation shell of the Br-anion can have a maximum number of molecules of acetonitrile bigger than 10 [9]. It should also be pointed out that in aqueous solutions coordination numbers increase when the concentration decrease [26].
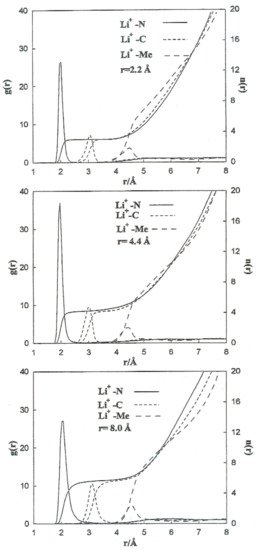
Figure 8.
Radial distribution functions and running coordination numbers for Li+ at various interionic separations for the Li+-Br− ion pair.
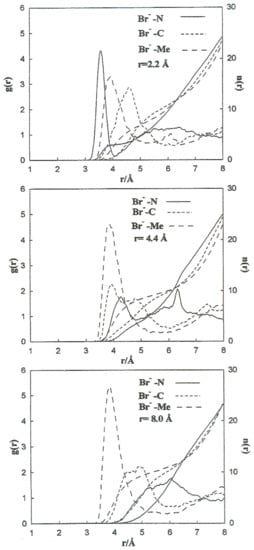
Figure 9.
Radial distribution functions and running coordination numbers for Br− at several interionic separations for the Li+-Br− ion pair.

Table 7.
Maximum () and minimum () radial distribution functions for the various cases.

Table 8.
Ion–solvent coordination numbers for each ion pair and interionic separation.
3.3. Li+-Br− Interconversion and Friction Kernels
The friction kernels depend on the ionic species and interionic distances [27].
We determined the transmission coefficient () of the barrier at 4.4 Å according to the Grote–Hynes theory of chemical reactions in a solution. In this model, the reaction coordinate develops by a global Langevin equation. The transmission coefficient (subscript GH or Kr stand for Grote–Hynes or Kramers) can be obtained as:
where is the barrier frequency, obtained by extrapolating an inverted parabola with an apex equivalent to the maximum PMF value. (reactive frequency) is the result of the next expression:
It is follows that is the characteristic frequency for the unstable motion at the transition state. For the coefficients involved in the previous theory regarding the Li+-Br−, Li+-Li+, and Br−-Br− systems, the initial values of the friction kernels ( are summarized in Table 9. The initial time values of the kernels are not only dependent on the ionic species but also show noticeable changes with the interionic separation. This interionic separation dependence of is strongly related to the magnitude of the changes in the solvent structure around the ion pairs as a function of these separations. The normalized friction kernels () related through all cases are displayed in Figure 10 and Figure 11. There are features common to the functions of both systems, all of which show a rapid and very similar initial decay before 0.2 ps. A lengthy decay follows, characterized for each individual system.

Table 9.
Initial values of the friction kernels for all ion pairs and interionic separations.
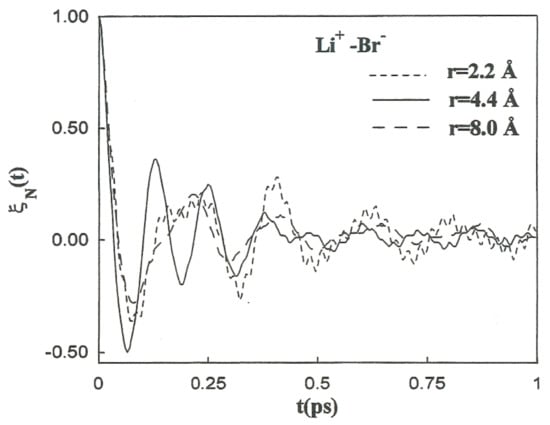
Figure 10.
Normalized friction kernels for the Li+-Br− ion pair at various interionic separations.
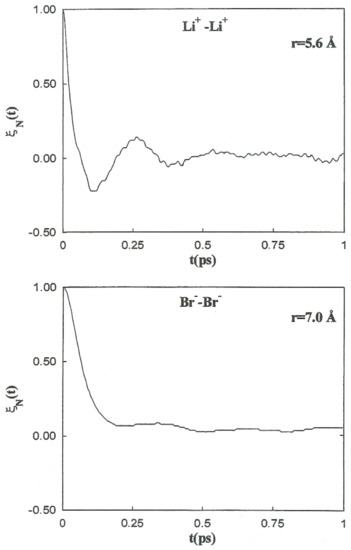
Figure 11.
Normalized friction kernels for the Li+-Li + ion pair (top) and Br −-Br− ion pair (bottom) at various interionic separations.
The coefficients involved in the Li+-Br− system are summarized in the Table 10.

Table 10.
Li+-Br− association-dissociation process parameters and reaction constants.
, gives us a temporal measure of the transition state in the presence of the solvent. We determined that, for acetonitrile, .
The correlation time of the friction of the solvent acting on the ion pair ( is defined by the value of the integral of the normalized kernel function:
In the case of acetonitrile, the correlation time is shorter than the reaction time.
A polarization caging regime is verified because a negative amount for the nonadiabatic barrier frequency ( was found [28]. In this regime, the solvent immediately catches the solute in a well or “polarization cage” of solvent molecules. Hence, the motion of solvent molecules is extremely crucial. A limiting case of the polarization caging regime is when and designated as adiabatic. In such circumstances, the predictions of the Grote–Hynes theory are reduced to Kramers doublets. Our results confirm that for the Li+-Br− ion pair, .
Lastly, we computed the full rate constants for the dissociation () and association () processes, given by [27,29]:
whereby is the reduced mass of the ion pair, is the transmission coefficient, is the interionic separation at the transition state (i.e., the top barrier), and is an arbitrary interionic distance beyond the outer boundary of the SSIP region, where there is no further interactivity. The results are summarized in Table 10. We have obtained a rate constant that is roughly smaller than . This is due to the greater stability of the CIP complex for the present model system since a value of was obtained for . Our overall constant rate corresponds to a relaxation time of approximately 835 ps. Values for were found. In such circumstances, the predictions of the Grote–Hynes theory are reduced to Kramers doublets. From the transmission coefficient values () results confirm the case called regime adiabatic and for the Li+-Br− ion pair, . A polarization caging regime is verified because a negative amount for the nonadiabatic barrier frequency ( was found.
4. Conclusions
The results reported in this paper on structural properties are in agreement with the experimental data; for instance, we carried out two unconstrained simulations of Li+ and Br−, with 215 solvent molecules. The information obtained from these ion–solvent structure simulations is compared to the neutron diffraction data (Table 3). We also obtain a coordination number for Li+ in acetonitrile, slightly higher than the experimental one (5.5 instead of 3—Table 4). This failure of simulations can be attributed to the deficiency in the interaction potentials used and the hydrogen atoms of the methyl group not being considered. We obtained PMF values for Li+-Br−, Li+-Li+, and Br−-Br−. For the Li+-Br− ion pair, the diluter allows sets two stable interionic separations, a CIP and a SSIP; where the CIP is more stable. The Li+-Li+ system is repulsive. The Br−-Br− pair composition is equilibrated at a distance corresponding to the lowest value (r = 7.0 Å) of W(r) by the adjacent acetonitrile molecules. The friction kernels and interconversion process of the Li+-Br− ion pair were evaluated. The passage of the barrier happens in the polarization caging regime. The correlation time of the solvent is much shorter than the reaction time and the Kramers regime of the Grote–Hynes theory was found for the system.
Funding
Dr. Reinhardt Pinzón acknowledges funding from SNI (Sistema Nacional de Investigación), the APC was covered by R.P. SNI funds, Contract No. 159-2018 of SENACYT (Secretaria Nacional de Ciencia y Tecnología e Innovación), project FID2016-275, and from a MUTIS fellowship from Institute Catalan de Cooperación Internacional.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank the editor and reviewers for their time and constructive comments, which have helped improve our manuscript. R.P. would like to acknowledge the support provided by Elvira Guardia I Manuel (EG), who is a professor at Department de Física i Enginyeria Nuclear Universitat Politècnica de Catalunya, Barcelona Spain.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Grote–Hynes Theory
We have seen that great progress has been made in the direction of linking the rate constants with microscopic properties. Several equivalent expressions involving time correlations functions have been deduced [27], so that it is clear what should be calculated. However, the theoretical calculation of rate constants is an extremely difficult task. Actually, we could regard computer simulations as the only feasible “theoretical” calculations for realistic systems.
The first contribution was that of Kramers [30]. The basic idea is borrowed from the Langevin formulation of the Brownian motion. He modeled the time evolution of the reaction coordinate of an active process as a Brownian particle under the influence of an external potential. This model has proven to be useful to describe the motion of a large and massive single particle inside a fluid. Mathematical:
the first term is the friction that acts on the particle of mass m and ξ is the friction coefficient. The second term , is a random force with zero mean and uncorrelated with the initial velocity, which mimics the chaotic impacts with solvent molecules. From the energy point of view, the friction drags energy from the particle, and the random force restores it. Therefore, if there is thermal equilibrium (a null mean flow of energy), the following equation should hold:
which is called the second fluctuation dissipation theorem.
However, if the model is applied to electrolytes, we cannot consider that the ions are massive and large particles in comparison with acetonitrile molecules. As a consequence, the random forces will keep some degree of correlation in a short time, because the time scales for the solvent and solute dynamics are comparable.
In the Grote–Hynes theory, the reaction coordinate obeys a generalized Langevin equation [30,31].
where the friction coefficient is replaced by a memory function of friction kernel , µ is a reduced mass of particles that conform the solute and . The first term of the above equation is the gradient of the potential of the mean force regarding the reaction coordinate. R(t) is a stochastic force with zero mean and is uncorrelated with the initial velocity and modeled by a Gaussian process. In this case,
If the dynamics are studied in the vicinity of the transition state, the barrier can be approximated as an inverted parabola of frequency . Grote and Hynes have deduced the following expression for the transmission coefficient,
From the analysis of the model, it follows that is the characteristic frequency for the unstable motion at the transition state. is determined through the equation,
is the Laplace transform of the time dependent friction coefficient,
The basic assumptions of this approach are:
- (a)
- The generalized Langevin equation is a valid description;
- (b)
- The friction kernel ξ ’ does not depend on the reaction coordinate;
- (c)
- The mean force barrier is parabolic.
If we approach the friction coefficient dependent on time to a delta function; namely, , with the friction coefficient constant given by,
Then, the Kramers theory can be recovered from this model and the transmission coefficient is given by,
Another case is the non-adiabatic limit, where the solvent remains essentially static during the time scale of the motion at the barrier. The effect of the friction is almost constant and equal to its time zero value . The transmission coefficient in the extreme case of constant friction is,
where is called the non-adiabatic barrier frequency. In this case it can be interpreted as the solute moving under the influence of an instantaneous barrier of frequency instead of ,
One particular situation is that in which is negative; it is called the polarization caging regime. The reaction coordinate is trapped in a well rather than moving on an inverted parabola. Here, it is clear that the movement of the solvent is key to allowing this instantaneous configuration to relax.
Appendix A.2. Friction Kernels from Molecular Dynamics
The Grote–Hynes description of the reaction coordinate assumes previous knowledge of the potential of mean force and the friction kernel. There is a method for evaluating the friction kernel in the limit case called the frozen bond approximation [31,32].
The method is based on the following idea: when we assume the generalized Langevin equation, one of the hypotheses is that the whole dependence on the reaction coordinate is contained in the potential of the mean force. On this basis, it seems reasonable that should not depend on the interparticle potential.
When there is a harmonic potential of interaction for the coordinate of interest, it is possible to obtain the corresponding memory function as,
Following the Mori formalism, it follows that
with
The renormalized frequency,
where can be obtained through the relations
Following this method, we can obtain the memory function parameterized as a function of and ω
It has been demonstrated that the limit corresponds to the aforementioned frozen bond approximation. This method is implemented in a molecular dynamics simulation program; the reaction coordinate is constrained to the x0 during the simulation and the friction kernel is calculated as the autocorrelation function,
where the instantaneous values ΔF(t, r0) are given by Equation (5) and,
Appendix B
Appendix B.1. Computer Simulation. Molecular Dynamics (MD)
We took a Molecular Dynamics approach for the present study. The basic assumption is the Born–Oppenheimer approximation. The motion of electrons and nuclei is treated separately. It rests on the fact that electrons are lighter than atomic nuclei. So, it is a good approximation to calculate the ground state of the electrons as if the nuclei were static.
The next is to treat the movement of the nuclei using classical mechanics. We are not interested in low temperatures or chemical reactions that involve electronic transitions from the ground state [31,32].
Appendix B.2. Interaction Potential
The full determination of the potential energy surface is an extremely complicated task even for a few atoms. Therefore, a solution is to split the potential function into a sum that will include terms depending on pairs of atoms, terms depending on triples of atoms, and terms involving quadruples. Each term will depend on a limited number of parameters. An alternative to determine these parameters is to fit them to theoretical as well as to experimental results and later on refine them until the properties calculated from the simulation are considered satisfactory [31,32].
The force field to simulate a lithium bromide solution (vectors represent the positions of the N atoms of the system) is given by:
The first term describes the interaction between pairs of ions. The second and third sums constitute the model for acetonitrile molecules. Finally, the last term represents the interaction between the ions and the acetonitrile molecules.
Appendix B.3. System Size and Periodic Conditions
The particles of interest lie in a central cell, which is surrounded by exact replicas. When one of the particles leaves the central shell through one face, its periodic image will enter it through the opposite face of the cube, so that we always have the same number of particles. The particles in the central cube are considered to interact with those of the neighboring images. The usual approximation is to fix a cut-off for the range of the interaction potentials. Each particle in the central box is considered to interact only with those that are at a distance lower than some value . In this work, was chosen equal to L/2, L being the length of the cubic central shell. This procedure is fine for the short-range interactions since they show a rapid decay with distance. However, the Coulomb interactions decay as r−1. To overcome this problem, we used the Ewald summation technique. The basic idea is that the potential energy associated with the Coulomb interactions should be computed as a sum over all pairs for which at least one of the atoms lies in the central box [31,32].
with integers. The prime indicates that the case i = j should not be considered for , and that the given pair i-j must be excluded when if the charges belong to the same molecule.
Appendix B.4. Integration Algorithms
If we are only considering the potential energy for the calculation of the forces, then the system is being studied at a fixed volume, number of particles, and energy [31,32]. The results obtained will correspond to the microcanonical ensemble. The corresponding equations of motion are:
The practical way to solve them is using the leap-frog algorithm of the following steps:
Evaluate forces at time t. Next, evaluate velocity for each particle. Evaluate positions for each particle. Here we are going to focus on simulations at a constant temperature. The equations that have to be solved in this approach are:
β is an arbitrary parameter that specifies the time scale of temperature fluctuations. T0 denotes the reference temperature of the system and T(t) the instantaneous temperature.
Appendix B.5. Implementation of Constraints
The Newton equations for a system with constraints can be derived from Hamilton’s principle [31,32],
are the direct forces, and λk is a set of Lagrange multipliers that has to be determined from the equations that define constraints,
In principle, can be found solving a system of linear equations and being substituted back in Equation (A25). The solution consists of approximating the exact Lagrange multipliers by a set of parameters which must guarantee that the constraints are maintained at each time step with a certain tolerance. These parameters are determined iteratively at each time step, considering the constraints in a sequential order within each iteration. This procedure is called SHAKE [17].
Appendix B.6. The Method of the Mean Force
The free energy A has the property that the work done by the system in a reversible process can be written [31,32],
If we take as additional parameters for A the positions of N solute particles (A (N, V, T, r1, …, rN)), the work done by the system in an ideal reversible process in which the N particles are infinitesimally moved is:
We are interested in the free energy as a function of the interionic vector . For this particular choice,
where is the force on the interionic axis. For symmetry reasons, A will only depend on the modulus of r and multiplying (A29) with a unitary vector , then , the equality comes from the fact that will be directed along . From this equation, we can calculate the free energy with a simple integration:
where , Fd is just the direct force that can be calculated from the interparticle potential and is the contribution from the solvent.
References
- Conway, B. Ionic Hydration. In Chemistry and Biophysics; Elsevier: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Guardia, E.; Rey, R.; Padro, J.A. Potential of mean force by constrained molecular dynamics: A sodium chloride ion-pair in water. Chem. Phys. 1991, 155, 187. [Google Scholar] [CrossRef]
- Guardia, E.; Rey, R.; Padro, J.A. Na+–Na+ and Cl−–Cl− ion pairs in water: Mean force potentials by constrained molecular dynamics. J. Chem. Phys. 1991, 95, 2823. [Google Scholar] [CrossRef]
- Sese, G.; Guardia, E.; Padro, J.A. Ionic association of Na+-Cl-, Na+-Na+ and Cl−-Cl− in methanol: Mean force potentials and friction kernels. J. Phys. Chem. 1995, 99, 12647. [Google Scholar] [CrossRef]
- Ciccotti, G.; Ferrario, M.; Hynes, J.T.; Kapral, R. Constrained molecular dynamics and the mean potential for an ion pair in a polar solvent. Chem. Phys. 1989, 129, 241. [Google Scholar] [CrossRef]
- Richardi, J.; Fries, P.H.; Krienke, H.J. The solvation of ions in acetonitrile and acetone: A molecular Ornstein–Zernike study. Chem. Phys. 1998, 108, 4079. [Google Scholar] [CrossRef]
- Cartailler, T.; Kunz, W.; Tung, P.; Bellisent-Funel, M.-C. Lithium bromide in acetonitrile and water: A neutron scattering study. J. Phys. Condens. Matter. 1991, 3, 9511. [Google Scholar] [CrossRef]
- Barthel, J.; Kleebaner, M.; Buchner, R. Dielectric relaxation of electrolyte solutions in acetonitrile. J. Solution Chem. 1995, 24, l. [Google Scholar] [CrossRef]
- Erkabaev, A.M.; Yaroslavtseva, T.V.; Reznitskikh, O.G.; Bushkova, O.V. Solvation of anions in acetonitrile solutions: FTIR and quantum chemical study for Br−, ClO4−, AsF6−, and CF3SO3. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020. [Google Scholar] [CrossRef]
- Erkabaev, A.M.; Yaroslavtseva, T.V.; Popov, S.E.; Bushkova, O.V. FTIR and quantum chemical study of LiBr solvation in acetonitrile solutions. Vib. Spectrosc. 2014, 75, 19–25. [Google Scholar] [CrossRef]
- Ayala, R.; Martínez, J.M.; Pappalardo, R.R.; Muñoz-Páez, A.; Marcos, E.S. The solvation of bromide anion in acetonitrile: A structural study based on the combination of theoretical calculations and X-ray absorption spectroscopy. Mol. Simul. 2006, 32, 1035–1043. [Google Scholar] [CrossRef]
- Guardia, E.; Pinzón, R.; Casulleras, J.; Orozco, M.; Luque, F.J. Comparison of Different Three-site Interaction Potentials for Liquid Acetonitrile. Mol. Simul. 2001, 26, 4. [Google Scholar] [CrossRef]
- Guardia, E.; Pinzón, R. On the solvation shell of Na+ and Cl− ions in acetonitrile: A computer simulation study. J. Mol. Liq. 2000, 85, 33–44. [Google Scholar] [CrossRef]
- Chandrasekhar, J.; Spellmeyer, D.C.; Jorgensen, W.L. Energy component analysis for dilute aqueous solutions of lithium(1+), sodium(1+), fluoride(1−), and chloride(1−) ions. J. Am. Chem. Soc. 1984, 106, 903. [Google Scholar] [CrossRef]
- Lybrand, T.P.; Closh, L.; McCammon, J.A. Hydration of chloride and bromide anions: Determination of relative free energy by computer simulation. J. Am. Chem. Soc. 1985, 107, 7793. [Google Scholar] [CrossRef]
- Berendsen, J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684. [Google Scholar] [CrossRef] [Green Version]
- Ciccotti, G.; Fenario, M.; Ryckaert, J.P. Molecular dynamics of rigid systems in cartesian coordinates A general formulation. Mol. Phys. 1982, 47, 1253. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987; Capitulo 5. [Google Scholar]
- Chandrasekhar, J.; Jorgensen, W.L. The nature of dilute solutions of sodium ion in water, methanol, and tetrahydrofuran. J. Chem. Phys. 1982, 77, 5080. [Google Scholar] [CrossRef]
- Marcus, Y. Ion Solvation; Wiley-Interscience: Chichester, UK, 1985. [Google Scholar]
- An, X.W.; Mansson, M. Enthalpies of combustion and formation of acetonitrile. J. Chem. Thermodyn. 1983, 15, 287. [Google Scholar] [CrossRef]
- Enderby, J.E. Neutron Scattering From Ionic Solutions. Ann. Rev. Phys. Chem. 1983, 34, 155. [Google Scholar] [CrossRef]
- Soper, A.K.; Neilson, G.W.; Enderby, J.E.; Howe, R.A. A neutron diffraction study of hydration effects in aqueous solutions. J. Phys. Chem. 1977, 10, 1793. [Google Scholar] [CrossRef]
- Guardia, E.; Rey, R.; Padro, J.A. Statistical Errors in Constrained Molecular Dynamics Calculations of the Mean Force Potential. Mol. Sim. 1992, 9, 201. [Google Scholar] [CrossRef]
- Justice, M.C.; Justice, J.C. Ionic interactions in solutions. I. The association concepts and the McMillan-Mayer theory. J. Sol. Chem. 1976, 5, 543. [Google Scholar] [CrossRef]
- Enderby, J.E.; Cummings, S.; Herdman, G.J.; Neilson, G.W.; Salmon, P.S.; Skippers, N.J. Diffraction and the study of aqua ions. Phys. Chem. 1987, 91, 5851. [Google Scholar] [CrossRef]
- Hynes, J.T. Theory of Chemical Reaction Dynamics; Baer, M., Ed.; CRC: Boca Raton, FL, USA, 1985. [Google Scholar]
- Der Zwan, G.V.; Hynes, J.T. Nonequilibrium solvation dynamics in solution reactions. J. Chem. Phys. 1983, 78, 4174. [Google Scholar] [CrossRef]
- Rey, R.; Guardia, E. Dynamical aspects of the sodium (1+)-chloride ion pair association in water. J. Phys. Chem. 1992, 96, 4712. [Google Scholar] [CrossRef]
- Kramers, H.A. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 1940, 7, 284. [Google Scholar] [CrossRef]
- Rey, R. Computer Simulation of Activated Processes in Solution: Ionic Association in Water. Ph.D. Thesis, Universität de Barcelona, Barcelona, Spain, 1992. [Google Scholar]
- Pinzon, R. El Acetonitrilo y sus Disoluciones Iónicas: Un Estudio mediante la Dinámica Molecular. Ph.D. Thesis, Universität Politécnica de Catalunya, Barcelona, Spain, December 1998. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).