Photoionization of Trans-Fe Ions: Se IV, Se V, and Se VI

Abstract

In the present study, the photoionization cross-sections are calculated for the trans-Fe ions Se IV, Se V, and Se VI over a wide energy region for ground and meta-stable states within the Dirac Atomic R-matrix approach (darc). Our cross-section results, when benchmarked against the available high-resolution measurements taken at the Advanced Light Source (ALS) for Se IV (Ga-like) and Se VI (Cu-like) selenium ions, show good agreement over the entire photon energy investigated. The present high quality cross-section data are suitable for use in many applications in astrophysics.

1. Introduction

Atomic selenium and its ions have been detected in the spectra of white dwarfs [1,2,3], sub-dwarfs [4], metal-poor stars [5,6], and planetary nebulae [7,8], despite its cosmic rarity. The chemical compositions of these objects highlight details of stellar nucleosynthesis and the chemical evolution of galaxies. The uncertainties in the atomic data can lead to an abundance errors of a factor of two or more in astrophysical nebulae [9,10]. Low-lying energy levels of Ga-like, Zn-like, and Cu-like ions of selenium have been extensively studied both theoretically and experimentally for fusion science applications [11], but photoabsorption studies are severely lacking. Elaborate non-local thermodynamical equilibrium (NLTE) models of stellar atmospheres include numerous generally reliable bound–bound transition data—see, for example, for Se V [3]—but radiative (bound-free) cross-sections are approximated using hydrogenic models [12,13], when other sources of data, for example, the Opacity Project, are not available for an ion of interest. Benchmarked calculations of the photoabsorption cross-sections for Se IV, Se V, and Se VI, presented in this paper, are therefore applicable to improving stellar atmosphere models.

2. Photoionization

The study of the photoabsorption spectra of trans-Fe elements such as selenium and its iso-nuclear sequence is interesting due to the open-shell features of these complexes and the role played by electron correlation effects. Similarly to our previous work on singly ionized selenium [14] and doubly ionized selenium [15], in order to gauge the quality of our theoretical work, large-scale close-coupling calculations were performed on the Se IV, Se V, and Se VI iso-nuclear ions of selenium, for which, respectively, the electronic structures are Ga-like, Zn-like, and Cu-like. We benchmark our theoretical results against the available experimental photoionization cross-section measurements from the Advanced Light Source (als) radiation facility in Berkeley, CA, USA [16]. When experimental results are available, our large-scale close-coupling photoionization cross-section calculations are in respectable agreement with other experiment, see Ref. [17] and references therein. In the absence of measurements, our darc calculations provide the necessary radiative data for astrophysical modeling. All our calculations were carried using the relativistic Dirac-Coulomb R-matrix approximation [18,19,20].

2.1. Se IV

The grasp0 code [19,21,22] was used to generate the residual ${\mathrm{Se}}^{4+}$ target wave functions that were employed in our collision work. The “physical” orbital basis (that is, corresponding to the orbitals of the actual, physical ion, such as might be produced by a bound state code) consisted of all orbitals up to $n=4$, and the $5s$ and $5p$ orbitals were also included in our basis set. We began by performing an extended averaged level (eal) calculation for the $n=4$ orbitals and extended these calculations with the addition of the $n=5$ orbitals. All eal calculations were performed on the lowest 16 fine-structure levels of the residual ${\mathrm{Se}}^{4+}$ ion in order to generate the target wave functions for our work. We retained 299 levels originating from one- and two-electron promotions from the $n=4$ levels into the orbital space of this ion. All 299 levels arising from the seventeen configurations were included in the darc close-coupling calculation, namely, the configurations, $3d^{10}4s^2$, $3d^{10}4s4p$, $3d^{10}4s4d$, $3d^{10}4p^2$, $3d^{10}4d^2$, $3d^{9}4s^{2}4p$, $3d^{9}4s^{2}4d$, $3d^{9}4s4p^2$, $3d^{9}4s4p4d$, $3d^{10}4s5s$, $3d^{10}4s5p$, $3d^{10}4p5s$, $3d^{10}4p5p$, $3d^{10}4d5s$, and $3d^{10}4d5p$. In addition, we include the two-electron promotions to the $n=5$ orbitals, $3d^{10}5s^2$ and $3d^{10}5p^2$.

This provides a suitable representation of the residual ${\mathrm{Se}}^{4+}$ ionic levels, as shown in Table 1, where the energies of the lowest 9 levels of the residual ${\mathrm{Se}}^{4+}$ ion from the 299-level grasp0 calculations are compared to the values from the nist tabulations [23]. The average percentage difference of our theoretical energy levels compared with the nist values is approximately 3%. Recently, experimental and theoretical energy levels for Zn-like ions were reviewed by [11]. Guided by this review, we tabulate the relativistic configuration interaction (RCI) calculations of [24], which are in good agreement with the nist data, as shown in Table 1. Additionally, all levels in Table 1 are in good agreement with the spectroscopic analysis of data from a triggered spark source by [25], giving us confidence in the tabulated data (Ref. [25] labels Level 9 of Table 1 as a $4p^2$ configuration, while nist lists the configuration as $4s4d$; however, according to [3,25], the $LS$ percentage decomposition is less than 20% $4s4d{}^1\mathrm{D}$. We have retained the nist labeling for consistency).

Table 1. Comparison of the theoretical energies for the ${\mathrm{Se}}^{4+}$ (Zn-like) ion from the grasp0 code [19,21,22] in the 299-level approximation with the available nist values [23]. Relative energies are given in Rydbergs. A sample of the 9 lowest levels for the ${\mathrm{Se}}^{4+}$ ion from the nist values are shown. The available relativistic configuration interaction with quantum electrodynamics (RCI + QED) atomic structure calculations [24] are included for completeness.

Level	Configuration	Term	nist	grasp0	rci + qed	Δ d	Δ e
			Energy a	Energy b	Energy c	(%)	(%)
			(Ry)	(Ry)	(Ry)	–
1	$3d^{10}4s^2$	${}^1\mathrm{S}_0$	0.00000	0.00000	-	0.0	0.0
2	$3d^{10}4s4p$	${}^3\mathrm{P}_0^{\mathrm{o}}$	0.81792	0.79144	0.81410	−3.2	−0.5
3	$3d^{10}4s4p$	${}^3\mathrm{P}_1^{\mathrm{o}}$	0.83245	0.80617	0.83296	−3.2	+0.1
4	$3d^{10}4s4p$	${}^3\mathrm{P}_2^{\mathrm{o}}$	0.86535	0.83827	0.86545	−3.1	+0.01
5	$3d^{10}4s4p$	${}^1\mathrm{P}_1^{\mathrm{o}}$	1.20044	1.24437	1.20010	+3.7	−0.03
6	$3d^{10}4p^2$	${}^3\mathrm{P}_0$	1.92996	1.91694	-	−0.7	0.0
7	$3d^{10}4p^2$	${}^3\mathrm{P}_1$	1.95091	1.93627	-	−0.8	0.0
8	$3d^{10}4p^2$	${}^3\mathrm{P}_2$	1.99217	2.04509	-	+2.7	0.0
9	$3d^{10}4s4d$	${}^1\mathrm{D}_2$	1.94277	1.96084	-	−0.9	0.0

^a nist values [23]. ^b grasp0 calculations using a 299-level approximation. ^c rci + qed calculations [24]. ${}^d\Delta$(%) of the grasp0 results with the nist [23] values. ${}^e\Delta$(%) of the rci+qed results with the nist [23] values.

The photoionization cross-section calculations were performed in the Dirac-Coulomb R-matrix approximation. In our 299-level darc photoionization cross-section section calculations, we used fifteen continuum orbitals and a boundary radius of 14.4 Bohr to accommodate the diffuse $n=5$ orbitals leading to Hamiltonian and dipole matrices of order 25,000, with approximately 1500 coupled channels. The suite of parallel darc codes allows one to concurrently form and diagonalise such large-scale Hamiltonian and dipole matrices. The outer region electron-residual ion collision problem was solved with a fine mesh of 2 × ${10}^{-8}$ Rydbergs ($0.272$ μeV) so that all the extremely narrow resonance features in the photoionization cross-sections were fully resolved. The photoionization cross-sections for both ground and metastable states were calculated. The Se V theoretical term energies were shifted to match the recommended experimental values of the nist tabulations [23]. Typical computer usage on a massively parallel processor was about 200 core-hours for the inner region and 3000 core-hours for the outer region, for each bound-free dipole transition matrix describing a photoionization channel.

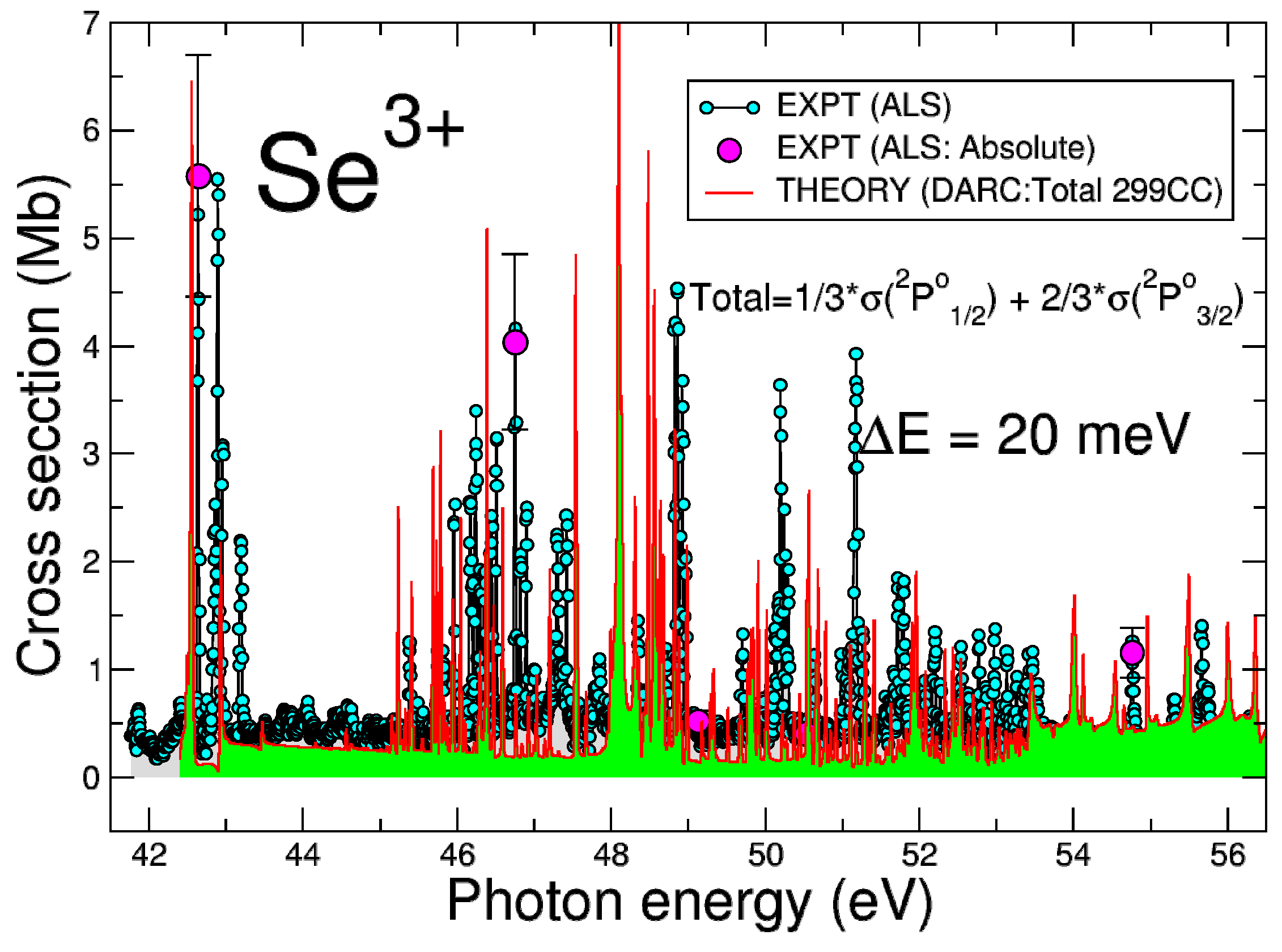
For the ${\mathrm{Se}}^{3+}$ ion, Figure 1 illustrates the comparison between our theoretical model used and the ALS experimental measurements made at a bandwidth of 20 meV FWHM. To compare directly with the experiment, we have convoluted the theoretical data with a Gaussian with a bandwidth of 20 meV FWHM and statistically averaged them over the ground and metastable states. The good agreement observed between theory and experiment is indicative of the large-scale high-quality target wave functions and collision model used in our theoretical model of this half collision process. The Rydberg resonance series observed in the Se IV spectrum are due to $4s\to 4p$ transitions converging to the $\left[4s4p\right]{}^3\mathrm{P}_0,{}^3\mathrm{P}_1,\mathrm{and}{}^3\mathrm{P}_2$ thresholds of the ${\mathrm{Se}}^{4+}$ ion.

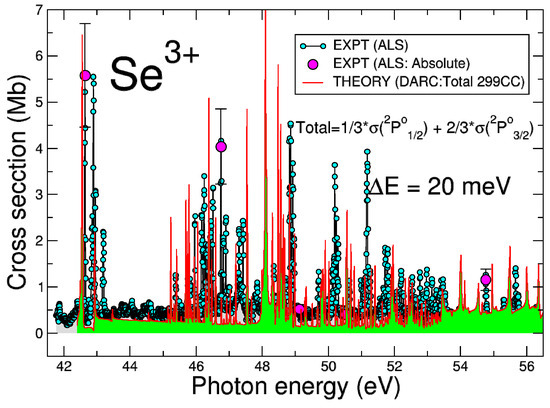
Figure 1. (Color online) darc photoionization cross-section results for the ${\mathrm{Se}}^{3+}$ ion in the 299-level approximation (solid red line with green fill). Illustrated are the statistical average of the ground $\left[4s^{2}4p\right]{}^2\mathrm{P}_{1/2}^{\mathrm{o}}$ and metastable $\left[4s^{2}4p\right]{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$ states for the ${\mathrm{Se}}^{3+}$ ion. We plot the convolution of the calculated cross-sections and a a Gaussian function of 20 meV at full width half maximum (fwhm). The als measurements (solid cyan circles connected by black line) and the absolute measurements (solid magenta circles) shown were taken at a resolution of 20 ± 3 meV fwhm. The ionization energy of Se IV is about 42.95 eV [23].

2.2. Se V

To generate the residual ${\mathrm{Se}}^{5+}$ target wave functions employed in our collision work, all orbitals were physical up to $n=4$. In addition, we included the $5s$ orbital in our basis set. The extended averaged level (eal) calculations for the $n=4$ orbitals were extended to include the $n=5$ orbitals. All eal calculations were performed on the lowest 16 fine-structure levels of the residual ${\mathrm{Se}}^{5+}$ ion in order to generate the target wave functions for our work. We included all 321 levels arising from the thirteen configurations in the close-coupling calculations. These configurations were, $3d^{10}4s$, $3d^{10}4p$, $3d^{10}4d$, $3d^{10}5s$, $3d^{9}4s^2$, $3d^{9}4p^2$, $3d^{9}4d^2$ $3d^{9}4s4p$, $3d^{9}4s4d$, $3d^{9}4p4d$, $3d^{10}4s5s$, $3d^{10}4p5s$, and $3d^{10}4d5s$.

This provides a suitable representation of the residual ${\mathrm{Se}}^{5+}$ ionic levels, as shown in Table 2, where the energies of the lowest 6 levels of the residual ${\mathrm{Se}}^{5+}$ ion from the 321-level grasp calculations are compared to the values from the nist tabulations [23]. The average percentage difference of our theoretical energy levels compared with the nist values is approximately 1%. The calculations of the Dirac–Fock method with QED and relativistic correlation corrections [11,26] agree to within 0.0009 Rydbergs (100 ${\mathrm{cm}}^{-1}$) with the NIST values for the transition energies between levels 1 and 2 and levels 1 and 3 listed in Table 2.

Table 2. Comparison of the theoretical energies for the ${\mathrm{Se}}^{5+}$ (Cu-like) ion from the grasp0 code [19,21,22] in the 321-level approximation with the available nist values [23]. Relative energies are given in Rydbergs. A sample of the lowest six energy levels for the ${\mathrm{Se}}^{5+}$ ion from the nist values are shown.

Level	Configuration	Term	nist	grasp0	Δ c
			Energy a	Energy b	(%)
			(Ry)	(Ry)	–
1	$3d^{10}4s$	${}^2\mathrm{S}_{1/2}$	0.000000	0.000000	0.00
2	$3d^{10}4p$	${}^2\mathrm{P}_{1/2}^{\mathrm{o}}$	1.027563	1.018557	−0.88
3	$3d^{10}4p$	${}^2\mathrm{P}_{3/2}^{\mathrm{o}}$	1.079505	1.068369	−1.03
4	$3d^{10}4d$	${}^2\mathrm{D}_{3/2}$	2.577337	2.546839	−1.18
5	$3d^{10}4d$	${}^2\mathrm{D}_{3/2}$	2.583524	2.553147	−1.18
6	$3d^{10}5s$	${}^2\mathrm{S}_{1/2}$	3.039932	2.981474	−1.92

^a nist values [23]. ^b Energies from the grasp0 code for the 321-level approximation. ${}^c\Delta$ (%) difference with the nist values [23].

For the 321-level darc photoionization cross-section calculations, we used fifteen continuum orbitals and a boundary radius of 8.91 Bohr to accommodate all the orbitals. This gave rise to Hamiltonian and dipole matrices of the order of 25,000, with approximately 1700 coupled channels. A similar energy mesh size was used as in the ${\mathrm{Se}}^{3+}$ work, and the energy levels of the residual ${\mathrm{Se}}^{5+}$ ion were adjusted to match those from the nist tabulations.

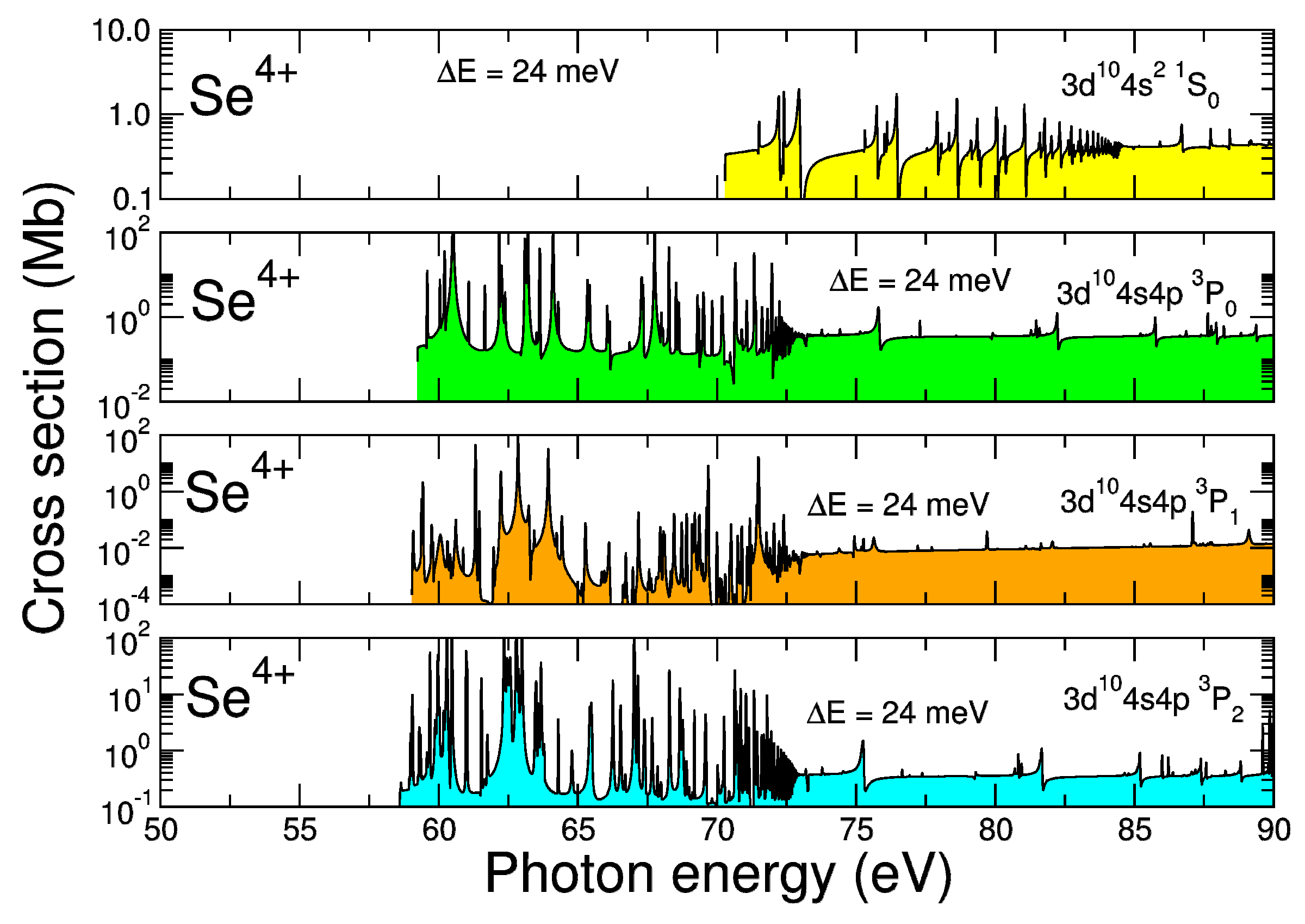
Figure 2, illustrates our results for the ${\mathrm{Se}}^{4+}$ ground state and metastable states convoluted at a band pass of 24 meV. The rich resonance features in the near threshold region dominate the cross section. Unfortunately, no experimental data are available at present for a comparison to be made between theory and experiment.

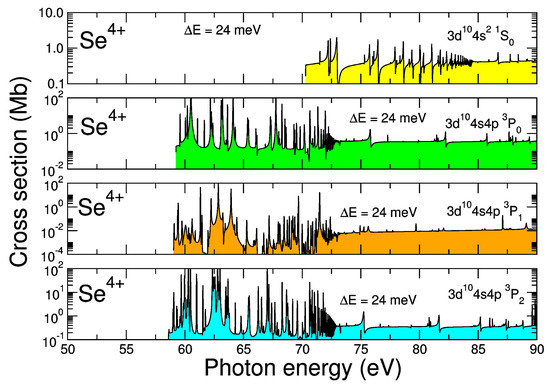
Figure 2. (Color online) darc photoionization cross-sections results for the ${\mathrm{Se}}^{4+}$ ion in the 321-level approximation, for the $\left[3d^{10}4s^2\right]{}^1\mathrm{S}_0$ ground state and the $\left[3d^{10}4s4p\right]{}^3\mathrm{P}_{0,1,2}$ metastable states, indicated, respectively, with yellow, green, orange, and cyan fill. We plot the convolution of the darc results with a Gaussian function having a profile of 24 meV at full width half maximum (fwhm). No data from the als synchrotron facility are available to compare with for this ion. Note the logarithmic scale for the cross-sections in each panel. The ionization energy of ${\mathrm{Se}}^{4+}$ is about 68.30 eV [23].

The Rydberg resonance pattern observed in the spectra for photoionization out of the ground and metastable states of the ${\mathrm{Se}}^{4+}$ ion is very similar to that for Be-like ions. For photoionization out of the $\left[3d^{10}4s^2\right]{}^1\mathrm{S}_0$ ground state, two-electron promotion yields the Rydberg series $[3d^{10}4pn\ell ]{}^1\mathrm{P}_1^{\mathrm{o}}$. For the metastable state, then, $4s4p\to 4pnp$ excitation of the $\left[3d^{10}4s4p\right]{}^3\mathrm{P}_{0,1,2}$ state give rise to the $\left[3d^{10}4pnp\right]{}^3\mathrm{S}_1{,}^3{\mathrm{P}}_{0,1,2}{,}^3{\mathrm{D}}_{1,2,3}$ resonance series. Similar types of Rydberg resonances have been observed in the als photoionization spectra of Be-like ions; B II, C III, and N IV [27,28,29]. Additional resonances are present in the spectra due to the inclusion of the opening of the $3d^{10}$ shell in the target wave functions and the close-coupling calculations.

2.3. Se VI

Finally, to generate the residual ${\mathrm{Se}}^{6+}$ target wave functions employed in our collision work, all orbitals included were physical up to $n=4$. The extended averaged level (eal) calculation for the $n=3$ orbitals were extended to include the $n=4$ orbitals. All eal calculations were performed on the lowest 16 fine-structure levels of the residual ${\mathrm{Se}}^{6+}$ ion in order to generate the target wave functions for our work. We included all 432 levels arising from the seven configurations in the close-coupling calculations. These configurations were the one-electron promotions, $3d^{10}$, $3d^{9}4s$, $3d^{9}4p$, $3d^{9}4d$, and the two-electron promotions, $3d^{8}4s^2$, $3d^{8}4p^2$, and $3d^{8}4d^2$.

As shown in Table 3, the energies of the lowest 12 levels of the residual ${\mathrm{Se}}^{6+}$ ion from the 432-level grasp calculations are compared to the values from the nist tabulations [23,30]. The average percentage difference of our theoretical energy levels compared with the nist values is approximately 3%.

Table 3. Comparison of the theoretical energies for the ${\mathrm{Se}}^{6+}$ (Ni-like) ion from the grasp0 code [19,21,22] in the 432-level approximation with the available nist values [23]. Relative energies are given in Rydbergs. A sample of the 12 lowest levels for the ${\mathrm{Se}}^{6+}$ ion from the nist tabuated values are shown.

Level	Configuration	Term	nist	grasp0	Δ c
			Energy a	Energy b	(%)
			(Ry)	(Ry)	–
1	$3d^{10}$	${}^1\mathrm{S}_0$	0.000000	0.000000	0.0
2	$3d^{9}4s$	${}^3\mathrm{D}_3$	4.007292	3.864936	−3.6
3	$3d^{9}4s$	${}^3\mathrm{D}_2$	4.028862	3.887010	−3.5
4	$3d^{9}4s$	${}^3\mathrm{D}_1$	4.071222	3.928608	−3.5
5	$3d^{9}4s$	${}^1\mathrm{D}_2$	4.103463	3.963003	−3.4
6	$3d^{9}4p$	${}^3\mathrm{P}_2^{\mathrm{o}}$	5.091267	4.938383	−3.0
7	$3d^{9}4p$	${}^3\mathrm{P}_1^{\mathrm{o}}$	5.154491	5.000593	−3.0
8	$3d^{9}4p$	${}^3\mathrm{P}_0^{\mathrm{o}}$	5.192190	5.037409	−3.0
9	$3d^{9}4p$	${}^3\mathrm{F}_3^{\mathrm{o}}$	5.136042	4.982794	−3.0
10	$3d^{9}4p$	${}^3\mathrm{F}_4^{\mathrm{o}}$	5.177072	5.021347	−3.0
11	$3d^{9}4p$	${}^3\mathrm{F}_2^{\mathrm{o}}$	5.180886	5.026563	−3.0
12	$3d^{9}4p$	${}^1\mathrm{D}_2^{\mathrm{o}}$	5.240788	5.090227	−2.9

^a nist values [23]. ^b Energies from the grasp0 code for the 432-level approximation. ${}^c\Delta$(%) difference with the nist values [23].

In the 432-level darc photoionization cross-section calculations for this ion, we used fifteen continuum orbitals and a boundary radius of 6.92 Bohr to accommodate all the n = 4 orbitals. This gave rise to Hamiltonian and dipole matrices of the order of 38,000, with approximately 2500 coupled channels. The energy mesh size used was similar to that used in the ${\mathrm{Se}}^{3+}$ work, and the energy levels of the residual ${\mathrm{Se}}^{6+}$ ion were adjusted to match those from the nist tabulations.

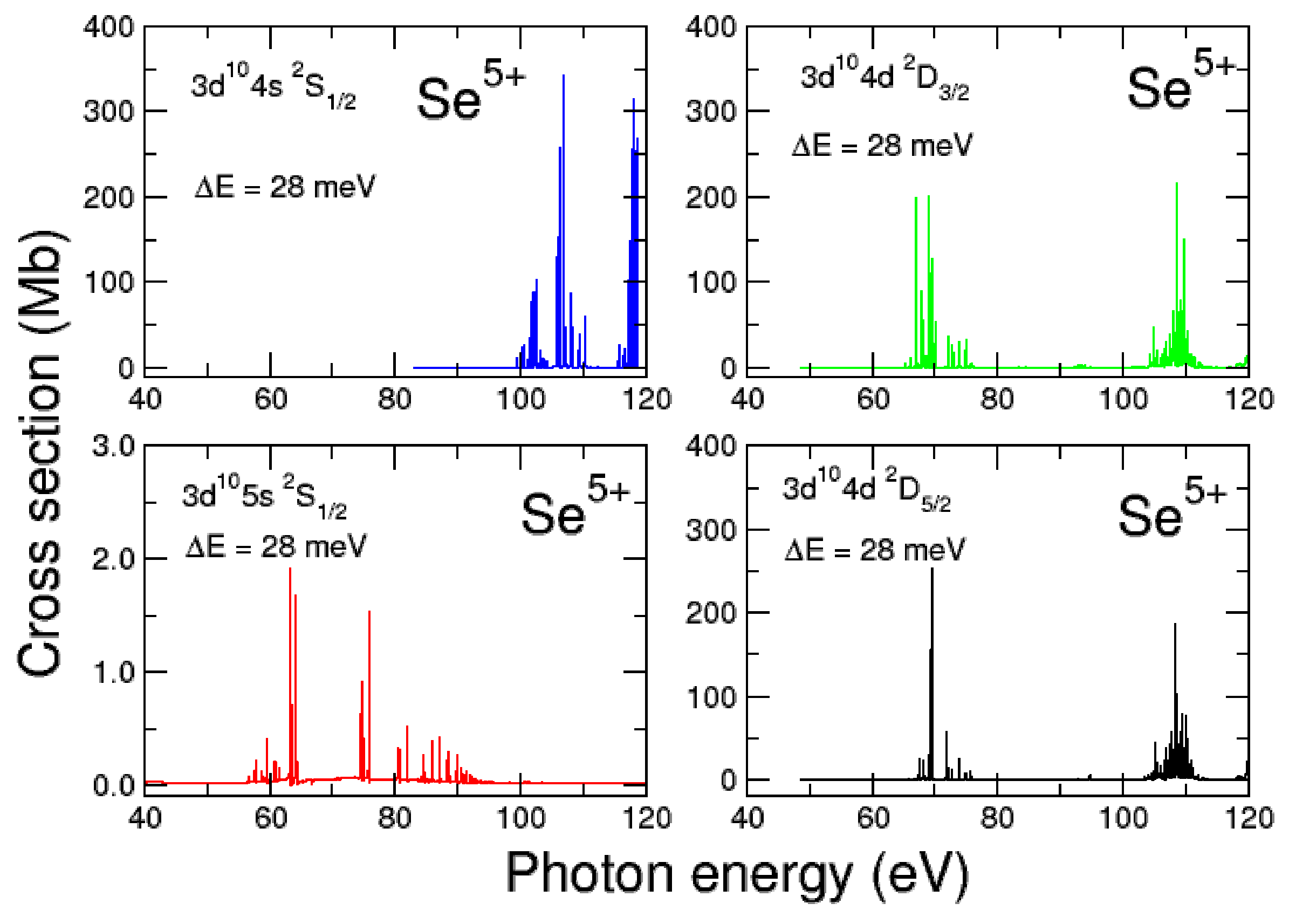
The Rydberg resonance series present in the spectra of the ${\mathrm{Se}}^{5+}$ ion arise due to $3d\to np$ promotions from the $\left[3d^{10}4s\right]{}^2\mathrm{S}_{1/2}$ ground state, yielding the $\left[3d^{9}4snp\right]{}^2\mathrm{P}_{1/2,3/2}^{\mathrm{o}}$ resonance series. Meanwhile, for the metastable states $\left[3d^{10}4d\right]{}^2\mathrm{D}_{3/2,5/2}$, $3d\to np$ promotions lead to the resonance series $\left[3d^{9}4dnp\right]{}^2\mathrm{P}_{1/2,3/2}^{\mathrm{o}}{,}^2{\mathrm{D}}_{3/2,5/2}^{\mathrm{o}}{,}^2{\mathrm{F}}_{5/2,7/2}^{\mathrm{o}}$. Note that the $3d\to nf$ promotion from the initial $\left[3d^{10}4d\right]{}^2\mathrm{D}_{3/2,5/2}$ metastable states would yield the $\left[3d^{9}4dnp\right]{}^2\mathrm{P}_{1/2,3/2}^{\mathrm{o}}{,}^2{\mathrm{D}}_{3/2,5/2}^{\mathrm{o}}{,}^2{\mathrm{F}}_{5/2,7/2}^{\mathrm{o}}$ resonance series.

The cross-sections for the ground states $\left[3d^{10}4s\right]{}^2\mathrm{S}_{1/2}$ and the metastable $\left[3d^{10}5s\right]{}^2\mathrm{S}_{1/2}$, $\left[3d^{10}4d\right]{}^2\mathrm{D}_{3/2}$ and $\left[3d^{10}4d\right]{}^2\mathrm{D}_{5/2}$ are shown in Figure 3. The cross-sections have been convoluted with a Gaussian distribution having a profile of 28 meV FWHM. As can be clearly seen from Figure 3, along with the ground state $\left[3d^{10}4s\right]{}^2\mathrm{S}_{1/2}$, only the $\left[3d^{10}4d\right]{}^2\mathrm{D}_{3/2}$ and $\left[3d^{10}4d\right]{}^2\mathrm{D}_{5/2}$ metastable states contribute to the total cross-section in the photon energy region 100–110 eV.

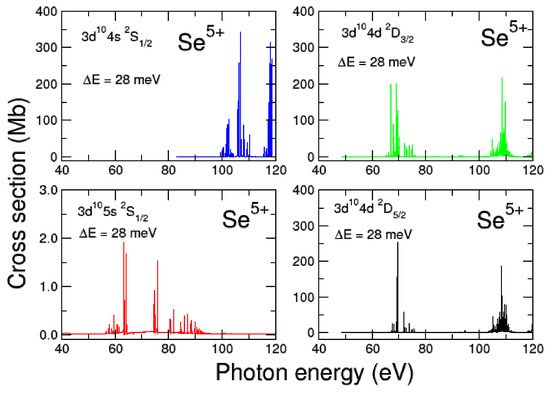
Figure 3. (Color online) darc photoionization cross-sections results for the ${\mathrm{Se}}^{5+}$ ion from the 432-level approximation. The ground state $\left[3d^{10}4s\right]{}^2\mathrm{S}_{1/2}$ (blue) of the ${\mathrm{Se}}^{5+}$ ion is shown along with the metastable states, $\left[3d^{10}5s\right]{}^2\mathrm{S}_{1/2}$ (red), $\left[3d^{10}4d\right]{}^2\mathrm{D}_{3/2}$ (green), and $\left[3d^{10}4d\right]{}^2\mathrm{D}_{5/2}$ (black), to indicate their various contributions. We plot the convolution of the darc results with a Gaussian function with a profile of 28 meV at full width half maximum (fwhm). The ionization energy of Se VI is about 81.83 eV [23].

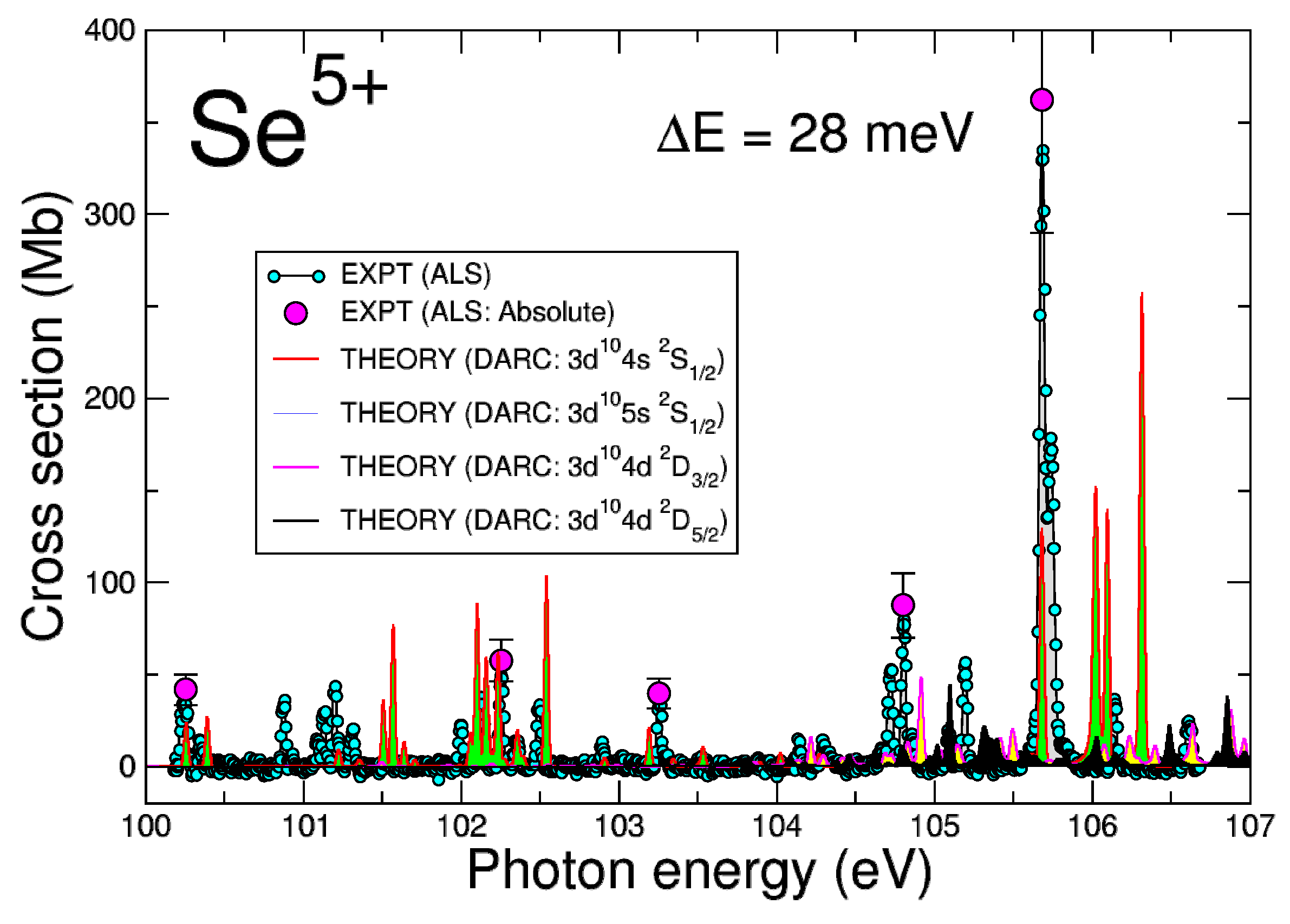
Figure 4 shows a comparison of our darc PI cross-sections with the published ALS data in the energy region 100–107 eV. We find that 80% of the $\left[3d^{10}4s\right]{}^2\mathrm{S}_{1/2}$ ground state and 20% of the statistically averaged $\left[3d^{10}4d\right]{}^2\mathrm{D}_{3/2}$ and $\left[3d^{10}4d\right]{}^2\mathrm{D}_{5/2}$ metastable states best match the experiment. The $\left[3d^{10}5s\right]{}^2\mathrm{S}_{1/2}$ metastable state does not contribute to the total photoionization cross-section in this photon energy region.

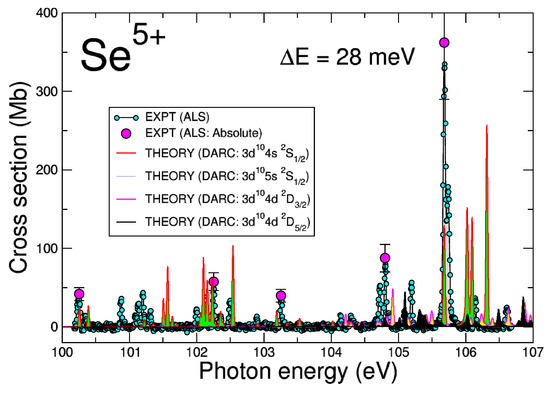
Figure 4. (Color online) darc photoionization cross-sections results for the ${\mathrm{Se}}^{6+}$ ion from the 432-level approximation. The ground state $\left[3d^{10}4s\right]{}^2\mathrm{S}_{1/2}$ of the ${\mathrm{Se}}^{5+}$ ion is illustrated (red line with green fill) together with the $\left[3d^{10}5s\right]{}^2\mathrm{S}_{1/2}$ (blue line, not visible), $\left[3d^{10}4d\right]{}^2\mathrm{D}_{3/2}$ (magenta line with yellow fill), and $\left[3d^{10}4d\right]{}^2\mathrm{D}_{5/2}$ (black line with black fill), metastable states. We plot the convolution of the darc results with a Gaussian function with a profile of 28 meV at full width half maximum (fwhm). The als measurements (solid cyan circles connected by a black line with gray fill) and the absolute measurements (solid magenta circle with error bars) shown were taken at an energy resolution of 28 ± 3 meV fwhm. The ionization energy of Se VI is about 81.83 eV [23].

We note that autoionization widths ($\Gamma$) for the $3d^{9}4p^2$ resonance states of Se VI (Cu-like) were observed and estimated for the J = 3/2 and 5/2 even parity symmetries (see Table IX of [31]), finding that the Auger widths are around 15 meV, or much less, which is below the resolution used in previous ALS experiments on Se ions [15,16,32,33]. Esteves et al. [16] (their Figure 6) searched the energy region near the threshold for Se VI with an experimental photon resolution of $60\pm 10\mathrm{meV}$ (∼$500\hspace{0.17em}{\mathrm{cm}}^{-1}$) and found no resonances. They determined the ionization potential of Se VI to be $81.780\pm 0.01$ eV, which is close to the earlier measurement of $660,100\pm 200{\mathrm{cm}}^{-1}$ ($81.842\pm 0.025\mathrm{eV}$) by Ryabtsev et al. (Table II of [31]).

3. Comparison of Theory and Experiment

A comparison of the theoretical and experimental values for the continuum oscillator strength f provides an additional check on our theoretical results. The integrated oscillator strength f of the experimental spectra was obtained using [34,35,36].

$$f=9.1075\times {10}^{-3}\int \sigma \left(h\nu \right)dh\nu .$$

For the ${\mathrm{Se}}^{3+}$ ion, the als measurements yielded a value of 0.080 ± 0.016, for the continuum f-value, and the darc calculations gave a value of 0.080, which is in excellent agreement with experiment. The darc results were obtained from the statistical average of the ground $\left[3d^{10}4s^{2}4p\right]{}^2\mathrm{P}_{1/2}^{\mathrm{o}}$ and metastable state $\left[3d^{10}4s^{2}4p\right]{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$ of the ${\mathrm{Se}}^{3+}$ ion and convoluted with a Gaussian distribution having a profile of 20 meV fwhm. For the ${\mathrm{Se}}^{4+}$ ion, no experimental data exist for comparison. For the the ${\mathrm{Se}}^{5+}$ ion, the darc results were convoluted with a Gaussian with a profile of 28 meV fwhm. The als measurements yielded a continuum f-value of 0.49 ± 0.10. Using 80% of the ground state $\left[3d^{10}4s\right]{}^2\mathrm{S}_{1/2}$ of the ${\mathrm{Se}}^{5+}$ ion and 20% of the statistical average of the $\left[3d^{10}4d\right]{}^2\mathrm{D}_{3/2}$ and $\left[3d^{10}4d\right]{}^2\mathrm{D}_{5/2}$ metastable states, the darc results gave a corresponding value of 0.547. This is within 12% of the experimental value and the approximate 20% experimental error.

4. Conclusions

Single photoionization theoretical cross-sections are presented for the following selenium ions: ${\mathrm{Se}}^{3+}$, ${\mathrm{Se}}^{4+}$, and ${\mathrm{Se}}^{5+}$, from the low-lying metastable state ionization region to the above the ground state ionization threshold. Comparison of the darc theoretical results with available measurements made at the als on ${\mathrm{Se}}^{3+}$ and ${\mathrm{Se}}^{5+}$ ions, taken at a photon energy resolution of 20 ± 3 meV and 28 ± 3 meV fwhm, respectively, show suitable agreement. Such comparisons of theory and experimental results provide confidence in the theoretical cross-section data for application in laboratory and astrophysical plasmas.

5. Summary

Single photoionization cross-section measurements made at the als on the selenium ions ${\mathrm{Se}}^{3+}$ and ${\mathrm{Se}}^{5+}$ over the photon energy ranges, 41.9–54.56 eV and 100.2–106.7 eV, respectively, are compared with large-scale darc calculations. Various Rydberg resonance series are visible in the spectra of these trans-Fe ions. The high resolution experimental measurements made at the als synchrotron radiation facility have been used to benchmark the theoretical calculations. In addition, we provide the photoionization cross-section results for the ${\mathrm{Se}}^{4+}$ ion over a wide photon energy range for the ground $\left[3d^{10}4s^2\right]{}^1\mathrm{S}_0$ and metastable states $\left[3d^{10}4s4p\right]{}^3\mathrm{P}_{0,1,2}$; for this trans-Fe ion, no such photoionization cross-section measurements are available from the als or from any other light source facility for comparison. The present results are suitable to be incorporated into astrophysical modeling codes such as the NLTE stellar atmosphere code tmap (Tübingen Model-Atmosphere Package) [3,12,13], cloudy [37,38], xstar [39], and atomdb [40], used to numerically simulate the thermal and ionization structure of ionized astrophysical nebulae.