The Validity of Long Wavelength Approximation in the Evaluation of Two-Photon Decay Rate

Abstract

This paper investigates the validity of the long wavelength approximation in the calculation of two-photon decay of $2s_{1/2}$ level in hydrogen-like ions with nuclear charge $Z=1-100$ based on time-dependent second-order perturbation theory and angular momentum algebra. While the relativistic structure effects on the two-photon decay rates are highlighted in the literature, the role of slowing effects in the photon electric dipole operators are not discussed extensively. The rate is computed by the sum-over-states method, with bound-bound and bound-free electric dipole matrix elements obtained in the Babushkin and Coulomb gauges, which satisfy the Lorenz gauge condition, as well as their non-relativistic limits in the long-wavelength approximation (Length and Velocity forms, respectively). The present results explicitly show how this approximation breaks gauge invariance by overestimating the Babushkin values by ∼24%${\left(\alpha Z\right)}^2$ while underestimating the Coulomb rates by ∼$31\%{\left(\alpha Z\right)}^2$. Using analytical eigenfunctions of the Dirac equation, we found that the contributions of the negative continuum states to the rate scale are ∼$0.0134{\left(\alpha Z\right)}^4$ in the Babushkin gauge and ∼$1.46{\left(\alpha Z\right)}^4$ in the Coulomb gauge, making the latter gauge more susceptible to errors when attempting to achieve basis completeness in multiphoton calculations. The present results are useful in assessing the complexity requirements of radiative transition rates for atomic systems of interest.

1. Introduction

The two-photon decay process is described by the simultaneous emission of photons with a continuous energy distribution through intermediate real or virtual states [1,2,3,4]. This process is encountered in atomic [5,6,7,8,9,10,11,12,13], nuclear [14,15], or solid-state physics [16]. It was first theoretically described by Maria Göppert-Mayer in her 1931 PhD dissertation [1], where she developed the quantum-mechanical formalism for multiphoton absorption and emission processes, laying the foundation for modern nonlinear optics. The two-photon decay has an important influence in the study of the cosmological hydrogen recombination epoch, where radiative recombination to 2 s metastable level of $H I$ did not result in fast ionization of neighboring atoms [17] and may also be used in the spectroscopy of long-lived states [18] in astrophysical plasmas such as planetary nebulae [3].

The two-photon decay rate of the metastable state 2 s in the hydrogen atom was first estimated by Breit and Teller [2] between 6.5 s⁻¹ and 8.7 s⁻¹, then computed by Spiltzer and Greenstein [3] arriving at the 8.23 s⁻¹ value, and later by Shapiro and Breit at 8.226 ± 0.001 s⁻¹. These authors used the sum over states $\left(SOS\right)$ method to include all virtual bound $np$ and continuum $ϵp$ states, and they subsequently applied increasingly accurate approximations for the non-relativistic radial integrals involved in the calculations. Klarsfeld [19] was the first to account for the summation over intermediate states using the closed form of the non-relativistic Coulomb–Green function [20], which was inspired by a similar function developed for Compton scattering of a bound electron [21], obtaining the value 8.2283 s⁻¹ for the two photon decay rate. Furthermore, Tung et al. [22] obtained the value of 8.2284 s⁻¹ and also extended the calculation of the two-photon decay rate to other excited levels of hydrogen-like ions. When computing the two-photon decay rate between two energy levels, the presence of real intermediate states lying energetically between them gives rise to resonances in the differential rate [23,24,25,26].

The first relativistic calculation was performed by Johnson [27], obtaining a value of 8.2290 s⁻¹, where he used Dirac orbitals to construct the Green function in the velocity gauge within the long wavelength approximation (LWA), computing the two-photon decay rate of $2s_{1/2}$ for the hydrogen-like isoelectronic series from $Z=1$ to $Z=100$. Goldman and Drake [28] performed a similar calculation using the discrete-basis-set method to construct the Dirac Coulomb–Green function [29], accounted for the slowing effects in the photon multipoles, and were also the first to check the gauge invariance of their results. Their values were larger by $20\%{\left(\alpha Z\right)}^2$ than those of Johnson [27], mainly due to the use of relativistic expansion of the radiation field in the corresponding length and velocity gauges. These effects become relevant at higher Z values, whereas for the $2s_{1/2}$ level in a hydrogen atom, they obtained a two-photon decay rate of 8.2291 s⁻¹. Parpia and Johnson [30] confirmed these results and also included contributions of the finite nuclear size, showing minor corrections for the high Z values.

Savukov and Johnson first noticed that negative Dirac energy states play a major role in $M1$ [31] and then in $E1M1$ [32] transitions for metastable states in higher Z helium-like ions. In the case of two-photon decay rates of excited states in hydrogen-like ions, the interference between the simultaneous emission process and the cascade terms has been investigated along with the influence of negative continuum [33,34,35,36,37,38]. The two-photon decay rates of high-lying energy levels in hydrogen atoms have shown that a dominant decay channel of $ns\to 1s$, with $2\le n\le 100$, is given by non-sequential $E1E1$ transition, while other multipoles ($M1M1$, $E2E2$) are negligible [39]. A cascade type $E1-E1$ transition can occur due to the Lamb shift [40], which places the relativistic $2p_{1/2}$ level below $2s_{1/2}$, allowing sequential $2s_{1/2}\to 2p_{1/2}\to 1s_{1/2}$ two-photon transition; however, the contribution to the total decay rate is ten orders of magnitude smaller than its non-sequential counterpart for the hydrogen atom.

Relativistic effects play a crucial role for higher Z elements through Dirac orbitals, providing the negative continuum contributions [41,42] that modify the two-photon decay rates of the $2s_{1/2}$ level up to $1\%$ and $40\%$ in H-like ions $X{e}^{53+}$ and $U^{91+}$, respectively. In the case of $E1M1$, $M1E1$ non-sequential two-photon decay of odd $1s^{2}2s2p$ ³$P_0^o$ levels in Be-like ions, the non-relativistic calculations [43,44] overestimate the two-photon decay rates by one and three orders of magnitude in $X{e}^{50+}$ and $U^{88+}$, respectively, compared to their relativistic counterpart [41]. For high Z hydrogen-like ions, higher-order multipole channels can provide small contributions to the total lifetime [42], as shown for $U^{91+}$, where the $E1E1$ rate is given by ${\Gamma }_{2s-1s}^{E1E1}=3.8256\times {10}^{12}$ s⁻¹, while $E2E2$ and $M1M1$ only give rise to ${\Gamma }_{2s-1s}^{E2E2}=1.7859\times {10}^8$ s⁻¹ and ${\Gamma }_{2s-1s}^{M1M1}=1.1093\times {10}^9$ s⁻¹, respectively. For $X{e}^{53+}$, these two higher-order multipole channels are roughly five orders of magnitude below the $E1E1$ rate, rendering them negligible.

The two-photon decay calculations can also be used as an initial assessment into multiphoton processes in highly charged heavy ions. Vanne and Saenz [45] theoretically investigated the interaction between a laser pulse and hydrogen-like ions by time-propagation of a free-field B-spline expansion of the Dirac equation and demonstrated a shift of ionization potential with increasing ionic charge. The dipole approximation has been used in both length and velocity gauges, while only the latter required the presence of negative continuum states, as expected. Avetissian et al. [46] determined the high-harmonic spectrum of hydrogen-like ions in a laser field using both analytical and numerical solutions of the Dirac equations. Ivanova et al. [47] developed scaling laws for the multiphoton ionization yields in hydrogen-like ions with different nuclear charges. The LWA approach is taken as a default in these kind of calculations. Telnov and Chu [48] computed the ionization probabilities of hydrogen-like ions using an eigenstates expansion of the Dirac equation while including the full plane wave form of the photon operators in the velocity gauge. The inclusion of negative states in a time-dependent Dirac equation calculation becomes computationally expensive [49,50,51], since the spectral domain is also extended by the $2m{c}^2$ gap in addition to the negative continuum and finer time steps up to two orders of magnitude compared to the time-dependent Schrödinger equation [52] are required to reach convergence.

In this paper, we investigate the validity of the long-wavelength approximation (LWA) on the non-sequential two-photon $E1E1$ decay of the $2s_{1/2}$ level in hydrogen-like ions from $Z=1$ to $Z=100$ using SOS method with Dirac bound and (positive + negative) continuum states. In Section 2, we describe the analytical formulation of the $E1E1$ two-photon decay rate, the evaluation of matrix elements in both relativistic (Babushkin and Coulomb) and non-relativistic (Length and Velocity, respectively) gauges, as well as the numerical methods used in our model. Section 3 contains the main results of this work, comprising data assessment in the form of gauge invariance, comparison with other works from literature, negative continuum contributions, and evaluation of LWA deviations compared to the relativistic treatment of the photon multipole operators. Conclusions are provided in Section 4. Furthermore, an extended data table containing the two-photon decay values of $2s_{1/2}$ level in hydrogen-like ions in both relativistic and non-relativistic gauges are provided in Appendix B.

2. Theoretical Background

2.1. Two-Photon Decay Rate Derivation

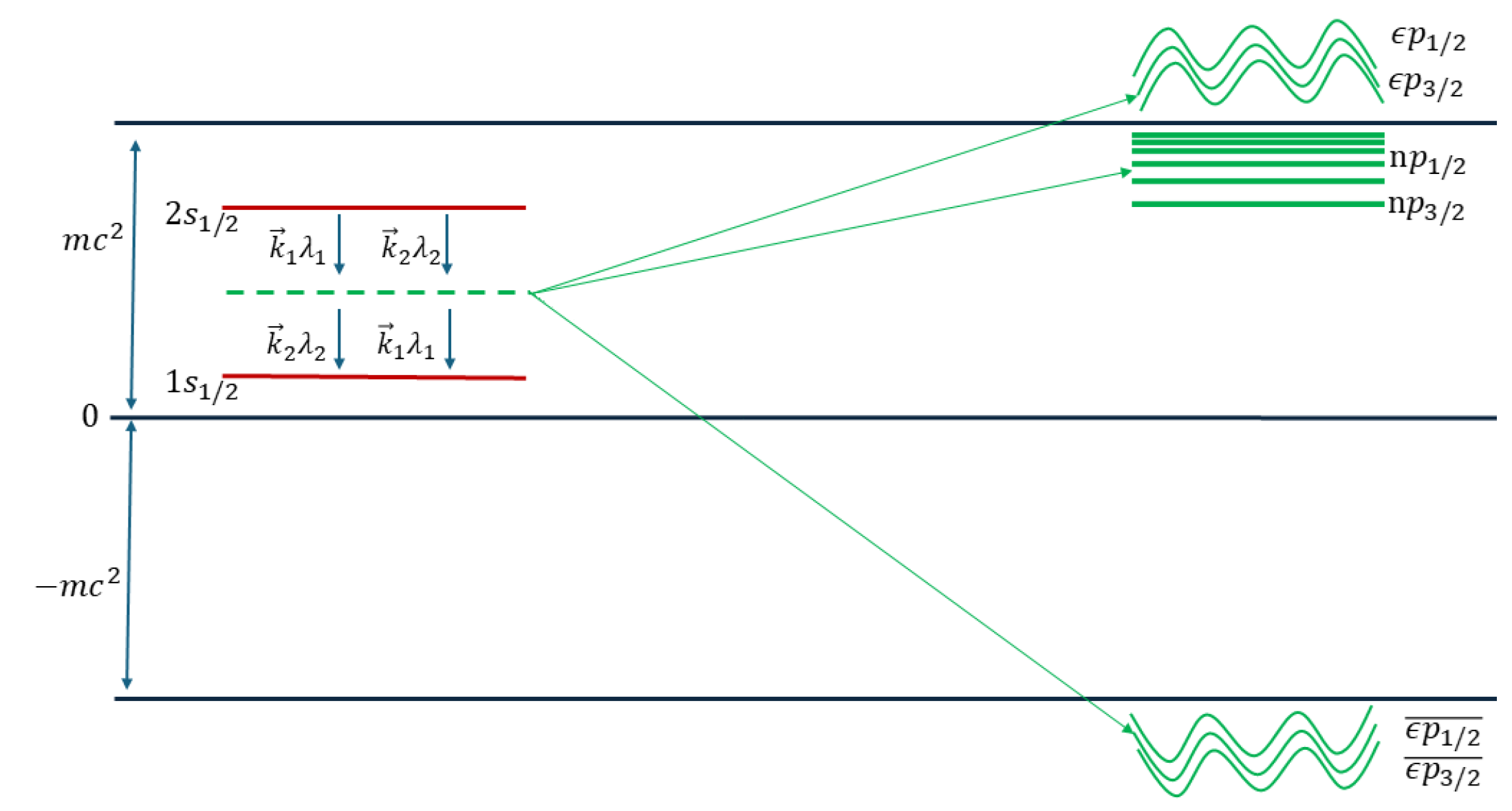
The two-photon decay process of $2s_{1/2}$ level in hydrogen-like ions is schematically drawn in Figure 1, showing the virtual bound $n{p}_{1/2,3/2}$, positive continuum $ϵp_{1/2,3/2}$ (where $ϵ=E-m{c}^2>0$), and negative continuum ${\overline{ϵp}}_{1/2,3/2}$ (where $ϵ=E+m{c}^2<0$) states. These Dirac states are described in Appendix A.

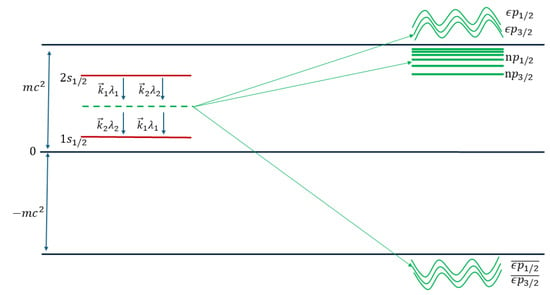
Figure 1. Two-photon decay scheme for hydrogen-like ions.

The Dirac interaction Hamiltonian [53], written using the volume V box quantization of the electromagnetic field [54] in $cgs \left(Gaussian\right)$ units, is given by:

$$\begin{array}{c}{\widehat{H}}_{int}(\overrightarrow{r},t)=e\hslash c\sum _{\overrightarrow{k}\lambda }\sqrt{{\displaystyle \frac{2\pi }{\hslash {\omega }_{k}V}}}{\displaystyle \frac{{(-1)}^{\lambda }}{\sqrt{2}}}\left\{\sum _{L=1}^{\infty }\sum _{M=-L}^L\left[\overrightarrow{\alpha }·\left({\overrightarrow{A}}_M^{L\left(e\right)}(\overrightarrow{r},{\omega }_k)+G_L{\overrightarrow{A}}_M^{L\left(l\right)}(\overrightarrow{r},{\omega }_k)\right.\right.\right.\hfill \\ \hfill \left.\left.\left.+\lambda {\overrightarrow{A}}_M^{L\left(m\right)}(\overrightarrow{r},{\omega }_k)\right)-G_L{\varphi }_M^L(\overrightarrow{r},{\omega }_k)\right]{\mathcal{D}}_{M,-\lambda }^{\left(L\right)}\left(\widehat{k}\right)\right\}{e}^{i{\omega }_{k}t}{\widehat{a}}_{\overrightarrow{k}\lambda }^{†}+c.c.\end{array}$$

(1)

where ${\overrightarrow{A}}_M^{L(e,l,m)}$ and ${\varphi }_M^L$ are the spherical tensor components of rank L and projection M of the vector and scalar potential, respectively, e stands for electric, l for longitudinal, and m for magnetic type multipole, as taken from Grant’s book [53]. The gauge parameter $G_L$ from the interaction Hamiltonian is taken as either 0 (Coulomb) or $\sqrt{{\displaystyle \frac{L+1}{L}}}$ (Babushkin).

The photon helicity states are written with respect to the quantization axis of the atomic system taken along the $\widehat{z}$ axis using the Wigner matrices. The matrix elements are then decomposed into reduced elements and Wigner $3j$ symbols:

$$\begin{array}{c}⟨E_{\beta }{\kappa }_{\beta }{m}_{\beta };\overrightarrow{k}\lambda \left|{\widehat{H}}_{int}\right|E_{\alpha }{\kappa }_{\alpha }{m}_{\alpha };0⟩=e\hslash c\sqrt{{\displaystyle \frac{\pi }{V}}}\sum _{\sigma =-1}^1{(-1)}^{j_{\beta }-m_{\beta }}\left(\begin{array}{ccc}{j}_{\beta }& 1& j_{\alpha }\\ -m_{\beta }& \sigma & m_{\alpha }\end{array}\right)\hfill \\ \hfill \times ⟨E_{\beta }{\kappa }_{\beta }\Vert T^{E1}\left({\omega }_k\right)\Vert E_{\alpha }{\kappa }_{\alpha }⟩{\displaystyle \frac{{(-1)}^{\lambda }{D}_{\sigma ,-\lambda }^{\left(1\right)}\left(\widehat{k}\right)}{\sqrt{\hslash {\omega }_k}}}\end{array}$$

(2)

The other matrix element type uses normalization for the two-photon state, leading to:

$$\begin{array}{c}⟨E_{\beta }{\kappa }_{\beta }{m}_{\beta };{\overrightarrow{k}}_1{\lambda }_1,{\overrightarrow{k}}_2{\lambda }_2\left|{\widehat{H}}_{int}\right|E_{\alpha }{\kappa }_{\alpha }{m}_{\alpha };\overrightarrow{k}\lambda ⟩=e\hslash c\sqrt{{\displaystyle \frac{\pi }{2V}}}\sum _{{\sigma }^{\prime }=-1}^1{(-1)}^{j_{\beta }-m_{\beta }}\left(\begin{array}{ccc}{j}_{\beta }& 1& j_{\alpha }\\ -m_{\beta }& {\sigma }^{\prime }& m_{\alpha }\end{array}\right)\hfill \\ \times \left[{\delta }_{{\overrightarrow{k}}_1,\overrightarrow{k}}{\delta }_{{\lambda }_1,\lambda }⟨E_{\beta }{\kappa }_{\beta }\Vert T^{E1}\left({\omega }_2\right)\Vert E_{\alpha }{\kappa }_{\alpha }⟩{\displaystyle \frac{{(-1)}^{{\lambda }_2}{\mathcal{D}}_{{\sigma }^{\prime },-{\lambda }_2}^{\left(1\right)}\left({\widehat{k}}_2\right)}{\sqrt{\hslash {\omega }_2}}}+\right.\\ \hfill \left.{\delta }_{{\overrightarrow{k}}_2,\overrightarrow{k}}{\delta }_{{\lambda }_2,\lambda }⟨E_{\beta }{\kappa }_{\beta }\Vert T^{E1}\left({\omega }_1\right)\Vert E_{\alpha }{\kappa }_{\alpha }⟩{\displaystyle \frac{{(-1)}^{{\lambda }_1}{\mathcal{D}}_{{\sigma }^{\prime },-{\lambda }_1}^{\left(1\right)}\left({\widehat{k}}_1\right)}{\sqrt{\hslash {\omega }_1}}}\right]\end{array}$$

(3)

The two-photon decay amplitude [54] between two atomic states is given by:

$$\begin{array}{c}\hfill {\mathcal{A}}_{if}\left(t\right)=⟨E_f{\kappa }_f{m}_f;{\overrightarrow{k}}_1{\lambda }_1,{\overrightarrow{k}}_2{\lambda }_2\left|\widehat{\mathcal{U}}\left(t\right)\right|E_i{\kappa }_i{m}_i;0⟩\end{array}$$

(4)

where the time evolution operator $\widehat{U}\left(t\right)$ is expanded as a Dyson series [54] as follows:

$$\widehat{U}\left(t\right)=1-{\displaystyle \frac{i}{\hslash }}{\int }_0^{t}d{t}^{\prime }{\left({\widehat{H}}_{int}\right)}_I\left(t^{\prime }\right)-{\left({\displaystyle \frac{i}{\hslash }}\right)}^2{\int }_0^{t}d{t}^{\prime }{\left({\widehat{H}}_{int}\right)}_I\left(t^{\prime }\right){\int }_0^{t^{\prime }}d{t}^{\prime \prime }{\left({\widehat{H}}_{int}\right)}_I\left(t^{\prime \prime }\right)-\dots$$

(5)

We insert the completeness relation containing the sum over all discrete and continuum available eigenstates $\nu$ of the unperturbed atomic Hamiltonian, as well as all the single-photon helicity states $\overrightarrow{k}\lambda$, and, by performing the time integrals of the second-order perturbation theory while eliminating highly oscillating terms corresponding to sequential processes, the non-resonant two-photon decay amplitude becomes:

$$\begin{array}{c}{\mathcal{A}}_{if}^{\left(non\right)}\left(t\right)={\displaystyle \frac{1}{{\hslash }^2}}\sum _{\nu {\kappa }_{\nu }{m}_{\nu }}\int \sum _{\overrightarrow{k}\lambda }⟨E_f{\kappa }_f{m}_f;{\overrightarrow{k}}_1{\lambda }_1{\overrightarrow{k}}_2{\lambda }_2\left|{\widehat{H}}_{int}\right|\nu {\kappa }_{\nu }{m}_{\nu };\overrightarrow{k}\lambda ⟩{\displaystyle \frac{⟨\nu {\kappa }_{\nu }{m}_{\nu };\overrightarrow{k}\lambda \left|{\widehat{H}}_{int}\right|E_i{\kappa }_i{m}_i;0⟩}{{\omega }_{\nu }+{\omega }_k-{\omega }_i}}\hfill \\ \hfill \times {\displaystyle \frac{e^{i({\omega }_f+{\omega }_1+{\omega }_2-{\omega }_i)t}-1}{{\omega }_f+{\omega }_1+{\omega }_2-{\omega }_i}}\end{array}$$

(6)

Here, the intermediate virtual states $\hslash {\omega }_{\nu }$ are situated above the initial and final energy levels; thus, no sequential contributions are possible. The time dependence of the ${\widehat{H}}_{int}$ operator has been included in the phase factor at the end of Equation (6).

The two-photon decay rate is obtained by averaging over all initial states $\left(m_i\right)$ and summing over all final states $(m_f;{\overrightarrow{k}}_1{\lambda }_1,{\overrightarrow{k}}_2{\lambda }_2)$:

$$\begin{array}{c}\hfill W_{if}=\underset{t\to \infty }{lim}{\displaystyle \frac{1}{t}} {\displaystyle \frac{1}{\left[j_i\right]}}\sum _{m_i=-j_i}^{j_i}\sum _{m_f=-j_f}^{j_f}\sum _{{\overrightarrow{k}}_1{\lambda }_1}\sum _{{\overrightarrow{k}}_2{\lambda }_2}{\left|{\mathcal{A}}_{if}^{\left(non\right)}\left(t\right)\right|}^2\end{array}$$

(7)

where $\left[j\right]=2j+1$ is the degeneracy of a state with total angular momentum j.

The temporal component of the diagonal non-resonant contribution becomes a parameterized Dirac $\delta$ function in the long interaction time limit [54]:

$$\begin{array}{c}{\left|{\displaystyle \frac{e^{i({\omega }_{fi}+{\omega }_1+{\omega }_2-{\omega }_i)t}-1}{{\omega }_f+{\omega }_1+{\omega }_2-{\omega }_i}}\right|}^2 = {\left|{\displaystyle \frac{sin\left[({\omega }_f+{\omega }_1+{\omega }_2-{\omega }_i)t/2\right]}{({\omega }_f+{\omega }_1+{\omega }_2-{\omega }_i)/2}}\right|}^2 \approx 2\pi t\delta ({\omega }_f+{\omega }_1+{\omega }_2-{\omega }_i)\hfill \\ \hfill \Rightarrow \underset{t\to \infty }{lim}{\displaystyle \frac{{\left|{\mathcal{A}}_{if}^{\left(non\right)}\left(t\right)\right|}^2}{t}}\propto 2\pi \delta ({\omega }_f+{\omega }_1+{\omega }_2-{\omega }_i)\end{array}$$

(8)

which results in the well-known energy conservation relation for the two-photon decay process. This is a standard result for calculations where no resonances are included.

The rate is obtained by dividing the two-photon probability to the interaction time:

$$\begin{array}{c}{W}_{if}={\displaystyle \frac{2\pi }{\left[j_i\right]{\hslash }^4}}\sum _{m_i=-j_i}^{j_i}\sum _{m_f=-j_f}^{j_f}\sum _{{\overrightarrow{k}}_1{\lambda }_1}\sum _{{\overrightarrow{k}}_2{\lambda }_2}\left|\sum _{\nu {\kappa }_{\nu }{m}_{\nu }}\sum _{\overrightarrow{k}\lambda }⟨E_f{\kappa }_f{m}_f;{\overrightarrow{k}}_1{\lambda }_1{\overrightarrow{k}}_2{\lambda }_2\left|{\widehat{H}}_{int}\right|\nu {\kappa }_{\nu }{m}_{\nu };\overrightarrow{k}\lambda ⟩\right.\hfill \\ \hfill {\left.\phantom{\sum _{\nu {\kappa }_{\nu }{m}_{\nu }}\sum _{\overrightarrow{k}\lambda }}⟨\nu {\kappa }_{\nu }{m}_{\nu };\overrightarrow{k}\lambda \left|{\widehat{H}}_{int}\right|E_i{\kappa }_i{m}_i;0⟩{\displaystyle \frac{1}{{\omega }_{\nu }+{\omega }_k-{\omega }_i}}\right|}^2\delta ({\omega }_f+{\omega }_1+{\omega }_2-{\omega }_i)\end{array}$$

(9)

By replacing the matrix elements, the rate becomes:

$$\begin{array}{c}{W}_{if}={\displaystyle \frac{{\pi }^3{e}^4{c}^4}{\left[j_i\right]{\hslash }^2{V}^2}}\sum _{{\overrightarrow{k}}_1{\lambda }_1}\sum _{{\overrightarrow{k}}_2{\lambda }_2}{\displaystyle \frac{1}{{\omega }_1{\omega }_2}}\delta ({\omega }_f+{\omega }_1+{\omega }_2-{\omega }_i)\hfill \\ \times \left|\sum _{\nu ,{\kappa }_{\nu },m_{\nu }}\sum _{\sigma ,{\sigma }^{\prime }=-1}^1{(-1)}^{j_f-m_f}{(-1)}^{j_{\nu }-m_{\nu }}\left(\begin{array}{ccc}{j}_f& 1& j_{\nu }\\ -m_f& {\sigma }^{\prime }& m_{\nu }\end{array}\right)\left(\begin{array}{ccc}{j}_{\nu }& 1& j_i\\ -m_{\nu }& \sigma & m_i\end{array}\right)\right.\\ \left[{\displaystyle \frac{⟨E_f{\kappa }_f\Vert T^{E1}\left({\omega }_2\right)\Vert \nu {\kappa }_{\nu }⟩⟨\nu {\kappa }_{\nu }\Vert T^{E1}\left({\omega }_1\right)\Vert E_i{\kappa }_i⟩}{{\omega }_{\nu }+{\omega }_1-{\omega }_i}}{\mathcal{D}}_{\sigma ,-{\lambda }_1}^{\left(1\right)}\left({\widehat{k}}_1\right){\mathcal{D}}_{{\sigma }^{\prime },-{\lambda }_2}^{\left(1\right)}\left({\widehat{k}}_2\right)\right.\\ \hfill {\left.+{\displaystyle \frac{⟨E_f{\kappa }_f\Vert T^{E1}\left({\omega }_1\right)\Vert \nu {\kappa }_{\nu }⟩⟨\nu {\kappa }_{\nu }\Vert T^{E1}\left({\omega }_2\right)\Vert E_i{\kappa }_i⟩}{{\omega }_{\nu }+{\omega }_2-{\omega }_i}}{\mathcal{D}}_{\sigma ,-{\lambda }_2}^{\left(1\right)}\left({\widehat{k}}_2\right){\mathcal{D}}_{{\sigma }^{\prime },-{\lambda }_1}^{\left(1\right)}\left({\widehat{k}}_1\right)]\right|}^2\end{array}$$

(10)

One can pass from the Cartesian box quantization [54] to spherical coordinates:

$$\begin{array}{c}\hfill \sum _{{\overrightarrow{k}}_1,{\overrightarrow{k}}_2}1\equiv {\displaystyle \frac{V^2}{{\left(2\pi c\right)}^6}}\int {\omega }_1^2 d{\omega }_1 \underset{0}{\overset{2\pi }{\int }} d{\varphi }_1 \underset{0}{\overset{\pi }{\int }} sin{\theta }_1 d{\theta }_1 \underset{0}{\overset{2\pi }{\int }} d{\varphi }_2 \underset{0}{\overset{\pi }{\int }} sin{\theta }_2 d{\theta }_2\end{array}$$

(11)

Combining two Wigner matrices that have the same Euler angles as arguments and then performing an integration over the corresponding solid angle, followed by a summation over the helicity states, yields the following:

$$\begin{array}{c}\hfill \sum _{{\lambda }_1=\pm 1}\int d{\Omega }_1{\mathcal{D}}_{{\sigma }_1,-{\lambda }_1}^{\left(1\right)}\left({\widehat{k}}_1\right){\mathcal{D}}_{{\sigma }_1^{\prime },-{\lambda }_1}^{\left(1\right)*}\left({\widehat{k}}_1\right)={(-1)}^{1+{\sigma }_1^{\prime }}{\displaystyle \frac{8\pi }{\sqrt{3}}}C\begin{array}{ccc}1& 1& 0\\ {\sigma }_1& -{\sigma }_1^{\prime }& 0\end{array}\end{array}$$

(12)

The result will now contain products of four Clebsch–Gordan coefficients that can either be reduced to Kronecker symbols or to $6j$ symbols by the appropriate sum rules. The Dirac $\delta ({\omega }_f+{\omega }_1+{\omega }_2-{\omega }_i)$ cancels the ${\omega }_2$ integral and, after performing the integrations and the corresponding sum rules, we arrive at:

$$\begin{array}{c}{W}_{2s_{1/2}\to 1s_{1/2}}={\displaystyle \frac{e^4}{18\pi c^2{\hslash }^2}}\int d{\omega }_1 {\omega }_1({\omega }_{2s_{1/2}}-{\omega }_{1s_{1/2}}-{\omega }_1)\hfill \\ \left\{{\displaystyle \frac{1}{2}}\left[{\left|g_{2s_{1/2}}^{[1/2]}\left({\omega }_1\right)\right|}^2+{\left|g_{1s_{1/2}}^{[1/2]}\left({\omega }_1\right)\right|}^2\right]+{\displaystyle \frac{1}{4}}\left[{\left|g_{2s_{1/2}}^{[3/2]}\left({\omega }_1\right)\right|}^2+{\left|g_{1s_{1/2}}^{[3/2]}\left({\omega }_1\right)\right|}^2\right]\right.\\ +{(-1)}^{{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}}\left\{\begin{array}{ccc}{\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& 1\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& 1\end{array}\right\}\left[g_{2s_{1/2}}^{[1/2]}\left({\omega }_1\right)g_{1s_{1/2}}^{[1/2]\ast }\left({\omega }_1\right)+g_{1s_{1/2}}^{[1/2]}\left({\omega }_1\right)g_{2s_{1/2}}^{[1/2]\ast }\left({\omega }_1\right)\right]\\ +{(-1)}^{{\displaystyle \frac{3}{2}}+{\displaystyle \frac{1}{2}}}\left\{\begin{array}{ccc}{\displaystyle \frac{3}{2}}& {\displaystyle \frac{1}{2}}& 1\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& 1\end{array}\right\}\left[g_{2s_{1/2}}^{[3/2]}\left({\omega }_1\right)g_{1s_{1/2}}^{[1/2]\ast }\left({\omega }_1\right)+g_{1s_{1/2}}^{[3/2]}\left({\omega }_1\right)g_{2s_{1/2}}^{[1/2]\ast }\left({\omega }_1\right)\right]\\ +{(-1)}^{{\displaystyle \frac{1}{2}}+{\displaystyle \frac{3}{2}}}\left\{\begin{array}{ccc}{\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& 1\\ {\displaystyle \frac{3}{2}}& {\displaystyle \frac{1}{2}}& 1\end{array}\right\}\left[g_{2s_{1/2}}^{[1/2]}\left({\omega }_1\right)g_{1s_{1/2}}^{[3/2]\ast }\left({\omega }_1\right)+g_{1s_{1/2}}^{[1/2]}\left({\omega }_1\right)g_{2s_{1/2}}^{[3/2]\ast }\left({\omega }_1\right)\right]\\ \hfill \left.+{(-1)}^{{\displaystyle \frac{3}{2}}+{\displaystyle \frac{3}{2}}}\left\{\begin{array}{ccc}{\displaystyle \frac{3}{2}}& {\displaystyle \frac{1}{2}}& 1\\ {\displaystyle \frac{3}{2}}& {\displaystyle \frac{1}{2}}& 1\end{array}\right\}\left[g_{2s_{1/2}}^{[3/2]}\left({\omega }_1\right)g_{1s_{1/2}}^{[3/2]\ast }\left({\omega }_1\right)+g_{1s_{1/2}}^{[3/2]}\left({\omega }_1\right)g_{2s_{1/2}}^{[3/2]\ast }\left({\omega }_1\right)\right]\right\}\end{array}$$

(13)

where $g_{1s_{1/2}}^{\left[j\right]}$ and $g_{2s_{1/2}}^{\left[j\right]}$ are the individual sums/integrals over intermediate states of angular momentum $j=1/2$ or $j=3/2$. The $1s$ and $2s$ subscripts show which state is connected to the “first” photon denoted by ${\hat{T}}^{E1}\left({\omega }_1\right)$:

$$\begin{array}{c}\hfill g_{2s_{1/2}}^{\left[j\right]}\left({\omega }_1\right)=\sum _{\nu }\int \sum _{{\kappa }_{\nu }}{\delta }_{j_{\nu },j}{\displaystyle \frac{⟨1s_{1/2}\Vert {\widehat{T}}^{E1}({\omega }_{2s_{1/2},1s_{1/2}}-{\omega }_1)\Vert \nu {\kappa }_{\nu }⟩⟨\nu {\kappa }_{\nu }\Vert {\widehat{T}}^{E1}\left({\omega }_1\right)\Vert 2s_{1/2}⟩}{{\omega }_{\nu }+{\omega }_1-{\omega }_{2s_{1/2}}}}\\ \hfill g_{1s_{1/2}}^{\left[j\right]}\left({\omega }_1\right)=\sum _{\nu }\int \sum _{{\kappa }_{\nu }}{\delta }_{j_{\nu },j}{\displaystyle \frac{⟨1s_{1/2}\Vert {\widehat{T}}^{E1}\left({\omega }_1\right)\Vert \nu {\kappa }_{\nu }⟩⟨\nu {\kappa }_{\nu }\Vert {\widehat{T}}^{E1}({\omega }_{2s_{1/2},1s_{1/2}}-{\omega }_1)\Vert 2s_{1/2}⟩}{{\omega }_{\nu }-{\omega }_1-{\omega }_{1s_{1/2}}}}\end{array}$$

(14)

These intermediate functions are evaluated for discretized values of ${\omega }_1$ after computing the matrix elements using Dirac orbitals in Babushkin and Coulomb gauges, as well as in their non-relativistic (LWA) counterparts, Length and Velocity, respectively.

2.2. Matrix Elements in Different Gauges

The Dirac electric multipole matrix elements, whether in Coulomb or Babushkin gauge, are structured using the following radial integrals [53,55]:

$$\begin{array}{c}\hfill {\mathcal{I}}_L^{\pm }\left(k\right)=\underset{0}{\overset{\infty }{\int }}\left[P_{E_{\beta }{\kappa }_{\beta }}^{*}\left(r\right)Q_{E_{\alpha }{\kappa }_{\alpha }}\left(r\right)\pm Q_{E_{\beta }{\kappa }_{\beta }}^{*}\left(r\right)P_{E_{\alpha }{\kappa }_{\alpha }}\left(r\right)\right]j_L\left(kr\right)dr\end{array}$$

(15)

$$\begin{array}{c}\hfill {\mathcal{J}}_L\left(k\right)=\underset{0}{\overset{\infty }{\int }}\left[P_{E_{\beta }{\kappa }_{\beta }}^{*}\left(r\right)P_{E_{\alpha }{\kappa }_{\alpha }}\left(r\right)+Q_{E_{\beta }{\kappa }_{\beta }}^{*}\left(r\right)Q_{E_{\alpha }{\kappa }_{\alpha }}\left(r\right)\right]j_L\left(kr\right)dr\end{array}$$

(16)

It is useful to define the reduced matrix element of the tensor-like spherical harmonic between relativistic $\left(\kappa \right)$ states:

$$\begin{array}{c}\hfill ⟨\kappa \Vert C^K\Vert {\kappa }^{\prime }⟩={(-1)}^{j+1/2}\sqrt{[j,j^{\prime }]}\left(\begin{array}{ccc}j& K& j^{\prime }\\ 1/2& 0& -1/2\end{array}\right)\end{array}$$

(17)

The electric dipole reduced matrix element for Dirac orbitals in Coulomb and Babushkin gauges is given by [53,55]:

$$\begin{array}{c}{⟨E_{\beta }{\kappa }_{\beta }\Vert {\widehat{T}}^{E1}\Vert E_{\alpha }{\kappa }_{\alpha }⟩}_{Coulomb}=(-i)⟨{\kappa }_{\beta }\Vert C^K\Vert {\kappa }_{\alpha }⟩\hfill \\ \times \left\{{\displaystyle \frac{1}{\sqrt{2}}}\left[({\kappa }_{\beta }-{\kappa }_{\alpha }){\mathcal{I}}_2^{+}+2{\mathcal{I}}_2^{-}\right]-\sqrt{2}\left[({\kappa }_{\beta }-{\kappa }_{\alpha }){\mathcal{I}}_0^{+}-{\mathcal{I}}_0^{-}\right]\right\}\hfill \end{array}$$

(18)

$$\begin{array}{c}{⟨E_{\beta }{\kappa }_{\beta }\Vert {\widehat{T}}^{E1}\Vert E_{\alpha }{\kappa }_{\alpha }⟩}_{Babuskin}=(-3i)⟨{\kappa }_{\beta }\Vert C^K\Vert {\kappa }_{\alpha }⟩\hfill \\ \times \left\{{\displaystyle \frac{1}{\sqrt{2}}}\left[({\kappa }_{\beta }-{\kappa }_{\alpha }){\mathcal{I}}_2^{+}+2{\mathcal{I}}_2^{-}\right]-\sqrt{2}{\mathcal{J}}_1\right\}\hfill \end{array}$$

(19)

In the LWA limit, only the integrals containing the lowest-order spherical Bessel functions are retained, and their first order approximation in the expansion is applied. The Coulomb and Babushkin gauges are reduced to Velocity and Length gauges, respectively:

$$\begin{array}{c}{⟨E_{\beta }{\kappa }_{\beta }\Vert {\widehat{T}}^{E1}\Vert E_{\alpha }{\kappa }_{\alpha }⟩}_{Coulomb}\underset{kr\ll 1}{\approx }{⟨E_{\beta }{\kappa }_{\beta }\Vert {\widehat{T}}^{E1}\Vert E_{\alpha }{\kappa }_{\alpha }⟩}_{Velocity}=i\sqrt{2}⟨{\kappa }_{\beta }\Vert C^K\Vert {\kappa }_{\alpha }⟩\hfill \\ \times \underset{0}{\overset{\infty }{\int }}\left[({\kappa }_{\beta }-{\kappa }_{\alpha }-1)P_{E_{\beta }{\kappa }_{\beta }}^{*}\left(r\right)Q_{E_{\alpha }{\kappa }_{\alpha }}\left(r\right)+({\kappa }_{\beta }-{\kappa }_{\alpha }+1)Q_{E_{\beta }{\kappa }_{\beta }}^{*}\left(r\right)P_{E_{\alpha }{\kappa }_{\alpha }}\left(r\right)\right]dr\hfill \end{array}$$

(20)

$$\begin{array}{c}{⟨E_{\beta }{\kappa }_{\beta }\Vert {\widehat{T}}^{E1}\Vert E_{\alpha }{\kappa }_{\alpha }⟩}_{Babuskin}\underset{kr\ll 1}{\approx }{⟨E_{\beta }{\kappa }_{\beta }\Vert {\widehat{T}}^{E1}\Vert E_{\alpha }{\kappa }_{\alpha }⟩}_{Length}=i\sqrt{2}⟨{\kappa }_{\beta }\Vert C^K\Vert {\kappa }_{\alpha }⟩\hfill \\ \times \underset{0}{\overset{\infty }{\int }}\left[P_{E_{\beta }{\kappa }_{\beta }}^{*}\left(r\right)P_{E_{\alpha }{\kappa }_{\alpha }}\left(r\right)+Q_{E_{\beta }{\kappa }_{\beta }}^{*}\left(r\right)Q_{E_{\alpha }{\kappa }_{\alpha }}\left(r\right)\right]k r dr\hfill \end{array}$$

(21)

2.3. Numerical Approach

The radial functions for the bound and continuum states were generated on a logarithmic grid of 5000 points between ${10}^{-8}/Z$ and $50/Z$ atomic units. All radial integrals contained either $1s_{1/2}$ or $2s_{1/2}$ orbitals in their arguments, ensuring that all the relevant contributions are included by using a maximum radius of $50/Z$ atomic units.

We included 1000 bound states of $n{p}_{1/2}$ and $n{p}_{3/2}$ types, while for the positive or negative continuum, we discretized the energy into 2000 logarithmic grid points from ${10}^{-5}{Z}^2$ to ${10}^3{Z}^2$ atomic units of energy for each $ϵp_{1/2}$ and $ϵp_{3/2}$ types. A fine tuning was performed for the minimum continuum energy cutoff in the ${10}^{-5}{Z}^2$ to ${10}^{-3}{Z}^2$ atomic units of energy range in order to avoid the singularity at $ϵ\to 0$ by maintaining gauge invariance between Babushkin and Coulomb treatments. The LWA radial integrals and matrix elements have also been evaluated for the same numerical parameters.

After computing the reduced elements, we discretized the photon energy ${\omega }_1$ into 513 points from ${\omega }_1=0$ to ${\omega }_1={\omega }_{2s_{1/2},1s_{1/2}}$. The functions $g^{\left[j\right]}\left({\omega }_1\right)$ containing the summation over intermediate states were evaluated at these points. The number of points $513(=2^9+1)$ has been chosen in order to optimally match the Clenshaw–Cutris quadratures scheme used to integrate the two-photon decay rate. Calculations were simultaneously performed for $257(=2^8+1)$ points, showing no deviation compared to the previous case within the five significant digits.

3. Results and Discussion

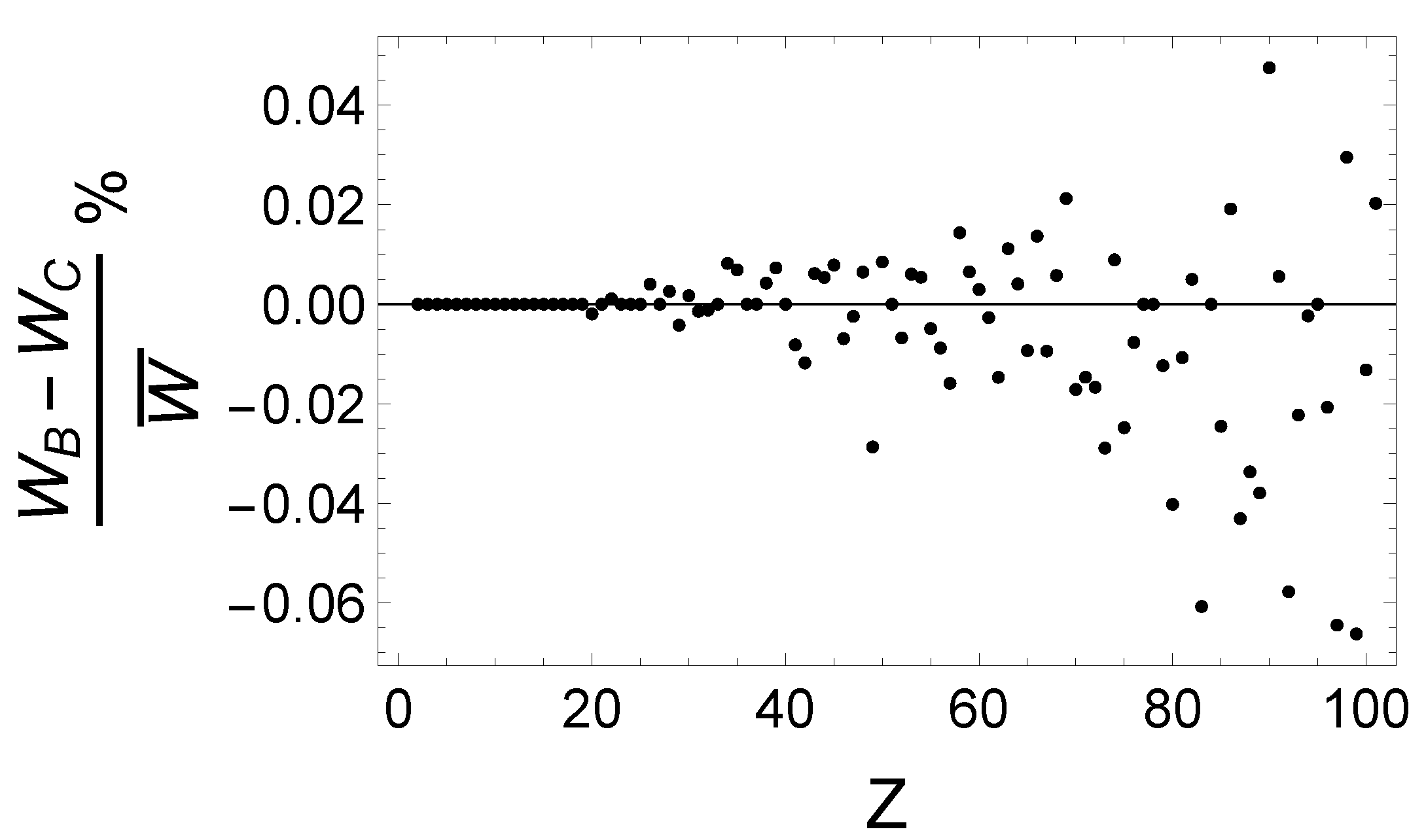
The two-photon decay rates of the $2s_{1/2}$ level in hydrogen-like ions with nuclear charges $Z=1-100$ have been calculated using the SOS method based on analytical Dirac eigenstates within Babushkin, Coulomb, Length (LWA), and Velocity (LWA) gauges. This section is dedicated to assessment of results, while the complete set of data are available in the extended table in Appendix B. In Figure 2, we check the gauge invariance of the present results in the relativistic Babuskin and Coulomb approaches:

$$\begin{array}{c}\hfill \epsilon ={\displaystyle \frac{W_{Babushkin}-W_{Coulomb}}{\left[W_{Babushkin}+W_{Coulomb}\right]/2}}\%\end{array}$$

(22)

For lighter ions, there is no difference up to 5 significant decimals; however, smaller deviations appear with increasing nuclear charge Z, no larger than $0.07\%$.

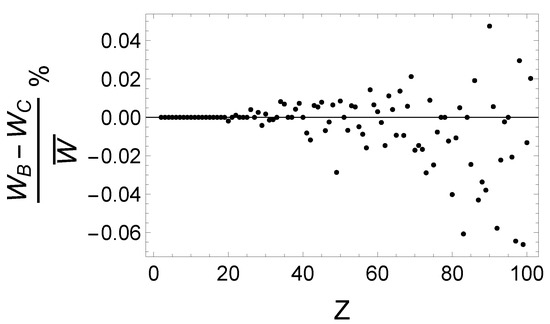
Figure 2. Relative deviations between Babushkin and Coulomb calculations based on Dirac orbitals for gauge invariance assessment.

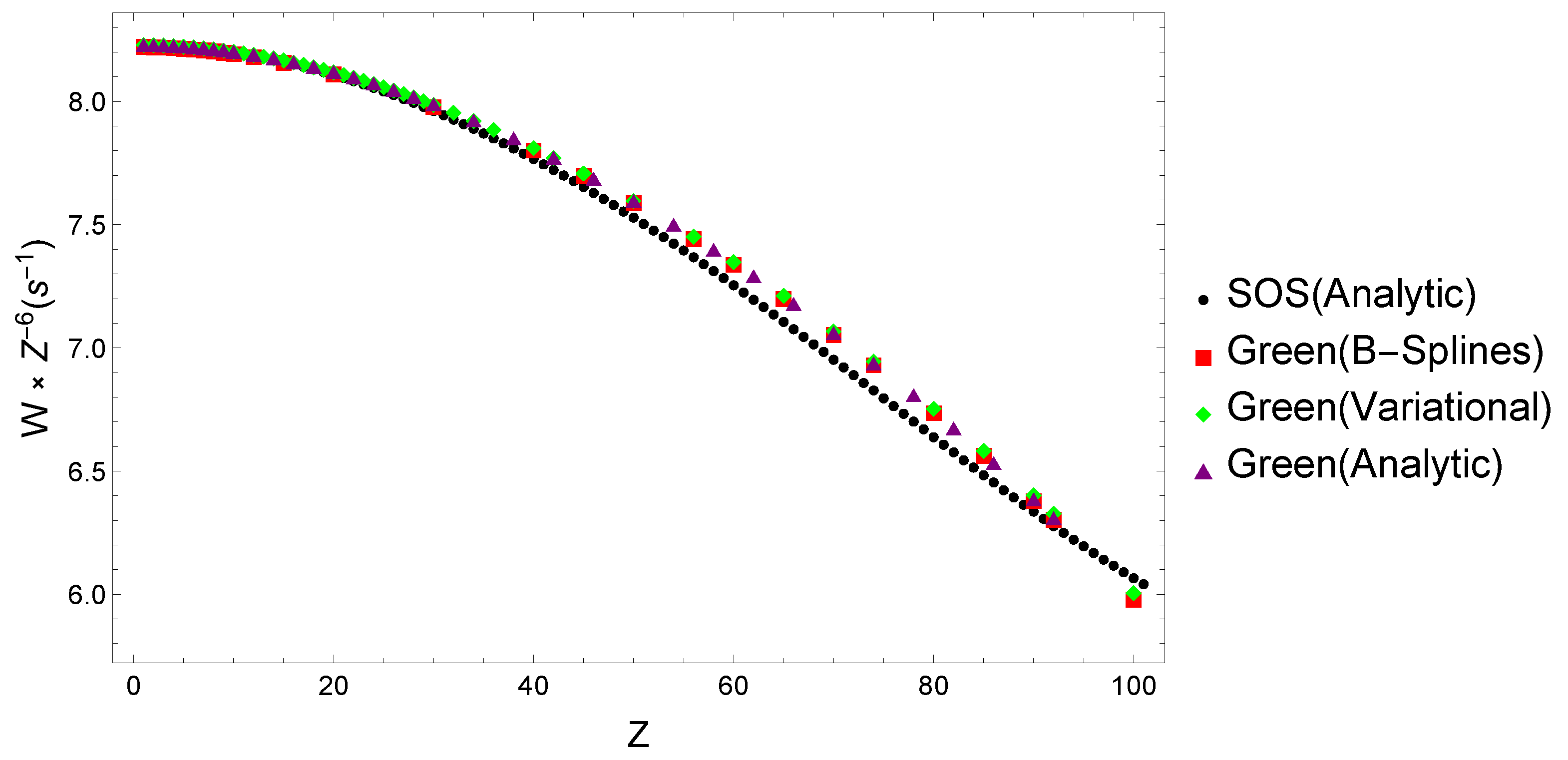
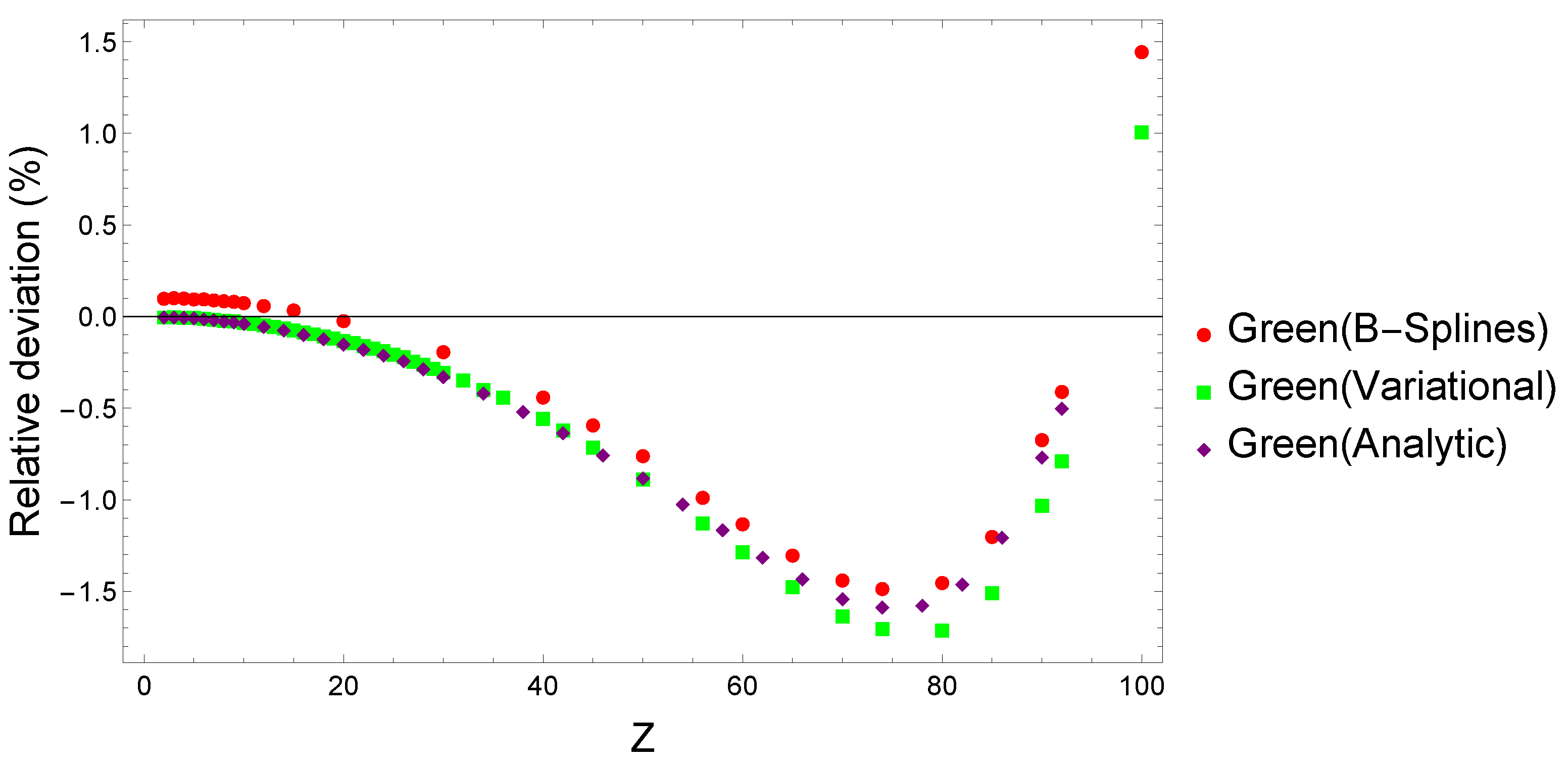
Present relativistic SOS results are compared with Dirac-Coulomb Green function expansion in finite basis calculations based on B-splines by Labzowsky et al. [37], variational eigenstates by Goldman and Drake [28], and analytical solutions by Parpia and Johnson [30]. These papers used the full expansion of the photon electric dipole operators demonstrating gauge invariance in their results. Figure 3 shows the present two-photon decay rates scaled with the nuclear charge $Z^6$ together with those from the works mentioned earlier. The relative deviations in % compared to present results are provided in Figure 4.

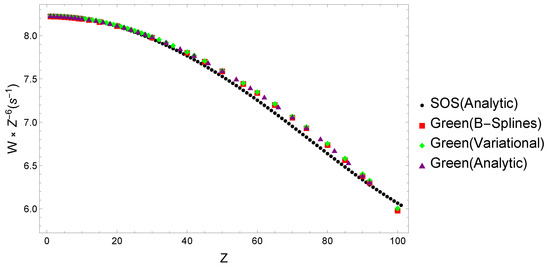
Figure 3. Relativistic two-photon decay rates for the $2s_{1/2}$ level in hydrogen-like ions scaled with the nuclear charge $Z^6$ determined using SOS (Present), and Dirac-Coulomb Green function approach based on B-Splines [37], variational states [28], and analytical eigenstates [30].

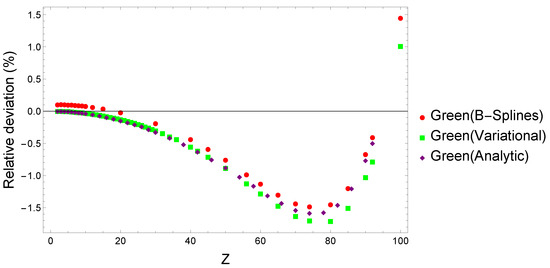
Figure 4. Relative deviations of the relativistic two-photon decay rates for the $2s_{1/2}$ level in hydrogen-like ions scaled with the nuclear charge $Z^6$ determined using Dirac-Coulomb Green function approach based on B-Splines [37], variational states [28], and analytical eigenstates [30] compared to present SOS results.

The present results, together with those from Labzowsky et al. [37] and Goldman and Drake [28], already attained gauge invariance (negligible differences between Coulomb and Babushkin gauges); hence, we only plot the Coulomb values to avoid overloading the figure.

For low nuclear charge $Z\le 20$, the results agree to better than $0.1\%$, but the deviations steadily increase up to around $Z\approx 80$, where they reach roughly 1.4–1.8% relative values. After $Z=80$, the deviations evolve in the opposite direction, first decreasing, then reaching roughly 1–1.5% relative error at $Z=100$. The Green function method assures completeness, while the SOS approach requires large numbers of bound, positive, and negative continuum states for convergence. However, the deviations are most likely caused by the numerical continuum energy cutoff near $ϵ\to 0$ at high Z values.

The negative continuum states contribution to the two-photon decay rate is gauge-dependent, which also implies method-dependence. Table 1 and Table 2 provide comparisons for rates belonging to $H^0$ and $U^{91+}$ between the present SOS approach based on Dirac analytical eigenstates and the Dirac B-splines approaches of Labzowski et al. [37] and Surzhykov et al. [42]. While the total rates loosely agree, one notices orders of magnitude differences between different works for positive- and negative-energy contributions to the total rates. Depending on how closely the pseudo-states (B-splines in those works) approximate the real eigenstates, the distribution of contributions from positive- and negative-energy states changes. When exact energy eigenstates are used (present study), the negative continuum contributions to Babushkin and Length (LWA) gauges are quite small, though not negligible for higher Z values. On the other hand, the Coulomb and Velocity (LWA) gauges are sensible to negative-energy states even for lower Z elements, and their inclusion is essential for achieving gauge invariance.

Table 1. Positive- $\left(W_{+}\right)$, negative- $\left(W_{-}\right)$, and full $\left(W_t\right)$ energy contributions to the two-photon decay rate provided by the present work, Labzowsky et al. [37], and Surzhykov et al. [42] in Babushkin gauge.

Ion	Rate	SOS (Present)	Labzowsky et al. [37]	Surzhykov et al. [42]
	$W_{+}$	$8.2281E+00$	$8.2206E+00$	$8.2291E+00$
$H^0$	$W_{-}$	$4.1584E-22$	$3.9975E-22$	$2.4949E-08$
	${\mathbf{W}}_{\mathbf{t}}$	$\mathbf{8}.\mathbf{2281}\mathbf{E}+\mathbf{00}$	$\mathbf{8}.\mathbf{2207}\mathbf{E}+\mathbf{00}$	$\mathbf{8}.\mathbf{2291}\mathbf{E}+\mathbf{00}$
	$W_{+}$	$3.8163E+12$	$3.8230E+12$	$2.9041E+12$
$U^{91+}$	$W_{-}$	$7.7250E+06$	$1.2851E+05$	$6.8066E+11$
	${\mathbf{W}}_{\mathbf{t}}$	$\mathbf{3}.\mathbf{8059}\mathbf{E}+\mathbf{12}$	$\mathbf{3}.\mathbf{8216}\mathbf{E}+\mathbf{12}$	$\mathbf{3}.\mathbf{8256}\mathbf{E}+\mathbf{12}$

Table 2. Positive- $\left(W_{+}\right)$, negative- $\left(W_{-}\right)$, and full $\left(W_t\right)$ energy contributions to the two-photon decay rate provided by the present work, Labzowsky et al. [37], and Surzhykov et al. [42] in Coulomb gauge.

Ion	Rate	SOS (Present)	Labzowsky et al. [37]	Surzhykov et al. [42]
	$W_{+}$	$8.2274E+00$	$8.2202E+00$	$8.2291E+00$
$H^0$	$W_{-}$	$1.3978E-08$	$6.2233E-09$	$6.2372E-09$
	${\mathbf{W}}_{\mathbf{t}}$	$\mathbf{8}.\mathbf{2281}\mathbf{E}+\mathbf{00}$	$\mathbf{8}.\mathbf{2206}\mathbf{E}+\mathbf{00}$	$\mathbf{8}.\mathbf{2291}\mathbf{E}+\mathbf{00}$
	$W_{+}$	$2.7157E+12$	$2.3914E+12$	$2.3939E+12$
$U^{91+}$	$W_{-}$	$9.4393E+10$	$1.7026E+11$	$1.7044E+11$
	${\mathbf{W}}_{\mathbf{t}}$	$\mathbf{3}.\mathbf{8081}\mathbf{E}+\mathbf{12}$	$\mathbf{3}.\mathbf{8216}\mathbf{E}+\mathbf{12}$	$\mathbf{3}.\mathbf{8256}\mathbf{E}+\mathbf{12}$

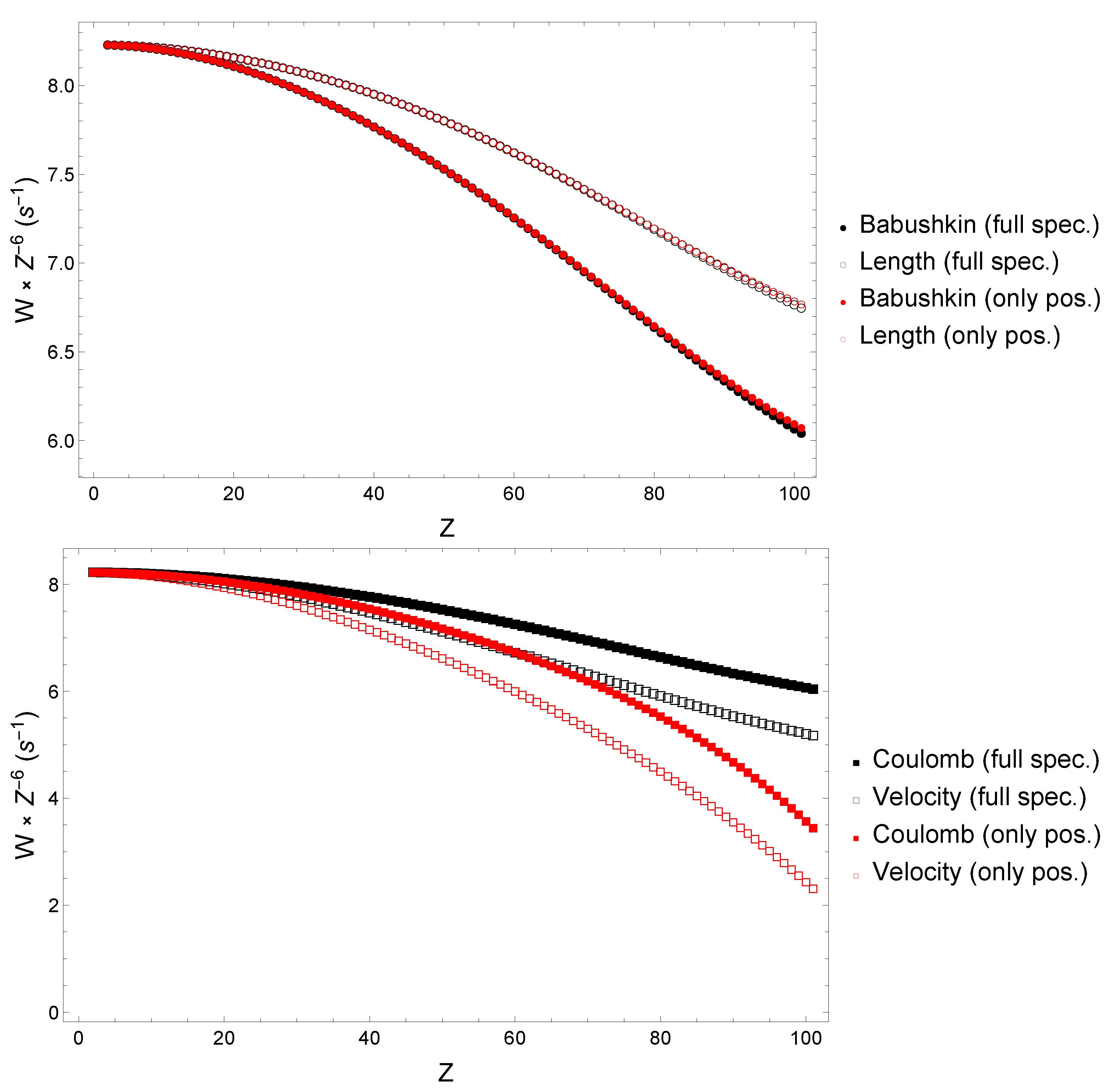
The gauge behaviors are better shown in Figure 5, where one can clearly see that Babushkin and Length gauges are only affected by the negative states at high nuclear charge Z, with contributions estimated at $-1.34\%{\left(\alpha Z\right)}^4$ and $-0.75\%{\left(\alpha Z\right)}^4$, respectively. However, the Coulomb and Velocity gauges are deeply affected by the negative states, even for low Z ions, with contributions estimated at $1.46{\left(\alpha Z\right)}^4$ and $1.99{\left(\alpha Z\right)}^4$, respectively.

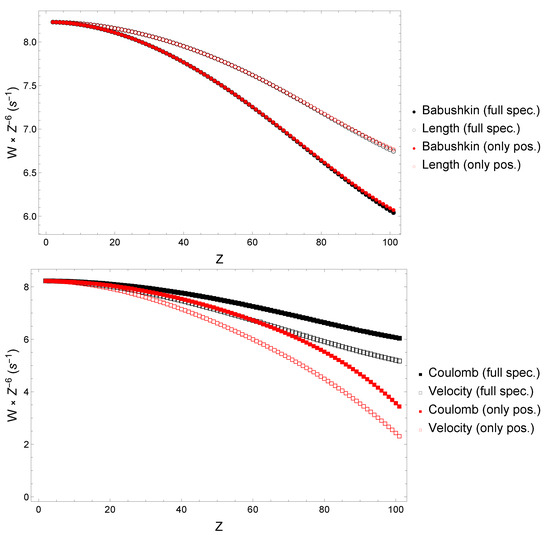
Figure 5. Two photon decay rates scaled by $Z^6$ computed with the full Dirac Hamiltonian spectrum $W_t$ (black symbols) or with positive states only $W_{+}$ (red symbols). Full symbols indicate results obtained in the relativistic Babushkin or Coulomb gauges, while empty symbols correspond to the LWA (Length and Velocity) gauge calculation. The top panel presents the Babushkin and Length gauge results, while the bottom panel indicates the Coulomb and Velocity gauge results.

These estimations have been achieved by minimizing the squared deviations between rates computed using the full Dirac spectrum versus rates using only the positive energy eigenstates.

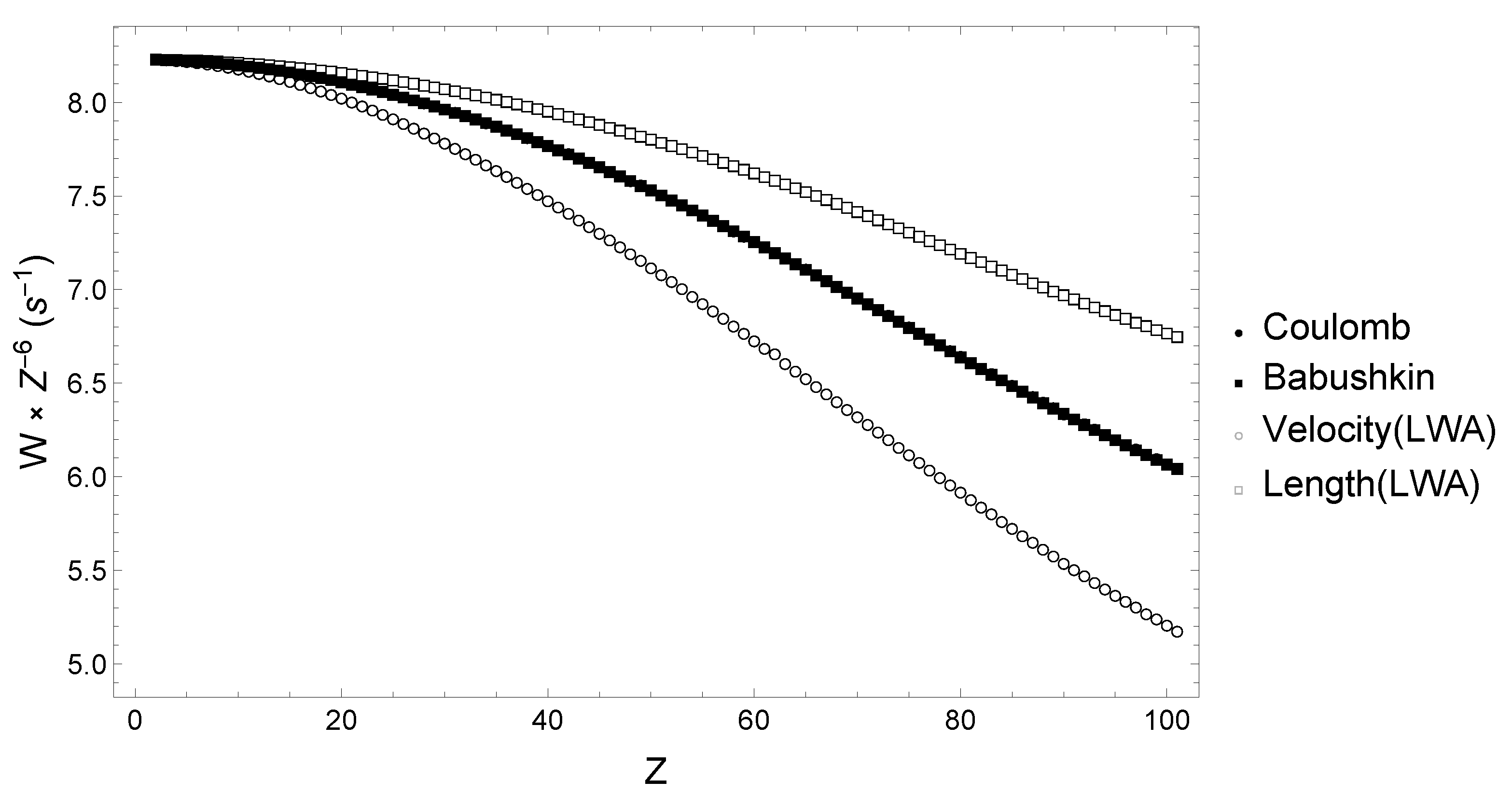
Because the Lorenz gauge condition is no longer satisfied in the LWA implementation, gauge invariance is increasingly broken as Z increases such that the Length gauge calculations overestimate the Babushkin result by ≈$24\%{\left(\alpha Z\right)}^2$, while the Velocity gauge calculations underestimate the Coulomb results by up to ≈$31\%{\left(\alpha Z\right)}^2$, as shown in Figure 6. Goldman and Drake [28] stated that the LWA values of Johnson [27] underestimate the Coulomb results by roughly ≈$20\%{\left(\alpha Z\right)}^2$. By minimizing the deviations between Coulomb [28] and Velocity [27] values from those works, we notice the deviations are closer to $24\%{\left(\alpha Z\right)}^2$. While the LWA limit behaves similarly in both approaches, the differences in deviations, $24\%{\left(\alpha Z\right)}^2$ compared to $31\%{\left(\alpha Z\right)}^2$, may arise due to the different methods used in the calculation, such as the relativistic Coulomb–Green function method versus the present SOS approach.

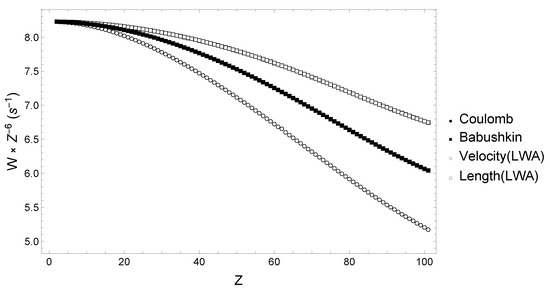
Figure 6. Two photon decay rates of $2s_{1/2}$ level in hydrogen-like ions scaled by $Z^6$ computed in relativistic, Babushkin (full black square) and Coulomb (full black disk), and non-relativistic, Length (empty black square) and Velocity (black circle), gauges. The full discrete and (positive+negative) continuum Dirac spectrum is considered.

Depending on the basis completeness and how closely the pseudo-states approach the true eigenstates, models involving simultaneous two-photon processes in highly charged heavy ions become sensitive to the electric dipole slowing effects in both the Babushkin and, in particular, the Coulomb gauge. The latter is especially sensitive to the negative continuum contribution along the whole hydrogen-like isoelectronic series.

4. Conclusions

The two-photon decay rate corresponding to the $2s_{1/2}-1s_{1/2}$ transition in hydrogen-like ions has been evaluated in the second-order perturbation theory by summing over intermediate states represented by the analytical Dirac bound and (positive and negative) continuum eigenstates in relativistic Babushkin and Coulomb gauges, as well as in their non-relativistic Length and Velocity counterparts by taking the LWA limit, respectively.

When the long-wavelength approximation is implemented, the present results show a $24\%{\left(\alpha Z\right)}^2$ overestimation of the Babushkin gauge values and a $31\%{\left(\alpha Z\right)}^2$ underestimation of the Coulomb results. The negative continuum contributions bear little effect on the Babushkin values when analytical energy eigenstates are used but are crucial in Coulomb calculations for obtaining gauge invariance.