A Comparative Study of COMPLET Code Predictions with Experimental Data on Alpha Particle-Induced Reactions on Cobalt Isotope up to 120 MeV

Cherie Sisay Mekonen; Ayyagari Venkata Mohan Rao

doi:10.3390/atoms13120096

and

¹

Department of Physics, Woldia University, Woldia P.O. Box 400, Ethiopia

²

Department of Physics, University of Gondar, Gondar P.O. Box 196, Ethiopia

^*

Author to whom correspondence should be addressed.

Atoms2025, 13(12), 96;https://doi.org/10.3390/atoms13120096
(registering DOI)

Version Notes

Order Reprints

Abstract

A comparative study of alpha-induced reactions on cobalt isotope with the predictions by COMPLET code is presented for nine excitation functions, ⁵⁹Co(α,p5n)⁵⁷Ni, ⁵⁹Co (α,p6n)⁵⁶Ni, ⁵⁹Co(α,2pn)⁶⁰Co, ⁵⁹Co(α,3pn)⁵⁹Fe, ⁵⁹Co(α,αn)⁵⁸Co, ⁵⁹Co(α,α2n)⁵⁷Co, ⁵⁹Co(α,α3n)⁵⁶Co, ⁵⁹Co(α,2αn)⁵⁴Mn, and ⁵⁹Co(α,2α3n)⁵²Mn. The experimental values were taken from the EXFOR data base. Theoretical cross-sections were calculated using initial exciton number n₀ = 4 (4p0h) and level density parameter a (=ACN/10) globally. While several reactions showed excellent agreement with experimental data, others displayed a notable discrepancy. This is because of the limitations of the COMPLET code to take the alpha emission in a pre-equilibrium phase.

Keywords:

pre-equilibrium emission; alpha-induced emission; excitation functions; cobalt isotope; COMPLET code

1. Introduction

Nuclear reaction models and simulation codes, grounded in nuclear physics principles, are used to calculate and analyze reactions when experimental data are limited or unavailable. Theoretical predictions for nuclear reaction models are crucial for generating reliable reaction cross-section data [1]. Code COMPLET is an invaluable tool in educational contexts when direct experimentation is not possible, allowing students and researchers to investigate nuclear physics concepts. COMPLET is the nuclear reaction code developed to generate theoretical data on reaction mechanisms and cross-sections [2,3,4,5,6]. The computational algorithms used in code COMPLET can efficiently calculate complex reactions and interactions, making it a powerful tool for researchers in the field. The code advances detailed modeling that helps accurately predict reaction rates, energy patterns, and directions of particles released. It incorporates modern theoretical frameworks and experimental data to enhance its predictive power, making it a valuable tool for researchers in nuclear physics and related fields. This study focuses on alpha-induced reactions on cobalt-59, aiming to reproduce excitation functions and compare theoretical outputs with experimental data from EXFOR [7,8,9]. The COMPLET code, based on the exciton model, was selected for its adaptability and reliability in predicting pre-equilibrium contributions. Despite previous uses of COMPLET, no systematic study has explored its performance across multiple alpha-induced cobalt reactions at energies up to 120 MeV. This gap motivates the present work, which aims to systematically compare COMPLET code predictions with existing experimental data across the full 10–120 MeV range, refine the model inputs, and assess the reliability and limitations of the COMPLET framework for alpha-induced reactions on cobalt.

2. Results and Discussion

The results of this study were gathered using the COMPLET code to explore how alpha particles interact with cobalt-59 targets in nuclear reactions. The data were analyzed through tables and graphs, which included projectile energy (E_α), theoretical cross-sections, and experimental values. Multiple parameters were used to establish theoretical predictions of excitation functions and evaluate their effects on reaction cross-sections. One key factor is the initial exciton number, which is essential for achieving accurate calculated values. The level density parameter also plays a crucial role in the statistical calculations used in nuclear reaction models. The COMPLET code calculated theoretical cross-sections using fixed input parameters: an initial exciton number (n₀ = 4) and level density parameter a = ACN/10. Here, the initial exciton numbers and the level density parameter (a) [8,9,10,11,12] have been adjusted to match the experimental data. The level density parameter a is determined using the formula a = ACN/K, where ACN is the mass number of the compound nucleus, and K is an adjustable constant selected and optimized to achieve the best agreement with the experimental data [13,14,15]. The K-value was adjusted from 8 to 10, and the level density parameter that produced the best agreement with the experimental data was used for each reaction channel. The specific value of the level density parameter was selected based on the degree of agreement between calculated and experimental excitation functions.

This study compared theoretical computations generated by the COMPLET code with experimental data obtained from various authors through the EXFOR library [16,17,18,19]. The current study can be divided into two categories: one involving alpha particles alongside nucleons in the exit channels, and another that includes only nucleons in the exit channels. Several authors [20,21,22,23,24,25] explain pre-equilibrium processes on exciton models. They calculate particle emission rates by applying reciprocity to the ejectiles under consideration, rather than the entire system. This approach works well when only nucleons are considered, as their presence within nuclei is generally accepted, and there is solid theoretical guidance regarding their behavior. However, when it comes to clusters, there is a lack of information about their pre-formation and behavior within the nuclei based on a priori knowledge. The predictions made by the COMPLET code exhibit different levels of consistency when compared to the experimental data.

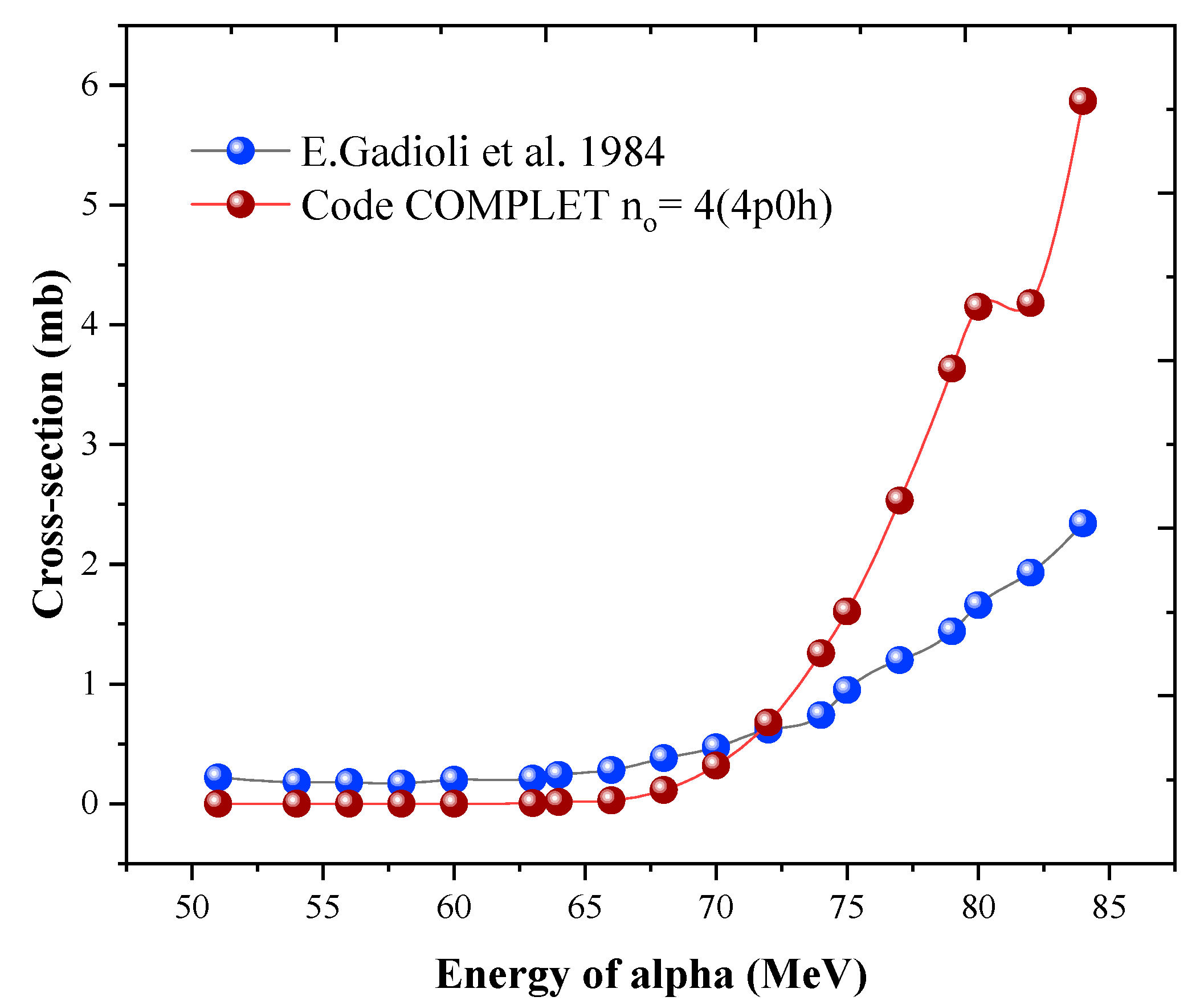
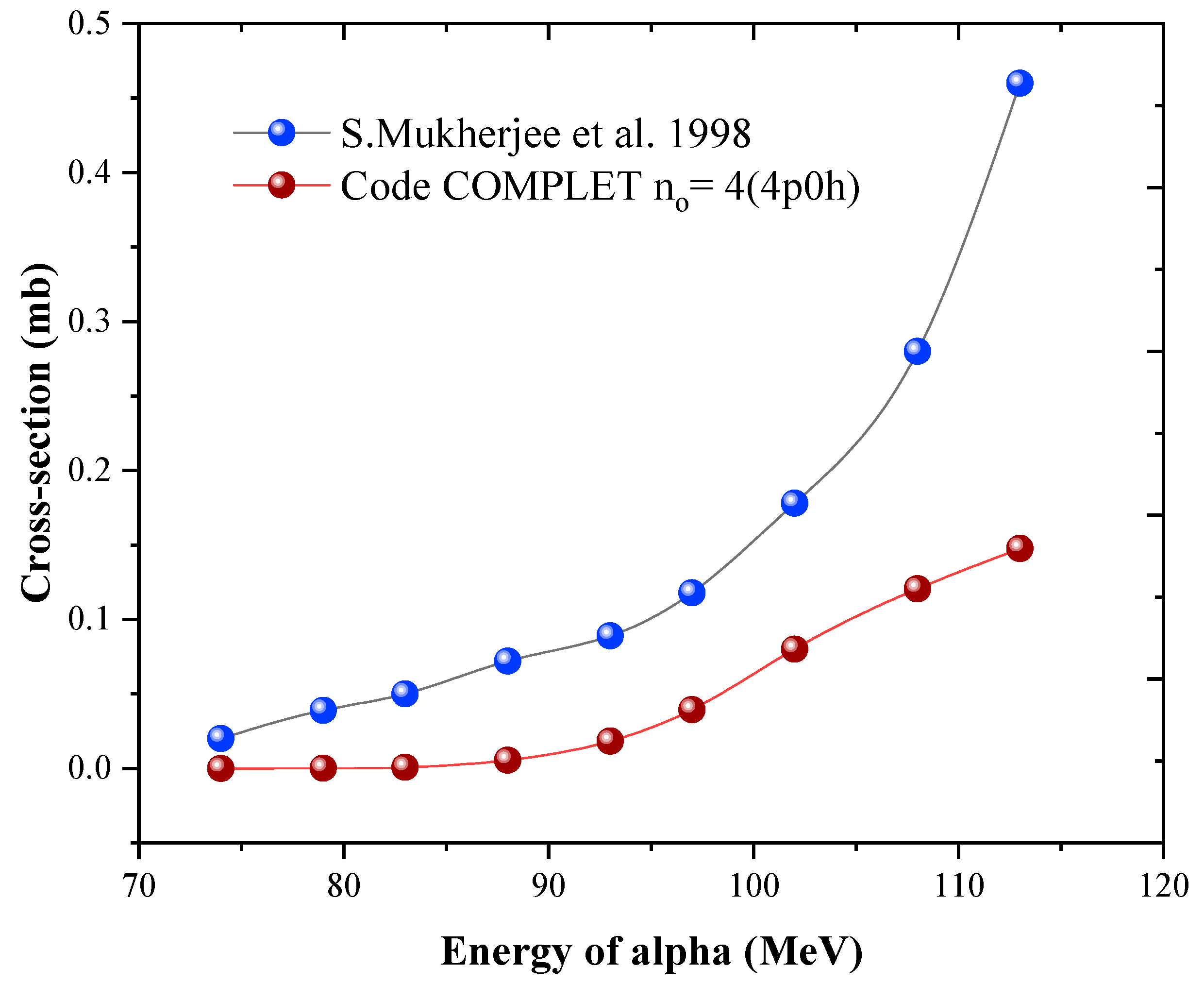
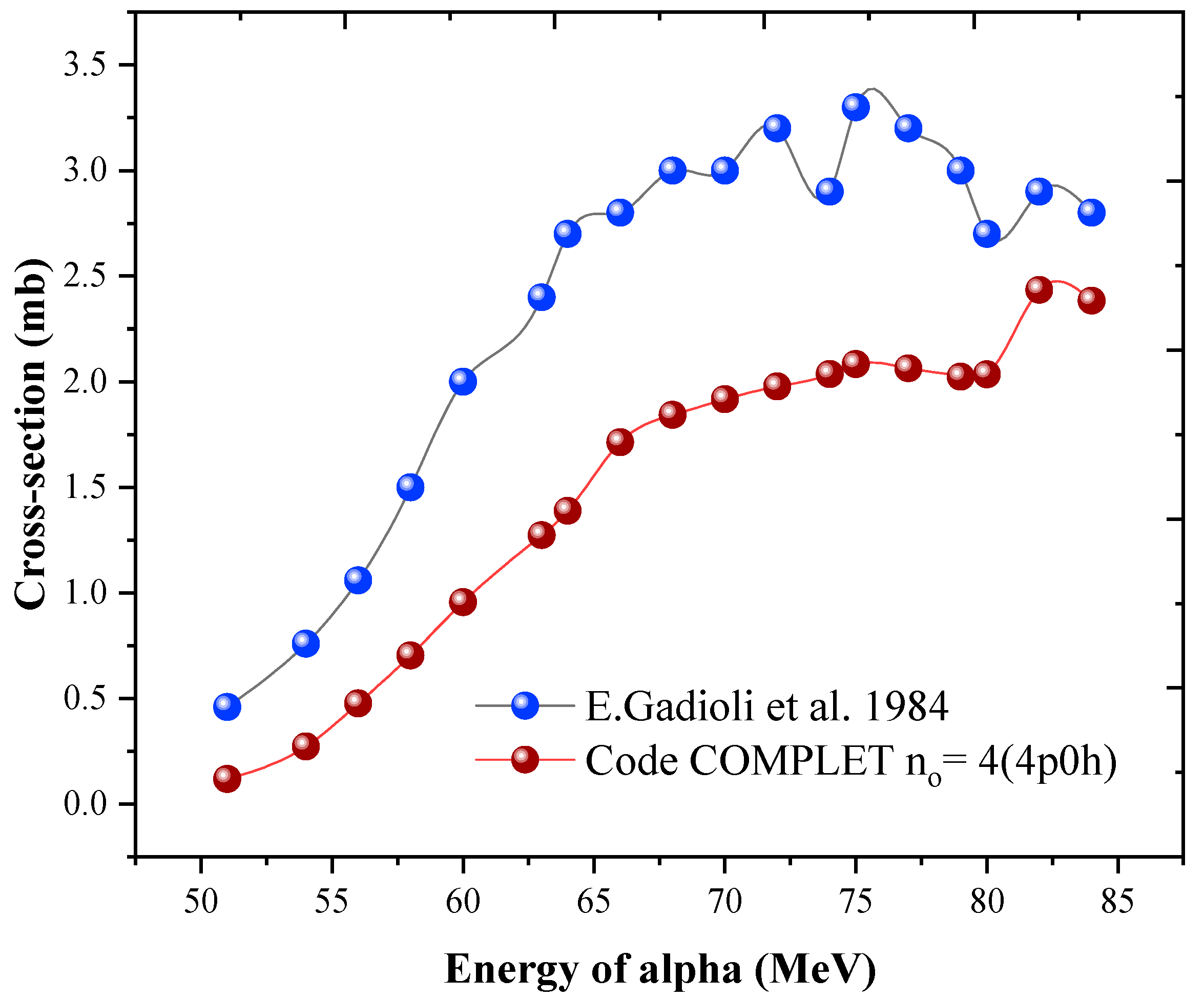
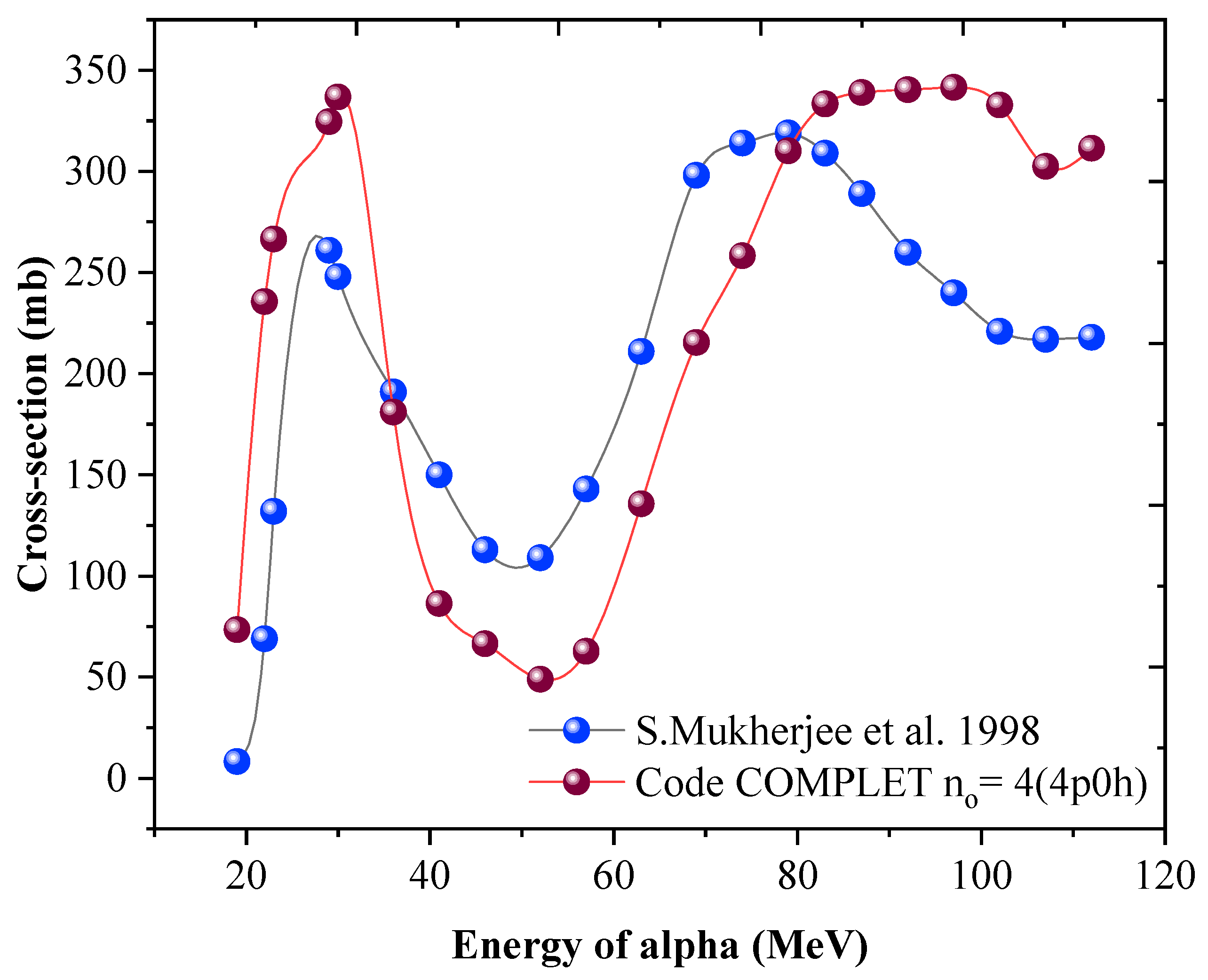
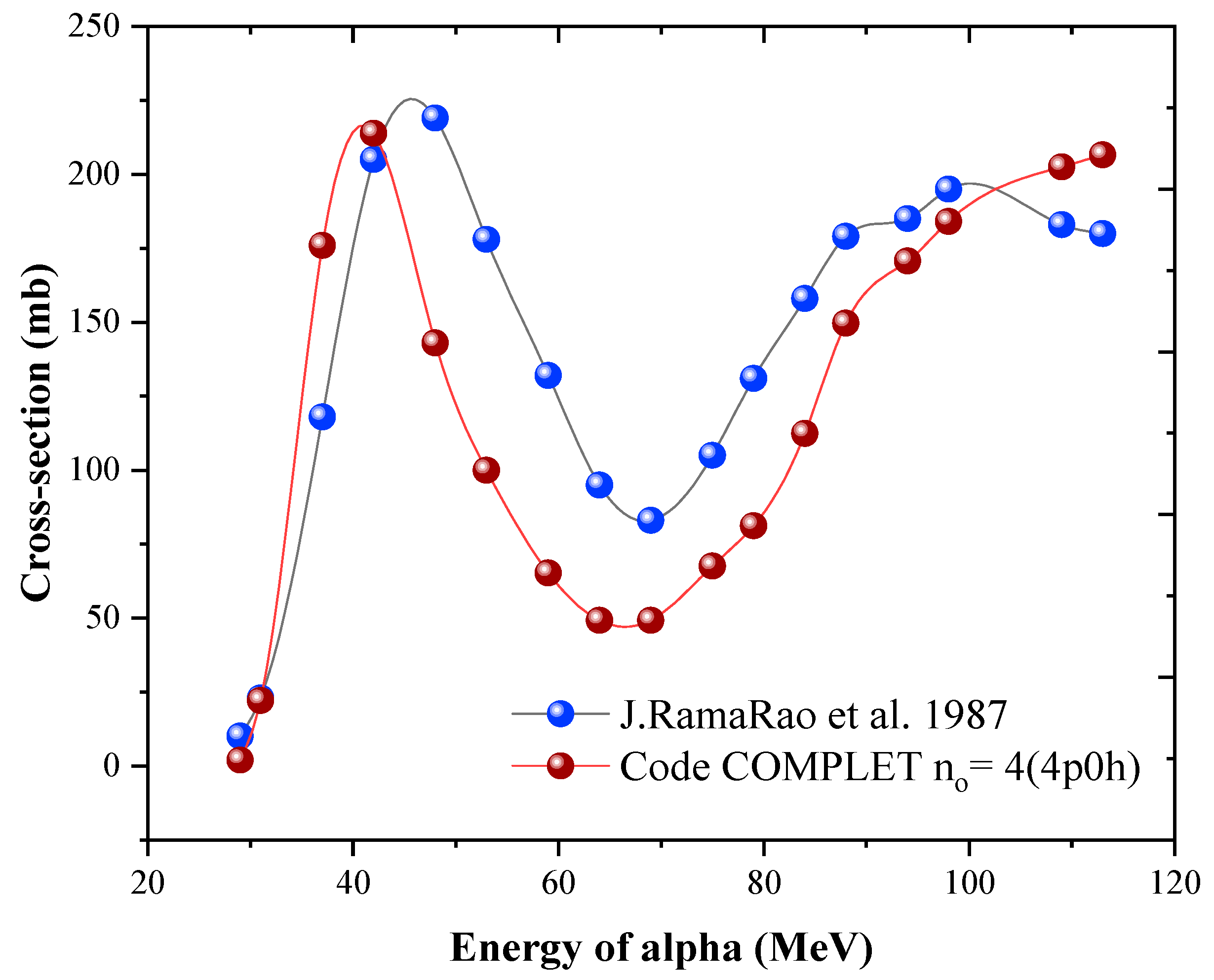
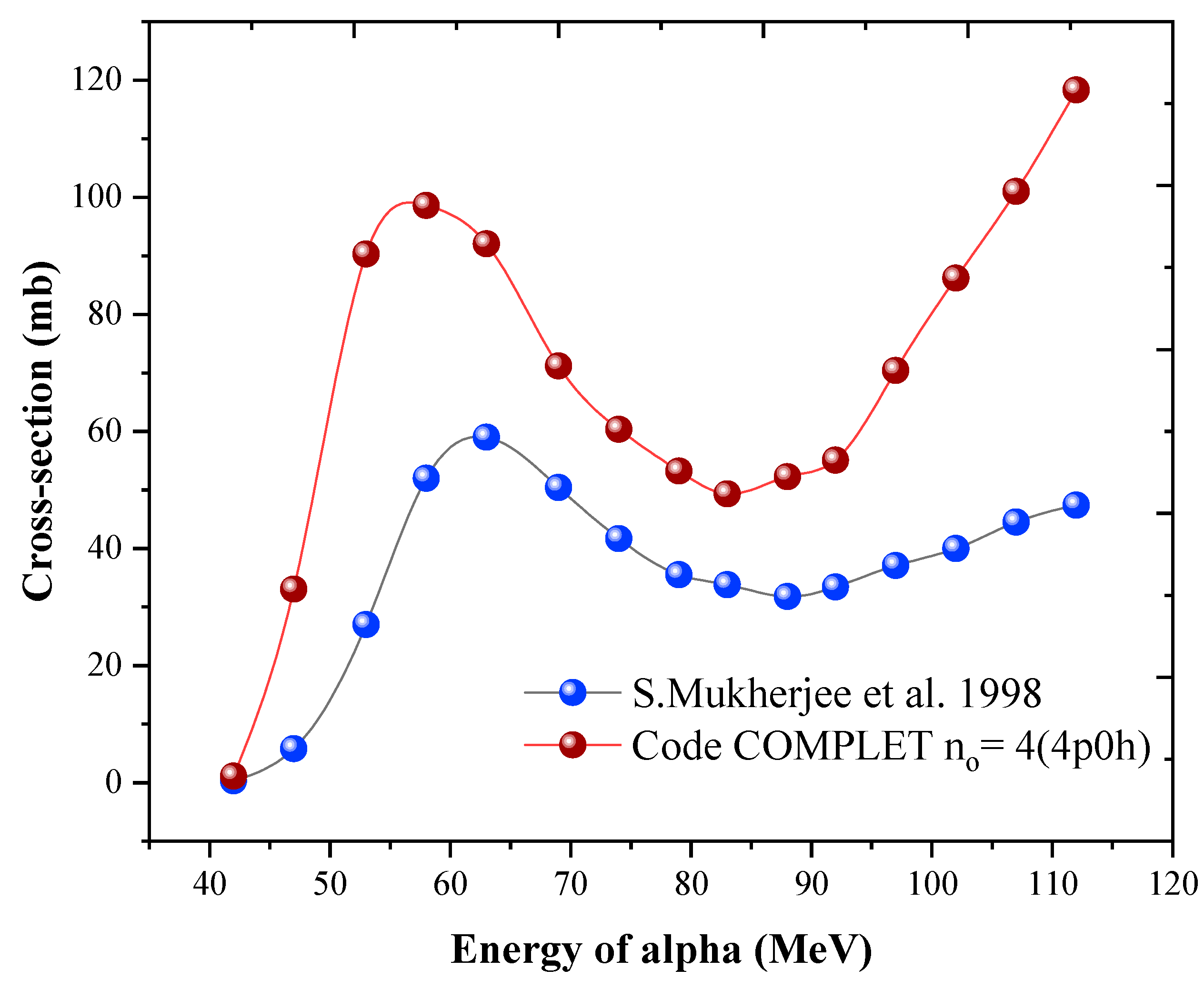
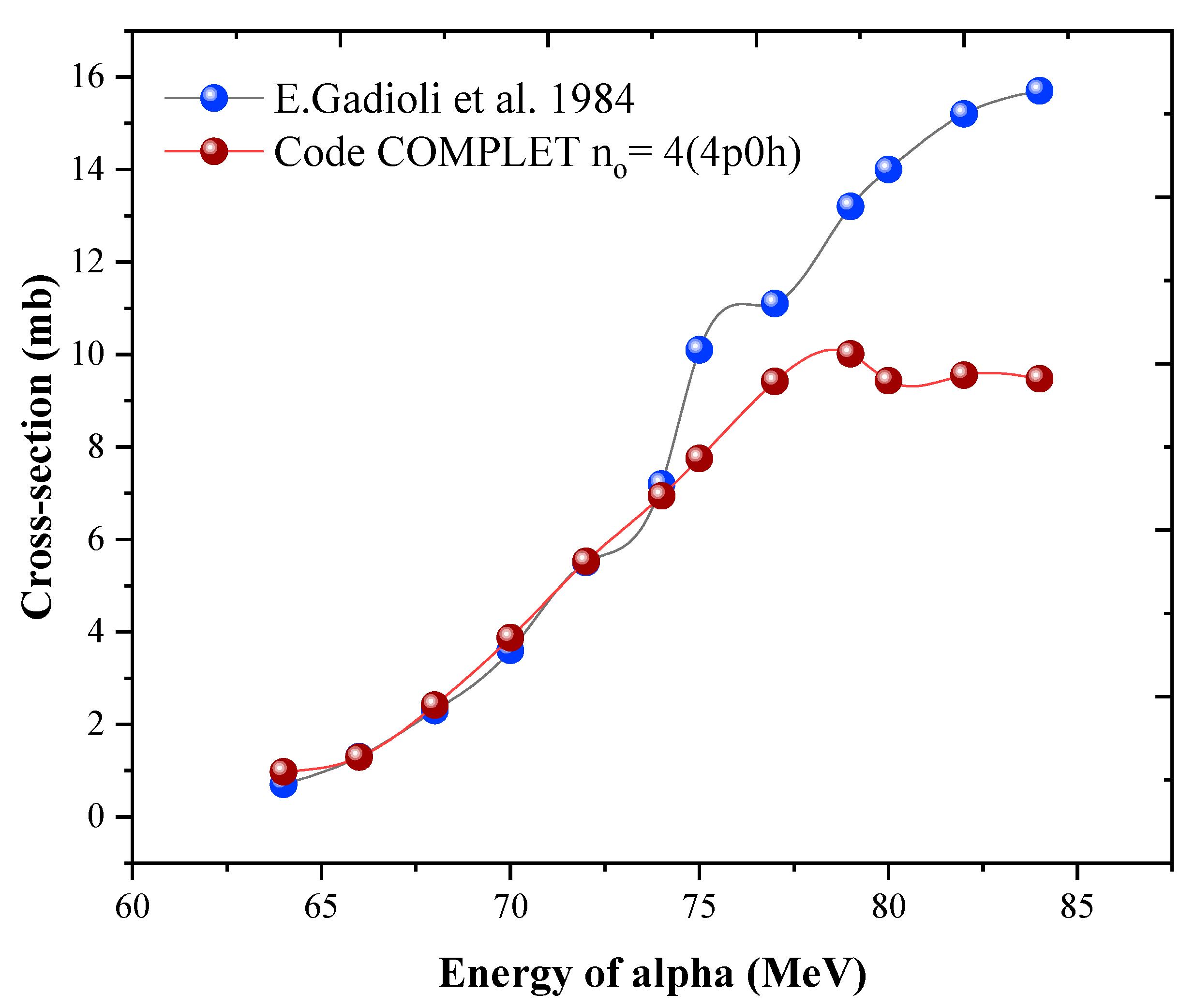
The first group includes the multiparticle emissions such us ⁵⁹Co(α, p5n), ⁵⁹Co(α, p6n), ⁵⁹Co(α, 2pn), and ⁵⁹Co(α, 3pn), these reactions are shown in Figure 1, Figure 2, Figure 3 and Figure 4. It is observed that in Figure 1 and Figure 2, while there is a good agreement between the experimental values and the COMPLET code predictions, there are discrepancies observed beyond 70 MeV. These differences are observed by a factor of 5 in Figure 3. The reaction ⁵⁹Co(α, 3pn) in Figure 4, has extremely low cross-section values both in experimental and theoretical predications. This reaction yield is suppressed by the emission of 3 protons hindered by coulomb barrier. Overall, in all these ⁵⁹Co(α, xynp) type of reactions, the code COMPLET predicts fairly good results up to 70 MeV.

Figure 1. Comparison of experimentally measured excitation functions [16] with theoretical model predictions for the formation of ⁵⁷Ni in the ⁵⁹Co(α, p5n)⁵⁷Ni reaction.

Figure 2. Comparison of experimentally measured excitation functions [17] with theoretical model predictions for the formation of ⁵⁶Ni in the ⁵⁹Co(α, p6n)⁵⁶Ni reaction.

Figure 3. Comparison of experimentally measured excitation functions [17] with theoretical model predictions for the formation of ⁶⁰Co in the ⁵⁹Co(α, 2pn)⁶⁰Co reaction.

Figure 4. Comparison of experimentally measured excitation functions [16] with theoretical model predictions for the formation of ⁵⁹Fe in the ⁵⁹Co(α, 3pn)⁵⁹Fe reaction.

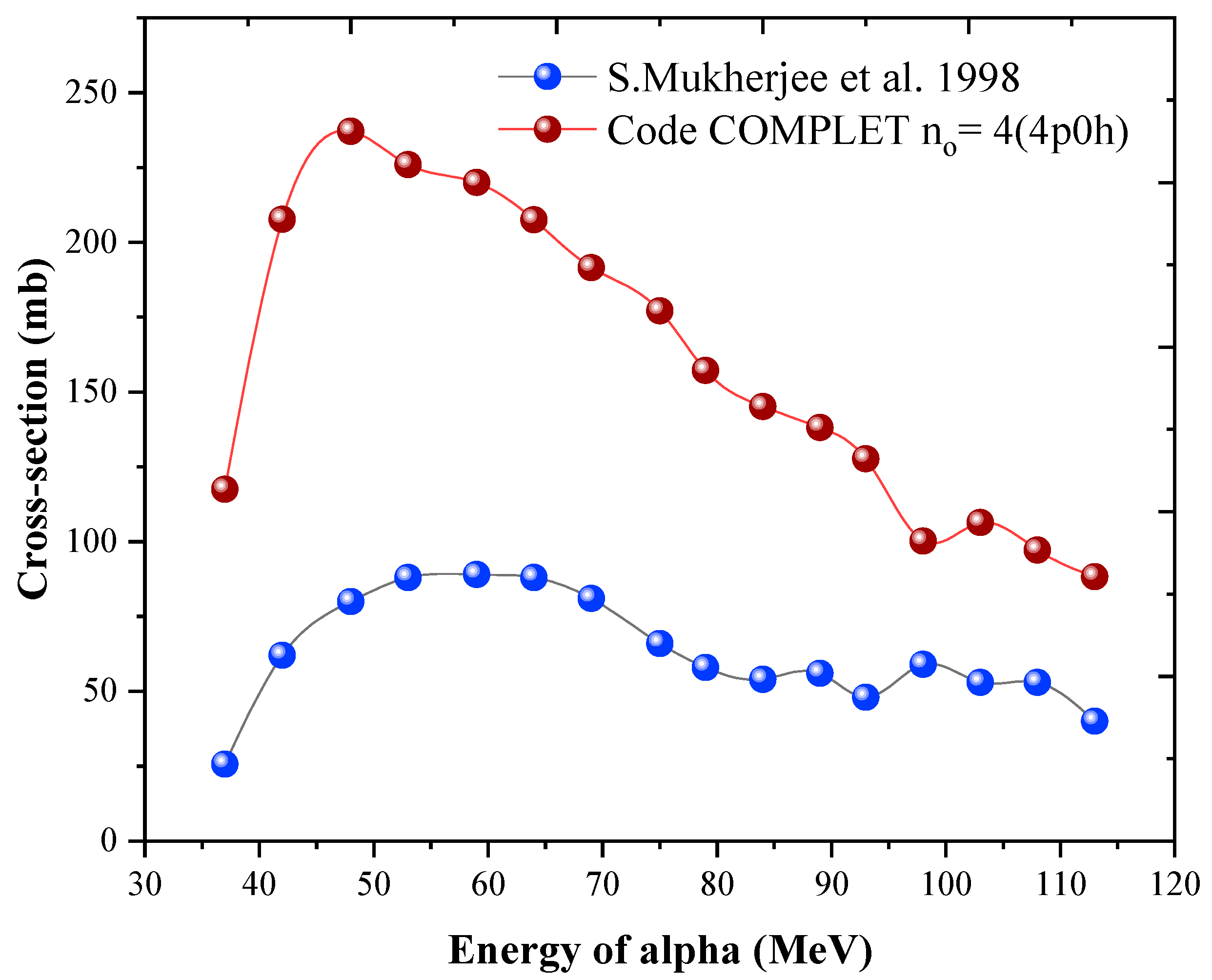
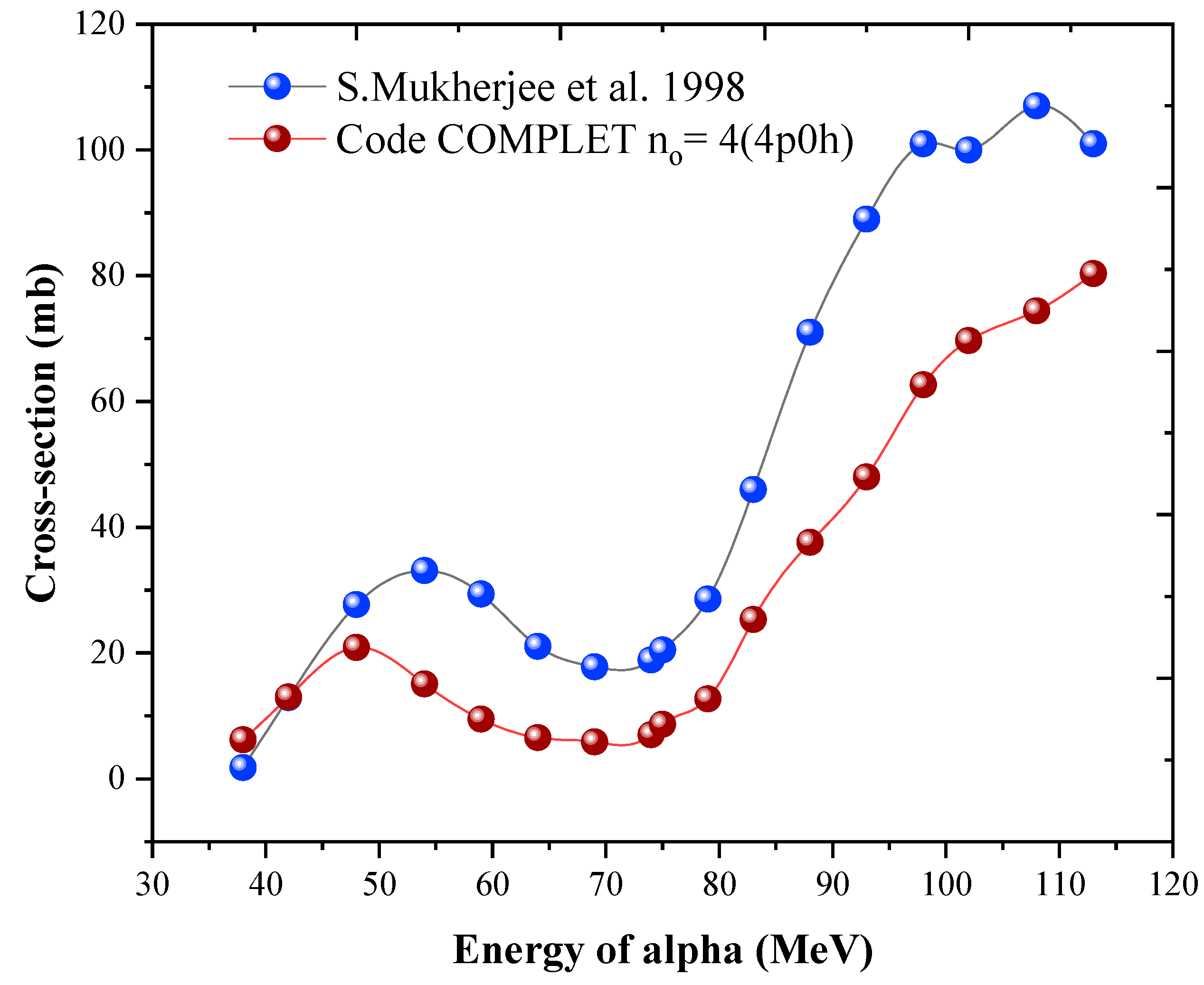
The second group includes reactions such as ⁵⁹Co (α, αn), (α, α2n), (α, α3n), (α, 2αn), and (α, 2α3n). For these reactions, the shapes of the excitation functions are reasonably well-reproduced by the COMPLET code as shown in Figure 5, Figure 6, Figure 7 and Figure 8. While the theoretical magnitudes generally fall below the experimental values by about a factor of two, one exception is the ⁵⁹Co(α, 2α3n)⁵²Mn reaction as observed in Figure 9, where a notable agreement occurs in the 65–75 MeV energy range. It may be observed that the peak-to-valley energy difference is around 30 MeV in all these reactions (Figure 5, Figure 6, Figure 7 and Figure 8), which is more than the binding energy of the alpha particle. Perhaps a different reaction mechanism may be operating in this energy range, and certainly not the pre-equilibrium emission. The detailed experimental and theoretical data supporting these findings are provided in the Appendix A.

Figure 5. Comparison of experimentally measured excitation functions [17] with theoretical model predictions for the formation of ⁵⁸Co in the ⁵⁹Co(α, αn)⁵⁸Co reaction.

Figure 6. Comparison of experimentally measured excitation functions [18] with theoretical model predictions for the formation of ⁵⁷Co in the ⁵⁹Co(α, α2n)⁵⁷Co reaction.

Figure 7. Comparison of experimentally measured excitation functions [17] with theoretical model predictions for the formation of ⁵⁶Co in the ⁵⁹Co(α, α3n)⁵⁶Co reaction.

Figure 8. Comparison of experimentally measured excitation functions [17] with theoretical model predictions for the formation of ⁵⁴Mn in the ⁵⁹Co(α, 2αn)⁵⁴Mn reaction.

Figure 9. Comparison of experimentally measured excitation functions [16] with theoretical model predictions for the formation of ⁵²Mn in the ⁵⁹Co(α, 2α3n)⁵²Mn reaction.

3. Materials and Methods

In this study, experimental cross-section data for alpha particle-induced reactions on the cobalt isotope (⁵⁹Co) were obtained from the EXFOR library, which provides a comprehensive collection of nuclear reaction data acquired from various experimental studies [26,27,28,29]. We utilized the experimental data as a benchmark to validate and refine our nuclear reaction models. The data selection focused on measurements relevant to incident alpha particle energies up to 120 MeV, ensuring the inclusion of high-energy reaction channels and minimizing uncertainties associated with low-energy measurements. Nine reactions were studied using datasets by [16,17,18]. To facilitate a meaningful comparison, only data with well-documented uncertainties and standardized measurement techniques were considered.

Theoretical predictions were generated using the COMPLET code, a sophisticated nuclear reaction modeling tool capable of simulating alpha particle interactions with target nuclei across a broad energy spectrum [6,30]. The COMPLET code provides reliable predications for many alpha-induced reactions on ⁵⁹Co, especially when model parameters are optimized. However, significant discrepancies can occur for certain reaction channels due to limitations in modeling complex nuclear mechanisms. The code incorporates various nuclear models, including pre-equilibrium and equilibrium reaction mechanisms, which are essential for accurately describing reactions at different energy ranges. In the present study, the input parameters such as target isotope (⁵⁹Co), incident energy grid (up to 120 MeV), nuclear level density options, and optical model potentials were carefully selected based on the recent literature and recommended standards to ensure the consistency and reliability of the simulations [6,31,32,33].

Simulation procedures involved setting up the input parameters within the COMPLET framework, executing the calculations across the specified energy range, and extracting the resulting cross-sections for various reaction channels. Graphical comparisons, including overlay plots of experimental and calculated cross-sections, complemented the quantitative analysis.

4. Conclusions

Nuclear data models often require precise parameter adjustments to align with experimental results, yet perfect agreement is sometimes unattainable. In such cases, the discrepancies must be factored into uncertainty assessments, while efforts continue to improve the models. Large, and occasionally unphysical, parameter changes can mask true physics, blending physical meaning with empirical corrections. Multiple parameter sets may fit data equally well, creating ambiguity. These challenges stress the need for advanced, microscopic nuclear models with fewer approximations. Although no model will be flawless, adopting superior models reduces parameter tuning and enhances agreement with experiments, thereby minimizing model-related uncertainties. This study highlights the strengths and limitations of the COMPLET code in modeling alpha-induced pre-equilibrium nuclear reactions on cobalt. Theoretically calculated results using the COMPLET code were compared with experimental data from the EXFOR library of the IAEA. The code performs well for simple reaction channels but has difficulty with complex ones, particularly those that emit multiple nucleons. The findings also show that the theoretical predictions are sensitive to input parameters such as exciton number and level density, which significantly affect the results. These demonstrate the significance of optimizing input parameters for accurate nuclear reaction modeling. Although the COMPLET code does not currently support built-in statistical error propagation, its importance is worth considering. Future studies should incorporate uncertainty analysis and compare COMPLET results with those from other nuclear reaction codes, such as TALYS and EMPIRE, to enhance the accuracy and reliability.

Author Contributions

Conceptualization, C.S.M. and A.V.M.R.; Methodology, C.S.M.; Software, C.S.M.; Validation, C.S.M. and A.V.M.R.; Formal analysis, C.S.M.; Investigation, C.S.M.; Resources, C.S.M. and A.V.M.R.; Data curation, C.S.M. and A.V.M.R.; Writing—original draft, C.S.M. and A.V.M.R.; Writing—review and editing, C.S.M. and A.V.M.R.; Visualization, C.S.M. and A.V.M.R.; Supervision, C.S.M.; Project administration, C.S.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The original contributions presented in this study are included in the article. Further enquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare that there are no conflicts of interest. The content and findings of this work are entirely the responsibility of the authors.

Appendix A

Table A1. Theoretical cross-section values compared with measured experimental data for the ⁵⁹Co(α, p + 5n)⁵⁷Ni reaction.

Eα (MeV)	E. Gadioli et al. (1984) [16]	Code COMPLET n_o = 4 (4p0h) (Present Work)
51.9 $\pm$ 1.2	0.22 $\pm$ 0.02	0.00
54.2 $\pm$ 1.15	0.18 $\pm$ 0.02	0.00
56.5 $\pm$ 1.15	0.18 $\pm$ 0.02	0.00
58.8 $\pm$ 1.1	0.17 $\pm$ 0.02	0.00
60.9 $\pm$ 1.05	0.2 $\pm$ 0.02	0.00
63 $\pm$ 1.05	0.21 $\pm$ 0.02	0.01
64.9 $\pm$ 0.8	0.24 $\pm$ 0.02	0.01
66.8 $\pm$ 1	0.28 $\pm$ 0.02	0.03
68.7 $\pm$ 0.95	0.38 $\pm$ 0.03	0.12
70.6 $\pm$ 0.9	0.47 $\pm$ 0.04	0.32
72.3 $\pm$ 0.8	0.62 $\pm$ 0.04	0.68
74.0 $\pm$ 0.95	0.74 $\pm$ 0.05	1.26
75.7 $\pm$ 0.75	0.95 $\pm$ 0.05	1.61
77.3 $\pm$ 0.85	1.2 $\pm$ 0.07	2.53
79.1 $\pm$ 0.9	1.44 $\pm$ 0.08	3.63
80.9 $\pm$ 0.9	1.66 $\pm$ 0.09	4.15
82.6 $\pm$ 0.8	1.93 $\pm$ 0.1	4.18
84.2 $\pm$ 0.8	2.34 $\pm$ 0.12	5.87

Table A2. Theoretical cross-section values compared with measured experimental data for the ⁵⁹Co(α, p + 6n)⁵⁶Ni reaction.

Eα (MeV)	S. Mukherjee et al. (1998) [17]	Code COMPLET n_o = 4 (4p0h) (Present Work)
74.51	0.02 $\pm$ 0.01	0.00
79.42	0.039 $\pm$ 0.01014	0.00
83.9	0.05 $\pm$ 0.01	0.00
88.56	0.072 $\pm$ 0.01008	0.01
93.17	0.089 $\pm$ 0.00801	0.02
97.81	0.118 $\pm$ 0.01416	0.04
102.9	0.178 $\pm$ 0.0178	0.08
108.1	0.28 $\pm$ 0.0308	0.12
113.4	0.46 $\pm$ 0.0506	0.15

Table A3. Theoretical cross-section values compared with measured experimental data for the ⁵⁹Co(α, 2p + n)⁶⁰Co reaction.

Eα (MeV)	S. Mukherjee et al. (1998) [17]	Code COMPLET n_o = 4 (4p0h) (Present Work)
37.9	25.7 $\pm$ 1.79	117.50
42.6	62 $\pm$ 3.72	207.70
48.1	80 $\pm$ 6.4	237.10
53.2	88 $\pm$ 6.16	226.00
59.4	89 $\pm$ 6.23	220.00
64.2	88 $\pm$ 5.28	207.50
69.9	81 $\pm$ 4.86	191.60
75.5	66 $\pm$ 5.94	177.10
79.7	58 $\pm$ 5.8	157.20
84.3	54 $\pm$ 5.94	145.10
89.1	56 $\pm$ 5.04	138.10
93.3	48 $\pm$ 4.8	127.70
98.5	59 $\pm$ 4.72	100.20
103	53 $\pm$ 4.77	106.40
108.1	53 $\pm$ 4.77	97.20
113.4	40 $\pm$ $5.2$	88.34

Table A4. Theoretical cross-section values compared with measured experimental data for the ⁵⁹Co(α, 3p + n)⁵⁹Fe reaction.

Eα (MeV)	E. Gadioli et al. (1984) [16]	Code COMPLET n_o = 4 (4p0h) (Present Work)
51.9 $\pm$ 1.2	0.46 $\pm$ 0.08	0.12
54.2 $\pm$ 1.15	0.76 $\pm$ 0.09	0.27
56.5 $\pm$ 1.15	1.06 $\pm$ 0.12	0.48
58.8 $\pm$ 1.1	1.5 $\pm$ 0.1	0.70
60.9 $\pm$ 1.05	2 $\pm$ 0.2	0.96
63.05 $\pm$ 1.05	2.4 $\pm$ 0.2	1.27
64.9 $\pm$ 0.85	2.7 $\pm$ 0.2	1.39
66.8 $\pm$ 1	2.8 $\pm$ 0.2	1.71
68.7 $\pm$ 0.95	3 $\pm$ 0.2	1.84
70.6 $\pm$ 0.9	3 $\pm$ 0.2	1.92
72.3 $\pm$ 0.8	3.2 $\pm$ 0.2	1.98
74 $\pm$ 0.95	2.9 $\pm$ 0.2	2.04
75.7 $\pm$ 0.75	3.3 $\pm$ 0.2	2.08
77.3 $\pm$ 0.85	3.2 $\pm$ 0.2	2.06
79.1 $\pm$ 0.9	3 $\pm$ 0.2	2.02
80.9 $\pm$ 0.9	2.7 $\pm$ 0.2	2.04
82.6 $\pm$ 0.8	2.9 $\pm$ 0.2	2.44
84.2 $\pm$ 0.8	2.8 $\pm$ 0.2	2.38

Table A5. Theoretical cross-section values compared with measured experimental data for the ⁵⁹Co(α, α + n)⁵⁸Co reaction.

Eα (MeV)	S. Mukherjee et al. (1998) [17]	Code COMPLET n_o = 4 (4p0h) (Present Work)
19.9	8.3 $\pm$ 0.996	73.51
22.2	69 $\pm$ 8.28	235.7
23.8	132 $\pm$ 13.2	266.6
29.1	261 $\pm$ 28.71	324.5
30.5	248 $\pm$ 19.84	336.7
36.2	191 $\pm$ 13.37	181
41.6	150 $\pm$ 9	86.43
46.1	113 $\pm$ 5.65	66.57
52.3	109 $\pm$ 6.54	49.04
57.5	143 $\pm$ 8.58	62.78
63.4	211 $\pm$ 14.77	135.7
69.2	298 $\pm$ 23.84	215.4
74	314 $\pm$ 21.98	258.3
79	319 $\pm$ 19.14	310.2
83.1	309 $\pm$ 18.54	333.4
87.5	289 $\pm$ 20.23	339
92.4	260 $\pm$ 15.6	340.4
97.4	240 $\pm$ 14.4	341.5
102.9	221 $\pm$ 11.05	332.8
107.3	217 $\pm$ 10.85	302.5
112.6	218 $\pm$ 10.9	311.4

Table A6. Theoretical cross-section values compared with measured experimental data for the ⁵⁹Co(α, α + 2n)⁵⁷Co reaction.

Eα (MeV)	J. RamaRao et al. (1987) [18]	Code COMPLET n_o = 4 (4p0h) (Present Work)
29.1	10.1 $\pm$ 0.909	1.98
31.5	23 $\pm$ 1.84	22.14
37.7	118 $\pm$ 8.26	176.00
42.3	205 $\pm$ 10.25	213.90
48.1	219 $\pm$ 10.95	143.00
53.3	178 $\pm$ 10.68	99.98
59.1	132 $\pm$ 6.6	65.26
64.3	95 $\pm$ 5.7	49.26
69.2	83 $\pm$ 4.15	49.24
75.6	105 $\pm$ 8.4	67.63
79.3	131 $\pm$ 7.86	81.25
84.5	158 $\pm$ 12.64	112.40
88.5	179 $\pm$ 12.53	149.70
94	185 $\pm$ 11.1	170.70
98.9	195 $\pm$ 13.65	184.10
109	183 $\pm$ 10.98	202.50
113.9	180 $\pm$ 12.6	206.60

Table A7. Theoretical cross-section values compared with measured experimental data for the ⁵⁹Co(α, α + 3n)⁵⁶Co reaction.

Eα (MeV)	S. Mukherjee et al. (1998) [17]	Code COMPLET n_o = 4 (4p0h) (Present Work)
42.19	0.302	1.13
47.71	5.8 $\pm$ 0.40	33.06
53.12	27 $\pm$ 1.35	90.32
58.29	52 $\pm$ 2.6	98.60
63.58	59 $\pm$ 2.95	92.05
69.51	50.4 $\pm$ 3.02	71.16
74.71	41.7 $\pm$ 2.91	60.35
79.2	35.5 $\pm$ 1.77	53.21
83.49	33.8 $\pm$ 2.02	49.36
88.01	31.8 $\pm$ 1.59	52.28
92.55	33.4 $\pm$ 1.67	55.08
97.59	37.1 $\pm$ 1.85	70.40
102.6	40 $\pm$ 1.6	86.17
107.9	44.5 $\pm$ 2.22	101.00
112.7	47.4 $\pm$ 2.37	118.30

Table A8. Theoretical cross-section values compared with measured experimental data for the ⁵⁹Co(α, 2α + n)⁵⁴Mn reaction.

Eα (MeV)	S. Mukherjee et al. (1998) [17]	Code COMPLET n_o = 4 (4p0h) (Present Work)
38.5	1.82 $\pm$ 0.091	6.24
42.6	12.9 $\pm$ 0.774	13.04
48.3	27.7 $\pm$ 1.662	20.89
54.1	33.1 $\pm$ 1.655	15.10
59.4	29.4 $\pm$ 1.764	9.48
64.2	21.1 $\pm$ 1.266	6.56
69.5	17.8 $\pm$ 1.068	5.89
74.4	18.9 $\pm$ 0.945	7.04
75	20.5 $\pm$ 1.435	8.68
79.4	28.6 $\pm$ 1.716	12.72
83.8	46 $\pm$ 3.22	25.34
88.2	71 $\pm$ 4.26	37.60
93.2	89 $\pm$ 5.34	48.00
98	101 $\pm$ 6.06	62.66
102.3	100 $\pm$ 6	69.67
108	107 $\pm$ 6.42	74.44
113.1	101 $\pm$ 7.07	80.34

Table A9. Theoretical cross-section values compared with measured experimental data for the ⁵⁹Co(α, 2α + 3n)⁵²Mn reaction.

Eα (MeV)	E. Gadioli et al. (1984) [16]	Code COMPLET n_o = 4 (4p0h) (Present Work)
64.9 $\pm$ 0.85	0.7 $\pm$ 0.2	0.98
66.8 $\pm$ 1	1.3 $\pm$ 0.2	1.29
68.7 $\pm$ 0.95	2.3 $\pm$ 0.2	2.42
70.6 $\pm$ 0.9	3.6 $\pm$ 0.2	3.88
72.3 $\pm$ 0.8	5.5 $\pm$ 0.3	5.53
74 $\pm$ 0.95	7.2 $\pm$ 0.4	6.94
75.7 $\pm$ 0.75	10.1 $\pm$ 0.5	7.75
77.3 $\pm$ 0.85	11.1 $\pm$ 0.6	9.42
79.1 $\pm$ 0.9	13.2 $\pm$ 0.7	10.01
80.9 $\pm$ 0.9	14 $\pm$ 0.7	9.43
82.6 $\pm$ 0.8	15.2 $\pm$ 0.8	9.55
84.2 $\pm$ 0.8	15.7 $\pm$ 0.8	9.47

References

Noori, S.S.; Akkurt, İ.; Demir, N.K. Comparison of Excitation Functions of Longer and Shorter Lived Radionuclides. Acta Phys. Pol. A 2017, 132, 1186–1188. [Google Scholar] [CrossRef]
Asres, Y.H.; Mathuthu, M.; Beyene, E.Y. The study of alpha particle induced reactions on bismuth-209 isotopes using computer code COMPLET. J. Phys. Commun. 2019, 3, 115006. [Google Scholar] [CrossRef]
Asres, Y.H.; Mathuthu, M.; Ferede, Y.A. Investigation of nuclear reaction mechanisms of Nickel isotopes at various energies induced by alpha particles. J. Phys. Commun. 2019, 3, 115018. [Google Scholar] [CrossRef]
Mekonen, C.S.; Rao, A.V.M. Analysis of Proton Induced Reactions on Yttrium Isotope Using Computer Code COMPLET. Int. J. High Energy Phys. 2023, 10, 20–26. [Google Scholar] [CrossRef]
Mekonen, C.S.; Aklie, M.T. Pre-equilibrium Effects on Alpha Particle Induced Reactions on Niobium Isotope from Threshold upto 100MeV using the Computer Code COMPLET. Int. J. Phys. Res. Appl. 2023, 6, 180–184. [Google Scholar] [CrossRef]
Mekonen, C.S.; Rao, A.V.M.; Dessie, Y.A. Analysis of excitation functions for alpha particle-induced reactions on stable copper and antimony isotopes up to 80 MeV energy region. Nucl. Energy Technol. 2025, 11, 259–269. [Google Scholar] [CrossRef]
Najm, S.A.; Salloum, A.D. Effect of Exciton Number on One-Component and Two-Component Partial Level Density Formulae. Baghdad Sci. J. 2025, 22, 170–176. [Google Scholar] [CrossRef]
Tel, E.; Aydin, A.; Kaplan, A.; Şarer, B. New calculation method for initial exciton numbers on nucleon induced pre-equilibrium reactions. Phys. Rev. C Nucl. Phys. 2008, 77, 054605. [Google Scholar] [CrossRef]
Elmaghraby, E.K. Initial exciton configuration in (p,n) pre-equilibrium emission reactions. Phys. Rev. C Nucl. Phys. 2008, 78, 014601. [Google Scholar] [CrossRef]
Furutachi, N.; Minato, F.; Iwamoto, O. Phenomenological level density model with hybrid parameterization of deformed and spherical state densities. J. Nucl. Sci. Technol. 2019, 56, 412–424. [Google Scholar] [CrossRef]
Hirdt, J.A.; Brown, D.A. Identifying Understudied Nuclear Reactions by Text-mining the EXFOR Experimental Nuclear Reaction Library. Nucl. Data Sheets 2016, 131, 377–399. [Google Scholar] [CrossRef]
Gezahegn, W.W. Investigation of Nuclear Reaction Cross Section by Proton, Deuteron, and alpha Particles Induced Reaction for the Production of Important Radioisotopes for PET Imaging. J. Radiat. Nucl. Appl. 2024, 226, 221–226. [Google Scholar] [CrossRef]
Benti, A.; Fekadu, H.; Birhanu, F. Excitation function of neutron induced reaction on isotopes of cadmium (¹⁰⁶ Cd, ¹⁰⁸ Cd & ¹¹⁰ Cd) in the energy range of 13–15 MeV. Int. J. Adv. Nucl. React. Des. Technol. 2023, 5, 137–143. [Google Scholar] [CrossRef]
Asres, Y.H.; Mathuthu, M.; Birhane, M.D. Analysis of reaction cross-section production in neutron induced fission reactions on uranium isotope using computer code COMPLET. Appl. Radiat. Isot. 2018, 139, 81–85. [Google Scholar] [CrossRef]
Degu Belete, G.; Asres, Y.H.; Zegeye, S.M.; Alemu, Y.E. Analysis of the excitation function of deuteron induced nuclear reaction on Neon-20 using COMPLET code. Nucl. Energy Technol. 2024, 10, 259–265. [Google Scholar] [CrossRef]
Gadioli, E.; Gadioli Erba, E.; Asher, J.; Parker, D.J. Analysis of ⁵⁹Co (α, x p y n z α) reactions up to 170 MeV incident α energy. Z Physik A. 1984, 317, 155–168. [Google Scholar] [CrossRef]
Mukherjee, S.; Sharma, A.K.; Bakhru, D.; Singh, N.L.; Kolev, D. Pre-equilibrium Alpha and Nucleon Emission in Co (α, zαypxn) Reactions Pre-equilibrium Alpha and Nucleon Emission in ⁵⁹ Co (a, zaypxn). Phys. Scr. 1998, 58, 319. [Google Scholar] [CrossRef]
Rao, J.R.; Rao, A.V.M.; Mukherjee, S.; Upadhyay, R.; Chaturvedi, L. Excitation Functions of Alpha Particle Induced reactions in Cobalt in the Energy Range upto 120Mev. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 1987, 25, 484–489. [Google Scholar] [CrossRef]
Smith, D.L.; Otuka, N. Experimental Nuclear Reaction Data Uncertainties: Basic Concepts and Documentation. Nucl. Data Sheets 2012, 113, 3006–3053. [Google Scholar] [CrossRef]
Blann, M. Preequilibrium decay. Annu. Rev. Nucl. Sci. 1975, 25, 123–166. [Google Scholar] [CrossRef]
Griffin, J.J. Statistical model of intermediate structure. Phys. Rev. Lett. 1966, 17, 478–481. [Google Scholar] [CrossRef]
Gadioli, E.; Erba, E.G.; Sona, P.G. Intermediate-state decay rates in the exciton model. Nucl. Phys. Sect. A 1973, 217, 589–610. [Google Scholar] [CrossRef]
Gruppelaar, H.; Nagel, P.; Hodgson, P.E. Pre-Equilibrium Processes in Nuclear Reaction Theory: The State of the Art and Beyond. Riv. Nuovo Cim. 1986, 9, 1–46. [Google Scholar] [CrossRef]
Hodgson, P.E.; Field, G.M.; Gruppelaar, H.; Nagel, P. Pre-equilibrium processes in nuclear reactions. Radiat. Eff. 1986, 95, 27–46. [Google Scholar] [CrossRef]
Blann, M. Hybrid Model For Pre-Equilibrium Decay in Nuclear Reactions. Phys. Rev. Lett. 1971, 27, 700. [Google Scholar] [CrossRef]
Otuka, N.; Dupont, E.; Semkova, V.; Pritychenko, B.; Blokhin, A.I.; Aikawa, M.; Babykina, S.; Bossant, M.; Chen, G.; Dunaeva, S.; et al. Towards a More complete and accurate experimental nuclear reaction data library (EXFOR): International collaboration between nuclear reaction data centres (NRDC). Nucl. Data Sheets 2014, 120, 272–276. [Google Scholar] [CrossRef]
Schnabel, G. A computational EXFOR database. EPJ Web Conf. 2020, 239, 16001. [Google Scholar] [CrossRef]
Semkova, V.; Otuka, N.; Simakov, S.P.; Zerkin, V. Experimental nuclear reaction data collection EXFOR. In Proceedings of the 2011 2nd International Conference on Advancements in Nuclear Instrumentation, Measurement Methods and Their Applications, Ghent, Belgium, 6–9 June 2011; pp. 2–4. [Google Scholar] [CrossRef]
Pritychenko, B. 75 Years of Experimental Nuclear Reaction Data Compilations. EPJ Web Conf. 2023, 284, 14002. [Google Scholar] [CrossRef]
Zegeye, S.M.; Asress, Y.H.; Belete, G.D.; Mekuriyaw, T.A.; Alemu, Y.E.; Worku, K.T.; Abeje, M.A. Analysis of excitation function for an induced reaction by nucleon on Arsenic-75 isotope using COMPLET code. Nucl. Energy Technol. 2025, 11, 183–193. [Google Scholar] [CrossRef]
Wiedeking, M.; Goriely, S. Photon strength functions and nuclear level densities: Invaluable input for nucleosynthesis. Philos. Trans. A Math. Phys. Eng. Sci. 2024, 382, 20230125. [Google Scholar] [CrossRef]
Capote, R.; Herman, M.; Obložinský, P.; Young, P.G.; Goriely, S.; Belgya, T.; Ignatyuk, A.V.; Koning, A.J.; Hilaire, S.; Plujko, V.A.; et al. RIPL—Reference Input Parameter Library for Calculation of Nuclear Reactions and Nuclear Data Evaluations. Nucl. Data Sheets 2009, 110, 3107–3214. [Google Scholar] [CrossRef]
MacHner, H. Validation of nuclear reaction models for incident α-particles. Radiochim. Acta 2021, 109, 1–25. [Google Scholar] [CrossRef]

Figure 1. Comparison of experimentally measured excitation functions [16] with theoretical model predictions for the formation of ⁵⁷Ni in the ⁵⁹Co(α, p5n)⁵⁷Ni reaction.

Figure 2. Comparison of experimentally measured excitation functions [17] with theoretical model predictions for the formation of ⁵⁶Ni in the ⁵⁹Co(α, p6n)⁵⁶Ni reaction.

Figure 3. Comparison of experimentally measured excitation functions [17] with theoretical model predictions for the formation of ⁶⁰Co in the ⁵⁹Co(α, 2pn)⁶⁰Co reaction.

Figure 4. Comparison of experimentally measured excitation functions [16] with theoretical model predictions for the formation of ⁵⁹Fe in the ⁵⁹Co(α, 3pn)⁵⁹Fe reaction.

Figure 5. Comparison of experimentally measured excitation functions [17] with theoretical model predictions for the formation of ⁵⁸Co in the ⁵⁹Co(α, αn)⁵⁸Co reaction.

Figure 6. Comparison of experimentally measured excitation functions [18] with theoretical model predictions for the formation of ⁵⁷Co in the ⁵⁹Co(α, α2n)⁵⁷Co reaction.

Figure 7. Comparison of experimentally measured excitation functions [17] with theoretical model predictions for the formation of ⁵⁶Co in the ⁵⁹Co(α, α3n)⁵⁶Co reaction.

Figure 8. Comparison of experimentally measured excitation functions [17] with theoretical model predictions for the formation of ⁵⁴Mn in the ⁵⁹Co(α, 2αn)⁵⁴Mn reaction.

Figure 9. Comparison of experimentally measured excitation functions [16] with theoretical model predictions for the formation of ⁵²Mn in the ⁵⁹Co(α, 2α3n)⁵²Mn reaction.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

A Comparative Study of COMPLET Code Predictions with Experimental Data on Alpha Particle-Induced Reactions on Cobalt Isotope up to 120 MeV

Abstract

1. Introduction

2. Results and Discussion

3. Materials and Methods

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Appendix A

References

Article Metrics

Citations

Article Access Statistics