Abstract
Against the backdrop of the world’s increasing reliance on renewable energy, the inherent intermittency and volatility of wind and solar energy pose significant challenges to the stability and economic benefits of the power system. In regions rich in renewable energy resources such as Gansu Province, due to low operational efficiency and underdeveloped market mechanisms, the potential of new energy storage systems is often not fully exploited. This paper proposes an integrated shared energy storage model designed to suppress wind power fluctuations and a two-way market trading mechanism designed to maximize social welfare to solve these problems. Firstly, a hybrid energy storage system combining electrochemical- and hydrogen-based energy storage is constructed. The modular coordination strategy is adopted to dynamically allocate power capacity, and the wind energy fluctuation suppression technology is proposed to achieve fluctuation suppression at multiple time scales. Secondly, a combined dual bidding mechanism is introduced, allowing for combined bidding across time periods and resource types, to better capture user preferences and enhance market flexibility. The model is represented as a mixed-integer nonlinear programming problem aimed at maximizing social welfare, and then transformed into a linear equivalence problem to enhance the traceability of the calculation. The branch and bound algorithm is adopted to solve this problem. Finally, the simulation results based on the bidding data of a certain area enhanced the participation of participants and improved the fairness of the market and the overall social welfare. This system effectively enhances the grid-friendliness of renewable energy grid connection and provides a scalable and replicable framework for highly renewable energy systems.
1. Introduction
Under increasing global dependence on renewable energy, the traditional power system is facing severe challenges due to the tightening of fossil energy resources and the constraints of ecological environment. The construction of a new power system with new energy as the main body has become a key path to promote the optimization of energy structure and achieve the strategic goal of ‘double carbon’ [1]. The optimization of a new energy system including wind energy is of great significance [2]. In this system, an integrated architecture of the multi-link deep integration of source, network, load, and storage is gradually formed. How to strengthen the collaborative interaction and dynamic regulation between the power supply side, the grid side, the load side, and the energy is becoming an important research direction in the field of electrical engineering [3,4,5,6]. Distributed wind power and photovoltaic power generation show significant intermittent and fluctuating characteristics, and their large-scale access to the power grid makes the system operation and scheduling face significant uncertainty challenges [7,8]. The new power system includes an energy storage system that can compensate for uncertainty and improve the operational flexibility of the energy system [9,10]. By optimizing the planning of the energy storage system, the rational allocation and storage and efficient utilization of multiple energy sources can be realized, so as to significantly improve the comprehensive energy utilization rate and effectively reduce carbon emissions.
Modern energy storage refers to the next generation of energy storage technology, which is different from pumped storage. It mainly includes electrochemical energy storage, physical energy storage, hydrogen energy storage, and heat storage. This kind of technology can realize the efficient storage and controllable release of energy, effectively alleviate the inherent intermittency and volatility of renewable energy power generation, enhance the flexible regulation and stable operation ability of power system, and provide key technical support for the construction of a new power system [11,12]. By introducing the empirical mode decomposition method and integrating it with the grid-connected power fluctuation, reference [13] separates the grid-connected reference power from the fluctuation component that needs to be stabilized by energy storage. On this basis, a hybrid energy storage system (HESS) composed of hydrogen energy storage and battery was constructed. This study provides a useful idea for the further development of the system’s application potential and the effective extension of battery cycle life. Reference [14] proposed a distributed market-assisted MDS recovery method considering the comprehensive uncertainty of typhoon disasters. The final results verify that the proposed method creates a win-win situation for all stakeholders. In reference [15], a multi-objective programming model of an electro-thermal integrated energy system (EHIES) based on non-dominated sorting genetic method III (NSGA-III) was proposed. The model takes the minimization of the planning cost of the system, the temperature fluctuation in the heating network node, and the voltage deviation in the node as the optimization objective and determines the output scheme of the coupling element in the system according to the operation strategy of ‘fixing power by heat’. In reference [16], the capacity optimization configuration of the production system in the natural gas hydrogen-doped park was carried out with the multi-objective of minimizing investment cost, operation cost, and carbon transaction cost, aiming at improving the overall economy of the integrated energy system. In reference [17], battery energy storage and hydrogen energy storage were used for short-term and long-term energy scheduling, respectively. By coordinating their dynamic response characteristics and taking into account the operating efficiency, an economic droop control strategy suitable for an electric–hydrogen hybrid energy storage system is proposed. Reference [18] improves the wind farm scheduling strategy in the Australian electricity market environment. By collaboratively optimizing the capacity configuration and real-time control instructions of the battery energy storage system (BES), the schedulability of the wind farm output power and the economic benefits of market operation are improved. The above literature mostly studies the optimization and algorithm of electric hydrogen production equipment, but does not consider the influence of real environmental factors, such as wind power fluctuation.
In reference [19], a bi-stage robust optimization formulation with a min–max–min paradigm considering the constraints of distribution network was constructed for the planning of a distributed energy storage system. The simulation results show that the energy storage planning method can effectively deal with the randomness and volatility of renewable energy generation and provide theoretical basis and method support for the investment decision of the energy storage system on the distribution network side. Combining long-term capacity planning with short-term operation optimization, a comprehensive method for collaborative optimization of capacity configuration, site selection, and sizing of energy storage systems is described in reference [20]. In reference [21], a risk-averse stochastic capacity planning and peer-to-peer (P2P) trading collaborative optimization method for multi-energy microgrids (MEMGs) considering carbon emission limits was proposed. The diagonal quadratic approximation method is used to linearize the quadratic penalty term in the enhanced Lagrangian function, and the parallel solution of all optimization sub-problems is realized. Finally, the effectiveness and superiority of the proposed method are verified by simulation. In references [22,23,24], the capacity configuration model of an energy storage system was constructed under the framework of two-stage stochastic optimization. By using multi-scenario generation and reduction technology, the original problem was transformed into a joint optimal power flow problem considering multi-probability scenarios and multi-time scales. Reference [25] constructed an electricity–hydrogen coupling energy model and established a distributed robust optimization planning model for the electricity–hydrogen energy storage system of new energy grid considering flexibility requirements with the goal of minimizing the total cost of the system. Through simulation verification, this method can effectively determine the optimal configuration capacity of energy storage and significantly improve the flexible adjustment ability of new energy power grid. Reference [26] proposed a two-stage stochastic programming model for an urban multi-energy system to coordinate the hybrid energy storage system. Based on the carbon trading mechanism, reference [27] established a virtual Power Plant (VPP) optimization model with the goal of maximizing daily operating income, and then established a distributed robust model. Finally, the alternating direction multiplier method was used to solve the cooperative game model. The above literature mostly studies the electro–hydrogen coupling but does not consider the impact of new shared energy storage. The specific comparison is shown in Table 1.

Table 1.
The comparation of the literature.
Although the above literature has made positive progress in electro–hydrogen coupling, energy storage configuration, and market mechanism, there are still some shortcomings in the following aspects:
- (1)
- Most studies focus on a single energy storage technology or a simple combination and lack a multi-time scale cooperative suppression strategy for wind power fluctuation characteristics. Especially in the modeling of a hydrogen energy storage system, most studies still limit it to the traditional peak regulation function and fail to give full play to its potential in fluctuation suppression.
- (2)
- The existing research mostly adopts one-way auction or fixed-price mechanisms, which are difficult to adapt to the ‘many-to-many’ trading characteristics of shared energy storage. The lack of mechanism design considering the coupling of technical performance and market value makes it difficult for the fluctuation mitigation service provided by the energy storage system to be reasonably compensated at the economic level.
- (3)
- The existing methods have the problem of energy aliasing when separating high- and low-frequency power, which affects the fluctuation suppression effect and operational reliability of the energy storage system, and then restricts its actual value in the market.
It is crucial to emphasize that the proposed fluctuation suppression technology and the two-way market mechanism are not isolated contributions but are intricately coupled within a unified framework. The technical operation of the hybrid energy storage system, specifically its ability to smooth wind power fluctuations via the optimized empirical mode decomposition (EMD)-based power allocation, directly creates and quantifies additional economic value. This value, represented as the fluctuation suppression service, is not merely a technical performance indicator but is explicitly embedded as premium compensation within the market’s social welfare objective function. Consequently, the market clearing process does not only consider traditional bids and offers but also internalizes the grid-stabilizing benefits provided by the storage system. This integration ensures that the economic signals from the market incentivize technically desirable operations, and conversely, the technical performance is accurately valued and rewarded in the market. Therefore, the framework seamlessly bridges the gap between physical operation and economic dispatch, creating a cohesive system where technological efficacy and market efficiency reinforce each other.
In summary, to solve the problems of abundant renewable resources with large fluctuations, low energy storage efficiency, and unreasonable configuration, the research is carried out based on the development of two-way sales and sharing of ES. The contributions of this paper are mainly divided into the following points:
- (1)
- Aiming at the problem of large fluctuation in wind and solar power output, this paper innovatively extends the hydrogen energy storage system from a single peak shaving function to a multi-module collaborative system with minute-level fluctuation suppression and realizes full coverage of multi-time scale fluctuation through dynamic power distribution, which significantly improves the flexibility and economy of the system.
- (2)
- Different from the traditional one-way auction, this paper designs a two-way transaction mechanism that allows ‘combinatorial bidding’, supports users’ complementary demand expression across time periods and capacities, and effectively improves market fairness and resource allocation efficiency through the social welfare maximization model and the ‘equal sharing principle’ pricing mechanism.
- (3)
- Aiming at the problem of energy aliasing in energy storage signal processing, the optimal segmentation boundary is determined by calculating the overlapping area of instantaneous frequency of adjacent intrinsic mode function (IMF) components, which realizes the effective separation of high- and low-frequency power, and improves the fluctuation suppression ability and operational reliability of energy storage systems.
The advantages of the trading mechanism proposed in this paper and the existing double auction trading mechanism are shown in Table 2.

Table 2.
Auction mechanism comparison.
2. A New ES System Based on Wind Power Stabilization
Based on the abundant renewable resource endowment and the features of new energy storage technology in Gansu Province, this paper constructs a new energy storage system as shown in Figure 1. The system takes the AC bus as the core hub, integrates the three major components of the power supply side, the load side, and the energy storage side, and forms a multi-energy complementary and flexible coordination architecture. On the power supply side, the wind power system is connected to the AC bus through the wind power converter system (PCS) to achieve reliable input of new energy power. The load side is connected to the power grid by measuring devices such as energy meters, and the exchange power between the real-time monitoring and the power grid is provided to provide data support for the system operation. The energy storage side is composed of an electrochemical energy storage unit and an electrolytic water hydrogen energy storage unit, which are connected to the AC bus in parallel through their respective PCS conversion devices to achieve two-way flow and multi-form storage of electrical energy.
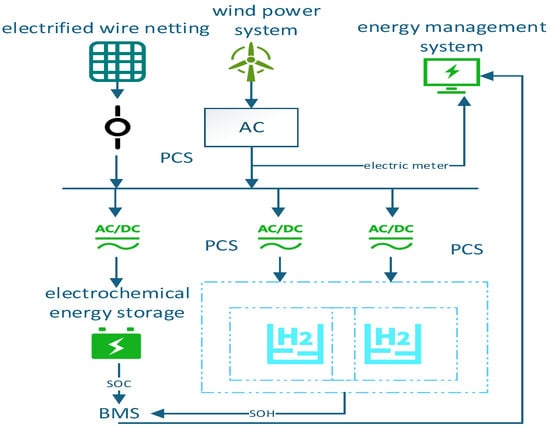
Figure 1.
New energy storage system.
In order to further suppress the stochastic and variable nature of wind power output, the system also introduces a fluctuation smoothing module and a peaking module. The fluctuation smoothing module improves the grid-connected friendliness by quickly responding to high-frequency power fluctuations; the peak regulation module releases energy reserves during peak system demand and relieves the power supply pressure of the power grid. The addition of the two types of modules not only enhances the controllability and reliability of the system but also enhances the overall utilization efficiency of energy storage assets. The integrated system structure leverages the resource advantages and technical characteristics of Gansu Province, and provides a replicable and scalable engineering demonstration model for energy storage applications in high-proportion renewable energy areas, which is helpful to new power system construction.
This chapter studies the deep coupling of hydrogen energy storage and wind power and proposes a modular coordination strategy of hydrogen energy storage while suppressing wind and solar fluctuations. Through the dynamic power distribution with electrochemical energy storage, the full-time scale smoothing of wind power fluctuations is realized. It lays the foundation for the two-way auction market mechanism proposed below.
2.1. Hydrogen Energy Storage System Model
As an energy-based energy storage technology, if the hydrogen energy storage system is limited to a single application scenario, its power output and capacity configuration may not be fully and efficiently utilized. Therefore, based on the original hydrogen energy storage for peak shaving operation, this paper proposes a modular collaborative utilization strategy: reserve some power and capacity resources in the hydrogen energy storage system, and construct a regulation module specially used for the minute-level fluctuation in wind power. This module fully leverages the advantages of the long life cycle of hydrogen energy storage, makes up for the features of fast response speed and poor cycle durability of the new electrochemical ES system, and jointly improves the stability effect and overall operation economy of the hybrid energy storage system in dealing with high volatility renewable energy.
Specifically, power capacity of the hydrogen energy storage is dynamically allocated.
To this end, the framework is built as follows:
where , , are the total power of each hydrogen energy storage sub-module; , , are power of each sub-module of the ripple suppression module; , , are power of each sub-module of the peaking module; α is the correction coefficient of smoothing fluctuation.
2.2. Signal Analysis Strategy of a Wind Power System
In order to quantify and suppress the adverse effects of this energy aliasing, it is necessary to objectively identify and select two adjacent components from all possible decomposition results, with the lowest instantaneous frequency overlap, as the optimal segmentation boundary of high-frequency and low-frequency power. In this paper, the selection process is formalized as an optimization problem. The goal is to find the segmentation point that minimizes the sum of the instantaneous frequency overlapping areas between adjacent IMF components.
where k is the number of candidate decomposition levels; is the area of the closed region enclosed by the instantaneous frequency curves of the i th and i + 1 th IMF components on the time–frequency plane.
For energy storage signal processing with wind turbines, empirical mode decomposition (EMD) is often used in existing research. Empirical mode decomposition is a data-driven method for analyzing nonlinear and non-stationary signals. Its core idea is to decompose a complex signal into several intrinsic mode functions and a residual term. By applying the empirical mode decomposition method to the energy storage system, the data are divided into several components and remainders, and the mathematical expression is
where is signal data; is data component; is the margin.
In the process of empirical mode decomposition, the signal to be decomposed is adaptively decomposed into a sequence of intrinsic mode functions (IMFs) based on its own time scale characteristics, and its order usually follows the law of instantaneous frequency from high to low. The instantaneous frequency of the component is generally higher than that of the subsequent component .
In the application of power signal reconstruction, ideally, it is expected that there is a clear time–frequency boundary, which can completely separate the high-frequency power from the low-frequency power, so that the supercapacitor and the battery are responsible for the compensation task, respectively, so as to avoid the coupling and mixing of power in different frequency bands. However, in the actual decomposition, the instantaneous frequency distribution of adjacent IMF components often has overlapping regions in the time–frequency plane, resulting in the frequency band crossing of power, that is, energy aliasing.
In order to suppress the adverse effects of this energy aliasing, it is necessary to identify and select two adjacent components with the lowest instantaneous frequency overlap as the optimal segmentation boundary. This paper uses a quantitative evaluation method: the area of the closed area enclosed by the time–frequency curve of any pair of adjacent IMF components is integrally calculated. By systematically comparing these integral values, the two adjacent components with the least instantaneous frequency crossover can be objectively determined, which can be used as the best boundary between high-frequency and low-frequency power for the final power reconstruction. The reconstructed expression is as follows:
where is a high-frequency component; is low-frequency component.
The average instantaneous frequency of the decomposed IMF component sequence should satisfy the order from high to low:
where is the average instantaneous frequency of the i th IMF component.
By solving the above optimization problem, we can systematically compare the overlapping area integral values corresponding to all possible segmentation points, so as to objectively determine the two adjacent components with the smallest instantaneous frequency crossover as the optimal boundary between high frequency and low frequency in the final power reconstruction.
2.3. Coupling Modeling of Energy Storage Output and Market Transaction
It is assumed that the fluctuation smoothing power actually provided by the ES system in the period t is , which can be calculated by the EMD and the hydrogen–electricity co-output model in Chapter 2:
where and are high-frequency and low-frequency components, respectively, which are obtained by EMD.
Defining the value contribution of the fluctuation smoothing service provided by the ES system to the system operation can be reflected as premium compensation or social welfare increment in the market:
where is the original wind power and λ is the unit value coefficient of the smoothing effect, which can be determined by the feedback of the market pricing mechanism.
5. Scene Example Analysis
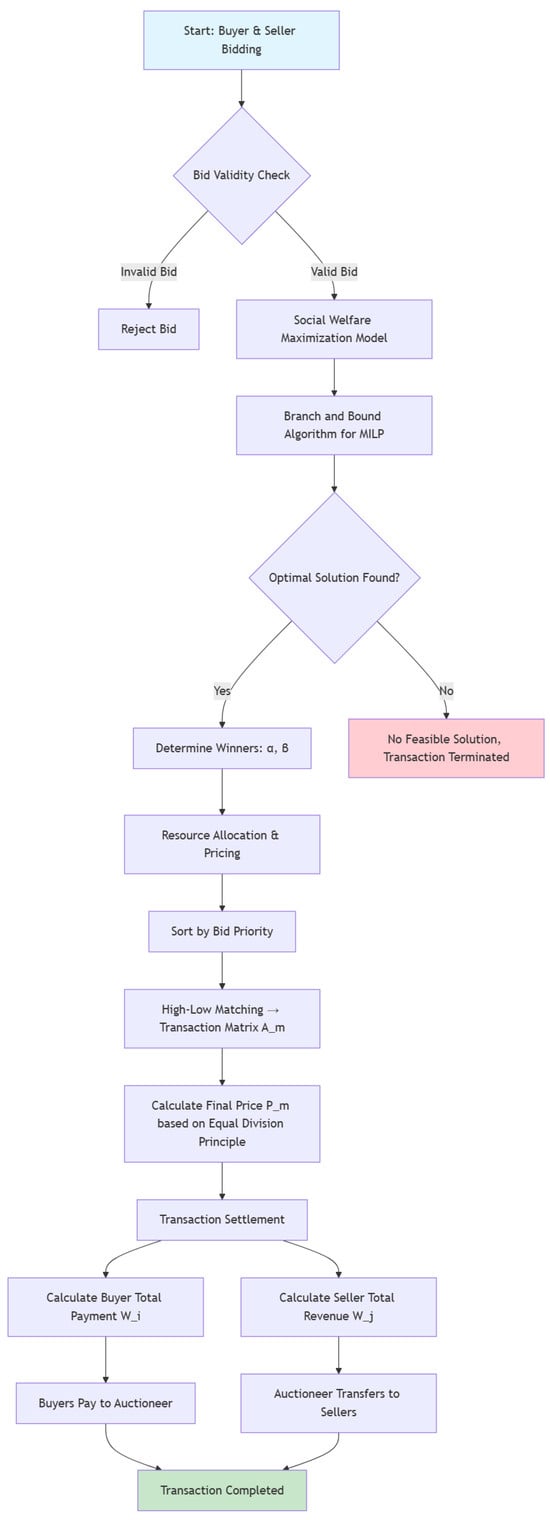
The process begins with the bidding declaration stage of the buyer and the seller. The seller submits the offer and the buyer submits the demand. Then, the validity check is carried out to ensure that all bids meet the requirements. Biddings that fail to pass the inspection will be rejected, while those that pass the inspection will enter the stage of winning the bid.
In the bid-winning stage, the two-party auction transaction model is used to determine the final bidder through model solution. Then, they enter the stage of resource allocation and price formation. First, the buyers and sellers are sorted according to the quotation and then matched according to the priority level to generate a transaction matrix. Finally, the final transaction price is calculated according to the ‘equal division principle’.
Finally, it enters the settlement stage, processes the corresponding data results, completes the fund settlement, and marks the end of the market transaction. The whole process reflects the fairness and efficiency of market transactions. Through scientific pricing mechanism and resource allocation, the interests of buyers and sellers being balanced and the promotion of the healthy operation of the market are ensured, as shown in Figure 4.
Figure 4.
Two-way transaction flow chart.
5.1. Data Description
The subject matter of the two-way trading mechanism proposed in this study is the total capacity available for the shared energy storage system in a specific period of time. Specifically, the energy storage operator (seller) plans all the rated capacity for market transactions, divides it according to different time periods, and declares it to the market. The buyer bids for the capacity of these periods according to their own needs. After the market is cleared, the winning buyer obtains a complete and exclusive right to use the energy storage capacity in the corresponding time period, rather than a percentage of the total capacity. This ‘capacity block’ trading model clearly defines property rights and is convenient for settlement. In addition, the value generated by the energy storage system by providing fluctuation smoothing services, as an additional social welfare increment, is coupled to the market objective function; however, it is not directly traded as physical power but indirectly returned to the energy storage operator through ‘premium compensation’ after the market clears or reflected in the final improved total social welfare.
The computing power data of this study are analyzed according to the actual demand data of buyers and sellers in a certain place. The data contain six sellers and seven buyers. The specific information is shown in Table 3 and Table 4.

Table 3.
Seller data.

Table 4.
Buyer data.
According to the seller’s bidding data shown in Table 3, the tender (5,0.9) indicates that the energy storage operator has declared 5 MW·h of electricity in the current period, and the declared electricity price is 0.9 yuan/kW·h. Energy storage operators can submit differentiated quotation schemes for different periods of time, that is, set the bidding power and bidding price independently in each period of time. This multi-period bidding mechanism can more fully reflect the operator’s differentiated evaluation of the value of energy storage capacity in different periods and enhance the flexibility of the market bidding strategy and the ability to express economic signals.
The data of buyers’ energy storage demand are shown in Table 4. Among them, the tender (10,1.2) indicates that the energy storage demand declared by the buyer in the current period is 10 MW·h, and the declared price is 1.2 yuan/(kW·h). Buyer 1 and buyer 4 adopt a combined bid for multiple periods, reflecting their complementary energy storage capacity requirements in multiple periods. Buyer 2 and buyer 6 adopt the strategy of ordering different energy storage requirements in different time periods, indicating that the energy storage capacity between these time periods is alternative or mutually exclusive. Buyer 3 and buyer 5 belong to the non-binding bidding type, and their ‘or’ bidding strategy allows winning any time period that meets the requirements. Buyer 7 only submitted a single-period energy demand for period 6.
According to the results of the seller’s winning bid shown in Table 3, the set of clearing sellers in each period can be determined. Taking the first period as an example, the winning seller set j = {1,3,4,6} in this period means that the energy storage capacity demand declared by buyer 1 and buyer 4 will be jointly met by the above four operators in a joint supply mode. The buyer’s and seller’s bidding information is shown in Table 5 and Table 6.

Table 5.
Sellers’ winning bid in the corresponding period.

Table 6.
Buyers’ winning bid in the corresponding period.
5.2. Analysis of Simulation Results
The energy storage demand of buyers in each period is shown in Figure 5. According to the transaction allocation results, it can be seen that the energy storage capacity demand of a single buyer may be realized through centralized or distributed supply mode during a specific operating period. Specifically, the capacity demand of buyer 2 in period 3 presents a single supply characteristic, which is independently satisfied by seller 5; the demand of buyer 1 in time period 1 adopts multi-source supply mode, and sellers 3, 4, and 6 jointly complete the delivery through capacity aggregation.
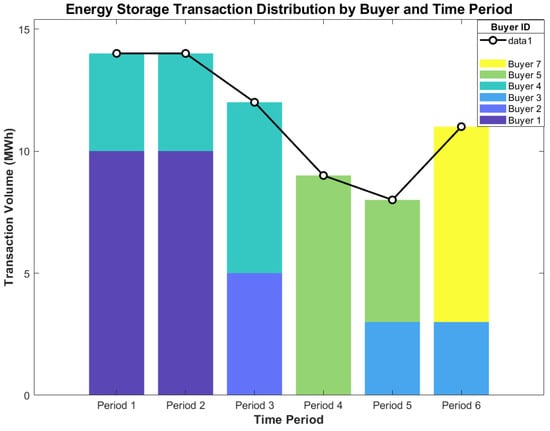
Figure 5.
Buyer’s energy storage demand in each period.
This transaction structure reflects the dual attributes of energy storage resources in the electricity market—both as a dedicated resource for targeted supply and as a public resource for shared regulation. Through the market-oriented trading mechanism, the optimal allocation of energy storage capacity in the space–time dimension is realized, and the overall utilization efficiency of system resources is improved.
The buyer’s transaction price in each period is shown in Figure 6. The analysis results show that there are some differences in the transaction prices reached by different buyers and specific sellers in the same period of time, which is mainly due to the different bidding strategies of various market players. The market adopts a high–low transaction-matching mechanism and a pricing rule based on social welfare equalization to ensure the fairness and efficiency of the transaction process.
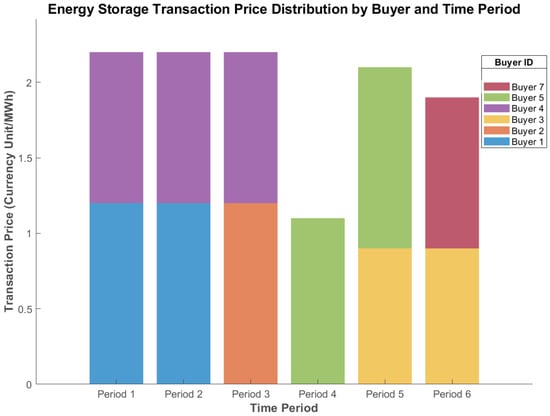
Figure 6.
Buyer’s transaction price in each period.
At the same time, the corresponding data of the seller are analyzed through data processing and application simulation, as shown in Figure 7.
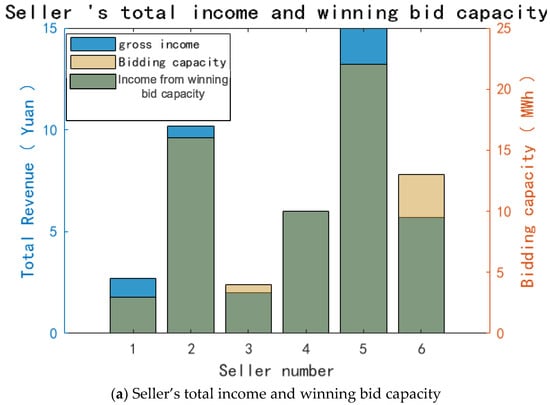
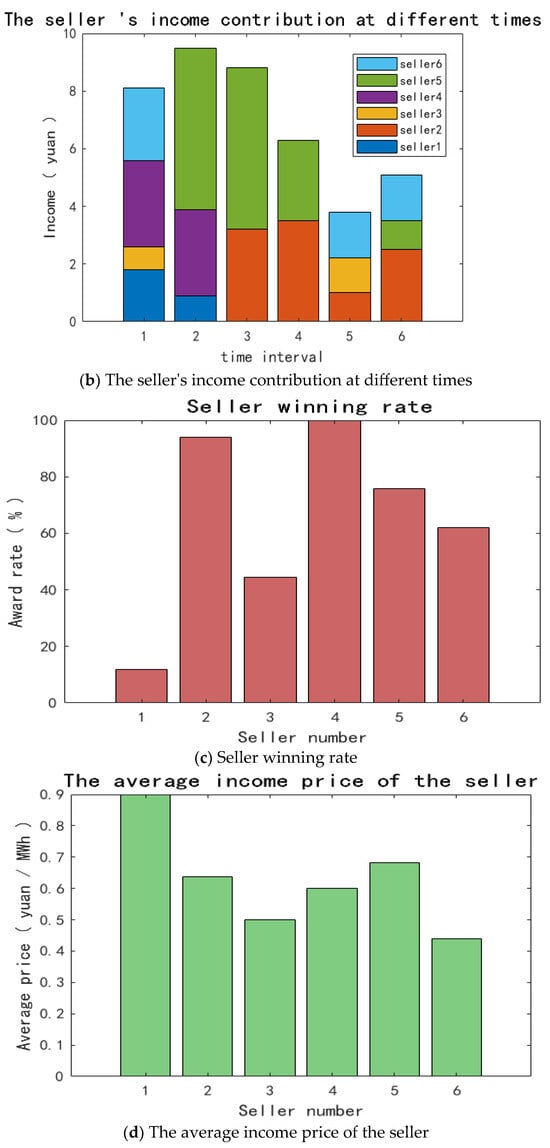
Figure 7.
Seller data analysis.
From seller data analysis in Figure 7, it can be seen that the market presents a significant head concentration effect. Seller 1 is far superior to other sellers in terms of total income, bid-winning ability and average income price. Its average price is close to 0.8 yuan/mm and the bid-winning rate is close to 100%, showing a strong market leading force; in contrast, the average income price and bidding rate of small- and medium-sized sellers are at a low level—the market competition pressure is large, and the market pattern differentiation is obvious.
In order to analyze the solution speed of the branch and bound method in this paper, according to the actual situation, the number of buyers and sellers is expanded, and then the simulation analysis is carried out. The analysis results are shown in Figure 8.
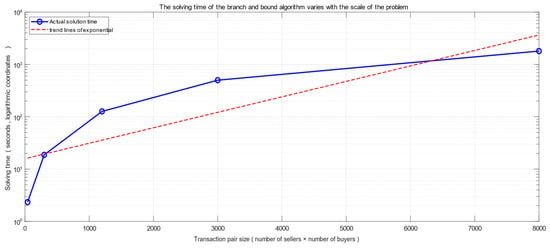
Figure 8.
Method accuracy analysis.
From the results, it can be seen that with the expansion of the scale of the problem, the solution time shows an approximate linear growth trend, indicating that the constructed mixed-integer linear programming model has good scalability. This method has a computational advantage in 2000–3000 trading pairs, and other methods should be found when the trading volume exceeds 3000 pairs.
In order to further analyze the impact of suppressing wind energy fluctuations and the two-way sales mechanism, a scenario analysis control experiment was set up, as shown in Table 7.

Table 7.
Scene settings.
From the data of Figure 9 and Table 8, it can be seen that when the wind energy suppression method and the two-way trading and sharing energy storage mechanism are applied, the social welfare is slightly lower in the fifth period, and it is in the first place in other periods. On average, the social welfare is the best, which can fully mobilize the enthusiasm of buyers and sellers.
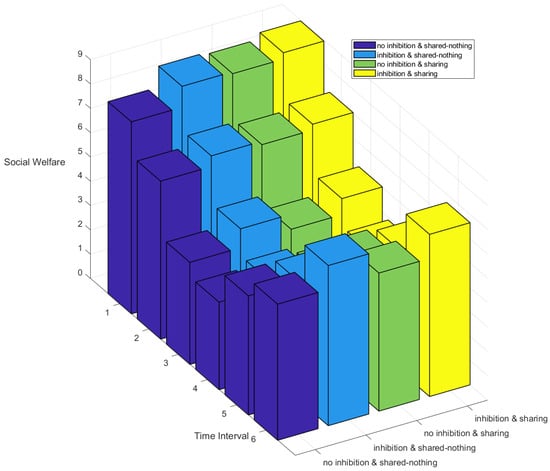
Figure 9.
Comparison of social welfare.

Table 8.
Social welfare table for each scene and period.
In order to further analyze the advantages of the proposed method, compared with other methods, the comparison results are shown in Table 9.

Table 9.
Methods comparison.
According to the comparison, the principle of equal sharing achieves the most balanced distribution of buyers and sellers’ surplus while maintaining the maximization of total social welfare. Although the VCG mechanism can achieve the optimal efficiency in theory, it has the problem of budget imbalance and high computational complexity. The marginal cost pricing calculation is simple, but the total social welfare and fairness indicators are poor. Therefore, the ‘equal sharing’ pricing principle adopted in this paper has achieved a good balance between efficiency, fairness, and practicality, which is especially suitable for application scenarios such as the shared energy storage market that need to take into account multiple interests.
In order to meet the actual power market situation, the total number of sellers and sellers is expanded to 100. The bid-winning situation of sellers and buyers is shown in Table 10 and Table 11. Because the data are too large, some data are listed here.

Table 10.
Seller’s winning bid in the corresponding period.

Table 11.
Buyers’ winning bid in the corresponding period.
According to the above four cases, the simulation analysis is carried out, and the results are as follows.
As shown in the data analysis of Figure 10 and Table 12, in the scenario with 50 participants, the social welfare is the highest in each period when the fluctuation suppression and sharing mechanism are adopted at the same time, and the total welfare is 36.51 yuan, which is significantly higher than the baseline scenario without any optimization. Compared with VCG mechanism and marginal cost pricing, the principle of equal sharing achieves a more balanced buyer–seller surplus distribution and a higher market participation rate while maintaining high social welfare. At the same time, the branch and bound method is used to solve the approximate linear growth of the solution time under the 2000–3000 transaction pair scale, which has good scalability, but more efficient algorithms are needed for larger scales.
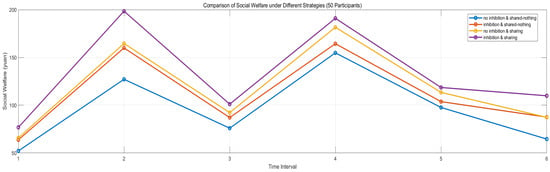
Figure 10.
Comparison of social welfare.

Table 12.
Social welfare table for each scene and period.
For further analysis, the impact of wind volatility on social welfare is carried out. As shown in Figure 11, when using the method in this paper, social welfare will increase with the increase in wind intensity. Although the second situation is also on the rise, the initial social welfare is low, so the method proposed in this paper has great advantages.
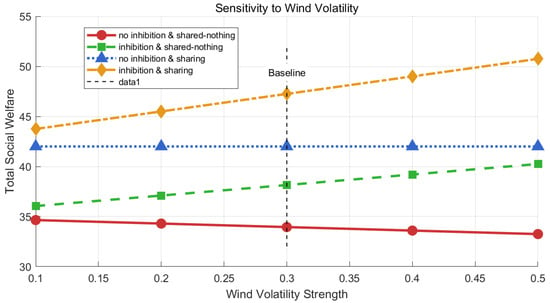
Figure 11.
Social welfare changes with wind intensity.
As shown in Figure 12, the line segments corresponding to each method will increase with the increase in energy storage capacity, but the method proposed in this paper has the largest upward trend, so the method proposed in this study can improve the coupling relationship with energy storage.
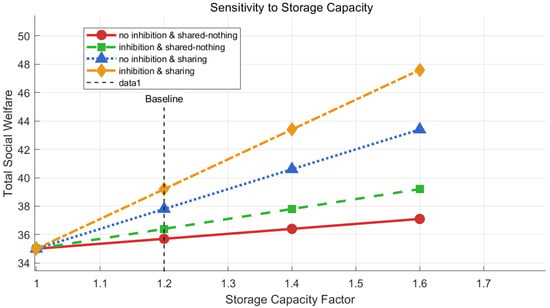
Figure 12.
Social welfare changes with wind energy storage capacity.
6. Discussion of Practical Limitations
While the proposed shared energy storage market mechanism demonstrates significant advantages in social welfare maximization and market fairness, several practical limitations must be addressed for real-world implementation.
6.1. Transmission Losses
The present formulation does not account for transmission losses, which can significantly affect the economic efficiency and actual deliverability of stored energy. Incorporating loss factors into the pricing and settlement mechanism—especially for long-distance or distributed storage resources—would enhance the model’s realism. A loss-allocated pricing scheme could be developed to reflect the true cost of energy delivery.
6.2. Grid Congestion and Physical Constraints
The current model assumes an idealized grid without transmission bottlenecks. In practice, grid congestion could restrict the power transfer between storage providers and consumers, especially in regions with high renewable penetration. Future work should integrate power flow constraints and nodal pricing to ensure that storage transactions are physically feasible and do not exacerbate grid congestion. Methods such as DC optimal power flow or distribution locational marginal pricing could be incorporated into the auction framework.
6.3. Transaction Costs
The model implicitly assumes negligible transaction costs. However, in real markets, costs related to metering, communication, settlement, and market administration can be substantial. These costs may discourage participation, especially for small-scale storage users. Future models could introduce a transaction fee structure or explore blockchain-based solutions to reduce administrative overhead and enhance market accessibility.
7. Conclusions
In this study, aiming at the characteristics of abundant but volatile wind and solar resources in some areas, a shared energy storage model for suppressing wind energy fluctuations is proposed, and a two-way trading market mechanism is designed. The simulation results show that the model can effectively mobilize the participation enthusiasm of buyers and sellers, significantly improve the fairness and impartiality of market transactions, and greatly increase the total social welfare. In the area where wind and solar resources are concentrated but the output is unstable, the energy storage system significantly improves the friendliness of the new energy grid connection by dynamically allocating energy storage capacity and smoothing power fluctuations. The market mechanism based on combinatorial double auction weakens the monopoly power of one party in the traditional one-way auction through the ‘many-to-many’ transaction structure and ensures the balance of interests between market entities of different scales.
However, there are still some shortcomings in this study. First of all, the proposed model algorithm is more complex, and it has higher requirements for computing resources in practical large-scale applications, which may affect its real-time decision-making ability in the actual power market. At the same time, the current model mainly runs under the day-ahead market framework. Future work will explore extending it to the real-time market and incorporating intra-day adjustment and balance mechanisms to better deal with wind power prediction errors and real-time fluctuations. Secondly, the research does not fully consider the coupling effect between the output characteristics of the power generation side and the market behavior and lacks the strategy modeling of the power producer participating in the energy storage sharing transaction. In view of the computational complexity of the mixed-integer linear programming model in large-scale applications, distributed optimization algorithms and reinforcement learning techniques are planned to be studied in the future to improve solution efficiency and achieve decentralized decision-making. In addition, the model does not introduce actual physical constraints such as grid congestion and transmission loss, which limits its application effect in the actual system to a certain extent. In view of the above problems, the follow-up research will focus on the following aspects: First, simplify and accelerate the model, adopt more efficient calculation methods such as distributed optimization, reinforcement learning, etc., to improve the practicability and scalability of the algorithm; the second is to include the power generation side as an active participant in the market structure and study its multilateral trading mechanism with energy storage operators and users. Thirdly, the power system operation constraints are further introduced to establish a collaborative planning and trading model of electric–hydrogen hybrid energy storage closer to the actual market, so as to enhance the engineering applicability and promotion value of the research results. Moreover, the model will be extended to take power producers as active market participants and realize multilateral transactions between power producers, energy storage operators and users. This will better capture the strategic interaction and value flow in a fully integrated energy market.
Author Contributions
Conceptualization, Y.C. and Y.T.; Methodology, Q.H.; Validation, C.W.; Formal analysis, J.P. and P.S.; Supervision, M.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Development Division of State Grid Gansu Electric Power Company of special cost project (B2273025Z125), ‘Adapt to Gansu new energy power system of new energy storage capacity dynamic planning and market mechanism research’.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Yi Chai, Yunfei Tian and Jing Peng were employed by the Development Division of State Grid Gansu Electric Power Company (Economic and Technological Research Institute), Qinghai Hao was employed by the Marketing Division of State Grid Gansu Electric Power Company (Marketing Service Center, Metrology Center). The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflicts of interest.
References
- Li, R.; Zhang, X.; Xu, Y.; Sun, W.; Zhou, X.; Guo, C.; Chen, H. Research on optimal configuration of hybrid energy storage capacity in wind-solar hybrid system. Energy Storage Sci. Technol. 2019, 8, 512–522. [Google Scholar]
- Yang, M.; Guo, Y.; Fan, F. Ultra-Short-Term Prediction of Wind Farm Cluster Power Based on Embedded Graph Structure Learning with Spatiotemporal Information Gain. IEEE Trans. Sustain. Energy 2025, 16, 308–322. [Google Scholar] [CrossRef]
- Zhou, P.; Sun, Y.; Kang, P.; Ma, J.; Yu, H.; Tian, H.; Hu, B.; Xie, K. Optimal configuration method of hybrid energy storage capacity for high proportion renewable energy system of photothermal power station. New Technol. Electr. Energy 2021, 40, 22–31. [Google Scholar]
- Yang, M.; Jiang, Y.; Xu, C.; Wang, B.; Wang, Z.; Su, X. Day-ahead wind farm cluster power prediction based on trend categorization and spatial information integration model. Appl. Energy 2025, 388, 125580. [Google Scholar] [CrossRef]
- Zhang, J.; Chang, X.; Xue, Y.; Bai, X.; Li, Z.; Wang, P.; Sun, H. Optimal Planning for Electricity–Gas–Hydrogen Integrated Energy Systems Considering Intertemporal Long-term Hydrogen Storage and Multiple Uncertainties. IEEE Trans. Power Syst. 2025, 1–14. [Google Scholar] [CrossRef]
- Yang, M.; Huang, Y.; Wang, Z.; Wang, B.; Su, X. A Framework of Day-Ahead Wind Supply Power Forecasting by Risk Scenario Perception. IEEE Trans. Sustain. Energy 2025, 16, 1659–1672. [Google Scholar] [CrossRef]
- Xi, J. Speech at the general debate of the 75th United Nations General Assembly. People’s Daily, 23 September 2020. [Google Scholar]
- Tang, J.; Zhai, Y.; Liu, M.; Ma, T.; Zhao, W.; Yao, Y. Research on the stability control strategy of new energy power grid based on logical operation. Renew. Energy 2022, 40, 675–682. [Google Scholar]
- Teamah, H.M.; Lightstone, M.F. Numerical study of the electrical load shift capability of a ground source heat pump system with phase change thermal storage. Energy Build. 2019, 199, 235–246. [Google Scholar] [CrossRef]
- Renaldi, R.; Friedrich, D. Techno-economic analysis of a solar district heating system with seasonal thermal storage in the UK. Appl. Energy 2019, 236, 388–400. [Google Scholar] [CrossRef]
- Zhou, L.; Huang, Y.; Guo, K.; Feng, Y. Review of research on energy storage technology in microgrid. Power Syst. Prot. Control 2011, 39, 147–152. [Google Scholar]
- Yang, M.; Jiang, R.; Wang, B.; Fang, G.; Jia, Y.; Fan, F. Multi-channel attention mechanism graph convolutional network considering cumulative effect and temporal causality for day-ahead wind power prediction. Energy 2025, 332, 137023. [Google Scholar] [CrossRef]
- Dash, V.; Bajpai, P. Power management control strategy for a stand-alone solar photovoltaic-fuel cell-battery hybrid system. Sustain. Energy Technol. Assess. 2015, 9, 68–80. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, H.; Wei, R.; Li, Z. A Distributed Market-Aided Restoration Approach of Multi-Energy Distribution Systems Considering Comprehensive Uncertainties From Typhoon Disaster. IEEE Trans. Smart Grid 2025, 16, 3743–3757. [Google Scholar] [CrossRef]
- Huang, Y.; Su, R.; He, G.; Luo, H.; Yang, J.; Shi, M.; Li, L. Optimal planning of electric-heat integrated energy system considering electric-hydrogen hybrid energy storage. Power Syst. Prot. Control 2025, 53, 152–162. [Google Scholar]
- Cen, Z.; Geng, B.; Gao, M.; Jiang, H.; Tabg, Y.; Shu, S. Optimal configuration of P2H in the park integrated energy system consider natural gas mixed with hydrogen. Electr. Power Eng. Technol. 2024, 43, 55–64. [Google Scholar]
- Li, L.; Han, Y.; Li, Q.; Chen, X.; Pu, Y.; Chen, W. Economic droop control strategy of a hybrid electric-hydrogen DC microgrid considering efficiency characteristics. Power Syst. Prot. Control 2022, 50, 69–80. [Google Scholar]
- Khatamianfar, A.; Khalid, M.; Savkin, A.V.; Agelidis, V.G. Improving wind farm dispatch in the Australian electricity market with battery energy storage using model predictive control. IEEE Trans. Sustain. Energy 2013, 4, 745–755. [Google Scholar] [CrossRef]
- Chen, X.; Li, T.; Li, R.; Liu, J.; Wang, L.; Zhang, Y.; Tian, C.; Cui, S.; Ai, X. A robust optimization method for distributed energy storage configuration in distribution network considering network constraints and optimal cost. J. Electr. Eng. 2025, 1–11. Available online: https://link.cnki.net/urlid/10.1289.TM.20250623.1557.004 (accessed on 12 October 2025).
- Awad, A.S.A.; El-Fouly, T.H.M.; Salama, M.M.A. Optimal ESS allocation for benefit maximization in distribution networks. IEEE Trans. Smart Grid 2015, 8, 1668–1678. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, H.; Zhao, B.; Zhang, L.; Shi, Y.; Xie, C. Risk-averse stochastic capacity planning and P2P trading collaborative optimization for multi-energy microgrids considering carbon emission limitations: An asymmetric Nash bargaining approach. Appl. Energy 2024, 357, 122505. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H. Wind farm energy storage configuration based on wiener stochastic process. Power Syst. Technol. 2022, 46, 3437–3446. [Google Scholar]
- Wu, W.; Hu, Z.; Song, Y. Optimal sizing of energy storage system for wind farms combining stochastic programming and sequential Monte Carlo simulation. Power Syst. Technol. 2018, 42, 1055–1062. [Google Scholar]
- Lin, S.; Han, M.; Zhao, G.; Niu, Z.; Hu, X. Capacity allocation of energy storage in distributed photovoltaic power system based on stochastic prediction error. Proc. CSEE 2013, 33, 25–33. [Google Scholar]
- Sun, K.; Chen, K.; Cen, H.; Li, T.; Zeng, H.; Lin, L. Stochastic planning method for energy storage capacity of interconnected microgrid considering demand response. Sci. Technol. Eng. 2023, 23, 14241–14247. [Google Scholar]
- Ji, X.; Hou, Y.; Bai, J.; Zhang, M.; Jiang, H.; Ye, P. Optimal planning method of electricity-hydrogen energy storage in new energy grid considering flexibility. Renew. Energy 2025, 43, 107–114. [Google Scholar]
- Lin, S.; Guo, Y.; Zhou, B.; Li, D.; Shen, Y.; Gu, C. Collaborative optimization scheduling method for multi-virtual power plants and shared energy storage considering price uncertainty. Smart Power 2025, 53, 20–27. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).