A Fault-Tolerant Proportional-Integral-Derivative Load Frequency Control for Power Systems Operating Under a Random Event-Triggered Scheme
Abstract
1. Introduction
- (1)
- Utilizing the unified model and actuator fault model for isolated power systems, a PID controller with fault tolerance is developed for power systems.
- (2)
- Unlike conventional PETSs [30], a series of randomly updated sampling intervals based on Poisson stochastic processes is introduced to depict communication patterns, leading to a reduction in the unnecessary use of communication resources.
- (3)
- By formulating suitable Lyapunov–Krasovskii functionals (LKFs), we establish a stability criterion for standalone power systems with performance. Following this, we conduct a comparative analysis to validate the efficacy of the proposed control strategy and demonstrate the benefits of RETS.
2. Preliminaries
2.1. Power System Load Frequency Control Model
- (a)
- The size of the bus voltage remains constant;
- (b)
- The power network is considered to be without losses.
2.2. A Fault-Tolerant PID Control
- Actuator fault model
- Fault-free: ;
- Fault of reduced effectiveness: ;
- Outage fault: .
- 2.
- A fault-tolerant PID control tactic.
2.3. Poisson Random Events to Trigger Communication Scheme
3. Primary Outcomes
3.1. Analysis of Controllability
3.2. Stability Assessment
3.3. Designing the Controller
4. Examples
The Example of Power System
- (a).
- Let , indicating that designed controller is free of faults. Next, utilize the LMIs toolbox to solve LMIs presented in Theorem 3. This will determine the PID control gain matrix as , and the event trigger weight matrix is determined as
- (b).
- Let , indicating that the designed controller comes with fault-tolerant capabilities. Next, utilize the LMIs toolbox to solve LMIs presented in Theorem 3. This will determine the PID control gain matrix as , and the event trigger weight matrix is determined as
- (c).
- Let , indicating that the designed controller comes with fault-tolerant capabilities. Because the actuator is completely faulty, K is meaningless.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dörfler, F.; Grammatico, S. Gather-and-broadcast frequency control in power systems. Automatica 2017, 79, 296–305. [Google Scholar] [CrossRef]
- Shangguan, X.C.; Zhang, C.K.; He, Y.; Jin, L.; Jiang, L.; Spencer, J.W.; Wu, M. Robust load frequency control for power system considering transmission delay and sampling period. IEEE Trans. Ind. Inform. 2020, 17, 5292–5303. [Google Scholar] [CrossRef]
- Xi, K.; Dubbeldam, J.L.; Lin, H.X.; van Schuppen, J.H. Power-imbalance allocation control of power systems-secondary frequency control. Automatica 2018, 92, 72–85. [Google Scholar] [CrossRef]
- Cheng, Z.; Hu, S.; Yue, D.; Dou, C.; Shen, S. Resilient distributed coordination control of multiarea power systems under hybrid attacks. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 7–18. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Tang, Y.; Liao, K.; Syed, M.H.; Guillo-Sansano, E.; Burt, G.M. Aggregated energy storage for power system frequency control: A finite-time consensus approach. IEEE Trans. Smart Grid 2018, 10, 3675–3686. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, D.; Yu, L.; Yan, H. Dynamic event-triggered output feedback control for load frequency control in power systems with multiple cyber attacks. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6246–6258. [Google Scholar] [CrossRef]
- Milano, F.; Manjavacas, Á.O. Frequency Variations in Power Systems: Modeling, State Estimation, and Control; John Wiley & Son: Hoboken, NJ, USA, 2020. [Google Scholar]
- Marinelli, M.; Martinenas, S.; Knezović, K.; Andersen, P.B. Validating a centralized approach to primary frequency control with series-produced electric vehicles. J. Energy Storage 2016, 7, 63–73. [Google Scholar] [CrossRef]
- Meesenburg, W.; Thingvad, A.; Elmegaard, B.; Marinelli, M. Combined provision of primary frequency regulation from Vehicle-to-Grid (V2G) capable electric vehicles and community-scale heat pump. Sustain. Energy Grids Netw. 2020, 23, 100382. [Google Scholar] [CrossRef]
- Wang, Z.; Mei, S.; Liu, F.; Low, S.H.; Yang, P. Distributed load-side control: Coping with variation of renewable generations. Automatica 2019, 109, 108556. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, J.; Lin, Z. Decentralized adaptive controller design for large-scale power systems. Automatica 2017, 79, 93–100. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Luo, W.; Wu, L. Resilient distributed fuzzy load frequency regulation for power systems under cross-layer random denial-of-service attacks. IEEE Trans. Cybern. 2020, 52, 2396–2406. [Google Scholar] [CrossRef] [PubMed]
- Tian, E.; Peng, C. Memory-based event-triggering H∞ load frequency control for power systems under deception attacks. IEEE Trans. Cybern. 2020, 50, 4610–4618. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhong, Q.; Ghias, A.M.; Dong, Z.Y.; Shi, K.; Yu, Y. Distributed fault-tolerant PI load frequency control for power system under stochastic event-triggered scheme. Appl. Energy 2023, 351, 121844. [Google Scholar] [CrossRef]
- Zhong, Q.; Yang, J.; Shi, K.; Zhong, S.; Li, Z.; Sotelo, M.A. Event-triggered H∞ load frequency control for multi-area nonlinear power systems based on non-fragile proportional integral control strategy. IEEE Trans. Intell. Transp. Syst. 2021, 23, 12191–12201. [Google Scholar] [CrossRef]
- Chowdhury, D.; Khalil, H.K. Dynamic consensus and extended high gain observers as a tool to achieve practical frequency synchronization in power systems under unknown time-varying power demand. Automatica 2021, 131, 109753. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H. Memory-Event-Triggered H∞ Load Frequency Control of Multi-Area Power Systems with Cyber-Attacks and Communication Delays. IEEE Trans. Netw. Sci. Eng. 2021, 8, 1571–1583. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Zhang, W.; Yang, W.; Zhang, Y.; Xu, D. Actuator fault-tolerant load frequency control for interconnected power systems with hybrid energy storage system. Energy Rep. 2020, 6, 1312–1317. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, S.; Wu, Z.G.; Chen, G.; Guan, X. Reliable event-triggered load frequency control of uncertain multiarea power systems with actuator failures. IEEE Trans. Autom. Sci. Eng. 2022, 20, 2516–2526. [Google Scholar] [CrossRef]
- Kirschen, D.S. Power Systems: Fundamental Concepts and the Transition to Sustainability; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Qi, W.-L.; Liu, K.-Z.; Wang, R.; Sun, X.-M. Data-Driven L2-Stability Analysis for Dynamic Event-Triggered Networked Control Systems: A Hybrid System Approach. IEEE Trans. Ind. Electron. 2022, 70, 6151–6158. [Google Scholar] [CrossRef]
- Shang-Guan, X.; He, Y.; Zhang, C.; Jiang, L.; Spencer, J.W.; Wu, M. Sampled-data based discrete and fast load frequency control for power systems with wind power. Appl. Energy 2020, 259, 114202. [Google Scholar] [CrossRef]
- Shen, B.; Wang, Z.; Huang, T. Stabilization for sampled-data systems under noisy sampling interval. Automatica 2016, 63, 162–166. [Google Scholar] [CrossRef]
- Lu, Z.; Guo, G. Control and communication scheduling co-design for networked control systems: A survey. Int. J. Syst. Sci. 2023, 54, 189–203. [Google Scholar] [CrossRef]
- Zhong, Q.; Han, S.; Shi, K.; Zhong, S.; Kwon, O.M. Co-design of adaptive memory event-triggered mechanism and aperiodic intermittent controller for nonlinear networked control systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4979–4983. [Google Scholar] [CrossRef]
- Yang, J.; Zhong, Q.; Shi, K.; Zhong, S. Dynamic-Memory Event-Triggered H∞ Load Frequency Control for Reconstructed Switched Model of Power Systems Under Hybrid Attacks. IEEE Trans. Cybern. 2022, 53, 3913–3925. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, J.; Yan, H. Adaptive event-triggering H∞ load frequency control for network-based power systems. IEEE Trans. Ind. Electron. 2017, 65, 1685–1694. [Google Scholar] [CrossRef]
- Liu, G.; Park, J.H.; Hua, C.; Li, Y. Hybrid dynamic event-triggered load frequency control for power systems with unreliable transmission networks. IEEE Trans. Cybern. 2022, 53, 806–817. [Google Scholar] [CrossRef]
- Shangguan, X.C.; He, Y.; Zhang, C.K.; Jin, L.; Yao, W.; Jiang, L.; Wu, M. Control performance standards-oriented event-triggered load frequency control for power systems under limited communication bandwidth. IEEE Trans. Control Syst. Technol. 2021, 30, 860–868. [Google Scholar] [CrossRef]
- Gu, Y.; Sun, Z.; Li, L.W.; Park, J.H.; Shen, M. Event-triggered security adaptive control of uncertain multi-area power systems with cyber attacks. Appl. Math. Comput. 2022, 432, 127344. [Google Scholar] [CrossRef]
- Milano, F.; Alhanjari, B.; Tzounas, G. Enhancing frequency control through rate of change of voltage feedback. IEEE Trans. Power Syst. 2023, 39, 2385–2388. [Google Scholar] [CrossRef]
- Park, P. A delay-dependent stability criterion for systems with uncertain time-invariant delays. IEEE Trans. Autom. Control 1999, 44, 876–877. [Google Scholar] [CrossRef]
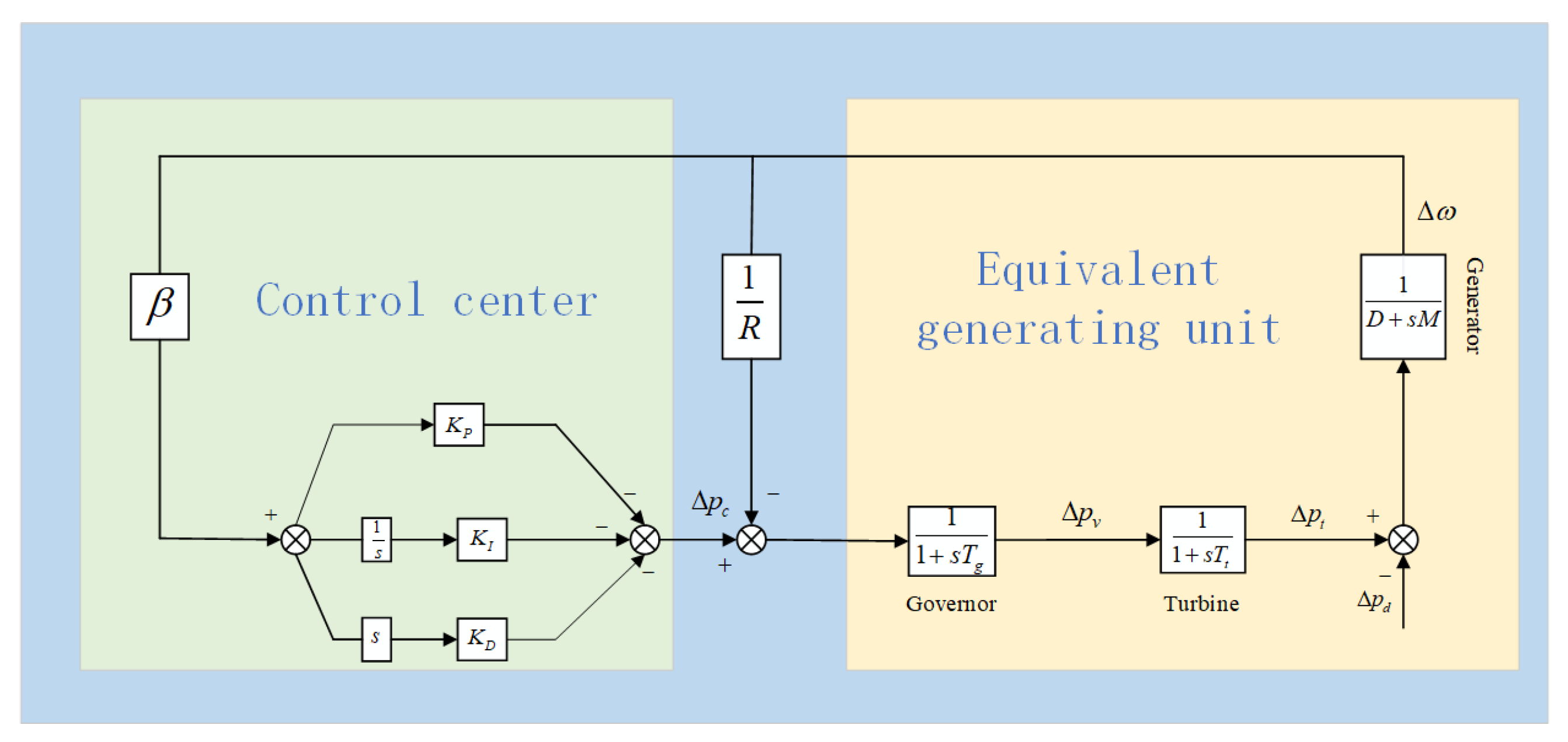








| D | Generator damping coefficient | Generator output deviation | |
| M | Generator inertia moment | Generator valve position deviation | |
| Turbine time constant | Control command deviation | ||
| Governor time constant | Load deviation | ||
| R | Speed drop factor | Frequency | |
| Frequency bias coefficient | Area control error signal |
| M (s2) | D (s) | (s) | (s) | R (Hz/pu) | (Hz/Hz) |
|---|---|---|---|---|---|
| 10.0 | 1.0 | 0.3 | 0.1 | 0.5 | 21.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, C.; Luo, J.; Shi, K.; Liu, Y. A Fault-Tolerant Proportional-Integral-Derivative Load Frequency Control for Power Systems Operating Under a Random Event-Triggered Scheme. Electronics 2025, 14, 2443. https://doi.org/10.3390/electronics14122443
Ling C, Luo J, Shi K, Liu Y. A Fault-Tolerant Proportional-Integral-Derivative Load Frequency Control for Power Systems Operating Under a Random Event-Triggered Scheme. Electronics. 2025; 14(12):2443. https://doi.org/10.3390/electronics14122443
Chicago/Turabian StyleLing, Chenyu, Junyi Luo, Kaibo Shi, and Yanjun Liu. 2025. "A Fault-Tolerant Proportional-Integral-Derivative Load Frequency Control for Power Systems Operating Under a Random Event-Triggered Scheme" Electronics 14, no. 12: 2443. https://doi.org/10.3390/electronics14122443
APA StyleLing, C., Luo, J., Shi, K., & Liu, Y. (2025). A Fault-Tolerant Proportional-Integral-Derivative Load Frequency Control for Power Systems Operating Under a Random Event-Triggered Scheme. Electronics, 14(12), 2443. https://doi.org/10.3390/electronics14122443







