Research on the Time-Varying Network Topology Characteristics of Cryptocurrencies on Uniswap V3
Abstract
1. Introduction
2. Related Works
3. Methods
3.1. Cryptocurrency Yield Correlation Coefficient Matrix
3.2. Random Matrix Theory
- Step 1: Assume there are N time series with identical sample size L, from which we construct a random linear correlation matrix R:where A is composed of N independent sequences of length L, each of which follows an distribution. Assume ; thus, the maximum and minimum values of the predicted eigenvalues of a random matrix can be expressed aswhere and are the upper and lower bounds of the random matrix’s predicted eigenvalue spectrum, which measures the range of market noise and unsystematic fluctuations, and is the variance of the random matrix R.
- Step 2: Performing feature decomposition on the cryptocurrency correlation coefficient matrix C:where P is an orthogonal matrix, is the transpose of matrix P(i.e., , and is a diagonal matrix containing eigenvalues. Its main diagonal elements are the eigenvalues of the cryptocurrency correlation coefficient matrix. Sort the eigenvalues in the matrix from small to large, and obtain the eigenvalue matrix , which takes the specific form ofwhere and . Simultaneously, perform feature decomposition on the random matrix R.
- Step 3: Replace the eigenvalues of the correlation coefficient matrix that fall within the predicted range of the random matrix theory with 0 [33] as follows:Meanwhile, the eigenvector matrix of the correlation coefficient also retains the eigenvectors at the same position. Therefore, the denoised correlation coefficient matrix can be expressed as follows:where is the new correlation coefficient matrix with its main diagonal elements set to 1, and is the new matrix of eigenvectors. By improving the correlation coefficient matrix of cryptocurrencies through the above method, the noise in the correlation coefficient matrix can be removed.
3.3. Cryptocurrency Network Topology Indicators
- (1)
- Average degree
- (2)
- Average clustering coefficient
- (3)
- Assortativity coefficient
4. Data and Correlation Coefficient Matrix Denoising
4.1. Data Description
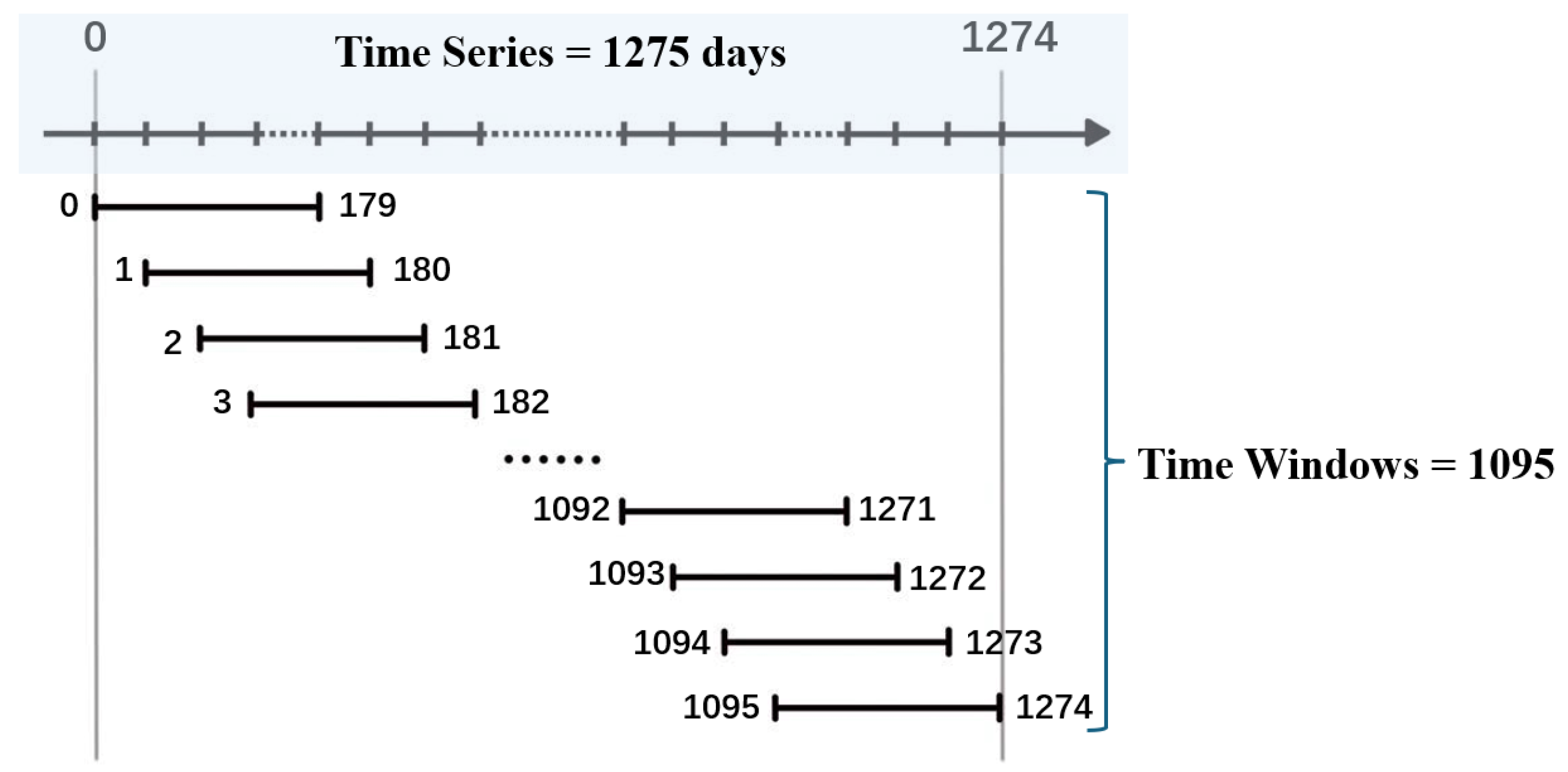
4.2. Sliding Window Processing
- Firstly, set the sliding window length to 180 days and the sliding step size to 1 day, as shown in Figure 1. There are a total of 1095 sliding windows in the research dataset of this article.
- Then, calculate the correlation coefficient matrix for the closing price of cryptocurrencies within each sliding window, and construct a random matrix to denoise the correlation coefficient matrix.
- Finally, within each sliding window, a cryptocurrency network is constructed based on the denoised correlation coefficient matrix, and the network topology index is calculated to perform time-varying feature analysis in the Uniswap V3 network.
4.3. Denoising of Uniswap V3 Cryptocurrency Correlation Coefficient Matrix Based on RMT Theory
- Firstly, the maximum and minimum eigenvalues of the random data correlation coefficient matrix almost coincide with the maximum and minimum predicted values of the random matrix theory, which conforms to the prediction principles of random matrices [31].
- Secondly, the maximum eigenvalue range of the correlation coefficient matrix is between 5 and 30, which deviates significantly from the range predicted by the random matrix theory. At the same time, the minimum eigenvalue range of the correlation coefficient matrix tends towards 0, which deviates to some extent from the range predicted by the random matrix theory, indicating the existence of special non-random attributes in the cryptocurrency correlation coefficient matrix.
- Thirdly, some eigenvalues of the linear correlation coefficient matrix fall within the range predicted by random matrix theory. The information contained in these eigenvalues cannot convey interactions between cryptocurrency variables and they are thus considered noise eigenvalues, indicating the presence of random noise in the cryptocurrency correlation coefficient matrix.
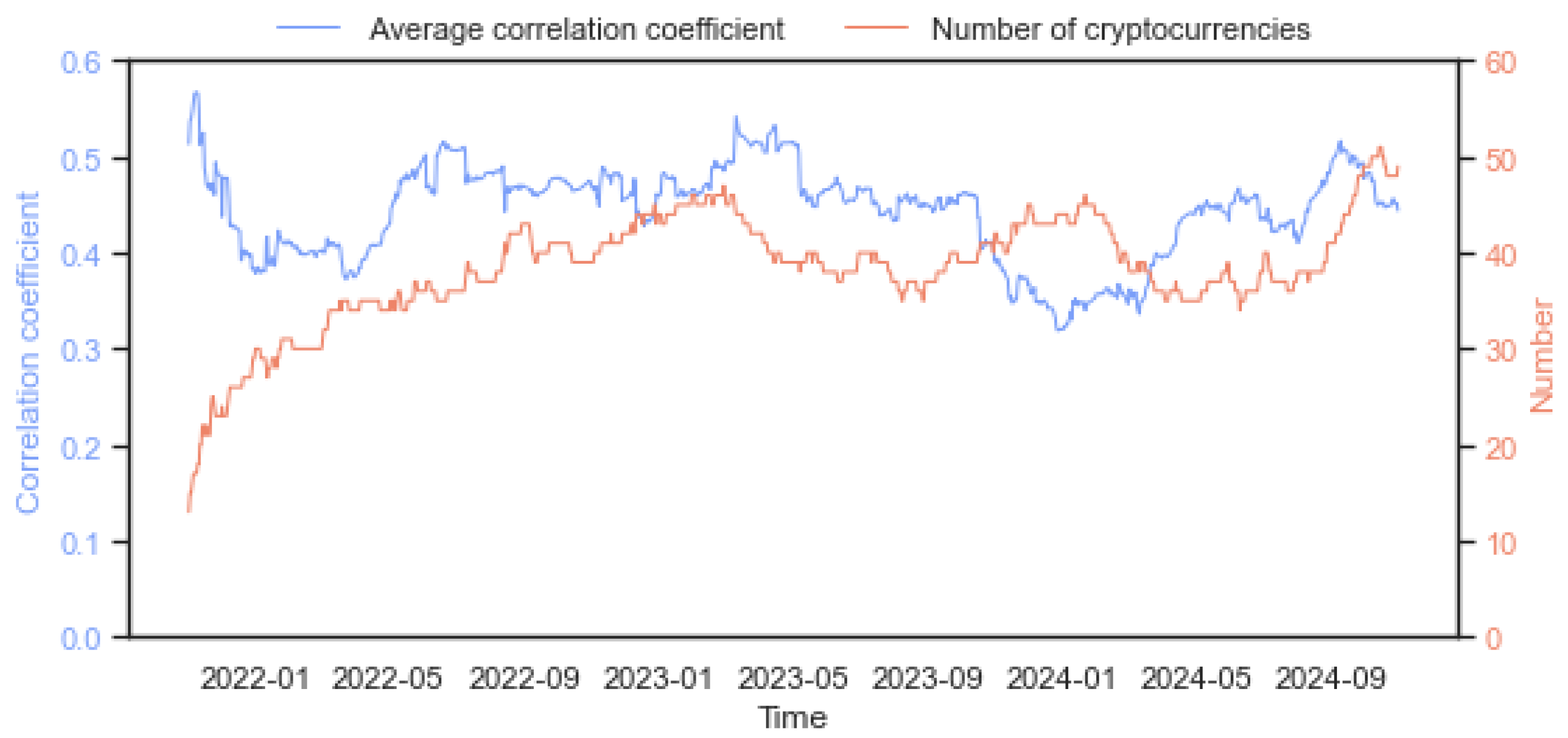
4.4. Distribution Attributes of Correlation Coefficient
5. Analysis of Uniswap V3 Network Topology Index Characteristics
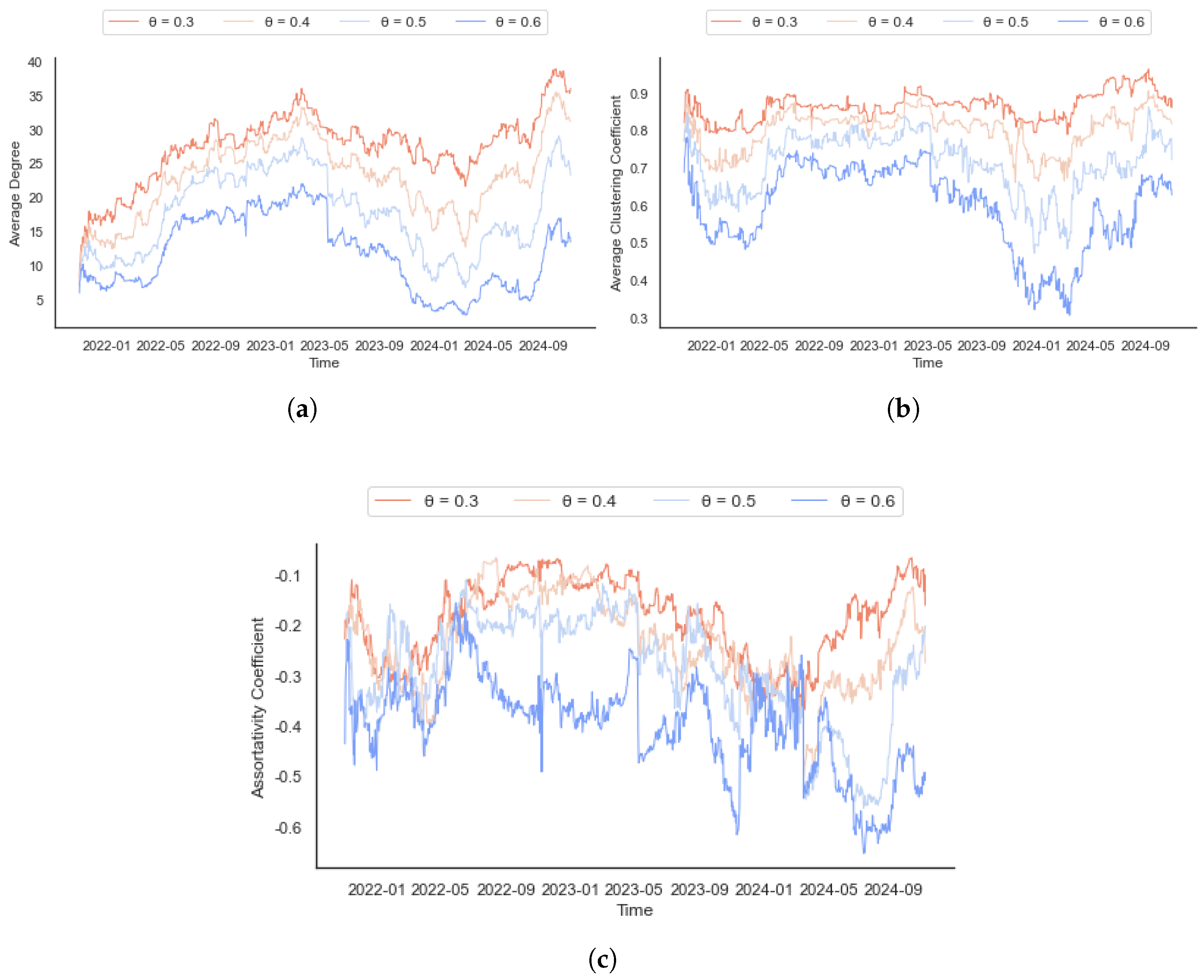
5.1. Uniswap V3 Network Topology Analysis
5.2. Analysis of Time-Varying Characteristics of Uniswap V3 Network Topology Indicators
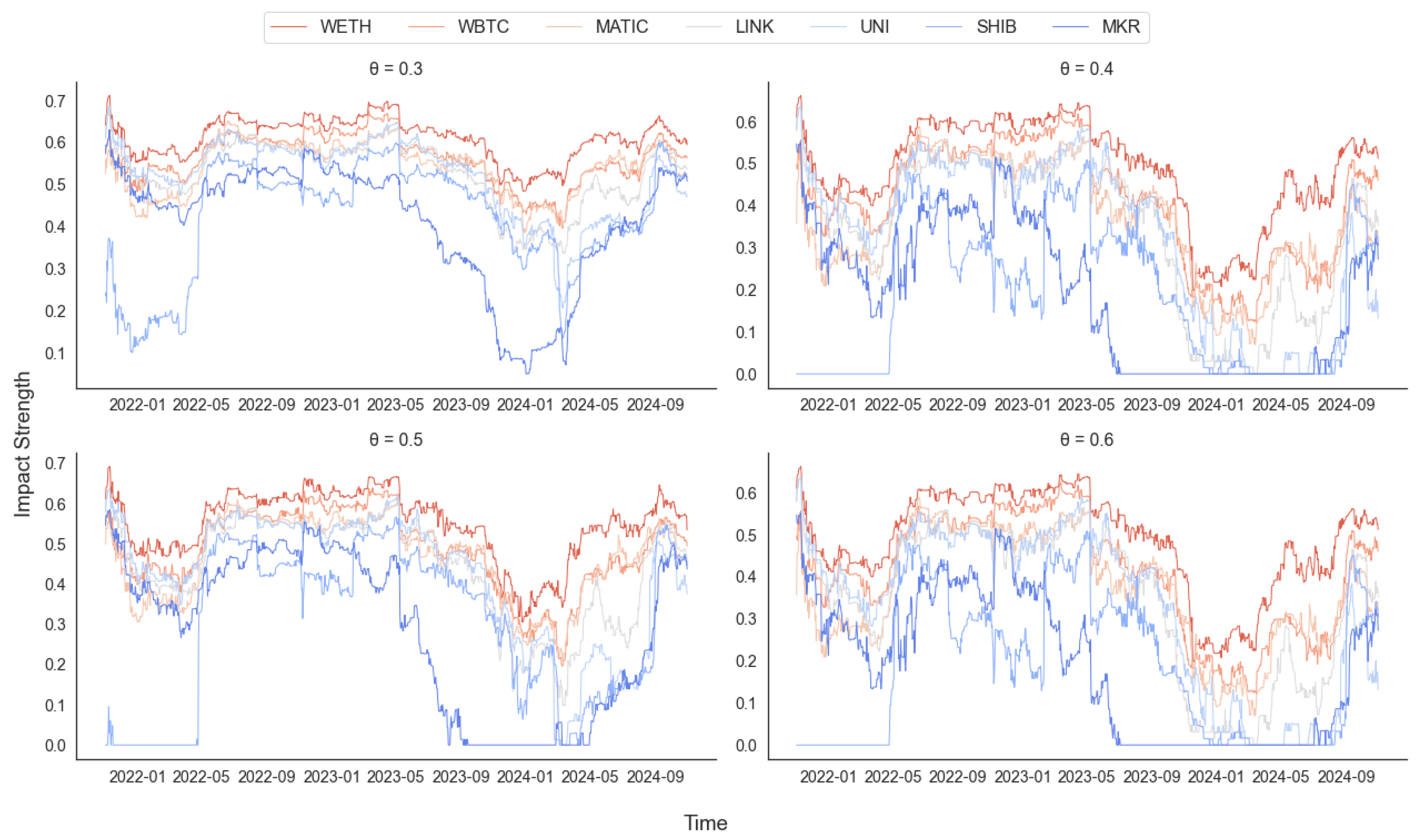
5.3. Analysis of the Impact Strength of Cryptocurrency on Uniswap V3
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wüst, K.; Gervais, A. Do you need a blockchain? In Proceedings of the 2018 Crypto Valley Conference on Blockchain Technology (CVCBT), Zug, Switzerland, 20–22 June 2018; Institute of Electrical and Electronics Engineers—IEEE: New York, NY, USA, 2018; pp. 1–10. [Google Scholar]
- Ankenbrand, T.; Bieri, D. Assessment of cryptocurrencies as an asset class by their characteristics. Invest. Manag. Financ. Innov. 2018, 15, 169–181. [Google Scholar] [CrossRef]
- Aigner, A.A.; Dhaliwal, G. Uniswap: Impermanent loss and risk profile of a liquidity provider. arXiv 2021, arXiv:2106.14404. [Google Scholar] [CrossRef]
- Asef, M.A.; Bamakan, S.M.H. From x* y= k to Uniswap Hooks: A Comparative Review of Decentralized Exchanges (DEX). arXiv 2024, arXiv:2410.10162. [Google Scholar]
- Heimbach, L.; Schertenleib, E.; Wattenhofer, R. Risks and Returns of Uniswap V3 Liquidity Providers. In Proceedings of the 4th ACM Conference on Advances in Financial Technologies, Cambridge, MA, USA, 19–21 September 2022; pp. 89–101. [Google Scholar]
- Lo, Y.C.; Medda, F. Uniswap and the Emergence of the Decentralized Exchange. J. Financ. Mark. Infrastructures 2021, 10, 1–25. [Google Scholar]
- Xia, P.; Wang, H.; Gao, B.; Su, W.; Yu, Z.; Luo, X.; Zhang, C.; Xiao, X.; Xu, G. Trade or Trick? Detecting and Characterizing Scam Tokens on Uniswap Decentralized Exchange. ACM Sigmetrics Perform. Eval. Rev. 2022, 50, 23–24. [Google Scholar] [CrossRef]
- Nguyen, A.P.N.; Mai, T.T.; Bezbradica, M.; Crane, M. The cryptocurrency market in transition before and after COVID-19: An opportunity for investors? Entropy 2022, 24, 1317. [Google Scholar] [CrossRef]
- Song, W.; Zhang, W.; Wang, J.; Zhai, L.; Jiang, P.; Huang, S.; Li, B. Blockchain data analysis from the perspective of complex networks: Overview. Tsinghua Sci. Technol. 2022, 28, 176–206. [Google Scholar] [CrossRef]
- Jing, R.; Rocha, L.E. A network-based strategy of price correlations for optimal cryptocurrency portfolios. Financ. Res. Lett. 2023, 58, 104503. [Google Scholar] [CrossRef]
- Yan, T.; Tessone, C.J. Network Analysis of Uniswap: Centralization and Fragility in the Decentralized Exchange Market. arXiv 2025, arXiv:2503.07834. [Google Scholar]
- Campajola, C.; Cristodaro, R.; De Collibus, F.M.; Yan, T.; Vallarano, N.; Tessone, C.J. The evolution of centralisation on cryptocurrency platforms. arXiv 2022, arXiv:2206.05081. [Google Scholar]
- Lin, J.H.; Marchese, E.; Tessone, C.J.; Squartini, T. The weighted bitcoin lightning network. Chaos Solitons Fractals 2022, 164, 112620. [Google Scholar] [CrossRef]
- Bovet, A.; Campajola, C.; Mottes, F.; Restocchi, V.; Vallarano, N.; Squartini, T.; Tessone, C.J. The evolving liaisons between the transaction networks of Bitcoin and its price dynamics. In Proceedings of the Blockchain Kaigi 2022 (BCK22), Sendai, Japan, 4–5 August 2022; p. 011002. [Google Scholar]
- Serena, L.; Ferretti, S.; D’Angelo, G. Cryptocurrencies activity as a complex network: Analysis of transactions graphs. Peer- Netw. Appl. 2022, 15, 839–853. [Google Scholar] [CrossRef]
- Qiao, X.; Zhu, H.; Tang, Y.; Peng, C. Time-frequency extreme risk spillover network of cryptocurrency coins, DeFi tokens and NFTs. Financ. Res. Lett. 2023, 51, 103489. [Google Scholar] [CrossRef]
- Yan, T.; Shang, Q.; Zhang, Y.; Tessone, C.J. Optimizing Arbitrage Strategies on Uniswap: The Impact of Trading Path Length on Profitability and Opportunity Frequency. In Proceedings of the Blockchain Kaigi 2023 (BCK23), Kobe, Japan, 28–29 October 2023; p. 011007. [Google Scholar]
- Ho, K.H.; Chiu, W.H.; Li, C. A network analysis of the cryptocurrency market. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, Australia, 1–4 December 2020; pp. 2178–2185. [Google Scholar]
- Mardan, M.; Khosravipour, I. Dynamic Evolution Analysis of Cryptocurrency Market: A Network Science Study. J. Interdiscip. Econ. 2024, 22, 02601079241265744. [Google Scholar] [CrossRef]
- Vidal-Tomás, D. Transitions in the cryptocurrency market during the COVID-19 pandemic: A network analysis. Financ. Res. Lett. 2021, 43, 101981. [Google Scholar] [CrossRef]
- Pagnottoni, P.; Famà, A.; Kim, J.M. Financial networks of cryptocurrency prices in time-frequency domains. Qual. Quant. 2024, 58, 1389–1407. [Google Scholar] [CrossRef]
- Chaudhari, H.; Crane, M. Cross-correlation dynamics and community structures of cryptocurrencies. J. Comput. Sci. 2020, 44, 101130. [Google Scholar] [CrossRef]
- Giudici, P.; Polinesi, G. Crypto price discovery through correlation networks. Ann. Oper. Res. 2021, 299, 443–457. [Google Scholar] [CrossRef]
- Soloviev, V.N.; Yevtushenko, S.P.; Batareyev, V.V. Comparative analysis of the cryptocurrency and the stock markets using the Random Matrix Theory. In Proceedings of the Computer Science & Software Engineering: Proceedings of the 2nd Student Workshop (CS&SE@ SW 2019), Kryvyi Rih, Ukraine, 29 November 2019; CEUR Workshop Proceedings. pp. 87–100. [Google Scholar]
- Tian, J.; Zhao, K. Optimal selection of financial risk investment portfolio based on random matrix method. J. Comput. Methods Sci. Eng. 2020, 20, 859–868. [Google Scholar] [CrossRef]
- Laloux, L.; Cizeau, P.; Bouchaud, J.P.; Potters, M. Noise dressing of financial correlation matrices. Sci. Financ. (CFM) Work. Pap. Arch. 1998, 83, 1467. [Google Scholar] [CrossRef]
- Chakraborti, A.; Sharma, K.; Pharasi, H.K.; Bakar, K.S.; Das, S.; Seligman, T.H. Emerging spectra characterization of catastrophic instabilities in complex systems. New J. Phys. 2020, 22, 063043. [Google Scholar] [CrossRef]
- Jalili, A.; Sabri, H.; Ahmadian, D.; Saleki, Z.; Luo, Y.A.; Chen, A.X. Spectral fluctuations in financial systems: An integrated random matrix theory and machine learning perspective. Eur. Phys. J. Plus 2024, 139, 980. [Google Scholar] [CrossRef]
- Potters, M.; Bouchaud, J.P. A First Course in Random Matrix Theory: For Physicists, Engineers and Data Scientists; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Tang, Y.; Xiong, J.; Cheng, Z.; Zhuang, Y.; Li, K.; Xie, J.; Zhang, Y. Looking into the Market Behaviors through the Lens of Correlations and Eigenvalues: An Investigation on the Chinese and US Markets Using RMT. Entropy 2023, 25, 1460. [Google Scholar] [CrossRef]
- Kwapień, J.; Drożdż, S.; Oświe¸cimka, P. The bulk of the stock market correlation matrix is not pure noise. Phys. A Stat. Mech. Its Appl. 2005, 359, 589–606. [Google Scholar] [CrossRef]
- Sharifi, S.; Crane, M.; Shamaie, A.; Ruskin, H. Random matrix theory for portfolio optimization: A stability approach. Phys. A Stat. Mech. Its Appl. 2004, 335, 629–643. [Google Scholar] [CrossRef]
- Plerou, V.; Gopikrishnan, P.; Rosenow, B.; Amaral, L.A.N.; Guhr, T.; Stanley, H.E. Random matrix approach to cross correlations in financial data. Phys. Rev. E 2002, 65, 066126. [Google Scholar] [CrossRef]
- Mantegna, R.N. Hierarchical structure in financial markets. Eur. Phys. J. B-Condens. Matter Complex Syst. 1999, 11, 193–197. [Google Scholar] [CrossRef]
- Tumminello, M.; Aste, T.; Di Matteo, T.; Mantegna, R.N. A tool for filtering information in complex systems. Proc. Natl. Acad. Sci. USA 2005, 102, 10421–10426. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex Networks: Structure and Dynamics. Complex Syst. Complex. Sci. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Rubi, M.; Diaz-Guilera, A. Statistical Mechanics of Complex Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003; Volume 625. [Google Scholar]
- Newman, M.E. Assortative mixing in networks. Phys. Rev. Lett. 2002, 89, 208701. [Google Scholar] [CrossRef]
- Chi, X.; Jue, H.; Gang-jin, W. Study on Topological Property of Stock Market’s Network Based on Random Matric Method. Oper. Res. Manag. Sci. 2018, 27, 144. [Google Scholar]

| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| Natural logarithmic return of cryptocurrency yield | Random matrix’s predicted eigenvalue spectrum | ||
| Correlation coefficient between cryptocurrencies | P | Eigenvector matrix of correlation coefficients | |
| C | Correlation coefficient matrix of cryptocurrency yields | Eigenvalue matrix of correlation coefficients | |
| R | Random linear correlation matrix | D | Adjacency matrix constructed by threshold method |
| N | Number of cryptocurrencies | E | Actual number of edges in the network |
| A | Random matrix | Average clustering coefficient | |
| L | Length of cryptocurrencies | r | Assortativity coefficient (degree correlation) |
| Long-Lived Coins | = 0.3 | = 0.4 | = 0.5 | = 0.6 |
|---|---|---|---|---|
| WETH | 0.611 | 0.590 | 0.549 | 0.488 |
| WBTC | 0.561 | 0.536 | 0.486 | 0.408 |
| MATIC | 0.543 | 0.517 | 0.465 | 0.369 |
| LINK | 0.526 | 0.499 | 0.439 | 0.342 |
| UNI | 0.519 | 0.486 | 0.423 | 0.330 |
| SHIB | 0.421 | 0.362 | 0.296 | 0.184 |
| MKR | 0.410 | 0.362 | 0.285 | 0.187 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, X.; Yu, M.; Yan, T.; Lin, J.; Tessone, C.J. Research on the Time-Varying Network Topology Characteristics of Cryptocurrencies on Uniswap V3. Electronics 2025, 14, 2444. https://doi.org/10.3390/electronics14122444
Feng X, Yu M, Yan T, Lin J, Tessone CJ. Research on the Time-Varying Network Topology Characteristics of Cryptocurrencies on Uniswap V3. Electronics. 2025; 14(12):2444. https://doi.org/10.3390/electronics14122444
Chicago/Turabian StyleFeng, Xiao, Mei Yu, Tao Yan, Jianhong Lin, and Claudio J. Tessone. 2025. "Research on the Time-Varying Network Topology Characteristics of Cryptocurrencies on Uniswap V3" Electronics 14, no. 12: 2444. https://doi.org/10.3390/electronics14122444
APA StyleFeng, X., Yu, M., Yan, T., Lin, J., & Tessone, C. J. (2025). Research on the Time-Varying Network Topology Characteristics of Cryptocurrencies on Uniswap V3. Electronics, 14(12), 2444. https://doi.org/10.3390/electronics14122444






