On the Trade-Off between Energy Efficiency and Spectral Efficiency in RIS-Aided Multi-User MISO Downlink

Abstract

As reconfigurable intelligent surfaces (RISs) have been gradually brought to reality, a large amount of research has been conducted to investigate the immense benefits of RISs. That is because RISs enable us to artificially direct the radio wave propagating through the environment at a relatively low cost. This paper investigates the trade-off between spectral efficiency (SE) and energy efficiency (EE) in the RIS-aided multi-user multiple-input single-output downlink. We develop an optimization framework for designing the transmitting precoding at the base station and the phase shift values at the RIS to balance the EE-SE trade-off. The proposed iterative optimization framework for the design includes quadratic transform, alternating optimization, and weighted minimization mean-square error conversion. Simulation results illustrate our optimization framework algorithm exhibits effectiveness and a fast convergence rate.

1. Introduction

As increasingly more 5G technology is being brought from concept to reality, the era of 5G has already started. A concept named reconfigurable intelligent surface (RIS) is proposed to achieve a higher data rate and increased availability and soon became a hot research topic. In practice, RIS is an artificial radio structure composed of low-cost units which can be programmed to reflect incoming radio-frequency waves to specified directions [1]. What makes RIS unique as a part of the environment is that it can control its reaction to the impinging radio wave by changing the inside current compared to the conventional surface [2,3]. According to the physical laws, the traditional surface, such as a wall, has a fixed reflection characteristic. As RIS can adapt to time-varying wireless communication environments, it makes the concept of intelligent radio environments possible [3]. The propagation environments become reconfigurable by adding RISs into the wireless environments. The process of installing RISs on or removing RISs from walls or ceilings has a low implementation cost as the hardware footprints are relatively low [4,5,6,7]. Therefore, RIS is expected to be the cost-efficient and energy-saving technology to improve system performance, becoming one of the hot topics in future communication networks [8,9,10,11].

Through the research of channel modeling [12,13], channel estimation [14], and performance evaluation of the communication system based on the RIS [15,16,17], the potential benefits of the communication environments based on RIS are discussed. In the resource allocation design of RIS-aided communication, large amounts of work focus on optimizing the spectral efficiency (SE) of the system [18]. Furthermore, we treat energy efficiency (EE), which is another important topic in the research on RIS [19,20], as one of the optimization objectives. However, most of the existing work has focused on the optimization of either SE or EE. SE performance is sometimes sacrificed for the maximization of EE, especially when the value of Signal to Interference plus Noise Ratio (SINR) is large [21,22]. Therefore, we try to find a way to attain a balance between EE and SE.

In this paper, a trade-off between SE and EE is investigated while the transmitting precoding at the base station (BS) side and the phase shift values at the RIS of RIS-aided multi-user multiple-input single-output (MISO) downlink are jointly optimized. The main contributions made by this paper are listed as follows.

We consider a RIS-aided multiuser downlink system to attain an EE-SE trade-off. Next, we propose an optimization framework for the problem in joint optimization. Then, we develop an optimization algorithm to design the transmitting precoding at the BS side and the phase shift values at the RIS to attain this trade-off. We first use the alternating optimization (AO) method to decouple the optimization variables. We also use quadratic transform and weighted minimization mean-square error (WMMSE) to turn the problem into a strictly convex problem.

The rest of this article is organized as follows. We introduce the optimization problem of the RIS-aided multiuser MISO downlink system in Section 2. Then, we present an algorithm framework to handle the problem in Section 3. In Section 4, we present further numerical analysis according to simulation results. At last, we provide the conclusion of this paper in Section 5.

Notation 1.

We use $\mathbf{A}$ to denote a matrix, while $a_{i,j}$ and ${\mathbf{a}}_k$ denote the $(i,j)$-th element and the k-th column vector of matrix $\mathbf{A}$, respectively. We also use $\mathbf{x}$ to denote a column vector, while $x_i$ and $\parallel \mathbf{x}\parallel$ denote the i-th element and the Euclidean norm of vector $\mathbf{x}$, respectively. An $M\times M$ identity matrix is denoted by ${\mathbf{I}}_M$ in this paper. The notation $\left|b\right|$ denotes the modulus value of complex scalar b. The operator $\mathsf{diag}\left\{·\right\}$ is used as the diagonalization operator in this paper. We use $\mathcal{CN}(\mathbf{a},\mathbf{B})$ to denote Circular symmetric complex Gaussian distribution. The conjugate, argument, and real part of a complex number Φ are denoted by ${\Phi }^{*}$, $\angle \Phi$, and $\Re \{\Phi \}$, respectively.

2. System Model and Problem Formulation

2.1. Channel Model

The paper considers a multiuser MISO downlink communication based on RIS, as shown in Figure 1. The messages are sent from one M-antenna BS to K users, and each user is equipped with a single antenna. The RIS in the system is equipped with N reflection elements to form a new communication path from the BS to the K users. We use ${\mathbf{h}}_{\mathrm{d},k}\in {\mathbb{C}}^{M\times 1}$, $\mathbf{G}\in {\mathbb{C}}^{M\times N}$, and ${\mathbf{h}}_{\mathrm{r},k}\in {\mathbb{C}}^{N\times 1}$, $k=1,\dots ,K$, to denote the channel vectors from the BS to user k, from the BS to RIS, and from RIS to user k, respectively.

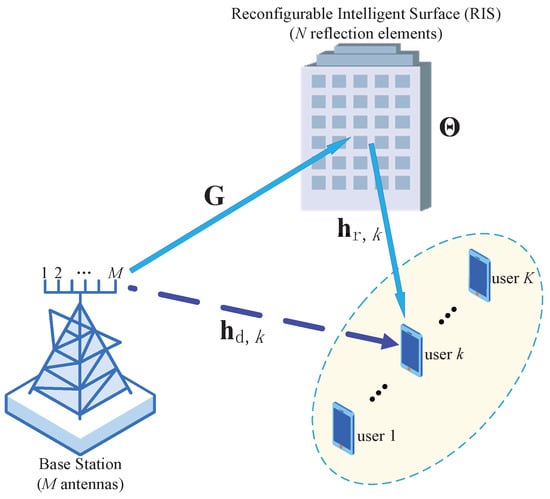
Figure 1. The reconfigurable intelligent surface (RIS)-aided multi-user multiple-input single-output (MISO) downlink system.

The reflection operation, which is finished by the N RIS elements, directed by an intelligent controller in RIS, will change the incident signal by multiplying it with ${\theta }_n\in \mathcal{F}$, where $\mathcal{F}$ refers to the feasible set of reflection coefficient (RC).The RIS will then forward this composite signal just like transmitting it from a point source [15].

Moreover, only the first-time-reflected signals are considered in the communication model considering substantially high path loss [18,23]. We use a diagonal matrix $\Theta =\sqrt{\eta }\mathsf{diag}\left({\theta }_1,\dots ,{\theta }_n,\dots ,{\theta }_N\right)$, where $\eta \le 1$ indicates the reflection efficiency, to denote the RIS phase-shift operation.

2.2. Signal Model

We can express the transmitted signal at the BS as

$$\mathbf{x}=\sum _{k=1}^K{\mathbf{w}}_k{s}_k$$

(1)

where ${\mathbf{w}}_k\in {\mathbb{C}}^{M\times 1}$ is used to denote corresponding transmit precoding vector, while $s_k$ denotes the transmit message to user k. It is assumed that $s_k$, $k=1,\dots ,K$, are independent random variables with zero mean and unit variance. Then, we use $y_k$ to denote the signal received by user k. The expression of $y_k$ is given below. Note that the difference between the two paths is usually negligible as the RIS is usually placed close to the transmitter or receiver to get minimal path loss. Otherwise, it needs to conduct an estimation of the delay at the BS [5,24] and phase compensation at the receiver when the difference between the two propagation delays gets large [25].

$$\begin{array}{cc}\hfill y_k& =\underset{\mathrm{Direct}\mathrm{link}}{\underbrace{{\mathbf{h}}_{\mathrm{d},k}^H\mathbf{x}}}+\underset{\mathrm{RIS}-\mathrm{aided}\mathrm{link}}{\underbrace{{\mathbf{h}}_{\mathrm{r},k}^H{\Theta }^H{\mathbf{G}}^H\mathbf{x}}}+u_k\hfill \\ \hfill & =({\mathbf{h}}_{\mathrm{d},k}^H+{\mathbf{h}}_{\mathrm{r},k}^H{\Theta }^H{\mathbf{G}}^H)\sum _{k=1}^K{\mathbf{w}}_k{s}_k+u_k\hfill \end{array}$$

(2)

where $u_k\sim \mathcal{CN}(0,{\sigma }_0^2)$ refers to the additive white Gaussian noise (AWGN) in the channel [26].

2.3. Problem Formulation

All the signals from other users (i.e., $s_1,\dots ,s_{k-1},$$s_{k+1},\dots ,s_K$) are treated as interference by the k-th user. Therefore, the decoding SINR of $s_k$ can be expressed as

$${\gamma }_k=\frac{{\left|({\mathbf{h}}_{\mathrm{d},k}^H+{\mathbf{h}}_{\mathrm{r},k}^H{\Theta }^H{\mathbf{G}}^H){\mathbf{w}}_k\right|}^2}{{\sum }_{i=1,i\ne k}^K{\left|({\mathbf{h}}_{\mathrm{d},k}^H+{\mathbf{h}}_{\mathrm{r},k}^H{\Theta }^H{\mathbf{G}}^H){\mathbf{w}}_i\right|}^2+{\sigma }_0^2}.$$

(3)

According to Equation (3), EE and SE of this RIS-aided downlink communication system can be expressed as

$$\begin{array}{cc}\hfill & \mathrm{EE}=\frac{{\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)}{\mu {\sum }_{k=1}^K\parallel {\mathbf{w}}_k{\parallel }^2+P_{\mathrm{s},\mathrm{total}}}\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill & \mathrm{SE}={\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)\hfill \end{array}$$

(4b)

where $\mu$ is the reciprocal of the transmit power amplifier efficiency, and ${\omega }_k$ refers to the weight in the SE of the system given to k-th user. In Equation (4a), the term $P_{\mathrm{s},\mathrm{total}}=P_{\mathrm{BS}}+N{P}_n+K{P}_k$ is the sum of the static hardware power consumed by the BS, the RIS, and the users. It refers to the fixed power consumed by the system [5]. Let $\mathbf{W}=\left[{\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_K\right]\in {\mathbb{C}}^{M\times K}$. Thus, we can get the joint optimization problem below.

$$\begin{array}{cc}\hfill \left(\mathrm{P}1\right)& \underset{\mathbf{W},\Theta }{max}a\frac{{\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)}{\mu {\sum }_{k=1}^K\parallel {\mathbf{w}}_k{\parallel }^2+P_{\mathrm{s},\mathrm{total}}}\hfill \\ & +\left(1-a\right){\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.{\sum }_{k=1}^K{\left|\left|{\mathbf{w}}_k\right|\right|}^2\le {\mathrm{P}}_{\mathrm{T}}\hfill \end{array}$$

(5b)

$$\begin{array}{cc}\hfill & {\theta }_n\in \mathcal{F},\forall n=1,\cdots ,N\hfill \end{array}$$

(5c)

where a refers to the weight of EE, $0<a<1$, and (5b) refers to the constraint on the transmit power at the BS side. In this paper, $\mathcal{F}$ is chosen as the continuous phase set [4,27,28,29], which means that ${∥{\theta }_n∥}^2=1$. Therefore, $\mathcal{F}$ can be expressed as

$$\mathcal{F}=\{{\theta }_n\mid {\theta }_n=e^{𝚥{\varphi }_n},{\varphi }_n\in [0,2\pi )\}.$$

(6)

The problem in (5a) is non-convex with the fractional expression of EE, and it is harder than the problem that only chooses SE as the objective. This paper tries to optimize the objective in problem $\left(\mathrm{P}1\right)$ with low computational complexity.

3. Joint Optimization of EE-SE

3.1. Quadratic Transform

As the fractional expression in the problem brings difficulties in designing an algorithm, we can get the equivalently transformed expression of $\left(\mathrm{P}1\right)$ by applying the quadratic transform in [30]. Therefore, we change the fractional problem into a new form without the fraction to simplify the optimization problem. The new problem is expressed as

$$\begin{array}{cc}\hfill \left(\mathrm{P}2\right)& \underset{\mathbf{W},\Theta ,y}{max}2y\sqrt{a{\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)}\hfill \\ & -y^2\left(\mu {\sum }_{k=1}^K\parallel {\mathbf{w}}_k{\parallel }^2+P_{\mathrm{s},\mathrm{total}}\right)\hfill \\ & +\left(1-a\right){\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)\hfill \\ & \mathrm{s}.\mathrm{t}.(5b),(5c)\hfill \end{array}$$

(7)

where $y\in \mathbb{R}$ is an auxiliary variable brought by the quadratic transform algorithm.

Next, the square root of the SE part contained in the objective function in problem $\left(\mathrm{P}2\right)$ is replaced with variable t. Furthermore, a new constraint on t needs to be added to ensure that the problem is reformulated equivalently.

$$\begin{array}{cc}\hfill \left(\mathrm{P}3\right)& \underset{\mathbf{W},\Theta ,y,t}{max}2y\sqrt{a}t-y^2\left(\mu {\sum }_{k=1}^K\parallel {\mathbf{w}}_k{\parallel }^2+P_{\mathrm{s},\mathrm{total}}\right)\hfill \\ & +\left(1-a\right){\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)\hfill \\ & \mathrm{s}.\mathrm{t}.(5b),(5c)\hfill \\ & t^2\le {\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)\hfill \end{array}$$

(8)

Therefore, optimizing the objective in problem $\left(\mathrm{P}1\right)$ over $\mathbf{W}$ and $\Theta$ is equivalently turned to the process of finding the optimal $\mathbf{W}$, $\Theta$, y, and t for the problem $\left(\mathrm{P}3\right)$. As the problem $\left(\mathrm{P}3\right)$ makes it difficult to find the optimal values of the four variables simultaneously, the AO method is then adopted to conduct the optimization by organizing the original problem into several sub-problems. The iteration step is repeated until the convergence is reached. First and foremost, y and t are optimized, while the algorithm to optimize $\Theta$ and $\mathbf{W}$ alternately will be introduced in Section 3.2. During the process of optimizing the objective over y and t, we can have

$$\begin{array}{cc}\hfill & t^{\mathrm{opt}}=\sqrt{{\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)}\hfill \end{array}$$

(9a)

$$\begin{array}{cc}\hfill & y^{\mathrm{opt}}=\frac{\sqrt{a{\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)}}{\mu {\sum }_{k=1}^K\parallel {\mathbf{w}}_k{\parallel }^2+P_{\mathrm{s},\mathrm{total}}}.\hfill \end{array}$$

(9b)

By setting the derivative of the target function in $\left(\mathrm{P}3\right)$ to zero, the expression of $y^{\mathrm{opt}}$ can be obtained. The objective function in $\left(\mathrm{P}1\right)$ appears after substituting $y^{\mathrm{opt}}$ and $t^{\mathrm{opt}}$ for y and t in problem $\left(\mathrm{P}3\right)$, which also proves that problem $\left(\mathrm{P}3\right)$ is equivalent to problem $\left(\mathrm{P}1\right)$.

3.2. WMMSE Algorithm

When optimizing $\Theta$ and $\mathbf{W}$ for problem $\left(\mathrm{P}3\right)$, we first focus on optimizing the latter part, which refers to the weighted sum-rate term, in problem $\left(\mathrm{P}3\right)$. Therefore, we obtain the new problem as

$$\begin{array}{cc}\hfill \left(\mathrm{P}4\right)& \underset{\mathbf{W},\Theta }{max}{\sum }_{k=1}^K{\omega }_k{log}_{}\left(1+{\gamma }_k\right)\hfill \\ & \mathrm{s}.\mathrm{t}.(5b),(5c).\hfill \end{array}$$

(10)

As problem $\left(\mathrm{P}4\right)$ is also non-convex, it is still hard to conduct the optimization. According to the work in [31], the WMMSE algorithm can be applied to optimize the SE of the system. We can equivalently transform problem $\left(\mathrm{P}4\right)$ into a convex optimization problem by introducing two auxiliary variables, while we can get the closed-form expression of the optimal solutions for these two variables. The equivalently formed problem is

$$\begin{array}{cc}\hfill \left(\mathrm{P}5\right)& \underset{\mathbf{W},\Theta ,\mathbf{u},\mathbf{\alpha }}{min}{\sum }_{k=1}^K{\omega }_k\left({\alpha }_k{e}_k-{log}_{}{\alpha }_k\right)\hfill \\ & \mathrm{s}.\mathrm{t}.(5b),(5c)\hfill \end{array}$$

(11)

where $\mathbf{u}\in {\mathbb{C}}^{K\times 1}$, $\mathbf{\alpha }\in {\mathbb{R}}^{K\times 1}$, and $e_k$ are auxiliary variables introduced by the algorithm. The first two variables $\mathbf{u}$ and $\mathbf{\alpha }$ refer to ${\left[u_1,\dots ,u_K\right]}^T$ and ${\left[{\alpha }_1,\dots ,{\alpha }_K\right]}^T$, respectively. The rest variable $e_k$ is expressed as

$$\begin{array}{cc}\hfill e_k=& |u_k^{*}\left({\mathbf{h}}_{\mathrm{d},k}^H+{\mathbf{h}}_{\mathrm{r},k}^H{\Theta }^H{\mathbf{G}}^H\right){\mathbf{w}}_k{-1|}^2\hfill \\ & +{\sum }_{i=1,i\ne k}^K{\left|u_i\left({\mathbf{h}}_{\mathrm{d},k}^H+{\mathbf{h}}_{\mathrm{r},k}^H{\Theta }^H{\mathbf{G}}^H\right){\mathbf{w}}_i\right|}^2+{\sigma }_0^2{\left|u_k\right|}^2.\hfill \end{array}$$

(12)

When optimizing $\Theta$ and $\mathbf{W}$ for problem $\left(\mathrm{P}3\right)$, we can remove some irrelevant items. With the equivalence relation between problems $\left(\mathrm{P}4\right)$ and $\left(\mathrm{P}5\right)$, we can turn problem $\left(\mathrm{P}3\right)$ into

$$\begin{array}{cc}\hfill \left(\mathrm{P}6\right)& \underset{\mathbf{W},\Theta ,\mathbf{u},\mathbf{\alpha }}{min}{y}^2\left(\mu {\sum }_{k=1}^K\parallel {\mathbf{w}}_k{\parallel }^2+P_{\mathrm{s},\mathrm{total}}\right)+\left(1-a\right){\sum }_{k=1}^K{\omega }_k\left({\alpha }_k{e}_k-{log}_{}{\alpha }_k\right)\hfill \\ & \mathrm{s}.\mathrm{t}.(5b),(5c).\hfill \end{array}$$

(13)

Next, we will alternately optimize $\mathbf{W}$, $\Theta$, $\mathbf{u}$, and $\mathbf{\alpha }$ for problem $\left(\mathrm{P}6\right)$. The optimization of $\Theta$ and $\mathbf{W}$ will be introduced in the following, while the optimal $u_k$ and ${\alpha }_k$ are obtained by setting the derivatives to zero, respectively:

$$\begin{array}{cc}\hfill & u_k^{\mathrm{opt}}=\frac{\left({\mathbf{h}}_{\mathrm{d},k}^H+{\mathbf{h}}_{\mathrm{r},k}^H{\Theta }^H{\mathbf{G}}^H\right){\mathbf{w}}_k}{{\sum }_{i=1}^K{\left|\left({\mathbf{h}}_{\mathrm{d},k}^H+{\mathbf{h}}_{\mathrm{r},k}^H{\Theta }^H{\mathbf{G}}^H\right){\mathbf{w}}_i\right|}^2+{\sigma }_0^2}\hfill \end{array}$$

(14a)

$$\begin{array}{cc}\hfill & {\alpha }_k^{\mathrm{opt}}=\frac{1}{e_k}\hfill \end{array}$$

(14b)

where $k=1,2,\cdots ,K$.

3.2.1. Optimization of Transmit Precoding for Given Phase-Shifting Values

To optimize the objective in problem $\left(\mathrm{P}6\right)$ over $\mathbf{W}$, we remove the terms that are independent of $\mathbf{W}$ and get

$$\begin{array}{cc}\hfill \left(\mathrm{P}7\right)& \underset{\mathbf{W}}{min}{y}^2\mu {\sum }_{k=1}^K{\left|\left|{\mathbf{w}}_k\right|\right|}^2+\left(1-a\right){\sum }_{k=1}^K{\omega }_k{\alpha }_k{e}_k\hfill \\ & \mathrm{s}.\mathrm{t}.(5b).\hfill \end{array}$$

(15)

Then, we rewrite $e_k$ as below. Therefore, we can rewrite the objective function and transform problem $\left(\mathrm{P}7\right)$ equivalently into new problem $\left(\mathrm{P}7\right)$ below.

$$\begin{array}{cc}\hfill e_k& =|u_k^{*}{\mathbf{h}}_k^H{\mathbf{w}}_k{-1|}^2+\sum _{i=1,i\ne k}^K{\left|u_i{\mathbf{h}}_k^H{\mathbf{w}}_i\right|}^2+{\sigma }_0^2{\left|u_k\right|}^2\hfill \\ \hfill & =\sum _{i=1}^K|u_i{|}^2{\mathbf{w}}_i^H{\mathbf{h}}_k{\mathbf{h}}_k^H{\mathbf{w}}_i-2\Re \left\{u_k{\mathbf{w}}_k^H{\mathbf{h}}_k\right\}+1+{\sigma }_0^2{\left|u_k\right|}^2\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \left(\mathrm{P}7\right)& \underset{\mathbf{W}}{min}{\sum }_{k=1}^K{\mathbf{w}}_k^H(y^2\mu {\mathrm{I}}_M+(1-a)|u_k{|}^2{\sum }_{i=1}^K{\omega }_i{\alpha }_i{\mathbf{h}}_i{\mathbf{h}}_i^H){\mathbf{w}}_k\hfill \\ & -2\Re \left\{\left(1-a\right){\omega }_k{\alpha }_k{u}_k{\mathbf{w}}_k^H{\mathbf{h}}_k\right\}+\left(1-a\right){\omega }_k{\alpha }_k(1+{\sigma }_0^2|u_k{|}^2)\hfill \\ & \mathrm{s}.\mathrm{t}.(5b)\hfill \end{array}$$

(17)

where ${\mathbf{h}}_i={\mathbf{h}}_{\mathrm{d},i}+\mathbf{G}\Theta {\mathbf{h}}_{\mathrm{r},i}$ and ${\mathrm{I}}_M$ denotes an $M\times M$ identity matrix.

Considering that $\mu >0$, $(1-a)>0$, ${\omega }_i\ge 0$, ${\alpha }_i>0$, new problem $\left(\mathrm{P}7\right)$ is convex. Then, we can use standard convex optimization algorithms [32] to find the optimal value of $\mathbf{W}$.

3.2.2. Optimization of Phase-Shifting Values for Given Transmitting Precoding

To optimize problem $\left(\mathrm{P}6\right)$ over $\Theta$, the terms which do not correlate with $\Theta$ can be omitted, and new problem forms as

$$\begin{array}{cc}\hfill \left(\mathrm{P}8\right)& \underset{\Theta }{min}{\sum }_{k=1}^K{\omega }_k{\alpha }_k{e}_k\hfill \\ & \mathrm{s}.\mathrm{t}.(5c).\hfill \end{array}$$

(18)

As variable $\Theta$ is a diagonal matrix, we can transform the variable of problem $\left(\mathrm{P}8\right)$ into vector $\mathbf{\theta }$ through some substitution and operation and rewrite the objective function in problem $\left(\mathrm{P}8\right)$ in the quadratic form of $\mathbf{\theta }$. Therefore, we add some auxiliary variables ${\mathbf{a}}_{i,k}=\sqrt{\eta }\mathsf{diag}\left({\mathbf{h}}_{\mathrm{r},k}^H\right){\mathbf{G}}^H{\mathbf{w}}_i$ and $b_{i,k}={\mathbf{h}}_{\mathrm{d},k}^H{\mathbf{w}}_i$. Thus, we have $\left({\mathbf{h}}_{\mathrm{d},k}^H+{\mathbf{h}}_{\mathrm{r},k}^H{\Theta }^H{\mathbf{G}}^H\right){\mathbf{w}}_i=b_{i,k}+{\mathbf{\theta }}^H{\mathbf{a}}_{i,k}$, where $\mathbf{\theta }={\left[{\theta }_1,\dots ,{\theta }_N\right]}^T$ [26]. Then, we can transform $e_k$ into the new form below to simplify the expression of the optimization problem. Therefore, we can rewrite the objective function in Equation (18), and problem $\left(\mathrm{P}8\right)$ can be equivalently expressed as new problem $\left(\mathrm{P}8\right)$ below.

$$\begin{array}{cc}\hfill e_k& =|u_k^{*}({\mathrm{b}}_{k,k}+{\mathbf{\theta }}^H{\mathbf{a}}_{k,k}){-1|}^2+\sum _{i=1,i\ne k}^K{\left|u_i({\mathrm{b}}_{i,k}+{\mathbf{\theta }}^H{\mathbf{a}}_{i,k})\right|}^2+{\sigma }_0^2{\left|u_k\right|}^2\hfill \\ \hfill & ={\mathbf{\theta }}^H\left(\sum _{i=1}^K{\left|u_i\right|}^2{\mathbf{a}}_{i,k}{\mathbf{a}}_{i,k}^H\right)\mathbf{\theta }+2\Re \left\{{\mathbf{\theta }}^H\left(\sum _{i=1}^K{\left|u_i\right|}^2{\mathrm{b}}_{i,k}^{*}{\mathbf{a}}_{i,k}-u_k^{*}{\mathbf{a}}_{k,k}\right)\right\}\hfill \\ & +\left(\sum _{i=1}^K{\left|u_i\right|}^2{\left|{\mathrm{b}}_{i,k}\right|}^2-2\Re \left\{u_k^{*}{\mathrm{b}}_{k,k}\right\}+{\sigma }_0^2{\left|u_k\right|}^2+1\right)\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \left(\mathrm{P}8\right)& \underset{\mathbf{\theta }}{min}{\mathbf{\theta }}^H\mathbf{U}\mathbf{\theta }+2\Re \left\{{\mathbf{\theta }}^H\mathbf{v}\right\}+\mathrm{C}\hfill \\ & \mathrm{s}.\mathrm{t}.(5c)\hfill \end{array}$$

(20)

where

$$\begin{array}{cc}\hfill & \mathbf{U}={\sum }_{k=1}^K{\omega }_k{\alpha }_k\left({\sum }_{i=1}^K|u_i{|}^2{\mathbf{a}}_{i,k}{\mathbf{a}}_{i,k}^H\right)\hfill \end{array}$$

(21a)

$$\begin{array}{cc}\hfill & \mathbf{v}={\sum }_{k=1}^K{\omega }_k{\alpha }_k\left({\sum }_{i=1}^K|u_i{|}^2{b}_{i,k}^{*}{\mathbf{a}}_{i,k}-u_k^{*}{\mathbf{a}}_{k,k}\right)\hfill \end{array}$$

(21b)

$$\begin{array}{cc}\hfill & \mathrm{C}={\sum }_{k=1}^K{\omega }_k{\alpha }_k({\sum }_{i=1}^K|u_i{|}^2|{\mathrm{b}}_{i,k}{|}^2-2\Re \left\{u_k^{*}{\mathrm{b}}_{k,k}\right\}+{\sigma }_0^2|u_k{|}^2+1).\hfill \end{array}$$

(21c)

Next, we change the variable $\Theta$ into $\mathbf{\theta }$ to conduct the optimization of new problem $\left(\mathrm{P}8\right)$. Then, we optimize the new problem $\left(\mathrm{P}8\right)$ over ${\theta }_1,\dots ,{\theta }_N$ in turn [26]. While conducting the optimization over one variable ${\theta }_n$, $n=1,\dots ,N$, the values of ${\theta }_j(j=1,\dots ,N,j\ne n)$ are fixed. In addition, the ${\mathbf{\theta }}^H\mathbf{U}\mathbf{\theta }$ and ${\mathbf{\theta }}^H\mathbf{v}$ in the new problem $\left(\mathrm{P}8\right)$ can be transformed as

$$\begin{array}{cc}\hfill {\mathbf{\theta }}^H\mathbf{U}\mathbf{\theta }& ={\sum }_{i=1}^N{\sum }_{j=1}^N{\theta }_i^{*}{\mathrm{u}}_{i,j}{\theta }_j\hfill \\ & ={\theta }_n^{*}{\mathrm{u}}_{n,n}{\theta }_n+2\Re \left\{{\sum }_{j=1,j\ne n}^{\mathrm{N}}{\theta }_n^{*}{\mathrm{u}}_{n,j}{\theta }_j\right\}\hfill \\ & +{\sum }_{i=1,i\ne n}^N{\sum }_{j=1,j\ne n}^N{\theta }_i^{*}{\mathrm{u}}_{i,j}{\theta }_j\hfill \end{array}$$

(22a)

$$\begin{array}{cc}\hfill {\mathbf{\theta }}^H\mathbf{v}& ={\theta }_n^{*}{\mathrm{v}}_{\mathrm{n}}+{\sum }_{i=1,i\ne n}^N{\theta }_i^{*}{\mathrm{v}}_i.\hfill \end{array}$$

(22b)

Then, we need to conduct the optimization over ${\theta }_n$. Therefore, the expression of problem $\left(\mathrm{P}8\right)$ can be adapted to the optimization problem below by removing the unrelated items.

$$\begin{array}{cc}\hfill \left(\mathrm{P}9\right)& \underset{{\theta }_n}{min}{\theta }_n^{*}{\mathrm{u}}_{n,n}{\theta }_n+2\Re \left\{{\theta }_n^{*}\left({\mathrm{v}}_n+{\sum }_{j=1,j\ne n}^N{\mathrm{u}}_{n,j}{\theta }_j\right)\right\}\hfill \\ & \mathrm{s}.\mathrm{t}.{\theta }_n={\mathrm{e}}^{j{\varphi }_n},{\varphi }_n\in [0,2\pi ).\hfill \end{array}$$

(23)

The value of the first part of the objective function is independent of ${\theta }_n$, so only the second part of the expression is needed to be considered while doing the optimization as ${\theta }_n={\mathrm{e}}^{𝚥{\varphi }_n}$. It can be easily seen that

$$\begin{array}{c}\hfill {\varphi }_n^{\mathrm{opt}}=\pi +\angle \left({\mathrm{v}}_n+{\sum }_{j=1,j\ne n}^N{\mathrm{u}}_{n,j}{\theta }_j\right)\end{array}$$

(24)

where $n=1,2,\cdots ,N$.

So far, we have managed to propose a complete framework for problem $\left(\mathrm{P}1\right)$ with low complexity. We first introduce auxiliary variable y by using the quadratic transform and replace the square root term with variable t, combining with the corresponding constraint, to turn the original problem into problem $\left(\mathrm{P}3\right)$ equivalently. Then, we use the AO method to decouple the optimization variables while optimizing the objective in the new problem. When optimizing the objective function in problem $\left(\mathrm{P}3\right)$, we use the WMMSE transform to turn problem $\left(\mathrm{P}3\right)$ into a convex problem. Then, we can use standard convex optimization algorithms [32] to find the solution.

4. Numerical Results

In this section, we will provide some simulation results to evaluate the performance of the framework for the trade-off of the EE and SE. During the simulation, we use the 3GPP spatial channel model under the suburban macro-cell propagation scenario [33,34]. The adopted parameters during the simulation are shown in the Table 1 below for clarity [35].

Table 1. Simulation setup parameters.

Parameters	Values
Path loss	$-110$ dB
Number of users K	4
Weight for each user in the system’s SE	$\frac{1}{K}$
Number of RIS reflecting units N	8
Number of BS antennas M	4
The reciprocal of the power amplifier efficiency at the BS $\mu$	5
The reflection efficiency of the RIS $\eta$	$0.8$
The noise variance at the users ${\sigma }_0^2$	$-130$ dBm
Static power consumption of each user $P_k$	10 dBm
Hardware dissipated power at the BS $P_{\mathrm{BS}}$	40 dBm
Per-element static power at the RIS $P_n$	20 dBm

The average convergence performance of the proposed algorithm is illustrated in Figure 2. The result demonstrates that the convergence is achieved with a small number of iterations.

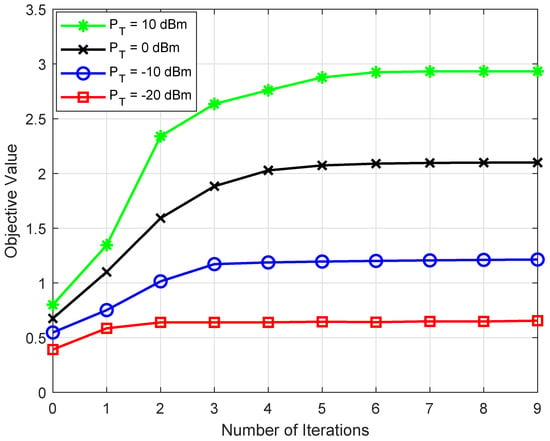
Figure 2. Average convergence performances versus the number of iterations for $a=0.5$.

The EE-SE trade-off curves attained by the algorithm framework under different values of BS power constraint $P_{\mathrm{T}}$ and weight a are shown in Figure 3. Obviously, EE-SE trade-offs under different weighting factors are similar to each other when the value of $P_{\mathrm{T}}$ is small, approximately when $P_{\mathrm{T}}<20$ dBm, as all available power of BS can be fully utilized and both EE and SE are maximized when $P_{\mathrm{T}}$ is small. Therefore, changes in values of a have little impact on the EE-SE trade-off when $P_{\mathrm{T}}$ is small. When $P_{\mathrm{T}}$ gets high, the EE-SE trade-offs under different a differ greatly. It is observed that the increasing of a brings about an increase in EE optimization and a decrease in SE, and the decreasing of a causes a decrease in EE and an increase in SE. That is because larger weight is given to EE for larger a, and thus more focus is transferred to EE when conducting the optimization. However, more focus is transferred to the SE optimization when a smaller weight is given to EE for smaller a.

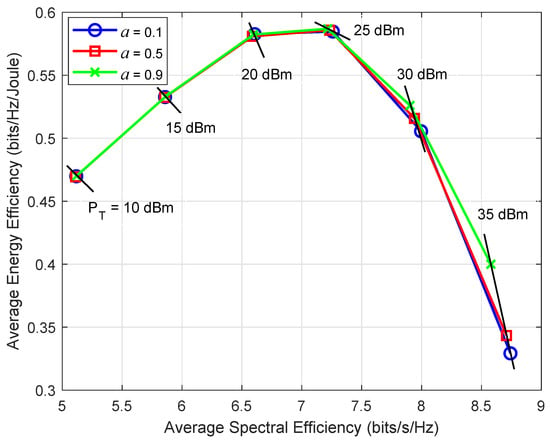
Figure 3. Average EE-SE trade-offs with different a under different transmit power budgets $P_{\mathrm{T}}$.

In Figure 4, we show the EE-SE trade-offs of the system under the condition of $a=0.5$. In order to illustrate the necessity of jointly optimizing the transmit precoding matrix and the phase shift values for optimizing the system SE and EE, the results of the EE-SE trade-off is provided in a baseline case. In the baseline, the phase shift values at the RIS are given randomly and are not optimized. It can also be observed that under the same transmission power constraint $P_{\mathrm{T}}$ of the BS, the EE and SE results of the joint optimization are greater than those of the baseline, respectively. It indicates that jointly optimizing the transmit precoding matrix and the phase shift values is beneficial for improving the SE and EE of the system.

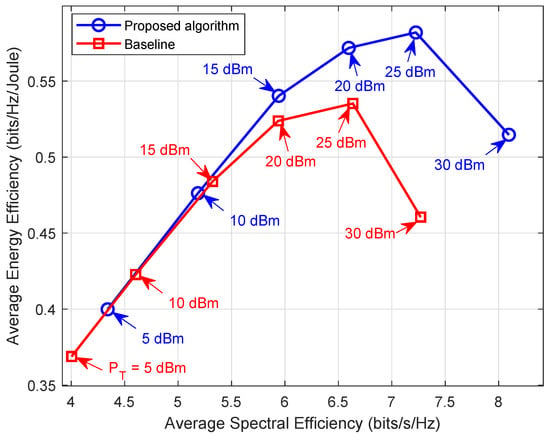
Figure 4. Average EE-SE trade-offs under proposed algorithm and baseline, with $a=0.5$.

5. Conclusions

A RIS-aided multi-user MISO downlink system was investigated in this paper. An optimization model was used to design the transmit precoding matrix at the BS and the phase shift values at the RIS to conduct the maximization of the weighted sum of EE and SE, considering the power constraint at the BS, RIS’s RC with constant modulus, and RIS’s phase shifters with continuous values. We finally attained EE-SE trade-off under different circumstances by changing the value of the weight factor and got the closed-form solution of phase shift values at the RIS, while the optimal precoding matrix was obtained through the standard convex optimization algorithms. Simulations results illustrated that the presented optimization algorithm possesses fast convergence rates under different values of the power budget at the BS. It also showed that the optimization over the RC of RIS could significantly improve the EE and SE of the system.