Slope Compensation and Bifurcation in a DC-DC, Single-Input, Multiple-Output, CMOS Integrated Converter Under Current-Mode and Comparator-Based Hybrid Control

Abstract

Single-Input, Multi-Output (SIMO) converters present significant challenges when operated under current-mode control, due to their strongly non-linear dynamics and susceptibility to bifurcation phenomena. To mitigate the effects on the converter’s steady-state, a double slope compensation solution is proposed. The compensation parameters play a critical role in shaping the system dynamics and rejecting the susceptibility to bifurcation. This paper proposes a detailed analysis methodology to investigate the design parameter space regarding the slope compensations with respect to bifurcation phenomena. The approach is validated on a CMOS integrated converter, where theoretical predictions are compared to the simulation results of a full transistor-level model of the circuit.

1. Introduction and State of Art

In the microcontroller (MCU) ecosystem, the innovation is driven by computation speed, power efficiency, and the integration of complex analog functions such as analog-to-digital converters (ADCs) or radio frequency (RF) transmitters [1]. A key advancement has been the integration of switch-mode power supplies (SMPSs), which reduce the bill of materials by eliminating external companion components, reduce the overall footprint and enhance both computation speed and energy efficiency. The latest MCUs feature at least three distinct power domains: digital glue, memories, and RF peripherals. Each power domain requires a different voltage level and power demand. A potential next step in power management integration is the use of a single-input multiple-output (SIMO) SMPS [2,3], as it can supply multiple domains using a single (off-chip) inductor. However, the implementation and stability analysis of such a topology are more complex compared to those of a standard one-output SMPS.

As the SIMO converter is a nonlinear system, subharmonic oscillations are likely to emerge. This phenomenon is characterized by the voltage outputs presenting a pattern at a frequency different from the switching frequency, generally a submultiple. Instead of returning to its initial state at the end of each switching cycle, the system alternates between multiple states over multiple switching cycles before possibly settling back to its initial state, which increases the time horizon of the system response. Moreover, in DC-DC power converters, the appearance of subharmonic oscillations is linked to the type of implemented control: hysteretic-based and current-mode control are more sensitive to the phenomenon than voltage-mode control, as an example. In power supplies, subharmonic oscillations lead to an increase in the inductor current and output voltage ripples. Consequently, the efficiency is eventually reduced compared to a DC-DC converter operating in a stable pattern, and components are more stressed, as mentioned in [4].

Stability issues and bifurcation analyses in the case of single-input single-output (SISO) DC-DC buck converters are extensively covered in the literature. In [5], multiple stability analysis methods are proposed.

Discrete-time modeling of a SISO DC-DC converter can be performed, as explained in [6,7]. Based on the discrete converter model, iterative simulations in the steady state can be conducted to determine the inductor current at the start of each switching cycle. If this current varies, the simulation results can then be plotted as bifurcation diagrams [8,9].

Circuit parameters, supply voltage, and output reference voltage directly impact the possible onset of a bifurcation phenomenon. In [10,11], the effective equivalent series resistance (ESR) of the output capacitor is used as the bifurcation parameter to plot bifurcation maps. In [8,12], bifurcation diagrams are provided concerning the equivalent series inductances (ESL). The supply voltage impact is also studied in [4,13,14], while the output voltage reference impact is addressed in [8,9,10].

In the context of SISO DC-DC converters with current-mode control, a commonly used approach to mitigate subharmonic oscillations is to add a compensating ramp to the image voltage of the sensed inductor current. Adaptive slope compensation that scales with the supply voltage or the output voltage level is proposed in [6,11,15,16]. The main advantage of an adaptive ramp over a fixed ramp is that it alleviates overcompensation when the output voltage is low [7]. In current-mode-controlled converters, transient performances are degraded when overcompensation occurs. Moreover, the compensating ramp slope can be used as the bifurcation parameter to plot bifurcation maps [12].

Further mathematical analyses are performed in [12,13,17,18]. Based on the discrete model of the SISO DC-DC converter, the local stability of the converter is determined by the eigenvalues of a state-space matrix. However, this methodology cannot be applied to a SIMO DC-DC converter due to the increased complexity of the system when more than one output is supplied.

A discrete model is derived for the single-input dual-output (SIDO) DC-DC converter in [19,20,21,22]. Simulations are conducted to obtain bifurcation maps. Similarly to the SISO converter, many circuit parameters impact the bifurcation phenomenon. In [21], the compensating ramp slope is considered as the bifurcation parameter. In [22], the impact of the output loads and the controller characteristics on the bifurcation phenomenon are studied.

In [19,23], an adaptive slope, similar to the one proposed in [22], is implemented in a SIMO converter with current-mode control to damp sub-harmonic oscillations.

This paper is organized as follows. First, Section 2 summarizes the scope of the analysis and the related original contributions regarding the state of the art. Then, the power stage of the vehicle three-output SIMO DC-DC converter and its control strategy are detailed in Section 3. Simulations of a full transistor-level model of the vehicle converter, designed in a ST-18nm-process, highlight that unwanted sub-harmonic oscillation phenomena occur during steady-state operation. In Section 4, a theorical analysis is provided on the implementation of double slope compensation to damp any tendency toward sub-harmonic oscillations. Stability conditions related to the circuit parameters are then derived to achieve a stable pattern. Afterward, the impacts of compensating ramp slopes and circuit parameters on the bifurcation phenomenon are verified through system-level simulations of the transistor-level model in Section 5. Finally, the double slope compensation scheme is implemented in a ST-18nm-process. Simulations of the full transistor-level model of the SIMO DC-DC converter are conducted in Section 6 to validate the effectiveness of the proposed solution to damp any tendency toward sub-harmonic oscillations.

2. Context of the Study

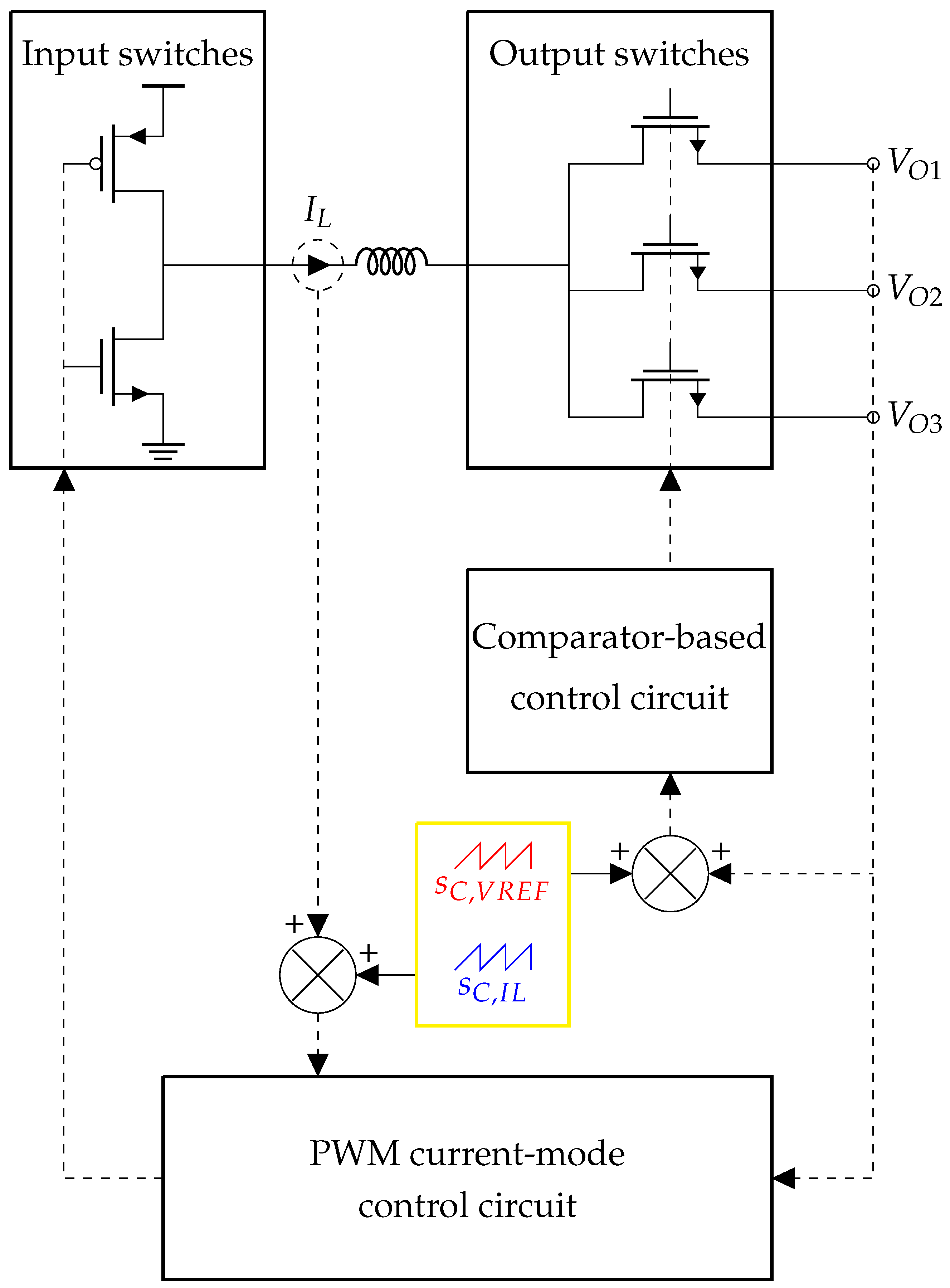
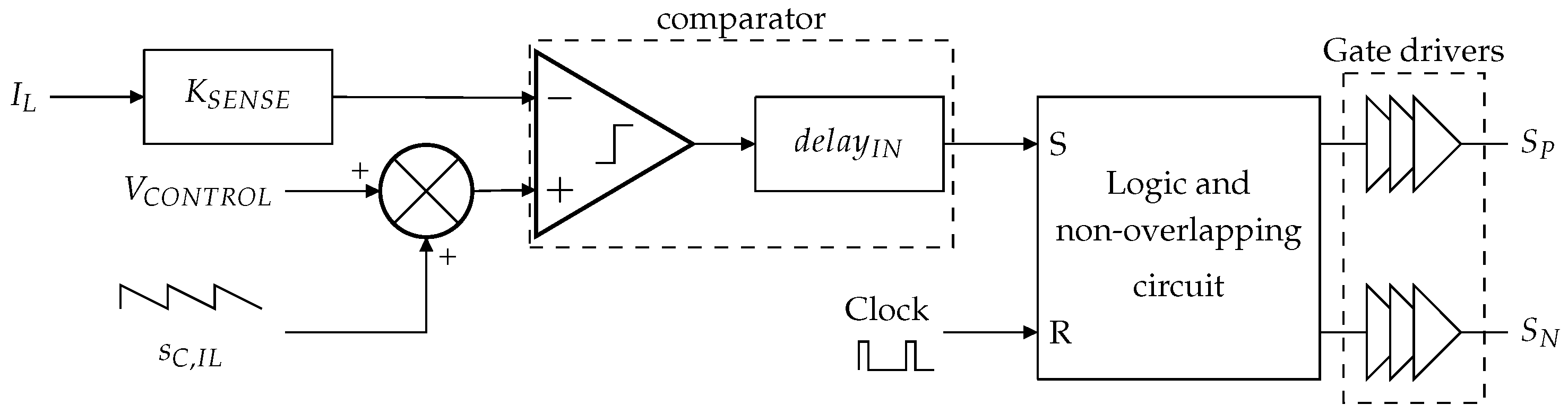
A simplified schematic of the SIMO converter with a double slope compensation strategy is shown in Figure 1. The compensating ramp, $s_{C,IL}$, is applied to the current-mode control loop for input switches, while $s_{C,VREF}$ impacts the comparator-based control loop for output switches. The double slope compensation strategy is proposed to counterfight the possible onset of sub-harmonic oscillations in the DC-DC three-output SIMO converter. The need for two compensating ramps is explained with separating the input switches and output switches control loops: PWM current-mode control and comparator-based control are respectively implemented. This choice of control is justified by previous work [24], which benchmarks several control strategies from the literature applied to the SIMO DC-DC converter in the context of the MCU power supply. Among all strategies studied, our proposed solution provides the most satisfying transient performance, which is a key metric of interest.

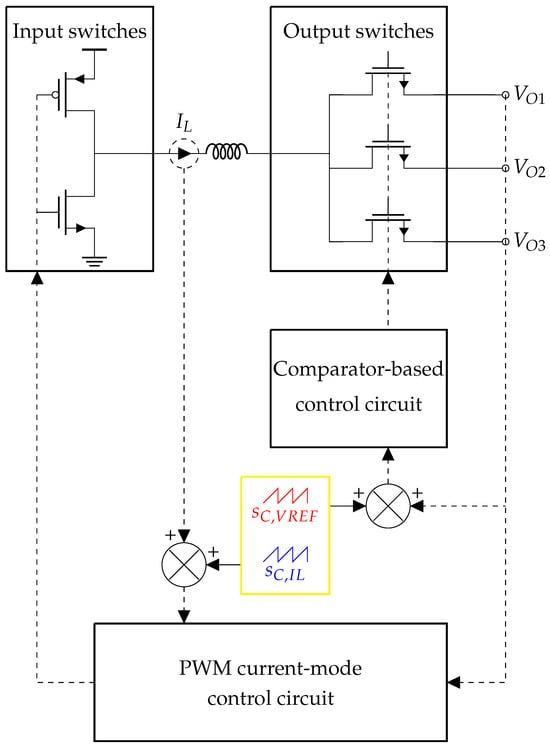
Figure 1. Double slope compensation implementation on a DC-DC SIMO converter.

The SIMO power stage and the control circuit are detailed in the following Section 3, while the implementation of the compensating ramps and the associated stability issues, topics not addressed in the previous work, are introduced in Section 4.

3. The SIMO Converter

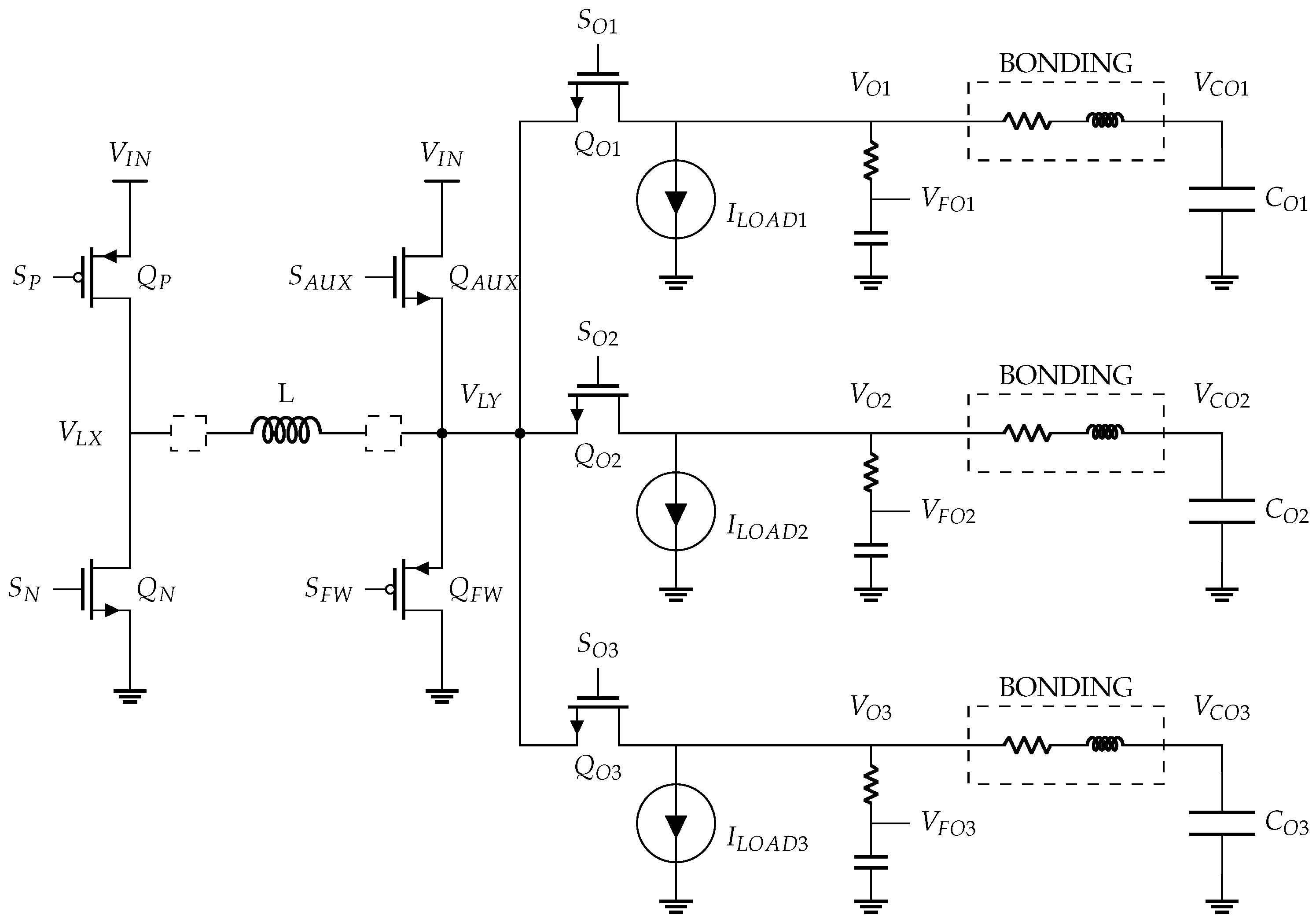
Figure 2 pictures the core schematic of the considered SIMO converter. The CMOS integrated converter is designed for 3 output voltages, $V_{O1}$, $V_{O2}$ and $V_{O3}$, regulated at 0.8 V, 1.0 V and 1.5 V, respectively. The nominal input supply voltage is set at 3.0 V, and only one inductance and three capacitors are necessary off-chip. Each output drives a current load: $I_{LOAD1}$ varies up to 500 mA, while $I_{LOAD2}$ and $I_{LOAD3}$ vary up to 200 mA respectively.

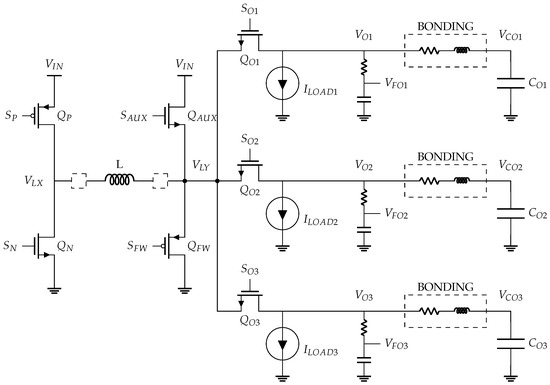
Figure 2. 3-output SIMO DC-DC converter power stage.

3.1. Power Stage Architecture

The off-chip inductor, L, is charged and then discharged over each operating period, by connecting the node, $V_{LX}$, to the input DC supply voltage or the ground node, respectively. This connection is performed by the two input switches, $Q_P$ and $Q_N$. The inductor current is dynamically split among the three outputs by three switches, $Q_{O1}$, $Q_{O2}$ and $Q_{O3}$ respectively. An off-chip capacitor is added in parallel on each output and acts as a charge tank when the output is not connected to the inductance with the goal to limit the voltage ripple.

A free-wheeling switch, $Q_{FW}$, is implemented between the ground node and the node $V_{LY}$. The latter switch can be considered as a fourth output switch that is used to derive an excess of inductance current that would otherwise overcharge the outputs above their reference voltage. An auxiliary current source is realized with the transistor, $Q_{AUX}$, added in parallel with the inductor regarding the input switches. When a load transient occurs, this source supplies additional current to assist the SMPS until the control feedback loop adjusts the current provided by the inductor to the outputs. The circuit is a simple copy of a fixed bias current, which means the source current amplitude is fixed and constant.

The connections between the outputs of the SIMO converter and the off-chip capacitors suffer from parasitic resistances and inductances due to the bonding of the off-chip power network. Thus, the swap of the inductor current from one output to another causes an important ripple on the output voltages. An RC low-pass filter is used to reject the effect of the ripple due to bonding parasitics on the output voltage for the purpose of voltage sensing with minimal impact on the control loops. Thus, the sensed output voltages $V_{FO1}$, $V_{FO2}$ and $V_{FO3}$ are obtained.

3.2. Control Scheme

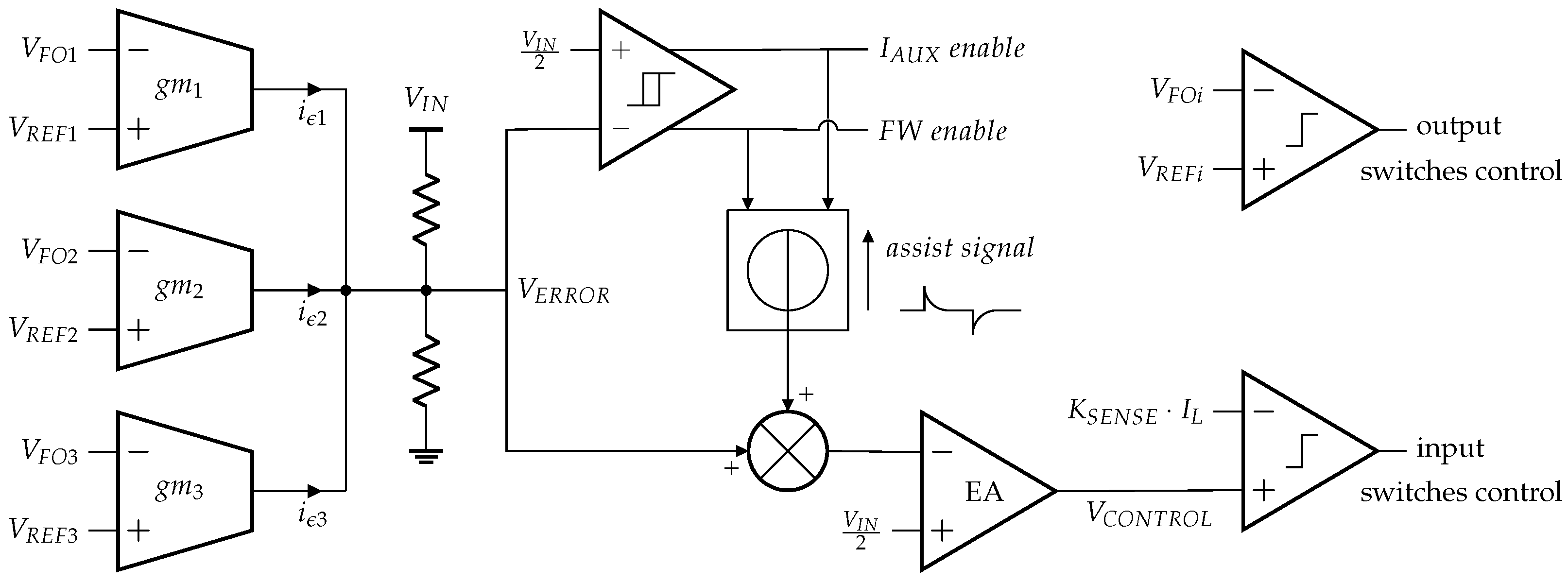
A current-mode control and a comparator-based hybrid control are proposed to operate the converter in Figure 2 as pictured in Figure 3. The first loop matches the average current flowing through the off-chip inductor to the sum of the instantaneous required output load currents. The second loop adjusts the duty cycle of the output switches, $Q_{Oi}$, to split optimally the inductor current into the three outputs. The first control loop is managed by a PWM peak-current mode control. The sensed output voltages $V_{FO1}$, $V_{FO2}$ and $V_{FO3}$ are forwarded to transconductance cells $g{m}_1$, $g{m}_2$ and $g{m}_3$, respectively. Depending on the difference between the actual output voltages and their nominal references, error currents are generated and summed into a resistor bridge to create the voltage, $V_{ERROR}$. A Proportional-Integral (PI) corrector is implemented to generate the voltage, $V_{CONTROL}$. The latter voltage signal is compared to a sensed image of the inductor current to control the duty cycle of input switches. The current sensing is performed by a current copy circuit on the high-side switch, $Q_P$. The second control loop implements a comparator-based voltage control. When the off-chip inductor charge or discharge phase starts, the first output is supplied until it reaches its reference voltage. Then the second output is supplied, and finally the third one is supplied until the inductor charge or discharge phase ends and the cycle restarts. When the free-wheeling switch is enabled, the charge of the third output stops when its reference is reached and the remaining current is sent to the ground node until the end of the period. This comparator-based control has the advantage for reducing the cross-regulation phenomenon on the output switches, compared to traditional PWM-based control. When a transient occurs, the duty cycles of the output switches immediately adapt instead of being negatively impacted by the response delay of a PI controller. Loads transients are detected by a hysteretic comparator on the voltage, $V_{ERROR}$. The auxiliary current source and free-wheeling switch are enabled when $V_{ERROR}$ reaches the hysteretic thresholds. Moreover, an assistance signal is added to the error amplifier input to speed up its response during a transient.

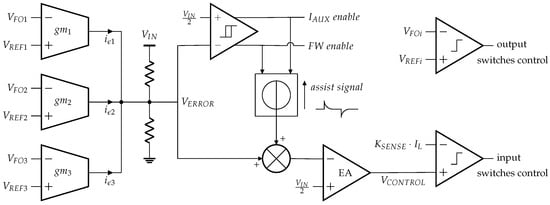
Figure 3. SIMO DC-DC converter proposed control.

3.3. Issue

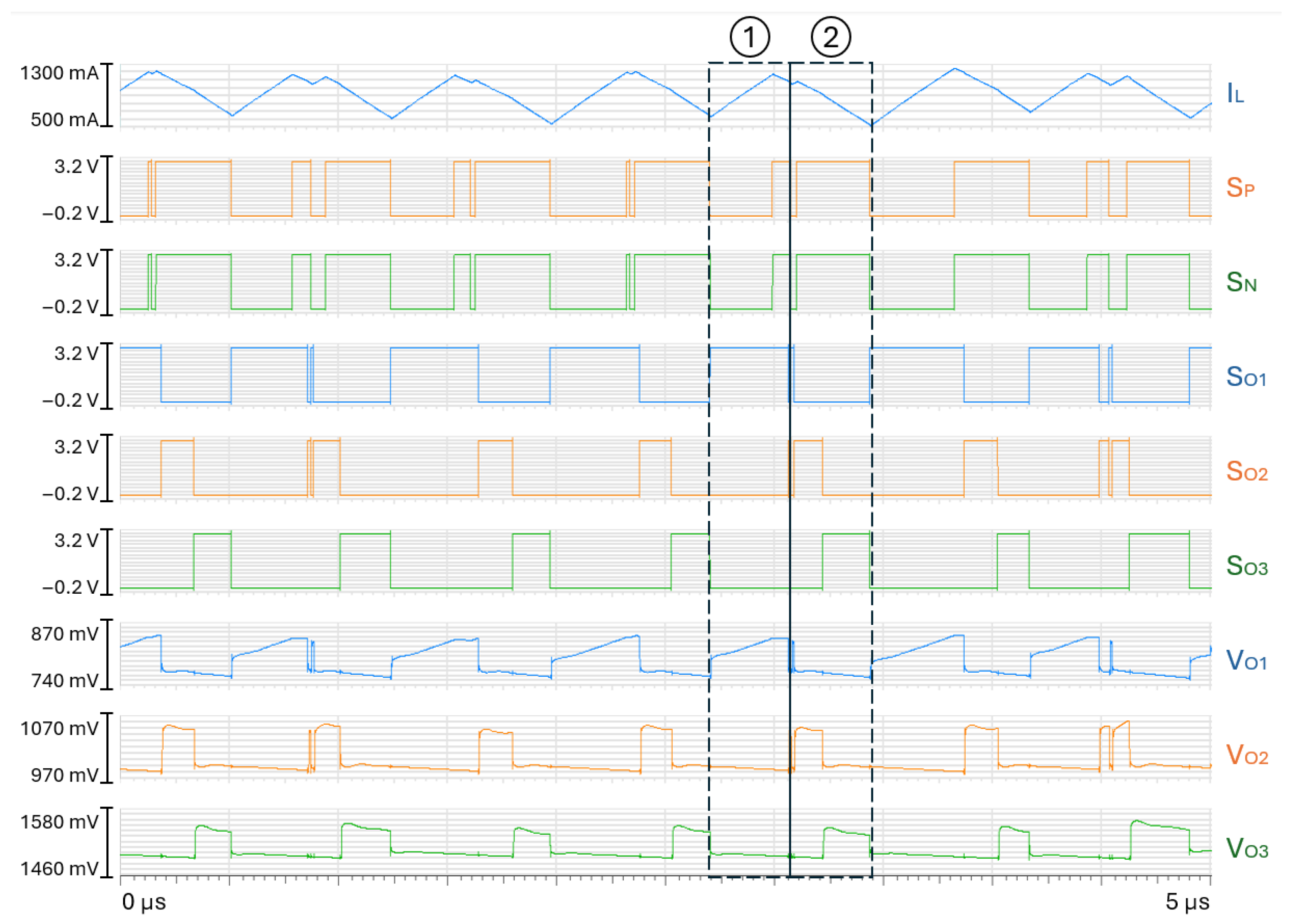
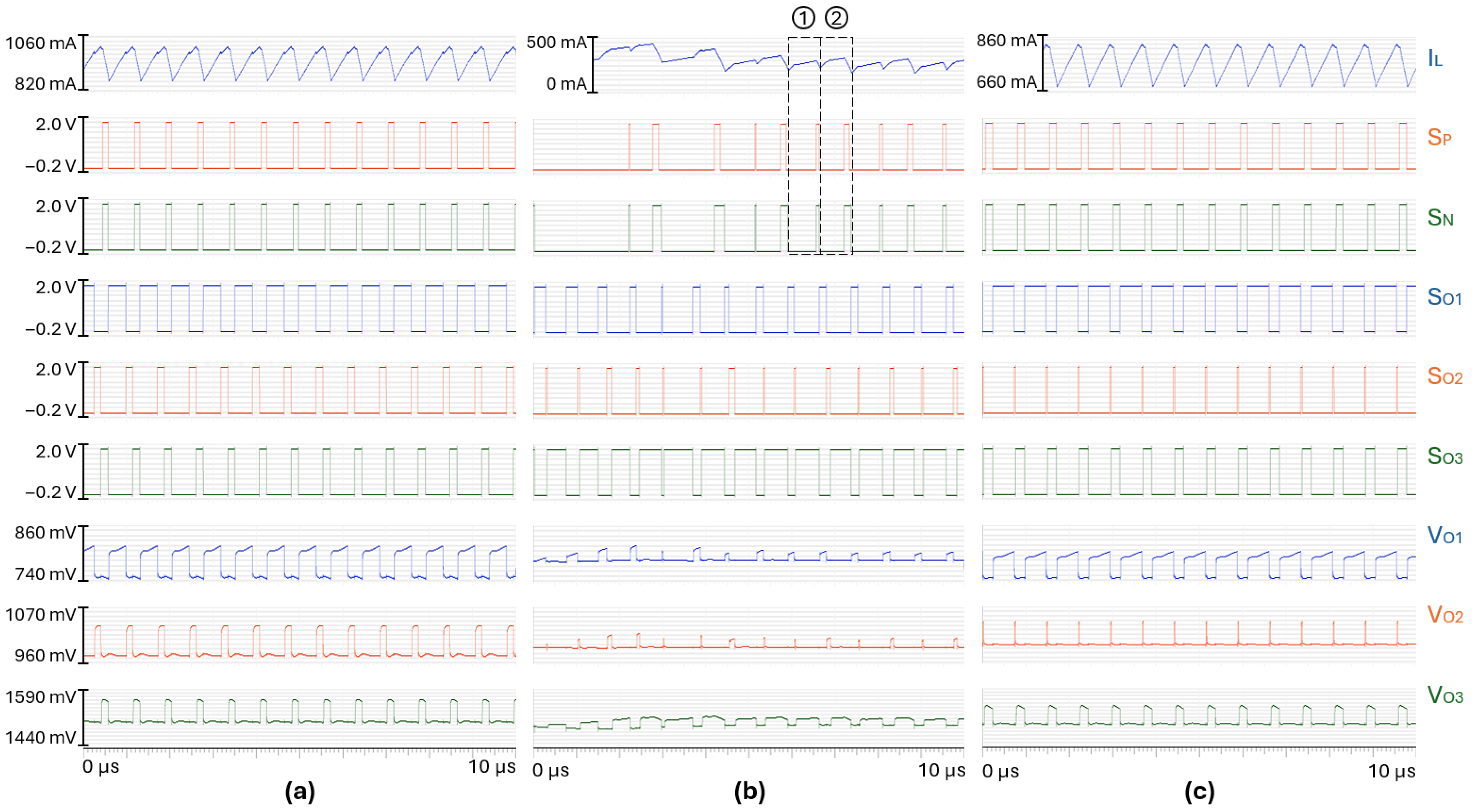
The SIMO DC-DC converter presented in the previous subsection is implemented in a ST-18nm-process. Figure 4 shows the main waveforms from the simulation of the transistor-level circuit model in a steady-state scenario under nominal supply voltage and maximum loads: $V_{IN}$ is set to 3.0 V, $I_{LOAD1}$ equals 500 mA, $I_{LOAD2}$ and $I_{LOAD3}$ equal 200 mA. The switching frequency is 2.73 MHz, which corresponds to a period T = 366 ns.

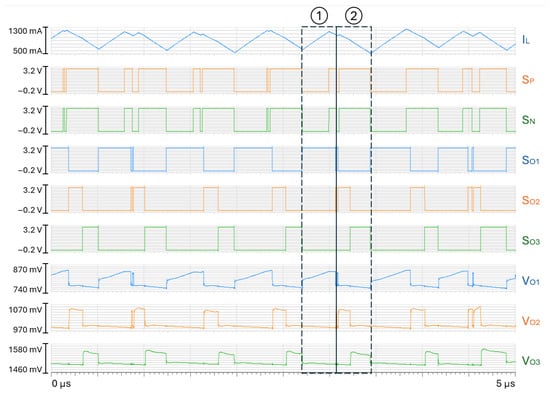
Figure 4. Sub-harmonic oscillations occuring during a steady-state scenario.

Sub-harmonic oscillations are visible on the inductor current waveform: as an example, the valley current is different between the two consecutive switching cycles (1) and (2) that are identified in Figure 4. The issue is characterized by alternating narrow and wide pulses on the switches’ signals $S_P$ and $S_N$, and the duty cycles of the switches are not the same from one period to the next.

The output voltage waveforms are also 2T-periodic rather than T-periodic. For the whole switching cycle ➀, only the first output is supplied. Then, all outputs are supplied during the switching cycle ➁, and this pattern repeats itself. However, the mean duty cycle of the input and output switches, over multiple periods, remains constant: the average inductor current is equal to the sum of output current loads on average and is correctly split between both 3 outputs. Thus, outputs are still regulated to their reference voltages. However, the phenomenon is not suitable as it is not controlled.

The inductor current ripple and the respective output voltage ripples are higher than in the case of a SIMO converter operating without sub-harmonic oscillations. The efficiency of power conversion is slightly degraded.

A bifurcation has occurred in the converter operation, shown by a more complex pattern of the transistor control signals than the expected nominal ones. During the converter design flow, it is mandatory to explore the conditions of the bifurcation onset prior to fabrication. It is the main interest of subsequent sections.

4. Theorical Analysis of Sub-Harmonic Oscillation Damping

Sub-harmonic oscillations, which occur when the duty cycle is higher than 50% in a Single-Input Single-Output (SISO) current-controlled DC-DC Buck converter, are a well-known phenomenon. The common solution presented in the state-of-the-art consists of adding a compensating ramp to the image voltage of the sensed inductor current. The same effect is achieved by adding a compensating ramp with a negative slope to the output signal of the error amplifier compared to the current image.

The DC-DC converter proposed in this article delivers multiple output voltages, simultaneously regulated at different voltage levels. In the literature, conventional control strategies for SIMO converters usually involve full PWM-based control for both input and output switches [2]. Thus, it is possible to apply a compensating ramp similarly to the one in a SISO converter to remove any tendency toward subharmonic oscillations.

However, the control strategy presented in this article has two different control loops: a current-mode control loop for the input switches and a comparator-based control loop for the output switches. This configuration has the advantage of minimizing the cross-regulation phenomenon compared with conventional control strategies. The drawback is that subharmonic oscillations can occur because of parallel control loops. Thus, a solution is proposed with double slope compensation, one for each control loop.

4.1. Implementation of a Double Slope Compensation

In the SIMO converter, the first control loop regulates the inductor current similarly to that of a PWM current-mode converter. Thus, it is possible to implement a slope compensation on that control loop as shown in Figure 5.

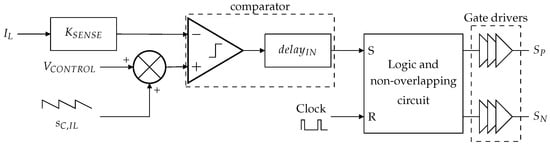
Figure 5. Slope compensation implementation on the input switch control loop.

The image voltage of the sensed inductor current, $K_{SENSE}$·$I_L$, with $K_{SENSE}$ the current sensor gain, is compared to the sum of a negative slope compensating ramp, $s_{C,IL}$, and the error amplifier output voltage, $V_{CONTROL}$. For simplicity in the analysis, the comparator is modeled as an ideal comparator and a delay block, $dela{y}_{IN}$, representing the switching latency of a real comparator. The comparator output is forwarded to the SET input of a logic glue and a non-overlapping circuit, while the SMPS clock signal drives the RESET input. This circuit generates the command signals of the input switches, $Q_P$ and $Q_N$, which are propagated through gate drivers to $S_P$ and $S_N$, respectively.

In the case of the proposed SIMO converter, a comparator-based control is applied to operate the output switches, $Q_{Oi}$. This implies that the duty cycle of an output switch can be different from one period to another, as long as the mean duty cycle remains coherent with the supplied load current and the inductor current. This opens the possibility of subharmonic oscillation phenomenon on the output voltages. Moreover, since the three outputs have their own and unique voltage levels, different duty cycle values from one period to another lead to different inductor current slopes from one period to another. Thus, it is another cause of subharmonic oscillation in the inductor current.

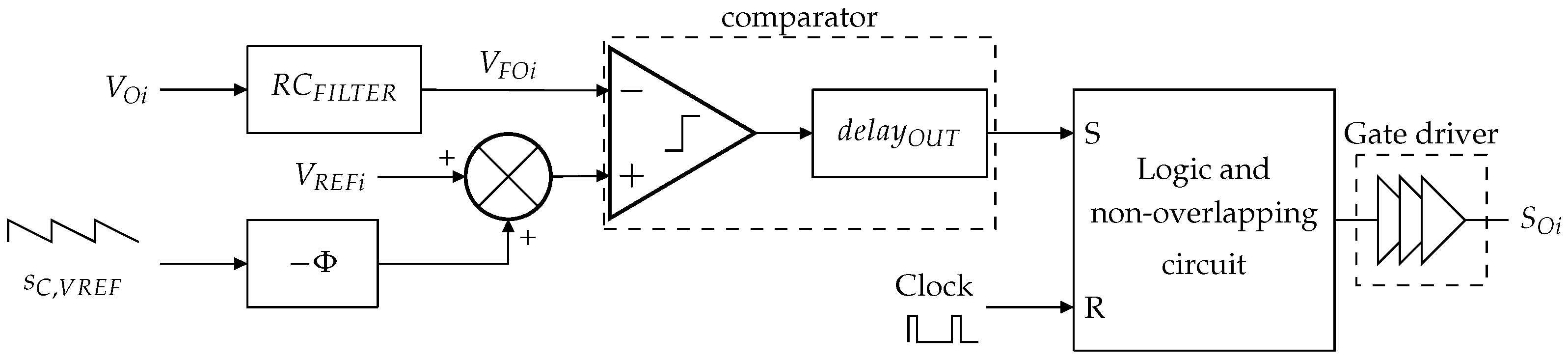
To address this issue, a compensation ramp is added to the output reference voltage as shown in Figure 6.

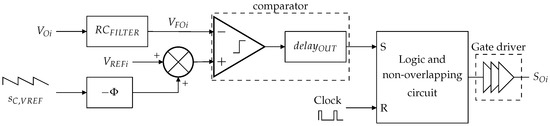
Figure 6. Slope compensation implementation on the output switch control loop.

The output voltages $V_{Oi}$ are filtered by a low-pass filter, $R{C}_{FILTER}$, to avoid glitches linked to parasitic resistance of the bonding. These glitches are visible on the output voltage waveforms in Figure 4. An offset occurs on an output voltage when its switch is turned on. The sensed output voltages, $V_{FOi}$, are compared to their respective reference voltages, $V_{REFi}$, plus a compensating ramp, $s_{C,VREF}$. For the sake of simplification during the analysis, the comparators are modeled by an ideal comparator and a delay block, $dela{y}_{OUT}$. The comparator outputs are connected to the SET inputs of logic glues and non-overlapping circuit, while the SMPS clock signal drives the RESET inputs. The circuit generates the duty cycles of the output switches and prevents any overlapping that would cause a shortcut between two outputs. Finally, the latter duty cycles are applied to $S_{Oi}$ through gate drivers.

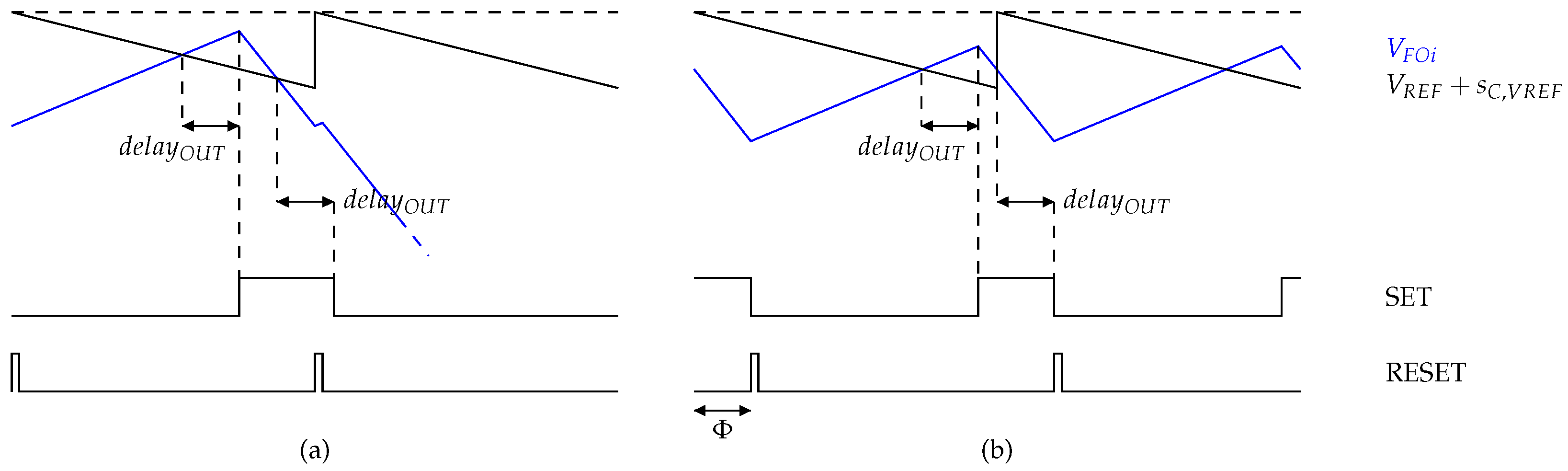
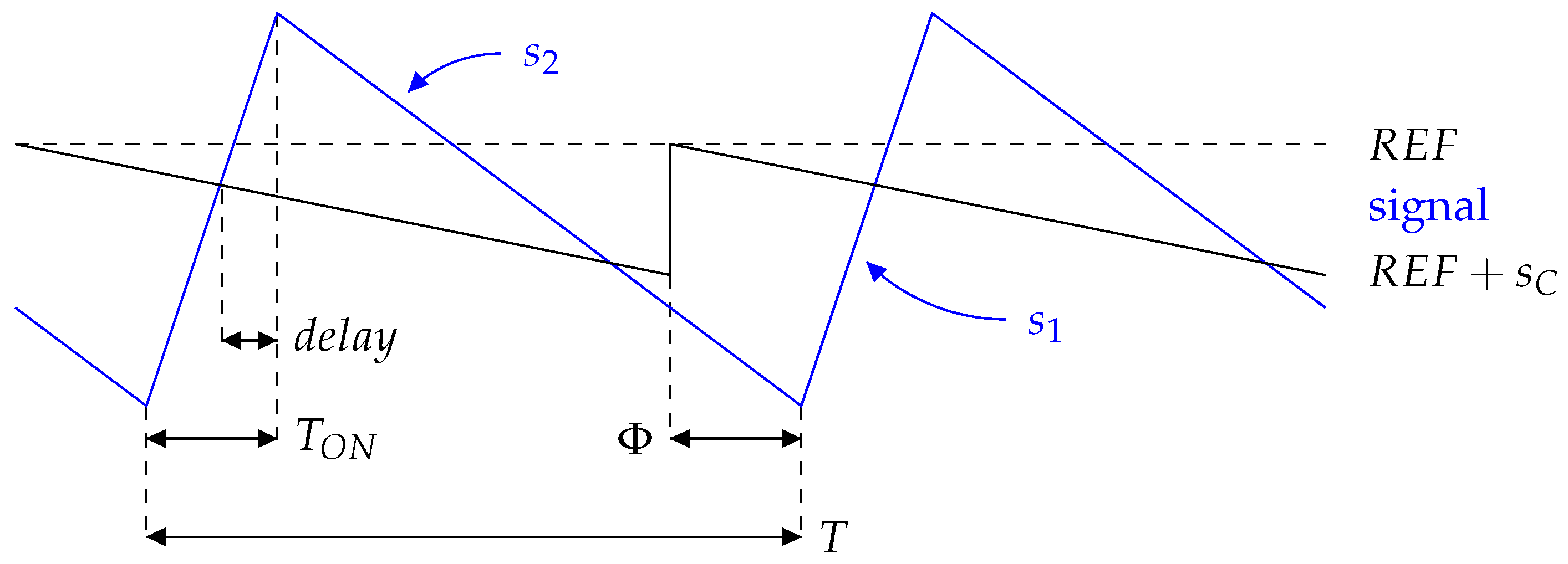
As shown in Figure 6, a phase shift, $\mathsf{\Phi }$, is added between the reset of the compensating ramp and the reset of the logic glues and non-overlapping circuit, to avoid both resets at the same time. Without this phase shift, if the sensed output voltage, $V_{FOi}$, becomes lower than its reference minus the slope compensation just before the logic glues and non-overlapping circuit is reset, the comparator’s propagation time, $dela{y}_{OUT}$, causes an incoherence between the comparator inputs and the output fed to the logic glues. This phenomenon is highlighted in Figure 7a. The RESET of the logic glues happens while the SET is still in a high state, even if the sensed output voltage is already lower than its reference minus the compensating ramp. As a result, the output voltage will decrease during the whole next period, then it will increase again, and this phenomenon will be repeated. It causes an unwanted pattern of subharmonic oscillations. This issue is also addressed in [25].

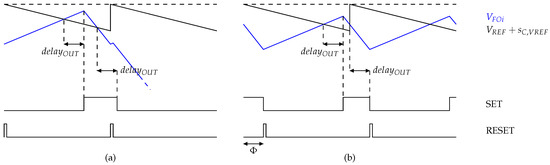
Figure 7. (a) Issue without phase shift and (b) benefit of the added phase shift.

Figure 7b shows the benefit of the phase shift between the compensating ramp reset and the logic glues reset, leading to a stable operation. During a steady-state, the signal is guaranteed to be lower than its reference when the compensating ramp resets. If the phase shift is higher than the propagation time (or delay) of the comparator, the comparator output is guaranteed to be coherent with respect to its input when the logic glues reset signal occurs. In [26], single-edge and dual-edge modulation techniques are applied to generate different PWM phase shifts, and the bifurcation diagram shows that the bifurcation phenomenon is impacted by the phase shift.

For the input switches control loop, the phase shift is not needed if the reset signal of the logic glues is implemented with a width slightly larger than $dela{y}_{IN}$. The priority of the reset over the set makes it possible to ignore the comparator output until it is matched again with its inputs when its propagation time has ended.

The drawback of increasing the reset signal width is that it forces the power stage in a fixed state for the whole reset signal duration. With the control strategy presented in this article, this fixed state corresponds to the charge of the first output, while the inductor current rises as the node, $V_{LY}$, is connected to the supply voltage, $V_{IN}$.

Through transistor-level simulation of the SIMO converter, $dela{y}_{IN}$ is estimated at 20 ns, while $dela{y}_{OUT}$ is estimated at 65 ns. When the first output load is relatively low compared to the total load supplied by the converter, it is not feasible to replace the phase shift in the output switches control loop with a logic glues reset signal wider than $dela{y}_{OUT}$. Doing so forces a fixed state for at least 65 ns during each period, causing the first output voltage to gradually rise significantly above its reference.

4.2. Damping Sub-Harmonic Oscillations

A theoretical analysis is proposed to demonstrate the suitable slope value needed by the compensating ramps to damp any tendency toward sub-harmonic oscillations.

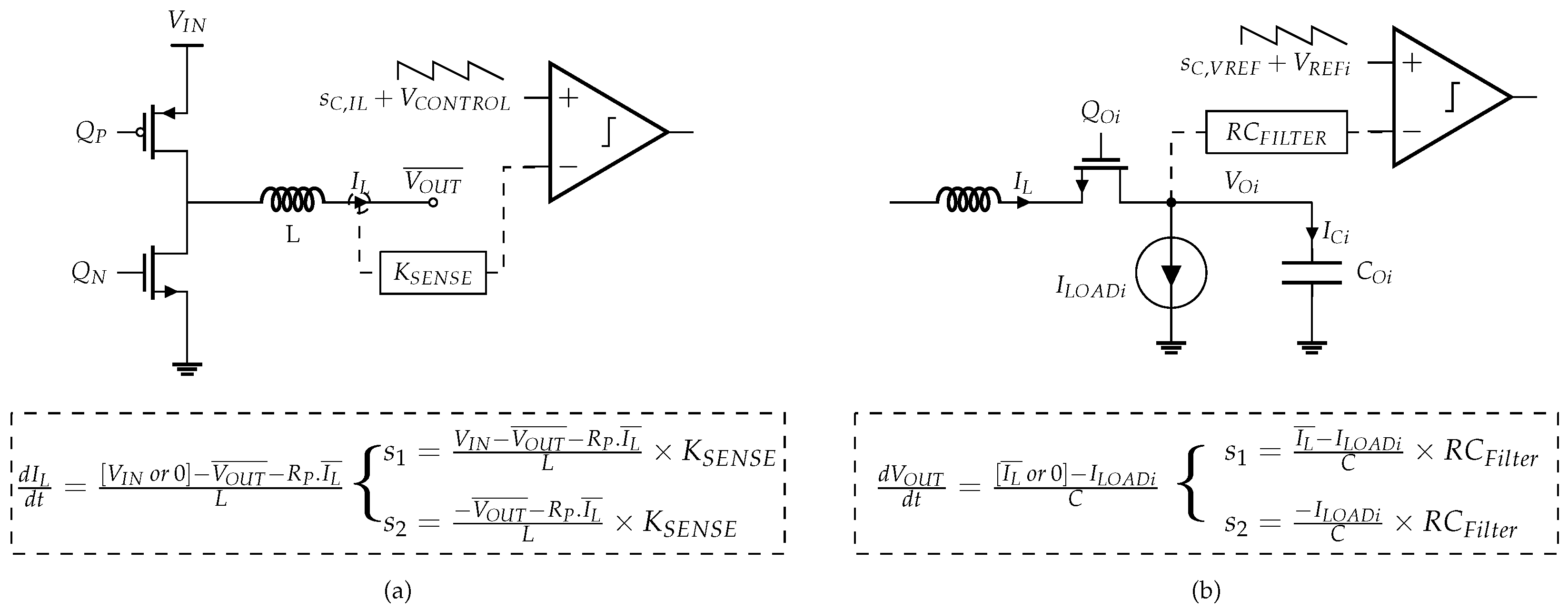
Figure 8 shows which signals from the SIMO converter power stage are compared to a reference signal plus a compensating ramp, for the input and output switches’ control loops, respectively, in Figure 8a and Figure 8b. Moreover, the expression of the slopes, $s_1$ and $s_2$ of the fed signals, are given as a function of the circuit parameters, voltages and currents.

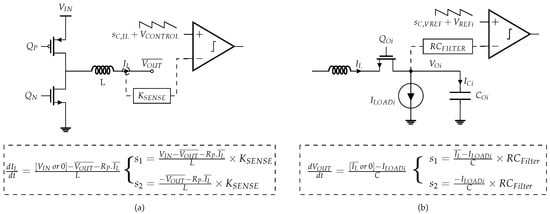
Figure 8. (a) Input switches’ control and (b) output switches’ control signals fed to comparators respectively.

The resistance, $R_P$, corresponds to the sum of the input and output switches, inductor and bonding parasitic resistances. Its value is estimated at 280 m$\mathsf{\Omega }$. The weighted output voltage, $\overline{V_{OUT}}$, in Figure 8 is evaluated from the nominal conditions of operation of the converter (1), while the inductor current is averaged by the mean value, $\overline{I_L}$, (2):

$$\overline{V_{OUT}}={\displaystyle \frac{I_{LOAD1}·V_{O1}+I_{LOAD2}·V_{O2}+I_{LOAD3}·V_{O3}}{\overline{I_L}}}$$

(1)

$$\overline{I_L}=I_{LOAD1}+I_{LOAD2}+I_{LOAD3}$$

(2)

For the bifurcation analysis, generalized figures and equations will be given, with only one signal and one compensating ramp represented at a time, as shown in Figure 9. However, the analysis is suited for the compensating ramp, $s_{C,IL}$, applied to the input switches’ control loop, and for the compensating ramp, $s_{C,VREF}$, applied to the output switches’ control loop.

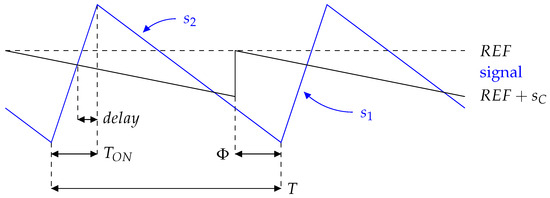
Figure 9. Steady-state pattern without sub-harmonic oscillations.

• For the input switches, REF refers to the error amplifier output, $V_{CONTROL}$, the compensating ramp, $s_C$, corresponds to a ramp of slope, $s_{C,IL}$, the delay corresponds to the propagation delay, $dela{y}_{IN}$ of the input comparator, and the signal corresponds to the sensed inductor current, $K_{SENSE}$·$I_L$.
• For each output switch, REF refers to the output reference voltage, $V_{REFi}$, the compensating ramp, $s_C$, corresponds to a ramp of slope, $s_{C,VREF}$, the delay corresponds to the propagation, delay $dela{y}_{OUT}$ of an output comparator, and the signal corresponds to the sensed output voltage, $V_{FOi}$.
• The signals’ slopes, $s_1$ and $s_2$, are pictured in Figure 8a and Figure 8b respectively.

The slope compensation is useful only if a stable steady-state pattern (without sub-harmonic oscillations) exists for a given operating point. Figure 9 shows a steady-state waveform with no sub-harmonic oscillations: the signal value at the end of the period T is the same as its starting value. The signal rises with a slope, $s_1$, for the duration, $T_{ON}$, and drops with a slope, $s_2$, for the duration, ($T-T_{ON}$).

A stable pattern without sub-harmonic oscillation, where the signal returns to its initial value at the end of the period T, can be described by the following inequality (3):

$$T_{ON}·s_1=-(T-T_{ON})·s_2$$

(3)

where $T_{ON}$ corresponds to the time needed by the signal to reach the reference, REF, minus the slope compensation, plus the comparator delay. Moreover, the propagation delay of the comparator must be lower than the rising time, $T_{ON}$, otherwise it would mean that the signal was already above its reference, minus the compensating ramp, at the start of a period. Thus, to guarantee a stable pattern without sub-harmonic oscillations, the comparator design is conditioned. Based on Equation (3), it is possible to express the design condition of the comparator’s propagation delay with respect to the rising slope and falling slope of the signal, as the following inequality (4):

$$delay<T_{ON}={\displaystyle \frac{-s_2·T}{s_1-s_2}}$$

(4)

When considering the comparator in the input switches’ control loop and its propagation delay, $dela{y}_{IN}$, the condition in (4) can be reviewed as the one in (5) using the expression of $s_1$ and $s_2$ from Figure 8a:

$$dela{y}_{IN}<{\displaystyle \frac{\overline{V_{OUT}}+R_P·\overline{I_L}}{V_{IN}}}·T$$

(5)

The specification range of the circuit parameters listed from the stability condition in (5) are given in Table 1.

Table 1. Specification range of the circuit parameters.

Parameter	Min	Max
$\overline{V_{OUT}}$	0.8 V	1.5 V
$\overline{I_L}$	0 A	0.9 A
$V_{IN}$	1.6 V	3.6 V

The minimum value for the right-side term in inequation (5) is reached when considering the minimum value of $\overline{V_{OUT}}$, the maximum value of $V_{IN}$ and the averaged inductor current, $\overline{I_L}$, equal to zero. Thus, the stability condition in (5) is satisfied if $dela{y}_{IN}$ is shorter than 74 ns, by numerical application of the converter specifications.

According to simulations of the transistor-level model of the circuit, the propagation delay of the comparator used in the input switches’ control loop, $dela{y}_{IN}$, is around 20 ns, which means that the inequality (5) is always satisfied, with some margin regarding the process variations.

Thus, a stable pattern without sub-harmonic oscillations exists for the output switches’ control loop, with the condition that the slope, $s_1$, remains identical from one switching period to another, as well as $s_2$.

When considering the comparators in the output switches’ control loops and their propagation delay, $dela{y}_{OUT}$, the condition of existence of a stable pattern without sub-harmonic oscillations, as described by the inequality (4), can be reworked as (6) using the slope expressions, $s_1$ and $s_2$, from Figure 8b:

$$dela{y}_{OUT}<{\displaystyle \frac{min\left(I_{LOADi}\right)}{\overline{I_L}}}·T$$

(6)

The propagation delay of the comparators used in the output switches’ control loop, $dela{y}_{OUT}$, is evaluated around 65 ns from simulations. A higher propagation delay than the one of the comparator implemented in the input switches’ control loop is expected: the sensed output voltage ripples are way lower than the sensed inductor current ripple. The stability condition in (6) is satisfied only if the load current at each output is higher than 19.5% of the converter total load current, which is not always the case.

The following analysis will consider the case where the stability condition in (6) is fulfilled and a stable pattern with no sub-harmonic oscillations exists for the three output switches’ control loops, while a solution to manage the cases where (6) is not fulfilled will be presented later on.

4.2.1. StabilityCondition in (6) Is Satisfied

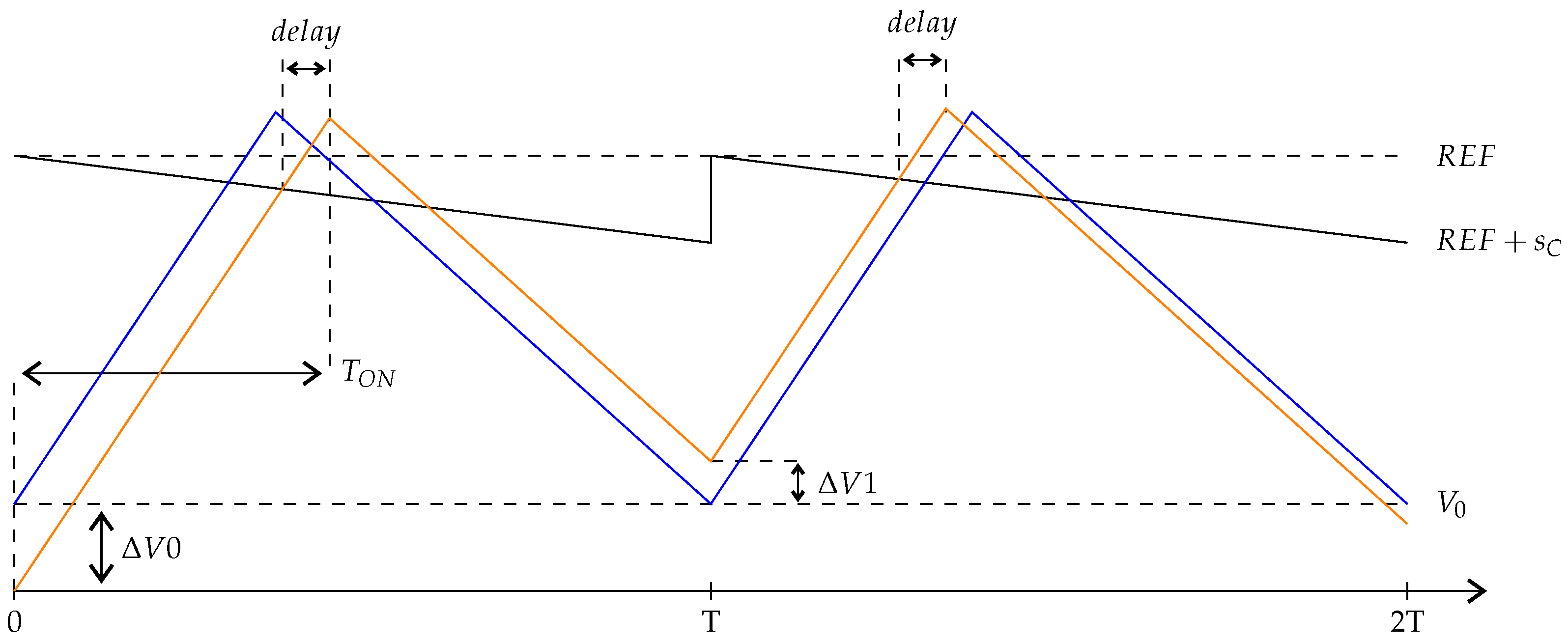
In Figure 10, the blue waveform corresponds to a signal of interest in steady-state condition, i.e., a stable pattern without sub-harmonic oscillations, while the orange waveform starts with an initial perturbation of $\mathsf{\Delta }{V}_0$. During each switching cycle, the signal is rising with a slope, $s_1$, until it reaches its reference minus the compensating ramp of slope, $s_C$. A delay, which corresponds to the comparator delay in the circuit implementation, is considered between the crossing and the start of the signal fall. The signal decreases with a slope, $s_2$, until the next switching cycle starts. The time during which the signal is rising is denoted $T_{ON}$, while the switching period is denoted T. When no sub-harmonic oscillations occur, the signal in blue returns to its initial value, $V_0$ at the start of the next switching cycle, while the perturbed signal in orange reaches $V_0+\mathsf{\Delta }{V}_1$ at the end of the cycle.

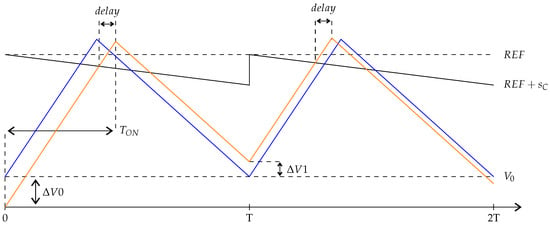
Figure 10. Slope compensation effect in nominal conditions.

Based on Figure 10, the expression of $T_{ON}$ for the perturbed signal comes as (7):

$$T_{ON}={\displaystyle \frac{REF-V_0-\mathsf{\Delta }{V}_0}{s_1-s_C}}+delay$$

(7)

Moreover, the signal value achieved at the end of a switching cycle ($V_0+\mathsf{\Delta }{V}_1$) can be expressed as:

$$V_0+\mathsf{\Delta }{V}_1=V_0+\mathsf{\Delta }{V}_0+s_1·T_{ON}+s_2(T-T_{ON})$$

(8)

Combining Equations (7) and (8) yields:

$$\mathsf{\Delta }{V}_1=\mathsf{\Delta }{V}_0+(s_1-s_2)\left({\displaystyle \frac{REF-V_0-\mathsf{\Delta }{V}_0}{s_1-s_C}}+delay\right)+T·s_2$$

(9)

In the case where no sub-harmonic oscillations occur, i.e., the signal in blue in Figure 10, the initial voltage value in each switching cycle, $V_0$, can be expressed as follows:

$$V_0=REF+(s_1-s_C)\left({\displaystyle \frac{T·s_2}{s_1-s_2}}+delay\right)$$

(10)

Combining Equations (9) and (10) gives a simple expression of $\mathsf{\Delta }{V}_1$, which depends only on the initial perturbation $\mathsf{\Delta }{V}_0$, the signal slopes and the compensating ramp slope:

$$\mathsf{\Delta }{V}_1=\mathsf{\Delta }{V}_0\left(1-{\displaystyle \frac{s_1-s_2}{s_1-s_C}}\right)$$

(11)

The sub-harmonic oscillation phenomenon is damped if the absolute value of $\mathsf{\Delta }{V}_1$ is lower than the absolute value of $\mathsf{\Delta }{V}_0$. Since the slopes $s_2$ and $s_C$ are negative, the damping condition can be written as:

$$s_C<{\displaystyle \frac{s_1+s_2}{2}}$$

(12)

The inequality in (12) gives a general expression of the slope compensation value needed as a function of the rising slope and falling slope of the signal to protect from sub-harmonic oscillation phenomena.

In the SIMO converter, two compensation ramps are implemented. Based on the expressions of $s_1$ and $s_2$ from Figure 8a and Figure 8b respectively, the inequality in (12) can be rewritten as (13) and (14), for the input switches’ control loop and output switches’ control loop respectively.

$$s_{C,I_L}<{\displaystyle \frac{V_{IN}-2\overline{V_{OUT}}-2R_P·\overline{I_L}}{2L}}\times K_{SENSE}$$

(13)

$$s_{C,V_{REF}}<{\displaystyle \frac{\overline{I_L}-2I_{LOAD}}{2C}}\times R{C}_{FILTER}$$

(14)

For a given operating point of the SIMO converter, if the conditions in (5), (6), (13) and (14) are both fulfilled, no sub-harmonic oscillations should be forcasted.

4.2.2. Stability Condition in (6) Is Not Satisfied

The condition in (6) is not fulfilled when the comparator propagation delay of the output switch control loop is longer than the theoretical supply duration needed by the output, which happens when one output current load is relatively low compared to the total current load supplied by the SIMO converter. In [23], this issue is addressed with a skip mechanism, while a phase interchange strategy is applied in [27]. However, both latter strategies are unsuited in the SIMO converter because they can be sources of bifurcation.

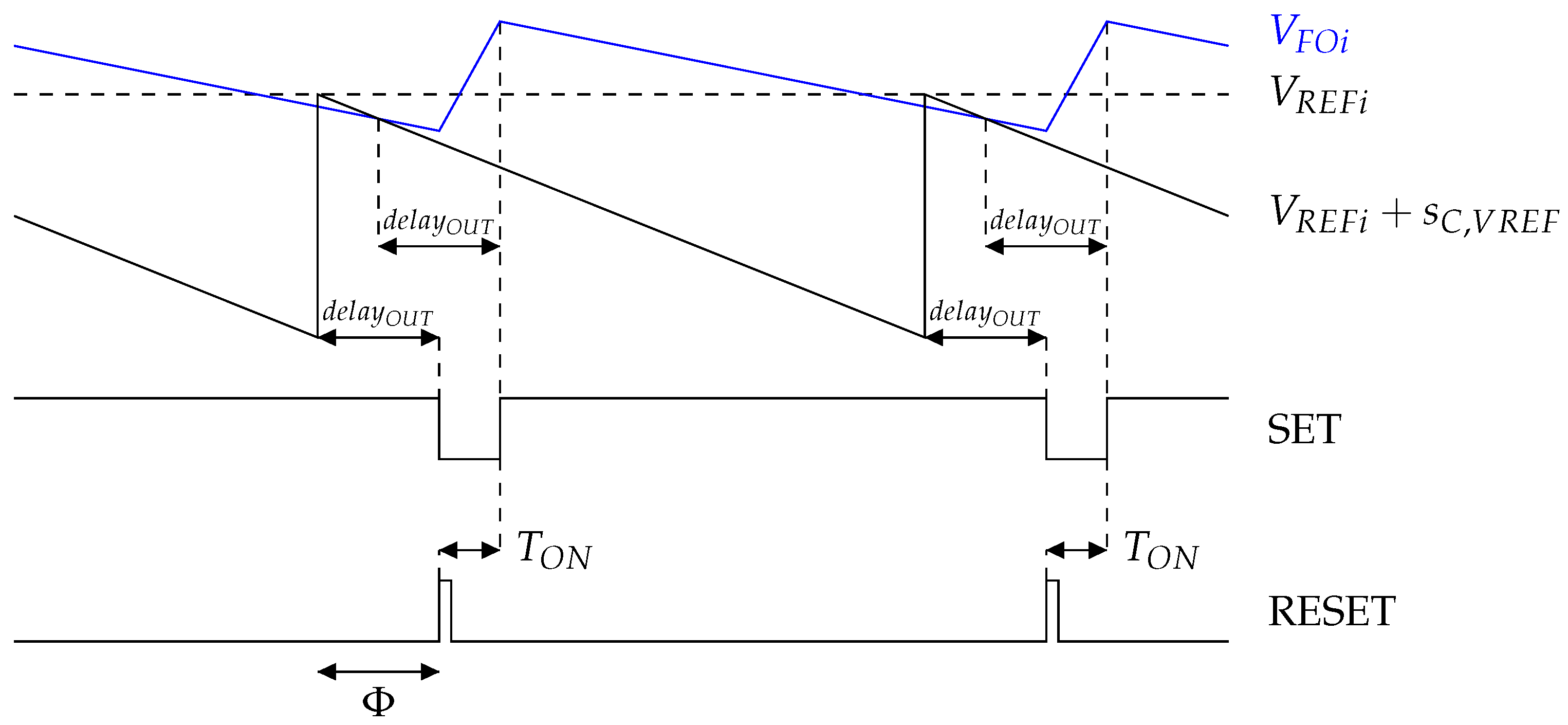
In the present context, it is possible to reach a supply duration lower than the comparator delay if the slope of the compensating ramp, $s_{C,VREF}$, is steeper than the decreasing slope, $s_2$, of the sensed output voltage, as shown in Figure 11.

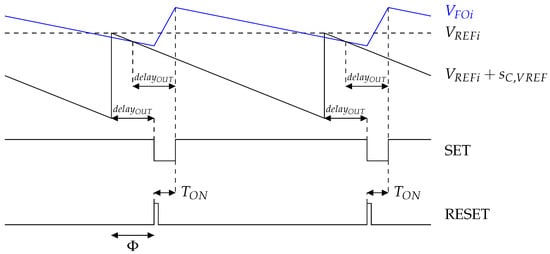
Figure 11. $T_{ON}$ lower than the delay, $dela{y}_{OUT}$.

With a compensation slope steeper than the decreasing slope of the sensed output voltage, $V_{FOi}$, the comparator triggers before the RESET pulse, which allows the supply duration, $T_{ON}$, to be shorter than the delay, $dela{y}_{OUT}$.

If a perturbation affects the signal, $V_{FOi}$, the intersection between the compensation slope and the sensed output voltage is shifted by $\mathsf{\Delta }{V}_0$ in value. It is possible to express the shift of the perturbed signal after one period T with respect to the slopes, $s_1$, $s_2$, and $s_{C,VREF}$, and the initial perturbation as expressed in (15):

$$\mathsf{\Delta }{V}_1=\mathsf{\Delta }{V}_0\left(1+{\displaystyle \frac{s_1-s_2}{s_{C,VREF}-s_2}}\right)$$

(15)

The sub-harmonic oscillation phenomenon is damped if the absolute value of $\mathsf{\Delta }{V}_1$ is lower than the absolute value of $\mathsf{\Delta }{V}_0$. Since $s_{C,VREF}$ is steeper than $s_2$, and since $s_1$ is higher than the absolute value of $s_2$, the damping condition can be written as (16):

$$s_{C,VREF}<{\displaystyle \frac{3·s_2-s_1}{2}}$$

(16)

Based on the expression of $s_1$ and $s_2$ from Figure 8b, (16) can be expressed as (17):

$$s_{C,VREF}<-{\displaystyle \frac{\overline{I_L}+2·I_{LOADi}}{2C}}\times R{C}_{FILTER}$$

(17)

For a given operating point of the SIMO converter, if the conditions in (5), (13) and (17), are both satisfied, no sub-harmonic oscillations should be forecasted.

5. Impact of Circuit Parameters on the Onset of Bifurcation

In the previous section, the stability conditions in (13), (14) and (17), were defined. They describe the minimum slope values required for the compensating ramps in order to damp sub-harmonic oscillations in the considered SIMO converter. However, many simplifications were considered that might have an impact on the boundaries found between sub-harmonic oscillation onset and stable patterns.

• The inductor current slope values are computed based on the weighted output voltage, $\overline{V_{OUT}}$, evaluated from the nominal conditions of the converter. In reality, the inductor current slopes depend on the output currently supplied: it is not a single value slope.
• Only the static gain of the current sensing filter, $K_{SENSE}$, is considered. The cut-off frequency of the filter is supposed to be well above the switching frequency of the converter so that the high frequency behavior is neglected and the current image is not distorted.
• The inductor current flowing through the output switches is averaged from the sum of the output current loads, and the current ripple is not considered in the output switches’ control loops and voltage drop on parasitic resistance, $R_P$, as well.
• The output voltage sensing filters, $R{C}_{FILTER}$, are considered as ideal low-pass filters with a gain of 1, that reject any voltage perturbations caused by the parasitic inductances and resistances from the bonding and the output capacitors.

Thus, the stability conditions described before need to be verified using a more accurate approach.

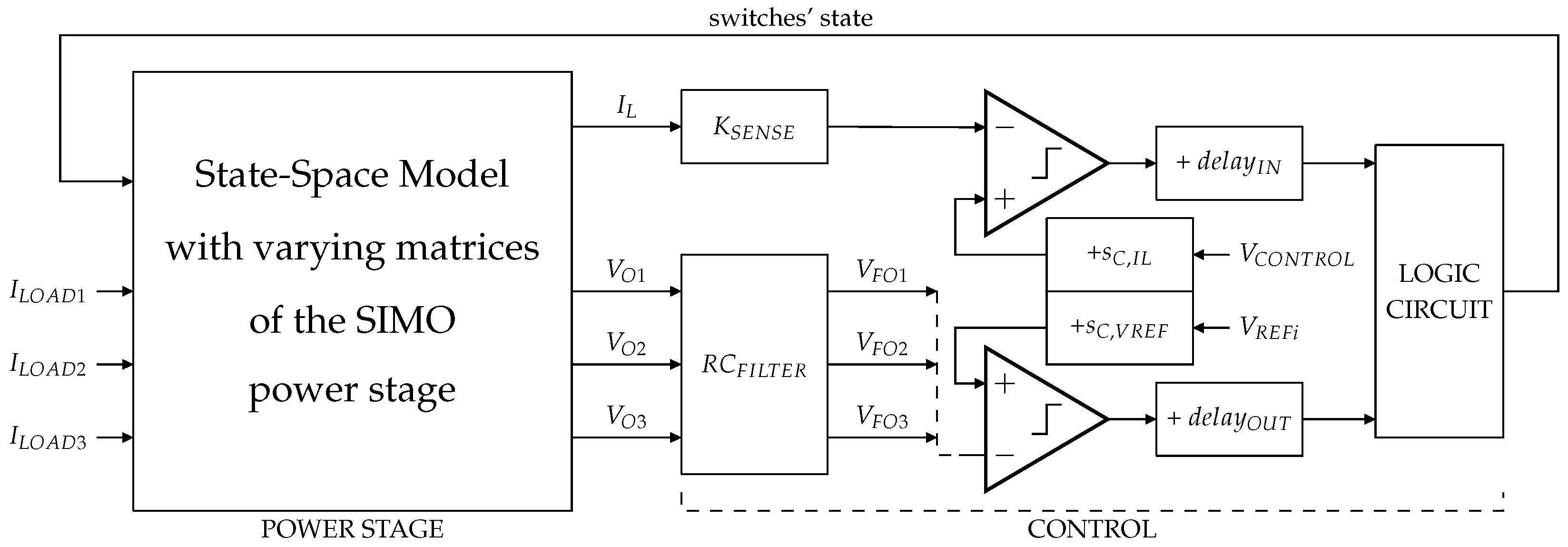
5.1. Modeling Using Matlab/Simulink

The SIMO converter architecture is implemented at system-level in Matlab/Simulink (version R2021b), as shown in Figure 12.

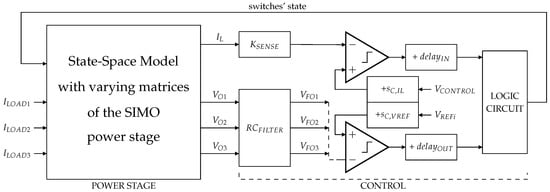
Figure 12. Implementation in Matlab/Simulink.

The power stage is represented by a state-space model, with adequate matrices depending on the switches’ states. The current sensor gain, $K_{SENSE}$, and the time-constants of output voltage sensing filters, $R{C}_{FILTER}$, are implemented as first-order transfer functions. The comparators are modeled as ideal comparator blocks and delay blocks. The input switches’ control loop in Figure 3 is implemented with transfer function blocks and basic mathematical blocks, yielding the signal $V_{CONTROL}$. The compensation ramp slopes, $s_{C,IL}$ and $s_{C,VREF}$, are added to $V_{CONTROL}$ and $V_{REFi}$ respectively. Finaly, a logic circuit determines the switches’ states depending on the comparators’ outputs.

In order to validate the inequalities in (5), (6), (13), (14) and (17), the SIMO converter is simulated in steady-state considering eight different load cases, as listed in Table 2:

Table 2. Load cases considered in the system-level simulations.

Case	${\mathit{I}}_{\mathit{LOAD}1}$	${\mathit{I}}_{\mathit{LOAD}2}$	${\mathit{I}}_{\mathit{LOAD}3}$
#1	500 mA	200 mA	200 mA
#2	500 mA	200 mA	20 mA
#3	500 mA	20 mA	200 mA
#4	500 mA	20 mA	20 mA
#5	50 mA	200 mA	200 mA
#6	50 mA	200 mA	20 mA
#7	50 mA	20 mA	200 mA
#8	50 mA	20 mA	20 mA

For each load case, multiple simulations are conducted, with simulation parameters changing from one simulation to another. The objective of the following results is to evaluate the impact of slope compensation across system parameters. So only one circuit parameter is considered as the primary simulation parameter, the other ones remain with their nominal values. Only one compensating ramp slope is considered as the second simulation parameter. The comparator delays are set to $dela{y}_{IN}$ = 20 ns and $dela{y}_{OUT}$ = 65 ns. The nominal supply voltage $V_{IN}$ is 3.0 V. The current sensing filter $K_{SENSE}$ has a static gain of 1.05, and a cut-off frequency, $f_{CUT,KSENSE}$ = 16 MHz. The low-pass RC filter inserted in the output voltage sensing scheme has a static gain of 1.0 and $f_{CUT,RCFILTER}$ = 400 kHz. The results will be presented as 2D-maps, with the circuit parameter range on the x-axis and the compensating ramp slope range on the y-axis. A yellow point on the 2D-map indicates that at least one of the load cases from Table 2 leads to sub-harmonic oscillation phenomenon for the considered set of simulation parameters. A blue point on the 2D-map indicates that for all load cases in Table 2, a stable pattern is achieved for the considered set of simulation parameters. The observed boundary between stable operation patterns and sub-harmonic oscillation appearance is compared to the theoretical predictions described by the stability conditions determined in the previous section.

5.2. Slope Compensation on the Input Switches’ Control Loop

The previous section shows the factors that can impact the boundaries between stable operation patterns and sub-harmonic oscillation appearance regarding the input switches’ control loop: the supply voltage, the current sensor characteristics, the comparator delay and the relative output load currents compared to the total current load supplied by the SIMO converter.

5.2.1. Impact of the Supply Voltage, $V_{IN}$

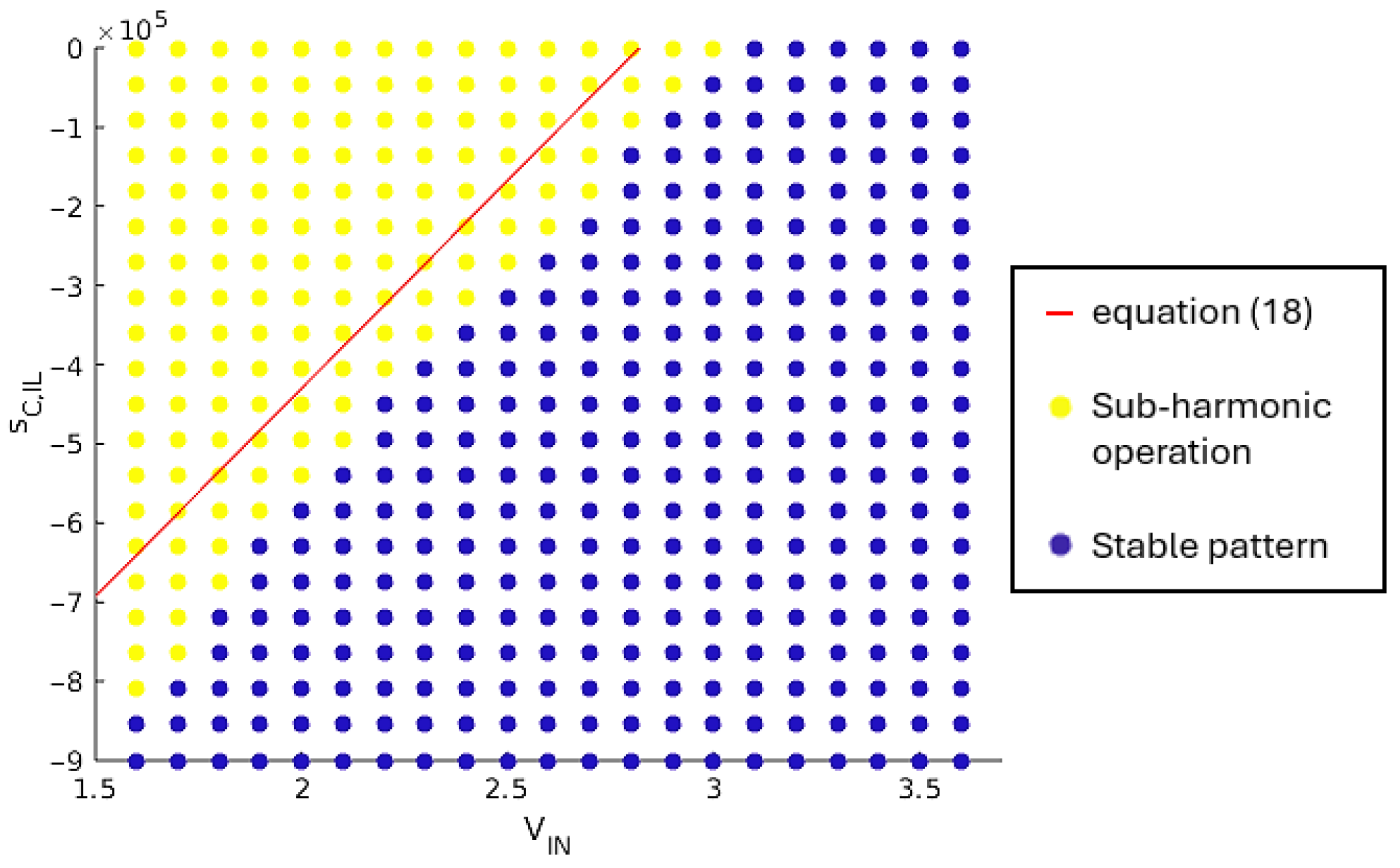
Considering the circuit parameters with their respective nominal values and $V_{IN}$ in the range [1.6 V; 3.6 V], the stability condition in (5) is fulfilled for all load cases. Thus, the mandatory condition for damping any tendency toward sub-harmonic oscillations is to satisfy the second stability condition (13).

When considering the supply voltage $V_{IN}$ as a simulation parameter, the load case #7 in Table 2 corresponds to the critical case: it is the load case that theoretically requires the highest compensating ramp slope. If a stable pattern is achieved for the load case #7, it should be achieved for all other load cases.

Load case #7, which corresponds to light loads on $V_{O1}$, $V_{O2}$ and large load on $V_{O3}$, was found to be the critical case when evaluating the numerical application of the stability condition in (13) for all load cases in Table 2, and considering the nominal values for circuit parameters, except for $V_{IN}$ which is the simulation parameter. For the load case #7, the stability condition is rewritten as (18).

$$s_{C,IL}=V_{IN}·5.25·{10}^5-1.48·{10}^6[V/s]$$

(18)

This boundary equation is verified through simulation. The supply voltage, $V_{IN}$, varies in the range [1.6 V; 3.6 V] with a 100 mV step. The compensation ramp slope, $s_{C,IL}$, varies between 0 V/s and 9·10⁵ V/s. The maximum value for this slope corresponds to an amplitude of 300 mV with 3 MHz switching frequency of the SIMO converter. Figure 13 shows the obtained results. For a given set of ($V_{IN}$, $s_{C,IL}$), a yellow point means that at least one load case is leading to sub-harmonic oscillations, while a blue point means that a stable operation pattern is achieved by the SIMO converter for all load cases in Table 2.

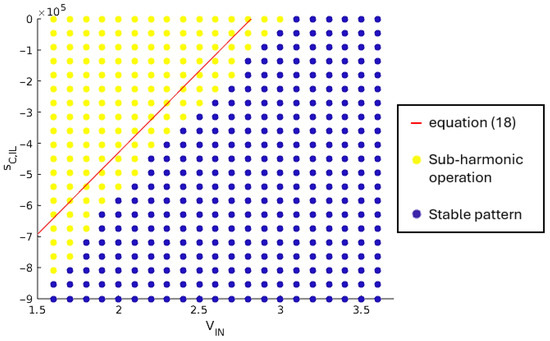
Figure 13. Correlation between $s_{C,IL}$ and $V_{IN}$ regarding sub-harmonic oscillations’ damping.

Similar behavior is observed between the theorical boundary Equation (18) and the simulation results, with a constant shift. This difference can be explained by the simplifications made to determine the theorical equation: $K_{SENSE}$ is considered as a static gain without high frequency behavior, inductor current and weighted output voltage are averaged over one period.

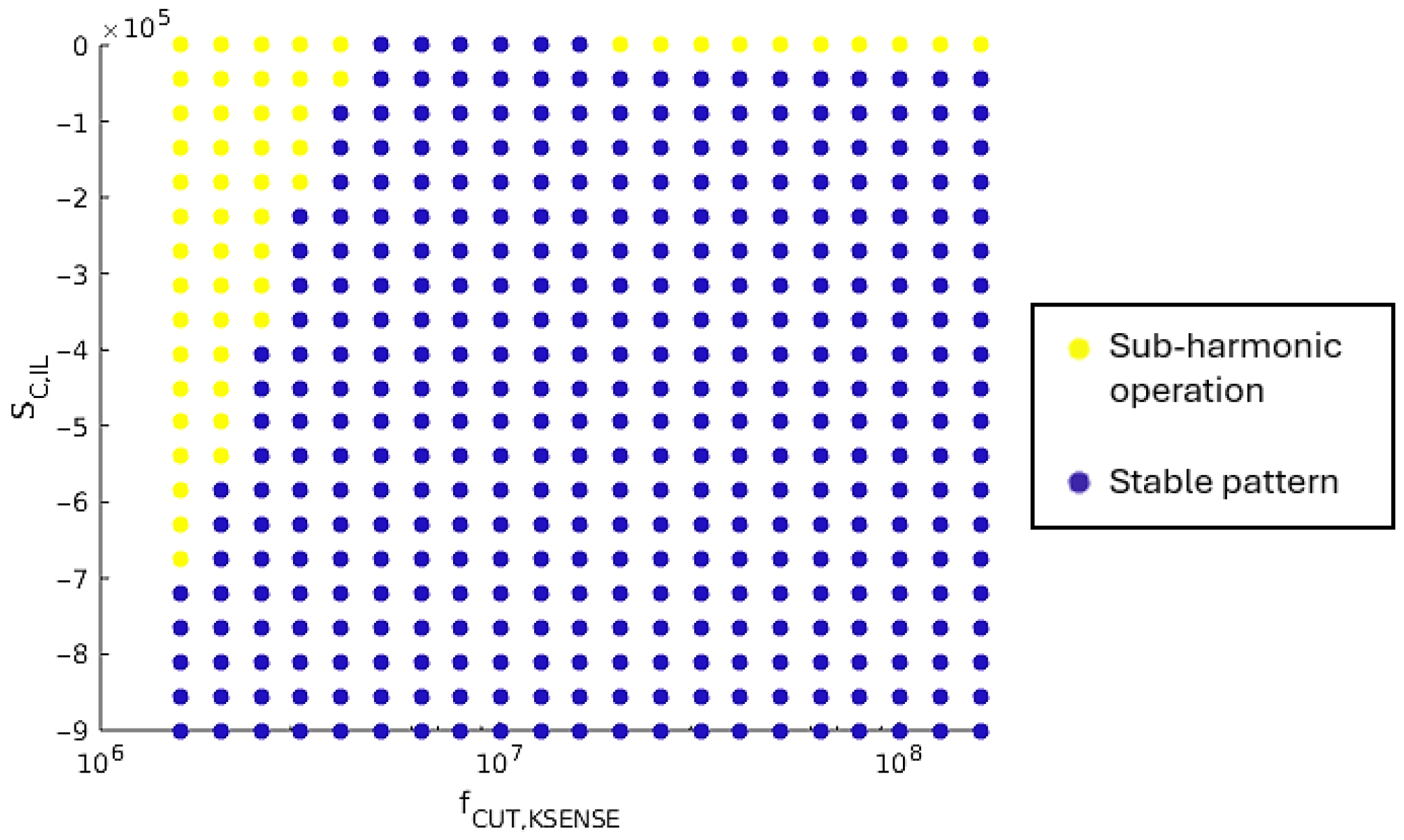
5.2.2. Impact of the Current Sensing Transfer Function, $K_{SENSE}$

As shown by the inequality in (13), the current sensing transfer function, $K_{SENSE}$, has a direct impact on the slope needed by the compensation ramp, $s_{C,IL}$, to damp any tendency toward sub-harmonic oscillations. Considering a first-order transfer function, its cut-off frequency has an impact on the current sensing gain for high-frequency signals. Moreover, an additional delay is introduced in the input switches’ control loop depending on the transfer function phase. Simulations are conducted to analyse this effect: the cut-off frequency varies between 1.6 MHz and 160 MHz, while $s_{C,IL}$ varies between 0 V/s and 9·10⁵ V/s.

Figure 14 shows the results obtained, with a logarithmic x-axis scale. For a cut-off frequency higher than 5 MHz, a stable operation pattern is achieved for all load cases, except for few points when no compensation ramp is applied: a steady-state with period doubling is reached by the SIMO converter. In this case, even a very low compensation ramp slope value is enough to make the converter converge to a stable operation pattern. For a cut-off frequency lower than 5 MHz, the value of the compensation ramp slope increases as the current sensing cut-off frequency decreases. The lower the cut-off frequency, the more distorted the sensed current image.

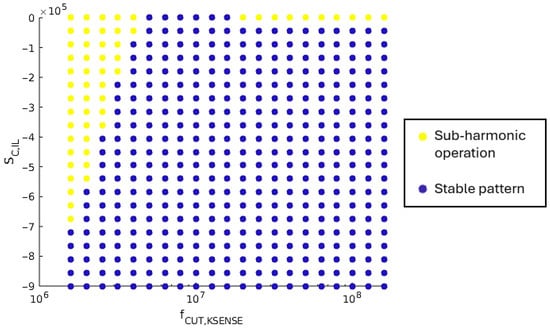
Figure 14. Correlation between $s_{C,IL}$ and $K_{SENSE}$ regarding the sub-harmonic oscillation damping.

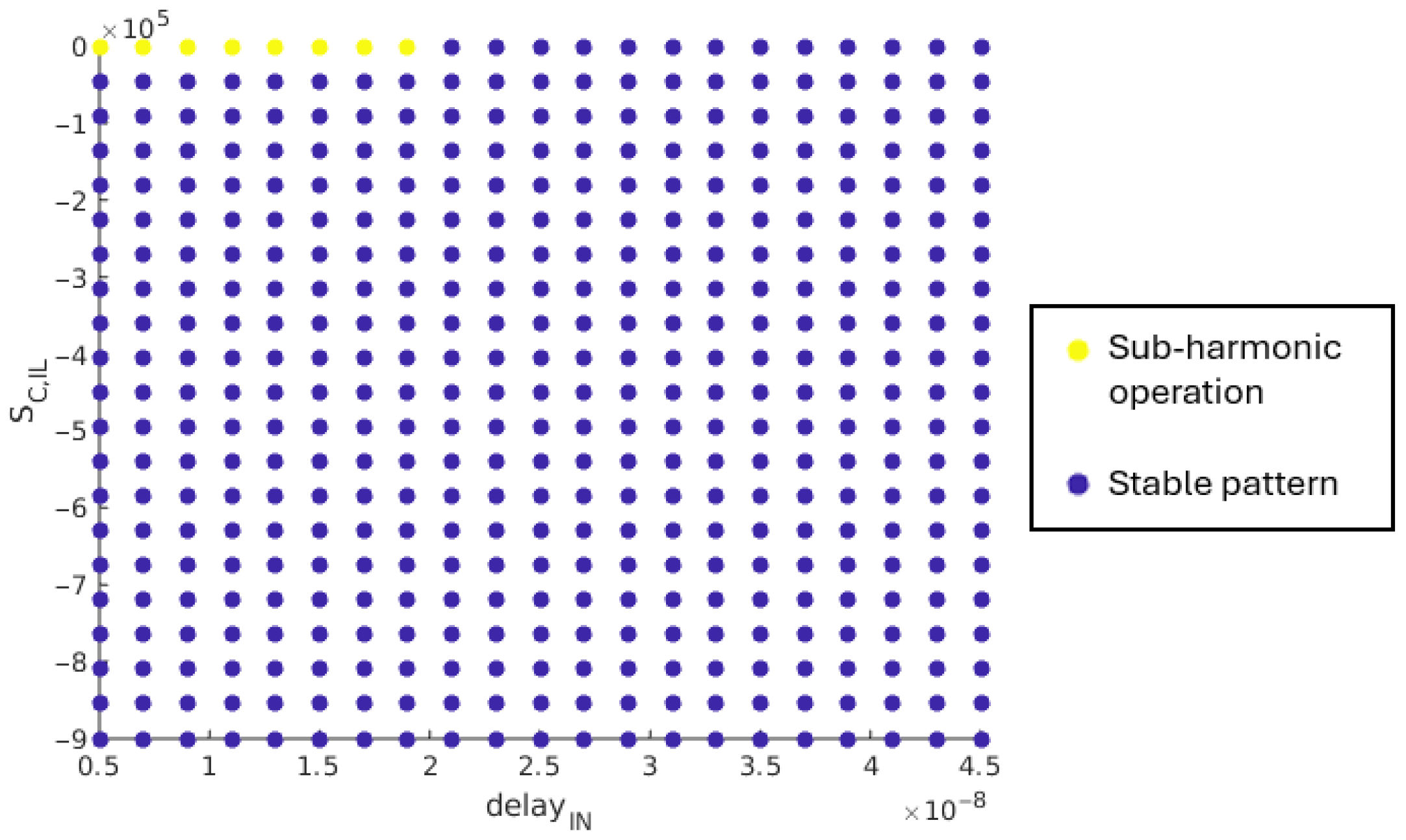
5.2.3. Impact of the Comparator’s Delay, $dela{y}_{IN}$

Considering the circuit parameters with their respective nominal values, the inequality in (5) is fulfilled for all load cases. This statement is verified through simulation, with the comparator delay $dela{y}_{IN}$ varying between 5 ns and 45 ns, as shown in Figure 15.

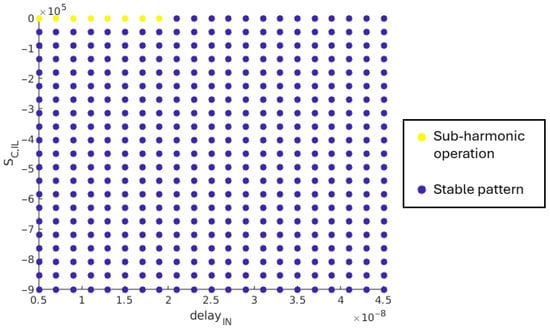
Figure 15. Correlation between $s_{C,IL}$ and $dela{y}_{IN}$ regarding the sub-harmonic oscillation damping.

Over the simulated $dela{y}_{IN}$ range, stable pattern is achieved for all load cases, except for few points when no slope compensation is applied.

5.3. Slope Compensation in the Output Switches’ Control Loops

Inequalities in (6), (14) and (17) from the previous section show the factors that can impact the boundaries between stable operation pattern and sub-harmonic oscillation appearance: the output load currents, the comparator delay and the output voltage sensing filter characteristics.

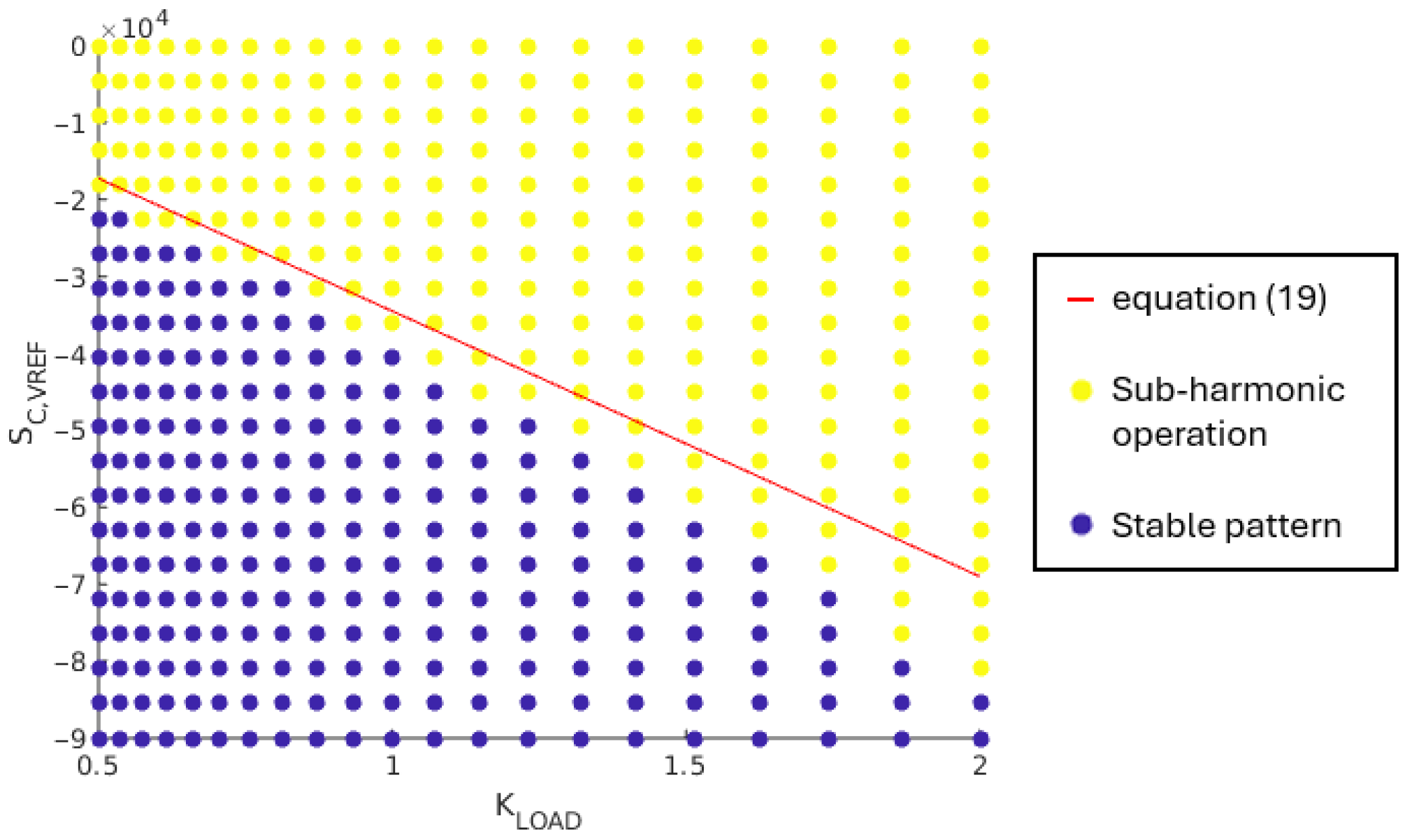
5.3.1. Impact of the Converter’s Total Current Load, $K_{LOAD}$

As described by the inequalities in (14) and (17), the compensating ramp slope needed in the output voltage control loops increases as the load current supplied by the SIMO converter increases. To study this phenomenon, for the eight load cases in Table 2, multiple simulations are conducted. However, a multiplicative coefficient, $K_{LOAD}$, between 0.5 and 2, is considered as the simulation parameter. This coefficient is multiplied with the load cases from Table 2 in order to generate the output load currents $I_{LOAD1}$, $I_{LOAD2}$ and $I_{LOAD3}$.

The load case #3 corresponds to the most critical case regarding the compensating ramp slope needed. For this case, the stability condition in (6) is not satisfied and the boundary between stable operation pattern and sub-harmonic oscillations is given by the inequality in (17). Doing the numerical application in this stability condition for the load case #3 and considering the nominal values for circuit parameters, the boundary between stable pattern and sub-harmonic oscillations is rewritten as (19):

$$s_{C,VREF}=-3.45·{10}^4·K_{LOAD}[V/s]$$

(19)

Figure 16 shows the obtained simulation results for a compensation ramp slope, $s_{C,VREF}$, between 0 V/s and 9· 10⁴ V/s. A behavior similar to the one given by the theorical Equation (19) is observed: the higher the load current, the steeper the required compensation ramp slope value.

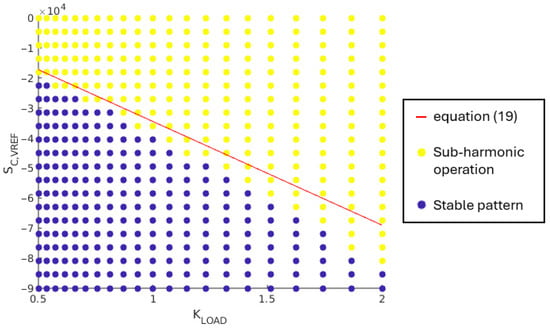
Figure 16. Correlation between $s_{C,VREF}$ and $K_{LOAD}$ regarding the sub-harmonic oscillation damping.

5.3.2. Impact of Comparators’ Delay, $dela{y}_{OUT}$

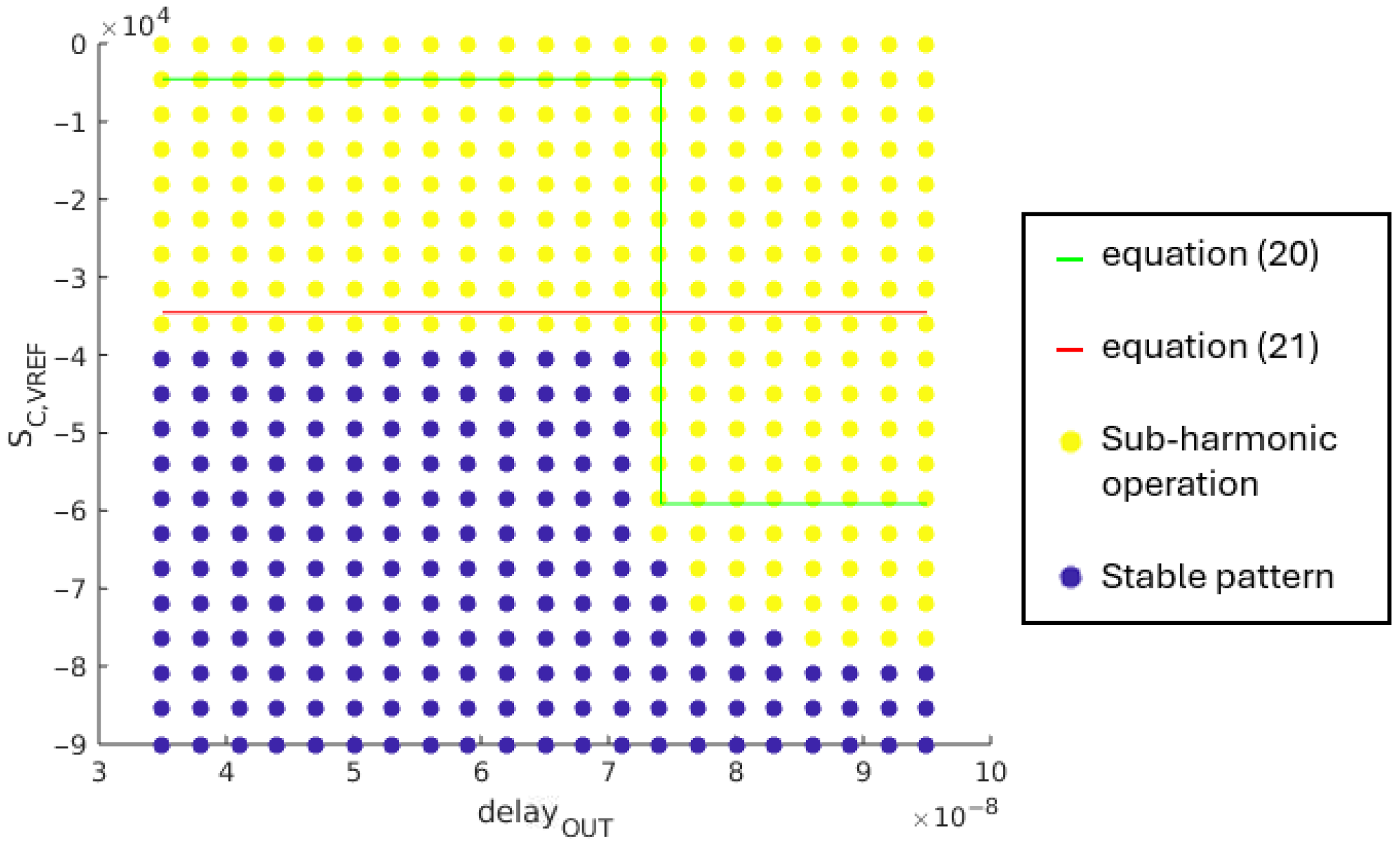
For the load case #1 in Table 2, the condition in (6) is fulfilled when the comparator’s delay, $dela{y}_{OUT}$, is lower than 74 ns. The compensating ramp slope needed to prevent sub-harmonic oscillation, given by the stability condition in (14), is rewritten as (20), considering the numerical application for the load case #1.

$$s_{C,VREF}=\left\{\begin{array}{cc}-4.55·{10}^3[V/s]\hfill & \mathrm{if}dela{y}_{OUT}<74\mathrm{ns}\hfill \\ -5.91·{10}^4[V/s]\hfill & \mathrm{if}dela{y}_{OUT}>74\mathrm{ns}\hfill \end{array}\right.$$

(20)

For load case #3 in Table 2, the stability condition in (6) is not satisfied when the comparator’s delay, $dela{y}_{OUT}$, is higher than 9 ns. The compensation ramp slope needed to damp sub-harmonic oscillation phenomenon is given by (17), which can be rewritten as (21), considering the numerical application for the load case #3.

$$s_{C,VREF}=\left\{\begin{array}{cc}-1.27·{10}^4[V/s]\hfill & \mathrm{if}dela{y}_{OUT}<9\mathrm{ns}\hfill \\ -3.45·{10}^4[V/s]\hfill & \mathrm{if}dela{y}_{OUT}>9\mathrm{ns}\hfill \end{array}\right.$$

(21)

Simulations results are given in Figure 17.

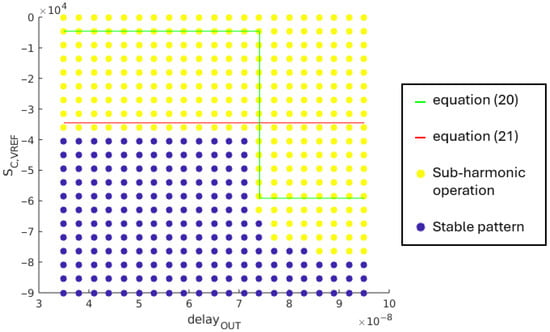
Figure 17. Correlation between $s_{C,VREF}$ and $dela{y}_{OUT}$ regarding the sub-harmonic oscillation damping.

When $dela{y}_{OUT}$ is higher than 74 ns, the simulation results differ from the ones given by the theoretical equations: the needed compensation ramp slope increases as the comparator’s delay increases. For a delay lower than 74 ns, simulation results are coherent with respect to the theoretical inequalities given in the previous section.

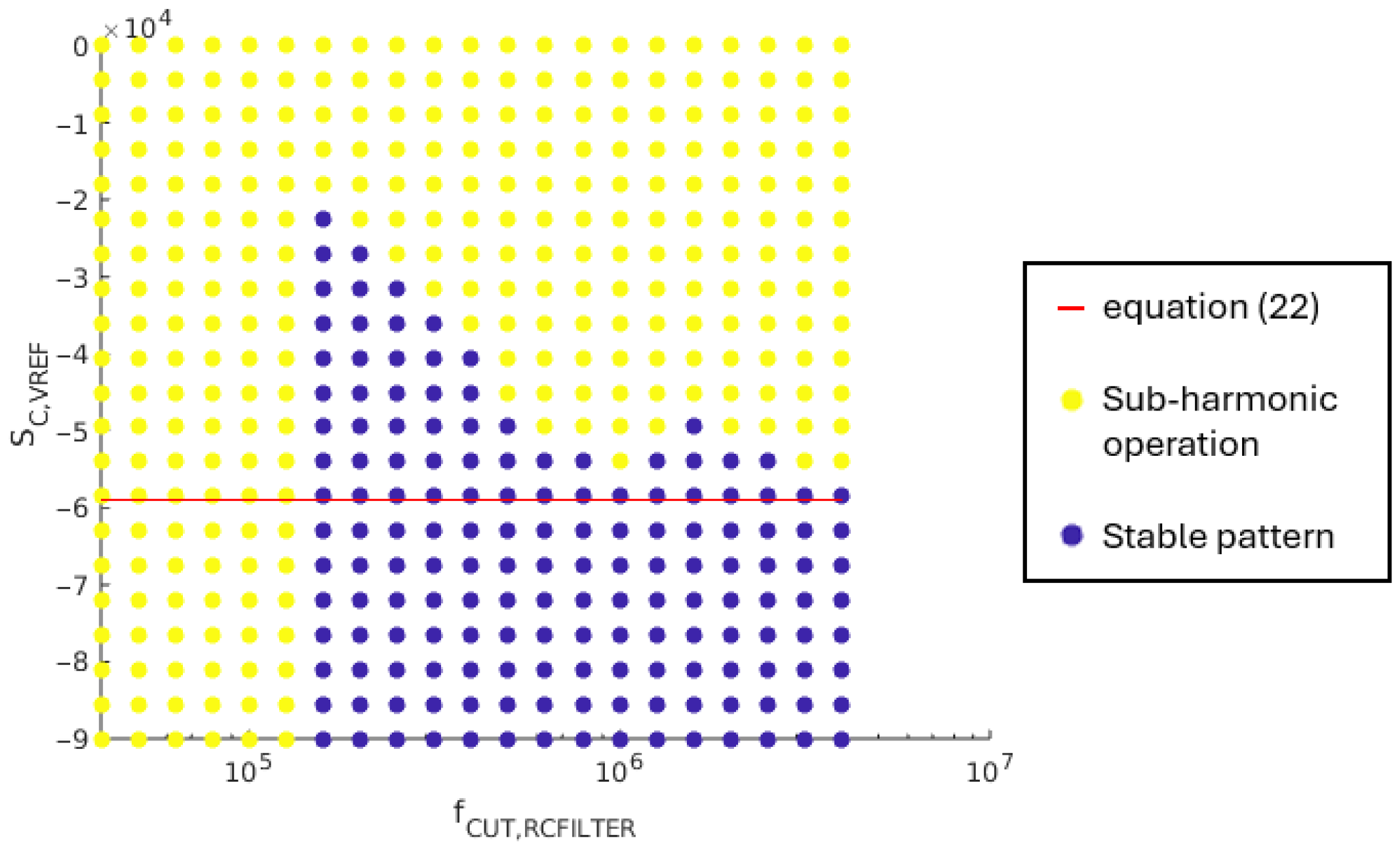
5.3.3. Impact of the Output Voltage Sensing Filter, $R{C}_{FILTER}$

The output voltage sensing filter, $R{C}_{FILTER}$, impacts the slope of the compensation ramp, $s_{C,VREF}$, as shown by the inequalities in (14) and (17). Since the filter is a first order one, the high-frequency gain is impacted by its cut-off frequency, $f_{CUT,RCFILTER}$. Moreover, the phase of this filter introduces another form of delay in the output switch control loops.

When the filter phase introduces a non-negligible delay and the condition in (6) is not fulfilled, the load case #1, high load on the three outputs, becomes the most critical case regarding the needed compensation ramp slope. The numerical application of the stability condition in (17) is given as (22) for the load case #1.

$$s_{C,VREF}=-5.91·{10}^4·G_{RCFILTER}[V/s]$$

(22)

The gain of the filter is limited by its static gain. Thus, the steeper compensation ramp is evaluated considering $G_{RCFILTER}$ = 1.

Simulations are conducted with a cut-off frequency varying between 40 kHz and 4 MHz, while $s_{C,VREF}$ varies between 0 V/s and 9· 10⁴ V/s. Figure 18 shows the obtained results, with a logarithmic x-axis scale.

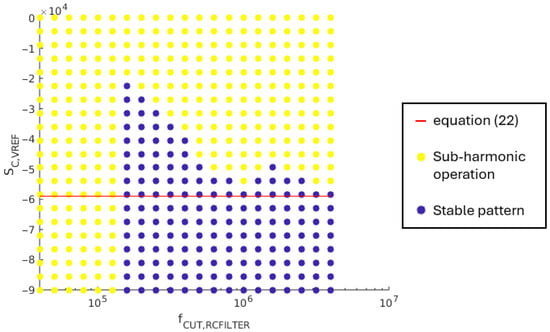
Figure 18. Correlation between $s_{C,VREF}$ and $f_{CUT,RCFILTER}$ regarding the sub-harmonic oscillation damping.

For a cut-off frequency lower than 150 kHz, no stable operation patterns are achieved whatever the load cases. It can be explained by the fact that the sensed output voltages are too distorted, and too much delay is introduced in the loop because of the filter’s phase. For frequencies of 150 kHz and higher, a stable operation pattern may be achieved for all load cases depending on the compensation ramp slope value. The required slope value varies with the gain and the phase of the filter. The boundary described by (22) is coherent.

6. Implementation and Transistor-Level Circuit Simulation

The double slope compensation is implemented in the SIMO converter transistor-level circuit, using the ST-18nm-process.

Regarding the bifurcation phenomenon, the worse simulation case is when the supply voltage, $V_{IN}$, is minimum. The previous section highlighted that a lower supply voltage requires a steeper compensating ramp to reach a stable pattern. Moreover, a lower supply voltage creates higher comparator propagation delays, which also require steeper slope compensation to damp any tendency toward sub-harmonic oscillations.

In this section, we will consider a minimum supply voltage $V_{IN}$ of 1.8 V instead of the 1.6 V value given in the previous section. This is because for $V_{IN}$ between 1.6 V and 1.8 V, the energy conversion is managed by a slightly different architecture than the SIMO DC-DC converter presented in this article: the third output of the SIMO converter is bypassed and is instead supplied by a linear regulator.

Depending on the circuit parameters, some load current cases are more critical than others, meaning that a steeper compensating ramp would be needed. The load current cases that are the most susceptible to sub-harmonic oscillations in the converter operation are #1, #3 and #7 from Table 2. Indeed, if no bifurcation occurs for these 3 cases, it won’t happen for the other load current cases.

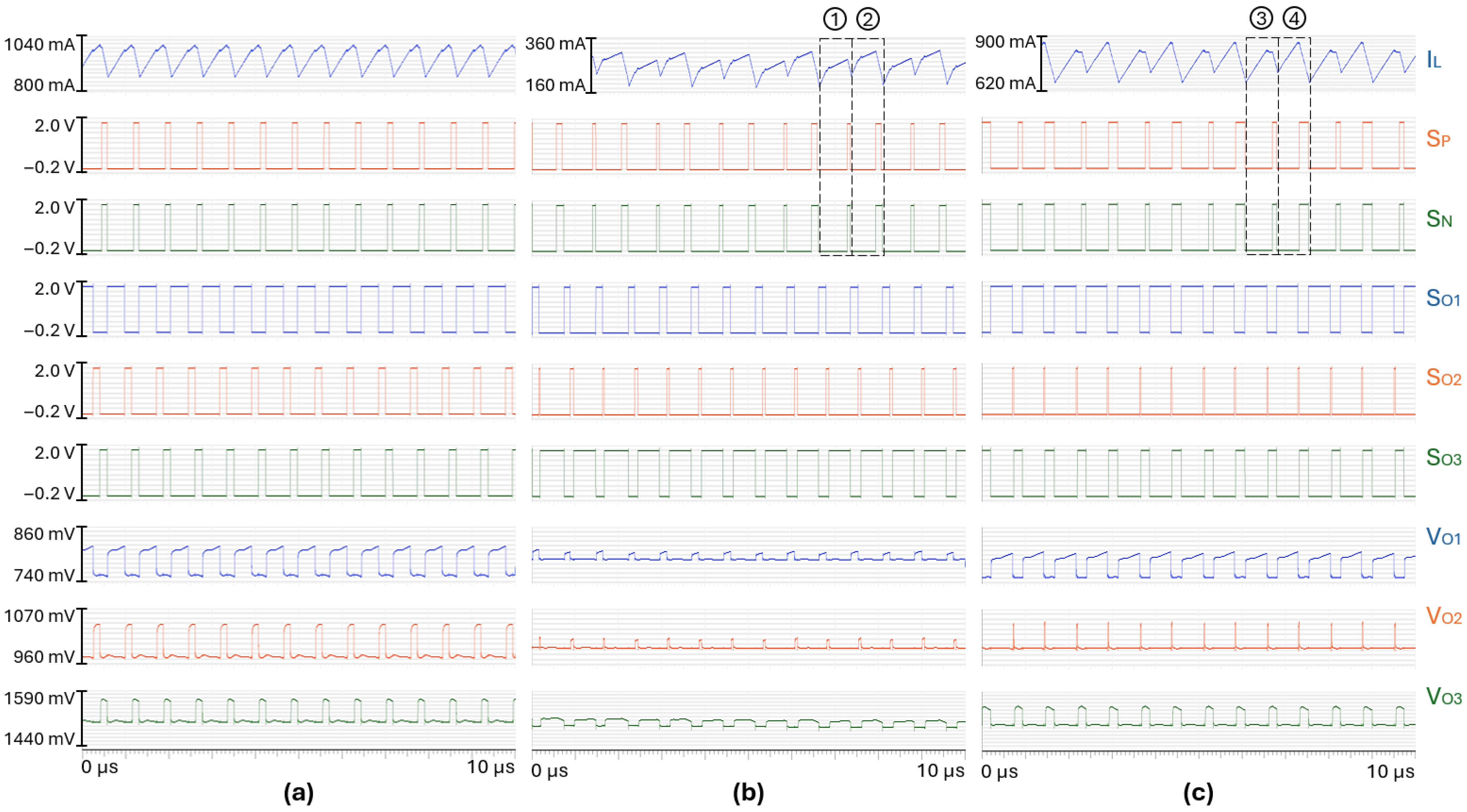
Figure 19 shows the waveforms obtained with $s_{C,IL}$ set to 8.3$·{10}^5$ V/s and $s_{C,VREF}$ set to 6.0$·{10}^4$ V/s. Based on the previous section, this set of compensating ramp slopes should damp any tendency toward sub-harmonic oscillations. However, a stable pattern is only achieved for the load case #1 as shown in Figure 19a. For the load cases #7 and #3, respectively shown in Figure 19b and Figure 19c, period doubling occurs. Between the two consecutive switching cycles ➀ and ➁, the valley current is different, as well as the duty cycles of the input switches. The same observation is done between the two consecutive switching cycles ➂ and ➃.

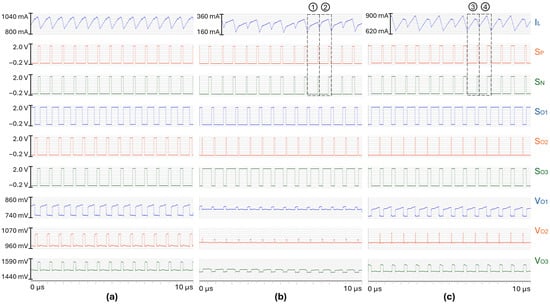
Figure 19. Steady-state waveforms achieved in (a) load case #1, (b) load case #7, (c) load case #3, for $s_{C,IL}$ = 8.3$·{10}^5$ V/s and $s_{C,VREF}$ = 6.0$·{10}^4$ V/s.

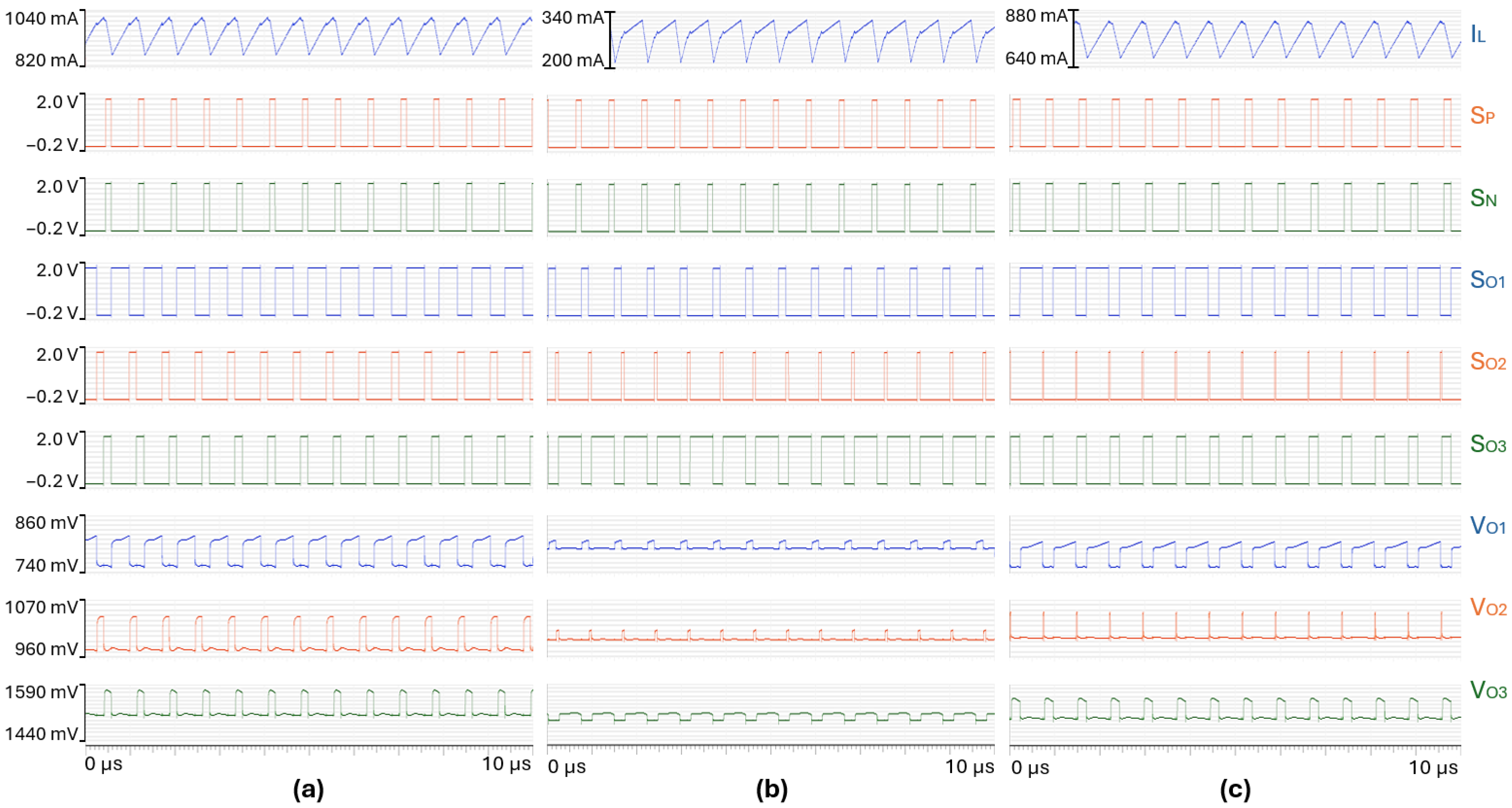
Since the previously implemented set of compensating ramp values is not suited for damping sub-harmonic oscillations, the slope of $s_{C,IL}$ is increased. Figure 20 shows the waveforms obtained with $s_{C,IL}$ set to 9.6$·{10}^5$ V/s and $s_{C,VREF}$ set to 6.0$·{10}^4$ V/s. A stable pattern is achieved for the three load cases.

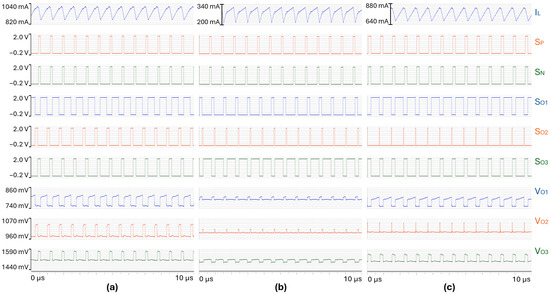
Figure 20. Steady-state waveforms achieved in (a) load case #1, (b) load case #7, (c) load case #3, for $s_{C,IL}$ = 9.6$·{10}^5$ V/s and $s_{C,VREF}$ = 6.0$·{10}^4$ V/s.

A shift is observed on the boundary between stable pattern and bifurcation, with respect to the compensating ramp $s_{C,IL}$, between system-level simulations and transistor-level circuit simulations. In the transistor-level circuit, a non-overlapping strategy is implemented to prevent any short-cut between two outputs when the supplied output changes from one to another. Because of this strategy, the inductor node, $V_{LY}$, rises above 2 V during the non-overlapping phase, which lasts for around 6 ns. It can be seen as an increase in the weighted output voltage. Thus, a steeper compensating ramp is needed to damp any tendency towards sub-harmonic oscillations.

Figure 21 shows the waveforms obtained with $s_{C,IL}$ set to 9.6$·{10}^5$ V/s and $s_{C,VREF}$ set to 5.0$·{10}^4$ V/s. A stable pattern is achieved for the load cases #1 and #3, respectively, as shown in Figure 21a and Figure 21c, while bifurcation occurs for the load case #7. Between the two consecutive switching cycles ➀ and ➁, the valley current is different, as well as the duty cycles of the input switches, as shown in Figure 21b.

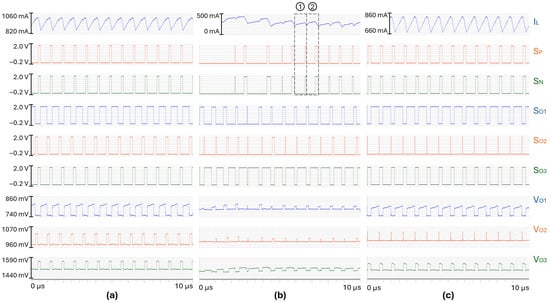
Figure 21. Steady-state waveforms achieved in (a) load case #1, (b) load case #7, (c) load case #3, for $s_{C,IL}$ = 9.6$·{10}^5$ V/s and $s_{C,VREF}$ = 5.0$·{10}^4$ V/s.

The value of $s_{C,VREF}$ decreases from 6.0$·{10}^4$ V/s to 5.0$·{10}^4$ V/s before the onset of period doubling. It is coherent with the theoretical analysis and system-level simulations from previous sections that predict a bifurcation onset when $s_{C,VREF}$ is lower than 5.91$·{10}^4$ V/s.

The transistor-level simulations, conducted for three different sets of compensating ramps, demonstrate that a well-calibrated pair of compensating ramps can effectively damp any tendency towards sub-harmonic oscillations in a DC-DC SIMO converter with a current-mode and comparator-based hybrid control, as shown in Figure 20. Moreover, the design of one of the compensating ramps might result in the occurrence of the bifurcation phenomenon, depending on the output load current case, as shown in Figure 19 and Figure 21.

Based on this observation, a safe statement is that over-designing the compensating ramp slopes would prevent any sub-harmonic oscillations, no matter what the output load current is. However, increasing the compensating ramp slopes degrades the transient performances of the SIMO converter. The steeper the ramp values, the closer the converter control becomes to voltage-mode control, and the lower the transient performances of the current-mode and comparator-based control.

The results in Table 3 illustrate this trade-off between the damping of sub-harmonic oscillations in steady-state and the transient performances.

Table 3. Impact of the compensating ramps on the steady-state and transient performances of the DC-DC SIMO converter.

Compensating Ramps	Load Case #1 Steady-State	Load Case #7 Steady-State	Load Case #3 Steady-State	#1 → #7 Transient Voltage Overshoot	#7 → #3 Transient Voltage Undershoot
no slope compensation	Bifurcation	Bifurcation	Bifurcation	35 mV	14 mV
$s_{C,IL}$ = 8.3$·{10}^5$ V/s $s_{C,VREF}$ = 6.0$·{10}^4$ V/s	Stable pattern (145 mA ripple)	Period-doubling (125 mA ripple)	Period-doubling (205 mA ripple)	46 mV	24 mV
$s_{C,IL}$ = 9.6$·{10}^5$ V/s $s_{C,VREF}$ = 6.0$·{10}^4$ V/s	Stable pattern (145 mA ripple)	Stable pattern (105 mA ripple)	Stable pattern (155 mA ripple)	47 mV	29 mV
$s_{C,IL}$ = 9.6$·{10}^5$ V/s $s_{C,VREF}$ = 5.0$·{10}^4$ V/s	Stable pattern (145 mA ripple)	Period-doubling (140 mA ripple)	Stable pattern (155 mA ripple)	44 mV	22 mV

7. Conclusions

This paper presents a SIMO DC-DC converter architecture with a current-mode and comparator-based hybrid control. Simulation of the full transistor-level circuit design of this topology highlighted the bifurcation phenomenon occurring during steady-state. Based on the classical slope compensation approach used in SISO current-controlled DC-DC converter, a new solution to damp any tendency toward sub-harmonic oscillations for the SIMO converter is proposed: a double slope compensation, with one implemented on the current-mode control loop and the other on the comparator-based control loop.

From a simplified theoretical analysis of the operating principle of the converter, inequalities are identified that describe the boundaries between stable operation and bifurcation. Moreover, the impactful circuit parameters are identified. An accurate model of the SIMO converter is implemented in Matlab/Simulink, with all possible switches’ states defined by a state-space model with varying matrices. Through system-level simulation, the boundaries between stable operation and bifurcation are verified with respect to the impactful parameters.

Finally, the double slope compensation is implemented in the circuit at transistor-level. Even in the worse steady-state scenario, calibrating the compensating ramps near the boundary between stable pattern and sub-harmonic oscillations allows us to prevent the bifurcation phenomenon’s occurrence, while keeping the advantage of comparator-based control in terms of transient performances.