Extreme Path Delay Estimation of Critical Paths in Within-Die Process Fluctuations Using Multi-Parameter Distributions

Abstract

Two multi-parameter distributions, namely the Pearson type IV and metalog distributions, are discussed and suggested as alternatives to the normal distribution for modelling path delay data that determines the maximum clock frequency (FMAX) of a microprocessor or other digital circuit. These distributions outperform the normal distribution in goodness-of-fit statistics for simulated path delay data derived from a fabricated microcontroller, with the six-term metalog distribution offering the best fit. Furthermore, 99.7% confidence intervals are calculated for some extreme quantiles on each dataset using the previous distributions. Considering the six-term metalog distribution estimates as the golden standard, the relative errors in single paths vary between 4 and 14% for the normal distribution. Finally, the within-die (WID) variation maximum critical path delay distribution for multiple critical paths is derived under the assumption of independence between the paths. Its density function is then used to compute different maximum delays for varying numbers of critical paths, assuming each path has one of the previous distributions with the metalog estimates as the golden standard. For 100 paths, the relative errors are at most 14% for the normal distribution. With 1000 and 10,000 paths, the corresponding errors extend up to 16 and 19%, respectively.

1. Introduction

Inadequately modelling variance in IC design increases design costs through performance loss, time-to-market delay, and yield loss. Variance components are usually lumped into ambient (addressed with design constraints), die-to-die or wafer-to-wafer process variations (corner models with possible spatial components), and within-die (WID) process variations (statistical transistor-level models). Even if the underlying model is normal, the sheer number of transistors leads to high dimensionality and non-linear transfer functions lead to non-normal distributions. The latter is especially exacerbated in the sub- and near-threshold regions, where energy optimality of digital circuits is achieved [1]. In these cases, transistor and gate delay is exponentially dependent on process and environmental parameters, such as the threshold voltage ($V_t$). The high dimensionality precludes analytical models and, for large circuits, Monte Carlo simulations of all parameters are impossible even with supercomputers.

Ultra-wide dynamic voltage and frequency scaling (UW-DVFS) is a flavour of conventional DVFS that operates down to the minimum-energy point [1]. The exact operating voltage will however be dynamically dependent on the process, temperature, architecture, data, among other things [2]. Designing for UW-DFVS is similar to conventional DVFS, with the exception of the re-characterization of the operating (and other sign-off) points. Additionally, due to the high susceptibility of performance to variance, liberty variation format (LVF) with moment gate libraries (which include skewness, the third-order statistical moments) are required in the design process. The inclusion of LVF makes the re-characterization an extremely time- and CAD-license-consuming design step. If re-characterization is also required at sign-off (due to, e.g., inaccurate operating points), it can cause major delays to the conventional design process.

A better option is to add accurate statistical modelling at higher abstraction levels to evaluate circuits at earlier design phases. Such early estimation has not yet been extensively studied in the literature. The best example is perhaps [3], where a model describing the maximum clock frequency (FMAX) distribution of a non-DVFS microprocessor is derived and compared with wafer data for a 250 nm process. The model uses normal distributions which are adequate for the 250 nm process. With the normality assumption, it is shown that within-die fluctuations cause the most significant performance degradation and a channel length deviation of 20% approximately projects a loss of a single performance process generation. For modern processes and especially near- and sub-threshold operation, transistor delay is a non-linear function of random process variables and this delay is non-Gaussian [4]. Due to the high dimensionality and exponential transfer functions, skewed distributions such as lognormal [5] are not enough to model the higher-level delay variance, and therefore multi-parameter distributions are required. Accurate early-phase statistical understanding could also be advantageous in design-phase power modelling. In [6], leakage and dynamic energy are co-optimized early in the design phase. Optimization across SS (slow–slow) and FF (fast–fast) corners, and SVT, HVT, and ULL gate libraries result in a gate library mix of 14% SVT, 50% HVT, and 36% ULL. Here, understanding the cross-library variance might result in a different library mix and/or lower voltages.

With skewed distributions, extreme quantile (high sigma) effects will show up in a smaller number of parts, possibly lowering the yield. Without an extremely large number of simulations, it is difficult to measure the effects of extreme quantile variation quickly and accurately. In this article, different methods of more accurately estimating the FMAX distribution are explored via multi-parameter distributions. They allow more precise margin additions or low-voltage effect estimations, which can be achieved, for example, with confidence intervals: e.g., by making sure that the cycle time is beyond the upper confidence bound.

The rest of this article is organized as follows. In Section 2, we present the problem statement of the paper, and Section 3 provides the mathematical framework as well as introducing the different mathematical methods used to generate the final results. Section 4 explains the origins of the data and presents the results along with their discussion. Finally, in Section 5 we close the article with our conclusions.

2. Problem Statement

When dealing with extreme quantiles, we are often faced with two primary challenges. First, we usually have limited data on the process of interest, and generating additional data may be costly or outright impossible. Second, we seldom know the underlying distribution of the data, which means we have to consider several different candidate distributions.

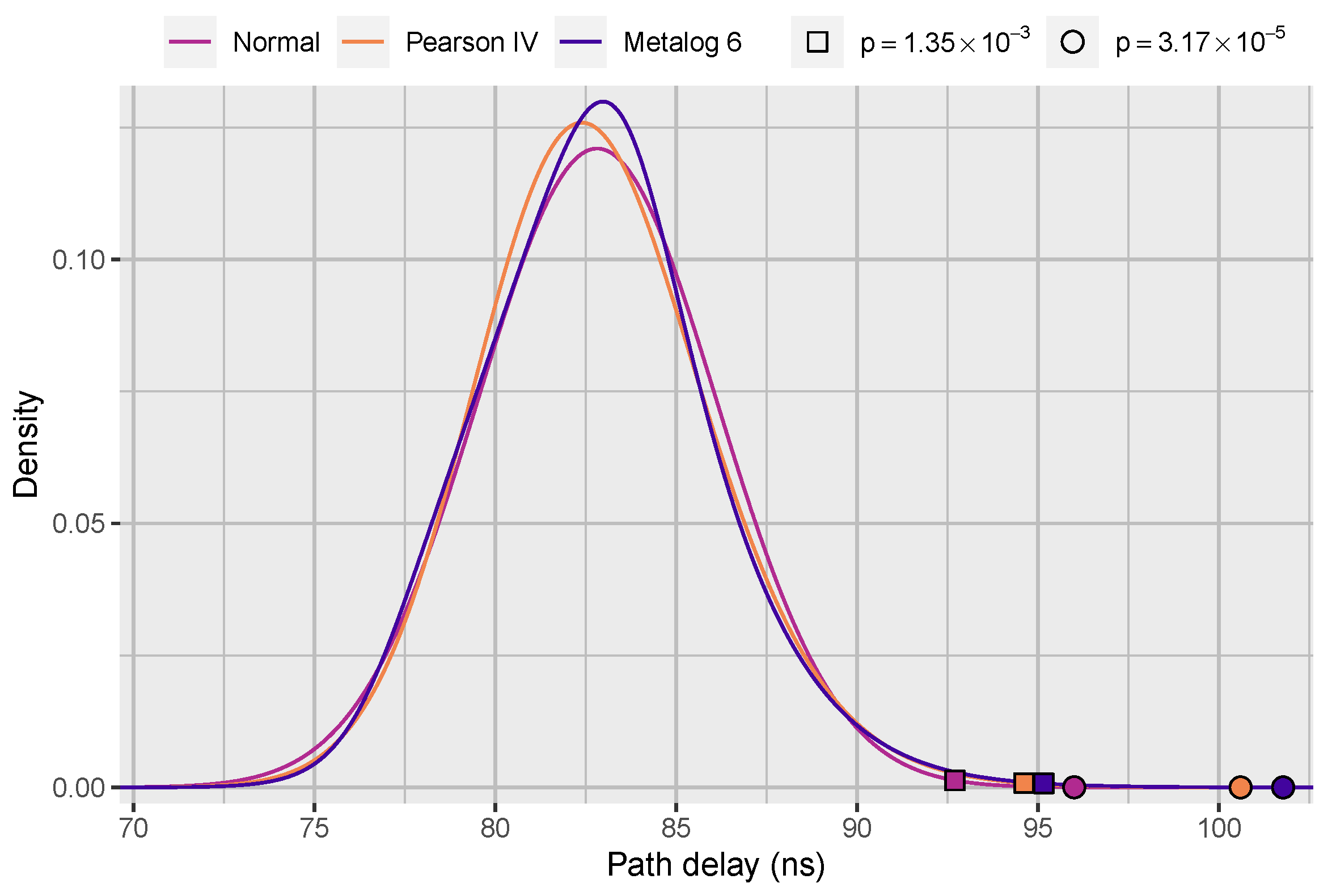
As an example, consider the three different distributions presented in Figure 1. In addition to the normal distribution, we have fitted the Pearson type IV and six-term metalog distributions (see Section 3.1 and Section 3.2) to path delay (signal propagation time from launch FF to capture FF) data from Monte Carlo simulations (see Section 4.1). Furthermore, we have plotted their theoretical $(1-p)$-quantiles corresponding to $p=1.35\times {10}^{-3}$ and $p=3.17\times {10}^{-5}$. In the case of normal distribution, these correspond to the so-called three- and four-sigma quantiles, i.e., quantiles which lie three and four standard deviations above the mean.

The $(1-p)$-quantiles are noticeably smaller for the normal distribution than for the Pearson type IV and six-term metalog distributions. Furthermore, the discrepancy in the point estimates is considerably larger for the quantile corresponding to $p=3.17\times {10}^{-5}$. In order to assess which distribution offers the best fit to the data, we have to consider different statistics that measure the goodness of fit (see Section 3.4).

However, point estimates of extreme quantiles are rarely useful on their own. This is due to the fact that the estimates depend on the sample used, and if we were to generate multiple samples of the same process we would always end up with different estimates for the statistic. Instead, we are interested in the confidence intervals of the extreme quantiles which give a range of values the unknown statistic is likely contained in. A common method to generate confidence intervals with relatively mild assumptions is bootstrapping (see, e.g., [7]).

3. Methods

3.1. The Pearson Distribution Family

The Pearson distribution is a family of continuous distributions originally introduced in a series of articles on biostatistics [8,9,10]. Whereas one- or two-parameter distributions can be used to fit data based on the sample mean and variance, there are often times they are unable to properly characterize skewed data. The Pearson distribution family allows distribution fitting on unimodal data that is potentially skewed or asymmetric via additional shape parameters. This makes the distribution family a compelling choice for fitting to skewed data and estimating its extreme quantiles. For a brief overview of applications of the distribution family in other work, see [11].

The Pearson distribution family consists of three main types, namely, types I, IV and VI, as well as other subtypes which are special cases of the main ones. The Pearson type I and VI distributions are generalizations of the beta and F-distributions, respectively, whereas type IV is not a generalization of any known distribution. However, based on our empirical observations, the type IV distribution usually offers the best fit on the data out of the three main types. We also noticed that it is the least likely distribution to fail to converge when optimizing parameters using non-linear optimization methods.

The density function of the Pearson type IV distribution is defined as [8]

$$p\left(x\right)=K{\left(1+{\left(\frac{x-\lambda }{\theta }\right)}^2\right)}^{-m}{e}^{-\nu arctan\left(\frac{x-\lambda }{\theta }\right)},$$

(1)

where $\theta ,m,\nu$ and $\lambda$ are parameters of the distribution, and K is a normalizing constant. See Appendix A for a detailed overview on the parametrization of the distribution. The parameters $\lambda$ and $\theta$ are also known as the location and scale parameters, respectively, while m and $\nu$ are called the shape parameters.

Maximum likelihood estimation is commonly used to solve the parameters of a multi-parameter distribution. Maximizing the log-likelihood is often achieved using quasi-Newton methods, such as the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm with a computational complexity of $\mathcal{O}\left(n^2\right)$, where n is the number of data points.

3.2. The Metalog Distribution Family

A more novel class of distributions are the so-called quantile-parameterized distributions, originally proposed for decision analysis in 2011 [12]. What makes them rather exceptional is the fact that, unlike most probability distributions, they are directly parameterized by the data. This eliminates the need for parameter estimation, which usually requires non-linear optimization for more complex distributions.

Introduced in 2016, one particular family of quantile-parameterized distributions is called the metalog distribution, which has virtually unlimited shape flexibility in addition to simple closed-form expressions for density and quantile functions [13]. Due to the aforementioned properties, the metalog distribution is an attractive candidate for modelling potentially skewed distributions and estimating extreme quantiles from simulation data.

The metalog distribution quantile function $M\left(y\right)$, expressed as a function of cumulative probability $0<y<1$, is defined as follows [13]:

$$M_k\left(y\right)=\left\{\begin{array}{c}\begin{array}{cc}{a}_1+a_{2}ln\frac{y}{1-y},\hfill & \hfill \mathrm{for}k=2,\\ a_1+a_{2}ln\frac{y}{1-y}+a_3\left(y-\frac{1}{2}\right)ln\frac{y}{1-y},\hfill & \hfill \mathrm{for}k=3,\\ a_1+a_{2}ln\frac{y}{1-y}+a_3\left(y-\frac{1}{2}\right)ln\frac{y}{1-y}\hfill \\ +a_4\left(y-\frac{1}{2}\right),\hfill & \hfill \mathrm{for}k=4,\\ M_{k-1}\left(y\right)+a_k{\left(y-\frac{1}{2}\right)}^{\frac{k-1}{2}},\hfill & \hfill \mathrm{for}\mathrm{odd}k\ge 5,\\ M_{k-1}\left(y\right)+a_k{\left(y-\frac{1}{2}\right)}^{\frac{k-2}{2}}ln\frac{y}{1-y},\hfill & \hfill \mathrm{for}\mathrm{even}k\ge 6,\end{array}\hfill \end{array}\right.$$

(2)

where $a_i$ are parameters of the distribution. The corresponding density function $m\left(y\right)$ for $0<y<1$ is then given by [13]

$$m_k\left(y\right)=\left\{\begin{array}{c}\begin{array}{cc}{\left[\frac{a_2}{y(1-y)}\right]}^{-1},\hfill & \hfill \mathrm{for}k=2,\\ {\left[\frac{a_2}{y(1-y)}+a_3\left(\frac{y-\frac{1}{2}}{y(1-y)}+ln\frac{y}{1-y}\right)\right]}^{-1},\hfill & \hfill \mathrm{for}k=3,\\ {\left[\frac{a_2}{y(1-y)}+a_3\left(\frac{y-\frac{1}{2}}{y(1-y)}+ln\frac{y}{1-y}\right)+a_4\right]}^{-1},\hfill & \hfill \mathrm{for}k=4,\\ {\left[m_{k-1}^{-1}\left(y\right)+a_k\frac{k-1}{2}{\left(y-\frac{1}{2}\right)}^{\frac{k-3}{2}}\right]}^{-1},\hfill & \hfill \mathrm{for}\mathrm{odd}k\ge 5,\\ \left[m_{k-1}^{-1}\left(y\right)+a_k\left(\frac{{\left(y-\frac{1}{2}\right)}^{\frac{k-2}{2}}}{y(1-y)}\right.\right.\hfill \\ {\left.\left.+\frac{k-2}{2}{\left(y-\frac{1}{2}\right)}^{\frac{k-4}{2}}ln\frac{y}{1-y}\phantom{\left(\frac{{\left(y-\frac{1}{2}\right)}^{\frac{k-2}{2}}}{y(1-y)}\right.}\right)\phantom{\left[q_{k-1}^{-1}\left(y\right)+a_k\left(\frac{{\left(y-\frac{1}{2}\right)}^{\frac{k-2}{2}}}{y(1-y)}\right.\right.}\right]}^{-1},\hfill & \hfill \mathrm{for}\mathrm{even}k\ge 6.\end{array}\hfill \end{array}\right.$$

(3)

The parameters $a_i$ are usually determined by linear least squares from the data [13]. When choosing the number of parameters, one has to be careful not to pick too many parameters to avoid overfitting. Assuming there are n data points, k parameters to be determined and $n>k$, the computational complexity of fitting a metalog distribution to the data is $\mathcal{O}\left(k^{2}n\right)$.

Despite its novelty, the metalog distribution has seen different applications in various branches of natural science and engineering. Recent examples of its applications include hydrology and fish biology [13], as well as risk assessment in astronomy [14] and cybersecurity [15].

3.3. Comparison of the Distributions

The normal distribution is the baseline distribution here due to its historical significance and prevalence in other works related to path delay modelling. Its clearest disadvantage is its inability to model asymmetric and heavy-tailed data. Additionally, the support of the normal distribution is the entire real line, even though path delays cannot obtain negative values. A better two-parameter alternative would be the log-normal distribution due to its support of strictly positive real numbers as well its ability to model skewed data.

The Pearson type IV distribution allows distribution fitting to data that is potentially skewed or asymmetric. However, in some cases it might not be adequate in the $({\beta }_1,{\beta }_2)$ space, where ${\beta }_1$ is the squared skewness and ${\beta }_2$ the kurtosis (see Appendix A for more information). In these cases, the other Pearson main-type distributions, namely types I and VI, may offer superior results.

The metalog distribution offers virtually unlimited shape flexibility. However, choosing the number of terms for the distribution is not unambiguous, since using too many terms may result in overfitting whereas using too few terms offers inferior results (in terms of goodness of fit). As such, one usually has to make a compromise when choosing the number of terms for the distribution.

3.4. Goodness-of-Fit Statistics

In order to assess the goodness of fit of a given distribution in observed data, we use different statistical tests that quantify the distance between the empirical and theoretical distributions in various ways. In the following, we introduce three goodness-of-fit test statistics with different emphases.

First, let $x=\{x_1,\cdots ,x_n\}$ be the set of observations. We define the empirical distribution function $F_n$ as

$$F_n\left(t\right)=\frac{1}{n}\sum _{i=1}^n{\mathbb{1}}_{x_i\le t},$$

(4)

where ${𝟙}_A$ is the indicator function of the event A. One of the simplest tests is the Kolmogorov–Smirnov (KS) test, for which the corresponding test statistic $\mathrm{KS}$ is [16,17]

$$\mathrm{KS}=\underset{x}{max}\left|F_n\left(x\right)-F\left(x\right)\right|,$$

(5)

where $F_n$ is the empirical distribution Function (4) and F the target cumulative distribution function. That is, (5) measures the largest absolute difference between the empirical and target cumulative distribution functions; therefore, a smaller value of the statistic indicates a better fit.

Another alternative to the KS test is the Cramér–von Mises (CM) criterion, originally proposed in [18,19]. The corresponding test statistic $\mathrm{CM}$ is computed as [20]

$$\mathrm{CM}=\frac{1}{12n}+\sum _{i=1}^n{\left(\frac{2i-1}{2n}-F\left(x_i\right)\right)}^2,$$

(6)

where $x_1,\cdots ,x_n$ are the observations sorted in increasing order. In other words, (6) computes a weighted average between the empirical and target distributions, with a lower value of the statistic corresponding to a better fit.

Another closely related quantity to the CM criterion is the Anderson–Darling (AD) distance [21]. The corresponding test statistic $\mathrm{AD}$ is defined as follows [22]:

$$\mathrm{AD}=-n-\sum _{i=1}^n\frac{2i-1}{n}\left[logF\left(x_i\right)+log(1-F\left(x_{n+1-i}\right))\right],$$

(7)

where $x_1,\cdots ,x_n$ are the observations sorted in ascending order. Compared to (6), (7) places more emphasis on observations in the distribution tails. Once again, a smaller value of the statistic indicates a better fit of the distribution.

3.5. WID Maximum Critical Path Delay Distribution

In [3], the critical path delay densities and WID parameter fluctuations are assumed to be normal. Here, we relax this assumption by allowing the WID fluctuation on a critical path to be modelled as some arbitrary density $f_{\mathrm{WID}}$ with a corresponding cumulative distribution $F_{\mathrm{WID}}$. However, a chip contains several critical paths which may or may not be correlated with one another. Assuming a number N of critical paths is independent, i.e., they have zero correlation, the probability of each path satisfying a specified maximum delay $t_{\max }$ is [3]

$${\mathbb{P}}_{\mathrm{WID},N}(t\le t_{\max })=F_{\mathrm{WID},N}\left(t_{\max }\right)={\left[F_{\mathrm{WID}}\left(t_{\max }\right)\right]}^N,$$

(8)

where $F_{\mathrm{WID},N}$ is the WID cumulative distribution of the chip. Consequently, the WID maximum critical path delay density $f_{\mathrm{WID},N}$ of the chip is calculated as [3]

$$f_{\mathrm{WID},N}\left(t_{\max }\right)=N{f}_{\mathrm{WID}}\left(t_{\max }\right){\left[F_{\mathrm{WID}}\left(t_{\max }\right)\right]}^{N-1}.$$

(9)

4. Simulations and Results

4.1. Origins of the Data

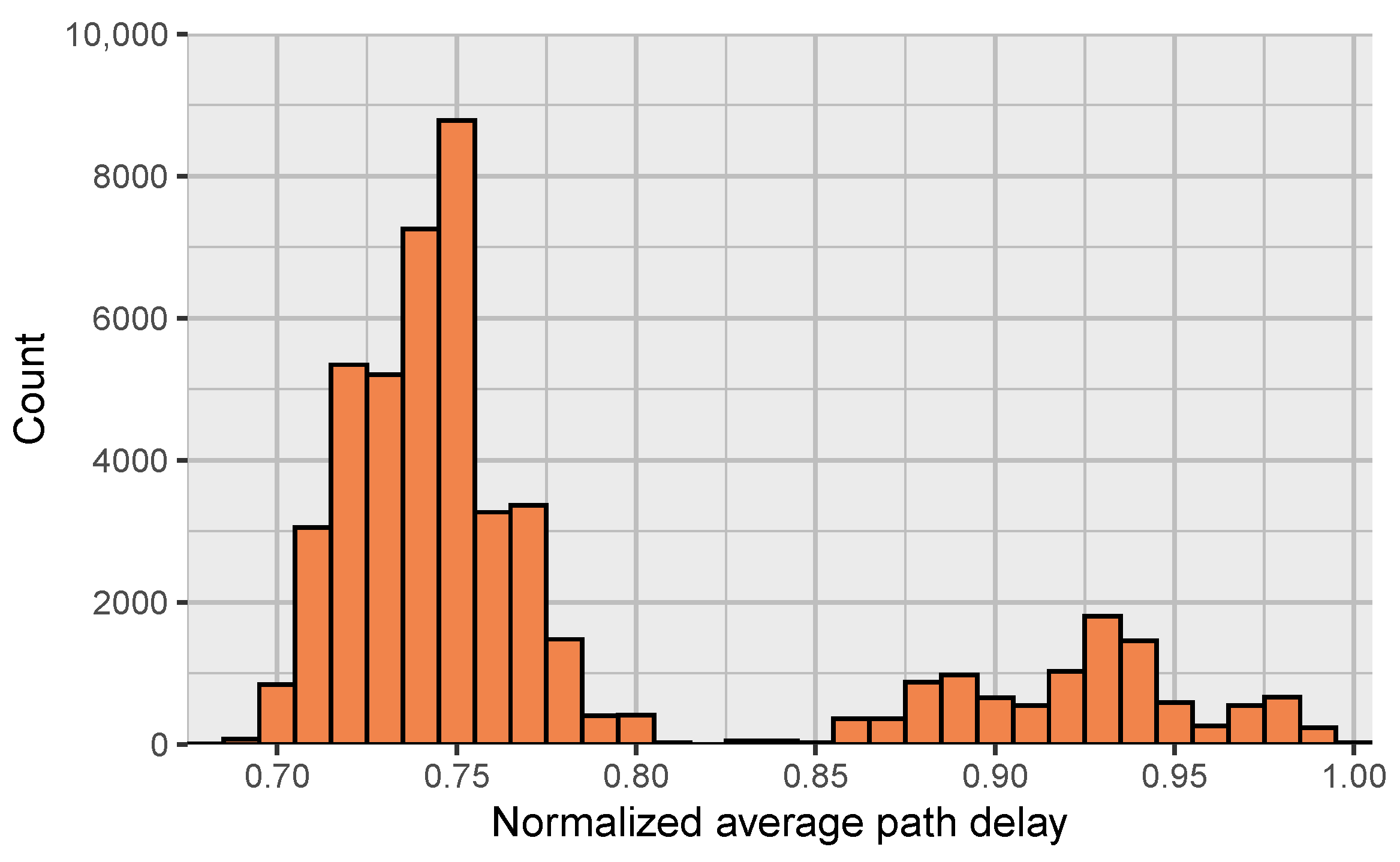
The simulation data is derived from a commercial microcontroller, similar to [23] in terms of performance and the number of gates. This UW-DVFS-capable microcontroller is a single-core embedded-class RISC core capable of near-threshold operations and has been fabricated by a 22 nm process. Post-layout statistical timing analysis (STA) data has been used to choose path groups which then have been simulated each with extensive Monte Carlo simulations. A histogram of normalized average path delays (signal propagation time from launch FF to capture FF) of all the paths is shown in Figure 2. The path delays are grouped as follows:

• Dataset 1 (DS 1) = Hold SS 0.51 V ${\mathrm{RC}}_{\mathrm{worst}}$;
• Dataset 2 (DS 2) = ${\mathrm{Setup}}_{\mathrm{win}}$ SS 0.51 V ${\mathrm{RC}}_{\mathrm{worst}}$;
• Dataset 3 (DS 3) = ${\mathrm{Setup}}_{\mathrm{critical}\mathrm{path}}$ SS 0.51 V ${\mathrm{RC}}_{\mathrm{worst}}$.

Even though the chip operates around 0.4 V nominally, the corner SS 0.51 V ${\mathrm{RC}}_{\mathrm{worst}}$ (worst resistance/capacitance) was chosen as it exhibited the most skewed distribution. DS 2 is critical for timing–event systems, such as [23], where it is important that all critical paths are monitored by the timing–event system. Therefore, the probability of non-monitored paths violating timing has to be known.

Figure 3 illustrates the path correlation of ${10}^4$ setup paths from STA in a heat map. Observe that the correlation matrix is not symmetrical. This is due to the fact that the path correlation ${\rho }_{A,B}\in [0,1]$ between paths A and B is calculated as

$${\rho }_{A,B}=\frac{\#\mathrm{Common}\mathrm{instances}\mathrm{between}A\mathrm{and}B}{\#\mathrm{Instances}\mathrm{in}A}.$$

As can be seen from Figure 3, few paths exhibit any path correlation. In total, only 14.8% of setup path pairs have non-zero correlation (0.56% for hold), that is, one or more common components with each other. Most of these have a common start point, and therefore all the paths with a common start point and large correlation (majority of shared gates) can be represented by a single distribution. As such, a reasonable approximation for critical path delay density can be obtained by assuming independence between the paths, which allows the usage of (9).

4.2. Goodness-of-Fit Statistics of the Data

In the following, we fit different probability distributions to the previously chosen datasets: normal, Pearson type IV (Pearson IV) (1) as well as the metalog (3) with six terms (metalog 6). The parameters for the former two are estimated using the maximum likelihood method; the metalog distribution is directly parameterized by the data via linear least squares [13]. The goodness-of-fit statistics (5)–(7) for each distribution and dataset are tabulated in

Table 1. Goodness-of-fit statistics for DS 1–3.

		KS	CM	AD
	Normal	0.039	0.585	4.395
DS 1	Pearson IV	0.027	0.096	0.586
	Metalog 6	0.020	0.055	0.460
	Normal	0.061	0.992	6.016
DS 2	Pearson IV	0.016	0.028	0.198
	Metalog 6	0.011	0.014	0.102
	Normal	0.022	0.107	0.918
DS 3	Pearson IV	0.017	0.051	0.370
	Metalog 6	0.016	0.025	0.211

.

The results suggest that the six-term metalog distribution offers the best fit among the candidates for each dataset, followed by the Pearson type IV distribution. The choice of six terms for the metalog distribution is based on obtaining the best possible fit while simultaneously avoiding overfitting. We observed that in some instances, having more than six terms in the metalog distribution will offer a slightly better fit, while fewer terms always yielded inferior results. However, graphical inspection revealed that having more than six terms sometimes introduces bi-modality to the distribution, which is a sign of overfitting which we wish to avoid.

While the differences in the KS test statistic values in Table 1 are somewhat negligible, the CM and AD test statistics are noticeably larger for the normal distribution than for the Pearson type IV and metalog distributions. Furthermore, the results imply the normal distribution fits rather poorly to the tails of the data, as indicated by the relatively large AD test statistic values.

4.3. Singular Path Delay Confidence Intervals

Next, we calculate the 99.7% confidence intervals of the $(1-p)$-quantiles for some values of p for DS 2–3 that are setup paths. Since DS 1 is a hold path, we compute the same confidence intervals for the p-quantiles instead. The confidence intervals are calculated with bootstrapping by resampling the original dataset with replacement ${10}^4$ times, yielding a new estimate for the quantiles in each resample. We consider the same three candidate distributions from earlier: normal, Pearson type IV and six-term metalog. The results are displayed in

Table 2. 99.7% confidence intervals of the $(1-p)$-quantiles (p-quantiles) for DS 2–3 (DS 1), in nanoseconds.

		$p=1.35\times {10}^{-3}$	$p=3.17\times {10}^{-5}$
	Normal	(5.77, 6.06)	(5.04, 5.43)
DS 1	Pearson IV	(6.02, 6.52)	(5.04, 6.23)
	Metalog 6	(5.90, 6.61)	(4.71, 6.36)
	Normal	(77.16, 79.48)	(81.07, 84.01)
DS 2	Pearson IV	(80.48, 89.28)	(87.63, 115.41)
	Metalog 6	(78.62, 85.13)	(82.96, 96.79)
	Normal	(91.85, 93.57)	(94.91, 97.13)
DS 3	Pearson IV	(92.37, 97.15)	(95.82, 107.94)
	Metalog 6	(92.43, 98.09)	(96.12, 108.12)

.

Previously, we concluded that the six-term metalog distribution appears to offer the best fit on our data. Therefore, we consider its estimates as the ’golden standard’ with which to compare other results and compute their relative errors.

The lower bounds for the quantiles in Table 2 appear to be similar across all datasets, distributions and quantiles—the relative error for the six-term metalog estimates is usually only a few percent at most. Instead, the discrepancy in the upper bound values is noticeably larger. For $p=1.35\times {10}^{-3}$, the relative errors for the six-term metalog estimates range between 4 and 8% for the normal distribution. When $p=3.17\times {10}^{-5}$, the corresponding errors vary from 10 to over 14%.

As for the Pearson type IV distribution, the relative errors for the upper bounds of the six-term metalog estimates vary between 1 and 5% for $p=1.35\times {10}^{-3}$. When $p=3.17\times {10}^{-5}$, the corresponding errors are less than 2% for DS 1 and DS 3, while it reaches over 19% for DS 2. Even though the AD statistic value for the Pearson type IV distribution is only around twice of the corresponding six-term metalog statistic for DS 2 in Table 1, it is entirely possible that the Pearson distribution does not adequately fit to the distribution tails when extrapolating far beyond the range of the data.

4.4. Multiple Critical Path Delay Distributions

As remarked earlier, the paths exhibit very little correlation, which allows us to use (9) to approximate the WID maximum critical path delay density for multiple critical paths. By assuming a single critical path has a normal, Pearson type IV or six-term metalog distribution, we can examine the effect of the number of critical paths N on the shape of the path delay density via (9).

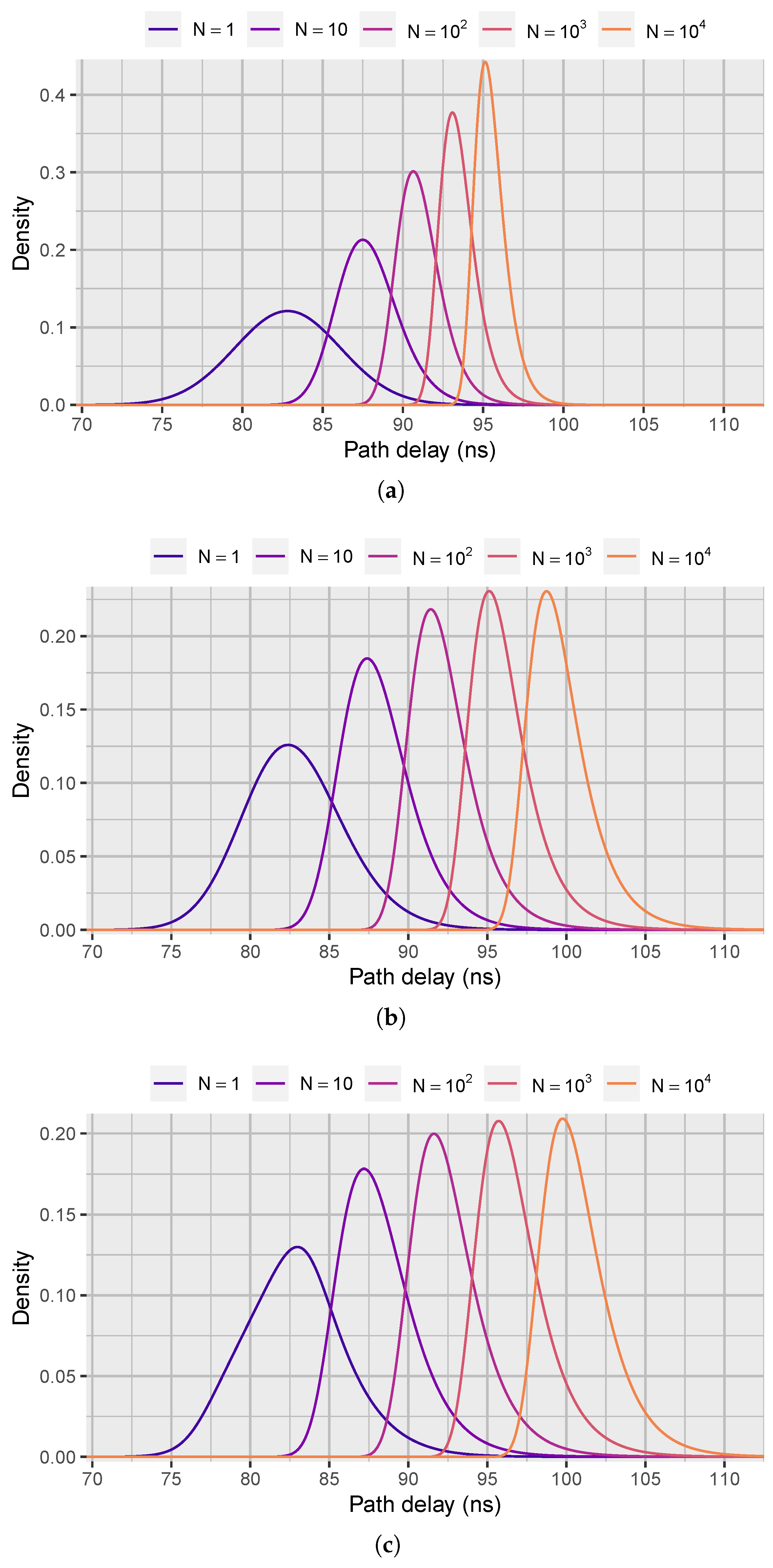
In Figure 4a–c, we have plotted the maximum critical path delay densities for different N using the three aforementioned distributions in DS 3. For the normal distributions, the variance decreases and the mean increases with N. However, increasing N from 1 to 10 has a greater impact on the shape of the distribution than increasing N from $N={10}^3$ to $N={10}^4$, as remarked in [3]. When N is larger than 1, the distribution is no longer symmetrical.

A similar decrease in variance and increase in mean with N is also observable for the Pearson type IV and six-term metalog distributions. It is worth noting, however, that the mean increases more and the variance decreases less for the two distributions than for the normal distributions. Furthermore, the normal distributions are less skewed than the other distributions.

Finally, we calculate some values of $t_{\max }$ when the probability from (8) is fixed for some N-independent critical paths. This is performed by numerically integrating the density from (9), coupled with a bisection method to find the correct $t_{\max }$. Once again, we assume a single critical path has a normal, Pearson type IV or six-term metalog distribution, and the metalog distribution estimates are considered to be the golden standard. The results are tabulated in

Table 3. The maximum (minimum) path delays of $N={10}^2$-independent critical paths corresponding to the $(1-p)$-quantile (p-quantile) for DS 2–3 (DS 1), in nanoseconds.

		$p=1.35\times {10}^{-3}$	$p=3.17\times {10}^{-5}$
	Normal	8.98	8.82
DS 1	Pearson IV	9.04	8.83
	Metalog 6	9.00	8.81
	Normal	83.41	86.72
DS 2	Pearson IV	100.77	118.30
	Metalog 6	92.60	101.04
	Normal	96.65	99.24
DS 3	Pearson IV	101.99	108.37
	Metalog 6	103.28	109.87

,

Table 4. The maximum (minimum) path delays of $N={10}^3$-independent critical paths corresponding to the $(1-p)$-quantile (p-quantile) for DS 2–3 (DS 1), in nanoseconds.

		$p=1.35\times {10}^{-3}$	$p=3.17\times {10}^{-5}$
	Normal	9.63	9.52
DS 1	Pearson IV	10.04	9.85
	Metalog 6	9.97	9.78
	Normal	85.50	88.53
DS 2	Pearson IV	111.00	131.49
	Metalog 6	97.78	106.17
	Normal	98.29	100.65
DS 3	Pearson IV	105.84	112.60
	Metalog 6	107.32	113.87

and

Table 5. The maximum (minimum) path delays of $N={10}^4$-independent critical paths corresponding to the $(1-p)$-quantile (p-quantile) for DS 2–3 (DS 1), in nanoseconds.

		$p=1.35\times {10}^{-3}$	$p=3.17\times {10}^{-5}$
	Normal	10.12	10.03
DS 1	Pearson IV	11.05	10.85
	Metalog 6	10.91	10.73
	Normal	87.40	90.21
DS 2	Pearson IV	122.94	147.00
	Metalog 6	102.96	110.87
	Normal	99.77	101.96
DS 3	Pearson IV	109.90	117.11
	Metalog 6	111.36	117.55

.

With only $N={10}^2$ critical paths, the relative errors to the six-term metalog estimates are at most 10% for the normal distribution, when $p=1.35\times {10}^{-3}$. For $p=3.17\times {10}^{-5}$, the corresponding relative errors reach 14%. When $N={10}^3$, the relative errors range from 3 to over 12% for the normal distribution for $p=1.35\times {10}^{-3}$; when $p=3.17\times {10}^{-5}$, the errors reach 16%. For $N={10}^4$, the corresponding errors are between 8 and 15% for $p=1.35\times {10}^{-3}$, and between 6 and 19% for $p=3.17\times {10}^{-5}$. It is worth noting that the relative errors are clearly higher for DS 2 and 3 than for DS 1. This is likely due to the fact that the former two sets contain paths with more atomic components than the paths in the latter.

For the Pearson type IV distribution, the relative errors to the six-term metalog estimates are less than a percentage for DS 1 and 3 with any N or p. However, the same errors are noticeably higher for DS 2, which we already noticed for the singular path confidence intervals earlier. Due to the dependence on the number of critical paths N in (9), the relative errors for the Pearson distribution in DS 2 increase with N.

5. Conclusions

Two multi-parameter distributions, namely the Pearson type IV and metalog distributions, are discussed and suggested as alternatives to the traditional normal distribution for modelling path delay data that determines the maximum clock frequency (FMAX) of a microprocessor or other digital circuit. These distributions are assessed and compared with different goodness-of-fit statistics for simulated path delay data derived from a fabricated microcontroller. The Pearson type IV and metalog distribution outperform the normal distribution for each statistic, with the six-term metalog distribution offering the best fit. Furthermore, 99.7% confidence intervals are calculated for some extreme quantiles on the datasets for each distribution. Considering the six-term metalog distribution estimates as the golden standard, the relative errors in single paths vary between 4 and 14% for the normal distribution. Finally, the within-die (WID) variation maximum critical path delay distribution for multiple critical paths is derived under the assumption of independence between the paths. Its density function is then used to compute different maximum delays $t_{\max }$ for varying numbers of critical paths N, assuming each path has one of the previous distributions with the metalog estimates as the golden standard. For $N={10}^2$ paths, the relative errors are at most 14% for the normal distribution. With $N={10}^3$ and $N={10}^4$, the corresponding errors reach 16 and 19%, respectively. The errors are clearly higher for longer paths that contain more atomic components than shorter paths with fewer components.

While this work is based on industry-standard Monte Carlo simulations, the underlying data is based on a functional integrated circuit [23], without which it would be impossible to conduct the work (or, if based on simulations of non-fabricated work, would severely undermine the validity of the results). It would be unfeasible to test a significant number of dies to prove these concepts—producing a similar amount of results via fabrication would require hundreds or thousands of fabricated chips in split lots (wafers tuned to the worst-case corners). This sort of cost is prohibitive to all academic institutions, small- and mid-sized companies, and are the sole opportunity of the largest companies and foundries.

In future work, other multi-parameter distributions which allow the study of extreme quantiles are worth exploring. For example, the Box–Cox elliptical distributions are a novel class of distributions that allow the modelling of marginally skewed and potentially heavy-tailed data [24]. In addition, parametric quantile regression models such as [25] offer an alternative approach to quantile estimation.