A Novel Combined Hybrid Group Multi-Criteria Decision-Making Model for the Selection of Power Generation Technologies
Abstract
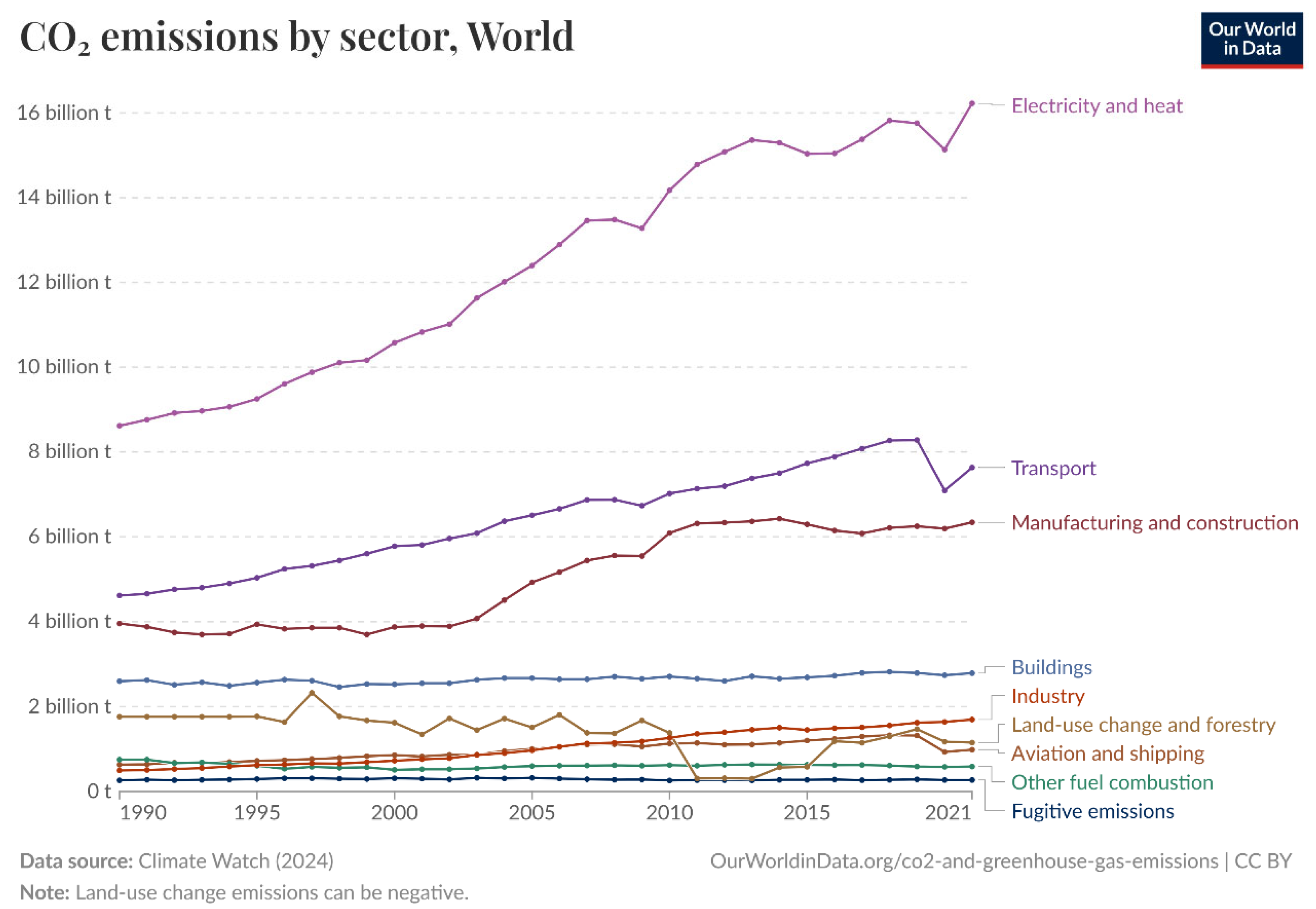
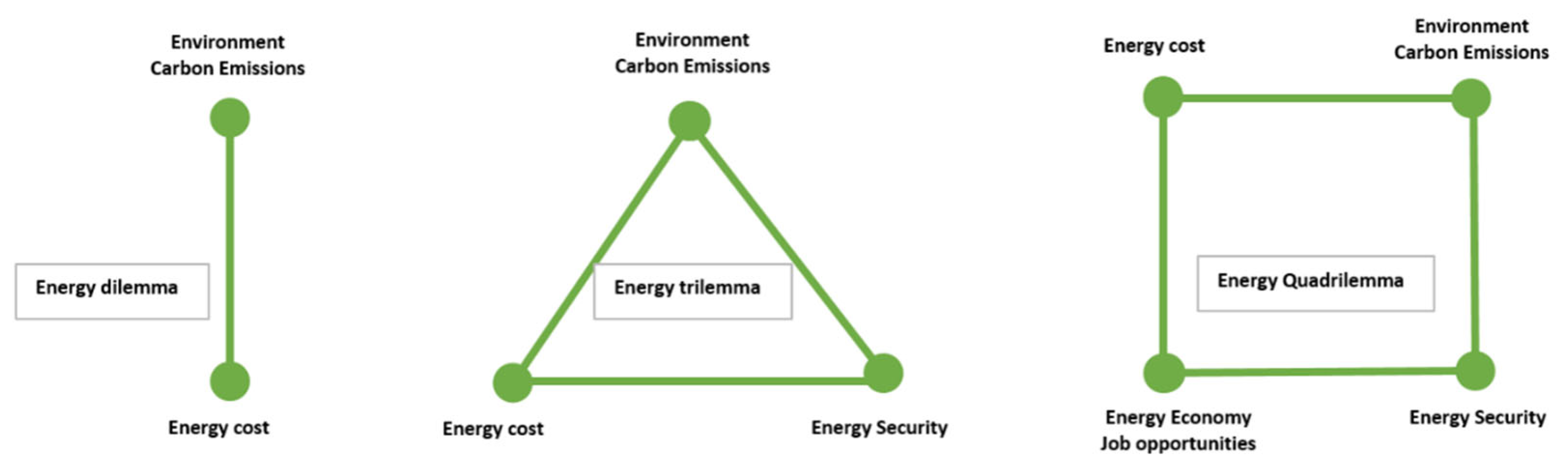
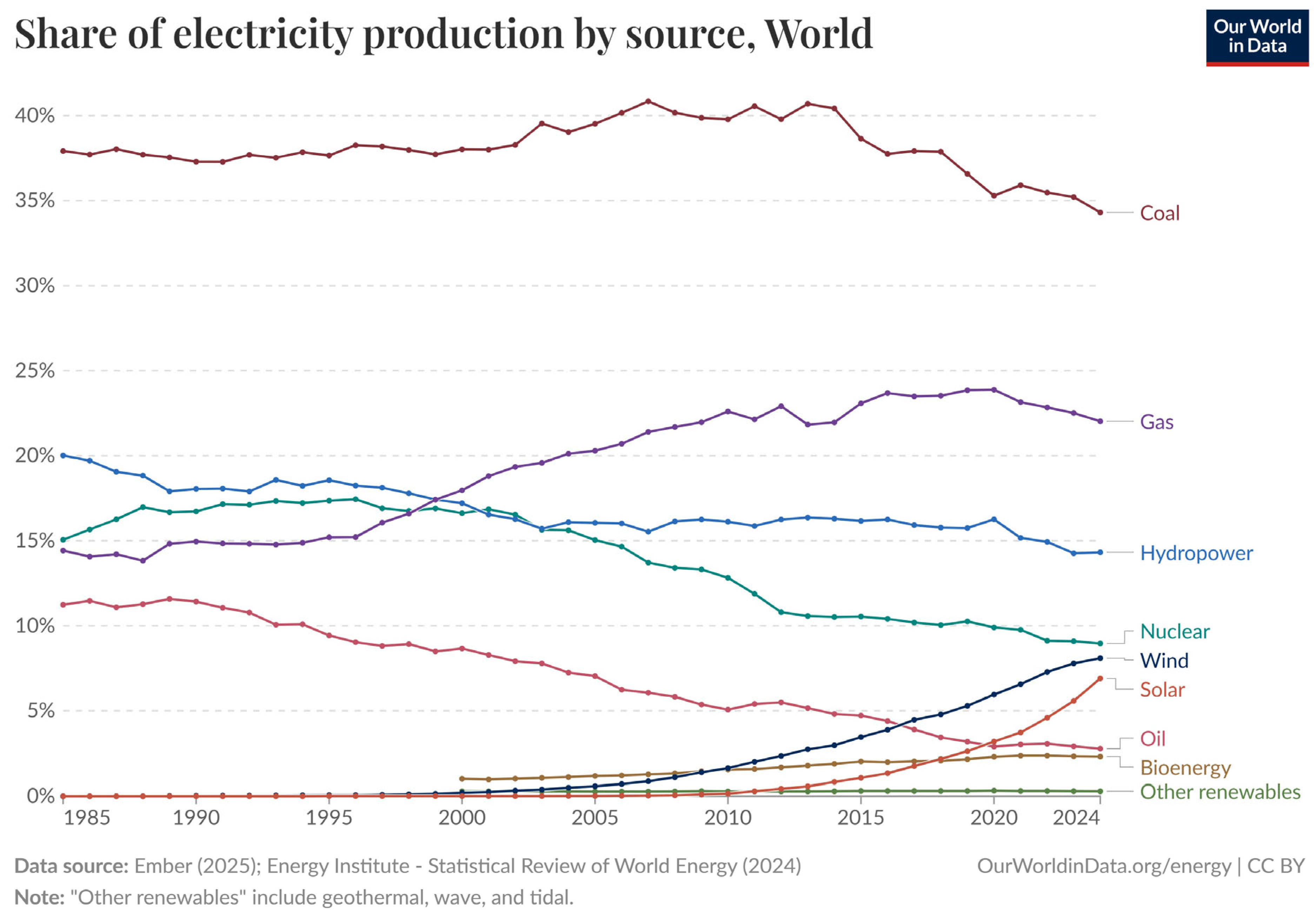
1. Introduction and Background
2. Literature Review
2.1. Methodologies
2.2. Criteria
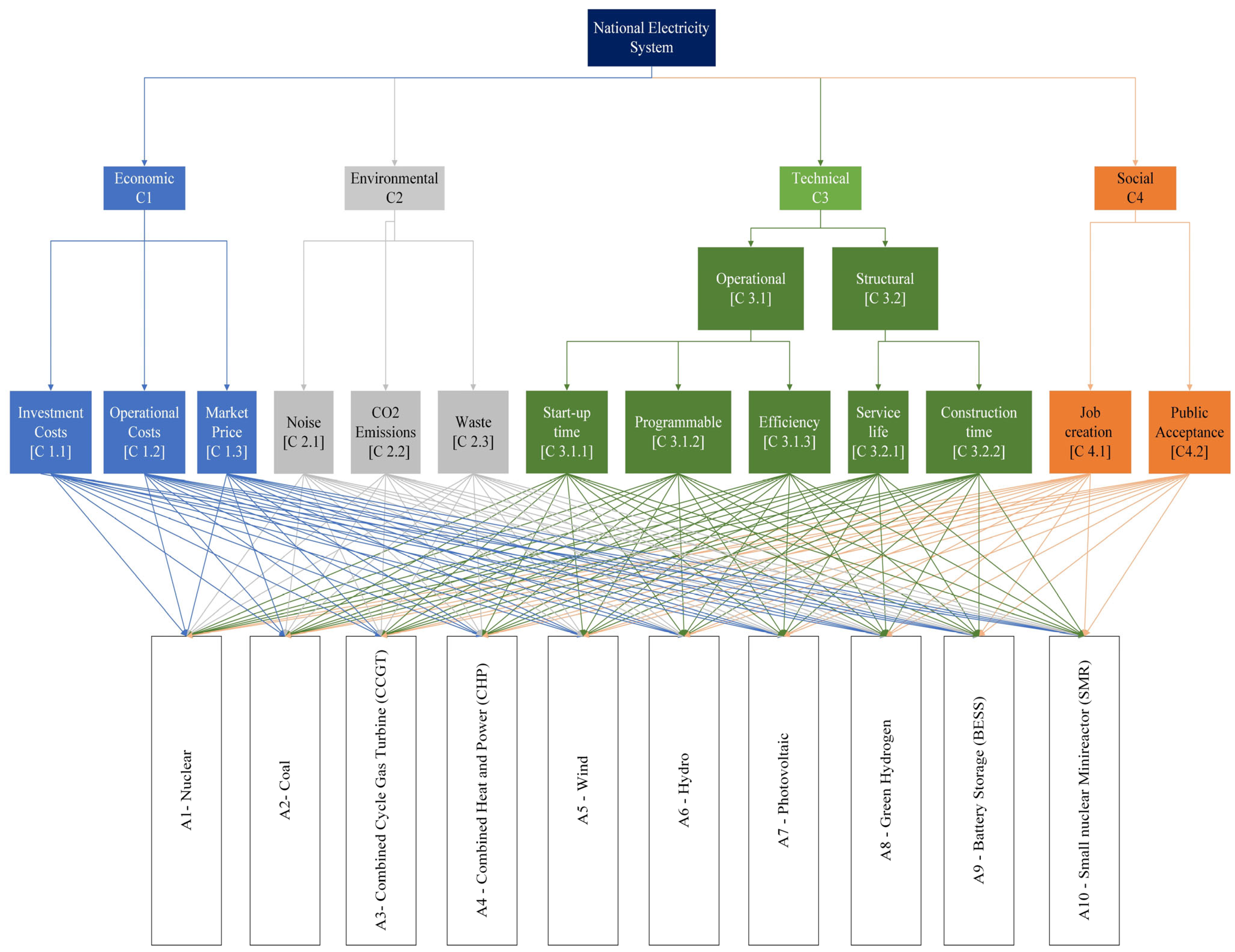
3. Proposed Model
3.1. Selected Alternatives
3.2. Selected Criteria
4. Methodology
4.1. Methodologies for the Combined Hybrid Decision Model (AHP + Fuzzy VIKOR)
4.1.1. Data Collection and Relevance Weights of Each Expert
- -
- Relevance weight of the expert “i”.
- -
- Years of professional activity of Expert “i”; Maximum among all experts.
- -
- Years of experience specialized in the Electricity Sector of Expert “i”; Maximum among all experts.
- -
- Studies degree of expert “i” [scale: 1-non-university degree, 2-bachelor’s degree, 3-master’s degree, 4-PhD]; Maximum among all experts.
- -
- Knowledge degree of the expert “i” (Likert scale [0–10]) in “m” different fields related to the Energy Sector (in our case, 4 fields: Economy, Environment, Technics and Society).
4.1.2. AHP (Weights of the Criteria)
4.1.3. Consensus Method
- (a)
- All experts reach an acceptable level of consensus (in our case all (are less than 1.01 (1%)).
- (b)
- All experts reject the modification of their PCMs.
- (c)
- A predetermined number of iterations is completed (10 in this case).
4.1.4. Fuzzy VIKOR (Ranking of Alternatives)
- (1)
- If Condition 1 is not met, iterations must be made with the next alternatives until it is fulfilled.
- (2)
- If Condition 2 is not met, the two first-ranked solutions that meet Condition 1 are accepted.
4.2. Methodologies for the Validation (BWM+ Fuzzy TOPSIS)
4.2.1. Best-Worst Method (Weights of the Criteria)
4.2.2. Fuzzy TOPSIS (Ranking of Alternatives)
5. Results, Validation and Discussion
5.1. Methodologies for the Combined Hybrid Decision Model (AHP + Fuzzy VIKOR)
5.1.1. Relevance Weights of Each Expert
5.1.2. Weights of the Criteria Using AHP
5.1.3. Consensus Method
5.1.4. Fuzzy VIKOR
5.2. Methodologies Used for the Validation (BWM + Fuzzy TOPSIS)
5.2.1. BWM (Weights of the Criteria)
5.2.2. Fuzzy TOPSIS (Ranking of Alternatives)
5.3. Comparison of Results
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Van Vactor, S.A. Historical Perspective on Energy Transitions (14 May 2018). USAEE Working Paper. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3178176 (accessed on 16 July 2025).
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Gregor, L.; Hauck, J.; Le Quéré, C.; Luijkx, I.T.; Olsen, A.; Peters, G.P.; et al. Global Carbon Budget 2022. Earth Syst. Sci. Data 2022, 14, 4811–4900. [Google Scholar] [CrossRef]
- Xu, Q.; Dhaundiyal, S.; Guan, C. Structural Conflict under the New Green Dilemma: Inequalities in Development of Renewable Energy for Emerging Economies. J. Environ. Manag. 2020, 273, 111117. [Google Scholar] [CrossRef]
- Khan, I.; Zakari, A.; Zhang, J.; Dagar, V.; Singh, S. A Study of Trilemma Energy Balance, Clean Energy Transitions, and Economic Expansion in the Midst of Environmental Sustainability: New Insights from Three Trilemma Leadership. Energy 2022, 248, 123619. [Google Scholar] [CrossRef]
- Olabi, A.G. Energy Quadrilemma and the Future of Renewable Energy. Energy 2016, 108, 1–6. [Google Scholar] [CrossRef]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2015. [Google Scholar]
- Marco-Lajara, B.; Martínez-Falcó, J.; Sánchez-García, E.; Millan-Tudela, L.A. Analyzing the Role of Renewable Energy in Meeting the Sustainable Development Goals: A Bibliometric Analysis. Energies 2023, 16, 3137. [Google Scholar] [CrossRef]
- Feng, J.-S.; Zheng, K.; Li, J.-T.; Fu, G.-J. A Re-Electrification Scenario Analysis at a Time of Worldwide Energy Transition. IOP Conf. Ser. Earth Environ. Sci. 2019, 237, 062028. [Google Scholar] [CrossRef]
- Lizana, J.; Halloran, C.E.; Wheeler, S.; Amghar, N.; Renaldi, R.; Killendahl, M.; Perez-Maqueda, L.A.; McCulloch, M.; Chacartegui, R. A National Data-Based Energy Modelling to Identify Optimal Heat Storage Capacity to Support Heating Electrification. Energy 2023, 262, 125298. [Google Scholar] [CrossRef]
- Vargas-Salgado, C.; Berna-Escriche, C.; Escriva-Castells, A.; Diaz-Bello, D. Optimization of All-Renewable Generation Mix According to Different Demand Response Scenarios to Cover All the Electricity Demand Forecast by 2040: The Case of the Grand Canary Island. Sustainability 2022, 14, 1738. [Google Scholar] [CrossRef]
- United Nations. Goal 7 Energy|Department of Economic and Social Affairs. Available online: https://sdgs.un.org/topics/energy (accessed on 7 June 2023).
- United Nations. Goal 13 Climate Change|Department of Economic and Social Affairs. Available online: https://sdgs.un.org/goals/goal13 (accessed on 4 May 2024).
- United Nations. The Paris Agreement; United Nations: New York, NY, USA, 2015. [Google Scholar]
- European Council. European Climate Law; Hart Publishing: Oxford, UK, 2016; ISBN 978-1-78225-864-3. [Google Scholar]
- European Commission. Fit for 55’: Delivering the EU’s 2030 Climate Target on the Way to Climate Neutrality; Publications Office of the European Union: Luxembourg, 2021. [Google Scholar]
- European Commission. Europe’s 2040 Climate Target and Path to Climate Neutrality by 2050 Building a Sustainable, Just and Prosperous Society; Publications Office of the European Union: Luxembourg, 2024. [Google Scholar]
- European Commission. The Net-Zero Industry Act; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar]
- European Commission. A Green Deal Industrial Plan for the Net-Zero Age; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar]
- European Commission. REPowerEU Plan; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar]
- Castillo, A.; Gayme, D.F. Grid-Scale Energy Storage Applications in Renewable Energy Integration: A Survey. Energy Conv. Manag. 2014, 87, 885–894. [Google Scholar] [CrossRef]
- Cama-Pinto, D.; Martínez-Lao, J.A.; Solano-Escorcia, A.F.; Cama-Pinto, A. Forecasted Datasets of Electric Vehicle Consumption on the Electricity Grid of Spain. Data Brief 2020, 31, 105823. [Google Scholar] [CrossRef]
- Abdin, Z.; Zafaranloo, A.; Rafiee, A.; Mérida, W.; Lipiński, W.; Khalilpour, K.R. Hydrogen as an Energy Vector. In Renewable and Sustainable Energy Reviews; Elsevier: Amsterdam, The Netherlands, 2020; Volume 120. [Google Scholar] [CrossRef]
- Li, X.; Du, M. China’s Green Industrial Policy and World Trade Law. East Asia 2025, 1–18. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A Review of Multi Criteria Decision Making (MCDM) towards Sustainable Renewable Energy Development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Martí, J.V.; Yepes, V. A Review of Multi-Criteria Decision-Making Methods Applied to the Sustainable Bridge Design. Sustainability 2016, 8, 1295. [Google Scholar] [CrossRef]
- Kaya, İ.; Çolak, M.; Terzi, F. A Comprehensive Review of Fuzzy Multi Criteria Decision Making Methodologies for Energy Policy Making. Energy Strategy Rev. 2019, 24, 207–228. [Google Scholar] [CrossRef]
- Herva, M.; Roca, E. Review of Combined Approaches and Multi-Criteria Analysis for Corporate Environmental Evaluation. J. Clean. Prod. 2013, 39, 355–371. [Google Scholar] [CrossRef]
- Bayod Rújula, A.A.; Dia, N.K. Application of a Multi-Criteria Analysis for the Selection of the Most Suitable Energy Source and Water Desalination System in Mauritania. Energy Policy 2010, 38, 99–115. [Google Scholar] [CrossRef]
- Ren, J.; Sovacool, B.K. Enhancing China’s Energy Security: Determining Influential Factors and Effective Strategic Measures. Energy Convers. Manag. 2014, 88, 589–597. [Google Scholar] [CrossRef]
- Solangi, Y.A.; Tan, Q.; Khan, M.W.A.; Mirjat, N.H.; Ahmed, I. The Selection of Wind Power Project Location in the Southeastern Corridor of Pakistan: A Factor Analysis, AHP, and Fuzzy-TOPSIS Application. Energies 2018, 11, 1940. [Google Scholar] [CrossRef]
- Taylan, O.; Alamoudi, R.; Kabli, M.; AlJifri, A.; Ramzi, F.; Herrera-Viedma, E. Assessment of Energy Systems Using Extended Fuzzy AHP, Fuzzy VIKOR, and TOPSIS Approaches to Manage Non-Cooperative Opinions. Sustainability 2020, 12, 2745. [Google Scholar] [CrossRef]
- Çolak, M.; Kaya, İ. Prioritization of Renewable Energy Alternatives by Using an Integrated Fuzzy MCDM Model: A Real Case Application for Turkey. Renew. Sustain. Energy Rev. 2017, 80, 840–853. [Google Scholar] [CrossRef]
- Rubio-Aliaga, A.; García-Cascales, M.S.; Sánchez-Lozano, J.M.; Molina-Garcia, A. MCDM-Based Multidimensional Approach for Selection of Optimal Groundwater Pumping Systems: Design and Case Example. Renew. Energy 2021, 163, 213–224. [Google Scholar] [CrossRef]
- Solangi, Y.A.; Tan, Q.; Mirjat, N.H.; Valasai, G.D.; Khan, M.W.A.; Ikram, M. An Integrated Delphi-AHP and Fuzzy TOPSIS Approach toward Ranking and Selection of Renewable Energy Resources in Pakistan. Processes 2019, 7, 118. [Google Scholar] [CrossRef]
- Al Garni, H.; Kassem, A.; Awasthi, A.; Komljenovic, D.; Al-Haddad, K. A Multicriteria Decision Making Approach for Evaluating Renewable Power Generation Sources in Saudi Arabia. Sustain. Energy Technol. Assess. 2016, 16, 137–150. [Google Scholar] [CrossRef]
- San Cristóbal, J.R. Multi-Criteria Decision-Making in the Selection of a Renewable Energy Project in Spain: The Vikor Method. Renew. Energy 2011, 36, 498–502. [Google Scholar] [CrossRef]
- Amer, M.; Daim, T.U. Selection of Renewable Energy Technologies for a Developing County: A Case of Pakistan. Energy Sustain. Dev. 2011, 15, 420–435. [Google Scholar] [CrossRef]
- Heo, E.; Kim, J.; Boo, K.-J. Analysis of the Assessment Factors for Renewable Energy Dissemination Program Evaluation Using Fuzzy AHP. Renew. Sustain. Energy Rev. 2010, 14, 2214–2220. [Google Scholar] [CrossRef]
- Faraji Abdolmaleki, S.; Esfandiary Abdolmaleki, D.; Bello Bugallo, P.M. Finding Sustainable Countries in Renewable Energy Sector: A Case Study for an EU Energy System. Sustainability 2023, 15, 10084. [Google Scholar] [CrossRef]
- Sakthivel, G.; Sivakumar, R.; Saravanan, N.; Ikua, B.W. A Decision Support System to Evaluate the Optimum Fuel Blend in an IC Engine to Enhance the Energy Efficiency and Energy Management. Energy 2017, 140, 566–583. [Google Scholar] [CrossRef]
- Gribiss, H.; Aghelinejad, M.M.; Yalaoui, F. Configuration Selection for Renewable Energy Community Using MCDM Methods. Energies 2023, 16, 2632. [Google Scholar] [CrossRef]
- Ecer, F. Sustainability Assessment of Existing Onshore Wind Plants in the Context of Triple Bottom Line: A Best-Worst Method (BWM) Based MCDM Framework. Environ. Sci. Pollut. Res. 2021, 28, 19677–19693. [Google Scholar] [CrossRef]
- Elena Arce, M.; Saavedra, Á.; Míguez, J.L.; Granada, E. The Use of Grey-Based Methods in Multi-Criteria Decision Analysis for the Evaluation of Sustainable Energy Systems: A Review. Renew. Sustain. Energy Rev. 2015, 47, 924–932. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, S. External Benefit Evaluation of Renewable Energy Power in China for Sustainability. Sustainability 2015, 7, 4783–4805. [Google Scholar] [CrossRef]
- Börcsök, E.; Groma, V.; Gerse, Á.; Osán, J. Determination of Country-Specific Criteria Weights for Long-Term Energy Planning in Europe. Energies 2023, 16, 4920. [Google Scholar] [CrossRef]
- Martínez-García, M.; Valls, A.; Moreno, A.; Aldea, A. A Semantic Multi-Criteria Approach to Evaluate Different Types of Energy Generation Technologies. Environ. Model. Softw. 2018, 110, 129–138. [Google Scholar] [CrossRef]
- Mousavi-Nasab, S.H.; Sotoudeh-Anvari, A. An Extension of Best-Worst Method with D Numbers: Application in Evaluation of Renewable Energy Resources. Sustain. Energy Technol. Assess. 2020, 40, 100771. [Google Scholar] [CrossRef]
- Ilbahar, E.; Kahraman, C.; Cebi, S. Evaluation of Sustainable Energy Planning Scenarios with a New Approach Based on FCM, WASPAS and Impact Effort Matrix. Environ. Dev. Sustain. 2022, 25, 11931–11955. [Google Scholar] [CrossRef]
- Ren, J.; Man, Y.; Lin, R.; Liu, Y. Chapter 16—Multicriteria Decision Making for the Selection of the Best Renewable Energy Scenario Based on Fuzzy Inference System. In Renewable-Energy-Driven Future; Ren, J., Ed.; Academic Press: London, UK, 2021; pp. 491–507. ISBN 978-0-12-820539-6. [Google Scholar]
- Rivero-Iglesias, J.M.; Puente, J.; Fernandez, I.; León, O. Integrated Model for the Assessment of Power Generation Alternatives through Analytic Hierarchy Process and a Fuzzy Inference System. Case Study of Spain. Renewable Energy 2023, 211, 563–581. [Google Scholar] [CrossRef]
- Neofytou, H.; Karakosta, C.; Gómez, N.C. Impact Assessment of Climate and Energy Policy Scenarios: A Multi-Criteria Approach. In Understanding Risks and Uncertainties in Energy and Climate Policy: Multidisciplinary Methods and Tools for a Low Carbon Society; Doukas, H., Flamos, A., Lieu, J., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 123–142. ISBN 978-3-030-03152-7. [Google Scholar]
- Martín-Gamboa, M.; Iribarren, D.; García-Gusano, D.; Dufour, J. Enhanced Prioritisation of Prospective Scenarios for Power Generation in Spain: How and Which One? Energy 2019, 169, 369–379. [Google Scholar] [CrossRef]
- Kahraman, C.; Kaya, İ.; Cebi, S. A Comparative Analysis for Multiattribute Selection among Renewable Energy Alternatives Using Fuzzy Axiomatic Design and Fuzzy Analytic Hierarchy Process. Energy 2009, 34, 1603–1616. [Google Scholar] [CrossRef]
- Sarkodie, W.O.; Ofosu, E.A.; Ampimah, B.C. Decision Optimization Techniques for Evaluating Renewable Energy Resources for Power Generation in Ghana: MCDM Approach. Energy Rep. 2022, 8, 13504–13513. [Google Scholar] [CrossRef]
- Kahraman, C.; Kaya, İ. A Fuzzy Multicriteria Methodology for Selection among Energy Alternatives. Expert Syst. Appl. 2010, 37, 6270–6281. [Google Scholar] [CrossRef]
- Ijadi Maghsoodi, A.; Ijadi Maghsoodi, A.; Mosavi, A.; Rabczuk, T.; Zavadskas, E.K. Renewable Energy Technology Selection Problem Using Integrated H-SWARA-MULTIMOORA Approach. Sustainability 2018, 10, 4481. [Google Scholar] [CrossRef]
- Hernández-Torres, J.A.; Sánchez-Lozano, D.; Sánchez-Herrera, R.; Vera, D.; Torreglosa, J.P. Integrated Multi-Criteria Decision-Making Approach for Power Generation Technology Selection in Sustainable Energy Systems. Renew. Energy 2025, 243, 122481. [Google Scholar] [CrossRef]
- Lotfipour, A.; Mohtavipour, S.S. A Multi-Criteria Decision-Making Model to Determine the Optimal Share of Variable Renewable Energy Sources in a Wholesale Electricity Market. Sustain. Energy Grids Netw. 2024, 39, 101408. [Google Scholar] [CrossRef]
- Parvaneh, F.; Hammad, A. Application of Multi-Criteria Decision-Making (MCDM) to Select the Most Sustainable Power-Generating Technology. Sustainability 2024, 16, 3287. [Google Scholar] [CrossRef]
- Arıkan Kargı, V.S.; Cesur, F. Renewable Energy Technology Selection for Hotel Buildings: A Systematic Approach Based on AHP and VIKOR Methods. Buildings 2024, 14, 2662. [Google Scholar] [CrossRef]
- Chen, Z.; Zhong, P.; Liu, M.; Ma, Q.; Si, G. An Integrated Expert Weight Determination Method for Design Concept Evaluation. Sci. Rep. 2022, 12, 6358. [Google Scholar] [CrossRef]
- Sánchez-Garrido, A.J.; Navarro, I.J.; Yepes, V. Multi-Criteria Decision-Making Applied to the Sustainability of Building Structures Based on Modern Methods of Construction. J. Clean. Prod. 2022, 330, 129724. [Google Scholar] [CrossRef]
- Saaty, R.W. The Analytic Hierarchy Process—What It Is and How It Is Used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Dong, Q.; Saaty, T.L. An Analytic Hierarchy Process Model of Group Consensus. J. Syst. Sci. Syst. Eng. 2014, 23, 362–374. [Google Scholar] [CrossRef]
- Dong, Q.; Zhü, K.; Cooper, O. Gaining Consensus in a Moderated Group: A Model with a Twofold Feedback Mechanism. Expert Syst. Appl. 2017, 71, 87–97. [Google Scholar] [CrossRef]
- Haseli, G.; Sheikh, R.; Wang, J.; Tomaskova, H.; Tirkolaee, E.B. A Novel Approach for Group Decision Making Based on the Best–Worst Method (G-BWM): Application to Supply Chain Management. Mathematics 2021, 9, 1881. [Google Scholar] [CrossRef]
- Minaei, B.; Akbarzadeh Khorshidi, H.; Aickelin, U.; Geramian, A. Cloud Model-Based Best-Worst Method for Group Decision Making under Uncertainty. INFOR Inf. Syst. Oper. Res. 2023, 62, 232–258. [Google Scholar] [CrossRef]
- Dumrul, C.; Bilgili, F.; Zarali, F.; Dumrul, Y.; Kiliçarslan, Z. The Evaluation of Renewable Energy Alternatives in Turkey Using Intuitionistic-Fuzzy EDAS Methodology. Environ. Sci. Pollut. Res. 2024, 31, 15503–15524. [Google Scholar] [CrossRef] [PubMed]
- Gul, M.; Ak, M.F.; Guneri, A.F. Pythagorean Fuzzy VIKOR-Based Approach for Safety Risk Assessment in Mine Industry. J. Saf. Res. 2019, 69, 135–153. [Google Scholar] [CrossRef]
- Hadadian, Z.; Mesbah, K. Selecting an Effective Leader-a Competency Based Fuzzy Vikor Analysis Model. QUID-Investig. Cienc. Tecnol. 2017, Special Issue 1, 2036–2045, ISSN:1692-343X. [Google Scholar]
- Jing, S.; Tang, Y.; Yan, J. The Application of Fuzzy VIKOR for the Design Scheme Selection in Lean Management. Math. Probl. Eng. 2018, 2018, e9253643. [Google Scholar] [CrossRef]
- Musani, S.; Jemain, A.A. Ranking Schools’ Academic Performance Using a Fuzzy VIKOR. J. Phys. Conf. Ser. 2015, 622, 012036. [Google Scholar] [CrossRef]
- Nuriyev, M.; Nuriyev, A.; Mammadov, J. Renewable Energy Transition Task Solution for the Oil Countries Using Scenario-Driven Fuzzy Multiple-Criteria Decision-Making Models: The Case of Azerbaijan. Energies 2023, 16, 8068. [Google Scholar] [CrossRef]
- Peleckis, K. Application of the Fuzzy VIKOR Method to Assess Concentration and Its Effects on Competition in the Energy Sector. Energies 2022, 15, 1349. [Google Scholar] [CrossRef]
- Saraswat, S.; Digalwar, A.; Yadav, S. Development of Assessment Model for Selection of Sustainable Energy Source in India: Hybrid Fuzzy MCDM Approach. In Proceedings of the Intelligent and Fuzzy Techniques: Smart and Innovative Solutions (INFUS 2020), Istanbul, Turkey, 21–23 July 2020; Springer: Cham, Switzerland, 2021; pp. 649–657, ISBN 978-3-030-51155-5. [Google Scholar]
- Savoji, H.; Mousavi Einehvarzani, M. Renewable Energy-Based Sustainable Oilseed Selection Problem: A New Integrated Group Decision Model under Dynamic Uncertainty. Environ. Dev. Sustain. 2024, 27, 13257–13286. [Google Scholar] [CrossRef]
- Taherdoost, H.; Madanchian, M. Multi-Criteria Decision Making (MCDM) Methods and Concepts. Encyclopedia 2023, 3, 77–87. [Google Scholar] [CrossRef]
- Muñoz Medina, B.; Romana García, M. Aplicación de métodos de decisión multicriterio discretos al análisis de alternativas en estudios informativos de infraestructuras de transporte. Pensam. Matemático 2016, 6, 27–45. [Google Scholar]
- Rezaei, J. Best-Worst Multi-Criteria Decision-Making Method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Liang, F.; Brunelli, M.; Rezaei, J. Consistency Issues in the Best Worst Method: Measurements and Thresholds. Omega 2020, 96, 102175. [Google Scholar] [CrossRef]
- Mohammadi, M.; Rezaei, J. Bayesian Best-Worst Method: A Probabilistic Group Decision Making Model. Omega 2020, 96, 102075. [Google Scholar] [CrossRef]
- Rezaei, J. Best-Worst Multi-Criteria Decision-Making Method: Some Properties and a Linear Model. Omega 2016, 64, 126–130. [Google Scholar] [CrossRef]
- Tavana, M.; Mina, H.; Santos-Arteaga, F.J. A General Best-Worst Method Considering Interdependency with Application to Innovation and Technology Assessment at NASA. J. Bus. Res. 2023, 154, 113272. [Google Scholar] [CrossRef]
- Van de Kaa, G.; Fens, T.; Rezaei, J. Residential Grid Storage Technology Battles: A Multi-Criteria Analysis Using BWM. Technol. Anal. Strateg. Manag. 2019, 31, 40–52. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, X.; Zhou, L.; Qin, J.; Rezaei, J. An Analytical Framework for the Best–Worst Method. Omega 2024, 123, 102974. [Google Scholar] [CrossRef]
- Rostampour, S. An Application of TOPSIS for Ranking Internet Web Browsers. Decis. Sci. Lett. 2012, 1, 53–58. [Google Scholar]
- Sun, C.-C.; Lin, G.T.R. Using Fuzzy TOPSIS Method for Evaluating the Competitive Advantages of Shopping Websites. Expert Syst. Appl. 2009, 36, 11764–11771. [Google Scholar] [CrossRef]
- Yang, T.; Chen, M.-C.; Hung, C.-C. Multiple Attribute Decision-Making Methods for the Dynamic Operator Allocation Problem. Math. Comput. Simul. 2007, 73, 285–299. [Google Scholar] [CrossRef]
- Galiano Bastarrica, L.A.; Buitrago Esquinas, E.M.; Caraballo Pou, M.Á.; Yñiguez Ovando, R. An Integrated Assessment Model for Comparing Electricity Decarbonisation Scenarios: The Case for Spain. Energy Policy 2023, 178, 113592. [Google Scholar] [CrossRef]
- García-Gusano, D.; Iribarren, D.; Dufour, J. Is Coal Extension a Sensible Option for Energy Planning? A Combined Energy Systems Modelling and Life Cycle Assessment Approach. Energy Policy 2018, 114, 413–421. [Google Scholar] [CrossRef]
- Navas-Anguita, Z.; García-Gusano, D.; Iribarren, D. Prospective Life Cycle Assessment of the Increased Electricity Demand Associated with the Penetration of Electric Vehicles in Spain. Energies 2018, 11, 1185. [Google Scholar] [CrossRef]
- Parrado-Hernando, G.; Pfeifer, A.; Frechoso, F.; Miguel González, L.J.; Duić, N. A Novel Approach to Represent the Energy System in Integrated Assessment Models. Energy 2022, 258, 124743. [Google Scholar] [CrossRef]
- San Miguel, G.; Cerrato, M. Life Cycle Sustainability Assessment of the Spanish Electricity: Past, Present and Future Projections. Energies 2020, 13, 1896. [Google Scholar] [CrossRef]
- Lu, Q.; Liu, M. A Multi-Criteria Compromise Ranking Decision-Making Approach for Analysis and Evaluation of Community-Integrated Energy Service System. Energy 2024, 306, 132439. [Google Scholar] [CrossRef]
- Sharaf, I.M.; Albahri, O.S.; Alsalem, M.A.; Alamoodi, A.H.; Albahri, A.S. A Novel Dual-Level Multi-Source Information Fusion Approach for Multicriteria Decision Making Applications. Appl. Intell. 2024, 54, 11577–11602. [Google Scholar] [CrossRef]
- Ji, Z.; Li, W.; Niu, D. Optimal Investment Decision of Agrivoltaic Coupling Energy Storage Project Based on Distributed Linguistic Trust and Hybrid Evaluation Method. Appl. Energy 2024, 353, 122139. [Google Scholar] [CrossRef]
- Taha Aljburi, M.; Albahri, A.S.; Albahri, O.S.; Alamoodi, A.H.; Mahdi Mohammed, S.; Deveci, M.; Tomášková, H. Exploring Decision-Making Techniques for Evaluation and Benchmarking of Energy System Integration Frameworks for Achieving a Sustainable Energy Future. Energy Strategy Rev. 2024, 51, 101251. [Google Scholar] [CrossRef]
- Xiao, D.; Peng, Z.; Lin, Z.; Zhong, X.; Wei, C.; Dong, Z.; Wu, Q. Incorporating Financial Entities into Spot Electricity Market with Renewable Energy via Holistic Risk-Aware Bilevel Optimization. Appl. Energy 2025, 398, 126449. [Google Scholar] [CrossRef]



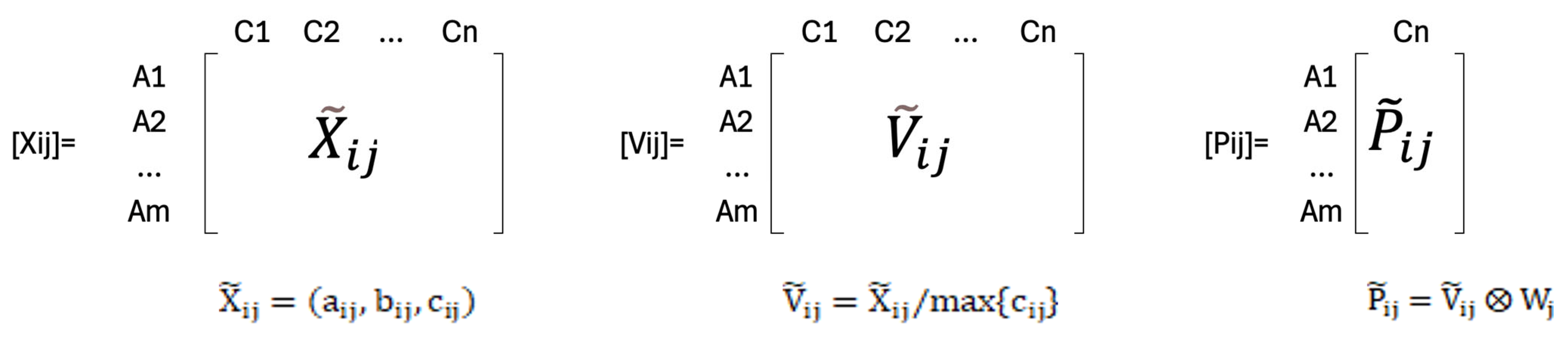


| Methodologies (*) | Reference Number | Consensus | RES (**), Fossil or Both | Country |
|---|---|---|---|---|
| AHP | [35] | RES | Saudi Arabia | |
| AHP | [37] | RES | Pakistan | |
| AHP, Fuzzy-GRA | [44] | RES | China | |
| AHP, TOPSIS | [33] | Global | ||
| AHP, VIKOR | [36] | RES | Spain | |
| AHP, ELECTRE, VIKOR, TOPSIS | [26] | RES | Turkey, global | |
| AHP and grey-based methods | [43] | RES | Global | |
| BWM | [42] | RES | Turkey | |
| D-BWM | [47] | RES | Iran | |
| Delphi, FAHP, FVIKOR, TOPSIS | [31] | X | RES | Saudi Arabia |
| ELECTRE | [46] | Both | Global | |
| Life-cycle assessment, DEA | [52] | Both | Spain | |
| FA, AHP, FTOPSIS | [30] | RES | Pakistan | |
| FAHP | [38] | RES | Korea | |
| FAHP | [39] | X | Both | Europe |
| FAHP | [29] | Both | China | |
| FAHP, Axiomatic Design | [53] | RES | Turkey | |
| FAHP, FTOPSIS | [32] | RES | Turkey | |
| FIS | [49] | RES | Global | |
| FIS | [50] | Both | Spain | |
| GAMS (Other) | [45] | Both | Europe | |
| PROMETHEE, Sim | [51] | Both | Europe | |
| WASPAS | [48] | RES | Global | |
| WS, WP, TOPSIS, EDAS | [41] | RES | Europe |
| Main Criteria | # | Sub-Criteria | # | Related References |
|---|---|---|---|---|
| Economic | 16 | Investment (Capital) cost | 12 | [29,31,34,35,36,42,44,50,51,53,54,55] |
| Operation and maintenance cost | 7 | [34,35,36,42,44,51,53] | ||
| National economic development | 5 | [30,31,34,50,51] | ||
| Technology cost | 2 | [34,45] | ||
| Electric cost | 1 | [36] | ||
| Fuel costs | 1 | [42] | ||
| Grid connection costs | 1 | [29] | ||
| R&D Cost | 1 | [36] | ||
| Levelized cost of energy (LCOE) | 3 | [31,45,51] | ||
| Operational life | 3 | [31,35,37] | ||
| Payback Period | 1 | [31] | ||
| Net present cost | 4 | [30,36,54,55] | ||
| Electricity price | 1 | [50] | ||
| Net import of energy | 1 | [50] | ||
| Road availability | 1 | [29] | ||
| Availability of funds | 4 | [31,37,54,55] | ||
| Power grid company revenue reduction | 1 | [43] | ||
| Power generation company cost increase | 1 | [43] | ||
| Electric power consumer expenditure increase | 1 | [43] | ||
| Economic growth promoting degree | 2 | [43,53] | ||
| Supply capability | 1 | [38] | ||
| Technical/Technological | 14 | Ease of decentralization | 2 | [34,51] |
| Efficiency | 7 | [30,31,34,36,42,51,53] | ||
| Exergy (rational efficiency) | 1 | [42] | ||
| Maturity | 6 | [31,34,36,37,42,51] | ||
| Implementation Period | 4 | [31,35,54,55] | ||
| Lead time | 4 | [31,36,54,55] | ||
| Risk | 5 | [31,44,53,54,55] | ||
| Safety | 2 | [30,34] | ||
| Production Capacity | 5 | [30,31,35,51,53] | ||
| Reliability | 6 | [31,36,37,53,54,55] | ||
| Possibility of acquiring original technology | 1 | [37] | ||
| Availability | 6 | [29,30,34,35,36,51] | ||
| On grid access | 1 | [36] | ||
| Installed capacity | 1 | [31] | ||
| HR experts | 5 | [29,31,36,54,55] | ||
| Programmable/Predictability | 4 | [31,53,54,55] | ||
| Feasibility | 3 | [31,54,55] | ||
| Climate | 1 | [29] | ||
| Energy intensity (2010=100) | 1 | [50] | ||
| Flexibility | 1 | [44] | ||
| Primary energy ratio | 2 | [37,42] | ||
| Storability | 1 | [30] | ||
| Environmental | 15 | CO2 emission | 3 | [35,36,51] |
| Air pollution | 4 | [30,44,54,55] | ||
| Greenhouse gas emissions | 3 | [31,42,53] | ||
| Land use/requirement | 8 | [29,31,34,36,37,51,54,55] | ||
| Impact on environment | 6 | [29,31,34,36,44,45] | ||
| Potential for reduction of greenhouse gases | 3 | [37,43,50] | ||
| Water consumption | 2 | [43,45] | ||
| Human health impact | 1 | [29] | ||
| Waste disposal | 4 | [31,45,54,55] | ||
| Other environmental effects | 3 | [29,31,43] | ||
| Renewables share overall | 1 | [50] | ||
| Energy savings | 1 | [50] | ||
| Social | 13 | Social acceptability | 6 | [29,31,36,37,54,55] |
| Job creation | 10 | [29,31,34,36,43,50,51,53,54,55] | ||
| Social Benefits | 2 | [29,36] | ||
| External costs (human health) | 2 | [42,50] | ||
| Maintain country’s leading position | 1 | [34] | ||
| Tax increase | 1 | [43] | ||
| Technical innovation promoting degree | 1 | [43] | ||
| Energy related expenditures of households | 1 | [50] | ||
| Sustainability | 1 | [31] | ||
| Durability | 1 | [31] | ||
| Distance to user | 2 | [29,31] | ||
| Political | 11 | Policy | 5 | [29,31,37,54,55] |
| Political acceptance | 6 | [31,34,51,53,54,55] | ||
| National economic benefits | 2 | [36,50] | ||
| National energy security | 3 | [36,37,43] | ||
| Relocation and rehabilitation | 2 | [29,37] | ||
| Geo-political factors | 2 | [37,44] | ||
| Government support | 1 | [30] | ||
| Market | 1 | Domestic market size and competitiveness | 1 | [38] |
| Global market size and competitiveness | 1 | [38] | ||
| Competitive power of domestic technology | 1 | [38] |
| Reference | [35] | [37] | [43] | [32] | [55] | [53] | [30] | [44] | [51] | [46] | [54] | [56] | [38] | [31] | [46] | [36] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alternatives | 5 | 4 | 7 | 9 | 5 | 8 | 3 | 5 | 9 | 5 | 6 | 8 | 9 | 13 | ||
| Experts | 20 | 3 | 4 | 4 | 5 | 4 | 8 | 25 | 9 | |||||||
| Criteria | 4 | 5 | 4 | 6 | 4 | 4 | 5 | 3 | 4 | 5 | 4 | 3 | 5 | 4 | 2 | 3 |
| Subcriteria | 14 | 20 | 9 | 29 | 17 | 17 | 16 | 11 | 12 | 7 | 13 | 11 | 17 | 9 | 5 | 7 |
| Country | Saudi Arabia | Pakistan | Turkey | Turkey | Turkey | Pakistan | China | EU | EU | Ghana | Iran | Korea | Saudi Arabia | United Kingdom | Spain |
| Intensity | Importance of One Over Another | Explanation |
|---|---|---|
| 1 | Equal importance | Two activities contribute equally to the objective |
| 3 | Moderate importance | Experience or judgements slightly favours one criterion over another |
| 5 | Essential or strong importance | Experience or judgements strongly favours one criterion over another |
| 7 | Very strong importance | An activity is strongly favoured, and its dominance demonstrated in practice |
| 9 | Extreme importance | The evidence favouring one activity over another is of the highest possible |
| 2, 4, 6, 8 | Intermediate values | When compromise is needed |
| Consistency Index (CI) | |||||||||
| aBW | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Consistency Index | 0 | 0.44 | 1 | 1.63 | 2.3 | 3 | 3.73 | 4.47 | 5.23 |
| Relevance weights of experts | Exp. 1 | Exp. 2 | Exp. 3 | Exp. 4 | Exp. 5 | Exp. 6 | |
|---|---|---|---|---|---|---|---|
| Experts’ individual experience: | |||||||
| Years of Professional Activity (PA) | 28 | 22 | 30 | 42 | 29 | 29 | |
| Years within the Energy Sector (ES) | 28 | 22 | 25 | 42 | 27 | 29 | |
| Academic Degree (AD) | 4 | 4 | 4 | 4 | 4 | 4 | |
| Knowledge Degree in energy sector fields (KD): | |||||||
| Economic Knowledge (KDEc) | 8 | 6 | 9 | 5 | 8 | 8 | |
| Environmental Knowledge (KDEnv) | 6 | 9 | 9 | 6 | 7 | 9 | |
| Technical Knowledge (KDTech) | 7 | 7 | 8 | 7 | 8 | 8 | |
| Social Knowledge (KDSoc) | 6 | 9 | 7 | 3 | 7 | 7 | |
| Expert Relevance | 1.298 | 1.400 | 1.509 | 1.179 | 1.405 | 1.483 | SUM: |
| Normalized Expert Relevance | 0.157 | 0.169 | 0.182 | 0.142 | 0.170 | 0.179 | 1.000 |
| Expert 1 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ1 = 0.157 | [Iij] | [I*ij] | Wi | ||||||||||
| C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | Consistency | |||||
| C1 | 1.0 | 2.0 | 2.0 | 2.0 | C1 | 0.40 | 0.36 | 0.50 | 0.29 | C1 | 0.39 | 0.041 | CI |
| C2 | 0.5 | 1.0 | 0.5 | 2.0 | C2 | 0.20 | 0.18 | 0.13 | 0.29 | C2 | 0.20 | 0.882 | RI |
| C3 | 0.5 | 2.0 | 1.0 | 2.0 | C3 | 0.20 | 0.36 | 0.25 | 0.29 | C3 | 0.27 | 0.046 | CR |
| C4 | 0.5 | 0.5 | 0.5 | 1.0 | C4 | 0.20 | 0.09 | 0.13 | 0.14 | C4 | 0.14 | 0.090 | Threshold |
| Sum | 2.5 | 5.5 | 4.0 | 7.0 | Sum | 1.00 | OK | ||||||
| Group of Experts | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G0 = [G0ij] | [G0*ij] | W0i | |||||||||||
| C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | Consistency | |||||
| C1 | 1.00 | 0.97 | 1.75 | 2.04 | C1 | 0.32 | 0.31 | 0.36 | 0.31 | C1 | 0.32 | 0.002 | CI |
| C2 | 1.03 | 1.00 | 1.42 | 2.13 | C2 | 0.33 | 0.32 | 0.29 | 0.32 | C2 | 0.32 | 0.882 | RI |
| C3 | 0.57 | 0.70 | 1.00 | 1.45 | C3 | 0.18 | 0.22 | 0.21 | 0.22 | C3 | 0.21 | 0.003 | CR |
| C4 | 0.49 | 0.47 | 0.69 | 1.00 | C4 | 0.16 | 0.15 | 0.14 | 0.15 | C4 | 0.15 | 0.090 | Threshold |
| Sum | 3.09 | 3.14 | 4.86 | 6.61 | Sum | 1.00 | OK | ||||||
| Criteria/Subcriteria | Local Weights | Global Weights | ID | ||||
|---|---|---|---|---|---|---|---|
| 1st level | 2nd Level | 3rd Level | 1st Level | 2nd Level | 3rd Level | ||
| Economic | Investment cost | 0.32 | 0.434 | 0.141 | C 1.1 | ||
| Operation cost | 0.236 | 0.077 | C 1.2 | ||||
| Market price | 0.330 | 0.107 | C 1.3 | ||||
| Environmental | Noise | 0.32 | 0.087 | 0.027 | C 2.1 | ||
| CO2 Emissions | 0.618 | 0.196 | C 2.2 | ||||
| Waste | 0.295 | 0.093 | C 2.3 | ||||
| Technical | Operational | Start-up time | 0.21 | 0.721 | 0.180 | 0.027 | C 3.1.1 |
| Programmable | 0.344 | 0.052 | C 3.1.2 | ||||
| Efficiency | 0.476 | 0.071 | C 3.1.3 | ||||
| Structural | Lifetime | 0.279 | 0.699 | 0.041 | C 3.2.1 | ||
| Construction time | 0.301 | 0.017 | C 3.2.2 | ||||
| Social | Job creation | 0.15 | 0.418 | 0.063 | C 4.1 | ||
| Public acceptance | 0.582 | 0.088 | C 4.2 | ||||
| Sum: | 1.000 | ||||||
| Criteria/Subcriteria | Local Weights | Global Weights | ID | ||||
|---|---|---|---|---|---|---|---|
| 1st Level | 2nd Level | 3rd Level | 1st Level | 2nd Level | 3rd Level | ||
| Economic | Investment cost | 0.32 | 0.354 | 0.114 | C 1.1 | ||
| Operation cost | 0.322 | 0.104 | C 1.2 | ||||
| Market price | 0.323 | 0.104 | C 1.3 | ||||
| Environmental | Noise | 0.34 | 0.072 | 0.024 | C 2.1 | ||
| CO2 Emissions | 0.653 | 0.219 | C 2.2 | ||||
| Waste | 0.276 | 0.092 | C 2.3 | ||||
| Technical | Operational | Start-up time | 0.18 | 0.661 | 0.23 | 0.028 | C 3.1.1 |
| Programmable | 0.389 | 0.046 | C 3.1.2 | ||||
| Efficiency | 0.381 | 0.046 | C 3.1.3 | ||||
| Structural | Lifetime | 0.339 | 0.696 | 0.043 | C 3.2.1 | ||
| Construction time | 0.304 | 0.019 | C 3.2.2 | ||||
| Social | Job creation | 0.16 | 0.33 | 0.054 | C 4.1 | ||
| Public acceptance | 0.67 | 0.109 | C 4.2 | ||||
| Sum: | 1.000 | ||||||
| Crisp | l | m | u |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 2 |
| 2 | 1 | 2 | 3 |
| 3 | 2 | 3 | 4 |
| 4 | 3 | 4 | 5 |
| 5 | 4 | 5 | 6 |
| 6 | 5 | 6 | 7 |
| 7 | 6 | 7 | 8 |
| 8 | 7 | 8 | 9 |
| 9 | 8 | 9 | 10 |
| 10 | 9 | 10 | 10 |
| Investment Cost | Operation Cost | … | Job Creation | Public Acceptance | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.08 | 0.20 | 0.31 | 0.58 | 0.68 | 0.79 | 0.79 | 0.91 | 1.00 | 0.07 | 0.18 | 0.29 | ||||
| A2 | 0.43 | 0.55 | 0.67 | 0.33 | 0.44 | 0.54 | 0.75 | 0.87 | 0.96 | 0.21 | 0.32 | 0.43 | ||||
| A3 | 0.71 | 0.82 | 0.94 | 0.44 | 0.54 | 0.65 | 0.55 | 0.66 | 0.77 | 0.46 | 0.57 | 0.68 | ||||
| A4 | 0.61 | 0.73 | 0.84 | 0.42 | 0.53 | 0.63 | 0.45 | 0.57 | 0.68 | 0.55 | 0.66 | 0.77 | ||||
| A5 | 0.76 | 0.88 | 0.98 | 0.72 | 0.82 | 0.91 | 0.34 | 0.45 | 0.57 | 0.71 | 0.82 | 0.93 | ||||
| Vij | A6 | 0.27 | 0.39 | 0.51 | 0.70 | 0.81 | 0.91 | … | 0.49 | 0.60 | 0.72 | 0.46 | 0.57 | 0.68 | ||
| A7 | 0.78 | 0.90 | 1.00 | 0.86 | 0.96 | 1.00 | 0.30 | 0.42 | 0.53 | 0.82 | 0.93 | 1.00 | ||||
| A8 | 0.24 | 0.35 | 0.47 | 0.28 | 0.39 | 0.49 | 0.51 | 0.62 | 0.74 | 0.64 | 0.75 | 0.86 | ||||
| A9 | 0.37 | 0.49 | 0.61 | 0.53 | 0.63 | 0.74 | 0.34 | 0.45 | 0.57 | 0.68 | 0.79 | 0.88 | ||||
| A10 | 0.20 | 0.31 | 0.43 | 0.51 | 0.61 | 0.72 | 0.68 | 0.79 | 0.91 | 0.21 | 0.32 | 0.43 | ||||
| FPIS | 0.78 | 0.90 | 1.00 | 0.86 | 0.96 | 1.00 | … | 0.79 | 0.91 | 1.00 | 0.82 | 0.93 | 1.00 | |||
| FNIS | 0.08 | 0.20 | 0.31 | 0.28 | 0.39 | 0.49 | 0.30 | 0.42 | 0.53 | 0.07 | 0.18 | 0.29 | ||||
| Wj | 0.114 | 0.104 | … | 0.054 | 0.109 | |||||||||||
| A1 | 0.06 | 0.11 | 0.22 | 0.01 | 0.05 | 0.12 | −0.02 | 0.00 | 0.04 | 0.06 | 0.11 | 0.19 | ||||
| A2 | 0.01 | 0.06 | 0.14 | 0.05 | 0.09 | 0.19 | −0.01 | 0.00 | 0.05 | 0.05 | 0.09 | 0.16 | ||||
| A3 | −0.02 | 0.01 | 0.07 | 0.03 | 0.08 | 0.16 | 0.00 | 0.03 | 0.09 | 0.02 | 0.05 | 0.11 | ||||
| A4 | −0.01 | 0.03 | 0.09 | 0.03 | 0.08 | 0.16 | 0.01 | 0.04 | 0.11 | 0.01 | 0.04 | 0.09 | ||||
| A5 | −0.02 | 0.00 | 0.06 | −0.01 | 0.03 | 0.08 | 0.02 | 0.05 | 0.13 | −0.01 | 0.02 | 0.06 | ||||
| M | A6 | 0.03 | 0.08 | 0.18 | −0.01 | 0.03 | 0.08 | … | 0.01 | 0.03 | 0.10 | 0.02 | 0.05 | 0.11 | ||
| A7 | −0.03 | 0.00 | 0.05 | −0.02 | 0.00 | 0.04 | 0.02 | 0.05 | 0.14 | −0.02 | 0.00 | 0.04 | ||||
| A8 | 0.04 | 0.09 | 0.19 | 0.05 | 0.10 | 0.20 | 0.00 | 0.03 | 0.10 | 0.00 | 0.03 | 0.07 | ||||
| A9 | 0.02 | 0.07 | 0.15 | 0.02 | 0.06 | 0.13 | 0.02 | 0.05 | 0.13 | −0.01 | 0.02 | 0.07 | ||||
| A10 | 0.04 | 0.09 | 0.19 | 0.02 | 0.06 | 0.14 | −0.01 | 0.01 | 0.07 | 0.05 | 0.09 | 0.16 | ||||
| Sj | Rj | Qj | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.16 | 0.53 | 1.31 | 0.06 | 0.11 | 0.22 | −0.77 | 0.52 | 1.88 |
| A2 | 0.29 | 0.70 | 1.55 | 0.14 | 0.22 | 0.33 | −0.40 | 0.98 | 2.43 |
| A3 | 0.11 | 0.47 | 1.22 | 0.07 | 0.14 | 0.22 | −0.78 | 0.53 | 1.80 |
| A4 | 0.16 | 0.55 | 1.36 | 0.09 | 0.16 | 0.26 | −0.67 | 0.67 | 2.02 |
| A5 | −0.07 | 0.22 | 0.85 | 0.02 | 0.05 | 0.13 | −1.10 | 0.05 | 1.21 |
| A6 | −0.04 | 0.27 | 0.89 | 0.03 | 0.08 | 0.18 | −1.02 | 0.19 | 1.36 |
| A7 | −0.11 | 0.17 | 0.77 | 0.02 | 0.05 | 0.14 | −1.12 | 0.01 | 1.15 |
| A8 | 0.15 | 0.55 | 1.41 | 0.03 | 0.10 | 0.33 | −0.86 | 0.50 | 2.29 |
| A9 | 0.08 | 0.45 | 1.23 | 0.01 | 0.07 | 0.26 | −0.99 | 0.30 | 1.91 |
| A10 | 0.14 | 0.51 | 1.28 | 0.04 | 0.09 | 0.19 | −0.83 | 0.45 | 1.77 |
| S+ | 0.29 | 0.70 | 1.55 | R+ | 0.14 | 0.22 | 0.33 | ||
| S− | −0.11 | 0.17 | 0.77 | R− | 0.02 | 0.05 | 0.13 |
| S | Ranking | R | Ranking | Q | Ranking | |||
|---|---|---|---|---|---|---|---|---|
| A1—Nuclear | 0635 | 7 | 0.127 | 6 | 0.538 | 7 | ||
| A2—Coal | 0.811 | 10 | 0.229 | 10 | 1.000 | 10 | ||
| A3—Combined Cycle | 0.566 | 5 | 0.142 | 7 | 0.522 | 6 | ||
| A4—CHP | 0.656 | 8 | 0.166 | 9 | 0.674 | 9 | ||
| A5—Wind | 0.308 | 2 | 0.063 | 1 | 0.053 | 2 | ||
| A6—Hydro | 0.348 | 3 | 0.094 | 3 | 0.181 | 3 | ||
| A7—PV | 0.249 | 1 | 0.067 | 2 | 0.014 | 1 | ||
| A8—Green Hydrogen | 0.663 | 9 | 0.143 | 8 | 0.610 | 8 | ||
| A9—Storage | 0.552 | 4 | 0.100 | 4 | 0.382 | 4 | ||
| A10—SMR | 0.614 | 6 | 0.107 | 5 | 0.458 | 5 |
| Level 1 Criteria | Economic Subcriteria | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Best | Worst | |||||||
| Environmental | Economic | Technical | Social | Investment Cost | Operation Cost | Market Price | ||||
| BO-> | 1 | 1.15 | 1.65 | 2.1 | BO-> | 1 | 1.09 | 1.1 | ||
| 2.1 | 1.83 | 1.27 | 1 | <-OW | 1.1 | 1.01 | 1 | <-OW | ||
| Operational subcriteria | Environmental subcriteria | |||||||||
| Best | Worst | Best | Worst | |||||||
| Programmable | Efficiency | Start-Up Time | CO2 Emissions | Waste | Noise | |||||
| BO-> | 1 | 1.03 | 1.66 | BO-> | 1 | 2.72 | 8.06 | |||
| 1.66 | 1.61 | 1 | <-OW | 8.06 | 2.97 | 1 | <-OW | |||
| Structural subcriteria | Technical subcriteria | |||||||||
| Best | Worst | Best | Worst | |||||||
| Lifetime | Construction time | Operational | Structural | |||||||
| BO-> | 1 | 2.29 | BO-> | 1 | 1.95 | |||||
| 2.29 | 1 | <-OW | 1.95 | 1 | <-OW | |||||
| Social subcriteria | ||||||||||
| Best | Worst | |||||||||
| Social acceptance | Job creation | |||||||||
| BO-> | 1 | 0.49 | ||||||||
| 2.03 | 1 | <-OW | ||||||||
| Criteria/Subcriteria | Local Weights | Global Weights | ID | ||||
|---|---|---|---|---|---|---|---|
| 1st Level | 2nd Level | 3rd Level | 1st Level | 2nd Level | 3rd Level | ||
| Economic | Investment cost | 0.33 | 0.333 | 0.111 | C 1.1 | ||
| Operation cost | 0.333 | 0.111 | C 1.2 | ||||
| Market price | 0.333 | 0.111 | C 1.3 | ||||
| Environmental | Noise | 0.33 | 0.091 | 0.030 | C 2.1 | ||
| CO2 Emissions | 0.727 | 0.242 | C 2.2 | ||||
| Waste | 0.182 | 0.061 | C 2.3 | ||||
| Technical | Operational | Start-up time | 0.17 | 0.661 | 0.333 | 0.037 | C 3.1.1 |
| Programmable | 0.333 | 0.037 | C 3.1.2 | ||||
| Efficiency | 0.333 | 0.037 | C 3.1.3 | ||||
| Structural | Lifetime | 0.339 | 0.696 | 0.039 | C 3.2.1 | ||
| Construction time | 0.304 | 0.017 | C 3.2.2 | ||||
| Social | Job creation | 0.17 | 0.33 | 0.055 | C 4.1 | ||
| Public acceptance | 0.67 | 0.112 | C 4.2 | ||||
| Sum: | 1.000 | ||||||
| Alternatives | Exp1 | … | Exp6 | Aggregated Mean | Normalised Assessment | Weighted Assessment | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1—Nuclear | 0 | 1 | 2 | 4 | 5 | 6 | 0.67 | 1.67 | 2.67 | 0.08 | 0.20 | 0.31 | 0.01 | 0.02 | 0.04 | |||
| A2—Coal | 2 | 3 | 4 | 6 | 7 | 8 | 3.67 | 4.67 | 5.67 | 0.43 | 0.55 | 0.67 | 0.05 | 0.06 | 0.08 | |||
| A3—Combined Cycle | 3 | 4 | 5 | 7 | 8 | 9 | 6.00 | 7.00 | 8.00 | 0.71 | 0.82 | 0.94 | 0.08 | 0.09 | 0.11 | |||
| A4—CHP | 4 | 5 | 6 | 6 | 7 | 8 | 5.17 | 6.17 | 7.17 | 0.61 | 0.73 | 0.84 | 0.07 | 0.08 | 0.10 | |||
| A5—Wind | 5 | 6 | 7 | … | 5 | 6 | 7 | 6.50 | 7.50 | 8.33 | 0.76 | 0.88 | 0.98 | 0.09 | 0.10 | 0.11 | ||
| A6—Hydro | 1 | 2 | 3 | 4 | 5 | 6 | 2.33 | 3.33 | 4.33 | 0.27 | 0.39 | 0.51 | 0.03 | 0.04 | 0.06 | |||
| A7—PV | 5 | 6 | 7 | 6 | 7 | 8 | 6.67 | 7.67 | 8.50 | 0.78 | 0.90 | 1.00 | 0.09 | 0.10 | 0.11 | |||
| A8—Green Hydrogen | 2 | 3 | 4 | 3 | 4 | 5 | 2.00 | 3.00 | 4.00 | 0.24 | 0.35 | 0.47 | 0.03 | 0.04 | 0.05 | |||
| A9—Storage | 2 | 3 | 4 | 5 | 6 | 7 | 3.17 | 4.17 | 5.17 | 0.37 | 0.49 | 0.61 | 0.04 | 0.06 | 0.07 | |||
| A10—SMR | 0 | 1 | 2 | 4 | 5 | 6 | 1.67 | 2.67 | 3.67 | 0.20 | 0.31 | 0.43 | 0.02 | 0.04 | 0.05 | |||
| Max: | 8.50 | Wi: | 0.11 | |||||||||||||||
| Investment Cost | … | Public Acceptance | D+ | D− | CC | Ranking | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.01 | 0.02 | 0.04 | 0.01 | 0.02 | 0.03 | A1 | 0.34 | 0.29 | 0.459 | 9 | |||
| A2 | 0.05 | 0.06 | 0.08 | 0.02 | 0.04 | 0.05 | A2 | 0.46 | 0.18 | 0.279 | 10 | |||
| A3 | 0.08 | 0.09 | 0.11 | 0.05 | 0.06 | 0.07 | A3 | 0.29 | 0.34 | 0.543 | 5 | |||
| A4 | 0.07 | 0.08 | 0.10 | 0.06 | 0.07 | 0.08 | A4 | 0.33 | 0.30 | 0.472 | 8 | |||
| A5 | 0.09 | 0.10 | 0.11 | … | 0.08 | 0.09 | 0.10 | A5 | 0.12 | 0.51 | 0.806 | 2 | ||
| A6 | 0.03 | 0.04 | 0.06 | 0.05 | 0.06 | 0.07 | A6 | 0.18 | 0.46 | 0.722 | 3 | |||
| A7 | 0.09 | 0.10 | 0.11 | 0.09 | 0.10 | 0.11 | A7 | 0.09 | 0.54 | 0.859 | 1 | |||
| A8 | 0.03 | 0.04 | 0.05 | 0.07 | 0.08 | 0.09 | A8 | 0.31 | 0.33 | 0.517 | 6 | |||
| A9 | 0.04 | 0.06 | 0.07 | 0.07 | 0.09 | 0.10 | A9 | 0.25 | 0.38 | 0.600 | 4 | |||
| A10 | 0.02 | 0.04 | 0.05 | 0.02 | 0.04 | 0.05 | A10 | 0.32 | 0.31 | 0.490 | 7 | |||
| FPIS | 0.09 | 0.10 | 0.11 | … | 0.09 | 0.10 | 0.11 | |||||||
| FNIS | 0.01 | 0.02 | 0.04 | 0.01 | 0.02 | 0.03 | ||||||||
| Criteria/Subcriteria | Global Weights | Diff (%) | |||
|---|---|---|---|---|---|
| 1st Level | 2nd Level | 3rd Level | AHP + Consensus | BWM | |
| Economic | Investment cost | 0.114 | 0.111 | 3% | |
| Operation cost | 0.104 | 0.111 | −7% | ||
| Market price | 0.104 | 0.111 | −6% | ||
| Environmental | Noise | 0.024 | 0.030 | −21% | |
| CO2 Emissions | 0.219 | 0.242 | −10% | ||
| Waste | 0.092 | 0.061 | 52% | ||
| Technical | Operational | Start-up time | 0.028 | 0.037 | −25% |
| Programmable | 0.046 | 0.037 | 26% | ||
| Efficiency | 0.046 | 0.037 | 24% | ||
| Structural | Lifetime | 0.043 | 0.039 | 8% | |
| Construction time | 0.019 | 0.017 | 9% | ||
| Social | Job creation | 0.054 | 0.055 | −2% | |
| Public acceptance | 0.109 | 0.112 | −2% | ||
| Sum: | 1.000 | 1.000 | 3.8% | ||
| # | Ranking by Technology | FVIKOR | FTOPSIS | Ranking by Technology | # |
|---|---|---|---|---|---|
| 1 | PV | A7 | A7 | PV | 1 |
| 2 | Wind | A5 | A5 | Wind | 2 |
| 3 | Hydro | A6 | A6 | Hydro | 3 |
| 4 | Battery Storage (BESS) | A9 | A9 | Battery Storage (BESS) | 4 |
| 5 | Small Modular Reactor (SMR) | A10 | A3 | Combined Cycle | 5 |
| 6 | Combined Cycle | A3 | A8 | Green Hydrogen | 6 |
| 7 | Nuclear | A1 | A10 | Small Modular Reactor (SMR) | 7 |
| 8 | Green Hydrogen | A8 | A4 | CHP | 8 |
| 9 | CHP | A4 | A1 | Nuclear | 9 |
| 10 | Coal | A2 | A2 | Coal | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivero-Iglesias, J.M.; Puente, J.; Fernandez, I.; León, O. A Novel Combined Hybrid Group Multi-Criteria Decision-Making Model for the Selection of Power Generation Technologies. Systems 2025, 13, 742. https://doi.org/10.3390/systems13090742
Rivero-Iglesias JM, Puente J, Fernandez I, León O. A Novel Combined Hybrid Group Multi-Criteria Decision-Making Model for the Selection of Power Generation Technologies. Systems. 2025; 13(9):742. https://doi.org/10.3390/systems13090742
Chicago/Turabian StyleRivero-Iglesias, Jose M., Javier Puente, Isabel Fernandez, and Omar León. 2025. "A Novel Combined Hybrid Group Multi-Criteria Decision-Making Model for the Selection of Power Generation Technologies" Systems 13, no. 9: 742. https://doi.org/10.3390/systems13090742
APA StyleRivero-Iglesias, J. M., Puente, J., Fernandez, I., & León, O. (2025). A Novel Combined Hybrid Group Multi-Criteria Decision-Making Model for the Selection of Power Generation Technologies. Systems, 13(9), 742. https://doi.org/10.3390/systems13090742







