First-Principles Study on Desolvation and Capacitive Performance of Bispyrrolidinium Cations in Pristine/Oxygen-Functionalized Bilayer Graphene Flat Pores

Abstract

Supercapacitors are limited by electrolyte cation desolvation, which directly impacts ion storage efficiency and capacitance. This study uses density functional tight-binding (DFTB+) first-principles calculations to investigate the desolvation of bispyrrolidinium cation complexes ([SBP(AN)]⁺, acetonitrile as solvent) in pristine (FP) and oxygen-functionalized (OFP: hydroxyl-HFP, carbonyl-CFP, aldehyde-AFP) bilayer graphene flat pores with AA/AB stacking. Critical desolvation diameters were determined: 5.0 Å (FP), 5.2 Å (HFP), 5.0 Å (AFP), and 4.6 Å (CFP). Hydroxyl functionalization expanded the critical diameter, reduced SBP⁺ intercalation energy, and increased relative capacitance by 1.02~1.03 times; carbonyl groups had the opposite effect, while aldehyde groups showed no significant impact. Density of States (DOS) analysis revealed enhanced conductivity for HFP and AFP after SBP⁺ embedding, but reduced conductivity for CFP. Charge density difference and Bader charge analysis confirmed electron transfer primarily between SBP⁺ (electron donor) and oxygen atoms in functional groups (electron acceptor), with SBP⁺ interacting mainly with functional groups rather than the carbon basal plane. This work provides theoretical guidance for optimizing graphene-based supercapacitor electrodes via pore structure and surface functionalization.

1. Introduction

The growth of portable electronics, electric vehicles, and renewable energy systems is driving demand for high-performance energy storage devices that offer high power, long life, and fast charge/discharge capabilities [1,2]. Supercapacitors, especially electric double-layer capacitors (EDLCs), are promising due to ultra-high power density (>10 kW kg⁻¹) and long cycle life (>10⁵ cycles) [3,4]. EDLCs store energy via electric double layers at electrode–electrolyte interfaces, where ions are adsorbed and desolvated, thereby building up charge [5]. However, capacitance and ion transport in EDLCs are limited by the extent of electrolyte cation desolvation—solvated cations must shed their solvent shells to enter nanoscale pores—and poor desolvation increases resistance and reduces storage [6,7].

Graphene, with its high specific surface area (~2630 m² g⁻¹), excellent electrical conductivity, and mechanical stability, is an ideal electrode material for EDLCs [8,9]. Bilayer graphene exhibits tunable interlayer spacing and a controllable pore structure. These features can be further adjusted by surface functionalization (e.g., hydroxyl (-OH), carbonyl (-CO), aldehyde (-CHO) groups) to control ion adsorption and desolvation [10,11]. Studies show that functional groups on graphene surfaces can alter the electronic structure of pores and the chemical environment, thereby influencing the interaction between electrolyte ions and the electrode [12,13]. For example, hydroxyl groups introduce hydrophilic sites that enhance ion–pore affinity; carbonyl groups may cause steric hindrance and inhibit ion entry [14]. However, critical knowledge gaps remain in this field: first, existing research mostly focuses on the effect of a single pore structure or functional group on ion adsorption, but lacks a systematic comparison of the differential roles of hydroxyl, carbonyl, and aldehyde groups in desolvation, while ignoring the synergistic effect of stacking configurations (AA/AB) of bilayer graphene. Second, the critical pore diameter for desolvation is a key parameter for electrode design, but quantitative data on the critical desolvation diameter of bispyrrolidinium cation (SBP⁺)—a commonly used cation in non-aqueous electrolytes—in functionalized bilayer graphene pores is still lacking. Third, the interaction mechanism between desolvated SBP⁺ and the electrode surface (e.g., charge transfer path, priority of interaction with functional groups or carbon basal plane) remains unclear, making it difficult to establish the structure–activity relationship between “functional groups-desolvation-capacitive performance”. In summary, how the stacking configuration and surface oxygen-containing functional groups of bilayer graphene synergistically regulate the desolvation behavior (critical pore diameter, intercalation energy) of SBP⁺, and how this process affects capacitance and electrode conductivity, has not been systematically elucidated at the atomic scale. The Manickam Minakshi team has made notable contributions to understanding EDL thickness in EDLCs. Their research revealed that EDL thickness is jointly determined by electrolyte ion hydration radius, solvent dielectric constant, and electrode surface functionalization, and that minimizing EDL thickness (without compromising ion transport) directly boosts capacitance by intensifying the interfacial electric field. However, their work focused on experimental characterizations, lacking atomic-scale insights into how electrode functionalization regulates EDL thickness via ion desolvation—this gap is addressed in our study by investigating SBP⁺ desolvation and dSBP⁺-C (EDL thickness proxy) in functionalized graphene pores.

SBP⁺ are widely used in non-aqueous electrolytes for supercapacitors for their high electrochemical stability and low viscosity [15,16]. AN is a benchmark solvent for non-aqueous supercapacitor electrolytes due to its high electrochemical stability (~5.5 V), low viscosity, and ability to form well-defined solvated complexes with SBP⁺. This ensures the simulated desolvation behavior is consistent with practical device operating conditions, while its simple molecular structure facilitates quantitative first-principles calculations. In acetonitrile (AN), SBP⁺ forms solvated complexes ([SBP(AN)]⁺) that must desolvate to enter graphene pores. Desolvation depends on pore size: pores that are too small cannot fit solvated cations, while oversized pores do not confine them enough to shed solvent shells [17,18]. Prior experimental studies have indirectly measured desolvation via capacitance tests; however, these methods cannot capture atomic-scale interactions (e.g., ion-solvent or ion-functional group interactions) [19]. First-principles calculations using density functional theory (DFT) simulate these interactions and quantify reaction energies, clarifying the desolvation mechanism at the molecular level [20,21].

To address these knowledge gaps, this study employs DFTB+ calculations to systematically investigate the desolvation of [SBP(AN)]⁺ in pristine and functionalized bilayer graphene pores with AA and AB stacking. The core research objective is to clarify the desolvation mechanism, critical pore diameter, and capacitance regulation law of [SBP(AN)]⁺ in bilayer graphene flat pores with different functionalizations/stacking configurations, thereby providing theoretical guidance for electrode structure optimization. Specifically, the objectives are to: (1) identify the critical pore diameters for complete desolvation of [SBP(AN)]⁺ in FP, HFP, CFP, and AFP; (2) evaluate functional group and stacking configuration effects on SBP⁺ intercalation energy and capacitance; (3) analyze the DOS and charge density differences between desolvated SBP⁺ and functionalized pores, thereby linking atomic-scale mechanisms to device performance.

The novelty of this work lies in three clarified findings: (1) quantitative relationships are established between functional group types or graphene stacking configurations and the critical diameter for desolvation; (2) hydroxyl groups are shown to enhance capacitance by promoting SBP⁺ storage, while carbonyl groups impede it; (3) electron transfer during desolvation occurs mainly between SBP⁺ and oxygen in the functional group, not the carbon basal plane. These findings provide explicit theoretical guidance for designing graphene-based electrodes with optimized pore size and chemistry for high-performance supercapacitors.

2. Calculation Method

This study conducted calculations using the density functional tight-binding (DFTB+, 2019 Version) software module, which is rooted in density functional theory (DFT). Given the large number of atoms in the system structure, a 1 × 1 × 1 k-point [22,23] grid within the Brillouin zone was employed, and its convergence was subsequently verified. For the optimization of the geometric structure, an intelligent algorithm was adopted, with the following convergence criteria strictly enforced:

• The total energy error of the system was controlled to be less than 0.05 kcal/mol;
• The total stress tensor was reduced to 0.1 GPa;
• The maximum ionic displacement was limited within 0.01 Å;
• The convergence accuracy of the forces acting on atoms was set to 0.5 kcal/mol/Å.

Pores in functionalized bilayer graphene are classified as either rigid (fixed structure) or flexible (deformable) pores [24]. Experimental observations showed that the structure of flat pores in functionalized bilayer graphene changes when bispyrrolidine cations—positively charged organic molecules—intercalate between the layers. Therefore, this study focused solely on simulating flexible pores. In the flat pore model, edge atoms (at the pore perimeter) were fixed to maintain pore size, while central atoms (within the pore) were allowed to move freely to model the dynamic behavior of flexible pores.

Both stacking types (AA and AB) of the flat pores in functionalized bilayer graphene have periodic hexagonal supercells, as shown in Figure 1 (black atoms on the base are fixed carbon, gray are free carbon). Pore sizes (4–10 Å) were modeled by adjusting interlayer spacing.

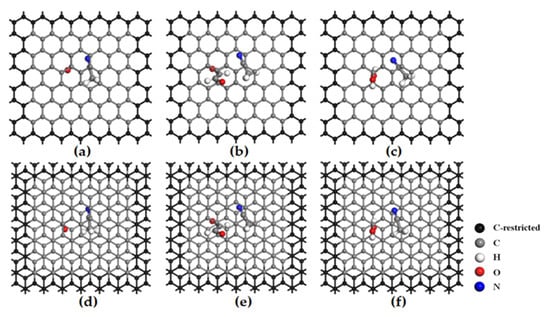
Figure 1. Stable structure of acetonitrile solvent in functionalized flat pores. (a) AA-stacked carbonyl flat pore. (b) AA-stacked aldehyde flat pore. (c) AA-stacked hydroxyl flat pore. (d) AB-stacked carbonyl flat pore. (e) AB-stacked aldehyde flat pore. (f) AB-stacked hydroxyl flat pore.

3. Results and Discussion

3.1. Reaction Principle

When hydroxyl (-OH) and aldehyde (-CHO) functional groups are introduced onto the surface of flat pores in bilayer graphene, these groups exhibit the highest stability when adsorbed onto carbon atoms. Concurrently, the configuration where hydrogen atoms point toward the center of the six-membered carbon ring is confirmed to be the most stable [25]. When hydroxyl and aldehyde groups are adsorbed on the inner walls of the flat pores, one of the three in-plane large π-bonds within the C-C framework is broken. This breakage induces a transition in the hybridization state of the affected carbon atoms from sp² to sp³, leading to the formation of unsaturated dangling bonds. To address this issue and enhance structural stability, hydroxyl and aldehyde groups were adsorbed on both sides of the graphene flat pores in this study, thereby improving the stability of hydroxyl- and aldehyde-functionalized flat pores in bilayer graphene. Simulation results further demonstrated that the most stable binding configuration is achieved when the hydroxyl and aldehyde groups are adsorbed on opposite sides and are in an orthogonal arrangement [26]. To investigate the intercalation behavior of acetonitrile (AN) solvent molecules between the layers of hydroxyl- and aldehyde-functionalized flat pores in bilayer graphene (with varying interlayer spacings), the adsorption characteristics of AN molecules on the bilayer graphene surface were systematically studied. Different orientations of AN molecules were considered, and their corresponding orientation energies were calculated. As presented in Figure 1, the adsorption site corresponding to the lowest energy value is identified as the most stable adsorption position for AN solvent molecules. This observation is consistent with the findings reported by Leenaerts et al. [27], who proposed that the adsorption energy of AN solvent molecules is primarily determined by their orientation. During the intercalation of bispyrrolidine cations into flat pores of pristine bilayer graphene (FP) or oxygen-containing functionalized bilayer graphene (OFP), three potential reaction pathways may occur: bispyrrolidine cations stably reside within the pores, while AN solvent molecules are expelled from the pores; AN solvent molecules are intercalated into the pores, while bispyrrolidine cations remain outside the pores; bispyrrolidine cation complexes are intercalated into the pores. These three reactions are expressed by, respectively, Equations (1)–(3):

A(AN) + FP/OFP → A(FP/OFP) + AN

(1)

A(AN) + FP/OFP → AN(FP/OFP) + A

(2)

A(AN) + FP/OFP → A(AN)FP/OFP

(3)

where

• A denotes SBP⁺;
• A(AN) represents bispyrrolidine cation complexes;
• FP refers to flat pores of pristine bilayer graphene;
• OFP denotes oxygen-containing functionalized flat pores of bilayer graphene, including hydroxyl-functionalized flat pores (HFP), carbonyl-functionalized flat pores (CFP), and aldehyde-functionalized flat pores (AFP);
• A(FP/OFP) stands for the intercalation compound of SBP⁺ in FP or OFP;
• AN(FP/OFP) represents the intercalation compound of AN molecules in FP or OFP;
• {A(AN)FP/OFP} denotes the intercalation compound of SBP⁺ complexes in FP or OFP.

To evaluate the intercalation feasibility of bispyrrolidine cations, solvated bispyrrolidine cations, and solvents into pores of different sizes, the reaction energies corresponding to the three reaction scenarios were calculated and defined as E_int1, E_int2, E_int3, E_int4, and E_int5, respectively. These reaction energies are mathematically expressed by Equations (4)–(8):

E_int1 = E_A(OFP) + E_AN − E_A(AN) − E_OFP

(4)

E_int2 = E_AN(OFP) + E_A − E_A(AN) − E_OFP

(5)

E_int3 = E_A(AN)OFP − E_A(AN) − E_OFP

(6)

E_int4 = E_A(FP) + E_AN − E_A(AN) − E_FP

(7)

E_int5 = E_A(AN)FP − E_A(AN) − E_FP

(8)

where

• E_A(AN) represents the energy of bispyrrolidine cation complexes;
• E_OFP denotes the energy of oxygen-containing functionalized flat pores of bilayer graphene;
• E_FP refers to the energy of flat pores of pristine bilayer graphene;
• E_A(OFP) stands for the energy of the intercalation compound of bispyrrolidine cations in OFP;
• E_A(FP) represents the energy of the intercalation compound of bispyrrolidine cations in FP;
• E_AN denotes the energy of AN molecules;
• E_AN(OFP) refers to the energy of the intercalation compound of AN molecules in OFP;
• E_A(AN)FP stands for the energy of the intercalation compound of bispyrrolidine cation complexes in FP;
• E_A represents the energy of bispyrrolidine cation;
• E_A(AN)OFP denotes the energy of the intercalation compound of bispyrrolidine cation complexes in OFP.

A lower value of E_int1, E_int2, E_int3, E_int4, or E_int5 indicates a higher probability of the corresponding reaction occurring.

3.2. Desolvation of SBP⁺ Complexes

3.2.1. Desolvation of SBP⁺ Complexes by Hydroxylated-Flat Pores

Figure 2 shows the desolvation reaction energy curves of [SBP(AN)]⁺ in hydroxyl-functionalized flat pores (HFP) and pristine flat pores (FP) of AA-stacked bilayer graphene. To determine the critical desolvation diameter of [SBP(AN)]⁺, we calculated the reaction energies of SBP⁺, AN, and [SBP(AN)]⁺ in HFP (denoted as E_int1, E_int2, E_int3) and of SBP⁺ and [SBP(AN)]⁺ in FP (denoted as E_int4, E_int5).

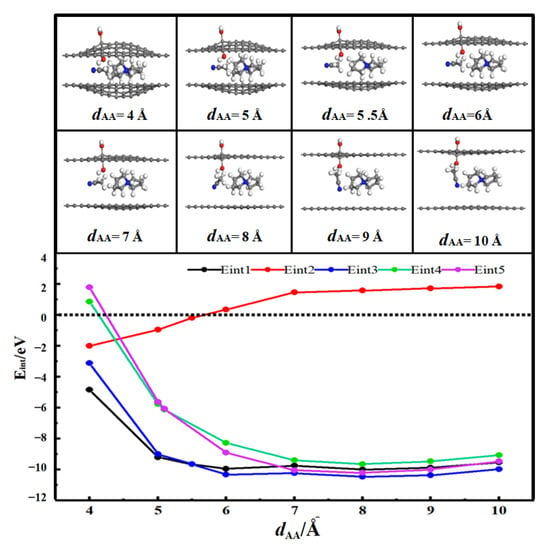
Figure 2. Reaction energy curves of SBP⁺, AN, and [SBP(AN)]⁺ in hydroxyl-functionalized flat pores (HFP) and of SBP⁺ and [SBP(AN)]⁺ in pristine flat pores (FP) of AA-stacked bilayer graphene [28].

When d_AA < 5.7 Å, E_int2 < 0, which means AN molecules can stably reside in the hydroxyl-functionalized flat pores of AA-stacked bilayer graphene independently. When the diameter of the hydroxyl-functionalized flat pores of AA-stacked bilayer graphene (d_AA) is 5.5 Å, the energy value of E_int1 (−9.65 eV) is close to that of E_int3 (−9.64 eV). This means 5.5 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the hydroxyl-functionalized flat pores of AA-stacked bilayer graphene. When the diameter of the hydroxyl-functionalized flat pores of AA-stacked bilayer graphene is less than 5.5 Å, E_int1 < E_int3 < 0, and SBP⁺ exists more stably in the pores than [SBP(AN)]⁺. Therefore, when the pore diameter is less than 5.5 Å, [SBP(AN)]⁺ can undergo complete desolvation in the hydroxyl-functionalized flat pores of AA-stacked bilayer graphene.

When the diameter of the flat pores of AA-stacked bilayer graphene (d_AA) is 5.1 Å, the energy value of E_int4 (−6.13 eV) is close to that of E_int5 (−6.08 eV). This indicates that 5.1 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the flat pores of AA-stacked bilayer graphene. When the diameter of the flat pores of AA-stacked bilayer graphene is less than 5.1 Å, E_int4 < E_int5 < 0, and SBP⁺ exists more stably in the pores than [SBP(AN)]⁺. Thus, when the pore diameter is less than 5.1 Å, [SBP(AN)]⁺ can undergo complete desolvation in the flat pores of AA-stacked bilayer graphene.

Figure 3 presents the desolvation reaction energy curves of [SBP(AN)]⁺ in hydroxyl-functionalized flat pores (HFP) and pristine flat pores (FP) of AB-stacked bilayer graphene. When d_AB < 5.8 Å, E_int2 < 0, which indicates that AN molecules can exist independently in the hydroxyl-functionalized flat pores of AB-stacked bilayer graphene. When the diameter of the hydroxyl-functionalized flat pores of AB-stacked bilayer graphene (d_AB) is 5.2 Å, the energy value of E_int1 (−9.63 eV) is close to that of E_int3 (−9.65 eV). This means 5.2 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the hydroxyl-functionalized flat pores of AB-stacked bilayer graphene. When the diameter of the hydroxyl-functionalized flat pores of AB-stacked bilayer graphene is less than 5.2 Å, E_int1 < E_int3 < 0, and SBP⁺ exists more stably in the pores than [SBP(AN)]⁺. Therefore, when the pore diameter is less than 5.2 Å, [SBP(AN)]⁺ can undergo complete desolvation in the hydroxyl-functionalized flat pores of AB-stacked bilayer graphene.

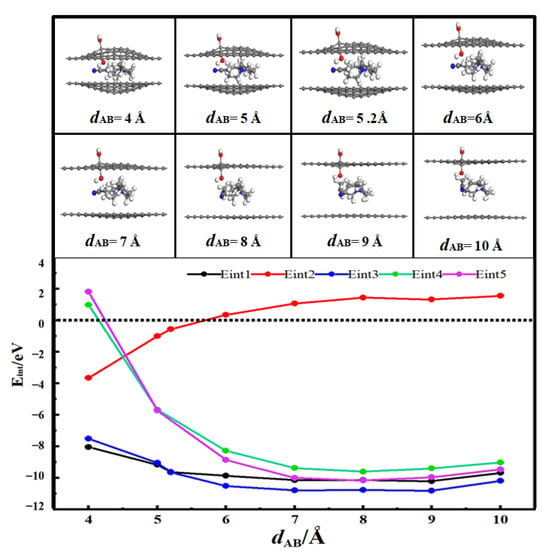
Figure 3. Reaction energy curves of SBP⁺, AN, and [SBP(AN)]⁺ in hydroxyl-functionalized flat pores (HFP) and of SBP⁺ and [SBP(AN)]⁺ in pristine flat pores (FP) of AB-stacked bilayer graphene [28].

When the diameter of the flat pores of AB-stacked bilayer graphene (d_AB) is 5.0 Å, the energy value of E_int4 (−5.68 eV) is close to that of E_int5 (−5.71 eV). This indicates 5.0 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the flat pores of AB-stacked bilayer graphene. When the diameter of the flat pores of AB-stacked bilayer graphene is less than 5.0 Å, E_int4 < E_int5 < 0, and SBP⁺ exists more stably in the pores than [SBP(AN)]⁺. Thus, when the pore diameter is less than 5.0 Å, [SBP(AN)]⁺ can undergo complete desolvation in the flat pores of AB-stacked bilayer graphene.

Therefore, this study concludes that the pore diameter required for the complete desolvation of [SBP(AN)]⁺ in the hydroxyl-functionalized flat pores of bilayer graphene is 5.2 Å, and the pore diameter range for partial desolvation is 5.2~5.5 Å. For the flat pores of bilayer graphene, the pore diameter for the complete desolvation of [SBP(AN)]⁺ is 5.0 Å, and the range for partial desolvation is 5.0~5.1 Å. Compared with the flat pores of bilayer graphene, the energy consumption for SBP⁺ to enter the hydroxyl-functionalized flat pores of bilayer graphene is lower, and SBP⁺ can enter more easily. The increase in SBP⁺ content can further enhance the capacitance of supercapacitors. Hydroxyl groups improve the adsorption capacity of flat pores for SBP⁺ and strengthen the ability of flat pores to store SBP⁺. Furthermore, the AA- and AB-stacking configurations of hydroxyl-functionalized flat pores play distinct regulatory roles. AA-stacked HFP favors ion diffusion with its symmetric channel, while AB-stacked HFP enhances ion adsorption via confined pores. This structural tunability based on stacking configuration provides a direct approach to balance the power density and energy density of supercapacitors.

3.2.2. Desolvation of SBP⁺ Complexes by Carbonylated-Flat Pores

Figure 4 shows the desolvation reaction energy curves of [SBP(AN)]⁺ in the carbonylated flat pores and flat pores of AA-stacked bilayer graphene. To determine the critical pore diameter for the desolvation of [SBP(AN)]⁺, the reaction energies of SBP⁺, AN, and [SBP(AN)]⁺ in the carbonylated flat pores, as well as those of SBP⁺ and [SBP(AN)]⁺ in the flat pores, were calculated and denoted as E_int1, E_int2, E_int3, E_int4, and E_int5, respectively.

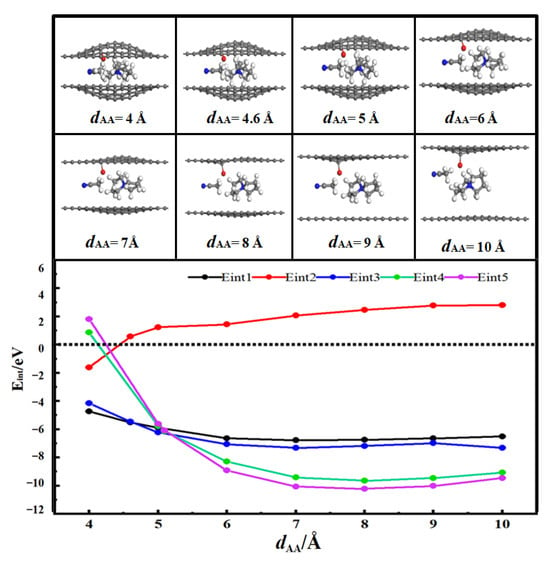
Figure 4. Reaction energy curves of SBP⁺, AN, [SBP(AN)]⁺ in carbonylated flat pores and SBP⁺ and [SBP(AN)]⁺ in flat pore AA stacks.

When d_AA < 4.5 Å, E_int2 < 0, indicating that AN molecules can exist independently in the carbonylated flat pores of AA-stacked bilayer graphene. When the diameter of the carbonylated flat pores of AA-stacked bilayer graphene (d_AA) is 4.6 Å, the energy value of Eint1 (−5.51 eV) is close to that of E_int3 (−5.47 eV). This means 4.6 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the carbonylated flat pores of AA-stacked bilayer graphene. When the diameter of the carbonylated flat pores of AA-stacked bilayer graphene is less than 4.6 Å, E_int1 < E_int3 < 0, and SBP⁺ exists more stably in the pores than [SBP(AN)]⁺. Therefore, when the pore diameter is less than 4.6 Å, [SBP(AN)]⁺ can undergo complete desolvation in the carbonylated flat pores of AA-stacked bilayer graphene.

When the diameter of the flat pores of AA-stacked bilayer graphene (d_AA) is 5.1 Å, the energy value of E_int4 (−6.13 eV) is close to that of E_int5 (−6.08 eV). This indicates 5.1 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the flat pores of AA-stacked bilayer graphene. When the diameter of the flat pores of AA-stacked bilayer graphene is less than 5.1 Å, E_int4 < E_int5 < 0, and SBP⁺ exists more stably in the pores than [SBP(AN)]⁺. Thus, when the pore diameter is less than 5.1 Å, [SBP(AN)]⁺ can undergo complete desolvation in the flat pores of AA-stacked bilayer graphene.

Figure 5 presents the desolvation reaction energy curves of [SBP(AN)]⁺ in the carbonylated flat pores and planar pores of AB-stacked bilayer graphene. When d_AB < 4.8 Å, E_int2 < 0, indicating that AN molecules can exist independently in the hydroxyl-functionalized flat pores of AB-stacked bilayer graphene. When the diameter of the carbonylated flat pores of AB-stacked bilayer graphene (d_AB) is 4.8 Å, the energy value of E_int1 (−5.75 eV) is close to that of E_int3 (−5.73 eV). This means 4.8 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the carbonylated flat pores of AB-stacked bilayer graphene. When the diameter of the carbonylated flat pores of AB-stacked bilayer graphene is less than 4.8 Å, E_int1 < E_int3 < 0, and SBP⁺ exists more stably in the pores than [SBP(AN)]⁺. Therefore, when the pore diameter is less than 4.8 Å, [SBP(AN)]⁺ can undergo complete desolvation in the carbonylated flat pores of AB-stacked bilayer graphene.

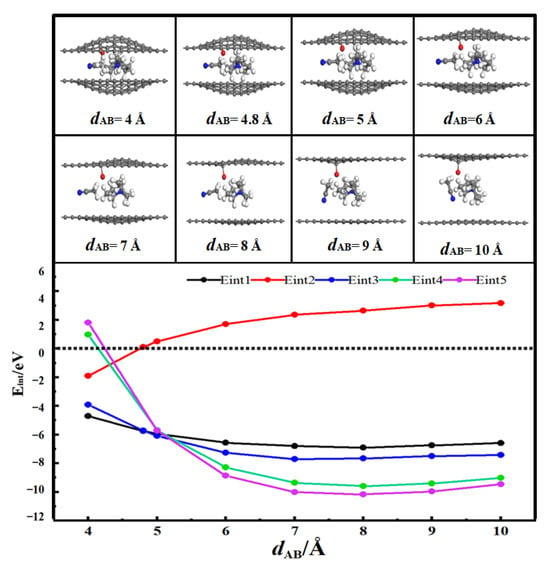
Figure 5. Reaction energy curves of SBP⁺, AN, [SBP(AN)]⁺ in carbonylated flat pores and SBP⁺ and [SBP(AN)]⁺ in flat pore AB stacks.

When the diameter of the flat pores of AB-stacked bilayer graphene (d_AB) is 5.0 Å, the energy value of E_int4 (−5.68 eV) is close to that of E_int5 (−5.71 eV). This indicates 5.0 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the flat pores of AB-stacked bilayer graphene. When the diameter of the flat pores of AB-stacked bilayer graphene is less than 5.0 Å, E_int4 < E_int5 < 0, and SBP⁺ exists more stably in the pores than [SBP(AN)]⁺. Thus, when the pore diameter is less than 5.0 Å, [SBP(AN)]⁺ can undergo complete desolvation in the flat pores of AB-stacked bilayer graphene.

Therefore, this study concludes that the pore diameter required for the complete desolvation of [SBP(AN)]⁺ in the carbonylated flat pores of bilayer graphene is 4.6 Å, and the pore diameter range for partial desolvation is 4.6~4.8 Å. For the flat pores of bilayer graphene, the pore diameter for the complete desolvation of [SBP(AN)]⁺ is 5.0 Å, and the range for partial desolvation is 5.0~5.1 Å. Compared with the flat pores of bilayer graphene, the energy consumption for SBP⁺ to enter the carbonylated flat pores of bilayer graphene is higher, and SBP⁺ is more difficult to enter. A decrease in the content of SBP⁺ can further reduce the capacitance of supercapacitors. Carbonyl groups reduce the adsorption capacity of flat pores for SBP⁺ and weaken the ability of flat pores to store SBP⁺.

3.2.3. Desolvation of SBP⁺ Complexes by Aldehydized-Flat Pores

Figure 6 shows the desolvation reaction energy curves of [SBP(AN)]⁺ in the AA-stacked bilayer graphene aldehyde-based flat pores and the flat pore models. To determine the critical size of the desolvation pore diameter for [SBP(AN)]⁺, the reaction energies of SBP⁺, AN, and [SBP(AN)]⁺ in the aldehyde-functionalized flat pores, as well as those of SBP⁺ and [SBP(AN)]⁺ in the flat pores, were calculated and denoted as E_int1, E_int2, E_int3, E_int4, and E_int5,respectively.

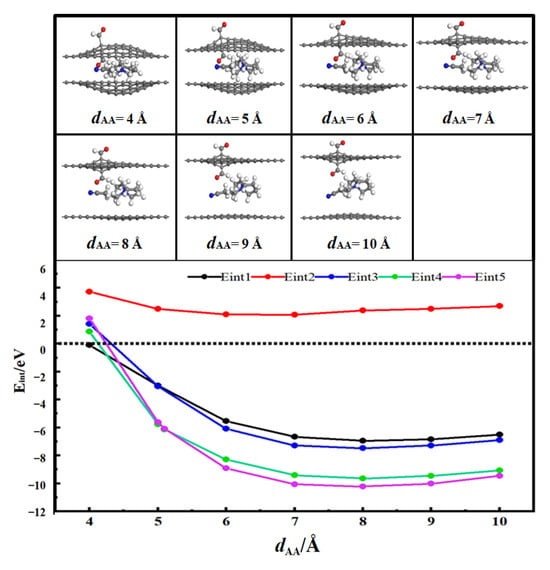
Figure 6. Reaction energy curves of SBP⁺, AN, [SBP(AN)]⁺ in aldehydized flat pores and SBP⁺ and [SBP(AN)]⁺ in flat pore AA stacks.

Among these, E_int2 > 0, indicating that AN molecules cannot exist independently in the AA-stacked bilayer graphene aldehyde-based flat pores. When the pore diameter of the AA-stacked bilayer graphene aldehyde-based flat pore (d_AA) is 5.0 Å, the energy value of E_int1 (−2.99 eV) is close to that of E_int3 (−3.05 eV); thus, 5.0 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the AA-stacked bilayer graphene aldehyde-based planar pores. When the diameter of the AA-stacked bilayer graphene aldehyde-based planar pore is less than 5.0 Å, E_int1 < E_int3 < 0, meaning SBP⁺ exists more stably in the pore than [SBP(AN)]⁺. Therefore, when the pore diameter is less than 5.0 Å, [SBP(AN)]⁺ can undergo complete desolvation in the AA-stacked bilayer graphene aldehyde-based flat pores.

When the pore diameter of the AA-stacked bilayer graphene flat pore (d_AA) is 5.1 Å, the energy value of E_int4 (−6.13 eV) is close to that of E_int5 (−6.08 eV); hence, 5.1 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the AA-stacked bilayer graphene flat pores. When the diameter of the AA-stacked bilayer graphene flat pore is less than 5.1 Å, E_int4 < E_int5 < 0, indicating that SBP⁺ exists more stably in the pore than [SBP(AN)]⁺. Therefore, when the pore diameter is less than 5.1 Å, [SBP(AN)]⁺ can undergo complete desolvation in the AA-stacked bilayer graphene flat pores.

Figure 7 shows the desolvation reaction energy curves of [SBP(AN)]⁺ in the AB-stacked bilayer graphene aldehyde functionalized flat pore model and flat pore model. Among the energy parameters, E_int2 > 0, indicating that AN molecules cannot exist alone in the AB-stacked bilayer graphene aldehyde-functionalized flat pores.

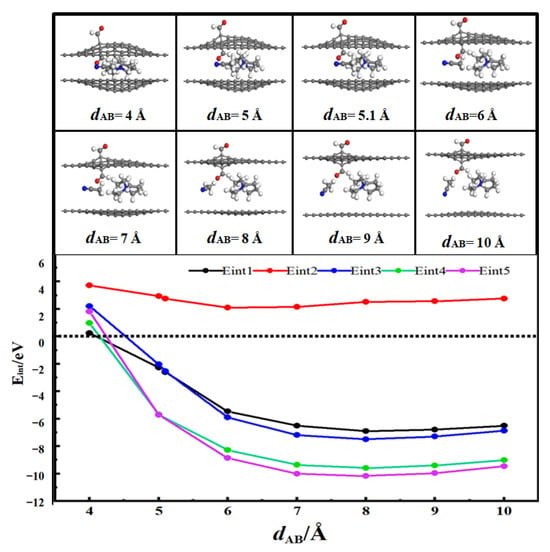
Figure 7. Reaction energy curves of SBP⁺, AN, [SBP(AN)]⁺ in aldehydized flat pores and SBP⁺ and [SBP(AN)]⁺ in flat pore AB stacks.

When the pore diameter of the AB-stacked bilayer graphene aldehyde functionalized flat pore (denoted as d_AB) is 5.1 Å, the energy value of E_int1 (−2.98 eV) is close to that of E_int3 (−3.00 eV). This means that 5.1 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the AB-stacked bilayer graphene aldehyde-functionalized flat pores. When the pore diameter of the AB-stacked bilayer graphene aldehyde functionalized flat pore is less than 5.1 Å, the condition E_int1 < E_int3 < 0 is satisfied. Under this condition, SBP⁺ exists more stably in the pores than [SBP(AN)]⁺. Therefore, when the pore diameter is less than 5.1 Å, [SBP(AN)]⁺ can undergo complete desolvation in the AB-stacked bilayer graphene aldehyde functionalized flat pores.

When the pore diameter of the AB-stacked bilayer graphene flat pore (d_AB) is 5.0 Å, the energy value of E_int4 (−5.68 eV) is close to that of E_int5 (−5.71 eV). That is, 5.0 Å is the critical point for the desolvation of [SBP(AN)]⁺ in the AB-stacked bilayer graphene flat pores. When the pore diameter of the AB-stacked bilayer graphene flat pore is less than 5.0 Å, the condition E_int4 < E_int5 < 0 is met. At this time, SBP⁺ exists more stably in the pores than [SBP(AN)]⁺. Hence, when the pore diameter is less than 5.0 Å, [SBP(AN)]⁺ can achieve complete desolvation in the AB-stacked bilayer graphene flat pores.

Therefore, this study concludes that: for [SBP(AN)]⁺ in bilayer graphene aldehyde-functionalized flat pores, the pore diameter enabling complete desolvation is 5.0 Å, and the pore diameter range for partial desolvation is 5.0~5.1 Å; for [SBP(AN)]⁺ in bilayer graphene flat pores, the pore diameter for complete desolvation is 5.0 Å, and the pore diameter range for partial desolvation is 5.0~5.1 Å.

Compared with bilayer graphene flat pores, the energy consumed for SBP⁺ to enter bilayer graphene aldehyde-functionalized flat pores is the same, and the capacitance of the supercapacitor remains unchanged. This indicates that the aldehyde group neither alters the adsorption capacity of flat pores for SBP⁺ nor affects the storage capacity of flat pores for SBP⁺.

3.2.4. Analysis of the Influence of Differently Functionalized Bilayer Graphene on the Desolvation Size of SBP⁺

To analyze the critical desolvation size of the SBP⁺ complex, Figure 8 presents the relationship between the desolvation sizes of SBP⁺ complexes and bilayer graphene with different functionalizations. In the acetonitrile solvent system, the simulation experiments measured the following results:

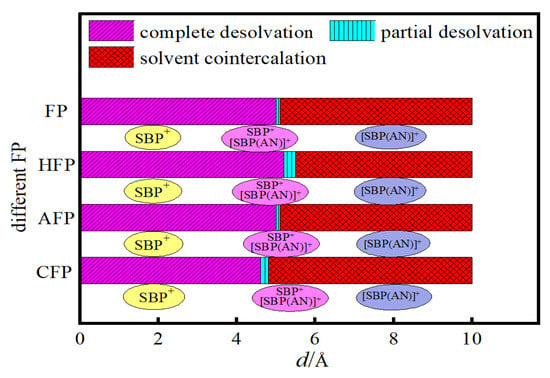
Figure 8. Relationship between the desolvation size of SBP⁺ Complexes and different functionalized bilayer graphene.

• For flat pores (FP), the complete desolvation size of the SBP⁺ complex is 5.0 Å, and the partial desolvation size ranges from 5.0 to 5.1 Å;
• For hydroxyl-functionalized flat pores (HFP), the complete desolvation size is 5.2 Å, and the partial desolvation size ranges from 5.2 to 5.5 Å;
• For aldehyde-functionalized flat pores (AFP), the complete desolvation size is 5.0 Å, and the partial desolvation size ranges from 5.0 to 5.1 Å;
• For carbonyl-functionalized flat pores (CFP), the complete desolvation size is 4.6 Å, and the partial desolvation size ranges from 4.6 to 4.8 Å.

The adsorption of hydroxyl groups on the surface of bilayer graphene flat pores enhances the pores’ ability to store SBP⁺, thereby increasing the supercapacitor’s capacitance. In contrast, the adsorption of carbonyl groups reduces the SBP⁺ storage capacity of the pores, thereby decreasing capacitance. The adsorption of aldehyde groups does not alter the SBP⁺ storage capacity, so the supercapacitor’s capacitance remains unchanged.

3.3. Analysis of the Relative Capacitance of SBP⁺ Embedded in Bilayer Graphene Flat Pores with Different Functional Groups

The capacitance calculation formula [29,30] of electric double-layer capacitors (EDLCs) is

C_EDLC = εA/d

(9)

In the formula, CEDLC represents the capacitance of EDLCs, ε denotes the local dielectric constant of the electrolyte, A stands for the surface area, and d is the thickness between the electric double layers. Formula (9) shows that the capacitance is inversely proportional to d: the smaller the value of d, the greater the capacitance. In the electrolyte, after the surface of the carbon material adsorbs a layer of positive ions, an electric double layer is formed, and the thickness between the double layers at this time equals the distance between the carbon layer and the ions. In the model constructed in this paper, since the dielectric constant in the model and the surface area of the electrode material cannot be accurately obtained, this paper compares the capacitance generated by the dipyrrolidinium ion complex after removing solvent molecules by using the ratio of d_SBP⁺_-C (where dipyrrolidinium cations are embedded in multiple systems of flat pores), i.e., the relative capacitance. To compare the capacitance generated by desolvated SBP⁺ in different pore systems, the relative capacitance (Crelative) is defined as the ratio of the capacitance of oxygen-functionalized flat pores (C_OFP) to that of pristine flat pores (C_FP). Based on the EDLC capacitance formula C_EDLC = εA/d (Equation (9)), where ε and A are constant across the same simulation setup, the relative capacitance can be simplified using the inverse ratio of d_SBP⁺_-C (Equation (10)):

C_relative = C_OFP/C_FP ≈ d_FP/d_OFP

(10)

A C_relative value greater than 1 indicates that the functionalized pores exhibit higher capacitance than pristine pores, while a value less than 1 indicates lower capacitance. Table 1 presents the d_SBP⁺-c values (interlayer distances between SBP⁺ and carbon basal plane) used to calculate relative capacitance via Equation (10). Smaller d_SBP⁺-c corresponds to higher capacitance.

Table 1. Interlayer distances between desolvated SBP⁺ and carbon basal plane of optimized pores with AA/AB stacking.

Structure	FP		HFP		AFP		CFP
	AA	AB	AA	AB	AA	AB	AA	AB
FP-4@ SBP+	2.83	2.86	2.87	2.92	2.75	2.75	2.72	2.76
FP-5@ SBP+	2.65	2.71	2.72	2.77	2.56	2.62	2.58	2.62
FP-6@ SBP+	2.58	2.59	2.60	2.64	2.42	2.46	2.47	2.50
FP-7@ SBP+	2.51	2.51	2.53	2.52	2.29	2.34	2.38	2.41
FP-8@ SBP+	2.43	2.40	2.44	2.44	2.23	2.27	2.29	2.30
FP-9@ SBP+	2.32	2.31	2.31	2.33	2.17	2.18	2.29	2.28
FP-10@ SBP+	2.14	2.19	2.21	2.23	2.03	2.08	2.24	2.24

In this paper, the capacitance generated by [SBP(AN)]⁺ after solvent molecule removal was compared by using the ratio of d_SBP⁺_-C when SBP⁺ was embedded in two systems: flat pores and functionalized flat pores. To investigate and compare the differences in d_SBP⁺_-C among different structures, relevant data were derived from Formula (9) and presented in Figure 9a,b. For data consistency, when measuring the distance within the structure, this paper adopted the shorter distance between SBP⁺ and the graphene layer. Since the upper and lower graphene layers in the bilayer graphene are identical, a consistent distance selection criterion is sufficient. It can be seen from the data in Figure 9c,d, the value of relative capacitance is closely related to the interlayer spacing between SBP⁺ and its surrounding layers.

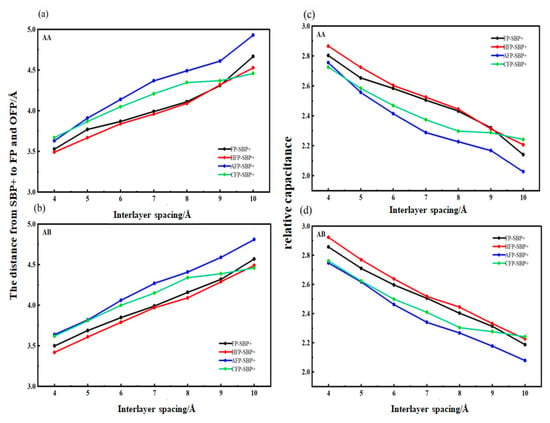
Figure 9. d_SBP⁺_-C and relative capacitance of SBP⁺ embedded into flat pores and functionalized flat pores. AA: (a,c); AB: (b,d).

From the relative capacitance data for AA and AB stackings (Figure 9c,d), under the same interlayer spacing, the relative capacitance from SBP⁺ intercalated in hydroxyl-functionalized flat pores (HFP) is significantly higher than that in pristine flat pores (FP), with the most prominent improvement observed at interlayer spacing x = 4 and x = 5. As shown in Table 1, the relative capacitance from SBP⁺ desolvation in HFP is consistently above 1.02 times that in FP, with a maximum of 1.03 times. This confirms that the confinement effect of small interlayer spacing exerts a notable influence on the structure of SBP⁺, thereby contributing to enhanced capacitance. By combining this conclusion with the findings obtained from the relationship between the desolvation size of SBP⁺ complexes and bilayer graphene with different functional groups (Figure 9), it can be deduced that the larger the desolvation size of SBP⁺ intercalated into bilayer graphene with different functional groups, the greater the relative capacitance provided; moreover, the relative capacitance of SBP⁺ complexes increases after desolvation.

3.4. Density of States Analysis of SBP⁺ After Desolvation in Functionalized Flat Pores

To further study the interaction between desolvated SBP⁺ and the pores of functionalized bilayer graphene flat, the Density of States (DOS) was calculated for two systems at the desolvation critical size of AA-stacked and AB-stacked pores in functionalized bilayer graphene flat: one being the functionalized bilayer graphene flat pores themselves, and the other being the functionalized bilayer graphene flat pores embedded with SBP⁺. The results are shown in Figure 10. The AA- and AB-stacking configurations of the functionalized flat pores have no significant impact on the DOS profiles, specifically:

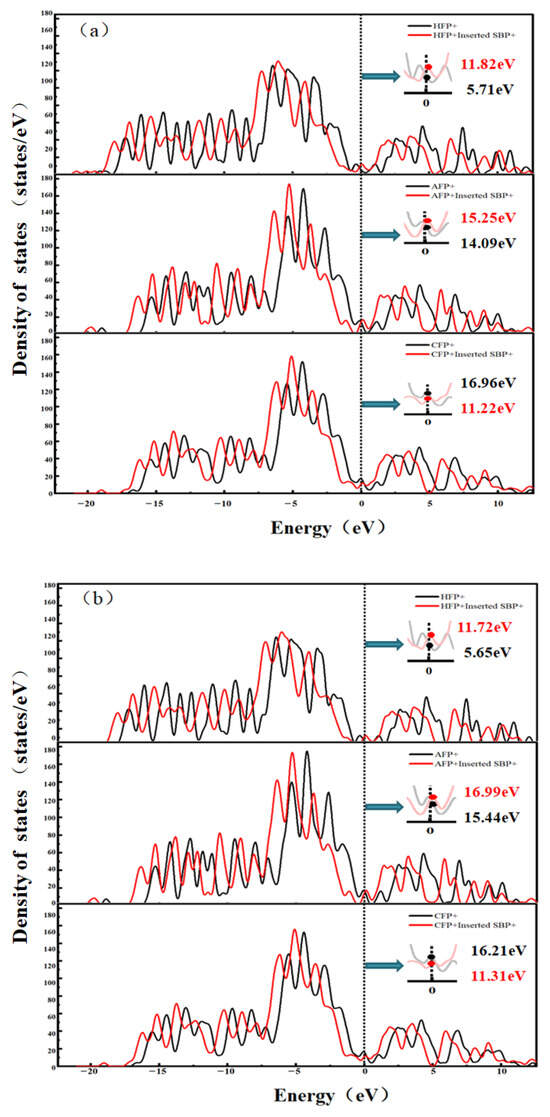
Figure 10. State density of SBP⁺ system: (a) AA stacking; (b) AB stacking.

For the hydroxyl-functionalized flat pores: In the AA stacking, the peak value at the Fermi level increases from 5.71 states/eV to 11.82 states/eV; in the AB stacking, the peak value at the Fermi level rises from 5.65 states/eV to 11.72 states/eV. This indicates a significant enhancement in the electrical conductivity of the hydroxylated sheet pores after embedding SBP⁺ [31].

For the aldehyde-functionalized flat pores: In the AA stacking, the peak value at the Fermi level increases from 14.09 states/eV to 15.25 states/eV; in the AB stacking, the peak value at the Fermi level goes up from 15.44 states/eV to 16.99 states/eV. This suggests a slight improvement in the electrical conductivity of the aldehyde-functionalized sheet pores after embedding SBP⁺.

For the carbonyl-functionalized flat pores: In the AA stacking, the DOS intensity at the Fermi level decreases from 16.96 states/eV to 11.22 states/eV; in the AB stacking, the peak value at the Fermi level drops from 16.21 states/eV to 11.31 states/eV. This demonstrates a reduction in the electrical conductivity of the carbonyl-functionalized flat pores after embedding SBP⁺.

After embedding SBP⁺ into the AA-stacked and AB-stacked functionalized flat pores, the shape of the DOS profiles of the functionalized flat pores does not change significantly. However, the overall positions of the DOS profiles for the three types of functionalized bilayer graphene flat pores shift to the left, which indicates that the basal plane of the functionalized flat pores gains electrons after embedding SBP⁺.

3.5. Charge Density Difference Analysis of SBP⁺ After Desolvation

To further investigate the interaction between desolvated SBP⁺ and functionalized bilayer graphene flat pores, the charge density difference at the desolvated dimension was calculated, as shown in Figure 11. The regions near oxygen atoms in the functional groups appear red, while those near hydrogen atoms are blue. This indicates that oxygen atoms gain electrons, whereas hydrogen atoms lose electrons. Additionally, the area surrounding desolvated SBP⁺ shows a blue color, suggesting that SBP⁺ loses electrons. These observations demonstrate that electron transfer primarily occurs between the functional groups and SBP⁺, and SBP⁺ mainly interacts with the oxygen atoms in the functional groups.

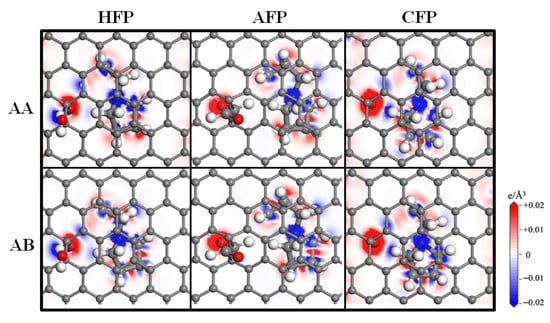
Figure 11. The electron density difference distributed graph of the charge transfer from SBP⁺ to OFP with the critical desolvated pore sizes.

The number of transferred electrons was calculated using the Bader charge analysis method [32,33], and the results are presented in Table 2. For the AA-stacked flat pores with hydroxyl (-OH), aldehyde (-CHO), and carbonyl (-CO) groups, the charges acquired from SBP⁺ are 0.757 e, 0.760 e, and 0.677 e, respectively; the charges gained by the oxygen atoms in the hydroxyl, aldehyde, and carbonyl groups are 0.624 e, 0.372 e, and 0.517 e, respectively. For the AB-stacked planar pores with hydroxyl, aldehyde, and carbonyl groups, the charges obtained from SBP⁺ are 0.732 e, 0.755 e, and 0.668 e, respectively; the charges gained by the oxygen atoms in these functional groups are 0.630 e, 0.374 e, and 0.523 e, respectively. In contrast, the four carbon atoms on the basal plane of the three types of functionalized flat pores, which are relatively close to SBP⁺, exhibit a relatively small amount of acquired charge.

Table 2. The charge transfer from SBP⁺ to OFP.

Charge/e	HFP	AFP	CFP
AA	+0.757	+0.760	+0.677
AB	+0.732	+0.755	+0.668

These results indicate that SBP⁺ primarily interacts with the functional groups rather than the carbon basal plane in the functionalized flat pores, which is consistent with the conclusion obtained by Dobrota et al. [34].

4. Conclusions

In this study, first-principles calculations were used to investigate the desolvation behavior, relative capacitance, density of states (DOS), and charge density difference of bispyrrolidinium cation ([SBP(AN)]⁺) complexes in AA/AB-stacked pristine flat pores (FP) and oxygen-functionalized flat pores (OFP: HFP, AFP, CFP) of bilayer graphene. The key conclusions are as follows:

• Critical desolvation diameters and capacitance effects: The minimum pore sizes enabling complete [SBP(AN)]⁺ desolvation (averaged across AA/AB stackings) are 5.0 Å (FP), 5.2 Å (HFP), 5.0 Å (AFP), and 4.6 Å (CFP), with partial desolvation ranges of 5.0~5.1 Å, 5.2~5.5 Å, 5.0~5.1 Å, and 4.6~4.8 Å, respectively. Hydroxyl functionalization expands the critical desolvation diameter by 0.2 Å and increases relative capacitance by 2%~3% (max 1.03× vs. FP) by enhancing SBP⁺ storage capacity. Carbonyl groups reduce the critical diameter by 0.4 Å and hinder SBP⁺ intercalation, lowering capacitance, while aldehyde groups show no significant impact on desolvation size or capacitance.
• Conductivity regulation via functional groups: DOS analysis reveals that embedding desolvated SBP⁺ enhances the conductivity of HFP and AFP (Fermi level peak increases by 2.0~10.1 states/eV) but reduces that of CFP (Fermi level peak decreases by 4.9~5.7 states/eV). AA- and AB-stacking configurations do not alter the trend of conductivity changes but tune ion transport properties—AA-stacked HFP favors diffusion, while AB-stacked HFP strengthens adsorption.
• Charge transfer mechanism: Charge density difference and Bader charge analysis confirm that SBP⁺ acts as an electron donor, transferring 0.67~0.76 e to OFP. Electron transfer primarily occurs between SBP⁺ and oxygen atoms in functional groups (oxygen gains 0.37~0.63 e), with negligible interaction between SBP⁺ and the carbon basal plane.
• This work provides quantitative guidance for electrode optimization: hydroxyl-functionalized bilayer graphene with 5.2 Å pores is preferred for high-performance supercapacitors. Future studies should extend to mixed electrolytes and experimental validation to further improve practical applicability.