Abstract
In this paper, we propose a deep learning-based surrogate model for Multivariate Empirical Mode Decomposition (MEMD) using Long Short-Term Memory (LSTM) networks, aimed at efficiently extracting Intrinsic Mode Functions (IMFs) from electroencephalographic (EEG) signals. Unlike traditional data-driven methods, our approach leverages temporal sequence modeling to learn the decomposition process in an end-to-end fashion. We further enhance the decomposition targets by employing Noise-Assisted MEMD (NA-MEMD), which stabilizes mode separation and mitigates mode mixing effects, leading to better supervised learning signals. Extensive experiments on synthetic and real EEG data demonstrate the superior performance of the proposed LSTM surrogate over conventional feedforward neural networks and standard MEMD-based targets. Specifically, the LSTM trained on NA-MEMD outputs achieved the lowest mean squared error (MSE) and the highest signal-to-noise ratio (SNR), significantly outperforming the feedforward baseline, even when compared using the Power Spectral Density (PSD). These results confirm the effectiveness of combining LSTM architectures with noise-assisted decomposition strategies to approximate nonlinear signal analysis tasks such as MEMD. The proposed surrogate model offers a fast and accurate alternative to classical empirical methods, enabling real-time and scalable EEG analysis.
1. Introduction
Decomposition of multivariate non-stationary signals overlapping in the time-frequency plane is a problem that is important for signal processing in applications related to EEG signals for source reconstruction [1], vibration signals for fault detection [2], power system oscillations [3], or similar multi-sensor data analysis.
The MEMD and its enhanced variant, NA-MEMD, have been widely adopted for the extraction of IMFs from multichannel biomedical signals such as EEG [4]. While these methods offer improved mode alignment and robustness to channel noise, their data-driven sifting process is inherently iterative and computationally intensive [5]. This high computational cost poses a significant challenge for real-time or low-latency applications, especially in embedded or edge computing scenarios. There are several implementations that try to reduce the computational cost by considering parallel implementations [6], or improvements based on Graphical Processing Units (GPUs) [7]. However, these approaches reduce the computational cost, but require a large amount of resources for their implementation. As a result, surrogate models that can approximate MEMD/NA-MEMD with reduced computational overhead have become increasingly valuable.
Deep Neural Networks (DNNs) and LSTM neural networks can be used as powerful alternatives to create surrogate models for complex, nonlinear systems. For example, in [8], an efficient framework to quantify the uncertainty of deep-learning surrogate models for most deep-learning surrogate architectures is proposed for data assimilation problems where the computational cost is reduced over . On the other hand, in [9], a DNN surrogate model to decouple the optimization process from the computational cost required by finite element analysis is proposed. Finally, in [10], an LSTM-based surrogate model for real-time flood forecasting that emulates a Physics-Based Model (PBM) is proposed. The surrogate LSTM-based model holds the high accuracy of the PBM but reduces its inherent high computational runtime and cost, which usually limits its use in real-time applications.
In this work, we propose a data-driven surrogate for MEMD using LSTM-based deep learning. Unlike conventional MEMD, our model learns to extract IMFs from EEG signals via sequence modeling, enabling end-to-end training and efficient inference. The proposed approach preserves temporal structure and frequency content more effectively than standard fully connected DNN architectures, as demonstrated in both synthetic EEG and frequency analysis benchmarks. We further enhanced the decomposition targets using NA-MEMD, which stabilizes mode separation and reduces mixing artifacts. In addition, we validate the proposed approach under real EEG signals, where the NA-MEMD LSTM-based surrogate model shows the better reconstruction performance in terms of signal approximation and IMF frequency-localized reconstruction. The novelty of our approach lies not in introducing new decomposition or neural architectures, but in designing a surrogate methodology that faithfully emulates MEMD and NA-MEMD while drastically reducing computational cost. Our contributions can be summarized as follows:
- We propose an LSTM-based surrogate model that reproduces full-sequence IMF extraction from multivariate EEG, preserving temporal and frequency structures more effectively than fully connected DNNs.
- We introduce the use of NA-MEMD outputs as surrogate training targets, which stabilizes decomposition learning and improves IMF fidelity.
- We provide a systematic evaluation of surrogate models using MSE, SNR, PSD overlap, and computational time, demonstrating that the LSTM surrogate achieves a favorable balance between accuracy and efficiency.
- We show that the proposed surrogate enables real-time and scalable EEG decomposition, outperforming conventional MEMD in both fidelity and computational speed.
The paper is organized as follows. In Section 2, the theoretical framework related to MEMD and NA-MEMD methods as well as the LSTM-based surrogates is presented. In Section 3, the simulation results and the comparison analysis are presented, and finally, in Section 4, the conclusions and final remarks are presented.
2. Theoretical Framework
2.1. EMD and Its Multivariate Extensions
EMD decomposes nonstationary signals into IMFs by iteratively estimating local means from envelope interpolation of local extrema [11]. While effective for univariate signals, applying EMD channel-wise to multivariate data like EEG can be problematic due to lack of synchronization between IMFs across channels [12].
To address this, MEMD extends EMD to multichannel signals by aligning local extrema across dimensions [12,13]. Instead of identifying local extrema directly (which is ill-defined in multivariate signals), MEMD projects the multichannel signal in multiple directions in an N-dimensional space, computes the 1D projections, and then averages their envelopes to form a multivariate local mean [1]. The multichannel input signal is represented as a vector-valued function of time, , where N is the number of channels.
The average of the envelopes of these projections forms the multivariate local mean. This is given by the equation:
being
- : The multivariate local mean.
- V: The total number of direction vectors used for projection. These vectors are typically uniformly distributed on an -dimensional sphere.
- : A specific direction vector for the projection. The angle is a conceptual representation of the direction in -dimensional space.
- : The envelope of the one-dimensional signal obtained by projecting the multivariate signal onto the direction vector . This envelope is calculated using standard EMD-like sifting on the projected signal.
The core of MEMD is an iterative sifting process to extract each IMF. For a given signal , the process works as follows:
- Calculate the multivariate local mean, .
- Subtract the local mean to obtain a “detail” signal: .
- If does not meet the IMF criteria (i.e., it is not an IMF), repeat the process using as the new signal.
- Once the IMF criteria are met, the resulting signal is the IMF, .
The IMFs are the fundamental components resulting from the decomposition. An IMF, denoted as , must satisfy two conditions:
- The number of extrema and zero-crossings must be equal or differ by at most one.
- The local mean, defined by the envelopes of the local maxima and local minima, must be zero. In MEMD, these are called joint rotational modes, as they represent synchronized oscillations across all channels.
The overall decomposition of the signal into IMFs and a residual is expressed as:
where:
- M: The total number of IMFs extracted from the signal. This number is determined by the decomposition process itself, not set beforehand.
- : The IMF or joint rotational mode, representing an oscillation component common to all channels.
- : The residual component. This is what remains after all IMFs have been extracted. It is a monotonic function, meaning it has at most one local extremum. It represents the trend or mean shift of the original signal and must satisfy the condition that no more IMFs can be extracted from it.
MEMD ensures a consistent number of IMFs across channels and improves frequency alignment, especially beneficial in EEG, where channels are strongly coupled. Compared to EMD, MEMD provides improved scale alignment and noise robustness.
NA-MEMD is an extension that adds white noise channels to the original signal before the MEMD decomposition. The added noise helps to regularize the extrema distribution across channels, improving the alignment and stability of the extracted IMFs [4]. By averaging across multiple realizations, NA-MEMD improves the estimation of local means and mitigates spurious modes. This makes NA-MEMD more robust for signals with overlapping or low-amplitude modes, improving the separation of true activity from noise. The NA-MEMD process can be summarized as follows:
- Generate a set of white noise signals.
- Concatenate these with the original signal to form an augmented signal.
- Apply MEMD to this augmented signal.
- The final IMFs are obtained by averaging the results across multiple independent realizations of the white noise, effectively canceling out the noise while preserving the true signal modes.
The main limitation of MEMD and NA-MEMD is the computational burden, which means high time complexity, particularly with increasing signal length and channels. Therefore, MEMD and NA-MEMD are not suitable for real-time or embedded systems due to iterative sifting and projection operations.
2.2. Surrogate Modeling and Neural Network Approaches
Surrogate models are fast, learnable approximations of expensive processes. DNNs can capture nonlinear mappings and are known for their fast inference once trained. Several examples of applications can be found in [9,14,15], where DNNs are used to emulate complex nonlinear processes. In contrast, the MEMD and NA-MEMD methods are computationally slow and require a lot of time. This feature makes them inappropriate for real-time tasks.
In Figure 1, the structure of a DNN-based surrogate of the MEMD is shown, where the inputs are the EEG channels, and the outputs are the corresponding IMFs.
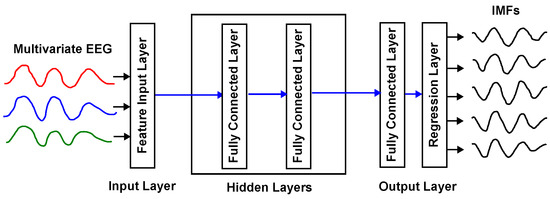
Figure 1.
Example of a DNN surrogate model of the MEMD with one input layer, two hidden layers, and one output layer.
The main hypothesis of this work is that the MEMD and NA-MEMD can be replaced by a surrogate model based on neural networks. However, since the EEG signals have an inherent temporal structure, the use of LSTM-based networks could be more adequate. LSTMs can capture temporal dependencies, which makes them ideal for sequential data like EEG. Several examples of LSTM-based surrogates can be found in [10,16,17]. In addition, bidirectional LSTM extends the standard LSTM by adding a second layer that processes the input sequence in reverse (from end to start). The outputs from both the forward and backward layers are combined (e.g., concatenated, summed, or averaged) to provide a richer representation of the sequence. In [18], a comparison is shown of the LSTM and bidirectional LSTM architectures for process modeling.
Therefore, in this work we propose a surrogate structure based on LSTM networks. This structure allows us to include in the learning process the underlying dynamics of the EEG, as well as the underlying dynamics related to its decomposition in IMFs. In Figure 2, the structure of a bidirectional LSTM-based surrogate of the MEMD is shown, where the inputs are the EEG channels, and the outputs are the corresponding IMFs.
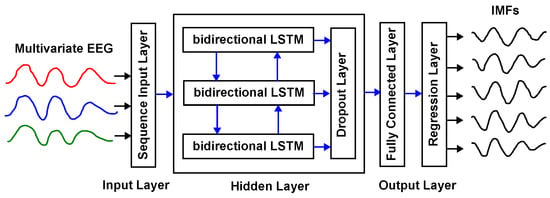
Figure 2.
Example of a bidirectional LSTM surrogate model of the MEMD with one input layer, one hidden layer, and one output layer.
It is worth noting from Figure 2 that the network receives the full multichannel EEG segment as input and outputs the corresponding IMF sequences across the entire time horizon (full-sequence prediction). This design contrasts with one-step-ahead or multi-step-ahead forecasting, and is aligned with the MEMD/NA-MEMD objective of producing complete IMF time series.
2.3. EEG Signal Characteristics
EEG signals are nonlinear, non-stationary signals composed of overlapping frequency bands (delta, theta, alpha, beta, gamma). In general, a multivariate EEG signal can be defined as
where is the leadfield matrix, which introduces the spatial mixing between the neural activity inside the brain and the EEG , which is measured on the scalp, and is the additive noise. Equation (3) clarifies why the resultant EEG signals have spatial and temporal correlation across channels. Therefore, in order to adequately analyze the underlying neural activity, it is important to decompose the EEG into intrinsic components for interpretability, diagnosis, and brain–computer interface applications.
3. Results and Discussion
In order to validate the proposed approach, we used both a synthetically generated EEG dataset and a real EEG dataset. Each multivariate EEG signal is decomposed using both traditional MEMD and NA-MEMD to extract the IMFs. The resulting IMFs for each MEMD and NA-MEMD decomposition are used to train the corresponding LSTM surrogates. Finally, the performance of the LSTM surrogates is evaluated by using three different metrics that evaluate the estimation in time and frequency.
3.1. Synthetic EEG Generation with Temporal and Spatial Mixing
Each trial of the EEG dataset is generated by simulating multichannel brain activity with well-defined temporal and spatial components. The signals are constructed as follows:
- Sampling frequency: Hz;
- Duration: seconds;
- Channels: ;
- Time vector: with samples;
- Noise level: Additive Gaussian noise with standard deviation .
Three frequency components are designed to simulate brain rhythms: a 10 Hz alpha wave (), a 20 Hz beta wave (), and a 6 Hz theta wave (). These components are linearly combined across channels to simulate temporal mixtures:
To introduce spatial mixing, a leadfield matrix is considered as follows:
Finally, the synthetic EEG signals with additive noised are obtained by considering Equation (3).
This synthetic configuration ensures both temporal dependencies and spatial cross-talk across channels, emulating key characteristics of real EEG signals. It provides a controlled environment to evaluate the decomposition and learning capabilities of MEMD-based and NA-MEMD-based surrogate models. The MEMD decomposition is obtained by using the Matlab 2023b toolbox described in [13], and the NA-MEMD is obtained according to the methodology described in [4]. A total of IMFs are selected for the MEMD case, and a total of IMFs are selected for the NA-MEMD case. For the NA-MEMD, C noise channels are added with 2 times the amplitude of the additive noise of the EEG dataset.
In Figure 3, an example is shown of one trial of the simulated EEG signals.
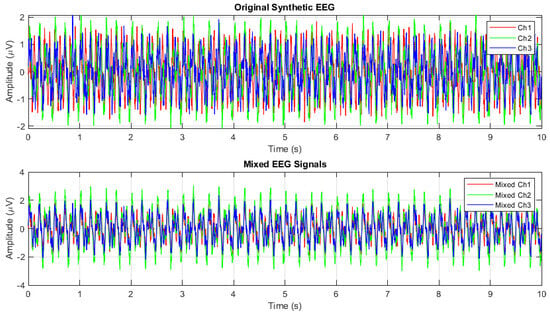
Figure 3.
Simulated EEG with temporal and spatial mixing.
In Figure 4, the IMF decomposition of the first four IMFs is shown for each EEG signal shown in Figure 3.
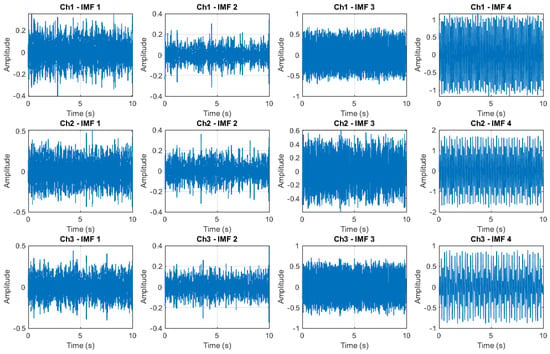
Figure 4.
IMF decomposition by using MEMD.
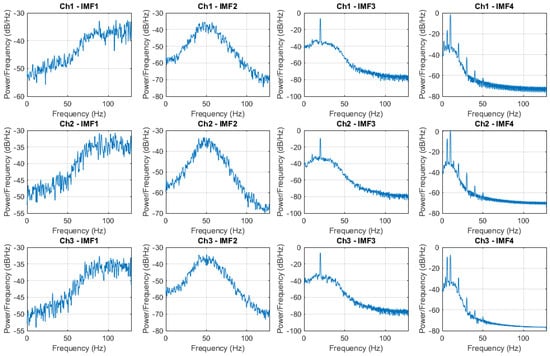
Figure 5.
PSD of the IMF decomposition by using MEMD.
- LSTM Surrogate Model
To learn the mapping from EEG signals to their corresponding IMFs, we trained a bidirectional LSTM-based neural network in MATLAB by considering the MEMD and the NA-MEMD decompositions. The model is defined as follows:
- Input Layer: sequenceInputLayer(inputSize);
- Bidirectional LSTM Layer: bilstmLayer(hiddenSize, ‘OutputMode’,‘sequence’);
- Fully Connected Layers: fullyConnectedLayer(outputSize), with optional ReLU activations;
- Output Layer: regressionLayer().
Where inputSize = C, hiddenSize = 64, outputSize = M × C with for the MEMD and for the NA-MEMD. The architecture of the LSTM surrogate is defined through an empirical trade-off analysis between accuracy and computational cost. We initially tested networks with one bidirectional LSTM layer, varying the hidden size from 4 to 512 neurons in powers of two (4, 8, 16, 32, 64, 128, 256, 512). For each configuration, the MSE on the training data and the computational runtime are measured. As expected, smaller models exhibited faster runtimes but higher errors, while larger models achieved slightly lower errors at the cost of significantly increased training and inference times. A hidden size of 64 neurons is selected as the best trade-off, offering stable convergence, low error, and efficient execution.
In this work, the LSTM surrogate is trained in a full-sequence prediction setting. The input to the network corresponds to the entire multichannel EEG segment, and the output is the corresponding set of IMF sequences across the full time horizon. This is implemented using a bidirectional LSTM layer with the ‘OutputMode’ set to ‘sequence’, ensuring that predictions are generated at every time step of the input sequence. In contrast to one-step-ahead or multi-step-ahead forecasting approaches, our design directly reconstructs the complete IMF time series, consistent with the objective of mimicking the MEMD and NA-MEMD decompositions, which inherently provide full-length intrinsic mode functions rather than short-term forecasts.
For comparison, a DNN is also tested using the following configuration:
- Input Layer: featureInputLayer(inputSize);
- Fully Connected Layers: Two dense layers with hiddenSize units each, followed by ReLU activations:
- –
- fullyConnectedLayer(hiddenSize), reluLayer();
- –
- fullyConnectedLayer(hiddenSize), reluLayer().
- Output Layer: fullyConnectedLayer(outputSize) followed by regressionLayer().
Where inputSize = C, hiddenSize = 128, and outputSize = 11 × C for the MEMD case or for the NA-MEMD case. The structure of the DNN surrogate is defined simply by considering one additional layer and double the number of hidden neurons than the LSTM surrogate.
- Training Details
The networks are trained using the trainNetwork function with the adam optimizer, a mini-batch size of 128, and a learning rate of . Training continued until convergence, with validation-based early stopping enabled. All models are trained to minimize the MSE between the predicted and ground-truth IMFs, which are the IMFs obtained from the MEMD decomposition.
In Figure 6 is shown the predicted IMFs decomposition (first four of a total of IMFs) based on an LSTM surrogate of the MEMD for the signals shown in Figure 3.
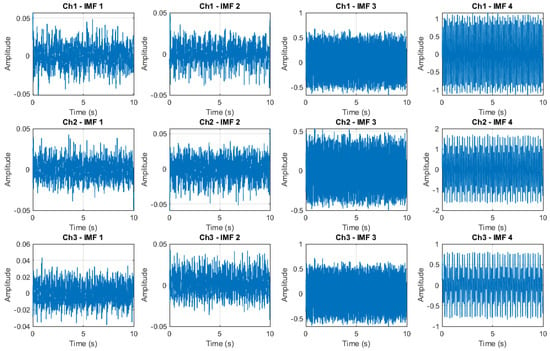
Figure 6.
Predicted IMF decomposition by using LSTM surrogate of the MEMD.
In Figure 7 is shown the PSD of the predicted IMFs based on an LSTM surrogate of the MEMD of Figure 4.
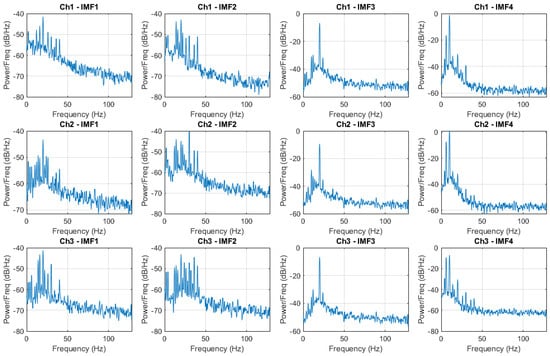
Figure 7.
PSD of the predicted IMF decomposition by using LSTM surrogate of the MEMD.
In Figure 8 is shown a zoom of IMF 3 of Channel 3 comparison between the original IMF (ground truth) and the predicted IMF decomposition based on an LSTM surrogate of the MEMD.
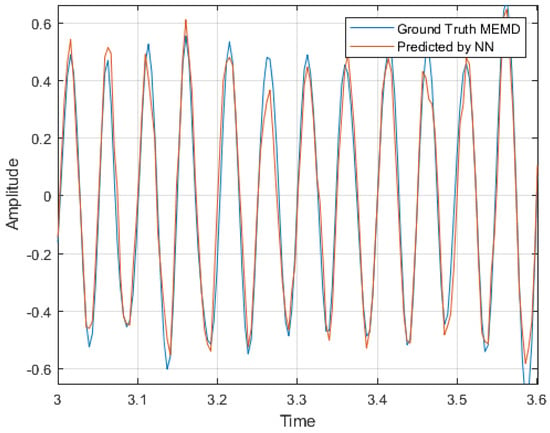
Figure 8.
Zoom of IMF 3 of Channel 3 comparison between the original IMF (ground truth) and the predicted IMF decomposition based on an LSTM surrogate of the MEMD.
- Evaluation Metrics
To assess the performance of the LSTM-based surrogates in replicating the MEMD and NA-MEMD decompositions, we used the following evaluation metrics:
- MSE: This metric quantifies the average squared difference between the predicted IMF signals and the reference MEMD/NA-MEMD IMFs :where M is the number of IMFs. A lower MSE indicates a more accurate reconstruction.
- SNR: This metric measures the relative strength of the true signal compared to the reconstruction error:Higher SNR values reflect better signal preservation and lower distortion in the reconstructed output.
- PSD Overlap: This metric assesses the similarity in frequency content between the true and predicted IMFs. It is computed by first estimating the power spectral densities and of the true and predicted signals using the Welch method, then normalizing them, and finally evaluating their overlap as:A value closer to 1 indicates a high similarity in spectral distribution, demonstrating that the predicted IMF retains the same frequency characteristics as the original.
These metrics are computed for each IMF and averaged across all test samples and channels. Together, they provide complementary insights into both the precision (MSE), the perceptual quality (SNR), and frequency similarity (PSD Overlap) of the surrogate models.
In Table 1 is shown a comparison of the training performance for one trial of the methods in terms of the MSE and SNR. It is worth noting that the data used for the comparison is the same data used for training the neural network.

Table 1.
Performance comparison using the training data of neural network architectures for IMF reconstruction.
It is worth mentioning that ↓ and ↑ symbols indicate that lower MSE and higher SNR are better. The proposed LSTM trained on NA-MEMD-preprocessed EEG signals achieves an MSE of 0.00337 and SNR of 12.68 dB, outperforming both a DNN and an LSTM trained on standard MEMD. The DNN had low SNR (0.02783 dB), meaning it poorly reconstructed the IMFs. The LSTM models, especially the one trained on NA-MEMD, achieved SNR above 12 dB, showing high-fidelity IMF reconstruction. This is due to the fact that the DNNs do not have sequence modeling, in contrast with the LSTM-based models. In addition, incorporating controlled noise channels in the decomposition stage leads to more robust and generalizable intrinsic mode representations for sequence learning. It can be seen that the DNN cannot describe the dynamic of the data, and therefore only the LSTM-based approaches are considered for the validation of the test data.
In Table 2 is shown the comparison of the LSTM-based approaches by considering a total of 6 trials. The trials are generated by considering random frequency variations as follows: for the wave, random frequencies between 8 Hz and 12 Hz, for the wave, random frequencies between 18 Hz and 22 Hz, and for the wave, random frequencies between 4 Hz and 8 Hz and also random noise. In this case, the neural networks are trained by considering one trial, and validated by considering five trials.

Table 2.
Performance comparison test data of neural network architectures for IMF reconstruction.
While the proposed LSTM-based surrogates show promising results, several limitations should be acknowledged. First, in contrast to MEMD, which adaptively determines the number of IMFs according to signal complexity, the surrogate network is constrained to a fixed output dimension (e.g., IMFs for MEMD and IMFs for NA-MEMD). This may limit its flexibility when analyzing signals that naturally produce a different number of modes. Second, although the surrogate achieves very low error and high SNR on the training distribution (Table 1), its performance decreases when tested on unseen signals with slightly different frequency content (Table 2). Specifically, the SNR dropped from above 12 dB on the training set to around 7.6 dB on test signals, indicating reduced generalization to out-of-distribution data.
On the other hand, in Table 3 is shown a computational time comparison.

Table 3.
Execution time comparison for IMF extraction methods.
In addition to improving signal fidelity, it can be seen from Table 3 that the proposed LSTM surrogate models significantly reduce the computational burden associated with classical MEMD and NA-MEMD methods. The test is performed on a workstation Intel Core i5, 8th Gen with 32 GB RAM. The implementation settings are the same for all the methods, including the additive random noise, which is generated by using the same seed. The traditional MEMD required approximately 10.56 seconds per signal, while NA-MEMD took over 21 seconds due to the added complexity of noise-assisted decomposition. In contrast, the LSTM surrogate trained on NA-MEMD achieved a runtime of only 0.23 s, representing a speedup of over 90× compared to classical NA-MEMD. Similarly, the MEMD-based LSTM model achieved a 63× speedup. A DNN trained on MEMD targets delivered the fastest inference time (0.045 s), corresponding to a 234× speedup; however, this came at the cost of significantly reduced reconstruction quality, as reflected in its lower SNR and higher MSE.
These results highlight a critical trade-off; while simpler models like DNNs offer extremely fast execution, they fail to preserve temporal and frequency structures adequately. LSTM-based surrogates, on the other hand, strike a favorable balance between speed and accuracy, making them suitable for real-time EEG analysis tasks that require high-fidelity signal decomposition.
An analysis of the PSD overlap is also performed for the LSTM surrogate of the MEMD and NA-MEMD. In Table 4 is shown the first 9 IMF PSD overlaps (of a total 11 IMF PSD overlaps) between the true and the LSTM-predicted MEMD.

Table 4.
PSD overlap between true and LSTM-predicted MEMD IMFs (first 9 modes).
Considering Table 4, it can be computed that the mean PSD overlap for the LSTM-based MEMD surrogate is . However, it can be seen that most IMFs in columns 3 to 5 show excellent overlap (), indicating good learning of key frequency bands. It is worth mentioning that these IMFs contain the synthetic generated EEG signals. Later IMFs (e.g., 6 to 11) show lower overlap, possibly due to residual noise or over-decomposition.
An analysis of the PSD overlap is also performed for the LSTM surrogate of the NA-MEMD, as shown in Table 5, where the first 9 IMF PSD overlaps are shown (of a total 13 IMF PSD overlaps).

Table 5.
PSD overlap between true and LSTM-predicted NA-MEMD IMFs (first 9 modes).
Considering Table 5, the mean PSD overlap for the LSTM-based NA-MEMD surrogate is approximately . Similar to previous results, IMFs in columns 4 to 6 demonstrate high spectral consistency (overlap ), indicating that the model effectively learns and preserves the main frequency bands of the synthetic EEG signals—namely alpha, beta, and theta rhythms. These IMFs are the most relevant for the simulated signal content, and their accurate reconstruction confirms the surrogate’s fidelity in capturing meaningful temporal and spectral structures. In contrast, IMFs beyond the fifth component (i.e., columns 7 to 9) exhibit reduced overlap, which may reflect the presence of noise, over-decomposition, or less significant frequency contributions.
The obtained results also underline the novelty and contributions of this work. First, it is verified that sequence modeling architectures, such as the LSTM-based surrogates for MEMD and NA-MEMD, can faithfully emulate nonlinear decomposition methods. Unlike classical MEMD, which required 10.56 s per signal, the proposed LSTM surrogate achieved similar decomposition quality in only 0.86 s, corresponding to a 63× speedup. When trained with NA-MEMD outputs, the surrogate reached the best performance while reducing the NA-MEMD runtime from 21.03 s to just 0.23 s, a 90× improvement. Second, by incorporating noise-assisted decomposition in the training targets, the surrogate benefits from stabilized mode separation, producing more robust IMF reconstructions. Third, our comparative analysis between DNN and LSTM surrogates highlights a novel trade-off; while DNNs achieve extreme computational speed, they fail to preserve temporal and frequency structures (SNR = 0.03 dB), whereas LSTM surrogates maintain high signal fidelity with only a modest increase in runtime. Finally, the LSTM-based NA-MEMD surrogate shows consistent performance across channels, especially in the IMFs with more relevant information, suggesting that the temporal dependencies modeled by the LSTM architecture contribute to more stable and reliable frequency-domain reconstructions.
3.2. Analysis of Real EEG Signals with Epileptic Seizures
An additional comparison analysis is performed for real EEG signals corresponding to epileptic seizures. This dataset includes the EEG of six epileptic patients recorded at the Epilepsy monitoring unit of the American University of Beirut Medical Center between January 2014 and July 2015. The data represents one-second measurements from scalp electrodes, following the 10–20 electrode system, sampled at 500 Hz for a total of samples [19]. A subset of 80 trials are considered for the evaluation of the proposed approach: 60 trials for training and 20 for testing. In addition, in order to obtain the same decomposition for all the trials, the number of IMFs for the MEMD and the NA-MEMD is truncated at .
In Table 6 is shown the performance comparison of the LSTM-based surrogates of the MEMD and the NA-MEMD.

Table 6.
Performance comparison of real EEG data of neural network architectures for IMF reconstruction.
It can be seen from Table 6 that the LSTM-based surrogate of the NA-MEMD outperforms the LSTM-based surrogate of the MEMD.
In addition, in Table 7 is shown the execution time for the classic and surrogate MEMD and NA-MEMD decompositions.

Table 7.
Execution time comparison for IMF extraction methods with EEG signals.
It can be seen from Table 7 that the LSTM-based surrogates are over 10 times faster that the classical MEMD and NA-MEMD decompositions.
As seen in the synthetic EEG signals, in the real signals the LSTM-based NA-MEMD surrogate also shows consistent performance across channels, and outperforms the LSTM-based MEMD. These results clearly demonstrate the novelty of combining NA-MEMD with LSTM sequence modeling to build efficient and accurate surrogates for nonlinear signal decomposition.
4. Conclusions
This work presents a novel LSTM-based surrogate model for MEMD, specifically tailored for EEG analysis. By using temporal sequence modeling, the LSTM network effectively learns to extract IMFs, outperforming traditional DNNs in both reconstruction accuracy and frequency preservation. The use of NA-MEMD as a training target further enhances performance by improving mode separation and stability.
In terms of computational efficiency, the proposed LSTM surrogate dramatically reduces execution time—achieving a 90× speedup over classical NA-MEMD while maintaining high fidelity. While DNNs offer even faster inference, their lack of temporal modeling leads to significant performance degradation.
Moreover, PSD overlap analysis confirms that the LSTM surrogate captures the dominant frequency components of the signal, particularly in the IMFs corresponding to the underlying EEG oscillations. These findings highlight the trade-off between speed and accuracy, and demonstrate that LSTM-based surrogates with noise-assisted decomposition offer a compelling balance for real-time, high-fidelity EEG signal analysis.
Finally, from the analysis performed over synthetic and real EEG signals, it can be concluded that the LSTM-based surrogate of the NA-MEMD is the method that can surrogate more adequately the classical nonlinear decomposition by significantly reducing the computational time while maintaining its characteristics.
Author Contributions
Conceptualization, P.A.M.-G. and D.F.R.-J.; methodology, E.G.; software, P.A.M.-G. and E.G.; investigation, D.F.R.-J.; project administration, P.A.M.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by Universidad del Quindio, research project 1054: “Solución del problema inverso dinámico con restricciones en frecuencia para la reconstrucción selectiva de la actividad cerebral usando señales simuladas de electroencefalografía”.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. However, all the parameters needed to replicate the simulated data are embedded in the results section. The real data experiments are performed by using a publicly archived Epileptic EEG data set at https://data.mendeley.com/datasets/5pc2j46cbc/1, accessed on 14 August 2025.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- Soler, A.; Muñoz-Gutiérrez, P.A.; Bueno-López, M.; Giraldo, E.; Molinas, M. Low-Density EEG for Neural Activity Reconstruction Using Multivariate Empirical Mode Decomposition. Front. Neurosci. 2020, 14, 175. [Google Scholar] [CrossRef] [PubMed]
- Lv, Y.; Yuan, R.; Song, G. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Zuo, Y.; Wang, X.; Zhang, B. Power System Dominant Oscillation Mode Analysis Based on Multivariate Empirical Mode Decomposition. In Proceedings of the 2023 3rd International Conference on Energy Engineering and Power Systems (EEPS), Dali, China, 28–30 July 2023; pp. 685–690. [Google Scholar] [CrossRef]
- Ur Rehman, N.; Park, C.; Huang, N.E.; Mandic, D.P. EMD via MEMD: Multivariate Noise-Aided Computation of Standard EMD. Adv. Adapt. Data Anal. 2013, 05, 1350007. [Google Scholar] [CrossRef]
- Stanković, L.; Mandić, D.; Daković, M.; Brajović, M. Time-frequency decomposition of multivariate multicomponent signals. Signal Process. 2018, 142, 468–479. [Google Scholar] [CrossRef]
- Wang, Z.; Juhasz, Z. Efficient GPU implementation of the multivariate empirical mode decomposition algorithm. J. Comput. Sci. 2023, 74, 102180. [Google Scholar] [CrossRef]
- Mujahid, T.; Rahman, A.U.; Khan, M.M. GPU-Accelerated Multivariate Empirical Mode Decomposition for Massive Neural Data Processing. IEEE Access 2017, 5, 8691–8701. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, K.; Liu, P.; Zhang, L.; Fu, W.; Chen, X.; Wang, J.; Liu, C.; Yang, Y.; Sun, H.; et al. Deep Bayesian surrogate models with adaptive online sampling for ensemble-based data assimilation. J. Hydrol. 2025, 649, 132457. [Google Scholar] [CrossRef]
- Zhou, X.; Cao, L.; Xie, W.; Qin, D. DNN surrogate model based cable force optimization for cantilever erection construction of large span arch bridge with concrete filled steel tube. Adv. Eng. Softw. 2024, 189, 103588. [Google Scholar] [CrossRef]
- Roy, B.; Goodall, J.L.; McSpadden, D.; Goldenberg, S.; Schram, M. Forecasting Multi-Step-Ahead Street-Scale Nuisance Flooding using a seq2seq LSTM Surrogate Model for Real-Time Application in a Coastal-Urban City. J. Hydrol. 2025, 656, 132697. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Multivariate empirical mode decomposition. Proc. R. Soc. Math. Phys. Eng. Sci. 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- ur Rehman, N.; Mandic, D.P. Filter Bank Property of Multivariate Empirical Mode Decomposition. IEEE Trans. Signal Process. 2011, 59, 2421–2426. [Google Scholar] [CrossRef]
- Hesthaven, J.; Ubbiali, S. Non-intrusive reduced order modeling of nonlinear problems using neural networks. J. Comput. Phys. 2018, 363, 55–78. [Google Scholar] [CrossRef]
- Kontou, M.G.; Asouti, V.G.; Giannakoglou, K.C. DNN surrogates for turbulence closure in CFD-based shape optimization. Appl. Soft Comput. 2023, 134, 110013. [Google Scholar] [CrossRef]
- Vlachas, P.R.; Byeon, W.; Wan, Z.Y.; Sapsis, T.P.; Koumoutsakos, P. Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks. Proc. R. Soc. Math. Phys. Eng. Sci. 2018, 474, 20170844. [Google Scholar] [CrossRef] [PubMed]
- Mora-Mariano, D.; Flores-Tlacuahuac, A. Bayesian LSTM framework for the surrogate modeling of process engineering systems. Comput. Chem. Eng. 2024, 181, 108553. [Google Scholar] [CrossRef]
- Joolee, J.B.; Raza, A.; Abdullah, M.; Jeon, S. Tracking of Flexible Brush Tip on Real Canvas: Silhouette-Based and Deep Ensemble Network-Based Approaches. IEEE Access 2020, 8, 115778–115788. [Google Scholar] [CrossRef]
- Nasreddine, W. Epileptic EEG Dataset. 2021. Available online: https://data.mendeley.com/datasets/5pc2j46cbc/1 (accessed on 30 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).